I. INTRODUCTION
Over the last few decades, the double-perovskite structure compounds with the general formula A 2BB’O6 (A = alkaline, alkaline-earth, or rare-earth ions, B and B’ = transition metal ions) have been studied extensively for their potential applications in ferroelectrics, catalysis, magnetic media, and microwave dielectrics (Gandhi and Keshri, Reference Gandhi and Keshri2015; Tasca et al., Reference Tasca, Lavata and Gloria González2017; Halder et al., Reference Halder, Nafday, Sanyal and Saha-Dasgupta2018; Li et al., Reference Li, Cho, Li, Li, Aimi, Inaguma, Antonio Alonso, Teresa Fernandez-Diaz, Yan, Downer, Henkelman, Goodenough and Zhou2018). Depending on their valences and relative radii, the B (B’) sites can be occupied by two different transition metal ions; therefore, a broad range of chemical and physical properties may be expected in this system (Zamkova et al., Reference Zamkova, Zhandun and Zinenko2013). The double perovskite oxides structures A 2BB’O6 can be reported as a modification of the simple structure ABO3 with the B positions occupying by the association of BO6 and B’O6 octahedral of acceptable charge and size. If B and B’ are satisfactorily different the ordered double perovskite structure is produced. However, the combinations of lattice distortions and orderings of different types of B (B’) cations lead to the reduction of symmetry from the ideal cubic structure Fm 
$\bar{3}$m, and even small changes produced in the tilting of the B/B’O6 octahedral can lead to either a tetragonal or a monoclinic distortion in these materials (Pena and Fierro, Reference Pena and Fierro2001; Knapp and Woodward, Reference Knapp and Woodward2006; Ochi et al., Reference Ochi, Yamada, Ohgushi, Kusano, Mizumaki, Takahashi, Yagi, Nishiyama, Inoue and Irifune2013). The distortions of double perovskite, sometimes very subtle, are often the cause of the important physical, electronic, and magnetic properties of them (Mugavero et al., Reference Mugavero, Puzdrjakova, Smith and zur Loye2005; Bernardo et al., Reference Bernardo, Ghivelder, Eslava, Amorim, Felner and Garcia2014; Ghimire et al., Reference Ghimire, Kaphle and Thapa2016).
The materials of double perovskite structure are known by a phase transition behavior under the effect of isomorphic substitutions in sites A and B of the double perovskite structure, temperature and/or pressure (Han et al., 2013; Orayech et al., Reference Orayech, Ortega-San-Martín, Urcelay-Olabarria, Lezama, Rojo, Arriortua and Igartuag2015; Zaraq et al., Reference Zaraq, Orayech, Faik, Igartua, Jouanneaux and El Bouari2016).
Many studies have been done on double perovskites with hexavalent cations, such as Sb, Nb, Mo, Re, W, Ta, and Te (Cecilia Blanco et al., Reference Cecilia Blanco, De Paoli, Ceppi, Tirao, Nassif, Guimpel and Carbonio2014; Musa Saad Reference Musa Saad2014). As reported by (Tang et al., Reference Tang, Hunter, Battle, Sena, Hadermann, Avdeev and Cadogan2016, Reference Tang, Sena, Avdeev, Battle, Cadogan, Hadermann and Hunter2017) the p-block elements such as tellurium can be strongly stabilized in the B-sites of the perovskite structure, presenting the required spherical symmetry and adequate ion size. From the 1940s, Sr2NiTeO6 oxide has been a great importance in the scientific community. The first studies focused on its properties, such as dielectric material for capacitors (Venevtsev et al., Reference Venevtsev, Politova and Zhdanov1974). The symmetry of the crystal of Sr2NiTeO6 is I2/m and its cell parameters are: a = 7.9174(4) Å, b = 7.8765(4) Å, c = 7.916(1) Å, and β = 90.378° (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Cuello, Gonzalez-Calbet, Arriortua and Rojo2005a, Reference Ortega-San Martin, Chapman, Lezama, Sanchez-Marcos, Rodriguez-Fernandez, Isabel Arriortuab and Rojo2005b). Concerning the oxides, Sr2MnTeO6 have shown that this material has a monoclinic structure with P21/n space group (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Hernandez Bocanegra, Insausti, Arriortua and Rojo2004).
In this work, we present a complete analysis by XRPD, Raman, and infrared (IF) spectroscopy of double perovskite oxides Sr2Mn1−xNixTeO6 (with x = 0.25, 0.5, and 0.75). The change in this series with the composition (x) is proposed for the first time. Furthermore, the structural phase transition at room temperature and with the nickel change is also analyzed.
II. EXPERIMENTAL
A. Sample preparation
The polycrystalline phases of the compositions Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5, and 0.75) were synthesized by conventional high-temperature solid-state reaction from stoichiometric amounts of TeO2 (99.9%), Mn(NO3)2.4H2O (99.999%), and Ni(NO3)2.6H2O (99.9%) with the appropriate metal carbonate of SrCO3 (99.9%). All compounds used as received from Sigma-Aldrich. The samples were heated in air, in alumina crucibles, at progressively higher temperatures (300 °C/6 h, 600 °C/12 h, 800 °C/12 h, 900 °C/24 h, 1000 °C/24 h, and 1180 °C/24 h) with periodic intermediate grinding.
The chemical reaction is:
2SrCO3 + (1−x)Mn(NO3)2.4H2O + xNi(NO3)2.6H2O + TeO2→Sr2Mn1−xNixTeO6 + 2CO2↑ + (1 + 2x)H2O↑ + 2NH3↑ + 5/2O2↑(x = 0.25, 0.5, and 0.75)
B. XRPD measurements
The final products of chemistry reactions were characterized by X-ray powder diffraction (XRPD) at room temperature with an Analytical X'Pert-PRO (θ−2θ) diffractometer, using CuKα radiation (45 kV, 40 mA). The data were collected from 13 to 80° 2θ, through steps of 0.01 (2θ). The refinements of the structures were achieved by the Rietveld method employing the FullProf program (Rodriguez-Carvajal, Reference Rodriguez-Carvajal1997; Roisnel and Rodriquez-Carvajal, Reference Roisnel and Rodriguez-Carvajal2001). The peaks of the XRPD lines were defined using a pseudo-Voigt function, concerning the background, is adapted with a fifth order polynomial. The structural refinement by the Rietveld method of the observed XXRPD data is begun with scale and the others parameters are refined according to this order: scale factor, zero shift, the cell parameters, background, atomic positions, asymmetry parameters, and the parameters of thermal motion of the atoms.
C. Raman and infrared spectroscopy
The Raman spectra were reported on DXR2 Raman Microscope. The spectral range is 3500–100 cm−1 captured with a single exposure of the CCD for avoids stitching artifacts, a laser type diode pumped, solid state (DPSS) (Spectra-Physics, 600 nm, 8 mW), and an optical system (with spectral resolution 2 cm−1 FWHM). All measurements were carried out at room temperature.
The IF spectra were recorded in the form of KBr pellets in the wave number range 4000–400 cm−1 using a Mattson 7000 spectrometer, then they are treated using the Win-IR software.
III. RESULTS AND DISCUSSION
A. Indexing and refinement of structures by the Rietveld method
The XRPD patterns of Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75) represented in Figure 1, indicated that the peak positions of the XRPD lines are analogous to those observed in the literature of the other double perovskite-type (e.g., Sr2CoTeO6; Sr2CaTeO6…) (Prior et al., Reference Prior, Couper and Battle2005; Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Cuello, Gonzalez-Calbet, Arriortua and Rojo2005a, Reference Ortega-San Martin, Chapman, Lezama, Sanchez-Marcos, Rodriguez-Fernandez, Isabel Arriortuab and Rojo2005b). The double perovskite formula Sr2Mn1−xNixTeO6 is isostructural with double perovskite-type phases Sr2MnTeO6 and Sr2NiTeO6 crystallizing in the space groups P21/n and I2/m, respectively (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Hernandez Bocanegra, Insausti, Arriortua and Rojo2004; Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Cuello, Gonzalez-Calbet, Arriortua and Rojo2005a, Reference Ortega-San Martin, Chapman, Lezama, Sanchez-Marcos, Rodriguez-Fernandez, Isabel Arriortuab and Rojo2005b).
Figure 1. (Colour online) X-ray powder diffraction patterns for Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75).
The tolerance factors, t, at room temperature of the titled series, have been calculated using the ionic radius suggested in Shannon database (Shannon, Reference Shannon1976) and the obtained values are listed in Table I. The values of tolerance factor suggest, in the one hand, that the room-temperature structures of both compounds should not be cubic, and, in the other hand, that Sr2Mn0.75Ni0.25TeO6 and Sr2Mn0.5Ni0.5TeO6 compounds will be more distorted than Sr2Mn0.25Ni0.75TeO6.
Table I. Tolerance factor calculated using the ionic radii suggested in (Shannon, Reference Shannon1976).
For a structural study of this double perovskite series Sr2Mn1−xNixTeO6, we had to choose between the two space groups (P21/n and I2/m). And of course, Miller's index always comes down to minimizing the number of space groups to be considered in the structural study, for that, two 2θ regions were analysis. The first region of (24–26°) corresponds to the reflections [(
$\bar{1}$ 11) (111)] and the second region of (52–53°) concerns the reflections [(−311) (311), (131) (−131)], these reflections characterize the primitive peaks h + k + l = 2n + 1 of the usual P21/n (a −a −c +) space group.
Moreover, in Figure 2, we have observed the presence of the characteristic systematic reflections [(
$\bar{1}$ 11) (111)] and [(−311) (311) (131) (−131)] in the X-ray diffraction pattern of the two compositions (x = 0.25 and 0.5), while these reflections disappeared from the X-ray diffraction pattern of the composition (x = 0.75).
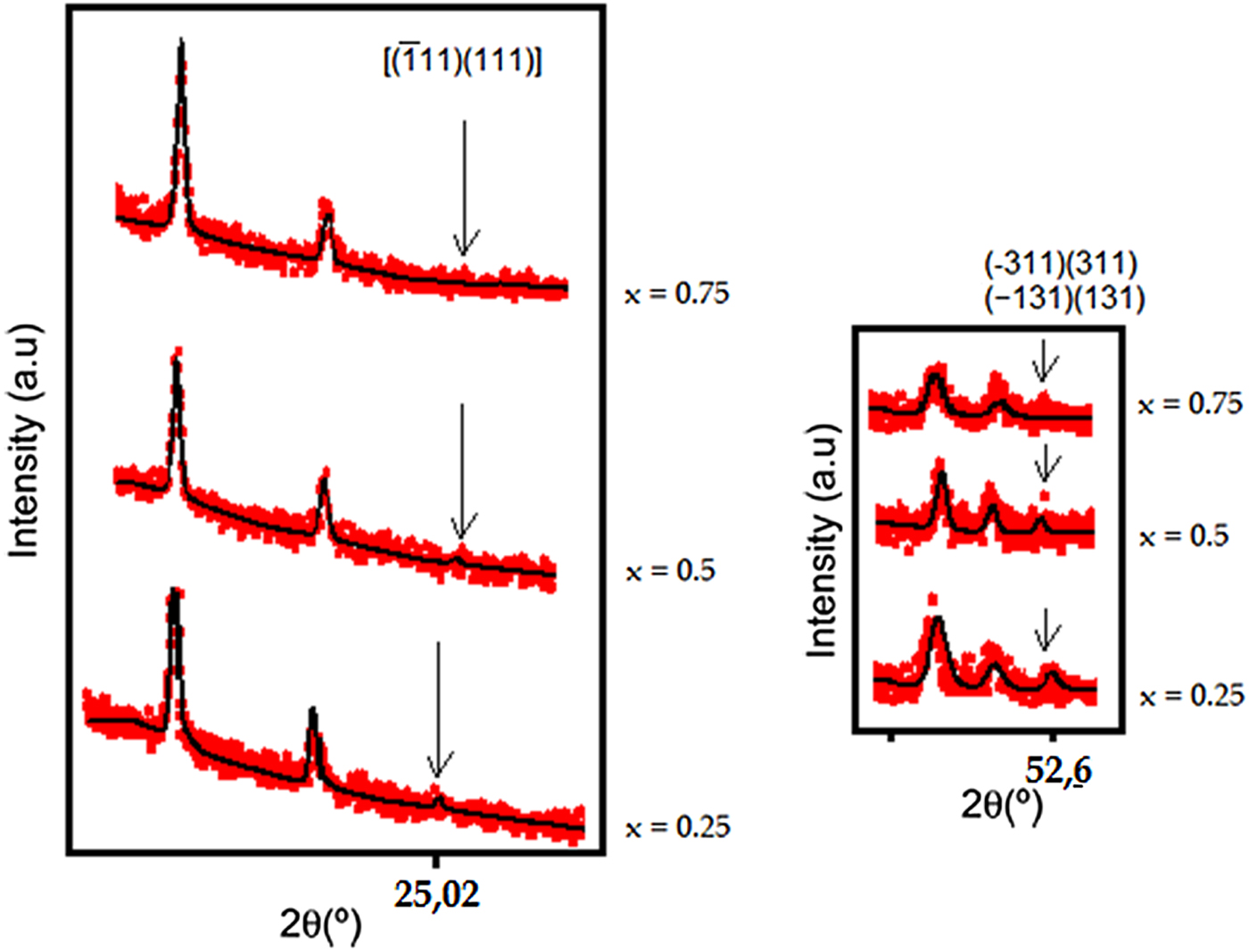
Figure 2. (Colour online) Selected 2θ intervals for the three compositions of the Sr2Mn1−xNixTeO6 series (x = 0.25, 0.5, and 0.75) determined the reflections characterizing the primitive peaks of the usual P21/n space group with h + k + l = 2n + 1. (a) The reflections [(
$\bar{1}$ 11)(111)] located around 25.01 and 25.06°. (b) The reflections [(−311)(311), (−131)(131)] located around 52.57 and 52.90°.
Via the method of Rietveld and using a FullProf analysis program the crystal structures of the compositions Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75) were tested. We have done the structural refinement with both models of symmetry P21/n and I2/m for all the series. We noticed good values of reliability factors for the compositions (x = 0.25 and 0.5) with the symmetry space group P21/n (International Tables, No. 14) (Glazer notation a +a −a −) (Glazer, Reference Glazer1975). While for the composition (x = 0.75) the refinement with the symmetry P21/n leads to relatively larger values of reliability factors (e.g., R B = 8.6%).
But when we have done the structural refinement with I2/m symmetry (International Tables, No. 12), (Glazer notation a 0b −b −) (Glazer, Reference Glazer1975) of the formula with (x = 0.75), surprisingly, this refinement led to acceptable reliability factors (e.g., R B = 4.24%). The details of Rietveld refinement conditions of this series are recorded in Table II.
Table II. Refined parameters for Sr2Mn1−xNixTeO6 at room temperature from XRPD data.
(PW), Present work.
The variation at room temperature of the lattice parameters and the unit cell volume as a function of the tolerance factor, of the series Sr2Mn1−xNixTeO6 is shown in Figure 3. As can be seen from Figure 3(a) there is a gradual decrease in the cell parameters when the nickel amount increases, and that owing to the lower ionic radius of Ni2+ (0.69 Å) compared to Mn2+ (0.83 Å). This difference between the size of Ni2+ and Mn2+ is responsible for the monoclinic distortion between the compositions of this double perovskite series. The decreasing of the volume of the BO6 octahedral leads to the decrease in the tilt systems which is observed by decreasing the monoclinic angle [see Figure 3(b)]. Therefore, when the size of the cations in site B is small, the tilt of the octahedron is weak and the structure is symmetrical.
Figure 3. (Colour online) Variations of (a) the cell parameters and (b) β angle as a function of the tolerance factor for Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75).
As indicated in several reports, in materials of double perovskite structure and holding rare earth ions, the kind and the size of the elements seems to be the reason of selective occupancy of their sites B and B’ (Azad et al., Reference Azad, Eriksson, Rundlöf and Eriksen2004). As many articles demonstrate that both B and B’ sites, in the double perovskite formula A 2BB’O6, are able to be occupied either by manganese and/or nickel and also tellurium atoms as it was noticed, for example, in Sr2MnTeO6 (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Hernandez Bocanegra, Insausti, Arriortua and Rojo2004) and Sr2NiTeO6 (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Cuello, Gonzalez-Calbet, Arriortua and Rojo2005a, Reference Ortega-San Martin, Chapman, Lezama, Sanchez-Marcos, Rodriguez-Fernandez, Isabel Arriortuab and Rojo2005b) [(Mn/Ni)B 6(Te)B’O6]. It is quite common that Te6+ (r VI Te6+ = 0.56 Å) ion favor to keep the octahedral B’ site of A 2BB’O6 double perovskite, and the Ni2+ and Mn2+ cations (r II Ni2+ = 0.69 Å, r II Mn2+ = 0.83 Å) prefer to be in site B, we recognize that there is a comparatively important difference between their ionic radii (Shannon, Reference Shannon1976). In order to clarify the cationic distribution in the double perovskite series Sr2Mn1−xNixTeO6, the structural refinement was based on two main assumptions.
In the first proposed Rietveld model, starting atomic positions for the Rietveld refinement of Sr2Mn0.75Ni0.25TeO6 and Sr2Mn0.5Ni0.5TeO6 were based on those reported for Sr2MnTeO6 (P21/n space group) (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Hernandez Bocanegra, Insausti, Arriortua and Rojo2004). For Sr2Mn0.25Ni0.75TeO6 the beginning atomic positions were based on those mentioned for Sr2NiTeO6 (I2/m space group) (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Cuello, Gonzalez-Calbet, Arriortua and Rojo2005a, Reference Ortega-San Martin, Chapman, Lezama, Sanchez-Marcos, Rodriguez-Fernandez, Isabel Arriortuab and Rojo2005b). For the two compositions (x = 0.25 and 0.5) the Mn and Ni atoms were restricted to be in the 2a (0 0 0) positions (B site) and the Te atoms are assumed to be only in the 2b (0, 0, ½) positions (B’ site). Concerning the material Sr2Mn0.25Ni0.75TeO6, the (Mn, Ni) and Te atoms are supposed to reside at the 2d (½, ½, 0) and 2a (0, 0, 0) positions, respectively. The occupancy factors for (Mn/Ni) and Te atoms within the two possible positions were not allowed to vary. This first refinement resulted in negative values for the displacement parameters (Biso) of Mn and Ni in (2a and 2d) sites, and big values of (Biso) for Te (2b and 2a) sites for the two symmetries P21/n and I2/m. Actually, the negative values for the displacement parameters of Mn and Ni indicate an electronic deficit within the 2a site in P21/n and the same thing happened into 2d site in the I2/m space group. Concerning the highest values of (Biso) for Tellerium atoms reveal an overabundance of electronic density. Even though the results of this refinement are not too favorable, they clearly demonstrate the essentiality of assuming the distribution of a heavier atom than Ni and Mn in the B sites of the compounds Sr2Mn1−xNixTeO6. Absolutely, given that Sr2Mn1−xNixTeO6 contains Tellerium atoms, which have a comparatively high atomic number [Z(Te) = 52].
In the second proposed Rietveld model for the two materials Sr2Mn0.75Ni0.25TeO6 and Sr2Mn0.5Ni0.5TeO6, (Mn, Ni, and Te) atoms are distributed between the two 2a and 2b positions of the B and B’ sites. The same thing about the compound Sr2Mn0.25Ni0.75TeO6, these atoms are distributed between 2d and 2a of the B and B’ sites of the double perovskite structure. The contrast provided between (Mn2+/Ni2+) and Te6+ allowed the free refinement of the occupancy factors of these atoms over the B and B’ sites during refining X-ray diffraction data. This fact is to conserve the total cation contents to be the same as the stoichiometry as the initial synthesized mixture. If not, the model is not able to correctly reproduce the experimental intensity of many peaks in the pattern. The occupancy rates of the oxygen atom sites have not been refined because they can only be measured accurately by neutron diffraction. In particular, this structural refinement leads to acceptable values for the coefficients of thermal motion (Biso) for all the double perovskite series, in addition it gave very satisfactory factors of reliability.
The final obtained cationic distribution that satisfactorily reproduces all the characteristics of the pattern is [Sr2 (Mn0.623Ni0.226Te0.177)B (Mn0.127Ni0.024Te0.823)B’O6 for x = 0.25, Sr2 (Mn0.434Ni0.366Te0.166)B (Mn0.066Ni0.134Te0.834)B’O6 for x = 0.5, and Sr2 (Mn0.195Ni0.605Te0.155)B (Mn0.055Ni0.145Te0.845)B’O6 for x = 0.75].
Concerning the Sr2+ and [O(1), O(2), and O(3)] atoms were allowed at the 4e (x, y, z) and 4e (x, y, z) positions, respectively, for both compositions (x = 0.25 and 0.5). About the composition (x = 0.75) crystalizing in I2/m space group, the Sr2+, O(1), and O(2) atoms occupy the 4i (x, 0, z), 4i (x, 0, z), and 8j (x, y, z) sites, respectively.
The experimental and calculated XRPD from the last proposed Rietveld model are compared in Figure 4, over the 2θ range from 17 to 100°, showing a good agreement between the profiles observed and calculated at ambient temperature. The refined position for the three phases is also displayed in Table III.
Figure 4. (Colour online) Experimental (symbols) and calculated (line) powder diffraction profiles for the Rietveld refinement of the series (a) Sr2Mn0.75Ni0.25TeO6, (b) Sr2Mn0.5Ni0.5TeO6 and (c) Sr2Mn0.25Ni0.75TeO6 at room temperature. The bars in the less part of the graphics symbolize the Bragg peak positions.
Table III. Atomic position, displacement parameters, fractional coordinates and occupation parameters for the series Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5, and 0.75) after Rietveld refinement from XRPD data collected at room temperature.
B. Description of the structure
In Figure 5(a), the crystal structures show the connection between the octahedras (Mn/Ni/Te)2aO6 and (Mn/Ni/Te)2bO6 and Figure 5(c) shows the perovskite structure with P21/n symmetry that is anticipated by the tilt system (a +a −a −) according to Glazer notation. Identically understanding from Figure 5(b) about the connection between the octahedras (Mn/Ni/Te)2dO6 and (Mn/Ni/Te)2aO6 defined by the I2/m model and Figure 5(d) provides the tilt system (a −a −c 0) as suggested by Glazer for this monoclinic centered system.
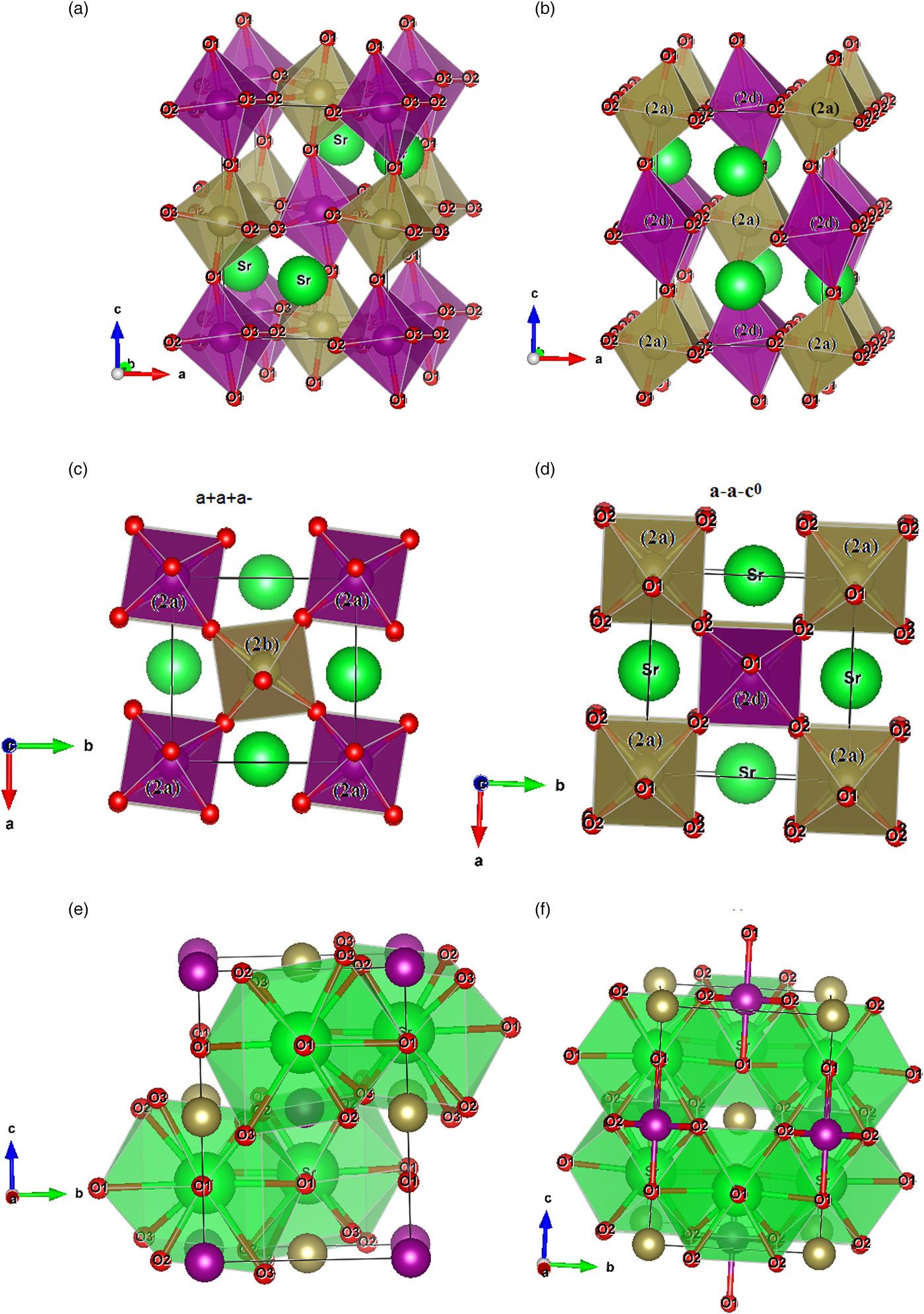
Figure 5. (Colour online) Crystal structures of a double perovskite series Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5 and 0.75) generated by VESTA program. (a) and (b) show the alternation and tilting of the octahedral for the compositions Sr2Mn0.5Ni0.5TeO6 and Sr2Mn0.25Ni0.75TeO6 crystallizing in space groups P21/n and I2/m, respectively. (c) and (d) indicate the structure in-phase (+) and out-of-phase (−) rotations of the compositions in P21/n and I2/m, respectively. (e) and (f) show the polyhedral (Sr)O12 setting in P21/n and I2/m symmetries.
A structural analysis of the monoclinic compositions of this series was carried out suggests that the sites of the (Ni2+/Mn2+) and Te6+ cations are coordinated by six oxygens in a distorted octahedral arrangement. The oxygen atoms (for x = 0.25 and 0.5) connect the (Mn/Ni/Te)2aO6 and (Mn/Ni/Te)2bO6 octahedra along the three directions. The same fact for the composition (x = 0.75), we have observed that the octahedra (Mn/Ni/Te)2dO6 and (Mn/Ni/Te)2aO6 are bound by the oxygen atoms in the three directions. The bond distance values (see Table IV) are in good agreement with those found in related double perovskite compounds (Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Hernandez Bocanegra, Insausti, Arriortua and Rojo2004; Ortega-San Martin et al., Reference Ortega-San Martin, Chapman, Cuello, Gonzalez-Calbet, Arriortua and Rojo2005a, Reference Ortega-San Martin, Chapman, Lezama, Sanchez-Marcos, Rodriguez-Fernandez, Isabel Arriortuab and Rojo2005b).
Table IV. The inter − atomic distances (Å) and angles (°) selected at room temperature for the monoclinic compositions in Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75) series.
Note that many reports show that if the charge of B and B’ are different in the ordered double perovskite structure, the oxygen ions are slightly displaced to the more charged cation despite the fact that the octahedral symmetry of the BO6 and B’O6 units is preserved. This determination is in agreement with the fact that Te6+ is more charged than (Mn2+/Ni2+), making a bigger distance between (Mn2+/Ni2+) and oxygen, unlike the Te6+ having a smaller distance with oxygen (see Table IV). We also noticed the values of the lengths and the angles of connection between the cations and the oxygens reveal some distortions of the octahedra [(Mn/NiTe)2aO6 and (Mn/Ni/Te)2bO6] for (x = 0.25 and 0.5), and the octahedra [(Mn/NiTe)2dO6 and (Mn/Ni/Te)2aO6] for (x = 0.75).
The liaison of the octahedra (Mn/Ni/Te)2aO6 and (Mn/Ni/Te)2bO6-octahedra for the two compositions (x = 0.25 and 0.5) of the series Sr2Mn1−xNixTeO6 is made by the oxygen O(1) atoms along the c-axis, and in the ab-plane the connection is made by the two oxygen atoms O(2) and O(3). The tilt of the octahedral is seen from the three bond angles (Mn/Ni/Te)2a–O(1)–(Mn/Ni/Te)2b (171.4°), (Mn/Ni/Te)2a–O(2)–(Mn/Ni/Te)2b (153.0°), and (Mn/Ni/Te)2a–O(3)–(Mn/Ni/Te)2b (167°). Concerning the composition (x = 0.75), the connection of the octahedra (Mn/Ni/Te)2dO6 and (Mn/Ni/Te)2aO6-octahedra is performed by the oxygen O(1) atoms along the c-axis, and in the ab-plane the linking is made by the O (2) atoms. The incline of the octahedral is noticed from the two bond angles (Mn/Ni/Te)2d–O(1)–(Mn/Ni/Te)2a (155°) and (Mn/Ni/Te)2d–O(2)–(Mn/Ni/Te)2a (171.1°) (see Table IV).
The Sr atoms form polyhedral (SrO12) with Sr–O bond lengths between 2.3 and 3.3 Å and an average value d of about 2.8 Å. For the two compositions (x = 0.25 and 0.5) with P21/n space group, the sharing faces of SrO12 polyhedral are connected by oxygen O(2) and O(3) along the axis c, in the ab-plane these polyhedral are connected by four oxygen atoms O(1) [see Figure 5(e)].
About the composition (x = 0.75) crystallizing in I2/m space group, the connection of the face of the polyhedral SrO12 is made by oxygen O(1) along the axis c, while in the ab-plane they are linked by four oxygen atoms O(2). We reveal the arrangement of atoms in the SrO12 polyhedron sites in Figure 5(f).
C. The Raman and IR spectroscopy studies
In this section of the paper Raman and IR spectroscopy studies were undertaken, to obtain further structural information about the nature of bonding in this series of double perovskite Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5, and 0.75). We have utilized group theory to classify the vibratory states of our double perovskite series.
The analysis of the site symmetry group (see Table V) of the compounds Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75) of the double perovskite structure [with P21/n and I2/m space group, (C2/m point group)] led to the following irreducible representation (Kroumova et al., Reference Kroumova, Aroyo, Perez-Mato, Kirov, Capillas, Ivantchev and Wondratschek2003).
Table V. Factor group analysis of the series Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5, and 0.75) at room temperature (Kroumova et al., Reference Kroumova, Aroyo, Perez-Mato, Kirov, Capillas, Ivantchev and Wondratschek2003).
T (P21/n) = 3A g (R) + 3B g (R) + 12A u (IR) + 12B u (IR) + A u (ac) 2B u (ac)
T (I2/m) = 7A g (R) + 5B g (R) + 7A u (IR) + 11B u (IR) + A u (ac) 2B u (ac)
The symbols stand for: R – Raman active modes, IR – IF active modes, ac – acoustic modes.
1. Raman spectroscopy
In Figure 6 we present the Raman spectra of the series Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5, and 0.75) recorded at room temperature CCD to avoid stitching artifacts, a laser type DPSS (Spectra-Physics, 600 nm, 8 mW). The Raman result is in good agreement with the literature of these double perovskite compounds that crystallize in a monoclinic symmetry.
Figure 6. (Colour online) Raman spectra of the series Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5, and 0.75) recorded at ambient conditions. The vertical lines on the bands of the Raman spectra to signal the small change in the modes produced into this series of double perovskite.
When we have analyzed the factor group, we have found that six active modes of Raman, represented by λ (Raman) = 3A g + 3B g, ought to be observed for monoclinic compositions with a space group of P21/n, and twelve active modes of Raman [λ (Raman) = 7A g(R) + 5B g (R)] should be observed for monoclinic compositions with a space group I2/m. From the analysis of the spectra, it has been found that most of the bands of our system are weak; there are only three bands and they are observed around (~412, ~550, and ~750 cm−1). The modes observed and the assignment, are recorded in Table VI.
Table VI. Raman and infrared shift (in cm−1) for the observed modes in Sr2Mn0.75Ni0.25TeO6, Sr2Mn0.5Ni0.5TeO6, and Sr2Mn0.25Ni0.75TeO6.
According to several studies already done on this type of material (Manoun et al., Reference Manoun, Ezzahi, Benmokhtar, Ider, Lazor, Bih and Igartua2012; Tamraoui et al., Reference Tamraoui, Manoun, Mirinioui, Haloui and Lazor2014), we can classify the Raman modes observed in our double perovskite series Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75) into three general families of network vibrations:
– At wavenumbers under <350 cm−1, there are translations of the cations Sr2+, also translational and rotational modes of the B’O6 octahedral.
– The region 350−500 cm−1, concerns the bending vibrations of O–(B’)–O.
– At wavenumbers above 550 cm−1, there are stretching modes of (B’)–O.
The investigation of Raman spectra recorded at room temperature of these double perovskite compounds Sr2Mn1−xNixTeO6 with (x = 0.25, 0.5 and 0.75) demonstrates that there are astounding changes in Raman modes in the arrangement of the series, this changing is between Sr2Mn0.5Ni0.5TeO6 and Sr2Mn0.25Ni0.75TeO6.
It was discovered that, other than its effect on the cell parameters, the concentration of the Ni and Mn cations likewise impacts the [(Mn/Ni)–O and Te–O] distances. We observed that the frequency of the υ 1 mode increments straightly with expanding of the Nickel concentration in this series of double pérovskite. To clarify these results, we considered that the frequency of the υ 1 is corresponding to the Te–O bonding energies. Table IV shows that the Te–O distances in connection to the apical and equatorial oxygens diminish. This effect expands the Te–O bonding energy, therefore we had an expanding of the υ 1 mode frequency (Ayala et al., Reference Ayala, Guedes, Silva, Augsburger, del C. Viola and Pedregosa2007).
2. Infrared spectroscopy
In Figure 7 we give the IF spectra, for the arrangement of the Sr2Mn1−xNixTeO6 mixes prepared. The most striking component obvious from this figure is the enormous closeness between the compounds in the IF spectra mostly for the two compounds Sr2Mn0.75Ni0.25TeO6 and Sr2Mn0.5Ni0.5TeO6, while the IF spectra of the compound Sr2Mn0.25Ni0.75TeO6 are different from the others, especially at the level of the band situated around the recurrence 750 cm−1.
Figure 7. (Colour online) The infrared spectra of Sr2Mn1−xNixTeO6 (x = 0.25, 0.5, and 0.75) compounds. The vertical lines on the bands show the little change in the modes produced into this series of double perovskite.
Accordingly, the point that can be promptly deduced from the vibrational spectra that the degree of cation order into each composition gives off an impression of the whole arrangement of mixes. The sharp bands present in these spectra are demonstrative of an arranged dissemination of Te.
IV. CONCLUSION
In this work we have presented the synthesis, the analyzed by conventional XRPD, the refinements using the Rietveld method. The structural analysis shows that (Mn2+ and Ni2+) and Te6+ are divided between the B and B’ sites of the double perovskite structure A 2BB'TeO6. We have introduced and confirmed by Raman and IR spectroscopy the phase transition producing the change in the double perovskite structure (from P21/n to I2/m) with the increase of the nickel composition in the series Sr2Mn1−xNixTeO6. Even though we observed from the Raman and IR spectra a small number of vibratory mode numbers, in contrast to those given by the group theory, all the spectra show the regular band pattern characteristic of the double perovskite structure. The vibrational modes were examined as far as the oxygen octahedra inward vibrations demonstrating that the fundamental unit in the structures of these materials is the TeO6. This exhibit gives a reason for the lessened number of groups seen in the Raman spectra and gives a helpful technique in describing the phase transitions as far as the gathering subgroup symmetry connection of these vibrational modes.
SUPPLEMENTARY MATERIAL
The supplementary material for this article can be found at https://doi.org/10.1017/S0885715619000411
ACKNOWLEDGEMENTS
The authors would like to acknowledge University Hassan II, Casablanca, Morocco, for their support. The authors are grateful to Engineers [in Service Centrale d'Analyse (CSA) de l'Unités d'Appui Technique à la Recherche Scientifique (UATRS) CNRS – Rabat, Morocco] for technical assistance.
