Introduction
The fast development of the laser technology has made the possibility of construction of super intense (I >1021 (W/cm2)), high contrast (up to ≤10−14) (Braenzel et al., Reference Braenzel, Andreev, Platonov, Klingsporn, Ehrentraut, Sandner and Schnürer2015) and short-laser pulses (on order of several tens of fs) (Yang et al., Reference Yang, Xu, Leng, Lu, Lin, Zhang, Li, Zhang, Yin and Tang2002; Waxer et al., Reference Waxer, Maywar, Kelly, Kessler, Kruschwitz, Loucks, McCrory, Meyerhofer, Morse, Stoeckl and Zuegel2005; Lozhkarev et al., Reference Lozhkarev, Freidman, Ginzburg, Katin, Khazanov, Kirsanov, Luchinin, Mal'shakov, Martyanov, Palashov and Poteomkin2006; Rus et al., Reference Rus, Bakule, Kramer, Naylon, Thoma, Green, Antipenkov, Fibrich, Novák, Batysta and Mazanec2015) in recent years. Nowadays, ion acceleration driven by super intense laser pulses is one of the most interesting fields of research (Daido et al., Reference Daido, Nishiuchi and Pirozhkov2012) because of potential applications such as cancer therapy (Bulanov et al., Reference Bulanov, Esirkepov, Khoroshkov, Kuznetsov and Pegoraro2002; Malka et al., Reference Malka, Fritzler, Lefebvre, d'Humières, Ferrand, Grillon, Albaret, Meyroneinc, Chambaret, Antonetti and Hulin2004; Fourkal et al., Reference Fourkal, Velchev, Fan, Luo and Ma2007), fast ignition (Roth et al., Reference Roth, Cowan, Key, Hatchett, Brown, Fountain, Johnson, Pennington, Snavely, Wilks and Yasuike2001; Tajima and Mourou, Reference Tajima and Mourou2002), ion imagining (Borghesi et al., Reference Borghesi, Schiavi, Campbell, Haines, Willi, MacKinnon, Gizzi, Galimberti, Clarke and Ruhl2001, Reference Borghesi, Campbell, Schiavi, Haines, Willi, MacKinnon, Patel, Gizzi, Galimberti, Clarke and Pegoraro2002) etc. Intense laser pulses, due to possessing very strong electric and magnetic fields, are capable of accelerating ions to high energies over very short distances (the acceleration gradients obtained in plasmas are 100–1000 GeV/m, orders of magnitude higher than 10–100 MeV/m typical values of conventional accelerators), allowing for what is called as a tabletop ion accelerator (Malka et al., Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc2008; Malka, Reference Malka2012).
In overdense plasma, depending on the laser parameters such as pulse duration, energy, intensity, and its polarization, and target properties such as density, species, and thickness, several mechanisms such as target normal sheath acceleration (TNSA) (Wilks et al., Reference Wilks, Langdon, Cowan, Roth, Singh, Hatchett, Key, Pennington, MacKinnon and Snavely2001), radiation pressure acceleration (RPA) (Henig et al., Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan and Meyer-ter-Vehn2009), and shock wave acceleration (SWA) (Haberberger et al., Reference Haberberger, Tochitsky, Fiuza, Gong, Fonseca, Silva, Mori and Joshi2012) can create high energetic protons and ion beams. All of these mechanisms are based on production of a strong electrostatic field due to charge separation. Because of lower mass of electrons with respect to ions, electrons are pushed forward by the laser ponderomotive force, and the charge separation electrostatic field pulls ions forwardly.
Producing energetic protons and ion beams by irradiating high-power laser pulses on the target has been investigated in recent years (Dover and Najmudin, Reference Dover and Najmudin2012; Wang et al., Reference Wang, Lin, Liu, Sheng, Lu, Ma, Bin, Schreiber, He, Chen and Zepf2014; Zhang et al., Reference Zhang, Shen, Wang, Xu, Liu, Liang, Leng, Li, Yan, Chen and Xu2015; Petrov et al., Reference Petrov, McGuffey, Thomas, Krushelnick and Beg2016). Origin of accelerating protons is contaminant layers of water vapor or hydrocarbon behind the surface of target or oil. The early experiments indicate that the maximum energy εmax of the accelerated protons scales with the laser intensity I and wavelength λ as εmax ∝ (Iλ2)1/2 (Borghesi et al., Reference Borghesi, Fuchs, Bulanov, Mackinnon, Patel and Roth2006; Fuchs et al., Reference Fuchs, Antici, d'Humières, Lefebvre, Borghesi, Brambrink, Cecchetti, Kaluza, Malka, Manclossi and Meyroneinc2006), consistent with the analytical model of TNSA.
The temporal structure of the laser pulse affects the laser–matter interaction and change the condition of the main pulse interaction with the target. The existing pre-pulse in laser pulse structure could ionize the front side of the target forming an expanding pre-plasma. Subsequent interaction of the main pulse with the target can be influenced by pre-plasma. Also, for long pulses (>100 ps), the main pulse itself can significantly takes place in the pre-plasma formation. Several techniques such as saturable absorbers (Itatani et al., Reference Itatani, Faure, Nantel, Mourou and Watanabe1998) and polarization rotation in a hollow fiber (Homoelle et al., Reference Homoelle, Gaeta, Yanovsky and Mourou2002) before pulse stretching, plasma mirrors (Thaury et al., Reference Thaury, Quéré, Geindre, Levy, Ceccotti, Monot, Bougeard, Réau, d'Oliveira, Audebert and Marjoribanks2007), and double chirped pulse amplification (Kalashnikov et al., Reference Kalashnikov, Risse, Schönnagel and Sandner2005) after pulse compression have been offered to modify temporal contrast of high-power lasers. Several experiments studied the effect of pre-plasma on generation and transportation electron and temperature of the hot electron generating by laser intensity (Lin et al., Reference Lin, Li, Liu, Liu, Du, Wang, Chen, Zhang, Liu, Liu and Wang2012; Yang et al., Reference Yang, Ma, Xu, Shao, Yu, Yin, Zhuo and Borghesi2013). These experiments show that the spectrum, spatial distribution, and divergence angle of the energetic electrons can be significantly changed in the presence of pre-plasma. Some experimental campaigns on the OMEGA-EP laser system show that the long-pulse length (of the order of ps) in conjunction with large initial pre-plasma has an impact on electron beam filamentation and creates multiple electron beams with large degrees of divergence (Peebles et al., Reference Peebles, Wei, Arefiev, McGuffey, Stephens, Theobald, Haberberger, Jarrott, Link, Chen and McLean2017). Shulyapov et al. showed that the acceleration efficiency of protons and multiply charged ions accelerated backwards under irradiation of the front surface of thick solid targets by high-power femtosecond laser radiation was determined by the contrast of this radiation (Shulyapov et al., Reference Shulyapov, Mordvintsev, Ivanov, Volkov, Zarubin, Ambrožová, Turek and Savel'ev2016). In the other work, experimental data represented that the presence of the pre-plasma leads to the decrease in the energy transfer efficiency of the laser beam to a solid target by fast electrons owing to the large divergence of streaming fast electrons which are generated far from the target surface (Pisarczyk et al., Reference Pisarczyk, Gus' kov, Renner, Demchenko, Kalinowska, Chodukowski, Rosinski, Parys, Smid, Dostal and Badziak2015).
PIC simulation in order to determine the influence of pre-plasma on the proton energy has been investigated in the TNSA regime. It shows that at the optimum pre-plasma density gradient, dense relativistic electron bunches can be produced by the laser-driven ponderomotive channel. Then, this energetic bunch of electrons can reach behind the target and accelerate rear side protons efficiently (Zheng et al., Reference Zheng, Wu, Zhang, Huang, Yu, Zhou and He2013). The influence of pre-plasma in the RPA regime of the ion acceleration was described by Liseykina et al. (Reference Liseykina, Borghesi, Macchi and Tuveri2008). They presented an optimum scale for pre-plasma as L pre = 0.5λ, for improvement of energy and efficiency of the acceleration in the RPA regime, but various scales for the laser pulse duration were not included in their analysis.
In this study, we focus on the effect of pre-plasma on the ion acceleration in the RPA regime when the laser pulses with different durations (of the order of several tens of fs) are irradiated on the target. We simulate interaction of high-power and short-laser pulses with thin the thickness of an aluminum target. Our simulation shows that the various laser pulse durations and pre-plasma scale lengths can affect ion energy. In the longer laser pulse regime (τp > 50 fs), pre-plasma is undesirable and the energy exchange between the laser pulse and underdense plasma is destroyed by the coupling of the laser pulse with the cut-off layer. But for the shorter laser pulse duration regime (τp < 50 fs), an optimum value for the pre-plasma scale length is obtained, in which the ion energy increase considerably.
In Section “Interaction of short-laser pulse with an aluminum target”, interaction of short-laser pulses with the aluminum target is demonstrated with the 1D3V particle-in-cell (PIC) code for four different pulse durations, τp = 20, 35, 100, 300 fs. In Section “Pre-plasma effect”, the effect of pre-plasma on the ion energy is demonstrated. Concluding remarks are given in Section “Conclusions”.
Interaction of short-laser pulse with an aluminum target
To study the interaction of short-laser pulses with an aluminum target, the relativistic 1D3V PIC code (UMPIC)Footnote 1 is used. Our targets are thin foils (L < 1 µm) of pure aluminum with a density of 27 g/cc and an initial charge state of +10, dealing with the ionization processes by pedestal or pre-pulse, corresponding to an electron density of n e = 4.3n c. In the simulations, circularly polarized pulses with the same intensity (I ~ 1021 W cm–2, a 0 = 15.2) and wavelength (λl = 0.8 μm), but four different durations 20, 35, 100, and 300 fs are employed. The dimension of the foil changes from few nanometers to hundreds of nanometers, but the length of the interaction zone can be increased by a few micrometers due to the presence of pre-plasma.
In the simulations, the size of each cell and the equivalent time step are δx = 6 nm (≃ 0.0075λl) and δt ≃ 0.02 fs, since 
$\widetilde{{{\rm \delta} t}} = \widetilde{{{\rm \delta} x}}$, where 
$\widetilde{{{\rm \delta} x}}$ and 
$\widetilde{{{\rm \delta} t}}$ are normalized cell length and time step, respectively. In each cell, 100 electrons and 10 ions are placed. Total interaction time is about 10 ns (~500 000 time steps), to cover all over the interaction area.
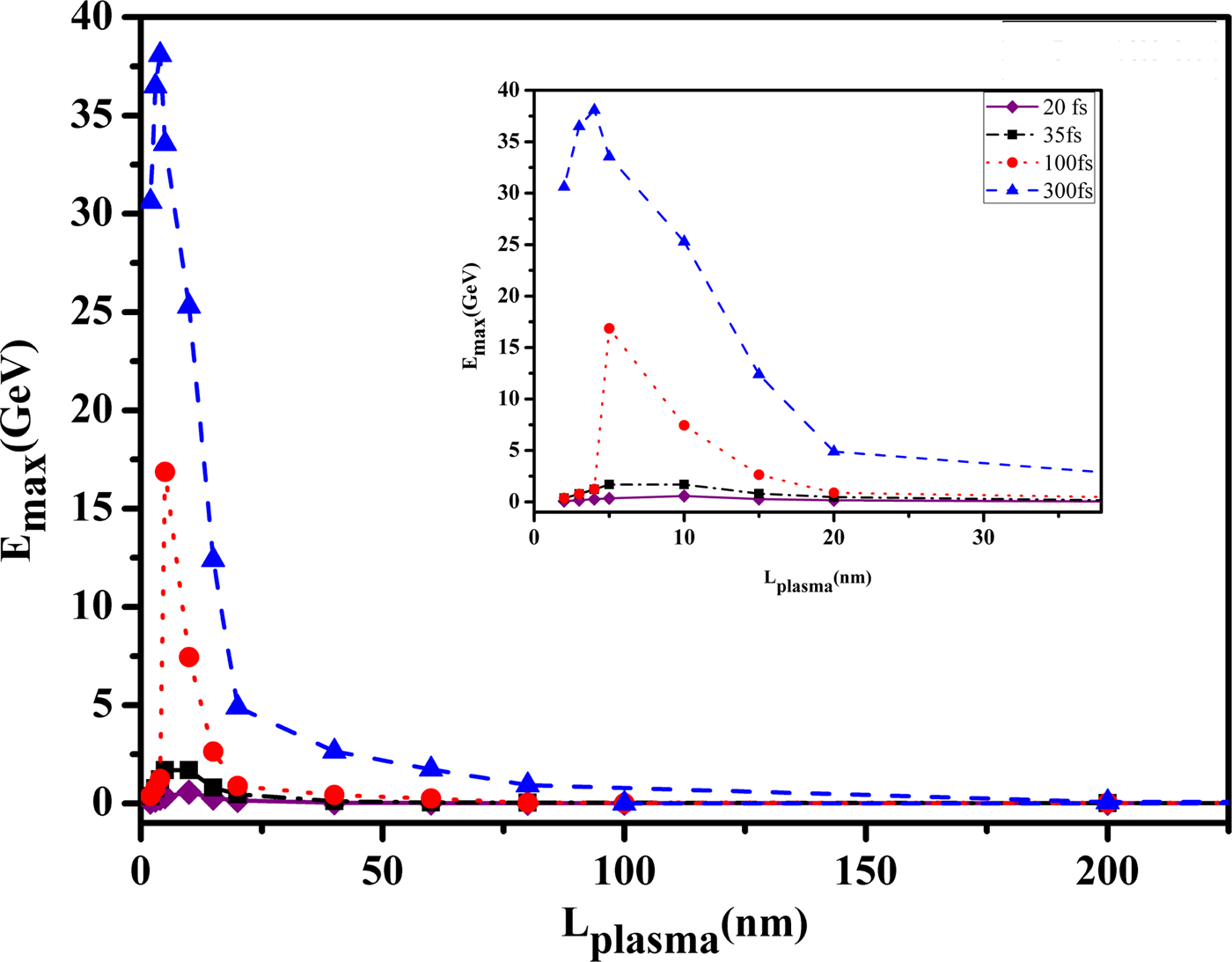
We first present the result of our simulations in the absence of pre-plasma (for very high contrast pulses). The maximum energy of ions as a function of target thickness is shown in Figure 1, for four different laser pulse durations. According to Figure 1, it seems that for targets with thicknesses more than 200 nm, different laser pulse durations almost deliver the same energy to the ions. In other words, for greater length foils, the increase of pulse duration is no longer effective on the ion acceleration. In contrast, maximum energy increases with decreasing target thickness up to an optimum thickness, which is obtained by the transparency condition of the thin foil (Bulanov et al., Reference Bulanov, Esarey, Schroeder, Bulanov, Esirkepov, Kando, Pegoraro and Leemans2016). Figure 1 (inset plot), shows that this optimum thickness increased with decreasing of the pulse duration. However, as one can see in Section “Pre-plasma effect”, it cannot happen in reality, since in the real experiments, pre-pulse and pulse pedestal make a spatial pre-plasma profile that will clearly change recent results.
Fig. 1. Maximum ion energy as a function of target thickness without pre-plasma for different laser pulse durations τp = 20 fs (purple solid line, diamonds), τp = 35 fs (black dash-dotted line, squares), τp = 100 fs (red dotted line, circles), and τp = 300 fs (blue dashed line, triangles).
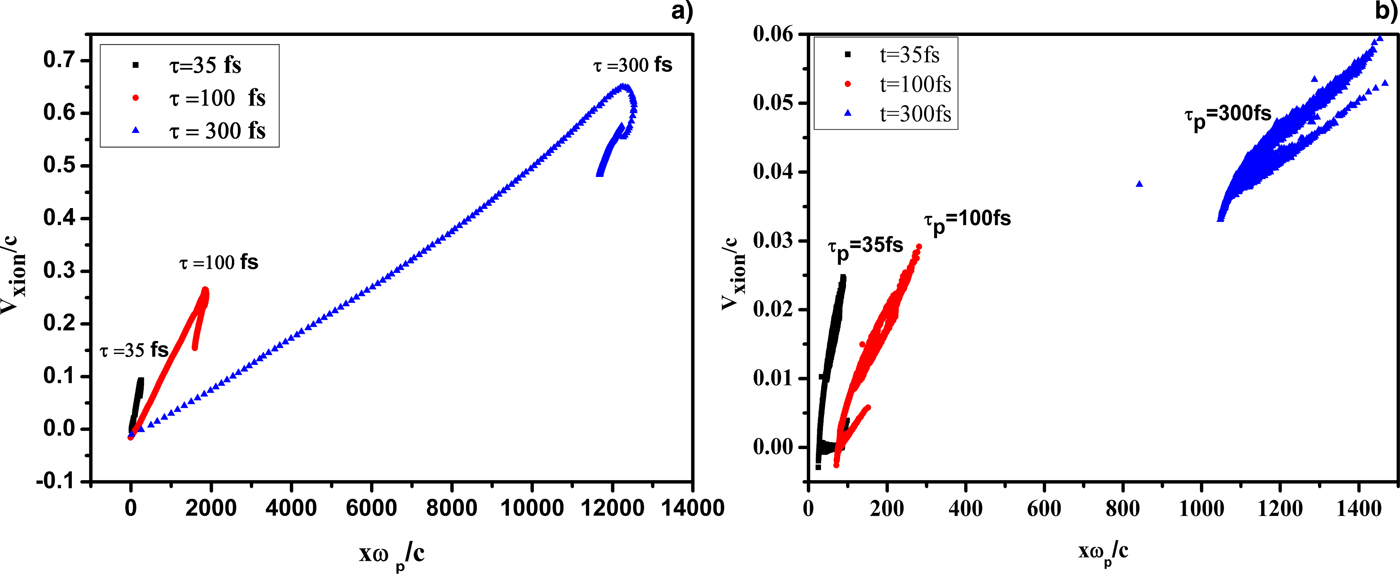
Regarding the phase space of the ions in Figure 2, it can be realized the involved ion acceleration regime. As one can see in Henig et al. (Reference Henig, Steinke, Schnürer, Sokollik, Hörlein, Kiefer, Jung, Schreiber, Hegelich, Yan and Meyer-ter-Vehn2009), in the RPA light sail regime the bulk of the target is displaced forward. For the thin foil targets (shorter than 200 nm), the dominant mechanism for the acceleration is RPA (Fig. 2a). It is clear in Figure 2b that for thick targets and shorter laser pulse duration, the TNSA mechanism can also appear behind the target.
Fig. 2. Phase space of ions for two target thicknesses whithout pre-plasma: (a) L plasma = 40 nm and (b) L plasma = 600 nm.
Pre-plasma effect
In this section, we consider pre-plasma with a linear-density ramp in front of the foil. We assume the Maxwellian equilibrium distribution of electrons in the pre-plasma, with equivalent temperature, which is obtained by laser pulse ponderomotive potential (Haines et al., Reference Haines, Wei, Beg and Stephens2009):
$$t_{\rm h} \approx 0.47a_{0{\rm p}}^{2/3},$$where t h is dimensionless temperature (it is dimensionless with the rest mass energy of an electron i.e. m 0c 2 = 0.511 MeV) and a 0p is dimensionless amplitudes of the electric field in the pre-pulse. This distribution of electrons propagates through the target and deposits its energy over stopping range R 0. As plasma is expanding in vacuum, a shock wave is formed and moves inside the cold plasma. According to Llor et al. (Reference Llor Aisa, Ribeyre, Gus' kov, Nicolaï and Tikhonchuk2015), there is a relationship between the electron energy ε1 and depth of electron penetration z as follows:
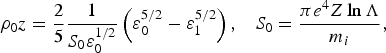$${\rm \rho} _0z = \displaystyle{2 \over 5}\displaystyle{1 \over {S_0 {\rm \varepsilon} _0^{1/2}}} \left( {{\rm \varepsilon} _0^{5/2} - {\rm \varepsilon} _1^{5/2}} \right){\rm,} \quad S_0 = \displaystyle{{{\rm \pi} e^4Z\ln \Lambda} \over {m_i}},$$
where ε0, S 0, and ρ0, respectively, are initial energy, angular scattering, and density of an electron. Ze and m i are charge and mass of plasma ions, respectively and lnΛ is the Coulomb logarithm. Then, stopping range is 
$R_0 = {\rm \rho} _0L_0 = (2 {\rm \varepsilon} _0^{1/2} /5S_0)$ where L 0 is the place that shock is formed. For our linear-density ramp of pre-plasma with the formula ρ = αz with α = (ρ0/L pre) (L pre is the pre-plasma length), we can find this stopping range as below:
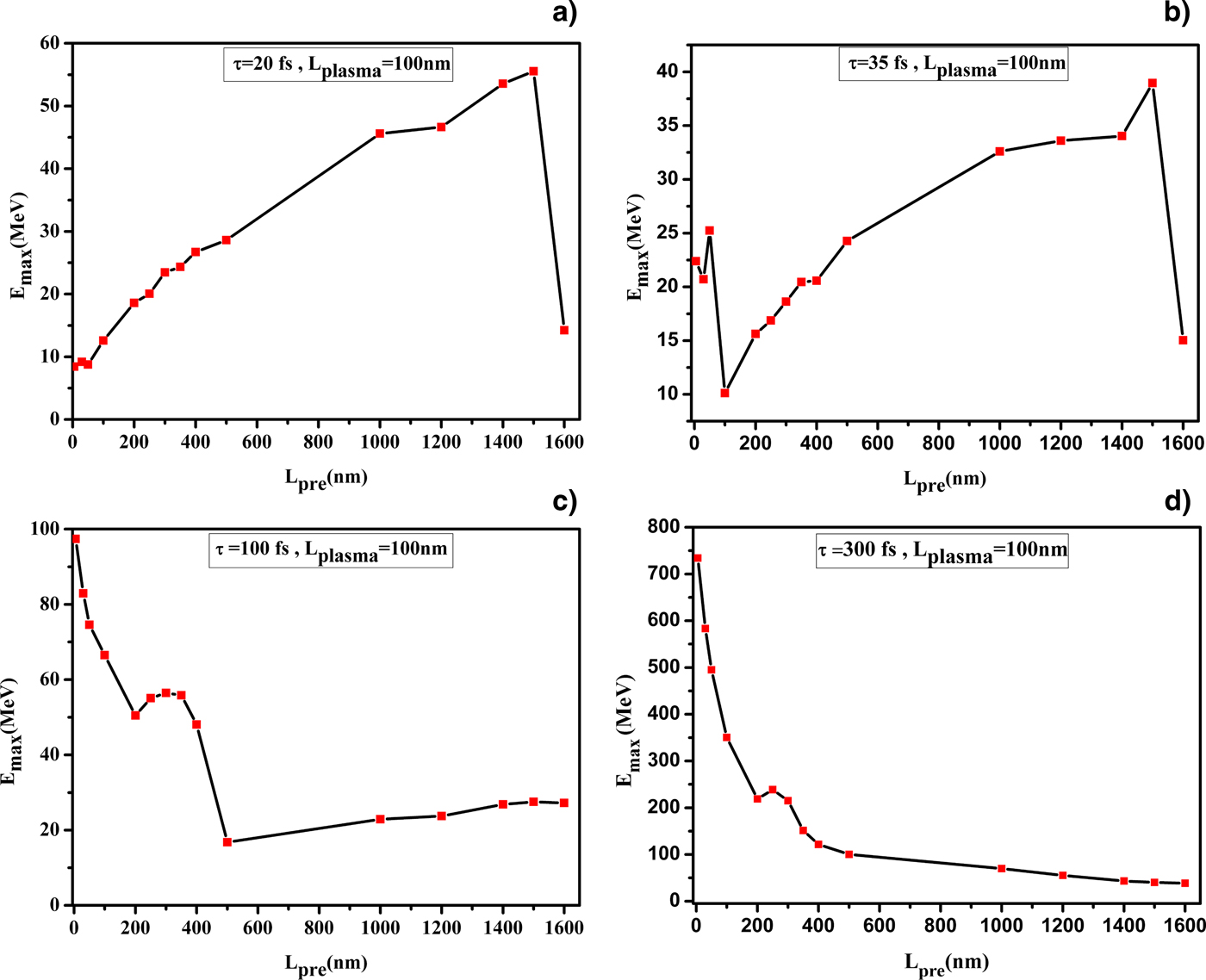
$$L_0 = \sqrt {\displaystyle{{2L_{{\rm pre}}} \over {{\rm \rho} _0S_0}}} {\rm \varepsilon} _0.$$Therefore, stopping range changes for different lengths of pre plasma. It shows that for our selected parameters, stopping range for L pre = 1500 nm is 420 nm which is almost coincident with the critical surface where laser pulse reflects from the target. Since, existing pre-pulse (or pedestal) in the temporal structure of the laser pulse creates pre-plasma on the target which is changing the interaction processes, we have chosen different intensity contrast ratio (I Main-Pulse/I Pre-Pulse) along with varying pre-plasma length from 5 nm to almost 1500 nm. Actually, different pre-plasma scale lengths may be obtained by various pre-pulse delays corresponding to the main laser pulse location. Figure 3 illustrates the maximum energy of ions as a function of pre-plasma length. Regarding Figures 3a and 3b, one can find an optimal pre-plasma thickness of ~1.5 µm for 20 and 35 fs laser pulses in order to take advantage of the maximum energy of ions. The decreasing of energy for larger values of L might be related to the weak coupling of the laser pulse with the cut-off layer (Liseykina et al., Reference Liseykina, Borghesi, Macchi and Tuveri2008). As the figures show, for longer pulses optimum pre-plasma length declines and reaches zero. Of course, in the case of pulse durations of 100 and 300 fs, the weak crest occurs at 350 and 300 nm, respectively. In other words, the maximum energy of ions occurs when pre-plasma does not create on the target. Then for long pulse durations, the use of lasers with high enough contrast is necessary to reach more energetic ions, in spite of the short pulse duration which long pre-plasma help to acquire energy by ions. Therefore, the 35 fs laser pulse creates ~40 MeV ions, which is twice the energy of producing ions by the 100 fs pulse with the same pre-plasma scale length. As a consequence, it proposes that the real experiment use of laser pulses with short durations can resolve concerns about creating pre-plasma due to pre-pulse.
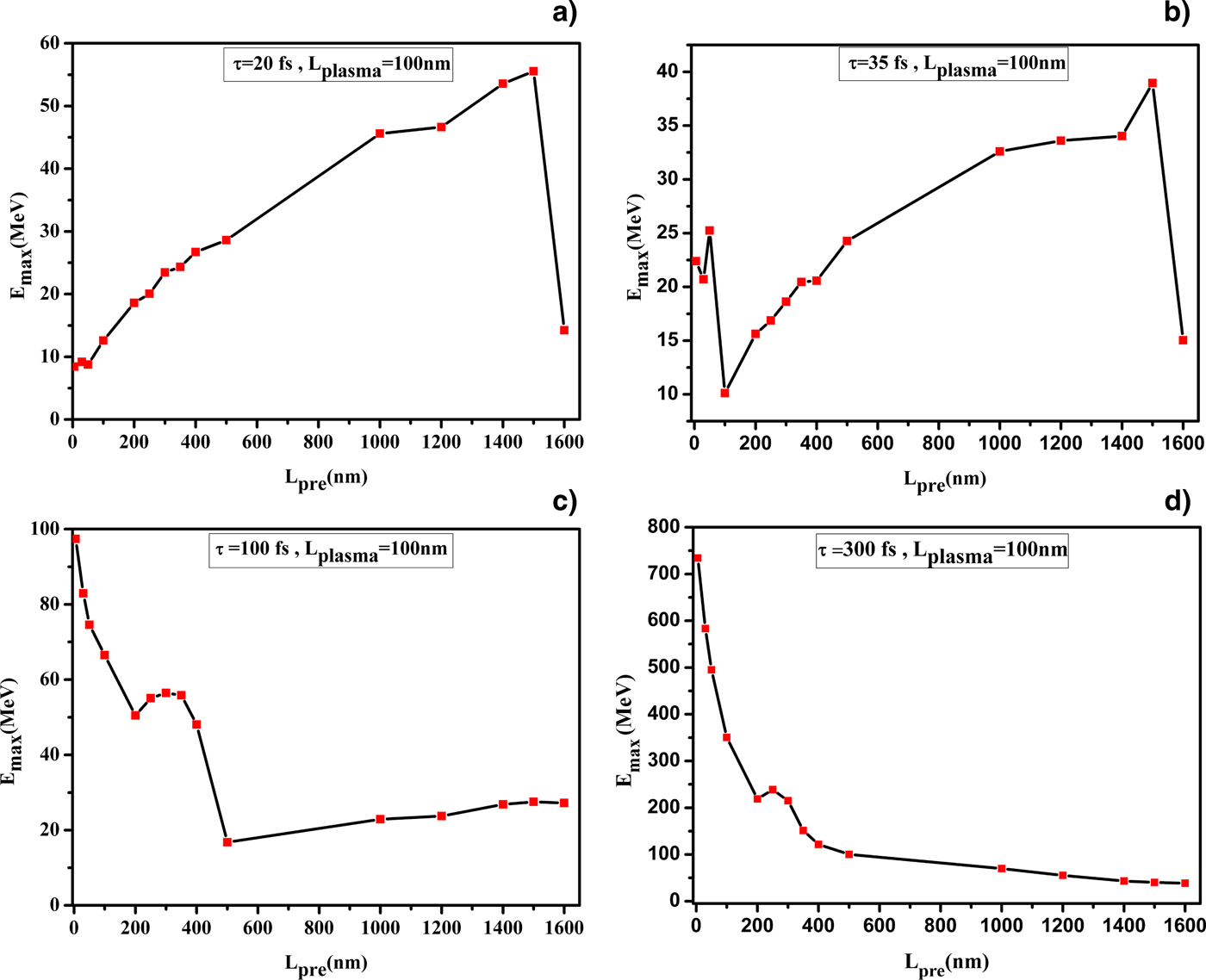
Fig. 3. Maximum ion energy as a function of pre-plasma thickness. For all diagrams, thickness of plasma is 100 nm. (a) τp = 20 fs, (b) τp = 35 fs, (c) τp = 100 fs, and (d) τp = 300 fs.
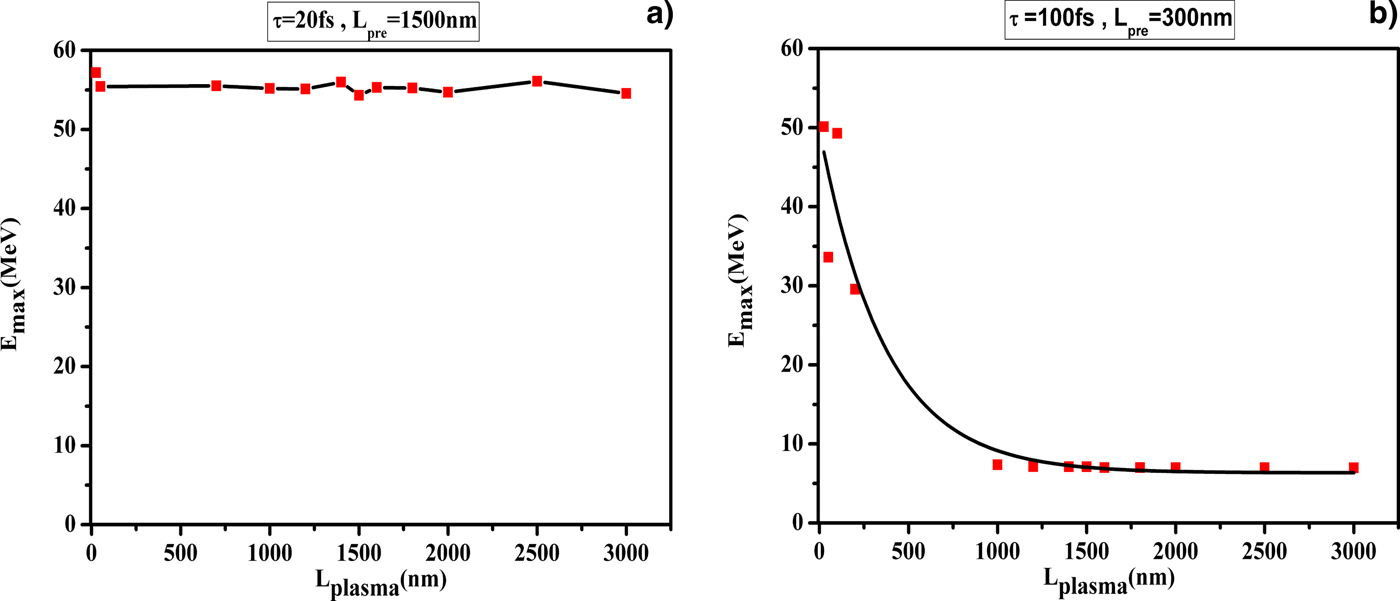
Our complementary simulation results show that for short-laser pulse (τp < 50 fs), changing the target thickness along with the optimal pre-plasma length obtained from previous section cannot affect the ion acceleration significantly. But for the longer pulses (τp > 50 fs), increasing target thicknesses decrease ion energy effectively. Figure 4 shows the maximum energy versus plasma length (a) for pulse duration τp = 20 fs and optimum pre-plasma length 1500 nm and (b) for pulse duration τp = 100 fs and optimum pre-plasma 350 nm.
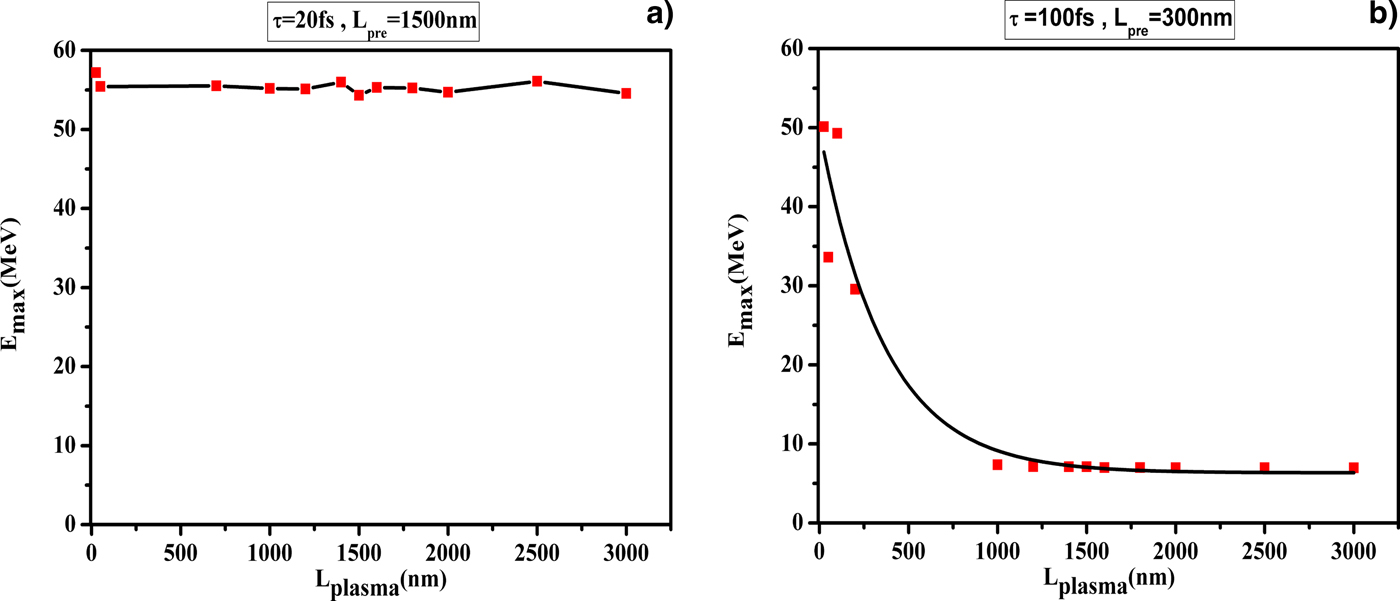
Fig. 4. Maximum energy versus plasma length: (a) for 
${{\rm \tau}} _{\rm p} = 20\;{\rm fs}$, pre-plasma length is 1500 nm and (b) for 
$ {\rm \tau} _{\rm p} = 100\; {\rm fs}$, pre-plasma length is 350 nm.
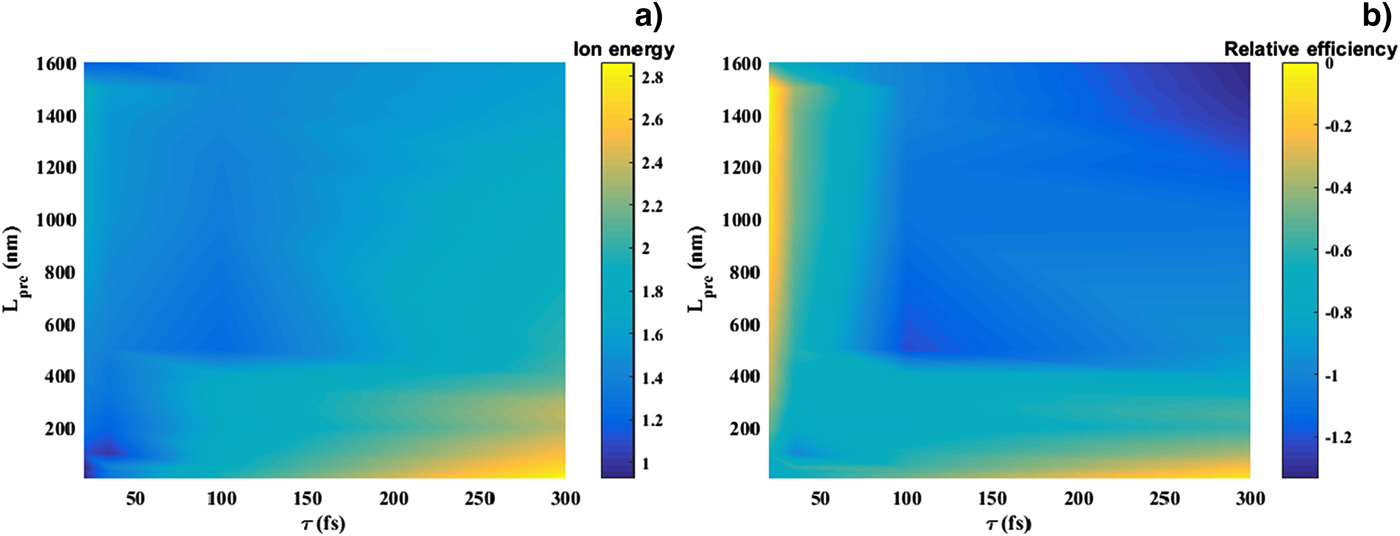
In Figure 5(a), the simultaneous effect of the laser pulse duration and pre-plasma scale length is demonstrated in two-dimensional color graded image. It is shown that small pre-plasma scale length (high contrast pulse) is required for longer laser pulses (τp > 50 fs), but large pre-plasma scale length has a suitable effect on shorter laser pulse (τp < 50 fs).
Fig. 5. (a) Ion energy (on logarithmic scale) as a function of pre-plasma length and laser pulse duration and (b) relative efficiency (η/η0 on logarithmic scale) as a function of pre-plasma length and laser pulse duration.
Two suitable regions for ion acceleration are indicated in Figure 5(a), one for longer pulses without pre-plasma and the other for short pulse with pre-plasma. The advantages of the short-laser pulse region are smaller input energy and low contrast requirement. Also, Figure 5b shows relative conversion efficiency η/η0 as a function of pulse duration and pre-plasma length (where η is the efficiency of each pulse and η0 is the efficiency of laser pulse with a duration of 20 fs and pre-plasma length of 1500 nm). As one can see, for longer pulses, relative efficiency decreases when pre-plasma length increases. Otherwise for shorter pulses (τ < 50 fs), efficiency increases when pre-plasma scale length increases up to an optimum value. It indicates that by using short-laser pulses, efficiency of energy transport from the laser to ions increases and the laser contrast is less important.
Conclusions
Recent advances in the construction of high intensity and short-laser pulses, as well as the production of thin nanometer foils, have led to a dramatic increase in ion acceleration in the interaction of laser pulses with solid targets. However, it seems that high contrast laser pulses are required in order to achieve considerable results in the interaction of intense laser pulses with a nanometer-scale foil. In fact, the presence of pre-pulses can create pre-plasma with a given scale length, or even in the case of very thin foils, damage the foils before arrival of the main pulse. Our simulation results from the interaction of femtosecond laser pulses with pure aluminum nanoscale foils show that pre-plasma presence has a destructive effect on the acceleration process for long pulses, while for pulses shorter than 50 fs, pre-plasma with optimal length can have a desirable effect on ion acceleration. In other words, laser pulses with less energy and short durations can transfer considerable energy to the ions with suitable efficiency. For instance, in the interaction of laser pulse with I ~ 1021 W cm–2, a 0 = 15.2 and pulse duration 35 fs with a 100 nm foil along with 1.5 μm pre-plasma can create ions with energy up to 40 MeV, which is twice the energy of Al10+ ions for laser pulse with 100 fs duration with the same target structure. Therefore, it is not required to serve high-energy long pulses with high contrast pulses in order to achieve energetic ions in the interaction of laser pulses with the solid target. In contrast, use of longer pulses with low contrast may be affordable. It should be noted that long-laser pulse durations with high contrast (≥1010) can create more energetic ions and more efficiency.
