2.1 Triggering of surface oscillations

An 8 cm-edge cubic water tank is filled with bidistilled undegassed water. The saturation of oxygen in the water is approximately $8.2~\text{mg}~\text{l}^{-1}$ depending slightly on temperature. As will be detailed later, tracer particles are added for the visualisation of microstreaming. An ultrasonic plane transducer (SinapTec^®, diameter of the active area 35 mm) is attached to the bottom of the tank. The voltage amplitude of the transducer is varied between 1 and 10 V, no gain amplifier is used. All experiments are conducted at a driving frequency set to 31.25 kHz.

For the bubbles, the driving frequency corresponds to a resonant radius $R_{res}\approx 104~\unicode[STIX]{x03BC}\text{m}$ according to Minnaert’s theory (Minnaert Reference Minnaert1933). The bubbles considered in this study have radii ranging between $40~\unicode[STIX]{x03BC}\text{m}$ and $80~\unicode[STIX]{x03BC}\text{m}$ . They are all smaller than resonant size and hence naturally driven towards pressure antinodes due to primary Bjerknes forces.

The distribution of the acoustic field has been simulated with Comsol Multiphysics^®. The driving frequency corresponds to a resonance frequency of the water tank, for which a pressure maximum is located on the $z$ -axis at a height of approximately 6 cm. This location corresponds to the experimental trapping position. Bubbles are trapped slightly above the pressure maximum, their stable position $\unicode[STIX]{x0394}z$ with respect to the pressure maximum can be estimated from an equilibrium between primary Bjerknes forces and buoyancy similar to calculations by (Eller Reference Eller1968),

(2.1) $$\begin{eqnarray}\unicode[STIX]{x0394}z=\frac{\unicode[STIX]{x1D706}_{z}}{4\unicode[STIX]{x03C0}}\arcsin \left(\frac{2\unicode[STIX]{x1D70C}gp_{0}\unicode[STIX]{x1D6FE}\unicode[STIX]{x1D706}_{z}\left(1-\displaystyle \frac{\unicode[STIX]{x1D714}^{2}}{\unicode[STIX]{x1D714}_{0}^{2}}\right)}{\unicode[STIX]{x03C0}p_{a}^{2}}\right).\end{eqnarray}$$

Here, $g$ is gravity, $\unicode[STIX]{x1D70C}$ the density of water, $p_{0}$ the static pressure, $p_{a}$ the acoustic pressure amplitude, $\unicode[STIX]{x1D6FE}=1.4$ , $\unicode[STIX]{x1D714}=2\unicode[STIX]{x03C0}f$ the driving frequency, $\unicode[STIX]{x1D714}_{0}$ the resonance frequency of the bubble and $\unicode[STIX]{x1D706}_{z}$ the wavelength along the $z$ -axis. The bubble is trapped between 0.3 mm and 2 mm above the pressure maximum, depending on the acoustic pressure and bubble size.

Single bubbles are nucleated by short laser pulses ( $\unicode[STIX]{x1D706}=532~\text{nm}$ , second harmonic of a Nd:YAG pulsed laser, New Wave Solo III, 6 ns pulse duration). The laser beam is focused by a set of three lenses: it is enlarged by a first spherical concave lens ( $f=-25~\text{mm}$ ), then collimated by a second spherical convex lens ( $f=125~\text{mm}$ ) and finally focused by an aspherical lens ( $f=40~\text{mm}$ ) to minimise optical aberrations. The size of the nucleated bubble depends strongly on how well focused the laser beam is. Furthermore, the size can be slightly influenced by tuning the energy of the laser. We nucleate bubbles with radii ranging between $20~\unicode[STIX]{x03BC}\text{m}$ and $40~\unicode[STIX]{x03BC}\text{m}$ . Larger bubbles can be obtained by coalescence of two smaller bubbles. For example, a bubble of radius $70~\unicode[STIX]{x03BC}\text{m}$ can typically be obtained from coalescing five to ten individual bubbles.

When bubble coalescence leads to a bubble size where a certain surface mode is expected to be unstable, the respective surface mode is triggered. We exploit this fact to obtain non-spherical bubble oscillations. As the technique is detailed elsewhere (Cleve et al. Reference Cleve, Guédra, Inserra, Mauger and Blanc-Benon2018a ), we will only recall some of the main features and important parameters. The conditions under which a surface mode $n$ can be triggered depend mainly on the bubble radius at rest $R_{0}$ , the acoustic driving frequency $f_{ac}$ and the acoustic pressure $p_{ac}$  (Brenner, Lohse & Dupont Reference Brenner, Lohse and Dupont1995). The driving frequency being a fixed variable in our experiments, a pressure threshold $p_{n,thresh}(R_{0})$ can be found above which the steady-state surface mode $n$ can be obtained. Consequently, a desired surface mode can be triggered by correctly choosing the bubble size and the acoustic pressure. This is a comparatively fast method to obtain a desired surface mode. As in other experiments, the hereby created surface modes are primarily shape deformations on zonal spherical harmonics and represent hence axisymmetric deformation. We have shown (Cleve et al. Reference Cleve, Guédra, Inserra, Mauger and Blanc-Benon2018a ) that the axis of symmetry is defined by the rectilinear motion between the two coalescing bubbles. This is a very important feature as the correct orientation of the bubble is essential to obtain unambiguous information on the bubble contour (Guédra et al. Reference Guédra, Cleve, Mauger, Blanc-Benon and Inserra2017). During our present experiments we thus take care that the bubbles are nucleated in the focal plane of the camera and that they remain in this plane all along their trajectory until coalescence. In conclusion, the bubble coalescence technique allows us to obtain bubbles of appropriate size for surface modes and furthermore to control their axis of symmetry.

The acoustic pressure is obtained indirectly by fitting the measured radial dynamics of bubbles driven at low acoustic amplitude to the analytical Keller–Miksis model (Keller & Miksis Reference Keller and Miksis1980). A large number of preliminary tests reveals a linear pressure–voltage relation.

2.2 Visualisation of the bubble dynamics

Experiments are captured with a CMOS camera (Vision Research^® V12.1) equipped with a $12\times$ objective lens (Navitar^® equipped with an additional 1.5 $\times$ lens). A frame size of $128\times 128~\text{pixels}$ and an acquisition rate of 180 kHz are used for the recordings of motion of the bubble interface. Backlight illumination is assured by a continuous light-emitting diode (LED). For this set-up and operating state, the depth of field of the camera objective and lenses is approximately $200~\unicode[STIX]{x03BC}\text{m}$ . The water tank is placed on a movable device which allows us to adjust its position in the three directions $x$ , $y$ and $z$ (defined in figure 1) to correct small variations of the bubble position.

Image processing is applied to extract the centroid and the bubble contour for each snapshot. Once the symmetry axis has been defined correctly, the contour can be described by the polar coordinates $(r_{s},\unicode[STIX]{x1D703})$ , (see figure 2). For each frame the contour is expanded on the basis of Legendre polynomials $P_{n}$ :

(2.2) $$\begin{eqnarray}r_{s}(\unicode[STIX]{x1D703},t)=\mathop{\sum }_{n=0}^{\infty }a_{n}(t)P_{n}(\cos \unicode[STIX]{x1D703}),\end{eqnarray}$$

where $a_{n}(t)$ are the modal coefficients (Guédra et al. Reference Guédra, Inserra, Mauger and Gilles2016)

(2.3) $$\begin{eqnarray}a_{n}(t)=\frac{2n+1}{2}\int _{-1}^{1}r_{s}(x,t)P_{n}(x)\,\text{d}x,\quad \text{with }x=\cos \unicode[STIX]{x1D703}.\end{eqnarray}$$

The coefficients can be interpreted as follows. The coefficient $a_{0}(t)=R(t)$ corresponds to the volume pulsations of the bubble, $a_{1}(t)$ can be related to translational oscillations and $a_{n}(t)$ for $n\geqslant 2$ are the amplitudes of shape modes. Figure 2(a) illustrates the theoretical shapes of different modes, and figure 2(b–d) presents three examples of modal decompositions obtained by experiments.

Figure 2. (a) Schematic representations of different bubble shape modes: radial mode $R$ , translation $a_{1}$ and surface modes $a_{n}$ for $n=2,\ldots ,7$ . The shapes are defined by the respective Legendre polynomial $P_{n}$ added to the rest radius $R_{0}$ , the two extreme deformations of the bubble are shown. (b–d) Experimentally obtained bubble shapes $r_{s}(\unicode[STIX]{x1D703})$ (left) and the respective modal decomposition (right). The dominance of different surface modes can be observed: (b) mode 2 for a bubble $R_{0}=46.9~\unicode[STIX]{x03BC}\text{m}$ , (c) mode 3 for a bubble $R_{0}=70.5~\unicode[STIX]{x03BC}\text{m}$ and (d) mode 4 for a bubble $R_{0}=55.7~\unicode[STIX]{x03BC}\text{m}$ . Note that the radial mode includes the radius at rest $R_{0}$ .

2.3 Visualisation of microstreaming

Red fluorescent polymer microspheres (diameter, $0.71~\unicode[STIX]{x03BC}\text{m}$ , Duke Scientific) are used to visualise the flow around the oscillating bubbles. The condition for inertial behaviour of the particles is fulfilled as the Stokes number $St$ is much smaller than 1,

(2.4) $$\begin{eqnarray}St=\frac{\unicode[STIX]{x1D70C}_{p}d_{p}v_{max}}{18\unicode[STIX]{x1D707}}\approx 0.04\ll 1,\end{eqnarray}$$

with $\unicode[STIX]{x1D707}\approx 1~\text{mPa}~\text{s}$ the liquid dynamic viscosity, $\unicode[STIX]{x1D70C}_{p}\approx 10^{3}~\text{kg}~\text{m}^{-3}$ the density of the particles, $d_{p}\approx 0.71~\unicode[STIX]{x03BC}\text{m}$ the diameter of the particles and $v_{max}\approx 2~\text{mm}~\text{s}^{-1}$ approximate maximum streaming velocity. In addition, the particles are small enough not to be influenced by the acoustic radiation force, since they are ten times smaller than the critical size estimated following Ben Haj Slama et al. (Reference Ben Haj Slama, Gilles, Chiekh and Béra2017). The particles are illuminated by a continuous wave laser source ( $\unicode[STIX]{x1D706}=532~\text{nm}$ , DPSS, CNI MLL-FN, 400 mW). A laser sheet is obtained by a cylindrical plano-concave lens ( $f=250~\text{mm}$ ). A cylindrical plano-convex lens ( $f=-25.4~\text{mm}$ ) is inserted just behind the first lens and oriented on the orthogonal axis to reduce the thickness of the laser sheet and obtain a beam waist estimated to approximately $250~\unicode[STIX]{x03BC}\text{m}$ . The fluorescence signal is recorded with the camera (see § 2.2) whose objective is equipped with a band reject filter (notch $532\pm 12~\text{nm}$ ) corresponding to the laser wavelength. A frame size of $1024\times 768~\text{pixels}$ and an acquisition rate of 600 Hz are used for the recordings of the motion of the tracer particles. The position of the continuous wave laser source including its lenses can be adjusted by a millimetre screw in order to precisely align the laser sheet with the bubble. Depending on the bubble size and exact position inside the laser sheet a more or less clear shadow might appear behind the bubble (see figure 9(a4) for a pronounced case). Note that all snapshots and streamline plots have been turned by $90^{\circ }$ for reasons of a more convenient image format. This has however no impact on the interpretation of the results.

Two types of post-processing for the microstreaming are conducted in the scope of this work, streak imaging and particle image velocimetry (PIV). The purpose of the streak imaging is to visualise the streaming patterns qualitatively. All snapshots of the videos are superposed and for each pixel the maximum value is kept. In this way, the trajectories of the tracer particles become visible. As the flow is a steady flow, trajectories, streaklines and streamlines coincide. PIV is used to obtain quantitative information on the streaming velocities. The software DaVis^® is used to extract a velocity vector field. Care has to be taken with the interpretation of the velocity data obtained for very small structures due to a limited number of tracer particles in these areas. Nevertheless, we choose to show PIV results in § 3.1 to give a rough idea about the occurring streaming velocities. The reader should keep in mind that the main aim of this work is not the discussion of streaming velocities but the overall characterisation of different types of streaming patterns.

2.4 Experimental procedure

In order to obtain information on bubble dynamics and microstreaming, the following experimental procedure is applied: a bubble is nucleated and trapped in the acoustic field of a fixed amplitude. This bubble is grown by multiple coalescences until it reaches a size slightly smaller than a bubble likely to show surface oscillations. If necessary, the position of the tank and of the focusing plane of the camera are adjusted. One further bubble is nucleated, which will trigger the surface oscillations. Once a steady-state regime is reached, we capture several sequences in the two operating states, visualisation of the bubble dynamics and visualisation of the microstreaming. Care is taken to rapidly switch between the operating states. A typical sequence is dynamics (a) – streaming (ab) – dynamics (b) – streaming (bc) – dynamics (c). If the bubble dynamics is the same on videos (a), (b) and (c), we can safely associate it with the obtained streaming pattern (ab) and (bc). Figure 3 visualises the experimental procedure with the associated time scales.

Figure 3. Schematic representations of the experimental procedure. As can be seen on the left zoom, the initial bubble shape caused by coalescence will lead to steady-state oscillations once the different modal components have decayed (here mode 2) or grown (here mode 3). After having adjusted the positions of camera and laser sheet, the measurement series begins, varying videos of bubble dynamics (abbreviated by dyn. in the figure) and streaming. The constant modal amplitudes, see superposed zooms on the right, lead us to conclude that we are in the steady-state regime.

2.5 Preliminary test for streaming without the presence of surface modes

Before conducting the experiments of streaming around bubbles with surface modes, we performed some preliminary tests (Cleve et al. Reference Cleve, Guédra, Mauger, Inserra and Blanc-Benon2018b ). For this, we recorded the fluorescent particles without the presence of any bubble and with the ultrasound field turned off. In the ideal case, no particle motion is visible at all. Frequently, a slight parasite flow (clearly smaller than the actual streaming) can be observed, which we suspect to be mainly due to thermal effects from the laser sheet. Switching on the ultrasound field does not lead to any further variations. Last, by adding a bubble that is purely oscillating on a radial mode, we still did not observe any particle motion. This observation is in agreement with several microstreaming models (Longuet-Higgins Reference Longuet-Higgins1998; Maksimov Reference Maksimov2007; Spelman & Lauga Reference Spelman and Lauga2017) that are not defined for purely radial oscillation. Indeed, even though not written explicitly, it becomes obvious from their derived fluid dynamics equations that no vorticity is induced by pure radial oscillations. Flows induced by pure radial motion have however been theoretically evidenced by Wu & Du (Reference Wu and Du1997). As a main difference to other models, their theory takes into account the gas phase inside the bubble as well as the incoming and the scattered acoustic field and it is based on the assumption of resonant size bubbles. As our bubbles are smaller than resonant size, this may explain why such liquid flows around a microbubble experiencing radial oscillations was never obtained in our experimental configuration. It is worth noting that, while focused on near-resonant bubbles, their theory may be applied to non-resonant bubbles as far as the applied acoustic field and the bubble equilibrium radius are known, which leads to small theoretical streaming velocities of the order of few micrometres per second for our experimental data.

In conclusion, in the present experimental conditions for a gas bubble in water and in a standing ultrasound field, other modes than the radial mode need to be present to obtain microstreaming. Note that the present set-up does not allow for pure translational motion.

3.1 Complete characterisation of a bubble: dynamics and streaming

The experimental procedure is conducted for approximately a hundred bubbles. Each of them is oscillating predominantly either in a mode 2, mode 3 or mode 4. The excited mode depends on the bubble size and driving pressure amplitude. All results are presented in a radius–pressure map in figure 4. The experimental results are indicated by the markers, and background colours indicate theoretically unstable areas (Brenner et al. Reference Brenner, Lohse and Dupont1995). The mode 2 and mode 3 presented on the map correspond to the first parametric resonance and the parametrically excited shape mode oscillates at half the driving frequency $f_{osc}/2$ . The mode 4 presented here corresponds to the second parametric resonance and the parametrically excited shape mode oscillates at the driving frequency $f_{osc}$ . The first parametric resonance of the mode 4 (obtained for bubble radii larger than $80~\unicode[STIX]{x03BC}\text{m}$ ) has not been investigated experimentally due to difficulties to keep surface oscillations stable for a sufficiently long time. A possible reason is that the first parametric resonance of the mode 4 (red zone on the right of figure 4) is close to the resonance size.

Figure 4. Radius–pressure map presenting experimental results classified according to the predominant mode of deformation ( $\times$  – mode 2, ▵ – mode 3, ▫ – mode 4) superimposed on numerically computed unstable areas (background colours: blue – mode 2, green – mode 3, red – mode 4).

Figure 5. Characterisation of a bubble ( $R_{0}=46.9~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=20.6~\text{kPa}$ ) oscillating predominantly on a surface mode 2 and its resulting streaming pattern: (a) consecutive snapshots over two acoustic periods $2T=0.064~\text{ms}$ recorded at 180 kHz (the axis of symmetry is indicated in the first screen shot, the image size is $180~\unicode[STIX]{x03BC}\text{m}\times 180~\unicode[STIX]{x03BC}\text{m}$ ); (b) modal decomposition of the bubble shape and (c) ‘zoom’ on two acoustic periods (500 measurement points reported on $2T=0.064~\text{ms}$ ); (d) streak photography of the streaming pattern (700 images corresponding to 1.2 ms of signal, image size $1200~\unicode[STIX]{x03BC}\text{m}\times 900~\unicode[STIX]{x03BC}\text{m}$ ); (e) PIV of the streaming flow and (f) velocity profiles along the line indicated in (e). See also supplementary movie 1 and movie 2.

Figure 6. Characterisation of a bubble ( $R_{0}=70.5~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=12.8~\text{kPa}$ ) oscillating predominantly on a surface mode 3 and its resulting streaming pattern: (a) consecutive snapshots over two acoustic periods $2T=0.064~\text{ms}$ recorded at 180 kHz (the axis of symmetry is indicated in the first screen shot, the image size is $180~\unicode[STIX]{x03BC}\text{m}\times 180~\unicode[STIX]{x03BC}\text{m}$ ); (b) modal decomposition of the bubble shape and (c) ‘zoom’ on two acoustic periods (500 measurement points reported on $2T=0.064~\text{ms}$ ); (d) streak photography of the streaming pattern (700 images corresponding to 1.2 ms of signal, images size $1200~\unicode[STIX]{x03BC}\text{m}\times 900~\unicode[STIX]{x03BC}\text{m}$ ); (e) PIV of the streaming flow and (f) velocity profiles along the line indicated in (e). See also supplementary movie 3 and movie 4.

Figure 7. Characterisation of a bubble ( $R_{0}=55.7~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=23.6~\text{kPa}$ ) oscillating predominantly on a surface mode 4 and its resulting streaming pattern: (a) consecutive snapshots over two acoustic periods $2T=0.064~\text{ms}$ recorded at $180~\text{kHz}$ (the axis of symmetry is indicated in the first screen shot, the image size is $180~\unicode[STIX]{x03BC}\text{m}\times 180~\unicode[STIX]{x03BC}\text{m}$ ); (b) modal decomposition of the bubble shape and (c) ‘zoom’ on two acoustic periods (500 measurement points reported on $2T=0.064~\text{ms}$ ); (d) streak photography of the streaming pattern (700 images corresponding to 1.2 ms of signal, images size $1200~\unicode[STIX]{x03BC}\text{m}\times 900~\unicode[STIX]{x03BC}\text{m}$ ); (e) PIV of the streaming flow and (f) velocity profiles along the line indicated in (e). See also supplementary movie 5 and movie 6.

Figures 5 to 7 present complete overviews on the characterisation of a bubble including its dynamics (a–c) and streaming (d–f). Respective videos can be found in the supplementary material (movie 1 to movie 6) available online at https://doi.org/10.1017/jfm.2019.511. Panel (a) presents a series of consecutive snapshots over two acoustic periods of the respective bubble. The modal decomposition over one millisecond is presented in (b). We recall that we restrict our analysis to the steady-state regime and that initial transient effects due to the coalescence process are no longer present. In (b) we only show 1 ms of signal out of 100 ms original recording length. Furthermore, we only present the decomposition of the first eight surface modes, which is sufficient to analyse the surface oscillations possibly generated through nonlinear coupling (Guédra et al. Reference Guédra, Cleve, Mauger, Blanc-Benon and Inserra2017). Similar information on the modal amplitude is presented in (c) in phase-averaged plots. It can be understood as a zoom on two acoustic periods, but more precisely it shows 2.7 ms of the signal that is recovered over two acoustic periods. This type of plot is introduced here, as it will facilitate the discussion in § 3.2. Panel (d) shows streak images where 700 snapshots covering 1.2 s are superposed to visualise the trajectories of the tracer particles. Panel (e) presents the velocity distribution resulting from PIV. The average over 100 PIV steps has been evaluated. Panel (f) shows the absolute velocity in dependence of the radial coordinate $r$ along the red line that is indicated in panel (e), coinciding with the axis of symmetry.

Figure 5 presents experimental results obtained for a bubble of mean radius $R_{0}=46.9~\unicode[STIX]{x03BC}\text{m}$ and pressure $p_{a}=20.6~\text{kPa}$ which is oscillating predominantly on a mode 2. The bubble dynamics shows the appearance of a radial component $R$ , a large modal amplitude $a_{2}$ and small modal amplitude $a_{4}$ . The parametric excitation of the mode 2 is naturally expected as the applied acoustic pressure is higher than the pressure threshold $p_{2,thresh}=17.5~\text{kPa}$ . The acoustic pressure is however below the pressure threshold of the mode 4 ( $p_{4,thresh}=44.1~\text{kPa}$ ), the appearance of the mode 4 is hence evidence of nonlinear coupling. The streaming pattern in figure 5(d) is a large cross-like structure with two pairs of small recirculation zones close to the bubble. The maximum absolute velocity is approximately $0.6~\text{mm}~\text{s}^{-1}$ on the axis of symmetry where the flow is flowing away from the bubble. Figure 6 presents experimental results obtained for a bubble of mean radius $R_{0}=70.5~\unicode[STIX]{x03BC}\text{m}$ and pressure $p_{a}=12.8~\text{kPa}$ which is oscillating predominantly on a mode 3. A large radial amplitude $R$ and a large modal amplitude $a_{3}$ can be observed. The apparently large translational mode $a_{1}$ will be discussed later. Furthermore, a modal amplitude $a_{6}$ is clearly visible, and small components of the modes $a_{2}$ and $a_{4}$ can be observed. The mode 3 is driven by parametric excitation ( $p_{3,thresh}=9.0~\text{kPa}$ ), whereas the other modes appear due to nonlinear coupling (for instance $p_{6,thresh}=39.5~\text{kPa}$ ). The streaming pattern in figure 6(d) consists of six lobes. Maximum velocities are approximately $1~\text{mm}~\text{s}^{-1}$ . Figure 7 presents experimental results obtained for a bubble of mean radius $R_{0}=55.7~\unicode[STIX]{x03BC}\text{m}$ and pressure $p_{a}=23.6~\text{kPa}$ which is oscillating predominantly on a mode 4. The bubble dynamics shows a radial amplitude $R$ , a modal amplitude $a_{4}$ and a slightly lower modal amplitude $a_{2}$ . The mode 4 is naturally excited ( $p_{4,thresh}=11.0~\text{kPa}$ ) whereas the acoustic pressure is below the threshold for the mode 2 ( $p_{2,thresh}=29.1~\text{kPa}$ ). The streaming pattern shows eight small lobes of the size of the bubble diameter. The PIV analysis results in maximum velocities of approximately $0.4~\text{mm}~\text{s}^{-1}$ .

Figure 8. Presentation of two different streaming patterns observed for a bubble oscillating in a mode 2: case (a) – Cross-shaped pattern with four small lobes close to the bubble ( $R_{0}=49.7~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=34.5~\text{kPa}$ ); case (b) – cross-shaped pattern without any lobes ( $R_{0}=44.0~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=23.4~\text{kPa}$ ). For each case (x), the information is structured as follows. (x1) schematic drawing of the bubble dynamics, and (x2) representative snapshot of the dynamics (image size $180~\unicode[STIX]{x03BC}\text{m}\times 180~\unicode[STIX]{x03BC}\text{m}$ ); (x3) schematic drawing of the streaming patterns, and (x4) streak photography of the streaming pattern (image size $1~\text{mm}\times 1~\text{mm}$ , 723 images corresponding to 1.2 ms of signal); (x5) maximum modal amplitudes; (x6) temporal evolution of: black line – $\unicode[STIX]{x1D709}_{0}$ , red dashed line – $\unicode[STIX]{x1D709}_{2}$ , and blue dotted line – $\unicode[STIX]{x1D709}_{4}$ .

Figure 9. Presentation of four different streaming patterns observed for a bubble oscillating in a mode 3: case (a) – pattern with 6 lobes confined around the bubble ( $R_{0}=70.8~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=9.2~\text{kPa}$ ); case (b) – pattern with 8 lobes confined around the bubble ( $R_{0}=70.1~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=12.4~\text{kPa}$ ); case (c) – cross-shaped pattern without any lobes ( $R_{0}=65.7~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=15.1~\text{kPa}$ ); case (d) – cross-shaped pattern with four circular zones of recirculation ( $R_{0}=68.6~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=13.3~\text{kPa}$ ). For each case (x), the information is structured as follows. (x1) schematic drawing of the bubble dynamics, and (x2) representative snapshot of the dynamics (image size $180~\unicode[STIX]{x03BC}\text{m}\times 180~\unicode[STIX]{x03BC}\text{m}$ ); (x3) schematic drawing of the streaming patterns, and (x4) streak photography of the streaming pattern (image size $1~\text{mm}\times 1~\text{mm}$ , 723 images corresponding to 1.2 ms of signal); (x5) maximum modal amplitudes; (x6) temporal evolution of: black line – $\unicode[STIX]{x1D709}_{0}$ , red dashed line – $\unicode[STIX]{x1D709}_{3}$ , and blue dotted line – $\unicode[STIX]{x1D709}_{6}$ .

Figure 10. Presentation of two different streaming patterns observed for a bubble oscillating in a mode 4: case (a) – pattern with 8 small lobes confined around the bubble ( $R_{0}=56.5~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=17.9~\text{kPa}$ ); case (b) – cross-shaped pattern ( $R_{0}=55.0~\unicode[STIX]{x03BC}\text{m}$ , $p_{a}=17.9~\text{kPa}$ ,). For each case (x), the information is structured as follows. (x1) schematic drawing of the bubble dynamics, and (x2) representative snapshot of the dynamics (image size $180~\unicode[STIX]{x03BC}\text{m}\times 180~\unicode[STIX]{x03BC}\text{m}$ ); (x3) schematic drawing of the streaming patterns, and (x4) streak photography of the streaming pattern (image size 1 mm $\times$ 1 mm, 723 images corresponding to 1.2 ms of signal); (x5) maximum modal amplitudes; (x6) temporal evolution of: black line – $\unicode[STIX]{x1D709}_{0}$ , green dash-dotted line – $\unicode[STIX]{x1D709}_{2}$ , and red dashed line –  $\unicode[STIX]{x1D709}_{4}$ .

Such complete characterisations can be obtained for a large number of bubbles. The examples shown in figures 5–7 are representative for several findings. However, it has been observed that the mode number is not the only parameter defining the shape of the streaming pattern. An extended set of different streaming patterns is presented in § 3.2.

3.2 Classification of streaming patterns

The streaming patterns shown in § 3.1 present one possible structure obtained for bubbles oscillating predominantly in mode 2, 3 or 4 respectively. These are, however, not unique possibilities and other streaming patterns can be observed. In this section we will present an extensive set of observed streaming patterns in figures 8 to 10. Figure 8 contains two different streaming patterns, (a) and (b), for a bubble oscillating in a mode 2, figure 9(a–d) shows four cases for a mode 3, and figure 10(a,b) two cases for a mode 4. For each streaming pattern (x), the following information is presented. The bubble dynamics is presented schematically in (x1), and by one representative snapshot in (x2). A schematic drawing of the streamlines is given in (x3) and is representative of the streak photography in (x4). More information on the modal amplitudes is given in (x5) and (x6). Panel (x5) presents the modal amplitudes $\hat{a}_{n}=\max (|a_{n}|)$ for the modes $n=0,\ldots ,8$ . Note that for the radial oscillation the value is obtained by first subtracting the mean radius $R_{0}$ so that $\hat{a}_{0}=\max (|a_{0}-R_{0}|)$ . Panel (x6) presents the temporal evolutions of some chosen modal amplitudes, less important modes are left out for clarity. Furthermore the evolutions have been normalised so that normalised temporal amplitude

(3.1) $$\begin{eqnarray}\unicode[STIX]{x1D709}_{n}(t)=\frac{a_{n}(t)-R_{0}\unicode[STIX]{x1D6FF}_{n0}}{\hat{a}_{n}}\end{eqnarray}$$

lies between $-1$ and 1. The Kronecker delta $\unicode[STIX]{x1D6FF}_{n0}$ is used here to subtract the radius at rest for the radial mode.

Figure 8 shows two characteristic streaming patterns for a bubble that is predominantly oscillating in a mode 2. Case 8(a) shows a cross-like structure with two pairs of recirculation zones close to the bubble surface and symmetric with respect to the axis of symmetry of the shape deformation. This case corresponds to the pattern already presented in figure 5 in § 3.1. Case 8(b) also shows a cross-like structure, but no small structures are visible. The main difference in the bubble dynamics between the two cases is that the modal amplitudes $a_{2}$ and $a_{4}$ are considerably larger for case 8(b) than for case 8(a). Taking into account all experimental results showing a mode 2, we observe that for the cross-like streaming pattern, case 8(a), the modal amplitudes range between $3~\unicode[STIX]{x03BC}\text{m}<a_{2}<6~\unicode[STIX]{x03BC}\text{m}$ and $a_{4}<2~\unicode[STIX]{x03BC}\text{m}$ . Opposed to those values, the modal amplitudes for the cross-like streaming patterns without any visible substructures, case 8(b), are larger and range between $10~\unicode[STIX]{x03BC}\text{m}<a_{2}<13~\unicode[STIX]{x03BC}\text{m}$ and $3~\unicode[STIX]{x03BC}\text{m}<a_{4}<4~\unicode[STIX]{x03BC}\text{m}$ .

Figure 9 shows four characteristic streaming patterns for a bubble that is predominantly oscillating in a mode 3. Case 9(a) shows a structure with six lobes. A similar pattern has already been presented in § 3.1 in figure 6. Case 9(b) shows a structure with 8 lobes. This kind of pattern is observed a large number of times. The 8 lobes may be arranged evenly around the circumference or irregularly as can be seen in the example presented here. The two lobes in the perpendicular direction to the axis of symmetry (on its right side) are very close to one another and could be described as one joint structure. Case 9(c) shows a cross-like structure. And finally case 9(d) shows a cross-like structure with four round zones of recirculation in every corner of the cross and close to the bubble. The cases presented here show larger modal amplitudes for the large cross-like structures, cases (c) and (d). These findings are however not representative of all experimental results as will be discussed later in this section. Besides the modal amplitude $a_{3}$ and the radial amplitude $a_{0}$ , a strong modal amplitude $a_{1}$ is visible. The corresponding dimensionless variable $\unicode[STIX]{x1D709}_{1}$ is not presented in the temporal information in (x6), as it is always in approximate phase opposition to $\unicode[STIX]{x1D709}_{3}$ it has hence been left out for clarity. Possible reasons for the appearance of $a_{1}$ will be discussed in § 4. A last look shall be taken at the modal amplitude $\unicode[STIX]{x1D709}_{6}$ as it is oscillating at the same frequency as the radial mode and hence at the driving frequency. The phase difference between these two modes $\unicode[STIX]{x1D709}_{0}$ and $\unicode[STIX]{x1D709}_{6}$ will be discussed later in this section.

Figure 10 shows two characteristic streaming patterns for a bubble that is predominantly oscillating in a mode 4. Case 10(a) shows a structure with 8 small lobes close to the bubble. The same case has already been presented in § 3.1 in figure 7. Case 10(b) is a cross-like structure. Generally, patterns with lobes, case (a), show smaller modal amplitudes ( $3~\unicode[STIX]{x03BC}\text{m}<a_{4}<8~\unicode[STIX]{x03BC}\text{m}$ , $a_{2}<4~\unicode[STIX]{x03BC}\text{m}$ ) than the cross-like structures ( $8~\unicode[STIX]{x03BC}\text{m}<a_{4}<18~\unicode[STIX]{x03BC}\text{m}$ , $2~\unicode[STIX]{x03BC}\text{m}<a_{2}<7~\unicode[STIX]{x03BC}\text{m}$ ). The modal amplitude $a_{8}$ is generally small and is left out in (x6) for clarity. As the mode 4 is a second parametric resonance, it is oscillating at the driving frequency $f_{osc}$ . The dimensionless variables $\unicode[STIX]{x1D709}_{0}(t)$ , $\unicode[STIX]{x1D709}_{2}(t)$ and $\unicode[STIX]{x1D709}_{4}(t)$ are oscillating at the same frequency. In all cases, $\unicode[STIX]{x1D709}_{0}(t)$ and $\unicode[STIX]{x1D709}_{4}(t)$ are in approximate phase opposition. As $\unicode[STIX]{x1D709}_{2}(t)$ has been observed to oscillate either in phase with $\unicode[STIX]{x1D709}_{0}(t)$ or with $\unicode[STIX]{x1D709}_{4}(t)$ for both cross-like structures and structures with 8 lobes, no certain rule can be deduced for the phase of $\unicode[STIX]{x1D709}_{2}(t)$ .

We can sort the observed patterns into two classes. The first class gathers patterns that only consist of lobes around the bubble. The streamlines start and end on the bubble surface. The second class gathers patterns that extend much further away from the bubble and have a cross-like structure. Some of those patterns show additional small zones of recirculation with closed streamlines. An overview of this classification is given in table 1. Streaming patterns induced by bubbles with a predominant mode 2 all belong to the second class (large cross-like structure), while patterns induced by modes 3 and 4 can be found in both classes.

Table 1. Definition of large patterns and confined lobe patterns as well as classification of the cases in figures 5–10.

All measurement points are reported in a radius–pressure map, figure 11(a), and a distinction between the two classes of patterns becomes visible. The confined lobes patterns are always found for bubbles larger than the $n$ th-mode resonance size, that is for frequencies below the $n$ th-mode resonance frequency. The large patterns are always found for bubbles smaller than the $n$ th-mode resonance size, that is for frequencies above the $n$ th-mode resonance frequency. The vertical lines indicated for modes 3 and 4 match well with the respective minima of the pressure threshold deduced from stability analysis by Brenner et al. (Reference Brenner, Lohse and Dupont1995) within the error margin on the bubble size. Furthermore, the line indicated for the mode 3 corresponds exactly to the 3rd-mode resonant radius calculated from first-order approximation analysis by Francescutto & Nabergoj (Reference Francescutto and Nabergoj1978). Note that such a linearised theory is only valid in the vicinity of the first parametric resonance, a similar analysis thus cannot be applied to the mode 4 presented in figure 11.

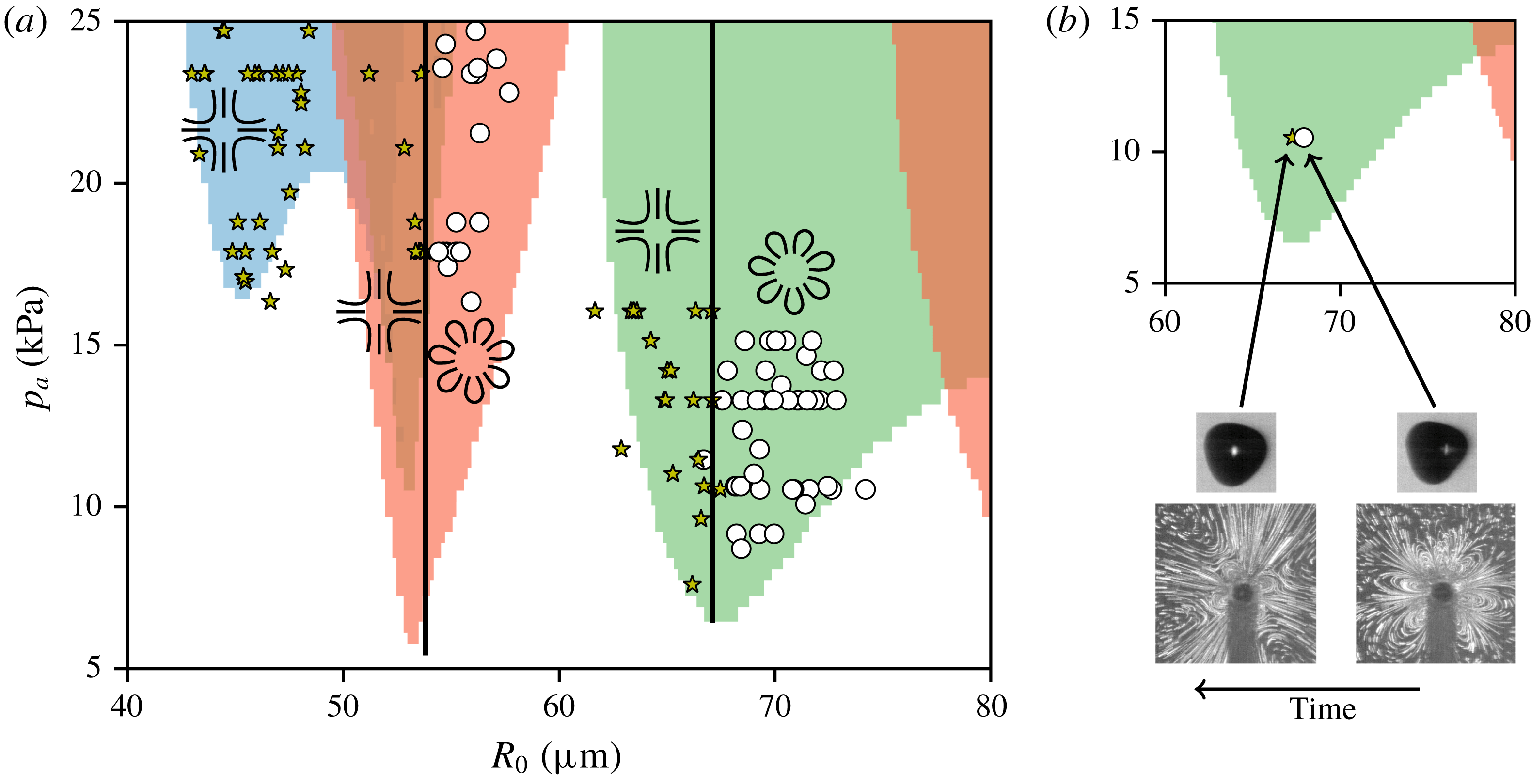
Figure 11. (a) Radius–pressure map with all results separated: $\star$ – large patterns; ○ – confined lobe patterns, (see table 1 for definition); background colours: blue – mode 2, green – mode 3, red – mode 4. (b) Example of one bubble whose pattern changes from a confined lobe pattern to a large pattern while the bubble is diminishing slightly in size, passing from above to below resonant size (within the error of measurement).

Normally, bubbles maintain an approximately stable size so that they show either lobe-shaped patterns or large patterns throughout one measurement series. However, in a few cases we succeeded in observing a bubble growing or shrinking over time while keeping the bubble oscillations otherwise stable. Such an example is shown in figure 11(b). In this particular case, we even managed to record the relatively fast switch (order of a few hundred milliseconds) between the two types of pattern. The beginning of the 1.2 s recording gives the lobe-shaped pattern on the right of figure 11(b), the end of the recording the large pattern on the left of figure 11(b). The corresponding bubble dynamics before and after the recording of the streaming shows a small decrease of the bubble size ( $R_{0}=69.2~\unicode[STIX]{x03BC}\text{m}$ and $69.0~\unicode[STIX]{x03BC}\text{m}$ ). Furthermore the modal amplitudes decrease (4 % for $a_{3}$ and 30 % for mode 6), but in particular an increased phase difference between the mode 0 and mode 6 becomes visible.

In figure 11(a), no zones can be seen that would allow us to further distinguish the observed patterns: For a mode 3, the patterns with six lobes and with eight lobes cannot be distinguished. For a mode 2, the cross-like patterns with and without zones of recirculation are in the same region.

We shall now take a closer look at the modal amplitudes and phases, focusing on bubbles in the vicinity of the first parametric resonance of mode 3 as presented in figure 9. As reported in the previous paragraph, the large patterns and lobe-shaped patterns can be distinguished by the bubble size. There are two other important parameters that were left out earlier in this section: the modal amplitudes $\hat{a}_{3}$ , $\hat{a}_{0}$ and $\hat{a}_{6}$ as well as the phase differences between modes. This information is presented in figure 12.

Figure 12. Study of amplitude and phasing for bubbles oscillating in a mode 3 and separated in large patterns – $\star$ and lobe pattern – ○. The $x$ -axis of all three panels is the maximum modal amplitude $\hat{a}_{3}$ , the $y$ -axis shows (a) the phase difference between $a_{0}$ and $a_{6}$ , (b) the maximum modal amplitude $\hat{a}_{0}$ and (c) the maximum modal amplitude $\hat{a}_{6}$ .

In all three panels the $x$ -axis is chosen to be the maximum modal amplitude $\hat{a}_{3}$ , which can be considered important information for a bubble oscillating predominantly on a mode 3. However, no distinction between large patterns and lobe patterns can be detected by this parameter. In figure 12(a), the $y$ -axis represents the phase difference between the mode $a_{0}$ and $a_{6}$ . Those two modal components are oscillating at the same frequency $f_{osc}$ , whereas $a_{3}$ is oscillating at $f_{osc}/2$ . A clear distinction between lobe patterns and large patterns can be observed. While lobe patterns range around zero phase difference, large patterns range around a phase difference of $\unicode[STIX]{x03C0}/8$ or in terms of acoustic period $T/16$ . We also show the modal amplitudes $\hat{a}_{0}$ , figure 12(b), and $\hat{a}_{6}$ , figure 12(c), as functions of $\hat{a}_{3}$ . It can be seen that $\hat{a}_{0}$ , $\hat{a}_{3}$ and $\hat{a}_{6}$ are linearly dependent on one another. However, no rule to distinguish large patterns and lobe patterns becomes obvious.