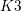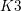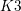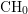0.1 Zero-cycles on $K3$ surfaces

Let $X$ be a nonsingular projective $K3$ surface. In [Reference Beauville and VoisinBV04], Beauville and Voisin showed that $X$ carries a canonical zero-cycle class of degree 1,

$$\begin{eqnarray}\displaystyle [o_{X}]\in \text{CH}_{0}(X), & & \displaystyle \nonumber\end{eqnarray}$$

where $o_{X}$ can be taken any point lying on a rational curve in  $X$ . It has the remarkable property that all intersections of divisor classes in  $X$ , as well as the second Chern class of  $X$ , lie in $\mathbb{Z}\cdot [o_{X}]$ .

In [Reference O’GradyO’Gr13], O’Grady introduced an increasing filtration $S_{\bullet }(X)$ on  $\text{CH}_{0}(X)$ ,

$$\begin{eqnarray}\displaystyle S_{0}(X)\subset S_{1}(X)\subset \cdots \subset S_{i}(X)\subset \cdots \subset \text{CH}_{0}(X), & & \displaystyle \nonumber\end{eqnarray}$$

where $S_{i}(X)$ is the union of $[z]+\mathbb{Z}\cdot [o_{X}]$ for all effective zero-cycles $z$ of degree  $i$ . In particular, we have

$$\begin{eqnarray}\displaystyle S_{0}(X)=\mathbb{Z}\cdot [o_{X}]. & & \displaystyle \nonumber\end{eqnarray}$$

An alternative characterization of $S_{\bullet }(X)$ via effective orbits is given by Voisin in [Reference VoisinVoi15].

0.2 Derived categories

Let $D^{b}(X)$ denote the bounded derived category of coherent sheaves on  $X$ . Given an object ${\mathcal{E}}\in D^{b}(X)$ , we write

$$\begin{eqnarray}\displaystyle v({\mathcal{E}})\in H^{0}(X,\mathbb{Z})\oplus H^{2}(X,\mathbb{Z})\oplus H^{4}(X,\mathbb{Z}) & & \displaystyle \nonumber\end{eqnarray}$$

for the Mukai vector of ${\mathcal{E}}$ , and define

$$\begin{eqnarray}\displaystyle d({\mathcal{E}})={\textstyle \frac{1}{2}}\dim \text{Ext}^{1}({\mathcal{E}},{\mathcal{E}})\in \mathbb{Z}_{{\geqslant}0}. & & \displaystyle \nonumber\end{eqnarray}$$

An interesting link between the second Chern classes of objects in $D^{b}(X)$ and the filtration $S_{\bullet }(X)$ was discovered by Huybrechts and O’Grady. In [Reference HuybrechtsHuy10], Huybrechts showed under certain assumptionsFootnote ¹ that if ${\mathcal{E}}\in D^{b}(X)$ is a spherical object (and hence $d({\mathcal{E}})=0$ ), then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in \mathbb{Z}\cdot [o_{X}]. & & \displaystyle \nonumber\end{eqnarray}$$

Later, O’Grady conjecturedFootnote ² in [Reference O’GradyO’Gr13] that if ${\mathcal{E}}$ is a Gieseker-stable sheaf with respect to a polarization $H$ on  $X$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

He verified the conjecture again under certain assumptions on the Picard rank of $X$ and/or on the Mukai vector $v({\mathcal{E}})$ . Further, in [Reference VoisinVoi15], Voisin proved (a generalization of) the conjecture for any simple vector bundle ${\mathcal{E}}$ on  $X$ .

Our first result completes the proof of O’Grady’s conjecture and generalizes it to arbitrary objects in  $D^{b}(X)$ .

Theorem 0.1. For any object ${\mathcal{E}}\in D^{b}(X)$ , we have

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Note that Theorem 0.1 does not involve any stability condition and should be viewed as a statement purely on the derived category $D^{b}(X)$ . However, the proof uses (slope) stability and ultimately relies on Voisin’s proof of the vector bundle case.

Theorem 0.1 has an important consequence. Let $\widetilde{S}_{\bullet }(X)$ be the extension of O’Grady’s filtration to the Chow ring $\text{CH}^{\ast }(X)$ by the trivial filtration on $\text{CH}^{0}(X)$ and $\text{CH}^{1}(X)$ . In particular, we have

$$\begin{eqnarray}\displaystyle \widetilde{S}_{0}(X)=R^{\ast }(X) & & \displaystyle \nonumber\end{eqnarray}$$

which is the Beauville–Voisin ring of $X$ generated by divisor classes. Let

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:D^{b}(X)\xrightarrow[{}]{{\sim}}D^{b}(X^{\prime }) & & \displaystyle \nonumber\end{eqnarray}$$

be a derived equivalence between two nonsingular projective $K3$ surfaces. It induces an isomorphism of (ungraded) Chow groups

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\text{CH}}:\text{CH}^{\ast }(X)\xrightarrow[{}]{{\sim}}\text{CH}^{\ast }(X^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

We have the following generalization of Huybrechts’ result in [Reference HuybrechtsHuy10] that $\unicode[STIX]{x1D6F7}^{\text{CH}}$ preserves the Beauville–Voisin ring.Footnote ³

The generality of Theorem 0.1 also suggests a natural increasing filtration on  $D^{b}(X)$ ,

$$\begin{eqnarray}\displaystyle S_{0}(D^{b}(X))\subset S_{1}(D^{b}(X))\subset \cdots \subset S_{i}(D^{b}(X))\subset \cdots \subset D^{b}(X), & & \displaystyle \nonumber\end{eqnarray}$$

where $S_{i}(D^{b}(X))$ consists of objects ${\mathcal{E}}\in D^{b}(X)$ with $c_{2}({\mathcal{E}})\in S_{i}(X)$ . By Corollary 0.2, this filtration does not depend on the $K3$ surface $X$ and is ‘intrinsic’ to the triangulated category $\mathbf{D}=D^{b}(X)$ .

0.3 Moduli spaces of stable objects

Moduli spaces of stable sheaves on  $X$ provide a large class of holomorphic symplectic varietiesFootnote ⁴ of $K3^{[d]}$ -type. The subject has been developed by many people, including Beauville, Mukai, Huybrechts, O’Grady, and Yoshioka; see [Reference BeauvilleBea83, Reference HuybrechtsHuy97, Reference HuybrechtsHuy99, Reference MukaiMuk84, Reference O’GradyO’Gr97, Reference YoshiokaYos01]. More recently, Bridgeland [Reference BridgelandBri07, Reference BridgelandBri08] and Bayer–Macrì [Reference Bayer and MacrìBM14a, Reference Bayer and MacrìBM14b] obtained all holomorphic symplectic birational models of these moduli spaces by considering moduli spaces of objects in  $D^{b}(X)$ satisfying certain stability conditions.

Let

$$\begin{eqnarray}\displaystyle \mathbf{v}\in H^{0}(X,\mathbb{Z})\oplus H^{2}(X,\mathbb{Z})\oplus H^{4}(X,\mathbb{Z}) & & \displaystyle \nonumber\end{eqnarray}$$

be a primitive algebraic class with Mukai self-intersection $\mathbf{v}^{2}>0$ . In [Reference BridgelandBri08], Bridgeland described a connected component $\text{Stab}^{\dagger }(X)$ of the space of stability conditions on $D^{b}(X)$ , which admits a chamber decomposition depending on  $\mathbf{v}$ . When $\unicode[STIX]{x1D70E}\in \text{Stab}^{\dagger }(X)$ is a genericFootnote ⁵ stability condition with respect to  $\mathbf{v}$ , there is a nonsingular projective moduli space $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ of $\unicode[STIX]{x1D70E}$ -stable objects ${\mathcal{E}}\in D^{b}(X)$ with Mukai vector $v({\mathcal{E}})=\mathbf{v}$ . The moduli space $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ only depends on the chamber containing $\unicode[STIX]{x1D70E}$ . It is of dimensionFootnote ⁶

$$\begin{eqnarray}\displaystyle 2d(\mathbf{v})=\mathbf{v}^{2}+2>2 & & \displaystyle \nonumber\end{eqnarray}$$

and is holomorphic symplectic by the pairing

$$\begin{eqnarray}\displaystyle \text{Ext}^{1}({\mathcal{E}},{\mathcal{E}})\times \text{Ext}^{1}({\mathcal{E}},{\mathcal{E}})\rightarrow \text{Ext}^{2}({\mathcal{E}},{\mathcal{E}})\xrightarrow[{}]{\text{tr}}\mathbb{C}. & & \displaystyle \nonumber\end{eqnarray}$$

When $\unicode[STIX]{x1D70E}$ is in the chamber corresponding to the large volume limit, the moduli space $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ recovers the moduli space of Gieseker-stable sheaves with respect to a generic polarization $H$ on  $X$ .

In the first version of this paper, we proposed the following conjecture relating the second Chern classes of objects in $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ to the corresponding point classes on $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ .

Conjecture 0.3. Two objects ${\mathcal{E}},{\mathcal{E}}^{\prime }\in M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ satisfy

(i) $$\begin{eqnarray}[{\mathcal{E}}]=[{\mathcal{E}}^{\prime }]\in \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))\end{eqnarray}$$

if and only if

(ii) $$\begin{eqnarray}c_{2}({\mathcal{E}})=c_{2}({\mathcal{E}}^{\prime })\in \text{CH}_{0}(X).\end{eqnarray}$$

Note that the two conditions above have different flavors. Condition (i) only depends on the triangulated category $\mathbf{D}=D^{b}(X)$ with a given stability condition, while (ii) requires the underlying $K3$ surface  $X$ .

Later, Marian and the third author found a short proof of Conjecture 0.3 in [Reference Marian and ZhaoMZ17]. This renders a number of subsequent statements unconditional.

0.4 Beauville–Voisin filtration for zero-cycles

Our study of zero-cycles on the moduli spaces $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ is motivated by the Beauville–Voisin conjecture for holomorphic symplectic varieties. The conjecture predicts that the Chow ring (with rational coefficients) of a holomorphic symplectic variety admits a multiplicative decomposition; see [Reference BeauvilleBea07, Reference VoisinVoi08, Reference VoisinVoi16]. Another way to phrase it is the existence of a new filtration on the Chow ring which is opposite to the conjectural Bloch–Beilinson filtration. Recently, rather than proving consequences of the Beauville–Voisin conjecture, much effort has been put to construct this new filtration, which we shall call the Beauville–Voisin filtration.

In the case of a moduli space $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ , our previous discussion suggests a natural candidate for the Beauville–Voisin filtration on the Chow group $\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))$ of zero-cycles. It is simply given by the restriction of the filtration $S_{\bullet }(\mathbf{D})$ to $\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))$ . More concretely, we have an increasing filtration

$$\begin{eqnarray}\displaystyle S_{0}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v})) & \subset & \displaystyle S_{1}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))\subset \cdots \nonumber\\ \displaystyle & \subset & \displaystyle S_{i}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))\subset \cdots \subset \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v})),\nonumber\end{eqnarray}$$

where $S_{i}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))$ is the subgroup spanned by $[{\mathcal{E}}]\in \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))$ for all ${\mathcal{E}}\in M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ with $c_{2}({\mathcal{E}})\in S_{i}(X)$ .

An immediate consequence of Theorem 0.1 is

$$\begin{eqnarray}\displaystyle S_{d(\mathbf{v})}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))=\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v})), & & \displaystyle \nonumber\end{eqnarray}$$

where $2d(\mathbf{v})=\mathbf{v}^{2}+2$ is the dimension of $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ . Moreover, by an argument in [Reference O’GradyO’Gr13], the subset

$$\begin{eqnarray}\displaystyle \{c_{2}({\mathcal{E}}):{\mathcal{E}}\in M_{\unicode[STIX]{x1D70E}}(\mathbf{v})\}\subset S_{d(\mathbf{v})}(X) & & \displaystyle \nonumber\end{eqnarray}$$

equals the full subset of $S_{d(\mathbf{v})}(X)$ of the given degree. In particular, we have

$$\begin{eqnarray}\displaystyle S_{0}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))\neq 0. & & \displaystyle \nonumber\end{eqnarray}$$

Further, since $S_{0}(X)=\mathbb{Z}\cdot [o_{X}]$ , Conjecture 0.3 (now proven) implies that

$$\begin{eqnarray}\displaystyle S_{0}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))\simeq \mathbb{Z}. & & \displaystyle \nonumber\end{eqnarray}$$

In other words, the moduli space $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ carries a canonical zero-cycle class of degree 1, which matches the predictions of the Beauville–Voisin conjecture.

We also show that the filtration $S_{\bullet }\text{CH}_{0}$ is independent of birational models or modular interpretations. Hence $S_{\bullet }\text{CH}_{0}$ is ‘intrinsic’ to $M=M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ as a moduli space of stable objects in the triangulated category $\mathbf{D}=D^{b}(X)$ .

Proposition 0.4. For any $(X^{\prime },\unicode[STIX]{x1D70E}^{\prime },\mathbf{v}^{\prime })$ such that $M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ is birational to $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ , the canonical isomorphism of Chow groups

$$\begin{eqnarray}\displaystyle \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))\xrightarrow[{}]{{\sim}}\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })) & & \displaystyle \nonumber\end{eqnarray}$$

preserves the filtration $S_{\bullet }\text{CH}_{0}$ .

In [Reference VoisinVoi16], Voisin proposed a filtration on $\text{CH}_{0}(M)$ for any holomorphic symplectic variety $M$ of dimension $2d$ . Given a (closed) point $x\in M$ , consider the orbit of $x$ under rational equivalence

$$\begin{eqnarray}\displaystyle O_{x}=\{x^{\prime }\in M:[x]=[x^{\prime }]\in \text{CH}_{0}(M)\}. & & \displaystyle \nonumber\end{eqnarray}$$

It is a countable union of constant cycle subvarieties.Footnote ⁷ We write $\dim O_{x}$ for the maximal dimension of these subvarieties. There is an increasing filtration

$$\begin{eqnarray}\displaystyle S_{0}^{V}\text{CH}_{0}(M) & \subset & \displaystyle S_{1}^{V}\text{CH}_{0}(M)\subset \cdots \subset S_{i}^{V}\text{CH}_{0}(M)\nonumber\\ \displaystyle & \subset & \displaystyle \cdots \subset S_{d}^{V}\text{CH}_{0}(M)=\text{CH}_{0}(M),\nonumber\end{eqnarray}$$

where $S_{i}^{V}\text{CH}_{0}(M)$ is the subgroup spanned by $[x]\in \text{CH}_{0}(M)$ for all $x\in M$ with $\dim O_{x}\geqslant d-i$ . Many questions around the filtration $S_{\bullet }^{V}\text{CH}_{0}(M)$ remain open, among which the existence of algebraically coisotropic subvarieties

where $Z_{i}$ is a subvariety of codimension $i$ and the general fibers of $q$ are constant cycle subvarieties (in  $M$ ) of dimension  $i$ .

The following result constructs such algebraically coisotropic varieties and connects the filtrations $S_{\bullet }\text{CH}_{0}(M)$ and $S_{\bullet }^{V}\text{CH}_{0}(M)$ in case $M=M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ . In particular, this verifies [Reference VoisinVoi16, Conjecture 0.4] when the holomorphic symplectic variety arises as a moduli space of stable objects in $D^{b}(X)$ .Footnote ⁸

0.5 Summary

We summarize the main themes of this paper by the following diagram.

1. (i) Theorem 0.1, i.e., O’Grady’s conjecture, provides a sheaf/cycle correspondence and lifts O’Grady’s filtration $S_{\bullet }(X)$ to $D^{b}(X)$ .

2. (ii) Conjecture 0.3, now proven in [Reference Marian and ZhaoMZ17], relates point classes on $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ to zero-cycles classes on  $X$ .

3. (iii) The lifted filtration $S_{\bullet }(D^{b}(X))$ in turn provides a natural candidate for the Beauville–Voisin filtration on $\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))$ , with many of the required properties.

In a sequel [Reference Shen and YinSY18] to this paper, we extend the picture above to more general $K3$ categories, especially Kuznetsov’s noncommutative $K3$ category associated to a nonsingular cubic 4-fold [Reference KuznetsovKuz10].

0.6 Conventions

Throughout, we work over the complex numbers  $\mathbb{C}$ . All varieties are assumed to be (quasi-)projective, and $K3$ surfaces are nonsingular and projective. Equivalences of triangulated categories are $\mathbb{C}$ -linear.

1.1 Preliminaries

We first list a few useful facts. Let $X$ be a $K3$ surface.

Corollary 1.2. Let

$$\begin{eqnarray}\displaystyle {\mathcal{F}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}\rightarrow {\mathcal{F}}[1] & & \displaystyle \nonumber\end{eqnarray}$$

be a distinguished triangle in $D^{b}(X)$ . If two of $c_{2}({\mathcal{E}}),c_{2}({\mathcal{F}}),c_{2}({\mathcal{G}})$ lie in $S_{i}(X)$ and $S_{i^{\prime }}(X)$ respectively, then the third lies in $S_{i+i^{\prime }}(X)$ .

Proof. By the distinguished triangle, we have

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})=c_{2}({\mathcal{F}})+c_{2}({\mathcal{G}})+D, & & \displaystyle \nonumber\end{eqnarray}$$

where $D$ is spanned by intersections of divisor classes. Hence $D\in S_{0}(X)$ by [Reference Beauville and VoisinBV04] and the statement follows immediately from Lemma 1.1.◻

We will need the following generalization of a lemma of Mukai [Reference MukaiMuk87, Corollary 2.8].

Lemma 1.3 [Reference Bayer and BridgelandBB17, Lemma 2.5].

Let

$$\begin{eqnarray}\displaystyle {\mathcal{F}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}\rightarrow {\mathcal{F}}[1] & & \displaystyle \nonumber\end{eqnarray}$$

be a distinguished triangle in $D^{b}(X)$ . If $\text{Hom}({\mathcal{F}},{\mathcal{G}})=0$ , then there is an inequality

$$\begin{eqnarray}\displaystyle d({\mathcal{F}})+d({\mathcal{G}})\leqslant d({\mathcal{E}}). & & \displaystyle \nonumber\end{eqnarray}$$

The following is a direct consequence of Corollary 1.2 and Lemma 1.3.

Proposition 1.4. Let

$$\begin{eqnarray}\displaystyle {\mathcal{F}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}\rightarrow {\mathcal{F}}[1] & & \displaystyle \nonumber\end{eqnarray}$$

be a distinguished triangle in $D^{b}(X)$ satisfying $\text{Hom}({\mathcal{F}},{\mathcal{G}})=0$ . If

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{F}})\in S_{d({\mathcal{F}})}(X)\quad \text{and}\quad c_{2}({\mathcal{G}})\in S_{d({\mathcal{G}})}(X), & & \displaystyle \nonumber\end{eqnarray}$$

then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

We also recall the theorems of Huybrechts and Voisin which serve as the starting point of our proof.

Theorem 1.5 ([Reference HuybrechtsHuy10, Theorem 1] and [Reference VoisinVoi15, Corollary 1.10]).

If ${\mathcal{E}}\in D^{b}(X)$ is spherical, i.e., $\text{Ext}^{\ast }({\mathcal{E}},{\mathcal{E}})=H^{\ast }(\mathbb{S}^{2},\mathbb{C})$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{0}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Theorem 1.6 [Reference VoisinVoi15, Theorem 1.9].

If ${\mathcal{E}}$ is a simple vector bundle on $X$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

1.2 Slope-stable sheaves

From now on, we fix a polarization $H$ on $X$ . The following proposition proves Theorem 0.1 for $\unicode[STIX]{x1D707}$ -stable sheaves.

Proposition 1.7. If ${\mathcal{E}}$ is torsion-free and $\unicode[STIX]{x1D707}$ -stable on $(X,H)$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. The double dual ${\mathcal{E}}^{\vee \vee }$ of ${\mathcal{E}}$ is locally free. There is a short exact sequence of sheaves

(1) $$\begin{eqnarray}0\rightarrow {\mathcal{E}}\rightarrow {\mathcal{E}}^{\vee \vee }\rightarrow {\mathcal{Q}}\rightarrow 0,\end{eqnarray}$$

where ${\mathcal{Q}}$ is a 0-dimensional sheaf whose support is of length  $l$ . A direct calculation yields $d({\mathcal{Q}})\geqslant l$ and

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{Q}})\in S_{l}(X)\subset S_{d({\mathcal{Q}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Now since ${\mathcal{E}}$ is $\unicode[STIX]{x1D707}$ -stable, the double dual ${\mathcal{E}}^{\vee \vee }$ is also $\unicode[STIX]{x1D707}$ -stable and hence simple. Applying Theorem 1.6, we find

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}}^{\vee \vee })\in S_{d({\mathcal{E}}^{\vee \vee })}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Consider (1) as a distinguished triangle

$$\begin{eqnarray}\displaystyle {\mathcal{Q}}[-1]\rightarrow {\mathcal{E}}\rightarrow {\mathcal{E}}^{\vee \vee }\rightarrow {\mathcal{Q}}. & & \displaystyle \nonumber\end{eqnarray}$$

Since ${\mathcal{Q}}$ is 0-dimensional and ${\mathcal{E}}^{\vee \vee }$ is locally free, we have

$$\begin{eqnarray}\displaystyle \text{Hom}({\mathcal{Q}}[-1],{\mathcal{E}}^{\vee \vee })=0. & & \displaystyle \nonumber\end{eqnarray}$$

Applying Proposition 1.4, we conclude that $c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X)$ .◻

We continue to treat sheaves which can be obtained as iterated extensions of $\unicode[STIX]{x1D707}$ -stable sheaves.

Proposition 1.8. Let ${\mathcal{F}}$ be torsion-free and $\unicode[STIX]{x1D707}$ -stable on $(X,H)$ . If ${\mathcal{E}}$ is an iterated extension of  ${\mathcal{F}}$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. Suppose ${\mathcal{E}}$ is an iterated extension of $m$ copies of ${\mathcal{F}}$ . Then we have

(2) $$\begin{eqnarray}c_{2}({\mathcal{E}})=c_{2}({\mathcal{F}}^{\oplus m})=mc_{2}({\mathcal{F}})+D,\end{eqnarray}$$

where $D$ is spanned by intersections of divisor classes and hence lies in  $S_{0}(X)$ . Combining Lemma 1.1 and Proposition 1.7, we find

(3) $$\begin{eqnarray}c_{2}({\mathcal{E}})\in S_{d({\mathcal{F}})}(X).\end{eqnarray}$$

If ${\mathcal{F}}$ is spherical, i.e., $v({\mathcal{F}})^{2}=-2$ , then $c_{2}({\mathcal{F}})\in S_{0}(X)$ by Theorem 1.5. By (2), we see that $c_{2}({\mathcal{E}})\in S_{0}(X)$ , and hence the statement holds.

We may focus on the case $v({\mathcal{F}})^{2}\geqslant 0$ . Then we have

$$\begin{eqnarray}\displaystyle 2d({\mathcal{E}}) & = & \displaystyle v({\mathcal{E}})^{2}+2\dim \text{Hom}({\mathcal{E}},{\mathcal{E}})\nonumber\\ \displaystyle & = & \displaystyle m^{2}v({\mathcal{F}})^{2}+2\dim \text{Hom}({\mathcal{E}},{\mathcal{E}})\nonumber\\ \displaystyle & {\geqslant} & \displaystyle v({\mathcal{F}})^{2}+2\nonumber\\ \displaystyle & = & \displaystyle 2d({\mathcal{F}}),\nonumber\end{eqnarray}$$

where we use that ${\mathcal{F}}$ is simple in the last equality. In this case the proposition follows from (3).◻

1.3 Torsion-free sheaves

The next step is to prove Theorem 0.1 for arbitrary torsion-free sheaves.

The following proposition provides a nice splitting of a $\unicode[STIX]{x1D707}$ -semistable vector bundle.

Proposition 1.9. Let ${\mathcal{E}}$ be a $\unicode[STIX]{x1D707}$ -semistable vector bundle on $(X,H)$ . There exists a short exact sequence of sheaves

(4) $$\begin{eqnarray}0\rightarrow {\mathcal{M}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}\rightarrow 0\end{eqnarray}$$

with the following properties:

1. (i) the sheaf ${\mathcal{M}}$ is an iterated extension of a $\unicode[STIX]{x1D707}$ -stable vector bundle ${\mathcal{F}}$ ;

2. (ii) the quotient sheaf ${\mathcal{G}}$ is torsion-free;

3. (iii) we have $\text{Hom}({\mathcal{M}},{\mathcal{G}})=0$ .

Proof. We only need to consider the case when ${\mathcal{E}}$ is not $\unicode[STIX]{x1D707}$ -stable. First, we can always find a $\unicode[STIX]{x1D707}$ -stable sub-vector bundle ${\mathcal{F}}\subset {\mathcal{E}}$ with $\unicode[STIX]{x1D707}({\mathcal{F}})=\unicode[STIX]{x1D707}({\mathcal{E}})$ .

The construction goes as follows. Let ${\mathcal{F}}_{0}$ be any $\unicode[STIX]{x1D707}$ -stable subsheaf of ${\mathcal{E}}$ with $\unicode[STIX]{x1D707}({\mathcal{F}}_{0})=\unicode[STIX]{x1D707}({\mathcal{E}})$ . The double dual ${\mathcal{F}}={\mathcal{F}}_{0}^{\vee \vee }$ is both $\unicode[STIX]{x1D707}$ -stable (of the same slope) and locally free, which admits a nontrivial map

$$\begin{eqnarray}\displaystyle i:{\mathcal{F}}={\mathcal{F}}_{0}^{\vee \vee }\rightarrow {\mathcal{E}}^{\vee \vee }={\mathcal{E}}. & & \displaystyle \nonumber\end{eqnarray}$$

The map $i$ is injective according to the stability condition. Hence we obtain a short exact sequence of sheaves

(5) $$\begin{eqnarray}0\rightarrow {\mathcal{F}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}_{0}\rightarrow 0.\end{eqnarray}$$

Claim. The quotient sheaf ${\mathcal{G}}_{0}$ is torsion-free and $\unicode[STIX]{x1D707}$ -semistable.

Proof of the Claim.

The stability condition ensures that the torsion part of ${\mathcal{G}}_{0}$ is at most 0-dimensional. Now assume that there is a short exact sequence of sheaves

$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{T}}\rightarrow {\mathcal{G}}_{0}\rightarrow {\mathcal{G}}_{0}^{F}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$

with ${\mathcal{T}}$ a nontrivial 0-dimensional sheaf and ${\mathcal{G}}_{0}^{F}$ torsion-free. We have a surjective map ${\mathcal{E}}\rightarrow {\mathcal{G}}_{0}^{F}$ given by ${\mathcal{E}}\rightarrow {\mathcal{G}}_{0}\rightarrow {\mathcal{G}}_{0}^{F}$ with kernel  ${\mathcal{F}}^{\prime }$ . It follows that ${\mathcal{F}}^{\prime }$ is a nontrivial extension of the 0-dimensional sheaf ${\mathcal{T}}$ by the vector bundle  ${\mathcal{F}}$ , which is a contradiction. This shows that ${\mathcal{G}}_{0}$ is torsion-free.

Since $\unicode[STIX]{x1D707}({\mathcal{G}}_{0})=\unicode[STIX]{x1D707}({\mathcal{F}})$ , the $\unicode[STIX]{x1D707}$ -semistability follows from a standard argument by considering quotients of ${\mathcal{G}}_{0}$ and comparing slopes.◻

If $\text{Hom}({\mathcal{F}},{\mathcal{G}}_{0})=0$ , then we are done by setting ${\mathcal{M}}={\mathcal{F}}$ and ${\mathcal{G}}={\mathcal{G}}_{0}$ , and (5) gives the desired exact sequence. Otherwise, there exists a nontrivial map

$$\begin{eqnarray}\displaystyle i_{1}:{\mathcal{F}}\rightarrow {\mathcal{G}}_{0}, & & \displaystyle \nonumber\end{eqnarray}$$

which must be injective according to the stability condition. We define ${\mathcal{G}}_{1}$ to be the quotient ${\mathcal{G}}_{0}/{\mathcal{F}}$ . The same argument as in the Claim implies that ${\mathcal{G}}_{1}$ is torsion-free and $\unicode[STIX]{x1D707}$ -semistable. Hence we obtain a short exact sequence of sheaves

$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{F}}_{1}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}_{1}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$

where ${\mathcal{F}}_{1}$ is a self-extension of ${\mathcal{F}}$ .

If $\text{Hom}({\mathcal{F}}_{1},{\mathcal{G}}_{1})\neq 0$ , we can continue this process until we reach the desired exact sequence (4).◻

Remark 1.10. One may expect a similar splitting for any $\unicode[STIX]{x1D707}$ -semistable sheaf via the Jordan–Hölder filtration (for slope stability). However, the difficulty is that there exist nontrivial morphisms between nonisomorphic $\unicode[STIX]{x1D707}$ -stable sheaves with the same slope. For example, there is the inclusion

$$\begin{eqnarray}\displaystyle {\mathcal{I}}_{Z}{\hookrightarrow}{\mathcal{O}}_{X} & & \displaystyle \nonumber\end{eqnarray}$$

with ${\mathcal{I}}_{Z}$ the ideal sheaf of a 0-dimensional subscheme $Z\subset X$ . Here we use a $\unicode[STIX]{x1D707}$ -stable locally free factor ${\mathcal{F}}$ to avoid this trouble.

Proposition 1.11. If ${\mathcal{E}}$ is a torsion-free sheaf on $X$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. We proceed by induction on the rank of ${\mathcal{E}}$ . If $\text{rank}({\mathcal{E}})=1$ , then ${\mathcal{E}}$ is $\unicode[STIX]{x1D707}$ -stable, and Proposition 1.7 gives the base case of the induction.

Now assume that ${\mathcal{E}}$ is torsion-free of rank $r>0$ . If ${\mathcal{E}}$ is not $\unicode[STIX]{x1D707}$ -semistable, then by the Harder–Narasimhan filtration (for slope stability), we have a short exact sequence of sheaves

$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{F}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}\rightarrow 0. & & \displaystyle \nonumber\end{eqnarray}$$

Here ${\mathcal{F}}$ and ${\mathcal{G}}$ are nonzero and torsion-free, and the slope of every $\unicode[STIX]{x1D707}$ -stable factor of ${\mathcal{F}}$ is greater than the slope of any $\unicode[STIX]{x1D707}$ -stable factor of  ${\mathcal{G}}$ . In particular, we have $\text{rank}({\mathcal{F}})<\text{rank}({\mathcal{E}})$ , $\text{rank}({\mathcal{G}})<\text{rank}({\mathcal{E}})$ , and $\text{Hom}({\mathcal{F}},{\mathcal{G}})=0$ . The induction hypothesis yields

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{F}})\in S_{d({\mathcal{F}})}(X)\quad \text{and}\quad c_{2}({\mathcal{G}})\in S_{d({\mathcal{G}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Applying Proposition 1.4, we find $c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X)$ .

It remains to treat the case when ${\mathcal{E}}$ is $\unicode[STIX]{x1D707}$ -semistable. By the same argument as in Proposition 1.7, it suffices to prove Theorem 0.1 for ${\mathcal{E}}^{\vee \vee }$ , which is a $\unicode[STIX]{x1D707}$ -semistable locally free sheaf satisfying $\text{rank}({\mathcal{E}})=\text{rank}({\mathcal{E}}^{\vee \vee })$ .

Hence we may assume ${\mathcal{E}}$ to be $\unicode[STIX]{x1D707}$ -semistable and locally free. We apply Proposition 1.9 to  ${\mathcal{E}}$ . Either ${\mathcal{E}}$ is an iterated extension of some $\unicode[STIX]{x1D707}$ -stable sheaf  ${\mathcal{F}}$ , or the extension (4) is nontrivial. In the first case, the statement of the proposition holds by Proposition 1.8. In the second case, the induction hypothesis and Proposition 1.4 complete the proof.◻

1.4 Torsion sheaves

Theorem 0.1 for torsion sheaves is essentially proven in [Reference O’GradyO’Gr13]. We begin by recalling the following criterion of O’Grady.

Lemma 1.12 [Reference O’GradyO’Gr13, Claim 0.2].

Let $C$ be an irreducible nonsingular curve of genus $g$ , and let $f:C\rightarrow X$ be a nonconstant map. Then

$$\begin{eqnarray}\displaystyle f_{\ast }\text{CH}_{0}(C)\subset S_{g}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Let ${\mathcal{E}}$ be a pure 1-dimensional torsion sheaf on $X$ with Mukai vector

$$\begin{eqnarray}\displaystyle v({\mathcal{E}})=(0,l,s)\in H^{0}(X,\mathbb{Z})\oplus H^{2}(X,\mathbb{Z})\oplus H^{4}(X,\mathbb{Z}). & & \displaystyle \nonumber\end{eqnarray}$$

By Lemma 1.12, we have at worst

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{g}(X), & & \displaystyle \nonumber\end{eqnarray}$$

where $g=\frac{1}{2}l^{2}+1$ is the arithmetic genus of the support curve of  ${\mathcal{E}}$ .

On the other hand, we find

$$\begin{eqnarray}\displaystyle d({\mathcal{E}})={\textstyle \frac{1}{2}}v({\mathcal{E}})^{2}+\dim \text{Hom}({\mathcal{E}},{\mathcal{E}})\geqslant {\textstyle \frac{1}{2}}l^{2}+1=g. & & \displaystyle \nonumber\end{eqnarray}$$

Hence for any pure 1-dimensional sheaf ${\mathcal{E}}$ , we have $c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X)$ .

Now we can prove Theorem 0.1 for arbitrary sheaves.

Proposition 1.13. If ${\mathcal{E}}$ is a coherent sheaf on $X$ , then

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. Given a torsion sheaf ${\mathcal{T}}$ , there is a short exact sequence of sheaves

$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{T}}_{0}\rightarrow {\mathcal{T}}\rightarrow {\mathcal{T}}_{1}\rightarrow 0, & & \displaystyle \nonumber\end{eqnarray}$$

where ${\mathcal{T}}_{0}$ is 0-dimensional and ${\mathcal{T}}_{1}$ is pure and 1-dimensional. Clearly

$$\begin{eqnarray}\displaystyle \text{Hom}({\mathcal{T}}_{0},{\mathcal{T}}_{1})=0. & & \displaystyle \nonumber\end{eqnarray}$$

By the discussion above, we have

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{T}}_{0})\in S_{d({\mathcal{T}}_{0})}(X)\quad \text{and}\quad c_{2}({\mathcal{T}}_{1})\in S_{d({\mathcal{T}}_{1})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Applying Proposition 1.4, we find $c_{2}({\mathcal{T}})\in S_{d({\mathcal{T}})}(X)$ which proves the statement for torsion sheaves.

Let ${\mathcal{E}}$ be an arbitrary sheaf. There is a short exact sequence of sheaves

$$\begin{eqnarray}\displaystyle 0\rightarrow {\mathcal{T}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{F}}\rightarrow 0 & & \displaystyle \nonumber\end{eqnarray}$$

with ${\mathcal{T}}$ torsion and ${\mathcal{F}}$ torsion-free. In particular, we have $\text{Hom}({\mathcal{T}},{\mathcal{F}})=0$ . Since the statement of the proposition holds for both ${\mathcal{T}}$ and ${\mathcal{F}}$ , we conclude by Proposition 1.4 that $c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X)$ .◻

1.5 Proof of Theorem 0.1 and Corollary 0.2

Given a bounded complex ${\mathcal{E}}\in D^{b}(X)$ , we define its length by

$$\begin{eqnarray}\displaystyle \ell ({\mathcal{E}})=\max \{|i-j|:h^{i}({\mathcal{E}})\neq 0,h^{j}({\mathcal{E}})\neq 0\}. & & \displaystyle \nonumber\end{eqnarray}$$

Clearly $\ell ({\mathcal{E}})=0$ if and only if ${\mathcal{E}}$ is a (shifted) sheaf.

Proof of Theorem 0.1.

We proceed by induction on $\ell ({\mathcal{E}})$ . Proposition 1.13 provides the base case of the induction.

Now consider a bounded complex ${\mathcal{E}}\in D^{b}(X)$ . Let $m$ be the largest integer such that $h^{m}({\mathcal{E}})\neq 0$ . There is a standard distinguished triangle

$$\begin{eqnarray}\displaystyle {\mathcal{F}}\rightarrow {\mathcal{E}}\rightarrow {\mathcal{G}}\rightarrow {\mathcal{F}}[1]. & & \displaystyle \nonumber\end{eqnarray}$$

Here ${\mathcal{G}}$ is the shifted sheaf $h^{m}({\mathcal{E}})[-m]$ and ${\mathcal{F}}\in D^{b}(X)$ is the truncated complex $\unicode[STIX]{x1D70F}^{{\leqslant}m-1}{\mathcal{E}}$ which satisfies

$$\begin{eqnarray}\displaystyle \ell ({\mathcal{F}})<\ell ({\mathcal{E}}). & & \displaystyle \nonumber\end{eqnarray}$$

By the induction hypothesis, we have

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{F}})\in S_{d({\mathcal{F}})}(X)\quad \text{and}\quad c_{2}({\mathcal{G}})\in S_{d({\mathcal{G}})}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Since ${\mathcal{F}}$ is concentrated in degrees ${<}m$ and ${\mathcal{G}}$ in degree  $m$ , we have $\text{Hom}({\mathcal{F}},{\mathcal{G}})=0$ . Applying Proposition 1.4, we find $c_{2}({\mathcal{E}})\in S_{d({\mathcal{E}})}(X)$ . The proof of Theorem 0.1 is complete.◻

Let $X$ and $X^{\prime }$ be two $K3$ surfaces. Suppose there is a derived equivalence

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:D^{b}(X)\xrightarrow[{}]{{\sim}}D^{b}(X^{\prime }) & & \displaystyle \nonumber\end{eqnarray}$$

with Fourier–Mukai kernel ${\mathcal{F}}\in D^{b}(X\times X^{\prime })$ . The induced isomorphism of (ungraded) Chow groups

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\text{CH}}:\text{CH}^{\ast }(X)\xrightarrow[{}]{{\sim}}\text{CH}^{\ast }(X^{\prime }) & & \displaystyle \nonumber\end{eqnarray}$$

is given by the correspondenceFootnote ⁹

$$\begin{eqnarray}\displaystyle v^{\text{CH}}({\mathcal{F}})=\text{ch}({\mathcal{F}})\sqrt{\text{td}_{X\times X^{\prime }}}\in \text{CH}^{\ast }(X\times X^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

Recall the following theorem of Huybrechts and Voisin.

Proof of Corollary 0.2.

Since $\unicode[STIX]{x1D6F7}$ is a derived equivalence, we only need to prove that

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}^{\text{CH}}(\widetilde{S}_{i}(X))\subset \widetilde{S}_{i}(X^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

Since $\unicode[STIX]{x1D6F7}^{\text{CH}}$ preserves the Beauville–Voisin ring by Theorem 1.14, it suffices to show that for any effective zero-cycle $z=x_{1}+\cdots +x_{i}$ , we have

(6) $$\begin{eqnarray}\unicode[STIX]{x1D6F7}^{\text{CH}}([z])\in \widetilde{S}_{i}(X^{\prime }).\end{eqnarray}$$

Further, we may assume $x_{1},\ldots ,x_{i}$ distinct, since multiplicities result in $[z]\in S_{i^{\prime }}(X)$ for some $i^{\prime }<i$ .

Let ${\mathcal{E}}$ be the direct sum of skyscraper sheaves

$$\begin{eqnarray}\displaystyle \mathbb{C}_{x_{1}}\oplus \cdots \oplus \mathbb{C}_{x_{i}}. & & \displaystyle \nonumber\end{eqnarray}$$

Then $c_{2}({\mathcal{E}})=[z]$ and $d(\unicode[STIX]{x1D6F7}({\mathcal{E}}))=d({\mathcal{E}})=i$ . Applying Theorem 0.1, we find

$$\begin{eqnarray}\displaystyle c_{2}(\unicode[STIX]{x1D6F7}({\mathcal{E}}))\in S_{i}(X^{\prime }), & & \displaystyle \nonumber\end{eqnarray}$$

which implies (6). ◻

2.1 Independence of modular interpretations

The proof of Proposition 0.4 uses Bayer and Macrì’s work [Reference Bayer and MacrìBM14a, Reference Bayer and MacrìBM14b] on the birational transforms of moduli spaces of stable objects.

Let $X$ be a $K3$ surface. Recall that given a primitive Mukai vectorFootnote ¹⁰   $\mathbf{v}$ with $\mathbf{v}^{2}>0$ , and a generic stability condition $\unicode[STIX]{x1D70E}\in \text{Stab}^{\dagger }(X)$ with respect to  $\mathbf{v}$ , there is a moduli space $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ of $\unicode[STIX]{x1D70E}$ -stable objects in $D^{b}(X)$ .

Bayer and Macrì realized all holomorphic symplectic birational models of  $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ as other moduli spaces of stable objects. Their following theorem describes the procedure concretely.

Theorem 2.1 [Reference Bayer and MacrìBM14a, Corollary 1.3].

With the notation above, let $(X^{\prime },\unicode[STIX]{x1D70E}^{\prime },\mathbf{v}^{\prime })$ be another triple. The moduli spaces $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ and $M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ are birational if and only if there exists a derived (anti-)equivalence

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:D^{b}(X)\xrightarrow[{}]{{\sim}}D^{b}(X^{\prime }) & & \displaystyle \nonumber\end{eqnarray}$$

which sends $\mathbf{v}$ to $\mathbf{v}^{\prime }$ and induces an isomorphism

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}:U\xrightarrow[{}]{{\sim}}U^{\prime } & & \displaystyle \nonumber\end{eqnarray}$$

between two nonempty open subsets $U\subset M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ and $U^{\prime }\subset M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ .Footnote ¹¹

It is well known that the $\text{CH}_{0}$ -group is invariant under birational transforms of nonsingular projective varieties.Footnote ¹² The statement can be made slightly more precise.

Lemma 2.2. Let $f:V{\dashrightarrow}V^{\prime }$ be a birational map between nonsingular projective varieties, and let

$$\begin{eqnarray}\displaystyle f_{\ast }:\text{CH}_{0}(V)\xrightarrow[{}]{{\sim}}\text{CH}_{0}(V^{\prime }) & & \displaystyle \nonumber\end{eqnarray}$$

be the induced isomorphism of Chow groups. Then for any point $x\in V$ , there exists a point $x^{\prime }\in V^{\prime }$ such that

$$\begin{eqnarray}\displaystyle [x^{\prime }]=f_{\ast }([x])\in \text{CH}_{0}(V^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. Consider a resolution

with $\widetilde{V}$ nonsingular and projective. Then $f_{\ast }$ is realized as $q_{\ast }p^{\ast }$ . By weak factorization, both $p$ and $q$ can be taken a sequence of blow-ups and blow-downs with nonsingular centers. We are reduced to the case of a blow-up, for which the statement is obvious.◻

Let $(X,\unicode[STIX]{x1D70E},\mathbf{v})$ and $(X^{\prime },\unicode[STIX]{x1D70E}^{\prime },\mathbf{v}^{\prime })$ be such that $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ and $M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ are birational. By Theorem 2.1, a derived (anti-)equivalence

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F7}:D^{b}(X)\xrightarrow[{}]{{\sim}}D^{b}(X^{\prime }) & & \displaystyle \nonumber\end{eqnarray}$$

induces a birational map

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6F4}:M_{\unicode[STIX]{x1D70E}}(\mathbf{v}){\dashrightarrow}M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime }), & & \displaystyle \nonumber\end{eqnarray}$$

which identifies two nonempty open subsets $U\subset M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ and $U^{\prime }\subset M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ . By further composing with $R{\mathcal{H}}om(-,{\mathcal{O}}_{X})$ , we may assume that $\unicode[STIX]{x1D6F7}$ is a derived equivalence.

Let ${\mathcal{E}}$ be an object in $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ . By Lemma 2.2, there exists an object ${\mathcal{F}}$ in $M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ such that

(7) $$\begin{eqnarray}[{\mathcal{F}}]=\unicode[STIX]{x1D6F4}_{\ast }([{\mathcal{E}}])\in \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })).\end{eqnarray}$$

Lemma 2.3. With the notation above, for any pair of objects ${\mathcal{E}}\in M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ and ${\mathcal{F}}\in M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ satisfying (7), we haveFootnote ¹³

$$\begin{eqnarray}\displaystyle v^{\text{CH}}({\mathcal{F}})=\unicode[STIX]{x1D6F7}^{\text{CH}}(v^{\text{CH}}({\mathcal{E}}))\in \text{CH}^{\ast }(X^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

Proof. Since any class in $\text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v}))$ is supported on  $U$ , we may write

$$\begin{eqnarray}\displaystyle [{\mathcal{E}}]=\mathop{\sum }_{j}a_{j}[{\mathcal{E}}_{j}]\in \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}}(\mathbf{v})) & & \displaystyle \nonumber\end{eqnarray}$$

for some ${\mathcal{E}}_{j}\in U$ . Using the (quasi-)universal family on $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})\times X$ , we have

(8) $$\begin{eqnarray}v^{\text{CH}}({\mathcal{E}})=\mathop{\sum }_{j}a_{j}v^{\text{CH}}({\mathcal{E}}_{j})\in \text{CH}^{\ast }(X).\end{eqnarray}$$

On the other hand, it is clear from the definition that

$$\begin{eqnarray}\displaystyle [{\mathcal{F}}]=\mathop{\sum }_{j}a_{j}[\unicode[STIX]{x1D6F4}({\mathcal{E}}_{j})]=\mathop{\sum }_{j}a_{j}[\unicode[STIX]{x1D6F7}({\mathcal{E}}_{j})]\in \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })). & & \displaystyle \nonumber\end{eqnarray}$$

Again using the (quasi-)universal family on $M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })\times X^{\prime }$ , we have

(9) $$\begin{eqnarray}v^{\text{CH}}({\mathcal{F}})=\mathop{\sum }_{j}a_{j}v^{\text{CH}}(\unicode[STIX]{x1D6F7}({\mathcal{E}}_{j}))\in \text{CH}^{\ast }(X^{\prime }).\end{eqnarray}$$

Combining (8) and (9) and using the commutative diagram

we find

$$\begin{eqnarray}\displaystyle v^{\text{CH}}({\mathcal{F}})=\unicode[STIX]{x1D6F7}^{\text{CH}}\biggl(\mathop{\sum }_{j}a_{j}v^{\text{CH}}({\mathcal{E}}_{j})\biggr)=\unicode[STIX]{x1D6F7}^{\text{CH}}(v^{\text{CH}}({\mathcal{E}}))\in \text{CH}^{\ast }(X^{\prime }).\Box & & \displaystyle \nonumber\end{eqnarray}$$

Proof of Proposition 0.4.

Let ${\mathcal{E}}$ be an object in $M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ such that

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{i}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Equivalently, we have

$$\begin{eqnarray}\displaystyle v^{\text{CH}}({\mathcal{E}})\in \widetilde{S}_{i}(X). & & \displaystyle \nonumber\end{eqnarray}$$

By Lemma 2.2, there exist an object ${\mathcal{F}}$ in $M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })$ satisfying

$$\begin{eqnarray}\displaystyle [{\mathcal{F}}]=\unicode[STIX]{x1D6F4}_{\ast }([{\mathcal{E}}])\in \text{CH}_{0}(M_{\unicode[STIX]{x1D70E}^{\prime }}(\mathbf{v}^{\prime })). & & \displaystyle \nonumber\end{eqnarray}$$

Applying Lemma 2.3, we find

$$\begin{eqnarray}\displaystyle v^{\text{CH}}({\mathcal{F}})=\unicode[STIX]{x1D6F7}^{\text{CH}}(v^{\text{CH}}({\mathcal{E}}))\in \text{CH}^{\ast }(X^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

Since $\unicode[STIX]{x1D6F7}^{\text{CH}}$ preserves the filtration $\widetilde{S}_{\bullet }$ by Corollary 0.2, we conclude that

$$\begin{eqnarray}\displaystyle v^{\text{CH}}({\mathcal{F}})\in \widetilde{S}_{i}(X^{\prime }), & & \displaystyle \nonumber\end{eqnarray}$$

or equivalently,

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{F}})\in S_{i}(X^{\prime }). & & \displaystyle \nonumber\end{eqnarray}$$

The proposition then follows from the definition of $S_{\bullet }\text{CH}_{0}$ .◻

2.2 The Beauville–Voisin filtration

As stated in Theorem 0.5, we compare two proposed filtrations on the $\text{CH}_{0}$ -group of a moduli space of stable objects.

Let $X$ be a $K3$ surface, let $M=M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ be a moduli space of stable objects in $D^{b}(X)$ of dimension $2d=2d(\mathbf{v})$ , and let $X^{[d]}$ be the Hilbert scheme of $d$ points on  $X$ . Consider the incidence variety

$$\begin{eqnarray}\displaystyle R=\{({\mathcal{E}},\unicode[STIX]{x1D709})\in M\times X^{[d]}:c_{2}({\mathcal{E}})=[\text{Supp}(\unicode[STIX]{x1D709})]+c[o_{X}]\in \text{CH}_{0}(X)\}, & & \displaystyle \nonumber\end{eqnarray}$$

where $\text{Supp}(\unicode[STIX]{x1D709})$ is the support of $\unicode[STIX]{x1D709}$ and $c\in \mathbb{Z}$ is a constant determined by the Mukai vector $\mathbf{v}$ . This incidence variety has already appeared in [Reference O’GradyO’Gr13, Reference VoisinVoi15].

A standard argument using Hilbert schemes shows that $R$ is a countable union of Zariski-closed subsets of $M\times X^{[d]}$ . Let

$$\begin{eqnarray}\displaystyle p_{M}:R\rightarrow M\quad \text{and}\quad p_{X^{[d]}}:R\rightarrow X^{[d]} & & \displaystyle \nonumber\end{eqnarray}$$

denote the two projections. By (the now proven) Conjecture 0.3 for $X^{[d]}$ or an explicit calculation, all points on the same fiber of $p_{M}$ have the same class in $\text{CH}_{0}(X^{[d]})$ . Similarly, by Conjecture 0.3 for  $M$ , all points on the same fiber of $p_{X^{[d]}}$ have the same class in $\text{CH}_{0}(M)$ .

An important consequence of Theorem 0.1 is that $p_{M}$ is dominant. Then, by the argument in [Reference O’GradyO’Gr13, Proposition 1.3] (see also [Reference VoisinVoi15, Corollary 3.4]), we also know that $p_{X^{[d]}}$ is dominant. More precisely, there exists a component $R_{0}\subset R$ which dominates both $M$ and  $X^{[d]}$ . Note that  $M$ and $X^{[d]}$ have the same dimension.

Further, up to taking hyperplane sections,Footnote ¹⁴ we may assume that $R_{0}$ is generically finite over both $M$ and  $X^{[d]}$ . To summarize, we have a diagram

(10)

where $U\subset M$ and $V\subset X^{[d]}$ are nonempty open subsets over which $p_{M}$ and $p_{X^{[d]}}$ are finite.

We recall two density results on $X$ and $X^{[d]}$ .

Proof of Theorem 0.5.

Given $d-i$ constant cycle curves in $X$ labeled as $C_{i+1},C_{i+2},\ldots ,C_{d}$ , we consider the rational map

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D719}:X^{[i]}\times C_{i+1}\times C_{i+2}\times \cdots \times C_{d}{\dashrightarrow}X^{[d]} & & \displaystyle \nonumber\end{eqnarray}$$

which (generically) sums up the points on the factors. By Lemma 2.4, the union of $\text{Im}(\unicode[STIX]{x1D719})$ for all choices of constant cycles curves is Zariski-dense in  $X^{[d]}$ . In particular, there exists such $\unicode[STIX]{x1D719}$ whose image meets $V\subset X^{[d]}$ .

Let $\unicode[STIX]{x1D719}^{\prime }:Z{\dashrightarrow}R_{0}$ denote the pull-back of $\unicode[STIX]{x1D719}$ via $p_{X^{[d]}}$ .Footnote ¹⁵ We have the following diagram.

Again by Lemma 2.4, we may assume that $\unicode[STIX]{x1D719}^{\prime }(Z)$ meets $p_{M}^{-1}(U)\subset R_{0}$ .

Let $q:Z{\dashrightarrow}X^{[i]}$ denote the composition of $p^{\prime }$ and the projection to  $X^{[i]}$ . For a general point $\unicode[STIX]{x1D709}\in X^{[i]}$ , consider the fiber $Z_{\unicode[STIX]{x1D709}}\subset Z$ . By construction, the image

$$\begin{eqnarray}\displaystyle p_{M}(\unicode[STIX]{x1D719}^{\prime }(Z_{\unicode[STIX]{x1D709}}))\subset M & & \displaystyle \nonumber\end{eqnarray}$$

consists of objects in $M$ with constant second Chern class. By (the now proven) Conjecture 0.3, this gives a constant cycle subvariety in  $M$ . The dimension of $p_{M}(\unicode[STIX]{x1D719}^{\prime }(Z_{\unicode[STIX]{x1D709}}))$ is $d-i$ since $p_{M}$ and $p_{X^{[d]}}$ are finite over $U$ and  $V$ .

We have shown that the image $p_{M}(\unicode[STIX]{x1D719}^{\prime }(Z))$ is generically covered by constant cycle subvarieties of dimension $d-i$ . We conclude by [Reference VoisinVoi16, Theorem 0.7] that $p_{M}(\unicode[STIX]{x1D719}^{\prime }(Z))$ is algebraically coisotropic of codimension  $d-i$ with constant cycle fibers. This proves part (i) of the theorem.

For part (ii), let ${\mathcal{E}}$ be an object in $M$ such that $c_{2}({\mathcal{E}})\in S_{i}(X)$ . By definition, there exists a point $\unicode[STIX]{x1D709}_{0}\in X^{[i]}$ satisfying

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})=[\text{Supp}(\unicode[STIX]{x1D709}_{0})]+(d-i)[o_{X}]+c[o_{X}]\in \text{CH}_{0}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Applying Lemma 2.5 to $\unicode[STIX]{x1D709}_{0}\in X^{[i]}$ , we may further assume that $p_{M}(\unicode[STIX]{x1D719}^{\prime }(Z_{\unicode[STIX]{x1D709}_{0}}))$ is well defined and is of dimension $d-i$ .

By construction, the subvariety $p_{M}(\unicode[STIX]{x1D719}^{\prime }(Z_{\unicode[STIX]{x1D709}_{0}}))$ consists of objects in $M$ whose second Chern class equals $c_{2}({\mathcal{E}})$ . By Conjecture 0.3, it is a subvariety of dimension $d-i$ in the orbit $O_{{\mathcal{E}}}\subset M$ . We conclude that $[{\mathcal{E}}]\in S_{i}^{V}\text{CH}_{0}(M)$ , which proves part (ii) of the theorem.◻

Remark 2.6. Our proof relies on the Zariski density of subvarieties of maximal dimension in an orbit of  $X^{[d]}$ . If one could prove such density for  $M$ , then an argument using [Reference VoisinVoi15, Theorem 2.1] would yield the other inclusion

$$\begin{eqnarray}\displaystyle S_{i}^{V}\text{CH}_{0}(M)\subset S_{i}\text{CH}_{0}(M). & & \displaystyle \nonumber\end{eqnarray}$$

3.1 The dimension $2$ case

In § 2, we focused on the Beauville–Voisin filtration for moduli spaces of dimension $2d(\mathbf{v})=\mathbf{v}^{2}+2>2$ . We discuss here the case $\mathbf{v}^{2}=0$ .

When $\mathbf{v}\in H^{\ast }(X,\mathbb{Z})$ is a primitive Mukai vector satisfying $\mathbf{v}^{2}=0$ , and $\unicode[STIX]{x1D70E}$ is a generic stability condition, the corresponding moduli space $M=M_{\unicode[STIX]{x1D70E}}(\mathbf{v})$ is a $K3$ surface. Although the Beauville–Voisin filtration on $\text{CH}_{0}(M)$ is clear by [Reference Beauville and VoisinBV04], its compatibility with the filtration on $\mathbf{D}=D^{b}(X)$ is not obvious.

If $M$ is a fine moduli space, then the universal family induces a derived equivalence

$$\begin{eqnarray}\displaystyle D^{b}(M)\xrightarrow[{}]{{\sim}}D^{b}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Theorem 1.14 shows that the corresponding isomorphism of Chow groups

$$\begin{eqnarray}\displaystyle \text{CH}^{\ast }(M)\xrightarrow[{}]{{\sim}}\text{CH}^{\ast }(X) & & \displaystyle \nonumber\end{eqnarray}$$

preserves the Beauville–Voisin ring. In particular, the canonical class $[o_{M}]\in \text{CH}_{0}(M)$ is represented by any object ${\mathcal{E}}\in M$ with $c_{2}({\mathcal{E}})\in \mathbb{Z}\cdot [o_{X}]$ . The Beauville–Voisin filtration $S_{\bullet }\text{CH}_{0}(M)$ indeed comes from the restriction of the filtration $S_{\bullet }(\mathbf{D})$ on the derived category.

If $M$ is not a fine moduli space, then $D^{b}(X)$ is equivalent to a derived category of twisted sheaves on  $M$ ,

$$\begin{eqnarray}\displaystyle D^{b}(M,\unicode[STIX]{x1D6FC})\xrightarrow[{}]{{\sim}}D^{b}(X). & & \displaystyle \nonumber\end{eqnarray}$$

Recently, Huybrechts showed in [Reference HuybrechtsHuy19, Corollary 2.2] that the universal twisted family induces an isomorphism of Chow groups

(11) $$\begin{eqnarray}\text{CH}^{\ast }(M)_{\mathbb{ Q}}\xrightarrow[{}]{{\sim}}\text{CH}^{\ast }(X)_{\mathbb{ Q}}.\end{eqnarray}$$

In this case, we also expect (11) to preserve the Beauville–Voisin ring. More generally, we ask the following question.Footnote ¹⁶

One may also ask the same question for arbitrary pairs of twisted $K3$ surfaces which are derived equivalent.

3.2 More on the Beauville–Voisin filtration

Let $M$ be a moduli space of stable objects in $D^{b}(X)$ as in § 2. Recall the filtration $S_{\bullet }\text{CH}_{0}(M)$ , where $S_{i}\text{CH}_{0}(M)$ is the subgroup spanned by the classes of ${\mathcal{E}}\in M$ satisfying $c_{2}({\mathcal{E}})\in S_{i}(X)$ . The following question asks for more precision.

Question 3.2. For an object ${\mathcal{E}}\in M$ , is it true that

$$\begin{eqnarray}\displaystyle [{\mathcal{E}}]\in S_{i}\text{CH}_{0}(M) & & \displaystyle \nonumber\end{eqnarray}$$

if and only if

$$\begin{eqnarray}\displaystyle c_{2}({\mathcal{E}})\in S_{i}(X)? & & \displaystyle \nonumber\end{eqnarray}$$

By (the proof of) Proposition 0.4, the answer to Question 3.2 is independent of birational models or modular interpretations.

Question 3.2 for the Hilbert schemes of points on $X$ alone has an interesting interpretation. Let $\unicode[STIX]{x1D6FE}\in \text{CH}_{0}(X)$ be a zero-cycle class of degree 0. We may assume

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}=[\text{Supp}(\unicode[STIX]{x1D709})]-d[o_{X}] & & \displaystyle \nonumber\end{eqnarray}$$

for some $\unicode[STIX]{x1D709}\in X^{[d]}$ with $d$ sufficiently large.

By an explicit calculation via the motivic decomposition of $X^{[d]}$ , we have

$$\begin{eqnarray}\displaystyle [\unicode[STIX]{x1D709}]\in S_{i}\text{CH}_{0}(X^{[d]}) & & \displaystyle \nonumber\end{eqnarray}$$

if and only if

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}^{\times (i+1)}=0\in \text{CH}_{0}(X^{i+1}). & & \displaystyle \nonumber\end{eqnarray}$$

A positive answer to Question 3.2 for $X^{[d]}$ is then equivalent to the statement that

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}\in S_{i}(X) & & \displaystyle \nonumber\end{eqnarray}$$

if and only if

$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D6FE}^{\times (i+1)}=0\in \text{CH}_{0}(X^{i+1}). & & \displaystyle \nonumber\end{eqnarray}$$

The latter is a new characterization of O’Grady’s filtration $S_{\bullet }(X)$ proposed by Voisin.