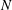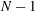1 Introduction
This study proposes a novel flow field expansion tailored to the construction of low-dimensional empirical Galerkin models. Such reduced-order models (1) help in data compression, (2) allow quick visualizations and kinematic mixing studies (Rom-Kedar, Leonard & Wiggins Reference Rom-Kedar, Leonard and Wiggins1990), (3) provide a testbed for physical understanding (Lorenz Reference Lorenz1963), (4) serve as computationally inexpensive surrogate models for optimization (Han, Stefan & Zimmermann Reference Han, Stefan and Zimmermann2013) or (5) may be used as a plant for control design (Gerhard et al. Reference Gerhard, Pastoor, King, Noack, Dillmann, Morzyński and Tadmor2003; Bergmann & Cordier Reference Bergmann and Cordier2008).
In 1858, Helmholtz laid the foundation for the first low-dimensional dynamical models in fluid mechanics with his famous theorems on vortices (see, e.g., Lugt Reference Lugt1995). Subsequently, a rich set of vortex models has been developed for vortex pairs, for the recirculation zone (Föppl Reference Föppl1913; Suh Reference Suh1993), for the vortex street (von Kármán & Rubach Reference von Kármán and Rubach1912) and for numerous combustion related problems (Coats Reference Coats1997), to name just a few. For non-periodic open flows, low-dimensional vortex models come at the expense of a hybrid state-space structure: new degrees of freedom (vortices) are created at the body, merged or removed. Most forms of applications, like dynamical systems analyses or control design, are not suitable for hybrid models but assume a continuous evolution in a fixed finite-dimensional state space. Hence, most currently developed reduced-order models are formulated by the Galerkin method and based on modal expansions (Fletcher Reference Fletcher1984).
In the last 100 years, Galerkin (Reference Galerkin1915)’s method of solving partial differential equations has enjoyed ample generalizations and applications, from high-dimensional grid-based computational methods to low-dimensional models. This study focuses on low-dimensional flow representations by an expansion in global modal structures. In principle, any space of square-integrable velocity fields has a complete set of orthonormal modes: any flow field can be arbitrarily closely approximated by a finite-dimensional expansion. In practice, however, the construction of such mathematical bases is restricted to simple geometries and the use of Fourier expansions or Chebyshev polynomials (Orszag Reference Orszag1971). Stability modes based on a linearization of the Navier–Stokes equations tend to be more efficient in terms of resolution for a given number
$N$
of modes. However, these physical modes generally lack a proof of completeness, and are afflicted by a reduced dynamic bandwidth and an
$O(N^{3})$
operation count for the quadratic terms, as opposed to
$O(N\log N)$
operations for Fourier or Chebyshev modes. The most efficient representations of a Navier–Stokes solution are obtained from empirical expansions based on flow snapshots. These data-driven Galerkin expansions are confined to a subspace spanned by the snapshots, i.e. have a narrow dynamic bandwidth defined by the training set.
This study focuses on data-driven expansions. A Galerkin expansion with guaranteed minimal residual over the training snapshots was first pioneered by Lorenz (Reference Lorenz1956) as principal axis modes and later popularized in fluid mechanics as proper orthogonal decomposition (POD) by Lumley (Reference Lumley, Yaglom and Tatarski1967). Proper orthogonal decomposition guarantees an optimal data reconstruction in a well-defined sense (see, e.g., Holmes, Lumley & Berkooz Reference Holmes, Lumley and Berkooz1998). Apart from data compression applications, Lumley devised POD as a mathematical tool for distilling coherent structures from data. Yet, only in rare cases have POD modes been found to resemble physically meaningful structures, like stability modes or base-flow deformations (Oberleithner et al. Reference Oberleithner, Sieber, Nayeri, Paschereit, Petz, Hege, Noack and Wygnanski2011). In particular, they tend to mix spatial and temporal frequencies in most modes, which complicates a physical interpretation. As a remedy for this shortcoming, the dynamic mode decomposition (DMD) – also referred to as Koopman analysis – was pioneered by Rowley et al. (Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009) and Schmid (Reference Schmid2010). Dynamic mode decomposition is able to distil stability eigenmodes from transient snapshot data and produce temporal Fourier modes for post-transient data. The downside of these DMD features – compared with POD – is non-orthogonality of the extracted modes, suboptimal convergence, the need for time-resolved snapshots and numerical challenges when filtering is omitted. Mezić (Reference Mezić2013) provides an excellent review of recent DMD developments.
In the past, numerous Galerkin models based on POD and DMD have been constructed. In addition, numerous generalizations have been proposed to address, among other topics, multi-operating conditions (Jørgensen, Sørensen & Brøns Reference Jørgensen, Sørensen and Brøns2003), changes during transients (Siegel et al. Reference Siegel, Seidel, Fagley, Luchtenburg, Cohen and Mclaughlin2008), optimal correlations to observables (Hoarau et al. Reference Hoarau, Borée, Laumonier and Gervais2006; Schlegel et al. Reference Schlegel, Noack, Jordan, Dillmann, Gröschel, Schröder, Wei, Freund, Lehmann and Tadmor2012) and control design (Brunton & Noack Reference Brunton and Noack2015).
This study proposes a novel data-driven expansion preserving key features of POD, such as orthonormality of the computed modes and a low residual, and of DMD, such as distilling the dominant frequencies and their associated structures contained in the data. The paper is organized as follows. Section 2 describes the cylinder wake configuration and gives details on the direct numerical simulation employed as well as the snapshots extracted. Section 3 outlines the computation of the proposed expansion, called ‘recursive DMD (RDMD)’ in what follows. Recursive DMD is then applied to a transient cylinder wake, demonstrating its advantages (§ 4) over previous decompositions. In § 5, a similar investigation is performed for the non-periodic wake behind three rotating cylinders. Our results are summarized in § 6.
2 Configuration and direct numerical simulation
As a test case, a two-dimensional incompressible viscous flow past a circular cylinder has been chosen. The flow is described in a Cartesian coordinate system where the
$x$
-axis is aligned with the streamwise direction and the
$y$
-axis is transverse and orthogonal to the cylinder axis. The origin of the coordinate system coincides with the cylinder axis. The location vector is denoted by
$\boldsymbol{x}=(x,y)$
. Analogously, the velocity is represented by
$\boldsymbol{u}=(u,v)$
, where
$u$
and
$v$
are the
$x$
- and
$y$
-components of the velocity. The time is represented by
$t$
. The Newtonian fluid is characterized by the density
$\unicode[STIX]{x1D70C}$
and dynamic viscosity
$\unicode[STIX]{x1D707}$
. In the following, all variables are assumed to be non-dimensionalized by the cylinder diameter
$D$
, the oncoming velocity
$U$
and the fluid density
$\unicode[STIX]{x1D70C}$
. The resulting Reynolds number
$\mathit{Re}=UD\unicode[STIX]{x1D70C}/\unicode[STIX]{x1D707}$
is set to 100, i.e. well above the onset of vortex shedding (Zebib Reference Zebib1987; Schumm, Berger & Monkewitz Reference Schumm, Berger and Monkewitz1994), but well below the onset of three-dimensional instabilities (Zhang et al.
Reference Zhang, Fey, Noack, König and Eckelmann1995; Barkley & Henderson Reference Barkley and Henderson1996; Williamson Reference Williamson1996).
A direct numerical simulation of the Navier–Stokes equations has been performed using an in-house solver based on a second-order finite-element discretization with Taylor–Hood elements (Taylor & Hood Reference Taylor and Hood1973) in primitive variables. The time stepping is performed using a third-order-accurate scheme and a time step equal to
$0.1$
. Following Noack et al. (Reference Noack, Afanasiev, Morzyński, Tadmor and Thiele2003), the computational domain extends from
$x=-5$
to
$x=25$
and
$y=-5$
to
$y=5$
and is discretized with 56 272 finite elements. The initial condition for the transient from
$t=0$
to
$t=150$
is a small perturbation of the steady Navier–Stokes solution
$\boldsymbol{u}_{s}$
and reads
$\boldsymbol{u}(\boldsymbol{x},0)=\boldsymbol{u}_{s}(\boldsymbol{x})+0.01\boldsymbol{f}_{1}(\boldsymbol{x})$
, where
$\boldsymbol{f}_{1}$
is the real part of the unstable complex eigenvector normalized to unit norm.
The simulation provides
$M=450$
equidistantly sampled velocity snapshots
$\boldsymbol{u}^{m}(\boldsymbol{x})=\boldsymbol{u}(\boldsymbol{x},t^{m})$
,
$m=1,\ldots ,M$
, covering the entire unforced transient phase, from the steady solution to the fully developed von Kármán vortex street. The snapshot times are
$t^{m}=30+m\unicode[STIX]{x0394}t$
based on a sampling interval of
$\unicode[STIX]{x0394}t=0.2$
and cover the time interval
$t\in [30,120]$
. The initial and final base flows are depicted in figure 1 together with the energy norm of the fluctuations
$\boldsymbol{v}=\boldsymbol{u}-\boldsymbol{u}_{s}$
around the steady solution
$\boldsymbol{u}_{s}$
. The transition from the unstable fixed point to the stable limit-cycle oscillation is characterized by the growing amplitude of the fluctuations accompanied by an increase in the Strouhal number (Zebib Reference Zebib1987; Schumm et al.
Reference Schumm, Berger and Monkewitz1994).
Figure 1. Incompressible two-dimensional flow around a circular cylinder at
$\mathit{Re}=100$
. The steady (a) and time-averaged (b) solutions are illustrated with streamlines. The total fluctuation level
$K$
normalized with its asymptotic value
$K_{\infty }$
is shown in (c).
Within the first 30 convective time units, the flow is governed by linear dynamics spanned by the steady solution and the unstable eigenmode. In the intermediate phase, approximately
$t\in [60,90]$
, the vortex shedding undergoes significant changes and moves farther upstream towards the cylinder. In the final 30 convective time units, the flow has converged to a limit-cycle dynamics exhibiting a fully developed von Kármán vortex street. These three characteristic stages of the transient evolution are depicted in figure 2. For the construction of the Galerkin expansions, we ignore the phase
$t\in [0,30]$
as there is hardly any noticeable fluctuation and the corresponding snapshots effectively duplicate the steady Navier–Stokes solution. We also ignore the converged limit-cycle data at
$t>120$
as this would also give emphasis to redundant information.
All modal decompositions are based on these fluctuations around the steady solution. The mean flow is discarded as a base flow because it is only well defined for this particular initial condition and the chosen time interval. Our sampling Strouhal frequency of 10 is approximately 30 times larger than the shedding frequency – a value that can be considered adequate for a Fourier transformation while avoiding excessive redundancy for the statistical POD.
3 Modal decomposition
In this section, a new snapshot-based modal decomposition is proposed. This decomposition comprises properties of the POD (Lumley Reference Lumley, Yaglom and Tatarski1967; Sirovich Reference Sirovich1987) and the DMD (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009; Schmid Reference Schmid2010). First (§§ 3.1 and 3.2), the snapshot-based POD and DMD are briefly recapitulated. In § 3.3, the RDMD is proposed as an appealing compromise inheriting the orthonormality and low truncation error of POD and the oscillatory representation of the flow behaviour of DMD.
Figure 2. Transient evolution of the cylinder wake illustrated with snapshots of the vorticity field at an initial (a,
$t=50$
), an intermediate (b,
$t=70$
) and a final state (c,
$t=90$
).
3.1 Proper orthogonal decomposition
We analyse a time-dependent velocity field
$\boldsymbol{u}(\boldsymbol{x},t)$
in a steady domain
$\boldsymbol{x}\in \unicode[STIX]{x1D6FA}$
and sample
$M$
flow snapshots with constant sampling frequency corresponding to a time step
$\unicode[STIX]{x0394}t$
. The velocity field at instant
$t^{m}=m\unicode[STIX]{x0394}t$
, with
$m=1,\ldots ,M$
, is denoted by
$\boldsymbol{u}^{m}:=\boldsymbol{u}(\boldsymbol{x},t^{m})$
.
Proper orthogonal decomposition requires the definition of an inner product and a time average. We assume the standard inner product of two square-integrable velocity fields
$\boldsymbol{u}^{1}$
,
$\boldsymbol{u}^{2}\in {\mathcal{L}}^{2}(\unicode[STIX]{x1D6FA})$
, given as
$$\begin{eqnarray}(\boldsymbol{u}^{1},\boldsymbol{u}^{2})_{\unicode[STIX]{x1D6FA}}:=\int _{\unicode[STIX]{x1D6FA}}\text{d}\boldsymbol{x}\,\boldsymbol{u}^{1}(\boldsymbol{x})\boldsymbol{\cdot }\boldsymbol{u}^{2}(\boldsymbol{x}).\end{eqnarray}$$
The corresponding norm reads
$\Vert \boldsymbol{u}\Vert _{\unicode[STIX]{x1D6FA}}:=\sqrt{(\boldsymbol{u},\boldsymbol{ u})_{\unicode[STIX]{x1D6FA}}}$
. The snapshot-based time average of a function
$F$
is defined in a canonical manner,
$$\begin{eqnarray}\langle F(\boldsymbol{u})\rangle _{M}:=\frac{1}{M}\mathop{\sum }_{m=1}^{M}F(\boldsymbol{u}^{m}).\end{eqnarray}$$
In the following, the snapshot-based POD (Sirovich Reference Sirovich1987) is applied to the fluctuations
$$\begin{eqnarray}\boldsymbol{v}^{m}(\boldsymbol{x}):=\boldsymbol{u}(\boldsymbol{x},t^{m})-\boldsymbol{u}_{s}(\boldsymbol{x})\end{eqnarray}$$
around the steady solution
$\boldsymbol{u}_{s}$
for the reasons mentioned in § 2. First, the correlation matrix
$\unicode[STIX]{x1D63E}=(\unicode[STIX]{x1D60A}^{mn})\in \mathbb{R}^{M\times M}$
of the fluctuations is determined,
$$\begin{eqnarray}\unicode[STIX]{x1D60A}^{mn}:=\frac{1}{M}(\boldsymbol{v}^{m},\boldsymbol{v}^{n})_{\unicode[STIX]{x1D6FA}}.\end{eqnarray}$$
Second, a spectral analysis of this matrix is performed. It should be noted that
$\unicode[STIX]{x1D63E}$
is a symmetric positive semi-definite Gramian matrix. Hence, its eigenvalues
$\unicode[STIX]{x1D706}_{i}$
are real and non-negative and can be assumed to be sorted according to
$\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \ldots \geqslant \unicode[STIX]{x1D706}_{M}\geqslant 0$
. The corresponding eigenvectors
$\boldsymbol{e}_{i}=[e_{i}^{1},\ldots ,e_{i}^{M}]^{\text{T}}$
satisfy
$$\begin{eqnarray}\unicode[STIX]{x1D63E}\boldsymbol{e}_{i}=\unicode[STIX]{x1D706}_{i}\boldsymbol{e}_{i},\quad i=1,\ldots ,M,\end{eqnarray}$$
and can – without loss of generality – be assumed to be orthonormalized, satisfying
$\boldsymbol{e}_{i}\boldsymbol{\cdot }\boldsymbol{e}_{j}=\unicode[STIX]{x1D6FF}_{ij}$
, with
$\unicode[STIX]{x1D6FF}_{ij}$
as the Kronecker symbol. Third, each POD mode is expressed as a linear combination of the snapshot fluctuations,
$$\begin{eqnarray}\boldsymbol{u}_{i}:=\frac{1}{\sqrt{M\unicode[STIX]{x1D706}_{i}}}\mathop{\sum }_{m=1}^{M}e_{i}^{m}\boldsymbol{v}^{m},\quad i=1,\ldots ,N.\end{eqnarray}$$
It follows that the POD modes are orthonormal, with
$(\boldsymbol{u}_{i},\boldsymbol{u}_{j})_{\unicode[STIX]{x1D6FA}}=\unicode[STIX]{x1D6FF}_{ij},\quad \forall i,j\in \{1,\ldots ,M\}$
. Finally, the mode amplitudes read
$$\begin{eqnarray}a_{i}^{m}:=\sqrt{\unicode[STIX]{x1D706}_{i}M}e_{m}^{i},\quad i=1,\ldots ,N.\end{eqnarray}$$
These amplitudes are uncorrelated (orthogonal in time), or in mathematical terms
$$\begin{eqnarray}\langle a_{i}a_{j}\rangle _{M}=\unicode[STIX]{x1D706}_{i}\unicode[STIX]{x1D6FF}_{ij},\quad i,j\in \{1,\ldots ,N\}.\end{eqnarray}$$
It should be noted that the first moments
$\langle a_{i}\rangle _{M}$
do not need to vanish as the fluctuations are based on the steady solution and not on the mean flow of this transient. The POD defines a second-order statistics providing the two-point autocorrelation function
$$\begin{eqnarray}\overline{\boldsymbol{v}(\boldsymbol{x},t)\boldsymbol{v}(\boldsymbol{y},t)}=\mathop{\sum }_{i=1}^{N}\unicode[STIX]{x1D706}_{i}\boldsymbol{u}_{i}(\boldsymbol{x})\boldsymbol{u}_{i}(\boldsymbol{y}).\end{eqnarray}$$
Hence, a minimum requirement imposed on the snapshot ensemble is the accuracy of the extracted mean flow and the second moments of the flow. This accuracy of the statistics for a given number of snapshots is increased by processing uncorrelated snapshots, as required in the original paper on the snapshot POD method (Sirovich Reference Sirovich1987).
The resulting expansion exactly reproduces the snapshots for
$N=M$
modes; we have
$$\begin{eqnarray}\boldsymbol{u}(\boldsymbol{x},t^{m})=\boldsymbol{u}_{s}(\boldsymbol{x})+\mathop{\sum }_{i=1}^{N}a_{i}(t^{m})\boldsymbol{u}_{i}(\boldsymbol{x}).\end{eqnarray}$$
For
$N<M$
, the truncated expansion (3.10) has a non-vanishing residual
$\boldsymbol{r}^{m}(\boldsymbol{x}):=\boldsymbol{r}(\boldsymbol{x},t^{m})$
. The corresponding time-averaged truncation error
$$\begin{eqnarray}\unicode[STIX]{x1D712}^{2}:=\langle \Vert \boldsymbol{r}^{m}\Vert _{\unicode[STIX]{x1D6FA}}^{2}\rangle _{M}\end{eqnarray}$$
can be shown to be minimal; in other words, no other Galerkin expansion with the same number of modes will have a smaller error (Holmes et al. Reference Holmes, Lumley and Berkooz1998). This optimality property makes POD an attractive data compression technique.
For later reference, the instantaneous truncation error
$\unicode[STIX]{x1D712}^{2}(t):=\Vert \boldsymbol{r}^{m}(\cdot ,t)\Vert _{\unicode[STIX]{x1D6FA}}^{2}$
is introduced. The size of this error may be compared with the corresponding fluctuation level on the limit cycle
$2K_{\infty }=\overline{\Vert \boldsymbol{v}\Vert ^{2}}$
, where
$K_{\infty }$
denotes the turbulent kinetic energy (TKE) and the overbar represents averaging over the post-transient phase. We also introduce
$K$
as the corresponding instantaneous quantity.
As a motivation for the proposed new decomposition, we recall that POD can also be defined in a recursive manner, following Courant & Hilbert (Reference Courant and Hilbert1989) on the spectral analysis of positive definite symmetric matrices. Taking
$\boldsymbol{u}_{1}$
as the first expansion mode, the resulting one-mode expansion reads
$$\begin{eqnarray}\boldsymbol{v}^{m}=a_{1}^{m}\boldsymbol{u}_{1}+\boldsymbol{r}_{1}^{m},\quad m=1,\ldots ,M.\end{eqnarray}$$
The mode amplitude
$a_{1}^{m}:=(\boldsymbol{v}^{m},\boldsymbol{u}_{1})_{\unicode[STIX]{x1D6FA}}$
minimizes the residual
$\Vert \boldsymbol{r}_{1}^{m}\Vert _{\unicode[STIX]{x1D6FA}}$
for a given
$\boldsymbol{u}_{1}$
. The first POD mode can be shown to minimize the averaged energy of the residual
$\langle \Vert \boldsymbol{r}_{1}^{m}\Vert _{\unicode[STIX]{x1D6FA}}^{2}\rangle _{M}$
. Furthermore, the residual
$\boldsymbol{r}_{1}^{m}$
,
$m=1,\ldots ,M$
is orthogonal to
$\boldsymbol{u}_{1}$
by construction. The second step then searches for a mode
$\boldsymbol{u}_{2}$
that best resolves the residual
$\boldsymbol{r}_{1}$
,
$$\begin{eqnarray}\boldsymbol{r}_{1}^{m}=a_{2}^{m}\boldsymbol{u}_{2}+\boldsymbol{r}_{2}^{m},\quad m=1,\ldots ,M,\end{eqnarray}$$
i.e. that minimizes
$\langle \Vert \boldsymbol{r}_{2}^{m}\Vert _{\unicode[STIX]{x1D6FA}}^{2}\rangle _{M}$
. The other remaining modes are computed in a similar manner.
3.2 Dynamic mode decomposition
Dynamic mode decomposition (Rowley et al.
Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009; Schmid Reference Schmid2010) is another data-driven modal expansion which can approximate stability eigenmodes from transient data or Fourier modes from post-transient data. The time step
$\unicode[STIX]{x0394}t$
needs to be sufficiently small for a meaningful Fourier analysis, but sufficiently large so that the changes in the flow state exceed the noise level.
We consider the fluctuation snapshots of § 3.1,
$\boldsymbol{v}^{m}$
,
$m=1,\ldots ,M-1$
, as linearly independent modes of an expansion and write
$$\begin{eqnarray}\boldsymbol{v}=\mathop{\sum }_{i=1}^{M-1}b_{i}\boldsymbol{v}^{i}.\end{eqnarray}$$
Evidently, the modes are generally not orthogonal. With this basis, the mode amplitude vector of the
$m$
th snapshot becomes a unit vector,
$$\begin{eqnarray}\boldsymbol{b}^{m}=[b_{1}^{m},\ldots ,b_{M-1}^{m}]^{\text{T}},\quad \text{where }b_{i}^{m}=\unicode[STIX]{x1D6FF}_{im}.\end{eqnarray}$$
Dynamic mode decomposition assumes a linear relationship between the
$(m+1)$
th and
$m$
th snapshot,
$$\begin{eqnarray}\boldsymbol{b}^{m+1}=\unicode[STIX]{x1D63C}\boldsymbol{b}^{m},\end{eqnarray}$$
where
$\unicode[STIX]{x1D63C}\in \mathbb{R}^{(M-1)\times (M-1)}$
is a square matrix which is generally identified from the data.
For
$m<M-1$
, (3.16) acts as a shift map: the
$m$
th unit vector is mapped on the
$(m+1)$
th unit vector, leading to unity in the first subdiagonal of
$\unicode[STIX]{x1D63C}$
and zeros in the remaining column. The
$M$
th snapshot has no successor in the time series and is expanded in terms of the previous snapshots,
$$\begin{eqnarray}\boldsymbol{v}^{M}=\mathop{\sum }_{i=1}^{M-1}c_{i}\boldsymbol{v}^{i}+\boldsymbol{r}.\end{eqnarray}$$
The coefficients
$c_{i}$
are chosen to minimize the residual norm
$\Vert \boldsymbol{r}\Vert _{\unicode[STIX]{x1D6FA}}$
.
From (3.16) and (3.17), the matrix is easily seen to be of companion type,
$$\begin{eqnarray}\unicode[STIX]{x1D63C}=\left[\begin{array}{@{}cccccc@{}}0 & 0 & \ldots & 0 & 0 & c_{1}\\ 1 & 0 & \ldots & 0 & 0 & c_{2}\\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \ldots & 1 & 0 & c_{M-2}\\ 0 & 0 & \ldots & 0 & 1 & c_{M-1}\end{array}\right].\end{eqnarray}$$
In what follows, we depart from the classical DMD literature and propose a simpler derivation of the DMD modes. Let
$P(s)=c_{1}+c_{2}s+\cdots +c_{M-1}s^{M-2}+s^{M-1}$
be a polynomial in
$s$
and let
$P(s)=(s-\unicode[STIX]{x1D706}_{1})(s-\unicode[STIX]{x1D706}_{2})\cdots (s-\unicode[STIX]{x1D706}_{M-1})$
be its factorization with distinct eigenvalues
$\unicode[STIX]{x1D706}_{i}$
. We introduce
$$\begin{eqnarray}\unicode[STIX]{x1D651}=\left[\begin{array}{@{}cccc@{}}1 & \unicode[STIX]{x1D706}_{1} & \ldots & \unicode[STIX]{x1D706}_{1}^{M-2}\\ 1 & \unicode[STIX]{x1D706}_{2} & \ldots & \unicode[STIX]{x1D706}_{2}^{M-2}\\ \vdots & \vdots & \vdots & \vdots \\ 1 & \unicode[STIX]{x1D706}_{M-1} & \ldots & \unicode[STIX]{x1D706}_{M-1}^{M-2}\end{array}\right]\end{eqnarray}$$
as the corresponding Vandermonde matrix. It can be easily verified that the Vandermonde matrix
$\unicode[STIX]{x1D651}$
diagonalizes the companion matrix
$\unicode[STIX]{x1D63C}$
. We obtain
$$\begin{eqnarray}\unicode[STIX]{x1D651}\unicode[STIX]{x1D63C}\unicode[STIX]{x1D651}^{-1}=\text{diag}(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{M-1}),\end{eqnarray}$$
where the right-hand side is a diagonal matrix with the eigenvalues as its elements. We introduce new variables
$\boldsymbol{a}$
defined by
$$\begin{eqnarray}\boldsymbol{a}=\unicode[STIX]{x1D651}\boldsymbol{b}.\end{eqnarray}$$
With these definitions, the evolution equation (3.16) can be cast into eigenform according to
$$\begin{eqnarray}\boldsymbol{a}^{m+1}=\unicode[STIX]{x1D651}\unicode[STIX]{x1D63E}\unicode[STIX]{x1D651}^{-1}\boldsymbol{a}^{m}=\unicode[STIX]{x1D63F}\boldsymbol{a}^{m}.\end{eqnarray}$$
Here,
$\unicode[STIX]{x1D63F}$
denotes the diagonal matrix
$$\begin{eqnarray}\unicode[STIX]{x1D63F}=\text{diag}(\unicode[STIX]{x1D706}_{1},\ldots ,\unicode[STIX]{x1D706}_{M-1})=\left[\begin{array}{@{}cccc@{}}\unicode[STIX]{x1D706}_{1} & 0 & \ldots & 0\\ 0 & \unicode[STIX]{x1D706}_{2} & \ldots & 0\\ \vdots & \vdots & \vdots & \vdots \\ 0 & 0 & \ldots & \unicode[STIX]{x1D706}_{M-1}\end{array}\right],\end{eqnarray}$$
where the
$i$
th eigenvalue is
$\unicode[STIX]{x1D706}_{i}$
, with corresponding eigenvector
$\boldsymbol{a}_{i}=\left[\unicode[STIX]{x1D6FF}_{1i},\ldots ,\unicode[STIX]{x1D6FF}_{(M-1)i}\right]^{\text{T}}$
.
Equations (3.15), (3.16) and (3.21) imply that the snapshots can be expressed as
$$\begin{eqnarray}\boldsymbol{v}^{m}=\mathop{\sum }_{i=1}^{M-1}\unicode[STIX]{x1D706}_{i}^{m-1}\unicode[STIX]{x1D731}_{i},\end{eqnarray}$$
where the
$\unicode[STIX]{x1D706}_{i}$
are referred to as DMD eigenvalues and the
$\unicode[STIX]{x1D731}_{i}$
as (complex) DMD modes. It should be noted that the derivation of (3.24) rests on the diagonalization of the companion matrix (3.20) and does not require the Koopman operator.
The choice of
$N$
DMD modes for the Galerkin expansion (3.10) minimizes the truncation error (3.11) following Chen, Tu & Rowley (Reference Chen, Tu and Rowley2012) and consistent with the optimal property of POD.
3.3 Recursive DMD
Recursive DMD serves a multi-objective task: extracting oscillatory modes from the snapshot sequence (like DMD) while ensuring orthogonality of the modes and a low truncation error (like POD).
The initialization step prepares the residual to be processed. We take
$$\begin{eqnarray}\boldsymbol{r}_{0}^{m}:=\boldsymbol{v}^{m},\quad m=1,\ldots ,M.\end{eqnarray}$$
During the
$i$
th step (
$0<i\leqslant N$
), the
$i$
th mode is determined from a DMD
$$\begin{eqnarray}\boldsymbol{r}_{i-1}^{m}=\mathop{\sum }_{j=1}^{M-1}\unicode[STIX]{x1D706}_{j}^{m-1}\unicode[STIX]{x1D731}_{j}^{i},\end{eqnarray}$$
where
$\unicode[STIX]{x1D731}_{j}^{i}$
represents the
$j$
th DMD mode of the
$i$
th step. The candidate modes to be considered are
$$\begin{eqnarray}\boldsymbol{u}_{k}^{\star }=\frac{\Re \{\unicode[STIX]{x1D731}_{k}^{i}\}}{\left\Vert \Re \{\unicode[STIX]{x1D731}_{k}^{i}\}\right\Vert _{\unicode[STIX]{x1D6FA}}},\quad k=1,\ldots ,M-1,\end{eqnarray}$$
and each mode reduces the residual
$\boldsymbol{r}_{i,k}^{m}$
according to
$$\begin{eqnarray}\displaystyle \boldsymbol{r}_{i-1}^{m} & = & \displaystyle a_{k}^{\star m}\boldsymbol{u}_{k}^{\star }+\boldsymbol{r}_{i,k}^{m},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle a_{k}^{\star m} & = & \displaystyle (\boldsymbol{r}_{i-1}^{m}\boldsymbol{\cdot }\boldsymbol{u}_{k}^{\star })_{\unicode[STIX]{x1D6FA}}.\end{eqnarray}$$
$\boldsymbol{r}_{i,k}^{m}$
depends on the index of iteration
$i$
, the snapshot index
$m$
and the trial mode index
$k$
. The truncation error of the
$i$
th candidate mode
$\boldsymbol{u}_{k}^{\star }$
for all snapshots is given by 
$$\begin{eqnarray}\unicode[STIX]{x1D712}_{i,k}^{2}:=\left\langle \left\Vert \boldsymbol{r}_{i,k}^{m}\right\Vert _{\unicode[STIX]{x1D6FA}}^{2}\right\rangle _{M}.\end{eqnarray}$$
As mode
$i$
we select the trial mode
$k$
with the lowest averaged error, i.e.
$$\begin{eqnarray}\boldsymbol{u}_{i}:=\boldsymbol{u}_{k}^{\star }\quad \text{so that}\quad \forall l\in \{1,\ldots ,M-1\}:\unicode[STIX]{x1D712}_{i,k}^{2}\leqslant \unicode[STIX]{x1D712}_{i,l}^{2}.\end{eqnarray}$$
The resulting expansion reads after the
$i$
th step
$$\begin{eqnarray}\boldsymbol{v}^{m}:=\mathop{\sum }_{j=1}^{i}a_{j}\boldsymbol{u}_{j}+\boldsymbol{r}_{i}^{m}.\end{eqnarray}$$
The
$(i+1)$
th mode is computed following the same steps. The iteration terminates when the desired number of modes is reached,
$i=N$
, or in the unlikely case that all residuals vanish,
$\boldsymbol{r}_{i}^{m}\equiv 0,\quad m=1,\ldots ,M$
– whichever criterion is satisfied first. We emphasize that the candidate modes are normalized (see (3.27)) and the
$(i+1)$
th mode is constructed from the orthogonal residual of the Galerkin expansion with the first
$i$
modes (see (3.28)). Hence, the modes form an orthonormal system.
4 Modal decomposition of the transient cylinder wake
The transient cylinder wake is analysed with POD (§ 4.1), DMD (§ 4.2) and the proposed new decomposition (§ 4.3) discussed in § 3. In § 4.4, all modal decompositions are subjected to a comparison with respect to the instantaneous residual, the averaged residual and the convergence with increasing number of modes. The transient wake snapshots are the same for all decompositions and have been described in § 2.
4.1 Proper orthogonal decomposition
The snapshots of the cylinder wake simulations described in § 2 are subjected to a snapshot POD outlined in § 3.1. The POD modes of the post-transient periodic cylinder wake mimic a Fourier decomposition. They arise in pairs representing the two phases at the first and higher harmonic frequencies (Deane et al.
Reference Deane, Kevrekidis, Karniadakis and Orszag1991; Noack et al.
Reference Noack, Afanasiev, Morzyński, Tadmor and Thiele2003). The energy level of each pair rapidly decreases with the order of the harmonics. The transient, however, exhibits a gradual change from the initial stability modes (with a fluctuation maximum far from the cylinder) to von Kármán vortex shedding (with fluctuations peaking near the cylinder). The other change is a base flow with a recirculation region that decreases in streamwise extent from approximately 7 diameters to approximately 1 diameter length. The resulting POD modes and associated mode amplitudes are depicted in figures 3 and 4 and appear to be different from the post-transient analogues. Proper orthogonal decomposition modes 1 and 2 effectively represent von Kármán vortex shedding growing from zero to asymptotic values. These values are larger than the corresponding fluctuation levels of the other modes. Modes 6 and 7 describe the second harmonics, as can be seen from the visualization and the amplitude evolution. Modes 9 and 10 look similar to the stability eigenmodes at slightly lower frequencies, with peak activity around
$t=55$
. Modes 4 and 5 also represent vortex shedding, with peak activity around
$t=65$
, i.e. two shedding periods later. Mode 3 depicts the shift mode (Noack et al.
Reference Noack, Afanasiev, Morzyński, Tadmor and Thiele2003), i.e. it characterizes the base-flow change between steady and time-averaged periodic solution. Mode 8 represents another base-flow correction with different topology and is mainly active during the most rapid changes of the transient around
$t=65$
. It has a small second harmonic component. The base-flow modes 3 and 8 correspond to an expansion with the steady solution as basic modes. Taking the post-transient averaged velocity as basic mode is numerically found to give rise to similar base-flow modes but with different energy content and thus different indices.
Figure 3. The first 10 POD modes of the transient phase of the flow, with
$t\in [30,120]$
and
$\mathit{Re}=100$
. (a,c,e,g,i) Modes 1–5, (b,d,f,h,j) modes 6–10. The vorticity of the mode is visualized in colour (green, zero; red, above a positive threshold; blue, below a negative threshold).
Figure 4. The mode amplitudes of the POD modes of figure 3.
All of the displayed POD modes show pronounced frequencies: six modes display oscillations near the shedding frequency, two resolve the second harmonics and two feature slowly varying base-flow changes. Unlike POD for periodic shedding, the third and higher harmonics are found as modes with indices after the first 10 ones displayed. This comparatively ‘clean’ frequency content may be attributed to the narrow-bandwidth transient dynamics, with dominant frequencies between the eigenfrequency of the steady solution and the shedding frequency of the post-transient wake. Moreover, the maximum of the fluctuation envelope moves upstream during the transient. For broadband dynamics, such as a mixing layer with multiple vortex pairings, POD modes with multiple frequency content are far more common (Noack et al. Reference Noack, Pelivan, Tadmor, Morzyński and Comte2004).
4.2 Dynamic mode decomposition
The snapshots of the transient flow have been decomposed with DMD. The DMD procedure can identify eigenmodes for the transient data and the Fourier modes for the attractor.
The result of the procedure is a set of complex Ritz vectors and complex eigenvalues characterizing the growth rate and the frequency of the respective mode. The first 10 eigenmodes are depicted in figure 5. The first DMD mode corresponds to a real eigenvalue leading to a real Ritz vector. The remaining modes represent the real and imaginary parts of complex Ritz vectors. The phase-shifted analogue of oscillatory mode 10 is mode 11 (not displayed). In figure 6, the corresponding amplitudes of the real modes are displayed.
Figure 5. The same as figure 3 but for the first 10 DMD modes.
Figure 6. The same as figure 4 but for the first 10 DMD modes.
Modes 1, 6 and 7 act as shift modes and resolve slow base-flow changes. This interpretation is corroborated by the behaviour of the mode amplitudes. The remaining modes describe vortex shedding (
$i=2,3,4,5,10$
) or its second harmonics (
$i=8,9$
). The oscillatory mode amplitudes are slowly growing, like the first vortex shedding pair (for
$i=2,3$
) and the second harmonics (for
$i=8,9$
), or slowly decaying (for
$i=4,5,10$
). Intriguingly, the DMD modes describing vortex shedding have nearly identical frequencies and nearly identical shapes. This implies a redundancy which constitutes a challenge for reduced-order modelling.
By construction, the mode amplitudes have an exponentially growing or decaying envelope and can thus give no indication of initial or asymptotic values or temporal periods of maximum activity. In particular, an extrapolation beyond the sampling interval
$t\in [30,120]$
is not meaningful. An additional potential challenge for reduced-order modelling is posed by the non-orthogonality of the DMD modes.
Already in the early literature (Rowley et al. Reference Rowley, Mezić, Bagheri, Schlatter and Henningson2009; Schmid Reference Schmid2010; Chen et al. Reference Chen, Tu and Rowley2012), DMD has been shown to accurately capture the onset of fluctuations in the linear regime or the post-transient behaviour on the attractor. The current results indicate difficulties of the DMD concerning the modal interpretation for a complete transient from the steady solution to the post-transient attractor. This issue has also been pointed out and analysed by Bagheri (Reference Bagheri2013). In the next section, we present an alternative DMD decomposition which addresses and removes the above-mentioned challenges.
4.3 Recursive DMD
In this section, the results of RDMD are presented. The procedure is demonstrated for the same set of snapshots as employed previously for POD and DMD.
The first 10 RDMD modes are depicted in figure 7. Intriguingly, RDMD resolves the first harmonics (modes
$i=1,2$
), the second harmonics (
$i=6,7$
) and the third harmonics (
$i=8,9$
). The associated mode amplitudes (see figure 8) show corresponding oscillations starting near zero and reaching asymptotic values on the limit cycle. Mode 3 shows a nearly pure shift mode, describing the transition of the base flow from the steady solution to the time-averaged flow. In contrast to Noack et al. (Reference Noack, Afanasiev, Morzyński, Tadmor and Thiele2003), the amplitude becomes negative, since the sign of the RDMD mode is arbitrary. Modes 4 and 5 resolve intermediate vortex shedding patterns with maximum activity around
$t=70$
and rather small residual fluctuations on the limit cycle. Modes 10 and 11 (not shown) are reminiscent of stability eigenmodes and peak near
$t=55$
, i.e. more than two periods earlier.
Figure 7. The same as figure 3 but for the first 10 RDMD modes.
The first seven modes have significant similarities with the POD modes of figures 3 and 4. Yet, the oscillations are more symmetric (compare RDMD and POD mode 6) and show no apparent frequency mixing, as in POD modes
$i=3,6,8$
. Recursive DMD modes have by definition a lower averaged residual, compared with POD modes, but they look much cleaner and even reveal the third harmonics. It appears that RDMD modes have more in common with POD modes than with DMD modes. This should not come as a surprise, since the primary construction principle is an orthonormal decomposition leading to minimization of the residual, while the secondary criterion is the emulation of single-frequency DMD-mode behaviour.
Figure 8. The same as figure 4 but for the first 10 RDMD modes.
4.4 Comparison of POD, DMD and RDMD
In this section, results from POD, DMD and RDMD are quantitatively compared.
Figure 9 shows the truncation error of the POD, DMD and RDMD expansions as a function of the number of modes. As expected, all errors decrease monotonically with the number of modes, and POD outperforms DMD and RDMD. The RDMD residual, however, follows the POD value remarkably well and stays within similar orders of magnitude. In contrast, DMD approaches an effective asymptote near 10 % of the final fluctuation level.
Figure 9. The time-averaged fluctuation level of the residual (3.11) for POD, DMD and RDMD with increasing number of modes. The value is normalized by the corresponding fluctuation level (
$2K_{\infty }$
) on the limit cycle.
Figure 10. The instantaneous normalized truncation error (3.11) as a function of time for 10 POD, DMD and RDMD modes. The figure displays the sampling interval.
The temporal evolution of the instantaneous truncation error is displayed in figure 10 for POD, DMD and RDMD at
$N=10$
. The maximum value in
$t\in [60,70]$
is lowest for POD and largest for DMD. Recursive DMD performs, as expected, between the alternative expansions. A surprising feature is the asymptotes. Proper orthogonal decomposition and DMD have similar truncation errors near 10 % of the terminal fluctuation level, while RDMD outperforms both with a final value at approximately 5 %. This is no contradiction to the optimal property of POD, as this property only guarantees a minimal time-averaged value, or, equivalently, a minimal value of the integral over the instantaneous truncation error, which it evidently has. The DMD-based frequency filtering included in RDMD appears to have ‘anticipated’ the limit-cycle behaviour. One indication of this ‘anticipation’ is the third harmonics which are featured in RDMD but absent in both POD and DMD. At this stage, RDMD appears to be more suitable for reduced-order modelling when compared with POD or DMD. Like POD, RDMD yields orthonormal modes, but with purer frequency content. Like DMD, RDMD extracts oscillatory modes, but with well-defined initial and asymptotic behaviour of the mode amplitudes. In this sense, a strength of RDMD is that its amplitudes depart from oscillatory behaviour with exponential growth or decay of the DMD decomposition. In addition, the cycle-to-cycle variation of amplitude and frequency of RDMD coefficients is smaller than for similar POD mode coefficients.
Figure 11. The same DMD modes as figure 5 but for the transient cylinder with
$t\in [30;120]$
and at
$\mathit{Re}=120$
.
The relative performance of POD, DMD and RDMD is rarely affected by a small change of the interval time under investigation. A numerical study with numerous time intervals indicates that the first modes keep their spatial structure but may have different energy content. Even significant changes of the interval only give rise to changes in the relative order of the modes. For instance, shifting the investigation interval to include more converged limit-cycle data decreases the energy content of slowly varying base-flow modes while higher harmonics become more dominant. In the extreme case of snapshots from the converged limit cycle, POD, DMD and RDMD become very similar. An opposite observation is made for intervals focusing on the initial transient.
4.5 Reconstruction of the flow at
$\mathit{Re}=120$
In the previous section (4.4), the data-driven Galerkin expansions have been evaluated for the training data. The residuals of these modal expansions are now tested for another data set: the transient cylinder wake at
$\mathit{Re}=120$
with the same initial conditions during the time
$t\in [30,120]$
.
Figure 12. The modal amplitudes of the DMD modes of figure 11.
The change of the wake transient may be appreciated when the new DMD mode basis displayed in figure 11 is compared with the
$\mathit{Re}=100$
reference in figure 5. While the first five modes have similar frequency content (see figure 12), modes 6–10 are distinctly different. For instance, the quasi-steady modes 6 and 7 of the
$\mathit{Re}=100$
reference have been replaced by the second harmonics for
$\mathit{Re}=120$
. The third harmonics do not appear in the top 10 of the reference data but are found as mode 10 for
$\mathit{Re}=120$
.
As cross-validation, the POD, DMD and RDMD expansions obtained from the transient wake at
$\mathit{Re}=100$
are employed to resolve the transient wake at
$\mathit{Re}=120$
. First, the residuals for the whole transients are plotted as a function of the number of modes in figure 13. The residuals of POD and RDMD decrease similarly to a low fluctuation level as the number of modes increases to 64. The observation that RDMD outperforms POD particularly for high-order expansion is not a contradiction to the optimality property of POD, as the residual is determined on new data. Intriguingly, DMD shows a particularly poor performance compared with POD and RDMD. As expected, the residual of DMD decreases when the training data (
$\mathit{Re}=100$
) are replaced by the testing data (
$\mathit{Re}=120$
). However, we emphasize that RDMD based on training data at
$\mathit{Re}=100$
performs much better for the new data at
$\mathit{Re}=120$
compared with DMD obtained and tested for these new data. In other words, RDMD obtained for some operating condition appears to be robust against new data from changing operating conditions.
Figure 13. The time-averaged fluctuation level of the residual (3.11) for POD, DMD and RDMD (obtained from the transient at
$\mathit{Re}=100$
), and DMD at
$\mathit{Re}=120$
with increasing number of modes. The value is normalized by the corresponding fluctuation level (
$2K_{\infty }$
) on the limit cycle.
Figure 14 shows the residual for the four modal expansions of figure 13 as a function of time for a modal order of
$N=10$
. The maximum instantaneous residuals are ordered like the averaged residual values at
$N=10$
: POD beats RDMD and RDMD beats DMD. The DMD obtained for the new transient data shows the largest maximum residual but is more accurate on the limit cycle.
Similar time-dependent residual behaviour is observed for expansions with more modes, except that RDMD is more often observed to outperform POD, keeping in mind that the expansions are obtained from
$\mathit{Re}=100$
data but tested for the
$\mathit{Re}=120$
transient.
5 Modal decomposition of the wake past three rotating cylinders
The performance of POD, DMD and RDMD is investigated for a non-periodic flow behind three rotating cylinders, which extends the previous cylinder wake simulations to a more complex configuration. All cylinders have unit diameter
$D=1$
. Their centres are on the vertices of an equilateral triangle with an edge length of
$1.5D$
. This triangle is centred at the origin and has one vertex on the negative
$x$
-axis and two vertices at same
$x$
-value downstream. The two rear cylinders rotate counterclockwise with tangential velocity
$v_{T}=1$
. The front cylinder rotates clockwise, and its tangential velocity
$v_{T}=(\sqrt{5}-1)/2\approx 0.618$
(figure 15
a). Due to the rotation speeds, the wake flow is intentionally not symmetrical. Figure 15(b) depicts the vorticity field.
Figure 15. Flow past three rotating cylinders. Details of the test case (a) and the instantaneous vorticity field (b).
In this section, we investigate the converged post-transient flow. The flow is computed with the same Navier–Stokes solver and the same accuracy as the cylinder wake in § 4. The computational domain is bounded by the rectangle
$-6\leqslant x\leqslant 20$
$-y\leqslant 6\leqslant y$
and is discretized by 4225 quadratic six-node elements. The Reynolds numbers, based on the diameter of a single cylinder, is 100.
We are working at companion experiments for this configuration. The motivation is to have a simple geometry with three actuation inputs, the rotations of the cylinders, which can display complex dynamics but remains easily computable and experimentally realizable. The front cylinder controls the stagnation point while the rear cylinders manipulate each shear-layer individually. Thus, many drag-reducing mechanisms can be realized, like stagnation point stabilization (front cylinder), symmetric and antisymmetric high-frequency shear-layer excitation (rear cylinders) or base bleeding (rear cylinders generating a jet on the
$x$
-axis), to name a few.
Figure 16. The first 10 POD modes of the flow past three rotating cylinders at
$\mathit{Re}=100$
. (a,c,e,g,i) Modes 1–5, (b,d,f,h,j) modes 6–10. The vorticity of the mode is visualized in colour (green, zero; red, above a positive threshold; blue, below a negative threshold).
Following the exposition of § 4, we discuss POD (§ 5.1), DMD (§ 5.2) and RDMD (§ 5.3), followed by a quantitative comparison of the residuals (§ 5.4).
5.1 Proper orthogonal decomposition
The snapshots representing the attractor of the flow past three rotating cylinders are decomposed using POD. The first 10 of them, representing more than 99 % of the fluctuation energy, are depicted in figure 16. The first two modes describe von Kármán vortex shedding and the next two modes resolve a low-frequency base-flow modulation. Modes 5–10 form pairs describing fluctuations at higher frequencies. The spatial mode interpretation is corroborated by the behaviour of the mode amplitudes in figure 17.
Figure 17. Flow past three rotating cylinders. The mode amplitudes of the POD modes of figure 16.
5.2 Dynamic mode decomposition
The same snapshots are subjected to DMD. The results, i.e. the eigenmodes and their amplitudes, are depicted in figures 18 and 19 respectively.
Figure 18. The same as figure 16 but for the first 10 DMD modes.
Figure 19. The same as figure 17 but for the first 10 DMD modes.
Figure 20. The same as figure 16 but for the first 10 RDMD modes.
Figure 21. The same as figure 17 but for the first 10 RDMD modes.
Figure 22. The time-averaged fluctuation level of the residual (3.11) for POD, DMD and RDMD for the flow past three rotating cylinders, with increasing number of modes. The value is normalized by the corresponding converged fluctuation level (
$2K_{\infty }$
) on the attractor.
The modal amplitudes show, as expected, pure harmonic behaviour, while the non-symmetric modes arise from a non-symmetrically forced wake.
5.3 Recursive DMD
In this section, the results of RDMD are presented. Again, the procedure is demonstrated for the same set of snapshots as employed previously for POD and DMD. Figures 20 and 21 depict the modes and their amplitudes respectively. The frequency contents of POD and RDMD are very similar, while the amplitude modulation of POD is less pronounced in RDMD, corroborating the very purpose or RDMD, namely more harmonic modes.
5.4 Comparison of POD, DMD and RDMD
In this section, results from POD, DMD and RDMD are quantitatively compared. Figure 22 shows the time-averaged residual as a function of the number of modes for all three expansions. The performance of RDMD follows POD closely, while the DMD residual is approximately one order of magnitude larger at
$N=32$
.
Table 1. Comparison of POD, DMD and RDMD for the transient cylinder wake. The maximum and asymptotic truncation errors are for expansions with
$N=10$
modes normalized with the post-transient fluctuation level
$2K_{\infty }$
.
6 Conclusions
We propose a novel data-driven flow decomposition which combines the modal orthonormality and low truncation error
$\unicode[STIX]{x1D712}^{2}$
(3.11) of POD with the frequency-distilling features of DMD. This decomposition is recursively defined. First, the data set is subjected to DMD, after which a normalized DMD mode is chosen which minimizes the averaged error
$\unicode[STIX]{x1D712}^{2}$
. This procedure is recursively repeated in the orthogonal subspace of computed modes. The resulting RDMD modes are orthonormal by construction and can be expected to have lower error
$\unicode[STIX]{x1D712}^{2}$
than DMD modes while retaining the monochromatic features of DMD.
Proper orthogonal decomposition, DMD and RDMD have been applied to the same snapshots of a transient cylinder wake starting near the steady solution and terminating on the limit cycle. As expected, RDMD significantly outperforms DMD in terms of the maximum, time-averaged and asymptotic truncation error for all considered mode numbers by a large margin. In addition, the exponentially growing or decaying DMD amplitudes resemble neither initial nor asymptotic flow behaviour in a meaningful manner, while the RDMD amplitudes clearly identify the initial, transient and post-transient flow phases.
Also as expected, RDMD modes have far purer frequency content than POD modes but maintain the residual at a comparable level. While the maximum and average truncation errors of POD outperform RDMD, the latter shows a better resolution of the limit cycle: the asymptotic value for
$N=10$
is half as large as the corresponding POD value, and the third harmonic frequency is only captured by RDMD in the first 10 modes. Table 1 provides a brief comparison of the main characteristics and features of POD, DMD and RDMD.
In the comparison, all modal decompositions were compared for the same data from which the modes were constructed. The robustness of the Galerkin expansions has also been tested for a transient at a higher Reynolds number of 120. Here, RDMD and POD performed very similarly, even better than DMD for the new data. A third investigation has been performed for a non-periodic and non-symmetric wake behind three rotating cylinders. Again, the main conclusions for RDMD, DMD and POD were corroborated.
The literature contains alternative approaches for spectrally purified POD modes. One important recent contribution is spectral POD (Sieber, Paschereit & Oberleithner Reference Sieber, Paschereit and Oberleithner2016), which interpolates between POD and DMD by filtering the correlation matrix. This continuous interpolation offers an additional degree of freedom not present in RDMD; the price is the loss of strict orthonormality of the modes for all interpolation parameters. In a similar vein, Bourgeois, Martinuzzi & Noack (Reference Bourgeois, Martinuzzi and Noack2013) construct orthogonal POD modes with purer frequency content after Morlet-filtering the flow data at design frequencies. Recursive DMD can be considered as a simpler approach, which can be expected to perform well in an unsupervised manner, but leaves little room for tuning the modes for special purposes or applications. As a word of warning, all data-driven Galerkin expansions are – by definition – based on modes that are linear combinations of the snapshots, i.e. they cannot leave the space spanned by the training data. The benefit of one reduced-order representation method over another may actually be small. Noack (Reference Noack2016) sketches how future data-driven low-dimensional flow representations may be generalized to cure inherent limitations of the Galerkin expansion.
Summarizing, the current study indicates that RDMD is an attractive ‘compromise’ between POD and DMD. It sacrifices little of the optimal residual property of POD while retaining the single-frequency behaviour of DMD. Its potential in control-oriented reduced-order modelling will be explored in a future study. In addition, a particularly attractive opportunity for RDMD is the unsupervised extraction of generalized mean-field models with few dominant frequencies (Brunton & Noack Reference Brunton and Noack2015).
Acknowledgements
B.N. acknowledges the funding and excellent working conditions of the Senior Chair of Excellence ‘Closed-loop control of turbulent shear flows using reduced-order models’ (TUCOROM 2010–2015) supported by the French Agence Nationale de la Recherche (ANR) and hosted by Institute PPRIME and the Collaborative Research Centre (CRC 880) ‘Fundamentals of High Lift of Future Civil Aircraft’ supported by the Deutsche Forschungsgemeinschaft (DFG) and hosted at the Technical University of Braunschweig. This work has also been funded by the Polish National Centre of Science under research grant no. DEC-2011/01/B/ST8/07264 ‘Novel Method of Physical Modal Basis Generation for Reduced Order Flow Models’. We have highly profited from stimulating discussions with M. Abel, S. Brunton, L. Cordier, R. Martinuzzi, B. Protas, R. Radespiel and R. Semaan. We thank the Ambrosys Ltd. Society for Complex Systems Management and the Bernd Noack Cybernetics Foundation for additional support.
