1. Introduction
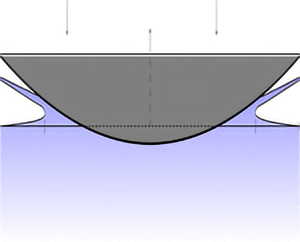
The two-dimensional unsteady problem of a rigid symmetric body entering water at constant speed, 
$V$, is considered. Before impact starts, the water is at rest, with a horizontal free surface, 
$y=0$. The body initially, at time 
$t=0$, touches the water surface at a single point, which is taken as the origin of the Cartesian coordinate system 
$Oxy$, where 
$y$ is directed upwards; see figure 1. The body is symmetric with respect to the vertical 
$y$-axis, rigid and convex. The angle between a tangent to the body surface in the wetted zone and the positive 
$x$-axis, which is known as the dead-rise angle, is small in the present analysis. As the body is forced into the water, the water is displaced. The subsequent flow is symmetric with respect to the 
$y$-axis. Hence, only half of the flow domain, 
$x \ge 0$, needs to be considered. In the right half of the flow domain, the water surface is elevated by the impact and overturns near the body surface, forming a jet that is thrown to the right, tangentially to the body surface; see figure 1. For small dead-rise angles, the jet is thin. The jet root is also known as the ‘overturning region’, or the ‘inner flow region’ (see Howison, Ockendon & Wilson Reference Howison, Ockendon and Wilson1991). The jet-root region is elevated above the 
$x$-axis (the equilibrium water level), and is adjacent to the body surface. The jet root moves to the right, along the surface of the body. The 
$x$-coordinate of the point on the free surface where the tangent to the free surface is vertical is denoted by 
$x=x_c(t)$. We also use the notation 
$x=x_{c}(t, 0)$ to describe the coordinate of this point in the absence of gravity, 
$g=0$; see § 3. Note that the elevation of the water surface, which is caused by displacement of the water by the entering body, increases the width of the wetted part of the body boundary. On the right of the turnover point 
$x_c(t)$, there is a separation point, where the jet separates from the surface of the body. The separation point is not shown in figure 1. The jet separates from the body surface because of the surface curvature (see Howison et al. Reference Howison, Ockendon and Wilson1991), and, because of gravity, this forces the jet to overturn and finally to collide with the free surface underneath (see Sun & Faltinsen Reference Sun and Faltinsen2007). The position of the separation point, and therefore the wetted part of the impacting body, is strongly affected by gravity. The jet flow with the effect of gravity is not covered in this paper; see Zekri (Reference Zekri2016) for more details.
Figure 1. Water impact by a symmetric body. Sketch of the flow and notation.
According to Wagner (Reference Wagner1932), the jet-root region is so small that one can make some approximations that allow one to neglect fine details of the flow in this region and hence calculate approximately the free-surface elevation, the distribution of the hydrodynamic pressure in the contact region, the size of this contact region and the total hydrodynamic force acting on the entering body. For small dead-rise angles, of the order of 
$O(\epsilon )$ say, where 
$\epsilon \ll 1$, the relative size of the jet-root region is of the order of 
$O(\epsilon ^2)$ (see Howison et al. Reference Howison, Ockendon and Wilson1991). Therefore, at leading order as 
$\epsilon \rightarrow 0$, the jet-root region can be treated as the point at which the slope of the water surface turns over to be vertical, producing a very thin spray jet; see figure 2. The hydrodynamic pressure peaks in the jet-root region and quickly decays down to atmospheric pressure with distance along the body surface towards the separation point. The thin spray jet starts at the periphery of the jet-root region there, where the hydrodynamic pressure is close to the ambient pressure above the liquid. The spray jet is neglected at leading order in this approximation as 
$\epsilon \rightarrow 0$. Then 
$x=x_c(t)$ becomes the coordinate of the right-hand contact point, where the free surface rises up and meets the surface of the body (see Wagner Reference Wagner1932; Howison et al. Reference Howison, Ockendon and Wilson1991). The jet-root region can be neglected, as it has little effect on the pressure field in the rest of the fluid domain far from the contact point 
$x=x_c(t)$. On the other hand, the jet-root region and the spray jet itself make a sink of mass, momentum and kinetic energy, from the viewpoint of the rest of the fluid domain. They also provide important contributions to higher-order solutions of the water impact problem (see Korobkin Reference Korobkin2007).
Figure 2. Sketch of the flow in the jet-root region. Note that there is a point on the free surface where the tangent to this surface is vertical.
There are several physical phenomena that affect the water entry process but are usually neglected in modelling. The surface tension on the liquid surface can be neglected at leading order when the size of the body is much larger than the capillary length 
$(\sigma / (\rho g))^{1/2}$, where 
$\sigma$ is the surface tension coefficient, 
$\rho$ is the liquid density and 
$g$ is the gravitational acceleration. This is the case for problems in ship hydrodynamics and wave impact on coastal and offshore structures. For an air–water interface, the capillary length is approximately 2.7 mm. The viscosity of the liquid can be neglected when the body velocity 
$V$ is not very small compared with 
$\nu /L$, where 
$\nu$ is the kinematic viscosity of the liquid and 
$L$ is the length scale of the body (see Korobkin & Pukhnachov Reference Korobkin and Pukhnachov1988). For water at room temperature, the kinematic viscosity is approximately 
$1.0035\times 10^{-6}$ m
$^2$ s
$^{-1}$. In water entry problems for a ship, we anticipate the Reynolds number 
$V L / \nu$ to be so much greater than unity that we may neglect viscosity. The presence of air between the water and the body may be important for hull shapes with very small dead-rise angles. Then air can be trapped as a single cavity or as several bubbles between the body and the water (see Wilson Reference Wilson1991; Khabakhpasheva, Korobkin & Malenica Reference Khabakhpasheva, Korobkin and Malenica2013).
The leading-order corrections of the simplified model solution during the initial stage for surface tension, liquid viscosity and nonlinear effects can be obtained independently for each effect using perturbation analysis. This technique was used in Korobkin & Pukhnachov (Reference Korobkin and Pukhnachov1988) to determine the correction due to a horizontal component of the impact velocity, and in Korobkin (Reference Korobkin1997) to determine the leading-order correction due to the liquid viscosity. These corrections were obtained for the main flow region and during the early impact stage. The leading-order corrections due to the surface tension and viscous effects on the flow in the jet-root region were obtained by Moore et al. (Reference Moore, Ockendon, Ockendon and Oliver2014). Uniformly valid solutions of the impact problems taking account of the mentioned corrections have not been obtained so far. The matching of the asymptotic solutions in the main flow region, in the jet-root region and in the spray jet requires comparison of the orders of all included effects, in contrast to the asymptotic solutions in each of the subregions separately. Note that the air-cushion effect is more difficult to account for and analyse because this effect changes the scenario of the impact. It is still unclear how to match the pre-impact stage with the air-cushion effect and the Wagner-type impact model; see recent papers by Ross & Hicks (Reference Ross and Hicks2019) and Moore (Reference Moore2021). In the present study, we focus on the correction to the solution in the main flow region, which lacks both the jet-root region and the spray jet, caused by gravity.
Gravity can be neglected in the leading order when the acceleration of the liquid particles caused by the impact is much greater than the acceleration due to gravity, 
$g$. The fluid acceleration depends on the impact speed 
$V$ and the dead-rise angle of the body surface, that is, on how quickly the impact occurs. A high speed of impact and/or a small dead-rise angle provide high accelerations of the liquid particles. If the fluid acceleration is comparable with 
$g$, then gravity should be included in the model, as occurs, for example, with slow impact speeds. However, even when gravity is formally of the same order of magnitude as the fluid inertia, the effect of gravity on the size of the wetted region, the elevation of the free surface and the hydrodynamic loads is still small and can be approximately neglected. Supporting evidence comes, in particular, from numerical studies of water entry problems (see Bertram Reference Bertram2000). This is also confirmed and explained in the present paper through asymptotic analyses of the early stage of water impact.
The effect of gravity changes the flow and the hydrodynamic pressure caused by the impact differently in different parts of the flow region and in different stages of the impact. The present study is focused on the initial stage, when the impact loads are high and the total hydrodynamic force peaks as a function of time. We do not consider the later stage, when the body is already completely wetted and continues to penetrate into the liquid with a cavity behind it. The cavity evolution and its final collapse are strongly dependent on gravity (see Bao, Wu & Xu Reference Bao, Wu and Xu2016). We do not consider also other impact configurations, such as wave impact and a floating plate impact, where gravity can provide an important contribution (see Sun & Wu Reference Sun and Wu2020).
The effect of gravity on the flow characteristics during the early stage is not obvious. The present study was, in particular, motivated by the paper of Khabakhpasheva et al. (Reference Khabakhpasheva, Korobkin, Maki and Seng2016), where water entry of a wedge with dead-rise angle of 45
$^{\circ }$, initial speed 
$4$ m s
$^{-1}$ and deceleration 
$3g$ was studied both by computational fluid dynamics (CFD) and simplified impact models. The maximum magnitude of the force, which occurs at 
$t=0.12$ s after the instant of impact, was overpredicted by 25 % without accounting for gravity. Here we concentrate on the effect of gravity on the characteristics of the flow in the main flow region. The fine details of the flow in the jet-root region and the spray jet are not included in the present analysis.
The results on the effects of gravity obtained so far are mainly numerical and experimental. We are unaware of any previous theoretical studies of gravity effects on water impact. As can be seen from the analysis of the present paper, the theoretical study of gravity effects is complicated even using the perturbation method for the initial stage of impact. Numerical analysis of gravity effects is more straightforward. Including gravity into a fully nonlinear potential flow solver does not significantly change the algorithms. There is a difficulty with numerical modelling in the position of the separation point on the body surface (see Sun & Faltinsen Reference Sun and Faltinsen2007), but, even by simply ignoring this difficulty (see Sun, Sun & Wu Reference Sun, Sun and Wu2015), the numerical solution is very reasonable. This might be caused by a small contribution of the position of the separation point to the total force. Careful determination of the separation point requires a special treatment (see Sun & Faltinsen Reference Sun and Faltinsen2007). Below, several papers that analyse the effects of gravity on water impact and on the results, which will be used as references in our study, are described.
Mackie (Reference Mackie1965) studied the free-surface elevation, with and without gravity, for the water entry of a slender symmetric wedge. His analysis showed that, far from the body, gravity raises the water surface and, near the body, gravity pulls it down, relative to the gravity-free case. He showed also that, far from the body, the increase in free-surface elevation due to gravity grows linearly with time. The asymptotic analysis of the present paper confirms this result, but for a blunt symmetric body. Greenhow (Reference Greenhow1987) studied numerically the vertical water entry of a wedge with gravity included. He concluded that it is acceptable to neglect gravity in computations when 
$t\leq V/(2g)$, except for the description of the jets. Compared with the zero-gravity results, he found a small difference in the magnitude of the hydrodynamic pressure in the wetted part of the wedge surface, with a slight decrease of the pressure in the jet region. The jets moved along the wedge surface slightly slower when gravity is included. He reported that the jets can separate from the surface of the wedge because of gravity (see also Sun & Faltinsen Reference Sun and Faltinsen2007). Asymptotic analysis of the effect of gravity on jet flow was performed by Zekri (Reference Zekri2016), who confirmed the numerical findings. An asymptotic analysis of the jets is not included in the present paper.
Seif et al. (Reference Seif, Mousaviraad, Saddathosseini and Bertram2005) used a CFD package to solve numerically the Reynolds-averaged Navier–Stokes equations. One of their example computations is for water entry of a semicircular cylinder, of radius 
$5.5$ m, descending into water at speed 
$V = 10$ m s
$^{-1}$. They computed the pressure peaks as the cylinder penetrates into the water. Surface tension, gravity and turbulence were included in their computations. They also performed computations in which these three effects were individually switched off. They wrote: ‘Only gravity was found to have a significant effect in this case, with results for the slamming force coefficient being approximately 
$23.2\,\%$ lower without gravity.’ Our asymptotic analysis reveals that the gravity contribution to the total hydrodynamic force increases in time as 
$t^{3/2}$ during the early stage.
Sun & Faltinsen (Reference Sun and Faltinsen2007) developed a ‘
$2\mathrm {D}+t$’ theory with gravity to describe steady three-dimensional planing flows at high and moderate Froude numbers. They used a time-dependent two-dimensional boundary-element method. Their results demonstrated that gravity becomes more important for moderate-Froude-number flows than for high-Froude-number ones. Gravity lowers the spray jets. They found a negligible effect of gravity on the vertical force before the chines are wetted. The effect of gravity is more pronounced after the flow reaches the chines and the hydrostatic force becomes dominant for the moderate-Froude-number case. By subtracting the hydrostatic force from the total vertical force, they found very close but not identical results for the dynamic component of the forces for Froude numbers equal to 
$2.5$ and 
$5$. They wrote: ‘So gravity also influences the hydrodynamic part of the force. This is because gravity will change the fluid flow around the hull and affect the free-surface elevation, as one can see from figure 14. Therefore, simply adding the hydrostatic force to the lift force obtained by neglecting gravity cannot fully account for the influence of gravity.’ Our asymptotic analysis reveals that the dynamic component of the gravity correction to the impact force increases the total force by 6 %.
Similar results were reported by Tveitnes, Fairlie-Clarke & Varyani (Reference Tveitnes, Fairlie-Clarke and Varyani2008). They performed an experimental investigation of the vertical water entry of wedges at constant speed. They estimated the impact force acting on the wedge from an empirical formula derived by Fairlie-Clarke & Tveitnes (Reference Fairlie-Clarke and Tveitnes2008). They explained that the total force comprises a ‘hydrostatic force’, a ‘residual gravity force’, which is defined as that part of the force that does some work against gravity to lift up the water splash above the still-water level, and a ‘hydrodynamic force’, which is due to the rate of change of the added-mass momentum and the flow momentum. In addition to hydrostatic forces, gravity can affect the water entry forces by changing the flow regime and the wetted width, and because work must be done to lift the water in the splash jets. In the present paper, we do not use the force decomposition as suggested by Tveitnes et al. (Reference Tveitnes, Fairlie-Clarke and Varyani2008) because we did not find an easy way to identify different contributions to the force from separate effects. Sun et al. (Reference Sun, Sun and Wu2015) studied the oblique water entry of a wedge into waves including gravity, using a boundary-element method with fully nonlinear boundary conditions. They concluded that: ‘The gravity effect is unimportant when the impact time is much less than the ratio of the entry speed to the acceleration due to the gravity. It becomes increasingly important for the pressure distribution as the impact time progresses. It will alter the shape of the pressure distribution, the location and the peak of pressure, and very noticeably the large pressure gradient near the jet root. As time continues, the gravity would eventually pull the water down and attached flow will no longer be valid.’
Khabakhpasheva et al. (Reference Khabakhpasheva, Korobkin, Maki and Seng2016) investigated the water entry and exit of a symmetric wedge with large displacement and non-constant speed. They used three mathematical models (see Korobkin Reference Korobkin2004), and CFD to study the pressure distribution along the wetted part of the wedge and the hydrodynamic force acting on the wedge during both the entry and exit stages. In their study, a significant contribution of gravity on the force appeared at the end of the entry stage. A similar problem (only for the entry stage) was previously studied by Khabakhpasheva, Kim & Korobkin (Reference Khabakhpasheva, Kim and Korobkin2014) using the generalised Wagner model and numerical conformal mapping.
In the present paper, we study the early stage of a two-dimensional, symmetric, potential flow caused by water entry of a parabolic body at constant speed 
$V$. The penetration depth of the body is much smaller that the horizontal dimension of the wetted part of the body surface during this early stage. The presence of air, surface tension and liquid viscosity are neglected but gravity is included in the model. The problem is formulated and its asymptotic analysis is performed in § 2. Two dimensionless parameters of the problem are identified. The first one, 
$\epsilon =(VT/R)^{1/2}$, where 
$T$ is the time scale of the impact and 
$R>0$ is the radius of curvature of the body surface at the point of first contact, appears as a coefficient of all the nonlinear terms in the boundary conditions and the Bernoulli equation for the hydrodynamic pressure. The second parameter, 
$\delta =\epsilon ^3gRV^{-2}$, is the coefficient of the gravity term in the Bernoulli equation. Our asymptotic analysis is based on the inequalities 
$\epsilon \ll \delta \ll 1$, which imply that the entry speed is small, and the stage immediately after the start of the body motion is not covered. The problem is complicated because both the equations of the flow and the dimension of the contact region, between the water and the entering body, depend on the small parameters. In the limit 
$\epsilon \to 0$, the equations and boundary conditions of the problem are linearised, but the limiting problem still depends on another small parameter 
$\delta$. An asymptotic two-term solution of the linearised problem as 
$\delta \to 0$ is obtained in § 3 in stretched coordinates. It is shown that the effect of gravity on the width of the contact region is small even for relatively large 
$\delta$. The leading-order corrections to the pressure distribution, hydrodynamic force and the free-surface elevation caused by gravity are studied in §§ 4, 5 and 6, respectively. Conclusions are drawn in § 7.
The aim of our paper is to quantify the meaning of ‘gravity is negligible during the impact stage’, putting the known results on a solid mathematical footing. We are unaware of existing estimates of gravity effects on water impact.
Let us think about water wave impact on a structure (see Zekri Reference Zekri2016). A water wave is governed by gravity. The impact conditions are governed by gravity. However, the impact loads caused by wave impact are only weakly dependent on gravity. We believe this is an interesting question. We show in this paper that arguments based on the Froude number, 
$Fr= V/({gR})^{1/2}$, where 
$V$ is the impact velocity, 
$g$ is the gravitational acceleration and 
$R$ is the linear scale of the problem, could be misleading. Gravity can still be neglected even though the Froude number is small. This is the parameter, 
$\delta =\epsilon ^3/Fr^2$, that is responsible for the gravity effects in water impact problems. Gravity can be neglected if 
$\delta$ is small. This is not the end of the story about gravity. The size of the wetted part of the body is weakly dependent on gravity, even if 
$\delta$ is moderate, say 
$\delta =2$. This is because the corrections for gravity in the asymptotic formulae of this paper are not only about the orders of these corrections (all of them are of the order of 
$O(\delta )$) but also about the coefficients in these formulae. If a coefficient is small, then the correction is small even if the parameter of the asymptotic analysis is not very small. This occurs with the size of the contact region but not with the pressure, the total force and the free-surface elevation. The asymptotic behaviour of the size of the contact region as 
$\delta$ tends to zero is important because this is the size of the contact region, which makes the problem nonlinear, even after all possible simplifications have been made. A surprising result is that this size is weakly dependent on gravity, even though gravity is important for other quantities of the flow.
2. Formulation of the problem
We consider the initial stage of water impact by a smooth body with constant speed 
$V$. The duration of this stage, 
$T$, is formal and such that the body penetration, 
$VT$, is much smaller than a characteristic length scale of the flow. The problem is formulated within the theory of two-dimensional, symmetric and potential flows.
2.1. Main unknowns and their scales
In this subsection, notation and the scales of the main variables describing the early stage of water impact are introduced. Initially, the liquid occupies the lower half-plane, 
$y<0$, and is bounded from above by the flat free surface, 
$y=0$. The position of the body surface is described by the equation
\begin{equation} y= \frac{x^2}{2R}-Vt, \end{equation}
where 
$R$ is the radius of curvature of the body's surface and 
$t$ is the time variable. Initially, 
$t=0$, the parabolic body (2.1) touches the liquid free surface, 
$y=0$, at a single point, 
$x=0$. In general, any smooth symmetric body can be approximated by a parabolic contour (2.1) near the impact point during the early stage of impact.
The linear scale of the flow region, 
$X_{sc}$, is proportional to the coordinate 
$x_c(T)$ of the turnover point; see figure 1. However, the function 
$x_c(t)$ is unknown in advance and should be determined as part of the solution. We can argue that, during the initial stage, 
$x_c(t)$ is of the same order as the coordinate 
$x_k(t)$ of the intersection point between the moving contour (2.1) and the initial position of the liquid free surface, 
$y=0$; see figure 1. The points 
$x=\pm x_k(t)$ are known as the von Kármán contact points (von Kármán Reference von Kármán1929), which separate the contact region 
$-x_k(t)<x<x_k(t)$ from the free surfaces, 
$y=0$, 
$x<-x_k(t)$ and 
$x>x_k(t)$, in the von Kármán water impact model, which does not account for the elevation of the free surface during the impact. Setting 
$y=0$ in (2.1), one finds 
$x_k(t)=\sqrt {2RVt}$. This gives 
$X_{sc}=\sqrt {RVT}$.
The duration of the initial stage, 
$T$, is defined by the condition that the displacement of the body during this stage, 
$VT$, is much smaller than the linear scale of the flow region, 
$X_{sc}$. Therefore, the duration 
$T$ is such that the ratio 
$VT/X_{sc}=\sqrt {VT/R}=\epsilon$ is small compared with unity. The non-dimensional parameter 
$\epsilon$ plays the role of a small parameter in the problem under consideration. Note that 
$T=\epsilon ^2 R/V$ and 
$X_{sc}=\epsilon R$, which imply that the length scale of the flow region during the initial stage is much smaller than the characteristic scale, 
$R$, of the body shape. This observation makes it possible to approximate any smooth shape by the parabolic contour (2.1), where 
$x=O(X_{sc})$.
The flow generated by the impact is described by a velocity potential 
$\varphi (x, y, t)$. The position of the free surface is given by the equation 
$y=\eta (x, t)$, where 
$|x|>x_c(t)$. The water entry problem is considered below in dimensionless variables. The dimensionless variables denoted by a hat are introduced by 
$x=X_{sc}\hat {x}$, 
$y=X_{sc} \hat {y}$ and 
$t=T \hat {t}$. The scales of the velocity potential, the free-surface elevation and the function 
$x_c(t)$ are 
$X_{sc}V$, 
$VT$ and 
$X_{sc}$, respectively. Then 
$\varphi =X_{sc}V\hat {\varphi }(\hat {x}, \hat {y}, \hat {t})$, 
$\eta =V T \hat {\eta }(\hat {x}, \hat {t})$ and 
$x_c(t)=X_{sc}\hat {x}_c(\hat {t})$. The hydrodynamic pressure 
$p(x, y, t)=\rho V^2 \epsilon ^{-1}\hat {p}(\hat {x}, \hat {y}, \hat {t})$ in the liquid is related to the velocity potential 
$\hat {\varphi }$ by the nonlinear Bernoulli equation, which reads
\begin{equation} -\hat{p} (\hat{x}, \hat{y}, \hat{t} )=\frac{{\partial}\hat{\varphi}}{{\partial}{\hat{t}}} +\frac{1}{2}\epsilon|\hat{\boldsymbol{\nabla}}\hat{\varphi}|^2 +\frac{\delta}{\epsilon}\hat{y},\quad \delta=\frac{gR}{V^2}\epsilon^3, \end{equation}
in the dimensionless variables, where 
$\rho$ is the liquid density and 
$g$ is the gravitational acceleration. The atmospheric pressure is set to zero. The last term in (2.2a,b) corresponds to the hydrostatic component of the pressure in the liquid, which is 
$\rho g y$ in the dimensional variables. The dimensionless parameter 
$\delta$ describes the gravity effect on the flow caused by the impact. This parameter can be presented as 
$\delta =\epsilon ^3 Fr^{-2}$, where 
$Fr=V/\sqrt {gR}$ is the Froude number and 
$\epsilon$ is the small parameter indicating that the early stage of the impact is of concern. Therefore, the effect of gravity is characterised not only by the Froude number but also by the small parameter 
$\epsilon$, which is specific for impact processes.
In the dimensionless variables, the position of the body is described by the equation 
$\hat {y}=\epsilon (\hat {x}^2/2-\hat {t})$, and the position of the free surface by the equation 
$\hat {y}=\epsilon \hat {\eta }(\hat {x},\hat {t})$, where 
$|\hat {x}|>\hat {x}_c(\hat {t})$. Note that the function 
$\hat {\eta }(\hat {x},\hat {t})$ can be multivalued; see figure 1 and Oliver (Reference Oliver2002). Only the dimensionless variables are used below. The hat is dropped for convenience.
2.2. Equations of the flow and boundary conditions
The mathematical formulation of the problem is presented in this subsection. The velocity potential 
$\varphi (x, y, t)$ satisfies Laplace's equation
\begin{equation} \frac{\partial^2 {\varphi}}{\partial {x}^2}+\frac{\partial^2 {\varphi}}{\partial { y}^2}=0 \end{equation}in the flow region
\begin{equation} \varOmega(t)= \{x, y\,|\, y < \epsilon(x^2/2-t),\ |x| < x_c(t)\ \mbox{and}\ y < \epsilon\eta(x, t), |x| > x_c(t) \},\end{equation}the boundary condition
\begin{equation} \frac{{\partial}\varphi}{{\partial} y}=\epsilon x \frac{{\partial}\varphi}{{\partial} x}-1 \end{equation}
on the wetted part of the body surface, 
$y=\epsilon (x^2/2-t)$, where 
$|x| < x_c(t)$, the kinematic boundary condition
\begin{equation} \frac{{\partial}\varphi}{{\partial} y}=\epsilon x \frac{{\partial}\eta}{{\partial} x} \frac{{\partial}\varphi}{{\partial} x}+\frac{{\partial}\eta}{{\partial} t} \end{equation}and the dynamic boundary condition
\begin{equation}
\frac{{\partial}\varphi}{{\partial}
t}+\frac{1}{2}\epsilon|\boldsymbol{\nabla} \varphi|^2
+\delta \eta= \frac{\epsilon}{{We}} \,\frac{\partial^2
{\eta}}{\partial { x}^2}\left(1+\epsilon^2
\left(\frac{{\partial}{\eta}}{{\partial}{x}}\right)^2\right)^{{-}3/2} \end{equation}
on the free surface, 
$y=\epsilon \eta (x,t)$, where 
$|x|>x_c(t)$. Here 
$We=\rho V^2R/\sigma$ is the Weber number and 
$\sigma$ is the coefficient of surface tension. The initial conditions are
\begin{equation} \varphi(x, y, 0)=0, \quad \eta(x, 0)=0 \quad\text{and}\quad x_c(0)=0 \end{equation}
at 
$t=0$, and the far-field conditions are
\begin{equation} \varphi\to 0 \quad\text{and}\quad \eta\to 0 \quad (x^2+y^2\to\infty ). \end{equation}In addition, we require that the free surface is below the surface of the moving body at any time of the motion,
\begin{equation} \eta(x, t)<\tfrac{1}{2}x^2-t \quad (|x|>x_c(t) ). \end{equation}2.3. Dimensionless parameters of the problem
In this subsection, we discuss the main parameters of the problem and their values in different situations. The conditions of the present study are also specified.
More details are given now about the three non-dimensional parameters, 
$\epsilon$, 
$\delta$ and 
$We$, in the formulated problem (2.3)–(2.10). The small parameter 
$\epsilon$ stands as the coefficient of the nonlinear terms. It can be considered as a parameter of the linearisation of the problem. The parameter 
$\delta$ is responsible for the gravitational effects. These effects can be neglected at leading order if the impact conditions are such that 
$\delta \ll 1$. The Weber number, 
$We$, describes the importance of the capillary effects on the flow generated by the blunt-body impact. The coefficient in (2.7) is equal to
\begin{equation} \frac{\epsilon}{{We}}=\left(\frac{a}{\epsilon R}\right)^2\delta, \end{equation}
where 
$a=\sqrt {\sigma /\rho g}$ is the capillary length; 
$a=2.7$ mm for water at temperature 
$20{\,}^{\circ }$C. Therefore, the capillary effects can be neglected in the dynamic condition (2.7) compared with the effect of gravity if 
$a/(\epsilon R)\ll 1$. That is, the length scale, 
$\epsilon R$, of the flow region is much greater than the capillary length. The capillary length depends only on the liquid characteristics.
The nonlinear term on the left-hand side of (2.7) can be neglected compared with the gravity term if 
$\epsilon \ll \delta$. This inequality together with the inequality obtained above, 
$\epsilon \gg a/R$, and the definition of the small parameter, 
$\delta =\epsilon ^3gR/V^2$, mean that both the nonlinear term and the capillary term in condition (2.7) can be neglected compared with the gravity term if
\begin{equation} \frac{V}{\sqrt{gR}}\ll \epsilon,\quad \frac{a}{R}\ll \epsilon. \end{equation}
The inequalities (2.12a,b) are not satisfied during the very early stage of impact when the size of the contact region is as small as either the capillary length 
$a$ or 
$O(V\sqrt {R/g})$. In the present study, we are concerned with the effect of gravity on the flow and the hydrodynamic loads during the early stage of water impact. This effect is not negligible only under conditions (2.12a,b).
The gravity effect is as important as the inertia effect during the water impact if we put 
$\delta =1$, which gives expressions for the parameter 
$\epsilon$ and the time scale 
$T$,
\begin{equation} \epsilon=\left(\frac{V^2}{{gR}}\right)^{1/3},\quad T=\left(\frac{RV}{{g^2}}\right)^{1/3}. \end{equation}
For example, for 
$V=0.5$ m s
$^{-1}$, 
$g=9.81$ m s
$^{-2}$ and 
$R=10$ m, we find 
$\epsilon =0.136$ and 
$T=0.373$ s. Such a parabolic body penetrates water to a depth less than 20 cm at 
$t=T$, which is much smaller than the characteristic length of the body 
$R$.
Below, we restrict ourselves to the case where the gravity effect is still small compared with the fluid inertia but stronger than both surface tension and nonlinear effects:
\begin{equation} \epsilon\ll \delta\ll 1. \end{equation}
This range of the parameter 
$\delta$ corresponds to the stage of the impact when
\begin{equation} \frac{V}{g}\ll T \ll \left(\frac{RV}{g^2}\right)^{1/3}, \end{equation}or, in terms of the quantity introduced by Greenhow (Reference Greenhow1987),
\begin{equation} 1\ll \frac{gT}{V}\ll \left(\frac{gR}{V^2}\right)^{1/3}. \end{equation}
Note that, on the basis of his numerical results, Greenhow (Reference Greenhow1987) suggested that gravity can be safely neglected during the early stage when 
$gT/V\leq 1/2$. For impact with 
$V=0.5$ m s
$^{-1}$, 
$g=9.81$ m s
$^{-2}$ and 
$R=10$ m, inequalities (2.15) provide 
$0.05~\mathrm {s} \ll T \ll 0.4~\mathrm {s}$.
2.4. Asymptotic model of water impact with gravity
A Wagner-type model of water impact is derived in this subsection for the initial stage of impact. Letting 
$\epsilon \to 0$ in (2.3)–(2.10) and using (2.14), we conclude that at leading order the flow domain (2.4) can be approximated by the lower half-plane, 
$y<0$, where
\begin{equation} \frac{\partial^2 {\varphi}}{\partial {x}^2}+\frac{\partial^2 {\varphi}}{\partial {y}^2}=0 \quad (y<0). \end{equation}
The kinematic boundary conditions (2.5) and (2.6) can be linearised and imposed on the undisturbed liquid boundary, 
$y=0$, in the intervals 
$|x|<x_c(t)$ and 
$|x|>x_c(t)$, respectively:
\begin{gather} \frac{{\partial}\varphi}{{\partial} y} ={-}1 \quad (y=0,\ |x| < x_c(t) ), \end{gather}
\begin{gather}\frac{{\partial}\varphi}{{\partial} y} = \frac{{\partial}\eta}{{\partial} t}\quad (y=0,\ |x|>x_c(t) ). \end{gather}The initial (2.8a–c) and far-field (2.9a,b) conditions do not change, and the dynamic condition (2.7) takes the form
\begin{equation} \frac{{\partial}\varphi}{{\partial} t}+\delta\eta=0\quad (y=0,\ |x|>x_c(t) ). \end{equation} Note that the original notation is used for the limiting values of the unknown functions as 
$\epsilon \to 0$. The linearised hydrodynamic problem (2.17)–(2.20), (2.8a–c) and (2.9a,b) should be supplemented by an equation for the coordinate of the contact point 
$x_c(t)$. Such an equation was suggested by Wagner (Reference Wagner1932) and it is known as the Wagner condition in water impact problems. The condition requires that the elevation of the free surface at the contact point, 
$x=x_c(t)$, is equal to the vertical coordinate of the body surface at this point,
\begin{equation} \eta(x_c(t), t)=\tfrac{1}{2}x_c^2(t)-t. \end{equation}
The Wagner condition (2.21) implies that the free surface, 
$y=\epsilon \eta (x, t)$, of the linearised water impact problem matches the body surface without the jet and without the jet-root region between them. Wagner (Reference Wagner1932) explained how to include both the jet-root and jet regions in the solution. The heuristic approach by Wagner was justified and formalised through asymptotic methods by Howison et al. (Reference Howison, Ockendon and Wilson1991). The jet root is attached to the body, but the jet flow is not necessarily attached to the body. We only assume that the upper edge of the jet root is tangent to the body surface (see Semenov & Wu Reference Semenov and Wu2019).
2.5. Displacement potential in the Wagner-type problem with gravity
The problem of the initial stage of water impact with gravity is formulated using a displacement potential. It is explained at the end of the subsection how the present problem is different from the classical Wagner problem and how this difference makes the problem complicated for analysis.
The Wagner condition (2.21) is difficult to implement within the formulated problem of impact with account for gravity. It is convenient to introduce a so-called displacement potential 
$\phi (x, y, t)$, defined as the time integral of the velocity potential,
\begin{equation} \phi (x, y, t ) = \int_{0}^{t}\varphi (x, y, \tau ) \, \mathrm{d}\tau \end{equation}
(see Korobkin Reference Korobkin1982, Reference Korobkin1996; Howison et al. Reference Howison, Ockendon and Wilson1991). The boundary-value problem with respect to the displacement potential 
$\phi (x, y, t)$ is derived by integrating (2.17)–(2.20) and (2.9a,b) in time, and using (2.22). The body boundary condition (2.18) is the most difficult one to integrate; the conditions (2.19) and (2.21) are used to perform the integration. The resulting boundary-value problem for 
$\phi (x, y, t)$ reads
\begin{gather} \frac{\partial^2 {\phi}}{\partial {x}^2}+\frac{\partial^2 {\phi}}{\partial {y}^2}=0\quad (y<0,\ t>0), \end{gather}
\begin{gather}\frac{\partial^2 {\phi}}{\partial {t}^2}+\delta\frac{\partial {\phi}}{\partial {y}}=0\quad (y=0,\ |x|>x_c(t,\delta)), \end{gather}
\begin{gather}\frac{\partial {\phi}}{\partial {y}}=\frac{1}{2}x^2-t\quad (y=0,\ |x| < x_c(t,\delta)), \end{gather}
\begin{gather}\phi(x, y, 0)=0,\quad \frac{\partial {\phi}}{\partial {t}}(x, y, 0)=0, \end{gather}
\begin{gather}\phi(x, y, t){\rightarrow 0} \quad (x^2+y^2\to \infty). \end{gather}The elevation of the free surface is given by
\begin{equation} \eta(x, t)= \frac{\partial {\phi}}{\partial {y}}(x, 0, t),\end{equation}and the pressure in the contact region is given by the linearised Bernoulli equation
\begin{equation} -p(x, 0, t)=\frac{\partial^2 {\phi}}{\partial {{t}}^2}+\delta\left(\frac{x^2}{2}-t\right)\quad (|x| < x_c(t,\delta)),\end{equation}
where the second term on the right-hand side corresponds to the hydrostatic pressure. The Wagner condition (2.21) together with (2.25) and (2.28) imply that the potential 
$\phi (x, y, t)$ is required to be continuous up to the boundary, together with its first derivatives in 
$x,\ y$ and 
$t$. In particular, continuity of the derivative 
$ {\partial }{\phi }/{ {\partial } y}$ on the boundary, 
$y=0$, at the contact point, 
$x=x_c(t)$, is equivalent to the Wagner condition (2.21) (see Korobkin Reference Korobkin1996). In the following, the function 
$x_c(t)$ is determined from the condition that the displacements 
$\phi _x$ and 
$\phi _y$ are finite in 
$y\leq 0$ including the contact points.
The hydrodynamic problem (2.23)–(2.28) is linear. However, the function 
$x=x_c(t)$ is unknown in advance and should be selected in such a way that the displacements, 
$\boldsymbol {\nabla } \phi$, of the liquid particles are finite in the flow region 
$y<0$ up to the boundary, 
$y=0$. The equation for 
$x=x_c(t)$ derived in Korobkin (Reference Korobkin1996) cannot be used for the present problem with gravity, where 
$\phi (x, 0, t)\neq 0$ on the free surface, in contrast to the entry problem without gravity, where 
$\phi (x, 0, t)=0$.
The parameter 
$\delta$ is the only parameter of the formulated problem (2.23)–(2.27). In the asymptotic analysis of this paper, we assume that 
$\delta \ll 1$ and investigate the corrections due to gravity to the solution of the problem without gravity, 
$\delta =0$. Only the leading-order corrections will be determined.
3. First-order displacement potential
Both the displacement potential 
$\phi (x, y, t, \delta )$ and the function 
$x_c(t, \delta )$ depend on the small parameter 
$\delta$. We are concerned with the asymptotic behaviours of these unknown functions as 
$\delta \to 0$. The asymptotic analysis is non-trivial because the positions of the contact points, 
$x=\pm x_c(t, \delta )$, which separate the boundary conditions (2.24) and (2.25), also depend on the parameter 
$\delta$. The solution of the problem for 
$\delta =0$ is well known (see Wagner Reference Wagner1932). In particular, 
$x_c(t, 0)=2\sqrt {t}$, and the velocity potential in the contact region is 
$\varphi (x, 0, t, 0)=-\sqrt {4t-x^2}$, where 
$|x|<2\sqrt {t}$.
To make the problem (2.23)–(2.28) suitable for asymptotic analysis as 
$\delta \to 0$, we introduce new stretched variables,
\begin{equation} \tilde{x}=x\frac{x_c(t, 0)}{x_c(t, \delta)}, \quad \tilde{y}=y\frac{x_c(t, 0)}{x_c(t, \delta)}, \quad \tilde{\phi} (\tilde{x}, \tilde{y}, t, \delta )=\phi(x, y, t, \delta), \end{equation}denoted by tilde, and search for asymptotic expansions of the unknown functions
\begin{gather} \tilde{\phi} (\tilde{x}, \tilde{y}, t, \delta ) =\tilde{\phi}_0 (\tilde{x}, \tilde{y}, t ) +\delta\tilde{\phi}_1 (\tilde{x}, \tilde{y}, t )+O (\delta^2), \end{gather}
\begin{gather}x_c (t, \delta )=x_{c} (t, 0 ) (1+\delta x_{1}(t)+O (\delta^2)). \end{gather}
Note that the size of the contact region is independent of 
$\delta$ in the new stretched variables, 
$|\tilde {x}| < x_c(t, 0)$. The potentials 
$\tilde {\phi }_0$ and 
$\tilde {\phi }_1$ satisfy the Laplace equation in 
$\tilde {y}<0$ and vanish at infinity. The boundary conditions for these potentials are derived below. The body boundary condition (2.25) in the new stretched variables reads
\begin{align} \frac{\partial {\phi}}{\partial {\tilde{y}}} &= \frac{x_c(t, \delta)}{x_c(t, 0)} \left(\frac{x_c^2(t, \delta)}{2x_c^2(t, 0)}\tilde{x}^2-t\right) \nonumber\\ &= (1+\delta x_1(t)+O (\delta^2)) \left( (1+2\delta x_1(t)+O (\delta^2))\frac{\tilde{x}^2}{2}-t\right). \end{align}This provides us with the boundary conditions
\begin{equation} \frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{y}}}=\frac{1}{2}\tilde{x}^2-t, \quad \frac{\partial {\tilde{\phi}_1}}{\partial {\tilde{y}}}=x_1(t)\left(\frac{3}{2}\tilde{x}^2-t\right) \quad (\tilde{y}=0, |\tilde{x}| < x_c(t, 0)).\end{equation}The second time derivative on the boundary is approximated as
\begin{equation} \frac{\partial^2 {\phi}}{\partial {{t}}^2}(x, 0, t, \delta)=\frac{\partial^2 {\tilde{\phi}_0}}{\partial {t}^2}(\tilde{x}, 0, t) +\delta\left(\frac{\partial^2 {\tilde{\phi}_1}}{\partial {t}^2}-2\tilde{x}x_1'(t) \frac{\partial^2\tilde{\phi}_0}{\partial \tilde{x}\partial t}-\tilde{x}x_1''(t) \frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{x}}}\right)+O(\delta^2).\end{equation}
The free-surface boundary condition (2.24) and the asymptotic expansions (3.2) and (3.6) provide 
$\partial ^2{\phi }_0/\partial {t^2}=0$, where 
$y=0$ and 
$|\tilde {x}|>x_c(t,0)$, at the leading order as 
$\delta \to 0$. This condition can be integrated in time twice using the initial conditions (2.26a,b), to give
\begin{equation} \tilde{\phi}_0=0 \quad (\tilde{y}=0,\ |\tilde{x}|>x_c(t, 0)). \end{equation}Substituting (3.6) in (2.24) and using (3.7), we find in the first approximation,
\begin{equation} \frac{\partial^2 {\tilde{\phi}_1}}{\partial {{t}}^2}+\frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{y}}}=0\quad (\tilde{y}=0,\ |\tilde{x}|>x_c(t, 0)).\end{equation}
The leading-order displacement potential, 
$\tilde {\phi }_0(\tilde {x}, \tilde {y}, t)$, satisfies the Laplace equation in 
$\tilde {y}<0$ and the boundary conditions (3.5a,b) and (3.7). The leading-order displacements, 
$\tilde {\phi }_{0x}$ and 
$\tilde {\phi }_{0y}$, are required to be bounded in 
$y\leq 0$. The solution of this leading-order problem with bounded displacements can be found in, for example, Korobkin (Reference Korobkin1996):
\begin{gather} x_c(t, 0) = 2\sqrt{t},\quad \tilde{\phi}_0 ({\tilde{x}}, 0, t )={-}\frac{1}{6} (4t-\tilde{x}^2 )^{3/2},\quad (|\tilde{x}|<2\sqrt{t}), \end{gather}
\begin{gather}\frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{y}}} ({\tilde{x}}, 0, t )= \frac{\tilde{x}}{2} (\tilde{x}-\sqrt{\tilde{x}^2-4t} \,)-t,\quad (|\tilde{x}|>2\sqrt{t}). \end{gather}Substituting (3.10) in (3.8) and integrating the condition twice in time by using the initial conditions (2.26a,b) and the far-field condition (2.27), we obtain the first-order displacement potential
\begin{equation} \tilde{\phi}_1 ({\tilde{x}}, 0, t ) =\frac{t^3}{6}-\frac{\tilde{x}^2}{4}t^2+\frac{\tilde{x}^4}{12}t -\frac{\tilde{x}^6}{120}+\frac{\tilde{x}}{120} (\tilde{x}^2-4t )^{5/2} \quad ({\tilde{y}}=0,\ \tilde{x}>2\sqrt{t}),\end{equation}and the first-order horizontal displacement
\begin{equation} \frac{\partial {\tilde{\phi}_1}}{\partial {\tilde{x}}} ({\tilde{x}}, 0,t ) ={-}\frac{\tilde{x}}{2}t^2+\frac{\tilde{x}^3}{3}t-\frac{\tilde{x}^5}{20} +\frac{1}{120} (\tilde{x}^2-4t )^{3/2}(6\tilde{x}^2-4t ) \quad ({\tilde{y}}=0,\ \tilde{x}>2\sqrt{t}),\end{equation}on the right-hand free surface.
The boundary conditions (3.5a,b) and (3.11) and the Laplace equation in 
$y<0$ indicate that the first-order potential 
$\tilde {\phi }_1(\tilde {x}, \tilde {y}, t)$ is self-similar, where
\begin{equation} \tilde{\phi}_1 (\tilde{x}, \tilde{y}, t )=2t^3\varPhi (\xi, \zeta ), \quad x_1(t)=\mu t^{3/2}, \end{equation}and the new self-similar variables are
\begin{equation} \xi=\frac{\tilde{x}}{2\sqrt{t}}, \quad \zeta=\frac{\tilde{y}}{2\sqrt{t}}, \end{equation}
with 
$\mu$ being a constant to be determined.
It is convenient to reformulate the first-order problem with respect to the complex displacement 
${ {\partial }\varPhi }/{ {\partial }\xi }-\mbox {i} { {\partial }\varPhi }/{ {\partial }\zeta }$, which is analytic in the flow region, 
$\zeta <0$, decays at infinity and satisfies the following boundary conditions:
\begin{gather} \frac{\partial {\varPhi}}{\partial {\xi}}={-}\xi+\frac{8}{3}\xi^3-\frac{8}{5}\xi^5+\frac{4}{15} (\xi^2-1 )^{3/2} (6\xi^2-1 )\,\mbox{sgn}(\xi), \quad (\zeta=0,\ |\xi|>1), \end{gather}
\begin{gather}\frac{\partial {\varPhi}}{\partial {\zeta}}=\mu (6\xi^2-1 ), \quad (\zeta=0,\ |\xi|<1). \end{gather} A new unknown function 
${W}(z)=({ {\partial } \varPhi }/{ {\partial }\xi }-\mbox {i} { {\partial }\varPhi }/{ {\partial }\zeta })\sqrt {z^2-1}$, with 
$z=\xi +\mbox {i} \zeta$, has been introduced by Zekri (Reference Zekri2016). The function 
$\sqrt {z^2-1}$ is defined in the complex 
$z$-plane with a cut along the interval 
$\zeta =0$, 
$-1<\xi <1$, in such a way that it is real and positive where 
$\zeta =0$ and 
$\xi >1$. The function 
${W}(z)$ is analytic in 
$\zeta <0$ and decays at infinity. The real part, 
$\mbox {Re}[{W}(\xi -\mbox {i} 0)]$, and imaginary part, 
$\mbox {Im}[{W}(\xi -\mbox {i} 0)]$, of this function on the boundary are related by the Hilbert formula (Gakhov Reference Gakhov1966),
\begin{equation} \mbox{Im}[{W}(\xi-i0)]=\frac{1}{\rm \pi}\,\mbox{p.v.}\int_{-\infty}^{\infty} \frac{\mbox{Re}[{W}(\tau-\mbox{i}0)]}{\tau-\xi}\,\mathrm{d}\tau, \end{equation}where the integral is understood as a Cauchy principal-value (p.v.) integral and
\begin{gather} \mbox{Re}[{W}(\xi-\mbox{i}0)]=\left\{\begin{array}{@{}ll} \displaystyle \dfrac{\partial {\varPhi}}{\partial {\xi}}(\xi, 0) \sqrt{\xi^2-1} & (\xi>1),\\ \displaystyle -\dfrac{\partial {\varPhi}}{\partial {\xi}}(\xi, 0) \sqrt{\xi^2-1} & (\xi<{-}1),\\ \displaystyle -\dfrac{\partial {\varPhi}}{\partial {\zeta}}(\xi, 0) \sqrt{1-\xi^2} & (|\xi|<1), \end{array}\right. \end{gather}
\begin{gather}\mbox{Im}[{W}(\xi-\mbox{i}0)]=\left\{\begin{array}{@{}ll} \displaystyle -\dfrac{\partial {\varPhi}}{\partial {\zeta}}(\xi, 0) \sqrt{\xi^2-1} & (\xi>1),\\ \displaystyle \dfrac{\partial {\varPhi}}{\partial {\zeta}}(\xi, 0) \sqrt{\xi^2-1} & (\xi<{-}1),\\ \displaystyle -\dfrac{\partial {\varPhi}}{\partial {\xi}}(\xi, 0) \sqrt{1-\xi^2} & (|\xi|<1). \end{array}\right. \end{gather} The boundary conditions (3.15) and (3.16) provide that the real part of the unknown function (3.18) on the boundary is given. Therefore, the integral in (3.17) can be evaluated, yielding the first-order vertical displacement, 
${ {\partial }\varPhi }/{ {\partial }\zeta }(\xi , 0)$, on the free surfaces and the horizontal displacement, 
${ {\partial }\varPhi }/{ {\partial }\xi }(\xi , 0)$, in the contact region, 
$|\xi |<1$; see (3.19). Equation (3.19) shows that the imaginary part, 
$\mbox {Im}[{W}(\xi -\mbox {i} 0)]$, is equal to zero at the contact points, 
$\xi =\pm 1$, for finite displacements 
${ {\partial }\varPhi }/{ {\partial }\xi }$ and 
${ {\partial }\varPhi }/{ {\partial }\zeta }$. Therefore, the integral in (3.17) should be equal to zero at 
$\xi =\pm 1$, which gives an equation for the constant 
$\mu$ and the leading-order gravity correction to the positions of the contact points. Owing to the flow symmetry, it is enough to equate the integral to zero only at 
$\xi =1$,
\begin{equation} \mbox{p.v.}\int_{-\infty}^{\infty} \frac{\mbox{Re}[{W}(\tau-\mbox{i}0)]}{\tau-1}\,\mathrm{d}\tau=0. \end{equation}The integral (3.20) is evaluated analytically using (3.15) and (3.16). The detailed calculations are not shown here. The result is
\begin{equation} \mu={-}\frac{8}{225{\rm \pi}}. \end{equation}Equations (3.3), (3.13a,b) and (3.21) yield the coordinate of the right contact point corrected for the gravity effect:
\begin{equation} x_c (t, \delta )=2\sqrt{t} (1-\delta|\mu| t^{3/2}+O (\delta^2)). \end{equation} We conclude that gravity reduces the size of the contact region. This reduction is small, even for moderate values of 
$\delta$. Indeed, in (3.22), 
$t=O(1)$ and 
$\mu \approx -0.0113$. Gravity also reduces the speed of the contact points,
\begin{equation} \frac{\mathrm{d}\kern0.05em x_c}{\mathrm{d}t} (t, \delta )= \frac{1}{\sqrt{t}}-4\delta|\mu| t+O (\delta^2). \end{equation} In the contact region, 
$|\xi | < 1$, the Hilbert formula (3.17) provides
\begin{align} \frac{\partial {\varPhi}}{\partial {\xi}}(\xi, 0)\sqrt{1-\xi^2} &= \frac{\mu}{\rm \pi}\,\mbox{p.v.}\int_{{-}1}^{1}\frac{(6\xi_0^2-1)(1-\xi_0^2)} {\sqrt{1-\xi_0^2}\,(\xi_0-\xi)}\,\mathrm{d}\xi_0 \nonumber\\ &\quad -\frac{2\xi}{\rm \pi}\int_{1}^{\infty} \frac{\partial {\varPhi}}{\partial {\xi}}(\xi_0, 0) \frac{\sqrt{\xi_0^2-1}}{\xi_0^2-\xi^2}\,\mathrm{d}\xi_0. \end{align}The integrals in (3.24) are evaluated analytically using (3.15) and (3.21) with the result
\begin{align} \frac{\partial {\varPhi}}{\partial {\xi}}(\xi, 0) &=\frac{24}{225{\rm \pi}}\xi\sqrt{1-\xi^2}(23-30\xi^2)+\frac{4}{15{\rm \pi}}(1-\xi^2)^{3/2} (1-6\xi^2)\ln\left|\frac{1+\xi}{1-\xi}\right| \nonumber\\ &\quad -\frac{1}{15}\xi(24\xi^4-40\xi^2+15)\quad (|\xi|<1). \end{align}
On the free surface, 
$\xi > 1$, the Hilbert formula provides
\begin{align} \frac{\partial {\varPhi}}{\partial {\zeta}}(\xi, 0)\sqrt{\xi^2-1} &= \frac{1}{\rm \pi}\int_{{-}1}^{1} \frac{\partial {\varPhi}}{\partial {\zeta}}(\xi_0, 0) \frac{\sqrt{1-\xi_0^2}}{\xi_0-\xi}\,\mathrm{d}\xi_0 \nonumber\\ &\quad -\frac{2\xi}{\rm \pi}\,\mbox{p.v.}\int_{1}^{\infty}\frac{\partial {\varPhi}}{\partial {\xi}} (\xi_0,0)\frac{\sqrt{\xi_0^2-1}}{\xi_0^2-\xi^2}\,\mathrm{d}\xi_0. \end{align}The integrals in (3.26) are evaluated analytically using (3.15), (3.16) and (3.21) with the result
\begin{align} \frac{\partial {\varPhi}}{\partial {\zeta}}(\xi, 0) &=\frac{8\xi}{75{\rm \pi}}\sqrt{\xi^2-1} (30\xi^2-23 ) \nonumber\\ &\quad +\frac{8(1-6\xi^2)}{225{\rm \pi}}\left(1+\frac{15}{2} (\xi^2-1 )^{{3}/{2}} \ln\left( \frac{\xi+1}{\xi-1}\right) \right). \end{align}By using the obtained first-order solution of the water entry problem with gravity, we can investigate the effect of gravity on both the dynamic and kinematic characteristics of the flow.
4. Pressure distribution in the contact region
In this section, the pressure distribution along the wetted part of the body during the impact is calculated with account taken for gravity. The asymptotic expansion of the hydrodynamic pressure in stretched variables (3.1a–c) for small 
$\delta$ is sought in the form
\begin{equation} \tilde{p} (\tilde{x}, \tilde{y}, t, \delta )=\tilde{p}_0 (\tilde{x}, \tilde{y}, t ) +\delta\tilde{p}_1 (\tilde{x}, \tilde{y}, t )+O (\delta^2). \end{equation}
In the contact region, 
$|\tilde {x}|<2\sqrt {t}$, (2.23), (3.6) and (3.9a,b) provide the leading-order pressure distribution without gravity (see Wagner Reference Wagner1932; Howison et al. Reference Howison, Ockendon and Wilson1991),
\begin{equation} \tilde{p}_0 (\tilde{x}, 0, t ) =\frac{2}{\sqrt{4t-\tilde{x}^2}}\quad (\tilde{y}=0,\ |\tilde{x}|<2\sqrt{t}). \end{equation}
The leading-order pressure (4.2) is positive with integrable singularity at the contact points, 
$\tilde {x}=\pm 2\sqrt {t}$. The leading-order correction to the pressure in the wetted area is given by the formula
\begin{equation} \tilde{p}_1(\tilde{x}, 0, t)={-}\frac{\partial^2 {\tilde{\phi}_1}}{\partial {t}^2}+ \tilde{x}\ddot{x}_{1}(t)\frac{\partial {\tilde{\phi}_0 }}{\partial {\tilde{x}}}+2\tilde{x} \dot{x}_{1}(t)\frac{\partial {^2\tilde{\phi}_0}}{\partial {\tilde{x}\partial t}}-\frac{\tilde{x}^2}{2}+t, \end{equation}
where 
$\tilde {\phi }_1(\tilde {x}, 0, t)$ and 
$x_1(t)$ are given by (3.13a,b) and (3.14a,b), and 
$\tilde {\phi }_0(\tilde {x}, 0, t)$ in the wetted area by (3.9a,b).
Equations (3.13a,b), (3.14a,b) and (3.9a,b) provide, after some algebra,
\begin{gather} \frac{\partial^2 {\tilde{\phi}_1}}{\partial {t}^2} (\tilde{x}, 0, t ) = \frac{t}{2} \left[24\varPhi-9\xi\frac{\partial {\varPhi}}{\partial {\xi}}+\xi^2\frac{\partial^2 {\varPhi}}{\partial {\xi}^2}\right] \quad (\tilde{y}=0,\ |\tilde{x}|<2\sqrt{t}), \end{gather}
\begin{gather}\frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{x}}} (\tilde{x}, 0, t ) = \frac{\tilde{x}}{2} (4t-\tilde{x}^2 )^{1/2},\quad \frac{\partial^2{\tilde{\phi}_0}}{\partial \tilde{x}\partial t} (\tilde{x}, 0, t ) =\frac{\tilde{x}}{\sqrt{4t-\tilde{x}^2}}\quad (\tilde{y}=0,\ |\tilde{x}|<2\sqrt{t}), \end{gather}
where the derivative 
$\varPhi _{\xi }$ in the wetted area is given by (3.25). The second derivative, 
$\varPhi _{\xi \xi }$, is obtained by differentiation of (3.25),
\begin{align} \frac{\partial^2 {\varPhi}}{\partial {\xi}^2}(\xi, 0) &={-}1+\frac{3600\xi^4-4104\xi^2+672}{225 {\rm \pi}\sqrt{1-\xi^2}} \nonumber\\ &\quad +8\xi^2(1-\xi^2)-\frac{4}{\rm \pi}\xi(1-2\xi^2)\sqrt{1-\xi^2} \ln\left|\frac{1+\xi}{1-\xi}\right|, \end{align}
and the function 
$\varPhi (\xi ,0)$ is obtained by integration of (3.25) in 
$\xi$ using the condition that this function is continuous at 
$\xi =1$; see Zekri (Reference Zekri2016) for more details. Then the first-order pressure in the wetted area reads
\begin{equation} \tilde{p}(\tilde{x}, 0, t)=\tilde{p}_0(\tilde{x}, 0, t) (1+\delta t^{3/2} P(\xi)+O (\delta^2)), \end{equation}where
\begin{gather} P(\xi)=3 \mu \xi^2 (3-\xi^2)+\sqrt{1-\xi^2}\,S(\xi), \end{gather}
\begin{gather}S(\xi)=1-2 \xi^2-12 \varPhi(\xi,0)+\tfrac{9}{2} \xi \varPhi_{\xi}(\xi,0) -\tfrac{1}{2}\xi^2 \varPhi_{\xi\xi}(\xi,0)\quad (|\xi|<1). \end{gather} Note that the pressure distribution with account for gravity (4.7) is also square-root singular as the pressure without gravity. However, the relative correction to the pressure, 
$\delta t^{3/2} P(\xi )$, is finite and small for the early stage of impact. This correction is not small for a later stage when 
$t=O(1)$ and 
$\delta =O(1)$, in contrast to the correction of the contact point position; see (3.22) where 
$\mu$ is small.
The even function 
$P(\xi )$ is shown by the solid line in figure 3 for 
$0<\xi <1$. It is seen that gravity increases the pressure in the central part of the contact region and decreases it near the periphery of this region. The hydrostatic part of the gravity correction, the second term on the right-hand side of (2.29), corresponds to 
$\sqrt {1-\xi ^2}(1-2\xi ^2)$ in (4.8) and (4.9). This term is shown in figure 3 by the dashed line. Therefore, the main contribution to the leading-order correction to the pressure comes from the hydrostatic pressure. The difference between the solid and dashed lines in figure 3 corresponds to the dynamic component of the gravity correction function 
$P(\xi )$. This dynamic component is shown in figure 4. It is 10 times smaller than the hydrostatic component of the pressure inside the wetted area, but it provides the main contribution at the periphery of the contact region. The dynamic pressure component depends on the free-surface pressure contribution (see the first term in (4.3)) and on the leading-order correction 
$x_1(t)$ to the contact point motion (see the second and third terms in (4.3)).
Figure 3. The function 
$P(\xi )$ (solid line) and its hydrostatic component (dashed line), where 
$P(0)=1.0863$. Also shown is minus-ten times the modified dynamic pressure component (dotted line).
Figure 4. The dynamic component of the gravity correction function 
$P(\xi )$. The curve has a terminal point 
$-$0.1867 at 
$\xi =1$ and 0.0863 at 
$\xi =0$.
Note that the dynamic component is approximately constant in the inner part of the contact region. This gives an idea to introduce a modified hydrostatic component with the zero-pressure level elevated by approximately 10 % of the body penetration depth. The resulting modified dynamic component with opposite sign is shown in figure 3 by the dotted line. It is seen that the modified dynamic correction is of the same order as the hydrostatic pressure near the contact points but is negligible in the inner part of the contact region. The idea of modified hydrostatic pressure was used in Khabakhpasheva et al. (Reference Khabakhpasheva, Korobkin, Maki and Seng2016) to identify different contributions to the total hydrodynamic force acting on a rigid wedge entering and then exiting fluid. We have no clear rational arguments for the modified components of the relative corrections of the impact pressure.
5. Hydrodynamic force
In this section, we evaluate the hydrodynamic force acting on the impacting body with account taken for gravity. The hydrodynamic force is obtained either by integration of the pressure over the wetted body surface (see Faltinsen Reference Faltinsen1993; Oliver Reference Oliver2002; Korobkin Reference Korobkin2007), or by using the energy arguments (see Miloh Reference Miloh1981). Wu (Reference Wu1998) used both these approaches and showed that they give the same results.
In this study, we evaluate the vertical force 
$F(t)$ acting on the symmetric body by integrating the pressure distribution along the wetted area. The scale of the force is 
$\rho V^2 R$. In the dimensionless variables, the force is given by
\begin{equation} F(t)=\int_{{-}x_c(t)}^{x_c(t)}p\left(x, \varepsilon \left(\frac{x^2}{2}-t\right), t \right)\mathrm{d}\kern0.05em x. \end{equation}
At the leading order as 
$\varepsilon \to 0$ and using the stretched variables (3.1a–c), formulae (4.7) and (5.1), we find
\begin{equation} F(t)=2\int_{0}^{x_c(t, 0)}\tilde{p}_0(\tilde{x}, 0, t) \left(1+ \delta t^{3/2} P\left(\frac{\tilde{x}}{2\sqrt{t}}\right)\right) (1-\delta|\mu| t^{3/2} )\,\mathrm{d}\tilde{x}+O(\varepsilon)+O(\delta^2), \end{equation}
where 
$\tilde {p}_0(\tilde {x}, 0, t)=t^{-1/2}/\sqrt {1-\xi ^2}$, 
$\xi =\tilde {x}/2\sqrt {t}$ and 
$P(\xi )$ is given by (4.8) and (4.9). The formula (5.2) can be simplified by using (4.8),
\begin{gather} F(t)=4\int_{0}^{1}\left(\frac{1}{\sqrt{1-\xi^2}} + \delta t^{3/2}\frac{P(\xi)+\mu}{\sqrt{1-\xi^2}}\right)\mathrm{d}\xi+O(\delta^2), \end{gather}
\begin{gather}F(t)=2{\rm \pi}+4\delta t^{3/2}\left(\mu \int_{0}^{1}\frac{3\xi^2(3-\xi^2)+1} {\sqrt{1-\xi^2}}\,\mathrm{d}\xi+\int_{0}^{1} S(\xi)\,\mathrm{d}\xi\right)+O(\delta^2), \end{gather}where
\begin{equation} \mu\int_{0}^{1} \frac{3\xi^2 (3-\xi^2)+1} {\sqrt{1-\xi^2}}\,\mathrm{d}\xi={-}\frac{7}{90},\quad \int_{0}^{1}S(\xi)\,\mathrm{d}\xi=\frac{1}{2}+\frac{35}{2}\int_{0}^{1}\xi \varPhi_{\xi}(\xi, 0)\,\mathrm{d}\xi. \end{equation}
The derivative 
$\varPhi _{\xi }$ in the wetted area is given by (3.25). Hence the coefficient of 
$\delta t^{3/2}$ in (5.4) is
\begin{equation} 4\left(-\frac{7}{90}+\frac{1}{2}+\frac{35}{2}\int_{0}^{1}\xi \varPhi_{\xi}(\xi, 0)\,\mathrm{d}\xi\right)=4\left(-\frac{7}{90}+ \frac{1}{2}+\frac{35}{2}({-}0.00381)\right)=1.4222 \end{equation}(see Zekri Reference Zekri2016).
Putting all these results together, we find
\begin{equation} F(t)=2{\rm \pi}+1.4222 \delta t^{3/2}+O(\delta^2). \end{equation}
Asymptotic formula (5.7) shows that gravity increases the hydrodynamic force. However, this increase is small for small time 
$t$. One may suggest a simplified model, where the dimension of the contact region does not depend on gravity because its contribution to the position of the contact point is small, see (3.22), and the pressure in the contact region depends on gravity only through the hydrostatic pressure, assuming that the dynamic pressure is not affected by gravity; see figure 3. In this model, the force is also given by (5.7) but with the coefficient 1.4222 of the correction term to be changed to 4/3, which is approximately 6 % smaller than the actual value.
6. Gravity correction to the free-surface shape
In this section, we shall investigate how significant is the contribution of gravity to the free-surface shape. The free-surface shape is given by (2.28),
\begin{equation} \eta(x, t)=\frac{x_c(t, 0)}{x_c(t, \delta)} \frac{\partial {\tilde{\phi}}}{\partial {\tilde{y}}}(\tilde{x}, 0, t) \end{equation}in the stretched variables. Asymptotic expansions (3.2) and (3.3) provide
\begin{equation} \eta(x, t)= (1-\delta x_1(t)+O (\delta^2)) \left(\frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{y}}}(\tilde{x}, 0, t)+\delta \frac{\partial {\tilde{\phi}_1}}{\partial {\tilde{y}}}(\tilde{x}, 0, t)+ O (\delta^2)\right) . \end{equation}Equations (3.10) and (3.13a,b) written in the self-similar variables yield
\begin{gather} \frac{\partial {\tilde{\phi}_0}}{\partial {\tilde{y}}}(\tilde{x}, 0, t)=t\eta_0(\xi),\quad \eta_0(\xi)=(\xi+\sqrt{\xi^2-1})^{{-}2},\quad \xi=\tilde{x}/2\sqrt{t}, \end{gather}
\begin{gather}\frac{\partial {\tilde{\phi}_1}}{\partial {\tilde{y}}}(\tilde{x}, 0, t) =t^{{5}/{2}}\frac{\partial {\varPhi}}{\partial {\zeta}}(\xi,0)\quad (\xi>1), \end{gather}
where the derivative 
$\varPhi _{\zeta }(\xi ,0)$ is given by (3.27). Then the asymptotic formula for the elevation of the right free surface, 
$\xi >1$, as 
$\delta \to 0$ reads
\begin{equation} \eta(x, t)=t\eta_0(\xi) + \delta t^{{5}/{2}} \eta_1(\xi) + O (\delta^2), \end{equation}
where 
$\eta _1(\xi )=-\mu \eta _0(\xi )+\varPhi _{\zeta }(\xi ,0)$. The functions 
$\eta _0(\xi )$ and 
$\eta _1(\xi )$ are shown in figure 5 by the dashed and solid lines, respectively. The gravity correction term, 
$\eta _1(\xi )$, is very small; it is shown in figure 5 multiplied by 10. It is seen that gravity lifts the free-surface elevation at a distance from the contact point 
$\xi =1$ but lowers it just next to the contact point. Both the elevation without account for gravity and the gravity correction term vanish quickly with increasing distance from the body surface.
Figure 5. The components of the free-surface shape in the self-similar variable 
$\xi$. The gravity correction term, 
$\eta _1(\xi )$, multiplied by 10 is shown by the solid line, and the free-surface elevation without gravity, 
$\eta _0(\xi )$, is shown by the dashed line. The terminal values at 
$\xi =1$ are 
$\eta _0(1)=0.7538$ and 
$\eta _1(1)=-0.019$.
The elevation of the free surface caused by the body entry can be considered as a reason for the increase of the hydrostatic pressure along the wetted part of the body. This idea was used in Khabakhpasheva et al. (Reference Khabakhpasheva, Korobkin, Maki and Seng2016), where the impact forces computed by CFD and by semi-analytical models were compared for a wedge of 45
$^{\circ }$ dead-rise angle taking account of gravity. The body moved vertically with non-zero initial velocity and a constant deceleration. The penetration depth was described by a quadratic function of time. Initially, the wedge penetrated water with a decreasing speed, then stopped and finally exited from the water. The first impact stage was well described by the modified Logvinovich model (MLM) from Korobkin (Reference Korobkin2004) and the generalised Wagner model (GWM) from Khabakhpasheva et al. (Reference Khabakhpasheva, Kim and Korobkin2014). At the end of the impact stage, the velocity of the wedge was small and the gravity effects are important. This is the stage that is similar to the process studied in the present paper. The semi-analytical models from Korobkin (Reference Korobkin2004) and Khabakhpasheva et al. (Reference Khabakhpasheva, Kim and Korobkin2014) do not provide forces comparable with the CFD forces at the transient stage from entry to exit. Both models were developed further including gravity in Khabakhpasheva et al. (Reference Khabakhpasheva, Korobkin, Maki and Seng2016). It was shown that the dynamic component of the gravity-induced correction can be reduced to an extra hydrostatic pressure within the GWM. Namely, the zero level of the hydrostatic pressure was supported to be placed at the pile-up height (elevation of the water surface at the contact points), increasing the hydrostatic pressure in the wetted part of the wedge. A similar idea was used to include gravity into the MLM. Note that the MLM was developed for water impact of bodies with small dead-rise angles. However, the MLM was shown to work well without gravity included even for a wedge of 45
$^{\circ }$ and moderate penetration depths. Gravity was included in the MLM by the zero level lifted to half of the pile-up height, without a rational explanation for this procedure. The modified GWM and MLM with gravity included provided hydrodynamic forces comparable to the CFD force up to the end of the entry stage, when the wedge speed dropped down to zero.
Figure 3 shows that the gravity-induced correction to the pressure (solid line) behaves similarly to the hydrostatic component (dashed line) but its magnitude is different. It is observed that, if the zero level for the hydrostatic pressure is increased from the equilibrium water level 
$y=0$ to 
$P(0)-1$, then the hydrostatic pressure becomes close to the correction 
$P(\xi )$. The difference between the correction by the modified hydrostatic pressure, 
$\sqrt {1-\xi ^2}(P(0)-2\xi ^2)$, and the calculated gravity correction, 
$P(\xi )$, multiplied by 10 is shown in figure 3 by the dotted line. We may conclude that the dynamic component of the gravity correction (see figure 4) is well approximated in the inner part of the contact region by an extra hydrostatic pressure. However, this approximation does not work near the contact point, where 
$\xi$ is close to 1 (see figure 3). We conclude that the dynamic effects are important in the gravity correction.
7. Conclusions
Impact by a symmetric two-dimensional and blunt body on a water surface was studied for small speeds of entry when gravity becomes formally important. Within the fully nonlinear theory of potential flows, a gravity term appears only in the dynamic boundary condition on the free surface if the body velocity is prescribed. There is numerical evidence that gravity can be well neglected even for impact conditions when this gravity term is formally of the same order as other terms in the problem.
To clarify this widely accepted observation, we formulated a problem for the early stage of water entry, when the penetration depth is small and the liquid inertia is dominant, with the nonlinear effects being negligible compared with both liquid inertia and gravity. At the leading order, this problem is an extension of the classical Wagner problem of water impact with an extra term in the free-surface boundary condition, which describes the effect of gravity on the flow. We assumed that this term is small compared with all other terms in the leading-order problem, and performed perturbation analysis of the flow, pressure distribution, hydrodynamic force and the free-surface elevation. The corrections obtained, accounting for the influence of gravity, are found to be small, even under conditions in which, formally, gravity should be dominant. The corrections were calculated in stretched variables to account for the dependence of the size of the wetted area of the body surface on gravity.
It was shown that the relative corrections to the length of the contact region, the pressure distribution along the contact region, the total hydrodynamic force acting on the entering body and the free-surface elevations are of the order of 
$O(\delta t^{3/2})$, where 
$\delta$ is a small parameter describing the gravity effects and 
$t$ is the dimensionless time, 
$t=O(1)$. The coefficients of 
$\delta t^{3/2}$ in the corrections have different orders for different corrections. The magnitudes of the coefficients are approximately 0.01 for the length of the wetted part of the body surface, and 0.02 for the free-surface correction. We may conclude that the kinematic characteristics of the flow are not sensitive to gravity, even for small entry speeds, when the parameter 
$\delta$ is not small. However, the dynamic characteristics of the flow, such as the hydrodynamic pressure and the total force, are significantly influenced by gravity, with the corresponding correction coefficients being of the order of 
$O(1)$.
The main contributions to the pressure and force corrections come from the hydrostatic pressure, which is easy to evaluate. Dynamic corrections are less than 6 % of the corresponding hydrostatic corrections. Physically, gravity changes the fluid from a region of passive inertia into a more active responder to the body being pushed downwards. There is now a pre-existing hydrostatic pressure distribution (and associated potential energy field) against which the body must force its way downwards. With this, the analysis shows an increase in pressure over the middle 70 % of the body's wetted region, and a surprising reduction in pressure near the contact points; see figure 3. The wetted part of the body is shortened by gravity. The total hydrodynamic force on the body is increased by gravity. The changes in water-surface elevation are harder to interpret in purely physical terms. Gravity acts to pull the contact point and the free surface nearby inwards and downwards, but everywhere else gravity pushes the water elevation up higher.
To sum up the conclusion, compared with gravity-free flow, gravity acts to: reduce the width of the wetted length of the body; slow down the speed of the contact point; increase the hydrodynamic pressure in the central part of the wetted body; decrease the pressure near the jet root; increase the total force exerted by the fluid on the body; and lower the free surface near the jet root and raise it everywhere else.
Acknowledgements
M.J.C. wishes to thank the Isaac Newton Institute for Mathematical Sciences, Cambridge, for time spent there during early work on this paper. H.J.Z. thanks the University of East Anglia and the University of Zakho for their support.
Funding
H.J.Z. is also grateful to the Ministry of Higher Education and Scientific Research, Kurdistan Region, Iraq, for financial support for this work.
Declaration of interests
The authors report no conflict of interest.
