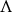1. Introduction
Contemporary cosmologists describe the universe with a strikingly simple concordance model, according to which the universe expands from a hot “big bang” state, then passes through a series of phases, with the expansion rate varying as different forms of mass-energy come to dominate the dynamics. Observations are needed to fix just a handful of parameters in this model. The parameters characterize the universe’s large-scale geometry and the relative densities of its primary constituents. Cosmologists’ confidence in this model has increased substantially with the advent of “precision cosmology,” which has led to determining the model parameters at the 1 percent level from a diverse array of observations. Peebles’s (Reference Peebles2020, 339) one-line summary reflects a widely shared view: “I emphasize again the broad variety of observations that probe the universe in such different ways and offer a story that is close enough to consistency to make the case for the
![]() $\Lambda$
CDM theory about as compelling as it gets in natural science.” Peebles takes this case to establish that the
$\Lambda$
CDM theory about as compelling as it gets in natural science.” Peebles takes this case to establish that the
![]() $\Lambda$
CDM model should be regarded as a permanent contribution, in the sense that it will be retained, at least as some form of approximation, in future cosmologies.
$\Lambda$
CDM model should be regarded as a permanent contribution, in the sense that it will be retained, at least as some form of approximation, in future cosmologies.
Philosophers have recently debated the nature and effectiveness of this kind of argument, exemplified by Perrin’s famous defense of atomism based on convergent measurements of Avogadro’s number. Van Fraassen (Reference Van Fraassen2009) takes Perrin to have shown how atomic theory can be “empirically grounded,” which requires that (1) significant theoretical parameters be measurable and (2) diverse theory-mediated measurements of them yield agreeing results. Clearly these arguments play a significant role in scientific practice, although it is more controversial what they establish. Van Fraassen contrasts his view, on which grounding does not imply that the parameters correspond to properties of real entities, with what he calls a “strange reading” offered by realists, who instead take Perrin to have established the reality of molecules. Smith and Seth (Reference Smith and Seth2020) frame their detailed historical case study as, in part, a rejoinder to van Fraassen. They argue that stable and convergent measurements of parameter values, amenable to increasing precision, did change the status of the molecular hypothesis: it began to be employed as a basic assumption guiding further inquiry, even though many pressing questions regarding molecules remained open. More generally, on their view, successful measurements of fundamental parameters can anchor subsequent work and impose constraints on future theory, in much the sense that Peebles suggests. Isaac (Reference Isaac2019) goes a step further, arguing in favor of a novel realist position: successful measurement gives us evidence for “fixed points” (modally stable phenomena) in the world. The main epistemic challenge facing such arguments for permanence is a threat of circularity: how can one establish that these parameters are physically meaningful and worthy of preservation, rather than merely artifacts of modeling assumptions?
The challenge is particularly salient in cosmology. The model relies on enormous extrapolations of physical theories, such as applying general relativity
![]() $\sim 14$
orders of magnitude beyond the solar-system scales where it is subject to high-precision tests. The model’s name—
$\sim 14$
orders of magnitude beyond the solar-system scales where it is subject to high-precision tests. The model’s name—
![]() $\Lambda$
CDM—highlights the two novel types of mass-energy it posits: a nonzero cosmological constant
$\Lambda$
CDM—highlights the two novel types of mass-energy it posits: a nonzero cosmological constant
![]() $\Lambda$
and cold dark matter. Without the freedom to introduce new types of mass-energy, with densities far larger than that of “normal” matter, the same high-precision data would decisively rule out the expanding universe models. A vocal minority regards this flexibility with skepticism and pursues models based on modified gravitational physics; even those who are not so skeptical often express dissatisfaction at treating the dark sector phenomenologically. These two points highlight the possibility of errors in the theoretical assumptions cosmologists rely on in turning data into parameter constraints. Finally, whether the story is close enough to consistency has come into question with the increasing precision of several different observational programs. I focus here on one prominent challenge to the
$\Lambda$
and cold dark matter. Without the freedom to introduce new types of mass-energy, with densities far larger than that of “normal” matter, the same high-precision data would decisively rule out the expanding universe models. A vocal minority regards this flexibility with skepticism and pursues models based on modified gravitational physics; even those who are not so skeptical often express dissatisfaction at treating the dark sector phenomenologically. These two points highlight the possibility of errors in the theoretical assumptions cosmologists rely on in turning data into parameter constraints. Finally, whether the story is close enough to consistency has come into question with the increasing precision of several different observational programs. I focus here on one prominent challenge to the
![]() $\Lambda$
CDM model: “local” measurements of the Hubble constant
$\Lambda$
CDM model: “local” measurements of the Hubble constant
![]() $H_0$
suggest a higher value than that based on “global,” early-universe observations of the cosmic microwave background (CMB).Footnote
1
$H_0$
suggest a higher value than that based on “global,” early-universe observations of the cosmic microwave background (CMB).Footnote
1
This case study supports two claims related to recent philosophical assessments of measurement (e.g., Chang Reference Chang2004; Tal Reference Tal2016). First, an effective response to the concerns regarding circularity requires a more fine-grained assessment of the role of theory in particular measurements. Philosophers have overstated circularity worries based on crude treatments of “theory dependence.” Smith and Seth (Reference Smith and Seth2020) distinguish three aspects of measurement, based on their case study of Perrin, that are illuminating when applied to the cosmological case as well: stability, amenability to increasing precision, and convergence. Stability refers to the constancy of a parameter value (or values) determined by a particular measurement technique over some range of observational data. Establishing whether a given technique is amenable to increasing precision requires a detailed physical account of how the measurement tracks a particular target quantity. Such an account can be used, among other things, to identify sources of systematic error. As we will see, both of these aspects of a measurement can often be assessed with aspects of physics or astrophysics that are relatively independent of the cosmological model. Cosmologists can then take the measurements as the basis for further inquiry while remaining agnostic on open research questions, and this makes it more plausible that the parameter measurements could anchor further research even through significant theory change. The degree of convergence among different measurements, by contrast, typically does depend sensitively on the cosmological model. In many cases, the model links together observations at different epochs through a description of the universe’s intervening evolution.
This leads to the second overall point, namely, to acknowledge the advantages of taking theory seriously as a starting point for further inquiry and what this stance entails. This stance allows cosmologists to bring data to bear on a variety of questions owing to the systematic relationships—such as those between parameter values at different epochs—
![]() $\Lambda$
CDM entails. Complementary measurements of the same parameters can be used to expose systematic errors in different measurement techniques. Taking
$\Lambda$
CDM entails. Complementary measurements of the same parameters can be used to expose systematic errors in different measurement techniques. Taking
![]() $\Lambda$
CDM seriously incurs an obligation to resolve any discrepancies in the parameter measurements, by (1) reanalyzing the measurements (changing calibration, identifying new sources of systematic error) or (2) adding further complexity to the model to mitigate the conflict. Persistent failure in pursuing either of these two options would force cosmologists to reject the physical significance of the model and abandon Peebles’s position that the
$\Lambda$
CDM seriously incurs an obligation to resolve any discrepancies in the parameter measurements, by (1) reanalyzing the measurements (changing calibration, identifying new sources of systematic error) or (2) adding further complexity to the model to mitigate the conflict. Persistent failure in pursuing either of these two options would force cosmologists to reject the physical significance of the model and abandon Peebles’s position that the
![]() $\Lambda$
CDM model makes a permanent contribution to cosmology.
$\Lambda$
CDM model makes a permanent contribution to cosmology.
The next section sets the stage with a sketch of the
![]() $\Lambda$
CDM model before turning to the debate regarding the Hubble constant in section 2. In section 3, I evaluate the limited sense in which this line of argument supports a realist stance regarding the theoretical parameters appearing in
$\Lambda$
CDM model before turning to the debate regarding the Hubble constant in section 2. In section 3, I evaluate the limited sense in which this line of argument supports a realist stance regarding the theoretical parameters appearing in
![]() $\Lambda$
CDM, before I conclude in section 4.
$\Lambda$
CDM, before I conclude in section 4.
2. The
 $\bf \Lambda$
CDM model
$\bf \Lambda$
CDM model
![]() $\Lambda$
CDM takes perturbed Friedmann–Lemaître (FL) models to represent the large-scale structure of the universe. These are solutions of Einstein’s field equations (EFE) with maximal symmetry: they describe space-time as foliated by a collection of three-dimensional hypersurfaces of constant curvature over cosmic time,
$\Lambda$
CDM takes perturbed Friedmann–Lemaître (FL) models to represent the large-scale structure of the universe. These are solutions of Einstein’s field equations (EFE) with maximal symmetry: they describe space-time as foliated by a collection of three-dimensional hypersurfaces of constant curvature over cosmic time,
![]() $\Sigma (t)$
(see, e.g., Weinberg Reference Weinberg2008). The world lines of “fundamental observers,” moving along geodesics and at rest with respect to matter, are orthogonal to these surfaces, and clocks carried by fundamental observers would measure cosmic time. The scale factor
$\Sigma (t)$
(see, e.g., Weinberg Reference Weinberg2008). The world lines of “fundamental observers,” moving along geodesics and at rest with respect to matter, are orthogonal to these surfaces, and clocks carried by fundamental observers would measure cosmic time. The scale factor
![]() $R(t)$
represents spatial distance in
$R(t)$
represents spatial distance in
![]() $\Sigma$
between nearby fundamental observers, flowing along with the cosmic evolution. Spatial volume changes as a function of cosmic time, proportional to
$\Sigma$
between nearby fundamental observers, flowing along with the cosmic evolution. Spatial volume changes as a function of cosmic time, proportional to
![]() ${\dot{R}(t)}/{R(t)}$
. This quantity is called the (time-varying) Hubble “constant”
${\dot{R}(t)}/{R(t)}$
. This quantity is called the (time-varying) Hubble “constant”
![]() $H(t)$
, with
$H(t)$
, with
![]() $H_0$
specifying the value at the present time. Owing to symmetries, EFE reduce to two ordinary differential equations for the scale factor, which can be solved given the equations of state and relative densities of the postulated material constituents. The pristine symmetry of these models has to be perturbed slightly to account for the existence of large-scale structures: structures like galaxies arise via gravitational enhancement of small “seed” perturbations in the early universe.
$H_0$
specifying the value at the present time. Owing to symmetries, EFE reduce to two ordinary differential equations for the scale factor, which can be solved given the equations of state and relative densities of the postulated material constituents. The pristine symmetry of these models has to be perturbed slightly to account for the existence of large-scale structures: structures like galaxies arise via gravitational enhancement of small “seed” perturbations in the early universe.
Free parameters in the
![]() $\Lambda$
CDM model characterize the space-time geometry and the constituents of the universe. One set of parameters characterizes the space-time geometry, given by a flat FL model (characterized in part by
$\Lambda$
CDM model characterize the space-time geometry and the constituents of the universe. One set of parameters characterizes the space-time geometry, given by a flat FL model (characterized in part by
![]() $H(t)$
) and the seed perturbations (fully characterized by two parameters, if they are Gaussian). A second set specifies how much of each different type of matter is present, in terms of density parameters
$H(t)$
) and the seed perturbations (fully characterized by two parameters, if they are Gaussian). A second set specifies how much of each different type of matter is present, in terms of density parameters
![]() $\Omega _i$
. The list of different “types of matter” extends beyond familar types of matter (such as baryonic matter,
$\Omega _i$
. The list of different “types of matter” extends beyond familar types of matter (such as baryonic matter,
![]() $\Omega _b$
) to include cold dark matter (
$\Omega _b$
) to include cold dark matter (
![]() $\Omega _c$
) and “dark energy.” The third and final set includes parameters that need to be specified to interpret observations, such as the ionization state of the early universe. There is some variation in the list of parameters cosmologists use in finding an optimal fit depending on the type of observations; cosmologists typically fit CMB data, for example, with six to nine parameters. The Hubble parameter is not included in this list for CMB observations but is treated instead as a derived quantity.
$\Omega _c$
) and “dark energy.” The third and final set includes parameters that need to be specified to interpret observations, such as the ionization state of the early universe. There is some variation in the list of parameters cosmologists use in finding an optimal fit depending on the type of observations; cosmologists typically fit CMB data, for example, with six to nine parameters. The Hubble parameter is not included in this list for CMB observations but is treated instead as a derived quantity.
Cosmologists have developed a number of independent observational techniques for constraining these parameters, exemplified by the baryonic mass density
![]() $\Omega _b$
(for a detailed discussion, see Peebles Reference Peebles2020). Two of the most precise constraints on
$\Omega _b$
(for a detailed discussion, see Peebles Reference Peebles2020). Two of the most precise constraints on
![]() $\Omega _b$
derive from early-universe physics. According to big bang nucleosynthesis, primordial light element abundances are fixed by nuclear physics applied to the early universe. Primordial isotope abundances, in particular that of deuterium, depend sensitively on
$\Omega _b$
derive from early-universe physics. According to big bang nucleosynthesis, primordial light element abundances are fixed by nuclear physics applied to the early universe. Primordial isotope abundances, in particular that of deuterium, depend sensitively on
![]() $\Omega _b$
(at the time of nucleosynthesis,
$\Omega _b$
(at the time of nucleosynthesis,
![]() $t \approx 10^2 s$
). A second constraint follows from observations of the acoustic peaks in the CMB (from
$t \approx 10^2 s$
). A second constraint follows from observations of the acoustic peaks in the CMB (from
![]() $t \approx 10^{11} s$
). Prior to recombination, the speed of sound in the coupled plasma–radiation oscillations that produced these peaks depends on
$t \approx 10^{11} s$
). Prior to recombination, the speed of sound in the coupled plasma–radiation oscillations that produced these peaks depends on
![]() $\Omega _b$
, and the relative magnitude of the second peak measures its value. In both cases, cosmologists have derived equations relating an observable quantity—the primordial deuterium abundance or features of the acoustic peaks in the CMB—to
$\Omega _b$
, and the relative magnitude of the second peak measures its value. In both cases, cosmologists have derived equations relating an observable quantity—the primordial deuterium abundance or features of the acoustic peaks in the CMB—to
![]() $\Omega _b$
. The great appeal of these early-universe parameter constraints is the relative simplicity of the physics involved: the equations follow from well-understood nuclear and plasma physics, respectively. Astrophysical estimates of
$\Omega _b$
. The great appeal of these early-universe parameter constraints is the relative simplicity of the physics involved: the equations follow from well-understood nuclear and plasma physics, respectively. Astrophysical estimates of
![]() $\Omega _b$
(from the “late universe,”
$\Omega _b$
(from the “late universe,”
![]() $t \approx 10^{17} s$
) are subject to much greater uncertainty, as they are based on a census of known baryonic matter or employ assumptions about how luminous objects trace the mass distribution. For example, applying the virial theorem to the motion of galaxies in clusters yields constraints on
$t \approx 10^{17} s$
) are subject to much greater uncertainty, as they are based on a census of known baryonic matter or employ assumptions about how luminous objects trace the mass distribution. For example, applying the virial theorem to the motion of galaxies in clusters yields constraints on
![]() $\Omega _b$
. Peebles (Reference Peebles2020, 337) reports a “crude estimate” of
$\Omega _b$
. Peebles (Reference Peebles2020, 337) reports a “crude estimate” of
![]() $\Omega _b h^2 \approx 0.015$
based on astrophysical constraints, compared to
$\Omega _b h^2 \approx 0.015$
based on astrophysical constraints, compared to
![]() $\Omega _b h^2 =0.022 \pm 0.001$
from Planck observations of the CMB and
$\Omega _b h^2 =0.022 \pm 0.001$
from Planck observations of the CMB and
![]() $0.021 \pm 0.002$
from big bang nucleosynthesis.
$0.021 \pm 0.002$
from big bang nucleosynthesis.
All three techniques for estimating
![]() $\Omega _b$
are strongly “theory dependent”—but the theory and background knowledge in each case are quite different. There is also a clear contrast between two different ways that assumptions about the background cosmological model play a role: first, in establishing a link between a specific observable quantity and
$\Omega _b$
are strongly “theory dependent”—but the theory and background knowledge in each case are quite different. There is also a clear contrast between two different ways that assumptions about the background cosmological model play a role: first, in establishing a link between a specific observable quantity and
![]() $\Omega _b$
, and then evaluating the stability of that link and how precision could be increased, and second, in making the case that different measurement techniques converge on the same physical quantity. Regarding the first, the connection between
$\Omega _b$
, and then evaluating the stability of that link and how precision could be increased, and second, in making the case that different measurement techniques converge on the same physical quantity. Regarding the first, the connection between
![]() $\Omega _b$
and isotopic ratios, for example, does not depend on the more contentious aspects of the
$\Omega _b$
and isotopic ratios, for example, does not depend on the more contentious aspects of the
![]() $\Lambda$
CDM model—dark matter and dark energy. The connection is also stable to variation of various other observable quantities, and physicists have clarified the impact of a wide variety of changes to background theory (including gravitational theory as well as nuclear physics). Cosmology enters into these calculations through the expansion timescale and its interplay with reaction rates, and little else.
$\Lambda$
CDM model—dark matter and dark energy. The connection is also stable to variation of various other observable quantities, and physicists have clarified the impact of a wide variety of changes to background theory (including gravitational theory as well as nuclear physics). Cosmology enters into these calculations through the expansion timescale and its interplay with reaction rates, and little else.
The background cosmological model plays a more substantial part, by contrast, in making the case that the three measurements (and several others) target the same quantity. Dynamical evolution as described by the
![]() $\Lambda$
CDM model connects measurements of
$\Lambda$
CDM model connects measurements of
![]() $\Omega _b$
at three different epochs—from
$\Omega _b$
at three different epochs—from
![]() $10^2 s$
all the way to
$10^2 s$
all the way to
![]() $10^{17} s$
. Making the case in favor of convergence, so that constraints obtained in different epochs can be used as cross-checks, depends directly on the validity of the
$10^{17} s$
. Making the case in favor of convergence, so that constraints obtained in different epochs can be used as cross-checks, depends directly on the validity of the
![]() $\Lambda$
CDM model. Hence worries about circularity are more pressing in evaluating the case that we have multiple convergent measurements. To the point in slightly different terms, accepting the
$\Lambda$
CDM model. Hence worries about circularity are more pressing in evaluating the case that we have multiple convergent measurements. To the point in slightly different terms, accepting the
![]() $\Lambda$
CDM model allows individual measurements of the fundamental parameters to be systematically interlinked. What the convergence of complementary measurement adds, over and above the fact that individual measurements are stable and well behaved, is evidence for these connections. In place of a general concern about circularity and theory dependence, cosmologists can then assess how robust the comparisons of different measurements of
$\Lambda$
CDM model allows individual measurements of the fundamental parameters to be systematically interlinked. What the convergence of complementary measurement adds, over and above the fact that individual measurements are stable and well behaved, is evidence for these connections. In place of a general concern about circularity and theory dependence, cosmologists can then assess how robust the comparisons of different measurements of
![]() $\Omega _b$
are to specific modifications of the
$\Omega _b$
are to specific modifications of the
![]() $\Lambda$
CDM model.Footnote
2
As we will see next, we can also turn this inference around: assuming the
$\Lambda$
CDM model.Footnote
2
As we will see next, we can also turn this inference around: assuming the
![]() $\Lambda$
CDM model makes it possible to assess systematic uncertainties in different measurement techniques.
$\Lambda$
CDM model makes it possible to assess systematic uncertainties in different measurement techniques.
3. Trouble with Hubble?
Hubble’s observations of a linear relationship between the redshift and distance of twenty-four nearby galaxies provided the first evidence that the universe is expanding. Astronomers have pursued more precise determinations of the Hubble constant ever since, with measured values decreasing substantially from Hubble’s value of
![]() $H_0 \approx 500$
(in units km s
$H_0 \approx 500$
(in units km s
![]() $^{-1}$
Mpc
$^{-1}$
Mpc
![]() $^{-1}$
). Astrophysical objects are not fundamental observers in an FL model, and their individual motions (also called “peculiar velocities”) result from gravitational interactions with nearby galaxies and clusters of galaxies, adding “noise” to the underlying “Hubble flow.” This is an obstacle to using local objects to measure
$^{-1}$
). Astrophysical objects are not fundamental observers in an FL model, and their individual motions (also called “peculiar velocities”) result from gravitational interactions with nearby galaxies and clusters of galaxies, adding “noise” to the underlying “Hubble flow.” This is an obstacle to using local objects to measure
![]() $H_0$
, but the error decreases at larger distances because the peculiar velocities become smaller, in ratio, to the ever-increasing recessional velocities due to the Hubble expansion. Ideally, one could measure the Hubble flow based on the distance–redshift relation for a population of standard candles or rulers, objects with known luminosity or scale, at sufficiently large distances. Astronomers have a variety of techniques for determining distances to astrophysical objects that apply at a variety of (often overlapping) scales. The distance ladder extends rung by rung to cosmological scales, starting with parallax measurements for nearby stars, using these to calibrate different distance indicators, and iterating the process. Observations of large samples of type Ia supernovae have significantly extended the distance ladder out into the pure Hubble flow, leading to the discovery that the expansion rate is accelerating and enabling higher-precision determinations of
$H_0$
, but the error decreases at larger distances because the peculiar velocities become smaller, in ratio, to the ever-increasing recessional velocities due to the Hubble expansion. Ideally, one could measure the Hubble flow based on the distance–redshift relation for a population of standard candles or rulers, objects with known luminosity or scale, at sufficiently large distances. Astronomers have a variety of techniques for determining distances to astrophysical objects that apply at a variety of (often overlapping) scales. The distance ladder extends rung by rung to cosmological scales, starting with parallax measurements for nearby stars, using these to calibrate different distance indicators, and iterating the process. Observations of large samples of type Ia supernovae have significantly extended the distance ladder out into the pure Hubble flow, leading to the discovery that the expansion rate is accelerating and enabling higher-precision determinations of
![]() $H_0$
.
$H_0$
.
As the precision of these “local” measurements of
![]() $H_0$
have increased, the contrast with “global” measurements based on observations of the CMB has become sharper. The Planck results led Bernal, etal. (Reference Bernal, Verde and Riess2016), for example, to prominently identify this as a serious tension in the
$H_0$
have increased, the contrast with “global” measurements based on observations of the CMB has become sharper. The Planck results led Bernal, etal. (Reference Bernal, Verde and Riess2016), for example, to prominently identify this as a serious tension in the
![]() $\Lambda$
CDM model. Local measurements favor a higher value, falling in the interval of 70–76, and are reasonably consistent given stated uncertainties, but they contrast with the lower value measured by the Planck Collaboration:
$\Lambda$
CDM model. Local measurements favor a higher value, falling in the interval of 70–76, and are reasonably consistent given stated uncertainties, but they contrast with the lower value measured by the Planck Collaboration:
![]() $67.27 \pm 0.6$
(assuming a flat model as a prior, with the stated uncertainty at
$67.27 \pm 0.6$
(assuming a flat model as a prior, with the stated uncertainty at
![]() $1 \sigma$
). Riess etal. (Reference Riess, Casertano, Yuan, Bowers, Macri, Zinn and Scolnic2021) find a value of
$1 \sigma$
). Riess etal. (Reference Riess, Casertano, Yuan, Bowers, Macri, Zinn and Scolnic2021) find a value of
![]() $73.2 \pm 1.3$
, leading to a
$73.2 \pm 1.3$
, leading to a
![]() $4.2 \sigma$
discrepancy given the stated uncertainties.Footnote
3
$4.2 \sigma$
discrepancy given the stated uncertainties.Footnote
3
CMB observations do not directly measure
![]() $H$
: they constrain the product of
$H$
: they constrain the product of
![]() $H$
with other cosmological parameters, such as
$H$
with other cosmological parameters, such as
![]() $\Omega _b$
and the total mass
$\Omega _b$
and the total mass
![]() $\Omega _m$
. Observations of the acoustic peaks essentially determine the geometry of the FL model at the time of last scattering. The angular scale of the first peak depends on the scale factor at that time and our distance from the surface. But observations of the acoustic peaks provide further parameter constraints: the relative height of the second peak measures
$\Omega _m$
. Observations of the acoustic peaks essentially determine the geometry of the FL model at the time of last scattering. The angular scale of the first peak depends on the scale factor at that time and our distance from the surface. But observations of the acoustic peaks provide further parameter constraints: the relative height of the second peak measures
![]() $\Omega _b h^2$
, and that of the third peak measures
$\Omega _b h^2$
, and that of the third peak measures
![]() $\Omega _m h^2$
. The degeneracy can be broken by assuming a flat model or by using other data sets to fix parameter values, leading to the value just cited. Although the determination of
$\Omega _m h^2$
. The degeneracy can be broken by assuming a flat model or by using other data sets to fix parameter values, leading to the value just cited. Although the determination of
![]() $H$
is indirect and depends on the background
$H$
is indirect and depends on the background
![]() $\Lambda$
CDM model, Planck can achieve such high precision in part because of the simplicity of the physics governing the CMB. Planck’s results agree well with those of other CMB observations, and it is striking that the conflict with local measurements seems to have had little impact in confidence on the Planck parameter values.
$\Lambda$
CDM model, Planck can achieve such high precision in part because of the simplicity of the physics governing the CMB. Planck’s results agree well with those of other CMB observations, and it is striking that the conflict with local measurements seems to have had little impact in confidence on the Planck parameter values.
The Hubble tension has already generated a vast literature, with Di Valentino etal. (Reference Di Valentino, Mena, Pan, Visinelli, Yang, Melchiorri, Mota, Riess and Silk2021) counting more than 850 papers exploring different theoretical resolutions. The expansion history according to the
![]() $\Lambda$
CDM models connects the CMB and local measurements, and the proposed resolutions nearly all modify this linkage without modifying the understanding of the CMB measurements. There are some proposals based on modifying general relativity and adopting a quite different framework, but the majority of these responses reflect cosmologists’ confidence in the
$\Lambda$
CDM models connects the CMB and local measurements, and the proposed resolutions nearly all modify this linkage without modifying the understanding of the CMB measurements. There are some proposals based on modifying general relativity and adopting a quite different framework, but the majority of these responses reflect cosmologists’ confidence in the
![]() $\Lambda$
CDM model: rather than abandoning the model entirely, these are minor modifications to the model’s dynamics, such as introducing a new form of dark energy that has a targeted impact on the expansion history. Specific modifications have often been criticized as ad hoc, but to my mind, there is a more striking downside of such changes. In effect, these modifications break the connection between these two types of measurements that allowed them to function as cross-checks of each other. Although one of these modifications could be correct, in general, they make it much more challenging to constrain cosmological models.
$\Lambda$
CDM model: rather than abandoning the model entirely, these are minor modifications to the model’s dynamics, such as introducing a new form of dark energy that has a targeted impact on the expansion history. Specific modifications have often been criticized as ad hoc, but to my mind, there is a more striking downside of such changes. In effect, these modifications break the connection between these two types of measurements that allowed them to function as cross-checks of each other. Although one of these modifications could be correct, in general, they make it much more challenging to constrain cosmological models.
A different line of response takes the conflict as a prompt to look for further possible sources of systematic error, a persistent challenge in measuring astrophysical distances since Hubble’s time. “Local” measurements extend into the Hubble flow using SNIa. There are different techniques to establish distances to the galaxies hosting the closest supernovae in order to calibrate the lowest rungs of the distance ladder. One approach relies primarily on Cepheids, a kind of variable star with a period–luminosity relationship discovered by Henrietta Leavitt. The advantages and disadvantages of using Cepheids as distance indicators have been scrutinized carefully, given the central role of this technique in earlier work, including the Hubble Space Telescope key project to measure
![]() $H_0$
. The SHoES collaboration (e.g., Riess etal. Reference Riess, Casertano, Yuan, Bowers, Macri, Zinn and Scolnic2021) uses Cepheids and claims to attain precision just below the 2 percent level, with a goal of reaching the 1 percent level based on new parallax measurements (compared to an approximately 5 percent level two decades ago).
$H_0$
. The SHoES collaboration (e.g., Riess etal. Reference Riess, Casertano, Yuan, Bowers, Macri, Zinn and Scolnic2021) uses Cepheids and claims to attain precision just below the 2 percent level, with a goal of reaching the 1 percent level based on new parallax measurements (compared to an approximately 5 percent level two decades ago).
The conflict with the Planck results suggests that unknown systematics may continue to plague local distance estimates. But a more compelling case has been made recently, relying on a new method using “tip of the red giant branch” (TRGB) stars. At the end of the red giant phase, stars undergo a core helium flash, leading to a sharp and readily observable discontinuity in the color-magnitude diagram, with a characteristic luminosity, for populations of low-mass stars. The CCHP project (e.g., Freedman etal. Reference Freedman, Madore, Hatt, Hoyt, Jang, Beaton and Burns2019) aims to avoid the systematics plaguing Cepheids by building an entirely new distance ladder using this feature as a standard candle. The results obtained so far provide compelling evidence that one or both of these projects has failed to identify some systematic errors (Freedman Reference Freedman2021). The two methods disagree even about the distance of nearby galaxies, with
![]() $2\sigma$
–3
$2\sigma$
–3
![]() $\sigma$
discrepancies. We can see the need for further scrutiny of the local distance ladder at this level of precision, even without comparison to early-universe parameter measurements. The resolution of this debate will directly impact the Hubble tension as well, if for no other reason than that the TRGB method leads to a lower value,
$\sigma$
discrepancies. We can see the need for further scrutiny of the local distance ladder at this level of precision, even without comparison to early-universe parameter measurements. The resolution of this debate will directly impact the Hubble tension as well, if for no other reason than that the TRGB method leads to a lower value,
![]() $H_0 = 69.6 \pm 1.9$
. But in addition, on Freedman’s (2021) analysis, contrasting zero-point calibrations for SNIa is not the primary reason for the divergence between the estimates given by the two methods, and unraveling the full reasons for the discrepancy is essential for assessing the Hubble tension and its ramifications.
$H_0 = 69.6 \pm 1.9$
. But in addition, on Freedman’s (2021) analysis, contrasting zero-point calibrations for SNIa is not the primary reason for the divergence between the estimates given by the two methods, and unraveling the full reasons for the discrepancy is essential for assessing the Hubble tension and its ramifications.
Although debates about the Hubble tension will certainly continue, to my mind, this episode illustrates the advantages of adopting the
![]() $\Lambda$
CDM model: it makes it possible to leverage high-precision measurements of the CMB to isolate systematic uncertainties as local distance ladder measurements are pushed to increasing levels of precision. This leverage is particularly valuable because the stability and agreement of closely related measurements often fail to expose systematic errors they all share. Smith and Seth (Reference Smith and Seth2020) pointedly note that this is true even of Perrin’s celebrated experimental measurements of Avogadro’s number: his preferred values fell in the range 65–
$\Lambda$
CDM model: it makes it possible to leverage high-precision measurements of the CMB to isolate systematic uncertainties as local distance ladder measurements are pushed to increasing levels of precision. This leverage is particularly valuable because the stability and agreement of closely related measurements often fail to expose systematic errors they all share. Smith and Seth (Reference Smith and Seth2020) pointedly note that this is true even of Perrin’s celebrated experimental measurements of Avogadro’s number: his preferred values fell in the range 65–
![]() $72 \times 10^{22}$
, and he substantially underestimated systematic errors shared by all these measurements. The introduction of novel techniques by Millikan and others led to a lower value and a reassessment of Perrin’s measurements.
$72 \times 10^{22}$
, and he substantially underestimated systematic errors shared by all these measurements. The introduction of novel techniques by Millikan and others led to a lower value and a reassessment of Perrin’s measurements.
4. Realism and the cosmological parameters
The strength of Peebles’s case that the
![]() $\Lambda$
CDM model is a permanent contribution to cosmology depends on the wide array of diverse data sets that yield stable, convergent measurements of its basic theoretical parameters. Obviously, I have the space here only to indicate the structure of the argument and to identify one area of active research and debate. Suppose, however, that we grant that the story is “close enough to consistency”: does that establish that we should regard the cosmological parameters as real properties of the universe? Here I will argue that even though we should, as van Fraassen (Reference Van Fraassen2009) suggested, resist a straightforwardly realist reading of the parameters, they can still anchor further work in cosmology.
$\Lambda$
CDM model is a permanent contribution to cosmology depends on the wide array of diverse data sets that yield stable, convergent measurements of its basic theoretical parameters. Obviously, I have the space here only to indicate the structure of the argument and to identify one area of active research and debate. Suppose, however, that we grant that the story is “close enough to consistency”: does that establish that we should regard the cosmological parameters as real properties of the universe? Here I will argue that even though we should, as van Fraassen (Reference Van Fraassen2009) suggested, resist a straightforwardly realist reading of the parameters, they can still anchor further work in cosmology.
A detailed description of the space-time geometry in the neighborhood of the Milky Way, according to general relativity, would resemble something like Swiss cheese—with the “holes” consisting of small-scale regions with large space-time curvature (say, near black holes), and sharp density contrasts, embedded within an expanding universe model. The parameters appearing in the
![]() $\Lambda$
CDM model characterize, by contrast, slight perturbations away from a completely uniform matter distribution at large scales. The relationship between the more realistic description and a “smoothed-out” or “averaged” model is far from straightforward in a nonlinear theory like general relativity. Ellis (Reference Ellis1984) showed that an “averaging operator” that smooths out nonuniformities below some length scale, when applied to a solution to EFE, does not generate a new solution (i.e., if the smoothing operator is applied to both the Einstein tensor and the stress-energy tensor for a given solution, the two new tensors generally do not satisfy EFE). More generally, there is not a straightforward procedure to generate a “best-fit” model from the bottom up, starting from a detailed description of space-time geometry at shorter length scales. It is a familiar lesson from other areas of physics that averaged parameters are not always physically meaningful—their utility depends on the relevant dynamics and justification for washing out details at different scales. These considerations block a straightforward reading of the parameters appearing in the
$\Lambda$
CDM model characterize, by contrast, slight perturbations away from a completely uniform matter distribution at large scales. The relationship between the more realistic description and a “smoothed-out” or “averaged” model is far from straightforward in a nonlinear theory like general relativity. Ellis (Reference Ellis1984) showed that an “averaging operator” that smooths out nonuniformities below some length scale, when applied to a solution to EFE, does not generate a new solution (i.e., if the smoothing operator is applied to both the Einstein tensor and the stress-energy tensor for a given solution, the two new tensors generally do not satisfy EFE). More generally, there is not a straightforward procedure to generate a “best-fit” model from the bottom up, starting from a detailed description of space-time geometry at shorter length scales. It is a familiar lesson from other areas of physics that averaged parameters are not always physically meaningful—their utility depends on the relevant dynamics and justification for washing out details at different scales. These considerations block a straightforward reading of the parameters appearing in the
![]() $\Lambda$
CDM model as corresponding, in some direct sense, to actual properties of the universe at cosmological scales.
$\Lambda$
CDM model as corresponding, in some direct sense, to actual properties of the universe at cosmological scales.
Setting aside a naive realist understanding of cosmological parameters does not, however, imply that they are merely artifacts, little more than a convenient way to summarize a large body of data. It is an old instrumentalist idea that the significance of a model should be characterized in terms of its role in guiding inquiry, not only in terms of fidelity to actual states of affairs. Miyake and Smith (Reference Miyake and Smith2021) articulate a version of this view in a discussion that has parallels to the cosmological case. As they describe in detail, molecular spectroscopy has led to the determination of (among other things) molecular constants that characterize the structural properties of diatomic molecules—represented as dumbbell-shaped bodies, with rotational and vibrational degrees of freedom. The constants specify structural features of this body, with the “rotation constant,” for example, interpreted as the inverse of its moment of inertia. Yet it would be a mistake to take this structural description as mapping onto the actual state of a molecule. For a molecule with an anharmonic potential, the rotational degrees of freedom couple to the vibrational modes; as a result, the atoms fluctuate around an equilibrium distance. Furthermore, taking electron–electron and electron–nuclei interactions into account requires time averaging over much shorter timescales. The full picture of a molecule includes fluctuations and interactions on several distinct timescales, and the simple interpretation of the rotation constant only applies if we, counterfactually, ignore all these details. Similarly, in the cosmological case, the parameters of the
![]() $\Lambda$
CDM model represent what the large-scale properties of the universe would be if we were to neglect complications due to structures at lower scales and the nonlinearities of general relativity. But, by contrast with spectroscopy, we lack a comparably clear understanding of the approximations involved in obtaining the large-scale model and the domain of validity of inferences based on it.
$\Lambda$
CDM model represent what the large-scale properties of the universe would be if we were to neglect complications due to structures at lower scales and the nonlinearities of general relativity. But, by contrast with spectroscopy, we lack a comparably clear understanding of the approximations involved in obtaining the large-scale model and the domain of validity of inferences based on it.
Miyake and Smith (Reference Miyake and Smith2021) propose that such counterfactual representations qualify as physically meaningful insofar as they can be used to guide inquiry, in the sense that systematic discrepancies between the model and observations have a physical source (as exemplified in the discovery of the isotopes of oxygen). On this view, a physically meaningful model is the first step in a series of successive approximations that are guided by ongoing comparisons with observations. Smith’s work has characteristically focused on long-term evaluation of the evidence developed in different areas of physics, to assess whether scientists have used physically meaningful models as a starting point and succeeded in identifying new features of nature through a process of refinement. Although we do not yet have a similarly long view in cosmology, the
![]() $\Lambda$
CDM model has clearly been the essential starting point for research in cosmology for several decades, and the model has (arguably) enabled the discovery of entirely new constituents of the universe (dark matter and dark energy).
$\Lambda$
CDM model has clearly been the essential starting point for research in cosmology for several decades, and the model has (arguably) enabled the discovery of entirely new constituents of the universe (dark matter and dark energy).
Returning to the second methodological theme from the introduction, “taking the model seriously” is precisely to take it as physically meaningful in this sense and hence to treat any discrepancies as targets for further investigation. This should not be read as a straightforwardly realist commitment, because the model has an essentially counterfactual character. The contrast here is not between realism and instrumentalism but rather, following Stein (Reference Stein1989), between a commitment to seeing the model as a source of further physical insights, such as opening up possibilities for measurements of the fundamental parameters, rather than merely a convenient tool for organizing a body of knowledge.
5. Conclusion
Ongoing disputes regarding
![]() $H_0$
illustrate the value of using a model to leverage high-precision measurements from one domain to gain further insight regarding systematic errors in another domain. Dedicated empirical work will be required to determine whether the current tension traces back to systematic errors in the local distance ladder or instead indicates a need to modify
$H_0$
illustrate the value of using a model to leverage high-precision measurements from one domain to gain further insight regarding systematic errors in another domain. Dedicated empirical work will be required to determine whether the current tension traces back to systematic errors in the local distance ladder or instead indicates a need to modify
![]() $\Lambda$
CDM. But in closing, we can return to the more philosophical issue: in what sense should we take
$\Lambda$
CDM. But in closing, we can return to the more philosophical issue: in what sense should we take
![]() $\Lambda$
CDM as a permanent contribution, based on convergent measurement of fundamental parameters? There is a common aspect of recent philosophical discussions of how successful measurements can establish permanence. Isaac (Reference Isaac2019) argues that measurement practices can identify objective fixed points in the world that are not subject to the familiar concerns about commitments shifting through periods of theory change. Permanence of these fixed points follows, on this account, from the theory neutrality of measurement: theory “factors out” in light of convergence, and success can be characterized in theory-neutral terms (namely, increasing precision). Despite several other contrasts, Smith and Seth (Reference Smith and Seth2020) similarly emphasize that in exemplary cases, the analysis of stability, convergence, and amenability to increasing precision of some set of measurements depends on “local regularities” (such as specific equations relating sets of accessible quantities, within a specified domain), rather than on fundamental laws. In both lines of argument, excessive reliance on higher-level theory opens up the possibility of impermanence. With this in mind, it is striking that efforts to develop an increasingly rich web of different measurement techniques in cosmology has led to the identification of many more “local regularities” and relatively weaker reliance on higher-level theory. Regardless of the fate of the
$\Lambda$
CDM as a permanent contribution, based on convergent measurement of fundamental parameters? There is a common aspect of recent philosophical discussions of how successful measurements can establish permanence. Isaac (Reference Isaac2019) argues that measurement practices can identify objective fixed points in the world that are not subject to the familiar concerns about commitments shifting through periods of theory change. Permanence of these fixed points follows, on this account, from the theory neutrality of measurement: theory “factors out” in light of convergence, and success can be characterized in theory-neutral terms (namely, increasing precision). Despite several other contrasts, Smith and Seth (Reference Smith and Seth2020) similarly emphasize that in exemplary cases, the analysis of stability, convergence, and amenability to increasing precision of some set of measurements depends on “local regularities” (such as specific equations relating sets of accessible quantities, within a specified domain), rather than on fundamental laws. In both lines of argument, excessive reliance on higher-level theory opens up the possibility of impermanence. With this in mind, it is striking that efforts to develop an increasingly rich web of different measurement techniques in cosmology has led to the identification of many more “local regularities” and relatively weaker reliance on higher-level theory. Regardless of the fate of the
![]() $\Lambda$
CDM model, taking the model seriously as a way of studying the universe has generated an enormous amount of detailed knowledge regarding the properties of systems, and local regularities governing how their properties relate to their cosmic environment, over an enormous range of scales.
$\Lambda$
CDM model, taking the model seriously as a way of studying the universe has generated an enormous amount of detailed knowledge regarding the properties of systems, and local regularities governing how their properties relate to their cosmic environment, over an enormous range of scales.
Acknowledgments
It is a pleasure to thank my co-symposiasts, as well as Sarah Gallagher, George Smith, Jim Weatherall, and especially Barry Madore, for helpful comments and discussions. Research on this article was supported in part by the John Templeton Foundation under grant 61048; the views expressed here are the author’s and do not necessarily reflect those of the Foundation.