INTRODUCTION
At present, the acceleration of electrons in extremely intense laser fields is an area of increasingly vigorous investigation. In the majority of studies, electron acceleration (a thorough review of laser acceleration of electrons can be found in Esarey et al. (Reference Esarey, Shroeder and Leemans2009), Malka (Reference Malka2012), and Umstadter (Reference Umstadter2003)) and bunch formation (for example, see Naumova et al. (Reference Naumova, Sokolov, Nees, Maksimchuk, Yanovsky and Mourou2004), Tajima and Dawson (Reference Tajima and Dawson1979), and Wagner et al. (Reference Wagner, Chen, Maksimchuk and Umstadter1997)) were examined in the context of laser interactions with plasma targets, with wakefields providing the acceleration mechanism. In the settings, the need for energy conversion from the laser field to the wakefield should limit the electron acceleration efficiency. Moreover, while the electron bunches formed in laser wakefields tend to be extremely short in the longitudinal direction, the corresponding size being considerably smaller than the laser wavelength and the durations falling within the attosecond range, the electron bunch transverses sizes remain comparable to the focal spot of the accelerating laser pulse.
An alternative mechanism of electron acceleration suggested by Galkin et al. (Reference Galkin, Korobkin, Romanovskiy, Trofimov and Shiryaev2012) is the direct interaction with the field of a standing wave formed by a pair of counter-propagating ultrashort laser pulses with amplitude fronts tilted relative to their phase fronts, in which an electron bunch gets compressed in one of the transverse dimensions to a size smaller than the laser wavelength. Driven by the standing wave, the electrons shift toward the symmetry plane of the field configuration and combine into bunches tightly compressed in one of the directions in space. The parameters of the bunch longitudinal compression in the process were found to be preferable compared to those achieved via wakefield acceleration.
In the present study, we propose a new concept of generating electron bunches compressed in all dimensions in the field of a standing wave generated by multiple laser pulses with tilted amplitude fronts. The corresponding simulations were carried out using the relativistic Newton equation with the Lorentz force arising from the laser field.
Usually, a standing wave represents the result of stationary interference between counter-propagating waves with equal amplitudes, which creates in space a periodic pattern of maxima and minima and involves no net energy flow. A more complex picture emerges in the case of the interference between several identical beams with the wave vectors belonging to the same plane. If the centers of the beams traverse the same point and all the angles between the wave vectors of the beams are equal, the resulting interference pattern is fairly symmetric relative to the line crossing the intersection point and perpendicular to the beam propagation plane. The corresponding field distribution can be described as a two-dimensional (2D) standing wave where, accordingly, a 2D trap for the electron acceleration can be created (a configuration of greater complexity, which can be interpreted as a three-dimensional (3D) standing wave, comes into being if several identical laser beams are launched to converge at a point in space from the centers of the faces of a polyhedron).
The use of laser pulses having amplitude fronts tilted relative to their phase fronts makes it possible to form bunches, compressed in all dimensions and consisting of electrons uniformly accelerated to extreme energies.
We explore the electron dynamics in 2D standing waves generated by three or four ultrashort laser pulses with tilted amplitude fronts. Simulations were performed for two schemes of the propagation of linearly polarized laser pulses. Three pulses were employed in the framework of the first scheme (Fig. 1a), so that in the reference frame chosen one travels along the z-axis and two propagate at an angle to it in the (y, z)-plane. The angle between the wave vectors of the pulses in this plane makes 120°. The amplitude fronts of the laser pulses are tilted relative to the phase fronts by an angle denoted as β (see Fig. 1b). The second scheme used four pulses, two of them propagating along the z and y-axes, and two — in the opposite directions. In the chosen reference frame the pulses overlap symmetrically with respect to the x-axis — central “axis” of the standing wave.
Fig. 1. Scheme of the propagation of linearly polarized laser pulses. The wave vectors k1k2, and k3 show the directions in which the beams propagate in the (y, z)-plane (Fig. 1a). One of the laser pulses with tilted amplitude fronts is designated as 1 on Figure 1b, β is the angle between the amplitude and phase fronts.
EQUATIONS OF MOTION
An electron in a laser pulse is driven by the Lorentz force, the equation of motion being:
$${d{\bf p} \over dt} = - e{\bf E} - {e \over c} \left[{\bf vH} \right]\comma \;$$where p, E, H are the electron momentum, the electric, and the magnetic fields, and e > 0 stands for the electron charge magnitude. Eq. (1) is combined with the initial conditions for the electron velocity and location.
Eq. (1) with initial conditions was used to simulate the electron dynamics in a 2D standing wave. It is assumed below that every laser pulse contributing to the standing wave is characterized by two distinct transverse sizes of the caustic waist 
${\rm \rho}_{0 \parallel}$ and 
${\rm \rho}_{0 \bot}$ in the directions, respectively, parallel and perpendicular to the pulse polarization. The transverse intensity distribution in every laser pulse is Gaussian. The coordinate dependencies of the pulse waist sizes in a given frame of reference such that the pulse propagates along the z-axis are expressed as:
$$\eqalign{{\rm \rho}_\parallel \left(z \right)&= {\rm \rho}_{0 \parallel} \sqrt{1 + {{z^2 } / {r_\parallel^2}}} \cr {\rm \rho}_{\bot} \left(z \right)&= {\rm \rho}_{0 \bot} \sqrt{1 + {{z^2} / {r_{\bot}^2}}}\comma \; }$$
where 
$r_{\parallel} = {\rm \pi} {\rm \rho}_{0\parallel}^2 / {\rm \lambda}$, 
$r_{\bot} = {\rm \pi} {\rm \rho}_{0 \bot}^2 / {\rm \lambda}$ are the asymmetric pulse Rayleigh ranges and λ is the radiation wavelength.
The structures of the electromagnetic fields in vacuum for Gaussian transverse intensity distributions were examined (Bochkarev & Bychenkov, Reference Bochkarev and Bychenkov2007; Hua et al., Reference Hua, Ho, Lin, Chen, Xiee, Zhang, Yan and Xu2004; Quesnel & Mora, Reference Quesnel and Mora1998). In the general case involving distinct waist sizes in the two transverse directions, the expressions for the fields in a pulse, linearly polarized along the x-axis and propagating in the z-direction are
$$\left\{\matrix{E_x = \displaystyle{{E_0 \left({\rm \xi} \right)\Lambda \left({x\comma \; y\comma \; z} \right)} \over {\left({\displaystyle{{z^2 } \over {r_\parallel ^2 }}+1} \right)^{1/4} \left({\displaystyle{{z^2 } \over {r_ \bot ^2 }}+1} \right)^{1/4} }}\sin {\rm \varphi}\comma \; \cr E_y=0\comma \; \cr E_z=\displaystyle{x \over {r_\parallel }}\displaystyle{{E_0 \left({\rm \xi} \right)\Lambda \left({x\comma \; y\comma \; z} \right)} \over {\left({\displaystyle{{z^2 } \over {r_\parallel ^2 }}+1} \right)^{3/4} \left({\displaystyle{{z^2 } \over {r_ \bot ^2 }}+1} \right)^{1/4} }}\cos \tilde {\rm \varphi}\comma \; \cr H_x=0\comma \; \cr H_y=E_x\comma \; \cr H_z=\displaystyle{y \over {r_ \bot }}\displaystyle{{E_0 \left({\rm \xi} \right)\Lambda \left({x\comma \; y\comma \; z} \right)} \over {\left({\displaystyle{{z^2 } \over {r_\parallel ^2 }}+1} \right)^{1/4} \left({\displaystyle{{z^2 } \over {r_ \bot ^2 }}+1} \right)^{3/4} }}\cos \tilde {\rm \varphi} . } \right.\comma \;$$
where 
$E_0 \left({\rm \xi} \right)= E_m \exp \left\{{ - \left[{{{\left({{\rm \xi} - {{z_d } / c}} \right)} / {\rm \tau} }} \right]^{2s} } \right\}$, 
$\Lambda \left({x\comma \; y\comma \; z} \right)=\exp \left\{{ - \displaystyle{{x^2 } \over {{\rm \rho} _\parallel ^2 \left(z \right)}} - \displaystyle{{y^2 } \over {{\rm \rho} _ \bot ^2 \left(z \right)}}} \right\}$, ξ = t − z/c, and the phase is given by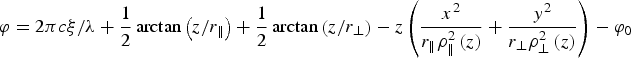 
${\rm \varphi}={{2{\rm \pi} c{\rm \xi} } / {\rm \lambda} }+\displaystyle{1 \over 2}\arctan \left({{z / {r_\parallel }}} \right)+\displaystyle{1 \over 2}\arctan \left({{z / {r_ \bot }}} \right)- z\left({\displaystyle{{x^2 } \over {r_\parallel {\rm \rho} _\parallel ^2 \left(z \right)}}+\displaystyle{{y^2 } \over {r_ \bot {\rm \rho} _ \bot ^2 \left(z \right)}}} \right)- {\rm \varphi} _0 $, 
$\tilde {\rm \varphi}={\rm \varphi}+\arctan \left({{z / {r_\parallel }}} \right)$, φ0 being the initial phase. Above, E m is the field peak strength, z d is the initial distance between the pulse and the electron (the quantity responsible for a gradual field rise), and τ is the pulse duration. The parameter s serves to define the temporal profile of the pulse and equals unity if the profile is Gaussian.
Eqs. (3) are derived as asymptotic solutions to the Maxwell equations to the first order in the small parameter ɛ = λ/(2πρ0i) (where ρ0i is the smaller of the beam waist sizes).
For a Gaussian pulse with the amplitude front tilted relative to the phase front by an angle β, the expressions for the fields can be obtained from the above by taking into account the dependence of ξ on β: ξ = t − (z + x tgβ) / c (for a pulse propagating in the direction of the z-axis) (Shuvaev et al., Reference Shuvaev, Nazarov, Shkurinov and Chirkin2007). The pulse intensity is
$$I = {c \over 4{\rm \pi}} \left\vert \overline{\left[{\bf E} \left({x\comma \; y\comma \; z\comma \; t} \right)\; {\bf H}\left({x\comma \; y\comma \; z\comma \; t} \right)\right]} \right\vert.$$Dimensionless intensities I m /I rel, where I m is the peak intensity, are introduced to characterize every pulse. The relativistic intensity I rel is defined as (Bochkarev & Bychenkov, Reference Bochkarev and Bychenkov2007):
$$I_{rel} = m^2 c^3 {\rm \omega}^2 /8{\rm \pi} e^2 = 1.37 \cdot 10^{18} \cdot \left({1 / {\rm \lambda}} \left[{\rm \mu} m \right]\right)^2 \left[W/cm^2 \right].$$ELECTRON DYNAMICS IN A STANDING WAVE
The expressions for the fields in a laser pulse propagating at an angle to the z-axis in the (y, z)-plane can be derived from Eqs. (3) with the help of a reference frame transformation such that the polarization direction remains parallel to the x-axis and the wave vector lies in the (y, z)-plane. The results of simulating the electron dynamics are shown below in the reference fame for which Eqs. (2) and (3) are written.
The present study is carried out for Gaussian beams with the amplitude fronts tilted relative to the phase fronts by an angle β in all cases. The results of the simulations performed for Gaussian pulses were compared against those generated assuming plane wave fronts. Beams having different waist sizes in different dimensions are advantageous in the context of the electron acceleration, since the zone where they overlap travels over greater distances for 
${\rm \rho}_{\parallel} \gt \gt {\rm \rho}_{\bot}$. Under the conditions, electrons interact with the optical fields during a longer period of time and therefore gain greater kinetic energies. Simulations were performed for ultrashort laser pulses with cτ/λ = 2.5, Gaussian transverse distributions, and Gaussian of hyper-Gaussian temporal profiles (s = 1, s = 2). The parameters of the focusing were 
${\rm \rho}_{\parallel} / {\rm \lambda} = 200$ and 
${\rm \rho}_{\bot} / {\rm \lambda} = 2.5$, with the length of the caustic waist being much greater than the size of the domain where electrons interact with the optical field.
The motions of an individual electron in the field of a standing wave generated by two laser pulses assumed to have plane phase fronts were investigated by Galkin et al. (Reference Galkin, Korobkin, Romanovskiy, Trofimov and Shiryaev2012). Note that in the case studied, the election gets trapped by the laser field and moves along the x-axis with a velocity close to the speed of light.
The intensity distribution in the standing wave generated by laser pulses under the arrangement described above in the case β = 45° has the shape of a 3D-lattice which travels with the speed of light along the x-axis.
Consider the dynamics of an electron in a standing wave generated by three Gaussian pulses. The electron coordinates, velocities, and accelerations, along with other electron trajectory parameters, were calculated by solving Eq. (1) numerically. Figure 2 shows, for the case of the linear polarization and the initial electron displacement given by x 0/λ = −20, y 0/λ = 0.06, z 0/λ = −0.24, the 2D electron trajectory in the normalized coordinates (x/λ, z/λ) (Fig. 2a), (x/λ, y/λ) (Fig. 2b), (y/λ, z/λ) (Fig. 2c), the dependence of the electron kinetic energy Wk/mc2 on time (Fig. 2d), and the velocity component in (Fig. 2e, Fig. 2f) for β = 45°. Figure 2f illustrates the dependence on time of the velocity component corresponding to the dashed part of the curve in Figure 2e. The circles in Figures 2a, 2b, 2c mark the initial location of the electron.
Fig. 2. The 2D trajectories of an electron in dimensionless coordinates x/λ, z/λ (Fig. 2a), x/λ, y/λ (Fig. 2b), z/λ, y/λ (Fig. 2c), and the dependencies on time of the electron kinetic energy Wk/mc2 (Fig. 2d) and the velocity components v x /c (Fig. 2e, Fig. 2f) for β = 45°. The parameters of the laser pulses are: s = 2, cτ/λ = 2.5, 
${\rm \rho}_{\parallel} /{\rm \lambda} = 200\comma \; {\rm \rho}_{\bot}/{\rm \lambda} = 2.5\comma \; I_m /I_{rel} = 1000$. The initial location of the electron is given by: x 0 /λ = −20, y 0 /λ = 0.06, z 0 /λ = −0.24.
The electron dynamics in the standing wave generated by three laser pulses includes two stages. At the first one, the electron rapidly gets shifted to a domain adjacent to the x-axis. The electron acceleration peaks in the process and the electron velocity approaches the speed of light. The impact of laser pulses forming the standing wave on an electron initially displaced in the (y, z)-plane is asymmetric: the pulse toward which the electron is initially displaced contributes most to the electron motion early during the interaction. At the second stage, the electron gets trapped by the optical field and moves along the x-axis on a straight-line segment of the trajectory with a velocity close to the speed of light. The electron exhibits slight oscillations in z and y symmetrically relative to the x-axis (see Figs. 2a, 2b, 2c; the axis scales in Figs. 2a and 2b differ considerably). The amplitudes of the oscillations in z and y differ slightly and depend on the respective initial displacements of the electron. The electron displacement in x over the interaction time far exceeds the amplitudes of the oscillations in z and y. The kinetic energy of the electron increases smoothly to reach the maximal value of Wk/mc2 = 5200 (2.6 GeV) by the end of the interaction.
Figure 3 shows the 2D trajectory of an electron in the normalized coordinates (z/λ, y/λ) (Fig. 3a), and the dependence of the kinetic energy Wk/mc2 on time (Fig. 3b) for the initial displacements given by x 0/λ = −35, y 0/λ = 0.18, z 0/λ = −0.18. Due to the difference in the initial locations of the electron, in this case, its trajectory in the (y, z)-plane also differs to an extent from the one observed in the previous case. The electron trajectories in the (x, z) and (x, y) planes are similar to those in the case illustrated by Figures 2a and 2b. At the second stage of the interaction, the electron having the trajectory shown in Figure 3 also moves along the x-axis with a velocity close to the speed of light, the energy gained in the interaction being Wk/mc2 = 5600 (2.8 GeV).
Fig. 3. The 2D trajectory of an electron in dimensionless coordinates z/λ, y/λ(Fig. 3a), and the dependence on time of the electron kinetic energy W k /mc 2 (Fig. 3b) for β = 45°. The parameters of the laser pulses are: s = 2, cτ/λ = 2.5, 
${\rm \rho}_{\parallel} /{\rm \lambda} = 200\comma \; {\rm \rho}_{\bot}/{\rm \lambda} = 2.5\comma \; I_m /I_{rel} = 1000$. The initial location of the electron is given by: x 0 /λ = −35, y 0 /λ = 0.18, z 0 /λ = −0.18.
The overall picture stays largely unchanged for all initial displacements of the electron such that |y 0/λ| ≤ 1, |z 0/λ| ≤ 1. At the second stage, the electron shifts along the x-axis, oscillating around it, the amplitude of the oscillations being fairly insensitive to the displacement values. Note that, as the initial electron displacement changes, the electron, when trapped, stays in a single cell of the field lattice where the field value is negative.
The conclusion stemming from the simulations is that the dynamics of practically all the electrons in the zone where they interact with the standing wave generated by three laser pulses with tilted amplitude fronts comprises the two consecutive stages described above.
The picture of the electron dynamics in a standing wave generated by four Gaussian pulses is similar to that for the standing wave formed by three pulses. The electron dynamics is again a two-stage process and the amplitudes of the oscillations in z and y are fairly close.
Moreover, the kinetic energy gained by the electron, its trajectory, the amplitudes of the oscillations in z and y, and other electron dynamics parameters in a standing wave generated by several laser pulses with the phase fronts assumed to be plane do not differ considerably from those in the cases considered above.
Importantly, efficient acceleration of electrons in standing waves for s = 1, s = 2 is possible only within a small interval of angles β around 45°. The velocity of displacement in x of the zone where the pulses overlap becomes different from the speed of light as the angle deviates from 45°. Due to the asymmetry of the impact of the pulses contributing to the standing wave, the electron gets trapped by one of the laser pulses and ejected from the domain where the standing wave is formed. The deviation of β by several dozen percent of a degree translates into a decrease in the electron energy gain by an order of magnitude.
The amplitude of the electron oscillations in z and y is higher for longer laser pulses, the result being that the electron can relocate from cell to cell at the second stage of the interaction. Accordingly, the electron energy gain decreases. For higher laser intensities, the amplitude of the electron oscillations goes down and the electron stays within the same cell during the second stage of the interaction.
As shown above, the dynamics of an individual electron in a standing wave formed by a group of laser pulses having relativistic intensities and amplitude fronts tilted relative to the phase fronts depends weakly on the initial location of the electron. Consequently, under optimal conditions the results obtained can be extended to describe the dynamics of an ensemble of electrons in a standing wave. The ensemble can, for example, be created as intense laser radiation propagates into a low-concentration neutral gas, causing ionization at the pulse front. Importantly, for the range of parameters of the laser acceleration scheme studied the Lorentz force exerted on the electrons by the laser field massively exceeds their Coulomb interactions. The simulations presented do not take the Coulomb forces or the magnetic fields generated by the laser driven electrons into account. The incorporation of the above effects is a subject for further study.
Traps are formed in a small domain near the x-axis due to the laser beam interference. The traps are cells of the lattice that move along the x-axis with the speed of light. Depending on the laser radiation parameters, the electrons starting to be driven within several wavelengths from the x-axis get trapped in one of the cells. Electrons with various initial coordinates in x undergo trapping successively. During the second stage of the interaction, the trapped electrons travel within cells along the x-axis with velocities close to the speed of light. The accelerated electrons therefore get concentrated within a small domain in space into a bunch. For relativistic intensities and s = 2, the bunch size in x is found to make ~10−3 λ. Traveling along the x-axis, the electrons oscillate slightly in z and y. The amplitudes of the oscillations are limited to percents of the wavelength. The eclectic field within the cell draws deviating electrons back to the x-axis. The result is the compression of the electron ensemble in z and y, the transverse size of the bunch in these coordinates making at most ~10−2 λ for s = 1 or s = 2. The bunch with the volume making 10−7λ3 collects the electrons from the domain having the transverse sizes on the order of about λ and the length on the order of about 100λ (which is the total distance over which the trap travels along the x-axis). The electron density in the bunch created can be about 109 times higher than in the target background. The electrons in the compressed bunch continue to interact individually with the standing wave field, the kinetic energy of the electrons in the bunch is several GeV. The resulting electron bunch is almost symmetric relative to the x-axis.
The electrons energy gain as high as several GeV occurs due to the direct action of the laser field. For the parameters of the laser pulses considered, its magnitude reaches 19 TV/m, which is roughly 200 times higher than the strength of the accelerating fields achieved during wakefield electron acceleration (Gordon et al., Reference Gordon, Tzeng, Clayton, Dangor, Malka, Marsh, Modena, Mori, Muggli, Najmudin, Neely, Danson and Joshi1998; Malka et al., Reference Malka, Fritzler, Lefebvre, Aleonard, Burgy, Chambaret, Chemin, Krushelnik, Malka, Mangles, Najmudin, Pittman, Rousseau, Scheurer, Walton and Dangor2002). The length over which electrons gain comparable energies is much shorter in the proposed scheme, and the electron bunches generated using the scheme discussed above are found to have extremely small longitudinal and transverse sizes.
CONCLUSIONS
A concept of laser acceleration of electrons using specially arranged field configurations acting as traps is proposed. The traps get formed via the interference between several relativistically intense laser pulses having amplitude fronts tilted relative to their phase fronts, all of which propagate in the same plane and converge at a single point, giving rise to a 2D standing wave. The traps travel with the speed of light in the direction perpendicular to the plane. For strongly asymmetric focal spots, such that one of the transverse sizes is comparable to the laser wavelength and the other, the one along which the laser field is polarized — much greater than the laser wavelength, the distances passed by the traps roughly equal the bigger of the focal spot transverse sizes. The shape of the electric field in a trap provides for the acceleration of the ensemble of the trapped electrons combined with its compression in the longitudinal and transverse directions. The resulting electron bunches, for the laser parameters studied, are shown to have the longitudinal sizes as short as about 10−3λ and the transverse sizes making about 10−2λ. Every bunch draws electrons from a volume of ionized gas with the transverse size comparable to the laser wavelength and the longitudinal size equal to the distance over which the trap travels. The latter depends on the transverse distribution of the intensity in the laser pulses and, under appropriate conditions, can be several orders of magnitude greater than the laser wavelength. The electron density in bunches can exceed the background value by nine orders of magnitude, with the electron energies as high as several GeV and beyond (for the currently available ultrashort laser pulse parameters). The electron acceleration scheme considered makes it possible to generate short bunches of high-energy electrons. The suggested acceleration technique can be used in basic research and various applications.
