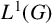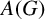1 Introduction
Let G be a locally compact group. By a classical result of Sakai [Reference Sakai14], G is compact if and only if the group algebra
![]() $L^1(G)$
has a nonzero (weakly) compact right multiplier. In [Reference Lau10], Lau showed that an analogous result is true on the dual side, that is, G is discrete if and only if its Fourier algebra
$L^1(G)$
has a nonzero (weakly) compact right multiplier. In [Reference Lau10], Lau showed that an analogous result is true on the dual side, that is, G is discrete if and only if its Fourier algebra
![]() $A(G)$
has a nonzero (weakly) compact multiplier. Along this line of research, Ghahramani and Lau proved that G is compact if and only if any symmetric Segal algebra
$A(G)$
has a nonzero (weakly) compact multiplier. Along this line of research, Ghahramani and Lau proved that G is compact if and only if any symmetric Segal algebra
![]() $S^1(G)$
of
$S^1(G)$
of
![]() $L^1(G)$
has a nonzero (weakly) compact right or left multiplier [Reference Ghahramani and Lau6].
$L^1(G)$
has a nonzero (weakly) compact right or left multiplier [Reference Ghahramani and Lau6].
Moreover, it was shown in [Reference Ghahramani and Lau4] that G is amenable if and only if
![]() $L^\infty (G)^*=L^1(G)^{**}$
, the second dual of
$L^\infty (G)^*=L^1(G)^{**}$
, the second dual of
![]() $L^1(G)$
equipped with the first Arens product, has a nonzero (weakly) compact right multiplier. Along the way, Ghahramani and Lau proved that G is compact if and only if
$L^1(G)$
equipped with the first Arens product, has a nonzero (weakly) compact right multiplier. Along the way, Ghahramani and Lau proved that G is compact if and only if
![]() $L^1(G)^{**}$
has a (weakly) compact left multiplier
$L^1(G)^{**}$
has a (weakly) compact left multiplier
![]() $ T $
with
$ T $
with
![]() $ \langle T(n),1\rangle \neq 0 $
for some
$ \langle T(n),1\rangle \neq 0 $
for some
![]() $ n\in L^{1}(G)^{**} $
[Reference Ghahramani and Lau5]. Dually, G is discrete if and only if
$ n\in L^{1}(G)^{**} $
[Reference Ghahramani and Lau5]. Dually, G is discrete if and only if
![]() $A(G)^{**}$
has a (weakly) compact left multiplier
$A(G)^{**}$
has a (weakly) compact left multiplier
![]() $ T $
with
$ T $
with
![]() $ \langle T(n),1\rangle \neq 0 $
for some
$ \langle T(n),1\rangle \neq 0 $
for some
![]() $ n\in A(G)^{**}$
.
$ n\in A(G)^{**}$
.
It is thus natural to try to determine when the second dual of a symmetric abstract Segal algebra of
![]() $L^{1}(G)$
or
$L^{1}(G)$
or
![]() $A(G)$
has a nonzero (weakly) compact left or right multiplier. We answer this question by proving that if
$A(G)$
has a nonzero (weakly) compact left or right multiplier. We answer this question by proving that if
![]() $ \mathcal {B} $
is a symmetric abstract Segal algebra of a Banach algebra
$ \mathcal {B} $
is a symmetric abstract Segal algebra of a Banach algebra
![]() $\mathcal {A} $
and
$\mathcal {A} $
and
![]() $ \varphi $
is a nonzero character on
$ \varphi $
is a nonzero character on
![]() ${\mathcal A}$
, then the existence of a (weakly) compact left or right multiplier on
${\mathcal A}$
, then the existence of a (weakly) compact left or right multiplier on
![]() $ \mathcal {B} $
is equivalent to the existence of the same multiplier on
$ \mathcal {B} $
is equivalent to the existence of the same multiplier on
![]() $ \mathcal {A}$
.
$ \mathcal {A}$
.
For a symmetric Segal algebra
![]() $S^1(G)$
of the group algebra
$S^1(G)$
of the group algebra
![]() $L^1(G)$
, we denote by
$L^1(G)$
, we denote by
![]() $ K $
the set of all right multipliers
$ K $
the set of all right multipliers
![]() $ T $
on
$ T $
on
![]() $ S^1(G)^{**} $
with rank one such that
$ S^1(G)^{**} $
with rank one such that
![]() $ \langle T(n),\varphi _{1}\rangle =1$
whenever
$ \langle T(n),\varphi _{1}\rangle =1$
whenever
![]() $ \langle n,\varphi _{1}\rangle =1 $
, where
$ \langle n,\varphi _{1}\rangle =1 $
, where
![]() $ \varphi _{1} $
is the nonzero character on
$ \varphi _{1} $
is the nonzero character on
![]() $ L^{1}(G) $
defined by
$ L^{1}(G) $
defined by
![]() $ \varphi _{1}(f)=\int _{G}f(x)\,dx$
for all
$ \varphi _{1}(f)=\int _{G}f(x)\,dx$
for all
![]() $f\in L^{1}(G) $
. We prove that if
$f\in L^{1}(G) $
. We prove that if
![]() $ G $
is amenable and noncompact and
$ G $
is amenable and noncompact and
![]() $ d(G) $
is the smallest possible cardinality of a covering of
$ d(G) $
is the smallest possible cardinality of a covering of
![]() $ G $
by compact sets, then
$ G $
by compact sets, then
![]() $ \lvert K\rvert \geq 2^{2^{d(G)}}\kern-1pt$
.
$ \lvert K\rvert \geq 2^{2^{d(G)}}\kern-1pt$
.
2 Preliminaries
We shall now fix some notation. We denote the closed linear span by
![]() $\overline {\langle \cdot \rangle }$
. Let
$\overline {\langle \cdot \rangle }$
. Let
![]() ${\mathcal A}$
be a Banach algebra. Then
${\mathcal A}$
be a Banach algebra. Then
![]() ${\mathcal A}^*$
is naturally a Banach
${\mathcal A}^*$
is naturally a Banach
![]() ${\mathcal A}$
-bimodule with the actions
${\mathcal A}$
-bimodule with the actions
for all
![]() $f\in {\mathcal A}^*$
and
$f\in {\mathcal A}^*$
and
![]() $a,b\in {\mathcal A}$
. It is known that there is a multiplication
$a,b\in {\mathcal A}$
. It is known that there is a multiplication
![]() $\Box $
on the second dual
$\Box $
on the second dual
![]() ${\mathcal A}^{**}$
of
${\mathcal A}^{**}$
of
![]() ${\mathcal A}$
, extending the multiplication on
${\mathcal A}$
, extending the multiplication on
![]() ${\mathcal A}$
. The first Arens product in
${\mathcal A}$
. The first Arens product in
![]() ${\mathcal A}^{**}$
is given as follows. For
${\mathcal A}^{**}$
is given as follows. For
![]() $m,n\in {\mathcal A}^{**}$
,
$m,n\in {\mathcal A}^{**}$
,
![]() $f\in {\mathcal A}^*$
and
$f\in {\mathcal A}^*$
and
![]() $a\in {\mathcal A}$
,
$a\in {\mathcal A}$
,
If
![]() $ \mathcal {A} $
is a Banach algebra, then a linear mapping
$ \mathcal {A} $
is a Banach algebra, then a linear mapping
![]() $ T:\mathcal {A}\rightarrow \mathcal {A} $
is a right (respectively left) multiplier if
$ T:\mathcal {A}\rightarrow \mathcal {A} $
is a right (respectively left) multiplier if
![]() $ T(ab)=aT(b)$
(respectively
$ T(ab)=aT(b)$
(respectively
![]() $T(ab)=T(a)b $
) for all
$T(ab)=T(a)b $
) for all
![]() $ a,b\in \mathcal {A} $
. In particular, for each
$ a,b\in \mathcal {A} $
. In particular, for each
![]() $ a\in \mathcal {A} $
, the multiplication operators
$ a\in \mathcal {A} $
, the multiplication operators
![]() $ \lambda _{a}:\mathcal {A}\rightarrow \mathcal {A} $
and
$ \lambda _{a}:\mathcal {A}\rightarrow \mathcal {A} $
and
![]() $ \rho _{a}:\mathcal {A}\rightarrow \mathcal {A} $
defined by
$ \rho _{a}:\mathcal {A}\rightarrow \mathcal {A} $
defined by
![]() $ \lambda _{a}(b)=ab $
and
$ \lambda _{a}(b)=ab $
and
![]() $ \rho _{a}(b)=ba $
are respectively left and right multipliers on
$ \rho _{a}(b)=ba $
are respectively left and right multipliers on
![]() $ \mathcal {A} $
. We also denote by
$ \mathcal {A} $
. We also denote by
![]() $\Delta ({\mathcal A})$
the set of all nonzero characters on
$\Delta ({\mathcal A})$
the set of all nonzero characters on
![]() ${\mathcal A}$
.
${\mathcal A}$
.
We recall from Burnham [Reference Burnham2] that a Banach algebra
![]() $\mathcal B$
is an abstract Segal algebra of
$\mathcal B$
is an abstract Segal algebra of
![]() $\mathcal A$
if:
$\mathcal A$
if:
-
(i)
 $\mathcal B$
is a dense left ideal in
$\mathcal B$
is a dense left ideal in
 $\mathcal A$
;
$\mathcal A$
; -
(ii) there exists
 $M> 0$
such that
$M> 0$
such that
 $\lVert b\rVert _{\mathcal A}\leq M \lVert b\rVert _{\mathcal B}$
for each
$\lVert b\rVert _{\mathcal A}\leq M \lVert b\rVert _{\mathcal B}$
for each
 $b\in \mathcal B$
;
$b\in \mathcal B$
; -
(iii) there exists
 $C> 0$
such that
$C> 0$
such that
 $\lVert ab\rVert _{\mathcal B}\leq C\lVert a\rVert _{\mathcal A} \lVert b\rVert _{\mathcal B}$
for each
$\lVert ab\rVert _{\mathcal B}\leq C\lVert a\rVert _{\mathcal A} \lVert b\rVert _{\mathcal B}$
for each
 $a, b\in \mathcal B$
.
$a, b\in \mathcal B$
.
We further say that
![]() ${\mathcal B}$
is symmetric if it is also a two-sided dense ideal in
${\mathcal B}$
is symmetric if it is also a two-sided dense ideal in
![]() ${\mathcal A}$
and for each
${\mathcal A}$
and for each
![]() $a,b \in {\mathcal B}$
,
$a,b \in {\mathcal B}$
,
In this case, by [Reference Burnham2, Theorem 2.1],
![]() $\Delta ({\mathcal A})$
and
$\Delta ({\mathcal A})$
and
![]() $\Delta ({\mathcal B})$
are homeomorphic.
$\Delta ({\mathcal B})$
are homeomorphic.
Throughout this paper, we assume that
![]() $ G $
is a locally compact group with a fixed left Haar measure and let
$ G $
is a locally compact group with a fixed left Haar measure and let
![]() $ L^{1}(G) $
be the group algebra of
$ L^{1}(G) $
be the group algebra of
![]() $ G $
. Then
$ G $
. Then
![]() $ L^{1}(G) $
is a Banach algebra with the convolution product defined by
$ L^{1}(G) $
is a Banach algebra with the convolution product defined by
 $$ \begin{align*} (f*g)(x)=\int_{G}f(y)g(y^{-1}x)\,dy\quad(f,g\in L^1(G)). \end{align*} $$
$$ \begin{align*} (f*g)(x)=\int_{G}f(y)g(y^{-1}x)\,dy\quad(f,g\in L^1(G)). \end{align*} $$
A linear subspace
![]() $ S^{1}(G) $
of
$ S^{1}(G) $
of
![]() $ L^{1}(G) $
is called a Segal algebra, if:
$ L^{1}(G) $
is called a Segal algebra, if:
-
(i)
 $ S^{1}(G) $
is dense in
$ S^{1}(G) $
is dense in
 $ L^{1}(G) $
;
$ L^{1}(G) $
; -
(ii)
 $ S^{1}(G) $
is a Banach space under some norm
$ S^{1}(G) $
is a Banach space under some norm
 $ \lVert \cdot \rVert _{S} $
and
$ \lVert \cdot \rVert _{S} $
and
 $ \lVert f\rVert _{1}\leq \lVert f\rVert _{S} $
for all
$ \lVert f\rVert _{1}\leq \lVert f\rVert _{S} $
for all
 $ f\in S^{1}(G) $
;
$ f\in S^{1}(G) $
; -
(iii)
 $ S^{1}(G) $
is left translation invariant and the map
$ S^{1}(G) $
is left translation invariant and the map
 $ x\mapsto l_{x}f $
of
$ x\mapsto l_{x}f $
of
 $ G $
into
$ G $
into
 $ S^{1}(G) $
is continuous;
$ S^{1}(G) $
is continuous; -
(iv)
 $ \lVert l_{x}f\rVert _{S}=\lVert f\rVert _{S} $
, for all
$ \lVert l_{x}f\rVert _{S}=\lVert f\rVert _{S} $
, for all
 $ x\in G $
and
$ x\in G $
and
 $ f\in S^1(G) $
.
$ f\in S^1(G) $
.
We note that every Segal algebra is an abstract Segal algebra of
![]() $ L^{1}(G)$
by [Reference Reiter13, Proposition 1]. A Segal algebra
$ L^{1}(G)$
by [Reference Reiter13, Proposition 1]. A Segal algebra
![]() $ S^{1}(G) $
is symmetric if it is right translation invariant,
$ S^{1}(G) $
is symmetric if it is right translation invariant,
![]() $ \lVert r_{x}f\rVert _{S}=\lVert f\rVert _{S} $
and the map
$ \lVert r_{x}f\rVert _{S}=\lVert f\rVert _{S} $
and the map
![]() $ x\mapsto r_{x}f $
from
$ x\mapsto r_{x}f $
from
![]() $ G $
into
$ G $
into
![]() $ S^{1}(G) $
is continuous for all
$ S^{1}(G) $
is continuous for all
![]() $ x\in G $
and
$ x\in G $
and
![]() $ f\in S^{1}(G) $
. Note that every symmetric Segal algebra is a two-sided ideal of
$ f\in S^{1}(G) $
. Note that every symmetric Segal algebra is a two-sided ideal of
![]() $ L^{1}(G) $
and has an approximate identity in which each term has norm one in
$ L^{1}(G) $
and has an approximate identity in which each term has norm one in
![]() $ L^{1}(G) $
(see [Reference Reiter13, Section 8, Proposition 1]).
$ L^{1}(G) $
(see [Reference Reiter13, Section 8, Proposition 1]).
3 Multipliers on the second dual
Let
![]() $ \mathcal {B} $
be a symmetric abstract Segal algebra of a Banach algebra
$ \mathcal {B} $
be a symmetric abstract Segal algebra of a Banach algebra
![]() $ \mathcal {A} $
. We note that for every
$ \mathcal {A} $
. We note that for every
![]() $ f\in \mathcal {B}^{*} $
,
$ f\in \mathcal {B}^{*} $
,
![]() $ a\in \mathcal {A} $
and
$ a\in \mathcal {A} $
and
![]() $ b\in \mathcal {B} $
, we can define
$ b\in \mathcal {B} $
, we can define
![]() $ f\bullet b\in \mathcal {A}^{*} $
by
$ f\bullet b\in \mathcal {A}^{*} $
by
Hence, for every
![]() $ m\in \mathcal {A}^{**} $
and
$ m\in \mathcal {A}^{**} $
and
![]() $ f\in \mathcal {B}^{*} $
, we may define the functional
$ f\in \mathcal {B}^{*} $
, we may define the functional
![]() $ m\bullet f\in \mathcal {B}^{*} $
by
$ m\bullet f\in \mathcal {B}^{*} $
by
Thus, for every
![]() $ m\in \mathcal {A}^{**} $
and
$ m\in \mathcal {A}^{**} $
and
![]() $ n\in \mathcal {B}^{**} $
, we can define the functional
$ n\in \mathcal {B}^{**} $
, we can define the functional
![]() $ n\odot m \in \mathcal {B}^{**} $
by
$ n\odot m \in \mathcal {B}^{**} $
by
For
![]() $ f\in \mathcal {B}^{*}$
and
$ f\in \mathcal {B}^{*}$
and
![]() $ a\in \mathcal {A} $
, we also can define
$ a\in \mathcal {A} $
, we also can define
![]() $ f\bullet a\in \mathcal {B}^{*} $
by
$ f\bullet a\in \mathcal {B}^{*} $
by
Thus for
![]() $ n\in \mathcal {B}^{**} $
and
$ n\in \mathcal {B}^{**} $
and
![]() $ f\in \mathcal {B}^{*} $
, we may define the functional
$ f\in \mathcal {B}^{*} $
, we may define the functional
![]() $ n\bullet f\in \mathcal {A}^{*} $
by
$ n\bullet f\in \mathcal {A}^{*} $
by
Therefore, for
![]() $ m\in \mathcal {A}^{**} $
and
$ m\in \mathcal {A}^{**} $
and
![]() $ n\in \mathcal {B}^{**} $
, we can define the functional
$ n\in \mathcal {B}^{**} $
, we can define the functional
![]() $ m\odot n \in \mathcal {B}^{**} $
by
$ m\odot n \in \mathcal {B}^{**} $
by
Let
![]() $ \iota :\mathcal {B}\rightarrow \mathcal {A} $
be the inclusion map. Then
$ \iota :\mathcal {B}\rightarrow \mathcal {A} $
be the inclusion map. Then
![]() $ \iota $
is an injective Banach
$ \iota $
is an injective Banach
![]() $ \mathcal {A} $
-bimodule morphism. Consider the adjoints
$ \mathcal {A} $
-bimodule morphism. Consider the adjoints
![]() $ \iota ^{*}:\mathcal {A}^{*}\rightarrow \mathcal {B}^{*} $
and
$ \iota ^{*}:\mathcal {A}^{*}\rightarrow \mathcal {B}^{*} $
and
![]() $ \iota ^{**}:\mathcal {B}^{**}\rightarrow \mathcal {A}^{**} $
of
$ \iota ^{**}:\mathcal {B}^{**}\rightarrow \mathcal {A}^{**} $
of
![]() $ \iota $
. Since
$ \iota $
. Since
![]() $ \iota $
has a dense range,
$ \iota $
has a dense range,
![]() $ \iota ^{*} $
is injective. It is not hard to see that
$ \iota ^{*} $
is injective. It is not hard to see that
![]() $ \iota ^{*} $
is in fact the restriction map. The following lemma will prove useful.
$ \iota ^{*} $
is in fact the restriction map. The following lemma will prove useful.
Lemma 3.1. Let
![]() $ \mathcal {B} $
be a symmetric abstract Segal algebra of
$ \mathcal {B} $
be a symmetric abstract Segal algebra of
![]() $ \mathcal {A} $
. Then for every
$ \mathcal {A} $
. Then for every
![]() $ {m\in \mathcal {A}^{**} }$
and
$ {m\in \mathcal {A}^{**} }$
and
![]() $ n,p\in \mathcal {B}^{**}$
, the following statements hold:
$ n,p\in \mathcal {B}^{**}$
, the following statements hold:
-
(i)
 $\lVert n\odot m\rVert \leq C\lVert n\rVert \,\lVert m\rVert $
;
$\lVert n\odot m\rVert \leq C\lVert n\rVert \,\lVert m\rVert $
; -
(ii)
 $\iota ^{**}(n\odot m)=\iota ^{**}(n)\square m $
;
$\iota ^{**}(n\odot m)=\iota ^{**}(n)\square m $
; -
(iii)
 $p\odot (m\square \iota ^{**}(n))=(p\odot m)\square n $
;
$p\odot (m\square \iota ^{**}(n))=(p\odot m)\square n $
; -
(iv)
 $\lVert m\odot n\rVert \leq C\lVert n\rVert \,\lVert m\rVert $
;
$\lVert m\odot n\rVert \leq C\lVert n\rVert \,\lVert m\rVert $
; -
(v)
 $\iota ^{**}(m\odot n)=m\square \iota ^{**}(n) $
;
$\iota ^{**}(m\odot n)=m\square \iota ^{**}(n) $
; -
(vi)
 $( \iota ^{**}(n)\square m)\odot p= n \square (m\odot p) $
.
$( \iota ^{**}(n)\square m)\odot p= n \square (m\odot p) $
.
Proof. The proofs of (i), (ii), (iv) and (v) are straightforward.
(iii) For
![]() $ f\in \mathcal {B}^{*} $
,
$ f\in \mathcal {B}^{*} $
,
![]() $ b\in \mathcal {B} $
and
$ b\in \mathcal {B} $
and
![]() $ a\in \mathcal {A} $
,
$ a\in \mathcal {A} $
,
 $$ \begin{align*} \langle \iota^{**}(n)\cdot(f\bullet b),a\rangle &=\langle \iota^{**}(n),f\bullet ba\rangle=\langle n,\iota^{*}(f\bullet ba)\rangle \\ &=\langle n,f\cdot ba\rangle=\langle n\cdot f,ba\rangle=\langle (n\cdot f)\bullet b,a\rangle. \end{align*} $$
$$ \begin{align*} \langle \iota^{**}(n)\cdot(f\bullet b),a\rangle &=\langle \iota^{**}(n),f\bullet ba\rangle=\langle n,\iota^{*}(f\bullet ba)\rangle \\ &=\langle n,f\cdot ba\rangle=\langle n\cdot f,ba\rangle=\langle (n\cdot f)\bullet b,a\rangle. \end{align*} $$
Therefore,
 $$ \begin{align*} \langle(m\square \iota^{**}(n))\bullet f),b\rangle&=\langle m\square \iota^{**}(n),f\bullet b\rangle=\langle m,\iota^{**}(n)\cdot(f\bullet b)\rangle\\ &=\langle m,(n\cdot f)\bullet b\rangle=\langle m\bullet(n\cdot f),b\rangle. \end{align*} $$
$$ \begin{align*} \langle(m\square \iota^{**}(n))\bullet f),b\rangle&=\langle m\square \iota^{**}(n),f\bullet b\rangle=\langle m,\iota^{**}(n)\cdot(f\bullet b)\rangle\\ &=\langle m,(n\cdot f)\bullet b\rangle=\langle m\bullet(n\cdot f),b\rangle. \end{align*} $$
Thus,
 $$ \begin{align*} \langle p\odot (m\square \iota^{**}(n)),f\rangle &=\langle p,(m\square \iota^{**}(n))\bullet f\rangle=\langle p,m\bullet (n\cdot f)\rangle\\ &=\langle p\odot m,n\cdot f\rangle=\langle(p\odot m)\square n,f\rangle. \end{align*} $$
$$ \begin{align*} \langle p\odot (m\square \iota^{**}(n)),f\rangle &=\langle p,(m\square \iota^{**}(n))\bullet f\rangle=\langle p,m\bullet (n\cdot f)\rangle\\ &=\langle p\odot m,n\cdot f\rangle=\langle(p\odot m)\square n,f\rangle. \end{align*} $$
Hence, we obtain
![]() $ p\odot (m\square \iota ^{**}(n))=(p\odot m)\square n $
, as required.
$ p\odot (m\square \iota ^{**}(n))=(p\odot m)\square n $
, as required.
(vi) Let
![]() $ f\in \mathcal {B}^{*} $
,
$ f\in \mathcal {B}^{*} $
,
![]() $ b\in \mathcal {B} $
and
$ b\in \mathcal {B} $
and
![]() $ a\in \mathcal {A} $
. Then
$ a\in \mathcal {A} $
. Then
 $$ \begin{align*} \langle (p\bullet f)\cdot b,a\rangle &=\langle p\bullet f,ba\rangle=\langle p,f\cdot ba\rangle\\ &=\langle p,(f\cdot b)\bullet a\rangle=\langle p\bullet(f\cdot b),a\rangle. \end{align*} $$
$$ \begin{align*} \langle (p\bullet f)\cdot b,a\rangle &=\langle p\bullet f,ba\rangle=\langle p,f\cdot ba\rangle\\ &=\langle p,(f\cdot b)\bullet a\rangle=\langle p\bullet(f\cdot b),a\rangle. \end{align*} $$
Therefore,
 $$ \begin{align*} \langle m\cdot (p\bullet f),b\rangle &=\langle m,(p\bullet f)\cdot b\rangle=\langle m,p\bullet(f\cdot b)\rangle \\ &=\langle m\odot p,f\cdot b\rangle=\langle (m\odot p)\cdot f,b\rangle. \end{align*} $$
$$ \begin{align*} \langle m\cdot (p\bullet f),b\rangle &=\langle m,(p\bullet f)\cdot b\rangle=\langle m,p\bullet(f\cdot b)\rangle \\ &=\langle m\odot p,f\cdot b\rangle=\langle (m\odot p)\cdot f,b\rangle. \end{align*} $$
Thus,
 $$ \begin{align*} \langle ( \iota^{**}(n)\square m)\odot p,f\rangle &= \langle\iota^{**}(n)\square m,p\bullet f\rangle=\langle\iota^{**}(n),m\cdot (p\bullet f)\rangle\\ &=\langle n, \iota^{*} (m\cdot (p\bullet f))\rangle =\langle n, m\cdot (p\bullet f)|_{\mathcal{B}}\rangle\\ &=\langle n,(m\odot p)\cdot f\rangle=\langle n\square(m\odot p),f\rangle. \end{align*} $$
$$ \begin{align*} \langle ( \iota^{**}(n)\square m)\odot p,f\rangle &= \langle\iota^{**}(n)\square m,p\bullet f\rangle=\langle\iota^{**}(n),m\cdot (p\bullet f)\rangle\\ &=\langle n, \iota^{*} (m\cdot (p\bullet f))\rangle =\langle n, m\cdot (p\bullet f)|_{\mathcal{B}}\rangle\\ &=\langle n,(m\odot p)\cdot f\rangle=\langle n\square(m\odot p),f\rangle. \end{align*} $$
Hence,
![]() $ ( \iota ^{**}(n)\square m)\odot p= n \square (m\odot p) $
and the proof is complete.
$ ( \iota ^{**}(n)\square m)\odot p= n \square (m\odot p) $
and the proof is complete.
Theorem 3.2. Let
![]() $ \mathcal {B} $
be a symmetric abstract Segal algebra of
$ \mathcal {B} $
be a symmetric abstract Segal algebra of
![]() $ \mathcal {A} $
and let
$ \mathcal {A} $
and let
![]() $ \varphi \in \Delta (\mathcal {A}) $
. Then the following statements are equivalent:
$ \varphi \in \Delta (\mathcal {A}) $
. Then the following statements are equivalent:
-
(i) there is a compact (weakly compact) left (right) multiplier
 $ T $
of
$ T $
of
 $ \mathcal {B}^{**} $
such that
$ \mathcal {B}^{**} $
such that
 $ \langle T(n),\varphi \rangle \neq 0$
for some
$ \langle T(n),\varphi \rangle \neq 0$
for some
 $ n\in \mathcal {B}^{**} $
;
$ n\in \mathcal {B}^{**} $
; -
(ii) there is a compact (weakly compact) left (right) multiplier
 $ T $
of
$ T $
of
 $ \mathcal {A}^{**} $
such that
$ \mathcal {A}^{**} $
such that
 $ \langle T(m),\varphi \rangle \neq 0 $
for some
$ \langle T(m),\varphi \rangle \neq 0 $
for some
 $m\in \mathcal {A}^{**} $
.
$m\in \mathcal {A}^{**} $
.
Proof. Suppose that
![]() $ T $
is a compact (weakly compact) left multiplier of
$ T $
is a compact (weakly compact) left multiplier of
![]() $ \mathcal {B}^{**} $
with
$ \mathcal {B}^{**} $
with
![]() $ \langle T(n),\varphi \rangle \neq 0 $
for some
$ \langle T(n),\varphi \rangle \neq 0 $
for some
![]() $ n\in \mathcal {B}^{**} $
. Putting
$ n\in \mathcal {B}^{**} $
. Putting
![]() $ p=T(n) $
makes
$ p=T(n) $
makes
![]() $ \lambda _{p}=T\circ \lambda _{n} $
a compact (weakly compact) left multiplier of
$ \lambda _{p}=T\circ \lambda _{n} $
a compact (weakly compact) left multiplier of
![]() $ \mathcal {B}^{**} $
. Now for each
$ \mathcal {B}^{**} $
. Now for each
![]() $ n\in \mathcal {B}^{**}$
, consider the continuous linear map
$ n\in \mathcal {B}^{**}$
, consider the continuous linear map
![]() $l_{n}:\mathcal {A}^{**}\rightarrow \mathcal {B}^{**} $
defined by
$l_{n}:\mathcal {A}^{**}\rightarrow \mathcal {B}^{**} $
defined by
![]() $ l_{n}(m)=n\odot m $
for all
$ l_{n}(m)=n\odot m $
for all
![]() $ m\in \mathcal {A}^{**} $
. Since
$ m\in \mathcal {A}^{**} $
. Since
![]() ${ \iota ^{**}\circ \lambda _{p}=\lambda _{\iota ^{**}(p)}\circ \iota ^{**} }$
, by using Lemma 3.1(ii),
${ \iota ^{**}\circ \lambda _{p}=\lambda _{\iota ^{**}(p)}\circ \iota ^{**} }$
, by using Lemma 3.1(ii),
![]() $\lambda _{\iota ^{**}(p^{2})}=\lambda _{\iota ^{**}(p)}\circ \iota ^{**}\circ l_{p} =\iota ^{**}\circ \lambda _{p} \circ l_{p} $
is a compact (weakly compact) left multiplier of
$\lambda _{\iota ^{**}(p^{2})}=\lambda _{\iota ^{**}(p)}\circ \iota ^{**}\circ l_{p} =\iota ^{**}\circ \lambda _{p} \circ l_{p} $
is a compact (weakly compact) left multiplier of
![]() $ \mathcal {A} ^{**}$
such that
$ \mathcal {A} ^{**}$
such that
Conversely, suppose that
![]() $ T $
is a compact (weakly compact) left multiplier of
$ T $
is a compact (weakly compact) left multiplier of
![]() $ \mathcal {A}^{**} $
such that
$ \mathcal {A}^{**} $
such that
![]() $ \langle T(m),\varphi \rangle \neq 0$
for some
$ \langle T(m),\varphi \rangle \neq 0$
for some
![]() $ m\in \mathcal {A}^{**} $
. Then
$ m\in \mathcal {A}^{**} $
. Then
![]() $ \lambda _{p} $
is a compact (weakly compact) left multiplier on
$ \lambda _{p} $
is a compact (weakly compact) left multiplier on
![]() $ \mathcal {A}^{**} $
, where
$ \mathcal {A}^{**} $
, where
![]() $ p=T(m) $
. Choose
$ p=T(m) $
. Choose
![]() $ n_0\in \mathcal {B} $
with
$ n_0\in \mathcal {B} $
with
![]() $ n_0(\varphi )=1 $
. Using Lemma 3.1(iii),
$ n_0(\varphi )=1 $
. Using Lemma 3.1(iii),
![]() $ n_0\odot (p \square \iota ^{**}(n)) =(n_{0}\odot p)\square n$
for all
$ n_0\odot (p \square \iota ^{**}(n)) =(n_{0}\odot p)\square n$
for all
![]() $n\in \mathcal {B}^{**} $
. Then the map
$n\in \mathcal {B}^{**} $
. Then the map
![]() $ \lambda _{n_{0}\odot p}=l_{n_{0}}\circ \lambda _{p}~\circ ~\iota ^{**} $
is a compact (weakly compact) left multiplier of
$ \lambda _{n_{0}\odot p}=l_{n_{0}}\circ \lambda _{p}~\circ ~\iota ^{**} $
is a compact (weakly compact) left multiplier of
![]() $ \mathcal {B}^{**} $
such that
$ \mathcal {B}^{**} $
such that
as required. The result for a right multiplier T can be proved similarly.
From [Reference Ghahramani and Lau4, Theorem 2.1] and the above theorem, we obtain the following corollary.
Corollary 3.3. Let
![]() $ S(G) $
be a symmetric abstract Segal algebra of
$ S(G) $
be a symmetric abstract Segal algebra of
![]() $ L^{1}(G) $
. Then
$ L^{1}(G) $
. Then
![]() $ G $
is amenable if and only if there is a compact (weakly compact) right multiplier T of
$ G $
is amenable if and only if there is a compact (weakly compact) right multiplier T of
![]() $ S(G)^{**} $
such that
$ S(G)^{**} $
such that
![]() $ \langle T(n),\varphi _{1}\rangle \neq 0 $
for some
$ \langle T(n),\varphi _{1}\rangle \neq 0 $
for some
![]() $ n\in L^{1}(G)^{**}$
.
$ n\in L^{1}(G)^{**}$
.
From [Reference Ghahramani and Lau5, Theorem 4.1] and Theorem 3.2, we also obtain the following result.
Corollary 3.4. Let
![]() $ S(G) $
be a symmetric abstract Segal algebra of
$ S(G) $
be a symmetric abstract Segal algebra of
![]() $ L^{1}(G) $
. Then
$ L^{1}(G) $
. Then
![]() $ G $
is compact if and only if there is a compact (weakly compact) left multiplier T of
$ G $
is compact if and only if there is a compact (weakly compact) left multiplier T of
![]() $ S(G)^{**} $
such that
$ S(G)^{**} $
such that
![]() $ \langle T(n),\varphi _{1}\rangle \neq 0 $
for some
$ \langle T(n),\varphi _{1}\rangle \neq 0 $
for some
![]() $ n\in S(G)^{**}$
.
$ n\in S(G)^{**}$
.
To state the next corollary, let
![]() $A(G)$
be the Fourier algebra of a locally compact group G as defined in [Reference Eymard3]. Combining Theorem 3.2 with [Reference Ghahramani and Lau5, Theorem 4.3], we obtain the following characterisation of discrete groups.
$A(G)$
be the Fourier algebra of a locally compact group G as defined in [Reference Eymard3]. Combining Theorem 3.2 with [Reference Ghahramani and Lau5, Theorem 4.3], we obtain the following characterisation of discrete groups.
Corollary 3.5. Let
![]() $SA(G) $
be an abstract Segal algebra of the Fourier algebra
$SA(G) $
be an abstract Segal algebra of the Fourier algebra
![]() $A(G)$
. Then
$A(G)$
. Then
![]() $ G $
is discrete if and only if there is a compact (weakly compact) left multiplier T of
$ G $
is discrete if and only if there is a compact (weakly compact) left multiplier T of
![]() $ SA(G)^{**} $
such that
$ SA(G)^{**} $
such that
![]() $ \langle T(n),1\rangle \neq 0 $
for some
$ \langle T(n),1\rangle \neq 0 $
for some
![]() $ n\in SA(G)^{**}$
.
$ n\in SA(G)^{**}$
.
4 Multipliers with rank one
Let
![]() ${\mathcal A}$
be a Banach algebra and let
${\mathcal A}$
be a Banach algebra and let
![]() $\varphi \in \Delta ({\mathcal A})$
. Following [Reference Kaniuth, Lau and Pym8], we call an element
$\varphi \in \Delta ({\mathcal A})$
. Following [Reference Kaniuth, Lau and Pym8], we call an element
![]() $ m\in {\mathcal A}^{**} $
a topologically left invariant
$ m\in {\mathcal A}^{**} $
a topologically left invariant
![]() $ \varphi $
-mean if
$ \varphi $
-mean if
![]() $ m(\varphi )=1 $
and
$ m(\varphi )=1 $
and
![]() $ m(f\cdot a)=\varphi (a)m(f) $
for every
$ m(f\cdot a)=\varphi (a)m(f) $
for every
![]() $f\in {\mathcal A}^{*}$
and
$f\in {\mathcal A}^{*}$
and
![]() $ a\in {\mathcal A}$
, or equivalently
$ a\in {\mathcal A}$
, or equivalently
![]() $ a\square m=\varphi (a)m$
. We denote the set of all topologically left invariant
$ a\square m=\varphi (a)m$
. We denote the set of all topologically left invariant
![]() $ \varphi $
-means on
$ \varphi $
-means on
![]() ${\mathcal A}^{*}$
by
${\mathcal A}^{*}$
by
![]() $ TLI_{\varphi }({\mathcal A}^{**})$
. We also put
$ TLI_{\varphi }({\mathcal A}^{**})$
. We also put
![]() $ {I_{\varphi }:=\lbrace a\in {\mathcal A}: \varphi (a)=0\rbrace }$
which is a co-dimension one closed ideal in
$ {I_{\varphi }:=\lbrace a\in {\mathcal A}: \varphi (a)=0\rbrace }$
which is a co-dimension one closed ideal in
![]() ${\mathcal A}$
. Recall that a locally compact group G is called amenable if there exists a topologically left invariant mean m on
${\mathcal A}$
. Recall that a locally compact group G is called amenable if there exists a topologically left invariant mean m on
![]() $L^\infty (G)$
, that is, a bounded linear functional with
$L^\infty (G)$
, that is, a bounded linear functional with
![]() $\lVert m\rVert = m(1)=1$
such that
$\lVert m\rVert = m(1)=1$
such that
![]() $m(f\cdot a)=a(1)m(f)$
for all
$m(f\cdot a)=a(1)m(f)$
for all
![]() $f\in L^\infty (G)$
and
$f\in L^\infty (G)$
and
![]() $a\in L^1({\Bbb G})$
. Topologically right invariant means and (two-sided) invariant means on
$a\in L^1({\Bbb G})$
. Topologically right invariant means and (two-sided) invariant means on
![]() $L^\infty (G)$
are defined similarly. It is known that the existence of a topologically right invariant mean and the existence of a topologically invariant mean are both equivalent to G being amenable.
$L^\infty (G)$
are defined similarly. It is known that the existence of a topologically right invariant mean and the existence of a topologically invariant mean are both equivalent to G being amenable.
A standard argument, used in the proof of [Reference Lau11, Theorem 4.1] on F-algebras, a class of Banach algebras including group algebras, shows that amenability of G is equivalent to the existence of a topologically left invariant
![]() $\varphi _1$
-mean on
$\varphi _1$
-mean on
![]() $L^\infty (G)$
(see also [Reference Kaniuth, Lau and Pym7, Remark 1.3]).
$L^\infty (G)$
(see also [Reference Kaniuth, Lau and Pym7, Remark 1.3]).
Theorem 4.1. Let
![]() $ S(G) $
be an abstract Segal algebra of
$ S(G) $
be an abstract Segal algebra of
![]() $ L^{1}(G)$
. Then G is amenable if and only if there is a nonzero idempotent
$ L^{1}(G)$
. Then G is amenable if and only if there is a nonzero idempotent
![]() $m\in S(G)^{**}$
such that
$m\in S(G)^{**}$
such that
![]() $\rho _{m}$
has rank one.
$\rho _{m}$
has rank one.
Proof. Suppose that G is amenable. Then by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4], there is a topologically left invariant
![]() $\varphi _1$
-mean m on
$\varphi _1$
-mean m on
![]() $S(G)^{*}$
. It is clear that m is a nonzero idempotent and the map
$S(G)^{*}$
. It is clear that m is a nonzero idempotent and the map
![]() $\rho _m$
on
$\rho _m$
on
![]() $S(G)^{**}$
, defined by
$S(G)^{**}$
, defined by
![]() $ \rho _{m}(n)=n\square m=\langle n,\varphi _{1}\rangle m$
for all
$ \rho _{m}(n)=n\square m=\langle n,\varphi _{1}\rangle m$
for all
![]() $n\in S(G)^{**}$
, has rank one.
$n\in S(G)^{**}$
, has rank one.
Conversely, let
![]() $m\in S(G)^{**}$
be a nonzero idempotent such that
$m\in S(G)^{**}$
be a nonzero idempotent such that
![]() $\rho _{m}$
on
$\rho _{m}$
on
![]() $S(G)^{**}$
has rank one. Then there is a functional
$S(G)^{**}$
has rank one. Then there is a functional
![]() $\varphi \in S(G)^{***}$
such that
$\varphi \in S(G)^{***}$
such that
![]() $n\square m=\varphi (n)m$
for all
$n\square m=\varphi (n)m$
for all
![]() $n\in S(G)^{**}$
. Since m is a nonzero idempotent, we obtain
$n\in S(G)^{**}$
. Since m is a nonzero idempotent, we obtain
![]() $\varphi (m)=1$
. Moreover,
$\varphi (m)=1$
. Moreover,
 $$ \begin{align*} \varphi (a*b)m&=(a*b)\square m=a\square (b\square m)\\ &=a\square (\varphi (b)m)=\varphi (b)a\square m\\ &=\varphi (b)\varphi (a)m, \end{align*} $$
$$ \begin{align*} \varphi (a*b)m&=(a*b)\square m=a\square (b\square m)\\ &=a\square (\varphi (b)m)=\varphi (b)a\square m\\ &=\varphi (b)\varphi (a)m, \end{align*} $$
for all
![]() $a,b\in S(G)$
. This implies that
$a,b\in S(G)$
. This implies that
![]() $\varphi (a*b)=\varphi (a)\varphi (b)$
for all
$\varphi (a*b)=\varphi (a)\varphi (b)$
for all
![]() $a,b\in S(G)$
. Since the map
$a,b\in S(G)$
. Since the map
![]() $n\mapsto n\square m$
on
$n\mapsto n\square m$
on
![]() $S(G)^{**}$
is weak
$S(G)^{**}$
is weak
![]() $^*$
-weak
$^*$
-weak
![]() $^*$
continuous and
$^*$
continuous and
![]() $\varphi (m)=1$
, it follows that
$\varphi (m)=1$
, it follows that
![]() ${\varphi \in \Delta (S(G))=\Delta (L^1(G))}$
. This shows that m is a topologically left invariant
${\varphi \in \Delta (S(G))=\Delta (L^1(G))}$
. This shows that m is a topologically left invariant
![]() $\varphi $
-mean on
$\varphi $
-mean on
![]() $S(G)^{*}$
. Hence,
$S(G)^{*}$
. Hence,
![]() ${G}$
is amenable by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4].
${G}$
is amenable by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4].
Lemma 4.2. Let
![]() $ S^1(G) $
be a symmetric Segal algebra of
$ S^1(G) $
be a symmetric Segal algebra of
![]() $ L^{1}(G)$
and let
$ L^{1}(G)$
and let
![]() $\varphi \in \Delta (L^1(G))$
. Then there is a one–one correspondence between the set of topologically left invariant
$\varphi \in \Delta (L^1(G))$
. Then there is a one–one correspondence between the set of topologically left invariant
![]() $\varphi $
-means on
$\varphi $
-means on
![]() $ S^1(G)^{*} $
and on
$ S^1(G)^{*} $
and on
![]() $L^{\infty }(G) $
.
$L^{\infty }(G) $
.
Proof. Let
![]() $ \iota :S^1(G)\rightarrow L^{1}(G) $
be the inclusion map. Consider the map
$ \iota :S^1(G)\rightarrow L^{1}(G) $
be the inclusion map. Consider the map
![]() $ \iota ^{**}:TLI_{\varphi }(S^1(G)^{**})\rightarrow L^{\infty }(G)^{*}$
. Let
$ \iota ^{**}:TLI_{\varphi }(S^1(G)^{**})\rightarrow L^{\infty }(G)^{*}$
. Let
![]() $ n\in TLI_{\varphi }(S^1(G)^{**}) $
and
$ n\in TLI_{\varphi }(S^1(G)^{**}) $
and
![]() $ m=\iota ^{**}(n) $
. It is clear that
$ m=\iota ^{**}(n) $
. It is clear that
![]() $ m(\varphi )=1 $
. Moreover, for every
$ m(\varphi )=1 $
. Moreover, for every
![]() $a\in L^{1}(G) $
, there is a sequence
$a\in L^{1}(G) $
, there is a sequence
![]() $ (a_{i})$
in
$ (a_{i})$
in
![]() $S^1(G) $
such that
$S^1(G) $
such that
![]() $ \lVert a_{i}-a\rVert _{1}\rightarrow 0 $
. Since
$ \lVert a_{i}-a\rVert _{1}\rightarrow 0 $
. Since
![]() $ \Delta (S^1(G))=\Delta (L^{1}(G)) $
, we have
$ \Delta (S^1(G))=\Delta (L^{1}(G)) $
, we have
 $$ \begin{align*} a\square m &=\lim_{i}(a_{i}\square \iota^{**}(n)) =\lim_{i}\iota^{**}(a_{i}\square n)\\ &=\lim_{i}\varphi(a_{i})\iota^{**}(n) =\varphi(a)\iota^{**}(n)=\varphi(a)m. \end{align*} $$
$$ \begin{align*} a\square m &=\lim_{i}(a_{i}\square \iota^{**}(n)) =\lim_{i}\iota^{**}(a_{i}\square n)\\ &=\lim_{i}\varphi(a_{i})\iota^{**}(n) =\varphi(a)\iota^{**}(n)=\varphi(a)m. \end{align*} $$
Therefore,
![]() $ \iota ^{**}(TLI_{\varphi }(S^1(G)^{**}))\subseteq TLI_{\varphi }(L^{\infty }(G)^{*})$
. We next show that
$ \iota ^{**}(TLI_{\varphi }(S^1(G)^{**}))\subseteq TLI_{\varphi }(L^{\infty }(G)^{*})$
. We next show that
is injective. In fact, suppose that
![]() $m, n\in TLI_{\varphi }(S^1(G)^{**})$
with
$m, n\in TLI_{\varphi }(S^1(G)^{**})$
with
![]() $m\neq n$
. Then there exists
$m\neq n$
. Then there exists
![]() $f\in S^1(G)^*$
such that
$f\in S^1(G)^*$
such that
![]() $m(f)\neq n(f)$
. Let
$m(f)\neq n(f)$
. Let
![]() $b_0\in S^1(G)$
be such that
$b_0\in S^1(G)$
be such that
![]() $\varphi (b_0)=1$
. Then
$\varphi (b_0)=1$
. Then
![]() ${m(f\cdot b_0)=m(f)\neq n(f)=n(f\cdot b_0)}$
. It follows that
${m(f\cdot b_0)=m(f)\neq n(f)=n(f\cdot b_0)}$
. It follows that
Therefore,
![]() $\iota ^{**}(m)\neq \iota ^{**}(n)$
. We now prove that
$\iota ^{**}(m)\neq \iota ^{**}(n)$
. We now prove that
![]() $ \iota ^{**} $
is surjective. Suppose that
$ \iota ^{**} $
is surjective. Suppose that
![]() $ {m\in TLI_{\varphi }(L^{\infty }(G)^*) }$
. Then for each
$ {m\in TLI_{\varphi }(L^{\infty }(G)^*) }$
. Then for each
![]() $ f\in S^1(G)^{*} $
and
$ f\in S^1(G)^{*} $
and
![]() $ a,b\in S^1(G) $
, we have
$ a,b\in S^1(G) $
, we have
Thus, for
![]() $ b\in I_{\varphi } $
, we have
$ b\in I_{\varphi } $
, we have
Since
![]() $S^1(G)$
has an approximate identity (not necessarily bounded), it follows that
$S^1(G)$
has an approximate identity (not necessarily bounded), it follows that
![]() $ \overline {\langle S^1(G)*I_{\varphi }\rangle }=I_{\varphi } $
. Thus
$ \overline {\langle S^1(G)*I_{\varphi }\rangle }=I_{\varphi } $
. Thus
![]() $ (m\bullet f)|_{I_{\varphi }}=0 $
. As
$ (m\bullet f)|_{I_{\varphi }}=0 $
. As
![]() $ a*b-b*a\in I_{\varphi } $
, we obtain
$ a*b-b*a\in I_{\varphi } $
, we obtain
Let
![]() $ \varphi (b_{0})=1 $
for some
$ \varphi (b_{0})=1 $
for some
![]() $ b_{0}\in S^1(G) $
and consider the functional
$ b_{0}\in S^1(G) $
and consider the functional
![]() $ \tilde {m}\in S^1(G)^{**} $
defined by
$ \tilde {m}\in S^1(G)^{**} $
defined by
Then for each
![]() $ b\in S^1(G) $
and
$ b\in S^1(G) $
and
![]() $ f\in S^1(G)^{*} $
, we have
$ f\in S^1(G)^{*} $
, we have
 $$ \begin{align*} \tilde{m}(f\cdot b)&=\langle m,(f\cdot b)\bullet b_{0}\rangle=\langle m,f\bullet(b* b_0)\rangle\\ &=\langle m,f\bullet(b_0* b)\rangle=\langle m,(f\bullet b_0)\cdot b)\rangle\\ &=\varphi(b)\langle m,f\bullet b_{0}\rangle=\varphi(b) \tilde{m}(f). \end{align*} $$
$$ \begin{align*} \tilde{m}(f\cdot b)&=\langle m,(f\cdot b)\bullet b_{0}\rangle=\langle m,f\bullet(b* b_0)\rangle\\ &=\langle m,f\bullet(b_0* b)\rangle=\langle m,(f\bullet b_0)\cdot b)\rangle\\ &=\varphi(b)\langle m,f\bullet b_{0}\rangle=\varphi(b) \tilde{m}(f). \end{align*} $$
Furthermore, it is obvious that
![]() $ \tilde {m}(\varphi )=1 $
. Hence,
$ \tilde {m}(\varphi )=1 $
. Hence,
![]() $ \tilde {m} \in TLI_{\varphi }(S^1(G)^{**}) $
. We have to show that
$ \tilde {m} \in TLI_{\varphi }(S^1(G)^{**}) $
. We have to show that
![]() $ \iota ^{**}(\tilde {m})=m $
. In fact, for every
$ \iota ^{**}(\tilde {m})=m $
. In fact, for every
![]() $ g\in L^{\infty }(G) $
, we have
$ g\in L^{\infty }(G) $
, we have
and the proof is complete.
Before giving the next result, recall that the compactness of G is equivalent to the existence of a topologically invariant mean in
![]() $L^{1}(G)$
. The following theorem is inspired by [Reference Ghahramani and Lau4, Theorem 2.15].
$L^{1}(G)$
. The following theorem is inspired by [Reference Ghahramani and Lau4, Theorem 2.15].
Theorem 4.3. Let
![]() $ S^1(G) $
be a symmetric Segal algebra of
$ S^1(G) $
be a symmetric Segal algebra of
![]() $ L^{1}(G)$
and
$ L^{1}(G)$
and
![]() $ K $
be the set of all right multipliers
$ K $
be the set of all right multipliers
![]() $ T $
of
$ T $
of
![]() $ S^1(G)^{**} $
with rank one such that
$ S^1(G)^{**} $
with rank one such that
![]() $ \langle T(n),\varphi _{1}\rangle =1$
whenever
$ \langle T(n),\varphi _{1}\rangle =1$
whenever
![]() $\langle n,\varphi _{1}\rangle =1 $
for
$\langle n,\varphi _{1}\rangle =1 $
for
![]() $ n\in S^1(G)^{**} $
. Then the following statements hold:
$ n\in S^1(G)^{**} $
. Then the following statements hold:
-
(i)
 $ K\neq \emptyset $
if and only if
$ K\neq \emptyset $
if and only if
 $ G $
is amenable;
$ G $
is amenable; -
(ii)
 $ \lvert K \rvert =1 $
if and only if
$ \lvert K \rvert =1 $
if and only if
 $ G $
is compact;
$ G $
is compact; -
(iii) if
 $ G $
is amenable and noncompact and
$ G $
is amenable and noncompact and
 $ d(G) $
is the smallest possible cardinality of a covering of
$ d(G) $
is the smallest possible cardinality of a covering of
 $ G $
by compact sets, then
$ G $
by compact sets, then
 $ \lvert K\rvert \geq 2^{2^{d(G)}}$
.
$ \lvert K\rvert \geq 2^{2^{d(G)}}$
.
Proof. (i) Suppose that
![]() $ G $
is amenable. Then by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4], there is a topologically left invariant
$ G $
is amenable. Then by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4], there is a topologically left invariant
![]() $ \varphi _{1}$
-mean
$ \varphi _{1}$
-mean
![]() $ m $
on
$ m $
on
![]() $ S^1(G)^{*}$
. Since
$ S^1(G)^{*}$
. Since
![]() $ \rho _{m}(n)=n\square m =\langle n,\varphi _{1}\rangle m$
for all
$ \rho _{m}(n)=n\square m =\langle n,\varphi _{1}\rangle m$
for all
![]() $n\in S^1(G)^{**}$
, it follows that
$n\in S^1(G)^{**}$
, it follows that
![]() $\rho _m$
belongs to
$\rho _m$
belongs to
![]() $ K $
.
$ K $
.
Conversely, suppose that
![]() $ T\in K $
and
$ T\in K $
and
![]() $ \langle n,\varphi _{1}\rangle =1 $
for some
$ \langle n,\varphi _{1}\rangle =1 $
for some
![]() $ n\in S^1(G)^{**} $
. Putting
$ n\in S^1(G)^{**} $
. Putting
![]() ${m=T(n) }$
, we have
${m=T(n) }$
, we have
![]() $\langle m,\varphi _{1}\rangle =1 $
. By the same argument as that used in the proof of Theorem 4.1, it is easy to show that m is a topologically left invariant
$\langle m,\varphi _{1}\rangle =1 $
. By the same argument as that used in the proof of Theorem 4.1, it is easy to show that m is a topologically left invariant
![]() $\varphi _1$
-mean on
$\varphi _1$
-mean on
![]() $S^1(G)^*$
. Thus, G is amenable by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4].
$S^1(G)^*$
. Thus, G is amenable by [Reference Alaghmandan, Nasr-Isfahani and Nemati1, Corollary 3.4].
(ii) Let
![]() $ T\in K $
and
$ T\in K $
and
![]() $ n\in TLI_{\varphi _{1}}(S^1(G)^{**}) $
. Putting
$ n\in TLI_{\varphi _{1}}(S^1(G)^{**}) $
. Putting
![]() $ m=T(n)$
, by (i),
$ m=T(n)$
, by (i),
![]() $ m $
is a topologically left invariant
$ m $
is a topologically left invariant
![]() $ \varphi _{1}$
-mean on
$ \varphi _{1}$
-mean on
![]() $ S^1(G)^{*}$
. In particular, for each
$ S^1(G)^{*}$
. In particular, for each
![]() $ p \in S(G)^{**} $
with
$ p \in S(G)^{**} $
with
![]() $\langle p,\varphi _{1}\rangle =1 $
, we obtain
$\langle p,\varphi _{1}\rangle =1 $
, we obtain
![]() $ p\square m= m$
. Thus,
$ p\square m= m$
. Thus,
By linearity, we conclude that
![]() $ \rho _{m}=T $
and so there is a one–one correspondence between
$ \rho _{m}=T $
and so there is a one–one correspondence between
![]() $ K $
and
$ K $
and
![]() $TLI_{\varphi _{1}}(S^1(G)^{**}) $
. By Lemma 4.2,
$TLI_{\varphi _{1}}(S^1(G)^{**}) $
. By Lemma 4.2,
![]() $ \lvert K\rvert = \lvert TLI_{\varphi _{1}}(L^{\infty }(G)^*)\rvert $
.
$ \lvert K\rvert = \lvert TLI_{\varphi _{1}}(L^{\infty }(G)^*)\rvert $
.
Now suppose that G is compact. Then there is a topologically invariant mean m in
![]() $L^{1}(G)$
. Thus, for each
$L^{1}(G)$
. Thus, for each
![]() $n\in TLI_{\varphi _{1}}(L^{\infty }(G)^{*})$
, we have
$n\in TLI_{\varphi _{1}}(L^{\infty }(G)^{*})$
, we have
This shows that
![]() $ \lvert K\rvert =\lvert TLI_{\varphi _{1}}(L^{\infty }(G)^{*})\rvert =1$
.
$ \lvert K\rvert =\lvert TLI_{\varphi _{1}}(L^{\infty }(G)^{*})\rvert =1$
.
Conversely, suppose that
![]() $ \lvert K\rvert =1 $
. Then
$ \lvert K\rvert =1 $
. Then
![]() $ \lvert TLI_{\varphi _{1}}(L^{\infty }(G)^{*})\rvert =1$
. Therefore, there is a unique topologically left invariant
$ \lvert TLI_{\varphi _{1}}(L^{\infty }(G)^{*})\rvert =1$
. Therefore, there is a unique topologically left invariant
![]() $\varphi _1$
-mean m on
$\varphi _1$
-mean m on
![]() $L^\infty (G)$
. It follows that m belongs to
$L^\infty (G)$
. It follows that m belongs to
![]() $L^1(G)$
(see [Reference Klawe9]), whence G is compact.
$L^1(G)$
(see [Reference Klawe9]), whence G is compact.
(iii) Suppose that
![]() $ G $
is noncompact. Then by [Reference Lau and Paterson12, Theorem 1], the cardinality of
$ G $
is noncompact. Then by [Reference Lau and Paterson12, Theorem 1], the cardinality of
![]() $TLI_{\varphi _{1}}(L^{\infty }(G)^{*})$
is at least
$TLI_{\varphi _{1}}(L^{\infty }(G)^{*})$
is at least
![]() $2^{2^{d(G)}}$
. Therefore,
$2^{2^{d(G)}}$
. Therefore,
![]() $ \lvert K\rvert = \lvert TLI_{\varphi _{1}}(L^{\infty }(G)^{*})\rvert \geq 2^{2^{d(G)}} $
.
$ \lvert K\rvert = \lvert TLI_{\varphi _{1}}(L^{\infty }(G)^{*})\rvert \geq 2^{2^{d(G)}} $
.
Acknowledgement
The authors would like to sincerely thank the referee for a careful reading of the paper.