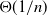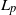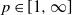1. Introduction
A (traditional) Pólya urn contains balls of several colours; we denote the number of colours by q. At discrete time steps, a ball is drawn at random from the urn, and it is replaced together with a balls of the same colour, where 
$a>0$ is some given constant. These urn models were studied by Markov in 1917 [Reference Markov11], but they are named after George Pólya who studied them with Eggenberger in the 1920s [Reference Eggenberger and Pólya2, Reference Pólya15]. (These early references studied the case 
$q=2$; the extension to general q is straightforward. See also [Reference Johnson and Kotz7, Chapter 4] and [Reference Mahmoud10], for example.)
Let the vector 
$\textbf{X}_n=(X_{n,1},\ldots,X_{n,q})$ (
$n\geqslant0$) describe the numbers of balls of the different colours at time n. (We assume that the colours are the integers 
$1,\ldots,q$.) The description above thus means that the random vectors 
$\textbf{X}_n$ evolve as a Markov chain, with some given (deterministic) initial vector 
$\textbf{X}_0=\textbf{x}_0=(x_1,\ldots,x_q)$ and
\begin{equation} \mathbb{P}({\textbf{X}_{n+1}=\textbf{X}_n+a\textbf e_i\mid\textbf{X}_n})=\dfrac{X_{n,i}}{|\textbf{X}_n|},\quad i=1,\ldots,q,\end{equation}
where 
$\textbf e_i=(\delta_{ij})_{j=1}^q$ are the unit vectors and 
$|\textbf{X}_n| \coloneqq \sum_{i=1}^q X_{n,i}$. Note that the total number of balls 
$|\textbf{X}_n|=an+|\textbf{x}_0|$ is deterministic.
Although the formulation in the first paragraph above talks about the ‘number of balls’, thus implying that the numbers are integers, we see that no such assumption is needed in the more formal definition using (1.1). Hence, from now on, a and 
$x_1,\ldots,x_q$ may be arbitrary positive real numbers, and thus the random vectors 
$\textbf{X}_n\in\mathbb R_{>0}^q$. We assume that a and 
$x_1,\ldots,x_q$ are strictly positive to avoid trivial complications; this implies that 
$X_{n,i}\geqslant x_i>0$ for all 
$n\geqslant0$ and 
$i\in[q] \coloneqq \ensuremath{\{{1,\ldots,q}\}}$. In particular, 
$|\textbf{X}_n|>0$, and the transition probabilities are well-defined by (1.1).
One advantage of the extension to real values is that the model is homogeneous in the sense that if we multiply all 
$X_n$ (including the initial values) and a by the same positive real number, then (1.1) still holds, so we have another Pólya urn. In particular, replacing 
$\textbf{X}_n$ with 
$\textbf{X}_n/a$, we may without loss of generality assume that 
$a=1$.
We also define the random vector 
$\textbf{Y}_n=(Y_{n,1},\ldots,Y_{n,q})$, where 
$Y_{n,i}$ is the number of the first n drawn balls that have colour i. Obviously
\begin{equation} \textbf{X}_n=\textbf{x}_0+a\textbf{Y}_n,\end{equation}
so it is equivalent to studying 
$\textbf{X}_n$ and 
$\textbf{Y}_n$.
It is easy to find the exact distribution of 
$\textbf{Y}_n$ and thus of 
$\textbf{X}_n$ (see e.g. [Reference Markov11], [Reference Olver, Lozier, Boisvert and Clark12], [Reference Pólya15], [Reference Johnson and Kotz7], [Reference Mahmoud10] and (3.3) below), and from this it is easy to see that as n→∞, the fraction of balls of a given colour converges in distribution to a beta distribution [Reference Pólya15]; more precisely
\begin{equation}\dfrac{X_{n,i}}{|\textbf{X}_n|}\overset{\textrm{d}}{\longrightarrow} \textrm{Beta}\bigg({x_i/a,\sum_{j\neq i}x_j/a}\bigg).\end{equation}
More generally, the vector 
$\textbf{X}_n/|\textbf{X}_n|$ of proportions converges to a Dirichlet distribution (see Section 2 for the definition):
\begin{equation}\dfrac{\textbf{X}_{n}}{|\textbf{X}_n|}\overset{\textrm{d}}{\longrightarrow} \textrm{Dir}({\textbf{x}_0/a}).\end{equation}
It follows by (1.2) that the same holds for the proportions 
$\textbf{Y}_n/|\textbf{Y}_n|$.
Remark 1.1. In fact it is easy to see that 
$\textbf{X}_n/|\textbf{X}_n|$ is a martingale, and thus 
$\textbf{X}_n/|\textbf{X}_n|$ converges a.s. to a limit, which thus has the Dirichlet distribution 
$\textrm{Dir}({\textbf{x}_0/a})$. It follows by (1.2) that the same holds for 
$\textbf{Y}_n/|\textbf{Y}_n|$. The a.s. convergence can also be seen in other ways, for example by de Finetti’s theorem and the fact that the sequence of colours of the drawn balls is exchangeable (see Remark 1.4) or by Martin boundary theory [Reference Blackwell and Kendall1, Reference Sawyer18].
The purpose of the present paper is to study the rate of convergence of the distributions in (1.3) and (1.4). For the Wasserstein metric 
$d_{\rm W}$, this was done by Goldstein and Reinert [Reference Goldstein and Reinert5], who proved, in the case 
$q=2$, a bound of the order 
${\textrm{O}}(1/n)$, with an explicit constant depending on a and 
$\textbf{x}_0$. More recently, Gan, Röllin, and Ross [Reference Gan, Röllin and Ross4] gave, for general q, a bound of the order 
${\textrm{O}}(1/n)$ for a weaker metric. Furthermore, for 
$q=2$, 
$a=1$, and 
$x_1,x_2$ integers, Peköz, Röllin, and Ross, in [Reference Peköz, Röllin and Ross13] (
$x_1=1$) and [Reference Peköz, Röllin and Ross14], gave a bound 
${\textrm{O}}(1/n)$ for the stronger metric 
$\ell_\infty$.
The Wasserstein metric equals the minimal 
$L_1$ metric 
$\ell_{1}$, and our main result is the following, which extends the result by Goldstein and Reinert [Reference Goldstein and Reinert5] to 
$\ell_{{p}}$ for all 
$p\leqslant\infty$, and to all numbers of colours 
$q\geqslant2$. See Section 2 for definitions and Sections 3–4 for proofs.
Theorem 1.1. For any 
$q\geqslant2$, any 
$a>0$, and any initial values 
$\textbf{X}_0=\textbf{x}_0\in\mathbb R_{>0}^q$, if 
$\textbf{W}\sim\textrm{Dir}({\textbf{x}_0/a})$, then for every 
$p\in[1,\infty]$ and all 
$n\geqslant1$,
\begin{align}\ell_{{p}}\bigg({\dfrac{\textbf{X}_n}{|\textbf{X}_n|},\textbf{W}}\bigg)&=\Theta\bigg({\dfrac{1}{{n}}}\bigg),\end{align}
\begin{align}\ell_{{p}}\bigg({\dfrac{\textbf{Y}_n}{n},\textbf{W}}\bigg)&=\Theta\bigg({\dfrac{1}{{n}}}\bigg).\end{align}
Corollary 1.1. For any 
$q\geqslant2$, any 
$a>0$, and any initial values 
$\textbf{X}_0=\textbf{x}_0\in\mathbb R_{>0}^q$, if 
$W_i\sim\textrm{Beta}({x_i/a,(|\textbf{x}_0|-x_i)/a})$, then for every 
$p\in[1,\infty]$, every 
$i\in[q]$, and all 
$n\geqslant1$,
\begin{align}\ell_{{p}}\bigg({\dfrac{X_{n,i}}{|\textbf{X}_n|},W_i}\bigg)&=\Theta\bigg({\dfrac{1}{{n}}}\bigg),\end{align}
\begin{align}\ell_{{p}}\bigg({\dfrac{Y_{n,i}}{n},W_i}\bigg)&=\Theta\bigg({\dfrac{1}{{n}}}\bigg){.}\end{align}
We prove Theorem 1.1 by induction on q. The main part of the proof is the base case 
$q=2$, which is proved in Section 3. The easy induction for general q is done in Section 4.
The proofs by Goldstein and Reinert [Reference Goldstein and Reinert5] and Gan, Röllin, and Ross [Reference Gan, Röllin and Ross4] are based on Stein’s method, where they develop versions for the beta distribution and Dirichlet distribution, respectively. In contrast, the present paper uses only direct calculations, based on the known exact distributions. This is similar in spirit to the proofs by Peköz, Röllin, and Ross [Reference Peköz, Röllin and Ross13, Reference Peköz, Röllin and Ross14], which use explicit couplings; however, their method seems difficult to generalize to non-integer 
$x_i/a$.
Since the 
$\ell_{{p}}$ metrics are monotone in p, it suffices to prove the lower bounds for 
$p=1$ and the upper bounds for 
$p=\infty$. Moreover, the lower bounds in (1.5)–(1.8) are trivial, since 
$W_i$ has a continuous distribution with continuous density function, while 
$X_{n,i}/|\textbf{X}_n|$ and 
$Y_{n,i}/n$ are discrete with values spaced by 
$a/(an+|\textbf{x}_0|)$ and 
$1/n$, respectively; see Section 3 for details. Since 
$|\textbf{X}_n|=an+|\textbf{x}_0|$, the upper bounds in (1.5) and (1.6) are for 
$p=\infty$ equivalent to, respectively,
\begin{align} \ell_{{\infty}}({{\textbf{X}_n},| \textbf{X}_n|\textbf{W}}) &={\textrm{O}}(1),\end{align}
\begin{align} \hspace*{6pt} \ell_{{\infty}}({{\textbf{Y}_n},n\textbf{W}}) &={\textrm{O}}(1).\hspace*{-6pt}\end{align}
Moreover, by (1.2), (1.9) is equivalent to 
$ \ell_{{\infty}}({a\textbf{Y}_n,an\textbf{W}}) ={\textrm{O}}(1)$ and thus to (1.10). Hence the upper bounds in the two assertions (1.5) and (1.6) in the theorem are equivalent.
For the one-dimensional variables 
$X_{n,i}$ and 
$Y_{n,i}$, we also give the corresponding results for the Kolmogorov–Smirnov distance 
$d_{\rm{KS}}$ and the Lévy distance 
$d_{\rm{L}}$. (Upper bounds for a multidimensional version of the Kolmogorov–Smirnov distance are given in [Reference Gan, Röllin and Ross4]; the rate obtained there is presumably not sharp, and is weaker than the one found here for the marginals, also when 
$q=2$.) The proofs are given in Section 5.
Theorem 1.2. With assumptions and notations as in Corollary 1, and
\begin{equation}\rho \coloneqq \min\ensuremath{\biggl\{{\dfrac{x_i}a,\dfrac{|\textbf{x}_0|-x_i}a,1}\biggr\}},\end{equation}
we have
\begin{align}d_{\rm{KS}}\bigg({\dfrac{X_{n,i}}{|\textbf{X}_n|},W_i}\bigg)&=\Theta({ n^{- \rho}}),\end{align}
\begin{align}d_{\rm{KS}}\bigg({\dfrac{Y_{n,i}}{n},W_i}\bigg)&=\Theta({ n^{- \rho}}).\end{align}
Theorem 1.3. With assumptions and notations as in Corollary 1.1,
\begin{align}d_{\rm{L}}\bigg({\dfrac{X_{n,i}}{|\textbf{X}_n|},W_i}\bigg)&=\Theta({ n^{- 1}}),
\end{align}
\begin{align}
d_{\rm{L}}\bigg({\dfrac{Y_{n,i}}{n},W_i}\bigg)&=\Theta({ n^{- 1}}).\end{align}
Remark 1.2. Note that the rate for the Kolmogorov–Smirnov distance differs from the other distances considered here, but only in the case when one of the parameters 
$\alpha \coloneqq {x_i}/a$ and 
$\beta \coloneqq ({|\textbf{x}_0|-x_i})/a$ of 
$W_i\sim\textrm{Beta}(\alpha,\beta)$ is less than 1. It follows from the proofs below that this difference can be attributed to the fact that the density (2.1) of 
$W_i$ is unbounded in (precisely) this case.
Remark 1.3. We do not attempt to find explicit values for the constant C in the upper bounds above, although in principle it should be possible by careful calculations in the proof. Note that the proof below treats the cases 
$x_i<a$, 
$x_i=a$ and 
$x_i>a$ separately, and the constants implicit in the calculations might blow up as 
$x_i\to a$ from above or below. We conjecture that the constant C can be chosen uniformly for, say, all 
$\textbf{x}_0$ with 
$a/2\leqslant x_i\leqslant 2a$, but it is not obvious whether this follows from (some version of) our method of proof or not, and we leave that as an open problem.
Remark 1.4. The present paper studies the rate of convergence of the distribution of 
$\textbf{X}_n/|\textbf{X}_n|$. As stated above, this sequence of random variables converges a.s. to a limit 
$\textbf{W}$, and one might also ask about the a.s. rate of convergence of the variables. In fact, the sequence of colours of the drawn balls is exchangeable, which (as noted by [Reference Pólya15]) follows from the simple formula for the probability distribution of the sequence (see (3.3) and the comments after it). Hence de Finetti’s theorem shows that, conditioned on the a.s. limit 
$\textbf{W}$, the sequence 
$\textbf{Y}_n$ is the sequence of partial sums of an independent and identically distributed (i.i.d.) sequence of random unit vectors 
$Z_n$, with the distribution 
$\mathbb{P}(Z_n=\textbf e_i)=W_i$; in particular, each coordinate is the sequence of sums of an i.i.d. Bernoulli sequence. (See e.g. [Reference Kallenberg8, Theorem 11.10].) Consequently we have the same a.s. rate of convergence for the trajectories 
$\textbf{Y}_n/n$ and 
$\textbf{X}_n/|\textbf{X}_n|$ as for the strong law of large numbers for i.i.d. Bernoulli sequences. Thus, by the central limit theorem, the distance 
$|\textbf{X}_n/|\textbf{X}_n|-\textbf{W}|$ is typically of order 
$n^{-1/2}$, and more precisely there is the law of the iterated logarithm.
Note that the distributions thus converge faster than the trajectories. This method with conditioning on the limit can be used to obtain an upper bound for the distance in (1.6), at least for 
$p<\infty$ (see [Reference Kuntschik and Neininger9, Lemma 2.1]), but it only yields a bound 
${\textrm{O}}(n^{-1/2})$, the 
$\ell_{{p}}$ rate of convergence of 
$n^{-1}\operatorname{Bi}(n,p')$ to the constant p’, for 
$p^{\prime}\in(0,1)$.
Remark 1.5. Generalized versions of the urn model above, where we may also add to the urn balls of colours other than the colour of the drawn one, have a rich theory with, typically, quite different behaviour. See e.g. [Reference Janson6]. Such urns will not be studied in the present paper.
Remark 1.6. The initial motivation for this study was a paper by Kuntschik and Neininger [Reference Kuntschik and Neininger9], where generalized Pólya urns (with other replacement schemes) were considered; one step in the proof in [Reference Kuntschik and Neininger9] was a weaker version of (1.8) with the bound 
${\textrm{O}}(n^{-1/2})$. I initially hoped that the sharper result in Corollary 1.1 would lead to an improvement of the result in [Reference Kuntschik and Neininger9] for generalized Pólya urns, but it turns out that this is not the case; the estimate found in [Reference Kuntschik and Neininger9] of the convergence rate is dominated by other terms in their proof.
2. Notation and other preliminaries
2.1. General
For a vector 
$\textbf{x}=(x_1,\ldots,x_q)\in\mathbb R^q$, we define 
$|\textbf{x}| \coloneqq \sum_i|x_i|$. (This is mainly for convenience, in for example (1.1). When defining the metrics below, the Euclidean distance would be just as good, within some constant factors in the result.)
Here 
$\lfloor{x}\rfloor$ denotes the integer part of a real number x, and 
$\{{x}\} \coloneqq x-\lfloor x\rfloor$ the fractional part. Here 
$F_X(x) \coloneqq \mathbb{P}(X\leqslant x)$ denotes the distribution function of a real-valued random variable X. Here C and c denote various positive constants that may depend on the parameters q, a and 
$\textbf{x}_0$, but not on n; they may change from one occurrence to another.
For sequences 
$a_n$ and 
$b_n$ of real numbers, with 
$b_n>0$, 
$a_n={\textrm{O}}(b_n)$ means 
$|a_n|\leqslant C b_n$, for some C. Similarly 
$a_n=\Theta(b_n)$ means 
$cb_n\leqslant |a_n|\leqslant C b_n$.
2.2. Beta and Dirichlet distributions
Recall that the beta distribution 
$\textrm{Beta}(\alpha,\beta)$, where 
$\alpha,\beta>0$, has the density function
\begin{equation} f_{\alpha,\beta}(x)=B(\alpha,\beta)^{-1} x^{\alpha-1}(1-x)^{\beta-1}\quad (0<x<1){,}\end{equation}
where the normalizing constant is given by the beta function
\begin{equation} B(\alpha,\beta) \coloneqq \dfrac{\Gamma(\alpha)\Gamma(\beta)}{\Gamma(\alpha+\beta)}.\end{equation}
Recall also that if 
$q\geqslant2$ and 
$\alpha_1,\ldots,\alpha_q>0$, then the Dirichlet distribution 
$\textrm{Dir}(\alpha_1,\ldots,\alpha_q)$ is the distribution on the simplex 
${\{{(x_1,\ldots,x_q)\in\mathbb R_{>0}^q\colon \sum_i x_i=1}\}}$ with density
\begin{equation}\dfrac{\Gamma(\alpha_1+\dots+\alpha_q)}{\Gamma(\alpha_1)\dotsm\Gamma(\alpha_q)}\, x_1^{\alpha_1}\dotsm x_q^{\alpha_q} \,\textrm{d} x_1\dotsm \,\textrm{d} x_{q-1}.\end{equation}
In the case 
$q=2$, this is essentially the same as a beta distribution; more precisely 
$\textbf{W}\in\textrm{Dir}(\alpha,\beta)$ if and only if 
$\textbf{W}=(V,1-V)$, with 
$V\in\textrm{Beta}(\alpha,\beta)$. More generally, if 
$(W_1,\ldots,W_q)\in\textrm{Dir}(\alpha_1,\ldots,\alpha_q)$, then 
$W_i\sim\textrm{Beta}(\alpha_i,\alpha^{\prime}_i)$, with 
$\alpha^{\prime}_i \coloneqq \sum_{j\neq i}\alpha_j$.
One well-known construction of Dirichlet-distributed random variables is that if 
$V_1,\ldots,V_q$ are independent random variables with 
$V_i\sim\Gamma(\alpha_i)$, then the vector of proportions
\begin{equation} \dfrac{(V_1,\ldots,V_q)}{\sum_i V_i}\sim\textrm{Dir}(\alpha_1,\ldots,\alpha_q),\end{equation}
and this vector is independent of 
$\sum_{i=1}^q V_i$. If 
$q>2$, then, letting 
$V' \coloneqq \sum_{i=2}^q V_i$,
\begin{equation} \dfrac{(V_1,\ldots,V_q)}{\sum_i V_i}=\biggl({\dfrac{V_1}{V_1+V^{\prime}},\dfrac{V^{\prime}}{V_1+V^{\prime}}\dfrac{(V_2,\ldots,V_q)}{V^{\prime}}}\biggr),\end{equation}
and it follows from (2.4) that if 
$Z\sim\textrm{Beta}(\alpha_1,\alpha')$ and 
$\textbf{V}\sim\textrm{Dir}(\alpha_2,\ldots,\alpha_q)$ are independent, with 
$\alpha'=\sum_{i=2}^q \alpha_i$, then
\begin{equation} ({Z,(1-Z)\textbf{V}})\sim\textrm{Dir}(\alpha_1,\ldots,\alpha_q).\end{equation}
2.3. Some probability metrics
A probability metric is a metric on a suitable set of probability distributions in some space 
${\mathcal S}$; in this paper we only consider 
${\mathcal S}=\mathbb R$ or 
$\mathbb R^q$ for some fixed q. (See e.g. [Reference Rachev, Klebanov, Stoyanov and Fabozzi16] for a general theory and many examples, including the ones below.) Although a probability metric 
$d(\mu,\nu)$ is formally defined for distributions 
$\mu$ and 
$\nu$, we follow common practice and write 
$d(X,Y) \coloneqq d({\mathcal L}(X),{\mathcal L}(Y))$ when X and Y are random variables with distributions 
${\mathcal L}(X)$ and 
${\mathcal L}(Y)$, and we state the definitions below in this form.
In the present paper we mainly study the minimal 
$L_p$ distance 
$\ell_{{p}}$ for 
$1\leqslant p\leqslant\infty$, defined by
\begin{equation} \ell_{{p}}(X,Y) \coloneqq \inf {\{{\|{X'-Y'}\|_p\colon X'\overset{\textrm{d}}{=} X,\,Y'\overset{\textrm{d}}{=} Y}\}},\end{equation}
where 
$\|{X'-Y'}\|_p$ is the usual 
$L_p$ distance, i.e. 
$(\mathbb{E}|X'-Y'|^p)^{1/p}$ for 
$p<\infty$, and the essential supremum of 
$|X'-Y'|$ if 
$p=\infty$, and the infimum is taken over all couplings of X and Y, i.e. all pairs (Xʹ,Yʹ) of random variables on a common probability space with the same (marginal) distributions as X and Y. (The infimum is actually attained; see [Reference Rachev, Klebanov, Stoyanov and Fabozzi16, Corollary 5.3.2].) This is a metric on the set of all probability distributions in 
$\mathbb R^q$ with finite pth absolute moment.
The metric 
$\ell_{1}$ is also known as the Wasserstein distance and the Kantorovich distance; see [Reference Rüschendorf17] for a history.
For random variables X and Y in 
$\mathbb R$, we also consider the Kolmogorov–Smirnov distance
\begin{equation} d_{\rm{KS}}(X,Y) \coloneqq \sup_{x \in \mathbb R} |F_X(x) - F_Y(x)|=\sup_{x \in \mathbb R} |P(X \leq x) - P(Y \leq x)|\end{equation}
and the Lévy distance
\begin{equation} d_{\rm{L}}(X,Y) \coloneqq \inf{\{{\varepsilon>0\colon F_X(x-\varepsilon)-\varepsilon \leqslant F_Y(x)\leqslant F_X(x+\varepsilon)+\varepsilon\text{ for all }x}\}}.\end{equation}
3. Proof of Theorem 1.1: 
$q=2$
As explained in the Introduction, we may assume without loss of generality that 
$a=1$, and we shall do so throughout the proof. For convenience, we call the two colours white and black, and we write 
$x_1=\alpha$ and 
$x_2=\beta$. We thus assume 
$a=1$ and 
$\textbf{x}_0=(\alpha,\beta)$, and note that then 
$|\textbf{X}_n|=n+\alpha+\beta$. Furthermore, 
$\textbf{W}=(W_1,W_2)=(W_1,1-W_1)$, where 
$W_1$ is a random variable with the distribution 
$\textrm{Beta}(\alpha,\beta)$,
The parameters 
$\alpha$ and 
$\beta$ are fixed throughout the section. Recall that C and c denote various constants that may depend on 
$\alpha$ and 
$\beta $, but not on n.
Recalling that 
$Y_{n,1}$ is the number of white balls drawn in the first n draws, define
\begin{align} \hspace*{-15pt} p_{n,i}& \coloneqq \mathbb{P}(Y_{n,1}=i),\hspace*{24pt}\end{align}
\begin{align}P_{n,k}& \coloneqq \mathbb{P}(Y_{n,1}\leqslant k)=\sum_{i=0}^k p_{n,i}{.}\end{align}
The basis of the proof is the well-known exact formula [Reference Eggenberger and Pólya2, Reference Johnson and Kotz7, Reference Mahmoud10, Reference Markov11, Reference Pólya15]
\begin{align} p_{n,i}&=\binom{n}{i}\dfrac{\alpha(\alpha+1)\dotsm(\alpha+i-1)\beta(\beta+1)\dotsm(\beta+n-i-1)}{(\alpha+\beta)(\alpha+\beta+1)\dotsm(\alpha+\beta+n-1)}\notag \\[3pt]&=\dfrac{n!}{i!\,(n-i)!}\dfrac{\Gamma(\alpha+i)\Gamma(\beta+n-i)\Gamma(\alpha+\beta)}{\Gamma(\alpha)\Gamma(\beta)\Gamma(\alpha+\beta+n)}\notag \\[3pt]&=B(\alpha,\beta)^{-1}\dfrac{\Gamma(i+\alpha)}{\Gamma(i+1)}\dfrac{\Gamma(n-i+\beta)}{\Gamma(n-i+1)}\dfrac{\Gamma(n+1)}{\Gamma(n+\alpha+\beta)}\end{align}
for 
$i=0,\ldots,n$. This formula is easily verified: if we draw i white balls in the first n draws, then this can be done in 
$\binom ni$ ways, and it follows from the definition (1.1) of the urn process that each of them has the same probability given by the fraction on the first line of (3.3). The rest is simple calculations with gamma functions. For future use we note the special cases
\begin{align} p_{n,0}&=\dfrac{\Gamma(\alpha+\beta)}{\Gamma(\beta)}\dfrac{\Gamma(n+\beta)}{\Gamma(n+\alpha+\beta)},\end{align}
\begin{align} p_{n,n}&=\dfrac{\Gamma(\alpha+\beta)}{\Gamma(\alpha)}\dfrac{\Gamma(n+\alpha)}{\Gamma(n+\alpha+\beta)}.\end{align}
Recall that 
$W_1\sim\textrm{Beta}(\alpha,\beta)$ has the density function 
$f_{\alpha,\beta}$ given in (2.1), and define
\begin{align} Q_{n,k}& \coloneqq \mathbb{P}(W_1\leqslant k/n) = \int_{0}^{k/n}f_{\alpha,\beta}(x)\,\textrm{d} x \end{align}
and
\begin{align}R_{n,k}& \coloneqq P_{n,k}-Q_{n,k}=\mathbb{P}(Y_{n,1}\leqslant k)-\mathbb{P}(W_1\leqslant k/n).\end{align}
We also define 
$\Delta P_{n,k} \coloneqq P_{n,k}-P_{n,k-1}=p_{n,k}$, 
$\Delta Q_{n,k} \coloneqq Q_{n,k}-Q_{n,k-1}$, and 
$\Delta R_{n,k} \coloneqq R_{n,k}-R_{n,k-1}$.
(i) If
$1\leqslant k\leqslant 3n/4$, then
(3.8)If further
\begin{equation}|\Delta R_{n,k}|\leqslant C {k^{\alpha-2}}/{n^\alpha}.\end{equation}
$\alpha=1$, this can be improved to
(3.9)
\begin{equation}|\Delta R_{n,k}|\leqslant C n^{-2}.\end{equation}
-
(ii) If
$n/4\leqslant k\leqslant n$, then
(3.10)If further
\begin{equation}|\Delta R_{n,k}|\leqslant C {(n-k+1)^{\beta-2}}/{n^\beta}.\end{equation}
$\beta=1$, this can be improved to
(3.11)
\begin{equation}|\Delta R_{n,k}|\leqslant C n^{-2}.\end{equation}
Proof. We recall the standard formula (an easy consequence of Stirling’s formula; see also [Reference Olver, Lozier, Boisvert and Clark12, 5.11.13])
\begin{equation} \dfrac{\Gamma(x+a)}{\Gamma(x+b)} = x^{a-b}\biggl({1+{\textrm{O}}\biggl({\dfrac{{1}}{{x}}}\biggr)}\biggr) \end{equation}
for, say, fixed 
$a,b\geqslant0$ and 
$x\geqslant1$.
Using (3.12) in (3.3), we find, for 
$1\leqslant k<n$,
\begin{align} p_{n,k}&= B(\alpha,\beta)^{-1} k^{\alpha-1}(n-k)^{\beta-1}n^{1-\alpha-\beta}\biggl({1+{\textrm{O}}\biggl({\dfrac{{1}}{{k}}}\biggr)+{\textrm{O}}\biggl({\dfrac{{1}}{{n-k}}}\biggr)+{\textrm{O}}\biggl({\dfrac{{1}}{{n}}}\biggr)}\biggr) \notag \\[3pt]
&=n^{-1} f_{\alpha,\beta} \biggl(\frac{k}{n}\biggr)
\biggl(1+\mathrm{O}\biggl(\frac{1}{k}\biggr)+\mathrm{O}\biggl(\frac{1}{n-k}\biggr)\biggr) .\end{align}
Furthermore, if 
$2\leqslant k<n$, then, for 
$x\in((k-1)/n,k/n]$,
\begin{equation} \dfrac{f_{\alpha,\beta}(x)}{f_{\alpha,\beta}(k/n)}=\biggl({\dfrac{{nx}}{{k}}}\biggr)^{\alpha-1}\biggl({\dfrac{{n-nx}}{{n-k}}}\biggr)^{\beta-1}={1+{\textrm{O}}\biggl({\dfrac{{1}}{{k}}}\biggr)+{\textrm{O}}\biggl({\dfrac{{1}}{{n-k}}}\biggr)}\end{equation}
and hence
\begin{equation} \Delta Q_{n,k}=\int_{(k-1)/n}^{k/n}f_{\alpha,\beta}(x)\,\textrm{d} x=n^{-1} f_{\alpha,\beta}\biggl(\frac{k}{n}\biggr)\biggl(1+\mathrm{O}\biggl(\frac{1}{k}\biggr)+\mathrm{O}\biggl(\frac{1}{n-k}\biggr)\biggr).\end{equation}
Moreover, for 
$k=1$, we have, crudely,
\begin{equation} \Delta Q_{n,1}=\int_{0}^{1/n}f_{\alpha,\beta}(x)\,\textrm{d} x\leqslant C \int_{0}^{1/n} x^{\alpha-1}\,\textrm{d} x=C n^{-\alpha}=n^{-1} f_{\alpha,\beta}\biggl(\frac{1}{n}\biggr)\mathrm{O}(1),\end{equation}
and thus (3.15) holds for 
$k=1$ as well.
Combining (3.13) and (3.15), we thus obtain, for 
$1\leqslant k< n$,
\begin{equation} \Delta R_{n,k}=\Delta P_{n,k}-\Delta Q_{n,k}=n^{-1} f_{\alpha,\beta}\biggl(\frac{k}{n}\biggr) \biggl(\mathrm{O}\biggl(\frac{1}{k}\biggr)+\mathrm{O}\biggl(\frac{1}{n-k}\biggr)\biggr).\end{equation}
If we further assume 
$1\leqslant k\leqslant 3n/4$, then 
$f_{\alpha,\beta}(k/n)\leqslant C(k/n)^{\alpha-1}$, and (3.8) follows. Similar calculations, or interchanging the colours and using (3.8), yield (3.10) for 
$n/4\leqslant k\leqslant n$.
Now assume 
$\alpha=1$. Then, using (3.12), for 
$k\leqslant 3n/4$, (3.3) simplifies to
\begin{equation} p_{n,k}=\beta \dfrac{\Gamma(n-k+\beta)}{\Gamma(n-k+1)}\dfrac{\Gamma(n+1)}{\Gamma(n+1+\beta)}=\beta (n-k)^{\beta-1}n^{-\beta}\biggl({1+{\textrm{O}}\biggl({\dfrac{{1}}{{n}}}\biggr)}\biggr).\end{equation}
Similarly, still for 
$k\leqslant 3n/4$, (3.15) simplifies to
\begin{equation} \Delta Q_{n,k}=\int_{(k-1)/n}^{k/n}\beta(1-x)^{\beta-1}\,\textrm{d} x=\beta (n-k)^{\beta-1}n^{-\beta}\biggl({1+{\textrm{O}}\biggl({\dfrac{{1}}{n}}\biggr)}\biggr)\end{equation}
and we obtain
\begin{equation} \Delta R_{n,k}=p_{n,k}-\Delta Q_{n,k}=\beta (n-k)^{\beta-1}n^{-\beta}{\textrm{O}}\biggl({\dfrac{{1}}{n}}\biggr)={\textrm{O}}({n^{-2}}),\end{equation}
showing (3.9). The proof of (3.11) is similar, or by interchanging the colours.□
(i) If
$0\leqslant k\leqslant n/2$, then
(3.21)
\begin{equation}|R_{n,k}|\leqslant C (k+1)^{\alpha-1}n^{-\alpha}.\end{equation}
-
(ii) If
$n/2\leqslant k\leqslant n$, then
(3.22)
\begin{equation}|R_{n,k}|\leqslant C (n-k+1)^{\beta-1}n^{-\beta}.\end{equation}
-
(iii) If
$1\leqslant k\leqslant n-1$, then
(3.23)
\begin{equation} |R_{n,k}|\leqslant Cn^{-1} f_{\alpha,\beta}({{{k}}/{n}}).\end{equation}
Proof. First consider (i), so 
$k\leqslant n/2$. First note that, by (3.4) and (3.12), since 
$Q_{n,0}=0$,
\begin{equation} R_{n,0}=P_{n,0}=p_{n,0}={\textrm{O}}({n^{-\alpha}}), \end{equation}
so (3.21) holds for 
$k=0$.
We now use Lemma 3.1. If 
$\alpha>1$, we have by (3.8), for 
$1\leqslant k\leqslant n/2$,
\begin{equation} R_{n,k}=R_{n,0}+\sum_{i=1}^k\Delta R_{n,i}={\textrm{O}}\biggl({n^{-\alpha}+n^{-\alpha}\sum_{i=1}^k i^{\alpha-2}}\biggr)={\textrm{O}}({n^{-\alpha}k^{\alpha-1}}),\end{equation}
yielding (3.21) in this case.
If 
$\alpha=1$, we obtain (3.21) in the same way, now using (3.9).
If 
$\alpha<1$, (3.8) yields for 
$0\leqslant k\leqslant \lfloor{n/2}\rfloor$ the preliminary result
\begin{align} R_{n,k}&=R_{n,\lfloor{n/2}\rfloor}-\sum_{i=k+1}^{\lfloor{n/2}\rfloor}\Delta R_{n,i}\notag \\*&=R_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}\biggl({n^{-\alpha}\sum_{i=k+1}^{\lfloor{n/2}\rfloor} i^{\alpha-2}}\biggr) \notag \\* &=R_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}({n^{-\alpha}(k+1)^{\alpha-1}}). \end{align}
It thus remains only to show the case 
$k=\lfloor{n/2}\rfloor$; we postpone this.
Now turn to (ii). If 
$\beta\geqslant1$, we obtain in the same way from (3.10) and (3.11), noting that 
$R_{n,n}=1-1=0$ by the definition (3.7), for 
$\lfloor{n/2}\rfloor\leqslant k\leqslant n$,
\begin{equation} R_{n,k}=-\sum_{i=k+1}^n\Delta R_{n,i}={\textrm{O}}({n^{-\beta}(n-k+1)^{\beta-1}}).\end{equation}
If 
$\beta<1$, we obtain instead, for 
$\lfloor{n/2}\rfloor\leqslant k\leqslant n$,
\begin{equation} R_{n,k}=R_{n,\lfloor{n/2}\rfloor}+\sum_{i=\lfloor{n/2}\rfloor+1}^k\Delta R_{n,i}=R_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}({n^{-\beta}(n-k+1)^{\beta-1}}).\end{equation}
We have thus shown, for 
$0\leqslant k\leqslant\lfloor{n/2}\rfloor$,
\begin{equation} R_{n,k}= \begin{cases} {\textrm{O}}({n^{-\alpha}(k+1)^{\alpha-1}}) &\alpha\geqslant1,\\ R_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}({n^{-\alpha}(k+1)^{\alpha-1}}) &\alpha<1, \end{cases}\end{equation}
and for 
$\lfloor{n/2}\rfloor\leqslant k\leqslant n$,
\begin{equation} R_{n,k}= \begin{cases} {\textrm{O}}({n^{-\beta}(n-k+1)^{\beta-1}}) &\beta\geqslant1,\\ R_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}({n^{-\beta}(n-k+1)^{\beta-1}}) &\beta<1. \end{cases}\end{equation}
This proves (3.21) and (3.22) when 
$\alpha\geqslant1$ and 
$\beta\geqslant1$.
Now suppose that 
$\alpha<1$ and 
$\beta\geqslant1$. Then (3.30) yields 
$R_{n,\lfloor{n/2}\rfloor}={\textrm{O}}({n^{-1}})$, and (3.29) shows that (3.21) holds in this case too.
Similarly, if 
$\alpha\geqslant1$ and 
$\beta<1$, then (3.29) yields 
$R_{n,\lfloor{n/2}\rfloor}={\textrm{O}}({n^{-1}})$ and (3.22) follows from (3.30).
It remains to consider the case 
$\alpha<1$ and 
$\beta<1$. In this case we sum 
$R_{n,k}$ over all k and obtain by (3.29) and (3.30), recalling 
$R_{n,n}=0$,
\begin{align} \sum_{k=0}^{n-1} R_{n,k}&=nR_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}\biggl({n^{-\alpha}\sum_{k=0}^{\lfloor{n/2}\rfloor} (k+1)^{\alpha-1}}\biggr)+{\textrm{O}}\biggl({n^{-\beta}\sum_{k=\lfloor{n/2}\rfloor+1}^{n-1} (n-k)^{\beta-1}}\biggr)\notag \\*&=nR_{n\lfloor{n/2}\rfloor}+{\textrm{O}}(1). \end{align}
On the other hand, by (3.7),
\begin{align}\sum_{k=0}^{n-1} R_{n,k}&=\sum_{k=0}^{n-1}({\mathbb{P}(Y_{n,1}\leqslant k)-\mathbb{P}(nW_1\leqslant k)})\notag \\*&=\sum_{k=0}^{n-1}({\mathbb{P}(nW_1>k)-\mathbb{P}(Y_{n,1}> k)})\notag \\&=\sum_{k=0}^{\infty}\mathbb{P}(\lceil{nW_1}\rceil>k)- \sum_{k=0}^{\infty}\mathbb{P}(Y_{n,1}> k)\notag \\&=\mathbb{E} \lceil{nW_1}\rceil-\mathbb{E} Y_{n,1} \notag \\*&=n\mathbb{E} W_1+{\textrm{O}}(1)-\mathbb{E} Y_{n,1}. \end{align}
However, 
$\mathbb{E} W_1=\alpha/(\alpha+\beta)$, and by (1.2), since 
$\textbf{X}_n/|\textbf{X}_n|$ is a martingale and 
$|\textbf{X}_n|=n+\alpha+\beta$,
\begin{equation} \mathbb{E}Y_{n,1}=\mathbb{E} X_{n,1}-\alpha=(n+\alpha+\beta)\dfrac{\alpha}{\alpha+\beta}-\alpha=n\dfrac{\alpha}{\alpha+\beta}=n\mathbb{E} W_1.\end{equation}
Hence (3.31)–(3.32) yield 
$nR_{n,\lfloor{n/2}\rfloor}+{\textrm{O}}(1)={\textrm{O}}(1)$, and thus 
$R_{n,\lfloor{n/2}\rfloor}={\textrm{O}}({n^{-1}})$ also in this case. The proof of (3.21) and (3.22) in this case is now completed by (3.29) and (3.30) as in the cases above.
This completes the proof of (i) and (ii). Finally, (iii) follows from (3.21), (3.22), and (2.1).□
Lemma 3.3. There exists an integer K such that, for all integers k and 
$n\geqslant1$,
\begin{equation}Q_{n,k-K}\leqslant P_{n,k}\leqslant Q_{n,k+K}.\end{equation}
Proof. Assume first 
$n\geqslant 3L$. For any integer 
$L\geqslant1$, if 
$L\leqslant k\leqslant n-2L$, then by (2.1),
\begin{equation}Q_{n,k+L}- Q_{n,k}=\int_{k/n}^{k/n+L/n}f_{\alpha,\beta}(x)\,\textrm{d} x\geqslant \dfrac{L}{n} c f_{\alpha,\beta}\biggl({\dfrac{{k}}{n}}\biggr).\end{equation}
It follows by (3.35) and Lemma 3.2(iii) that if L is chosen large enough, then, for all n and 
$L\leqslant k\leqslant n-2L$,
\begin{equation} Q_{n,k+L}-Q_{n,k} \geqslant R_{n,k} = P_{n,k}-Q_{n,k},\end{equation}
and thus
\begin{equation} P_{n,k}\leqslant Q_{n,k+L}.\end{equation}
Furthermore, using (3.37) for 
$k=L$ (assuming 
$n\geqslant 3L$), we see that if 
$0\leqslant k<L$, then
\begin{equation} P_{n,k}\leqslant P_{n,L}\leqslant Q_{n,2L}\leqslant Q_{n,k+2L}.\end{equation}
Moreover, if 
$k\geqslant n-2L$, then trivially
\begin{equation} P_{n,k} \leqslant 1=Q_{n,n}=Q_{n,k+2L}.\end{equation}
We conclude that if 
$n\geqslant 3L$, then for any 
$k\geqslant0$
\begin{equation} P_{n,k}\leqslant Q_{n,k+2L}.\end{equation}
Moreover, this is trivially true also if 
$k<0$; thus (3.40) holds for all 
$k\in\mathbb Z$ when 
$n\geqslant3L$.
In the same way we see that if L was chosen large enough, also 
$Q_{n,k}-Q_{n,k-L}\geqslant -R_{n,k}$ whenever 
$2L\leqslant k\leqslant n-L$, and it follows that 
$P_{n,k}\geqslant Q_{n,k-2L}$ for all 
$k\in\mathbb Z$ when 
$n\geqslant3L$.
This proves (3.34) with 
$K=3L$ for all 
$n\geqslant1$, since the case 
$n<3L$ is trivial. □
Proof of upper bounds in Theorem 1.1 for 
$q=2$. We use the monotone coupling of 
$Y_{n,1}$ and 
$nW_1$. Since 
$nW_1$ has a continuous distribution, while 
$Y_{n,1}$ is discrete, this coupling can be constructed as follows. Define 
$t_0<\dots<t_n=n$ such that 
$\mathbb{P}(nW_1\leqslant t_k)=P_{n,k}=\mathbb{P}(Y_{n,1}\leqslant k)$, and define the function 
$g\colon (0,n]\to\ensuremath{\{{0,\ldots,n}\}}$ by 
$g(t)=k$ if 
$t\in(t_{k-1},t_k]$ (with 
$t_{-1} \coloneqq 0$). Then
\begin{equation*}\mathbb{P}({g(nW_1)\leqslant k})=\mathbb{P}(nW_1\leqslant t_k)=\mathbb{P}(Y_{n,1}\leqslant k)\quad\text{for $k=0,\ldots,n$,}\end{equation*}
and thus 
$Y_{n,1}^* \coloneqq g(nW_1)$ has the same distribution as 
$Y_{n,1}$.
For K as in Lemma 3.3, we have by (3.34) and (3.6)
\begin{equation} \mathbb{P}(nW_1\leqslant k-K) =Q_{n,k-K}\leqslant P_{n,k}=\mathbb{P}(nW_1\leqslant t_k) \leqslant Q_{n,k+K}=\mathbb{P}(nW_1\leqslant k+K), \end{equation}
and thus 
$k-K\leqslant t_k\leqslant k+K$ for every k. Hence, if 
$Y_{n,1}^*=k$, so 
$nW_1\in(t_{k-1},t_k]$, then 
$nW_1\leqslant t_k\leqslant k+K=Y_{n,1}^*+K$, and similarly 
$nW_1>t_{k-1}\geqslant k-1-K=Y_{n,1}^*-K-1$. Consequently, almost surely, 
$|nW_1-Y_{n,1}^*|\leqslant K+1$, which yields the desired coupling of 
$nW_1$ and 
$Y_{n,1}$. We have thus shown
\begin{equation} \ell_{{\infty}}({Y_{n,1},nW_1})\leqslant\|{{Y_{n,1}^*-nW_1}}\|_{L_\infty}\leqslant K_1 \coloneqq K+1.\end{equation}
Since 
$\textbf{Y}=(Y_{n,1},n-Y_{n,1})$ and 
$\textbf{W}=(W_1,1-W_1)$, this coupling also shows 
$ \ell_{{\infty}}({\textbf{Y},n\textbf{W}})\leqslant K_1$, i.e. (1.10). As stated in the Introduction, by (1.2) this is equivalent to (1.9), and the upper bounds in (1.5)–(1.6) follow.□
For the proof of the lower bounds, we record a simple general fact.
Lemma 3.4. If W is a continuous random variable, then 
$\{{nW}\}\overset{\textrm{d}}{\longrightarrow} U(0,1)$ as
n→∞. In particular,
\begin{equation} \mathbb{P}\biggl({\dfrac{1}4<\{{nW}\}<\dfrac{3}4}\biggr)\to\dfrac12\quad\text{as \ensuremath{{n\to\infty}}}.\end{equation}
Proof. As is well known, by considering the Fourier transform on 
$\mathbb T=\mathbb R/\mathbb Z$, 
$\{{nW}\}\overset{\textrm{d}}{\longrightarrow} U(0,1)$ is equivalent to
\begin{equation}\mathbb{E} \,{\textrm{e}}^{2\pi\textrm{i} m\{{nW}\}}\to0\quad\text{as \ensuremath{{n\to\infty}}}\end{equation}
for every 
$m\in\mathbb Z\setminus\ensuremath{\{0\}}$. We have
\begin{equation}\mathbb{E} \,{\textrm{e}}^{2\pi\textrm{i} m\{{nW}\}}=\mathbb{E} \,{\textrm{e}}^{2\pi\textrm{i} m{nW}}=\varphi(2\pi mn),\end{equation}
where 
$\varphi$ is the characteristic function of W, and thus (3.44) follows by the Riemann–Lebesgue lemma. □
Proof of lower bounds in Theorem 1.1 and Corollary 1.1. (This proof holds for any 
$q\geqslant2$.) Note that 
$W_1$ is a continuous random variable while 
$Y_{n,1}$ is integer-valued. Hence, in any coupling of 
$Y_{n,1}$ and 
$W_1$,
\begin{equation}\mathbb{P}\biggl({|{Y_{n,1}-nW_1}|>\dfrac{1}4}\biggr)\geqslant \mathbb{P}\biggl({\dfrac14<\{{nW_1}\}<\dfrac34}\biggr)\geqslant c\end{equation}
for some 
$c>0$ and all 
$n\geqslant1$, since the last probability in (3.46) is strictly positive for every n and converges to 
$\frac12$ as n→∞ by Lemma 3.4. It follows that 
$\ell_{{p}}(Y_{n,1},nW_1)\geqslant\ell_{1}(Y_{n,1},nW_1)\geqslant c/4$. The lower bound in (1.8) follows. The proof of the lower bound in (1.7) is similar, and the lower bounds in (1.5) and (1.6) follow trivially from these. □
4. Proof of Theorem 1.1: $q>2$
We show here how the general case of Theorem 1.1 follows from the case 
$q=2$ shown in Section 3. Recall that the lower bounds were proved for general q in (3.46). Hence it suffices to show the upper bounds.
Proof of upper bounds in Theorem 1.1 for 
$q>2$. We may still assume 
$a=1$ for simplicity. We focus on the version (1.10); this implies (1.9) and (1.5)–(1.6), as stated in the Introduction.
We use induction on q. Thus, let 
$q>2$, and assume that (1.10) holds when the number of colours is 
$q-1$, and when it is 2.
We call the first colour white and all other colours dark. It is then obvious from the definition of the urn, in words or by (1.1), that if we are colour-blind and only notice whether balls are white or dark, we obtain another Pólya urn, with two colours. Formally, we define 
$\textbf{X}_n^{\prime} \coloneqq (X_{n,2},\ldots,X_{n,q})$ and 
$X_n^{\prime} \coloneqq |\textbf{X}_n^{\prime}|$, and then 
$(X_{n,1},X_n^{\prime})$ is a Pólya urn with initial state 
$\textbf{x}_0^{\prime}=(x_1,x')$ where 
$x' \coloneqq \sum_{j\neq1} x_j$, and the same 
$a=1$.
Let also 
$\textbf{Y}^{\prime}_n \coloneqq (Y_{n,2},\ldots,Y_{n,q})=\textbf{X}_n^{\prime}-\textbf{x}_0^{\prime}$ and 
$Y_n^{\prime} \coloneqq |\textbf{Y}_n^{\prime}|$, the number of times in the n first draws that a dark ball is drawn. Then it follows from the case 
$q=2$ of (1.10) applied to the urn with white and dark balls that if 
$Z\sim\textrm{Beta}(x_1,x')$, then, for each 
$n\geqslant1$,
\begin{equation} \ell_{{\infty}}({Y_{n,1},nZ} )\leqslant C.\end{equation}
In other words, there exists a random variable 
$Z^*\sim\textrm{Beta}(x_1,x')$ such that a.s. 
$|{Y_{n,1}-nZ^*}|\leqslant C$, that is,
\begin{equation}Y_{n,1}=nZ^*+O_{L_\infty}(1),\end{equation}
where, as in the rest of this proof, 
$O_{L_\infty}(1)$ denotes a random variable that is a.s. bounded by some constant C. (These random variables, and other variables in the proof such as 
$Z^*$, may depend on n, but the bound C does not.) Note also that 
$Y_{n,1}+Y_n^{\prime}=|\textbf{Y}_n|=n$, and thus
\begin{equation}Y_n^{\prime}=n-Y_{n,1}=n(1-Z^*)+O_{L_\infty}(1).\end{equation}
Moreover, it also follows from the definition that, conditioned on 
$Y_n^{\prime}=m$, the vector 
$\textbf{X}_n^{\prime}$ is distributed as the mth stage of a Pólya urn with 
$q-1$ colours and initial state 
$\textbf{X}^{\prime}_0$. Consequently, using the induction hypothesis on this urn, if 
$\textbf{W}'\sim\textrm{Dir}(x_2,\ldots,x_q)$, then
\begin{equation*}\ell_{{\infty}}({(\textbf{Y}^{\prime}_n\mid Y_n^{\prime}=m),m\textbf{W}'})\leqslant C.\end{equation*}
This means that for every 
$m\in\ensuremath{\{{0,\ldots,n}\}}$ there exists a random vector 
$\textbf{W}^*_m$ defined on the event 
$\ensuremath{\{{Y_n^{\prime}=m}\}}$ such that
\begin{equation}({\textbf{W}_m^*\mid Y_n^{\prime}=m})\overset{\textrm{d}}{=} \textbf{W}'\end{equation}
and, if 
$Y_n^{\prime}=m$, then a.s.
\begin{equation} |\textbf{Y}_n^{\prime}-m\textbf{W}^*_m|\leqslant C.\end{equation}
Define the random vector 
$\textbf{W}^*$ on our probability space 
$\Omega$ by 
$\textbf{W}^* \coloneqq \textbf{W}^*_{Y_n^{\prime}}$, i.e. 
$\textbf{W}^*=\textbf{W}^*_m$ when 
$Y_n^{\prime}=m$. Then (4.4) means that
\begin{equation*} \textbf{W}^*\overset{\textrm{d}}{=} \textbf{W}'\sim\textrm{Dir}(x_2,\ldots,x_q), \end{equation*}
and that 
$\textbf{W}^*$ is independent of 
$Y_n^{\prime}$, while (4.5) means that 
$|\textbf{Y}_n^{\prime}-Y_n^{\prime}\textbf{W}^*|\leqslant C$, or equivalently
\begin{equation}\textbf{Y}_n^{\prime}=Y_n^{\prime}\textbf{W}^*+O_{L_\infty}(1).\end{equation}
Note also that since 
$\textbf{W}^*$ is independent of 
$Y_n^{\prime}$, and thus of 
$Y_{n,1}$, we may assume that 
$Z^*$ in (4.2)–(4.3) is chosen to be independent of 
$\textbf{W}^*$.
Combining (4.6) and (4.2)–(4.3), we obtain, recalling that the Dirichlet distribution is supported on a bounded set,
\begin{align} \textbf{Y}_n&=({Y_{1,n},\textbf{Y}^{\prime}_n})=({Y_{1,n},Y_n^{\prime}\textbf{W}^*})+O_{L_\infty}(1) \notag \\[2pt]&=({nZ^*,n(1-Z^*)\textbf{W}^*})+O_{L_\infty}(1) \notag \\[2pt] & =n({Z^*,(1-Z^*)\textbf{W}^*})+O_{L_\infty}(1).\end{align}
Since 
$Z^*\sim\textrm{Beta}(x_1,x')$ and 
$\textbf{W}^*\sim\textrm{Dir}(x_2,\ldots,x_q)$, with 
$Z^*$ and 
$\textbf{W}^*$ independent,
\begin{equation*}\textbf{W} \coloneqq ({Z^*,(1-Z^*)\textbf{W}^*})\sim\textrm{Dir}(x_1,\ldots,x_q)\end{equation*}
by (2.6). Consequently (4.7) shows that 
$\ell_{{\infty}}({\textbf{Y}_n,n\textbf{W}})\leqslant\|{{\textbf{Y}_n-n\textbf{W}}}\|_{L_\infty}={\textrm{O}}(1)$ with 
$\textbf{W}\sim\textrm{Dir}(x_1,\ldots,x_q)$, which completes the induction.
This completes the proof of Theorem 1.1.□
Proof of Corollary 1.1. The upper bounds follow by Theorem 1.1, and the lower bounds were proved above by (3.46) and the corresponding argument for 
$X_{n,i}$.□
5. Proofs of Theorems 1.2 and 1.3
Proof of Theorem 1.2. We may assume 
$a=1$, and by symmetry, it suffices to consider 
$i=1$. Furthermore, by regarding the colours as white or dark as in Section 4, it suffices to consider 
$q=2$. As in Section 3, let 
$\alpha \coloneqq x_1$ and 
$\beta \coloneqq |\textbf{x}_0|-x_1$, so (1.11) becomes
\begin{equation}\rho=\min\ensuremath{\{{\alpha,\beta,1}\}}.\end{equation}
For simplicity, we consider only (1.13). Similar arguments yield (1.12); note that by (1.2),
\begin{align} d_{\rm{KS}}\biggl({\dfrac{X_{n,1}}{|\textbf{X}_n|},W_1}\biggr)&= d_{\rm{KS}}\biggl({\dfrac{Y_{n,1}+x_1}{n+|\textbf{x}_0|},W_1}\biggr) \notag \\[2pt] &= d_{\rm{KS}}\biggl({\dfrac{Y_{n,1}+x_1}n,\dfrac{n+|\textbf{x}_0|}n W_1}\biggr) \notag\\[2pt] &= d_{\rm{KS}}\biggl({\dfrac{Y_{n,1}}n,\biggl({1+\dfrac{|\textbf{x}_0|}n}\biggr) W_1-\dfrac{x_1}{n}}\biggr).\end{align}
Since 
$Y_{n,1}$ is integer-valued, we have, for 
$x\in[k/n,(k+1)/n)$ with integer k, recalling the definitions (3.2), (3.6), (3.7),
\begin{align} \mathbb{P}(Y_{n,1}/n \leqslant x)-\mathbb{P}(W_1\leqslant x)&=\mathbb{P}(Y_{n,1}\leqslant k)-\mathbb{P}(W_1\leqslant x)\notag\\[2pt] &=R_{n,k} -\int_{k/n}^x f_{\alpha,\beta}(x)\,\textrm{d} x .\end{align}
The integral in (5.3) is less than 
$\Delta Q_{n,k+1}$, and thus, recalling also (2.8),
\begin{equation} d_{\rm{KS}}({{Y_{n,1}}/n,W_1})\leqslant\sup_k |R_{n,k}| + \sup_k|\Delta Q_{n,k}|.\end{equation}
Furthermore, by taking 
$x=k/n$ in (5.3),
\begin{equation}\sup_k |R_{n,k}| \leqslant d_{\rm{KS}}({{Y_{n,1}}/n,W_1}){,}\end{equation}
and by instead letting 
$x\nearrow (k+1)/n$,
\begin{equation}\sup_k |R_{n,k}-\Delta Q_{n,k+1}| \leqslant d_{\rm{KS}}({{Y_{n,1}}/n,W_1}).\end{equation}
Hence, combining (5.5) and (5.6),
\begin{equation}\sup_k |\Delta Q_{n,k+1}| \leqslant 2d_{\rm{KS}}({{Y_{n,1}}/n,W_1}).\end{equation}
It follows from (3.6) and (2.1) that
\begin{align*} \Delta Q_{n,1} \geqslant c n^{-\alpha},
\end{align*}
\begin{align*} \Delta Q_{n,n} \geqslant c n^{-\beta},\end{align*}
\begin{align*} \Delta Q_{n,\lfloor{(n+1)/2}\rfloor} \geqslant c/n.\end{align*}
Consequently (5.7) yields the lower bound, using (5.1),
\begin{equation} d_{\rm{KS}}({{Y_{n,1}}/n,W_1}) \geqslant c \max({ n^{-\alpha},n^{-\beta},n^{-1}})=c n^{- \rho}.\end{equation}
For an upper bound, we similarly have (see (3.15)–(3.16))
\begin{equation} \max_k \Delta Q_{n,k}\leqslant C \max_{1\leqslant k\leqslant n-1} n^{-1} f_{\alpha,\beta}\biggl({\dfrac{{k}}{n}}\biggr)\leqslant C n^{- \rho}.\end{equation}
Furthermore, Lemma 3.2 yields
\begin{equation} \max_k| R_{n,k}|\leqslant C n^{- \min\ensuremath{\{{\alpha,\beta,1}\}}}= C n^{- \rho}.\end{equation}
Consequently the upper bound in (1.13) follows from (5.4).□
Proof of Theorem 1.3. We use the same simplifying assumptions and notations as in the proof of Theorem 1.2. Again we consider only 
$Y_{n,1}/n$; the proof for 
$X_{n,1}/|\textbf{X}_n|$ is similar. Lemma 3.3 implies that
\begin{equation}d_{\rm{L}}\biggl({\dfrac{Y_{n,1}}{n},W_1}\biggr) \leqslant \dfrac{K}{n}.\end{equation}
Conversely, suppose that 
$d_{\rm{L}}({{Y_{n,1}}/{n},W_1}) < {1}/{4n}$. Take any 
$\delta$ such that 
$d_{\rm{L}}({{Y_{n,1}}/{n},W_1}) < \delta<{1}/{4n}$, and let 
$w_0 \coloneqq \lfloor{n/2}\rfloor/n$. Then, by (2.9) and the fact that 
$Y_{n,1}$ takes only integer values,
\begin{align} F_{W_1}\biggl({w_0+\dfrac{3}{4n}}\biggr)&\leqslant F_{Y_{n,1}/n}\biggl({w_0+\dfrac{3}{4n}+\delta}\biggr)+\delta \notag \\[2pt] &= F_{Y_{n,1}/n}\biggl({w_0+\dfrac{1}{4n}-\delta}\biggr)+\delta\notag\\[2pt] &\leqslant F_{W_1}\biggl({w_0+\dfrac{1}{4n}}\biggr) +2\delta.\end{align}
We have 
$W_1\sim \textrm{Beta}({\alpha,\beta})$ for some 
$\alpha,\beta>0$, and thus (2.1) yields
\begin{equation} F_{W_1}\biggl({w_0+\dfrac{3}{4n}}\biggr) -F_{W_1}\biggl({w_0+\dfrac{1}{4n}}\biggr)=\int_{w_0+{{1}/{(4n)}}} ^{w_0+{{3}/{(4n)}}} f_{\alpha,\beta}(x)\,\textrm{d} x\geqslant \dfrac{c}n.\end{equation}
Together, (5.12) and (5.13) yield 
$2\delta\geqslant c/n$. We may choose 
$\delta$ arbitrarily close to 
$d_{\rm{L}}({{Y_{n,1}}/{n},W_1})$, and thus it follows that if
\begin{equation*}d_{\rm{L}}({{Y_{n,1}}/{n},W_1})
< \dfrac{1}{4n},\end{equation*}
then
\begin{equation*}d_{\rm{L}}({{Y_{n,1}}/{n},W_1}) \geqslant \dfrac{c}{2n}.\end{equation*}
Consequently, in any case,
\begin{equation} d_{\rm{L}}\biggl({\dfrac{Y_{n,1}}{n},W_1}\biggr) \geqslant \dfrac{\min\ensuremath{\{{1/4,c/2}\}}}{n}.\end{equation}
This together with (5.11) completes the proof.□
Acknowledgement
This work was partly carried out during a visit to the Isaac Newton Institute for Mathematical Sciences during the programme ‘Theoretical Foundations for Statistical Network Analysis’ in 2016 (EPSCR grant EP/K032208/1) and was partially supported by a grant from the Simons foundation and a grant from the Knut and Alice Wallenberg Foundation. I thank Ralph Neininger for posing the problem, and Gesine Reinert and two anonymous referees for helpful comments.
