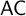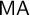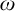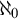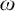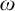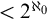1 Notation and terminology
Notation 1.1.
-
(1) Let
 $X,Y$
be two sets. We write:
$X,Y$
be two sets. We write:-
(a)
 $|X|=|Y|$
if there exists a bijection from X onto Y. Otherwise, we write
$|X|=|Y|$
if there exists a bijection from X onto Y. Otherwise, we write
 $|X|\neq |Y|$
;
$|X|\neq |Y|$
; -
(b)
 $|X|\leq |Y|$
if there exists an injection from X into Y;
$|X|\leq |Y|$
if there exists an injection from X into Y; -
(c)
 $|X|<|Y|$
if
$|X|<|Y|$
if
 $|X|\leq |Y|$
and
$|X|\leq |Y|$
and
 $|X|\neq |Y|$
.
$|X|\neq |Y|$
.
-
-
(2) For a set X,
 $[X]^{<\omega }$
denotes the set of all finite subsets of X.
$[X]^{<\omega }$
denotes the set of all finite subsets of X. -
(3) For an infinite set X,
 $\wp ^{\infty }(X)$
denotes the set of all infinite subsets of X.
$\wp ^{\infty }(X)$
denotes the set of all infinite subsets of X.
Definition 1.2. A set X is called:
-
(1) denumerable if
 $|X|=\aleph _{0}$
;
$|X|=\aleph _{0}$
; -
(2) countable if
 $|X|\leq \aleph _{0}$
;
$|X|\leq \aleph _{0}$
; -
(3) Dedekind-finite if
 $\aleph _{0}\not \leq |X|$
. Otherwise, X is called Dedekind-infinite.
$\aleph _{0}\not \leq |X|$
. Otherwise, X is called Dedekind-infinite.
Definition 1.3. Let
![]() $(P,\leq )$
be a poset (that is, a partially ordered set).
$(P,\leq )$
be a poset (that is, a partially ordered set).
-
(1) A non-empty subset F of P is called a filter in P if it satisfies the following two properties:
-
(a)
 $\forall p\in F\forall q\in F\exists r\in F(r\le p\wedge r\leq q)$
;
$\forall p\in F\forall q\in F\exists r\in F(r\le p\wedge r\leq q)$
; -
(b)
 $\forall p\in P\forall q\in F(q\le p\rightarrow p\in F)$
.
$\forall p\in P\forall q\in F(q\le p\rightarrow p\in F)$
.
A filter F in P is called:
-
(c) a free filter in P if F has no lower bound in P;
-
(d) an ultrafilter in P if for every filter G in P with
 $F\subseteq G$
, we have
$F\subseteq G$
, we have
 $F=G$
.
$F=G$
.
-
-
(2) A non-empty subset B of P is called a filter base in P if it satisfies the following property:
 $\forall a\in B\forall b\in B\exists c\in B(c\leq a\wedge c\leq b$
).
$\forall a\in B\forall b\in B\exists c\in B(c\leq a\wedge c\leq b$
). -
(3) Two elements p and q of P are called compatible if there exists
 $r\in P$
such that
$r\in P$
such that
 $r\le p$
and
$r\le p$
and
 $r\le q$
. Otherwise, p and q are called incompatible.
$r\le q$
. Otherwise, p and q are called incompatible. -
(4) A set
 $A\subseteq P$
is called an antichain in P if any two distinct elements of A are incompatible.
$A\subseteq P$
is called an antichain in P if any two distinct elements of A are incompatible. -
(5)
 $(P,\le )$
has the countable chain condition (c.c.c.) if every antichain in P is countable.
$(P,\le )$
has the countable chain condition (c.c.c.) if every antichain in P is countable. -
(6) A set
 $D\subseteq P$
is called dense in P if it satisfies the following property:
$D\subseteq P$
is called dense in P if it satisfies the following property:
 $\forall p\in P \exists d\in D (d\le p)$
.
$\forall p\in P \exists d\in D (d\le p)$
.
Remark 1.4. If
![]() $(P,\leq )$
is a poset and B is a filter base in P, then
$(P,\leq )$
is a poset and B is a filter base in P, then
is a filter in P; F is called the filter generated by B, and B is called a base for F.
Definition 1.5. Let X be a non-empty set. A non-empty set
![]() $\mathscr {F}\subseteq \wp (X)\setminus \{\emptyset \}$
is called a filter (filter base, ultrafilter) on X if
$\mathscr {F}\subseteq \wp (X)\setminus \{\emptyset \}$
is called a filter (filter base, ultrafilter) on X if
![]() $\mathscr {F}$
is a filter (respectively, filter base, ultrafilter) in the poset
$\mathscr {F}$
is a filter (respectively, filter base, ultrafilter) in the poset
![]() $(\wp (X)\setminus \{\emptyset \},\subseteq )$
.
$(\wp (X)\setminus \{\emptyset \},\subseteq )$
.
Remark 1.6. Let X be a non-empty set. A filter
![]() $\mathscr {F}$
on X is
$\mathscr {F}$
on X is
-
(1) free if
 $\bigcap \mathscr {F}=\emptyset $
;
$\bigcap \mathscr {F}=\emptyset $
; -
(2) an ultrafilter on X if, for every
 $A\subseteq X$
, either
$A\subseteq X$
, either
 $A\in \mathscr {F}$
or
$A\in \mathscr {F}$
or
 $A^{c}=X\setminus A\in \mathscr {F}$
.
$A^{c}=X\setminus A\in \mathscr {F}$
.
Definition 1.7.
-
(1) For any infinite set X,
 $\mathsf {AC}(X)$
: Every family of non-empty subsets of X has a choice function.
$\mathsf {AC}(X)$
: Every family of non-empty subsets of X has a choice function. -
(2) The Axiom of Countable Choice,
 $\mathsf {AC}^{\aleph _{0}}$
[Reference Howard and Rubin11, Form 8]: Every denumerable family of non-empty sets has a choice function.
$\mathsf {AC}^{\aleph _{0}}$
[Reference Howard and Rubin11, Form 8]: Every denumerable family of non-empty sets has a choice function. -
(3)
 $\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
[Reference Howard and Rubin11, Form 94]: Every denumerable family of non-empty subsets of
$\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
[Reference Howard and Rubin11, Form 94]: Every denumerable family of non-empty subsets of
 $\mathbb {R}$
has a choice function.
$\mathbb {R}$
has a choice function. -
(4)
 $\mathsf {CUT}(\mathbb {R})$
[Reference Howard and Rubin11, Form 6]: The union of a countable family of countable subsets of
$\mathsf {CUT}(\mathbb {R})$
[Reference Howard and Rubin11, Form 6]: The union of a countable family of countable subsets of
 $\mathbb {R}$
is countable.
$\mathbb {R}$
is countable. -
(5)
 $\mathsf {DFF}(\mathbb {R})$
[Reference Howard and Rubin11, Form 13]: Every Dedekind-finite subset of
$\mathsf {DFF}(\mathbb {R})$
[Reference Howard and Rubin11, Form 13]: Every Dedekind-finite subset of
 $\mathbb {R}$
is finite.
$\mathbb {R}$
is finite. -
(6) The Principle of Dependent Choices,
 $\mathsf {DC}$
[Reference Howard and Rubin11, Form 43]: Let X be a non-empty set and let R be a binary relation on X such that, for every
$\mathsf {DC}$
[Reference Howard and Rubin11, Form 43]: Let X be a non-empty set and let R be a binary relation on X such that, for every
 $x\in X$
, there exists
$x\in X$
, there exists
 $y\in X$
such that
$y\in X$
such that
 $xRy$
. Then there exists a sequence
$xRy$
. Then there exists a sequence
 $(x_{n})_{n\in \omega }$
of elements of X such that
$(x_{n})_{n\in \omega }$
of elements of X such that
 $x_{n}Rx_{n+1}$
for all
$x_{n}Rx_{n+1}$
for all
 $n\in \omega $
.
$n\in \omega $
. -
(7) Let X be a set.
-
(a)
 $\mathsf {BPI}(X)$
: Every filter on X can be extended to an ultrafilter.
$\mathsf {BPI}(X)$
: Every filter on X can be extended to an ultrafilter. -
(b)
 $\mathsf {BPI_{wob}}(X)$
: Every filter on X can be extended to an ultrafilter with a well-orderable base.
$\mathsf {BPI_{wob}}(X)$
: Every filter on X can be extended to an ultrafilter with a well-orderable base. -
(c) If X is infinite, then:
 $\mathsf {UF}(X)$
: There exists a free ultrafilter on X;
$\mathsf {UF}(X)$
: There exists a free ultrafilter on X; $\mathsf {UF_{wob}}(X)$
: There exists a free ultrafilter on X with a well-orderable base.Footnote
1
$\mathsf {UF_{wob}}(X)$
: There exists a free ultrafilter on X with a well-orderable base.Footnote
1
-
-
(8) The Boolean Prime Ideal Theorem,
 $\mathsf {BPI}$
[Reference Howard and Rubin11, Form 14]: Every Boolean algebra has a prime ideal.
$\mathsf {BPI}$
[Reference Howard and Rubin11, Form 14]: Every Boolean algebra has a prime ideal. -
(9)
 $\aleph _{1}\le 2^{\aleph _{0}}$
[Reference Howard and Rubin11, Form 170]: There exists an injection from
$\aleph _{1}\le 2^{\aleph _{0}}$
[Reference Howard and Rubin11, Form 170]: There exists an injection from
 $\omega _{1}$
into
$\omega _{1}$
into
 $2^{\omega }$
.
$2^{\omega }$
. -
(10) Let
 $\kappa $
be a well-ordered cardinal.
$\kappa $
be a well-ordered cardinal. $\kappa $
-Martin’s Axiom,
$\kappa $
-Martin’s Axiom,
 $\mathsf {MA}(\kappa )$
: If
$\mathsf {MA}(\kappa )$
: If
 $(P,\le )$
is a non-empty c.c.c. poset and if
$(P,\le )$
is a non-empty c.c.c. poset and if
 $\mathcal D$
is a family of
$\mathcal D$
is a family of
 $\le \kappa $
dense sets in P, then there is a filter F of P such that, for all
$\le \kappa $
dense sets in P, then there is a filter F of P such that, for all
 $D\in \mathcal D$
,
$D\in \mathcal D$
,
 $F\cap D\ne \emptyset $
. Such a filter F of P is called a
$F\cap D\ne \emptyset $
. Such a filter F of P is called a
 $\mathcal D$
-generic filter in P.
$\mathcal D$
-generic filter in P. -
(11) Martin’s Axiom,
 $\mathsf {MA}$
:
$\mathsf {MA}$
:
 $\forall \kappa <2^{\aleph _0}(\mathsf {MA}(\kappa ))$
(where the parameter
$\forall \kappa <2^{\aleph _0}(\mathsf {MA}(\kappa ))$
(where the parameter
 $\kappa $
ranges over the well-ordered cardinal numbers less than
$\kappa $
ranges over the well-ordered cardinal numbers less than
 $2^{\aleph _{0}}$
).
$2^{\aleph _{0}}$
). -
(12) The Continuum Hypothesis,
 $\mathsf {CH}$
:
$\mathsf {CH}$
:
 $2^{\aleph _{0}}=\aleph _{1}$
.
$2^{\aleph _{0}}=\aleph _{1}$
.
Remark 1.8.
-
(1) Let X be any infinite set. Since
 $\mathsf {AC}(X)$
is clearly equivalent to “
$\mathsf {AC}(X)$
is clearly equivalent to “
 $\wp (X)\setminus \{\emptyset \}$
has a choice function”, it is part of the folklore that
$\wp (X)\setminus \{\emptyset \}$
has a choice function”, it is part of the folklore that  $$ \begin{align*}\mathsf{AC}(X)\Longleftrightarrow "X\ \text{can be well ordered".}\end{align*} $$
$$ \begin{align*}\mathsf{AC}(X)\Longleftrightarrow "X\ \text{can be well ordered".}\end{align*} $$
Let us also note here that
 $\mathsf {AC}(\mathbb {R})$
, “
$\mathsf {AC}(\mathbb {R})$
, “
 $\mathbb {R}$
can be well ordered”, and “
$\mathbb {R}$
can be well ordered”, and “
 $\wp (\mathbb {R})$
can be well ordered” are, respectively, Form 79 A, Form 79, and Form 130 in [Reference Howard and Rubin11].
$\wp (\mathbb {R})$
can be well ordered” are, respectively, Form 79 A, Form 79, and Form 130 in [Reference Howard and Rubin11]. -
(2)
 $\mathsf {BPI} \Longleftrightarrow \forall X(\mathsf {BPI}(X))$
(see [Reference Howard and Rubin11]).
$\mathsf {BPI} \Longleftrightarrow \forall X(\mathsf {BPI}(X))$
(see [Reference Howard and Rubin11]). -
(3) The statement “there exists an infinite set X such that
 $\mathsf {UF}(X)$
” is not provable in
$\mathsf {UF}(X)$
” is not provable in
 $\mathsf {ZF}$
; in particular, the latter statement is false in Blass’ model
$\mathsf {ZF}$
; in particular, the latter statement is false in Blass’ model
 $\mathcal {M}15$
of [Reference Howard and Rubin11] (see [Reference Blass1, Reference Howard and Rubin11]).
$\mathcal {M}15$
of [Reference Howard and Rubin11] (see [Reference Blass1, Reference Howard and Rubin11]). -
(4)
 $\mathsf {UF}(\omega )$
[Reference Howard and Rubin11, Form 70] is strictly weaker than
$\mathsf {UF}(\omega )$
[Reference Howard and Rubin11, Form 70] is strictly weaker than
 $\mathsf {BPI}(\omega )$
[Reference Howard and Rubin11, Form 225] in
$\mathsf {BPI}(\omega )$
[Reference Howard and Rubin11, Form 225] in
 $\mathsf {ZF}$
(see [Reference Hall, Keremedis and Tachtsis6]).
$\mathsf {ZF}$
(see [Reference Hall, Keremedis and Tachtsis6]). -
(5) It is clear that
and since $$ \begin{align*}\mathsf{ZF}\vdash\forall X(\mathsf{UF_{wob}}(X)\Rightarrow\mathsf{UF}(X)),\end{align*} $$
$$ \begin{align*}\mathsf{ZF}\vdash\forall X(\mathsf{UF_{wob}}(X)\Rightarrow\mathsf{UF}(X)),\end{align*} $$
 $\mathsf {AC}$
is equivalent to the Well-Ordering Theorem, i.e., “Every set can be well ordered”, (where
$\mathsf {AC}$
is equivalent to the Well-Ordering Theorem, i.e., “Every set can be well ordered”, (where $$ \begin{align*}\mathsf{ZFC}\vdash\forall X(\mathsf{UF_{wob}}(X) \Longleftrightarrow\mathsf{UF}(X)),\end{align*} $$
$$ \begin{align*}\mathsf{ZFC}\vdash\forall X(\mathsf{UF_{wob}}(X) \Longleftrightarrow\mathsf{UF}(X)),\end{align*} $$
 $\mathsf {ZFC}=\mathsf {ZF}+\mathsf {AC}$
). In Theorem 5.13, we will show that
$\mathsf {ZFC}=\mathsf {ZF}+\mathsf {AC}$
). In Theorem 5.13, we will show that  $$ \begin{align*}\mathsf{ZF}\nvdash "\mathsf{UF}(\omega)\Rightarrow\mathsf{UF_{wob}}(\omega)".\end{align*} $$
$$ \begin{align*}\mathsf{ZF}\nvdash "\mathsf{UF}(\omega)\Rightarrow\mathsf{UF_{wob}}(\omega)".\end{align*} $$
-
(6)
 $\mathsf {MA}(\aleph _0)$
is Form 339 in [Reference Howard and Rubin11]. For a recent study on
$\mathsf {MA}(\aleph _0)$
is Form 339 in [Reference Howard and Rubin11]. For a recent study on
 $\mathsf {MA}$
,
$\mathsf {MA}$
,
 $\mathsf {MA}(\aleph _{0})$
,
$\mathsf {MA}(\aleph _{0})$
,
 $\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras, and weak forms of
$\mathsf {MA}(\aleph _{0})$
restricted to complete Boolean algebras, and weak forms of
 $\mathsf {AC}$
, the reader is referred to Tachtsis [Reference Tachtsis26, Reference Tachtsis27].
$\mathsf {AC}$
, the reader is referred to Tachtsis [Reference Tachtsis26, Reference Tachtsis27]. -
(7) “
 $\aleph _{1}$
is regular” and “
$\aleph _{1}$
is regular” and “
 $\mathbb {R}$
cannot be written as a countable union of countable sets” are, respectively, Form 34 and Form 38 in [Reference Howard and Rubin11]. Recall that 34 implies 38 (see Jech [Reference Jech13, Problem 2, p. 148]) and that in the Feferman–Lévy model,
$\mathbb {R}$
cannot be written as a countable union of countable sets” are, respectively, Form 34 and Form 38 in [Reference Howard and Rubin11]. Recall that 34 implies 38 (see Jech [Reference Jech13, Problem 2, p. 148]) and that in the Feferman–Lévy model,
 $\mathbb {R}$
is a countable union of countable sets; so,
$\mathbb {R}$
is a countable union of countable sets; so,
 $\aleph _{1}$
is singular in that model (see [Reference Jech13, Theorem 10.6] and [Reference Howard and Rubin11, Model
$\aleph _{1}$
is singular in that model (see [Reference Jech13, Theorem 10.6] and [Reference Howard and Rubin11, Model
 $\mathcal{M}9$
]). Therefore, none of 34 and 38 are provable in
$\mathcal{M}9$
]). Therefore, none of 34 and 38 are provable in
 $\mathsf {ZF}$
. Furthermore, 170 (i.e., “
$\mathsf {ZF}$
. Furthermore, 170 (i.e., “
 $\aleph _{1}\leq 2^{\aleph _{0}}$
”) implies 38 and the implication is not reversible in
$\aleph _{1}\leq 2^{\aleph _{0}}$
”) implies 38 and the implication is not reversible in
 $\mathsf {ZF}$
(see Specker [Reference Specker25] and the forthcoming Theorem 4.1). Finally, 34 and 170 are mutually independent in
$\mathsf {ZF}$
(see Specker [Reference Specker25] and the forthcoming Theorem 4.1). Finally, 34 and 170 are mutually independent in
 $\mathsf {ZF}$
and 38 does not imply 34 in
$\mathsf {ZF}$
and 38 does not imply 34 in
 $\mathsf {ZF}$
(see [Reference Howard, Keremedis, Rubin, Stanley and Tachtsis10, Reference Howard and Rubin11]).
$\mathsf {ZF}$
(see [Reference Howard, Keremedis, Rubin, Stanley and Tachtsis10, Reference Howard and Rubin11]).
Definition 1.9. Let
![]() $\kappa $
be an infinite well-ordered cardinal number. A family
$\kappa $
be an infinite well-ordered cardinal number. A family
![]() $\mathcal {A}\subseteq \wp (\kappa )$
is called independent in
$\mathcal {A}\subseteq \wp (\kappa )$
is called independent in
![]() $\kappa $
if whenever
$\kappa $
if whenever
![]() $\mathcal C$
and
$\mathcal C$
and
![]() $\mathcal D$
are disjoint finite subsets of
$\mathcal D$
are disjoint finite subsets of
![]() $\mathcal {A}$
, then
$\mathcal {A}$
, then
![]() $|\bigcap \mathcal C\cap (\kappa \setminus \bigcup \mathcal D)|=\kappa $
.
$|\bigcap \mathcal C\cap (\kappa \setminus \bigcup \mathcal D)|=\kappa $
.
Remark 1.10. It is a renowned
![]() $\mathsf {ZF}$
-result that there is an independent family in
$\mathsf {ZF}$
-result that there is an independent family in
![]() $\omega $
of size
$\omega $
of size
![]() $2^{\aleph _{0}}$
. This was proved by Fichtenholz and Kantorovich [Reference Fichtenholz and Kantorovich4], using the density of
$2^{\aleph _{0}}$
. This was proved by Fichtenholz and Kantorovich [Reference Fichtenholz and Kantorovich4], using the density of
![]() $\mathbb {Q}$
(the set of rational numbers) in
$\mathbb {Q}$
(the set of rational numbers) in
![]() $\mathbb {R}$
, and we include the elegant and short argument here. Let
$\mathbb {R}$
, and we include the elegant and short argument here. Let
![]() $X=[\mathbb {Q}]^{<\omega }$
. Then
$X=[\mathbb {Q}]^{<\omega }$
. Then
![]() $|X|=\aleph _{0}$
since
$|X|=\aleph _{0}$
since
![]() $|\mathbb {Q}|=\aleph _{0}$
. For each
$|\mathbb {Q}|=\aleph _{0}$
. For each
![]() $r\in \mathbb {R}$
, let
$r\in \mathbb {R}$
, let
It is easy to verify that the collection
is an independent family in X having cardinality
![]() $2^{\aleph _{0}}$
.
$2^{\aleph _{0}}$
.
A more general
![]() $\mathsf {ZF}$
-result was established by Hausdorff, namely that for any infinite well-ordered cardinal
$\mathsf {ZF}$
-result was established by Hausdorff, namely that for any infinite well-ordered cardinal
![]() $\kappa $
, there exists an independent family in
$\kappa $
, there exists an independent family in
![]() $\kappa $
of size
$\kappa $
of size
![]() $2^{\kappa }$
; see Kunen [Reference Kunen16, Exercise (A6), p. 288].
$2^{\kappa }$
; see Kunen [Reference Kunen16, Exercise (A6), p. 288].
2 Motivation and aim
In a private communication, Mauro Di Nasso inquired about the relative strength of
![]() $\mathsf {UF_{wob}}(\omega )$
and its position in the hierarchy of weak choice principles. (For a detailed—and by no means complete—list comprising more than 350 weak forms of
$\mathsf {UF_{wob}}(\omega )$
and its position in the hierarchy of weak choice principles. (For a detailed—and by no means complete—list comprising more than 350 weak forms of
![]() $\mathsf {AC}$
, the reader is referred to Howard and Rubin’s book [Reference Howard and Rubin11].) It was exactly Di Nasso’s inquiry which gave us the motivation for the research in this paper, and we are most thankful to him for drawing our attention to this intriguing theme. The investigation of the open problem of determining the relationship of
$\mathsf {AC}$
, the reader is referred to Howard and Rubin’s book [Reference Howard and Rubin11].) It was exactly Di Nasso’s inquiry which gave us the motivation for the research in this paper, and we are most thankful to him for drawing our attention to this intriguing theme. The investigation of the open problem of determining the relationship of
![]() $\mathsf {UF_{wob}}(\omega )$
with weak choice principles lead us to a fairly recent paper by Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9]. To the best of our knowledge,
$\mathsf {UF_{wob}}(\omega )$
with weak choice principles lead us to a fairly recent paper by Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9]. To the best of our knowledge,
![]() $\mathsf {UF_{wob}}(\omega )$
was introduced for the first time in [Reference Herzberg, Kanovei, Katz and Lyubetsky9] (and was denoted by
$\mathsf {UF_{wob}}(\omega )$
was introduced for the first time in [Reference Herzberg, Kanovei, Katz and Lyubetsky9] (and was denoted by
![]() $\mathbf {WOB}$
therein). The authors [Reference Herzberg, Kanovei, Katz and Lyubetsky9] studied
$\mathbf {WOB}$
therein). The authors [Reference Herzberg, Kanovei, Katz and Lyubetsky9] studied
![]() $\mathsf {UF_{wob}}(\omega )$
from the viewpoint of nonstandard analysis and showed (among other results) that
$\mathsf {UF_{wob}}(\omega )$
from the viewpoint of nonstandard analysis and showed (among other results) that
and thus neither does
![]() $\mathsf {UF_{wob}}(\omega )+\mathsf {AC}^{\aleph _{0}}$
imply
$\mathsf {UF_{wob}}(\omega )+\mathsf {AC}^{\aleph _{0}}$
imply
![]() $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
![]() $\mathsf {ZF}$
; see [Reference Herzberg, Kanovei, Katz and Lyubetsky9, Section 4.1].Footnote
2
On the other hand, the question whether or not
$\mathsf {ZF}$
; see [Reference Herzberg, Kanovei, Katz and Lyubetsky9, Section 4.1].Footnote
2
On the other hand, the question whether or not
![]() $\mathsf {UF}(\omega )$
implies
$\mathsf {UF}(\omega )$
implies
![]() $\mathsf {UF_{wob}}(\omega )$
was left open in [Reference Herzberg, Kanovei, Katz and Lyubetsky9]. We will answer this question in the negative; in fact, we will prove (in Theorem 5.13) a properly stronger result, namely that
$\mathsf {UF_{wob}}(\omega )$
was left open in [Reference Herzberg, Kanovei, Katz and Lyubetsky9]. We will answer this question in the negative; in fact, we will prove (in Theorem 5.13) a properly stronger result, namely that
![]() $\mathsf {UF}(\omega )$
does not imply
$\mathsf {UF}(\omega )$
does not imply
![]() $\aleph _{1}\leq 2^{\aleph _{0}}$
(which is strictly weaker than
$\aleph _{1}\leq 2^{\aleph _{0}}$
(which is strictly weaker than
![]() $\mathsf {UF_{wob}}(\omega )$
in
$\mathsf {UF_{wob}}(\omega )$
in
![]() $\mathsf {ZF}$
—see Theorem 4.1) in
$\mathsf {ZF}$
—see Theorem 4.1) in
![]() $\mathsf {ZF}$
, and thus also filling the gap in information in Howard and Rubin [Reference Howard and Rubin11] about the relationship between the latter two principles.
$\mathsf {ZF}$
, and thus also filling the gap in information in Howard and Rubin [Reference Howard and Rubin11] about the relationship between the latter two principles.
Whether or not there is a model of
![]() $\mathsf {ZF}$
in which
$\mathsf {ZF}$
in which
![]() $\mathsf {BPI}$
is true and
$\mathsf {BPI}$
is true and
![]() $\mathsf {UF_{wob}}(\omega )$
is false is still an open problem; in particular, it is unknown if
$\mathsf {UF_{wob}}(\omega )$
is false is still an open problem; in particular, it is unknown if
![]() $\mathsf {UF_{wob}}(\omega )$
fails in the Basic Cohen Model in which
$\mathsf {UF_{wob}}(\omega )$
fails in the Basic Cohen Model in which
![]() $\mathsf {BPI}$
is true (see [Reference Howard and Rubin11, Model
$\mathsf {BPI}$
is true (see [Reference Howard and Rubin11, Model
![]() $1$
]). Moreover, the relationship between
$1$
]). Moreover, the relationship between
![]() $\mathsf {UF_{wob}}(\omega )$
and
$\mathsf {UF_{wob}}(\omega )$
and
![]() $\mathsf {BPI}(\omega )$
is unknown. However, in Theorem 5.20(ii), we will show that
$\mathsf {BPI}(\omega )$
is unknown. However, in Theorem 5.20(ii), we will show that
![]() $\mathsf {BPI}(\omega )$
implies “there exists a free ultrafilter on
$\mathsf {BPI}(\omega )$
implies “there exists a free ultrafilter on
![]() $\omega $
which has no well-orderable base of cardinality
$\omega $
which has no well-orderable base of cardinality
![]() $<2^{\aleph _{0}}$
”. From this result, we will deduce (in Theorem 5.20(iii)) that the statement “there exists a free ultrafilter on
$<2^{\aleph _{0}}$
”. From this result, we will deduce (in Theorem 5.20(iii)) that the statement “there exists a free ultrafilter on
![]() $\omega $
which has no well-orderable base” is true in the Basic Cohen Model, and (in Theorem 5.20(iv)) we will observe that
$\omega $
which has no well-orderable base” is true in the Basic Cohen Model, and (in Theorem 5.20(iv)) we will observe that
![]() $\mathsf {BPI}(\omega )$
does not imply the latter principle in
$\mathsf {BPI}(\omega )$
does not imply the latter principle in
![]() $\mathsf {ZF}$
. Furthermore, in view of (1) and the above open problems, we introduce the following natural strengthening of
$\mathsf {ZF}$
. Furthermore, in view of (1) and the above open problems, we introduce the following natural strengthening of
![]() $\mathsf {UF_{wob}}(\omega )$
, which we denote by
$\mathsf {UF_{wob}}(\omega )$
, which we denote by
![]() $\mathsf {BPI_{wob}}(\omega )$
: Every filter on
$\mathsf {BPI_{wob}}(\omega )$
: Every filter on
![]() $\omega $
can be extended to an ultrafilter with a well-orderable base. We will show in Theorem 5.22(i) that
$\omega $
can be extended to an ultrafilter with a well-orderable base. We will show in Theorem 5.22(i) that
![]() $\mathsf {BPI_{wob}}(\omega )$
is equivalent to
$\mathsf {BPI_{wob}}(\omega )$
is equivalent to
![]() $\mathsf {AC}(\mathbb {R})$
; thus (by (1))
$\mathsf {AC}(\mathbb {R})$
; thus (by (1))
![]() $\mathsf {UF_{wob}}(\omega )$
is strictly weaker than
$\mathsf {UF_{wob}}(\omega )$
is strictly weaker than
![]() $\mathsf {BPI_{wob}}(\omega )$
in
$\mathsf {BPI_{wob}}(\omega )$
in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
As it is apparent by now, the chief aim of this paper is the study of the set-theoretic strength of
![]() $\mathsf {UF_{wob}}(\omega )$
mostly in terms of weak choice principles, and, in this direction, we provide several positive and independence results, which (together with (1) and the research in [Reference Herzberg, Kanovei, Katz and Lyubetsky9]) shed light on this enthralling (and fairly unexplored) topic, and also set a basis for further research in the future.
$\mathsf {UF_{wob}}(\omega )$
mostly in terms of weak choice principles, and, in this direction, we provide several positive and independence results, which (together with (1) and the research in [Reference Herzberg, Kanovei, Katz and Lyubetsky9]) shed light on this enthralling (and fairly unexplored) topic, and also set a basis for further research in the future.
In pursue of our goal, we will also investigate the relative strength of the following four statements, which are closely related to
![]() $\mathsf {UF_{wob}}(\omega )$
:
$\mathsf {UF_{wob}}(\omega )$
:
-
(1) Every filter base on
 $\omega $
can be well ordered.
$\omega $
can be well ordered. -
(2) Every filter on
 $\omega $
has a well-orderable base.
$\omega $
has a well-orderable base. -
(3) Every filter base on
 $\mathbb {R}$
can be well ordered.
$\mathbb {R}$
can be well ordered. -
(4) Every filter on
 $\mathbb {R}$
has a well-orderable base.
$\mathbb {R}$
has a well-orderable base.
We will prove (in Theorem 5.1 of Subsection 5.1) the following results:
-
(5) For any infinite linearly orderable set X, the following are equivalent:
-
(a)
 $\mathsf {AC}(\wp (X))$
.
$\mathsf {AC}(\wp (X))$
. -
(b) Every filter base on X can be well ordered.
-
(c) Every filter on X has a well-orderable base.
In particular,
 $\mathsf {AC}(\mathbb {R})$
is equivalent to each of (1) and (2), and
$\mathsf {AC}(\mathbb {R})$
is equivalent to each of (1) and (2), and
 $\mathsf {AC}(\wp (\mathbb {R}))$
is equivalent to each of (3) and (4).
$\mathsf {AC}(\wp (\mathbb {R}))$
is equivalent to each of (3) and (4).
Figure 1 Results on
 $\mathsf {UF_{wob}}(\omega )$
and related principles.
$\mathsf {UF_{wob}}(\omega )$
and related principles. -
-
(6)
 $\mathsf {CH}$
(and thus
$\mathsf {CH}$
(and thus
 $\mathsf {AC}(\mathbb {R})$
, (1), (2))
$\mathsf {AC}(\mathbb {R})$
, (1), (2))
 $\nRightarrow \mathsf {AC}(\wp (\mathbb {R}))$
(and thus (3), (4)) in
$\nRightarrow \mathsf {AC}(\wp (\mathbb {R}))$
(and thus (3), (4)) in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
From the above results, and the fact (from [Reference Herzberg, Kanovei, Katz and Lyubetsky9]) that
![]() $\mathsf {UF_{wob}}(\omega )$
is strictly weaker than
$\mathsf {UF_{wob}}(\omega )$
is strictly weaker than
![]() $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
![]() $\mathsf {ZF}$
, we will derive (in Corollary 5.7) the following striking result:
$\mathsf {ZF}$
, we will derive (in Corollary 5.7) the following striking result:
-
(7) Each of the statements (1)-(4) implies
 $\mathsf {UF_{wob}}(\omega )$
, and none of these implications are reversible in
$\mathsf {UF_{wob}}(\omega )$
, and none of these implications are reversible in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Typical results of the paper are listed in the abstract, and the majority of the main results (concerning implications and non-implications between the various principles studied here) is depicted in Figure 1 of Section 3.
Concluding this section, let us point out here that our approach is completely different from [Reference Herzberg, Kanovei, Katz and Lyubetsky9] in the sense that no nonstandard methods are considered.
3 Diagram of results
We summarize the majority of our main results in Figure 1 below. A couple of comments about the diagram are in order:
-
• A dashed arrow with initial vertex
 $\mathsf {A}$
and final vertex
$\mathsf {A}$
and final vertex
 $\mathsf {B}$
means that
$\mathsf {B}$
means that
 $\mathsf {A}$
implies
$\mathsf {A}$
implies
 $\mathsf {B}$
, but the implication is not reversible in
$\mathsf {B}$
, but the implication is not reversible in
 $\mathsf {ZF}$
;
$\mathsf {ZF}$
; -
• A negated arrow with initial vertex
 $\mathsf {A}$
and final vertex
$\mathsf {A}$
and final vertex
 $\mathsf {B}$
means that
$\mathsf {B}$
means that
 $\mathsf {A}$
does not imply
$\mathsf {A}$
does not imply
 $\mathsf {B}$
in
$\mathsf {B}$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
For use in the diagram only, we also insert the following abbreviations:
-
• “
 $\mathsf {NUF_{b}}(\omega ,<2^{\aleph _{0}})$
” abbreviates “No free ultrafilter on
$\mathsf {NUF_{b}}(\omega ,<2^{\aleph _{0}})$
” abbreviates “No free ultrafilter on
 $\omega $
has a base of cardinality
$\omega $
has a base of cardinality
 $<2^{\aleph _{0}}$
”;
$<2^{\aleph _{0}}$
”; -
• “
 $\mathsf {NUF_{wob}}(\omega ,<2^{\aleph _{0}})$
” abbreviates “No free ultrafilter on
$\mathsf {NUF_{wob}}(\omega ,<2^{\aleph _{0}})$
” abbreviates “No free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”;
$<2^{\aleph _{0}}$
”; -
• “
 $\mathsf {FWOB}(X)$
”, where
$\mathsf {FWOB}(X)$
”, where
 $X\in \{\omega ,\mathbb {R}\}$
, abbreviates “Every filter on X has a well-orderable base”.
$X\in \{\omega ,\mathbb {R}\}$
, abbreviates “Every filter on X has a well-orderable base”. -
• “
 $\mathbb {R}$
is not cuc” abbreviates “
$\mathbb {R}$
is not cuc” abbreviates “
 $\mathbb {R}$
is not a countable union of countable sets”; recall that this is Form 38 in [Reference Howard and Rubin11].
$\mathbb {R}$
is not a countable union of countable sets”; recall that this is Form 38 in [Reference Howard and Rubin11].
Implications and/or nonimplications which appear in the diagram, but are not established here, are either straightforward or known. In the second case, the reader is referred to: Howard and Rubin [Reference Howard and Rubin11]; Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9] for “
![]() $\mathsf {UF_{wob}}(\omega )$
(
$\mathsf {UF_{wob}}(\omega )$
(
![]() $+\mathsf {DC}$
) does not imply
$+\mathsf {DC}$
) does not imply
![]() $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
![]() $\mathsf {ZF}$
”; and Hall et al. [Reference Hall, Keremedis and Tachtsis6] for “
$\mathsf {ZF}$
”; and Hall et al. [Reference Hall, Keremedis and Tachtsis6] for “
![]() $\mathsf {UF}(\omega )$
does not imply
$\mathsf {UF}(\omega )$
does not imply
![]() $\mathsf {BPI}(\omega )$
in
$\mathsf {BPI}(\omega )$
in
![]() $\mathsf {ZF}$
”.
$\mathsf {ZF}$
”.
4 Known and preliminary results
Recall that in
![]() $\mathsf {ZFC}$
, the character of an ultrafilter
$\mathsf {ZFC}$
, the character of an ultrafilter
![]() $\mathscr {U}$
on
$\mathscr {U}$
on
![]() $\omega $
, denoted by
$\omega $
, denoted by
![]() $\chi (\mathscr {U})$
, is defined to be the least well-ordered cardinal number
$\chi (\mathscr {U})$
, is defined to be the least well-ordered cardinal number
![]() $\kappa $
for which there exists a base
$\kappa $
for which there exists a base
![]() $\mathscr {B}$
for
$\mathscr {B}$
for
![]() $\mathscr {U}$
with
$\mathscr {U}$
with
![]() $|\mathscr {B}|=\kappa $
. It is known that, in
$|\mathscr {B}|=\kappa $
. It is known that, in
![]() $\mathsf {ZFC}$
, if
$\mathsf {ZFC}$
, if
![]() $\mathscr {U}$
is a free ultrafilter on
$\mathscr {U}$
is a free ultrafilter on
![]() $\omega $
, then
$\omega $
, then
![]() $\aleph _{1}\le \chi (\mathscr {U})$
(see Kunen [Reference Kunen16, Exercise (A9), p. 289]) and, for any ultrafilter
$\aleph _{1}\le \chi (\mathscr {U})$
(see Kunen [Reference Kunen16, Exercise (A9), p. 289]) and, for any ultrafilter
![]() $\mathscr {V}$
on
$\mathscr {V}$
on
![]() $\omega $
,
$\omega $
,
![]() $\chi (\mathscr {V})\le |\mathscr {V}|=2^{\aleph _{0}}$
. Note that the latter equality holds in
$\chi (\mathscr {V})\le |\mathscr {V}|=2^{\aleph _{0}}$
. Note that the latter equality holds in
![]() $\mathsf {ZF}$
. Indeed, let
$\mathsf {ZF}$
. Indeed, let
![]() $\mathcal {J}=\{\{A,A^{c}\}:A\in \wp (\omega )\}$
. By Remark 1.6(2), it easily follows that
$\mathcal {J}=\{\{A,A^{c}\}:A\in \wp (\omega )\}$
. By Remark 1.6(2), it easily follows that
![]() $|\mathcal {J}|=|\mathscr {V}|$
. Furthermore,
$|\mathcal {J}|=|\mathscr {V}|$
. Furthermore,
![]() $|\mathcal {J}|=2^{\aleph _{0}}$
. To see this, fix an almost disjoint subfamily of
$|\mathcal {J}|=2^{\aleph _{0}}$
. To see this, fix an almost disjoint subfamily of
![]() $\wp ^{\infty }(\omega )$
of cardinality
$\wp ^{\infty }(\omega )$
of cardinality
![]() $2^{\aleph _{0}}$
,
$2^{\aleph _{0}}$
,
![]() $\mathcal {D}$
say. That is, any two distinct elements of
$\mathcal {D}$
say. That is, any two distinct elements of
![]() $\mathcal {D}$
have a finite intersection. It is well known that such a family
$\mathcal {D}$
have a finite intersection. It is well known that such a family
![]() $\mathcal {D}$
can be constructed without using any form of choice (see, for example, Kunen [Reference Kunen16, Theorem 1.3, p. 48]). Since
$\mathcal {D}$
can be constructed without using any form of choice (see, for example, Kunen [Reference Kunen16, Theorem 1.3, p. 48]). Since
![]() $\mathcal {D}$
is almost disjoint, it is reasonably clear that the function
$\mathcal {D}$
is almost disjoint, it is reasonably clear that the function
![]() $f:\mathcal {D}\rightarrow \mathcal {J}$
defined by
$f:\mathcal {D}\rightarrow \mathcal {J}$
defined by
![]() $f(D)=\{D,D^{c}\}$
for all
$f(D)=\{D,D^{c}\}$
for all
![]() $D\in \mathcal {D}$
, is an injection. Therefore,
$D\in \mathcal {D}$
, is an injection. Therefore,
![]() $2^{\aleph _{0}}=|\mathcal {D}|\leq |\mathcal {J}|$
and since we also have
$2^{\aleph _{0}}=|\mathcal {D}|\leq |\mathcal {J}|$
and since we also have
![]() $|\mathcal {J}|\leq 2^{\aleph _{0}}$
(because, in
$|\mathcal {J}|\leq 2^{\aleph _{0}}$
(because, in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $|[\wp (\omega )]^{<\omega }|=2^{\aleph _{0}}$
), it follows that
$|[\wp (\omega )]^{<\omega }|=2^{\aleph _{0}}$
), it follows that
![]() $|\mathcal {J}|=2^{\aleph _{0}}$
, i.e.,
$|\mathcal {J}|=2^{\aleph _{0}}$
, i.e.,
![]() $|\mathscr {V}|=2^{\aleph _{0}}$
.
$|\mathscr {V}|=2^{\aleph _{0}}$
.
So, essentially, “
![]() $\mathsf {ZF}\vdash \mathsf {UF_{wob}}(\omega )\Rightarrow \aleph _{1}\leq 2^{\aleph _{0}}$
” is a known result. Since the latter result is not explicitly mentioned in the literature (it is neither mentioned in Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9], where
$\mathsf {ZF}\vdash \mathsf {UF_{wob}}(\omega )\Rightarrow \aleph _{1}\leq 2^{\aleph _{0}}$
” is a known result. Since the latter result is not explicitly mentioned in the literature (it is neither mentioned in Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9], where
![]() $\mathsf {UF_{wob}}(\omega )$
was considered), we will include it here along with its short proof. In fact, all the results of Theorem 4.1 below are part of the folklore and we present them for the sake of completeness and the reader’s convenience.
$\mathsf {UF_{wob}}(\omega )$
was considered), we will include it here along with its short proof. In fact, all the results of Theorem 4.1 below are part of the folklore and we present them for the sake of completeness and the reader’s convenience.
Theorem 4.1. Each of the following statements implies the one beneath it
![]() $:$
$:$
-
(i)
 $\mathsf {AC}(\mathbb {R})$
.
$\mathsf {AC}(\mathbb {R})$
. -
(ii)
 $\mathsf {UF_{wob}}(\omega )$
.
$\mathsf {UF_{wob}}(\omega )$
. -
(iii)
 $\aleph _{1}\le 2^{\aleph _{0}}$
.
$\aleph _{1}\le 2^{\aleph _{0}}$
. -
(iv)
 $\mathbb {R}$
cannot be written as a countable union of countable sets.
$\mathbb {R}$
cannot be written as a countable union of countable sets.
None of the above implications are reversible in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. (i)
![]() $\Rightarrow $
(ii) This follows from the following facts:
$\Rightarrow $
(ii) This follows from the following facts:
![]() $\mathsf {AC}(\mathbb {R})\Rightarrow \mathsf {UF}(\omega )$
;
$\mathsf {AC}(\mathbb {R})\Rightarrow \mathsf {UF}(\omega )$
;
![]() $\mathsf {AC}(\mathbb {R})$
is equivalent to “
$\mathsf {AC}(\mathbb {R})$
is equivalent to “
![]() $\mathbb {R}$
can be well ordered”; and
$\mathbb {R}$
can be well ordered”; and
![]() $|\mathbb {R}|=|\wp (\omega )|$
.
$|\mathbb {R}|=|\wp (\omega )|$
.
(ii)
![]() $\Rightarrow $
(iii) Assume
$\Rightarrow $
(iii) Assume
![]() $\mathsf {UF_{wob}}(\omega )$
. We first prove the following claim.
$\mathsf {UF_{wob}}(\omega )$
. We first prove the following claim.
Claim 4.2. (
![]() $\mathsf {ZF}$
) No free ultrafilter on any infinite set has a base of cardinality
$\mathsf {ZF}$
) No free ultrafilter on any infinite set has a base of cardinality
![]() $\aleph _{0}$
.
$\aleph _{0}$
.
Proof. Assume, on the contrary, that there exist an infinite set X and a free ultrafilter
![]() $\mathscr {U}$
on X which has a denumerable base, say
$\mathscr {U}$
on X which has a denumerable base, say
![]() $\mathscr {C}=\{C_{n}:n\in \omega \}$
. Since
$\mathscr {C}=\{C_{n}:n\in \omega \}$
. Since
![]() $\mathscr {U}$
is free and
$\mathscr {U}$
is free and
![]() $\mathscr {C}$
is a filter base, we may assume, without loss of generality, that for every
$\mathscr {C}$
is a filter base, we may assume, without loss of generality, that for every
![]() $n\in \omega $
,
$n\in \omega $
,
![]() $C_{n}\supsetneq C_{n+1}$
. For every
$C_{n}\supsetneq C_{n+1}$
. For every
![]() $n\in \omega $
, we let
$n\in \omega $
, we let
and we also let
It is clear that
![]() $D\cap C_{n}\ne \emptyset $
for all
$D\cap C_{n}\ne \emptyset $
for all
![]() $n\in \omega $
. Since
$n\in \omega $
. Since
![]() $\mathscr {C}$
is a base for the ultrafilter
$\mathscr {C}$
is a base for the ultrafilter
![]() $\mathscr {U}$
, we conclude that
$\mathscr {U}$
, we conclude that
![]() $D\in \mathscr {U}$
. But then, there exists
$D\in \mathscr {U}$
. But then, there exists
![]() $n\in \omega $
such that
$n\in \omega $
such that
![]() $C_{n}\subseteq D$
, which is impossible. This completes the proof of the claim.
$C_{n}\subseteq D$
, which is impossible. This completes the proof of the claim.
By
![]() $\mathsf {UF_{wob}}(\omega )$
, there exists a free ultrafilter
$\mathsf {UF_{wob}}(\omega )$
, there exists a free ultrafilter
![]() $\mathscr {V}$
on
$\mathscr {V}$
on
![]() $\omega $
with a well-orderable base
$\omega $
with a well-orderable base
![]() $\mathscr {B}=\{B_{\alpha }:\alpha <\kappa \}$
, where
$\mathscr {B}=\{B_{\alpha }:\alpha <\kappa \}$
, where
![]() $\kappa $
is an infinite well-ordered cardinal number. By Claim 4.2, we obtain that
$\kappa $
is an infinite well-ordered cardinal number. By Claim 4.2, we obtain that
![]() $\aleph _{1}\le \kappa $
. Since
$\aleph _{1}\le \kappa $
. Since
![]() $\kappa =|\mathscr {B}|\leq |\mathscr {V}|=2^{\aleph _{0}}$
, we conclude that
$\kappa =|\mathscr {B}|\leq |\mathscr {V}|=2^{\aleph _{0}}$
, we conclude that
![]() $\aleph _{1}\le 2^{\aleph _{0}}$
, as required.
$\aleph _{1}\le 2^{\aleph _{0}}$
, as required.
(iii)
![]() $\Rightarrow $
(iv) [Reference Specker25] Assume that
$\Rightarrow $
(iv) [Reference Specker25] Assume that
![]() $\aleph _{1}\le 2^{\aleph _{0}}$
. Let
$\aleph _{1}\le 2^{\aleph _{0}}$
. Let
![]() $H:\omega _{1}\to 2^{\omega }$
be an injection. We argue by contradiction that (iv) holds. So, since in
$H:\omega _{1}\to 2^{\omega }$
be an injection. We argue by contradiction that (iv) holds. So, since in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $|\mathbb {R}|=|(2^{\omega })^{\omega }|$
, we assume that
$|\mathbb {R}|=|(2^{\omega })^{\omega }|$
, we assume that
where
![]() $C_{i}$
is countable for all
$C_{i}$
is countable for all
![]() $i\in \omega $
. For every
$i\in \omega $
. For every
![]() $i\in \omega $
, we let
$i\in \omega $
, we let
![]() $G_{i}:C_{i}\to 2^{\omega }$
be the mapping defined by
$G_{i}:C_{i}\to 2^{\omega }$
be the mapping defined by
Since, for every
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $C_{i}$
is countable, so is
$C_{i}$
is countable, so is
![]() $G_{i}(C_{i})$
. We define an
$G_{i}(C_{i})$
. We define an
![]() $F\in (2^{\omega })^{\omega }$
by letting, for all
$F\in (2^{\omega })^{\omega }$
by letting, for all
![]() $i\in \omega $
,
$i\in \omega $
,
Note that, for every
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $\lambda _{i}$
is well defined; otherwise, for some
$\lambda _{i}$
is well defined; otherwise, for some
![]() $i\in \omega $
,
$i\in \omega $
,
![]() $H(\lambda )\in G_{i}(C_{i})$
for all
$H(\lambda )\in G_{i}(C_{i})$
for all
![]() $\lambda \in \aleph _{1}$
, and thus (since H is injective)
$\lambda \in \aleph _{1}$
, and thus (since H is injective)
![]() $\aleph _{1}=|H(\omega _{1})|\leq |G_{i}(C_{i})|\le \aleph _{0}$
, which is a contradiction. It follows that
$\aleph _{1}=|H(\omega _{1})|\leq |G_{i}(C_{i})|\le \aleph _{0}$
, which is a contradiction. It follows that
and thus
![]() $F\not \in \bigcup \{C_{i}:i\in \omega \}=(2^{\omega })^{\omega }$
, a contradiction. Therefore, (iv) holds, as required.
$F\not \in \bigcup \{C_{i}:i\in \omega \}=(2^{\omega })^{\omega }$
, a contradiction. Therefore, (iv) holds, as required.
The last assertion of the theorem follows from the subsequent facts:
-
(a) In [Reference Herzberg, Kanovei, Katz and Lyubetsky9], it was shown that
 $\mathsf {UF_{wob}}(\omega )$
does not imply
$\mathsf {UF_{wob}}(\omega )$
does not imply
 $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(b) In Feferman’s model
 $\mathcal {M}2$
of [Reference Howard and Rubin11], “
$\mathcal {M}2$
of [Reference Howard and Rubin11], “
 $\aleph _{1}\le 2^{\aleph _{0}}$
” is true, whereas
$\aleph _{1}\le 2^{\aleph _{0}}$
” is true, whereas
 $\mathsf {UF}(\omega )$
is false in
$\mathsf {UF}(\omega )$
is false in
 $\mathcal {M}2$
. Therefore,
$\mathcal {M}2$
. Therefore,
 $\mathsf {UF_{wob}}(\omega )$
is also false in
$\mathsf {UF_{wob}}(\omega )$
is also false in
 $\mathcal {M}2$
.
$\mathcal {M}2$
. -
(c) (iv) is true in Solovay’s model
 $L(\mathbb {R})$
(labeled as Model
$L(\mathbb {R})$
(labeled as Model
 $\mathcal {M}5(\aleph )$
in [Reference Howard and Rubin11]—also see the proof of the forthcoming Theorem 5.13 for the description of
$\mathcal {M}5(\aleph )$
in [Reference Howard and Rubin11]—also see the proof of the forthcoming Theorem 5.13 for the description of
 $L(\mathbb {R})$
), whereas
$L(\mathbb {R})$
), whereas
 $\aleph _{1}\nleq 2^{\aleph _{0}}$
in
$\aleph _{1}\nleq 2^{\aleph _{0}}$
in
 $L(\mathbb {R})$
(see [Reference Howard and Rubin11]).
$L(\mathbb {R})$
(see [Reference Howard and Rubin11]).
The above arguments complete the proof of the theorem.
Remark 4.3. Note that in view of Claim 4.2 (of the proof of Theorem 4.1),
![]() $\mathsf {CH}$
implies the statement “No free ultrafilter on
$\mathsf {CH}$
implies the statement “No free ultrafilter on
![]() $\omega $
has a base of cardinality
$\omega $
has a base of cardinality
![]() $<2^{\aleph _{0}}$
”. The open problem of the deductive strength of the principle “No free ultrafilter on
$<2^{\aleph _{0}}$
”. The open problem of the deductive strength of the principle “No free ultrafilter on
![]() $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
![]() $<2^{\aleph _{0}}$
”, which is introduced in this paper, will be investigated in the forthcoming Subsection 5.2. Among other results therein, we will show that the latter principle does not imply back
$<2^{\aleph _{0}}$
”, which is introduced in this paper, will be investigated in the forthcoming Subsection 5.2. Among other results therein, we will show that the latter principle does not imply back
![]() $\mathsf {CH}$
(see Theorem 5.23).
$\mathsf {CH}$
(see Theorem 5.23).
As a corollary to Theorem 4.1, we have the following result.
Corollary 4.4. The following hold
![]() $:$
$:$
-
(i)
 $\mathsf {UF_{wob}}(\omega ) +\mathsf {CUT}(\mathbb {R})$
implies “
$\mathsf {UF_{wob}}(\omega ) +\mathsf {CUT}(\mathbb {R})$
implies “
 $\aleph _{1}$
is regular”.
$\aleph _{1}$
is regular”. -
(ii) Neither
 $\mathsf {CUT}(\mathbb {R})$
nor “
$\mathsf {CUT}(\mathbb {R})$
nor “
 $\aleph _{1}$
is regular” imply
$\aleph _{1}$
is regular” imply
 $\mathsf {UF}(\omega )$
(and thus
$\mathsf {UF}(\omega )$
(and thus
 $\mathsf {UF_{wob}}(\omega )$
) in
$\mathsf {UF_{wob}}(\omega )$
) in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. (i) By Theorem 4.1, we have
![]() $\aleph _{1}\le 2^{\aleph _{0}}$
. This, together with
$\aleph _{1}\le 2^{\aleph _{0}}$
. This, together with
![]() $\mathsf {CUT}(\mathbb {R})$
, yields
$\mathsf {CUT}(\mathbb {R})$
, yields
![]() $\aleph _{1}$
is regular.
$\aleph _{1}$
is regular.
(ii) Both
![]() $\mathsf {CUT}(\mathbb {R})$
and “
$\mathsf {CUT}(\mathbb {R})$
and “
![]() $\aleph _{1}$
is regular” are true in Feferman’s model
$\aleph _{1}$
is regular” are true in Feferman’s model
![]() $\mathcal {M}2$
of [Reference Howard and Rubin11] (as well as in Solovay’s model
$\mathcal {M}2$
of [Reference Howard and Rubin11] (as well as in Solovay’s model
![]() $\mathcal {M}5(\aleph )$
of [Reference Howard and Rubin11], in which
$\mathcal {M}5(\aleph )$
of [Reference Howard and Rubin11], in which
![]() $\aleph _{1}\not \leq 2^{\aleph _{0}}$
), whereas
$\aleph _{1}\not \leq 2^{\aleph _{0}}$
), whereas
![]() $\mathsf {UF}(\omega )$
is false in
$\mathsf {UF}(\omega )$
is false in
![]() $\mathcal {M}2$
(and in
$\mathcal {M}2$
(and in
![]() $\mathcal {M}5(\aleph )$
); see [Reference Howard and Rubin11]. Thus,
$\mathcal {M}5(\aleph )$
); see [Reference Howard and Rubin11]. Thus,
![]() $\mathsf {UF_{wob}}(\omega )$
is false in
$\mathsf {UF_{wob}}(\omega )$
is false in
![]() $\mathcal {M}2$
(and in
$\mathcal {M}2$
(and in
![]() $\mathcal {M}5(\aleph )$
) also.
$\mathcal {M}5(\aleph )$
) also.
Theorem 4.5. The following hold
![]() $:$
$:$
-
(i) [Reference Hall, Keremedis and Tachtsis6]
 $\mathsf {UF}(\omega )$
if and only if
$\mathsf {UF}(\omega )$
if and only if
 $\mathsf {UF}(\mathbb {R})$
if and only if “every countable filter base on
$\mathsf {UF}(\mathbb {R})$
if and only if “every countable filter base on
 $\omega $
can be extended to an ultrafilter on
$\omega $
can be extended to an ultrafilter on
 $\omega $
”.Footnote
3
$\omega $
”.Footnote
3
-
(ii)
 $\mathsf {UF_{wob}}(\omega )$
if and only if
$\mathsf {UF_{wob}}(\omega )$
if and only if
 $\mathsf {UF_{wob}}(\mathbb {R})$
if and only if “every countable filter base on
$\mathsf {UF_{wob}}(\mathbb {R})$
if and only if “every countable filter base on
 $\omega $
can be extended to an ultrafilter on
$\omega $
can be extended to an ultrafilter on
 $\omega $
with a well-orderable base”.
$\omega $
with a well-orderable base”.In particular, given an infinite well-ordered cardinal number
 $\kappa $
, “there exists a free ultrafilter on
$\kappa $
, “there exists a free ultrafilter on
 $\omega $
with a base of cardinality
$\omega $
with a base of cardinality
 $\kappa $
” if and only if “there exists a free ultrafilter on
$\kappa $
” if and only if “there exists a free ultrafilter on
 $\mathbb {R}$
with a base of cardinality
$\mathbb {R}$
with a base of cardinality
 $\kappa $
”.
$\kappa $
”.
Proof. The proof of (ii) is almost identical to the proofs of [Reference Hall, Keremedis and Tachtsis6, Theorem 3.1] and [Reference Hall, Keremedis and Tachtsis6, Theorem 3.3] (“
![]() $\mathsf {UF}(\omega )$
if and only if “every countable filter base on
$\mathsf {UF}(\omega )$
if and only if “every countable filter base on
![]() $\omega $
can be extended to an ultrafilter on
$\omega $
can be extended to an ultrafilter on
![]() $\omega $
””). We thus refer the interested reader to [Reference Hall, Keremedis and Tachtsis6] for filling in the details.
$\omega $
””). We thus refer the interested reader to [Reference Hall, Keremedis and Tachtsis6] for filling in the details.
5 Main results
5.1 Filters on
 $\omega $
and
$\omega $
and
 $\mathbb {R}$
with well-orderable bases and
$\mathbb {R}$
with well-orderable bases and
 $\mathsf {UF_{wob}}(\omega )$
$\mathsf {UF_{wob}}(\omega )$
In Theorem 5.1 below, we show that, for any infinite linearly ordered set X,
![]() $\mathsf {AC}(\wp (X))$
is equivalent to each of “every filter base on X can be well ordered” and “every filter on X has a well-orderable base”, and that
$\mathsf {AC}(\wp (X))$
is equivalent to each of “every filter base on X can be well ordered” and “every filter on X has a well-orderable base”, and that
![]() $\mathsf {CH}$
, and thus “every filter on
$\mathsf {CH}$
, and thus “every filter on
![]() $\omega $
has a well-orderable base” (equivalently,
$\omega $
has a well-orderable base” (equivalently,
![]() $\mathsf {AC}(\mathbb {R})$
), does not imply “every filter on
$\mathsf {AC}(\mathbb {R})$
), does not imply “every filter on
![]() $\mathbb {R}$
has a well-orderable base” (equivalently,
$\mathbb {R}$
has a well-orderable base” (equivalently,
![]() $\mathsf {AC}(\wp (\mathbb {R}))$
) in
$\mathsf {AC}(\wp (\mathbb {R}))$
) in
![]() $\mathsf {ZF}$
; for the latter independence result, we will construct a suitable symmetric model. For the reader’s convenience, we have included an appendix with a brief account on the construction of symmetric extension models; a detailed account can be found in Halbeisen [Reference Halbeisen5, Chapter 17] and Jech [Reference Jech13, Chapter 5].
$\mathsf {ZF}$
; for the latter independence result, we will construct a suitable symmetric model. For the reader’s convenience, we have included an appendix with a brief account on the construction of symmetric extension models; a detailed account can be found in Halbeisen [Reference Halbeisen5, Chapter 17] and Jech [Reference Jech13, Chapter 5].
Theorem 5.1.
-
(i) Let X be an infinite linearly orderable set. The following are equivalent
 $:$
$:$
-
(a)
 $\mathsf {AC}(\wp (X))$
.
$\mathsf {AC}(\wp (X))$
. -
(b)
 $\wp (X)$
can be well ordered.
$\wp (X)$
can be well ordered. -
(c) Every filter base on X can be well ordered.
-
(d) Every filter on X has a well-orderable base.
In particular,
 $\mathsf {AC}(\mathbb {R})$
is equivalent to each of “every filter base on
$\mathsf {AC}(\mathbb {R})$
is equivalent to each of “every filter base on
 $\omega $
can be well ordered” and “every filter on
$\omega $
can be well ordered” and “every filter on
 $\omega $
has a well-orderable base”, and
$\omega $
has a well-orderable base”, and
 $\mathsf {AC}(\wp (\mathbb {R}))$
is equivalent to each of “every filter base on
$\mathsf {AC}(\wp (\mathbb {R}))$
is equivalent to each of “every filter base on
 $\mathbb {R}$
can be well ordered” and “every filter on
$\mathbb {R}$
can be well ordered” and “every filter on
 $\mathbb {R}$
has a well-orderable base”.
$\mathbb {R}$
has a well-orderable base”. -
-
(ii)
 $\mathsf {CH}$
, and thus (by part (i)) “every filter on
$\mathsf {CH}$
, and thus (by part (i)) “every filter on
 $\omega $
has a well-orderable base”, does not imply “every filter on
$\omega $
has a well-orderable base”, does not imply “every filter on
 $\mathbb {R}$
has a well-orderable base” in
$\mathbb {R}$
has a well-orderable base” in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. (i) By hypothesis, let
![]() $\preceq $
be a linear order on X.
$\preceq $
be a linear order on X.
(a)
![]() $\Longleftrightarrow $
(b) This is well known and, moreover, is true for any infinite set Y in place of
$\Longleftrightarrow $
(b) This is well known and, moreover, is true for any infinite set Y in place of
![]() $\wp (X)$
.
$\wp (X)$
.
(b)
![]() $\Rightarrow $
(c)
$\Rightarrow $
(c)
![]() $\Rightarrow $
(d) These are straightforward.
$\Rightarrow $
(d) These are straightforward.
(d)
![]() $\Rightarrow $
(a) We first prove the following lemma.
$\Rightarrow $
(a) We first prove the following lemma.
Lemma 5.2. “Every filter on X has a well-orderable base” implies
![]() $\mathsf {AC}(X)$
.
$\mathsf {AC}(X)$
.
Proof. Since
![]() $\preceq $
is a linear ordering of X, the family of all non-empty finite subsets of X has a choice function. So, it suffices to show that the family
$\preceq $
is a linear ordering of X, the family of all non-empty finite subsets of X has a choice function. So, it suffices to show that the family
![]() $\wp ^{\infty }(X)$
of all infinite subsets of X has a choice function. To this end, let
$\wp ^{\infty }(X)$
of all infinite subsets of X has a choice function. To this end, let
![]() $\mathscr {F}$
be the Fréchet filter on X, that is,
$\mathscr {F}$
be the Fréchet filter on X, that is,
By hypothesis,
![]() $\mathscr {F}$
has a well-orderable base, say
$\mathscr {F}$
has a well-orderable base, say
![]() $\mathscr {B}=\{B_{\alpha }:\alpha <\kappa \}$
for some well-ordered cardinal
$\mathscr {B}=\{B_{\alpha }:\alpha <\kappa \}$
for some well-ordered cardinal
![]() $\kappa $
. We assert the following:
$\kappa $
. We assert the following:
To see this, fix
![]() $Y\in \wp ^{\infty }(X)$
. Let
$Y\in \wp ^{\infty }(X)$
. Let
![]() $y\in Y$
. Then
$y\in Y$
. Then
![]() $X\setminus \{y\}\in \mathscr {F}$
, so since
$X\setminus \{y\}\in \mathscr {F}$
, so since
![]() $\mathscr {B}$
is a base for
$\mathscr {B}$
is a base for
![]() $\mathscr {F}$
, there exists
$\mathscr {F}$
, there exists
![]() $\alpha <\kappa $
such that
$\alpha <\kappa $
such that
![]() $B_{\alpha }\subseteq X\setminus \{y\}$
. As
$B_{\alpha }\subseteq X\setminus \{y\}$
. As
![]() $y\in Y$
, we obtain that
$y\in Y$
, we obtain that
![]() $|Y\setminus B_{\alpha }|>0$
. Therefore, (2) holds, as asserted.
$|Y\setminus B_{\alpha }|>0$
. Therefore, (2) holds, as asserted.
By (2), for every
![]() $Y\in \wp ^{\infty }(X)$
, let
$Y\in \wp ^{\infty }(X)$
, let
Since
![]() $\mathscr {B}\subseteq \mathscr {F}$
, we have that
$\mathscr {B}\subseteq \mathscr {F}$
, we have that
Then the function
![]() $h:\wp ^{\infty }(X)\rightarrow \bigcup \wp ^{\infty }(X)$
defined by
$h:\wp ^{\infty }(X)\rightarrow \bigcup \wp ^{\infty }(X)$
defined by
is a choice function for
![]() $\wp ^{\infty }(X)$
. Thus,
$\wp ^{\infty }(X)$
. Thus,
![]() $\mathsf {AC}(X)$
is true, as required.
$\mathsf {AC}(X)$
is true, as required.
By (d) and Lemma 5.2, we conclude that X is well orderable. We recall here the following
![]() $\mathsf {ZF}$
-fact (see Rubin and Rubin [Reference Rubin and Rubin23, Theorem 5.5, p. 76]):
$\mathsf {ZF}$
-fact (see Rubin and Rubin [Reference Rubin and Rubin23, Theorem 5.5, p. 76]):
(*) The power set of a well-ordered set can be linearly ordered.
By (*) and the fact that X is well orderable, we infer that
![]() $\wp (X)$
is linearly orderable. By (the second paragraph of) Remark 1.10, let
$\wp (X)$
is linearly orderable. By (the second paragraph of) Remark 1.10, let
![]() $\mathcal {\mathcal {I}}$
be an independent family in X of cardinality
$\mathcal {\mathcal {I}}$
be an independent family in X of cardinality
![]() $|\wp (X)|$
. Since
$|\wp (X)|$
. Since
![]() $\wp (X)$
is linearly orderable, so is its subset
$\wp (X)$
is linearly orderable, so is its subset
![]() $\mathcal {I}$
. Our plan is to show that
$\mathcal {I}$
. Our plan is to show that
![]() $\mathcal {I}$
is well orderable, which will give us that
$\mathcal {I}$
is well orderable, which will give us that
![]() $\wp (X)$
is well orderable since
$\wp (X)$
is well orderable since
![]() $|\wp (X)|=|\mathcal {I}|$
. By way of contradiction, we assume that
$|\wp (X)|=|\mathcal {I}|$
. By way of contradiction, we assume that
![]() $\mathcal {I}$
is not well orderable. Let
$\mathcal {I}$
is not well orderable. Let
Since
![]() $\mathcal {I}$
is independent,
$\mathcal {I}$
is independent,
![]() $\mathscr {B}$
is a filter base. Let
$\mathscr {B}$
is a filter base. Let
![]() $\mathscr {F}_{\mathscr {B}}$
be the filter on X generated by
$\mathscr {F}_{\mathscr {B}}$
be the filter on X generated by
![]() $\mathscr {B}$
. By hypothesis,
$\mathscr {B}$
. By hypothesis,
![]() $\mathscr {F}_{\mathscr {B}}$
has a well-orderable base, say
$\mathscr {F}_{\mathscr {B}}$
has a well-orderable base, say
for some well-ordered cardinal
![]() $\kappa $
. For every
$\kappa $
. For every
![]() $\alpha <\kappa $
, we let
$\alpha <\kappa $
, we let
As
![]() $\mathcal {I}\subseteq \mathscr {F}_{\mathscr {B}}$
and
$\mathcal {I}\subseteq \mathscr {F}_{\mathscr {B}}$
and
![]() $\mathscr {C}$
is a base for
$\mathscr {C}$
is a base for
![]() $\mathscr {F}_{\mathscr {B}}$
, we have
$\mathscr {F}_{\mathscr {B}}$
, we have
Since
![]() $\mathcal {I}$
is not well orderable and the union of a well-ordered family of finite subsets of
$\mathcal {I}$
is not well orderable and the union of a well-ordered family of finite subsets of
![]() $\mathcal {I}$
is well orderable (because
$\mathcal {I}$
is well orderable (because
![]() $\mathcal {I}$
is linearly orderable), it follows that, for some
$\mathcal {I}$
is linearly orderable), it follows that, for some
![]() $\alpha <\kappa $
,
$\alpha <\kappa $
,
![]() $\mathcal {D}_{\alpha }$
is infinite. As
$\mathcal {D}_{\alpha }$
is infinite. As
![]() $\mathscr {B}$
is a base for
$\mathscr {B}$
is a base for
![]() $\mathscr {F}_{\mathscr {B}}$
and
$\mathscr {F}_{\mathscr {B}}$
and
![]() $C_{\alpha }\in \mathscr {F}_{\mathscr {B}}$
, there exists
$C_{\alpha }\in \mathscr {F}_{\mathscr {B}}$
, there exists
![]() $\mathcal {Q}\in [\mathcal {I}]^{<\omega }\setminus \{\emptyset \}$
such that
$\mathcal {Q}\in [\mathcal {I}]^{<\omega }\setminus \{\emptyset \}$
such that
![]() $\bigcap \mathcal {Q}\subseteq C_{\alpha }$
. Since
$\bigcap \mathcal {Q}\subseteq C_{\alpha }$
. Since
![]() $\mathcal {D}_{\alpha }$
is infinite and
$\mathcal {D}_{\alpha }$
is infinite and
![]() $\mathcal {Q}$
is finite, there exists
$\mathcal {Q}$
is finite, there exists
![]() $z\in \mathcal {D}_{\alpha }\setminus \mathcal {Q}$
. It follows that
$z\in \mathcal {D}_{\alpha }\setminus \mathcal {Q}$
. It follows that
![]() $\mathcal {Q},\{z\}$
are two disjoint finite subsets of the independent family
$\mathcal {Q},\{z\}$
are two disjoint finite subsets of the independent family
![]() $\mathcal {I}$
such that
$\mathcal {I}$
such that
But then, we have
contradicting the fact that
![]() $\mathcal {I}$
is independent. From the above arguments, we conclude that
$\mathcal {I}$
is independent. From the above arguments, we conclude that
![]() $\mathcal {I}$
is well orderable, and thus so is
$\mathcal {I}$
is well orderable, and thus so is
![]() $\wp (X)$
since
$\wp (X)$
since
![]() $|\wp (X)|=|\mathcal {I}|$
. Therefore,
$|\wp (X)|=|\mathcal {I}|$
. Therefore,
![]() $\mathsf {AC}(\wp (X))$
holds, as required.
$\mathsf {AC}(\wp (X))$
holds, as required.
(ii) For the independence result, we will construct a new symmetric model of
![]() $\mathsf {ZF}$
and prove that it has the required properties. To this end, we start with a countable transitive model M of
$\mathsf {ZF}$
and prove that it has the required properties. To this end, we start with a countable transitive model M of
![]() $\mathsf {ZFC}+\mathsf {CH}$
. As a forcing notion, we use the set
$\mathsf {ZFC}+\mathsf {CH}$
. As a forcing notion, we use the set
of all countable partial functions from
![]() $\omega \times \omega _{1}\times \omega _{1}$
into
$\omega \times \omega _{1}\times \omega _{1}$
into
![]() $2=\{0,1\}$
equipped with the partial order of reverse inclusion, that is, for all
$2=\{0,1\}$
equipped with the partial order of reverse inclusion, that is, for all
![]() $p,q\in \mathbb {P}$
,
$p,q\in \mathbb {P}$
,
![]() $p\leq q\Longleftrightarrow p\supseteq q$
. Note that the maximum element
$p\leq q\Longleftrightarrow p\supseteq q$
. Note that the maximum element
![]() $\mathbf {1}_{\mathbb {P}}$
of
$\mathbf {1}_{\mathbb {P}}$
of
![]() $\mathbb {P}$
is the empty function. Let G be a
$\mathbb {P}$
is the empty function. Let G be a
![]() $\mathbb {P}$
-generic filter over M, and also let
$\mathbb {P}$
-generic filter over M, and also let
![]() $M[G]$
be the corresponding generic extension model of M. Since
$M[G]$
be the corresponding generic extension model of M. Since
![]() $\aleph _{1}$
is a regular cardinal,
$\aleph _{1}$
is a regular cardinal,
![]() $(\mathbb {P},\leq )$
is
$(\mathbb {P},\leq )$
is
![]() $\aleph _{1}$
-closed, that is, for every
$\aleph _{1}$
-closed, that is, for every
![]() $\gamma \in \aleph _{1}$
and every decreasing sequence
$\gamma \in \aleph _{1}$
and every decreasing sequence
![]() $(p_{\xi })_{\xi <\gamma }$
of elements of
$(p_{\xi })_{\xi <\gamma }$
of elements of
![]() $\mathbb {P}$
, there exists
$\mathbb {P}$
, there exists
![]() $q\in \mathbb {P}$
such that
$q\in \mathbb {P}$
such that
![]() $q\leq p_{\xi }$
for all
$q\leq p_{\xi }$
for all
![]() $\xi <\gamma $
. It follows from Kunen [Reference Kunen16, Theorem 6.14, p. 214] that no new functions
$\xi <\gamma $
. It follows from Kunen [Reference Kunen16, Theorem 6.14, p. 214] that no new functions
![]() $g:\omega \rightarrow 2$
, and thus no new reals, are added. Moreover, by [Reference Kunen16, Corollary 6.15, p. 215], we have that
$g:\omega \rightarrow 2$
, and thus no new reals, are added. Moreover, by [Reference Kunen16, Corollary 6.15, p. 215], we have that
![]() $(\mathbb {P},\leq )$
preserves cofinalities
$(\mathbb {P},\leq )$
preserves cofinalities
![]() $\leq \aleph _{1}$
, and hence cardinals
$\leq \aleph _{1}$
, and hence cardinals
![]() $\leq \aleph _{1}$
. Therefore,
$\leq \aleph _{1}$
. Therefore,
![]() $\mathsf {CH}$
is true in
$\mathsf {CH}$
is true in
![]() $M[G]$
, as well as in every model N with
$M[G]$
, as well as in every model N with
![]() $M\subseteq N\subseteq M[G]$
.
$M\subseteq N\subseteq M[G]$
.
Forcing with
![]() $\mathbb {P}$
over M yields, in
$\mathbb {P}$
over M yields, in
![]() $M[G]$
, the following generic subsets of
$M[G]$
, the following generic subsets of
![]() $\omega _{1}$
:
$\omega _{1}$
:
Note that, via standard density arguments, the family
is independent in
![]() $\omega _{1}$
. The sets
$\omega _{1}$
. The sets
![]() $a_{n,k}$
,
$a_{n,k}$
,
![]() $(n,k)\in \omega \times \omega _{1}$
, and
$(n,k)\in \omega \times \omega _{1}$
, and
![]() $\mathcal {A}$
, have respectively the following
$\mathcal {A}$
, have respectively the following
![]() $\mathbb {P}$
-names:
$\mathbb {P}$
-names:
and
Every permutation
![]() $\phi $
of
$\phi $
of
![]() $\omega \times \omega _{1}$
induces an order-automorphism of
$\omega \times \omega _{1}$
induces an order-automorphism of
![]() $(\mathbb {P},\leq )$
by requiring, for every
$(\mathbb {P},\leq )$
by requiring, for every
![]() $p\in \mathbb {P}$
, the following:
$p\in \mathbb {P}$
, the following:
 $$ \begin{align} \begin{aligned} \operatorname{\mathrm{{dom}}}\phi(p)&=\{(\phi(i,j),k):(i,j,k)\in\operatorname{\mathrm{{dom}}}(p)\},\\ \phi(p)(\phi(i,j),k)&=p(i,j,k). \end{aligned} \end{align} $$
$$ \begin{align} \begin{aligned} \operatorname{\mathrm{{dom}}}\phi(p)&=\{(\phi(i,j),k):(i,j,k)\in\operatorname{\mathrm{{dom}}}(p)\},\\ \phi(p)(\phi(i,j),k)&=p(i,j,k). \end{aligned} \end{align} $$
Let
![]() $\mathcal G$
be the group of all order-automorphisms of
$\mathcal G$
be the group of all order-automorphisms of
![]() $(\mathbb {P},\le )$
which are induced by permutations
$(\mathbb {P},\le )$
which are induced by permutations
![]() $\phi $
of
$\phi $
of
![]() $\omega \times \omega _{1}$
, as in (3). Note that
$\omega \times \omega _{1}$
, as in (3). Note that
By (4), we obtain that
For every
![]() $E\in [\omega \times \omega _{1}]^{<\omega }$
, we let
$E\in [\omega \times \omega _{1}]^{<\omega }$
, we let
![]() $\operatorname {\mathrm {{fix}}}_{\mathcal G}(E)=\{\phi \in \mathcal G:{\forall e\in E}(\phi (e)=e)\}$
, and we also let
$\operatorname {\mathrm {{fix}}}_{\mathcal G}(E)=\{\phi \in \mathcal G:{\forall e\in E}(\phi (e)=e)\}$
, and we also let
![]() $\Gamma $
be the filter of subgroups of
$\Gamma $
be the filter of subgroups of
![]() $\mathcal G$
generated by the filter base
$\mathcal G$
generated by the filter base
![]() $\{\operatorname {\mathrm {{fix}}}_{\mathcal G}(E):E\in [\omega \times \omega _{1}]^{<\omega }\}$
. It is not hard to verify that
$\{\operatorname {\mathrm {{fix}}}_{\mathcal G}(E):E\in [\omega \times \omega _{1}]^{<\omega }\}$
. It is not hard to verify that
![]() $\Gamma $
is a normal filter on
$\Gamma $
is a normal filter on
![]() $\mathcal {G}$
. If
$\mathcal {G}$
. If
![]() $\dot {x}$
is a
$\dot {x}$
is a
![]() $\mathbb {P}$
-name and
$\mathbb {P}$
-name and
![]() $E\in [\omega \times \omega _{1}]^{<\omega }$
is such that
$E\in [\omega \times \omega _{1}]^{<\omega }$
is such that
![]() $\operatorname {\mathrm {{fix}}}_{\mathcal G}(E)\subseteq \operatorname {\mathrm {{sym}}}_{\mathcal {G}}(\dot {x})$
(
$\operatorname {\mathrm {{fix}}}_{\mathcal G}(E)\subseteq \operatorname {\mathrm {{sym}}}_{\mathcal {G}}(\dot {x})$
(
![]() $=\{\phi \in \mathcal {G}:\phi (\dot {x})=\dot {x}\}$
), then we call E a support of
$=\{\phi \in \mathcal {G}:\phi (\dot {x})=\dot {x}\}$
), then we call E a support of
![]() $\dot {x}$
. Let
$\dot {x}$
. Let
be the symmetric extension model of M. By the definitions of
![]() $\Gamma $
and
$\Gamma $
and
![]() $\operatorname {\mathrm {{HS}}}^{\Gamma }$
, it follows that every
$\operatorname {\mathrm {{HS}}}^{\Gamma }$
, it follows that every
![]() $\dot {x}\in \operatorname {\mathrm {{HS}}}^{\Gamma }$
has a support in the above sense.
$\dot {x}\in \operatorname {\mathrm {{HS}}}^{\Gamma }$
has a support in the above sense.
In view of the observations at the beginning of the proof (of part (ii)), we have:
and thus
Claim 5.3. For every
![]() $(n,m)\in \omega \times \omega _{1}$
,
$(n,m)\in \omega \times \omega _{1}$
,
![]() $a_{n,m}\in N$
, and also
$a_{n,m}\in N$
, and also
![]() $\mathcal {A}\in N$
.
$\mathcal {A}\in N$
.
Proof. Fix
![]() $(n,m)\in \omega \times \omega _{1}$
. By (4), it readily follows that
$(n,m)\in \omega \times \omega _{1}$
. By (4), it readily follows that
![]() $E=\{(n,m)\}$
is a support of
$E=\{(n,m)\}$
is a support of
![]() $\dot {a}_{n,m}$
, and thus
$\dot {a}_{n,m}$
, and thus
![]() $\dot {a}_{n,m}$
is
$\dot {a}_{n,m}$
is
![]() $\Gamma $
-symmetric. Since, for every
$\Gamma $
-symmetric. Since, for every
![]() $(\check {k},p)\in \dot {a}_{n,m}$
,
$(\check {k},p)\in \dot {a}_{n,m}$
,
![]() $\check {k}\in \operatorname {\mathrm {{HS}}}^{\Gamma }$
, we conclude that
$\check {k}\in \operatorname {\mathrm {{HS}}}^{\Gamma }$
, we conclude that
![]() $a_{n,m}\in N$
.
$a_{n,m}\in N$
.
The fact that
![]() $\mathcal {A}\in N$
follows immediately from (5).
$\mathcal {A}\in N$
follows immediately from (5).
Claim 5.4. The set
![]() $\mathcal {A}=\{a_{n,m}:(n,m)\in \omega \times \omega _{1}\}$
is not well orderable in N.
$\mathcal {A}=\{a_{n,m}:(n,m)\in \omega \times \omega _{1}\}$
is not well orderable in N.
Proof. Assume the contrary. Since
![]() $|\mathcal {A}|=\aleph _{1}$
in
$|\mathcal {A}|=\aleph _{1}$
in
![]() $M[G]$
, our assumption yields
$M[G]$
, our assumption yields
![]() $|\mathcal {A}|=\aleph _{1}$
in N also. So, let
$|\mathcal {A}|=\aleph _{1}$
in N also. So, let
![]() $f:\omega _{1}\rightarrow \mathcal {A}$
be a bijection in N. Let
$f:\omega _{1}\rightarrow \mathcal {A}$
be a bijection in N. Let
![]() $\dot {f}$
be an
$\dot {f}$
be an
![]() $\operatorname {\mathrm {{HS}}}^{\Gamma }$
-name for f. There exists
$\operatorname {\mathrm {{HS}}}^{\Gamma }$
-name for f. There exists
![]() $p\in G$
such that
$p\in G$
such that
Let
![]() $E\in [\omega \times \omega _{1}]^{<\omega }$
be a support of
$E\in [\omega \times \omega _{1}]^{<\omega }$
be a support of
![]() $\dot {f}$
. Since f is a bijection and E is finite, there exist
$\dot {f}$
. Since f is a bijection and E is finite, there exist
![]() $i\in \omega _{1}$
and
$i\in \omega _{1}$
and
![]() $(n_{0},m_{0})\in \omega \times \omega _{1}$
such that
$(n_{0},m_{0})\in \omega \times \omega _{1}$
such that
![]() $E\cap (\{n_{0}\}\times \omega _{1})=\emptyset $
and
$E\cap (\{n_{0}\}\times \omega _{1})=\emptyset $
and
![]() $f(i)=a_{n_{0},m_{0}}$
. Let
$f(i)=a_{n_{0},m_{0}}$
. Let
![]() $q\in G$
be such that
$q\in G$
be such that
![]() $q\leq p$
and
$q\leq p$
and
Since
![]() $|q|<\aleph _{1}$
, there exists
$|q|<\aleph _{1}$
, there exists
![]() $k\in \omega _{1}$
such that
$k\in \omega _{1}$
such that
![]() $k>m_{0}$
and, for all
$k>m_{0}$
and, for all
![]() $i\in \omega _{1}$
with
$i\in \omega _{1}$
with
![]() $i\geq k$
,
$i\geq k$
,
![]() $(n_{0},i)\not \in \operatorname {\mathrm {{dom}}}(\operatorname {\mathrm {{dom}}}(q))$
. Let
$(n_{0},i)\not \in \operatorname {\mathrm {{dom}}}(\operatorname {\mathrm {{dom}}}(q))$
. Let
![]() $\eta :[0,k)\rightarrow [k,2k)$
be an order-isomorphism. Then
$\eta :[0,k)\rightarrow [k,2k)$
be an order-isomorphism. Then
![]() $\eta $
induces a permutation
$\eta $
induces a permutation
![]() $\eta ^{*}$
of
$\eta ^{*}$
of
![]() $\omega _{1}$
defined by
$\omega _{1}$
defined by
 $$\begin{align*}\eta^{*}(i)= \begin{cases} \eta(i), & \text{if }i\in [0,k);\\ \eta^{-1}(i), & \text{if }i\in [k,2k);\\ i, & \text{if }2k\leq i. \end{cases} \end{align*}$$
$$\begin{align*}\eta^{*}(i)= \begin{cases} \eta(i), & \text{if }i\in [0,k);\\ \eta^{-1}(i), & \text{if }i\in [k,2k);\\ i, & \text{if }2k\leq i. \end{cases} \end{align*}$$
Note that, as
![]() $m_{0}\in [0,k)$
,
$m_{0}\in [0,k)$
,
![]() $\eta ^{*}(m_{0})>m_{0}$
, since
$\eta ^{*}(m_{0})>m_{0}$
, since
![]() $\eta ^{*}(m_{0})=\eta (m_{0})\in [k,2k)$
. We define a permutation
$\eta ^{*}(m_{0})=\eta (m_{0})\in [k,2k)$
. We define a permutation
![]() $\phi $
of
$\phi $
of
![]() $\omega \times \omega _{1}$
by stipulating, for all
$\omega \times \omega _{1}$
by stipulating, for all
![]() $(n,m)\in \omega \times \omega _{1}$
,
$(n,m)\in \omega \times \omega _{1}$
,
 $$\begin{align*}\phi(n,m)= \begin{cases} (n_{0},\eta^{*}(m)), & \text{if }n=n_{0};\\ (n,m), &\text{if }n\ne n_{0}. \end{cases} \end{align*}$$
$$\begin{align*}\phi(n,m)= \begin{cases} (n_{0},\eta^{*}(m)), & \text{if }n=n_{0};\\ (n,m), &\text{if }n\ne n_{0}. \end{cases} \end{align*}$$
Denoting by
![]() $\phi $
the element of
$\phi $
the element of
![]() $\mathcal {G}$
induced by
$\mathcal {G}$
induced by
![]() $\phi $
, as well as the extension of
$\phi $
, as well as the extension of
![]() $\phi $
to an automorphism of
$\phi $
to an automorphism of
![]() $M^{\mathbb {P}}$
(the class of all
$M^{\mathbb {P}}$
(the class of all
![]() $\mathbb {P}$
-names), we have that the following hold:
$\mathbb {P}$
-names), we have that the following hold:
-
(a)
 $\phi \in \operatorname {\mathrm {{fix}}}_{\mathcal {G}}(E)$
, since
$\phi \in \operatorname {\mathrm {{fix}}}_{\mathcal {G}}(E)$
, since
 $E\cap (\{n_{0}\}\times \omega _{1})=\emptyset $
and
$E\cap (\{n_{0}\}\times \omega _{1})=\emptyset $
and
 $\phi $
fixes
$\phi $
fixes
 $\{n\}\times \omega _{1}$
pointwise for all
$\{n\}\times \omega _{1}$
pointwise for all
 $n\in \omega \setminus \{n_{0}\}$
. It follows that
$n\in \omega \setminus \{n_{0}\}$
. It follows that
 $\phi (\dot {f})=\dot {f}$
, since E is a support of
$\phi (\dot {f})=\dot {f}$
, since E is a support of
 $\dot {f}$
and
$\dot {f}$
and
 $\phi \in \operatorname {\mathrm {{fix}}}_{\mathcal {G}}(E)$
.
$\phi \in \operatorname {\mathrm {{fix}}}_{\mathcal {G}}(E)$
. -
(b)
 $\phi (\dot {a}_{n_{0},m_{0}})=\dot {a}_{\phi (n_{0},m_{0})}=\dot {a}_{n_{0},\eta ^{*}(m_{0})}$
.
$\phi (\dot {a}_{n_{0},m_{0}})=\dot {a}_{\phi (n_{0},m_{0})}=\dot {a}_{n_{0},\eta ^{*}(m_{0})}$
. -
(c)
 $\phi (\dot {\mathcal {A}})=\dot {\mathcal {A}}$
(by (5)).
$\phi (\dot {\mathcal {A}})=\dot {\mathcal {A}}$
(by (5)). -
(d) q and
 $\phi (q)$
are compatible conditions. It follows that
$\phi (q)$
are compatible conditions. It follows that
 $q\cup \phi (q)$
is a well-defined extension of q,
$q\cup \phi (q)$
is a well-defined extension of q,
 $\phi (q)$
, and p (recall that
$\phi (q)$
, and p (recall that
 $q\leq p$
).
$q\leq p$
).
By (7), (a), and (b), we obtain that
By (c) and (d), together with (6), (7) and (8), we conclude that
 $$ \begin{align} &q\cup\phi(q)\Vdash"\dot{f}\text{ is a bijection from }\check{\omega_{1}}\text{ onto }\dot{\mathcal{A}}\text{"}\wedge \dot{f}(\check{i})=\dot{a}_{n_{0},m_{0}}\nonumber\\ &\qquad\qquad\qquad\wedge\dot{f}(\check{i})=\dot{a}_{n_{0},\eta^{*}(m_{0})}. \end{align} $$
$$ \begin{align} &q\cup\phi(q)\Vdash"\dot{f}\text{ is a bijection from }\check{\omega_{1}}\text{ onto }\dot{\mathcal{A}}\text{"}\wedge \dot{f}(\check{i})=\dot{a}_{n_{0},m_{0}}\nonumber\\ &\qquad\qquad\qquad\wedge\dot{f}(\check{i})=\dot{a}_{n_{0},\eta^{*}(m_{0})}. \end{align} $$
But then, (9) clearly yields a contradiction. Therefore,
![]() $\mathcal {A}$
is not well orderable in the model N, as required.
$\mathcal {A}$
is not well orderable in the model N, as required.
Claim 5.5. The principle “Every filter on
![]() $\mathbb {R}$
has a well-orderable base” is false in N.
$\mathbb {R}$
has a well-orderable base” is false in N.
Proof. We first note that, by (*) of the proof of “(i)[(d)
![]() $\Rightarrow $
(a)]”,
$\Rightarrow $
(a)]”,
![]() $\wp (\omega _{1})$
can be linearly ordered in N. Following now the aforementioned proof with
$\wp (\omega _{1})$
can be linearly ordered in N. Following now the aforementioned proof with
![]() $\mathcal {A}$
(
$\mathcal {A}$
(
![]() $=\{a_{n,k}:(n,k)\in \omega \times \omega _{1}\}$
) in place of
$=\{a_{n,k}:(n,k)\in \omega \times \omega _{1}\}$
) in place of
![]() $\mathcal {I}$
therein, and taking into account Claim 5.4, the fact that
$\mathcal {I}$
therein, and taking into account Claim 5.4, the fact that
![]() $\mathcal {A}$
is independent in
$\mathcal {A}$
is independent in
![]() $\omega _{1}$
, and the fact that
$\omega _{1}$
, and the fact that
![]() $\mathcal {A}\subseteq \wp (\omega _{1})$
is linearly orderable in N, we may derive that the filter
$\mathcal {A}\subseteq \wp (\omega _{1})$
is linearly orderable in N, we may derive that the filter
![]() $\mathscr {F}_{\mathscr {B}}$
on
$\mathscr {F}_{\mathscr {B}}$
on
![]() $\omega _{1}$
(generated by
$\omega _{1}$
(generated by
![]() $\mathscr {B}=\{\bigcap \mathcal {Q}:\mathcal {Q}\in [\mathcal {A}]^{<\omega }\setminus \{\emptyset \}\}$
) does not have a well-orderable base in the model N. As
$\mathscr {B}=\{\bigcap \mathcal {Q}:\mathcal {Q}\in [\mathcal {A}]^{<\omega }\setminus \{\emptyset \}\}$
) does not have a well-orderable base in the model N. As
![]() $|\mathbb {R}|=\aleph _{1}$
in N (since
$|\mathbb {R}|=\aleph _{1}$
in N (since
![]() ${N\models \mathsf {CH}}$
), we conclude that “every filter on
${N\models \mathsf {CH}}$
), we conclude that “every filter on
![]() $\mathbb {R}$
has a well-orderable base” is false in N, as required.
$\mathbb {R}$
has a well-orderable base” is false in N, as required.
The above arguments complete the proof of (ii) and of the theorem.
Let us recall here that in the forthcoming Theorem 5.22, we will prove that in
![]() $\mathsf {ZF}$
,
$\mathsf {ZF}$
,
![]() $\mathsf {AC}(\mathbb {R})$
is also equivalent to
$\mathsf {AC}(\mathbb {R})$
is also equivalent to
![]() $\mathsf {BPI_{wob}}(\omega )$
(“Every filter on
$\mathsf {BPI_{wob}}(\omega )$
(“Every filter on
![]() $\omega $
can be extended to an ultrafilter with a well-orderable base”) and that the principle “every ultrafilter on
$\omega $
can be extended to an ultrafilter with a well-orderable base”) and that the principle “every ultrafilter on
![]() $\omega $
has a well-orderable base” is strictly weaker than
$\omega $
has a well-orderable base” is strictly weaker than
![]() $\mathsf {AC}(\mathbb {R})$
.
$\mathsf {AC}(\mathbb {R})$
.
Remark 5.6. We note that the fact that
![]() $\mathsf {AC}(\mathbb {R})$
does not imply
$\mathsf {AC}(\mathbb {R})$
does not imply
![]() $\mathsf {AC}(\wp (\mathbb {R}))$
in
$\mathsf {AC}(\wp (\mathbb {R}))$
in
![]() $\mathsf {ZF}$
was first established by Keremedis and Tachtsis [Reference Keremedis and Tachtsis15]. However, our proof here of the latter independence result is, on the one hand, different since it is modeled on the novel result of Theorem 5.1(i) and its proof, and, on the other hand, it is easier and substantially more informative than the one from [Reference Keremedis and Tachtsis15].
$\mathsf {ZF}$
was first established by Keremedis and Tachtsis [Reference Keremedis and Tachtsis15]. However, our proof here of the latter independence result is, on the one hand, different since it is modeled on the novel result of Theorem 5.1(i) and its proof, and, on the other hand, it is easier and substantially more informative than the one from [Reference Keremedis and Tachtsis15].
As a corollary to Theorem 4.1 and Theorem 5.1, and taking into account the fact (from [Reference Herzberg, Kanovei, Katz and Lyubetsky9]) that
![]() $\mathsf {UF_{wob}}(\omega )$
does not imply
$\mathsf {UF_{wob}}(\omega )$
does not imply
![]() $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
![]() $\mathsf {ZF}$
, we obtain the following striking, and surprising, result.
$\mathsf {ZF}$
, we obtain the following striking, and surprising, result.
Corollary 5.7. Each of the following statements
![]() $:$
$:$
-
(a) Every filter on
 $\mathbb {R}$
has a well-orderable base.
$\mathbb {R}$
has a well-orderable base. -
(b) Every filter base on
 $\mathbb {R}$
can be well ordered.
$\mathbb {R}$
can be well ordered. -
(c) Every filter on
 $\omega $
has a well-orderable base.
$\omega $
has a well-orderable base. -
(d) Every filter base on
 $\omega $
can be well ordered,
$\omega $
can be well ordered,
implies
![]() $\mathsf {UF_{wob}}(\omega )$
, and none of these implications are reversible in
$\mathsf {UF_{wob}}(\omega )$
, and none of these implications are reversible in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Concluding this subsection, we consider it important to draw the reader’s attention to the fact that Theorem 5.1(i) also yields interesting, and novel, characterizations of the principle “every linearly ordered set can be well ordered” [Reference Howard and Rubin11, Form 90] in
![]() $\mathsf {ZFA}$
(i.e., Zermelo–Fraenkel set theory with atoms), and of
$\mathsf {ZFA}$
(i.e., Zermelo–Fraenkel set theory with atoms), and of
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
, as the subsequent Theorem 5.8 clarifies (also recall (*) of the proof of Theorem 5.1(i)). It is known that “every linearly ordered set can be well ordered” is equivalent to
$\mathsf {ZF}$
, as the subsequent Theorem 5.8 clarifies (also recall (*) of the proof of Theorem 5.1(i)). It is known that “every linearly ordered set can be well ordered” is equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
, but is not equivalent to
$\mathsf {ZF}$
, but is not equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
; see Jech [Reference Jech13, Theorems 9.1 and 9.2]. For a quite recent, and extensive, study of models of
$\mathsf {ZFA}$
; see Jech [Reference Jech13, Theorems 9.1 and 9.2]. For a quite recent, and extensive, study of models of
![]() $\mathsf {ZFA}+\neg \mathsf {AC}$
in which every linearly ordered set can be well ordered, the reader is referred to Howard and Tachtsis [Reference Howard and Tachtsis12].
$\mathsf {ZFA}+\neg \mathsf {AC}$
in which every linearly ordered set can be well ordered, the reader is referred to Howard and Tachtsis [Reference Howard and Tachtsis12].
Theorem 5.8. The following are equivalent in
![]() $\mathsf {ZFA}{:}$
$\mathsf {ZFA}{:}$
-
(a) For every linearly ordered set X,
 $\mathsf {AC}(\wp (X))$
.
$\mathsf {AC}(\wp (X))$
. -
(b) For every linearly ordered set X,
 $\wp (X)$
can be well ordered.
$\wp (X)$
can be well ordered. -
(c) For every linearly ordered set X, every filter base on X can be well ordered.
-
(d) For every linearly ordered set X, every filter on X has a well-orderable base.
-
(e) Every linearly ordered set can be well ordered.
In particular, each of (a), (b), (c), and (d) is equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZF}$
, but is not equivalent to
$\mathsf {ZF}$
, but is not equivalent to
![]() $\mathsf {AC}$
in
$\mathsf {AC}$
in
![]() $\mathsf {ZFA}$
.
$\mathsf {ZFA}$
.
5.2
 $\mathsf {UF_{wob}}(\omega )$
,
$\mathsf {UF_{wob}}(\omega )$
,
 $\mathsf {UF}(\omega )$
,
$\mathsf {UF}(\omega )$
,
 $\mathsf {BPI}(\omega )$
,
$\mathsf {BPI}(\omega )$
,
 $\mathsf {BPI_{wob}}(\omega )$
, and
$\mathsf {BPI_{wob}}(\omega )$
, and
 $\mathsf {MA}$
$\mathsf {MA}$
Recall that (by [Reference Herzberg, Kanovei, Katz and Lyubetsky9])
![]() $\mathsf {UF_{wob}}(\omega )+\mathsf {AC}^{\aleph _{0}}$
does not imply
$\mathsf {UF_{wob}}(\omega )+\mathsf {AC}^{\aleph _{0}}$
does not imply
![]() $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
![]() $\mathsf {ZF}$
. However, it is an open problem whether or not
$\mathsf {ZF}$
. However, it is an open problem whether or not
![]() $\mathsf {UF_{wob}}(\omega )$
implies (
$\mathsf {UF_{wob}}(\omega )$
implies (
![]() $\mathsf {AC}^{\aleph _{0}}$
, or)
$\mathsf {AC}^{\aleph _{0}}$
, or)
![]() $\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
, or the weaker principle
$\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
, or the weaker principle
![]() $\mathsf {DFF}(\mathbb {R})$
. On the other hand, the axiom of choice for well-ordered families of non-empty sets [Reference Howard and Rubin11, Form 40], and thus
$\mathsf {DFF}(\mathbb {R})$
. On the other hand, the axiom of choice for well-ordered families of non-empty sets [Reference Howard and Rubin11, Form 40], and thus
![]() $\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
and
$\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
and
![]() $\mathsf {DFF}(\mathbb {R})$
, does not imply
$\mathsf {DFF}(\mathbb {R})$
, does not imply
![]() $\mathsf {UF}(\omega )$
(and thus
$\mathsf {UF}(\omega )$
(and thus
![]() $\mathsf {UF_{wob}}(\omega )$
) in
$\mathsf {UF_{wob}}(\omega )$
) in
![]() $\mathsf {ZF}$
; see [Reference Howard and Rubin11, Feferman’s Model
$\mathsf {ZF}$
; see [Reference Howard and Rubin11, Feferman’s Model
![]() $\mathcal {M} 2$
].
$\mathcal {M} 2$
].
Theorem 4.1 (of Section 4) yields
![]() $\mathsf {UF_{wob}}(\omega )$
is also false in another famous model of
$\mathsf {UF_{wob}}(\omega )$
is also false in another famous model of
![]() $\mathsf {ZF}$
, namely the Feferman–Lévy Model
$\mathsf {ZF}$
, namely the Feferman–Lévy Model
![]() $\mathcal {M}9$
of [Reference Howard and Rubin11]. Indeed, in
$\mathcal {M}9$
of [Reference Howard and Rubin11]. Indeed, in
![]() $\mathcal {M}9$
,
$\mathcal {M}9$
,
![]() $\mathbb {R}$
is written as a countable union of countable sets, and thus (by Theorem 4.1)
$\mathbb {R}$
is written as a countable union of countable sets, and thus (by Theorem 4.1)
![]() $\mathsf {UF_{wob}}(\omega )$
is false in
$\mathsf {UF_{wob}}(\omega )$
is false in
![]() $\mathcal {M}9$
. In Howard and Rubin [Reference Howard and Rubin11], the status of
$\mathcal {M}9$
. In Howard and Rubin [Reference Howard and Rubin11], the status of
![]() $\mathsf {DFF}(\mathbb {R})$
in
$\mathsf {DFF}(\mathbb {R})$
in
![]() $\mathcal {M}9$
is not specified. The above result of Feferman and Lévy about
$\mathcal {M}9$
is not specified. The above result of Feferman and Lévy about
![]() $\mathbb {R}$
in
$\mathbb {R}$
in
![]() $\mathcal {M}9$
, together with Proposition 5.9 below, immediately yields
$\mathcal {M}9$
, together with Proposition 5.9 below, immediately yields
![]() $\mathsf {DFF}(\mathbb {R})$
is true in
$\mathsf {DFF}(\mathbb {R})$
is true in
![]() $\mathcal {M}9$
; we label the latter result, together with the failure of
$\mathcal {M}9$
; we label the latter result, together with the failure of
![]() $\mathsf {UF_{wob}}(\omega )$
in
$\mathsf {UF_{wob}}(\omega )$
in
![]() $\mathcal {M}9$
, as Theorem 5.11 below. Let us point out here that it is an (intriguing) open problem whether or not
$\mathcal {M}9$
, as Theorem 5.11 below. Let us point out here that it is an (intriguing) open problem whether or not
![]() $\mathsf {UF}(\omega )$
is true in
$\mathsf {UF}(\omega )$
is true in
![]() $\mathcal {M}9$
.
$\mathcal {M}9$
.
Proposition 5.9. Let X be an infinite linearly orderable set. If X is a union of a well-orderable family of well-orderable sets, then every infinite subset of X has an infinite well-orderable subset. In particular, if
![]() $\mathbb {R}$
is a countable union of countable sets, then
$\mathbb {R}$
is a countable union of countable sets, then
![]() $\mathsf {DFF}(\mathbb {R})$
holds.
$\mathsf {DFF}(\mathbb {R})$
holds.
Proof. Let
![]() $\preceq $
be a linear order on X. Let
$\preceq $
be a linear order on X. Let
![]() $\mathcal {B}=\{B_{\alpha }:\alpha <\kappa \}$
, where
$\mathcal {B}=\{B_{\alpha }:\alpha <\kappa \}$
, where
![]() $\kappa $
is a well-ordered cardinal, be a family of well-orderable sets such that
$\kappa $
is a well-ordered cardinal, be a family of well-orderable sets such that
![]() $X=\bigcup \mathcal {B}$
.
$X=\bigcup \mathcal {B}$
.
Let A be an infinite subset of X. If, for some
![]() $\alpha \in \kappa $
,
$\alpha \in \kappa $
,
![]() $A\cap B_{\alpha }$
is infinite, then (since
$A\cap B_{\alpha }$
is infinite, then (since
![]() $B_{\alpha }$
is well orderable)
$B_{\alpha }$
is well orderable)
![]() $A\cap B_{\alpha }$
is well orderable. If
$A\cap B_{\alpha }$
is well orderable. If
![]() $A\cap B_{\alpha }$
is finite for all
$A\cap B_{\alpha }$
is finite for all
![]() $\alpha \in \kappa $
, then
$\alpha \in \kappa $
, then
![]() $A=\bigcup \{A\cap B_{\alpha }:\alpha <\kappa \}$
is well orderable as a union of a well-ordered family of finite linearly ordered sets.
$A=\bigcup \{A\cap B_{\alpha }:\alpha <\kappa \}$
is well orderable as a union of a well-ordered family of finite linearly ordered sets.
Remark 5.10. We note here that a stronger result than the second assertion of Proposition 5.9 holds. In particular, arguing similarly to the proof of Proposition 5.9, one may show that if
![]() $\mathbb {R}$
is a countable union of countable unions of countable sets, then
$\mathbb {R}$
is a countable union of countable unions of countable sets, then
![]() $\mathsf {DFF}(\mathbb {R})$
holds. On the other hand, Arnold Miller [Reference Miller18, Appendix] has constructed a variant of the Feferman–Lévy model
$\mathsf {DFF}(\mathbb {R})$
holds. On the other hand, Arnold Miller [Reference Miller18, Appendix] has constructed a variant of the Feferman–Lévy model
![]() $\mathcal {M}9$
in which
$\mathcal {M}9$
in which
![]() $\mathbb {R}$
is a countable union of countable unions of countable sets (and thus
$\mathbb {R}$
is a countable union of countable unions of countable sets (and thus
![]() $\mathsf {DFF}(\mathbb {R})$
holds in Miller’s model), but is not a countable union of countable sets.
$\mathsf {DFF}(\mathbb {R})$
holds in Miller’s model), but is not a countable union of countable sets.
We do not know if
![]() $\mathsf {UF_{wob}}(\omega )$
implies “
$\mathsf {UF_{wob}}(\omega )$
implies “
![]() $\mathbb {R}$
is not a countable union of countable unions of countable sets”, or if
$\mathbb {R}$
is not a countable union of countable unions of countable sets”, or if
![]() $\mathsf {UF_{wob}}(\omega )$
is false in Miller’s model.
$\mathsf {UF_{wob}}(\omega )$
is false in Miller’s model.
Theorem 5.11. Let
![]() $\mathcal {M}9$
(in the notation of [Reference Howard and Rubin11]) be the Feferman–Lévy model in which
$\mathcal {M}9$
(in the notation of [Reference Howard and Rubin11]) be the Feferman–Lévy model in which
![]() $\mathbb {R}$
is a countable union of countable sets. Then
$\mathbb {R}$
is a countable union of countable sets. Then
In Howard and Rubin [Reference Howard and Rubin11], it is not specified whether or not there is a model of
![]() $\mathsf {ZF}$
which satisfies
$\mathsf {ZF}$
which satisfies
![]() $\mathsf {UF}(\omega )\wedge \aleph _{1}\not \leq 2^{\aleph _{0}}$
, and thus (by Theorem 4.1)
$\mathsf {UF}(\omega )\wedge \aleph _{1}\not \leq 2^{\aleph _{0}}$
, and thus (by Theorem 4.1)
![]() $\mathsf {UF}(\omega )\wedge \neg \mathsf {UF_{wob}}(\omega )$
. We show next (in Theorem 5.13) that
$\mathsf {UF}(\omega )\wedge \neg \mathsf {UF_{wob}}(\omega )$
. We show next (in Theorem 5.13) that
![]() $\mathsf {ZF}+\mathsf {UF}(\omega )+ \aleph _{1}\not \leq 2^{\aleph _{0}}$
is relatively consistent with
$\mathsf {ZF}+\mathsf {UF}(\omega )+ \aleph _{1}\not \leq 2^{\aleph _{0}}$
is relatively consistent with
![]() $\mathsf {ZFC} +$
“there exists a strongly inaccessible cardinal”, and thus filling the gap in information in [Reference Howard and Rubin11], as well as in Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9]. Nevertheless, it is an open question whether or not the assumption (in the aforementioned result) of the consistency of large cardinals can be dropped.
$\mathsf {ZFC} +$
“there exists a strongly inaccessible cardinal”, and thus filling the gap in information in [Reference Howard and Rubin11], as well as in Herzberg et al. [Reference Herzberg, Kanovei, Katz and Lyubetsky9]. Nevertheless, it is an open question whether or not the assumption (in the aforementioned result) of the consistency of large cardinals can be dropped.
Before embarking to Theorem 5.13, let us provide the following definition.
Definition 5.12.
-
(1) A set
 $\mathcal {A}\subseteq \wp ^{\infty }(\omega )$
is called a Ramsey-set if there is an
$\mathcal {A}\subseteq \wp ^{\infty }(\omega )$
is called a Ramsey-set if there is an
 $H\in \wp ^{\infty }(\omega )$
which is homogeneous for the two-element partition
$H\in \wp ^{\infty }(\omega )$
which is homogeneous for the two-element partition
 $\{\mathcal {A},\wp ^{\infty }(\omega )\setminus \mathcal {A}\}$
of
$\{\mathcal {A},\wp ^{\infty }(\omega )\setminus \mathcal {A}\}$
of
 $\wp ^{\infty }(\omega )$
, that is,
$\wp ^{\infty }(\omega )$
, that is,
 $\wp ^{\infty }(H)$
is contained in one of the pieces of the above partition.
$\wp ^{\infty }(H)$
is contained in one of the pieces of the above partition. -
(2) The statement “every set
 $\mathcal {A}\subseteq \wp ^{\infty }(\omega )$
is a Ramsey-set”Footnote
4
is denoted by “
$\mathcal {A}\subseteq \wp ^{\infty }(\omega )$
is a Ramsey-set”Footnote
4
is denoted by “
 $\omega \rightarrow (\omega )^{\omega }$
”.
$\omega \rightarrow (\omega )^{\omega }$
”.
Theorem 5.13. If
![]() $\mathsf {ZFC} +$
“there exists a strongly inaccessible cardinal” is consistent, then so is
$\mathsf {ZFC} +$
“there exists a strongly inaccessible cardinal” is consistent, then so is
![]() $\mathsf {ZF} + \mathsf {UF}(\omega )+ \aleph _{1}\not \leq 2^{\aleph _{0}}$
. Hence,
$\mathsf {ZF} + \mathsf {UF}(\omega )+ \aleph _{1}\not \leq 2^{\aleph _{0}}$
. Hence,
![]() $\mathsf {UF}(\omega )$
does not imply “
$\mathsf {UF}(\omega )$
does not imply “
![]() $\aleph _{1}\leq 2^{\aleph _{0}}$
” in
$\aleph _{1}\leq 2^{\aleph _{0}}$
” in
![]() $\mathsf {ZF}$
, and consequently (by Theorem 4.1)
$\mathsf {ZF}$
, and consequently (by Theorem 4.1)
![]() $\mathsf {UF}(\omega )$
does not imply
$\mathsf {UF}(\omega )$
does not imply
![]() $\mathsf {UF_{wob}}(\omega )$
in
$\mathsf {UF_{wob}}(\omega )$
in
![]() $\mathsf {ZF}$
either.
$\mathsf {ZF}$
either.
Proof. First, we consider Solovay’s model
![]() $L(\mathbb {R})$
from [Reference Solovay24], labeled as ‘Model
$L(\mathbb {R})$
from [Reference Solovay24], labeled as ‘Model
![]() $\mathcal {M}5(\aleph )$
’ in [Reference Howard and Rubin11], for which the following facts are well known (see [Reference Howard and Rubin11, Reference Solovay24]):
$\mathcal {M}5(\aleph )$
’ in [Reference Howard and Rubin11], for which the following facts are well known (see [Reference Howard and Rubin11, Reference Solovay24]):
Our plan is to force over
![]() $L(\mathbb {R})$
with a suitable poset of conditions so that a free ultrafilter on
$L(\mathbb {R})$
with a suitable poset of conditions so that a free ultrafilter on
![]() $\omega $
is added, and in the generic extension it is still true that
$\omega $
is added, and in the generic extension it is still true that
![]() $\aleph _{1}\not \leq 2^{\aleph _{0}}$
.
$\aleph _{1}\not \leq 2^{\aleph _{0}}$
.
For the reader’s convenience, we give a brief description of
![]() $L(\mathbb {R})$
. We first recall that for a well-ordered cardinal
$L(\mathbb {R})$
. We first recall that for a well-ordered cardinal
![]() $\kappa $
, the Lévy collapsing order for
$\kappa $
, the Lévy collapsing order for
![]() $\kappa $
, Lv
$\kappa $
, Lv
![]() $(\kappa )$
(in the notation of Kunen [Reference Kunen16, Definition 8.6, p. 231]), is the set of all finite functions p with
$(\kappa )$
(in the notation of Kunen [Reference Kunen16, Definition 8.6, p. 231]), is the set of all finite functions p with
![]() $\operatorname {\mathrm {{dom}}}(p)\subseteq \kappa \times \omega $
,
$\operatorname {\mathrm {{dom}}}(p)\subseteq \kappa \times \omega $
,
![]() $\operatorname {\mathrm {{ran}}}(p)\subseteq \kappa $
and for each
$\operatorname {\mathrm {{ran}}}(p)\subseteq \kappa $
and for each
![]() $(\alpha ,n)\in p$
,
$(\alpha ,n)\in p$
,
![]() $p(\alpha ,n)<\alpha $
. Lv
$p(\alpha ,n)<\alpha $
. Lv
![]() $(\kappa )$
is partially ordered by reverse inclusion, i.e.,
$(\kappa )$
is partially ordered by reverse inclusion, i.e.,
![]() $p\leq q$
if and only if
$p\leq q$
if and only if
![]() $p\supseteq q$
.
$p\supseteq q$
.
![]() $L(\mathbb {R})$
is constructed in two steps, starting with a model M of
$L(\mathbb {R})$
is constructed in two steps, starting with a model M of
![]() $\mathsf {ZFC}$
with a strongly inaccessible cardinal
$\mathsf {ZFC}$
with a strongly inaccessible cardinal
![]() $\kappa $
. First, we force with Lv
$\kappa $
. First, we force with Lv
![]() $(\kappa )$
over M, so that if G is an Lv
$(\kappa )$
over M, so that if G is an Lv
![]() $(\kappa )$
-generic filter over M, we obtain the generic extension model
$(\kappa )$
-generic filter over M, we obtain the generic extension model
![]() $M[G]$
in which all cardinals less than
$M[G]$
in which all cardinals less than
![]() $\kappa $
have been collapsed to
$\kappa $
have been collapsed to
![]() $\omega $
, i.e.,
$\omega $
, i.e.,
![]() $\kappa =(\omega _{1})^{M[G]}$
(see Kunen [Reference Kunen16, Theorem 8.8, p. 231]). Second, if
$\kappa =(\omega _{1})^{M[G]}$
(see Kunen [Reference Kunen16, Theorem 8.8, p. 231]). Second, if
![]() $\mathbb {R}$
is the set of real numbers of
$\mathbb {R}$
is the set of real numbers of
![]() $M[G]$
, then
$M[G]$
, then
![]() $L(\mathbb {R})$
is the inner model
$L(\mathbb {R})$
is the inner model
![]() $\mathsf {HOD}(\mathbb {R})$
(defined within
$\mathsf {HOD}(\mathbb {R})$
(defined within
![]() $M[G]$
), i.e., the class of those sets of
$M[G]$
), i.e., the class of those sets of
![]() $M[G]$
which are hereditarily ordinal-definable from a finite number of elements of
$M[G]$
which are hereditarily ordinal-definable from a finite number of elements of
![]() $\mathrm {On}\cup \mathbb {R}\cup \{\mathbb {R}\}$
, where
$\mathrm {On}\cup \mathbb {R}\cup \{\mathbb {R}\}$
, where
![]() $\mathrm {On}$
is the class of all ordinal numbers; for “Ordinal-definable sets”, see Jech [Reference Jech14, pp. 194–196] or Kunen [Reference Kunen16, Chapter V, Section 2, p. 157].
$\mathrm {On}$
is the class of all ordinal numbers; for “Ordinal-definable sets”, see Jech [Reference Jech14, pp. 194–196] or Kunen [Reference Kunen16, Chapter V, Section 2, p. 157].
Fact 5.14. (Mathias [Reference Mathias17])
![]() $L(\mathbb {R})\models \omega \rightarrow (\omega )^{\omega }$
.
$L(\mathbb {R})\models \omega \rightarrow (\omega )^{\omega }$
.
In
![]() $L(\mathbb {R})$
, we let
$L(\mathbb {R})$
, we let
where for
![]() $x\in \wp ^{\infty }(\omega )$
,
$x\in \wp ^{\infty }(\omega )$
,
![]() $[x]=\{x\triangle y:y\in [\omega ]^{<\omega }\}$
(where “
$[x]=\{x\triangle y:y\in [\omega ]^{<\omega }\}$
(where “
![]() $\triangle $
” denotes the operation of symmetric difference between sets). We define a binary relation on
$\triangle $
” denotes the operation of symmetric difference between sets). We define a binary relation on
![]() $\mathbb {P}$
by stipulating, for all
$\mathbb {P}$
by stipulating, for all
![]() $p,q\in \mathbb {P}$
,
$p,q\in \mathbb {P}$
,
It is easy to verify that
![]() $\leq $
is a partial order on
$\leq $
is a partial order on
![]() $\mathbb {P}$
.Footnote
5
Let G be a
$\mathbb {P}$
.Footnote
5
Let G be a
![]() $\mathbb {P}$
-generic set over
$\mathbb {P}$
-generic set over
![]() $L(\mathbb {R})$
and let
$L(\mathbb {R})$
and let
![]() $L(\mathbb {R})[G]$
be the generic extension model of
$L(\mathbb {R})[G]$
be the generic extension model of
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
Fact 5.15. (Henle–Mathias–Woodin; [Reference Henle, Mathias, Woodin and Di Prisco8]) Let M be a transitive model of
![]() $\mathsf {ZF} + \omega \rightarrow (\omega )^{\omega }$
and N be its generic extension model (called Hausdorff extension in [Reference Henle, Mathias, Woodin and Di Prisco8]) obtained by forcing with
$\mathsf {ZF} + \omega \rightarrow (\omega )^{\omega }$
and N be its generic extension model (called Hausdorff extension in [Reference Henle, Mathias, Woodin and Di Prisco8]) obtained by forcing with
![]() $(\wp ^{\infty }(\omega )/[\omega ]^{<\omega },\leq )$
(as defined above) over M. Then every map in N from an ordinal into the ground model M lies in M; in particular, no new sets of ordinals are added.
$(\wp ^{\infty }(\omega )/[\omega ]^{<\omega },\leq )$
(as defined above) over M. Then every map in N from an ordinal into the ground model M lies in M; in particular, no new sets of ordinals are added.
Claim 5.16.
![]() $L(\mathbb {R})[G]$
has the same reals as
$L(\mathbb {R})[G]$
has the same reals as
![]() $L(\mathbb {R})$
.
$L(\mathbb {R})$
.
Proof. Since, by Fact 5.14,
![]() $L(\mathbb {R})$
is a transitive model of
$L(\mathbb {R})$
is a transitive model of
![]() $\mathsf {ZF} + \omega \rightarrow (\omega )^{\omega }$
and
$\mathsf {ZF} + \omega \rightarrow (\omega )^{\omega }$
and
![]() $L(\mathbb {R})[G]$
is its Hausdorff extension, it follows from Fact 5.15 that
$L(\mathbb {R})[G]$
is its Hausdorff extension, it follows from Fact 5.15 that
![]() $(2^{\omega })^{L(\mathbb {R})[G]}=(2^{\omega })^{L(\mathbb {R})}$
.
$(2^{\omega })^{L(\mathbb {R})[G]}=(2^{\omega })^{L(\mathbb {R})}$
.
In
![]() $L(\mathbb {R})[G]$
, we let
$L(\mathbb {R})[G]$
, we let
Claim 5.17.
![]() $\mathscr {U}$
is a free ultrafilter on
$\mathscr {U}$
is a free ultrafilter on
![]() $\omega $
in
$\omega $
in
![]() $L(\mathbb {R})[G]$
. Thus,
$L(\mathbb {R})[G]$
. Thus,
Proof. First, we show that
![]() $\mathscr {U}$
is a free filter on
$\mathscr {U}$
is a free filter on
![]() $\omega $
.
$\omega $
.
-
(1)
 $\emptyset \not \in \mathscr {U}$
. Otherwise,
$\emptyset \not \in \mathscr {U}$
. Otherwise,
 $[\emptyset ]=[\omega ]^{<\omega }\in \mathbb {P}$
, a contradiction.
$[\emptyset ]=[\omega ]^{<\omega }\in \mathbb {P}$
, a contradiction. -
(2)
 $\forall x\in \wp (\omega )(|\omega \setminus x|<\aleph _{0}\rightarrow x\in \mathscr {U})$
. Since G is a filter in
$\forall x\in \wp (\omega )(|\omega \setminus x|<\aleph _{0}\rightarrow x\in \mathscr {U})$
. Since G is a filter in
 $\mathbb {P}$
,
$\mathbb {P}$
,
 $G\neq \emptyset $
. So, there exists
$G\neq \emptyset $
. So, there exists
 $x\in \wp ^{\infty }(\omega )$
such that
$x\in \wp ^{\infty }(\omega )$
such that
 $[x]\in G$
. Since
$[x]\in G$
. Since
 $[x]\leq [\omega ]$
and G is a filter,
$[x]\leq [\omega ]$
and G is a filter,
 $[\omega ]\in G$
. As
$[\omega ]\in G$
. As
 $[\omega ]=\{z\in \wp (\omega ):|\omega \setminus z|<\aleph _{0}\}$
, we conclude that every co-finite subset of
$[\omega ]=\{z\in \wp (\omega ):|\omega \setminus z|<\aleph _{0}\}$
, we conclude that every co-finite subset of
 $\omega $
is an element of
$\omega $
is an element of
 $\mathscr {U}$
.
$\mathscr {U}$
. -
(3)
 $\forall x\in \mathscr {U}\forall y\in \mathscr {U}(x\cap y\in \mathscr {U})$
. Fix
$\forall x\in \mathscr {U}\forall y\in \mathscr {U}(x\cap y\in \mathscr {U})$
. Fix
 $x,y\in \mathscr {U}$
. Then
$x,y\in \mathscr {U}$
. Then
 $[x],[y]\in G$
and since G is a filter in
$[x],[y]\in G$
and since G is a filter in
 $\mathbb {P}$
, there exists
$\mathbb {P}$
, there exists
 $z\in \wp ^{\infty }(\omega )$
such that
$z\in \wp ^{\infty }(\omega )$
such that
 $[z]\in G$
,
$[z]\in G$
,
 $[z]\leq [x]$
, and
$[z]\leq [x]$
, and
 $[z]\leq [y]$
. By definition of
$[z]\leq [y]$
. By definition of
 $\leq $
, we have that both
$\leq $
, we have that both
 $z\setminus x$
and
$z\setminus x$
and
 $z\setminus y$
are finite. Therefore,
$z\setminus y$
are finite. Therefore,
 $z\setminus (x\cap y)$
is finite and, since z is infinite,
$z\setminus (x\cap y)$
is finite and, since z is infinite,
 $x\cap y$
is infinite. It follows that
$x\cap y$
is infinite. It follows that
 $[x\cap y]\in \mathbb {P}$
and
$[x\cap y]\in \mathbb {P}$
and
 $[z]\leq [x\cap y]$
. Since
$[z]\leq [x\cap y]$
. Since
 $[z]\in G$
and G is a filter, we obtain that
$[z]\in G$
and G is a filter, we obtain that
 $[x\cap y]\in G$
. Thus,
$[x\cap y]\in G$
. Thus,
 $x\cap y\in \mathscr {U}$
.
$x\cap y\in \mathscr {U}$
. -
(4)
 $\forall x\in \mathscr {U}\forall y\in \wp (\omega )(x\subseteq y\rightarrow y\in \mathscr {U})$
. Fix
$\forall x\in \mathscr {U}\forall y\in \wp (\omega )(x\subseteq y\rightarrow y\in \mathscr {U})$
. Fix
 $x\in \mathscr {U}$
and
$x\in \mathscr {U}$
and
 $y\in \wp (\omega )$
with
$y\in \wp (\omega )$
with
 $x\subseteq y$
. Then
$x\subseteq y$
. Then
 $[x]\in G$
,
$[x]\in G$
,
 $[y]\in \mathbb {P}$
, and
$[y]\in \mathbb {P}$
, and
 $[x]\leq [y]$
. Since
$[x]\leq [y]$
. Since
 $[x]\in G$
and G is a filter, we conclude that
$[x]\in G$
and G is a filter, we conclude that
 $[y]\in G$
, and so
$[y]\in G$
, and so
 $y\in \mathscr {U}$
.
$y\in \mathscr {U}$
.
From (1)-(4), we infer that
![]() $\mathscr {U}$
is a free filter on
$\mathscr {U}$
is a free filter on
![]() $\omega $
.
$\omega $
.
Now, we show that
![]() $\mathscr {U}$
is an ultrafilter on
$\mathscr {U}$
is an ultrafilter on
![]() $\omega $
in
$\omega $
in
![]() $L(\mathbb {R})[G]$
. Since, by (2),
$L(\mathbb {R})[G]$
. Since, by (2),
![]() $\mathscr {U}$
contains every co-finite subset of
$\mathscr {U}$
contains every co-finite subset of
![]() $\omega $
, it suffices to show that, for every
$\omega $
, it suffices to show that, for every
![]() $x\in \wp ^{\infty }(\omega )$
with
$x\in \wp ^{\infty }(\omega )$
with
![]() $x^{c}\in \wp ^{\infty }(\omega )$
, either
$x^{c}\in \wp ^{\infty }(\omega )$
, either
![]() $x\in \mathscr {U}$
or
$x\in \mathscr {U}$
or
![]() $x^{c}\in \mathscr {U}$
. So, fix such an
$x^{c}\in \mathscr {U}$
. So, fix such an
![]() $x\in \wp ^{\infty }(\omega )$
in
$x\in \wp ^{\infty }(\omega )$
in
![]() $L(\mathbb {R})[G]$
. By Claim 5.16, we have that
$L(\mathbb {R})[G]$
. By Claim 5.16, we have that
![]() $x,x^{c}\in L(\mathbb {R})$
. Due to this fact, we may let within
$x,x^{c}\in L(\mathbb {R})$
. Due to this fact, we may let within
![]() $L(\mathbb {R})$
,
$L(\mathbb {R})$
,
Then D is a dense subset of
![]() $\mathbb {P}$
. To see this, fix
$\mathbb {P}$
. To see this, fix
![]() $p\in \mathbb {P}$
. There exists
$p\in \mathbb {P}$
. There exists
![]() $z\in \wp ^{\infty }(\omega )$
such that
$z\in \wp ^{\infty }(\omega )$
such that
![]() $p=[z]$
. Since z is infinite and
$p=[z]$
. Since z is infinite and
![]() $z=(z\cap x)\cup (z\cap x^{c})$
, it follows that
$z=(z\cap x)\cup (z\cap x^{c})$
, it follows that
![]() $z\cap x$
is infinite or
$z\cap x$
is infinite or
![]() $z\cap x^{c}$
is infinite. If the first case holds, then
$z\cap x^{c}$
is infinite. If the first case holds, then
![]() $[z\cap x]\in D$
and
$[z\cap x]\in D$
and
![]() $[z\cap x]\leq p$
, and, if the second case holds, then
$[z\cap x]\leq p$
, and, if the second case holds, then
![]() $[z\cap x^{c}]\in D$
and
$[z\cap x^{c}]\in D$
and
![]() $[z\cap x^{c}]\leq p$
. Therefore, either of the above two cases yields an extension of p in D, i.e., D is dense in
$[z\cap x^{c}]\leq p$
. Therefore, either of the above two cases yields an extension of p in D, i.e., D is dense in
![]() $\mathbb {P}$
, as required.
$\mathbb {P}$
, as required.
Since G is
![]() $\mathbb {P}$
-generic over
$\mathbb {P}$
-generic over
![]() $L(\mathbb {R})$
,
$L(\mathbb {R})$
,
![]() $G\cap D\neq \emptyset $
. So, let
$G\cap D\neq \emptyset $
. So, let
![]() $g\in G\cap D$
. It follows that
$g\in G\cap D$
. It follows that
![]() $g\leq [x]$
or
$g\leq [x]$
or
![]() $g\leq [x^{c}]$
and, as G is a filter, we obtain that
$g\leq [x^{c}]$
and, as G is a filter, we obtain that
![]() $[x]\in G$
or
$[x]\in G$
or
![]() $[x^{c}]\in G$
, i.e.,
$[x^{c}]\in G$
, i.e.,
![]() $x\in \mathscr {U}$
or
$x\in \mathscr {U}$
or
![]() $x^{c}\in \mathscr {U}$
. Therefore,
$x^{c}\in \mathscr {U}$
. Therefore,
![]() $\mathscr {U}$
is an ultrafilter, finishing the proof of the claim.
$\mathscr {U}$
is an ultrafilter, finishing the proof of the claim.
Claim 5.18.
![]() $L(\mathbb {R})[G]\models \aleph _{1}\not \leq 2^{\aleph _{0}}$
. In particular,
$L(\mathbb {R})[G]\models \aleph _{1}\not \leq 2^{\aleph _{0}}$
. In particular,
![]() $L(\mathbb {R})[G]\models \neg \mathsf {UF_{wob}}(\omega )$
.
$L(\mathbb {R})[G]\models \neg \mathsf {UF_{wob}}(\omega )$
.
Proof. Since, by Fact 5.14,
![]() $L(\mathbb {R})$
is a transitive model of
$L(\mathbb {R})$
is a transitive model of
![]() $\mathsf {ZF} + \omega \rightarrow (\omega )^{\omega }$
and
$\mathsf {ZF} + \omega \rightarrow (\omega )^{\omega }$
and
![]() $L(\mathbb {R})[G]$
is its Hausdorff extension, it follows from Claim 5.16 and Fact 5.15 that, in
$L(\mathbb {R})[G]$
is its Hausdorff extension, it follows from Claim 5.16 and Fact 5.15 that, in
![]() $L(\mathbb {R})[G]$
, there is no injection
$L(\mathbb {R})[G]$
, there is no injection
![]() $f:\omega _{1}\rightarrow \mathbb {R}$
; otherwise, since (by Claim 5.16)
$f:\omega _{1}\rightarrow \mathbb {R}$
; otherwise, since (by Claim 5.16)
![]() $\mathbb {R}^{L(\mathbb {R})}=\mathbb {R}^{L(\mathbb {R})[G]}$
, such an injection would be (by Fact 5.15) in
$\mathbb {R}^{L(\mathbb {R})}=\mathbb {R}^{L(\mathbb {R})[G]}$
, such an injection would be (by Fact 5.15) in
![]() $L(\mathbb {R})$
, contradicting that
$L(\mathbb {R})$
, contradicting that
![]() $L(\mathbb {R})$
satisfies “
$L(\mathbb {R})$
satisfies “
![]() $\aleph _{1}\not \leq 2^{\aleph _{0}}$
”. Therefore,
$\aleph _{1}\not \leq 2^{\aleph _{0}}$
”. Therefore,
![]() $L(\mathbb {R})[G]\models \aleph _{1}\not \leq 2^{\aleph _{0}}$
, and consequently (by Theorem 4.1)
$L(\mathbb {R})[G]\models \aleph _{1}\not \leq 2^{\aleph _{0}}$
, and consequently (by Theorem 4.1)
![]() $L(\mathbb {R})[G]\models \neg \mathsf {UF_{wob}}(\omega )$
.
$L(\mathbb {R})[G]\models \neg \mathsf {UF_{wob}}(\omega )$
.
The above arguments complete the proof of the theorem.
Remark 5.19.
-
(1) It is an open problem whether or not either of
 $\mathsf {BPI}$
and
$\mathsf {BPI}$
and
 $\mathsf {BPI}(\omega )$
imply
$\mathsf {BPI}(\omega )$
imply
 $\aleph _{1}\leq 2^{\aleph _{0}}$
in
$\aleph _{1}\leq 2^{\aleph _{0}}$
in
 $\mathsf {ZF}$
. Since
$\mathsf {ZF}$
. Since
 $\mathsf {UF}(\omega )$
is weaker than
$\mathsf {UF}(\omega )$
is weaker than
 $\mathsf {BPI}(\omega )$
, Theorem 5.13 provides a partial answer to the above problem.
$\mathsf {BPI}(\omega )$
, Theorem 5.13 provides a partial answer to the above problem.It is unknown to us whether or not
 $\mathsf {BPI}(\omega )$
is false in the model
$\mathsf {BPI}(\omega )$
is false in the model
 $L(\mathbb {R})[G]$
of the proof of Theorem 5.13.
$L(\mathbb {R})[G]$
of the proof of Theorem 5.13. -
(2) Note that since
 $L(\mathbb {R})[G]$
satisfies
$L(\mathbb {R})[G]$
satisfies
 $\mathsf {UF}(\omega )+\neg \mathsf {UF_{wob}}(\omega )$
, the formally weaker statement “there exists a free ultrafilter on
$\mathsf {UF}(\omega )+\neg \mathsf {UF_{wob}}(\omega )$
, the formally weaker statement “there exists a free ultrafilter on
 $\omega $
which has no well-orderable base” is true in
$\omega $
which has no well-orderable base” is true in
 $L(\mathbb {R})[G]$
; in particular, the free ultrafilter
$L(\mathbb {R})[G]$
; in particular, the free ultrafilter
 $\mathscr {U}$
on
$\mathscr {U}$
on
 $\omega $
(of the proof of Theorem 5.13) has no well-orderable base in
$\omega $
(of the proof of Theorem 5.13) has no well-orderable base in
 $L(\mathbb {R})[G]$
(otherwise, by Claim 4.2 of the proof of Theorem 4.1, we would have that in
$L(\mathbb {R})[G]$
(otherwise, by Claim 4.2 of the proof of Theorem 4.1, we would have that in
 $L(\mathbb {R})[G]$
,
$L(\mathbb {R})[G]$
,
 $\aleph _{1}\leq 2^{\aleph _{0}}$
which is not true, as shown above).
$\aleph _{1}\leq 2^{\aleph _{0}}$
which is not true, as shown above).
Since for an ultrafilter
![]() $\mathscr {U}$
on
$\mathscr {U}$
on
![]() $\omega $
it is true that
$\omega $
it is true that
![]() $|\mathscr {U}|=2^{\aleph _{0}}$
, and from Claim 4.2 (of the proof of Theorem 4.1) no free ultrafilter on
$|\mathscr {U}|=2^{\aleph _{0}}$
, and from Claim 4.2 (of the proof of Theorem 4.1) no free ultrafilter on
![]() $\omega $
has a countable base, it is natural to ask about the relative strength of the following statements:
$\omega $
has a countable base, it is natural to ask about the relative strength of the following statements:
-
(1) There exists a free ultrafilter on
 $\omega $
with a base of cardinality
$\omega $
with a base of cardinality
 $<2^{\aleph _{0}}$
.
$<2^{\aleph _{0}}$
. -
(2) There exists a free ultrafilter on
 $\omega $
which has no base of cardinality
$\omega $
which has no base of cardinality
 $<2^{\aleph _{0}}$
.
$<2^{\aleph _{0}}$
.
With regard to (1), Kunen [Reference Kunen16, Exercise (A10), p. 289] has constructed a forcing model of
![]() $\mathsf {ZFC}$
in which
$\mathsf {ZFC}$
in which
![]() $\aleph _{1}< 2^{\aleph _{0}}$
and there exists a free ultrafilter on
$\aleph _{1}< 2^{\aleph _{0}}$
and there exists a free ultrafilter on
![]() $\omega $
having a base of cardinality
$\omega $
having a base of cardinality
![]() $\aleph _{1}$
.
$\aleph _{1}$
.
Statement (2) is a
![]() $\mathsf {ZFC}$
-result of Pospíšil [Reference Pospíšil22]; Hajnal and Juhász also established (2) in
$\mathsf {ZFC}$
-result of Pospíšil [Reference Pospíšil22]; Hajnal and Juhász also established (2) in
![]() $\mathsf {ZFC}$
, and a hint for their proof is given by Kunen [Reference Kunen16, Exercise (A11), p. 289]. Based on that hint of [Reference Kunen16], we will prove (2) in the weaker axiomatic system
$\mathsf {ZFC}$
, and a hint for their proof is given by Kunen [Reference Kunen16, Exercise (A11), p. 289]. Based on that hint of [Reference Kunen16], we will prove (2) in the weaker axiomatic system
![]() $\mathsf {ZF} + \mathsf {BPI}(\omega ) +$
“if
$\mathsf {ZF} + \mathsf {BPI}(\omega ) +$
“if
![]() $\mathcal {A}=\{A_{i}:i\in I\}$
is a family of subsets of
$\mathcal {A}=\{A_{i}:i\in I\}$
is a family of subsets of
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $|I|<2^{\aleph _{0}}$
and
$|I|<2^{\aleph _{0}}$
and
![]() $|A_{i}|<2^{\aleph _{0}}$
for all
$|A_{i}|<2^{\aleph _{0}}$
for all
![]() $i\in I$
, then
$i\in I$
, then
![]() $|\bigcup \mathcal {A}|<2^{\aleph _{0}}$
”. Indeed, we have the following theorem.
$|\bigcup \mathcal {A}|<2^{\aleph _{0}}$
”. Indeed, we have the following theorem.
Theorem 5.20. The following hold
![]() $:$
$:$
-
(i)
 $\mathsf {BPI}(\omega ) +$
“if
$\mathsf {BPI}(\omega ) +$
“if
 $\mathcal {A}=\{A_{i}:i\in I\}$
is a family of subsets of
$\mathcal {A}=\{A_{i}:i\in I\}$
is a family of subsets of
 $\mathbb {R}$
such that
$\mathbb {R}$
such that
 $|I|<2^{\aleph _{0}}$
and
$|I|<2^{\aleph _{0}}$
and
 $|A_{i}|<2^{\aleph _{0}}$
for all
$|A_{i}|<2^{\aleph _{0}}$
for all
 $i\in I$
, then
$i\in I$
, then
 $|\bigcup \mathcal {A}|<2^{\aleph _{0}}$
” implies “there exists a free ultrafilter on
$|\bigcup \mathcal {A}|<2^{\aleph _{0}}$
” implies “there exists a free ultrafilter on
 $\omega $
which has no base of cardinality
$\omega $
which has no base of cardinality
 $<2^{\aleph _{0}}$
”.
$<2^{\aleph _{0}}$
”. -
(ii)
 $\mathsf {BPI}(\omega )$
implies “there exists a free ultrafilter on
$\mathsf {BPI}(\omega )$
implies “there exists a free ultrafilter on
 $\omega $
which has no well-orderable base of cardinality
$\omega $
which has no well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”.
$<2^{\aleph _{0}}$
”. -
(iii) “There exists a free ultrafilter on
 $\omega $
which has no well-orderable base” is true in the Basic Cohen Model.
$\omega $
which has no well-orderable base” is true in the Basic Cohen Model. -
(iv)
 $\mathsf {AC}(\mathbb {R})$
and “there exists a free ultrafilter on
$\mathsf {AC}(\mathbb {R})$
and “there exists a free ultrafilter on
 $\omega $
which has no well-orderable base” are mutually independent in
$\omega $
which has no well-orderable base” are mutually independent in
 $\mathsf {ZF}$
. In particular,
$\mathsf {ZF}$
. In particular,
 $\mathsf {BPI}(\omega )$
does not imply “there exists a free ultrafilter on
$\mathsf {BPI}(\omega )$
does not imply “there exists a free ultrafilter on
 $\omega $
which has no well-orderable base” in
$\omega $
which has no well-orderable base” in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. (i) Let
![]() $\mathcal {I}$
be an independent family in
$\mathcal {I}$
be an independent family in
![]() $\omega $
of size
$\omega $
of size
![]() $2^{\aleph _{0}}$
, and also let
$2^{\aleph _{0}}$
, and also let
 $$ \begin{align*}\mathcal{F}=\mathcal{I}\cup\left\{\bigcup_{A\in\mathcal{J}}A^{c}:\mathcal{J}\in\wp^{\infty}(\mathcal{I})\right\}.\end{align*} $$
$$ \begin{align*}\mathcal{F}=\mathcal{I}\cup\left\{\bigcup_{A\in\mathcal{J}}A^{c}:\mathcal{J}\in\wp^{\infty}(\mathcal{I})\right\}.\end{align*} $$
Since
![]() $\mathcal {I}$
is independent, it is easy to see that
$\mathcal {I}$
is independent, it is easy to see that
![]() $\mathcal {F}$
has the finite intersection property. Furthermore,
$\mathcal {F}$
has the finite intersection property. Furthermore,
![]() $\bigcap \mathcal {F}=\emptyset $
since
$\bigcap \mathcal {F}=\emptyset $
since
![]() $\bigcap \mathcal {F}\subseteq (\bigcap \mathcal {I})\cap (\bigcup _{A\in \mathcal {I}}A^{c})=\emptyset $
.
$\bigcap \mathcal {F}\subseteq (\bigcap \mathcal {I})\cap (\bigcup _{A\in \mathcal {I}}A^{c})=\emptyset $
.
By
![]() $\mathsf {BPI}(\omega )$
, there exists an ultrafilter
$\mathsf {BPI}(\omega )$
, there exists an ultrafilter
![]() $\mathscr {U}$
on
$\mathscr {U}$
on
![]() $\omega $
which extends
$\omega $
which extends
![]() $\mathcal {F}$
. Since
$\mathcal {F}$
. Since
![]() $\bigcap \mathcal {F}=\emptyset $
,
$\bigcap \mathcal {F}=\emptyset $
,
![]() $\mathscr {U}$
is free. We assert that
$\mathscr {U}$
is free. We assert that
![]() $\mathscr {U}$
has no base of cardinality
$\mathscr {U}$
has no base of cardinality
![]() $<2^{\aleph _{0}}$
. Assume the contrary, and let
$<2^{\aleph _{0}}$
. Assume the contrary, and let
![]() $\mathscr {C}$
be a base for
$\mathscr {C}$
be a base for
![]() $\mathscr {U}$
such that
$\mathscr {U}$
such that
![]() $|\mathscr {C}|<2^{\aleph _{0}}$
. For each
$|\mathscr {C}|<2^{\aleph _{0}}$
. For each
![]() $C\in \mathscr {C}$
, let
$C\in \mathscr {C}$
, let
Then
Since
![]() $|\mathscr {C}|< 2^{\aleph _{0}}$
and
$|\mathscr {C}|< 2^{\aleph _{0}}$
and
![]() $|\mathcal {I}|=2^{\aleph _{0}}$
, it follows from the second principle of our hypothesis that for some
$|\mathcal {I}|=2^{\aleph _{0}}$
, it follows from the second principle of our hypothesis that for some
![]() $C\in \mathscr {C}$
,
$C\in \mathscr {C}$
,
![]() $S_{C}$
is an infinite set. By the definition of
$S_{C}$
is an infinite set. By the definition of
![]() $S_{C}$
, we have
$S_{C}$
, we have
![]() $C\subseteq \bigcap S_{C}$
, and hence
$C\subseteq \bigcap S_{C}$
, and hence
![]() $\bigcap S_{C}\in \mathscr {U}$
since
$\bigcap S_{C}\in \mathscr {U}$
since
![]() $C\in \mathscr {C}\subseteq \mathscr {U}$
and
$C\in \mathscr {C}\subseteq \mathscr {U}$
and
![]() $\mathscr {U}$
is a filter. Furthermore, since
$\mathscr {U}$
is a filter. Furthermore, since
![]() $S_{C}\in \wp ^{\infty }(\mathcal {I})$
, it follows that
$S_{C}\in \wp ^{\infty }(\mathcal {I})$
, it follows that
![]() $(\bigcap S_{C})^{c}=\bigcup _{A\in S_{C}}A^{c}\in \mathcal {F}\subseteq \mathscr {U}$
and thus
$(\bigcap S_{C})^{c}=\bigcup _{A\in S_{C}}A^{c}\in \mathcal {F}\subseteq \mathscr {U}$
and thus
![]() $(\bigcap S_{C})^{c}\in \mathscr {U}$
. This, together with
$(\bigcap S_{C})^{c}\in \mathscr {U}$
. This, together with
![]() $\bigcap S_{C}\in \mathscr {U}$
, contradicts
$\bigcap S_{C}\in \mathscr {U}$
, contradicts
![]() $\mathscr {U}$
’s being a filter. Therefore,
$\mathscr {U}$
’s being a filter. Therefore,
![]() $\mathscr {U}$
has no base of cardinality
$\mathscr {U}$
has no base of cardinality
![]() $<2^{\aleph _{0}}$
.
$<2^{\aleph _{0}}$
.
(ii) Assuming
![]() $\mathsf {BPI}(\omega )$
and following the proof of (i), we have that, if
$\mathsf {BPI}(\omega )$
and following the proof of (i), we have that, if
![]() $\mathscr {C}$
is a well-ordered base for the ultrafilter
$\mathscr {C}$
is a well-ordered base for the ultrafilter
![]() $\mathscr {U}$
which extends
$\mathscr {U}$
which extends
![]() $\mathcal {F}$
and
$\mathcal {F}$
and
![]() $|\mathscr {C}|<2^{\aleph _{0}}$
, then again for some
$|\mathscr {C}|<2^{\aleph _{0}}$
, then again for some
![]() $C\in \mathscr {C}$
,
$C\in \mathscr {C}$
,
![]() $\mathcal {S}_{C}$
is infinite; otherwise,
$\mathcal {S}_{C}$
is infinite; otherwise,
![]() $2^{\aleph _{0}}=|\mathcal {I}|=|\bigcup \{\mathcal {S}_{C}:C\in \mathscr {C}\}|=|\mathscr {C}|< 2^{\aleph _{0}}$
, a contradiction. We may now complete the proof as in (i), obtaining again a contradiction to
$2^{\aleph _{0}}=|\mathcal {I}|=|\bigcup \{\mathcal {S}_{C}:C\in \mathscr {C}\}|=|\mathscr {C}|< 2^{\aleph _{0}}$
, a contradiction. We may now complete the proof as in (i), obtaining again a contradiction to
![]() $\mathscr {U}$
’s being a filter.
$\mathscr {U}$
’s being a filter.
(iii) This follows from (ii) and the fact that the Basic Cohen Model [Reference Howard and Rubin11, Model
![]() $1$
] satisfies
$1$
] satisfies
![]() $\mathsf {BPI}+\neg \mathsf {AC}(\mathbb {R})$
(see [Reference Jech13], or [Reference Howard and Rubin11]).
$\mathsf {BPI}+\neg \mathsf {AC}(\mathbb {R})$
(see [Reference Jech13], or [Reference Howard and Rubin11]).
(iv) The first assertion follows from Theorem 5.1(i) and part (iii), and the second assertion follows from the first and the fact that
![]() $\mathsf {AC}(\mathbb {R})$
(strictly) implies
$\mathsf {AC}(\mathbb {R})$
(strictly) implies
![]() $\mathsf {BPI}(\omega )$
in
$\mathsf {BPI}(\omega )$
in
![]() $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Remark 5.21. The statement “if
![]() $\mathcal {A}=\{A_{i}:i\in I\}$
is a family of subsets of
$\mathcal {A}=\{A_{i}:i\in I\}$
is a family of subsets of
![]() $\mathbb {R}$
such that
$\mathbb {R}$
such that
![]() $|I|<2^{\aleph _{0}}$
and
$|I|<2^{\aleph _{0}}$
and
![]() $|A_{i}|<2^{\aleph _{0}}$
for all
$|A_{i}|<2^{\aleph _{0}}$
for all
![]() $i\in I$
, then
$i\in I$
, then
![]() $|\bigcup \mathcal {A}|<2^{\aleph _{0}}$
” is provable in
$|\bigcup \mathcal {A}|<2^{\aleph _{0}}$
” is provable in
![]() $\mathsf {ZFC}+\mathsf {MA}$
; see [Reference Kunen16, Corollary 2.19, p. 58], which states that (in
$\mathsf {ZFC}+\mathsf {MA}$
; see [Reference Kunen16, Corollary 2.19, p. 58], which states that (in
![]() $\mathsf {ZFC}$
)
$\mathsf {ZFC}$
)
![]() $\mathsf {MA}$
implies
$\mathsf {MA}$
implies
![]() $2^{\aleph _{0}}$
is a regular cardinal; in fact,
$2^{\aleph _{0}}$
is a regular cardinal; in fact,
![]() $\mathsf {AC}(\mathbb {R})+\mathsf {MA}$
suffices for the proof of the latter result.Footnote
6
$\mathsf {AC}(\mathbb {R})+\mathsf {MA}$
suffices for the proof of the latter result.Footnote
6
Furthermore, the above statement is false in both the Basic Cohen Model
![]() $\mathcal {M}1$
of [Reference Howard and Rubin11] (in
$\mathcal {M}1$
of [Reference Howard and Rubin11] (in
![]() $\mathcal {M}1$
,
$\mathcal {M}1$
,
![]() $\mathbb {R}$
has a partition
$\mathbb {R}$
has a partition
![]() $\{A,B\}$
such that
$\{A,B\}$
such that
![]() $|A|<2^{\aleph _{0}}$
and
$|A|<2^{\aleph _{0}}$
and
![]() $|B|<2^{\aleph _{0}}$
—see Monro [Reference Monro19], or [Reference Howard and Rubin11, Form 369 and Model
$|B|<2^{\aleph _{0}}$
—see Monro [Reference Monro19], or [Reference Howard and Rubin11, Form 369 and Model
![]() $\mathcal {M}1$
]) and the Feferman–Lévy Model
$\mathcal {M}1$
]) and the Feferman–Lévy Model
![]() $\mathcal {M}9$
of [Reference Howard and Rubin11] (since, in
$\mathcal {M}9$
of [Reference Howard and Rubin11] (since, in
![]() $\mathcal {M}9$
,
$\mathcal {M}9$
,
![]() $\mathbb {R}$
is a countable union of countable sets).
$\mathbb {R}$
is a countable union of countable sets).
Theorem 5.22. The following hold
![]() $:$
$:$
-
(i)
 $\mathsf {BPI_{wob}}(\omega )$
is equivalent to
$\mathsf {BPI_{wob}}(\omega )$
is equivalent to
 $\mathsf {AC}(\mathbb {R})$
. It follows that
$\mathsf {AC}(\mathbb {R})$
. It follows that
 $\mathsf {BPI}$
(and thus
$\mathsf {BPI}$
(and thus
 $\mathsf {BPI}(\omega )$
) does not imply
$\mathsf {BPI}(\omega )$
) does not imply
 $\mathsf {BPI_{wob}}(\omega )$
in
$\mathsf {BPI_{wob}}(\omega )$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(ii)
 $\mathsf {AC}(\mathbb {R})$
implies “every ultrafilter on
$\mathsf {AC}(\mathbb {R})$
implies “every ultrafilter on
 $\omega $
has a well-orderable base” and the implication is not reversible in
$\omega $
has a well-orderable base” and the implication is not reversible in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. (i) (
![]() $\mathsf {AC}(\mathbb {R}) \Rightarrow \mathsf {BPI_{wob}}(\omega )$
) This is an immediate consequence of the fact that
$\mathsf {AC}(\mathbb {R}) \Rightarrow \mathsf {BPI_{wob}}(\omega )$
) This is an immediate consequence of the fact that
![]() $|\wp (\omega )|=|\mathbb {R}|$
and the fact that
$|\wp (\omega )|=|\mathbb {R}|$
and the fact that
![]() $\mathsf {AC}(\mathbb {R})$
is equivalent to “
$\mathsf {AC}(\mathbb {R})$
is equivalent to “
![]() $\mathbb {R}$
can be well ordered”.
$\mathbb {R}$
can be well ordered”.
(
![]() $\mathsf {BPI_{wob}}(\omega ) \Rightarrow \mathsf {AC}(\mathbb {R})$
) Let
$\mathsf {BPI_{wob}}(\omega ) \Rightarrow \mathsf {AC}(\mathbb {R})$
) Let
![]() $\mathcal {I}$
and
$\mathcal {I}$
and
![]() $\mathcal {F}$
be defined as in the proof of Theorem 5.20(i). By
$\mathcal {F}$
be defined as in the proof of Theorem 5.20(i). By
![]() $\mathsf {BPI_{wob}}(\omega )$
,
$\mathsf {BPI_{wob}}(\omega )$
,
![]() $\mathcal {F}$
can be extended to an ultrafilter
$\mathcal {F}$
can be extended to an ultrafilter
![]() $\mathscr {U}$
with a well-orderable base,
$\mathscr {U}$
with a well-orderable base,
![]() $\mathscr {C}$
say. Then
$\mathscr {C}$
say. Then
![]() $|\mathscr {C}|\leq 2^{\aleph _{0}}$
and, by the proof of Theorem 5.20(i),
$|\mathscr {C}|\leq 2^{\aleph _{0}}$
and, by the proof of Theorem 5.20(i),
![]() $|\mathscr {C}|\not < 2^{\aleph _{0}}$
. Therefore,
$|\mathscr {C}|\not < 2^{\aleph _{0}}$
. Therefore,
![]() $|\mathscr {C}|=2^{\aleph _{0}}$
, i.e.,
$|\mathscr {C}|=2^{\aleph _{0}}$
, i.e.,
![]() $\mathbb {R}$
can be well ordered. So,
$\mathbb {R}$
can be well ordered. So,
![]() $\mathsf {AC}(\mathbb {R})$
holds true.
$\mathsf {AC}(\mathbb {R})$
holds true.
The second assertion of (i) follows from the first and the fact that
![]() $\mathsf {BPI}$
(and thus
$\mathsf {BPI}$
(and thus
![]() $\mathsf {BPI}(\omega )$
) does not imply
$\mathsf {BPI}(\omega )$
) does not imply
![]() $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
![]() $\mathsf {ZF}$
(see [Reference Howard and Rubin11, Basic Cohen Model
$\mathsf {ZF}$
(see [Reference Howard and Rubin11, Basic Cohen Model
![]() $1$
]).
$1$
]).
(ii) The first assertion follows from (i) (or Theorem 5.1(i)), and the second one follows from the fact that “every ultrafilter on
![]() $\omega $
has a well-orderable base” is true in Feferman’s model
$\omega $
has a well-orderable base” is true in Feferman’s model
![]() $\mathcal {M}2$
of [Reference Howard and Rubin11] since, in
$\mathcal {M}2$
of [Reference Howard and Rubin11] since, in
![]() $\mathcal {M}2$
, every ultrafilter on
$\mathcal {M}2$
, every ultrafilter on
![]() $\omega $
is principal, but
$\omega $
is principal, but
![]() $\mathsf {AC}(\mathbb {R})$
is false in
$\mathsf {AC}(\mathbb {R})$
is false in
![]() $\mathcal {M}2$
(see [Reference Feferman3] or [Reference Jech13, Problem 24, p. 82]).
$\mathcal {M}2$
(see [Reference Feferman3] or [Reference Jech13, Problem 24, p. 82]).
In view of Theorem 5.20 and Remark 5.21, it is plausible to ask about the possible relationship between
![]() $\mathsf {MA}$
and
$\mathsf {MA}$
and
![]() $\mathsf {UF_{wob}}(\omega )$
. In Theorem 5.23 below, we will prove (among other results) that
$\mathsf {UF_{wob}}(\omega )$
. In Theorem 5.23 below, we will prove (among other results) that
![]() $\mathsf {MA}$
and
$\mathsf {MA}$
and
![]() $\mathsf {UF_{wob}}(\omega )$
are mutually independent in
$\mathsf {UF_{wob}}(\omega )$
are mutually independent in
![]() $\mathsf {ZF}$
, and that
$\mathsf {ZF}$
, and that
![]() $\mathsf {MA}+\mathsf {UF_{wob}}(\omega )$
implies
$\mathsf {MA}+\mathsf {UF_{wob}}(\omega )$
implies
![]() $\mathsf {AC}(\mathbb {R})$
(or equivalently,
$\mathsf {AC}(\mathbb {R})$
(or equivalently,
![]() $\mathbb {R}$
can be well ordered).
$\mathbb {R}$
can be well ordered).
Theorem 5.23. The following hold
![]() $:$
$:$
-
(i)
 $\mathsf {MA}$
does not imply
$\mathsf {MA}$
does not imply
 $\mathsf {UF_{wob}}(\omega )$
in
$\mathsf {UF_{wob}}(\omega )$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(ii)
 $\mathsf {MA}$
implies “no free ultrafilter on
$\mathsf {MA}$
implies “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”, and the implication is not reversible in
$<2^{\aleph _{0}}$
”, and the implication is not reversible in
 $\mathsf {ZF}$
. Moreover, by (i), “no free ultrafilter on
$\mathsf {ZF}$
. Moreover, by (i), “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
” does not imply
$<2^{\aleph _{0}}$
” does not imply
 $\mathsf {UF_{wob}}(\omega )$
in
$\mathsf {UF_{wob}}(\omega )$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(iii) “No free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”
$<2^{\aleph _{0}}$
”
 $+ \mathsf {UF_{wob}}(\omega )$
implies
$+ \mathsf {UF_{wob}}(\omega )$
implies
 $\mathsf {AC}(\mathbb {R})$
. Thus, by (ii),
$\mathsf {AC}(\mathbb {R})$
. Thus, by (ii),
 $\mathsf {MA}+\mathsf {UF_{wob}}(\omega )$
implies
$\mathsf {MA}+\mathsf {UF_{wob}}(\omega )$
implies
 $\mathsf {AC}(\mathbb {R})$
. Furthermore, by Theorem 4.1 and (i),
$\mathsf {AC}(\mathbb {R})$
. Furthermore, by Theorem 4.1 and (i),
 $\mathsf {MA}$
does not imply
$\mathsf {MA}$
does not imply
 $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(iv)
 $\mathsf {AC}(\mathbb {R})$
(and thus
$\mathsf {AC}(\mathbb {R})$
(and thus
 $\mathsf {UF_{wob}}(\omega )$
) does not imply “no free ultrafilter on
$\mathsf {UF_{wob}}(\omega )$
) does not imply “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
” in
$<2^{\aleph _{0}}$
” in
 $\mathsf {ZF}$
. Hence, by (ii),
$\mathsf {ZF}$
. Hence, by (ii),
 $\mathsf {AC}(\mathbb {R})$
(and thus
$\mathsf {AC}(\mathbb {R})$
(and thus
 $\mathsf {UF_{wob}}(\omega ))$
does not imply
$\mathsf {UF_{wob}}(\omega ))$
does not imply
 $\mathsf {MA}$
in
$\mathsf {MA}$
in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(v)
 $\mathsf {CH}$
implies “no free ultrafilter on
$\mathsf {CH}$
implies “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”
$<2^{\aleph _{0}}$
”
 $+ \mathsf {UF_{wob}}(\omega )$
, and the implication is not reversible in
$+ \mathsf {UF_{wob}}(\omega )$
, and the implication is not reversible in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
. -
(vi) “
 $\aleph _{1}\not \leq 2^{\aleph _{0}}$
” implies “no free ultrafilter on
$\aleph _{1}\not \leq 2^{\aleph _{0}}$
” implies “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”, and the implication is not reversible in
$<2^{\aleph _{0}}$
”, and the implication is not reversible in
 $\mathsf {ZF}$
.
$\mathsf {ZF}$
.
Proof. (i) In Solovay’s model
![]() $L(\mathbb {R})$
[Reference Howard and Rubin11, Model
$L(\mathbb {R})$
[Reference Howard and Rubin11, Model
![]() $5\left(\mathrm{\aleph}\right)$
],
$5\left(\mathrm{\aleph}\right)$
],
![]() $\aleph _{1}\not \le 2^{\aleph _{0}}$
, and hence the only well-orderable subsets of
$\aleph _{1}\not \le 2^{\aleph _{0}}$
, and hence the only well-orderable subsets of
![]() $\mathbb {R}$
in
$\mathbb {R}$
in
![]() $L(\mathbb {R})$
are the countable ones. It follows that in
$L(\mathbb {R})$
are the countable ones. It follows that in
![]() $L(\mathbb {R})$
,
$L(\mathbb {R})$
,
![]() $\mathsf {MA}$
is equivalent to
$\mathsf {MA}$
is equivalent to
![]() $\mathsf {MA}(\aleph _{0})$
. Since
$\mathsf {MA}(\aleph _{0})$
. Since
![]() $\mathsf {DC}$
implies
$\mathsf {DC}$
implies
![]() $\mathsf {MA}(\aleph _{0})$
(see Kunen [Reference Kunen16, Lemma 2.6(c), pp. 54–55]) and
$\mathsf {MA}(\aleph _{0})$
(see Kunen [Reference Kunen16, Lemma 2.6(c), pp. 54–55]) and
![]() $\mathsf {DC}$
is true in
$\mathsf {DC}$
is true in
![]() $L(\mathbb {R})$
, we conclude that
$L(\mathbb {R})$
, we conclude that
![]() $\mathsf {MA}$
is true in
$\mathsf {MA}$
is true in
![]() $L(\mathbb {R})$
. However,
$L(\mathbb {R})$
. However,
![]() $\mathsf {UF}(\omega )$
is false in
$\mathsf {UF}(\omega )$
is false in
![]() $L(\mathbb {R})$
, and thus so is
$L(\mathbb {R})$
, and thus so is
![]() $\mathsf {UF_{wob}}(\omega )$
.
$\mathsf {UF_{wob}}(\omega )$
.
(ii) Assume
![]() $\mathsf {MA}$
. By way of contradiction, suppose that there exists a free ultrafilter
$\mathsf {MA}$
. By way of contradiction, suppose that there exists a free ultrafilter
![]() $\mathscr {U}$
on
$\mathscr {U}$
on
![]() $\omega $
with a well-orderable base
$\omega $
with a well-orderable base
![]() $\mathscr {B}$
such that
$\mathscr {B}$
such that
![]() $|\mathscr {B}|<2^{\aleph _{0}}$
. We let
$|\mathscr {B}|<2^{\aleph _{0}}$
. We let
and define a binary relation
![]() $\preceq $
on P by stipulating, for all
$\preceq $
on P by stipulating, for all
![]() $(x,y),(z,w)\in P$
,
$(x,y),(z,w)\in P$
,
It is easy to verify that
![]() $\preceq $
is a partial order on P. Furthermore, since
$\preceq $
is a partial order on P. Furthermore, since
![]() $|[\omega ]^{<\omega }|=\aleph _{0}$
, it follows that
$|[\omega ]^{<\omega }|=\aleph _{0}$
, it follows that
![]() $|P|=\aleph _{0}$
. Hence, the poset
$|P|=\aleph _{0}$
. Hence, the poset
![]() $(P,\preceq )$
has the c.c.c.
$(P,\preceq )$
has the c.c.c.
For each
![]() $B\in \mathscr {B}$
, we let
$B\in \mathscr {B}$
, we let
Claim 5.24. For every
![]() $B\in \mathscr {B}$
,
$B\in \mathscr {B}$
,
![]() $D_{B}$
is dense in P.
$D_{B}$
is dense in P.
Proof. Fix
![]() $B\in \mathscr {B}$
and let
$B\in \mathscr {B}$
and let
![]() $(z,w)\in P$
. Since
$(z,w)\in P$
. Since
![]() $\mathscr {U}$
is a free filter, every element of
$\mathscr {U}$
is a free filter, every element of
![]() $\mathscr {U}$
is an infinite set, and so B is infinite since
$\mathscr {U}$
is an infinite set, and so B is infinite since
![]() $B\in \mathscr {B}\subseteq \mathscr {U}$
. Therefore, there exist distinct elements
$B\in \mathscr {B}\subseteq \mathscr {U}$
. Therefore, there exist distinct elements
![]() $b_1$
and
$b_1$
and
![]() $b_2$
of B such that
$b_2$
of B such that
![]() $\{b_1,b_2\}\cap (z\cup w)=\emptyset $
. Let
$\{b_1,b_2\}\cap (z\cup w)=\emptyset $
. Let
![]() $x=z\cup \{b_{1}\}$
and
$x=z\cup \{b_{1}\}$
and
![]() $y=w\cup \{b_{2}\}$
. Then
$y=w\cup \{b_{2}\}$
. Then
![]() $(x,y)\in D_{B}$
and
$(x,y)\in D_{B}$
and
![]() $(x,y)\preceq (z,w)$
. Thus,
$(x,y)\preceq (z,w)$
. Thus,
![]() $D_{B}$
is dense in P, as required.
$D_{B}$
is dense in P, as required.
We let
Then we have:
since the mapping
![]() $B\mapsto D_{B}$
,
$B\mapsto D_{B}$
,
![]() $B\in \mathscr {B}$
, is onto, and thus
$B\in \mathscr {B}$
, is onto, and thus
![]() $|\mathcal {D}|\le |\mathscr {B}|$
since
$|\mathcal {D}|\le |\mathscr {B}|$
since
![]() $\mathscr {B}$
is well ordered. By
$\mathscr {B}$
is well ordered. By
![]() $\mathsf {MA}$
(in particular, by
$\mathsf {MA}$
(in particular, by
![]() $\mathsf {MA}(|\mathscr {B}|)$
) applied to
$\mathsf {MA}(|\mathscr {B}|)$
) applied to
![]() $(P,\preceq )$
and
$(P,\preceq )$
and
![]() $\mathcal {D}$
, we obtain a
$\mathcal {D}$
, we obtain a
![]() $\mathcal {D}$
-generic filter in P, G say. Let
$\mathcal {D}$
-generic filter in P, G say. Let
Claim 5.25.
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
are infinite disjoint sets.
$F_{2}$
are infinite disjoint sets.
Proof. If, for some
![]() $i\in \{1,2\}$
,
$i\in \{1,2\}$
,
![]() $F_{i}$
is finite, then since
$F_{i}$
is finite, then since
![]() $\mathscr {U}$
is a free ultrafilter,
$\mathscr {U}$
is a free ultrafilter,
![]() $\omega \setminus F_{i}\in \mathscr {U}$
. Since
$\omega \setminus F_{i}\in \mathscr {U}$
. Since
![]() $\mathscr {B}$
is a base for
$\mathscr {B}$
is a base for
![]() $\mathscr {U}$
, there exists
$\mathscr {U}$
, there exists
![]() $B\in \mathscr {B}$
such that
$B\in \mathscr {B}$
such that
![]() $B\subseteq \omega \setminus F_{i}$
. As G is a
$B\subseteq \omega \setminus F_{i}$
. As G is a
![]() $\mathcal {D}$
-generic filter in P,
$\mathcal {D}$
-generic filter in P,
![]() $G\cap D_{B}\ne \emptyset $
. So, let
$G\cap D_{B}\ne \emptyset $
. So, let
![]() $(x,y)\in G\cap D_{B}$
. By (10) and (11), we obtain that
$(x,y)\in G\cap D_{B}$
. By (10) and (11), we obtain that
![]() $x\subseteq F_{1}$
,
$x\subseteq F_{1}$
,
![]() $y\subseteq F_{2}$
,
$y\subseteq F_{2}$
,
![]() $B\cap x\ne \emptyset $
, and
$B\cap x\ne \emptyset $
, and
![]() $B\cap y\ne \emptyset $
, which is a contradiction since
$B\cap y\ne \emptyset $
, which is a contradiction since
![]() $B\subseteq \omega \setminus F_{i}$
. Therefore,
$B\subseteq \omega \setminus F_{i}$
. Therefore,
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
are infinite.
$F_{2}$
are infinite.
For the second assertion of the claim, assume on the contrary that
![]() $F_{1}\cap F_{2}\neq \emptyset $
. Let
$F_{1}\cap F_{2}\neq \emptyset $
. Let
![]() $r\in F_{1}\cap F_{2}$
. By (11), there exist
$r\in F_{1}\cap F_{2}$
. By (11), there exist
![]() $(x_{1},y_{1}),(x_{2},y_{2})\in G$
such that
$(x_{1},y_{1}),(x_{2},y_{2})\in G$
such that
![]() $r\in x_{1}\cap y_{2}$
. Since G is a filter in P, there exists
$r\in x_{1}\cap y_{2}$
. Since G is a filter in P, there exists
![]() $(x_3,y_3)\in G$
such that
$(x_3,y_3)\in G$
such that
![]() $(x_3,y_3)\preceq (x_1,y_1)$
and
$(x_3,y_3)\preceq (x_1,y_1)$
and
![]() $(x_3,y_3)\preceq (x_2,y_2)$
. By definition of
$(x_3,y_3)\preceq (x_2,y_2)$
. By definition of
![]() $\preceq $
, we have
$\preceq $
, we have
![]() $x_1\subseteq x_3$
and
$x_1\subseteq x_3$
and
![]() $y_2\subseteq y_3$
, and thus
$y_2\subseteq y_3$
, and thus
![]() ${r\in x_3\cap y_3}$
. But this contradicts the fact
${r\in x_3\cap y_3}$
. But this contradicts the fact
![]() $x_3\cap y_3=\emptyset $
since
$x_3\cap y_3=\emptyset $
since
![]() $(x_3,y_3)\in P$
. Therefore,
$(x_3,y_3)\in P$
. Therefore,
![]() $F_{1}$
and
$F_{1}$
and
![]() $F_{2}$
are disjoint, finishing the proof of the claim.
$F_{2}$
are disjoint, finishing the proof of the claim.
Now, we let
Claim 5.26. The families
![]() $\mathscr {C}_1$
and
$\mathscr {C}_1$
and
![]() $\mathscr {C}_2$
have the finite intersection property.
$\mathscr {C}_2$
have the finite intersection property.
Proof. Let
![]() $\mathcal {B}\in [\mathscr {B}]^{<\omega }\setminus \{\emptyset \}$
. Since
$\mathcal {B}\in [\mathscr {B}]^{<\omega }\setminus \{\emptyset \}$
. Since
![]() $\mathscr {B}$
is a filter base, there exists
$\mathscr {B}$
is a filter base, there exists
![]() $B\in \mathscr {B}$
such that
$B\in \mathscr {B}$
such that
![]() $B\subseteq \bigcap \mathcal {B}$
. Since G is
$B\subseteq \bigcap \mathcal {B}$
. Since G is
![]() $\mathcal {D}$
-generic, we have
$\mathcal {D}$
-generic, we have
![]() $G\cap D_B\ne \emptyset $
, and so we may let
$G\cap D_B\ne \emptyset $
, and so we may let
![]() $(x,y)\in G\cap D_B$
. By (10) and (11), we obtain that
$(x,y)\in G\cap D_B$
. By (10) and (11), we obtain that
![]() $x\cap B\ne \emptyset $
and
$x\cap B\ne \emptyset $
and
![]() $x\subseteq F_1$
. So,
$x\subseteq F_1$
. So,
![]() $F_1\cap B\ne \emptyset $
, and consequently (as
$F_1\cap B\ne \emptyset $
, and consequently (as
![]() $B\subseteq \bigcap \mathcal {B}$
)
$B\subseteq \bigcap \mathcal {B}$
)
![]() $F_1\cap (\bigcap \mathcal {B})\ne \emptyset $
. Thus,
$F_1\cap (\bigcap \mathcal {B})\ne \emptyset $
. Thus,
![]() $\mathscr {C}_1$
has the finite intersection property. The argument that
$\mathscr {C}_1$
has the finite intersection property. The argument that
![]() $\mathscr {C}_2$
also has the finite intersection property is fairly similar to the one for
$\mathscr {C}_2$
also has the finite intersection property is fairly similar to the one for
![]() $\mathscr {C}_{1}$
, and thus is left to the reader.
$\mathscr {C}_{1}$
, and thus is left to the reader.
Since
![]() $\mathscr {B}$
is a base for
$\mathscr {B}$
is a base for
![]() $\mathscr {U}$
and (by Claim 5.26)
$\mathscr {U}$
and (by Claim 5.26)
![]() $\mathscr {C}_{1}$
and
$\mathscr {C}_{1}$
and
![]() $\mathscr {C}_{2}$
have the finite intersection property, it follows that
$\mathscr {C}_{2}$
have the finite intersection property, it follows that
and thus, as
![]() $\mathscr {U}$
is an ultrafilter, we deduce that
$\mathscr {U}$
is an ultrafilter, we deduce that
This, together with Claim 5.25, yields a contradiction to the fact that
![]() $\mathscr {U}$
is a filter. Therefore,
$\mathscr {U}$
is a filter. Therefore,
![]() $\mathscr {U}$
cannot have a well-orderable base of cardinality
$\mathscr {U}$
cannot have a well-orderable base of cardinality
![]() $<2^{\aleph _{0}}$
, as required.
$<2^{\aleph _{0}}$
, as required.
For the second assertion of (ii), we first note that Tachtsis [Reference Tachtsis26] had constructed a Fraenkel–Mostowski permutation model
![]() $\mathcal {N}$
in which
$\mathcal {N}$
in which
![]() $\mathsf {CH}$
is true, but
$\mathsf {CH}$
is true, but
![]() $\mathsf {MA}(\aleph _{0})$
(and thus
$\mathsf {MA}(\aleph _{0})$
(and thus
![]() $\mathsf {MA}$
) is false (see [Reference Tachtsis26, Theorem 2.15]). By Remark 4.3, it follows that “no free ultrafilter on
$\mathsf {MA}$
) is false (see [Reference Tachtsis26, Theorem 2.15]). By Remark 4.3, it follows that “no free ultrafilter on
![]() $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
![]() $< 2^{\aleph _{0}}$
” is true in
$< 2^{\aleph _{0}}$
” is true in
![]() $\mathcal {N}$
. On the other hand, it is easy to verify that the latter statement and
$\mathcal {N}$
. On the other hand, it is easy to verify that the latter statement and
![]() $\neg \mathsf {MA}(\aleph _{0})$
are both boundable (for the definition of the term “boundable statement”, see [Reference Howard and Rubin11, Note 103] or [Reference Jech13, Problem 1, p. 94]), and that this yields their conjunction is also boundable. Since this conjunction has a permutation model, it follows from the Jech–Sochor First Embedding Theorem [Reference Jech13, Theorem 6.1] that it also has a symmetric model of
$\neg \mathsf {MA}(\aleph _{0})$
are both boundable (for the definition of the term “boundable statement”, see [Reference Howard and Rubin11, Note 103] or [Reference Jech13, Problem 1, p. 94]), and that this yields their conjunction is also boundable. Since this conjunction has a permutation model, it follows from the Jech–Sochor First Embedding Theorem [Reference Jech13, Theorem 6.1] that it also has a symmetric model of
![]() $\mathsf {ZF}$
. Therefore, “no free ultrafilter on
$\mathsf {ZF}$
. Therefore, “no free ultrafilter on
![]() $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
![]() $< 2^{\aleph _{0}}$
” does not imply
$< 2^{\aleph _{0}}$
” does not imply
![]() $\mathsf {MA}$
in
$\mathsf {MA}$
in
![]() $\mathsf {ZF}$
, as required.
$\mathsf {ZF}$
, as required.
(iii) The first assertion follows immediately from the hypothesis and the fact that any base for a filter on
![]() $\omega $
has cardinality
$\omega $
has cardinality
![]() $\leq 2^{\aleph _{0}}$
.
$\leq 2^{\aleph _{0}}$
.
(iv) As mentioned in the paragraph preceding Theorem 5.20, there is a model of
![]() $\mathsf {ZFC}$
in which
$\mathsf {ZFC}$
in which
![]() $\aleph _{1}< 2^{\aleph _{0}}$
and there exists a free ultrafilter on
$\aleph _{1}< 2^{\aleph _{0}}$
and there exists a free ultrafilter on
![]() $\omega $
having a base of cardinality
$\omega $
having a base of cardinality
![]() $\aleph _{1}$
; see Kunen [Reference Kunen16, Exercise (A10), p. 289]. Thus, in that model,
$\aleph _{1}$
; see Kunen [Reference Kunen16, Exercise (A10), p. 289]. Thus, in that model,
![]() $\mathsf {AC}(\mathbb {R})$
(and hence
$\mathsf {AC}(\mathbb {R})$
(and hence
![]() $\mathsf {UF_{wob}}(\omega )$
) is true, whereas “no free ultrafilter on
$\mathsf {UF_{wob}}(\omega )$
) is true, whereas “no free ultrafilter on
![]() $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
![]() $< 2^{\aleph _{0}}$
” (and thus
$< 2^{\aleph _{0}}$
” (and thus
![]() $\mathsf {MA}$
by part (ii)) is false.
$\mathsf {MA}$
by part (ii)) is false.
(v) The first assertion follows from Theorem 4.1 and Claim 4.2 of the proof of that theorem.
The second assertion follows from (ii), Theorem 4.1, and Corollary 6.4 on p. 281 of [Reference Kunen16] which states that if
![]() $\mathsf {ZFC}$
is consistent, then so is
$\mathsf {ZFC}$
is consistent, then so is
![]() $\mathsf {ZFC}+\mathsf {MA}+ 2^{\omega }=\omega _{83}$
.
$\mathsf {ZFC}+\mathsf {MA}+ 2^{\omega }=\omega _{83}$
.
(vi) This follows immediately from Claim 4.2 of the proof of Theorem 4.1 and the proof of part (v).
Remark 5.27.
-
(1) By Theorem 5.23(iii) and the fact (from [Reference Herzberg, Kanovei, Katz and Lyubetsky9]) that
 ${\mathsf {DC}+\mathsf {UF_{wob}}(\omega )}$
does not imply
${\mathsf {DC}+\mathsf {UF_{wob}}(\omega )}$
does not imply
 $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
 $\mathsf {ZF}$
, it follows that in
$\mathsf {ZF}$
, it follows that in
 $\mathsf {ZF}$
,
$\mathsf {ZF}$
,  $$ \begin{align*}&\mathsf{DC}\nRightarrow\text{"no free ultrafilter on }\omega\text{ has a well-orderable base of}\\ &\quad\text{ cardinality }<2^{\aleph_{0}}\text{"}.\end{align*} $$
$$ \begin{align*}&\mathsf{DC}\nRightarrow\text{"no free ultrafilter on }\omega\text{ has a well-orderable base of}\\ &\quad\text{ cardinality }<2^{\aleph_{0}}\text{"}.\end{align*} $$
In particular, as
 $\mathsf {DC}$
implies
$\mathsf {DC}$
implies
 $\mathsf {MA}(\aleph _{0})$
, we have that in
$\mathsf {MA}(\aleph _{0})$
, we have that in
 $\mathsf {ZF}$
,
$\mathsf {ZF}$
,  $$ \begin{align*}&\mathsf{MA}(\aleph_{0})\nRightarrow\text{"no free ultrafilter on }\omega\text{ has a well-orderable base of}\\ &\quad\text{cardinality } <2^{\aleph_{0}}\text{"}.\end{align*} $$
$$ \begin{align*}&\mathsf{MA}(\aleph_{0})\nRightarrow\text{"no free ultrafilter on }\omega\text{ has a well-orderable base of}\\ &\quad\text{cardinality } <2^{\aleph_{0}}\text{"}.\end{align*} $$
-
(2) Since Solovay’s model
 $L(\mathbb {R})$
satisfies “
$L(\mathbb {R})$
satisfies “
 $\aleph _{1}\nleq 2^{\aleph _{0}}$
”, it follows from Theorem 5.23(vi) that
$\aleph _{1}\nleq 2^{\aleph _{0}}$
”, it follows from Theorem 5.23(vi) that
 $L(\mathbb {R})$
also satisfies “no free ultrafilter on
$L(\mathbb {R})$
also satisfies “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
”. This is also readily derivable from the fact that
$<2^{\aleph _{0}}$
”. This is also readily derivable from the fact that
 $\mathsf {UF_{wob}}(\omega )$
is false in
$\mathsf {UF_{wob}}(\omega )$
is false in
 $L(\mathbb {R})$
(see Theorems 4.1, 5.13). Furthermore, as
$L(\mathbb {R})$
(see Theorems 4.1, 5.13). Furthermore, as
 $L(\mathbb {R})$
satisfies
$L(\mathbb {R})$
satisfies
 $\mathsf {DC}$
, we obtain that in
$\mathsf {DC}$
, we obtain that in
 $\mathsf {ZF}$
,
$\mathsf {ZF}$
,  $$ \begin{align*} &\mathsf{DC}+\text{"no free ultrafilter on }\omega\text{ has a well-orderable base of cardinality}\\ &\quad<2^{\aleph_{0}}\text{"}\nRightarrow\mathsf{UF_{wob}}(\omega). \end{align*} $$
$$ \begin{align*} &\mathsf{DC}+\text{"no free ultrafilter on }\omega\text{ has a well-orderable base of cardinality}\\ &\quad<2^{\aleph_{0}}\text{"}\nRightarrow\mathsf{UF_{wob}}(\omega). \end{align*} $$
-
(3) From the proofs of Theorem 5.13 and Theorem 5.23(i), we infer that
 $$ \begin{align*}\mathsf{MA}\nRightarrow\mathsf{BPI}\text{ in }\mathsf{ZF}.\end{align*} $$
$$ \begin{align*}\mathsf{MA}\nRightarrow\mathsf{BPI}\text{ in }\mathsf{ZF}.\end{align*} $$
In particular, Solovay’s model
 $L(\mathbb {R})$
[Reference Howard and Rubin11, Model
$L(\mathbb {R})$
[Reference Howard and Rubin11, Model
 $5\left(\mathrm{\aleph}\right)$
] satisfies
$5\left(\mathrm{\aleph}\right)$
] satisfies
 $\mathsf {MA}\wedge \neg \mathsf {BPI}$
. On the other hand, in Howard and Rubin [Reference Howard and Rubin11], no model (either a permutation model or a forcing model) is specified for
$\mathsf {MA}\wedge \neg \mathsf {BPI}$
. On the other hand, in Howard and Rubin [Reference Howard and Rubin11], no model (either a permutation model or a forcing model) is specified for
 $\mathsf {BPI}\wedge \neg \mathsf {MA}$
. However, from Tachtsis [Reference Tachtsis27], it follows that
$\mathsf {BPI}\wedge \neg \mathsf {MA}$
. However, from Tachtsis [Reference Tachtsis27], it follows that  $$ \begin{align*}\mathsf{BPI}\nRightarrow\mathsf{MA}\text{ in }\mathsf{ZF}.\end{align*} $$
$$ \begin{align*}\mathsf{BPI}\nRightarrow\mathsf{MA}\text{ in }\mathsf{ZF}.\end{align*} $$
Indeed, in [Reference Tachtsis27, Theorem 3.7], it was shown that
 $\mathsf {MA}(\aleph _{0})$
for complete Boolean algebras is false in the Mostowski Linearly Ordered Model [Reference Howard and Rubin11, Model
$\mathsf {MA}(\aleph _{0})$
for complete Boolean algebras is false in the Mostowski Linearly Ordered Model [Reference Howard and Rubin11, Model
 $\mathcal{N}3$
] in which
$\mathcal{N}3$
] in which
 $\mathsf {BPI}$
is famously known to be true (see Halpern [Reference Halpern7]). By a transfer theorem of Pincus which states: If a conjunction of injectively boundable statements and
$\mathsf {BPI}$
is famously known to be true (see Halpern [Reference Halpern7]). By a transfer theorem of Pincus which states: If a conjunction of injectively boundable statements and
 $\mathsf {BPI}$
has a permutation model, then it also has a
$\mathsf {BPI}$
has a permutation model, then it also has a
 $\mathsf {ZF}$
-model (see Pincus [Reference Pincus21, Added in proof] or Howard and Rubin [Reference Howard and Rubin11, third theorem, p. 286], and for the definition of the term “injectively boundable statement” see [Reference Howard and Rubin11, Note 103] or Pincus [Reference Pincus20]), it follows that
$\mathsf {ZF}$
-model (see Pincus [Reference Pincus21, Added in proof] or Howard and Rubin [Reference Howard and Rubin11, third theorem, p. 286], and for the definition of the term “injectively boundable statement” see [Reference Howard and Rubin11, Note 103] or Pincus [Reference Pincus20]), it follows that
 $\mathsf {BPI}\wedge \neg \mathsf {MA}(\aleph _{0})$
is relatively consistent with
$\mathsf {BPI}\wedge \neg \mathsf {MA}(\aleph _{0})$
is relatively consistent with
 $\mathsf {ZF}$
(and note that
$\mathsf {ZF}$
(and note that
 $\neg \mathsf {MA}(\aleph _{0})$
is a boundable, and thus injectively boundable statement).
$\neg \mathsf {MA}(\aleph _{0})$
is a boundable, and thus injectively boundable statement).Let us note here that it is an open question whether or not
 $\mathsf {MA}(\aleph _{0})$
is false in the Basic Cohen Model [Reference Howard and Rubin11, Model
$\mathsf {MA}(\aleph _{0})$
is false in the Basic Cohen Model [Reference Howard and Rubin11, Model
 $1$
]—this question has also been posed by Tachtsis [Reference Tachtsis27, Problem 3.17(3)].
$1$
]—this question has also been posed by Tachtsis [Reference Tachtsis27, Problem 3.17(3)].
6 Open questions
-
(1) Does
 $\mathsf {UF_{wob}}(\omega )$
imply any of the following principles: “
$\mathsf {UF_{wob}}(\omega )$
imply any of the following principles: “
 $\aleph _{1}$
is regular”;
$\aleph _{1}$
is regular”;
 $\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
;
$\mathsf {AC}^{\aleph _{0}}(\mathbb {R})$
;
 $\mathsf {AC}^{\aleph _{0}}_{\aleph _{0}}(\mathbb {R})$
(that is,
$\mathsf {AC}^{\aleph _{0}}_{\aleph _{0}}(\mathbb {R})$
(that is,
 $\mathsf {AC}$
restricted to denumerable sets of denumerable subsets of
$\mathsf {AC}$
restricted to denumerable sets of denumerable subsets of
 $\mathbb {R}$
—also see [Reference Howard and Rubin11, Form 5]);
$\mathbb {R}$
—also see [Reference Howard and Rubin11, Form 5]);
 $\mathsf {CUT}(\mathbb {R}); \mathsf {DFF}(\mathbb {R})$
; and
$\mathsf {CUT}(\mathbb {R}); \mathsf {DFF}(\mathbb {R})$
; and
 $\mathsf {BPI}(\omega )$
.
$\mathsf {BPI}(\omega )$
. -
(2) Does
 $\mathsf {UF_{wob}}(\omega )+\mathsf {AC^{WO}}(\mathbb {R})$
(i.e., “every well-orderable family of non-empty subsets of
$\mathsf {UF_{wob}}(\omega )+\mathsf {AC^{WO}}(\mathbb {R})$
(i.e., “every well-orderable family of non-empty subsets of
 $\mathbb {R}$
has a choice function”) imply:
$\mathbb {R}$
has a choice function”) imply:-
(a)
 $\mathsf {AC}(\mathbb {R})$
(recall that
$\mathsf {AC}(\mathbb {R})$
(recall that
 $\mathsf {UF_{wob}}(\omega )+\mathsf {AC}^{\aleph _{0}}(\mathbb {R})\nRightarrow \mathsf {AC}(\mathbb {R})$
); or
$\mathsf {UF_{wob}}(\omega )+\mathsf {AC}^{\aleph _{0}}(\mathbb {R})\nRightarrow \mathsf {AC}(\mathbb {R})$
); or -
(b) “Every continuum sized family of non-empty subsets of
 $\mathbb {R}$
has a choice function”; or
$\mathbb {R}$
has a choice function”; or -
(c) “Every family of pairwise disjoint non-empty subsets of
 $\mathbb {R}$
has a choice function”; or
$\mathbb {R}$
has a choice function”; or -
(d) “Every partition of
 $\mathbb {R}$
has cardinality
$\mathbb {R}$
has cardinality
 $\leq 2^{\aleph _{0}}$
”.
$\leq 2^{\aleph _{0}}$
”.
The weak choice principles given by (b) and (c) are, respectively, Form 212 and Form 203 in [Reference Howard and Rubin11]; 212 is strictly weaker than 203 in
 $\mathsf {ZF}$
(see Truss [Reference Truss28]). We also note that it is a long-standing open problem whether or not 203 implies
$\mathsf {ZF}$
(see Truss [Reference Truss28]). We also note that it is a long-standing open problem whether or not 203 implies
 $\mathsf {AC}(\mathbb {R})$
in
$\mathsf {AC}(\mathbb {R})$
in
 $\mathsf {ZF}$
. Furthermore,
$\mathsf {ZF}$
. Furthermore,
 $\mathsf {AC}^{\aleph _{0}}$
is strictly weaker than
$\mathsf {AC}^{\aleph _{0}}$
is strictly weaker than
 $\mathsf {AC^{WO}}$
(the axiom of well-ordered choice) in
$\mathsf {AC^{WO}}$
(the axiom of well-ordered choice) in
 $\mathsf {ZF}$
since in Solovay’s model
$\mathsf {ZF}$
since in Solovay’s model
 $L(\mathbb {R})$
,
$L(\mathbb {R})$
,
 $\mathsf {DC}$
(and thus
$\mathsf {DC}$
(and thus
 $\mathsf {AC}^{\aleph _{0}}$
) and “
$\mathsf {AC}^{\aleph _{0}}$
) and “
 $\aleph _{1}\nleq 2^{\aleph _{0}}$
” are true; thus
$\aleph _{1}\nleq 2^{\aleph _{0}}$
” are true; thus
 $\mathsf {AC^{WO}}(\mathbb {R})$
is false in
$\mathsf {AC^{WO}}(\mathbb {R})$
is false in
 $L(\mathbb {R})$
—recall that in
$L(\mathbb {R})$
—recall that in
 $\mathsf {ZF}$
, there is a partition of
$\mathsf {ZF}$
, there is a partition of
 $\mathbb {R}$
of cardinality
$\mathbb {R}$
of cardinality
 $\aleph _{1}$
(see Jech [Reference Jech13, Hint for Problem 2, p. 148]).
$\aleph _{1}$
(see Jech [Reference Jech13, Hint for Problem 2, p. 148]). -
-
(3) Is
 $\mathsf {UF}(\omega )$
true in the Feferman–Lévy model [Reference Howard and Rubin11, Model
$\mathsf {UF}(\omega )$
true in the Feferman–Lévy model [Reference Howard and Rubin11, Model
 $\mathcal{M}9$
]?
$\mathcal{M}9$
]? -
(4) Is
 $\mathsf {ZF}+\mathsf {BPI}+\neg \mathsf {UF_{wob}}(\omega )$
relatively consistent with
$\mathsf {ZF}+\mathsf {BPI}+\neg \mathsf {UF_{wob}}(\omega )$
relatively consistent with
 $\mathsf {ZFC}$
?
$\mathsf {ZFC}$
? -
(5) Is
 $\mathsf {UF_{wob}}(\omega )$
false in the Basic Cohen Model [Reference Howard and Rubin11, Model
$\mathsf {UF_{wob}}(\omega )$
false in the Basic Cohen Model [Reference Howard and Rubin11, Model
 $1$
]?
$1$
]? -
(6) Does
 $\mathsf {BPI}(\omega )$
imply “there exists a free ultrafilter on
$\mathsf {BPI}(\omega )$
imply “there exists a free ultrafilter on
 $\omega $
which has no base of cardinality
$\omega $
which has no base of cardinality
 $<2^{\aleph _{0}}$
”?
$<2^{\aleph _{0}}$
”? -
(7) What is the status of “there exists a free ultrafilter on
 $\omega $
which has no base of cardinality
$\omega $
which has no base of cardinality
 $<2^{\aleph _{0}}$
” in the Basic Cohen Model?
$<2^{\aleph _{0}}$
” in the Basic Cohen Model? -
(8) Is the statement “no free ultrafilter on
 $\omega $
has a well-orderable base of cardinality
$\omega $
has a well-orderable base of cardinality
 $<2^{\aleph _{0}}$
” true in the Basic Cohen Model?
$<2^{\aleph _{0}}$
” true in the Basic Cohen Model?
7 Appendix: A brief account of the construction of symmetric extension models of
 $\mathsf {ZF}$
$\mathsf {ZF}$
Assume that M is a countable transitive model of
![]() $\mathsf {ZFC}$
and that
$\mathsf {ZFC}$
and that
![]() $(\mathbb {P},\leq )\in M$
is a poset with a maximum element denoted by
$(\mathbb {P},\leq )\in M$
is a poset with a maximum element denoted by
![]() $\mathbf {1}_{\mathbb {P}}$
; such a poset
$\mathbf {1}_{\mathbb {P}}$
; such a poset
![]() $(\mathbb {P},\leq )$
in M is said to be a notion of forcing. Let
$(\mathbb {P},\leq )$
in M is said to be a notion of forcing. Let
![]() $M^{\mathbb {P}}$
be the (proper) class of all
$M^{\mathbb {P}}$
be the (proper) class of all
![]() $\mathbb {P}$
-names, which is defined by transfinite recursion within M (see [Reference Kunen16, Definitions 2.5 and 2.6, pp. 188–189]). We denote a
$\mathbb {P}$
-names, which is defined by transfinite recursion within M (see [Reference Kunen16, Definitions 2.5 and 2.6, pp. 188–189]). We denote a
![]() $\mathbb {P}$
-name by
$\mathbb {P}$
-name by
![]() $\dot {x}$
and, following the notation of [Reference Kunen16, Definition 2.10, p. 190], for
$\dot {x}$
and, following the notation of [Reference Kunen16, Definition 2.10, p. 190], for
![]() $x\in M$
, we denote by
$x\in M$
, we denote by
![]() $\check {x}$
the canonical name
$\check {x}$
the canonical name
![]() $\{(\check {y},\mathbf {1}_{\mathbb {P}}):y\in x\}$
for x.
$\{(\check {y},\mathbf {1}_{\mathbb {P}}):y\in x\}$
for x.
If
![]() $\phi $
is an order-automorphism of
$\phi $
is an order-automorphism of
![]() $(\mathbb {P},\leq )$
, then
$(\mathbb {P},\leq )$
, then
![]() $\phi $
can be extended to an automorphism
$\phi $
can be extended to an automorphism
![]() $\tilde {\phi }$
of
$\tilde {\phi }$
of
![]() $M^{\mathbb {P}}$
defined by recursion,
$M^{\mathbb {P}}$
defined by recursion,
For every
![]() $x\in M$
,
$x\in M$
,
![]() $\tilde {\phi }(\check {x})=\check {x}$
. We use
$\tilde {\phi }(\check {x})=\check {x}$
. We use
![]() $\phi $
to denote both the automorphism of
$\phi $
to denote both the automorphism of
![]() $(\mathbb {P},\leq )$
and the automorphism
$(\mathbb {P},\leq )$
and the automorphism
![]() $\tilde {\phi }$
of the
$\tilde {\phi }$
of the
![]() $\mathbb {P}$
-names.
$\mathbb {P}$
-names.
Let
![]() $\mathcal {G}$
be a group of order-automorphisms of
$\mathcal {G}$
be a group of order-automorphisms of
![]() $(\mathbb {P},\leq )$
, and also let
$(\mathbb {P},\leq )$
, and also let
![]() $\Gamma $
be a normal filter on
$\Gamma $
be a normal filter on
![]() $\mathcal {G}$
, that is,
$\mathcal {G}$
, that is,
![]() $\Gamma $
is a filter of subgroups of
$\Gamma $
is a filter of subgroups of
![]() $\mathcal {G}$
closed under conjugation, i.e., for all
$\mathcal {G}$
closed under conjugation, i.e., for all
![]() $\phi \in \mathcal {G}$
and
$\phi \in \mathcal {G}$
and
![]() $H\in \Gamma $
,
$H\in \Gamma $
,
![]() $\phi H\phi ^{-1}\in \Gamma $
. A
$\phi H\phi ^{-1}\in \Gamma $
. A
![]() $\mathbb {P}$
-name
$\mathbb {P}$
-name
![]() $\dot {x}$
is called
$\dot {x}$
is called
![]() $\Gamma $
-symmetric if
$\Gamma $
-symmetric if
![]() $\operatorname {\mathrm {{sym}}}_{\mathcal {G}}(\dot {x})\in \Gamma $
, where
$\operatorname {\mathrm {{sym}}}_{\mathcal {G}}(\dot {x})\in \Gamma $
, where
![]() $\operatorname {\mathrm {{sym}}}_{\mathcal {G}}(\dot {x})$
is the stabilizer of the name
$\operatorname {\mathrm {{sym}}}_{\mathcal {G}}(\dot {x})$
is the stabilizer of the name
![]() $\dot {x}$
, i.e., the subgroup
$\dot {x}$
, i.e., the subgroup
![]() $\{\phi \in \mathcal {G}:\phi (\dot {x})=\dot {x}\}$
of
$\{\phi \in \mathcal {G}:\phi (\dot {x})=\dot {x}\}$
of
![]() $\mathcal {G}$
.
$\mathcal {G}$
.
![]() $\dot {x}$
is called hereditarily
$\dot {x}$
is called hereditarily
![]() $\Gamma $
-symmetric if
$\Gamma $
-symmetric if
![]() $\dot {x}$
is
$\dot {x}$
is
![]() $\Gamma $
-symmetric and, for every
$\Gamma $
-symmetric and, for every
![]() $(\dot {y},p)\in \dot {x}$
,
$(\dot {y},p)\in \dot {x}$
,
![]() $\dot {y}$
is hereditarily
$\dot {y}$
is hereditarily
![]() $\Gamma $
-symmetric. The class of hereditarily
$\Gamma $
-symmetric. The class of hereditarily
![]() $\Gamma $
-symmetric
$\Gamma $
-symmetric
![]() $\mathbb {P}$
-names (which, in view of the above, is defined by transfinite recursion over the rank of
$\mathbb {P}$
-names (which, in view of the above, is defined by transfinite recursion over the rank of
![]() $\dot {x}$
) is denoted by
$\dot {x}$
) is denoted by
![]() $\operatorname {\mathrm {{HS}}}^{\Gamma }$
.
$\operatorname {\mathrm {{HS}}}^{\Gamma }$
.
Let G be a
![]() $\mathbb {P}$
-generic filter over M and also let
$\mathbb {P}$
-generic filter over M and also let
where
![]() $\dot {x}_{G}$
denotes the value of the name
$\dot {x}_{G}$
denotes the value of the name
![]() $\dot {x}$
by G, that is,
$\dot {x}$
by G, that is,
![]() $\dot {x}_{G}=\{\dot {y}_{G}:\exists p\in G((\dot {y},p)\in \dot {x})\}$
. Then, N is a transitive model of
$\dot {x}_{G}=\{\dot {y}_{G}:\exists p\in G((\dot {y},p)\in \dot {x})\}$
. Then, N is a transitive model of
![]() $\mathsf {ZF}$
and
$\mathsf {ZF}$
and
![]() $M\subseteq N\subseteq M[G]$
(see [Reference Halbeisen5, Proposition 17.1, p. 385], or [Reference Jech13, Section 5.2, p. 64]), where
$M\subseteq N\subseteq M[G]$
(see [Reference Halbeisen5, Proposition 17.1, p. 385], or [Reference Jech13, Section 5.2, p. 64]), where
![]() $M[G]=\{\dot {x}_{G}:\dot {x}\in M^{\mathbb {P}}\}$
is the generic extension model of M. N is called a symmetric extension model of M generated by
$M[G]=\{\dot {x}_{G}:\dot {x}\in M^{\mathbb {P}}\}$
is the generic extension model of M. N is called a symmetric extension model of M generated by
![]() $\Gamma $
.
$\Gamma $
.
Acknowledgements
The author is deeply grateful to Mauro Di Nasso whose inquiry about the deductive strength of
![]() $\mathsf {UF_{wob}}(\omega )$
motivated the research in this paper. I would also like to express my gratitude to the anonymous referee for careful reading and valuable comments and suggestions which helped improve the quality and the exposition of the paper.
$\mathsf {UF_{wob}}(\omega )$
motivated the research in this paper. I would also like to express my gratitude to the anonymous referee for careful reading and valuable comments and suggestions which helped improve the quality and the exposition of the paper.
Funding
The author declares no financial support for this research.