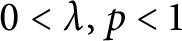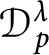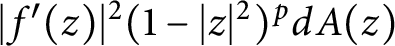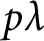1 Introduction
Let
![]() ${\mathbb D} $
and
${\mathbb D} $
and
![]() $\partial {\mathbb D}$
be the open unit disc and the unit circle in the complex plane, respectively. Denote by
$\partial {\mathbb D}$
be the open unit disc and the unit circle in the complex plane, respectively. Denote by
![]() $H({\mathbb D})$
the space of all analytic functions on
$H({\mathbb D})$
the space of all analytic functions on
![]() ${\mathbb D}$
. For any interval
${\mathbb D}$
. For any interval
![]() $I\subset \partial {\mathbb D}$
, let
$I\subset \partial {\mathbb D}$
, let
be the Carleson box based on I, where
![]() $|I|$
is the normalized arc length of I. Let
$|I|$
is the normalized arc length of I. Let
![]() $0<\alpha <\infty $
and
$0<\alpha <\infty $
and
![]() $\mu $
be a positive Borel measure on
$\mu $
be a positive Borel measure on
![]() ${\mathbb D}$
. We say that
${\mathbb D}$
. We say that
![]() $\mu $
is an
$\mu $
is an
![]() $\alpha $
-Carleson measure (see [Reference Pau and Zhao19]) if
$\alpha $
-Carleson measure (see [Reference Pau and Zhao19]) if
 $$ \begin{align*}\|\mu\|_{\alpha}=\sup_{I\subset \partial{\mathbb D}}{ \mu(S(I)) \over |I|^\alpha }< \infty.\end{align*} $$
$$ \begin{align*}\|\mu\|_{\alpha}=\sup_{I\subset \partial{\mathbb D}}{ \mu(S(I)) \over |I|^\alpha }< \infty.\end{align*} $$
![]() $\mu $
is the classical Carleson measure when
$\mu $
is the classical Carleson measure when
![]() $\alpha =1$
.
$\alpha =1$
.
For
![]() $0<p<\infty $
, the Hardy space
$0<p<\infty $
, the Hardy space
![]() $H^p$
is the set of all
$H^p$
is the set of all
![]() $f\in H(\mathbb {D})$
with
$f\in H(\mathbb {D})$
with
 $$ \begin{align*}\|f\|^p_{H^p}= \sup_{0<r<1}\frac{1}{2\pi}\int_0^{2\pi}|f(re^{i\theta})|^pd\theta <\infty.\end{align*} $$
$$ \begin{align*}\|f\|^p_{H^p}= \sup_{0<r<1}\frac{1}{2\pi}\int_0^{2\pi}|f(re^{i\theta})|^pd\theta <\infty.\end{align*} $$
Let
![]() $H^\infty $
denote the space of all bounded analytic functions with the supremum norm
$H^\infty $
denote the space of all bounded analytic functions with the supremum norm
![]() $\|f\|_{H^{\infty }}=\sup _{z\in {\mathbb D}}|f(z)|.$
For
$\|f\|_{H^{\infty }}=\sup _{z\in {\mathbb D}}|f(z)|.$
For
![]() $0<p<\infty $
, the weighted Dirichlet space
$0<p<\infty $
, the weighted Dirichlet space
![]() $\mathcal {D}_p$
is the space consisting of all
$\mathcal {D}_p$
is the space consisting of all
![]() $f\in H({\mathbb D})$
such that
$f\in H({\mathbb D})$
such that
 $$ \begin{align*}\|f\|^2_{\mathcal{D}_p}=|f(0)|^2+ \int_{{\mathbb D}}|f'(z)|^2(1-|z|^2)^{p} dA(z) <\infty,\end{align*} $$
$$ \begin{align*}\|f\|^2_{\mathcal{D}_p}=|f(0)|^2+ \int_{{\mathbb D}}|f'(z)|^2(1-|z|^2)^{p} dA(z) <\infty,\end{align*} $$
where
 $dA(z)={1\over \pi }dxdy$
is the normalized Lebesgue area measure in
$dA(z)={1\over \pi }dxdy$
is the normalized Lebesgue area measure in
![]() ${\mathbb D}$
. Clearly,
${\mathbb D}$
. Clearly,
![]() $\mathcal {D}_1$
is the classical Hardy space
$\mathcal {D}_1$
is the classical Hardy space
![]() $H^2$
, and
$H^2$
, and
![]() $\mathcal {D}_0$
is the classical Dirichlet space
$\mathcal {D}_0$
is the classical Dirichlet space
![]() $\mathcal {D}$
.
$\mathcal {D}$
.
Let
![]() $K:\lbrack 0,\infty )\to \lbrack 0,\infty )$
be a nondecreasing function and not identically zero. The space
$K:\lbrack 0,\infty )\to \lbrack 0,\infty )$
be a nondecreasing function and not identically zero. The space
![]() $Q_K$
consists of those functions
$Q_K$
consists of those functions
![]() $f\in H({\mathbb D})$
such that (see, e.g., [Reference Essén and Wulan7, Reference Wulan and Zhu25])
$f\in H({\mathbb D})$
such that (see, e.g., [Reference Essén and Wulan7, Reference Wulan and Zhu25])
 $$ \begin{align*}\|f\|^2_{Q_K}=|f(0)|^2+\sup_{a\in {\mathbb D}} \int_{{\mathbb D}} |f'(z)|^2K(g(z,a))dA(z) <\infty,\end{align*} $$
$$ \begin{align*}\|f\|^2_{Q_K}=|f(0)|^2+\sup_{a\in {\mathbb D}} \int_{{\mathbb D}} |f'(z)|^2K(g(z,a))dA(z) <\infty,\end{align*} $$
where
![]() $g(z,a)=-\log |\varphi _{a}(z)|$
is the Green function at a and
$g(z,a)=-\log |\varphi _{a}(z)|$
is the Green function at a and
![]() $\varphi _a(z)={a-z \over 1-\bar {a}z}$
is the Möbius map that interchanges points
$\varphi _a(z)={a-z \over 1-\bar {a}z}$
is the Möbius map that interchanges points
![]() $0$
and a. When
$0$
and a. When
![]() $K(t)=t^p, 0<p<\infty $
,
$K(t)=t^p, 0<p<\infty $
,
![]() $Q_K$
is the
$Q_K$
is the
![]() $Q_p$
space (see, e.g., [Reference Xiao27]). For the case
$Q_p$
space (see, e.g., [Reference Xiao27]). For the case
![]() $p=1$
,
$p=1$
,
![]() $Q_1$
coincides with
$Q_1$
coincides with
![]() $BMOA$
, the class of holomorphic functions of bounded mean oscillation on
$BMOA$
, the class of holomorphic functions of bounded mean oscillation on
![]() ${\mathbb D}$
(see [Reference Girela10]), meanwhile for
${\mathbb D}$
(see [Reference Girela10]), meanwhile for
![]() $p>1$
,
$p>1$
,
![]() $Q_p$
is the Bloch space.
$Q_p$
is the Bloch space.
Let
![]() $0\leq \lambda ,p \leq 1$
. Galanopoulos, Merch
$0\leq \lambda ,p \leq 1$
. Galanopoulos, Merch
![]() $\acute {{\textrm {a}}}$
n, and Siskakis [Reference Galanopoulos, Merchán and Siskakis8] defined the Dirichlet–Morrey space
$\acute {{\textrm {a}}}$
n, and Siskakis [Reference Galanopoulos, Merchán and Siskakis8] defined the Dirichlet–Morrey space
![]() $\mathcal {D}_p^{\lambda }$
, which consists of all functions
$\mathcal {D}_p^{\lambda }$
, which consists of all functions
![]() $f\in \mathcal {D}_p$
such that
$f\in \mathcal {D}_p$
such that
 $$ \begin{align*}\|f\|_{\mathcal{D}_p^{\lambda}}=|f(0)|+\sup_{a\in {\mathbb D}}(1-|a|^2)^{p(1-\lambda)\over 2}\|f\circ\varphi_{a}-f(a)\|_{\mathcal{D}_p}<\infty.\end{align*} $$
$$ \begin{align*}\|f\|_{\mathcal{D}_p^{\lambda}}=|f(0)|+\sup_{a\in {\mathbb D}}(1-|a|^2)^{p(1-\lambda)\over 2}\|f\circ\varphi_{a}-f(a)\|_{\mathcal{D}_p}<\infty.\end{align*} $$
By a simple calculation, we see that
 $$ \begin{align*}\|f\|_{\mathcal{D}_p^{\lambda}}^2\approx \sup_{a\in {\mathbb D}}(1-|a|^2)^{p(1-\lambda)}\int_{{\mathbb D}}|f'(z)|^2(1-|\varphi_a(z)|^2)^pdA(z).\end{align*} $$
$$ \begin{align*}\|f\|_{\mathcal{D}_p^{\lambda}}^2\approx \sup_{a\in {\mathbb D}}(1-|a|^2)^{p(1-\lambda)}\int_{{\mathbb D}}|f'(z)|^2(1-|\varphi_a(z)|^2)^pdA(z).\end{align*} $$
It is easy to check that
![]() $\mathcal {D}_1^{\lambda }=\mathcal {L}^{2,\lambda }$
, the Morrey space (see [Reference Li, Liu and Lou13, Reference Liu and Lou14, Reference Wu and Xie23, Reference Wulan and Zhou24]). Moreover,
$\mathcal {D}_1^{\lambda }=\mathcal {L}^{2,\lambda }$
, the Morrey space (see [Reference Li, Liu and Lou13, Reference Liu and Lou14, Reference Wu and Xie23, Reference Wulan and Zhou24]). Moreover,
 $\mathcal {D}_p^{1}=Q_p,\mathcal {D}_p^{0}=\mathcal {D}_p$
, and
$\mathcal {D}_p^{1}=Q_p,\mathcal {D}_p^{0}=\mathcal {D}_p$
, and
 $$ \begin{align*}Q_p\subset \mathcal{D}_p^{\lambda}\subset \mathcal{D}_p,\,\,\,\,\, 0<\lambda<1 .\end{align*} $$
$$ \begin{align*}Q_p\subset \mathcal{D}_p^{\lambda}\subset \mathcal{D}_p,\,\,\,\,\, 0<\lambda<1 .\end{align*} $$
Let X be a Banach space of analytic functions on
![]() ${\mathbb D} $
and
${\mathbb D} $
and
![]() $ M(X)$
be the algebra of pointwise multipliers of
$ M(X)$
be the algebra of pointwise multipliers of
![]() $X $
, that is,
$X $
, that is,
In this paper, we investigate the corona problem for
 $M(\mathcal {D}^\lambda _p) $
when
$M(\mathcal {D}^\lambda _p) $
when
![]() $0<\lambda ,p<1$
. This problem can be stated as follows.
$0<\lambda ,p<1$
. This problem can be stated as follows.
The
 $M(\mathcal {D}^\lambda _p) $
corona problem. Let
$M(\mathcal {D}^\lambda _p) $
corona problem. Let
![]() $0<\lambda ,p<1$
, and let
$0<\lambda ,p<1$
, and let
 $g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
. What are the sufficient and necessary conditions on these functions such that there exist
$g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
. What are the sufficient and necessary conditions on these functions such that there exist
 $ f_1,f_2,\ldots ,f_n\in M(\mathcal {D}_p^{\lambda })$
such that
$ f_1,f_2,\ldots ,f_n\in M(\mathcal {D}_p^{\lambda })$
such that
The corona theorem holds for
![]() $H^\infty $
by a famous result of Carleson (see [Reference Carleson6]). In [Reference Nicolau and Xiao15], Nicolau and Xiao gave the corona theorem on spaces
$H^\infty $
by a famous result of Carleson (see [Reference Carleson6]). In [Reference Nicolau and Xiao15], Nicolau and Xiao gave the corona theorem on spaces
![]() $H^\infty \cap Q_p$
, which has been extended to
$H^\infty \cap Q_p$
, which has been extended to
![]() $Q_p$
space by Xiao in [Reference Xiao26]. In addition, the same results on
$Q_p$
space by Xiao in [Reference Xiao26]. In addition, the same results on
![]() $ M(Q_p)$
and
$ M(Q_p)$
and
![]() $H^\infty \cap Q_K$
were established by Pau in [Reference Pau16, Reference Pau17], respectively. In [Reference Li and Wulan12], Li and Wulan also showed that the corona theorem holds for
$H^\infty \cap Q_K$
were established by Pau in [Reference Pau16, Reference Pau17], respectively. In [Reference Li and Wulan12], Li and Wulan also showed that the corona theorem holds for
![]() $M(Q_K)$
. See [Reference Bao, Lou, Qian and Wulan4, Reference Treil21, Reference Trent22] and the references therein for more results of the corona theorem.
$M(Q_K)$
. See [Reference Bao, Lou, Qian and Wulan4, Reference Treil21, Reference Trent22] and the references therein for more results of the corona theorem.
In this paper, we first show that the corona theorem holds for
 $M(\mathcal {D}^\lambda _p) $
when
$M(\mathcal {D}^\lambda _p) $
when
![]() ${0<\lambda},{p<1}$
, that is, the unit disc is dense in the maximal ideal space of
${0<\lambda},{p<1}$
, that is, the unit disc is dense in the maximal ideal space of
 $M(\mathcal {D}^\lambda _p) $
. This can be reformulated in the following way.
$M(\mathcal {D}^\lambda _p) $
. This can be reformulated in the following way.
Theorem 1 Let
![]() $0<\lambda ,p<1$
, and let
$0<\lambda ,p<1$
, and let
 $g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
with
$g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
with
 $$ \begin{align} \inf_{z\in {\mathbb D}}\sum_{j=1}^{n}|g_j(z)|=\delta>0. \end{align} $$
$$ \begin{align} \inf_{z\in {\mathbb D}}\sum_{j=1}^{n}|g_j(z)|=\delta>0. \end{align} $$
Then there exist
 $ f_1,f_2,\ldots ,f_n\in M(\mathcal {D}_p^{\lambda })$
such that
$ f_1,f_2,\ldots ,f_n\in M(\mathcal {D}_p^{\lambda })$
such that
Banjade and Trent showed that the Wolff theorem holds for the multipliers of the Dirichlet space and weighted Dirichlet spaces in [Reference Banjade and Trent2, Reference Banjade and Trent3], respectively. Banjade also gave the Wolff theorem on spaces
![]() $H^\infty \cap Q_p$
and
$H^\infty \cap Q_p$
and
![]() $M(Q_p)$
in [Reference Banjade1]. In [Reference Li and Wulan12], Li and Wulan showed that the Wolff theorem holds for the space
$M(Q_p)$
in [Reference Banjade1]. In [Reference Li and Wulan12], Li and Wulan showed that the Wolff theorem holds for the space
![]() $M(Q_K)$
. Motivated by these results, we investigate the Wolff theorem on the space
$M(Q_K)$
. Motivated by these results, we investigate the Wolff theorem on the space
 $M(\mathcal {D}_p^{\lambda })$
. The second main result can be reformulated in the following way.
$M(\mathcal {D}_p^{\lambda })$
. The second main result can be reformulated in the following way.
Theorem 2 Let
![]() $0<\lambda ,p<1$
, and let
$0<\lambda ,p<1$
, and let
 $g,g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
with
$g,g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
with
 $$ \begin{align} \sum_{j=1}^{n}|g_j(z)|^2\ge|g(z)|^2,\,\,\,\,z\in{\mathbb D}. \end{align} $$
$$ \begin{align} \sum_{j=1}^{n}|g_j(z)|^2\ge|g(z)|^2,\,\,\,\,z\in{\mathbb D}. \end{align} $$
Then there exist
 $ f_1,f_2,\ldots ,f_n\in M(\mathcal {D}_p^{\lambda })$
such that
$ f_1,f_2,\ldots ,f_n\in M(\mathcal {D}_p^{\lambda })$
such that
The paper is organized as follows. In Section 2, we give some auxiliary properties, which will be used in the proofs of Theorems 1 and 2. In Section 3, we give a detail proof for Theorem 1. In Section 4, we give a proof for Theorem 2.
In this paper, we write
![]() $F\approx G$
if
$F\approx G$
if
![]() $F\lesssim G \lesssim F$
, where
$F\lesssim G \lesssim F$
, where
![]() $G \lesssim F$
means that there exists a nonnegative constant C such that
$G \lesssim F$
means that there exists a nonnegative constant C such that
![]() $ G\le CF$
.
$ G\le CF$
.
2 Some auxiliary properties
In this section, we state some lemmas that are useful for the proof of the corona theorem on spaces
 $ M(\mathcal {D}^\lambda _p)$
.
$ M(\mathcal {D}^\lambda _p)$
.
Lemma 1 [Reference Galanopoulos, Merchán and Siskakis8, Propositions 2.1 and 2.2]
Let
![]() $0<\lambda ,p<1$
,
$0<\lambda ,p<1$
,
![]() $f\in H({\mathbb D})$
. Then the following statements hold:
$f\in H({\mathbb D})$
. Then the following statements hold:
-
(a) f belongs to
 $\mathcal {D}_p^{\lambda }$
if and only if
$\mathcal {D}_p^{\lambda }$
if and only if  $$ \begin{align*}\sup_{I\subset \partial{\mathbb D}} {1\over |I|^{p\lambda }}\int_{S(I)}|f'(z)|^2(1-|z|^2)^pdA(z) <\infty.\end{align*} $$
$$ \begin{align*}\sup_{I\subset \partial{\mathbb D}} {1\over |I|^{p\lambda }}\int_{S(I)}|f'(z)|^2(1-|z|^2)^pdA(z) <\infty.\end{align*} $$
-
(b) If
 $f\in \mathcal {D}_p^{\lambda }$
, then
$f\in \mathcal {D}_p^{\lambda }$
, then  $$ \begin{align*}|f(z)|\lesssim{\|f\|_{\mathcal{D}_p^{\lambda}} \over (1-|z|^2)^{{p\over 2}(1-\lambda)}}.\end{align*} $$
$$ \begin{align*}|f(z)|\lesssim{\|f\|_{\mathcal{D}_p^{\lambda}} \over (1-|z|^2)^{{p\over 2}(1-\lambda)}}.\end{align*} $$
Lemma 2 [Reference Zhu28, Lemma 3.10]
Let
![]() $z\in {\mathbb D}$
,
$z\in {\mathbb D}$
,
![]() $\alpha>-1$
, and
$\alpha>-1$
, and
![]() $\beta>0$
. Then
$\beta>0$
. Then
 $$ \begin{align*}\int_{{\mathbb D}}{ (1-|w|^2)^\alpha \over |1-z\bar{w}|^{2+\alpha+\beta}}dA(w)\approx(1-|z|^2)^{-\beta}.\end{align*} $$
$$ \begin{align*}\int_{{\mathbb D}}{ (1-|w|^2)^\alpha \over |1-z\bar{w}|^{2+\alpha+\beta}}dA(w)\approx(1-|z|^2)^{-\beta}.\end{align*} $$
Lemma 3 [Reference Pau16, Lemma 2.2]
Let
![]() $0<p<1$
. If
$0<p<1$
. If
![]() $ |f(z)|^2(1-|z|^2)^pdA(z)$
is a p-Carleson measure, then
$ |f(z)|^2(1-|z|^2)^pdA(z)$
is a p-Carleson measure, then
![]() $ |f(z)|dA(z)$
is a Carleson measure.
$ |f(z)|dA(z)$
is a Carleson measure.
Lemma 4 Let
![]() $0<\lambda ,p<1$
such that
$0<\lambda ,p<1$
such that
 $$ \begin{align*}T_f(z)=\int_{{\mathbb D}}{f(z)\over |1-\bar{w}z|^2}dA(w)\end{align*} $$
$$ \begin{align*}T_f(z)=\int_{{\mathbb D}}{f(z)\over |1-\bar{w}z|^2}dA(w)\end{align*} $$
has sense and it defines an analytic function. If
![]() $ |f(z)|^2(1-|z|^2)^pdA(z)$
is a
$ |f(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure, then
$p\lambda $
-Carleson measure, then
 $ |T_f(z)|^2(1-|z|^2)^pdA(z)$
is also a
$ |T_f(z)|^2(1-|z|^2)^pdA(z)$
is also a
![]() $p\lambda $
-Carleson measure.
$p\lambda $
-Carleson measure.
Proof For the Carleson box
![]() $S(I)$
, it is obvious that
$S(I)$
, it is obvious that
 $$ \begin{align*} &\int_{S(I)}|T_f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \int_{S(I)}\left( \int_{S(2I)}{ |f(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\qquad{}+\int_{S(I)}\left( \int_{{\mathbb D} \backslash S(2I)}{ |f(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)=I_1+I_2. \end{align*} $$
$$ \begin{align*} &\int_{S(I)}|T_f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \int_{S(I)}\left( \int_{S(2I)}{ |f(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\qquad{}+\int_{S(I)}\left( \int_{{\mathbb D} \backslash S(2I)}{ |f(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)=I_1+I_2. \end{align*} $$
From Lemma 7.2.2 in [Reference Xiao27], we have
 $$ \begin{align*}I_1\lesssim\int_{S(2I)}|f(z)|^2(1-|z|^2)^pdA(z)\lesssim|I|^{p\lambda}.\end{align*} $$
$$ \begin{align*}I_1\lesssim\int_{S(2I)}|f(z)|^2(1-|z|^2)^pdA(z)\lesssim|I|^{p\lambda}.\end{align*} $$
Applying the Cauchy–Schwarz inequality, we obtain that
 $$ \begin{align*} \int_{S(I)}{|f(z)|}dA(z) &\le \left(\int_{S(I)} { |f(z)|^2(1-|z|^2)^p } dA(z) \right)^{1/2}\left( \int_{S(I)}{ (1-|z|^2)^{-p} }dA(z) \right)^{1/2}\\ &\lesssim |I|^{p\lambda\over 2}|I|^{1-{p\over 2}}=|I|^{1+{p\lambda\over 2}-{p\over 2}}. \end{align*} $$
$$ \begin{align*} \int_{S(I)}{|f(z)|}dA(z) &\le \left(\int_{S(I)} { |f(z)|^2(1-|z|^2)^p } dA(z) \right)^{1/2}\left( \int_{S(I)}{ (1-|z|^2)^{-p} }dA(z) \right)^{1/2}\\ &\lesssim |I|^{p\lambda\over 2}|I|^{1-{p\over 2}}=|I|^{1+{p\lambda\over 2}-{p\over 2}}. \end{align*} $$
Therefore,
![]() $ |f(z)|dA(z)$
is a
$ |f(z)|dA(z)$
is a
 $1+{p\lambda \over 2}-{p\over 2} $
-Carleson measure. This deduces that
$1+{p\lambda \over 2}-{p\over 2} $
-Carleson measure. This deduces that
 $$ \begin{align*} I_2 &\lesssim \int_{S(I)}\left( \sum_{n=1}^{\infty}\int_{S(2^{n+1}I)\backslash S(2^nI)}{ |f(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\lesssim\int_{S(I)}\left( \sum_{n=1}^{\infty} { 2^{n+1}|I|^{1+{p\lambda\over 2}-{p\over 2}} \over (2^n|I|)^2 }\right)^2(1-|z|^2)^pdA(z)\lesssim|I|^{p\lambda}. \end{align*} $$
$$ \begin{align*} I_2 &\lesssim \int_{S(I)}\left( \sum_{n=1}^{\infty}\int_{S(2^{n+1}I)\backslash S(2^nI)}{ |f(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\lesssim\int_{S(I)}\left( \sum_{n=1}^{\infty} { 2^{n+1}|I|^{1+{p\lambda\over 2}-{p\over 2}} \over (2^n|I|)^2 }\right)^2(1-|z|^2)^pdA(z)\lesssim|I|^{p\lambda}. \end{align*} $$
So
 $ |T_f(z)|^2(1-|z|^2)^pdA(z)$
is a
$ |T_f(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure. The proof is complete.▪
$p\lambda $
-Carleson measure. The proof is complete.▪
Let
![]() $f\in H({\mathbb D})$
. The Volterra integral operator
$f\in H({\mathbb D})$
. The Volterra integral operator
![]() $J_f$
, which was first introduced by Pommerenke in [Reference Pommerenke20], is defined as
$J_f$
, which was first introduced by Pommerenke in [Reference Pommerenke20], is defined as
 $$ \begin{align*}J_f(g)(z)=\int_0^zg(\zeta)f'(\zeta)d\zeta, \,\,z\in {\mathbb D}, g\in H({\mathbb D}).\end{align*} $$
$$ \begin{align*}J_f(g)(z)=\int_0^zg(\zeta)f'(\zeta)d\zeta, \,\,z\in {\mathbb D}, g\in H({\mathbb D}).\end{align*} $$
Its related operator
![]() $I_f$
is defined by
$I_f$
is defined by
 $$ \begin{align*}I_f(g)(z)=\int_0^zg'(\zeta)f(\zeta)d\zeta, \,\,z\in {\mathbb D}, g\in H({\mathbb D}).\end{align*} $$
$$ \begin{align*}I_f(g)(z)=\int_0^zg'(\zeta)f(\zeta)d\zeta, \,\,z\in {\mathbb D}, g\in H({\mathbb D}).\end{align*} $$
It is clear that
![]() $M_f(g)(z)=J_f(g)(z)+I_f(g)(z)+f(0)g(0)$
, where
$M_f(g)(z)=J_f(g)(z)+I_f(g)(z)+f(0)g(0)$
, where
![]() $M_f(g)(z)=f(z)g(z)$
, called the multiplication operator.
$M_f(g)(z)=f(z)g(z)$
, called the multiplication operator.
Lemma 5 Let
![]() $0<\lambda ,p<1$
. Then
$0<\lambda ,p<1$
. Then
 $f\in M(\mathcal {D}_p^{\lambda })$
if and only if
$f\in M(\mathcal {D}_p^{\lambda })$
if and only if
![]() $f\in H^\infty $
and the measure
$f\in H^\infty $
and the measure
![]() $d\mu (z)=|f'(z)|^2|g(z)|^2(1-|z|^2)^pdA(z)$
is a
$d\mu (z)=|f'(z)|^2|g(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure for any
$p\lambda $
-Carleson measure for any
 $g\in \mathcal {D}_p^{\lambda }$
.
$g\in \mathcal {D}_p^{\lambda }$
.
Proof Suppose first that
 $f\in M(\mathcal {D}_p^{\lambda })$
. For any
$f\in M(\mathcal {D}_p^{\lambda })$
. For any
 $g\in \mathcal {D}_p^{\lambda }$
, we have
$g\in \mathcal {D}_p^{\lambda }$
, we have
 $M_f(g)\in \mathcal {D}_p^{\lambda }$
. Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8] gives that
$M_f(g)\in \mathcal {D}_p^{\lambda }$
. Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8] gives that
![]() $f\in H^\infty $
, which implies that
$f\in H^\infty $
, which implies that
 $I_f(g)\in \mathcal {D}_p^{\lambda }$
. Therefore,
$I_f(g)\in \mathcal {D}_p^{\lambda }$
. Therefore,
 $J_f(g)\in \mathcal {D}_p^{\lambda }$
, that is, the measure
$J_f(g)\in \mathcal {D}_p^{\lambda }$
, that is, the measure
![]() $d\mu (z)=|f'(z)|^2|g(z)|^2(1-|z|^2)^pdA(z)$
is a
$d\mu (z)=|f'(z)|^2|g(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure.
$p\lambda $
-Carleson measure.
Conversely, suppose that
![]() $f\in H^\infty $
and the measure
$f\in H^\infty $
and the measure
![]() $\mu $
is a
$\mu $
is a
![]() $p\lambda $
-Carleson measure. For any
$p\lambda $
-Carleson measure. For any
 $g\in \mathcal {D}_p^{\lambda }$
, using the norm of
$g\in \mathcal {D}_p^{\lambda }$
, using the norm of
![]() $\mathcal {D}_p^{\lambda }$
, we can easily obtain the desired result.▪
$\mathcal {D}_p^{\lambda }$
, we can easily obtain the desired result.▪
Let
![]() $0<\lambda ,p<1$
,
$0<\lambda ,p<1$
,
![]() $f\in L^2(\partial {\mathbb D})$
. We say that
$f\in L^2(\partial {\mathbb D})$
. We say that
 $f\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D}) $
if
$f\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D}) $
if
 $$ \begin{align*}\|f\|_{\mathcal{D}_p^{\lambda}(\partial{\mathbb D})}=\left( \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{I}\int_{I}{ |f(\varsigma)-f(\eta)|^2 \over |\varsigma-\eta|^{2-p} }|d\varsigma||d\eta| \right)^{1/2}<\infty.\end{align*} $$
$$ \begin{align*}\|f\|_{\mathcal{D}_p^{\lambda}(\partial{\mathbb D})}=\left( \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{I}\int_{I}{ |f(\varsigma)-f(\eta)|^2 \over |\varsigma-\eta|^{2-p} }|d\varsigma||d\eta| \right)^{1/2}<\infty.\end{align*} $$
A function of
![]() $H^2$
belongs to
$H^2$
belongs to
![]() $\mathcal {D}_p^{\lambda }$
if and only if its boundary values belong to
$\mathcal {D}_p^{\lambda }$
if and only if its boundary values belong to
 $ \mathcal {D}_p^{\lambda }(\partial {\mathbb D}) $
(see [Reference Galanopoulos, Merchán and Siskakis8, Theorem 2.1]).
$ \mathcal {D}_p^{\lambda }(\partial {\mathbb D}) $
(see [Reference Galanopoulos, Merchán and Siskakis8, Theorem 2.1]).
Lemma 6 [Reference Bao and Pau5, Lemma 2.2]
Let
![]() $0<p<1$
and
$0<p<1$
and
![]() $f\in L^2(\partial {\mathbb D})$
. Let
$f\in L^2(\partial {\mathbb D})$
. Let
![]() $F\in \mathcal {C}^1({\mathbb D})$
such that
$F\in \mathcal {C}^1({\mathbb D})$
such that
![]() $\lim _{r\to 1^-}F(re^{i\theta })=f(e^{i\theta })$
for almost everywhere
$\lim _{r\to 1^-}F(re^{i\theta })=f(e^{i\theta })$
for almost everywhere
![]() $ e^{i\theta }\in \partial {\mathbb D}$
. For any interval
$ e^{i\theta }\in \partial {\mathbb D}$
. For any interval
![]() $I\subset \partial {\mathbb D}$
,
$I\subset \partial {\mathbb D}$
,
 $$ \begin{align*}\int_{I}\int_{I}{|f(e^{it})-f(e^{is})|^2 \over| e^{it}-e^{is}|^{2-p} }dtds\lesssim\int_{S(3I)}|\nabla F(z)|^2(1-|z|^2)^{p}dA(z).\end{align*} $$
$$ \begin{align*}\int_{I}\int_{I}{|f(e^{it})-f(e^{is})|^2 \over| e^{it}-e^{is}|^{2-p} }dtds\lesssim\int_{S(3I)}|\nabla F(z)|^2(1-|z|^2)^{p}dA(z).\end{align*} $$
Using Lemma 6, we get the following result.
Corollary 1 Let
![]() $0<\lambda ,p<1$
and
$0<\lambda ,p<1$
and
![]() $f\in L^2(\partial {\mathbb D})$
. Let
$f\in L^2(\partial {\mathbb D})$
. Let
![]() $F\in \mathcal {C}^1({\mathbb D})$
such that
$F\in \mathcal {C}^1({\mathbb D})$
such that
![]() $\lim _{r\to 1^-}F(re^{i\theta })=f(e^{i\theta })$
for almost everywhere
$\lim _{r\to 1^-}F(re^{i\theta })=f(e^{i\theta })$
for almost everywhere
![]() $ e^{i\theta }\in \partial {\mathbb D}$
. If
$ e^{i\theta }\in \partial {\mathbb D}$
. If
![]() $ |\nabla F(z)|^2(1-|z|^2)^pdA(z)$
is a
$ |\nabla F(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure, then
$p\lambda $
-Carleson measure, then
 $ f\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
.
$ f\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
.
For
![]() $z=x+i y$
, define
$z=x+i y$
, define
 $$ \begin{align*}\bar{\partial}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i \frac{\partial}{\partial y}\right) ,\quad \partial=\frac{1}{2}\left(\frac{\partial}{\partial x}-i \frac{\partial}{\partial y}\right). \end{align*} $$
$$ \begin{align*}\bar{\partial}=\frac{1}{2}\left(\frac{\partial}{\partial x}+i \frac{\partial}{\partial y}\right) ,\quad \partial=\frac{1}{2}\left(\frac{\partial}{\partial x}-i \frac{\partial}{\partial y}\right). \end{align*} $$
Let f be
![]() $\mathcal {C}^{1}$
and bounded on
$\mathcal {C}^{1}$
and bounded on
![]() ${\mathbb D}$
. Then the
${\mathbb D}$
. Then the
![]() $\bar {\partial }$
-equation
$\bar {\partial }$
-equation
![]() $\bar {\partial } g=f$
has a standard solution
$\bar {\partial } g=f$
has a standard solution
 $$ \begin{align*}g(z)=\frac{1}{\pi} \int_{{\mathbb D}} \frac{f(w)}{z-w} d A(w) \end{align*} $$
$$ \begin{align*}g(z)=\frac{1}{\pi} \int_{{\mathbb D}} \frac{f(w)}{z-w} d A(w) \end{align*} $$
on
![]() ${\mathbb D}$
. In this paper, Jones’ solution of the
${\mathbb D}$
. In this paper, Jones’ solution of the
![]() $\bar {\partial }$
-equation is suitable for our purpose, i.e., the following lemma (see [Reference Jones11, Reference Xiao26]).
$\bar {\partial }$
-equation is suitable for our purpose, i.e., the following lemma (see [Reference Jones11, Reference Xiao26]).
Lemma 7 Let
![]() $ \mu $
be a Carleson measure on
$ \mu $
be a Carleson measure on
![]() ${\mathbb D}$
. If for
${\mathbb D}$
. If for
![]() $z \in {\mathbb D} \cup \partial {\mathbb D}$
and
$z \in {\mathbb D} \cup \partial {\mathbb D}$
and
![]() $\varsigma \in {\mathbb D}$
,
$\varsigma \in {\mathbb D}$
,
 $$ \begin{align*}K_\mu(z,\varsigma)={ 2i(1-|\varsigma|^2)\over\pi(1-\bar{\varsigma}z)(z-\varsigma) }\exp\left\{\int_{ |w|\ge |\varsigma|} \left ({1+\bar{w}\varsigma \over 1-\bar{w}\varsigma }- {1+\bar{w}z \over 1-\bar{w}z } \right){d\mu(w)\over \|\mu\|_1}\right\}, \end{align*} $$
$$ \begin{align*}K_\mu(z,\varsigma)={ 2i(1-|\varsigma|^2)\over\pi(1-\bar{\varsigma}z)(z-\varsigma) }\exp\left\{\int_{ |w|\ge |\varsigma|} \left ({1+\bar{w}\varsigma \over 1-\bar{w}\varsigma }- {1+\bar{w}z \over 1-\bar{w}z } \right){d\mu(w)\over \|\mu\|_1}\right\}, \end{align*} $$
then
 $$ \begin{align*}G(z)=\int_{{\mathbb D}}K_\mu(z,\varsigma)d\mu(\varsigma)\end{align*} $$
$$ \begin{align*}G(z)=\int_{{\mathbb D}}K_\mu(z,\varsigma)d\mu(\varsigma)\end{align*} $$
satisfies
![]() $\bar {\partial }G=\mu $
. Moreover, if
$\bar {\partial }G=\mu $
. Moreover, if
![]() $z \in \partial {\mathbb D}$
, then the above integral converges absolutely and obeys
$z \in \partial {\mathbb D}$
, then the above integral converges absolutely and obeys
 $$ \begin{align*}\int_{{\mathbb D}}|K_\mu(e^{i\theta},\varsigma)|d\mu(\varsigma) \le C\|\mu\|_1,\end{align*} $$
$$ \begin{align*}\int_{{\mathbb D}}|K_\mu(e^{i\theta},\varsigma)|d\mu(\varsigma) \le C\|\mu\|_1,\end{align*} $$
and hence
![]() $G\in L^\infty (\partial {\mathbb D})$
and
$G\in L^\infty (\partial {\mathbb D})$
and
![]() $\|G\|_{L^\infty (\partial {\mathbb D})}\le C\|\mu \|_1.$
$\|G\|_{L^\infty (\partial {\mathbb D})}\le C\|\mu \|_1.$
Thus, if
![]() $|g(z)|dA(z)$
is a Carleson measure, then the equation
$|g(z)|dA(z)$
is a Carleson measure, then the equation
![]() $\bar {\partial }G=g $
has a solution
$\bar {\partial }G=g $
has a solution
![]() $G\in L^\infty (\partial {\mathbb D})$
.
$G\in L^\infty (\partial {\mathbb D})$
.
3 Proof of Theorem 1
Proof of Theorem 1
Let
 $g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
such that (1) holds. Without loss of generality, we suppose that
$g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
such that (1) holds. Without loss of generality, we suppose that
![]() $\|g_j\|_{H^\infty }\le 1,j=1,2,\ldots ,n$
. Consider the equation
$\|g_j\|_{H^\infty }\le 1,j=1,2,\ldots ,n$
. Consider the equation
and its nonanalytic solutions
 $$ \begin{align*}\varPhi_j(z)={ \bar{g}_j(z) \over \sum_{k=1}^n|g_k(z)|^2 },\,\,\,\,\,\,j=1,2,\ldots,n.\end{align*} $$
$$ \begin{align*}\varPhi_j(z)={ \bar{g}_j(z) \over \sum_{k=1}^n|g_k(z)|^2 },\,\,\,\,\,\,j=1,2,\ldots,n.\end{align*} $$
For
![]() $ 1\le k,j\le n$
, we assume that the
$ 1\le k,j\le n$
, we assume that the
![]() $\bar {\partial }$
-equation
$\bar {\partial }$
-equation
 $$ \begin{align*}\bar{\partial}b_{j,k}=\varPhi_j\bar{\partial}\varPhi_k\end{align*} $$
$$ \begin{align*}\bar{\partial}b_{j,k}=\varPhi_j\bar{\partial}\varPhi_k\end{align*} $$
has solution
![]() $b_{j,k}$
such that
$b_{j,k}$
such that
 $b_{j,k} f \in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
for every
$b_{j,k} f \in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
for every
 $f\in \mathcal {D}_p^{\lambda }$
. By a simple calculation, we see that
$f\in \mathcal {D}_p^{\lambda }$
. By a simple calculation, we see that
 $$ \begin{align*}f_j=\varPhi_j+\sum_{k=1}^n(b_{j,k}-b_{k,j})g_k,\,\,\,\,j=1,2,\ldots,n,\end{align*} $$
$$ \begin{align*}f_j=\varPhi_j+\sum_{k=1}^n(b_{j,k}-b_{k,j})g_k,\,\,\,\,j=1,2,\ldots,n,\end{align*} $$
satisfy
 $\sum _{j=1}^ng_jf_j=\sum _{j=1}^ng_j\varPhi _j=1$
.▪
$\sum _{j=1}^ng_jf_j=\sum _{j=1}^ng_j\varPhi _j=1$
.▪
Since
 $$ \begin{align*}{\partial f_j \over \partial\bar{z}}={ \partial \varPhi_j\over\partial\bar{z} }+\sum_{k=1}^ng_k\bigg(\varPhi_j{ \partial \varPhi_k\over\partial\bar{z} }-\varPhi_k{ \partial \varPhi_j\over\partial\bar{z} }\bigg)=0,\end{align*} $$
$$ \begin{align*}{\partial f_j \over \partial\bar{z}}={ \partial \varPhi_j\over\partial\bar{z} }+\sum_{k=1}^ng_k\bigg(\varPhi_j{ \partial \varPhi_k\over\partial\bar{z} }-\varPhi_k{ \partial \varPhi_j\over\partial\bar{z} }\bigg)=0,\end{align*} $$
we have
![]() $f_j\in H({\mathbb D})$
. By (1), we have that (see also [Reference Pau16])
$f_j\in H({\mathbb D})$
. By (1), we have that (see also [Reference Pau16])
 $$ \begin{align*}|\varPhi_j(z)|\le\delta^{-1} ~{\textrm{and}}~|\nabla\varPhi_j|^2 \lesssim\delta^{-3}\sum_{k=1}^n|g^{\prime}_k|^2.\end{align*} $$
$$ \begin{align*}|\varPhi_j(z)|\le\delta^{-1} ~{\textrm{and}}~|\nabla\varPhi_j|^2 \lesssim\delta^{-3}\sum_{k=1}^n|g^{\prime}_k|^2.\end{align*} $$
To obtain that
 $ f_j\in M(\mathcal {D}_p^{\lambda })$
, we need to show that
$ f_j\in M(\mathcal {D}_p^{\lambda })$
, we need to show that
 $ ff_j\in \mathcal {D}_p^{\lambda }$
for any
$ ff_j\in \mathcal {D}_p^{\lambda }$
for any
 $ f\in \mathcal {D}_p^{\lambda }$
. Applying Lemmas 1 and 5, we get
$ f\in \mathcal {D}_p^{\lambda }$
. Applying Lemmas 1 and 5, we get
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|\nabla\varPhi_j(z)f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}\sum_{k=1}^n{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g^{\prime}_k(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|\nabla\varPhi_j(z)f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}\sum_{k=1}^n{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g^{\prime}_k(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
Since
![]() $|\varPhi _j(z)|\le \delta ^{-1}$
, we obtain
$|\varPhi _j(z)|\le \delta ^{-1}$
, we obtain
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|\varPhi_j(z)\nabla f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f'(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|\varPhi_j(z)\nabla f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f'(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
Therefore,
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|\nabla(\varPhi_jf)(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}(|\nabla\varPhi_j(z)f(z)|^2+|\varPhi_j(z)\nabla f(z)|^2)(1-|z|^2)^pdA(z)<\infty, \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|\nabla(\varPhi_jf)(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}(|\nabla\varPhi_j(z)f(z)|^2+|\varPhi_j(z)\nabla f(z)|^2)(1-|z|^2)^pdA(z)<\infty, \end{align*} $$
which implies that
 $\varPhi _j f \in \mathcal {D}_p^{\lambda }$
. Since
$\varPhi _j f \in \mathcal {D}_p^{\lambda }$
. Since
 $ g_k\in M(\mathcal {D}_p^{\lambda })$
,
$ g_k\in M(\mathcal {D}_p^{\lambda })$
,
 $b_{j,k}f\in \mathcal {D}_p^{\lambda }, 1\le j,k\le n$
, we obtain that
$b_{j,k}f\in \mathcal {D}_p^{\lambda }, 1\le j,k\le n$
, we obtain that
 $$ \begin{align*}\sum_{j=1}^n(b_{j,k}-b_{k,j})g_kf\in\mathcal{D}_p^{\lambda}.\end{align*} $$
$$ \begin{align*}\sum_{j=1}^n(b_{j,k}-b_{k,j})g_kf\in\mathcal{D}_p^{\lambda}.\end{align*} $$
This implies that
 $$ \begin{align*}f_jf=\varPhi_jf+\sum_{k=1}^n(b_{j,k}-b_{k,j})g_kf \in\mathcal{D}_p^{\lambda}.\end{align*} $$
$$ \begin{align*}f_jf=\varPhi_jf+\sum_{k=1}^n(b_{j,k}-b_{k,j})g_kf \in\mathcal{D}_p^{\lambda}.\end{align*} $$
To finish the proof, we only need to show that there exists a
![]() $ b_{j,k}$
such that
$ b_{j,k}$
such that
 $\bar {\partial }b_{j,k}=\varPhi _j\bar {\partial }\varPhi _k$
, where
$\bar {\partial }b_{j,k}=\varPhi _j\bar {\partial }\varPhi _k$
, where
 $b_{j,k} f \in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
for every
$b_{j,k} f \in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
for every
 $f\in \mathcal {D}_p^{\lambda }$
. Consider the
$f\in \mathcal {D}_p^{\lambda }$
. Consider the
![]() $\bar {\partial }$
-equation
$\bar {\partial }$
-equation
![]() $ \bar {\partial }u=G$
, where
$ \bar {\partial }u=G$
, where
 $G=\varPhi _j\bar {\partial }\varPhi _k$
. Applying (1), we get that
$G=\varPhi _j\bar {\partial }\varPhi _k$
. Applying (1), we get that
 $$ \begin{align} |G(z)|^2\lesssim \delta^{-6}\left(\sum_{k=1}^n|g^{\prime}_k(z)|\right)^2. \end{align} $$
$$ \begin{align} |G(z)|^2\lesssim \delta^{-6}\left(\sum_{k=1}^n|g^{\prime}_k(z)|\right)^2. \end{align} $$
Since
 $g_k\in M(\mathcal {D}_p^{\lambda })\subset Q_p $
(see Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8]), then
$g_k\in M(\mathcal {D}_p^{\lambda })\subset Q_p $
(see Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8]), then
![]() $ |g^{\prime }_k(z)|^2(1-|z|^2)^pdA(z)$
is a p-Carleson measure. So,
$ |g^{\prime }_k(z)|^2(1-|z|^2)^pdA(z)$
is a p-Carleson measure. So,
![]() $|G(z)|^2(1-|z|^2)^pdA(z) $
is also a p-Carleson measure. Using Lemma 3, we have that
$|G(z)|^2(1-|z|^2)^pdA(z) $
is also a p-Carleson measure. Using Lemma 3, we have that
![]() $|G(z)|dA(z) $
is a Carleson measure. So, by Lemma 7, we get Jones’ solution u of the
$|G(z)|dA(z) $
is a Carleson measure. So, by Lemma 7, we get Jones’ solution u of the
![]() $\bar {\partial } $
problem
$\bar {\partial } $
problem
![]() $\bar {\partial }u=G$
. Moreover, u has the boundary values in
$\bar {\partial }u=G$
. Moreover, u has the boundary values in
![]() $L^\infty (\partial {\mathbb D})$
. Let
$L^\infty (\partial {\mathbb D})$
. Let
 $$ \begin{align*} v(z)&={2i\over \pi}\int_{{\mathbb D}}{ 1-|\varsigma|^2 \over |1-\bar{\varsigma}z|^2 }\\ &\cdot\exp\left( \int_{ |w|\ge |\varsigma|} \left({1+\bar{w}\varsigma \over 1-\bar{w}\varsigma }- {1+\bar{w}z \over 1-\bar{w}z } \right)|G(w)|dA(w) \right)G(\varsigma)dA(\varsigma). \end{align*} $$
$$ \begin{align*} v(z)&={2i\over \pi}\int_{{\mathbb D}}{ 1-|\varsigma|^2 \over |1-\bar{\varsigma}z|^2 }\\ &\cdot\exp\left( \int_{ |w|\ge |\varsigma|} \left({1+\bar{w}\varsigma \over 1-\bar{w}\varsigma }- {1+\bar{w}z \over 1-\bar{w}z } \right)|G(w)|dA(w) \right)G(\varsigma)dA(\varsigma). \end{align*} $$
From the proof of Theorem 3.1 of [Reference Nicolau and Xiao15], we have that v has the same boundary values as
![]() $zu$
and
$zu$
and
 $$ \begin{align} |\nabla v(z)|\lesssim \int_{{\mathbb D}} { |G(w)| \over |1-\bar{w}z |^2 }dA(w). \end{align} $$
$$ \begin{align} |\nabla v(z)|\lesssim \int_{{\mathbb D}} { |G(w)| \over |1-\bar{w}z |^2 }dA(w). \end{align} $$
Since
![]() $|G(z)|dA(z) $
is a Carleson measure, then
$|G(z)|dA(z) $
is a Carleson measure, then
![]() $ v\in L^\infty ({\mathbb D})$
from [Reference Jones11].
$ v\in L^\infty ({\mathbb D})$
from [Reference Jones11].
Now, we show that
 $vf\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
for every
$vf\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
for every
 $f\in \mathcal {D}_p^{\lambda }$
. For this purpose, we need to prove that for any
$f\in \mathcal {D}_p^{\lambda }$
. For this purpose, we need to prove that for any
 $f\in \mathcal {D}_p^{\lambda }$
,
$f\in \mathcal {D}_p^{\lambda }$
,
is a
![]() $p\lambda $
-Carleson measure by Corollary 1.
$p\lambda $
-Carleson measure by Corollary 1.
Since
 $f\in \mathcal {D}_p^{\lambda }$
and
$f\in \mathcal {D}_p^{\lambda }$
and
![]() $ v\in L^\infty ({\mathbb D})$
, we see that
$ v\in L^\infty ({\mathbb D})$
, we see that
![]() $ |v(z)|^2|\nabla f(z)|^2(1-|z|^2)^pdA(z)$
is a
$ |v(z)|^2|\nabla f(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure. Then it remains to verify that
$p\lambda $
-Carleson measure. Then it remains to verify that
![]() $ |\nabla v(z)|^2| f(z)|^2(1-|z|^2)^pdA(z)$
is also a
$ |\nabla v(z)|^2| f(z)|^2(1-|z|^2)^pdA(z)$
is also a
![]() $p\lambda $
-Carleson measure. By inequalities (3) and (4), we obtain that
$p\lambda $
-Carleson measure. By inequalities (3) and (4), we obtain that
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)\nabla v(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)|^2\left(\int_{{\mathbb D}}{ |G(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)|^2\left( \sum_{k=1}^n\int_{{\mathbb D}}{ |g^{\prime}_k(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sum_{k=1}^n\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)|^2|T_{|g^{\prime}_k|}(z)|^2(1-|z|^2)^pdA(z), \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)\nabla v(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)|^2\left(\int_{{\mathbb D}}{ |G(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)|^2\left( \sum_{k=1}^n\int_{{\mathbb D}}{ |g^{\prime}_k(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sum_{k=1}^n\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)|^2|T_{|g^{\prime}_k|}(z)|^2(1-|z|^2)^pdA(z), \end{align*} $$
where
 $$ \begin{align*}T_h(z)=\int_{{\mathbb D}}{ h(w) \over |1-\bar{w}z|^2 }dA(w).\end{align*} $$
$$ \begin{align*}T_h(z)=\int_{{\mathbb D}}{ h(w) \over |1-\bar{w}z|^2 }dA(w).\end{align*} $$
We write
 $ fT_{|g^{\prime }_k|}=T_{f|g^{\prime }_k|}+(fT_{|g^{\prime }_k|}-T_{f|g^{\prime }_k|} )$
. Since
$ fT_{|g^{\prime }_k|}=T_{f|g^{\prime }_k|}+(fT_{|g^{\prime }_k|}-T_{f|g^{\prime }_k|} )$
. Since
 $g_k\in M(\mathcal {D}_p^{\lambda })$
, by Lemma 5, we get that
$g_k\in M(\mathcal {D}_p^{\lambda })$
, by Lemma 5, we get that
![]() $ |f(z)|^2|g^{\prime }_k(z)|^2(1-|z|^2)^pdA(z)$
is a
$ |f(z)|^2|g^{\prime }_k(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure. Lemma 4 yields that
$p\lambda $
-Carleson measure. Lemma 4 yields that
 $|T_{f|g^{\prime }_k|}|^2(1-|z|^2)^pdA(z)$
is also a
$|T_{f|g^{\prime }_k|}|^2(1-|z|^2)^pdA(z)$
is also a
![]() $p\lambda $
-Carleson measure. Applying the identity
$p\lambda $
-Carleson measure. Applying the identity
 $$ \begin{align*}f(z)T_{|g^{\prime}_k|}(z)-T_{f|g^{\prime}_k|}(z)=\int_{{\mathbb D}}(f(z)-f(w)){ |g^{\prime}_k(w)| \over |1-\bar{w}z|^2 }dA(w),\end{align*} $$
$$ \begin{align*}f(z)T_{|g^{\prime}_k|}(z)-T_{f|g^{\prime}_k|}(z)=\int_{{\mathbb D}}(f(z)-f(w)){ |g^{\prime}_k(w)| \over |1-\bar{w}z|^2 }dA(w),\end{align*} $$
the Cauchy–Schwarz inequality, and
 $g_k\in M(\mathcal {D}_p^{\lambda })\subset Q_p\subset \mathcal {D}_p^{\lambda } $
(see Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8]), we obtain that
$g_k\in M(\mathcal {D}_p^{\lambda })\subset Q_p\subset \mathcal {D}_p^{\lambda } $
(see Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8]), we obtain that
 $$ \begin{align*} &|f(z)T_{|g^{\prime}_k|}(z)-T_{f|g^{\prime}_k|}(z)|^2\le\left( \int_{{\mathbb D}}|f(z)-f(w)|{ |g^{\prime}_k(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2\\ &\quad\le \left( \int_{{\mathbb D}}{ |f(z)-f(w)|^2(1-|w|^2)^{-p} \over |1-\bar{w}z|^{4-2p} }dA(w) \right)\left( \int_{{\mathbb D}}{ |g^{\prime}_k(w)|^2(1-|w|^2)^p \over |1-\bar{w}z|^{2p} } dA(w) \right)\\ &\quad\le \left( \int_{{\mathbb D}}{ |f(z)-f(w)|^2(1-|w|^2)^{-p} \over |1-\bar{w}z|^{4-2p} }dA(w) \right)\|g_k\|_{Q_p}^2(1-|z|^2)^{-p}. \end{align*} $$
$$ \begin{align*} &|f(z)T_{|g^{\prime}_k|}(z)-T_{f|g^{\prime}_k|}(z)|^2\le\left( \int_{{\mathbb D}}|f(z)-f(w)|{ |g^{\prime}_k(w)| \over |1-\bar{w}z|^2 }dA(w) \right)^2\\ &\quad\le \left( \int_{{\mathbb D}}{ |f(z)-f(w)|^2(1-|w|^2)^{-p} \over |1-\bar{w}z|^{4-2p} }dA(w) \right)\left( \int_{{\mathbb D}}{ |g^{\prime}_k(w)|^2(1-|w|^2)^p \over |1-\bar{w}z|^{2p} } dA(w) \right)\\ &\quad\le \left( \int_{{\mathbb D}}{ |f(z)-f(w)|^2(1-|w|^2)^{-p} \over |1-\bar{w}z|^{4-2p} }dA(w) \right)\|g_k\|_{Q_p}^2(1-|z|^2)^{-p}. \end{align*} $$
Using Proposition 4.27 of [Reference Wulan and Zhu25] and following the ideas of the proof of Lemma 1 in [Reference Liu and Lou14], we obtain that
 $$ \begin{align*}|f\circ\varphi_w(u)-f(w)|\lesssim\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|{ (1-|\xi|^2)^{2} \over |1-\bar{\xi}u|^{3} }dA(\xi). \end{align*} $$
$$ \begin{align*}|f\circ\varphi_w(u)-f(w)|\lesssim\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|{ (1-|\xi|^2)^{2} \over |1-\bar{\xi}u|^{3} }dA(\xi). \end{align*} $$
The Cauchy–Schwarz inequality and Lemma 2 yield that
 $$ \begin{align*} |f\circ\varphi_w(u)-f(w)|^2 &\le \int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p} \over |1-\bar{\xi}u|^2 }dA(\xi)\int_{{\mathbb D}}{ (1-|\xi|^2)^{1+p} \over |1-\bar{\xi}u|^4 }dA(\xi)\\ &\lesssim (1-|u|^2)^{p-1}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p} \over |1-\bar{\xi}u|^2 }dA(\xi). \end{align*} $$
$$ \begin{align*} |f\circ\varphi_w(u)-f(w)|^2 &\le \int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p} \over |1-\bar{\xi}u|^2 }dA(\xi)\int_{{\mathbb D}}{ (1-|\xi|^2)^{1+p} \over |1-\bar{\xi}u|^4 }dA(\xi)\\ &\lesssim (1-|u|^2)^{p-1}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p} \over |1-\bar{\xi}u|^2 }dA(\xi). \end{align*} $$
Since
 $$ \begin{align*}|1-\bar{a}\varphi_w(u)|={ |1-a\bar{w}||1-\bar{u}\varphi_w(a)| \over |1-\bar{w}u| },\end{align*} $$
$$ \begin{align*}|1-\bar{a}\varphi_w(u)|={ |1-a\bar{w}||1-\bar{u}\varphi_w(a)| \over |1-\bar{w}u| },\end{align*} $$
applying Lemma 2 and Lemma D in [Reference Pau and Peláez18] and changing the variable
![]() $z=\varphi _w(u)$
, we have
$z=\varphi _w(u)$
, we have
 $$ \begin{align*} &(1-|a|^2)^{p(1-\lambda)}\int_{{\mathbb D}}|f(z)T_{|g^{\prime}_k|}(z)-T_{f|g^{\prime}_k|}(z)|^2(1-|\varphi_a(z)|^2)^pdA(z)\\&\lesssim \|g_k\|_{Q_p}^2(1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}} \int_{{\mathbb D}}{ |f(z)-f(w)|^2(1-|w|^2)^{-p} \over |1-\bar{w}z|^{4-2p} }dA(w) {dA(z) \over|1-\bar{a}z|^{2p}} \\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}{| f(\varphi_w(u))-f(w)|^2 \over |1-\bar{w}\varphi_w(u)|^{4-2p} }\\&\quad\cdot{ (1-|w|^2)^{2-p} \over |1-\bar{w}u|^4|1-\bar{a}\varphi_w(u)|^{2p} }dA(u)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}| f(\varphi_w(u))-f(w)|^2\\&\quad\cdot{ (1-|w|^2)^{p-2} \over |1-\bar{w}u|^{2p} |1-\bar{a}\varphi_w(u)|^{2p}}dA(u)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}}\int_{{\mathbb D}}| f(\varphi_w(u))-f(w)|^2\\&\quad\cdot { (1-|w|^2)^{p-2} \over |1-\bar{w}a|^{2p} |1-\bar{u}\varphi_w(a)|^{2p}}dA(u)dA(w)\\&\lesssim \|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}}\int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p} (1-|w|^2)^{p-2} \over |1-\bar{\xi}u|^2 |1-\bar{w}a|^{2p} }\\&\quad\cdot{ (1-|u|^2)^{p-1} \over |1-\bar{u}\varphi_w(a)|^{2p} }dA(\xi)dA(u)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p}(1-|w|^2)^{p-2}\over |1-\bar{w}a|^{2p} }\\&\quad\cdot\int_{{\mathbb D}}{ (1-|u|^2)^{p-1}\over |1-\bar{\xi}u|^2 |1-\bar{u}\varphi_w(a)|^{2p}}dA(u)dA(\xi)dA(w)\\&\lesssim \|g_k\|_{Q_p}^2 (1\!-\!|a|^2)^{p(2-\lambda)}\!\int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^2 (1-|w|^2)^{p-2} \over |1-\bar{w}a|^{2p} |1-\bar{\xi}\varphi_w(a)|^{2p}}dA(\xi)dA(w)\\&=\|g_k\|_{Q_p}^2 (1\!-\!|a|^2)^{p(2-\lambda)}\!\int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^2 (1-|w|^2)^{p-2} \over |1-\bar{w}\xi|^{2p} |1-\bar{a}\varphi_w(\xi)|^{2p}}dA(\xi)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}|f'(\eta)|^2{ (1-|\varphi_w(\eta)|^2)^2 (1-|w|^2)^{p-2} \over |1-\bar{w}\varphi_w(\eta)|^{2p} |1-\bar{a}\eta|^{2p}}dA(\eta)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}|f'(\eta)|^2{ (1-|w|^2)^{-p} (1-|\eta|^2)^2 \over|1-\bar{w}\eta|^{4-2p}|1-\bar{a}\eta|^{2p} }dA(\eta)dA(w)\\ &=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}|f'(\eta)|^2{(1-|\eta|^2)^2 \over|1-\bar{a}\eta|^{2p} }\int_{{\mathbb D}}{ (1-|w|^2)^{-p} \over |1-\bar{w}\eta|^{4-2p} }dA(w)dA(\eta)\\&\lesssim \|g_k\|_{Q_p}^2(1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}|f'(\eta)|^2{(1-|\eta|^2)^p\over |1-\bar{a}\eta|^{2p} }dA(\eta)\\&=\|g_k\|_{Q_p}^2(1-|a|^2)^{p(1-\lambda)}\int_{{\mathbb D}}|f'(\eta)|^2(1-|\varphi_a(\eta)|^2)^pdA(\eta)\\&\lesssim \|g_k\|_{\mathcal{D}_p^{\lambda}}^2\|f\|_{\mathcal{D}_p^{\lambda}}^2. \end{align*} $$
$$ \begin{align*} &(1-|a|^2)^{p(1-\lambda)}\int_{{\mathbb D}}|f(z)T_{|g^{\prime}_k|}(z)-T_{f|g^{\prime}_k|}(z)|^2(1-|\varphi_a(z)|^2)^pdA(z)\\&\lesssim \|g_k\|_{Q_p}^2(1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}} \int_{{\mathbb D}}{ |f(z)-f(w)|^2(1-|w|^2)^{-p} \over |1-\bar{w}z|^{4-2p} }dA(w) {dA(z) \over|1-\bar{a}z|^{2p}} \\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}{| f(\varphi_w(u))-f(w)|^2 \over |1-\bar{w}\varphi_w(u)|^{4-2p} }\\&\quad\cdot{ (1-|w|^2)^{2-p} \over |1-\bar{w}u|^4|1-\bar{a}\varphi_w(u)|^{2p} }dA(u)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}| f(\varphi_w(u))-f(w)|^2\\&\quad\cdot{ (1-|w|^2)^{p-2} \over |1-\bar{w}u|^{2p} |1-\bar{a}\varphi_w(u)|^{2p}}dA(u)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}}\int_{{\mathbb D}}| f(\varphi_w(u))-f(w)|^2\\&\quad\cdot { (1-|w|^2)^{p-2} \over |1-\bar{w}a|^{2p} |1-\bar{u}\varphi_w(a)|^{2p}}dA(u)dA(w)\\&\lesssim \|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}}\int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p} (1-|w|^2)^{p-2} \over |1-\bar{\xi}u|^2 |1-\bar{w}a|^{2p} }\\&\quad\cdot{ (1-|u|^2)^{p-1} \over |1-\bar{u}\varphi_w(a)|^{2p} }dA(\xi)dA(u)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)} \int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^{3-p}(1-|w|^2)^{p-2}\over |1-\bar{w}a|^{2p} }\\&\quad\cdot\int_{{\mathbb D}}{ (1-|u|^2)^{p-1}\over |1-\bar{\xi}u|^2 |1-\bar{u}\varphi_w(a)|^{2p}}dA(u)dA(\xi)dA(w)\\&\lesssim \|g_k\|_{Q_p}^2 (1\!-\!|a|^2)^{p(2-\lambda)}\!\int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^2 (1-|w|^2)^{p-2} \over |1-\bar{w}a|^{2p} |1-\bar{\xi}\varphi_w(a)|^{2p}}dA(\xi)dA(w)\\&=\|g_k\|_{Q_p}^2 (1\!-\!|a|^2)^{p(2-\lambda)}\!\int_{{\mathbb D}}\int_{{\mathbb D}}|(f\circ\varphi_w)'(\xi)|^2{ (1-|\xi|^2)^2 (1-|w|^2)^{p-2} \over |1-\bar{w}\xi|^{2p} |1-\bar{a}\varphi_w(\xi)|^{2p}}dA(\xi)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}|f'(\eta)|^2{ (1-|\varphi_w(\eta)|^2)^2 (1-|w|^2)^{p-2} \over |1-\bar{w}\varphi_w(\eta)|^{2p} |1-\bar{a}\eta|^{2p}}dA(\eta)dA(w)\\&=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}\int_{{\mathbb D}}|f'(\eta)|^2{ (1-|w|^2)^{-p} (1-|\eta|^2)^2 \over|1-\bar{w}\eta|^{4-2p}|1-\bar{a}\eta|^{2p} }dA(\eta)dA(w)\\ &=\|g_k\|_{Q_p}^2 (1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}|f'(\eta)|^2{(1-|\eta|^2)^2 \over|1-\bar{a}\eta|^{2p} }\int_{{\mathbb D}}{ (1-|w|^2)^{-p} \over |1-\bar{w}\eta|^{4-2p} }dA(w)dA(\eta)\\&\lesssim \|g_k\|_{Q_p}^2(1-|a|^2)^{p(2-\lambda)}\int_{{\mathbb D}}|f'(\eta)|^2{(1-|\eta|^2)^p\over |1-\bar{a}\eta|^{2p} }dA(\eta)\\&=\|g_k\|_{Q_p}^2(1-|a|^2)^{p(1-\lambda)}\int_{{\mathbb D}}|f'(\eta)|^2(1-|\varphi_a(\eta)|^2)^pdA(\eta)\\&\lesssim \|g_k\|_{\mathcal{D}_p^{\lambda}}^2\|f\|_{\mathcal{D}_p^{\lambda}}^2. \end{align*} $$
This implies that
![]() $ |\nabla (vf)(z)|^2(1-|z|^2)^pdA(z)$
is a
$ |\nabla (vf)(z)|^2(1-|z|^2)^pdA(z)$
is a
![]() $p\lambda $
-Carleson measure. Then Corollary 1 deduces that
$p\lambda $
-Carleson measure. Then Corollary 1 deduces that
 $vf\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
.▪
$vf\in \mathcal {D}_p^{\lambda }(\partial {\mathbb D})$
.▪
Let
![]() $g=(g_1,g_2,\ldots ,g_n)\in H({\mathbb D})^n$
and
$g=(g_1,g_2,\ldots ,g_n)\in H({\mathbb D})^n$
and
![]() $f=(f_1,f_2,\ldots ,f_n)\in H({\mathbb D})^n$
. Consider the operator
$f=(f_1,f_2,\ldots ,f_n)\in H({\mathbb D})^n$
. Consider the operator
![]() $M_g$
defined by
$M_g$
defined by
 $$ \begin{align*}M_g(f)=\sum_{k=1}^nf_kg_k.\end{align*} $$
$$ \begin{align*}M_g(f)=\sum_{k=1}^nf_kg_k.\end{align*} $$
Similarly to the proof of Theorem 1.2 in [Reference Pau16] (using the ideas of Theorem 3.1 of [Reference Xiao26]), by Theorem 1, we obtain the following result. We omit the details of the proof.
Theorem 3 Let
![]() $0<\lambda ,p<1$
and
$0<\lambda ,p<1$
and
![]() $g\in H({\mathbb D})^n$
. The following statements are equivalent:
$g\in H({\mathbb D})^n$
. The following statements are equivalent:
-
(a)
 $M_g: M(\mathcal {D}_p^{\lambda })\times \cdots \times M(\mathcal {D}_p^{\lambda })\to M(\mathcal {D}_p^{\lambda })$
is surjective;
$M_g: M(\mathcal {D}_p^{\lambda })\times \cdots \times M(\mathcal {D}_p^{\lambda })\to M(\mathcal {D}_p^{\lambda })$
is surjective; -
(b)
 $M_g: \mathcal {D}_p^{\lambda }\times \cdots \times \mathcal {D}_p^{\lambda }\to \mathcal {D}_p^{\lambda }$
is surjective; and
$M_g: \mathcal {D}_p^{\lambda }\times \cdots \times \mathcal {D}_p^{\lambda }\to \mathcal {D}_p^{\lambda }$
is surjective; and -
(c)
 $g_1,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
and (1) holds.
$g_1,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
and (1) holds.
4 Proof of Theorem 2
In this section, we give a detail proof for Theorem 2, i.e., we show that the Wolff theorem holds for the algebra of pointwise multipliers of the Dirichlet–Morrey space
![]() $\mathcal {D}_p^{\lambda } $
.
$\mathcal {D}_p^{\lambda } $
.
Proof of Theorem 2
First, considering the trivial case
![]() $g\equiv 0$
, we can choose
$g\equiv 0$
, we can choose
![]() $f_j\equiv 0, j=1,2,\ldots ,n$
. Then the desired result is obtained. Next, we consider the nontrivial case. Let
$f_j\equiv 0, j=1,2,\ldots ,n$
. Then the desired result is obtained. Next, we consider the nontrivial case. Let
 $g,g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
satisfying (2). Without loss of generality, we suppose that
$g,g_1,g_2,\ldots ,g_n\in M(\mathcal {D}_p^{\lambda })$
satisfying (2). Without loss of generality, we suppose that
![]() $g,g_1,g_2,\ldots ,g_n$
are the analytic function on
$g,g_1,g_2,\ldots ,g_n$
are the analytic function on
![]() $\bar {{\mathbb D}}$
and satisfying
$\bar {{\mathbb D}}$
and satisfying
![]() $\|g\|_{H^\infty }\le 1$
,
$\|g\|_{H^\infty }\le 1$
,
![]() $\|g_j\|_{H^\infty }\le 1,j=1,2,\ldots ,n$
(see [Reference Garnett9, Proof of Theorem 2.3, p. 319]). Let
$\|g_j\|_{H^\infty }\le 1,j=1,2,\ldots ,n$
(see [Reference Garnett9, Proof of Theorem 2.3, p. 319]). Let
 $$ \begin{align*}\Psi_j(z)={g(z)\bar{g}_j(z) \over \sum_{k=1}^n|g_k(z)|^2 },\,\,\,\,j=1,2,\ldots,n.\end{align*} $$
$$ \begin{align*}\Psi_j(z)={g(z)\bar{g}_j(z) \over \sum_{k=1}^n|g_k(z)|^2 },\,\,\,\,j=1,2,\ldots,n.\end{align*} $$
It is obvious that
![]() $\Psi _j $
, satisfying
$\Psi _j $
, satisfying
![]() $|\Psi _j(z)|\le 1$
, is the
$|\Psi _j(z)|\le 1$
, is the
![]() $C^\infty $
function on
$C^\infty $
function on
![]() $\bar {{\mathbb D}}$
such that
$\bar {{\mathbb D}}$
such that
 $ \sum _{j=1}^ng_j\Psi _j=g$
. For
$ \sum _{j=1}^ng_j\Psi _j=g$
. For
![]() $ 1\le k,j\le n$
, we assume that the following equation
$ 1\le k,j\le n$
, we assume that the following equation
 $$ \begin{align*}\bar{\partial}b_{j,k}=g\Psi_j\bar{\partial}\Psi_k\end{align*} $$
$$ \begin{align*}\bar{\partial}b_{j,k}=g\Psi_j\bar{\partial}\Psi_k\end{align*} $$
has solution
 $b_{j,k}\in M(\mathcal {D}_p^{\lambda })$
and
$b_{j,k}\in M(\mathcal {D}_p^{\lambda })$
and
![]() $\|b_{j,k}\|_{H^\infty }\le 1$
. We write
$\|b_{j,k}\|_{H^\infty }\le 1$
. We write
 $$ \begin{align*}f_j(z)=g^2(z)\Psi_j(z)+\sum_{k=1}^n(b_{j,k}(z)-b_{k,j}(z) )g_k(z),\,\,\,\,j=1,2,\ldots,n.\end{align*} $$
$$ \begin{align*}f_j(z)=g^2(z)\Psi_j(z)+\sum_{k=1}^n(b_{j,k}(z)-b_{k,j}(z) )g_k(z),\,\,\,\,j=1,2,\ldots,n.\end{align*} $$
Then we get that
 $$ \begin{align*}\sum_{j=1}^n g_jf_j=g^2\sum_{j=1}^ng_j\Psi_j=g^3.\end{align*} $$
$$ \begin{align*}\sum_{j=1}^n g_jf_j=g^2\sum_{j=1}^ng_j\Psi_j=g^3.\end{align*} $$
In addition,
 $$ \begin{align*}{\partial f_j\over \partial\bar{z}}=g^2{ \partial \Psi_j \over \partial\bar{z}}+\sum_{k=1}^ngg_k\bigg( \Psi_j{ \partial\Psi_k \over \partial\bar{z} }-\Psi_k{\partial\Psi_j \over \partial\bar{z}} \bigg)=0.\end{align*} $$
$$ \begin{align*}{\partial f_j\over \partial\bar{z}}=g^2{ \partial \Psi_j \over \partial\bar{z}}+\sum_{k=1}^ngg_k\bigg( \Psi_j{ \partial\Psi_k \over \partial\bar{z} }-\Psi_k{\partial\Psi_j \over \partial\bar{z}} \bigg)=0.\end{align*} $$
Therefore,
![]() $f_j\in H({\mathbb D})$
. Moreover,
$f_j\in H({\mathbb D})$
. Moreover,
![]() $\|f_j\|_{H^\infty } \leq 1+2n$
, and hence
$\|f_j\|_{H^\infty } \leq 1+2n$
, and hence
![]() $f_j\in H^\infty $
.▪
$f_j\in H^\infty $
.▪
Since
 $ { \partial \overline {g_j}\over \partial \bar {z}}=\overline {g^{\prime }_j}$
, and
$ { \partial \overline {g_j}\over \partial \bar {z}}=\overline {g^{\prime }_j}$
, and
 $$ \begin{align*}{\partial\Psi_j \over\partial\bar{z} }={ g\overline{g^{\prime}_j} \over \sum_{k=1}^n|g_k|^2 }-{ g\overline{g_j}\sum_{k=1}^ng_k\overline{g^{\prime}_k} \over \left( \sum_{k=1}^n|g_k|^2\right)^2 }={ g\sum_{k=1}^ng_k(\overline{g_k}\overline{g^{\prime}_j} -\overline{g_j}\overline{g^{\prime}_k} ) \over \left( \sum_{k=1}^n|g_k|^2\right)^2},\end{align*} $$
$$ \begin{align*}{\partial\Psi_j \over\partial\bar{z} }={ g\overline{g^{\prime}_j} \over \sum_{k=1}^n|g_k|^2 }-{ g\overline{g_j}\sum_{k=1}^ng_k\overline{g^{\prime}_k} \over \left( \sum_{k=1}^n|g_k|^2\right)^2 }={ g\sum_{k=1}^ng_k(\overline{g_k}\overline{g^{\prime}_j} -\overline{g_j}\overline{g^{\prime}_k} ) \over \left( \sum_{k=1}^n|g_k|^2\right)^2},\end{align*} $$
we see that
 $$ \begin{align*}\left| {\partial\Psi_j \over\partial\bar{z}} \right|{}^2\lesssim{ |g|^2\left( \sum_{k=1}^n|g_k|^2\right)^2\sum_{k=1}^n|g^{\prime}_k|^2 \over \left( \sum_{k=1}^n|g_k|^2\right)^4 } \lesssim { \sum_{k=1}^n|g^{\prime}_k|^2 \over \sum_{k=1}^n|g_k|^2}.\end{align*} $$
$$ \begin{align*}\left| {\partial\Psi_j \over\partial\bar{z}} \right|{}^2\lesssim{ |g|^2\left( \sum_{k=1}^n|g_k|^2\right)^2\sum_{k=1}^n|g^{\prime}_k|^2 \over \left( \sum_{k=1}^n|g_k|^2\right)^4 } \lesssim { \sum_{k=1}^n|g^{\prime}_k|^2 \over \sum_{k=1}^n|g_k|^2}.\end{align*} $$
Similarly,
 $$ \begin{align*}\left| {\partial\Psi_j \over\partial z} \right|{}^2\lesssim{|g'|^2 \sum_{k=1}^n|g_k|^2 \over\left( \sum_{k=1}^n|g_k|\right)^2 }+{ |g|^2\left( \sum_{k=1}^n|g_k|^2\right)^2\sum_{k=1}^n|g^{\prime}_k|^2 \over \left( \sum_{k=1}^n|g_k|^2\right)^4 }\lesssim{|g'|^2+ \sum_{k=1}^n|g^{\prime}_k|^2 \over \sum_{k=1}^n|g_k|^2}.\end{align*} $$
$$ \begin{align*}\left| {\partial\Psi_j \over\partial z} \right|{}^2\lesssim{|g'|^2 \sum_{k=1}^n|g_k|^2 \over\left( \sum_{k=1}^n|g_k|\right)^2 }+{ |g|^2\left( \sum_{k=1}^n|g_k|^2\right)^2\sum_{k=1}^n|g^{\prime}_k|^2 \over \left( \sum_{k=1}^n|g_k|^2\right)^4 }\lesssim{|g'|^2+ \sum_{k=1}^n|g^{\prime}_k|^2 \over \sum_{k=1}^n|g_k|^2}.\end{align*} $$
Therefore, by the assumption, we get that
 $$ \begin{align*}|g\nabla\Psi_j|^2 \lesssim |g'|^2+ \sum_{k=1}^n|g^{\prime}_k|^2.\end{align*} $$
$$ \begin{align*}|g\nabla\Psi_j|^2 \lesssim |g'|^2+ \sum_{k=1}^n|g^{\prime}_k|^2.\end{align*} $$
Now, we show that
 $ f_j\in M(\mathcal {D}_p^{\lambda })$
. To do this, we need to show that
$ f_j\in M(\mathcal {D}_p^{\lambda })$
. To do this, we need to show that
 $ ff_j\in \mathcal {D}_p^{\lambda }$
for any
$ ff_j\in \mathcal {D}_p^{\lambda }$
for any
 $ f\in \mathcal {D}_p^{\lambda }$
. First of all, we are going to prove that
$ f\in \mathcal {D}_p^{\lambda }$
. First of all, we are going to prove that
 $fg^2\Psi _j \in \mathcal {D}_p^{\lambda }$
. Since
$fg^2\Psi _j \in \mathcal {D}_p^{\lambda }$
. Since
![]() $g\in H^\infty $
and
$g\in H^\infty $
and
![]() $|\Psi _j(z) |\leq 1$
, we get that
$|\Psi _j(z) |\leq 1$
, we get that
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|g^2(z)\Psi_j(z)f'(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\le \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f'(z)|^2(1-|z|^2)^pdA(z) <\infty. \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|g^2(z)\Psi_j(z)f'(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\le \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f'(z)|^2(1-|z|^2)^pdA(z) <\infty. \end{align*} $$
Since
 $g\in M(\mathcal {D}_p^{\lambda }) $
, applying Lemma 5, we get
$g\in M(\mathcal {D}_p^{\lambda }) $
, applying Lemma 5, we get
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|g(z)g'(z)\Psi_j(z)f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g'(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|g(z)g'(z)\Psi_j(z)f(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g'(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
Using the fact that
![]() $|g\nabla \Psi _j|^2\lesssim |g'|^2+ \sum _{k=1}^n|g^{\prime }_k|^2 $
and Lemma 5 again, we obtain that
$|g\nabla \Psi _j|^2\lesssim |g'|^2+ \sum _{k=1}^n|g^{\prime }_k|^2 $
and Lemma 5 again, we obtain that
 $$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|g^2(z)f(z)\nabla\Psi_j(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g'(z)|^2(1-|z|^2)^pdA(z)\\ &\qquad{}+\sum_{j=1}^n\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g^{\prime}_j(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
$$ \begin{align*} &\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|g^2(z)f(z)\nabla\Psi_j(z)|^2(1-|z|^2)^pdA(z)\\ &\quad\lesssim \sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g'(z)|^2(1-|z|^2)^pdA(z)\\ &\qquad{}+\sum_{j=1}^n\sup_{I\subset \partial{\mathbb D}}{1\over |I|^{p\lambda}}\int_{S(I)}|f(z)g^{\prime}_j(z)|^2(1-|z|^2)^pdA(z)<\infty. \end{align*} $$
So, using the fact that
 $$ \begin{align*} |\nabla(fg^2\Psi_j)|^2 \lesssim|g^2\Psi_jf'|^2+|gg'\Psi_jf|^2+|g^2f\nabla\Psi_j|^2,\end{align*} $$
$$ \begin{align*} |\nabla(fg^2\Psi_j)|^2 \lesssim|g^2\Psi_jf'|^2+|gg'\Psi_jf|^2+|g^2f\nabla\Psi_j|^2,\end{align*} $$
we get that
 $fg^2\Psi _j \in \mathcal {D}_p^{\lambda }$
.
$fg^2\Psi _j \in \mathcal {D}_p^{\lambda }$
.
Now, we are going to prove that the other part of
![]() $ f_jf$
belongs to
$ f_jf$
belongs to
![]() $ \mathcal {D}_p^{\lambda } $
. Since
$ \mathcal {D}_p^{\lambda } $
. Since
 $ g_k\in M(\mathcal {D}_p^{\lambda })$
,
$ g_k\in M(\mathcal {D}_p^{\lambda })$
,
 $b_{j,k}f\in \mathcal {D}_p^{\lambda }, 1\le j,k\le n$
, we obtain that
$b_{j,k}f\in \mathcal {D}_p^{\lambda }, 1\le j,k\le n$
, we obtain that
 $$ \begin{align*}\sum_{k=1}^n(b_{j,k}-b_{k,j})g_kf\in\mathcal{D}_p^{\lambda}.\end{align*} $$
$$ \begin{align*}\sum_{k=1}^n(b_{j,k}-b_{k,j})g_kf\in\mathcal{D}_p^{\lambda}.\end{align*} $$
Hence,
 $f_jf \in \mathcal {D}_p^{\lambda },$
that is,
$f_jf \in \mathcal {D}_p^{\lambda },$
that is,
 $ f_j\in M(\mathcal {D}_p^{\lambda }),j=1,2,\ldots ,n$
.
$ f_j\in M(\mathcal {D}_p^{\lambda }),j=1,2,\ldots ,n$
.
Now, it remains to show that we can find a solution of
 $\bar {\partial }b_{j,k}=g\Psi _j\bar {\partial }\Psi _k$
satisfying
$\bar {\partial }b_{j,k}=g\Psi _j\bar {\partial }\Psi _k$
satisfying
 $ b_{j,k}\in M(\mathcal {D}_p^{\lambda })$
. To do this, it is sufficient to deal with the equation
$ b_{j,k}\in M(\mathcal {D}_p^{\lambda })$
. To do this, it is sufficient to deal with the equation
![]() $ \bar {\partial }u=G$
, where
$ \bar {\partial }u=G$
, where
 $G=g\Psi _j\bar {\partial }\Psi _k$
. It is easy to see that
$G=g\Psi _j\bar {\partial }\Psi _k$
. It is easy to see that
 $$ \begin{align*}|G(z)|^2=|g\Psi_j\bar{\partial}\Psi_k|^2\lesssim|g|^2 \sum_{k=1}^n|g^{\prime}_k|^2 \le \sum_{k=1}^n|g^{\prime}_k |^2. \end{align*} $$
$$ \begin{align*}|G(z)|^2=|g\Psi_j\bar{\partial}\Psi_k|^2\lesssim|g|^2 \sum_{k=1}^n|g^{\prime}_k|^2 \le \sum_{k=1}^n|g^{\prime}_k |^2. \end{align*} $$
Since
 $ M(\mathcal {D}_p^{\lambda })\subset Q_p$
(see Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8]) and
$ M(\mathcal {D}_p^{\lambda })\subset Q_p$
(see Corollary 3.1 in [Reference Galanopoulos, Merchán and Siskakis8]) and
 $ g_k\in M(\mathcal {D}_p^{\lambda })$
, we obtain that
$ g_k\in M(\mathcal {D}_p^{\lambda })$
, we obtain that
![]() $|G(z)|^2(1-|z|^2)^pdA(z) $
is a p-Carleson measure. Lemma 3 yields that
$|G(z)|^2(1-|z|^2)^pdA(z) $
is a p-Carleson measure. Lemma 3 yields that
![]() $|G(z)|dA(z) $
is a Carleson measure. Then we can obtain a solution
$|G(z)|dA(z) $
is a Carleson measure. Then we can obtain a solution
 $v\in M(\mathcal {D}_p^{\lambda })$
by a similar method to Theorem 1.
$v\in M(\mathcal {D}_p^{\lambda })$
by a similar method to Theorem 1.