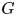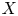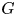1. Introduction
The goal of this paper is to provide a novel approach to the central limit theorem (CLT) on groups acting on hyperbolic spaces, for sampling with respect to the word length in the group. We shall replace the traditional approach based on thermodynamic formalism with techniques coming from the theory of random walks on groups. This allows us to establish new applications, including CLTs for lengths of geodesics in geometrically finite hyperbolic manifolds, for intersection numbers with submanifolds, and for homomorphisms between hyperbolic groups.
Motivation
The distribution of lengths of closed orbits for smooth flows on manifolds has long been a topic of considerable interest. For instance, Sinai [Reference SinaiSin60] and then Ratner [Reference RatnerRat73] proved a CLT for the geodesic flow on a hyperbolic manifold (see also Lalley [Reference LalleyLal87]). One prominent technique, pioneered by Sinai [Reference SinaiSin72], Bowen [Reference BowenBow75], Ruelle [Reference RuelleRue04], Parry and Pollicott [Reference Parry and PollicottPP90], and others, uses Markov partitions to reduce the study of smooth flows to symbolic dynamics to which one can apply tools from thermodynamic formalism. This approach has been successful in a variety of settings, especially applied to Anosov flows and their generalizations.
More recently, there has been renewed interest in the statistical properties of geodesic length and other geometric quantities with respect to a different sampling, namely according to the counting measure, that is to say, uniform measure on spheres in a Cayley graph of a finitely generated group ![]() $G$. For instance, Pollicott and Sharp [Reference Pollicott and SharpPS98] considered the ratio between the word length and the geometric length, Calegari and Fujiwara [Reference Calegari and FujiwaraCF10] compared word lengths with respect to different generating sets for general hyperbolic groups, and Horsham and Sharp [Reference Horsham and SharpHS09] established a CLT for quasimorphisms on free groups.
$G$. For instance, Pollicott and Sharp [Reference Pollicott and SharpPS98] considered the ratio between the word length and the geometric length, Calegari and Fujiwara [Reference Calegari and FujiwaraCF10] compared word lengths with respect to different generating sets for general hyperbolic groups, and Horsham and Sharp [Reference Horsham and SharpHS09] established a CLT for quasimorphisms on free groups.
In [Reference Gekhtman, Taylor and TiozzoGTT19] the authors, building on [Reference Gekhtman, Taylor and TiozzoGTT18], settled a conjecture of Chas, Li and Maskit [Reference Chas, Li and MaskitCLM13] about the distribution of hyperbolic lengths of closed geodesics on compact surfaces when sampling with respect to word length. Further, a CLT and statistical laws have been established for cocompact, proper actions of hyperbolic groups on CAT![]() $(-1)$ spaces by Cantrell [Reference CantrellCan21].
$(-1)$ spaces by Cantrell [Reference CantrellCan21].
All of these results are based on a symbolic coding and thermodynamic formalism. Although these techniques are quite powerful, they necessarily impose strong constraints on the actions of interest, usually requiring that the space ![]() $X$ is CAT
$X$ is CAT![]() $(-1)$ and that the action
$(-1)$ and that the action ![]() $G \curvearrowright X$ is proper cocompact. While this is the case in the classical setting, they are not satisfied for most actions on Gromov hyperbolic spaces.
$G \curvearrowright X$ is proper cocompact. While this is the case in the classical setting, they are not satisfied for most actions on Gromov hyperbolic spaces.
The goal of this paper is to provide a new approach to the CLT on groups ![]() $G \curvearrowright X$ acting on hyperbolic spaces, which will allow us to consider in particular:
$G \curvearrowright X$ acting on hyperbolic spaces, which will allow us to consider in particular:
(i) groups
 $G$ which are not necessarily word hyperbolic;
$G$ which are not necessarily word hyperbolic;(ii) actions on spaces
 $(X, d)$ which are
$(X, d)$ which are  $\delta$-hyperbolic, but not necessarily CAT
$\delta$-hyperbolic, but not necessarily CAT $(-1)$ or proper;
$(-1)$ or proper;(iii) group actions
 $G \curvearrowright X$ which need not be free, convex cocompact or even proper.
$G \curvearrowright X$ which need not be free, convex cocompact or even proper.
For the sake of concreteness, we will now present a version of our main theorem (Theorem 1.1) from which we will then derive several applications. Our discussion here will be a special case of the most general theorems (Theorems 7.3 and 7.4) which we will state and prove in § 7.
Main results
Let ![]() $G$ be a finitely generated group acting by isometries on a
$G$ be a finitely generated group acting by isometries on a ![]() $\delta$-hyperbolic metric space
$\delta$-hyperbolic metric space ![]() $(X, d)$, and fix a finite generating set
$(X, d)$, and fix a finite generating set ![]() $S$. We require that the action is nonelementary in the sense that there are two independent loxodromic elements.
$S$. We require that the action is nonelementary in the sense that there are two independent loxodromic elements.
Let ![]() $S_n := \{ g \in G: \Vert g \Vert = n \}$ be the sphere of radius
$S_n := \{ g \in G: \Vert g \Vert = n \}$ be the sphere of radius ![]() $n$ for the word metric with respect to
$n$ for the word metric with respect to ![]() $S$. We denote by
$S$. We denote by ![]() $\mathcal {N}_\sigma$ the Gaussian measure
$\mathcal {N}_\sigma$ the Gaussian measure ![]() $d \mathcal {N}_\sigma (t) = ({1}/{\sqrt {2 \pi } \sigma }) e^{-t^{2}/2\sigma ^{2}}\ dt$ if
$d \mathcal {N}_\sigma (t) = ({1}/{\sqrt {2 \pi } \sigma }) e^{-t^{2}/2\sigma ^{2}}\ dt$ if ![]() $\sigma > 0$, and the Dirac measure at
$\sigma > 0$, and the Dirac measure at ![]() $0$ if
$0$ if ![]() $\sigma = 0$. We require that
$\sigma = 0$. We require that ![]() $G$ admits a thick geodesic combing for
$G$ admits a thick geodesic combing for ![]() $S$ and we refer the reader to § 2.1 for definitions. We note here that these general conditions are satisfied in a variety of settings; for example, see the applications below and Lemma 8.1.
$S$ and we refer the reader to § 2.1 for definitions. We note here that these general conditions are satisfied in a variety of settings; for example, see the applications below and Lemma 8.1.
Theorem 1.1 Let ![]() $G$ be a group which admits a thick geodesic combing for the generating set
$G$ be a group which admits a thick geodesic combing for the generating set ![]() $S$. Let
$S$. Let ![]() $G \curvearrowright X$ be a nonelementary action by isometries on a
$G \curvearrowright X$ be a nonelementary action by isometries on a ![]() $\delta$-hyperbolic space
$\delta$-hyperbolic space ![]() $(X, d)$, and let
$(X, d)$, and let ![]() $o \in X$ be a base point.
$o \in X$ be a base point.
(i) (CLT for displacement) Then there exist
 $\ell > 0$,
$\ell > 0$,  $\sigma \geq 0$ such that for any
$\sigma \geq 0$ such that for any  $a < b$ we have
$a < b$ we have
 \begin{align*} \lim_{n \to \infty} \frac{1}{\# S_n} \# \bigg\{ g \in S_n : \frac{d(o, g o) - \ell n}{\sqrt{n}} \in [a, b] \bigg\} = \int_a^{b} d \mathcal{N}_\sigma(t). \end{align*}
\begin{align*} \lim_{n \to \infty} \frac{1}{\# S_n} \# \bigg\{ g \in S_n : \frac{d(o, g o) - \ell n}{\sqrt{n}} \in [a, b] \bigg\} = \int_a^{b} d \mathcal{N}_\sigma(t). \end{align*}(ii) (CLT for translation length) Moreover, if
 $\tau (g)$ denotes the translation length of
$\tau (g)$ denotes the translation length of  $g$ on
$g$ on  $X$, we also have for any
$X$, we also have for any  $a < b$,
$a < b$,
 \begin{align*} \lim_{n \to \infty} \frac{1}{\# S_n} \# \bigg\{ g \in S_n : \frac{\tau(g) - \ell n }{\sqrt{n}} \in [a, b] \bigg\} = \int_a^{b} d \mathcal{N}_\sigma(t). \end{align*}
\begin{align*} \lim_{n \to \infty} \frac{1}{\# S_n} \# \bigg\{ g \in S_n : \frac{\tau(g) - \ell n }{\sqrt{n}} \in [a, b] \bigg\} = \int_a^{b} d \mathcal{N}_\sigma(t). \end{align*}(iii) Further,
 $\sigma = 0$ if and only if there exists a constant
$\sigma = 0$ if and only if there exists a constant  $C$ such that
for any
$C$ such that
for any \begin{align*} |d(o, go) - \ell \Vert g \Vert | \leq C \end{align*}
\begin{align*} |d(o, go) - \ell \Vert g \Vert | \leq C \end{align*} $g \in G$.
$g \in G$.
We remark that as a consequence of (iii), if ![]() $\sigma =0$ then the translation length of any
$\sigma =0$ then the translation length of any ![]() $g\in G$ with respect to its action on
$g\in G$ with respect to its action on ![]() $X$ is a constant multiple of its translation length in the word metric. Moreover, if the action
$X$ is a constant multiple of its translation length in the word metric. Moreover, if the action ![]() $G\curvearrowright X$ is not proper, then
$G\curvearrowright X$ is not proper, then ![]() $\sigma > 0$.
$\sigma > 0$.
Another way to formulate (i) is to say that we have the convergence in distribution
hence from now on we will use the above notation as a shorthand.
Applications
There are a number of applications to the above theorems and we summarize a few of them here. For the proofs, see § 8.
Geometrically finite hyperbolic manifolds
First, let us state an extension of our previous work on surfaces [Reference Gekhtman, Taylor and TiozzoGTT19] to general hyperbolic manifolds, possibly with cusps. If ![]() $M = \mathbb {H}^{n} / \Gamma$ is a hyperbolic manifold and
$M = \mathbb {H}^{n} / \Gamma$ is a hyperbolic manifold and ![]() $\gamma \in \Gamma = \pi _1(M)$, then we set
$\gamma \in \Gamma = \pi _1(M)$, then we set ![]() $\ell (\gamma )$ to be the length of the geodesic freely homotopic to
$\ell (\gamma )$ to be the length of the geodesic freely homotopic to ![]() $\gamma$ unless
$\gamma$ unless ![]() $\gamma$ is peripheral (i.e. homotopic into a cusp), in which case we set
$\gamma$ is peripheral (i.e. homotopic into a cusp), in which case we set ![]() $\ell (\gamma )=0$.
$\ell (\gamma )=0$.
Theorem 1.2 Suppose that ![]() $M$ is a geometrically finite hyperbolic manifold and let
$M$ is a geometrically finite hyperbolic manifold and let ![]() $S'$ be any generating set for
$S'$ be any generating set for ![]() $\pi _1 (M)$. Then there is a finite generating set
$\pi _1 (M)$. Then there is a finite generating set ![]() $S \supset S'$ and
$S \supset S'$ and ![]() $\ell,\sigma >0$ such that
$\ell,\sigma >0$ such that
where ![]() $\gamma$ is chosen uniformly at random in the sphere of radius
$\gamma$ is chosen uniformly at random in the sphere of radius ![]() $n$ with respect to
$n$ with respect to ![]() $S$.
$S$.
If, moreover, ![]() $\pi _1(M)$ is word hyperbolic, then we can take
$\pi _1(M)$ is word hyperbolic, then we can take ![]() $S = S'$.
$S = S'$.
The statement includes the cases where ![]() $M$ is either finite volume or convex cocompact, and is new even when
$M$ is either finite volume or convex cocompact, and is new even when ![]() $M$ is a finite area surface. We remark that when
$M$ is a finite area surface. We remark that when ![]() $M$ is either convex cocompact or a surface, the above theorem works for any generating set
$M$ is either convex cocompact or a surface, the above theorem works for any generating set ![]() $S$. In the convex cocompact case, the needed action
$S$. In the convex cocompact case, the needed action ![]() $\pi _1(M) \curvearrowright \mathbb {H}^{n}$ is sufficiently tame so that the techniques of thermodynamics may be applicable [Reference Pollicott and SharpPS98, Reference CantrellCan21]. However, this is not the case when the manifold
$\pi _1(M) \curvearrowright \mathbb {H}^{n}$ is sufficiently tame so that the techniques of thermodynamics may be applicable [Reference Pollicott and SharpPS98, Reference CantrellCan21]. However, this is not the case when the manifold ![]() $M$ has cusps.
$M$ has cusps.
We note that Theorem 1.2 further extends to manifolds of variable negative curvature, as long as the peripheral subgroups are virtually abelian, and the same proof applies.
Geometrically infinite 3-manifolds
In the case of ![]() $3$-manifolds, the previous result can be strengthened further as follows.
$3$-manifolds, the previous result can be strengthened further as follows.
Theorem 1.3 Let ![]() $M$ be a hyperbolic
$M$ be a hyperbolic ![]() $3$-manifold such that
$3$-manifold such that ![]() $\pi _1(M)$ is finitely generated and not virtually abelian. Suppose further that
$\pi _1(M)$ is finitely generated and not virtually abelian. Suppose further that ![]() $M$ does not have any rank
$M$ does not have any rank ![]() $2$ cusps. Then for any finite generating set
$2$ cusps. Then for any finite generating set ![]() $S$ of
$S$ of ![]() $\pi _1(M)$, there are
$\pi _1(M)$, there are ![]() $\ell,\sigma >0$ such that
$\ell,\sigma >0$ such that
where ![]() $\gamma$ is chosen uniformly at random in the sphere of radius
$\gamma$ is chosen uniformly at random in the sphere of radius ![]() $n$ with respect to
$n$ with respect to ![]() $S$.
$S$.
Moreover, if ![]() $M$ has rank
$M$ has rank ![]() $2$ cusps, the same statement holds after enlarging the generating set as in Theorem 1.2.
$2$ cusps, the same statement holds after enlarging the generating set as in Theorem 1.2.
To the authors’ knowledge, this is the first CLT for lengths of closed geodesics for possibly geometrically infinite ![]() $3$-manifolds.
$3$-manifolds.
Intersection numbers with a submanifold
For our next application, the required actions are on locally infinite trees, which are nonproper hyperbolic spaces.
Let ![]() $M$ be a smooth orientable manifold and
$M$ be a smooth orientable manifold and ![]() $\Sigma$ a smooth orientable codimension
$\Sigma$ a smooth orientable codimension ![]() $1$ submanifold which is
$1$ submanifold which is ![]() $\pi _1$-injective on each component. We say
$\pi _1$-injective on each component. We say ![]() $\Sigma$ is fiber-like if for each boundary component of the cut manifold
$\Sigma$ is fiber-like if for each boundary component of the cut manifold ![]() $M|\Sigma$ its induced subgroup in the fundamental group of the corresponding component of
$M|\Sigma$ its induced subgroup in the fundamental group of the corresponding component of ![]() $M|\Sigma$ has index at most
$M|\Sigma$ has index at most ![]() $2$.
$2$.
For ![]() $\gamma \in \pi _1 (M)$, let
$\gamma \in \pi _1 (M)$, let ![]() $i(\gamma, \Sigma )$ denote the minimal intersection number of
$i(\gamma, \Sigma )$ denote the minimal intersection number of ![]() $\Sigma$ with loops in
$\Sigma$ with loops in ![]() $M$ freely homotopic to
$M$ freely homotopic to ![]() $\gamma$.
$\gamma$.
Theorem 1.4 Suppose that ![]() $M$ is a closed orientable hyperbolic manifold and let
$M$ is a closed orientable hyperbolic manifold and let ![]() $S$ be any generating set for
$S$ be any generating set for ![]() $\pi _1 (M)$. Let
$\pi _1 (M)$. Let ![]() $\Sigma$ be a smooth orientable codimension
$\Sigma$ be a smooth orientable codimension ![]() $1$ submanifold that is
$1$ submanifold that is ![]() $\pi _1$-injective but not fiber-like. Then there are
$\pi _1$-injective but not fiber-like. Then there are ![]() $\ell,\sigma >0$ such that
$\ell,\sigma >0$ such that
where ![]() $\gamma$ is chosen uniformly at random in the sphere of radius
$\gamma$ is chosen uniformly at random in the sphere of radius ![]() $n$ with respect to
$n$ with respect to ![]() $S$.
$S$.
The theorem is new even for surfaces; in that context, Chas and Lalley [Reference Chas and LalleyCL12] proved a CLT for self-intersection numbers of curves with respect to word length. Following Theorem 1.2, a similar result could be formulated for more general hyperbolic manifolds.
Homomorphisms between hyperbolic groups
Our next application is to homomorphisms between hyperbolic groups. Interestingly, the condition for nonzero variance can be recast in terms of the induced Patterson–Sullivan measures.
Theorem 1.5 Suppose that ![]() $\phi \colon G \to G'$ is a homomorphism between hyperbolic groups such that the image of
$\phi \colon G \to G'$ is a homomorphism between hyperbolic groups such that the image of ![]() $\phi$ is not virtually cyclic. For any fixed generating sets
$\phi$ is not virtually cyclic. For any fixed generating sets ![]() $S$ and
$S$ and ![]() $S'$ of
$S'$ of ![]() $G$ and
$G$ and ![]() $G'$, respectively, there are
$G'$, respectively, there are ![]() $\ell >0$ and
$\ell >0$ and ![]() $\sigma \ge 0$ such that
$\sigma \ge 0$ such that
for ![]() $g\in G$ chosen uniformly at random in the sphere of radius
$g\in G$ chosen uniformly at random in the sphere of radius ![]() $n$ with respect to
$n$ with respect to ![]() $S$.
$S$.
Moreover, ![]() $\sigma = 0$ (i.e. the Gaussian is degenerate) if and only if
$\sigma = 0$ (i.e. the Gaussian is degenerate) if and only if ![]() $\phi$ has finite kernel and there is an induced embedding
$\phi$ has finite kernel and there is an induced embedding ![]() $\partial \phi \colon \partial G \to \partial G'$ that pushes the Patterson–Sullivan measure class for
$\partial \phi \colon \partial G \to \partial G'$ that pushes the Patterson–Sullivan measure class for ![]() $(G,d_S)$ to the Patterson–Sullivan measure class for
$(G,d_S)$ to the Patterson–Sullivan measure class for ![]() $(\phi (G), d_{S'})$.
$(\phi (G), d_{S'})$.
The above result generalizes a result due to Calegari and Fujiwara [Reference Calegari and FujiwaraCF10, Corollary 4.27]. It is also related to [Reference CantrellCan21, Theorem 1.6], who proved a CLT where ![]() $\phi$ is the abelianization homomorphism, which in turn generalizes work of Rivin [Reference RivinRiv10] for free groups.
$\phi$ is the abelianization homomorphism, which in turn generalizes work of Rivin [Reference RivinRiv10] for free groups.
Hyperplanes crossed in right-angled Artin and Coxeter groups
Our final application is to a collection of groups that is not necessarily relatively hyperbolic.
Suppose that ![]() $G$ is a right-angled Artin group or right-angled Coxeter group that is not a direct product. Let
$G$ is a right-angled Artin group or right-angled Coxeter group that is not a direct product. Let ![]() $V$ be its set of vertex generators. For each
$V$ be its set of vertex generators. For each ![]() $v \in V$, define a function
$v \in V$, define a function ![]() $\#_v \colon G \to \mathbb {Z}$ that counts the number of occurrences of
$\#_v \colon G \to \mathbb {Z}$ that counts the number of occurrences of ![]() $v^{\pm 1}$ in a shortest spelling of
$v^{\pm 1}$ in a shortest spelling of ![]() $g \in G$ with respect to
$g \in G$ with respect to ![]() $V$. Equivalently,
$V$. Equivalently, ![]() $\#_v(g)$ is the number of hyperplanes labeled by
$\#_v(g)$ is the number of hyperplanes labeled by ![]() $v$ separating
$v$ separating ![]() $o$ and
$o$ and ![]() $go$ in the cube complex associated to
$go$ in the cube complex associated to ![]() $G$.
$G$.
Theorem 1.6 For ![]() $G$ as above, there are
$G$ as above, there are ![]() $\ell,\sigma > 0$ such that for any vertex
$\ell,\sigma > 0$ such that for any vertex ![]() $v$,
$v$,
where ![]() $g$ is chosen uniformly at random in the sphere of radius
$g$ is chosen uniformly at random in the sphere of radius ![]() $n$ with respect to the vertex generators.
$n$ with respect to the vertex generators.
We conclude by noting that our methods are sufficiently general to apply beyond the case of ‘nonpositively curved’ groups. Moreover, we do not need to assume that our counting measures are associated to geodesic combings. See Theorems 7.3 and 7.4 for the most general result. For example, by using the standard graph structure associated to the language of geodesics for a free group, we obtain a CLT for nonbacktracking random walks on any group with a nonelementary action on a hyperbolic space ![]() $X$.
$X$.
From thermodynamics to random walks
Most CLTs for counting measures established so far use a coding for geodesics with finite paths, and then apply classical results in thermodynamic formalism, like the existence and uniqueness of Gibbs measures for shifts of finite type. There, the observable is assumed to be Hölder continuous with respect to the standard metric on the shift space.
In this paper, instead, we do not assume any good geometric property on the action. Let us recall that displacement is not a quasimorphism, is in general not weakly combable (in the language of [Reference Calegari and FujiwaraCF10]) if the action is not convex cocompact, and is not a Hölder weight function in the sense of [Reference Pollicott and SharpPS98, Proposition 1] if ![]() $X$ is not CAT
$X$ is not CAT![]() $(-1)$. Thus, the observable need not be Hölder and the thermodynamic approach does not appear to work. We also do not use transfer operators or
$(-1)$. Thus, the observable need not be Hölder and the thermodynamic approach does not appear to work. We also do not use transfer operators or ![]() $\zeta$-functions (e.g. as in [Reference Parry and PollicottPP90, Reference CantrellCan21]).
$\zeta$-functions (e.g. as in [Reference Parry and PollicottPP90, Reference CantrellCan21]).
Rather, our general strategy is as follows.
(i) We start with a graph structure, that is, a graph whose paths parameterize the group elements we want to count. We first consider a vertex
 $v$ of this graph, and consider a random walk on the semigroup
$v$ of this graph, and consider a random walk on the semigroup  $\Gamma _v$ of loops based at this vertex. Here, we apply the CLT for cocycles for groups acting on hyperbolic spaces, as devised by Benoist and Quint [Reference Benoist and QuintBQ16] and generalized by Horbez [Reference HorbezHor18] to actions on nonproper spaces.
$\Gamma _v$ of loops based at this vertex. Here, we apply the CLT for cocycles for groups acting on hyperbolic spaces, as devised by Benoist and Quint [Reference Benoist and QuintBQ16] and generalized by Horbez [Reference HorbezHor18] to actions on nonproper spaces.(ii) Then we consider the set of paths in a maximal component for the graph as a suspension on the space of loops at
 $v$, and we apply results of Melbourne and Török [Reference Maher and TiozzoMT18] to ‘lift’ the CLT to the suspended transformation. To be precise, we need to consider a skew product over the shift space.
$v$, and we apply results of Melbourne and Török [Reference Maher and TiozzoMT18] to ‘lift’ the CLT to the suspended transformation. To be precise, we need to consider a skew product over the shift space.(iii) Now we note that a thick graph structure is almost semisimple, hence there exists a power
 $p$ for which the transition matrix
$p$ for which the transition matrix  $M^{p}$ is semisimple. We use this to prove that the counting measure starting at an initial vertex converges to a convex combination of stationary measures for the Markov chains on the maximal components.
$M^{p}$ is semisimple. We use this to prove that the counting measure starting at an initial vertex converges to a convex combination of stationary measures for the Markov chains on the maximal components.(iv) Using a coherence condition on the graph structure, we show that all the CLTs for all Markov chains have the same mean and variance. This implies a CLT for the counting measure on the set of paths starting at any vertex in a semisimple structure.
(v) Finally, for a general thick structure of period
 $p$ we condition on the first prefix of length
$p$ we condition on the first prefix of length  $r$; since all these distributions for the conditional measures converge to the same law (by (iv) above), the CLT for the entire sequence holds.
$r$; since all these distributions for the conditional measures converge to the same law (by (iv) above), the CLT for the entire sequence holds.
We conclude by mentioning some natural generalizations of this work, which we do not attempt here. A Berry–Esseen type estimate of the error term appears within reach, using the corresponding result for random walks and the bounds we work out here comparing the counting and random walk measures. It would also be very interesting to obtain a local limit theorem, for which, however, much further work is needed.
2. Background
2.1 Graph structures for countable groups
Given a countable group ![]() $G$, we define a graph structure on
$G$, we define a graph structure on ![]() $G$ as a triple
$G$ as a triple ![]() $(\Gamma, v_0, \mathrm {ev})$, where
$(\Gamma, v_0, \mathrm {ev})$, where ![]() $\Gamma$ is a finite, directed graph,
$\Gamma$ is a finite, directed graph, ![]() $v_0$ is a vertex of
$v_0$ is a vertex of ![]() $\Gamma$ which we call its initial vertex, and
$\Gamma$ which we call its initial vertex, and ![]() $\mathrm {ev} \colon E(\Gamma ) \to G$ is a map that labels the edges of
$\mathrm {ev} \colon E(\Gamma ) \to G$ is a map that labels the edges of ![]() $\Gamma$ with group elements. Given this data, we extend the map
$\Gamma$ with group elements. Given this data, we extend the map ![]() $\mathrm {ev}$ by defining for each finite path
$\mathrm {ev}$ by defining for each finite path ![]() $g = g_1 \cdots g_n$ the group element
$g = g_1 \cdots g_n$ the group element ![]() $\mathrm {ev}(g) = \mathrm {ev}(g_1) \cdots \mathrm {ev}(g_n)$. We remark that here and throughout, a path in
$\mathrm {ev}(g) = \mathrm {ev}(g_1) \cdots \mathrm {ev}(g_n)$. We remark that here and throughout, a path in ![]() $\Gamma$ will always mean a directed path. To simplify notation, we will use
$\Gamma$ will always mean a directed path. To simplify notation, we will use ![]() $\overline {g} = \mathrm {ev}(g)$ to denote the group element associated to the path
$\overline {g} = \mathrm {ev}(g)$ to denote the group element associated to the path ![]() $g$. We denote by
$g$. We denote by ![]() $\Vert g \Vert$ the length of the path
$\Vert g \Vert$ the length of the path ![]() $g$. The graph structure is bounded if there is a uniform bound on the number of paths in
$g$. The graph structure is bounded if there is a uniform bound on the number of paths in ![]() $\Gamma$ mapping to any single element of
$\Gamma$ mapping to any single element of ![]() $G$.
$G$.
For a graph structure ![]() $\Gamma$, we define
$\Gamma$, we define ![]() $\Omega$ to be the set of all infinite paths starting at any vertex of
$\Omega$ to be the set of all infinite paths starting at any vertex of ![]() $\Gamma$ and
$\Gamma$ and ![]() $\sigma \colon \Omega \to \Omega$ to be the shift map. Given a path
$\sigma \colon \Omega \to \Omega$ to be the shift map. Given a path ![]() $\omega = (g_1, \ldots, g_n, \ldots )$, we denote by
$\omega = (g_1, \ldots, g_n, \ldots )$, we denote by ![]() $w_n := g_1 \cdots g_n$ its prefix of length
$w_n := g_1 \cdots g_n$ its prefix of length ![]() $n$. The set of all finite paths starting at any vertex of
$n$. The set of all finite paths starting at any vertex of ![]() $\Gamma$ will be denoted by
$\Gamma$ will be denoted by ![]() $\Omega ^{*}$.
$\Omega ^{*}$.
We define two vertices ![]() $v_i, v_j$ to be equivalent if there is a path from
$v_i, v_j$ to be equivalent if there is a path from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ and a path from
$v_j$ and a path from ![]() $v_j$ to
$v_j$ to ![]() $v_i$, and the components of
$v_i$, and the components of ![]() $\Gamma$ as the equivalence classes for this relation.
$\Gamma$ as the equivalence classes for this relation.
We will denote by ![]() $M$ the transition matrix for
$M$ the transition matrix for ![]() $\Gamma$. By Perron–Frobenius,
$\Gamma$. By Perron–Frobenius, ![]() $M$ has a real eigenvalue of largest modulus, which we will denote by
$M$ has a real eigenvalue of largest modulus, which we will denote by ![]() $\lambda$. Moreover, such a matrix is almost semisimple if for any eigenvalue of maximal modulus, its geometric and algebraic multiplicity agree. Furthermore, such a matrix is semisimple if its only eigenvalue of maximal modulus is real positive. We call a graph structure (almost) semisimple if its associated transition matrix is.
$\lambda$. Moreover, such a matrix is almost semisimple if for any eigenvalue of maximal modulus, its geometric and algebraic multiplicity agree. Furthermore, such a matrix is semisimple if its only eigenvalue of maximal modulus is real positive. We call a graph structure (almost) semisimple if its associated transition matrix is.
Let ![]() $\Gamma$ be almost semisimple, and let
$\Gamma$ be almost semisimple, and let ![]() $\lambda$ be the leading eigenvalue of
$\lambda$ be the leading eigenvalue of ![]() $M$. Then we define a vertex
$M$. Then we define a vertex ![]() $v$ to be of large growth if
$v$ to be of large growth if
and of small growth otherwise (in which case, the limit above is less than ![]() $\lambda$). Furthermore, a component
$\lambda$). Furthermore, a component ![]() $C$ is maximal if
$C$ is maximal if
As discussed in [Reference Gekhtman, Taylor and TiozzoGTT20], the global structure of ![]() $\Gamma$ is as follows: there is no path between maximal components, and vertices of large growth are precisely the ones which have a path to a maximal component.
$\Gamma$ is as follows: there is no path between maximal components, and vertices of large growth are precisely the ones which have a path to a maximal component.
Given a vertex ![]() $v$, we denote by
$v$, we denote by ![]() $\Gamma _v$ the loop semigroup of
$\Gamma _v$ the loop semigroup of ![]() $v$, that is, the set of all finite paths from
$v$, that is, the set of all finite paths from ![]() $v$ to itself. This is a semigroup under concatenation, and all its elements lie entirely in the component of
$v$ to itself. This is a semigroup under concatenation, and all its elements lie entirely in the component of ![]() $v$. We denote by
$v$. We denote by ![]() $\overline {\Gamma }_v$ the image of
$\overline {\Gamma }_v$ the image of ![]() $\Gamma _v$ in
$\Gamma _v$ in ![]() $G$ under the evaluation map.
$G$ under the evaluation map.
Definition 2.1 (Thick graph structure)
A graph structure ![]() $\Gamma$ is thick if, for any vertex
$\Gamma$ is thick if, for any vertex ![]() $v$ in a maximal component, there exists a finite set
$v$ in a maximal component, there exists a finite set ![]() $B \subseteq G$ such that
$B \subseteq G$ such that
where the equality is in the group ![]() $G$.
$G$.
In what follows, we often make the evaluation map implicit in our notation. In particular, if ![]() $G$ acts on a metric space
$G$ acts on a metric space ![]() $(X, d)$,
$(X, d)$, ![]() $o \in X$ is a base point, and
$o \in X$ is a base point, and ![]() $g$ is a finite path in
$g$ is a finite path in ![]() $\Gamma$, we will often write
$\Gamma$, we will often write ![]() $go$ to mean the point
$go$ to mean the point ![]() $\overline {g}o \in X$.
$\overline {g}o \in X$.
2.1 Geodesic combings
For particular applications, it is also useful to define the notion of a geodesic graph structure. A graph structure ![]() $\Gamma$ is geodesic if the length
$\Gamma$ is geodesic if the length ![]() $\Vert g \Vert$ of any path
$\Vert g \Vert$ of any path ![]() $g$ is equal the word length of
$g$ is equal the word length of ![]() $\overline {g}$ in the subgroup generated by the edge labels, using edge labels as the (finite) generating set. A geodesic graph structure is called a geodesic combing if, in addition, there is a directed path from
$\overline {g}$ in the subgroup generated by the edge labels, using edge labels as the (finite) generating set. A geodesic graph structure is called a geodesic combing if, in addition, there is a directed path from ![]() $v_0$ to any other vertex of
$v_0$ to any other vertex of ![]() $\Gamma$ and the evaluation map is a bijection from the set of finite paths starting at
$\Gamma$ and the evaluation map is a bijection from the set of finite paths starting at ![]() $v_0$ to the set of elements of
$v_0$ to the set of elements of ![]() $G$. Note that a geodesic combing is automatically a bounded graph structure. We say that
$G$. Note that a geodesic combing is automatically a bounded graph structure. We say that ![]() $\Gamma$ is a geodesic combing associated to a finite generating set
$\Gamma$ is a geodesic combing associated to a finite generating set ![]() $S$ if, up to adding inverses,
$S$ if, up to adding inverses, ![]() $S$ is the set of edge labels for the graph structure. In this case,
$S$ is the set of edge labels for the graph structure. In this case, ![]() $\Vert g \Vert$ is equal to the word length of
$\Vert g \Vert$ is equal to the word length of ![]() $\overline {g}$ with respect to
$\overline {g}$ with respect to ![]() $S$.
$S$.
We emphasize that although the geodesic condition is used in the applications of our main theorem (as in Theorems 1.1–1.6), it is not required for the most general results; see Theorems 7.3 and 7.4. There we use the following more general notion.
Definition 2.2 (Coherent graph structure)
A graph structure ![]() $\Gamma$ for
$\Gamma$ for ![]() $G$ is coherent if it is bounded and if for any finite set
$G$ is coherent if it is bounded and if for any finite set ![]() $B \subseteq G$ there exists a constant
$B \subseteq G$ there exists a constant ![]() $\mathcal {B} \ge 0$ such that if
$\mathcal {B} \ge 0$ such that if ![]() $g$ and
$g$ and ![]() $h$ are finite length paths in
$h$ are finite length paths in ![]() $\Gamma$, and
$\Gamma$, and ![]() $\overline {g} = b_1 \overline {h} b_2$ in
$\overline {g} = b_1 \overline {h} b_2$ in ![]() $G$, then
$G$, then
The idea of coherence is simple; informally, if two group elements are close in ![]() $G$ then a coherent graph structure
$G$ then a coherent graph structure ![]() $\Gamma$ codes them with paths that are roughly the same length, and the coding is uniformly bounded-to-one.
$\Gamma$ codes them with paths that are roughly the same length, and the coding is uniformly bounded-to-one.
Our first lemma summarizes some properties of thick, coherent graph structures that we will need in the sequel.
Lemma 2.3 A thick, coherent graph structure ![]() $\Gamma$ is almost semisimple.
$\Gamma$ is almost semisimple.
Moreover, if ![]() $G \curvearrowright X$ is a nonelementary action on a hyperbolic space, then the actions of both semigroups
$G \curvearrowright X$ is a nonelementary action on a hyperbolic space, then the actions of both semigroups ![]() $\Gamma _v$ and
$\Gamma _v$ and ![]() $\Gamma _v^{-1}$ on
$\Gamma _v^{-1}$ on ![]() $X$ are also nonelementary, for each vertex
$X$ are also nonelementary, for each vertex ![]() $v$ contained in a maximal component.
$v$ contained in a maximal component.
Proof. Suppose the graph structure ![]() $\Gamma$ is thick and coherent. Since a coherent graph structure is bounded, there is a
$\Gamma$ is thick and coherent. Since a coherent graph structure is bounded, there is a ![]() $\mathfrak b \ge 0$ so that the evaluation map
$\mathfrak b \ge 0$ so that the evaluation map ![]() $\mathrm {ev} \colon \Omega ^{*} \to G$ is at most
$\mathrm {ev} \colon \Omega ^{*} \to G$ is at most ![]() $\mathfrak b$-to-one. Let
$\mathfrak b$-to-one. Let ![]() $B\subset G$ be the finite set given by thickness of
$B\subset G$ be the finite set given by thickness of ![]() $\Gamma$ (Definition 2.1) and let
$\Gamma$ (Definition 2.1) and let ![]() $\mathcal {B}$ be the resulting constant from Definition 2.2. By thickness and coherence we have
$\mathcal {B}$ be the resulting constant from Definition 2.2. By thickness and coherence we have
where ![]() $S_n \subset \Omega ^{*}$ is the set of all length
$S_n \subset \Omega ^{*}$ is the set of all length ![]() $n$ paths starting at any vertex. Then the definition of
$n$ paths starting at any vertex. Then the definition of ![]() $\mathfrak b$ implies that
$\mathfrak b$ implies that
This, in turn, is bounded by a constant times ![]() $\lambda ^{n}$ since it is no more than the growth of paths in the maximal component of
$\lambda ^{n}$ since it is no more than the growth of paths in the maximal component of ![]() $\Gamma$ containing
$\Gamma$ containing ![]() $v$, and
$v$, and ![]() $k$ is uniformly bounded. On the other hand, if the transition matrix
$k$ is uniformly bounded. On the other hand, if the transition matrix ![]() $M$ of
$M$ of ![]() $\Gamma$ is not almost semisimple, then
$\Gamma$ is not almost semisimple, then ![]() $M$ has a Jordan block for an eigenvalue of modulus
$M$ has a Jordan block for an eigenvalue of modulus ![]() $\lambda$ of size
$\lambda$ of size ![]() $k\ge 2$ (see [Reference Gekhtman, Taylor and TiozzoGTT18, § 2]). In particular, the growth of paths in
$k\ge 2$ (see [Reference Gekhtman, Taylor and TiozzoGTT18, § 2]). In particular, the growth of paths in ![]() $\Gamma$ is at least a constant times
$\Gamma$ is at least a constant times ![]() $n^{k-1}\lambda ^{n}$. We conclude that
$n^{k-1}\lambda ^{n}$. We conclude that ![]() $\Gamma$ is almost semisimple.
$\Gamma$ is almost semisimple.
The statement that the action of ![]() $\Gamma _v$ (and hence
$\Gamma _v$ (and hence ![]() $\Gamma _v^{-1}$) on
$\Gamma _v^{-1}$) on ![]() $X$ is nonelementary is proven in [Reference Gekhtman, Taylor and TiozzoGTT20, Proposition 6.3].
$X$ is nonelementary is proven in [Reference Gekhtman, Taylor and TiozzoGTT20, Proposition 6.3].
The following lemma is immediate from the definitions.
Lemma 2.4 A geodesic combing for ![]() $G$ is coherent.
$G$ is coherent.
Other sources of (not necessarily geodesic) coherent graph structures come from biautomatic groups, in the sense of [Reference MosherMos97] or [Reference Epstein, Paterson, Cannon, Holt, Levy and ThurstonEPC+92, Lemma 2.5.5].
2.2 Cocycles and horofunctions
Let ![]() $(X, d)$ be a metric space, and let
$(X, d)$ be a metric space, and let ![]() $o \in X$ be a base point. Given
$o \in X$ be a base point. Given ![]() $z \in X$, we define the Busemann function
$z \in X$, we define the Busemann function ![]() $\rho _z : X \to \mathbb {R}$ as
$\rho _z : X \to \mathbb {R}$ as
Thus, setting
defines a map
where ![]() $\text {Lip}^{1}_o(X)$ is the space of
$\text {Lip}^{1}_o(X)$ is the space of ![]() $1$-Lipschitz functions on
$1$-Lipschitz functions on ![]() $X$ which vanish at
$X$ which vanish at ![]() $o$.
$o$.
We define the horofunction compactification ![]() $\overline {X}^{h}$ as the closure of
$\overline {X}^{h}$ as the closure of ![]() $\Phi (X)$ in
$\Phi (X)$ in ![]() $\text {Lip}^{1}_o(X)$, with respect to the topology of pointwise convergence. Elements of
$\text {Lip}^{1}_o(X)$, with respect to the topology of pointwise convergence. Elements of ![]() $\overline {X}^{h}$ will be called horofunctions. We denote by
$\overline {X}^{h}$ will be called horofunctions. We denote by ![]() $\overline {X}_\infty ^{h}$ the space of infinite horofunctions, that is, the set of
$\overline {X}_\infty ^{h}$ the space of infinite horofunctions, that is, the set of ![]() $h \in \overline {X}^{h}$ such that
$h \in \overline {X}^{h}$ such that ![]() $\inf _{x \in X} h(x) = - \infty$.
$\inf _{x \in X} h(x) = - \infty$.
For any ![]() $\xi \in \overline {X}^{h}$, the Busemann cocycle is defined as
$\xi \in \overline {X}^{h}$, the Busemann cocycle is defined as
 \begin{align*} \beta_{\xi}(x, y) &:= \lim_{z_n \to \xi} [ d(y, z_n) - d(x, z_n)] \\ &= h_\xi(y) - h_\xi(x), \end{align*}
\begin{align*} \beta_{\xi}(x, y) &:= \lim_{z_n \to \xi} [ d(y, z_n) - d(x, z_n)] \\ &= h_\xi(y) - h_\xi(x), \end{align*}
where ![]() $h_\xi$ is the horofunction associated to
$h_\xi$ is the horofunction associated to ![]() $\xi$. This has the usual cocycle property
$\xi$. This has the usual cocycle property ![]() $\beta _{\xi }(x, z) =\beta _{\xi }(x, y) +\beta _{\xi }(y, z)$.
$\beta _{\xi }(x, z) =\beta _{\xi }(x, y) +\beta _{\xi }(y, z)$.
Remark 2.5 Benoist and Quint [Reference Benoist and QuintBQ16] and Horbez [Reference HorbezHor18] define ![]() $B \colon G \times \overline {X}^{h} \to \mathbb {R}$ by
$B \colon G \times \overline {X}^{h} \to \mathbb {R}$ by
To compare their definition with ours:
3. Central limit theorem for random walks on the loop semigroups
Let ![]() $\Gamma$ be a graph structure for
$\Gamma$ be a graph structure for ![]() $G$, and let
$G$, and let ![]() $v$ be a vertex in a maximal component. Recall that a (directed) loop is prime if it is not itself a product of nontrivial loops; since every loop can be decomposed uniquely as a concatenation of prime loops, prime loops freely generate
$v$ be a vertex in a maximal component. Recall that a (directed) loop is prime if it is not itself a product of nontrivial loops; since every loop can be decomposed uniquely as a concatenation of prime loops, prime loops freely generate ![]() $\Gamma _v$ as a semigroup.
$\Gamma _v$ as a semigroup.
Given a probability measure ![]() $\mu$ on the set of edges of
$\mu$ on the set of edges of ![]() $\Gamma$, one defines the first return measure
$\Gamma$, one defines the first return measure ![]() $\mu _v$ on
$\mu _v$ on ![]() $\Gamma _v$ as follows. If
$\Gamma _v$ as follows. If ![]() $l = g_1 \cdots g_n$ is a prime loop in
$l = g_1 \cdots g_n$ is a prime loop in ![]() $\Gamma _v$, then we set
$\Gamma _v$, then we set
We set ![]() $\mu _v(l) = 0$ for all other loops. Note that inversion defines a map
$\mu _v(l) = 0$ for all other loops. Note that inversion defines a map ![]() $\Gamma _v \to \Gamma ^{-1}_v$ and we define the measure
$\Gamma _v \to \Gamma ^{-1}_v$ and we define the measure ![]() $\check \mu$ on
$\check \mu$ on ![]() $\Gamma ^{-1}_v$ by
$\Gamma ^{-1}_v$ by ![]() $\check \mu (l) = \mu (l^{-1})$. These measures push forward to measures on the group
$\check \mu (l) = \mu (l^{-1})$. These measures push forward to measures on the group ![]() $G$ under the evaluation map. We say that
$G$ under the evaluation map. We say that ![]() $\mu _v$ is nondegenerate if it gives positive measure to any prime loop of
$\mu _v$ is nondegenerate if it gives positive measure to any prime loop of ![]() $\Gamma _v$.
$\Gamma _v$.
Let ![]() $\mathcal {M}$ be a metric space on which
$\mathcal {M}$ be a metric space on which ![]() $G$ acts by homeomorphisms. A measure
$G$ acts by homeomorphisms. A measure ![]() $\nu$ on
$\nu$ on ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\mu$-stationary if
$\mu$-stationary if ![]() $\nu = \int _G g_\star \nu \,d\mu (g)$, and
$\nu = \int _G g_\star \nu \,d\mu (g)$, and ![]() $\mu$-ergodic if it cannot be written as a nontrivial convex combination of
$\mu$-ergodic if it cannot be written as a nontrivial convex combination of ![]() $\mu$-stationary measures.
$\mu$-stationary measures.
3.1 Central limit theorems for cocycles
Recall that a cocycle is a function ![]() $\sigma \colon G \times \mathcal {M} \to \mathbb {R}$ such that
$\sigma \colon G \times \mathcal {M} \to \mathbb {R}$ such that
A cocycle ![]() $\sigma \colon G \times \mathcal {M} \to \mathbb {R}$ has constant drift
$\sigma \colon G \times \mathcal {M} \to \mathbb {R}$ has constant drift ![]() $\lambda$ if there exists
$\lambda$ if there exists ![]() $\lambda \in \mathbb {R}$ such that
$\lambda \in \mathbb {R}$ such that
for any ![]() $x \in \mathcal {M}$. A cocycle
$x \in \mathcal {M}$. A cocycle ![]() $\sigma \colon G \times \mathcal {M} \to \mathbb {R}$ is centerable if it can be written as
$\sigma \colon G \times \mathcal {M} \to \mathbb {R}$ is centerable if it can be written as
where ![]() $\sigma _0$ is a cocycle with constant drift and where
$\sigma _0$ is a cocycle with constant drift and where ![]() $\psi \colon \mathcal {M} \to \mathbb {R}$ is a bounded, measurable function. In this case, we say that
$\psi \colon \mathcal {M} \to \mathbb {R}$ is a bounded, measurable function. In this case, we say that ![]() $\sigma _0$ is the centering of
$\sigma _0$ is the centering of ![]() $\sigma$; note that
$\sigma$; note that ![]() $\lambda = \int _{G \times \mathcal {M}} \sigma (g, x) \, d\mu (g) \,d \nu (x)$ for any
$\lambda = \int _{G \times \mathcal {M}} \sigma (g, x) \, d\mu (g) \,d \nu (x)$ for any ![]() $\mu$-stationary
$\mu$-stationary ![]() $\nu$. We say that the cocycle
$\nu$. We say that the cocycle ![]() $\sigma$ has finite second moment with respect to a measure
$\sigma$ has finite second moment with respect to a measure ![]() $\mu$ on
$\mu$ on ![]() $G$ if
$G$ if
We now use the following CLT for centerable cocycles; as remarked in [Reference HorbezHor18, Remark 1.7], the proof is exactly the same as the proof of [Reference Benoist and QuintBQ16, Theorem 4.7].
Theorem 3.1 (Central limit theorem for cocycles)
Let ![]() $G$ be a discrete group,
$G$ be a discrete group, ![]() $\mathcal {M}$ be a compact metrizable
$\mathcal {M}$ be a compact metrizable ![]() $G$-space and
$G$-space and ![]() $\mu$ a probability measure on
$\mu$ a probability measure on ![]() $G$. Let
$G$. Let ![]() $\nu$ be a
$\nu$ be a ![]() $\mu$-ergodic,
$\mu$-ergodic, ![]() $\mu$-stationary probability measure on
$\mu$-stationary probability measure on ![]() $\mathcal {M}$, and let
$\mathcal {M}$, and let ![]() $\mathcal {M}_0$ be a
$\mathcal {M}_0$ be a ![]() $G$-invariant subset of
$G$-invariant subset of ![]() $\mathcal {M}$ of full
$\mathcal {M}$ of full ![]() $\nu$-measure. Let
$\nu$-measure. Let ![]() $\sigma \colon G \times \mathcal {M}_0 \to \mathbb {R}$ be a centerable cocycle with drift
$\sigma \colon G \times \mathcal {M}_0 \to \mathbb {R}$ be a centerable cocycle with drift ![]() $\lambda$ and finite second moment. Then there exist
$\lambda$ and finite second moment. Then there exist ![]() $\sigma \geq 0$ such that for any continuous
$\sigma \geq 0$ such that for any continuous ![]() $F \colon \mathbb {R} \to \mathbb {R}$ with compact support, we have for
$F \colon \mathbb {R} \to \mathbb {R}$ with compact support, we have for ![]() $\nu$-almost every (a.e.)
$\nu$-almost every (a.e.) ![]() $x \in \mathcal {M}$,
$x \in \mathcal {M}$,
We now apply this result to the loop semigroup. Let ![]() $F_v$ be the group freely generated by the prime loops in
$F_v$ be the group freely generated by the prime loops in ![]() $\Gamma _v$.
$\Gamma _v$.
Let ![]() $N\colon \Gamma _v \to \mathbb {Z}$ be the semigroup homomorphism
$N\colon \Gamma _v \to \mathbb {Z}$ be the semigroup homomorphism ![]() $N(g) := - \Vert g \Vert$, where
$N(g) := - \Vert g \Vert$, where ![]() $\Vert g \Vert$ is the length in
$\Vert g \Vert$ is the length in ![]() $\Gamma$ of the loop
$\Gamma$ of the loop ![]() $g$. There is a natural inclusion
$g$. There is a natural inclusion ![]() $\Gamma _v \to F_v$ as a subsemigroup and we can extend the semigroup homomorphism above to a group homomorphism
$\Gamma _v \to F_v$ as a subsemigroup and we can extend the semigroup homomorphism above to a group homomorphism ![]() $N\colon F_v \to \mathbb {Z}$. Moreover, we also extend the natural semigroup homomorphism
$N\colon F_v \to \mathbb {Z}$. Moreover, we also extend the natural semigroup homomorphism ![]() $\Gamma _v \to G$, induced by evaluation, to a group homomorphism
$\Gamma _v \to G$, induced by evaluation, to a group homomorphism ![]() $e \colon F_v \to G$. Now, using the homomorphism
$e \colon F_v \to G$. Now, using the homomorphism ![]() $e \colon F_v \to G$, the free group
$e \colon F_v \to G$, the free group ![]() $F_v$ has a nonelementary action on
$F_v$ has a nonelementary action on ![]() $X$, and, moreover,
$X$, and, moreover, ![]() $\mu _v^{*n}$ is supported on
$\mu _v^{*n}$ is supported on ![]() $\Gamma _v \subseteq F_v$ for all
$\Gamma _v \subseteq F_v$ for all ![]() $n\ge 1$.
$n\ge 1$.
Finally, for some ![]() $\ell \in \mathbb {R}$ to be specified below, we define
$\ell \in \mathbb {R}$ to be specified below, we define ![]() $\eta \colon F_v \times \overline X^{h} \to \mathbb {R}$ as
$\eta \colon F_v \times \overline X^{h} \to \mathbb {R}$ as
Lemma 3.2 Suppose that the action of ![]() $\Gamma _v$ on
$\Gamma _v$ on ![]() $X$ is nonelementary and
$X$ is nonelementary and ![]() $\mu _v$ is nondegenerate. Then, for any
$\mu _v$ is nondegenerate. Then, for any ![]() $\ell \in \mathbb {R}$, the restriction of
$\ell \in \mathbb {R}$, the restriction of ![]() $\eta : F_v \times \overline X^{h} \to \mathbb {R}$ to
$\eta : F_v \times \overline X^{h} \to \mathbb {R}$ to ![]() $F_v \times \overline {X}_\infty ^{h}$ is a centerable cocycle.
$F_v \times \overline {X}_\infty ^{h}$ is a centerable cocycle.
Proof. We have
 \begin{align*} \eta(gh, \xi) &= \beta_\xi(o, h^{-1} g^{-1} o) - \ell N(gh) \\ &= \beta_\xi(o, h^{-1} o) + \beta_{\xi}(h^{-1} o, h^{-1} g^{-1} o) - \ell N(g) - \ell N(h) \\ &= \beta_\xi(o, h^{-1} o) + \beta_{h \xi}(o, g^{-1} o) - \ell N(g) - \ell N(h) \\ &= \eta(h, \xi) + \eta(g, h\xi), \end{align*}
\begin{align*} \eta(gh, \xi) &= \beta_\xi(o, h^{-1} g^{-1} o) - \ell N(gh) \\ &= \beta_\xi(o, h^{-1} o) + \beta_{\xi}(h^{-1} o, h^{-1} g^{-1} o) - \ell N(g) - \ell N(h) \\ &= \beta_\xi(o, h^{-1} o) + \beta_{h \xi}(o, g^{-1} o) - \ell N(g) - \ell N(h) \\ &= \eta(h, \xi) + \eta(g, h\xi), \end{align*}
hence ![]() $\eta$ is a cocycle. Moreover, by [Reference HorbezHor18, Proposition 1.5], using [Reference HorbezHor18, Corollary 2.7] and [Reference HorbezHor18, Proposition 2.8], the cocycle
$\eta$ is a cocycle. Moreover, by [Reference HorbezHor18, Proposition 1.5], using [Reference HorbezHor18, Corollary 2.7] and [Reference HorbezHor18, Proposition 2.8], the cocycle ![]() $B(g, \xi ) = \beta _\xi (o, g^{-1}o)$ is centerable on
$B(g, \xi ) = \beta _\xi (o, g^{-1}o)$ is centerable on ![]() $F_v \times \overline {X}_\infty ^{h}$. Then, since
$F_v \times \overline {X}_\infty ^{h}$. Then, since ![]() $\eta (g, \xi ) - B(g, \xi ) = \ell N(g)$ is a homomorphism and depends only on
$\eta (g, \xi ) - B(g, \xi ) = \ell N(g)$ is a homomorphism and depends only on ![]() $g$, we have that
$g$, we have that ![]() $\eta (g, \xi )$ is also centerable on
$\eta (g, \xi )$ is also centerable on ![]() $F_v \times \overline {X}_\infty ^{h}$.
$F_v \times \overline {X}_\infty ^{h}$.
Thus, we obtain the following consequence of Theorem 3.1.
Corollary 3.3 Let ![]() $\Gamma$ be a thick structure, let
$\Gamma$ be a thick structure, let ![]() $v$ be a vertex in a maximal component of
$v$ be a vertex in a maximal component of ![]() $\Gamma$. Suppose that the first return measure
$\Gamma$. Suppose that the first return measure ![]() $\mu _v$ is nondegenerate, and let
$\mu _v$ is nondegenerate, and let ![]() $\nu _v$ be a
$\nu _v$ be a ![]() $\check {\mu }_v$-ergodic,
$\check {\mu }_v$-ergodic, ![]() $\check {\mu }_v$-stationary measure on
$\check {\mu }_v$-stationary measure on ![]() $\overline {X}^{h}$. Then there exist
$\overline {X}^{h}$. Then there exist ![]() $\ell, \sigma \ge 0$ such that for any continuous
$\ell, \sigma \ge 0$ such that for any continuous ![]() $F \colon \mathbb {R} \to \mathbb {R}$ with compact support, we have for
$F \colon \mathbb {R} \to \mathbb {R}$ with compact support, we have for ![]() $\nu _v$-a.e.
$\nu _v$-a.e. ![]() $\xi$,
$\xi$,
Proof. We apply Theorem 3.1 to the measure ![]() $\check {\mu }_v$, supported on
$\check {\mu }_v$, supported on ![]() $\Gamma _v^{-1}$, where
$\Gamma _v^{-1}$, where ![]() $\ell$ is chosen so that
$\ell$ is chosen so that ![]() $\lambda = \int _{F_v \times \overline X^{h}} \eta (g, \xi ) \, d\check {\mu }_v(g) \,d\nu _v(\xi ) = 0$. Note that, by [Reference Maher and TiozzoMT18, Proposition 4.4] and the fact that
$\lambda = \int _{F_v \times \overline X^{h}} \eta (g, \xi ) \, d\check {\mu }_v(g) \,d\nu _v(\xi ) = 0$. Note that, by [Reference Maher and TiozzoMT18, Proposition 4.4] and the fact that ![]() $\Gamma _v^{-1}$ is nonelementary (Lemma 2.3), we have
$\Gamma _v^{-1}$ is nonelementary (Lemma 2.3), we have ![]() $\nu _v(\overline {X}^{h}_\infty ) = 1$. Moreover, for any
$\nu _v(\overline {X}^{h}_\infty ) = 1$. Moreover, for any ![]() $g \in \Gamma _v$ we have
$g \in \Gamma _v$ we have
3.2 Skew products and invariance on the loop semigroup
Let ![]() $\mathcal {M}$ be a compact metric space with a continuous
$\mathcal {M}$ be a compact metric space with a continuous ![]() $G$-action. We define the skew product
$G$-action. We define the skew product ![]() $T\colon \Omega \times \mathcal {M} \to \Omega \times \mathcal {M}$ as
$T\colon \Omega \times \mathcal {M} \to \Omega \times \mathcal {M}$ as
where ![]() $\omega = (g_1, g_2, \ldots )$.
$\omega = (g_1, g_2, \ldots )$.
A graph structure ![]() $\Gamma$ is primitive if its associated transition matrix
$\Gamma$ is primitive if its associated transition matrix ![]() $M$ is primitive, that is, has a positive power. Now let
$M$ is primitive, that is, has a positive power. Now let ![]() $\Gamma$ be a primitive graph structure, let
$\Gamma$ be a primitive graph structure, let ![]() $v$ be a vertex of
$v$ be a vertex of ![]() $\Gamma$, let
$\Gamma$, let ![]() $\Gamma _v$ be the loop semigroup, and let
$\Gamma _v$ be the loop semigroup, and let ![]() $\mu _v$ be the first return measure.
$\mu _v$ be the first return measure.
Finally, let ![]() $\Omega _v = (\Gamma _v)^{\mathbb{N}}$ with shift map
$\Omega _v = (\Gamma _v)^{\mathbb{N}}$ with shift map ![]() $\sigma _v$. To highlight the difference, we denote the elements of
$\sigma _v$. To highlight the difference, we denote the elements of ![]() $\Gamma _v^{\mathbb{N}}$ by
$\Gamma _v^{\mathbb{N}}$ by ![]() $(l_1, l_2, \ldots )$, since each element of the sequence is a loop, while the elements of
$(l_1, l_2, \ldots )$, since each element of the sequence is a loop, while the elements of ![]() $\Omega$ will be denoted by
$\Omega$ will be denoted by ![]() $\omega = (g_1, g_2, \ldots )$, since its elements are edges. Let us define the map
$\omega = (g_1, g_2, \ldots )$, since its elements are edges. Let us define the map ![]() $T_v : \Omega _v \times \mathcal {M} \to \Omega _v \times \mathcal {M}$ as
$T_v : \Omega _v \times \mathcal {M} \to \Omega _v \times \mathcal {M}$ as
Lemma 3.4 A measure ![]() $\nu$ on
$\nu$ on ![]() $\mathcal {M}$ is
$\mathcal {M}$ is ![]() $\check {\mu }_v$-stationary if and only if
$\check {\mu }_v$-stationary if and only if ![]() $\mu _v^{\mathbb{N}} \otimes \nu$ is
$\mu _v^{\mathbb{N}} \otimes \nu$ is ![]() $T_v$-invariant.
$T_v$-invariant.
Proof. Fix ![]() $C \subset \Omega _v$ measurable and let
$C \subset \Omega _v$ measurable and let ![]() $C_l \subset \Omega _v$ be the subset consisting of sequences beginning with
$C_l \subset \Omega _v$ be the subset consisting of sequences beginning with ![]() $l \in \Gamma _v$ such that
$l \in \Gamma _v$ such that ![]() $\sigma _v (C_l) = C$. Then, for any
$\sigma _v (C_l) = C$. Then, for any ![]() $A \subset \mathcal {M}$ measurable,
$A \subset \mathcal {M}$ measurable,
Since
 \begin{align*} \mu_v^{\mathbb{N}} \otimes \nu \bigg(\bigcup_l C_l \times l A\bigg) &= \mu(C) \sum_l \mu(l) \nu(lA) \\ &= \mu(C) \sum_l \check \mu(l) l_*\nu(A), \end{align*}
\begin{align*} \mu_v^{\mathbb{N}} \otimes \nu \bigg(\bigcup_l C_l \times l A\bigg) &= \mu(C) \sum_l \mu(l) \nu(lA) \\ &= \mu(C) \sum_l \check \mu(l) l_*\nu(A), \end{align*}the lemma follows.
Lemma 3.5 There exists an ergodic ![]() $\check {\mu }_v$-stationary measure
$\check {\mu }_v$-stationary measure ![]() $\nu _v$ on
$\nu _v$ on ![]() $\mathcal {M}$ such that the product measure
$\mathcal {M}$ such that the product measure ![]() $\mu _v^{\mathbb{N}} \otimes \nu _v$ is
$\mu _v^{\mathbb{N}} \otimes \nu _v$ is ![]() $T_v$-invariant and ergodic.
$T_v$-invariant and ergodic.
Proof. Since ![]() $\mathcal {M}$ is a compact metric space, there exists a
$\mathcal {M}$ is a compact metric space, there exists a ![]() $\check {\mu }_v$-stationary measure
$\check {\mu }_v$-stationary measure ![]() $\nu _1$ on
$\nu _1$ on ![]() $\mathcal {M}$ [Reference FurstenbergFur63, Lemma 1.2]. Then by Lemma 3.4 the measure
$\mathcal {M}$ [Reference FurstenbergFur63, Lemma 1.2]. Then by Lemma 3.4 the measure ![]() $\lambda _1 := \mu _v^{\mathbb{N}} \otimes \nu _1$ is
$\lambda _1 := \mu _v^{\mathbb{N}} \otimes \nu _1$ is ![]() $T_v$-invariant. If
$T_v$-invariant. If ![]() $\lambda _1$ is not ergodic, let us consider its ergodic decomposition, and take one of its ergodic components
$\lambda _1$ is not ergodic, let us consider its ergodic decomposition, and take one of its ergodic components ![]() $\lambda _v$. By definition,
$\lambda _v$. By definition, ![]() $\lambda _v \ll \lambda _1$ and
$\lambda _v \ll \lambda _1$ and ![]() $\lambda _v$ is
$\lambda _v$ is ![]() $T_v$-invariant and ergodic. Then, by [Reference MoritaMor88, Corollary 3.1],
$T_v$-invariant and ergodic. Then, by [Reference MoritaMor88, Corollary 3.1], ![]() $\lambda _v$ is of the form
$\lambda _v$ is of the form ![]() $\lambda _v = \mu _v^{\mathbb{N}} \otimes \nu _v$ for some measure
$\lambda _v = \mu _v^{\mathbb{N}} \otimes \nu _v$ for some measure ![]() $\nu _v$ on
$\nu _v$ on ![]() $\mathcal {M}$. Finally, again by Lemma 3.4, the measure
$\mathcal {M}$. Finally, again by Lemma 3.4, the measure ![]() $\nu _v$ is
$\nu _v$ is ![]() $\check {\mu }_v$-stationary.
$\check {\mu }_v$-stationary.
Lemma 3.6 Consider the function ![]() $f\colon \Omega \times \overline {X}^{h} \to \mathbb {R}$ defined as
$f\colon \Omega \times \overline {X}^{h} \to \mathbb {R}$ defined as
Then for any ![]() $n$ we have
$n$ we have
 \begin{equation} \sum_{j = 0}^{n-1} f(T^{j}(\omega, \xi)) = \beta_{\xi}(o, w_n o). \end{equation}
\begin{equation} \sum_{j = 0}^{n-1} f(T^{j}(\omega, \xi)) = \beta_{\xi}(o, w_n o). \end{equation}Proof. The cocycle property implies
 \begin{align*} \beta_{\xi} (o, w_n o) = \sum_{j =0}^{n-1} \beta_{\xi} (w_j o, w_{j+1} o) = \sum_{j = 0}^{n-1} \beta_{w_j^{-1} \xi}(o, g_{j+1} o) \end{align*}
\begin{align*} \beta_{\xi} (o, w_n o) = \sum_{j =0}^{n-1} \beta_{\xi} (w_j o, w_{j+1} o) = \sum_{j = 0}^{n-1} \beta_{w_j^{-1} \xi}(o, g_{j+1} o) \end{align*}
for any ![]() $\xi \in \overline {X}^{h}$. Moreover, by definition and
$\xi \in \overline {X}^{h}$. Moreover, by definition and ![]() $G$-equivariance we have
$G$-equivariance we have
and the claim follows.
An analogous statement holds by replacing ![]() $T, \Omega$ by
$T, \Omega$ by ![]() $T_v, \Omega _v$.
$T_v, \Omega _v$.
4. Central limit theorem for Markov chains of primitive graph structures
We begin by recalling the following. If ![]() $\Gamma$ is a directed graph whose transition matrix
$\Gamma$ is a directed graph whose transition matrix ![]() $M$ is primitive with leading eigenvalue
$M$ is primitive with leading eigenvalue ![]() $\lambda$, then
$\lambda$, then
where ![]() $M \rho = \lambda \rho$,
$M \rho = \lambda \rho$, ![]() $u^{T} M = \lambda u^{T}$, and
$u^{T} M = \lambda u^{T}$, and ![]() $u^{T} \rho = 1$ [Reference WaltersWal00, Theorem 0.17]. We will consider the following measures associated to
$u^{T} \rho = 1$ [Reference WaltersWal00, Theorem 0.17]. We will consider the following measures associated to ![]() $\Gamma$. The stationary measure on vertices for the corresponding Markov chain is given by setting the starting probability at vertex
$\Gamma$. The stationary measure on vertices for the corresponding Markov chain is given by setting the starting probability at vertex ![]() $v_i$ to be
$v_i$ to be ![]() $\pi _i = \rho _i u_i$. Assigning the probability
$\pi _i = \rho _i u_i$. Assigning the probability ![]() $ {\rho _j}/{\lambda \rho _i}$ to an edge
$ {\rho _j}/{\lambda \rho _i}$ to an edge ![]() $e$ from
$e$ from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ then determines the transition probability
$v_j$ then determines the transition probability ![]() $p_{ij}$ from
$p_{ij}$ from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ to be
$v_j$ to be ![]() $p_{ij} = {M_{ij} \rho _j}/{\lambda \rho _i}$ (see, for example, [Reference WaltersWal00, § 6.6 (7)]). The corresponding Markov measure
$p_{ij} = {M_{ij} \rho _j}/{\lambda \rho _i}$ (see, for example, [Reference WaltersWal00, § 6.6 (7)]). The corresponding Markov measure ![]() $\mathbb {P}$ on the path space
$\mathbb {P}$ on the path space ![]() $\Omega$ determined by these probabilities gives the measure of maximal entropy for the shift on
$\Omega$ determined by these probabilities gives the measure of maximal entropy for the shift on ![]() $\Omega$ (which in this section is unique since the graph structure is assumed to be primitive) and is known as the Parry measure [Reference ParryPar64]. For a vertex
$\Omega$ (which in this section is unique since the graph structure is assumed to be primitive) and is known as the Parry measure [Reference ParryPar64]. For a vertex ![]() $v$ of
$v$ of ![]() $\Gamma$, we use
$\Gamma$, we use ![]() $\mathbb {P}_v$ to denote the measure on the space of paths
$\mathbb {P}_v$ to denote the measure on the space of paths ![]() $\Omega _v \subset \Omega$ starting at
$\Omega _v \subset \Omega$ starting at ![]() $v$ obtained by beginning the Markov chain at
$v$ obtained by beginning the Markov chain at ![]() $v$ and using the above transition probabilities. From now on we use these edge probabilities to define the first return measure
$v$ and using the above transition probabilities. From now on we use these edge probabilities to define the first return measure ![]() $\mu _v$ as in § 3.
$\mu _v$ as in § 3.
We also define ![]() $\mu _n$ as the distribution on the space of paths of length
$\mu _n$ as the distribution on the space of paths of length ![]() $n$ induced by the Markov measure
$n$ induced by the Markov measure ![]() $\mathbb {P}$; that is,
$\mathbb {P}$; that is, ![]() $\mu _n$ is the pushforward of
$\mu _n$ is the pushforward of ![]() $\mathbb {P}$ to
$\mathbb {P}$ to ![]() $\Omega ^{*}$ under the map which sends an infinite path to its prefix of length
$\Omega ^{*}$ under the map which sends an infinite path to its prefix of length ![]() $n$. In this section we prove the following result.
$n$. In this section we prove the following result.
Theorem 4.1 Suppose that ![]() $\Gamma$ is a primitive graph structure and let
$\Gamma$ is a primitive graph structure and let ![]() $\mu _n$ be the associated distribution on the space of paths of length
$\mu _n$ be the associated distribution on the space of paths of length ![]() $n$. There are constants
$n$. There are constants ![]() $\ell$ and
$\ell$ and ![]() $\sigma$ such that, for any continuous function
$\sigma$ such that, for any continuous function ![]() $F \colon \mathbb {R} \to \mathbb {R}$ with compact support, we have
$F \colon \mathbb {R} \to \mathbb {R}$ with compact support, we have
The main technique to obtain the CLT for the Markov chain as above from that from the random walk on the loop semigroup is using a suspension flow, adapting the approach of Melbourne and Török [Reference Melbourne and TörökMT04] for dynamical systems.
4.1 Suspension flows
Let ![]() $S \colon (\mathcal {X}, \lambda ) \to (\mathcal {X}, \lambda )$ be a measure-preserving dynamical system, and let
$S \colon (\mathcal {X}, \lambda ) \to (\mathcal {X}, \lambda )$ be a measure-preserving dynamical system, and let ![]() $r \colon \mathcal {X} \to \mathbb {N}$ be a measurable, integrable function, which we call the roof function. Then the discrete suspension flow of
$r \colon \mathcal {X} \to \mathbb {N}$ be a measurable, integrable function, which we call the roof function. Then the discrete suspension flow of ![]() $S$ with roof function
$S$ with roof function ![]() $r$ is the dynamical system given by the map
$r$ is the dynamical system given by the map ![]() $\widehat {S} : \widehat {\mathcal {X}} \to \widehat {\mathcal {X}}$ where
$\widehat {S} : \widehat {\mathcal {X}} \to \widehat {\mathcal {X}}$ where
with measure ![]() $\widehat {\lambda } := ({1}/{\overline {r}}) (\lambda \otimes \delta )$, where
$\widehat {\lambda } := ({1}/{\overline {r}}) (\lambda \otimes \delta )$, where ![]() $\delta$ is the counting measure on
$\delta$ is the counting measure on ![]() $\mathbb {N}$ and
$\mathbb {N}$ and ![]() $\overline {r} := \int _{\mathcal {X}} r \, d\lambda$. Then the map
$\overline {r} := \int _{\mathcal {X}} r \, d\lambda$. Then the map ![]() $\widehat {S}$ is defined as
$\widehat {S}$ is defined as
Since in this case the system has discrete time, the above construction is also called a Kakutani skyscraper.
We now state the main theorem of Melbourne and Törok [Reference Melbourne and TörökMT04, Theorem 1.1].
Theorem 4.2 Let ![]() $S\colon (\mathcal {X}, \lambda ) \to (\mathcal {X}, \lambda )$ be an ergodic, measure-preserving transformation, and let
$S\colon (\mathcal {X}, \lambda ) \to (\mathcal {X}, \lambda )$ be an ergodic, measure-preserving transformation, and let ![]() $\widehat {S} \colon (\widehat {\mathcal {X}}, \widehat {\lambda }) \to (\widehat {\mathcal {X}}, \widehat {\lambda })$ be the suspension flow with roof function
$\widehat {S} \colon (\widehat {\mathcal {X}}, \widehat {\lambda }) \to (\widehat {\mathcal {X}}, \widehat {\lambda })$ be the suspension flow with roof function ![]() $r$. Let
$r$. Let ![]() $\phi \colon \widehat {\mathcal {X}} \to \mathbb {R}$ be such that
$\phi \colon \widehat {\mathcal {X}} \to \mathbb {R}$ be such that ![]() $\int \phi \, d\widehat {\lambda } = 0$, and define
$\int \phi \, d\widehat {\lambda } = 0$, and define ![]() $\Phi (x) := \sum _{k = 0}^{r(x) -1} \phi (x, k)$. Let
$\Phi (x) := \sum _{k = 0}^{r(x) -1} \phi (x, k)$. Let ![]() $\phi \in L^{b}(\widehat {\mathcal {X}})$ and let
$\phi \in L^{b}(\widehat {\mathcal {X}})$ and let ![]() $r \in L^{a}(\mathcal {X})$ be the roof function, with
$r \in L^{a}(\mathcal {X})$ be the roof function, with ![]() $(1 - 1/a)(1-1/b) \geq 1/2$. Suppose that
$(1 - 1/a)(1-1/b) \geq 1/2$. Suppose that ![]() $\Phi$ and
$\Phi$ and ![]() $r$ satisfy a CLT. Then
$r$ satisfy a CLT. Then ![]() $\phi$ satisfies a CLT.
$\phi$ satisfies a CLT.
Moreover, if the CLT for ![]() $\Phi$ has variance
$\Phi$ has variance ![]() $\sigma _1^{2}$, then the CLT for
$\sigma _1^{2}$, then the CLT for ![]() $\phi$ has variance
$\phi$ has variance ![]() $\sigma ^{2} = {\sigma _1^{2}}/{\overline {r}}$.
$\sigma ^{2} = {\sigma _1^{2}}/{\overline {r}}$.
4.2 Invariant measure on the suspended space
For any ![]() $\omega \in \Omega _v$, let
$\omega \in \Omega _v$, let ![]() $r(\omega )$ be the length in
$r(\omega )$ be the length in ![]() $\Gamma$ of
$\Gamma$ of ![]() $l_1(\omega )$. This is the first return time for the loop determined by
$l_1(\omega )$. This is the first return time for the loop determined by ![]() $\omega$. Let us define the suspension of the skew product
$\omega$. Let us define the suspension of the skew product
and
Let us now denote ![]() $R := \int _{\Gamma _v} \Vert g \Vert \, d \mu _v(g) = \int r(\omega ) \, d \mathbb {P}_v(\omega )$ and define the probability measure
$R := \int _{\Gamma _v} \Vert g \Vert \, d \mu _v(g) = \int r(\omega ) \, d \mathbb {P}_v(\omega )$ and define the probability measure ![]() $\nu ^{(s)} := ({1}/{R})(\mu _v^{\mathbb{N}} \otimes \delta \otimes \nu _v)$ on
$\nu ^{(s)} := ({1}/{R})(\mu _v^{\mathbb{N}} \otimes \delta \otimes \nu _v)$ on ![]() $\Omega ^{(s)}$.
$\Omega ^{(s)}$.
Lemma 4.3 Let ![]() $\nu _v$ be the
$\nu _v$ be the ![]() $\check {\mu }_v$-stationary measure constructed in Lemma 3.5. Then
$\check {\mu }_v$-stationary measure constructed in Lemma 3.5. Then ![]() $\nu ^{(s)}$ on
$\nu ^{(s)}$ on ![]() $\Omega ^{(s)}$ is
$\Omega ^{(s)}$ is ![]() $\widehat {T}$-invariant and ergodic.
$\widehat {T}$-invariant and ergodic.
Proof. It suffices to check invariance of the measure using cylinder sets ![]() $C_{l_1, \ldots, l_n}$ consisting of loops beginning with
$C_{l_1, \ldots, l_n}$ consisting of loops beginning with ![]() $l_1\cdots l_n$. We have
$l_1\cdots l_n$. We have
 \[ \widehat{T}^{-1}(C_{l_1, \ldots, l_n} \times \{ k \} \times A) = \left\{ \begin{array}{@{}ll} C_{l_1, \ldots, l_n} \times \{ k-1 \} \times A & \text{if }k > 0,\\ \displaystyle\bigsqcup_{l \in P_v} C_{l, l_1, \ldots, l_n} \times \{ \Vert l \Vert -1 \} \times l A & \text{if }k = 0,\\ \end{array}\right. \]
\[ \widehat{T}^{-1}(C_{l_1, \ldots, l_n} \times \{ k \} \times A) = \left\{ \begin{array}{@{}ll} C_{l_1, \ldots, l_n} \times \{ k-1 \} \times A & \text{if }k > 0,\\ \displaystyle\bigsqcup_{l \in P_v} C_{l, l_1, \ldots, l_n} \times \{ \Vert l \Vert -1 \} \times l A & \text{if }k = 0,\\ \end{array}\right. \]
where ![]() $P_v \subseteq \Gamma _v$ is the set of prime loops. Hence, in the first case, the equality
$P_v \subseteq \Gamma _v$ is the set of prime loops. Hence, in the first case, the equality
is obvious. In the second case,
 \begin{align*} \nu^{(s)}(\widehat{T}^{-1}(C_{l_1, \ldots, l_n} \times \{ k \} \times A)) &= \frac{1}{R} \sum_{l \in P_v} \mu_v(l) \mu_v(l_1)\cdots \mu_v(l_n) \nu_v(lA) \\ &= \frac{1}{R} \mu_v(l_1)\cdots \mu_v(l_n) \sum_{l \in P_v} \mu_v(l) \nu_v(lA) \\ &= \frac{1}{R} \mu_v(l_1)\cdots \mu_v(l_n) \nu_v(A) \\ &= \nu^{(s)}(C_{l_1, \ldots, l_n} \times \{ k \} \times A), \end{align*}
\begin{align*} \nu^{(s)}(\widehat{T}^{-1}(C_{l_1, \ldots, l_n} \times \{ k \} \times A)) &= \frac{1}{R} \sum_{l \in P_v} \mu_v(l) \mu_v(l_1)\cdots \mu_v(l_n) \nu_v(lA) \\ &= \frac{1}{R} \mu_v(l_1)\cdots \mu_v(l_n) \sum_{l \in P_v} \mu_v(l) \nu_v(lA) \\ &= \frac{1}{R} \mu_v(l_1)\cdots \mu_v(l_n) \nu_v(A) \\ &= \nu^{(s)}(C_{l_1, \ldots, l_n} \times \{ k \} \times A), \end{align*}
hence ![]() $\nu ^{(s)}$ is
$\nu ^{(s)}$ is ![]() $\widehat {T}$-invariant. Moreover, the suspension of an ergodic measure is ergodic (see, for example, [Reference SarigSar20, Proposition 1.11]).
$\widehat {T}$-invariant. Moreover, the suspension of an ergodic measure is ergodic (see, for example, [Reference SarigSar20, Proposition 1.11]).
4.3 Pushforward of the  $\widehat {T}$-invariant measure to
$\widehat {T}$-invariant measure to  $\Omega \times \mathcal {M}$
$\Omega \times \mathcal {M}$
Recall that ![]() $\Omega$ is the space of all infinite sample paths in
$\Omega$ is the space of all infinite sample paths in ![]() $\Gamma$ starting at any vertex. Let us define the projection
$\Gamma$ starting at any vertex. Let us define the projection ![]() $\pi : \Omega ^{(s)} \to \Omega \times \mathcal {M}$ as
$\pi : \Omega ^{(s)} \to \Omega \times \mathcal {M}$ as
and recall that the skew product ![]() $T: \Omega \times \mathcal {M} \to \Omega \times \mathcal {M}$ is
$T: \Omega \times \mathcal {M} \to \Omega \times \mathcal {M}$ is
Lemma 4.4 The following diagram commutes.

As a consequence, in the hypotheses of the previous lemmas, the measure ![]() $\overline {\nu } := \pi _\star \nu ^{(s)}$ is
$\overline {\nu } := \pi _\star \nu ^{(s)}$ is ![]() $T$-invariant and ergodic.
$T$-invariant and ergodic.
Proof. We show that the horizontal arrow is equivariant for the shifts. This follows from the fact that if we write ![]() $l_1(\omega )$ for the first return loop of
$l_1(\omega )$ for the first return loop of ![]() $\omega$ then
$\omega$ then ![]() $l_1(\omega ) = g_1(\omega )\ldots g_{r(\omega )}(\omega )$. Hence,
$l_1(\omega ) = g_1(\omega )\ldots g_{r(\omega )}(\omega )$. Hence,
 \begin{align*} \pi \circ \widehat T (\omega, r(\omega) -1, \xi) &= \pi ((\sigma_v(\omega),0, l_1^{-1}\xi))\\ &= (\sigma^{r(\omega)}(\omega), (g_1\cdots g_{r(\omega)})^{-1}\xi), \end{align*}
\begin{align*} \pi \circ \widehat T (\omega, r(\omega) -1, \xi) &= \pi ((\sigma_v(\omega),0, l_1^{-1}\xi))\\ &= (\sigma^{r(\omega)}(\omega), (g_1\cdots g_{r(\omega)})^{-1}\xi), \end{align*}
which is equal to ![]() $T \circ \pi ((\omega, r(\omega ) -1, \xi ))$. The other cases being trivial, this proves the first statement.
$T \circ \pi ((\omega, r(\omega ) -1, \xi ))$. The other cases being trivial, this proves the first statement.
Finally, since ![]() $\overline \nu$ is the pushforward of an ergodic measure, it is ergodic.
$\overline \nu$ is the pushforward of an ergodic measure, it is ergodic.
4.4 Return times and invariant measures for the Markov chain
Recall that in the previous section we produced a measure ![]() $\nu _v$ on
$\nu _v$ on ![]() $\mathcal {M}$ which is
$\mathcal {M}$ which is ![]() $\check {\mu }_v$-stationary and such that the product measure
$\check {\mu }_v$-stationary and such that the product measure ![]() $\mu _v^{\mathbb{N}} \otimes \nu _v$ is
$\mu _v^{\mathbb{N}} \otimes \nu _v$ is ![]() $T_v$-invariant and ergodic. Then, by lifting it to the suspension and pushing it forward to
$T_v$-invariant and ergodic. Then, by lifting it to the suspension and pushing it forward to ![]() $\Omega \times \mathcal {M}$, we have an ergodic,
$\Omega \times \mathcal {M}$, we have an ergodic, ![]() $T$-invariant measure
$T$-invariant measure ![]() $\overline {\nu }$ on
$\overline {\nu }$ on ![]() $\Omega \times \mathcal {M}$.
$\Omega \times \mathcal {M}$.
Now, for any vertex ![]() $w$ other than
$w$ other than ![]() $v$ we define the measure
$v$ we define the measure ![]() $\nu _w$ on
$\nu _w$ on ![]() $\mathcal {M}$ as
$\mathcal {M}$ as
where the sum is over the set ![]() $\Gamma _{v, w}$ of all paths
$\Gamma _{v, w}$ of all paths ![]() $\gamma$ from
$\gamma$ from ![]() $v$ to
$v$ to ![]() $w$ which do not pass through
$w$ which do not pass through ![]() $v$ in their middle, and
$v$ in their middle, and ![]() $\mu (\gamma )$ is the product of the measures of the edges of
$\mu (\gamma )$ is the product of the measures of the edges of ![]() $\gamma$. Recall also we denote by
$\gamma$. Recall also we denote by ![]() $\mathbb {P}_w$ the Markov measure on the space of infinite sample paths starting at
$\mathbb {P}_w$ the Markov measure on the space of infinite sample paths starting at ![]() $w$.
$w$.
Lemma 4.5 We have
Proof. Let ![]() $w$ be a vertex, and let
$w$ be a vertex, and let ![]() $g_1, g_2, \ldots, g_n$ be a finite path starting from
$g_1, g_2, \ldots, g_n$ be a finite path starting from ![]() $w$. We have for any measurable
$w$. We have for any measurable ![]() $A \subseteq \mathcal {M}$
$A \subseteq \mathcal {M}$
 \[ \pi^{-1}(C_{g_1, \ldots, g_n} \times A) = \left\{ \begin{array}{@{}ll} C_{g_1, \ldots, g_n} \times \{0 \} \times A & \text{if }w = v, \\ \displaystyle\bigsqcup_{\gamma \in \Gamma_{v, w}} C_{\gamma, g_1, \ldots, g_n} \times \{|\gamma|\} \times \gamma A & \text{if }w \neq v, \\ \end{array}\right. \]
\[ \pi^{-1}(C_{g_1, \ldots, g_n} \times A) = \left\{ \begin{array}{@{}ll} C_{g_1, \ldots, g_n} \times \{0 \} \times A & \text{if }w = v, \\ \displaystyle\bigsqcup_{\gamma \in \Gamma_{v, w}} C_{\gamma, g_1, \ldots, g_n} \times \{|\gamma|\} \times \gamma A & \text{if }w \neq v, \\ \end{array}\right. \]
where the union is over the set ![]() $\Gamma _{v, w}$ of all paths
$\Gamma _{v, w}$ of all paths ![]() $\gamma$ from
$\gamma$ from ![]() $v$ to the initial vertex
$v$ to the initial vertex ![]() $w$ of
$w$ of ![]() $g_1$ which do not pass through
$g_1$ which do not pass through ![]() $v$ in their middle. Thus we have
$v$ in their middle. Thus we have
 \begin{align*} \overline{\nu}(C_{g_1, \ldots, g_n} \times A) &= \frac{1}{R} \sum_{\gamma \in \Gamma_{v, w}} \mu(\gamma) \mu(g_1) \cdots \mu(g_n) \nu_v(\gamma A) \\ & = \frac{1}{R} \mu(g_1) \cdots \mu(g_n) \nu_w( A) \\ & = \frac{1}{R} \mathbb{P}_w(C_{g_1, \ldots, g_n}) \nu_w(A) \end{align*}
\begin{align*} \overline{\nu}(C_{g_1, \ldots, g_n} \times A) &= \frac{1}{R} \sum_{\gamma \in \Gamma_{v, w}} \mu(\gamma) \mu(g_1) \cdots \mu(g_n) \nu_v(\gamma A) \\ & = \frac{1}{R} \mu(g_1) \cdots \mu(g_n) \nu_w( A) \\ & = \frac{1}{R} \mathbb{P}_w(C_{g_1, \ldots, g_n}) \nu_w(A) \end{align*}which proves the claim, since both measures agree on all rectangles.
Recall that ![]() $R = \int r(\omega ) \, d\mathbb {P}_v(\omega )$, and set
$R = \int r(\omega ) \, d\mathbb {P}_v(\omega )$, and set ![]() $n_w = \nu _w(\mathcal {M})$. Here we show the following lemma.
$n_w = \nu _w(\mathcal {M})$. Here we show the following lemma.
Lemma 4.6 We have the identities
(i)
 $R = {1}/{\pi _v}$, and
$R = {1}/{\pi _v}$, and(ii)
 $\pi _w = {n_w}/{R}$ for any vertex
$\pi _w = {n_w}/{R}$ for any vertex  $w$ of
$w$ of  $\Gamma$.
$\Gamma$.
Note that if we replace ![]() $\Gamma$ with the graph
$\Gamma$ with the graph ![]() $\overline \Gamma$ obtained by reversing the direction of each edge, then the transition matrix for
$\overline \Gamma$ obtained by reversing the direction of each edge, then the transition matrix for ![]() $\overline \Gamma$ is
$\overline \Gamma$ is ![]() $M^{T}$ and so we have that
$M^{T}$ and so we have that ![]() $\rho$ and
$\rho$ and ![]() $u$ switch roles. In particular, the new transition probability from
$u$ switch roles. In particular, the new transition probability from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ is (in terms of the quantities defined in § 4)
$v_j$ is (in terms of the quantities defined in § 4) ![]() $\overline {p}_{ij} = {M_{ji}u_j}/{\lambda u_i}$ but the stationary measure on vertices is unchanged.
$\overline {p}_{ij} = {M_{ji}u_j}/{\lambda u_i}$ but the stationary measure on vertices is unchanged.
Proof of Lemma 4.6 Assertion (i) is the well-known Kac lemma [Reference KacKac47, Theorem 2’]. To prove (ii), recall that ![]() $\Gamma _{v, w}$ is the set of all paths
$\Gamma _{v, w}$ is the set of all paths ![]() $\gamma$ from
$\gamma$ from ![]() $v$ to
$v$ to ![]() $w$ which do not pass through
$w$ which do not pass through ![]() $v$ in their middle. Hence, if we reverse all the paths in this set, we obtain
$v$ in their middle. Hence, if we reverse all the paths in this set, we obtain ![]() $\overline \Gamma _{v,w}$, the set of all paths
$\overline \Gamma _{v,w}$, the set of all paths ![]() $\overline \gamma$ from
$\overline \gamma$ from ![]() $w$ to
$w$ to ![]() $v$ which do not pass through
$v$ which do not pass through ![]() $v$ in their middle. Note that since almost every path starting at
$v$ in their middle. Note that since almost every path starting at ![]() $w$ passes through
$w$ passes through ![]() $v$,
$v$,
 \begin{align*} 1&= \sum_{\overline \gamma \in \overline \Gamma_{v,w}} \overline \mu(\overline \gamma)\\ &= \frac{u_v}{u_w} \sum_{\overline \gamma \in \overline \Gamma_{v,w}} \lambda^{-|\overline \gamma|}, \end{align*}
\begin{align*} 1&= \sum_{\overline \gamma \in \overline \Gamma_{v,w}} \overline \mu(\overline \gamma)\\ &= \frac{u_v}{u_w} \sum_{\overline \gamma \in \overline \Gamma_{v,w}} \lambda^{-|\overline \gamma|}, \end{align*}
where ![]() $\overline \mu (\overline \gamma )$ is the product of the measures of the edges of
$\overline \mu (\overline \gamma )$ is the product of the measures of the edges of ![]() $\overline \gamma$ with respect to
$\overline \gamma$ with respect to ![]() $\overline p$ and we have used our previous observation about
$\overline p$ and we have used our previous observation about ![]() $\overline p$.
$\overline p$.
Using this and the fact that
we compute
 \begin{align*} n_w &= \nu_w(\mathcal{M}) \\ &= \sum_{\gamma \in \Gamma_{v, w}} \mu(\gamma) = \frac{\rho_w}{\rho_v} \sum_{\gamma \in \Gamma_{v, w}} \lambda^{-|\gamma|}\\ &= \frac{\rho_w}{\rho_v} \cdot \frac{u_w}{u_v}= \frac{\pi_w}{\pi_v}. \end{align*}
\begin{align*} n_w &= \nu_w(\mathcal{M}) \\ &= \sum_{\gamma \in \Gamma_{v, w}} \mu(\gamma) = \frac{\rho_w}{\rho_v} \sum_{\gamma \in \Gamma_{v, w}} \lambda^{-|\gamma|}\\ &= \frac{\rho_w}{\rho_v} \cdot \frac{u_w}{u_v}= \frac{\pi_w}{\pi_v}. \end{align*}Hence, the lemma follows from (i).
4.5 The central limit theorem for the Markov chain
We are now in a position to prove Theorem 4.1. By Melbourne and Török [Reference Melbourne and TörökMT04, Theorem 1.1], we have the following proposition.
Proposition 4.7 Let ![]() $\phi \colon \Omega \times \overline {X}^{h} \to \mathbb {R}$ belong to
$\phi \colon \Omega \times \overline {X}^{h} \to \mathbb {R}$ belong to ![]() $L^{b}(\Omega \times \overline {X}^{h}, \overline {\nu })$ for some
$L^{b}(\Omega \times \overline {X}^{h}, \overline {\nu })$ for some ![]() $b > 2$, and let
$b > 2$, and let ![]() $m := \int \phi \, d\overline {\nu }$. Define
$m := \int \phi \, d\overline {\nu }$. Define ![]() $\Phi \colon \Omega _v \times \overline X^{h} \to \mathbb {R}$ as
$\Phi \colon \Omega _v \times \overline X^{h} \to \mathbb {R}$ as ![]() $\Phi (\omega, \xi ) := \sum _{k = 0}^{r(\omega ) -1} \phi (T^{k}(\omega,\xi )) - m r(\omega )$, and suppose that
$\Phi (\omega, \xi ) := \sum _{k = 0}^{r(\omega ) -1} \phi (T^{k}(\omega,\xi )) - m r(\omega )$, and suppose that
 \begin{align*} \frac{\sum_{j = 0}^{n-1} \Phi \circ T_v^{j} }{\sqrt{n}} \end{align*}
\begin{align*} \frac{\sum_{j = 0}^{n-1} \Phi \circ T_v^{j} }{\sqrt{n}} \end{align*}
converges to a normal distribution in probability on ![]() $(\Omega _v \times \overline {X}^{h}, \mu _v^{\mathbb {N}} \otimes \nu _v)$. Then the sequence
$(\Omega _v \times \overline {X}^{h}, \mu _v^{\mathbb {N}} \otimes \nu _v)$. Then the sequence
 \begin{align*} \frac{\sum_{j = 0}^{n-1} \phi \circ T^{j} - n m}{\sqrt{n}} \end{align*}
\begin{align*} \frac{\sum_{j = 0}^{n-1} \phi \circ T^{j} - n m}{\sqrt{n}} \end{align*}
converges to a normal distribution in probability on ![]() $(\Omega \times \overline {X}^{h}, \overline {\nu })$.
$(\Omega \times \overline {X}^{h}, \overline {\nu })$.
Proof. Note that since ![]() $r$ has exponential tail (see, for example, [Reference Gekhtman, Taylor and TiozzoGTT18, Lemma 3.2 (2)]), it belongs to
$r$ has exponential tail (see, for example, [Reference Gekhtman, Taylor and TiozzoGTT18, Lemma 3.2 (2)]), it belongs to ![]() $L^{a}(\Omega _v)$ for any
$L^{a}(\Omega _v)$ for any ![]() $a \geq 1$. Then the condition
$a \geq 1$. Then the condition ![]() $(1-1/a)(1-1/b) \geq 1/2$ is satisfied as long as
$(1-1/a)(1-1/b) \geq 1/2$ is satisfied as long as ![]() $b > 2$. Moreover,
$b > 2$. Moreover, ![]() $(r \circ T_v^{n}(\omega ))_{n}$ is a sequence of independent random variables and so it satisfies a CLT. Hence, we can apply Theorem 4.2 to obtain a central limit theorem for the observable
$(r \circ T_v^{n}(\omega ))_{n}$ is a sequence of independent random variables and so it satisfies a CLT. Hence, we can apply Theorem 4.2 to obtain a central limit theorem for the observable ![]() $\phi \circ \pi - m$ and the system
$\phi \circ \pi - m$ and the system ![]() $\widehat {T}$, with measure
$\widehat {T}$, with measure ![]() $\nu ^{(s)}$. Moreover, since
$\nu ^{(s)}$. Moreover, since ![]() $\phi \circ \pi \circ \widehat {T}^{n} = \phi \circ T^{n} \circ \pi$ by Lemma 4.4, this is equivalent to a CLT for the observable
$\phi \circ \pi \circ \widehat {T}^{n} = \phi \circ T^{n} \circ \pi$ by Lemma 4.4, this is equivalent to a CLT for the observable ![]() $\phi$ on the system
$\phi$ on the system ![]() $T$ with the measure
$T$ with the measure ![]() $\pi _*(\nu ^{(s)}) = \overline {\nu }$.
$\pi _*(\nu ^{(s)}) = \overline {\nu }$.
Proposition 4.8 There exist ![]() $\ell, \sigma$ such that for any continuous, compactly supported
$\ell, \sigma$ such that for any continuous, compactly supported ![]() $F \colon \mathbb {R} \to \mathbb {R}$ one has
$F \colon \mathbb {R} \to \mathbb {R}$ one has
as ![]() $n \to \infty$.
$n \to \infty$.
Proof. Let us apply the previous proposition with ![]() $\phi = f$ where
$\phi = f$ where ![]() $f \colon \Omega \times \overline X^{h} \to \mathbb {R}$ is defined as
$f \colon \Omega \times \overline X^{h} \to \mathbb {R}$ is defined as ![]() $f(\omega, \xi ) := \beta _\xi (o, g_1 o)$. Then by definition of
$f(\omega, \xi ) := \beta _\xi (o, g_1 o)$. Then by definition of ![]() $\Phi$ and
$\Phi$ and ![]() $f$, Lemma 3.6 gives that for every
$f$, Lemma 3.6 gives that for every ![]() $\omega \in \Omega _v$,
$\omega \in \Omega _v$,
 \begin{align*} \Phi(\omega, \xi) &= \sum_{k = 0}^{r(\omega) - 1} f(T^{k}(\omega,\xi)) - \ell r(\omega)\\ &= \beta_{\xi}(o, w_{r(\omega)} o) - \ell r(\omega) =: f_v(\omega, \xi), \end{align*}
\begin{align*} \Phi(\omega, \xi) &= \sum_{k = 0}^{r(\omega) - 1} f(T^{k}(\omega,\xi)) - \ell r(\omega)\\ &= \beta_{\xi}(o, w_{r(\omega)} o) - \ell r(\omega) =: f_v(\omega, \xi), \end{align*}where
Now, by Corollary 3.3, integrating in ![]() $d\nu _v$, we have for some
$d\nu _v$, we have for some ![]() $\sigma _1 \geq 0$,
$\sigma _1 \geq 0$,
Note, moreover, that ![]() $\beta _\xi (o, l_1 \cdots l_n o) - \ell \Vert l_1 \cdots l_n \Vert = \sum _{j = 0}^{n-1} f_v (T_v^{j}(\omega, \xi ))$, hence we can rewrite the above equation as
$\beta _\xi (o, l_1 \cdots l_n o) - \ell \Vert l_1 \cdots l_n \Vert = \sum _{j = 0}^{n-1} f_v (T_v^{j}(\omega, \xi ))$, hence we can rewrite the above equation as
 \begin{align*} \int_{\Omega_v \times \overline{X}^{h}} F\bigg(\frac{\sum_{j = 0}^{n-1} f_v( T_v^{j}(\omega, \xi))}{\sqrt{n}}\bigg) d(\mu_v^{\mathbb{N}} \otimes \nu_v)(\omega, \xi) \to \int_{\mathbb{R}} F(t) \, d \mathcal{N}_{\sigma_1}(t). \end{align*}
\begin{align*} \int_{\Omega_v \times \overline{X}^{h}} F\bigg(\frac{\sum_{j = 0}^{n-1} f_v( T_v^{j}(\omega, \xi))}{\sqrt{n}}\bigg) d(\mu_v^{\mathbb{N}} \otimes \nu_v)(\omega, \xi) \to \int_{\mathbb{R}} F(t) \, d \mathcal{N}_{\sigma_1}(t). \end{align*}
Thus, by Proposition 4.7 and the above calculation, we also have (for some different ![]() $\sigma$)
$\sigma$)
 \begin{align*} \int_{\Omega \times \overline{X}^{h}} F\bigg(\frac{\sum_{j = 0}^{n-1} f \circ T^{j}(\omega, \xi) - \ell n}{\sqrt{n}}\bigg) d \overline{\nu}(\omega, \xi) \to \int_{\mathbb{R}} F(t) \, d \mathcal{N}_\sigma(t). \end{align*}
\begin{align*} \int_{\Omega \times \overline{X}^{h}} F\bigg(\frac{\sum_{j = 0}^{n-1} f \circ T^{j}(\omega, \xi) - \ell n}{\sqrt{n}}\bigg) d \overline{\nu}(\omega, \xi) \to \int_{\mathbb{R}} F(t) \, d \mathcal{N}_\sigma(t). \end{align*}
The claim follows by again using that, by Lemma 3.6, we have ![]() $\sum _{j = 0}^{n-1} f \circ T^{j}(\omega, \xi ) = \beta _\xi (o, g_1 \cdots g_n o)$.
$\sum _{j = 0}^{n-1} f \circ T^{j}(\omega, \xi ) = \beta _\xi (o, g_1 \cdots g_n o)$.
We will now need to go from the CLT for the Busemann cocycle to that for displacement. To do so, we use the following variation of [Reference Benoist and QuintBQ16, Proposition 3.3].
By [Reference Maher and TiozzoMT18, Proposition 4.4] and the fact that ![]() $\Gamma _v^{-1}$ is nonelementary (Lemma 2.3), we have
$\Gamma _v^{-1}$ is nonelementary (Lemma 2.3), we have ![]() $\nu _v(\overline {X}^{h}_\infty ) = 1$ for any vertex
$\nu _v(\overline {X}^{h}_\infty ) = 1$ for any vertex ![]() $v$.
$v$.
Lemma 4.9 For any ![]() $\epsilon > 0$ there exists
$\epsilon > 0$ there exists ![]() $T$ such that for all vertices
$T$ such that for all vertices ![]() $w$ in
$w$ in ![]() $\Gamma$, all
$\Gamma$, all ![]() $\xi \in \overline {X}^{h}_\infty$ and all
$\xi \in \overline {X}^{h}_\infty$ and all ![]() $n \geq 1$ we have
$n \geq 1$ we have
Proof. Recall that by [Reference Maher and TiozzoMT18, § 3.3] there exists a ![]() $G$-equivariant map
$G$-equivariant map ![]() $\pi \colon \overline {X}^{h}_\infty \to \partial X$, where
$\pi \colon \overline {X}^{h}_\infty \to \partial X$, where ![]() $\partial X$ is the Gromov boundary. Then, by definition of Gromov product and
$\partial X$ is the Gromov boundary. Then, by definition of Gromov product and ![]() $\delta$-hyperbolicity, we have
$\delta$-hyperbolicity, we have
for any ![]() $\xi \in \overline {X}^{h}_\infty$ (see, for example, [Reference HorbezHor18, Lemma 2.4]). Now, since the pushforward of the stationary measure
$\xi \in \overline {X}^{h}_\infty$ (see, for example, [Reference HorbezHor18, Lemma 2.4]). Now, since the pushforward of the stationary measure ![]() $\mathbb {P}_w$ for the Markov chain starting at
$\mathbb {P}_w$ for the Markov chain starting at ![]() $w$ to the Gromov boundary of
$w$ to the Gromov boundary of ![]() $X$ is not atomic [Reference Gekhtman, Taylor and TiozzoGTT20, Lemma 4.2], we have that for every
$X$ is not atomic [Reference Gekhtman, Taylor and TiozzoGTT20, Lemma 4.2], we have that for every ![]() $\epsilon > 0$ there exists
$\epsilon > 0$ there exists ![]() $T$ such that
$T$ such that
for all ![]() $\xi \in \overline {X}^{h}_\infty$ and for all
$\xi \in \overline {X}^{h}_\infty$ and for all ![]() $w$. This, combined with (3), yields the desired estimate.
$w$. This, combined with (3), yields the desired estimate.
Proof of Theorem 4.1 Let ![]() $F \colon \mathbb {R} \to \mathbb {R}$ be continuous with compact support. Since
$F \colon \mathbb {R} \to \mathbb {R}$ be continuous with compact support. Since ![]() $F$ is uniformly continuous and by Lemma 4.9, for any
$F$ is uniformly continuous and by Lemma 4.9, for any ![]() $\eta > 0$ there exists
$\eta > 0$ there exists ![]() $n_0$ such that for any
$n_0$ such that for any ![]() $n \geq n_0$, any
$n \geq n_0$, any ![]() $w$ and any
$w$ and any ![]() $\xi \in \overline {X}^{h}_\infty$ one has
$\xi \in \overline {X}^{h}_\infty$ one has
with probability ![]() $\mathbb {P}_w$ at least
$\mathbb {P}_w$ at least ![]() $1 - \epsilon$. Thus, since
$1 - \epsilon$. Thus, since ![]() $\overline {\nu } = ({1}/{R}) \sum _w \mathbb {P}_w \otimes \nu _w$, for any
$\overline {\nu } = ({1}/{R}) \sum _w \mathbb {P}_w \otimes \nu _w$, for any ![]() $\eta > 0$ there exists
$\eta > 0$ there exists ![]() $n_0$ such that for any
$n_0$ such that for any ![]() $n \geq n_0$ we have
$n \geq n_0$ we have
on a subset of ![]() $\Omega \times \overline {X}^{h}$ of
$\Omega \times \overline {X}^{h}$ of ![]() $\overline {\nu }$-measure
$\overline {\nu }$-measure ![]() $\geq 1 - \epsilon$. On the other hand, by Proposition 4.8, we have
$\geq 1 - \epsilon$. On the other hand, by Proposition 4.8, we have
Hence,
Since the integrand does not depend on ![]() $\xi$, then we also have
$\xi$, then we also have
where ![]() $P$ is the pushforward of
$P$ is the pushforward of ![]() $\overline {\nu }$ to
$\overline {\nu }$ to ![]() $\Omega$. Finally, since
$\Omega$. Finally, since ![]() $\overline {\nu } = ({1}/{R}) \sum _w \mathbb {P}_w \otimes \nu _w$, the pushforward of
$\overline {\nu } = ({1}/{R}) \sum _w \mathbb {P}_w \otimes \nu _w$, the pushforward of ![]() $\overline {\nu }$ to
$\overline {\nu }$ to ![]() $\Omega$ equals
$\Omega$ equals ![]() $P = \sum _w \frac {n_w}{R} \mathbb {P}_w$, where
$P = \sum _w \frac {n_w}{R} \mathbb {P}_w$, where ![]() $n_w = \nu _w(M)$. Hence, Lemma 4.6 implies that
$n_w = \nu _w(M)$. Hence, Lemma 4.6 implies that ![]() $P = \sum _w \pi _w \mathbb {P}_w = \mathbb {P}$, thus we also have
$P = \sum _w \pi _w \mathbb {P}_w = \mathbb {P}$, thus we also have
as required.
5. Uniqueness of drift and variance
Now suppose that ![]() $\Gamma$ is a semisimple graph structure. In particular, each maximal component
$\Gamma$ is a semisimple graph structure. In particular, each maximal component ![]() $C_i$ of
$C_i$ of ![]() $\Gamma$ gives a primitive graph structure (without an initial vertex) on
$\Gamma$ gives a primitive graph structure (without an initial vertex) on ![]() $G$ to which the results of the previous section (in particular, Theorem 4.1) apply. Hence, for each maximal component
$G$ to which the results of the previous section (in particular, Theorem 4.1) apply. Hence, for each maximal component ![]() $C_i$ of
$C_i$ of ![]() $\Gamma$, Theorem 4.1 gives constants
$\Gamma$, Theorem 4.1 gives constants ![]() $\ell _i$ and
$\ell _i$ and ![]() $\sigma _i$ for the associated CLT.
$\sigma _i$ for the associated CLT.
In this section we show that the CLTs for the recurrent components of ![]() $\Gamma$ are compatible in the sense that they have the same drift and variance. This is the primary place where we will use thickness and coherence of
$\Gamma$ are compatible in the sense that they have the same drift and variance. This is the primary place where we will use thickness and coherence of ![]() $\Gamma$. For this, first recall that
$\Gamma$. For this, first recall that ![]() $\Omega ^{*}$ is the set of finite length paths in
$\Omega ^{*}$ is the set of finite length paths in ![]() $\Gamma$ starting at any vertex and that the graph structure is bounded if there exists a constant
$\Gamma$ starting at any vertex and that the graph structure is bounded if there exists a constant ![]() $\mathfrak {b}\ge 1$ so that the evaluation map
$\mathfrak {b}\ge 1$ so that the evaluation map ![]() $\mathrm {ev} \colon \Omega ^{*} \to G$ is at worst
$\mathrm {ev} \colon \Omega ^{*} \to G$ is at worst ![]() $\mathfrak {b}$-to-one, that is,
$\mathfrak {b}$-to-one, that is, ![]() $\# (\mathrm {ev}^{-1}(g)) \le \mathfrak {b}$ for all
$\# (\mathrm {ev}^{-1}(g)) \le \mathfrak {b}$ for all ![]() $g \in G$. Also recall the definition of coherence from Definition 2.2.
$g \in G$. Also recall the definition of coherence from Definition 2.2.
Remark 5.1 Our standing assumption until § 7 is that ![]() $\Gamma$ is a semisimple graph structure on
$\Gamma$ is a semisimple graph structure on ![]() $G$. This implies that the transition matrix for each component of maximal growth is primitive.
$G$. This implies that the transition matrix for each component of maximal growth is primitive.
5.1 Uniformly bicontinuous functions
Let us begin by introducing a class of functions that are well behaved under bounded perturbations in the group.
Definition 5.2 A function ![]() $f \colon \Omega ^{*} \to \mathbb {R}$ is uniformly bicontinuous if, for any finite set
$f \colon \Omega ^{*} \to \mathbb {R}$ is uniformly bicontinuous if, for any finite set ![]() $B \subseteq G$ and any
$B \subseteq G$ and any ![]() $\eta > 0$, there exists
$\eta > 0$, there exists ![]() $N\ge 0$ such that if
$N\ge 0$ such that if ![]() $\Vert g \Vert \geq N$ and
$\Vert g \Vert \geq N$ and ![]() $b_1 \overline g b_2 = \overline h$ in
$b_1 \overline g b_2 = \overline h$ in ![]() $G$ for some
$G$ for some ![]() $b_1, b_2 \in B$, then
$b_1, b_2 \in B$, then
In our application, the uniformly bicontinuous property will be a consequence of the fact that displacement is Lipschitz in both the right and left word metric on ![]() $G$. This definition is inspired by [Reference Calegari and FujiwaraCF10] (in particular, the proof of [Reference Calegari and FujiwaraCF10, Lemma 4.24]), where the bi-Lipschitz property is extensively used.
$G$. This definition is inspired by [Reference Calegari and FujiwaraCF10] (in particular, the proof of [Reference Calegari and FujiwaraCF10, Lemma 4.24]), where the bi-Lipschitz property is extensively used.
We next introduce the primary functions of interest used throughout this section. Define the following functions on ![]() $\Omega ^{*}$: for any
$\Omega ^{*}$: for any ![]() $\ell \in \mathbb {R}$,
$\ell \in \mathbb {R}$,
We remark that the constant ![]() $\ell$ will be chosen once and for all after the proof of Lemma 5.6.
$\ell$ will be chosen once and for all after the proof of Lemma 5.6.
Lemma 5.3 If the graph structure is coherent, then the functions ![]() $\psi$ and
$\psi$ and ![]() $\varphi$ defined above are uniformly bicontinuous for any
$\varphi$ defined above are uniformly bicontinuous for any ![]() $\ell$.
$\ell$.
Proof. Fix a finite set ![]() $B \subset G$, and let
$B \subset G$, and let ![]() $\mathcal {B}$ be the resulting constant from Definition 2.2. Suppose that
$\mathcal {B}$ be the resulting constant from Definition 2.2. Suppose that ![]() $\overline {h} = b_1 \overline {g} b_2$ for some
$\overline {h} = b_1 \overline {g} b_2$ for some ![]() $b_1, b_2 \in B$. Then
$b_1, b_2 \in B$. Then ![]() $|\Vert g \Vert - \Vert h \Vert | \leq \mathcal {B}$ and by the triangle inequality
$|\Vert g \Vert - \Vert h \Vert | \leq \mathcal {B}$ and by the triangle inequality ![]() $|d(o, g o) - d(o, h o)| \leq \mathcal {B}_1$ where
$|d(o, g o) - d(o, h o)| \leq \mathcal {B}_1$ where ![]() $\mathcal {B}_1 := 2 \max _{b \in B} d(o, bo)$. Finally, denote by
$\mathcal {B}_1 := 2 \max _{b \in B} d(o, bo)$. Finally, denote by ![]() $\mathcal {L}$ the Lipschitz constant so that
$\mathcal {L}$ the Lipschitz constant so that ![]() $d(o, g o) \leq \mathcal {L} \Vert g \Vert$ for any
$d(o, g o) \leq \mathcal {L} \Vert g \Vert$ for any ![]() $g \in \Omega ^{*}$.
$g \in \Omega ^{*}$.
(1) By the above estimates,
 \begin{align*} \bigg|\frac{d(o, h o)}{\Vert h \Vert} - \frac{d(o, g o)}{\Vert g \Vert}\bigg| &= \frac{| (d(o, ho) - d(o, go)) \Vert g \Vert + d(o,go) (\Vert g \Vert - \Vert h \Vert )|}{\Vert g \Vert \Vert h \Vert} \\ &\leq \frac{| d(o, ho) - d(o, go)| }{\Vert h \Vert} + \frac{ d(o,go) }{\Vert g \Vert } \cdot \frac{| \Vert g \Vert - \Vert h \Vert |}{ \Vert h \Vert} \\ &\leq \frac{\mathcal{B}_1 + \mathcal{L} \mathcal{B}}{\Vert g \Vert - \mathcal{B}}, \end{align*}
\begin{align*} \bigg|\frac{d(o, h o)}{\Vert h \Vert} - \frac{d(o, g o)}{\Vert g \Vert}\bigg| &= \frac{| (d(o, ho) - d(o, go)) \Vert g \Vert + d(o,go) (\Vert g \Vert - \Vert h \Vert )|}{\Vert g \Vert \Vert h \Vert} \\ &\leq \frac{| d(o, ho) - d(o, go)| }{\Vert h \Vert} + \frac{ d(o,go) }{\Vert g \Vert } \cdot \frac{| \Vert g \Vert - \Vert h \Vert |}{ \Vert h \Vert} \\ &\leq \frac{\mathcal{B}_1 + \mathcal{L} \mathcal{B}}{\Vert g \Vert - \mathcal{B}}, \end{align*}
and the right-hand side tends to ![]() $0$ as
$0$ as ![]() $\Vert g \Vert \to \infty$.
$\Vert g \Vert \to \infty$.
(2) We can write
where ![]() $x = d(o, g o) - \ell \Vert g \Vert$,
$x = d(o, g o) - \ell \Vert g \Vert$, ![]() $y = d(o, h o) - \ell \Vert h \Vert - d(o, g o) + \ell \Vert g \Vert$,
$y = d(o, h o) - \ell \Vert h \Vert - d(o, g o) + \ell \Vert g \Vert$, ![]() $n = \Vert g \Vert$, and
$n = \Vert g \Vert$, and ![]() $d = \Vert h \Vert - \Vert g \Vert$.
$d = \Vert h \Vert - \Vert g \Vert$.
Recall that by the above inequalities ![]() $|d| \leq \mathcal {B}$, hence also
$|d| \leq \mathcal {B}$, hence also ![]() $|y| \leq \mathcal {B}_1 + \ell \mathcal {B}$ and
$|y| \leq \mathcal {B}_1 + \ell \mathcal {B}$ and ![]() $|x| \leq (\mathcal {L}+\ell ) \Vert g \Vert$. Thus,
$|x| \leq (\mathcal {L}+\ell ) \Vert g \Vert$. Thus,
 \begin{align*} \bigg|\frac{x}{\sqrt{n}} - \frac{x + y}{\sqrt{n + d}}\bigg| &= \bigg|\frac{x(\sqrt{n+d}-\sqrt{n})}{\sqrt{n (n+d)}} - \frac{y}{\sqrt{n+d}}\bigg| \\ &\leq \frac{|x|}{n} \frac{n}{\sqrt{n(n+d)}} |\sqrt{n+d}-\sqrt{n}| + \frac{|y|}{\sqrt{n+d}} \\ &\leq (\mathcal{L}+\ell) \frac{n}{\sqrt{n(n- \mathcal{B})}} (\sqrt{n+ \mathcal{B}}-\sqrt{n}) + \frac{\mathcal{B}_1 + \ell \mathcal{B}}{\sqrt{n-\mathcal{B}}} \end{align*}
\begin{align*} \bigg|\frac{x}{\sqrt{n}} - \frac{x + y}{\sqrt{n + d}}\bigg| &= \bigg|\frac{x(\sqrt{n+d}-\sqrt{n})}{\sqrt{n (n+d)}} - \frac{y}{\sqrt{n+d}}\bigg| \\ &\leq \frac{|x|}{n} \frac{n}{\sqrt{n(n+d)}} |\sqrt{n+d}-\sqrt{n}| + \frac{|y|}{\sqrt{n+d}} \\ &\leq (\mathcal{L}+\ell) \frac{n}{\sqrt{n(n- \mathcal{B})}} (\sqrt{n+ \mathcal{B}}-\sqrt{n}) + \frac{\mathcal{B}_1 + \ell \mathcal{B}}{\sqrt{n-\mathcal{B}}} \end{align*}
and the right-hand side tends to ![]() $0$ uniformly in
$0$ uniformly in ![]() $n$.
$n$.
Remark 5.4 (Logarithmic perturbations)
As a consequence of the proof that ![]() $\varphi$ is uniformly bicontinuous, we observe that for any
$\varphi$ is uniformly bicontinuous, we observe that for any ![]() $\eta > 0$ there is an
$\eta > 0$ there is an ![]() $N$ such that if
$N$ such that if ![]() $\Vert g \Vert \geq N$ then for any decomposition
$\Vert g \Vert \geq N$ then for any decomposition ![]() $g = g_0 g_1 g_2$ with
$g = g_0 g_1 g_2$ with ![]() $\Vert g_0 \Vert, \Vert g_2 \Vert \leq \log N$ we have
$\Vert g_0 \Vert, \Vert g_2 \Vert \leq \log N$ we have
The main reason why we introduce the bicontinuous functions is the following property. For each ![]() $i$, we denote by
$i$, we denote by ![]() $\mu _n^{(i)}$ the distribution on the space of paths of length
$\mu _n^{(i)}$ the distribution on the space of paths of length ![]() $n$ induced by the Markov measure associated to the maximal component
$n$ induced by the Markov measure associated to the maximal component ![]() $C_i$, as defined in § 4. In particular,
$C_i$, as defined in § 4. In particular, ![]() $\mu _n^{(i)}$ is supported on length
$\mu _n^{(i)}$ is supported on length ![]() $n$ paths of
$n$ paths of ![]() $\Gamma$ that are contained in
$\Gamma$ that are contained in ![]() $C_i$.
$C_i$.
Lemma 5.5 Suppose that the graph structure ![]() $\Gamma$ is thick and coherent. Let
$\Gamma$ is thick and coherent. Let ![]() $f \colon \Omega ^{*} \to \mathbb {R}$ be a uniformly bicontinuous function, and suppose that for each maximal component
$f \colon \Omega ^{*} \to \mathbb {R}$ be a uniformly bicontinuous function, and suppose that for each maximal component ![]() $C_i$ there is a finite measure
$C_i$ there is a finite measure ![]() $\mathcal {D}_i$ on
$\mathcal {D}_i$ on ![]() $\mathbb {R}$ so that
$\mathbb {R}$ so that
in distribution with respect to the Markov measure on ![]() $C_i$. If each
$C_i$. If each ![]() $\mathcal {D}_i$ is nonatomic, then there exists
$\mathcal {D}_i$ is nonatomic, then there exists ![]() $a \ge 1$ such that for any interval
$a \ge 1$ such that for any interval ![]() $I \subset \mathbb {R}$,
$I \subset \mathbb {R}$,
Similarly, if each ![]() $\mathcal {D}_i$ is a Dirac measure, then
$\mathcal {D}_i$ is a Dirac measure, then ![]() $\mathcal {D}_i = \mathcal {D}_j$.
$\mathcal {D}_i = \mathcal {D}_j$.
Proof. Let ![]() $v$ be a vertex of
$v$ be a vertex of ![]() $C_i$, and let
$C_i$, and let ![]() $C_j$ be another maximal component. Let
$C_j$ be another maximal component. Let ![]() $B\subset G$ be the finite set given by thickness of
$B\subset G$ be the finite set given by thickness of ![]() $\Gamma$ (Definition 2.1) and let
$\Gamma$ (Definition 2.1) and let ![]() $\mathcal {B}$ be the resulting constant from Definition 2.2. Similar to the proof of Lemma 2.3, by thickness and coherence we have
$\mathcal {B}$ be the resulting constant from Definition 2.2. Similar to the proof of Lemma 2.3, by thickness and coherence we have
 \begin{align*} \overline{S_n^{(j)}} \subseteq \bigcup_{b_1, b_2 \in B} \bigcup_{|k| \leq \mathcal{B}} b_1 (\overline{\Gamma_v \cap S_{n + k}}) b_2 \end{align*}
\begin{align*} \overline{S_n^{(j)}} \subseteq \bigcup_{b_1, b_2 \in B} \bigcup_{|k| \leq \mathcal{B}} b_1 (\overline{\Gamma_v \cap S_{n + k}}) b_2 \end{align*}
where ![]() $S_n^{(j)}$ is the set of paths of length
$S_n^{(j)}$ is the set of paths of length ![]() $n$ which lie entirely in
$n$ which lie entirely in ![]() $C_j$. Hence, by uniform continuity, for any
$C_j$. Hence, by uniform continuity, for any ![]() $\epsilon > 0$ there exists
$\epsilon > 0$ there exists ![]() $n_0$ such that for all
$n_0$ such that for all ![]() $n \geq n_0$,
$n \geq n_0$,
for any interval ![]() $I = [x,y]$. Here, we have used that the evaluation map is at most
$I = [x,y]$. Here, we have used that the evaluation map is at most ![]() $\mathfrak {b}$-to-one. Now, note that there exists
$\mathfrak {b}$-to-one. Now, note that there exists ![]() $C > 0$ such that
$C > 0$ such that
for any ![]() $i$, any
$i$, any ![]() $n$ and any set
$n$ and any set ![]() $A$. Hence, by noting that
$A$. Hence, by noting that ![]() $\Gamma _v \cap S_{n+k} \subseteq S_{n+k}^{(i)}$,
$\Gamma _v \cap S_{n+k} \subseteq S_{n+k}^{(i)}$,
Now taking limits and using the portmanteau theorem, we obtain that
for any ![]() $\epsilon > 0$. So if
$\epsilon > 0$. So if ![]() $c = 2\mathcal {B}\mathfrak {b}|B|^{2} C^{2}$, we have that
$c = 2\mathcal {B}\mathfrak {b}|B|^{2} C^{2}$, we have that ![]() $\mathcal {D}_j((x,y)) \le c \mathcal {D}_i([x,y])$ because
$\mathcal {D}_j((x,y)) \le c \mathcal {D}_i([x,y])$ because ![]() $\mathcal {D}_i([x,y]) = \bigcap _{\epsilon > 0} \mathcal {D}_i([x-\epsilon,y+\epsilon ])$ for any finite measure.
$\mathcal {D}_i([x,y]) = \bigcap _{\epsilon > 0} \mathcal {D}_i([x-\epsilon,y+\epsilon ])$ for any finite measure.
Now if each ![]() $\mathcal {D}_i$ is nonatomic, we get
$\mathcal {D}_i$ is nonatomic, we get ![]() $\mathcal {D}_j([x,y]) \le c \mathcal {D}_i([x,y])$, and reversing the roles of
$\mathcal {D}_j([x,y]) \le c \mathcal {D}_i([x,y])$, and reversing the roles of ![]() $i$ and
$i$ and ![]() $j$ completes the proof in this case. Similarly, if
$j$ completes the proof in this case. Similarly, if ![]() $\mathcal {D}_i$ and
$\mathcal {D}_i$ and ![]() $\mathcal {D}_j$ were distinct Dirac measures, we would obtain a contradiction by letting
$\mathcal {D}_j$ were distinct Dirac measures, we would obtain a contradiction by letting ![]() $(x,y)$ be a small interval about the atom for
$(x,y)$ be a small interval about the atom for ![]() $\mathcal {D}_j$ and taking
$\mathcal {D}_j$ and taking ![]() $\epsilon$ small enough so that
$\epsilon$ small enough so that ![]() $[x-\epsilon,y+\epsilon ]$ does not contain the atom for
$[x-\epsilon,y+\epsilon ]$ does not contain the atom for ![]() $\mathcal {D}_i$. This completes the proof.
$\mathcal {D}_i$. This completes the proof.
5.2 Uniqueness of drift
We now show that all maximal components of ![]() $\Gamma$ determine the same drift.
$\Gamma$ determine the same drift.
Lemma 5.6 If the graph structure ![]() $\Gamma$ is thick and coherent, then all
$\Gamma$ is thick and coherent, then all ![]() $\ell _i$ for each maximal component
$\ell _i$ for each maximal component ![]() $C_i$ are the same.
$C_i$ are the same.
Proof. By the subadditive ergodic theorem, for each maximal component ![]() $C_i$ we have
$C_i$ we have
almost surely (and hence in distribution) with respect to the measure ![]() $\mu _n^{(i)}$. Since
$\mu _n^{(i)}$. Since ![]() $\psi (g) = {d(o, g o)}/{\Vert g \Vert }$ is uniformly bicontinuous by Lemma 5.3, the claim then follows by Lemma 5.5.
$\psi (g) = {d(o, g o)}/{\Vert g \Vert }$ is uniformly bicontinuous by Lemma 5.3, the claim then follows by Lemma 5.5.
By the above lemma, we now define ![]() $\varphi$ using
$\varphi$ using ![]() $\ell = \ell _i$ for any (equivalently all)
$\ell = \ell _i$ for any (equivalently all) ![]() $i$.
$i$.
5.3 Uniqueness of variance
To show that all maximal components of ![]() $\Gamma$ determine the same variance, we use the simple fact that distinct normal distributions with mean
$\Gamma$ determine the same variance, we use the simple fact that distinct normal distributions with mean ![]() $0$ can be distinguished by the decay of their tails.
$0$ can be distinguished by the decay of their tails.
Lemma 5.7 If the graph structure ![]() $\Gamma$ is thick and coherent, then for any two maximal components
$\Gamma$ is thick and coherent, then for any two maximal components ![]() $C_i$ and
$C_i$ and ![]() $C_j$ we have
$C_j$ we have ![]() $\sigma _i = \sigma _j$.
$\sigma _i = \sigma _j$.
Proof. We have already shown that for ![]() $\ell$ fixed as above and any maximal component
$\ell$ fixed as above and any maximal component ![]() $C_i$ of
$C_i$ of ![]() $\Gamma$,
$\Gamma$,
in distribution with respect to the Markov measure on ![]() $C_i$ (Theorem 4.1). Since
$C_i$ (Theorem 4.1). Since ![]() $\phi$ is uniformly bicontinuous by Lemma 5.3, Lemma 5.5 states that there exists an
$\phi$ is uniformly bicontinuous by Lemma 5.3, Lemma 5.5 states that there exists an ![]() $a\ge 1$ so that for any interval
$a\ge 1$ so that for any interval ![]() $I$ in
$I$ in ![]() $\mathbb {R}$,
$\mathbb {R}$,
But since this holds for every interval, Lemma 5.8 implies that ![]() $\sigma _i = \sigma _j$ as required.
$\sigma _i = \sigma _j$ as required.
Lemma 5.8 If there exists ![]() $a \geq 1$ such that
$a \geq 1$ such that
for any interval ![]() $I$, then
$I$, then ![]() $\sigma _i = \sigma _j$.
$\sigma _i = \sigma _j$.
Proof. If we let
we get
which yields
Then, if (6) holds, then
hence, by (7)
which yields ![]() $\sigma _i = \sigma _j$.
$\sigma _i = \sigma _j$.
6. The semisimple case
In this section we prove our main theorem for semisimple graph structures. This is completed in Theorem 6.3.
6.1 Convergence to the Markov measure
So far our work has been for maximal components of a semisimple graph structure. In this section we consider the whole graph structure, still in the semisimple case.
Let ![]() $\Gamma$ be a semisimple graph structure for
$\Gamma$ be a semisimple graph structure for ![]() $G$ with transition matrix
$G$ with transition matrix ![]() $M$ of spectral radius
$M$ of spectral radius ![]() $\lambda > 1$. Let
$\lambda > 1$. Let ![]() $v_i$ be the vertices of the graph, and let
$v_i$ be the vertices of the graph, and let ![]() $v_0$ be a vertex of large growth, which we take as the initial vertex. Then recall that
$v_0$ be a vertex of large growth, which we take as the initial vertex. Then recall that ![]() $e_i^{T} M^{n} e_j$ is the number of paths of length
$e_i^{T} M^{n} e_j$ is the number of paths of length ![]() $n$ from
$n$ from ![]() $v_i$ to
$v_i$ to ![]() $v_j$. Since
$v_j$. Since ![]() $M$ is semisimple, the limit
$M$ is semisimple, the limit
exists. In particular, in keeping with notation at the beginning of § 4, we denote by ![]() $e_i$ the
$e_i$ the ![]() $i$th vector of the standard basis, and define
$i$th vector of the standard basis, and define
By construction, ![]() $\rho = (\rho _i)$ satisfies
$\rho = (\rho _i)$ satisfies ![]() $\rho = M_\infty 1$ and
$\rho = M_\infty 1$ and ![]() $M \rho = \lambda \rho$, while
$M \rho = \lambda \rho$, while ![]() $u = (u_i)$ satisfies
$u = (u_i)$ satisfies ![]() $u^{T} M = \lambda u^{T}$. Finally,
$u^{T} M = \lambda u^{T}$. Finally, ![]() $\sum _i u_i = \rho _0$ and
$\sum _i u_i = \rho _0$ and ![]() $\sum _i u_i \rho _i = \rho _0$.
$\sum _i u_i \rho _i = \rho _0$.
Note that vertices ![]() $v_i$ for which
$v_i$ for which ![]() $\rho _i > 0$ and
$\rho _i > 0$ and ![]() $u_i > 0$ are precisely vertices of components of maximal growth. The large growth vertices are those with
$u_i > 0$ are precisely vertices of components of maximal growth. The large growth vertices are those with ![]() $\rho _i >0$.
$\rho _i >0$.
As before, we use a standard construction to define a Markov measure ![]() $\mathbb {P}$ on the space
$\mathbb {P}$ on the space ![]() $\Omega$ of infinite paths starting at any vertex of
$\Omega$ of infinite paths starting at any vertex of ![]() $\Gamma$. First define the initial distribution of the Markov chain to start at vertex
$\Gamma$. First define the initial distribution of the Markov chain to start at vertex ![]() $v_i$ with probability
$v_i$ with probability ![]() $\pi _i := {u_i \rho _i}/{\rho _0}$. Then assign to an edge from
$\pi _i := {u_i \rho _i}/{\rho _0}$. Then assign to an edge from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ the probability
$v_j$ the probability ![]() $ {\rho _j }/{\lambda \rho _i}$ so that the transition probability from
$ {\rho _j }/{\lambda \rho _i}$ so that the transition probability from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ is
$v_j$ is ![]() $p_{ij} := {M_{ij} \rho _j }/{\lambda \rho _i}$. Obviously,
$p_{ij} := {M_{ij} \rho _j }/{\lambda \rho _i}$. Obviously, ![]() $\mathbb {P}$ is supported on paths that are entirely contained in components of maximal growth. We denote by
$\mathbb {P}$ is supported on paths that are entirely contained in components of maximal growth. We denote by ![]() $\mathbb {P}_n$ the distribution on the space of paths of length
$\mathbb {P}_n$ the distribution on the space of paths of length ![]() $n$ induced by the Markov measure
$n$ induced by the Markov measure ![]() $\mathbb {P}$.
$\mathbb {P}$.
Remark 6.1 We remark that the induced measure on each maximal component ![]() $C$ of
$C$ of ![]() $\Gamma$ rescales to give the Markov measure on
$\Gamma$ rescales to give the Markov measure on ![]() $C$ previously considered. This follows immediately from the construction.
$C$ previously considered. This follows immediately from the construction.
The following result relates the Markov measure on the semisimple graph structure to the counting measure. For its statement, let ![]() $v_0$ be any vertex of large growth. For each
$v_0$ be any vertex of large growth. For each ![]() $n$, consider the path given by selecting uniformly a path
$n$, consider the path given by selecting uniformly a path ![]() $\gamma$ starting at
$\gamma$ starting at ![]() $v_0$ of length
$v_0$ of length ![]() $n$, and take its subpath
$n$, and take its subpath ![]() $\tilde {\gamma }$ from position
$\tilde {\gamma }$ from position ![]() $\lfloor \log n \rfloor$ to position
$\lfloor \log n \rfloor$ to position ![]() $n - \lfloor \log n \rfloor$. To avoid writing the integer part every time, we set
$n - \lfloor \log n \rfloor$. To avoid writing the integer part every time, we set ![]() $\lg (n) := \lfloor \log n \rfloor$. Let
$\lg (n) := \lfloor \log n \rfloor$. Let ![]() $\tilde {\lambda }_n$ denote the distribution of
$\tilde {\lambda }_n$ denote the distribution of ![]() $\tilde {\gamma }$.
$\tilde {\gamma }$.
Lemma 6.2 With notation as above, the total variation
as ![]() $n \to \infty$.
$n \to \infty$.
Proof. Denote ![]() $n' := n - 2 \lg (n)$. Let
$n' := n - 2 \lg (n)$. Let ![]() $\gamma$ be a path in the graph, starting at
$\gamma$ be a path in the graph, starting at ![]() $v_i$ and ending at
$v_i$ and ending at ![]() $v_j$. Then by definition the proportion of paths of length
$v_j$. Then by definition the proportion of paths of length ![]() $n$, starting at
$n$, starting at ![]() $v_0$, that have
$v_0$, that have ![]() $\gamma$ as ‘middle subpath’ of length
$\gamma$ as ‘middle subpath’ of length ![]() $n'$ is
$n'$ is
 \begin{align*} \tilde{\lambda}_n(\gamma) = \frac{(e_0^{T} M^{\lg(n)} e_i) (e_j^{T} M^{\lg(n)} 1)}{e_0^{T} M^{n} 1}. \end{align*}
\begin{align*} \tilde{\lambda}_n(\gamma) = \frac{(e_0^{T} M^{\lg(n)} e_i) (e_j^{T} M^{\lg(n)} 1)}{e_0^{T} M^{n} 1}. \end{align*}On the other hand,
 \[ \mathbb{P}_{n'}(\gamma) = \left\{\begin{array}{@{}ll} \dfrac{\pi_i \rho_j}{\rho_i \lambda^{n'}} & \text{if }v_i\text{ has large growth,} \\ 0 & \text{otherwise,} \end{array}\right. \]
\[ \mathbb{P}_{n'}(\gamma) = \left\{\begin{array}{@{}ll} \dfrac{\pi_i \rho_j}{\rho_i \lambda^{n'}} & \text{if }v_i\text{ has large growth,} \\ 0 & \text{otherwise,} \end{array}\right. \]
which is nonzero if both ![]() $v_i$ and
$v_i$ and ![]() $v_j$ belong to a maximal component. In this case,
$v_j$ belong to a maximal component. In this case,
 \begin{align*} \frac{d\mathbb{P}_{n'}}{d \tilde{\lambda}_{n}}(\gamma) &= \frac{\lambda^{\lg(n)}}{e_0^{T} M^{\lg(n)}e_i}\cdot \frac{\lambda^{\lg(n)}}{e_j^{T} M^{\lg(n)} 1} \cdot \frac{e_0^{T} M^{n} 1}{\lambda^{n}} \cdot \frac{\pi_i \rho_j}{\rho_i}\\ &\longrightarrow \frac{1}{u_i} \cdot \frac{1}{\rho_j} \cdot \frac{\rho_0}{1} \cdot \frac{\pi_i \rho_j}{\rho_i} =1 \end{align*}
\begin{align*} \frac{d\mathbb{P}_{n'}}{d \tilde{\lambda}_{n}}(\gamma) &= \frac{\lambda^{\lg(n)}}{e_0^{T} M^{\lg(n)}e_i}\cdot \frac{\lambda^{\lg(n)}}{e_j^{T} M^{\lg(n)} 1} \cdot \frac{e_0^{T} M^{n} 1}{\lambda^{n}} \cdot \frac{\pi_i \rho_j}{\rho_i}\\ &\longrightarrow \frac{1}{u_i} \cdot \frac{1}{\rho_j} \cdot \frac{\rho_0}{1} \cdot \frac{\pi_i \rho_j}{\rho_i} =1 \end{align*}
using that ![]() $\pi _i = {u_i \rho _i}/{\rho _0}$. Moreover, if
$\pi _i = {u_i \rho _i}/{\rho _0}$. Moreover, if ![]() $S_n^{i,j}$ denotes the set of paths of length
$S_n^{i,j}$ denotes the set of paths of length ![]() $n'$ from
$n'$ from ![]() $v_i$ to
$v_i$ to ![]() $v_j$, we have
$v_j$, we have
 \begin{align*} \tilde{\lambda}_{n}(S_n^{i,j}) &= \frac{(e_i^{T} M^{n'} e_j) (e_0^{T} M^{\lg(n)} e_i) (e_j^{T} M^{\lg(n)} 1)}{e_0^{T} M^{n} 1} \\ &\leq \frac{(e_i^{T} M^{n'} 1) (e_0^{T} M^{\lg(n)} e_i) (e_j^{T} M^{\lg(n)} 1)}{e_0^{T} M^{n} 1} \\ &\to \frac{\rho_i u_i \rho_j}{\rho_0}, \end{align*}
\begin{align*} \tilde{\lambda}_{n}(S_n^{i,j}) &= \frac{(e_i^{T} M^{n'} e_j) (e_0^{T} M^{\lg(n)} e_i) (e_j^{T} M^{\lg(n)} 1)}{e_0^{T} M^{n} 1} \\ &\leq \frac{(e_i^{T} M^{n'} 1) (e_0^{T} M^{\lg(n)} e_i) (e_j^{T} M^{\lg(n)} 1)}{e_0^{T} M^{n} 1} \\ &\to \frac{\rho_i u_i \rho_j}{\rho_0}, \end{align*}
hence such a probability tends to ![]() $0$ unless both
$0$ unless both ![]() $v_i$ and
$v_i$ and ![]() $v_j$ belong to a maximal component.
$v_j$ belong to a maximal component.
Finally, if we denote by ![]() $\mathcal {L}_n$ the set of paths of length
$\mathcal {L}_n$ the set of paths of length ![]() $n'$ which lie entirely in a maximal component, we have for any set
$n'$ which lie entirely in a maximal component, we have for any set ![]() $A$,
$A$,
 \begin{align*} | \mathbb{P}_{n'}(A) - \tilde{\lambda}_{n}(A)| &\leq \sum_{x \in A \cap \mathcal{L}_n} \bigg|\frac{\mathbb{P}_{n'}(x)}{\tilde{\lambda}_{n}(x)}\tilde{\lambda}_{n}(x) - \tilde{\lambda}_{n}(x)\bigg| + \tilde{\lambda}_{n}(A \setminus \mathcal{L}_n) \\ &\leq \sup_{x \in \mathcal{L}_n} \bigg|\frac{\mathbb{P}_{n'}(x)}{\tilde{\lambda}_{n}(x)} - 1\bigg| + \tilde{\lambda}_{n}(\mathcal{L}_n^{c}) \end{align*}
\begin{align*} | \mathbb{P}_{n'}(A) - \tilde{\lambda}_{n}(A)| &\leq \sum_{x \in A \cap \mathcal{L}_n} \bigg|\frac{\mathbb{P}_{n'}(x)}{\tilde{\lambda}_{n}(x)}\tilde{\lambda}_{n}(x) - \tilde{\lambda}_{n}(x)\bigg| + \tilde{\lambda}_{n}(A \setminus \mathcal{L}_n) \\ &\leq \sup_{x \in \mathcal{L}_n} \bigg|\frac{\mathbb{P}_{n'}(x)}{\tilde{\lambda}_{n}(x)} - 1\bigg| + \tilde{\lambda}_{n}(\mathcal{L}_n^{c}) \end{align*}
and both terms tend to ![]() $0$ as
$0$ as ![]() $n \to \infty$, independently of
$n \to \infty$, independently of ![]() $A$.
$A$.
6.2 Central limit theorem for the counting measure in the semisimple case
We are now ready to prove the following result. For its statement, let ![]() $S_n$ denote the set of length
$S_n$ denote the set of length ![]() $n$ paths beginning at the initial vertex
$n$ paths beginning at the initial vertex ![]() $v_0$.
$v_0$.
Theorem 6.3 Let ![]() $\Gamma$ be a semisimple, thick, coherent graph structure for a nonelementary group
$\Gamma$ be a semisimple, thick, coherent graph structure for a nonelementary group ![]() $G$ of isometries of a
$G$ of isometries of a ![]() $\delta$-hyperbolic space
$\delta$-hyperbolic space ![]() $(X, d)$, and let
$(X, d)$, and let ![]() $o \in X$ be a base point. Then there exist
$o \in X$ be a base point. Then there exist ![]() $\ell \geq 0$,
$\ell \geq 0$, ![]() $\sigma \geq 0$ such that for any
$\sigma \geq 0$ such that for any ![]() $a < b$ we have
$a < b$ we have
In the following proof and later on, we will use the notation ![]() $N_\sigma (x) := \int _{-\infty }^{x} d\mathcal {N}_\sigma (t)$.
$N_\sigma (x) := \int _{-\infty }^{x} d\mathcal {N}_\sigma (t)$.
Remark 6.4 Note that if the graph structure ![]() $\Gamma$ is semisimple and has a unique maximal component, then Theorem 6.3 holds even without assuming that the structure is coherent.
$\Gamma$ is semisimple and has a unique maximal component, then Theorem 6.3 holds even without assuming that the structure is coherent.
Proof. Let ![]() $C_1, \ldots, C_k$ be the maximal components, and let
$C_1, \ldots, C_k$ be the maximal components, and let ![]() $\mu _n^{(i)}$ be the distribution on the space of paths of length
$\mu _n^{(i)}$ be the distribution on the space of paths of length ![]() $n$ induced by the Markov measure associated to that component, as in § 4. Theorem 4.1 shows a CLT for all such measures, and by Lemmas 5.6 and 5.7 all such measures have the same drift and variance, which we denote by
$n$ induced by the Markov measure associated to that component, as in § 4. Theorem 4.1 shows a CLT for all such measures, and by Lemmas 5.6 and 5.7 all such measures have the same drift and variance, which we denote by ![]() $\ell$ and
$\ell$ and ![]() $\sigma$.
$\sigma$.
Now, since the starting probability ![]() $(\pi _i)$ in the above construction is nonzero precisely on the set of vertices which belong to a maximal component, there exist weights
$(\pi _i)$ in the above construction is nonzero precisely on the set of vertices which belong to a maximal component, there exist weights ![]() $c_i \geq 0$ with
$c_i \geq 0$ with ![]() $\sum _i c_i = 1$ such that
$\sum _i c_i = 1$ such that
 \begin{align*} \mathbb{P}_n = \sum_{i = 1}^{k} c_i \mu_n^{(i)} \end{align*}
\begin{align*} \mathbb{P}_n = \sum_{i = 1}^{k} c_i \mu_n^{(i)} \end{align*}
for any ![]() $n$. Thus, for any
$n$. Thus, for any ![]() $x \in \mathbb {R}$,
$x \in \mathbb {R}$,
 \begin{equation} \mathbb{P}_n (g: \varphi(g) \leq x ) = \sum_{i = 1}^{k} c_i \mu_n^{(i)} (g: \varphi(g) \leq x ) \to N_\sigma(x), \end{equation}
\begin{equation} \mathbb{P}_n (g: \varphi(g) \leq x ) = \sum_{i = 1}^{k} c_i \mu_n^{(i)} (g: \varphi(g) \leq x ) \to N_\sigma(x), \end{equation}where we recall that
We now use that the counting measure can be approximated by the distribution on finite paths for the Markov chain. If ![]() $g$ is a path of length
$g$ is a path of length ![]() $n$, we denote
$n$, we denote ![]() $g = g_0 g_1 g_2$ where
$g = g_0 g_1 g_2$ where ![]() $g_0$ is the prefix of length
$g_0$ is the prefix of length ![]() $\lg (n)$,
$\lg (n)$, ![]() $g_1$ is the middle part of length
$g_1$ is the middle part of length ![]() $n - 2 \lg (n)$ and
$n - 2 \lg (n)$ and ![]() $g_2$ is the final part of length
$g_2$ is the final part of length ![]() $\lg (n)$. By Remark 5.4, there exists
$\lg (n)$. By Remark 5.4, there exists ![]() $n_0$ such that
$n_0$ such that
for any ![]() $n \geq n_0$ and
$n \geq n_0$ and ![]() $g$ with
$g$ with ![]() $\Vert g \Vert = n$.
$\Vert g \Vert = n$.
Fix ![]() $x \in \mathbb {R}$ and
$x \in \mathbb {R}$ and ![]() $\epsilon > 0$. Then we have
$\epsilon > 0$. Then we have
 \begin{align*} \lambda_n (g: \varphi(g) \leq x ) &= \lambda_n ( g = g_0 g_1 g_2: \varphi(g) \leq x) \\ &\le \lambda_n ( g = g_0 g_1 g_2: \varphi(g_1) \leq x + \epsilon ) \quad\ \ \, \text{by 9, for $n$ large }\\ &= \tilde{\lambda}_n ( g_1: \varphi(g_1) \leq x + \epsilon ) \quad\quad\quad\quad\quad\ \, \text{by definition of $\tilde{\lambda}_n$} \\ &\le \mathbb{P}_{n - 2 \lg(n)} ( g_1: \varphi(g_1) \leq x + \epsilon ) + \epsilon \quad \text{by Lemma 6.2, for $n$ large.} \end{align*}
\begin{align*} \lambda_n (g: \varphi(g) \leq x ) &= \lambda_n ( g = g_0 g_1 g_2: \varphi(g) \leq x) \\ &\le \lambda_n ( g = g_0 g_1 g_2: \varphi(g_1) \leq x + \epsilon ) \quad\ \ \, \text{by 9, for $n$ large }\\ &= \tilde{\lambda}_n ( g_1: \varphi(g_1) \leq x + \epsilon ) \quad\quad\quad\quad\quad\ \, \text{by definition of $\tilde{\lambda}_n$} \\ &\le \mathbb{P}_{n - 2 \lg(n)} ( g_1: \varphi(g_1) \leq x + \epsilon ) + \epsilon \quad \text{by Lemma 6.2, for $n$ large.} \end{align*}Hence, by (8) we obtain
and, by taking ![]() $\epsilon$ smaller and smaller and using the continuity of
$\epsilon$ smaller and smaller and using the continuity of ![]() $N_\sigma$,
$N_\sigma$,
The lower bound follows analogously.
Indeed, the same proof shows the following stronger statement. Let ![]() $\lambda _n^{(l)}$ denote the counting measure on the set of paths of length
$\lambda _n^{(l)}$ denote the counting measure on the set of paths of length ![]() $n$ starting at
$n$ starting at ![]() $v_l$.
$v_l$.
Corollary 6.5 Let ![]() $\Gamma$ be a semisimple, thick, coherent graph structure for a nonelementary group
$\Gamma$ be a semisimple, thick, coherent graph structure for a nonelementary group ![]() $G$ of isometries of a
$G$ of isometries of a ![]() $\delta$-hyperbolic space
$\delta$-hyperbolic space ![]() $(X, d)$, and let
$(X, d)$, and let ![]() $o \in X$ be a base point. Then there exist
$o \in X$ be a base point. Then there exist ![]() $\ell \geq 0$,
$\ell \geq 0$, ![]() $\sigma \geq 0$ such that for any vertex
$\sigma \geq 0$ such that for any vertex ![]() $v_l$ of large growth for
$v_l$ of large growth for ![]() $\Gamma$ and any
$\Gamma$ and any ![]() $a < b$ we have
$a < b$ we have
 \begin{align*} \lim_{n \to \infty} \lambda_n^{(l)} \bigg(g: \frac{d(o, g o) - \ell \Vert g \Vert}{\sqrt{\Vert g \Vert}} \in [a, b]\bigg) = \int_a^{b} d N_\sigma(t). \end{align*}
\begin{align*} \lim_{n \to \infty} \lambda_n^{(l)} \bigg(g: \frac{d(o, g o) - \ell \Vert g \Vert}{\sqrt{\Vert g \Vert}} \in [a, b]\bigg) = \int_a^{b} d N_\sigma(t). \end{align*}Proof. Let us fix a vertex ![]() $v_l$ of large growth for
$v_l$ of large growth for ![]() $M$. Then we can define a Markov measure
$M$. Then we can define a Markov measure ![]() $\mathbb {P}^{(l)}$ on the space of infinite paths as follows. The transition probabilities will always be the same
$\mathbb {P}^{(l)}$ on the space of infinite paths as follows. The transition probabilities will always be the same ![]() $p_{ij} = {\rho _j}/{\lambda ^{p} \rho _i}$, while for each vertex
$p_{ij} = {\rho _j}/{\lambda ^{p} \rho _i}$, while for each vertex ![]() $v_l$ one finds a different set of starting probabilities
$v_l$ one finds a different set of starting probabilities ![]() $\pi _i^{(l)}$ given by
$\pi _i^{(l)}$ given by
Just as before, there exist constants ![]() $c_i^{(l)} \geq 0$ such that
$c_i^{(l)} \geq 0$ such that ![]() $\sum _i c_i^{(l)} = 1$ and
$\sum _i c_i^{(l)} = 1$ and
 \begin{align*} \mathbb{P}_n^{(l)} = \sum_{i =1}^{k} c_i^{(l)} \mu_n^{(i)}. \end{align*}
\begin{align*} \mathbb{P}_n^{(l)} = \sum_{i =1}^{k} c_i^{(l)} \mu_n^{(i)}. \end{align*}The proof then proceeds exactly as for Theorem 6.3.
7. The central limit theorem for displacement and translation length
Now suppose that ![]() $\Gamma$ is an almost semisimple graph structure for
$\Gamma$ is an almost semisimple graph structure for ![]() $G$ with transition matrix
$G$ with transition matrix ![]() $M$. Then
$M$. Then ![]() $M$ has some period
$M$ has some period ![]() $p\ge 1$ such that
$p\ge 1$ such that ![]() $M^{p}$ is semisimple. We denote by
$M^{p}$ is semisimple. We denote by ![]() $\Gamma ^{p}$ the corresponding
$\Gamma ^{p}$ the corresponding ![]() $p$-step graph structure on
$p$-step graph structure on ![]() $G$. That is,
$G$. That is, ![]() $\Gamma ^{p}$ is the graph with the same vertex set as
$\Gamma ^{p}$ is the graph with the same vertex set as ![]() $\Gamma$ and an edge joining
$\Gamma$ and an edge joining ![]() $v_i$ to
$v_i$ to ![]() $v_j$ for each directed path from
$v_j$ for each directed path from ![]() $v_i$ to
$v_i$ to ![]() $v_j$ of length
$v_j$ of length ![]() $p$, whose label is the word in
$p$, whose label is the word in ![]() $G$ spelled by the corresponding path. The transition matrix for
$G$ spelled by the corresponding path. The transition matrix for ![]() $\Gamma ^{p}$ is
$\Gamma ^{p}$ is ![]() $M^{p}$, hence
$M^{p}$, hence ![]() $\Gamma$ is a semisimple graph structure for
$\Gamma$ is a semisimple graph structure for ![]() $G$.
$G$.
Since the previous results require this structure to be thick and coherent, we need the following lemma.
Lemma 7.1 The following properties pass to the ![]() $p$-step graph structure.
$p$-step graph structure.
– If
 $v$ is a large growth vertex of
$v$ is a large growth vertex of  $\Gamma$, then it is also a large growth vertex of
$\Gamma$, then it is also a large growth vertex of  $\Gamma ^{p}$.
$\Gamma ^{p}$.– If
 $\Gamma$ is a thick structure, then
$\Gamma$ is a thick structure, then  $\Gamma ^{p}$ is also thick.
$\Gamma ^{p}$ is also thick.– If
 $\Gamma$ is coherent, then so is
$\Gamma$ is coherent, then so is  $\Gamma ^{p}$.
$\Gamma ^{p}$.
Proof. The first statement holds because any path from ![]() $v$ that ends in a component of maximal growth can be extended to a path whose length is a multiple of
$v$ that ends in a component of maximal growth can be extended to a path whose length is a multiple of ![]() $p$ by adding on a path in that component of length less than
$p$ by adding on a path in that component of length less than ![]() $p$.
$p$.
Now suppose that ![]() $\Gamma$ is thick. Let
$\Gamma$ is thick. Let ![]() $v$ be a vertex in a maximal component of
$v$ be a vertex in a maximal component of ![]() $\Gamma ^{p}$. Then
$\Gamma ^{p}$. Then ![]() $v$ is also a vertex in a maximal component of
$v$ is also a vertex in a maximal component of ![]() $\Gamma$. Let
$\Gamma$. Let ![]() $\Gamma _{v, p}$ be the semigroup of loops based at
$\Gamma _{v, p}$ be the semigroup of loops based at ![]() $v$ of lengths multiple of
$v$ of lengths multiple of ![]() $p$. Consider the semigroup homomorphism
$p$. Consider the semigroup homomorphism
given by taking the length and reducing it mod ![]() $p$. Clearly, the image of
$p$. Clearly, the image of ![]() $f$ is a subsemigroup of
$f$ is a subsemigroup of ![]() $\mathbb {N}/p\mathbb {N}$, which is a finite group, hence the image contains the inverse of each element and so is also a group. Let
$\mathbb {N}/p\mathbb {N}$, which is a finite group, hence the image contains the inverse of each element and so is also a group. Let ![]() $\gamma _i, \ldots, \gamma _k \subseteq \Gamma _v$ be a set of representatives for each remainder class in the image of
$\gamma _i, \ldots, \gamma _k \subseteq \Gamma _v$ be a set of representatives for each remainder class in the image of ![]() $f$. Now let
$f$. Now let ![]() $\gamma \in \Gamma _v$. Then
$\gamma \in \Gamma _v$. Then ![]() $\Vert \gamma \Vert$ belongs to the image of
$\Vert \gamma \Vert$ belongs to the image of ![]() $f$, hence there exists
$f$, hence there exists ![]() $\gamma _i$ (the representative of the inverse modulo
$\gamma _i$ (the representative of the inverse modulo ![]() $p$), such that
$p$), such that ![]() $\gamma \gamma _i$ has length a multiple of
$\gamma \gamma _i$ has length a multiple of ![]() $p$, hence it belongs to
$p$, hence it belongs to ![]() $\Gamma _{v, p}$. Hence, by setting
$\Gamma _{v, p}$. Hence, by setting ![]() $B'$ the set
$B'$ the set ![]() $\{ \gamma _i^{-1}: 1 \leq i \leq k \}$, we have
$\{ \gamma _i^{-1}: 1 \leq i \leq k \}$, we have ![]() $\Gamma _v \subseteq \Gamma _{v, p} B'$ in the group. Since
$\Gamma _v \subseteq \Gamma _{v, p} B'$ in the group. Since ![]() $\Gamma$ is thick, there exists
$\Gamma$ is thick, there exists ![]() $B''$ such that
$B''$ such that ![]() $G = B'' \Gamma _v B''$, hence also
$G = B'' \Gamma _v B''$, hence also ![]() $G = B'' \Gamma _{v, p} B' B''$, hence
$G = B'' \Gamma _{v, p} B' B''$, hence ![]() $\Gamma ^{p}$ is also thick.
$\Gamma ^{p}$ is also thick.
Finally, note that any path ![]() $g$ in
$g$ in ![]() $\Gamma ^{p}$ of length
$\Gamma ^{p}$ of length ![]() $k$ can be naturally thought of as a path
$k$ can be naturally thought of as a path ![]() $g_{{\dagger} }$ in
$g_{{\dagger} }$ in ![]() $\Gamma$ of length
$\Gamma$ of length ![]() $pk$ such that, for all
$pk$ such that, for all ![]() $i\ge 0$,
$i\ge 0$, ![]() $\overline {g_{{\dagger} }(pi)} = \overline g(i)$. From this, it follows that
$\overline {g_{{\dagger} }(pi)} = \overline g(i)$. From this, it follows that ![]() $\Gamma ^{p}$ is bounded whenever
$\Gamma ^{p}$ is bounded whenever ![]() $\Gamma$ is. Moreover, if
$\Gamma$ is. Moreover, if ![]() $B\subset G$ and
$B\subset G$ and ![]() $\mathcal {B} \ge 0$ are as in the definition of coherence of
$\mathcal {B} \ge 0$ are as in the definition of coherence of ![]() $\Gamma$ (Definition 2.2) and
$\Gamma$ (Definition 2.2) and ![]() $g,h$ are paths in
$g,h$ are paths in ![]() $\Gamma ^{p}$ with
$\Gamma ^{p}$ with ![]() $\overline g = b_1\overline h b_2$ for
$\overline g = b_1\overline h b_2$ for ![]() $b_1,b_2 \in B$, then we also have that
$b_1,b_2 \in B$, then we also have that ![]() $\overline {g_{{\dagger} }} = b_1\overline {h_{{\dagger} }} b_2$. Then coherence of
$\overline {g_{{\dagger} }} = b_1\overline {h_{{\dagger} }} b_2$. Then coherence of ![]() $\Gamma$ implies that
$\Gamma$ implies that
and so coherence of ![]() $\Gamma ^{p}$ follows.
$\Gamma ^{p}$ follows.
Now let us consider the semisimple matrix ![]() $M^{p}$. Note that irreducible components of
$M^{p}$. Note that irreducible components of ![]() $M^{p}$ may be proper subsets of irreducible components of
$M^{p}$ may be proper subsets of irreducible components of ![]() $M$. Given a vertex
$M$. Given a vertex ![]() $v_i$, let us denote by
$v_i$, let us denote by ![]() $\lambda _{k}^{(i)}$ the counting measure on paths starting at
$\lambda _{k}^{(i)}$ the counting measure on paths starting at ![]() $v_i$ of length
$v_i$ of length ![]() $k$ for
$k$ for ![]() $\Gamma$. Note that if
$\Gamma$. Note that if ![]() $k = np$, then this also counts paths of length
$k = np$, then this also counts paths of length ![]() $n$ in
$n$ in ![]() $\Gamma ^{p}$ starting at
$\Gamma ^{p}$ starting at ![]() $v_i$.
$v_i$.
Since a bounded, thick graph structure ![]() $\Gamma$ is almost semisimple (Lemma 2.3), by applying Corollary 6.5 to
$\Gamma$ is almost semisimple (Lemma 2.3), by applying Corollary 6.5 to ![]() $\Gamma ^{p}$, we immediately obtain the following result.
$\Gamma ^{p}$, we immediately obtain the following result.
Corollary 7.2 Let ![]() $\Gamma$ be a thick, coherent structure of period
$\Gamma$ be a thick, coherent structure of period ![]() $p$ for a nonelementary group
$p$ for a nonelementary group ![]() $G$ of isometries of a
$G$ of isometries of a ![]() $\delta$-hyperbolic space
$\delta$-hyperbolic space ![]() $(X, d)$, and let
$(X, d)$, and let ![]() $o \in X$ be a base point. Then there exist
$o \in X$ be a base point. Then there exist ![]() $\ell, \sigma$ such that the following assertion holds. For any vertex
$\ell, \sigma$ such that the following assertion holds. For any vertex ![]() $v_i$ of large growth for
$v_i$ of large growth for ![]() $\Gamma$ and for any
$\Gamma$ and for any ![]() $x$, we have
$x$, we have
as ![]() $n \to \infty$.
$n \to \infty$.
We are now ready to prove the following theorem. Recall that ![]() $S_n$ denotes the set of length
$S_n$ denotes the set of length ![]() $n$ paths beginning at the initial vertex
$n$ paths beginning at the initial vertex ![]() $v_0$.
$v_0$.
Theorem 7.3 Let ![]() $\Gamma$ be a thick, coherent graph structure for a nonelementary group
$\Gamma$ be a thick, coherent graph structure for a nonelementary group ![]() $G$ of isometries of a
$G$ of isometries of a ![]() $\delta$-hyperbolic space
$\delta$-hyperbolic space ![]() $(X, d)$, and let
$(X, d)$, and let ![]() $o \in X$ be a base point. Then there exist
$o \in X$ be a base point. Then there exist ![]() $\ell \geq 0$,
$\ell \geq 0$, ![]() $\sigma \geq 0$ such that for any
$\sigma \geq 0$ such that for any ![]() $a < b$ we have
$a < b$ we have
Proof. Let ![]() $v_0$ be the initial vertex, let
$v_0$ be the initial vertex, let ![]() $S_{n}$ be the set of paths of length
$S_{n}$ be the set of paths of length ![]() $n$ based at
$n$ based at ![]() $v_0$, and let
$v_0$, and let ![]() $\lambda _n$ be the uniform measure on
$\lambda _n$ be the uniform measure on ![]() $S_n$.
$S_n$.
Let us fix ![]() $0 \leq r \leq p-1$. Then we can write the counting measure on
$0 \leq r \leq p-1$. Then we can write the counting measure on ![]() $S_{pn+r}$, starting at the initial vertex
$S_{pn+r}$, starting at the initial vertex ![]() $v_0$, by first picking randomly a path
$v_0$, by first picking randomly a path ![]() $g_0$ of length
$g_0$ of length ![]() $r$ from
$r$ from ![]() $v_0$ with a certain probability
$v_0$ with a certain probability ![]() $\mu$, and then picking a random path starting at
$\mu$, and then picking a random path starting at ![]() $v_i = t(g_0)$ with respect to the counting measure on the set of paths of length
$v_i = t(g_0)$ with respect to the counting measure on the set of paths of length ![]() $n$ starting at
$n$ starting at ![]() $v_i$.
$v_i$.
To compute ![]() $\mu$, let us consider a path
$\mu$, let us consider a path ![]() $g_0$ of length
$g_0$ of length ![]() $r$ starting at
$r$ starting at ![]() $v_0$ and ending at
$v_0$ and ending at ![]() $v_i$. Then, if
$v_i$. Then, if ![]() $v_i$ is of large growth for
$v_i$ is of large growth for ![]() $\Gamma ^{p}$,
$\Gamma ^{p}$,
Thus, we define
Note that ![]() $\mu (g_0) = 0$ if the end vertex of
$\mu (g_0) = 0$ if the end vertex of ![]() $g_0$ has small growth and, moreover,
$g_0$ has small growth and, moreover,
 \begin{align*} \sum_{\Vert g_0 \Vert = r} \mu(g_0) = \sum_i \mu(g_0) \# \{ g_0 \in S_r: t(g_0) = v_i \} = \sum_i e_0 M^{r} e_i \frac{e_i M_{\infty} 1}{e_0 M^{r} M_\infty 1} = 1. \end{align*}
\begin{align*} \sum_{\Vert g_0 \Vert = r} \mu(g_0) = \sum_i \mu(g_0) \# \{ g_0 \in S_r: t(g_0) = v_i \} = \sum_i e_0 M^{r} e_i \frac{e_i M_{\infty} 1}{e_0 M^{r} M_\infty 1} = 1. \end{align*} Let ![]() $\lambda '_{pn+r}$ be the measure on
$\lambda '_{pn+r}$ be the measure on ![]() $S_{pn + r}$ given by first taking randomly a path
$S_{pn + r}$ given by first taking randomly a path ![]() $g_0$ of length
$g_0$ of length ![]() $r$ from
$r$ from ![]() $v_0$ with distribution
$v_0$ with distribution ![]() $\mu$ and then taking uniformly a path of length
$\mu$ and then taking uniformly a path of length ![]() $pn$ starting from
$pn$ starting from ![]() $t(g_1)$.
$t(g_1)$.
Now we show that the CLT holds for ![]() $\lambda '_{pn+r}$. Let
$\lambda '_{pn+r}$. Let ![]() $\ell, \sigma$ be given by Corollary 7.2, and let
$\ell, \sigma$ be given by Corollary 7.2, and let ![]() $\varphi (g) := ({d(o, go) - \ell \Vert g\Vert })/{\sqrt { \Vert g \Vert }}$. By Corollary 7.2, for any vertex
$\varphi (g) := ({d(o, go) - \ell \Vert g\Vert })/{\sqrt { \Vert g \Vert }}$. By Corollary 7.2, for any vertex ![]() $v_i$ of large growth, we have
$v_i$ of large growth, we have
Then if ![]() $g = g_0 g_1$, and
$g = g_0 g_1$, and ![]() $t(g_0)$ denotes the (index of the) end vertex of
$t(g_0)$ denotes the (index of the) end vertex of ![]() $g_0$,
$g_0$,
 \begin{align*} \lambda'_{pn+r} (g: \varphi(g) \leq x ) &= \sum_{g_0 \in S_r} \mu(g_0) \lambda^{(t(g_0))}_{pn} ( g_1 : \varphi(g_0 g_1) \leq x) \\ &\longrightarrow \sum_{g_0} \mu(g_0) N_{\sigma}(x) = N_\sigma(x), \end{align*}
\begin{align*} \lambda'_{pn+r} (g: \varphi(g) \leq x ) &= \sum_{g_0 \in S_r} \mu(g_0) \lambda^{(t(g_0))}_{pn} ( g_1 : \varphi(g_0 g_1) \leq x) \\ &\longrightarrow \sum_{g_0} \mu(g_0) N_{\sigma}(x) = N_\sigma(x), \end{align*}
where we used that ![]() $\varphi$ is uniformly bicontinuous as in the proof of Theorem 6.3.
$\varphi$ is uniformly bicontinuous as in the proof of Theorem 6.3.
Now we prove that
as ![]() $n \to \infty$. Indeed, if
$n \to \infty$. Indeed, if ![]() $\gamma = g_0 g_1$ is a path from
$\gamma = g_0 g_1$ is a path from ![]() $v_0$ of length
$v_0$ of length ![]() $pn+r$ and
$pn+r$ and ![]() $g_0$ is its prefix of length
$g_0$ is its prefix of length ![]() $r$ ending at a vertex
$r$ ending at a vertex ![]() $v_i$ of large growth, then
$v_i$ of large growth, then
On the other hand, if the end vertex of ![]() $g_0$ is of small growth, then
$g_0$ is of small growth, then ![]() $\lambda '_{pn+r}(g) = 0$, and also
$\lambda '_{pn+r}(g) = 0$, and also
as ![]() $n \to \infty$. Now, let
$n \to \infty$. Now, let ![]() $A_x := \{ g:\varphi (g) \leq x \}$ and
$A_x := \{ g:\varphi (g) \leq x \}$ and ![]() $L_r$ be the set of paths starting at
$L_r$ be the set of paths starting at ![]() $v_0$ whose prefix of length
$v_0$ whose prefix of length ![]() $r$ ends in a vertex of large growth. Then
$r$ ends in a vertex of large growth. Then
 \begin{align*} \lambda_{pn+r}(g: \varphi(g) \leq x ) &= \lambda_{pn+r} (g \in L_r: \varphi(g) \leq x ) + \lambda_{pn+r} (g \notin L_r: \varphi(g) \leq x ) \\ &= \frac{\lambda_{pn+r}(A_x \cap L_r) }{\lambda'_{pn+r}(A_x \cap L_r)} \lambda'_{pn+r}(A_x \cap L_r) + \lambda_{pn+r}(A_x \setminus L_r) \\ &\to 1 \cdot N_\sigma(x) + 0 = N_\sigma(x). \end{align*}
\begin{align*} \lambda_{pn+r}(g: \varphi(g) \leq x ) &= \lambda_{pn+r} (g \in L_r: \varphi(g) \leq x ) + \lambda_{pn+r} (g \notin L_r: \varphi(g) \leq x ) \\ &= \frac{\lambda_{pn+r}(A_x \cap L_r) }{\lambda'_{pn+r}(A_x \cap L_r)} \lambda'_{pn+r}(A_x \cap L_r) + \lambda_{pn+r}(A_x \setminus L_r) \\ &\to 1 \cdot N_\sigma(x) + 0 = N_\sigma(x). \end{align*}
We have thus obtained a CLT for ![]() $\lambda _{pn+r}$, for any
$\lambda _{pn+r}$, for any ![]() $0 \leq r \leq p-1$, always with the same
$0 \leq r \leq p-1$, always with the same ![]() $\ell, \sigma$. Since there are only finitely many values
$\ell, \sigma$. Since there are only finitely many values ![]() $r$, the claim follows.
$r$, the claim follows.
7.1 A central limit theorem for translation length
We now prove a more general version of our second main result, Theorem 1.1(ii).
Theorem 7.4 Let ![]() $\Gamma$ be a thick, coherent graph structure for a nonelementary group
$\Gamma$ be a thick, coherent graph structure for a nonelementary group ![]() $G$ of isometries of a
$G$ of isometries of a ![]() $\delta$-hyperbolic space
$\delta$-hyperbolic space ![]() $(X, d)$, let
$(X, d)$, let ![]() $o \in X$ be a base point, and let
$o \in X$ be a base point, and let ![]() $\ell,\sigma$ be as in Theorem 7.3. Then for any
$\ell,\sigma$ be as in Theorem 7.3. Then for any ![]() $a < b$ we have
$a < b$ we have
Proof. Let us recall that the translation length of an isometry ![]() $g$ of a
$g$ of a ![]() $\delta$-hyperbolic space can be computed by (see, for example, [Reference Maher and TiozzoMT18, Proposition 5.8])
$\delta$-hyperbolic space can be computed by (see, for example, [Reference Maher and TiozzoMT18, Proposition 5.8])
where ![]() $O(\delta )$ is a constant which only depends on the hyperbolicity constant of
$O(\delta )$ is a constant which only depends on the hyperbolicity constant of ![]() $X$. Now, by choosing
$X$. Now, by choosing ![]() $f(n) = \epsilon \sqrt {n}$ in [Reference Gekhtman, Taylor and TiozzoGTT20, Proposition 5.8], for any
$f(n) = \epsilon \sqrt {n}$ in [Reference Gekhtman, Taylor and TiozzoGTT20, Proposition 5.8], for any ![]() $\epsilon$ we have
$\epsilon$ we have
as ![]() $n \to \infty$. The claim then follows by combining this statement and the statement of Theorem 7.3 into formula (10).
$n \to \infty$. The claim then follows by combining this statement and the statement of Theorem 7.3 into formula (10).
7.2 Zero variance
We finally complete our main theorem by characterizing the case where ![]() $\sigma = 0$. First, we give a general criterion.
$\sigma = 0$. First, we give a general criterion.
Proposition 7.5 In the hypotheses of Theorem 7.3 we have ![]() $\sigma =0$ if and only if there is
$\sigma =0$ if and only if there is ![]() $C \ge 0$ such that for all finite length paths
$C \ge 0$ such that for all finite length paths ![]() $g$ in
$g$ in ![]() $\Gamma$,
$\Gamma$,
We note that the proposition implies that ![]() $\sigma >0$ whenever the action
$\sigma >0$ whenever the action ![]() $G \curvearrowright X$ is nonproper.
$G \curvearrowright X$ is nonproper.
Proof. Suppose that ![]() $\sigma = 0$ for the CLT for the counting measure. Then, by our previous discussion, we have
$\sigma = 0$ for the CLT for the counting measure. Then, by our previous discussion, we have ![]() $\sigma = 0$ also for the Markov chain on any maximal components. Then, by Theorem 4.2, we also have
$\sigma = 0$ also for the Markov chain on any maximal components. Then, by Theorem 4.2, we also have ![]() $\sigma = 0$ for the random walk on the loop semigroup driven by
$\sigma = 0$ for the random walk on the loop semigroup driven by ![]() $\check {\mu }_v$. Hence, as in [Reference Benoist and QuintBQ16, Proof of Theorem 4.7 (b)], for any
$\check {\mu }_v$. Hence, as in [Reference Benoist and QuintBQ16, Proof of Theorem 4.7 (b)], for any ![]() $n$,
$n$,
where ![]() $\eta _0$ is the centering of
$\eta _0$ is the centering of ![]() $\eta$. This implies
$\eta$. This implies
for any ![]() $g \in \Gamma _v^{-1}$ and
$g \in \Gamma _v^{-1}$ and ![]() $\nu _v$-a.e.
$\nu _v$-a.e. ![]() $\xi \in \overline X^{h}$. Thus, since
$\xi \in \overline X^{h}$. Thus, since ![]() $|\eta - \eta _0| \leq 2 \Vert \psi \Vert _\infty$ is bounded, we have
$|\eta - \eta _0| \leq 2 \Vert \psi \Vert _\infty$ is bounded, we have
hence by [Reference HorbezHor18, Corollary 2.3] there exists a constant ![]() $C$ for which
$C$ for which
for any ![]() $g$ in the support of
$g$ in the support of ![]() $\check {\mu }_v^{*n}(g)$.
$\check {\mu }_v^{*n}(g)$.
Hence, by thickness we have that for any ![]() $g \in \Omega ^{*}$ there exist
$g \in \Omega ^{*}$ there exist ![]() $b_1, b_2 \in B$ and
$b_1, b_2 \in B$ and ![]() $h \in \Gamma _v^{-1}$ such that
$h \in \Gamma _v^{-1}$ such that ![]() $\overline {h} = b_1 \overline {g} b_2$, thus by coherence and the triangle inequality
$\overline {h} = b_1 \overline {g} b_2$, thus by coherence and the triangle inequality
thus there exists a constant ![]() $C'$ such that
$C'$ such that
for any ![]() $g \in \Omega ^{*}$. This completes the proof.
$g \in \Omega ^{*}$. This completes the proof.
We conclude with a corollary that applies when the graph structure is geodesic. For the action ![]() $G \curvearrowright X$, denote the translation length of
$G \curvearrowright X$, denote the translation length of ![]() $h$ by
$h$ by ![]() $\tau _X(h)$. We use the notation
$\tau _X(h)$. We use the notation ![]() $\tau _G(h)$ to denote the translation length of
$\tau _G(h)$ to denote the translation length of ![]() $h$ with respect to the word metric
$h$ with respect to the word metric ![]() $d_G$ induced by the graph structure
$d_G$ induced by the graph structure ![]() $\Gamma$:
$\Gamma$:
Corollary 7.6 Suppose that ![]() $\Gamma$ is a thick geodesic combing of
$\Gamma$ is a thick geodesic combing of ![]() $G$. If
$G$. If ![]() $\sigma = 0$ in the CLT, then for all
$\sigma = 0$ in the CLT, then for all ![]() $h \in G$,
$h \in G$,
where ![]() $\ell$ is the corresponding drift.
$\ell$ is the corresponding drift.
Proof. Recall that a geodesic combing is coherent by Lemma 2.4. Let ![]() $g_n$ be a path in
$g_n$ be a path in ![]() $\Gamma$ representing
$\Gamma$ representing ![]() $h^{n}$ for
$h^{n}$ for ![]() $h\in G$. That is,
$h\in G$. That is, ![]() $h^{n} = \overline g_n$. Since the structure is geodesic,
$h^{n} = \overline g_n$. Since the structure is geodesic, ![]() $||g_n|| = d_G(1,h^{n})$. Applying Proposition 7.5, we get that
$||g_n|| = d_G(1,h^{n})$. Applying Proposition 7.5, we get that
The corollary follows after dividing by ![]() $n$ and taking a limit.
$n$ and taking a limit.
8. Applications
The main theorem of § 1 now follows easily from the results in § 7.
Proof of Theorem 1.1 Since ![]() $G$ has a thick geodesic combing with respect to
$G$ has a thick geodesic combing with respect to ![]() $S$, the length
$S$, the length ![]() $\Vert g \Vert$ of a path in the graph equals the word length with respect to
$\Vert g \Vert$ of a path in the graph equals the word length with respect to ![]() $S$ of its evaluation
$S$ of its evaluation ![]() $\overline {g} \in G$, and the sphere of radius
$\overline {g} \in G$, and the sphere of radius ![]() $n$ in the Cayley graph of
$n$ in the Cayley graph of ![]() $G$ is in bijection with the set of paths of length
$G$ is in bijection with the set of paths of length ![]() $n$ in the graph. Moreover, the associated graph structure is coherent by Lemma 2.4. Then (i) follows immediately from Theorem 7.3, (ii) follows from 7.4 and (iii) from Corollary 7.6.
$n$ in the graph. Moreover, the associated graph structure is coherent by Lemma 2.4. Then (i) follows immediately from Theorem 7.3, (ii) follows from 7.4 and (iii) from Corollary 7.6.
We now give proofs of the applications in the introduction. We first recall some examples of groups which admit thick geodesic combings; for further details, see also [Reference Gekhtman, Taylor and TiozzoGTT20].
Lemma 8.1 The following groups admit thick geodesic combings.
(i) A (word) hyperbolic group
 $G$ admits a thick geodesic combing with respect to any generating set.
$G$ admits a thick geodesic combing with respect to any generating set.(ii) If
 $G$ is relatively hyperbolic with virtually abelian peripheral subgroups, then every finite generating set
$G$ is relatively hyperbolic with virtually abelian peripheral subgroups, then every finite generating set  $S'$ can be extended to a finite generating set
$S'$ can be extended to a finite generating set  $S$ for
$S$ for  $G$ which admits a thick geodesic combing.
$G$ which admits a thick geodesic combing.(iii) If
 $G$ is a right-angled Artin group or right-angled Coxeter group that does not decompose as a product and
$G$ is a right-angled Artin group or right-angled Coxeter group that does not decompose as a product and  $S$ is the vertex generating set, then
$S$ is the vertex generating set, then  $G$ admits a thick geodesic combing for
$G$ admits a thick geodesic combing for  $S$ whose graph structure has only one maximal component, which is primitive.
$S$ whose graph structure has only one maximal component, which is primitive.
Proof. (i) By [Reference CannonCan84], a hyperbolic ![]() $G$ has a geodesic combing with respect to any generating set. By [Reference Arzhantseva and LysenokAL02, Theorem 3], this geodesic combing has the growth quasitightness property (see [Reference Gekhtman, Taylor and TiozzoGTT20, Definition 1.2], inspired by [Reference Arzhantseva and LysenokAL02]). Since growth quasitightness implies thickness by [Reference Gekhtman, Taylor and TiozzoGTT20, Proposition 7.2], such a structure is thick. Alternatively, thickness can also be deduced from the proof of [Reference Gouëzel, Mathéus and MaucourantGMM18, Lemma 4.6].
$G$ has a geodesic combing with respect to any generating set. By [Reference Arzhantseva and LysenokAL02, Theorem 3], this geodesic combing has the growth quasitightness property (see [Reference Gekhtman, Taylor and TiozzoGTT20, Definition 1.2], inspired by [Reference Arzhantseva and LysenokAL02]). Since growth quasitightness implies thickness by [Reference Gekhtman, Taylor and TiozzoGTT20, Proposition 7.2], such a structure is thick. Alternatively, thickness can also be deduced from the proof of [Reference Gouëzel, Mathéus and MaucourantGMM18, Lemma 4.6].
(ii) By [Reference Antolin and CiobanuAC16, Corollary 1.9], the generating set ![]() $S'$ of
$S'$ of ![]() $G$ can be enlarged to a generating set
$G$ can be enlarged to a generating set ![]() $S$, so that the pair
$S$, so that the pair ![]() $(G,S)$ admits a geodesic combing. Yang [Reference YangYan19] proves that any relatively hyperbolic group has the growth quasitightness property with respect to any finite generating set, hence the proof is complete, observing as above that growth quasitightness implies thickness.
$(G,S)$ admits a geodesic combing. Yang [Reference YangYan19] proves that any relatively hyperbolic group has the growth quasitightness property with respect to any finite generating set, hence the proof is complete, observing as above that growth quasitightness implies thickness.
(iii) In [Reference Gekhtman, Taylor and TiozzoGTT20, Corollary 10.4], building on Hermiller and Meier [Reference Hermiller and MeierHM95], we proved that the language of lexicographically first geodesics in the vertex generators is parameterized by a thick graph structure. In fact, the graph structure we construct has only one maximal component, which is primitive.
Proof of Theorem 1.2 Note that ![]() $\pi _1(M)$ is hyperbolic relative to its parabolic subgroups, which are virtually abelian since
$\pi _1(M)$ is hyperbolic relative to its parabolic subgroups, which are virtually abelian since ![]() $M$ has constant curvature. Hence, by Lemma 8.1(ii) the given generating set
$M$ has constant curvature. Hence, by Lemma 8.1(ii) the given generating set ![]() $S'$ can be enlarged to a finite generating set
$S'$ can be enlarged to a finite generating set ![]() $S$ that is associated to a thick geodesic combing on
$S$ that is associated to a thick geodesic combing on ![]() $\pi _1(M)$. The theorem then follows from Theorem 1.1. Finally,
$\pi _1(M)$. The theorem then follows from Theorem 1.1. Finally, ![]() $\sigma > 0$ by (iii) since the length spectrum is not arithmetic [Reference Guivarc'h and RaugiGR86, Reference KimKim06].
$\sigma > 0$ by (iii) since the length spectrum is not arithmetic [Reference Guivarc'h and RaugiGR86, Reference KimKim06].
Proof of Theorem 1.3 In the case where ![]() $M$ has no rank
$M$ has no rank ![]() $2$ cusps, we have that
$2$ cusps, we have that ![]() $\pi _1(M)$ is hyperbolic. Indeed, by the tameness theorem [Reference Calegari and GabaiCG06, Reference AgolAgo04],
$\pi _1(M)$ is hyperbolic. Indeed, by the tameness theorem [Reference Calegari and GabaiCG06, Reference AgolAgo04], ![]() $M$ is the interior of a compact manifold
$M$ is the interior of a compact manifold ![]() $\overline M$, which by assumption does not have tori as boundary components. Then Thurston's hyperbolization theorem (see [Reference KapovichKap01]),
$\overline M$, which by assumption does not have tori as boundary components. Then Thurston's hyperbolization theorem (see [Reference KapovichKap01]), ![]() $\overline M$ admits a convex cocompact hyperbolic structure on its interior. Hence,
$\overline M$ admits a convex cocompact hyperbolic structure on its interior. Hence, ![]() $\pi _1(M)$ is hyperbolic. The result now follows from Lemma 8.1 and Theorem 1.1.
$\pi _1(M)$ is hyperbolic. The result now follows from Lemma 8.1 and Theorem 1.1.
For the moreover statement, the argument above gives that ![]() $\overline M$ admits a geometrically finite hyperbolic structure. Hence,
$\overline M$ admits a geometrically finite hyperbolic structure. Hence, ![]() $\pi _1(M)$ is hyperbolic relative to its rank
$\pi _1(M)$ is hyperbolic relative to its rank ![]() $2$ parabolic subgroups, which are virtually
$2$ parabolic subgroups, which are virtually ![]() $\mathbb {Z} \times \mathbb {Z}$. The proof then proceeds as in Theorem 1.2
$\mathbb {Z} \times \mathbb {Z}$. The proof then proceeds as in Theorem 1.2
Proof of Theorem 1.4 First, since ![]() $\pi _1(M)$ is word hyperbolic, by Lemma 8.1(i) it has a thick geodesic combing with respect to any generating set.
$\pi _1(M)$ is word hyperbolic, by Lemma 8.1(i) it has a thick geodesic combing with respect to any generating set.
Second, let ![]() $T =T_\Sigma$ be the dual tree associated to
$T =T_\Sigma$ be the dual tree associated to ![]() $\Sigma \subset M$. For details of this standard construction and the properties we need, see [Reference Shalen, Daverman and SherSha02, § 1.4]. Alternatively,
$\Sigma \subset M$. For details of this standard construction and the properties we need, see [Reference Shalen, Daverman and SherSha02, § 1.4]. Alternatively, ![]() $T$ is the Bass–Serre tree associated to the splitting of
$T$ is the Bass–Serre tree associated to the splitting of ![]() $\pi _1(M)$ induced by
$\pi _1(M)$ induced by ![]() $\Sigma$. Since
$\Sigma$. Since ![]() $\Sigma$ is not fiber-like,
$\Sigma$ is not fiber-like, ![]() $T$ is not the real line, and since the quotient
$T$ is not the real line, and since the quotient ![]() $\mathcal {G}$ of the action
$\mathcal {G}$ of the action ![]() $\pi _1(M) \curvearrowright T$ is compact (it is the underlying graph of the associated graph of groups), the action is nonelementary.
$\pi _1(M) \curvearrowright T$ is compact (it is the underlying graph of the associated graph of groups), the action is nonelementary.
Finally, the intersection number ![]() $i(\gamma, \Sigma )$ equals the translation length of
$i(\gamma, \Sigma )$ equals the translation length of ![]() $\gamma$ with respect to the action
$\gamma$ with respect to the action ![]() $\pi _1(M) \curvearrowright T$. To see this, note that the translation length of
$\pi _1(M) \curvearrowright T$. To see this, note that the translation length of ![]() $\gamma$ for this action is equal to the number of edges
$\gamma$ for this action is equal to the number of edges ![]() $\#_e\gamma$ crossed by the shortest representative of
$\#_e\gamma$ crossed by the shortest representative of ![]() $\gamma$ in
$\gamma$ in ![]() $\mathcal {G}$. If we embed
$\mathcal {G}$. If we embed ![]() $\mathcal {G}$ in
$\mathcal {G}$ in ![]() $M$ dual to
$M$ dual to ![]() $\Sigma$, this shows that
$\Sigma$, this shows that ![]() $i(\gamma, \Sigma ) \le \#_e\gamma$. For the opposite inequality, recall that there is a retraction
$i(\gamma, \Sigma ) \le \#_e\gamma$. For the opposite inequality, recall that there is a retraction ![]() $r \colon M \to \mathcal {G}$ mapping each component of
$r \colon M \to \mathcal {G}$ mapping each component of ![]() $\Sigma$ to the midpoint of some edge. Thus by taking a representative of
$\Sigma$ to the midpoint of some edge. Thus by taking a representative of ![]() $\gamma$ intersecting
$\gamma$ intersecting ![]() $\Sigma$ minimally, considering its image under the retraction, and homotoping it off edges that it does not fully cross, we obtain that
$\Sigma$ minimally, considering its image under the retraction, and homotoping it off edges that it does not fully cross, we obtain that ![]() $\#_e\gamma \le i(\gamma, \Sigma ).$ Hence,
$\#_e\gamma \le i(\gamma, \Sigma ).$ Hence, ![]() $i(\gamma,\Sigma ) = \ell (\gamma )$ for the action on
$i(\gamma,\Sigma ) = \ell (\gamma )$ for the action on ![]() $T$.
$T$.
We now obtain the CLT by applying Theorem 1.1 to this action. If ![]() $\sigma = 0$, then Theorem 1.1(iii) implies that the action
$\sigma = 0$, then Theorem 1.1(iii) implies that the action ![]() $\pi _1(M) \curvearrowright T$ is proper and hence vertex stabilizers are finite. However, this is impossible since only virtually free groups admit cocompact actions on trees with finite vertex stabilizers (see, for example, [Reference Scott and WallSW79, Theorem 7.3]).
$\pi _1(M) \curvearrowright T$ is proper and hence vertex stabilizers are finite. However, this is impossible since only virtually free groups admit cocompact actions on trees with finite vertex stabilizers (see, for example, [Reference Scott and WallSW79, Theorem 7.3]).
For the following application, let us assume ![]() $G$ is a hyperbolic group, let
$G$ is a hyperbolic group, let ![]() $\partial G$ be its Gromov boundary, and let
$\partial G$ be its Gromov boundary, and let ![]() $d$ be a metric on
$d$ be a metric on ![]() $G$. We define the growth rate of the metric
$G$. We define the growth rate of the metric ![]() $d$ as
$d$ as
and for each ![]() $s > v$ let us consider the measure on
$s > v$ let us consider the measure on ![]() $G \cup \partial G$:
$G \cup \partial G$:
 \begin{align*} \nu_s := \frac{\sum_{g \in G} e^{-s d(1, g)} \delta_{g}}{ \sum_{g \in G} e^{-s d(1, g)}}. \end{align*}
\begin{align*} \nu_s := \frac{\sum_{g \in G} e^{-s d(1, g)} \delta_{g}}{ \sum_{g \in G} e^{-s d(1, g)}}. \end{align*}
Then any limit point of ![]() $(\nu _s)$ as
$(\nu _s)$ as ![]() $s \to v$ is supported on
$s \to v$ is supported on ![]() $\partial G$ and is called a Patterson–Sullivan measure. By Coornaert [Reference CoornaertCoo93], any two limit measures are absolutely continuous with respect to each other, with bounded Radon–Nikodym derivative, so the Patterson–Sullivan measure class is well defined.
$\partial G$ and is called a Patterson–Sullivan measure. By Coornaert [Reference CoornaertCoo93], any two limit measures are absolutely continuous with respect to each other, with bounded Radon–Nikodym derivative, so the Patterson–Sullivan measure class is well defined.
The following rigidity statement about Patterson–Sullivan measures is essentially due to Furman [Reference FurmanFur02], at least in the torsion-free case. For the reader's convenience, we assemble a complete proof from results in the literature. Let ![]() $G\curvearrowright X$ be a properly discontinuous and cocompact action on a geodesic Gromov hyperbolic metric space
$G\curvearrowright X$ be a properly discontinuous and cocompact action on a geodesic Gromov hyperbolic metric space ![]() $(X,d)$. Let
$(X,d)$. Let ![]() $o\in X$, and
$o\in X$, and ![]() $\partial X$ be the Gromov boundary. Given
$\partial X$ be the Gromov boundary. Given ![]() $\zeta \in \partial X$, we define the Busemann function on the Gromov boundary by setting, for
$\zeta \in \partial X$, we define the Busemann function on the Gromov boundary by setting, for ![]() $x, y \in X$,
$x, y \in X$, ![]() $\mathfrak {b}_\zeta (x, y) := \liminf _{z \to \zeta } \beta _{z}(x, y)$, where
$\mathfrak {b}_\zeta (x, y) := \liminf _{z \to \zeta } \beta _{z}(x, y)$, where ![]() $z$ are points in
$z$ are points in ![]() $X$. A measure
$X$. A measure ![]() $\nu$ on
$\nu$ on ![]() $\partial X$ is called quasiconformal with respect to
$\partial X$ is called quasiconformal with respect to ![]() $d$ if there are constants
$d$ if there are constants ![]() $\alpha, C > 0$ such that
$\alpha, C > 0$ such that
for any ![]() $g \in G$,
$g \in G$, ![]() $\nu$-a.e.
$\nu$-a.e. ![]() $\zeta \in \partial X$. The constant
$\zeta \in \partial X$. The constant ![]() $\alpha$ is called the quasiconformal dimension of
$\alpha$ is called the quasiconformal dimension of ![]() $\nu$. The Patterson–Sullivan measure on the boundary of a hyperbolic group is quasiconformal with respect to the associated word metric [Reference CoornaertCoo93].
$\nu$. The Patterson–Sullivan measure on the boundary of a hyperbolic group is quasiconformal with respect to the associated word metric [Reference CoornaertCoo93].
Proposition 8.2 Let ![]() $G\curvearrowright X$ be a properly discontinuous and cocompact action on a metric space
$G\curvearrowright X$ be a properly discontinuous and cocompact action on a metric space ![]() $X$. Let
$X$. Let ![]() $d_1$ and
$d_1$ and ![]() $d_2$ be
$d_2$ be ![]() $G$-equivariant, geodesic, Gromov hyperbolic metrics on
$G$-equivariant, geodesic, Gromov hyperbolic metrics on ![]() $X$. Let
$X$. Let ![]() $\nu _1$ and
$\nu _1$ and ![]() $\nu _2$ be measures on
$\nu _2$ be measures on ![]() $\partial X$, quasiconformal with respect to
$\partial X$, quasiconformal with respect to ![]() $d_1$ and
$d_1$ and ![]() $d_2$, respectively. Then
$d_2$, respectively. Then ![]() $\nu _1$ and
$\nu _1$ and ![]() $\nu _2$ are in the same measure class if and only if there are constants
$\nu _2$ are in the same measure class if and only if there are constants ![]() $a,b>0$ with
$a,b>0$ with ![]() $|ad_1(x, y)-d_2(x, y)|\leq b$ for any
$|ad_1(x, y)-d_2(x, y)|\leq b$ for any ![]() $x, y \in X.$
$x, y \in X.$
Proof. Suppose ![]() $|ad_1-d_2| \leq b$. Then, letting
$|ad_1-d_2| \leq b$. Then, letting ![]() $\mathfrak {b}^{i}$ be the Busemann functions associated to
$\mathfrak {b}^{i}$ be the Busemann functions associated to ![]() $d_i$, we have
$d_i$, we have ![]() $|a\mathfrak {b}_\zeta ^{1}( \cdot, \cdot ) -\mathfrak {b}_\zeta ^{2}(\cdot, \cdot ) | \leq 2b$ for any
$|a\mathfrak {b}_\zeta ^{1}( \cdot, \cdot ) -\mathfrak {b}_\zeta ^{2}(\cdot, \cdot ) | \leq 2b$ for any ![]() $\zeta \in \partial X$. Therefore any
$\zeta \in \partial X$. Therefore any ![]() $d_1$-quasiconformal measure is
$d_1$-quasiconformal measure is ![]() $d_2$-quasiconformal and vice versa. By Coornaert [Reference CoornaertCoo93, Theorem 7.7], any two
$d_2$-quasiconformal and vice versa. By Coornaert [Reference CoornaertCoo93, Theorem 7.7], any two ![]() $d_1$-quasiconformal measures are absolutely continuous with bounded Radon–Nikodym derivative. Therefore
$d_1$-quasiconformal measures are absolutely continuous with bounded Radon–Nikodym derivative. Therefore ![]() $\nu _1$ and
$\nu _1$ and ![]() $\nu _2$ are in the same measure class.
$\nu _2$ are in the same measure class.
To prove the converse, we assume that ![]() $\nu _1, \nu _2$ are in the same measure class. First, we prove that their Radon–Nikodym derivative is bounded, as follows. As claimed in [Reference FurmanFur02] for the torsion-free case and proved by Bader and Furman [Reference Bader and FurmanBF17, Theorem 1.4] in general (see also [Reference Coulon, Dougall, Schapira and TapieCDST18, Theorem 4.1] for a generalization beyond cocompact actions), the action of
$\nu _1, \nu _2$ are in the same measure class. First, we prove that their Radon–Nikodym derivative is bounded, as follows. As claimed in [Reference FurmanFur02] for the torsion-free case and proved by Bader and Furman [Reference Bader and FurmanBF17, Theorem 1.4] in general (see also [Reference Coulon, Dougall, Schapira and TapieCDST18, Theorem 4.1] for a generalization beyond cocompact actions), the action of ![]() $G$ on
$G$ on ![]() $\partial X \times \partial X$ is ergodic with respect to
$\partial X \times \partial X$ is ergodic with respect to ![]() $\nu _i \times \nu _i$ for
$\nu _i \times \nu _i$ for ![]() $i = 1, 2$. By [Reference Coulon, Dougall, Schapira and TapieCDST18, Lemma 2.6], there exists for any
$i = 1, 2$. By [Reference Coulon, Dougall, Schapira and TapieCDST18, Lemma 2.6], there exists for any ![]() $i = 1, 2$ a rescaling
$i = 1, 2$ a rescaling ![]() $m_i$ of
$m_i$ of ![]() $d\nu _i \times d\nu _i$, known as Bowen–Margulis measure, which is
$d\nu _i \times d\nu _i$, known as Bowen–Margulis measure, which is ![]() $G$-invariant. Hence, by e.g. [Reference Gekhtman and TiozzoGT20, Lemma 5.2],
$G$-invariant. Hence, by e.g. [Reference Gekhtman and TiozzoGT20, Lemma 5.2], ![]() $\nu _1$ and
$\nu _1$ and ![]() $\nu _2$ have bounded Radon–Nikodym derivative.
$\nu _2$ have bounded Radon–Nikodym derivative.
Now, by the chain rule, the ratio between ![]() $ {dg\nu _1}/{d\nu _1}$ and
$ {dg\nu _1}/{d\nu _1}$ and ![]() $ {dg\nu _2}/{d\nu _2}$ is bounded independently of
$ {dg\nu _2}/{d\nu _2}$ is bounded independently of ![]() $g\in G$. Quasiconformality implies that there are
$g\in G$. Quasiconformality implies that there are ![]() $\alpha _1,\alpha _2,D>0$ such that
$\alpha _1,\alpha _2,D>0$ such that
for ![]() $\nu _i$-a.e.
$\nu _i$-a.e. ![]() $\zeta \in \partial X$ and every
$\zeta \in \partial X$ and every ![]() $g\in G$. Now recall that Busemann functions are coarsely continuous (see, for example, [Reference Coulon, Dougall, Schapira and TapieCDST18, Proposition 2.1]), that is, there exists
$g\in G$. Now recall that Busemann functions are coarsely continuous (see, for example, [Reference Coulon, Dougall, Schapira and TapieCDST18, Proposition 2.1]), that is, there exists ![]() $D_1$ such that
$D_1$ such that
for any ![]() $\zeta \in \partial X$, any
$\zeta \in \partial X$, any ![]() $x, y \in X$. Since the
$x, y \in X$. Since the ![]() $\nu _i$ have full support on the infinite
$\nu _i$ have full support on the infinite ![]() $\partial X$ [Reference CoornaertCoo93, Corollary 5.2], this implies that there exists
$\partial X$ [Reference CoornaertCoo93, Corollary 5.2], this implies that there exists ![]() $D_2$ such that
$D_2$ such that
for every ![]() $\zeta \in \partial X$ and every
$\zeta \in \partial X$ and every ![]() $g\in G$. Since
$g\in G$. Since ![]() $d_i(o,go)=\sup _{\zeta \in \partial X} \mathfrak {b}^{i}_{\zeta }(g o, o)$, we obtain
$d_i(o,go)=\sup _{\zeta \in \partial X} \mathfrak {b}^{i}_{\zeta }(g o, o)$, we obtain ![]() $|\alpha _1 d_1(o,go)-\alpha _2 d_2(o,go)| \leq D_2$. Since the action of
$|\alpha _1 d_1(o,go)-\alpha _2 d_2(o,go)| \leq D_2$. Since the action of ![]() $G$ is cocompact and the metrics
$G$ is cocompact and the metrics ![]() $d_i$ are
$d_i$ are ![]() $G$-equivariant, this implies
$G$-equivariant, this implies ![]() $|\alpha _1 d_1-\alpha _2 d_2| \leq D_3$ for some constant
$|\alpha _1 d_1-\alpha _2 d_2| \leq D_3$ for some constant ![]() $D_3$, as required.
$D_3$, as required.
Proof of Theorem 1.5 Since ![]() $G$ is word hyperbolic, it has a thick geodesic combing by Lemma 8.1(i). The first statement then follows immediately from Theorem 1.1, by considering the action of
$G$ is word hyperbolic, it has a thick geodesic combing by Lemma 8.1(i). The first statement then follows immediately from Theorem 1.1, by considering the action of ![]() $G$ on the Cayley graph of
$G$ on the Cayley graph of ![]() $G'$.
$G'$.
For the moreover statement, if ![]() $\sigma =0$, Theorem 1.1(iii) implies that
$\sigma =0$, Theorem 1.1(iii) implies that
is bounded independently of ![]() $g\in G$, hence
$g\in G$, hence ![]() $\phi$ has finite kernel.
$\phi$ has finite kernel.
Now consider the factorization ![]() $G \overset {\pi }{\rightarrow } \overline G : = ({G}/{\ker \phi }) \overset {\overline {\phi }}{\rightarrow } G'$, and define
$G \overset {\pi }{\rightarrow } \overline G : = ({G}/{\ker \phi }) \overset {\overline {\phi }}{\rightarrow } G'$, and define ![]() $\overline {S} := \pi (S)$. Then the Cayley graph of
$\overline {S} := \pi (S)$. Then the Cayley graph of ![]() $\overline G$ carries the two metrics
$\overline G$ carries the two metrics
and they satisfy
for any ![]() $g, h \in \overline {G}$. In particular,
$g, h \in \overline {G}$. In particular, ![]() $\phi \colon G \to G'$ is a quasi-isometric embedding and so it admits a continuous extension
$\phi \colon G \to G'$ is a quasi-isometric embedding and so it admits a continuous extension ![]() $\partial \phi \colon \partial G \to \partial G'$ to an embedding.
$\partial \phi \colon \partial G \to \partial G'$ to an embedding.
Now, by Proposition 8.2, inequality (11) holds if and only if the Patterson–Sullivan measure classes for ![]() $d_1$,
$d_1$, ![]() $d_2$ on
$d_2$ on ![]() $\partial \overline {G}$ are the same. Finally, if
$\partial \overline {G}$ are the same. Finally, if ![]() $\phi$ has finite kernel, there exists
$\phi$ has finite kernel, there exists ![]() $C > 0$ for which
$C > 0$ for which
for any ![]() $g, h \in G$. Hence, the Patterson–Sullivan measure class for
$g, h \in G$. Hence, the Patterson–Sullivan measure class for ![]() $(G, d_S)$ on
$(G, d_S)$ on ![]() $\partial G$ pushes forward to the Patterson–Sullivan measure class for
$\partial G$ pushes forward to the Patterson–Sullivan measure class for ![]() $(\phi (G), d_{S'})$ if and only if
$(\phi (G), d_{S'})$ if and only if ![]() $\sigma = 0$.
$\sigma = 0$.
Proof of Theorem 1.6 By Lemma 8.1(iii), a right-angled Artin or Coxeter group has a graph structure with respect to the vertex generating set, which is semisimple with only one maximal component. Hence, the CLT follows from Theorem 6.3 (see Remark 6.4). To complete the proof, we note that ![]() $\#_v(g)$ is equal to the displacement of
$\#_v(g)$ is equal to the displacement of ![]() $g$ with respect to the action of
$g$ with respect to the action of ![]() $G$ on the Bass–Serre tree for the hyperplane associated to
$G$ on the Bass–Serre tree for the hyperplane associated to ![]() $v$. The details are similar to those of Theorem 1.4.
$v$. The details are similar to those of Theorem 1.4.