INTRODUCTION
The investigations of transport and focusing of charged ion beams have a variety of important applications, such as warm dense matter physics (Ng et al., Reference Ng, Ao, Perror, Dharma-Wardana and Foord2005), high-energy-density physics (Drake, Reference Drake2006), and heavy ion fusion (Roy et al., Reference Roy, Yu, Henestroza, Anders, Bieniosek, Coleman, Eylon, Greenway, Leitner, Logan, Waldron, Welch, Thoma, Sefkow, Gilson, Efthimion and Davidson2005). For these applications, the ion beam should be simultaneously compressed in transverse and longitudinal direction to small spot sizes and short pulses, respectively, due to the reason that the power per unit area that delivered by the beam to the target is inversely proportional to the square of beam radius and the pulse duration. Also, the building cost of an ion beam driver dramatically decreases with the amount of compression (in space and time) that can be achieved.
Simulations (Kaganovich et al., Reference Kaganovich, Startsev, Sefkow and Davidson2007; Dorf et al., Reference Dorf, Kaganovich, Startsev and Davidson2009) and experiments (Henestroza et al., Reference Henestroza, Eylon, Roy, Yu, Anders, Bieniosek, Greenway, Logan, Macgill, Derek, Vanecek and Waldron2004; Roy et al., Reference Roy, Yu, Eylon, Henestroza, Anders, Bieniosek, Greenway, Logan, Waldron, Vanecek, Welch, Rose, Davidson, Efthimion, Gilson, Sefkow and Sharp2004; Reference Roy, Yu, Henestroza, Anders, Bieniosek, Coleman, Eylon, Greenway, Leitner, Logan, Waldron, Welch, Thoma, Sefkow, Gilson, Efthimion and Davidson2005) have proven that background plasma can be provided as an ideal media for ion beam focusing and transport. It is shown that for long, nonrelativistic ion beams, charge neutralization is complete even for very tenuous background plasmas (Kaganovich et al., Reference Kaganovich, Shvets, Startsev and Davidson2001). At the same time, experiments have shown that a 60-fold longitudinal pulse compression of ion beams can be achieved by applying a time-dependent velocity tilt to the charge bunch and subsequently allowing it to drift through background plasma (Roy et al., Reference Roy, Yu, Henestroza, Anders, Bieniosek, Coleman, Eylon, Greenway, Leitner, Logan, Waldron, Welch, Thoma, Sefkow, Gilson, Efthimion and Davidson2005). To our knowledge, most of these investigations focus on the compression of high energy ion beams. However, the low energy ion beams may be desirable because they can be produced more efficiently. In this paper, we are concerned with the self-modulation of low energy ion beam in background plasmas. As we shall demonstrate below, a low energy continuous ion beam can be compressed into short pulses of high densities by induced wakefield.
The wakefield induced by the propagation beam shows important impact on the beam transport and also the background plasmas. It can accelerate electrons to high velocities, as indicated in plasma-based wakefield accelerator scheme (Chen et al., Reference Chen, Dawson, Huff and Katsouleas1985; Caldwell et al., Reference Caldwell, Lotov, Pukhov and Simon2009), and influence the stability of ion beams. In addition to the wakefield driven by the ion beam, the wakefield driven by the laser pulse can also show important applications (Xie et al., Reference Xie, Aimidula, Niu, Liu and Yu2009; Bonatto et al., Reference Bonatto, Pakter and Rizzato2011). Krasovitskiy (Reference Krasovitskiy2008) investigated the self-bunching of relativistic electron beams in background plasmas. Kumar et al. (Reference Kumar, Pukhov and Lotov2010) developed an analytical model for the self-modulation instability of a long relativistic proton bunch, which can resonantly excite the wakefield needed for the Tev regime electron acceleration. There are few experiments devoted to observe this self-bunching effect until now. In this paper, we show that the wakefield excited by a low energy continuous ion beam can modulate the beam into periodic short pulses of high densities. The separation between the periodic pulses can be controlled by the plasma density and beam drift velocity. An enhanced longitudinal beam compression can be achieved by plasma density gradient due to the phase lock of ion pulses in the focusing regions of wakefield and reduced heating of plasma electrons. This phase lock effect by density gradient has been routinely used in both laser and plasma wakefield accelerations (Katsouleas et al., Reference Katsouleas1986; Geddes et al., Reference Geddes, Nakamura, Plateau, Toth, Cormier-Michel, Esarey, Schroeder, Cary and Leemans2008; Pukhov et al., Reference Pukhov, Kumar, Tuckmantel, Upadhyay, Lotov, Muggli, Khudik, Siemon and Shvets2011).
MODULATION IN UNIFORM PLASMAS
Now, consider the propagation of a continuous ion beam through uniform plasma with a constant density and drift velocity V b0 in the z-direction and a Gaussian shape in the radial r-direction. We can then obtain the wakefield inside the continuous ion beam from linearized fluid equations and Poisson's equation through Fourier transforming in both time and spatial space (Jones & Keinigs, Reference Jones and Keinigs1987),
$$\eqalign{{\rm E}_{\rm z} \left({{\rm r\comma \; {\rm \zeta} }} \right)& =- \displaystyle{{{\rm {\rm \rho}_{ b0}}} \over {{\rm {\rm \varepsilon} }_{\rm 0} {\rm k}_{\rm p} }}{\rm sin}\left({{\rm k}_{\rm p} {\rm {\rm \zeta} }} \right)\vint_{\rm 0}^\infty {{\rm k}_{\rm p} {\rm r}} {\rm ^{\prime}exp}\left({-\displaystyle{{{\rm r^{\prime}}^{\rm 2} } \over {{\rm r}_{\rm b}^{\rm 2} }}} \right){\rm I}_{\rm 0} \left({{\rm k}_{\rm p} {\rm r}_{\rm\lt } } \right)\cr & \quad {\rm K}_{\rm 0} \left({{\rm k}_{\rm p} {\rm r}_{\rm\gt } } \right){\rm d}\left({{\rm k}_{\rm p} {\rm r^{\prime}}} \right)}$$
where ρb0 is the peak beam density and r b is the beam radius. Here, 
${\rm {\rm \zeta}=V}_{{\rm b0}} {\rm t - z}$, 
${\rm k}_{\rm p} =\displaystyle{{{\rm {\rm \omega} }_{{\rm pe}} } \over {{\rm V}_{{\rm b0}} }}$, I 0 and K 0 are the modified Bessel functions of the first and second kind, respectively, and r < and r > denote, respectively, the smaller and larger of r and r′. In the longitudinal direction, an oscillation in the structure of wakefield can be clearly observed from Eq. (1). This oscillation wakefield can, in turn, show modulation effects on the structure of ion beam. As one can see, the wakefield induced by foregoing ions in the beam may show significant effects on the incoming ions. To show this modulation effects, we thus perform in the following two-dimensional electrostatic particle-in-cell (PIC) simulations. In the simulation, hydrogen plasma with mass ratio (m p/m e) = 1836 and plasma ion charge Z p = e is considered. Also the injection beam ions are taken to be protons with mass m b = 1836m e and charge Z b = e. The plasma and beam parameters adopted in the simulation are as follows. The proton beam with perveance 10−3, energy of 20 keV and current of 0.8 mA is assumed. The plasma temperature is taken to be T e = 10 eV and the plasma density is treated as a variable parameter in the simulation.
We first show in Figure 1 the density of a continuous ion beam propagating in uniform plasmas with different densities at time t = 4.2 ns. As the time progresses, the beam ions are continually injected into the plasma with the initial velocity prescription on the left boundary and absorbed as they reach the right boundary. One can clearly observe from all three figures that the initial continuous ion beam is modulated into periodic short ion pulses with a constant separation S b. The produced pulses have a period of typically about 1.2 ns with full width at half maximum (FWHM) of about 0.1 ns. Estimation can be made on the constant separation S b from Eq. (1) as 
${\rm S}_{\rm b} =\displaystyle{{{\rm 2}{\rm \pi} {\rm V}_{{\rm b0}} } \over {{\rm {\rm \omega} }_{{\rm pe}} }}{\rm \propto V}_{{\rm b0}} {\rm n}_{{\rm e0}}^{ - {{\rm 1} \over {\rm 2}}}$ and agreements between this analytical estimation and simulation results can be found in Figure 1. The modulation effect can be easily explained from the corresponding oscillation wakefield induced by the ion beam, as shown in Figure 2, where the oscillations with decreasing magnitude can be observed. This damping of the magnitude is due to the kinetic effects, which can not be included in fluid equations, but can be properly treated in particle simulations.
Fig. 1. The ion beam density propagating in uniform plasmas at time t = 4.2 ns in the cases of different plasma densities (a) n e0 = 2 × 1011 cm−3, (b) n e0 = 5 × 1011 cm−3, and (c) n e0 = 1012 cm−3. A continuous ion beam with initial drift velocity V b0 = 8 × 106(m/s), radius r b = 2.2 mm, and unperturbed density n b0 = 1.5 × 1011 cm−3 is assumed.
Fig. 2. The corresponding wakefield with the same parameters as in Figure 1.
In the oscillation wakefield, the beam ions are accelerated and decelerated by the positive and negative wakefield, respectively. One can see that the beam ions located in regions with maximum positive and negative field on the left and right, respectively, are compressed toward the zero field region in the middle as propagating through the plasma. While, the beam ions located in the regions with a revised field profile are defocused. In Figure 3, we show the on-axis ion beam density and wakefield at time (1) t = 1.8 ns and (2) t = 3.52 ns with the same parameters as in Figure 1b, except the unperturbed beam density adopted here n b0 = 3 × 1011 cm−3. One can clearly see from Figure 3a that the produced ion pulses are indeed located in the focusing regions of the wakefield.
Fig. 3. The on-axis ion beam density and wakefield at time (a) t = 1.8 ns and (b) 3.52 ns with the same beam and plasma parameters as in Fig. 1(b), except the unperturbed beam density adopted here n b0 = 3 × 1011 cm−3.
However, due to the self-consistent beam-plasma interaction, the ion beam and excited wakefield are modified, and difference arises between the phase and drift velocity of wakefield and ion pulses, respectively. The produced ion pulses then travel gradually into the defocusing regions of the wakefield, as shown in Figure 3b at time t = 3.52 ns. A large number of simulations are performed for uniform plasmas and similar conclusion is found. This indicates a maximum compression density that can be achieved in uniform plasma. Simulations with different beam and plasma parameters show that this maximum compression density has a close relation to the initial beam and plasma density for a fixed beam drift velocity. For a uniform plasma with density n e0 = 1012 cm−3, and an ion beam with initial density n b0 = 8 × 1010 cm−3 and drift velocity V b0 = 8 × 106(m/s) the maximum pulse density is shown to be n bmax ≈ 1.2 × 1012 cm−3, indicating a maximum density compression ratio R bmax = (n bmax/n b0) = 15.
Here, we are mainly concerned with the longitudinal focusing of ion beam. In the radial direction, the oscillation radial field is weak and the compression of the ion beam is not significant, due to the low beam velocity. Thus, for the focusing of low energy ion beam, one may first compress a long continuous ion beam into short ion pulses by background plasmas in the longitudinal direction, and then in radial direction through the magnetic lens (Roy et al., Reference Roy, Yu, Henestroza, Anders, Bieniosek, Coleman, Eylon, Greenway, Leitner, Logan, Waldron, Welch, Thoma, Sefkow, Gilson, Efthimion and Davidson2005). For relativistic ion beam, the longitudinal self-bunching is mainly caused by the transverse wakefield, due to the very anisotropic response of relativistic beam particles to longitudinal and transverse forces, as indicated by Kumar et al. (Reference Kumar, Pukhov and Lotov2010).
MODULATION IN NONUNIFORM PLASMAS
To further increase the density compression ratio, we propose to transport the continuous ion beam through nonuniform plasma with positive density gradient in the beam propagation direction. As we shall show in the following, by a plasma density gradient, the produced ion pulses can be locked in the focusing regions of wakefield, which is essential for continuous beam focusing. This scheme is also used in plasma wakefield acceleration using high energy ion pulses (Katsouleas et al., Reference Katsouleas1986; Pukhov et al., Reference Pukhov, Kumar, Tuckmantel, Upadhyay, Lotov, Muggli, Khudik, Siemon and Shvets2011).
Thus, we further investigate the propagation of ion beams in nonuniform plasmas with linear increasing density 
${\rm n}_{{\rm e0}} \left({\rm z} \right)={\rm n}_{{\rm e0}} \left({\rm 0} \right)\left({{\rm 1+a}_{\rm 0} \displaystyle{{\rm z} \over {{\rm L}_{\rm z} }}} \right)$, and make comparisons with the uniform case. Here, L z is the simulation length and 
${\rm a}_0 = \displaystyle{{{\rm L}_{\rm z} } \over {{\rm n}_{{\rm e0}} \left({\rm 0} \right)}}\displaystyle{{\partial {\rm n}_{{\rm e0}} } \over {\partial {\rm z}}}$ is a dimensionless quantity for describing the strength of density gradient. In the following simulations of nonuniform plasmas, we fix the simulation length and vary the plasma density to show the inhomogeneity effects. Figure 4a shows the on-axis wakefield induced by a continuous ion beam propagating in nonuniform plasma with density increasing linearly from n e0(0) = 2.7 × 1011 cm−3 on the left to n e0(L z) = 1012 cm−3 (a 0 = 2.7) at time t = 3.52 ns. For comparisons, the on-axis wakefield in the uniform plasma case (a 0 = 0) with unperturbed density n e0 = 1012 cm−3 is also displayed in the figure. The wakefield in nonuniform plasma case, with a rapid damping in the oscillation tail, is found to be three times smaller than that in uniform plasma case. As one can see, for plasma with inhomogeneity in the longitudinal direction, the region over which any given wave can experience growth is limited, due to the dependence of plasma frequency on the position. With this incoherence effect, one can expect a reduced magnitude and oscillation length of wakefield in the nonuniform plasma case. Similar characteristics can be found in the electron density profile, as indicated in Figure 4b.
Fig. 4. The comparisons of on-axis wakefield (a) and electron density (b) at time t = 3.52 ns between the cases of uniform plasma with unperturbed density n e0 = 1012 cm−3 and nonuniform plasma with density increasing linearly from n e0(0) = 2.7 × 1011 cm−3on the left to n e0(L z) = 1012 cm−3 (a 0 = 2.7) on the right. The corresponding on-axis ion beam density (c) at time t = 3.87 ns and radial distribution of two ion pulses with peak density in each case (the insert small figure) are also shown. A continuous ion beam with drift velocity V b0 = 8 × 106(m/s), beam radius r b = 0.2 mm and peak beam density n b0 = 3 × 1011 cm−3 is assumed in both cases.
With such wakefield structure, we further show in Figure 4c the corresponding on-axis ion beam density at time t = 3.87 ns. From the figure, the number of ion pulses produced by the longitudinal compression is seen to be reduced greatly, which can be readily explained from the limited oscillation length in the wakefield profile indicated in Figure 4a. The radial density distributions of two ion pulses with peak density in each case are also displayed in Figure 4c, where the radius of beam pulse in nonuniform case (r b ≈ 0.06 mm) is found to be smaller than that in uniform case (r b ≈ 0.085 mm). The compression of beam radius is not significant compared to the initial beam distribution, due to weak radial electric field.
It is important to note that the peak density of ion pulses that produced in nonuniform plasma (about 4.8 × 1012 cm−3) is approximately two times larger than that produced in uniform plasma (about 2.4 × 1012 cm−3) as indicated in Figure 4c, showing an enhanced compression by plasma density gradient. To further show this enhanced density compression, we show the time evolution of maximum pulse density in the cases of uniform plasma a 0 = 0, and nonuniform plasmas with a 0 = 1 and 2.7 in Figure 5. For all three cases, the background plasma density at the right boundary is fixed to be 1012 cm−3. From the figure, a linear growth following with an exponential growth of the pulse density can be observed before density saturation. As the density gradient a 0 increases, the maximum density that a beam pulse can reach increases significantly, indicating an enhanced compression by density gradient. Then, with a proper plasma length, one can obtain ion pulses of higher densities and smaller radius from nonuniform plasmas.
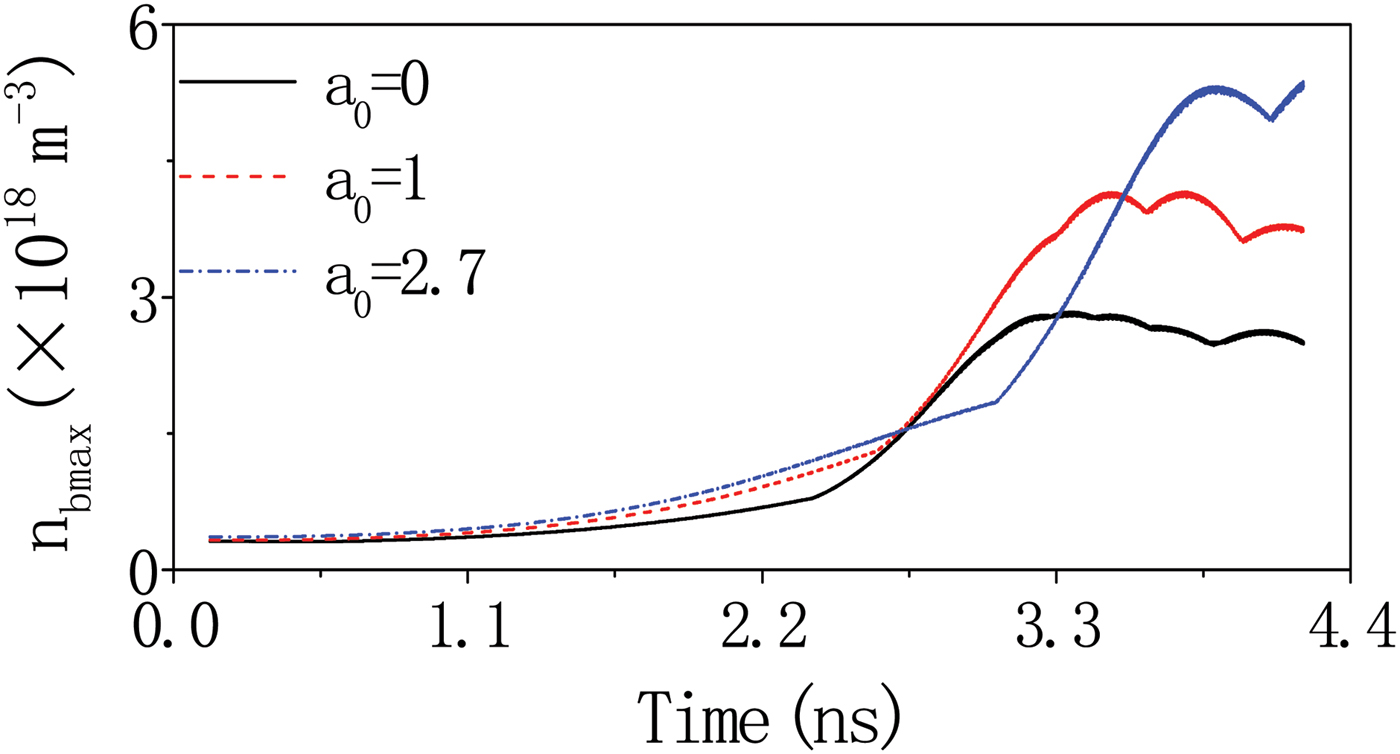
Fig. 5. The time evolution of maximum pulse density for density gradient a 0 = 0 (uniform plasma), 1, and 2.7, with the same beam parameters in Figure 4. For all three cases, the simulation length L z is the same and background plasma density at the right boundary is fixed to be 1012 cm−3.
Consider the wakefield induced by the initial unperturbed continuous ion beam moving up a plasma density gradient. Its wavelength will decrease according to 
${\rm {\rm \lambda} }_{\rm p} \approx \displaystyle{{{\rm 2{\rm \pi} V}_{{\rm b0}} } \over {{\rm {\rm \omega} }_{{\rm pe}} \left({\rm Z} \right)}}{\rm \propto n}_{{\rm e0}}^{ - {{\rm 1} \over {\rm 2}}} \left({\rm z} \right)$. Hence, as the ion beam progresses up the density gradient, the wakefield will appear to be compressed toward the beam head. Similar to the uniform plasma case, the produced ion pulses stay in the compression phase of wakefield at the early stage, as shown in Figure 6a. At the later stage, as shown in Figure 6b at time t = 3.52 ns, although the first ion pulse is located in the defocusing field, the following pulses are still in the focusing regions, due to the decreasing wavelength with increasing plasma density. This shows important difference to the case of uniform plasma as indicated in Figure 3b, where all the ion pulses have traveled into the defocusing regions. This difference should be the main reason for the enhanced compression by the density gradient.
Fig. 6. The on-axis ion beam density and wakefield at time (a) t = 1.8 ns and (b) 3.52 ns for the case of nonuniform plasma a 0 = 2.7. The beam and plasma parameters are the same as those of nonuniform plasma case in Figure 4.
As shown in Figure 4 of nonuniform plasma, the magnitude of wakefield decreases significantly due to the incoherence effect, which can suppress the heating of plasma electrons effectively. For beam focusing, any heating of plasma electrons should be avoided to get optimal compression, due to the decreased charge neutralization with increasing electron temperature. Thus, from the above discussion, we can see that the plasma with density gradient can effectively suppress the heating of plasma electrons, which can also lead to the enhanced ion beam compression.
CONCLUSIONS
In summary, we have performed two-dimensional PIC simulations to investigate the propagation of low energy continuous ion beams in background plasmas. Simulation results show that the continuous ion beam can be modulated into periodic short beam pulses by the induced wakefield, which can be adopted as a method to compress the ion beam in temporal space to short pulses. The separation between the periodic pulses can be controlled by the plasma density and beam drift velocity. Furthermore, plasma with density gradient in the longitudinal direction is proposed to transport the continuous ion beam and the produced ion pulse is found to have a higher density and smaller beam radius compared to that produced in uniform plasma. This is shown mainly due to the phase lock of ion pulses in the focusing regions of wakefield by plasma density gradient. Also, a decrease in the magnitude and oscillation length of wakefield is observed, leading to the reduced heating of plasma electrons.
ACKNOWLEDGMENTS
This work is supported by the National Basic Research Program of China (Grant No. 2010CB832901) and the Fundamental Research Funds for the Central Universities (DUT10ZD111).
