I. INTRODUCTION
In time-of-flight-based localization systems, the user's position can be determined by using the time-of-arrival (TOA) method. To distinguish between different users, code division multiple access (CDMA) signals are used. Major errors in the estimated position result from a bias in TOA values due to reflections, which lead to the motivation of our approach in achieving very precise TOA measurements to increase the overall accuracy of the localization system.
For static multipath environments, the maximum likelihood (ML) approach performs very well, and such estimators are capable to achieve theoretical limits given by the Cramer Rao bound. Several ML approaches, which address the multipath problem, have also been published in the literature [Reference Jones, Fenton and Smith2–Reference Weill5].
Our approach is motivated by iltis [Reference Iltis6] proposing joint estimation of delay and multipath coefficients. Here the channel is characterized by a time-varying tapped-delay line. As the estimator's objectives are communication systems, channel approximation is limited to the sampling instance. For localization systems, this restriction is not suitable.
Several waveforms and techniques for the accurate determination of TOA values have been investigated at Fraunhofer Institute for Integrated Circuits IIS. An internal research at the Fraunhofer Institute on TOA estimation has lead to a precise method for TOA calculation using inflection points on the correlation curve [Reference Hofmann7, Reference Hofmann and Breiling8], hereafter referred to as inflection-point method (IPM). Simulations have shown that the inflection point as characteristic point on the correlation performs better in terms of time resolution than the maximum. This algorithm is examined as reference for the new TOA estimator based on the unscented Kalman filter (UKF). In terms of performance the IPM can be compared to the pulse aperture correlator [Reference Jones, Fenton and Smith2] or the vision correlator [Reference Fenton and Jones1].
In this article, a robust TOA estimator suitable for dynamic multipath channels is presented. An overview of the used time-of-flight-based localization system and an introduction of the concept of Bayesian filtering, especially UKFs, is given. The main issue is the proposed estimator itself. Thereby emphasis is placed on the models describing the multipath channel, the state prediction and the measurement update, and the dynamic adaption of the state space to the time-varying channel. Simulation results evaluating data from synthetic channel models and measurement campaigns conclude this paper.
II. DESCRIPTION OF THE LOCALIZATION SYSTEM
The application of the localization system that is referred to is tracking players and balls in a soccer game or at the training grounds. The tracking system has been presented in [Reference Rohmer, Dünkler and von der Grün9] and Fig. 1 roughly shows the setup for the soccer application. Such an application has high demands on the accuracy of the positioning and on the dynamics of the moving targets. To incorporate the targets’ dynamics, the system can run at a rate of 2000 Hz for each transmitter which requires real-time data processing with low latency.
Fig. 1. Overview of the examined time-of-flight-based localization system.
The examined real-time localization system can be described as an inverted global navigation satellite system, i.e. receivers and transmitters switch positions. This way miniaturized and inexpensive tags with low power consumption can be used for the transmission of the localization signals. In order to differentiate between the users’ tags, direct-sequence spread spectrum techniques are used to realize code division multiple access to the channel. For this purpose pseudo noise sequences (so-called M-sequences) are used. However, Gold codes could be applied, too. Spreading also makes the localization system more robust against narrowband interference.
All receivers are synchronized by a common reference clock source. However, the time of transmission is unknown as the transmitters are not synchronized (free running oscillators). The time of transmission is not relevant for the position calculation thanks, to the use of the time difference of arrival (TDOA). TDOA values are obtained by calculating the difference of the TOA values to the TOA value of the receiver used as reference. Positions can be calculated by hyperbolic triangulation of TDOA values. Apparently errors in TOA values result in incorrect TDOA values, which finally lead to a bias in the calculated position of the transmitter. So, the TOA values have a dominant influence on the precision of time-of-flight-based localization system.
The transmitted signal is received by multiple antenna units located in direct proximity to the corresponding antenna and sampled at Nyquist rate. The sampled signal is transmitted via an optical network to the receiver units, which are arranged in a central computing cluster. Receiving units can be separated into hardware and software parts. The correlation of the received sequences is realized by a Field Programmable Gate Array (FPGA)-based hardware component. Acquisition (which is not subject to this paper) and rough tracking of the line-of-sight (LOS) path (i.e. extracting smaller correlation windows out of the data stream) is done by the correlation hardware.
The input of the TOA estimator is a correlation window which includes 60 complex samples roughly gathered around the hardware-detected LOS path (which not necessarily has to be the real LOS path). Both, the IPM and the UKF approaches are implemented in software running on the receiver units. Fig. 2 describes the integration of the TOA estimator into the localization system. After pre-processing of the correlation data, it is used for the filter initialization and the measurement in the update step of the UKF.
Fig. 2. Integration of the TOA estimator into the localization system.
III. IMPLEMENTATION OF THE ESTIMATOR
Optimal filtering, or Bayesian filtering, addresses the problem of estimating the state of a time-varying system that can be observed by measurements. Bayesian filtering [Reference Rohmer, Dünkler and von der Grün9–Reference Särkkä, Tamminen, Vehtari and Lampinen12] considers state estimation problems in the form
with mk being the unknown hidden state, which is indirectly observable by noisy measurements yk with known distribution given by p(yk | mk), and p(mK | mk−1) being the state transition PDF of the Markov process. As mk denotes the desired state, the objective is to describe the posterior probability density function (PDF) of a possible state representation given all observations p(mk | y1:k). For a given posterior PDF p(mk−1) | y1:k−1) at time k − 1, the prior PDF p(mk | y1:k−1) can be derived applying Chapman–Kolmogorov equation:
where p(mk | mk−1) is the PDF of the state transition used in the prediction step. In the update step, the successive posterior PDF is calculated applying the rule of Bayes to p(mk | yk, y1:k−1) leading to the normalized product of the likelihood p(yk | mk) and the prior PDF:
As the denominator is constant relative to mk, it can be computed by integrating the nominator over mk. In summary, the posterior PDF can be calculated recursively applying prediction and update starting with an initial value for p(m0 | y0) = p(m0).
The proposed TOA estimator is based on recursive Bayesian estimation [Reference Bar-Shalom, Li and Kirubarajan13–Reference van der Merwe15]. Since the journal paper [Reference Kalman16], optimal filtering has become quite popular in many fields, which lead to several different approaches addressed to non-linear problems like the extended Kalman filter, UKF, or sequential Monte Carlo methods. In particular, the UKF framework is used to realize the prediction and update steps of the estimator, as shown in Fig. 2 before. The UKF [Reference Julier and Uhlmann17] is a non-linear extension of the original Kalman filter [Reference Kalman16] which was designed for linear systems. As the UKF is based on the unscented transformation [Reference Julier, Uhlmann and Durrant-Whyte18], this method differs essentially from Monte Carlo methods (e.g. particle filters) as the sampling is done in a deterministic way [Reference van der Merwe, Wan and Julier19, Reference Wan and van der Merwe20].
A) Channel model for multipath environments
It is assumed that the complex baseband-equivalent signal reaching the receiver is equal to
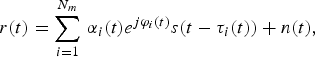
where s(t) is the transmitted CDMA signal, and α i(t)e φ(t) and τ i are the complex amplitudes and time delays, respectively, for each multipath component i. The received signal is disturbed by additive white Gaussian noise n(t). As the receiver includes a matched filter, the received and sampled signal r(k) is convoluted with the transmitted signal s(k).
The state vector mi,k for a single propagation path i covers delay, phase, and amplitude as well as delay and phase rates:
![{\bf m}_{i,k}=[\tau _{i,k} \;\varphi _{i,k} \;\alpha _{i,k} \;\mathop {\dot \tau }\nolimits_{i,k} \;\mathop {\dot \varphi }\nolimits_{i,k} ].\eqno (5)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn5.gif?pub-status=live){kind=small}
The first three parameters follow directly from the channel model above. Delay and phase rates are added to the state vector to incorporate frequency offsets between transmitter and receiver (clock drift of free running oscillators).
In order to model multiple propagation paths using just one Kalman filter, the state vectors of the propagations paths are stacked:
![{\bf m}_k=[{\bf m}_{1,k} \; \ldots \;{\bf m}_{N_m, k} ].\eqno (6)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn6.gif?pub-status=live){kind=small}
B) Process and measurement models
Process and measurement model are central parts of the UKF framework. The process model realizes the transition from the current timestep k − 1 to the next step k. The state prediction is a constant-velocity model:
As the process model is purely linear, the basic Kalman filter is used for the prediction of the state ahead. The prediction of the state mk− and its covariance Pk− can be obtained from the previous state using
where A denotes the transition matrix and Qk−1 the noise matrix of the linear process model.
Given the predicted state, the measurement model h is used to obtain the expected measurement
In an ideal case the output of the matched filter should be the autocorrelation of the transmitted signal.
Inside the measurement model the state vector mk is again divided into sub-states mi,k for each path. For simplicity mi,k will be denoted as mi.
The presented measurement model reconstructs the expected received signal by examining the ideal autocorrelation of the transmitted signal. The transmitted signal s(k) is convoluted with itself to obtain the autocorrelation C xx. The autocorrelation is upsampled by the factor f up = 8:
The estimated delay τ i is multiplied with the interpolation factor f up and rounded to the next integer
where the unit for the internal representation of the delay is the sampling interval (≈10ns). C xxReference Hofmann and Breiling8(τ iReference Hofmann and Breiling8) returns the upsampled autocorrelation for the given delay τ i. The autocorrelation is scaled and phase shifted according to α i and φ i from the state vector mi. The expected measurement μ i for one path can be expressed as
In this realization the precision is limited to the eighth of a sample for the delay τ i. But, on the other hand, the method can be implemented for higher time resolutions very efficiently by a lookup table. Thus, in general the measurement model has no limitations in terms of precision. The expected measurement μ can be calculated as the sum
of the expected measurements μ i of all individual propagation paths i. Sigma points Xk are determined according to [Reference Särkkä, Tamminen, Vehtari and Lampinen12, Reference Hartikainen and Särkkä21] for the predicted state mk with
![{\bf X}_k=\left[ {{\bf m}_k \cdots {\bf m}_k } \right]+\sqrt c \left[ {0\;\sqrt {{\bf P}_k } \; - \sqrt {{\bf P}_k } } \right],\eqno (15)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn15.gif?pub-status=live){kind=small}
where c = n + λ and 
is the square root of the covariance matrix. All sigma points are propagated through the non-linear function
where the function h is applied to each sigma point vector of the matrix Xk separately. The transformed sigma points are scaled according to their weights
and the Kalman gain can be computed using the matrix form [Reference Hartikainen and Särkkä21]:
![{\bf S}_k ={\bf Y}_k^ - {\bf W}[{\bf Y}_{k}^ - ]^T+{\bf R}_k, \eqno (18)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn18.gif?pub-status=live){kind=small}
![{\bf C}_k ={\bf X}_k^ - {\bf W}[{\bf Y}_{k}^ - ]^T, \eqno (19)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn19.gif?pub-status=live){kind=small}
The predicted state mean mk− and covariance Pk− are updated applying the Kalman filter equations:
![{\bf m}_k ={\bf m}_k^ -+{\bf K}_k [{\bf y}_k - \mu _k ],\eqno (21)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn21.gif?pub-status=live){kind=small}
The TOA value of the LOS path can be calculated directly from the estimated state by extracting the minimal delay
from the state vector mk. Triangulation of multiple TOA values leads to the user's position.
C) Dynamic adaption of the state space
In order to incorporate channel dynamics, the estimator has to be capable of adjusting the number of propagation paths. The filter's state space is dynamically adapted to the channel. An arbitrary number of propagation paths N m ∈ [1, N max] can be modeled by the TOA estimator. Initially, the UKF is set up with one propagation path which has not necessarily to be the LOS path. In case of changes in the dimension of the state space, the state vector as well as the transition and process noise matrices have to be resized.
The state vector mk and covariance Pk have to be adapted to the new dimension of state space. The same is necessary for the process noise Qk and the transition matrix A. After the measurement step of the Kalman filter, the expected measurement μ k is subtracted from the current measurement yk. Multiple criteria are verified on the remaining error signal
to determine candidates for new propagation paths. These candidates are approved in the next timestep to avoid instabilities and to determine good estimates for delay and phase rates. If a candidate passes all tests, the candidate's state vector ci,k is initialized for the new propagation path i and appended to the state vector:
![{\bf m}_k \leftarrow [{\bf m}_k \quad {\bf c}_{i,k} ].\eqno (25)](https://static.cambridge.org/binary/version/id/urn:cambridge.org:id:binary:20151022075027002-0349:S1759078711000274_eqn25.gif?pub-status=live){kind=small}
The noise and covariance matrices of the filter have to be resized accordingly.
For the reason of stability and to reduce the computational load propagation paths with delays out of range, negative amplitude, or weak signal strength are discarded. In this case sub-states are removed from the state vector. As mentioned before, the filter matrices have to be resized accordingly. Fig. 9 illustrates the tracking of multiple propagation paths and the channel dynamics.
IV. RESULTS
In order to demonstrate the performance of the proposed TOA estimator, we ran simulations and did field tests in indoor and outdoor environments. Evaluations of synthetic data show the theoretical limits of the formerly used IPM and the UKF approach. Indoor measurements show the channel sounding capabilities of the presented algorithm. Results from a measurement campaign in a soccer stadium reveal the superior performance of the UKF in comparison to the IPM. The error of the TOA value is significantly reduced in all evaluated scenarios.
All results have been generated running the filter algorithms in a Matlab environment on previously recorded data. The next sections will illustrate the results of the three scenarios which have been evaluated.
A) Simulations
To assess the performance of the presented approach in comparison to the IPM, a channel with two propagation paths has been simulated. Two propagation paths have been simulated with equal attenuation but varying delays and phases. Additionally, some white noise was added. However, because of the nature of pseudo noise sequences, the noise has no real significant impact on the simulations. Although the measurement noise is neglectable for synthetic data, no special parameterization of the UKF has been performed for the simulations. Since then simulation results would be lacking practical relevance.
Fig. 3 shows the performance of the IPM in an artificial multipath environment with two propagation paths. The extent of the TOA error depends on the phase and delay between the two simulated propagation paths. For the IPM the error in delay estimation does not exceed an absolute value of 7 ns. For larger path delays (>30 ns) no notable TOA errors exist.
Fig. 3. TOA estimation error for the IPM. The TOA error is shown for delays up to 50 ns and phases from 0 to 165° in steps of 15° between the two propagation paths. Both paths are equal in terms of signal strength.
The same channel is evaluated in Fig. 4 for the UKF. In comparison to the IPM the performance of the UKF is superior. Only minor errors exist in TOA estimation for delays, larger than 7 ns. For very short path delays, the modeled number of paths is reduced to one for stability reasons in some cases. Thus, a two-path channel is modeled by only one path that leads to a larger error of approximately e toa ≈ 0.5τ p1,p 2. For a smaller LOS amplitude, the benefit of the presented approach over the IPM is even larger.
Fig. 4. The proposed UKF tracking algorithm clearly outperforms the formerly used algorithm using the inflection point method (IPM). Especially for delays between 5 and 30 ns the UKF-based TOA estimator performs excellent.
Especially, if one compares the errors relative to the path delay in Figs 3 and 4, it becomes obvious that the IPM results in large TOA errors for delays below 25 ns whereas the UKF performs excellently for delays down to 7 ns with a relative error under 10%. In addition the error is not phase dependent for the UKF approach.
B) Indoor measurements
For the evaluation of the precision of delay and range estimation between propagation paths, we built a symmetric setup splitting the signal of one transmitter to two transmitting antennas with equal delays. Fig. 5 shows the setup we used for our simulations.
Fig. 5. Symmetric transmitter setup. RF splitters are used to distribute the transmitted signal to two antennas with known distance to generate defined path delays.
Measurements have been done with varying distances between the transmitter's antennas to generate different path delays between both propagation paths. From the estimated delays pseudo ranges are calculated and compared to the real distance between the antennas. Fig. 6 shows the measured delays for the setup described above, where the distance between the transmitter's antennas is 8 m. A snapshot of the received correlation and Kalman filter estimates of the channel is depicted in Fig. 7. Path-to-path delay measurements applying the UKF result in a mean of 26 ns ≈ 7.8 m. These results are remarkable as the measurements were taken in an indoor environment causing additional reflections, and the signal strength of the artificially delayed path is at a level of 20% compared to the LOS path. The estimation error is in the range of a few centimeters for this scenario.
Fig. 6. Delay estimation between two propagation paths. The distance between the transmitting antennas is 8m. Dark red lines show the LOS estimate and the light line denotes the reflected path.
Fig. 7. Snapshot of an indoor multipath channel. The UKF estimate is shown in red while the blue line denotes the measured signal. Dashed lines denote delay estimations.
C) Outdoor measurements in a soccer stadium
Simulation runs of the proposed TOA estimator on data from measurement campaigns show the performance of the new algorithm in comparison to the formerly used IPM. Even though this is an outdoor scenario, signals are massively disturbed by reflections from the ground, concrete walls, or metal slabs used for advertisement.
Fig. 8 depicts a real-world measured channel with strong multipath propagation. As seen in Fig. 9 the IPM is occasionally tracking the first or second echo, whereas the UKF estimator is tracking the LOS path throughout the whole measurement. Such a bias in the TOA results in a pseudo range error of 45 m, which indeed will have an extensive influence on the position accuracy of the overall localization system.
Fig. 8. Performance of the UKF tracking a moving target with up to N max = 4 paths in a dynamic multipath environment. The figure shows the direct path estimate of the UKF (red) and the estimate from the algorithm using the inflection point (blue).
Fig. 9. Comparison of tracking performance of the UKF (red) and inflection point algorithm (blue). Dark lines show the LOS estimate and light lines denote the reflected paths. Up to three delayed propagation paths are tracked in addition to the LOS path by the UKF.
A snapshot of the channel discussed before can be seen in Fig. 10. The channel is characterized by a weak LOS path and some non-linear distortions. The IPM is tracking the first replica. Estimating the channel parameters of the multipath channel, the UKF is able to eliminate the influence of reflected paths and distortions on the TOA value.
Fig. 10. Snapshot of an outdoor multipath channel. The UKF estimate is shown in red whereas the blue line denotes the measured signal. Dashed lines denote delay estimations.
V. CONCLUSION
In this paper we have proposed an algorithm for the precise determination of the TOA value of a user's signal in case of multipath propagation. By modeling the channels multipath characteristics, the error in the TOA value due to reflections can be reduced considerably. We have demonstrated how sequential Bayesian estimation methods can be applied to the problem of multipath mitigation in localization systems. Results on synthetic and measured data confirm the benefit of the proposed TOA estimator. Furthermore, the estimator can be used for the purpose of channel parameter estimation and tracking.
As the results of the TOA estimator promise a significant gain in the overall positioning accuracy, the filter algorithms are currently being ported from Matlab to C ++ and integrated into the localization system to meet the high demands of real-time data processing. Further research work will involve benchmarking the positioning accuracy using the UKF TOA estimator and the IPM with reference data sets. Optimization of the filter models and parameterization will also be a subject of future work.
Thorsten Nowak received his diploma in engineering from the University of Ulm, Germany, in 2009. Since 2008, he is with Fraunhofer Institute for Integrated Circuits. He is a research assistant at the RF and Microwave Design Department within the Wireless Location Systems Group, where he is working on multipath mitigation techniques and multisensor data fusion. His research interests include wireless communications, signal processing, and localization position systems. Further interests are in the fields of communication systems and software development.
Andreas Eidloth received his Dipl.-Ing. degree in electrical engineering from the Friedrich-Alexander University of Erlangen-Nurem berg in 2005. Since then he is employed at the Fraunhofer-Institute for Integrated Circuits IIS in Erlangen. He is working at the RF and Microwave Design Department within the Wireless Location Systems Group. His fields of work are system design of time-of-flight radio localization systems, localization algorithms, and system simulation.
