I. INTRODUCTION
Filters in microwave systems must provide not only maximum transmission in the passband, but also as much isolation as possible in the stopband. However, owing to their distributed form, as well as the notorious inequality of even- and odd-mode phase velocities, microstrip coupled-line filters often suffer from spurious responses in the stopband, especially at the harmonics of the center frequency. This has inspired researchers to develop various means of effectively suppressing spurious responses in the stopband [Reference Lin, Ku, Wang and Chen1–Reference Hung, Weng, Lan and Huang22]. For instance, a bandpass filter is constructed with a combination of low- and high-pass filters [Reference Lin, Ku, Wang and Chen1]. Although this may be a simple solution to improve the stopband response, the filter suffers from relatively large size and high insertion loss. To resolve these problems, a complementary split-ring resonator (CSRR) can be utilized to reject the harmonic responses without increasing loss and circuit size [Reference Karthikeyan and Kshetrimayum2–Reference García-García5]. However, an optimization process through time-consuming full-wave simulation is required to compensate for the altered passband performance. While the popular defected ground structure (DGS) [Reference Ardakani, Fallahzadeh and Rashed-Mohassel6–Reference Kumar and Machavaram9] or its variations such as inductive compensation [Reference Phromloungsri, Chongcheawchamnan and Robertson10], stepped-impedance structure [Reference Denis, Person, Toutain, Theron and Vigneron11], and wiggly line [Reference Lopetegi12] can be utilized to equalize the even- and odd-mode phase velocities, its effect is limited to suppression of spurious response at the second harmonic of the center frequency only. A wider bandwidth of spurious suppression can be realized with miniaturized coupled-line filters [Reference Lee and Lee13–Reference Myoung and Yook15]. As the lengths of the coupled lines are reduced, the frequencies of spurious response are shifted to higher frequencies. This leads to improved out-of-band performance. However, the enhancement is limited since excessive reduction of coupled lines requires coupling that is too tight to realize. This work demonstrates two methods of constructing microstrip filters with coupled lines of incommensurate lengths. With the length of each coupled-line section, the frequencies of not only resonance, but also transmission zeros can be controlled. Therefore, when the coupled lines in a microstrip are of different lengths, these frequencies do not overlap. This allows substantial enhancement in the stopband response, without having to reduce the lengths of the coupled lines extremely. The previous method in [Reference Sanchez-Soriano, Torregrosa-Penalva and Bronchalo16] that is also based on coupled lines of different lengths improves stopband response by designing these lines to suppress coupling between two resonators at the harmonics of the resonant frequencies. Therefore, it relies largely on full-wave simulations to calculate the coupling coefficients. Furthermore, the method is valid for coupled-line filters only, whereas the proposed method can be applied to any type of filters that can be synthesized using inverters and resonators, including transmission-line filters [Reference Yim, Wong and Cheng17, Reference Ha, Lee, Min and Lee23]. Most importantly, size reduction accompanies the proposed method, which can be controlled at the initial design step. For verification of the proposed method, experimental results are provided that maintain the transmission level below −20 dB up to as high as 11.9 f 0 for a third-order filter, where f 0 is the center frequency.
II. DESIGN PROCEDURES
Figure 1(a) shows the schematic of an N th-order filter that consists of (N + 1) reduced-length (θ i < 90°) coupled lines. The reduction in the length is compensated by inductive loading. Detailed conditions of length reduction are given by equations (20) and (21) in [Reference Lee and Lee13]. Figure 1(b) shows the equivalent circuit of the filter based on K inverters and resonators.
Fig. 1. Nth-order inductively loaded coupled-line filter.
A) Non-overlapping resonant frequencies
For a conventional bandpass filter based on equi-length ideal coupled lines of 90°, spurious response occurs at the odd harmonics of the center frequency where all resonators of its equivalent circuit resonate. On the other hand, spurious response of the filter in Fig. 1(a) occurs at a higher frequency since it consists of reduced-length coupled lines. For instance, when all sections are reduced to 60°, the lowest frequency that the identical resonators resonate is 3.44 f 0, where f 0 is the center frequency.
Moreover, by designing each coupled line with a different length, each resonator can be made to resonate at different frequencies. Since the resonant responses of all coupled-line sections do not add up constructively at a certain frequency, no distinctive transmission will be seen in the stopband, and the transmission will be maintained at low levels. The resonant frequencies of an inductively loaded coupled-line section can be calculated by finding the frequencies at which the reactance of each resonator vanishes.
$$X_1 = - \lpar Z_{0e\comma 1} + Z_{0o\comma 1} \rpar {\rm cot}\theta _1 + \omega L_1\comma \; $$
$$\eqalign{X_{i + 1} & = - \lpar Z_{0e\comma i} + Z_{0o\comma i} \rpar {\rm cot}\theta _i - \lpar Z_{0e\comma i + 1} + Z_{0o\comma i + 1} \rpar {\rm cot}\theta _{i + 1} \cr & \quad + \omega \lpar L_i + L_{i + 1} \rpar \comma \; } $$
$$X_{N + 2} =- \lpar Z_{0e\comma N + 1} + Z_{0o\comma N + 1} \rpar {\rm cot}\theta _{N + 1} + \omega L_{N + 1}\comma \; $$where i = 1,2, …, N.
Equations (1)–(3) imply that the frequencies at which X vanishes can be controlled by the length of each coupled-line section, θ i. Therefore, by carefully choosing θ i, so that these frequencies do not overlap, substantial improvement in the stopband response can be achieved. Although rigorous mathematical analysis remain as future work, to the authors' experience, no major difference in the enhancement of stopband response is observed as long as no more than two resonant frequencies are included in a 0.5 GHz bandwidth for filters at low-GHz frequencies.
Figure 2 shows the resonant frequencies calculated by (1)–(3), which are compared with the frequencies of spurious responses in ideal-circuit simulation results, for a third-order 0.1-dB Chebyshev filter with 10% bandwidth and θ 1 = 75.35°, θ 2 = 42.97°, θ 3 = 54.73°, and θ 4 = 66.94°. The frequencies are normalized by the center frequency. As can be seen, the calculated resonant frequencies and the frequencies of spurious response from ideal simulation results match exactly. This implies that the frequencies of spurious response can be controlled by the lengths of coupled lines, since the resonant frequencies are governed by the lengths. By designing a filter such that all coupled lines are of incommensurate lengths, these resonant frequencies can be distributed over a wide bandwidth. Since the resonant responses do not add up constructively, no distinctive transmission occurs at a certain frequency, and therefore a substantial improvement in the stopband can be accomplished.
Figure 3 shows the ideal transmission characteristic for the same filter. For comparison, transmission for the same filter but consisting of equi-length (θ i = 60°) inductively loaded coupled lines while maintaining the same total length of 240°, as well as conventional θ i = 90° coupled lines is also shown. Results show that while the passband characteristics are maintained perfectly, the stopband response is improved substantially without any periodic spurious responses.
Fig. 3. Ideal simulation results of proposed filter (Filter A) with θ 1 = 75.35°, θ 2 = 42.97°, θ 3 = 54.73°, θ 4 = 66.94°, and total length of 240° for non-overlapping resonant frequencies, with equi-length (θ i = 60°) inductively loaded coupled lines and total length of 240°, and with conventional coupled lines of θ i = 90° and total length of 360°. All filters are 0.1 dB Chebyshev-type with 10% bandwidth.
B) Non-overlapping frequencies of transmission zeros
Microstrip-coupled lines are notorious for unequal even- and odd-mode phase velocities. One of the consequences of this is that when a filter is constructed with 90° microstrip-coupled lines, a transmission zero occurs around, and in general at frequencies slightly higher than, the even harmonics of the center frequency. Taking advantage of this for the improvement of the stopband response, a microstrip filter can be constructed with incommensurate coupled lines, so that the frequencies of the transmission zeros do not overlap. The distributed transmission zeros will interfere destructively with spurious responses, therefore allowing significant improvement in the stopband response. The optimum combination of electrical lengths will provide suppression of spurious response over a substantially wide bandwidth.
To determine the optimum combination of coupled-line lengths, the frequencies of the transmission zeros must first be calculated for a given microstrip-coupled line. This can be done simply with a circuit simulator, an example of which is given in Fig. 4, which shows the frequencies of the first four transmission zeros with respect to the electrical length of a coupled line with Z 0e = 129.7 Ω and Z 0o = 79.3 Ω in an RF-35 substrate from Taconic with ε r = 3.5 and a thickness of 0.76 mm. This is the first section of the example third-order 0.1-dB Chebyshev filter with a 10% bandwidth, of which the microstrip simulation results are shown in Fig. 5. Based on the frequencies of the transmission zeros for all sections, the optimum combination of electrical lengths can be determined through iterative simulation. For the widest possible bandwidth, to the authors' experience, no more than two transmission zeroes should occur within a 0.5 GHz band for filters at low GHz frequencies.
Fig. 4. Frequencies of transmission zeros (TZ) for reduced-length, inductively loaded microstrip-coupled line with Z 0e = 129.7 Ω, Z 0o = 79.3 Ω in substrate with ε r = 3.5 and h = 0.76 mm.
Fig. 5. Microstrip simulation results of the proposed filter (Filter B) with θ 1 = 90°, θ 2 = 48°, θ 3 = 29°, θ 4 = 73°, and total length of 240° for non-overlapping frequencies of transmission zeros, with equi-length coupled lines (θ i = 60°) and total length of 240°, and with conventional coupled lines of θ i = 90°. All filters are 0.1 dB Chebyshev-type with 10% bandwidth.
The lengths of coupled lines of the proposed filter, shown in Fig. 5 are θ 1 = 90°, θ 2 = 48°, θ 3 = 29°, and θ 4 = 73°, with a total length of 240°. Also shown are the microstrip simulation results for another inductively loaded microstrip filter with a total length of 240°, but with equi-length (θ i = 60°) coupled lines, as well as a conventional filter with θ i = 90° coupled lines. Comparison reveals that although the passband performance remains nearly intact, a remarkable enhancement in stopband response can be observed.
To investigate the sensitivity of the proposed filters on fabrication tolerances, Monte Carlo analysis with 250 iterations has been performed for both filters. Figure 6 shows the results of the ideal and the worst responses due to 5% tolerance in the inductance of all inductors. Results reveal that although the passband may be shifted in frequency, its effect is negligible on the stopband response for both filters. The effects on passband response can be relieved by making the total length longer since then the required reactance or susceptance is smaller. Although it is not shown here, similar trends are observed with other practical errors such as dimensional errors as well as the Q factors of inductors: the improvement in the stopband response remains virtually intact, whereas the effects on passband response may not be negligible.
Fig. 6. Effects of ±5% tolerance in inductance from stochastic simulation.
III. EXPERIMENTAL RESULTS
For experimental verification, the proposed filters shown in Fig. 3 (Filter A) and Fig. 5 (Filter B) and centered at 1 GHz are designed and fabricated in an RF-35 substrate from Taconic with ε r = 3.5 and a thickness of 0.76 mm. Layout optimization is achieved with high frequency structural simulator (HFSS) to compensate for parasitic effects associated with the 0603-sized SMD-type inductors, as well as the junction discontinuities. Figure 7 shows a photograph of the fabricated filters, the design parameters of which are summarized in Table 1. The filters are measured in the 0.5–20 GHz range with a 37247D vector network analyzer from Anritsu. The results shown in Fig. 8 demonstrate that while the passband response is maintained, the transmission remains below −40 dB up to 7 f 0 and 6.4 f 0, and below −20 dB up to 11.9 f 0 and 8.8 f 0, for Filters A and B, respectively, where f 0 is the center frequency. The improvement in the measured stopband response may be somewhat less evident than in the circuit-simulated results in Figs 3 and 5. This is mostly due to the parasitic effects of the lumped inductors that need to be modeled more accurately in such a wide bandwidth of spurious suppression. This is especially important since the parasitic effects become much more detrimental as the frequency increases. Nevertheless, both filters show substantial improvement in the stopband response that has rarely been achieved with third-order coupled-line filters. Additionally, further improvement in the passband performance is expected with more accurate modeling of the lumped inductors.
Fig. 7. Photograph of fabricated filters.
Fig. 8. Measured and full-wave simulated results. Solid–: proposed with 240° total length, dash dot -.-: equi-length (θ i = 60°) with 240° total length, dotted …: conventional with θ i = 90°, thin-solid–: full-wave simulated results of proposed filters.
Table 1. Electrical parameters of demonstrated filters.
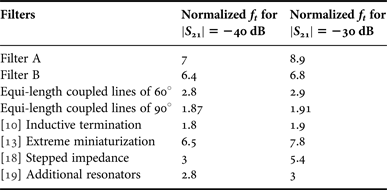
Table 2 compares the stopband performance of the proposed filters with those of state-of-the-art third-order coupled-line filters with enhanced stopband performance. As seen, the proposed filters show unprecedented stopband performance that cannot be matched by other methods of suppressing spurious responses, comparable only with the one that has a substantially shorter total length of 122° [Reference Lee and Lee13]. The performance of Filter A, which is based on non-overlapping resonant frequencies, can be improved further by reducing the total lengths, since the frequencies of resonance are then shifted to higher frequencies. In addition, further enhancement of Filter B is expected by increasing the number of stages, since more frequencies of transmission zeroes can then be employed. However, accurate modeling of the lumped elements over the very wide bandwidth of spurious suppression must be accompanied for both cases.
Table 2. Comparison of stopband performance of N = 3 coupled-line filters.
IV. CONCLUSION
Simple yet effective methods of improving the stopband response in microstrip coupled-line filters are demonstrated. With the length of each section, the frequencies of the resonance or transmission zeros can be controlled. Therefore, with coupled lines of incommensurate lengths, a microstrip filter can be designed so that the resonant responses do not add up constructively at a certain frequency. In addition, the length of each section can be chosen so that the frequencies of the transmission zeros are distributed to suppress spurious responses over a wide bandwidth. Both approaches lead to substantial enhancement of the stopband response over a wide bandwidth. Experimental results verify the effectiveness of the proposed methods. The methods are fully compatible with the conventional filter synthesis method based on inverters and resonators, allowing for a very systematic design procedure to develop filters with various types of coupled lines [Reference Lee and Lee13–Reference Myoung and Yook15, Reference Ha, Lee, Min and Lee23] as well as transmission lines [Reference Yim, Wong and Cheng17, Reference Ha, Lee, Min and Lee23]. Moreover, the filter has a compact size with superior stopband performance that can be predicted easily. Finally, experimental results are demonstrated in which the transmission level is maintained below −20 dB up to as high as 11.9 f 0, where f 0 is the center frequency. This outperforms all previous methods of enhancing the stopband response for microstrip coupled-line filters, which can be improved even further by reducing the total length or by increasing the number of stages.
ACKNOWLEDGEMENTS
This work has been supported by the Low Observable Technology Research Center program of Defense Acquisition Program Administration and Agency for Defense Development.
Sang-Ho Lee received his B.S. and M.S. degrees from Yonsei University, Seoul, Korea, in 1998 and 2000, respectively, and now he is working toward the Ph.D. degree in Electrical and Electronic Engineering at Yonsei University, and working for Korea Evaluation Institute of Industrial Technology. His current research interests include passive and active circuits for various microwave applications.
Hobyung Yoon received his B.S. degree from Chungnam National University, Daejeon, Korea, in 2010, and the M.S. degree in Electrical Engineering from Yonsei University, Seoul, Korea, in 2013, and now he is currently working with LG Chem Ltd., Daejeon, Korea. His current research interests include various planar circuits for microwave applications.
Jungje Ha received his B.S. and M.S. degrees from Yonsei University, Seoul, Korea, in 2009 and 2011, respectively, and he is currently working toward the Ph.D. degree in Electrical and Electronic Engineering at Yonsei University. His current research interests include multi-band planar circuits and systems for microwave applications.
Yongshik Lee received his B.S. degree from Yonsei University, Seoul, Korea, in 1998, and M.S. and Ph.D. degrees in Electrical Engineering from The University of Michigan at Ann Arbor in 2001 and 2004, respectively. In 2004, he was a postdoctoral research associate at Purdue University, West Lafayette, IN. From 2004 to 2005, he was with EMAG Technologies, Inc., Ann Arbor, MI, as a Research Engineer. In September 2005, he joined Yonsei University, Seoul, Korea, where he is currently an Associate Professor. His current research interests include passive and active circuitry for microwave and millimeter-wave applications, and electromagnetic metamaterials.
