1. INTRODUCTION
The experimental studies of a hydrodynamic instability between two
media of different densities at their accelerated motion have been
successfully conducted for the case of incompressible media at moderate
physical parameters (Kucherenko et al.,
1991; Youngs, 1992; Schneider et al., 1998).
The basic goal of the present study was to define the quantitative
characteristics of the given phenomenon developing in compressible
media.
2. THE EXPERIMENTAL SETUP
The investigation was carried out in a vertical tube closed at both
ends (Zaytsev et al., 1991). The
sketch of the setup is given in Figure 1.
Prior to the experiment, the tube was hermetically divided into two
parts with a plate P. After evacuation of the tube its upper part B was
filled with a combustible mixture (gas B, density
ρb), the lower part was filled with gas A
(density ρa [gl ] ρb).
The pressure of gases A and B was precisely set at 0.5 bar. As a
combustible mixture, we use the hydrogen–oxygen mixture
(0.45H2 + 0.55O2).
The sketch of the experimental setup. 1: channel (inner section 72
× 72 mm2, full length l = 1010–730 mm,
length of the upper part lk = 63.5 cm). 2,
3: upper and lower endwalls. 4: ignition spark. P: dividing
plate. F: flame front, B0: combustible
mixture. A0: inert gas.
K0b, K0a:
interfaces, separating the initial mixing zone from “pure”
gases.
After removing the plate P from the tube, a mixing zone K0
forms and the combustion of gas B is initialized. The flame front F,
descending in the tube, generates a compression wave C in gas B. As a
result of interaction of C with the mixing zone K0, the
latter accelerates downward. The refracted compression wave, being
reflected on the bottom plate of the tube, forms the reflected
compression wave that moves towards the mixing zone. The interaction of
the reflected compression wave and the mixing zone results in the
deceleration of the latter.
The diagnostic of the process is carried out using Mach–Zehnder
interferometry. The flow patterns in the tube and the density
distribution in vicinity of K at the stages of accelerated and
decelerated motion were defined.
3. FUNDAMENTAL REGIMES OF THE MIXING ZONES
EVOLUTION
The flame front F acquires a meniscus form during its motion in the
tube. A characteristic peculiarity of the motion of the meniscus-shaped
flame front F is the formation of one-dimensional flow—a planar
compression wave—ahead of F at a distance over a few diameters of
a tube (Salamandra, 1974). The analysis of
the motion shows that the essential changes of the flow parameters come
from the dilatation of the combustion products behind F. This process
determines the properties of the incident compression
wave—C0. The distribution of parameters within
C0 is modulated by a system of secondary compression
waves.
The existence of secondary compression waves is clearly recorded in
gases A, which have a large enough value of refraction coefficient (see
Fig. 2). The density change in the front of
secondary compression waves turns out to be smaller than in the
incident compression wave—C0. The secondary system of
compression waves results from the interaction of the meniscus-shaped
flame front with the lateral walls of the channel.
Interferograms of the mixing zone motion, K, separating the
combustible mixture from SF6 (p0 = 0.5
bar, g ≈ 1.3 cm·s−2).
CT: front of the first from the set of
refracted compression waves.
If the length of the upper part of the channel filled with the
combustible mixture does not exceed a given threshold, then the
compression wave C0 during its motion does not succeed in
turning into a shock wave. In that case, the initial mixing zone
K0 is involved in the accelerated motion by the compression
wave. Hence, the following regimes of continuous acceleration of the
mixing zone K are possible (see Fig. 3).
Possible regimes of interaction between the mixing zone K and
refracted CT and reflected CR compression
waves.
3.1. ρa >
ρb
In this case, the direction of gravitational acceleration coincides
with the direction of the density gradient and the mixing zone
K0 stays hydrodynamically stable until the beginning of the
interaction with the compression wave C0 (t =
t0). For t ≥ t0 the
mixing zone K is accelerated down the channel by the incident
compression wave. Here an effective gravitational field directed upward
appears. The value of the acceleration of this field is
|g1| ≃
104g0, where g0 is
the acceleration of the Earth's gravity. The Rayleigh–Taylor
instability, (RTI), is excited in the mixing zone K
(∇ρ·∇p < 0).
The RTI development continues until the moment t =
tQ, when K deceleration, created by the
interaction with the reflected compression wave CR, begins.
For t ≥ tQ RTI “is
switched off” as the effective gravitational field turns in the
downward direction (∇ρ·∇p < 0). The
value of this acceleration field is
|g2| ≃
104g0. At this stage of the mixing zone
evolution, a “stratification” process “is switched
on”—separation in the field of effective gravitation.
At t = t, the mixing zone K reaches the
section l = l, located at the minimum
distance from the lower end of the channel. Later the mixing zone
oscillates near I under the action of
reverberating compression or rarefaction waves.
3.2. ρa <
ρb
The change of the density gradient direction results in excitation of
the hydrodynamic instability in the mixing zone K0 in the
Earth's gravitational field (acceleration g0).
This state continues until the compression wave arrival. In the stage
of accelerated motion at t0 < t <
tQ, K is subjected to an effective field
(|g2| ≃
104g0), in the upward direction. Here
the RTI “is switched off”
(∇ρ·∇p < 0). K is subjected to a
compression, created by C0.
In the deceleration stage created by the interaction of K with
CR at tQ < t <
t, the RTI is excited and developed, as
∇ρ·∇p < 0.
Having reached the closest proximity from the lower channel plate
(section l) K oscillates under the action of
reverberating waves in the compressed gas A.
4. THE INITIAL MIXING ZONE: MEASURED
PARAMETERS
The plate P is removed from the channel with the help of a spring
mechanism. The full time of removal of P from the channel ranges from
40 to 100 ms. The thickness of K0 is determined by a
diffusion coefficient of the gases A and B and by the time of mixing.
The resulting mixing zone has the form of a layer that becomes thinner
in the direction of the plate motion. The undulating perturbances on
borders of the layer occur when the Reynolds number (Re =
udv−1, where u is a flow velocity,
d is a thickness of plate P, and v is a viscosity of
gas A) exceeds 100. In Figure 4, a schematic
representation of the mixing zone is given and the characteristic
points Ji, Bj
are indicated on the surfaces separating the mixing zone K0
from gases B and A. The coordinates of the indicated points are used
for definition of the following parameters of the mixing zone:
amplitude ai maximum penetration depth of
one gas into the other Li wave lengths of
the chosen perturbation λi, trajectory of the
mixing zone motion xk(t),
thickness of mixing zone δi:
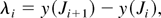
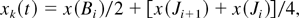
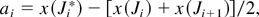
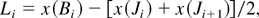
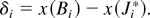
A scheme of the initial mixing zone. Ji,
Ji*, Ji+1,
Bi: position of characteristic
points.
The value λi for the initial mixing zone
decreases roughly by a factor of 2 along the direction of the plate
motion (y axis). Near the channel axis (y = 36 mm),
the quantity λi has the following values: 20,
18, 15, 12, 9, and 6 mm ±2 for He, Ne, Ar, Kr, Xe, and
SF6, respectively, when the full time of the plate P removal
equals 100 ms.
5. ONE-DIMENSIONAL MODEL
A flame front simulation is carried out using the subsequent heat
release in the domain filled with the combustible mixture (gas B). In
this domain, each cell of the computational mesh contains a source that
releases a distributed quantity of energy q(x). This
energy is released in a precise time evolution such that the
temperature in a given cell reaches the level of ignition temperature
Ti. The temperature change in gas B comes
as a result of the temperature wave propagation resulting from the
energy release in the cells where combustion took place.
The flow in the channel closed at two ends is described by the system
of conservation equation for mass, momentum, and energy in Lagrangian form:
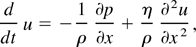
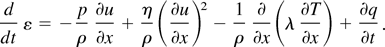
This system is completed by the equation of state in the form
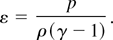
Here ρ, ε, u, and λ are a density, internal
energy, velocity, and thermal conductivity, respectively, Δ is the
size of a cell of the Lagrangian mesh, η ∼ ρΔ is the
factor of artificial viscosity. The variable x represents a
Euler coordinate. As a respective Lagrangian coordinate, the so-called
mass variable s, ds = ρdx, was used.
Thus equation (6) expresses both the condition of conservation of mass,
and natural conditions of a constant of Lagrangian coordinate
ds/dt = 0. For the solution of this equation
system, the explicit numerical scheme (first-order time accuracy and
second-order coordinate accuracy) was applied. The equation system was
numerically solved with the following conditions: at the top x
= 0 and bottom x = l ends of the channel, the flow
velocity is u(t) = 0. The combustible mixture (gas B)
is set in the sector 0 ≤ x ≤
xk − δ/2. Here, for
xk—the position of the median line
of the mixing zone—at t = 0,
xk = lk. The
molar mass of the combustible mixture is μb =
18.5. The specific thermal capacity ratio is γb
= 7/5, where δ is the mixing zone thickness. One of the
experimental gases A fills the sector xk +
δ/2 < x < l, for which μ =
μa, γ = γa,
q = 0. The mixing zone is set in the interval
xk − δ/2 < x
< xk + δ/2, within which the
density ρ varies according to a linear law from the density value
ρb of gas B at the point
xk − δ/2 to the value of
density ρa of gas A at the point
xk + δ/2. The flow in 0 <
x < l is adiabatic.
Initial conditions are: the pressure of gas B,
pb, and the pressure of gas A,
pa, at t = 0 are equal to
pb = pa =
p0. The ignition energy is q =
q0 at t = 0 for x = 0.
The shape of function q(x) is determined from the
agreement of calculated and experimentally measured position of
trajectory of the mixing zone K at the initial stage of motion
t < tQ.
In Figure 5, the calculated density
distribution ρ(t) at the abscissa x = 685 mm is
shown. The points in this picture are the experimentally measured
values (Zaytsev et al., 1999).
Calculated (one-dimensional model) and experimental values of density
ρ(t, x1), x1 =
68.5 cm. K separates the combustible mixture from argon.
6. TWO-DIMENSIONAL MODEL
To calculate the evolution of the RTI, the solution of
two-dimensional conservation equations is carried out with a nonlinear
quasi-monotonic scheme of high precision (Nikishin
et al., 1994). The problem is investigated in a
rectangular domain 7.2 × 100 cm2, filled with gases A
and B, which are separated by the mixing zone. The latter is
accelerated by the compression wave propagating from B to A. The upper
boundary of the calculated domain is set above the initial mixing zone
at a distance of 2 cm from the upper boundary of K. The lower boundary
is set at a distance of 12 cm from the upper one.
The quantities for density ρ(t), pressure
p(t), temperature T(t) and velocity
u(t) found from the one-dimensional numerical
simulation are given on the upper boundary (see Sec. 5).
7. RESULTS OF EXPERIMENTS AND NUMERICAL
CALCULATIONS: DISCUSSION
7.1. Trajectory of the mixing zone motion
The wave diagram of the process (Fig. 6) is
represented by the trajectories of the mixing zone and the incident,
transmitted, and reflected compression waves.
Wave diagram of interaction between the mixing zone, separating the
combustible mixture from argon, with incident and reflected compression
waves. C0, CT, CR: incident,
refracted, and reflected compression waves. Position of curves
C0, CT and CR is defined from a
condition (∂2ρ/∂t2) =
0. Curve K corresponds to the motion calculated based on
one-dimensional simulation. Within the limits of the measurement error
the calculated and measured positions K coincide. Vz. F: visualization
area.
The complete numerical simulation of the mixing zone trajectory shows
that if calculated and experimental points of the mixing zone
trajectory coincide at the beginning stage of motion t <
tQ, one can also observe such a
coincidence at the final stage t >
tQ.
Trajectories of an incident, refracted, and reflected compression
wave are presented in the wave diagram by points C0,
CT, and CR. The second derivative in these points
∂2ρ/∂x2 is equal to
zero.
7.2. Excitation and development of the RTI
The evolution of the initial perturbation that has an amplitude
ai(0) = a0 < 0.5
λi, can be approximated by the relation
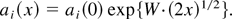
Here ai(0) is the amplitude of the
ith perturbation of the initial mixing zone, x is the
travel distance of the mixing zone, counted from its initial position
W = (At°k)1/2, where At° is
the Atwood number.
Table 1 contains experimental data
W for different Atwood numbers. The table also contains values
of wavelength λ of the perturbations and thickness δ of layers
at which these perturbations are formed. The table also presents the
perturbation amplitude growth rate W(T) calculated
from the Taylor relation (Taylor, 1950), and
W(D), the rate obtained with the method proposed by
Duff et al. (1962) for a mixing zone of a finite thickness.
The quantities W(T) describe the evolution of the
linear stage of instability in incompressible media with a
discontinuous change of density (δ = 0). The quantities
W(D) are also obtained for incompressible media, but
the initial mixing zone has a finite thickness δ. Unlike
W(T) and W(D), the experimental
values W were obtained under the conditions when the RTI
development occurs during the simultaneous compression of the mixing
zone by waves CT or CR. As seen from the table,
values W are much less then W(T) and
W(D). The latter indicates the influence of
compressibility on the RTI evolution. Figure
7 gives results (ai) of
two-dimensional numerical simulations and experimental data for the
mixing zone between the combustible mixture and helium at the stage of
deceleration. The data are presented in the coordinate system moving
with a constant velocity equal to that of the mixing zone at the moment
of change of acceleration sign. The principal scheme of definition of
traveled distance η in this case is given in Figure 8.
The data of the linear stage of RTI
Comparison of experimental results and calculated ones based on
two-dimensional simulation. Thicker part of the solid line: linear
stage of the RTI, approximation
.
The principal scheme
of definition η.
At ai ≃ 0.5
λi, one can observe the beginning and
subsequent growth of characteristic distortion of the perturbation form
of the surfaces separating the mixing zone from the “pure”
gases. The heavy gas penetrates into the light one in the form of
narrowing “jets.” The light gas penetrates into the heavy
one as widening “bubbles”—the nonlinear stage of the
RTI. Interferograms of the RTI evolution presented in Figure 2 clearly show this phenomenon. Beginning
from this phase, the penetration depth L of one gas into the
other, as measured in the experiment, is satisfactorily approximated by
a relation
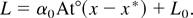
Here x* is the distance traveled by K at the moment of the
beginning of the nonlinear stage (ai ∼
λi), At° is the Atwood number,
L0 is a penetration depth of one gas into the other
at the moment of transition to the nonlinear stage, and x is
the distance traveled by K counted from its initial position.
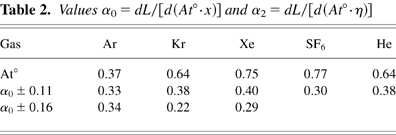
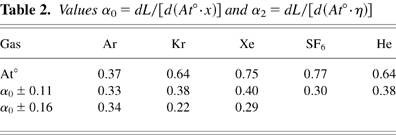
In Figure 9, the values of L,
measured for mixing zones between the combustible mixture and Ar, Kr,
Xe, SF6, and He are given. In Table
2, the values of α0 are given.
Values α0 =
dL/[d(At°·x)]
and α2 =
dL/[d(At°·η)]
The penetration depth of gases, L(x), at nonlinear
and transitional stages of the RTI. Values L(η) are given
for He.
Let us emphasize the combination with helium. Here the instability
develops at the stage of the mixing zone deceleration. To calculate
α0 correctly, one needs to take into account only the
part of the distance that the mixing zone traveled after the change of
acceleration sign. To do this, we have to switch into a coordinate
system moving with the constant velocity equal to velocity at the
moment t = t0 (see Fig.
8). Then
Here zero points of the coordinate system and time coincide with a
point of change of acceleration sign, that is, with the moment when the
perturbation growth starts. η* is the mixing zone position and
L0 is the penetration depth of one gas into the
other in the moment of transition to the nonlinear stage of the
instability evolution.
7.3. Measurement of mass involved in mixing
Data presented in Table 2 show the growth
rate of penetration depth of gases of different densities (the growth
rate of distance between the most distant points placed on the
different boundaries of the mixing zone). In the case of incompressible
media, the growth rate of penetration depth coincides with the growth
rate of mass involved in mixing. In conditions of the given experiment,
the parameters of media separating the mixing zone from
“pure” gases are changing continuously during the motion,
so we had to make a direct measurement of the mass of gas involved in
mixing. To do this, a method for the definition of the forms of the
surfaces separating the mixing zone from the “pure” gases A
and B was prepared, on a given level of density change. When defining a
volume of the mixing zone in the given moment of time t =
ti, the boundaries were set by two
tabulated point sets xj(y),
ymin ≤ y ≤ ymax,
j = 1, 2. j = 1 corresponds to the upper boundary
Kb separating the mixing zone from the
combustible mixture. j = 2 corresponds to the lower boundary
Ka separating the mixing zone from gas A.
The mixing zone volume is defined as
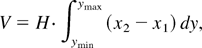
where H is a distance between lateral walls of the tube
(H = 7.2 cm).
The mass of matter involved in mixing is defined by a relation
where ρ = 0.5(ρa +
ρb), and ρa and
ρb are densities of gases A and B on boundaries
separating the mixing zone from the “pure” gases.
The data presented in Figure 10 correspond
to the growth of the penetration depth L, volume
V, and mass M of gases of different
densities as a function of the traveled distance x between
the combustible mixture and krypton (At° = 0.64). The data
correspond to the nonlinear and subsequent stages of the RT instability
evolution. L, V, and
M are penetration depth, volume, and mass of gases
divided by their values at the moment of transition to the nonlinear
stage of the RTI evolution. The traveled distance is nondimensionalized
by dividing by L0,
(x/L0 = x).
Values of function L(x),
V(x), M(x) for
the mixing zone between the combustible mixture and krypton at the
stage of accelerated motion.
The end plate in the given experiment was placed 230 mm away from the
dividing plate. The action of the reflected wave and its
“forerunners” within the visualization area did not affect
the instability development. It is worth noting that the volume
V occupied with the mixing zone increases more rapidly as
compared to the growth of the penetration depth L.
This may be linked to development of small scale turbulence inside the
mixing zone. The growth rate of mass involved in mixing turns out to be
an order higher than the rate of the penetration depth because of the
density increase caused by compression. Similar results were obtained
in experiments with hydrogen (At° = 0.8), where the instability was
developed at the stage of interaction with the reflected compression
wave.
7.4. Interaction of the mixing zone with reflected
compression wave or shock wave
The study of this process has been carried out for the mixing zone
between the combustible mixture and argon. The length of the upper part
of the channel lk is 635 mm. The length of
the lower part of the channel
l–Ik ranged from 100 to 155
mm. In the performed experiments, the density of the driver
gas—hydrogen-oxygen mixture—is less than the density of the
driven gas—argon. In the stage of accelerated motion of the
mixing zone, the RTI was excited. Hence, the penetration depth
L of one gas into the other grows. After the beginning of the
decelerated motion (x > xQ)
the RTI mechanism is “switched off” and the stratification
process begins—separation of gases of different densities, by
which L decreases in the sector x >
xQ. Such a character of the process is
called shockless deceleration.
Figure 11 presents a trajectory of the
mixing zone and L values obtained in this experiment. As seen
(x = xQ), the character of
function L(x) is changed: Increase is replaced by
decrease.
A trajectory of motion (points 1, 2) and function
L(x) (points 3) for the mixing zone between the
combustible mixture and argon. Shockless deceleration.
In Table 3 are given the values of the
parameters measured in experiments with shockless deceleration. The
first column gives the number of the experiment. The second one gives
the distance between the channel end plate and the initial position of
the mixing zone. In the third and fifth columns, the values of the
mixing zone acceleration in the stage of accelerated and decelerated
motion are given. In the fourth and sixth columns are the values of
dL/dx corresponding to these stages.
Values of parameters for nonshocked deceleration
To evaluate the suppression of the RTI caused by interaction of the
mixing zone with the reflected wave, the following relation was used
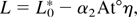
where η is calculated using the procedure presented in Figure 8, excluding the fact that the zero point of
the coordinate system and time were counted here from the beginning of
the decrease of L. Here only the distance traveled by the
mixing zone under action of the negative acceleration was taken into
account. The obtained mean value for α2 is presented in
Table 2. The analogous values
α2 were obtained for the combination of the
oxygen–hydrogen mixture with krypton or xenon.
An essential change in the evolution of the above-described process
is brought by the appearance of a shock wave. The latter is formed in
the interval between the end plate and the mixing zone. The collision
between this shock wave with the mixing zone leads to the growth of the
penetration depth L.
In Figure 12, the diagrams are analogous to
ones given in Figure 11, but obtained for a
case of shock-induced deceleration are presented.
A trajectory of motion (points 1, 2) and function
L(x) (points 5). A trajectory of the reflected shock
motion (points 3). A trajectory of the refracted shock motion after
interaction with the mixing zone (points 4). Shock-induced
deceleration.
In all experiments, included in Table 4,
the wave fronts that intersect the mixing zone trajectory at
xQ < x <
l have been distinctly recorded on the
interferograms. This interval corresponds to the domain of interaction
of the “forerunner” of the reflected compression wave with
the mixing zone. The discontinuity of the interferometric bands at the
fronts of these waves is roughly 0.5 mm, corresponding to a density
change Δρ ≃ 2.38·10−5
g/cm3. The velocity of the motion of these waves in the
system attached to the mixing zone lies just above the speed of sound
(the Mach number equal to 1.05). Such aspect of the function
L(x) allows the supposition that the growth of
L(x) in the interval x0 <
x < l originates from the
Richtmyer–Meshkov instability, excited by the interaction of the
mixing zone with the shock waves, which appeared as a result of the
evolution of the system of secondary compression waves.
Values of parameters for shocked deceleration
8. CONCLUSION
- The surfaces that separate the mixing zone from the
“pure” gases in the process of the RTI evolution proceed
through all the forms well known from the research in incompressible
media, which correspond to the linear, nonlinear, and transitional RTI
stages.
- For the linear stage, the growth rate of the amplitude a
in compressible media turns out to be significantly less than for
incompressible media.
- For the nonlinear and following phases (transitional, the stage of
the ever-growing structures) the penetration depth L of one
gas into the other is approximated by a linear dependence on the
distance x, traveled by the mixing zone.
- Inside the mixing zone, a small scale turbulence is excited, which
results in increase of the volume V growth rate as compared
to the penetration depth L growth rate.
- The braking of the mixing zone, brought by the interaction with the
reflected compression wave, is linked to the decrease of the
penetration depth L of one gas into the other.
- In a series of experiments, the braking process, created by the
action of the reflected compression wave, is linked to the development
of shock waves. At the origin of the development of the latter are
secondary compression waves, brought by the interaction of the
meniscus-shaped flame front with the channel walls. The mixing zone
interaction with the above-mentioned shock waves of low intensity (Mach
number near 1.05) leads to the growth of the penetration depth
L in the braking process.
