INTRODUCTION
The study of ultrashort laser pulses (picosecond and femtosecond) is one of the important evolving research fields because of its unique advantage of having high precision material ablation by extreme high-energy intensities with negligible thermal affected zone. This is because of the very short interacting time period, which is less than the time needed to reach the thermal equilibrium. The ultrashort laser pulses interacting with materials is used for many applications such as drilling, welding, cutting, micro-machining, precise processing of highly sensitive materials, surface alloying (Sonntag et al., Reference Sonntag, Roth, Gaehler and Trebin2009; Furusawa et al., Reference Furusawa, Takahashi, Cho, Kumagai, Midorikawa and Obara2000; Gurevich et al., Reference Gurevich, Kittel and Hergenröder2012), and various medical applications such as brain surgery and removing tumor tissue (Oraevsky et al., Reference Oraevsky, DaSilva, Feit, Glinsky, Mammini, Paquette, Perry, Rubenchik, Small IV and Stuart1995; Lee et al., Reference Lee, Jeong and Chan2009). The physics of ultrashort pulses differs from that for the nanosecond or millisecond range pulses because the pulse width is less than the time needed to reach the equilibrium state between the electrons and the phonons. During the irradiation of metals by picosecond or femtosecond laser pulses the electrons absorb the photon energy and then the heating of the metal lattice occurs by the electron-phonon collisions (Sonntag et al., Reference Sonntag, Roth, Gaehler and Trebin2009; Ihtesham et al., Reference Ihtesham, Chowdhury and Xianfan2003; Ihtesham and Xianfan, 2007).
The non-equilibrium heat transfer between the electrons and the lattice can be described by a two temperature model which was first proposed by Anisimov et al. (Reference Anisimov, Kapeliovich and Perel'man1974) In this model, the heat conduction by the lattice was neglected. After that, Qiu and Tien (Reference Qiu and Tien1993) used the Boltzmann heat equation and developed the hyperbolic two step radiation heating model and was simplified to the parabolic two step model in which the heating, melting, and evaporation of the materials irradiated by short laser pulses have been solved numerically and have a reasonable agreement with experimental results. Then Qiu and Tien (Reference Qiu and Tien1993) model was modified by Chen and Beraun (Reference Chen2001) dual hyperbolic two step radiation model in which the heat conduction of the lattice was considered, the electron temperature from both models was very close while there was a remarkable difference in the lattice temperature.
The energy equations that describe the non-equilibrium heat transfer in the two step model are given below (Sonntag et al., Reference Sonntag, Roth, Gaehler and Trebin2009; Ihtesham et al., Reference Ihtesham, Chowdhury and Xianfan2003; Zhang and Chen, Reference Zhang and Chen2007; Lin et al., Reference Lin, Zhigilei and Celli2008):
$$C_e \; \displaystyle{{\partial T_e } \over {\partial t}}\; =\; \nabla .\left({K_e \nabla T_e } \right)- G\left({T_e - T_l } \right)+Q\lpar \mathop{r}\limits^{\rightharpoonup}\comma \; t\rpar \comma \;$$
$$C_l \; \displaystyle{{\partial T_l } \over {\partial t}}\; =\; \nabla . \left({K_l \nabla T_l } \right) + G_{ \left({T_e - T_l } \right)}.$$Where T is the temperature, t is the time, C is the volumetric specific heat, K is the thermal conductivity, where the subscripts e and l are associated with the electron and lattice, respectively, G is the coupling factor that describes the interaction between the electrons and the lattice, Q is the volumetric laser energy deposition rate as a function of space and time. Eq. (1) describes the heat absorbed by electrons, the electronic heat conduction, the transfer of heat between the electrons and the lattice, and the energy distribution of the laser in time and space. The second equation describes the heat transfer through the lattice, heat conduction and the coupling heat with the electron system.
The laser-heating source as a function of space and time can be described by the following expression:
$$Q\left({x\comma \; y\comma \; z\comma \; t} \right)=I_0 \left({1 - R} \right)I\lpar t\rpar I\lpar x\comma \; y\comma \; z\rpar.$$Where I 0 is the maximum power density, R is the reflectivity, I(t), and I(x,y,z) are the temporal distribution and the spatial distribution of the power density, respectively.
INPUT AND ASSUMPTIONS
In this work, a two-dimensional model for the solution of the transient heat transfer equations was developed with temperature and phase change dependent thermal properties (density, thermal conductivity, and specific heat) for both the electron and the lattice. The heat conduction term in the lattice energy equation was neglected because of the slow diffusion in the lattice system during the pulse duration. The Gaussian distribution was assumed for both the time (Tan et al., Reference Tan, Zhang, Mao, Li, Yi and Zhang2009) and the space (Hassanein, Reference Hassanein1983) for the heating source. Therefore, the energy transport equations become (Hassanein, Reference Hassanein1983):
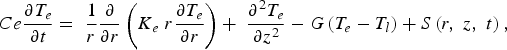$$Ce\displaystyle{{\partial T_e } \over {\partial t}}=\; \displaystyle{1 \over r}\displaystyle{\partial \over {\partial r}}\left({K_e \; r\displaystyle{{\partial T_e } \over {\partial r}}} \right)+\; \displaystyle{{\partial ^2 T_e } \over {\partial z^2 }} - G\left({T_e - T_l } \right)+S\left({r\comma \; z\comma \; t} \right)\comma \;$$
$$Cl\displaystyle{{\partial T_l } \over {\partial t}}=\; G\left({T_e - T_l } \right).$$Eq. (4) describes the heat transfer in cylindrical coordinate system where r is the radial direction and z is the direction along the depth inside the target, s(r,z,t) is the volumetric energy from the laser and it depends on r, z, and t as follows:
$$S\left({r\comma \; z\comma \; t} \right)=I_0 \left({1 - R} \right){\rm \alpha} {\rm \; }I_{surf\; } {\rm }\left({r\rpar I\lpar t} \right)\exp \left({ - {\rm {\rm \alpha} }z} \right)\comma \;$$
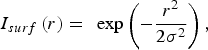$$I_{surf} {\rm}\left(r \right)={\rm \; }\exp \left({ - \displaystyle{{r^2 } \over {2{\rm {\rm \sigma} }^2 }}} \right)\comma \;$$
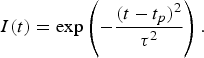$$I\lpar t\rpar = \exp \left(- \displaystyle{{\lpar t - t_p \rpar ^2 } \over {{\rm \tau} ^2 }}\right).\eqno \lpar 8\rpar$$Where α is the absorption coefficient, I 0 is the maximal power density, tp is the laser pulse width in time, and σ = r beam/2 where r beam is the spot radius of the laser beam.
Thermo Physical Properties and Temperature Dependence
In this work, the thermal properties of electron and lattice such as thermal conductivity, density, and heat capacity were assumed to be dependent on temperature, the following equations describe such dependency (Ihtesham et al., Reference Ihtesham, Chowdhury and Xianfan2003; Zhang and Chen, Reference Zhang and Chen2007; Lin et al., Reference Lin, Zhigilei and Celli2008; Chen et al., Reference Chen, Jiang, Sui, Ding, Liu and Jin2011; Ren et al., Reference Ren, Chen and Zhang2011). The thermal conductivity of electron is given by:
$$k_{e} = {\rm \; {\rm \chi} }\left({\displaystyle{{\lpar {\rm \mu} _e^2+0.16\rpar ^{5 \over 4} \;\lpar {\rm \mu} _e^2+0.44\rpar {\rm \mu} _e^2 } \over {\lpar {\rm \mu} _e^2+0.092\rpar ^{1 \over 2} \;\lpar {\rm \mu} _e^2+{\rm \eta} {\rm \mu} _l \rpar }}} \right).$$Where χ and η are constants, μe = T e/T F, μl = T l/T F, and T F is the Fermi temperature. The specific heat of the electron is usually a linear function of electron temperature, given by
$$C_e = B_e T_e\comma \;$$where B e = π2n ek B/2T F, n e is the density of the free electrons, and k B is the Boltzmann's constant. The lattice specific heat is in the form of (Jovanović et al., Reference Jovanović, Knežević-Stevanović and Grozdanić2009; Garg et al., Reference Garg, Banipal and Ahluwalia1993):
$$C_{l}=a+b T_{l}+c T_{l}^{2}+d T_{l}^{3}.$$Where a, b, c, and d are constants which depend on the material.
The density of the material have been assumed temperature and phase dependent and it is given by (Garg et al., Reference Garg, Banipal and Ahluwalia1993; Sangwal, Reference Sangwal1987):
$${\rm \rho} =c_{0}+c_{1} T_{l}+c_{2} T_{l}^{2}+c_{3} T_{l}^{3}\comma \;$$where c 0, c 1, c 2, and c 3 are constants that depend on the material and it's phase. Most of the constants in these equations are tabulated in Table 1.
Table 1. Thermal and optical properties of Cu
Initial and Boundary Conditions
The initial value of the target temperature is assumed to be the ambient temperature (300 K) as well as the temperature far away from the exposed surface in r direction and also very far from the center in z direction.
$$T\lpar r\comma \; z\comma \; t=0\rpar =T_{amb}=300\, K\comma \;$$
$$T\lpar r=\infty\comma \; z\comma \; t\rpar =T_{amb}=300\, K\comma \;$$
$$T\lpar r\comma \; z=\infty\comma \; t\rpar =T_{amb} =300\, K.$$The adiabatic boundary conditions have been assumed for both sides in r and z directions
$$\displaystyle{dT \over dr}\; = 0 \quad \hbox{for} \, \, r = 0\comma \; \infty\comma \;$$
$$\displaystyle{{{\rm \; }dT} \over {dz}}\; = 0 \quad \,\hbox{for} \, \, z = 0\comma \; \infty.$$In this paper, the two temperature model was used to predict the thermal response of Cu target with an ambient temperature of 300 K when exposed to ultrashort laser pulse of 100 fs, spot size of 40 µm, and with a total laser energy of 3.5 µJ. Using Eqs. (6), (7), and (8) the maximum power density was calculated to be 1.5 × 1013 W/cm2.
RESULTS AND DISCUSSION
The calculation for our two-dimensional heat transfer equations was implemented using non-equilibrium heat transfer equations by modifying the A*THERMAL-2 computer code developed by Hassanein (Reference Hassanein1996). The finite difference methods were used to calculate both the electron temperature and the lattice temperature. For the 100 fs laser pulse with 40 µm spot size the time step was 0.5 fs up to 100 fs and then increased to 5 fs to the end of the run time. The mesh size in r direction was 0.5 µm and it was changing in z direction to speed up the calculations but maintain the accuracy. The results of the calculated temperatures of lattice and electron and their distribution in space and time as well as the impact of laser spot size, coupling factor, and the material reflectivity are shown and discussed below.
Electron and Lattice Temperature Evaluation
The temporal temperature distribution at the center of the laser beam for both the electron and the lattice is shown in Figure 1, the electron temperature increases very fast within few femtoseconds and reaches to about 11700 K while the lattice temperature increases very slow, at this stage the electrons absorb the photons from the laser and their temperature remains constant to the end of the pulse duration as shown in the upper part of this figure. Then the electrons transfer the absorbed energy to other electrons as well as through the coupling with the phonons, so the temperature of electrons decreases while the lattice temperature increases as shown. However, the decreasing in the electron temperature is much faster than the increasing in the lattice temperature because the rate of electron-electron interaction is higher than the rate of electron phonon interactions (Lee et al., Reference Lee, Kang and Lee2011). At about 4.8 picoseconds the system reaches thermal equilibrium with temperature about 1330 K.
Fig. 1. (Color online) Electron and lattice temperatures of Cu target at the center heated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm. The upper part is the amplification of the same figure up to 100 fs.
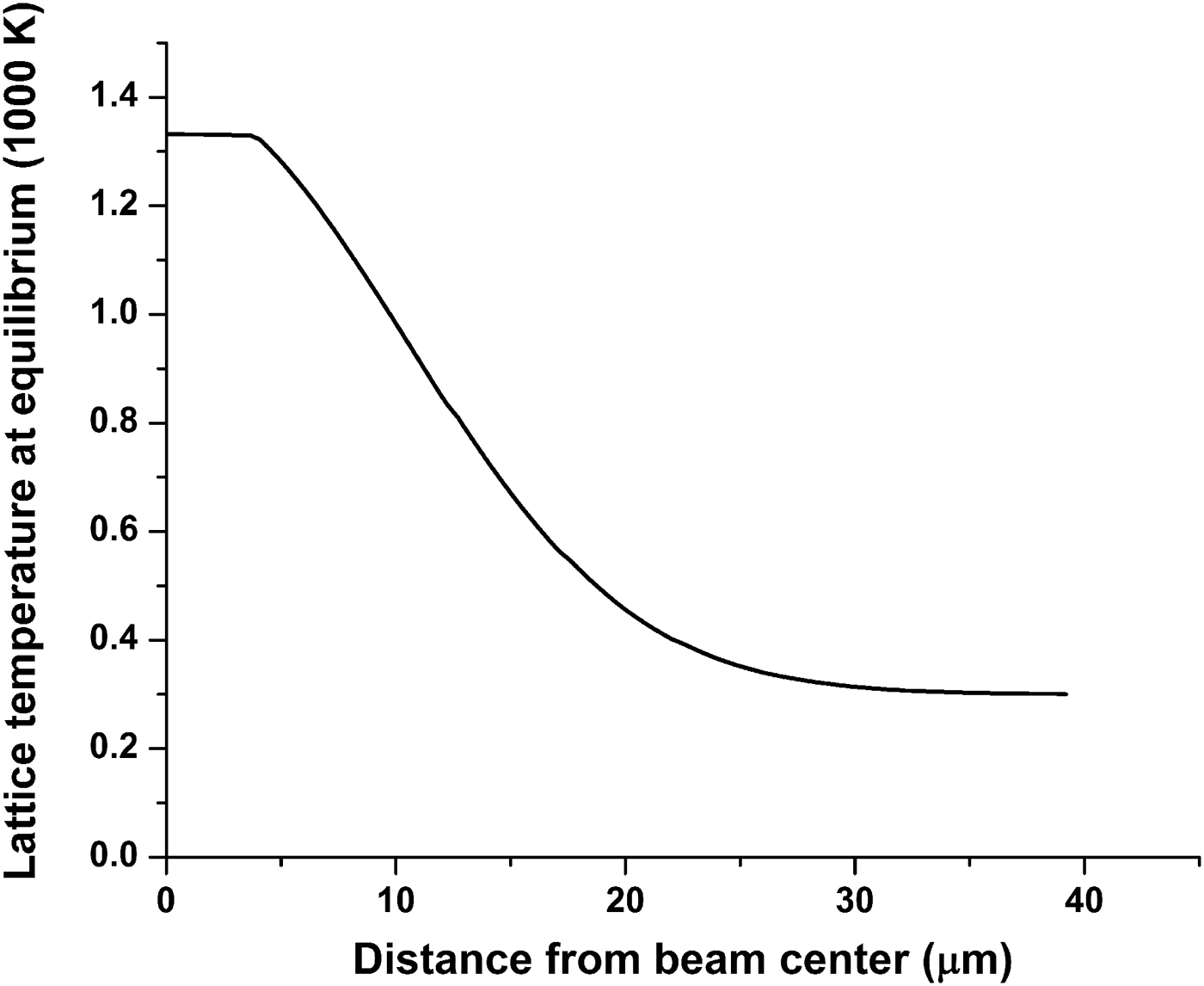
The equilibrium distribution of the lattice temperature at the surface as a function of r is shown in Figure 2, the temperature has its maximum value at the center of the laser beam (r = 0) since the maximum power density of the laser is at the center and according to Eq. (7) the temperature decreases gradually until it reaches 300 K which is the assumed initial temperature at about 34 µm.
Fig. 2. Lattice equilibrium temperature at the surface as a function of r heated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm.
Figure 3 shows the temporal and spatial distribution of the electron temperature at the surface. At fixed location the electron temperature increases suddenly until it reaches the maximum value then it decreases gradually until reaching the thermal equilibrium. Figure 3 was extended up to 100 fs which is the value of pulse duration as shown in Figure 4. It can be seen that when the electron temperature reaches its maximum value it remains constant to the end of the pulse width before the decrease in temperature takes place as a result of the electron-phonon coupling. On the other hand, for fixed time the electrons have their maximum value at the center then decreases with r due to the Gaussian distribution of the power density.
Fig. 3. (Color online) Two-dimensional temporal distribution of the electron temperature at the surface as a function of r irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm.
Fig. 4. (Color online) Two-dimensional temporal distribution of the electron temperature at the surface up to 100 fs as a function of r irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm.
The temporal and spatial distribution of the lattice temperature at the surface is shown in Figure 5 for fixed location the temperature increases with low rate compared to electrons until reaching the thermal equilibrium and for fixed time the temperature decreases far away from the center as discussed above.
Fig. 5. (Color online) Two-dimensional temporal distribution of the lattice temperature at the surface as a function of r irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm.
The electron and lattice temperature distribution in z direction at the center as a function of time is shown in Figures 6 and 7. The temperature at the center is the maximum and then decreases along with the depth exponentially according to the absorption in z direction as in Eq. (6). The energy needs longer time to be absorbed inside the material. The behavior of the temporal distribution for both electron and lattice at any point along with depth is the same as discussed before.
Fig. 6. (Color online) Two-dimensional temporal distribution of the electron temperature at the center as a function of z irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm.
Fig. 7. (Color online) Two-dimensional temporal distribution of the lattice temperature at the center as a function of z irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm.
Parametric Study
The impact of the spot size of the laser beam on the thermal response in the interacting Cu is shown in Figure 8. As the spot size increases the equilibrium temperature decreases because at the fixed total energy the smaller spot size causes higher power density and more heat is deposited at the surface leading to higher temperature. A 40% reduction in the temperature at equilibrium was observed when the spot size increased by 25%. For the spot size of 40 µm using Eqs. (6), (7), and (8), the maximal power density is 1.5 × 1013 W/cm2 and the thermal equilibrium temperature is about 1330 K whereas for spot size of 50 µm the maximum power density is 8.8 × 1012 W/cm2 and the equilibrium temperature is only 800 K. On the other hand, smaller spot size causes less heat dissipated in r direction.
Fig. 8. (Color online) Electron and lattice temperatures at the center irradiated by laser pulse with pulse width of 100 fs, at different values of spot size.
Figure 9 shows the impact of the electron-phonon coupling factor. When the value of the coupling factor is 2.5 × 1011 W/cm3 K the thermal equilibrium between the electron and lattice occurs at about 4.8 ps whereas when its value is 5 × 1011 W/cm3 K the equilibrium occurs at about 2.6 ps because the higher value of coupling factor increases the rate of the electron phonon interaction such that the thermal equilibrium occurs earlier. Therefore, doubling the coupling factor resulted in reducing the equilibrium time by a factor of 1.8.
Fig. 9. (Color online) Electron and lattice temperatures at the center irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm at different values of electron-phonon coupling factor.
The final parameter studied was surface laser reflectivity, which is shown in Figure 10. For the Cu reflectivity of 0.94, the maximum electron temperature is about 11700 and the equilibrium lattice temperature is 1330 K. Whereas for a reflectivity of 0.85 the maximum electron temperature is about 18500 K and the equilibrium temperature is about 2700 K, this is because as the reflectivity increases more photons from the input laser are reflected which leads to less laser power deposited on the surface. In this case, a 10% decrease in target surface reflectivity increased the equilibrium temperature by a factor of 2. This is in contrast to nanosecond laser pulses where the reflected laser light will be absorbed in the evolving plasma of the target materials and additionally heating such plasma that can further contribute to erosion of target materials.
Fig. 10. (Color online) Electron and lattice temperatures at the center irradiated by laser pulse with pulse width of 100 fs, I 0 of 1.5 × 1013 W/cm2, and spot radius of 20 µm at different values of reflectivity.
CONCLUSION
In this work, a two-step temperature model was developed and used to study the non-equilibrium thermal two-dimensional heat distribution when Cu target is irradiated by femtosecond laser pulse with temperature dependent thermal properties. Gaussian temporal and spatial distributions of laser power density were assumed in our simulation. The predicted behavior of the temperature distribution of the electron and the lattice as a function of t, r, and z was explained by the physics of the heat exchange mechanisms among electrons, photons, and lattice atoms. The electrons initially absorb the laser photons and their temperature increase rapidly to maximum value then remains constant to the end of the femtosecond pulse. Then the heat is transferred to other electrons and phonons such that the electron temperature decreases and lattice temperature increases till reaching the thermal equilibrium. The impact of the spot size of the femtosecond laser beam was also studied and the larger spot size for a fixed total energy leads to smaller maximum power density so less heat deposited to the material and finally lower equilibrium temperature. The coupling factor has an impact on the rate of interaction between the electrons and the lattice, higher values causes higher rate of interaction and faster thermal equilibrium. Finally, the effect of laser reflectivity was studied and that higher value of reflectivity leads to high rate of photons reflection and less absorption of the energy in the target. This process should also be function of target condition during irradiation, as reflectivity changes as the state of the material changes from solid to liquid to gas/vapor phases. This will be studied in future work.
ACKNOWLEDGEMENT
This work is partially supported by the US Department of Energy, Office of Fusion Energy Sciences.
