1. INTRODUCTION
Due to availability of the high power lasers, laser plasma interaction at higher intensity (1018–1021 W/cm2) becomes an important nonlinear phenomenon in recent years. The propagation of an intense laser beam through the plasma results into various instabilities namely, self-focusing, filamentation, stimulated Raman scattering (SRS), stimulated Brillouin scattering (SBS), two plasmon decay, etc. (Krall et al., Reference Krall and Trivelpiece1973; Kruer, Reference Kruer1974; Liu et al., Reference Liu and Tripathri1994; Guérin et al., Reference Guérin, Mora and Laval1998). These instabilities play a very important role in many areas like fast-ignitor thermonuclear fusion (Deutsch et al., Reference Deutsch, Furukawa, Mima, Murukami and Nishihara1996), compact laser-driven accelerators (Tajima et al., Reference Tajima and Dawson1979), X-ray lasers (Li et al., Reference Li, Wang, Zhu, Ye, Li and Yu2011), laboratory astrophysics (Remington et al., Reference Remington, Drake, Takabe and Arnett1999), and many more (Tajima et al., Reference Tajima and Mourou2002), where laser plasma interaction takes place. In particular, SRS corresponds to the decay of the incident electromagnetic wave into a scattered electromagnetic wave and an electron plasma wave (EPW), while during SBS the incident electromagnetic wave decays into a scattered electromagnetic wave and an ion acoustic wave (IAW). In this paper, we are mainly concerned about SRS and SBS because due to these instabilities, a large fraction of the high power laser energy is not efficiently coupled with plasma as well as modification of the intensity distribution takes place which affect the uniformity of energy deposition (Kruer, Reference Kruer1974; Liu et al., Reference Liu and Tripathri1994; Lindl et al., Reference Lindl, Amendt, Berger, Glendining, Glenzer, Hann, Kauffman, Landen and Suter2004; Omatsu et al., Reference Omatsu, Kong, Park, Cha, Yoshida, Tsubakimoto, Fujita, Miyanaga, Nakatsuka, Wang, Lu, Zheng, Zhang, Kalal, Slezak, Ashihara, Yoshino, Hayashi, Tokizane, Okida, Miyamoto, Toyoda, Grabar, Kabir, Oishi, Suzuki, Kannari, Schaefer, Pandiri, Katsuragawa, Wang, Lu, Wang, Zheng, He, Lin, Hasi, Guo, Lu, Fu, Gong, Geng, Sharma, Sharma, Rajput, Bhardwaj, Zhu and Gao2012). Apart from SRS and SBS, the self-focusing of the laser beam is also a crucial problem in high power laser plasma interactions. For the propagation of a non-uniform intense laser beam inside the plasma, both ponderomotive nonlinearity and relativistic nonlinearity can lead to the self-focusing process. The relativistic self-focusing occurs because at such higher intensities the field associated with the light wave becomes very high which accelerates the plasma electrons at relativistic velocities and hence the relativistic mass correction must be taken into account. This relativistic change in the electron mass modifies the dielectric constant of plasma 
${\rm \varepsilon} = 1 - {{{\rm \omega} _{\,pe}^2 } / {{\rm \gamma} {\rm \omega} _0^2 }}$, where 
${\rm \omega} _{\,pe} \, = ( 4{\rm \pi} N_{e} e^2 / m_0 )^{1/2}$ is the plasma frequency, ω0 is the laser frequency, N e is the plasma electron density, e and m 0 are the charge and rest mass of the electron, respectively, and γ is the relativistic Lorentz factor. Therefore, plasma refractive index (
$\sqrt {\rm \varepsilon} $) seen by the intense laser beam becomes γ dependent which leads to the relativistic self-focusing and breakup of the laser beam into intense filaments (Umstadter, Reference Umstadter2003). On the other hand, ponderomotive nonlinearity modifies the refraction index by expulsion of the electrons from the higher intensity region. However, these nonlinearities are operative at different time scales according to the inequalities (1) τ < τpe or (2) τpe < τ< τpi; here, τ is laser pulse duration, τpe is the electron plasma period, and τpi is ion plasma period. In case (1), the relativistic nonlinearity is set up (almost instantaneously) while for case (2), both the nonlinearities (relativistic and ponderomotive) are operative (Brandi et al., Reference Brandi, Manus, Mainfray and Lehner1993). So, relativistic nonlinearity will set up almost instantaneously in the system and requires relatively higher threshold laser power than the ponderomotive nonlinearity (Brandi et al., Reference Brandi, Manus, Mainfray and Lehner1993). This relativistic nonlinearity (self-focusing) creates a hindrance in uniform energy deposition of the laser inside the plasma. So both SRS and SBS along with the relativistic self-focusing greatly affect the laser plasma coupling. Relativistic self-focusing occurs when the laser power exceeds the critical (threshold) power, given by 
$P_c = 17 {\rm \gamma} \left(\left. {\rm \omega}_{0}\right/{{\rm \omega}_{\,pe}} \right)^2\rm GW$ (Sun et al., Reference Sun, Ott, Lee and Guzdar1987; Sprangle et al., Reference Sprangle, Tang and Esarey1987), which is available for experiments due to the recent advancement in laser technology. Therefore, these instabilities at high power laser flux have been very actively studied experimentally (Monot et al., Reference Monot, Auguste, Gibbon, Jakober, Mainfray, Dulieu, Louis-Jacquet, Malka and Miquel1995; Borghesi et al., Reference Borghesi, Mackinnon, Barringer, Gaillard, Gizzi, Meyer, Willi, Pukhov and Meyer-Ter-Vehn1997; Wang et al., Reference Wang, Krishnan, Saleh, Wang and Umstadter2000; Rousseaux et al., Reference Rousseaux, Le Gloahec, Baton, Amiranoff, Fuchs, Gremillet, Adam, Héron and Mora2002).
In the past, a lot of theoretical and numerical works at high power laser flux has been done in which SRS and SBS are carried out separately (three wave interaction = 3WI), ignoring the interplay among them (Guérin et al., Reference Guérin, Laval, Mora, Adam, Heron and Bendib1995; Barr et al., Reference Barr, Berwick and Mason1998; Mahmoud et al., Reference Mahmoud and Sharma2001; Shuller et al., Reference Shuller and Porzio2010; Paknezhad et al., Reference Paknezhad2012). However, SRS and SBS can coexist upto N cr /4 inside the plasma (SRS exists upto N cr /4 while SBS exists upto N cr) (Kruer, Reference Kruer1974; Liu et al., Reference Liu and Tripathri1994), where N cr is the electron critical density, defined as the density above which the propagation of the electromagnetic wave is not allowed. Although, the interplay between SRS and SBS has been theoretically studied earlier (Kolber et al., Reference Kolber, Rozmus and Tikhonchuk1995; Sharma et al., Reference Sharma, Vyas and Singh2013; Hao et al., Reference Hao, Liu, Hu and Zheng2013). Recently, Sharma et al. (Reference Sharma, Vyas and Singh2013) have studied the effect of ponderomotive nonlinearity on coexisting stimulated Raman and Brillouin scattering, but these studies are carried out at relatively low powers. Therefore, not applicable at ultra-intense laser plasma interaction where the relativistic nonlinearity plays a very important role. In order to understand the interplay among SRS and SBS at relativistic laser power, it is essential to study these instabilities along with the relativistic self-focusing in the regime where they co-exist and affect each other.
The interplay between SRS and SBS has been observed in many experiments (Walsh et al., Reference Walsh, Villeneuve D and Baldis1984; Labaune et al., Reference Labaune, Baldis, Renard, Schifano and Michard1997; Michel et al., Reference Michel, Depierreux, Stenz, Tassin and Labaune2010). The first experimental observation of this competitive phenomenon was made by Walsh et al. (Reference Walsh, Villeneuve D and Baldis1984) in which they observed that the quenching of SRS plasma waves were strongly correlated to the initiation of SBS ion waves. Recently, it has been found experimentally that for plasma based laser amplifiers, it is essential to study SRS and SBS simultaneous at relativistic laser power (Turnbull et al., Reference Turnbull, Li, Morozov and Suckewer2012; Weber et al., Reference Weber, Riconda, Lancia, Marquès, Mourou and Fuchs2013). Therefore, the motivation of the present work is to understand the effect of the coexistence on the growth, saturation, and the reflectivity of SRS and SBS including the effect of relativistic self-focusing of intense Gaussian laser beam.
This paper presents the simultaneous study of stimulated Raman and Brillouin scattering along with the effect of relativistic filamentation of the pump beam within the paraxial-ray approximation. The back reflectivity is a very important parameter to assure the amount of energy dissipated in laser plasma interaction therefore we have simulated the back-reflectivity of the scattered waves (SRS and SBS) and studied how it gets modified due to this coexistence process. We have also examined how the pump depletion affects the filamentation process (of the pump beam as well as scattered beams) and the back reflectivity of scattered beams. It has been demonstrated that the relativistic filamentation modifies the SRS and SBS gain parameters which further modifies the back-reflectivities of the scattered beams.
This paper is arranged as follows. In Section 2, we have described a three-dimensional theoretical model to study the effect of relativistic filamentation of the pump on the coexistence of SRS and SBS and derived the expression for SRS and SBS back-reflectivity. Section 3 presents the detailed discussion of the results followed by the conclusion in Section 4.
2. MODEL EQUATION
In this section, we have developed a five wave interaction (5WI) model to study the interplay between SRS and SBS at relativistic laser power. A high power laser beam with Gaussian intensity profile is treated as the pump which is polarized along the x-axis and propagating along the z-axis in collisionless plasma. The expression of the initial intensity distribution along the wave front is given by:
$${\overrightarrow {E_0 } .\overrightarrow {E_0^{\ast} } \vert _{Z = 0} = \, \, E_{00}^2 \exp \lpar\!\! - r^2 / r_0^2 \rpar }\comma \;$$
where r 0 is the initial beam width, E 00 is the axial amplitude, and r refers to the radial coordinate in cylindrical co-ordinate system. To study the coexistence case, we are mainly concern about the coupling of three fields — the incident pump field 
$\vec E_0 $, the Raman backscattered field 
$\vec E_R $, and the Brillouin backscattered field 
$\vec E_B $. Following the standard technique used by Sharma et al. (Reference Sharma, Vyas and Singh2013) including the relativistic mass correction, one can obtain the following governing equations for the pump and scattered fields:
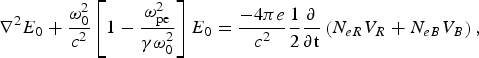$$\eqalign{& {\nabla ^2}{E_0} + \displaystyle{{{\rm \omega} _0^2 } \over {{c^2}}}\left[{1 - \displaystyle{{{\rm \omega} _{{\rm pe}}^2} \over {{\rm \gamma} {\rm \omega} _0^2 }}} \right]{E_0} = \displaystyle{{ - 4 {\rm \pi} e} \over {{c^2}}}\displaystyle{1 \over 2}\displaystyle{\partial \over {\partial {\rm t}}}\left({{N_{eR}} {V_R} + {N_{eB}} {V_B} } \right)\comma \; }$$
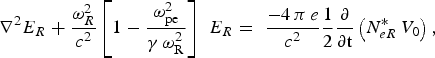$$\nabla ^2 E_R + \displaystyle{{{\rm \omega} _R^2 } \over {c^2 }}\left[{1 - \displaystyle{{{\rm \omega} _{{\rm pe}}^2 } \over {{\rm \gamma} \, {\rm \omega} _{\rm R}^2 }}} \right]\, \, E_R = \, \, \displaystyle{{ - 4\, {\rm \pi} \, e} \over {c^2 }}\displaystyle{1 \over 2}\displaystyle{\partial \over {\partial {\rm t }}}\left({N_{eR}^{\ast} \, V_0 } \right)\comma \;$$
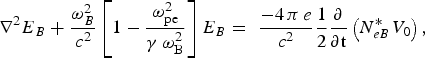$$\nabla ^2 E_B + \displaystyle{{{\rm \omega} _B^2 } \over {c^2 }}\left[{1 - \displaystyle{{{\rm \omega} _{{\rm pe}}^2 } \over {{\rm \gamma} \, {\rm \omega} _{\rm B}^2 }}} \right]E_B = \, \, \displaystyle{{ - 4\, {\rm \pi} \, e} \over {c^2 }}\displaystyle{1 \over 2}\displaystyle{\partial \over {\partial {\rm t }}}\left({N_{eB}^{\ast} V_0 } \right)\comma \;$$where γ is the relativistic Lorentz factor and other symbols have their usual meanings. Here N eR and N eB are the electron density perturbations in the EPW and IAW, respectively. Using the heavy damping limit one can obtain:
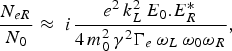$${{\displaystyle{{N_{eR} } \over {N_0 }} \approx \, \, i\displaystyle{{e^2 \, k_L^2 \, E_0 .E_R^{\ast} } \over {4\, m_0^2 \, {\rm \gamma} ^2 \Gamma _e \, {\rm \omega} _L \, {\rm \omega} _{0} {\rm \omega}_R }}}}\comma \;$$
$$\displaystyle{{{N_{eB}}} \over {{N_0}}} \approx i\displaystyle{{{e^2}{{\rm \omega} _A}{E_0}.E_B^ * {\rm }} \over {4 {m_0} {\rm \gamma} M {\Gamma _i}{{\rm \omega} _0}{{\rm \omega} _B}c_s^2 }}\comma \;$$where Γe and Γi are the Landau damping coefficients for EPW and IAW, respectively, T e and T i are electron and ion temperatures, k β is the Boltzmann's constant, and λd is the Debye length. Using Eqs (5) and (6), the following equations are obtained:
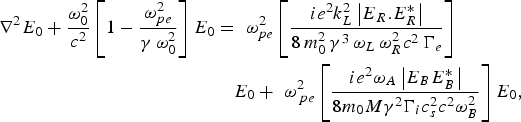$$\eqalign{ \nabla ^2 E_0 + \displaystyle{{{\rm \omega} _0^2 } \over {c^2 }}\left[{1 - \displaystyle{{{\rm \omega} _{pe}^2 } \over {{\rm \gamma} \, {\rm \omega} _0^2 }}} \right]E_0 &= \, \, {\rm \omega} _{pe}^2 \left[{\displaystyle{{ie^2 k_L^2 \left\vert {E_R .E_R^ {\ast} } \right\vert } \over {8\, m_0^2 \, {\rm \gamma} ^3 \, {\rm \omega} _L \, {\rm \omega} _R^2 c^2 \, \Gamma _e }}} \right]\cr & \quad E_0 + \, \, {\rm \omega} _{\,pe}^2 \left[{\displaystyle{ie^2 {\rm \omega}_A \left\vert E_B E_B^{\ast} \right\vert \over 8m_0 M {\rm \gamma} ^2 \Gamma_i c_s^2 c^2 {\rm \omega} _B^2 }} \right]E_0\comma \; }$$
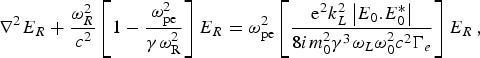$$\eqalign{& {\nabla ^2}{E_R} + \displaystyle{{{\rm \omega} _R^2 } \over {{c^2}}}\left[{1 - \displaystyle{{{\rm \omega} _{{\rm pe}}^2 } \over {{\rm \gamma} {\rm \omega} _{\rm R}^2 }}} \right] {E_R} = {\rm \omega} _{{\rm pe}}^2 \left[{\displaystyle{{{{\rm e}^2}k_L^2 \left\vert {{E_0}.E_0^{\ast}} \right\vert } \over {8 i m_0^2 {{\rm \gamma} ^3} {{\rm \omega} _L}{\rm \omega} _0^2 {c^2} {\Gamma _e}}}} \right]{E_R}}\comma \;$$
$$\eqalign{& {\nabla ^2}{E_B} + \displaystyle{{{\rm \omega} _B^2 } \over {{c^2}}}\left[{1 - \displaystyle{{{\rm \omega} _{\,pe}^2 } \over {{\rm \gamma} {\rm \omega} _B^2 }}} \right] {E_B} = {\rm \omega} _{\,pe}^2 \left[{\displaystyle{{{e^2}{{\rm \omega} _A}\left\vert {{E_0}E_0^ * } \right\vert } \over {8 i {m_0} {{\rm \gamma} ^2} M c_s^2 {c^2} {\rm \omega} _0^2 {\Gamma _i}}}} \right]{E_B}}$$One can solve Eqs (7), (8), and (9) by using the paraxial ray approximation. Writing
$$E_0 = A_{00} \lpar r\comma \; z\rpar \, \, \exp \left\{{ - ik_0 \left({z\, \, + \, \, S_0 \lpar r\comma \; z\rpar } \right)} \right\}\comma \;$$
$$E_R = A_{R0} \lpar r\comma \; z\rpar \, \, \exp \left\{{ - ik_R \left({z\, \, + \, \, S_R \lpar r\comma \; z\rpar } \right)} \right\}\comma \;$$
$$E_B = A_{B0} \lpar r\comma \; z\rpar \, \, \exp \left\{{ - ik_B \left({z\, \, + \, \, S_B \lpar r\comma \; z\rpar } \right)} \right\}.$$Using the above equations in Eqs (7), (8), and (9) and on separating real and imaginary parts, one can obtain a set of coupled equations. Eq. (7) gives (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968)
$$\eqalign{ 2\displaystyle{\partial A_{00} \over \partial z} + &2\displaystyle{\partial A_{00} \over \partial r} \displaystyle{\partial S_0 \over \partial r} + \left(\displaystyle{\partial^2 S_0 \over \partial r^2} + \displaystyle{1 \over r}\displaystyle{\partial S_0 \over \partial r} \right) A_{00} \cr &\quad + {\rm e}^2 {\rm \omega} _{\rm pe}^2 \left[\displaystyle{k_L^2 \left\vert A_{R0} \right\vert^2 \over 8 m_0^2 {\rm \gamma} ^3} {\rm \omega}_L {\rm \omega}_0 {\rm \omega}_R^2 \Gamma_e c {\rm \varepsilon}_0^{1/2} \right. \cr & \left. + \displaystyle{{\rm \omega}_A \vert A_{B0} \vert^2 \over 8{m_0}M {\rm \gamma}^2 \Gamma_i c_s^2 {\rm \omega}_B^2 {\rm \omega}_0 c {\rm \varepsilon}_0^{1/2}} \right] A_{00}^2 = 0\comma \;}$$and
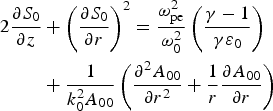$$\eqalign{2\displaystyle{{\partial {S_0}} \over {\partial z}} & + {\left({\displaystyle{{\partial {S_0}} \over {\partial r}}} \right)^2} = \displaystyle{{{\rm \omega} _{{\rm pe}}^2 } \over {{\rm \omega} _0^2 }}\left({\displaystyle{{{\rm \gamma} - 1} \over {{\rm \gamma} {{\rm \varepsilon} _0}}}} \right)\cr & + \displaystyle{1 \over {k_0^2 {A_{00}}}}\left({\displaystyle{{{\partial ^2}{A_{00}}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {A_{00}}} \over {\partial r}}} \right)}$$similarly, Eq. (8) gives:
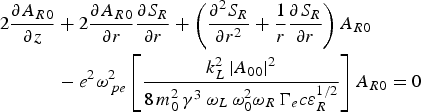$$\eqalign{ 2\displaystyle{{\partial A_{R0}} \over {\partial z}} &+ 2\displaystyle{{\partial A_{R0}} \over {\partial r}}\displaystyle{{\partial S_R } \over {\partial r}} + \left({\displaystyle{{\partial ^2 S_R } \over {\partial r^2 }} + \displaystyle{1 \over r}\displaystyle{{\partial S_R } \over {\partial r}}} \right)A_{R0}\cr & -e^2 {\rm \omega} _{\,pe}^2 \left[{\displaystyle{{k_L^2 \left\vert {A_{00} } \right\vert ^2 } \over {8\, m_0^2 \, {\rm \gamma} ^3 \, {\rm \omega} _L \, {\rm \omega} _0^2 {\rm \omega} _R \, \Gamma _e c{\rm \varepsilon} _R ^{{1 / 2}} }}} \right]A_{R0} = 0 \cr & }$$and
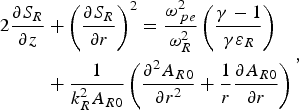$$\eqalign{ 2\displaystyle{{\partial {S_R}} \over {\partial z}} &+ {\left({\displaystyle{{\partial {S_R}} \over {\partial r}}} \right)^2} = \displaystyle{{{\rm \omega} _{\,pe}^2 } \over {{\rm \omega} _R^2 }}\left({\displaystyle{{{\rm \gamma} - 1} \over {{\rm \gamma} {{\rm \varepsilon} _R}}}} \right)\cr & + \displaystyle{1 \over {k_R^2 {A_{R0}}}}\left({\displaystyle{{{\partial ^2}{A_{R0}}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {A_{R0}}} \over {\partial r}}} \right)}\comma \;$$similarly, Eq. (9) gives:
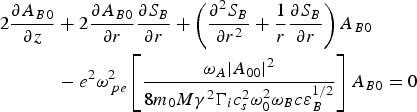$$\eqalign{ 2\displaystyle{{\partial {A_{B0}}} \over {\partial z}} &+ 2\displaystyle{{\partial {A_{B0}}} \over {\partial r}}\displaystyle{{\partial {S_B}} \over {\partial r}} + \left({\displaystyle{{{\partial ^2}{S_B}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {S_B}} \over {\partial r}}} \right){A_{B0}}\cr & - {e^2} {\rm \omega} _{\,pe}^2 \left[{\displaystyle{{{{\rm \omega} _A} {{\left\vert {{A_{00}}} \right\vert }^2}} \over {8 {m_0}M {{\rm \gamma} ^2} {\Gamma _i}c_s^2 {\rm \omega} _0^2 {{\rm \omega} _B}c {\rm \varepsilon} _B^{1/2} }}} \right]{A_{B0}} = 0}$$and
$$\eqalign{ 2\displaystyle{{\partial {S_B}} \over {\partial z}} &+ {\left({\displaystyle{{\partial {S_B}} \over {\partial r}}} \right)^2} = \displaystyle{{{\rm \omega} _{\,pe}^2 } \over {{\rm \omega} _B^2 }}\left({\displaystyle{{{\rm \gamma} - 1} \over {{\rm \gamma} {{\rm \varepsilon} _B}}}} \right)\cr & + \displaystyle{1 \over {k_B^2 {A_{B0}}}}\left({\displaystyle{{{\partial ^2}{A_{B0}}} \over {\partial {r^2}}} + \displaystyle{1 \over r}\displaystyle{{\partial {A_{B0}}} \over {\partial r}}} \right)}.$$The solution for the pump wave (Eqs (13) and (14)) can be written as (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968)
$${A_{00}^2 = \displaystyle{{E_{00}^2 \lpar z = 0\rpar } \over {{\rm f}_0^2 \lpar z\rpar }}\exp \left[{ - \, \displaystyle{{r^2 } \over {r_0^2 \, {\rm f}_0^2 \lpar z\rpar }}\, - \, 2G_0 z} \right]}\comma \;$$
$${{\rm S}_0} = \displaystyle{{{r^2}} \over 2}\displaystyle{1 \over {{{\rm f}_0}\lpar z\rpar }}\displaystyle{{d {{\rm f}_0}\lpar z\rpar } \over {dz}} + {\Phi _0}\lpar z\rpar \comma \;$$
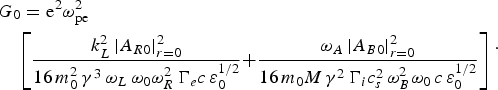$$\eqalign{& G_0 = {\rm e}^2 {\rm \omega} _{{\rm pe}}^2\cr & \quad \left[{\displaystyle{{k_L^2 \left\vert {A_{R0} } \right\vert _{r = 0}^2 } \over {16\, m_0^2 \, {\rm \gamma} ^3 \, {\rm \omega} _L \, {\rm \omega} _0 {\rm \omega} _R^2 \, \Gamma _e c\, {\rm \varepsilon} _0 ^{{1 / 2}} }}{ + \displaystyle{{{\rm \omega} _A \left\vert {A_{B0} } \right\vert _{r = 0}^2 } \over {16\, m_0 M\, {\rm \gamma} ^2 \, \Gamma_i c_s^2 \, {\rm \omega} _B^2 {\rm \omega} _0 \, c\, {\rm \varepsilon} _0 ^{{1 / 2}} }}}} \right]}.$$Similarly, the following solutions are obtained for the Raman scattered beam (Eqs (15) and (16)):
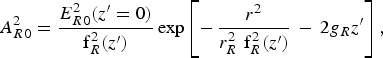$$A_{R0}^2 = \displaystyle{{E_{R0}^2 \lpar z^{\prime} = 0\rpar } \over {{\rm f}_R^2 \lpar z^{\prime}\rpar }}\exp \left[{ - \, \displaystyle{{r^2 } \over {r_R^2 \, \, {\rm f}_R^2 \lpar z^{\prime}\rpar }}\, - \, 2g_R z^{\prime}} \right]\comma \;$$
$$S_R = \displaystyle{{r^2 } \over 2}\displaystyle{1 \over {{\rm f}_R \lpar z^{\prime}\rpar }}\displaystyle{{d{\rm f}_R \lpar z^{\prime}\rpar } \over {dz}} + \Phi _R \lpar z^{\prime}\rpar \comma \;$$
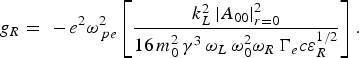$$g_{R} = \, \, - \, e^2 {\rm \omega} _{\,pe}^2 \left[{\displaystyle{{k_L^2 \left\vert {A_{00} } \right\vert _{r = 0}^2 } \over {16\, m_0^2 \, {\rm \gamma} ^3 \, {\rm \omega} _L \, {\rm \omega} _0^2 {\rm \omega} _R \, \Gamma _e c{\rm \varepsilon} _R ^{{1 / 2}} }}} \right].$$Here z' = L z – z, L z is the interaction length. Similarly, the solutions for the Brillouin scattered beam (Eqs (17) and (18)) are:
$${A_{B0}^2 = \displaystyle{{E_{B0}^2 \lpar z^{\prime} = 0\rpar } \over {{\rm f}_B^2 \lpar z^{\prime}\rpar }}\exp \, \, \left[{ - \displaystyle{{r^2 } \over {r_B^2 {\rm f}_B^2 \lpar z^{\prime}\rpar }}\, { - \, 2g_B z^{\prime}}} \right]}\comma \;$$
$$S_B = \displaystyle{{r^2 } \over 2}\displaystyle{1 \over {{\rm f}_B \lpar z^{\prime}\rpar }}\displaystyle{{d{\rm f}_B \lpar z^{\prime}\rpar } \over {dz}} + \Phi _B \lpar z^{\prime}\rpar \comma \;$$
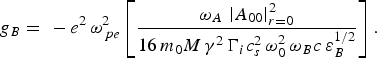$$g_{B} = \, \, - \, e^2 \, {\rm \omega} _{\,pe}^2 \left[{\displaystyle{{{\rm \omega} _A \, \left\vert {A_{00} } \right\vert _{r = 0}^2 } \over {16\, m_0 M\, {\rm \gamma} ^2 \, \Gamma_i c_s^2 \, {\rm \omega} _0^2 \, {\rm \omega} _B c\, {\rm \varepsilon} _B^{1/2} }}} \right].$$Here G 0, g R and g B are the gain factors for the pump wave, SRS wave and SBS wave, respectively, in 5WI case and other symbols have their usual meaning. Here the relativistic factor γ is given by
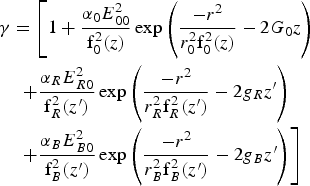$$\eqalign{& {\rm \gamma} = \left[{1 + \displaystyle{{{{\rm \alpha} _0}E_{00}^2 } \over {{\rm f}_0^2 \lpar z\rpar }}\exp \left({\displaystyle{{ - {r^2}} \over {r_0^2 {\rm f}_0^2 \lpar z\rpar }} - 2{G_0}z} \right)} \right. \cr & \quad \left.+ \displaystyle{{{{\rm \alpha} _R}E_{R0}^2 } \over {{\rm f}_R^2 \lpar {z^{\prime}}\rpar }} \exp \left({\displaystyle{{ - {r^2}} \over {r_R^2 {\rm f}_R^2 \lpar {z^{\prime}}\rpar }} - 2{g_{R}}{z^{\prime}}} \right)\right. \cr & \quad \left. { + \displaystyle{{{{\rm \alpha} _B}E_{B0}^2 } \over {{\rm f}_B^2 \lpar {z^{\prime}}\rpar }} \exp \left({\displaystyle{{ - {r^2}} \over {r_B^2 {\rm f}_B^2 \lpar {z^{\prime}}\rpar }} - 2{g_{B}}{z^{\prime}}} \right)} \right]}$$where
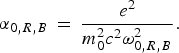$${\rm \alpha} _{0\comma R\comma B} \, = \, \displaystyle{{e^2 } \over {m_0^2 c^2 {\rm \omega} _{0\comma R\comma B}^2 }}.$$Here f0, fR and fB are the dimensionless beam width parameters of the pump beam , SRS and SBS beam, respectively. The governing differential equations for the dimensionless beam width parameters are given by:
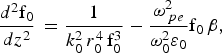$$\displaystyle{{d^2 {\rm f}_0 } \over {dz^2 }} \, = \displaystyle{1 \over {k_0^2 \, r_0^4 \, {\rm f}_0^3 }} - \displaystyle{{{\rm \omega} _{\,pe}^2 } \over {{\rm \omega} _0^2 {\rm \varepsilon} _0 }}{\rm f}_0 \, {\rm \beta}\comma \;$$
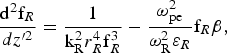$$\displaystyle{{{{\rm d}^2}{{\rm f}_R}} \over {d{z^{\prime 2}}}} = \displaystyle{1 \over {{\rm k}_{\rm R}^2 r_R^4 {\rm f}_R^3 }} - \displaystyle{{{\rm \omega} _{{\rm pe}}^2 } \over {{\rm \omega} _{\rm R}^2 {{\rm \varepsilon} _R}}}{{\rm f}_R} {\rm \beta}\comma \;$$
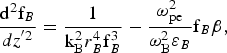$$\displaystyle{{{{\rm d}^2}{{\rm f}_B}} \over {d{z^{^\prime 2}}}} = \displaystyle{1 \over {{\rm k}_{\rm B}^2 r_B^4 {\rm f}_B^3 }} - \displaystyle{{{\rm \omega} _{{\rm pe}}^2 } \over {{\rm \omega} _{\rm B}^2 {{\rm \varepsilon} _B}}}{{\rm f}_B} {\rm \beta} \comma \;$$where β is given by
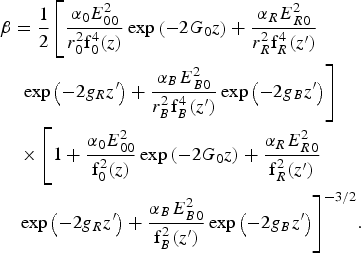$$\eqalign{& {\rm \beta} = \displaystyle{1 \over 2}\left[{\displaystyle{{{{\rm \alpha} _0} E_{00}^2 } \over {r_0^2 {\rm f}_0^4 \lpar z\rpar }} \exp \left({ - 2{G_0}z} \right)+ \displaystyle{{{{\rm \alpha} _R} E_{R0}^2 } \over {r_R^2 {\rm f}_R^4 \lpar {z^{\prime}}\rpar }} } \right. \cr & \quad \left. {\exp \left({ - 2{g_{R}}{z^{\prime}}} \right)+ \displaystyle{{{{\rm \alpha} _B} E_{B0}^2 } \over {r_B^2 {\rm f}_B^4 \lpar {z^{\prime}}\rpar }} \exp \left({ - 2{g_{B}}{z^{\prime}}} \right)} \right]\cr & \quad \times \left[{1 + \displaystyle{{{{\rm \alpha} _0} E_{00}^2 } \over {{\rm f}_0^2 \lpar z\rpar }}\exp \left({ - 2{G_0}z} \right)+ \displaystyle{{{{\rm \alpha} _R} E_{R0}^2 } \over {{\rm f}_R^2 \lpar {z^{\prime}}\rpar }}} \right. \cr & \quad {\left. {\exp \left({ - 2{g_R}{z^{\prime}}} \right)+ \displaystyle{{{{\rm \alpha} _B} E_{B0}^2 } \over {{\rm f}_B^2 \lpar {z^{\prime}}\rpar }}\exp \left({ - 2{g_B}{z^{\prime}}} \right)} \right]^{ - 3/2}}.}$$In order to see the effect of filamentation on the backscattered beams, we have derived the expression of the back reflectivity for the SRS wave and the SBS wave:
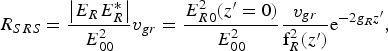$${R_{SRS}} = \displaystyle{{\left\vert {{E_R}E_R^ * } \right\vert } \over {E_{00}^2 }}{v_{gr}} = \displaystyle{{E_{R0}^2 \lpar {z^{\prime}} = 0\rpar } \over {E_{00}^2 }}\displaystyle{{{v_{gr}}} \over {{\rm f}_R^2 \lpar {z^{\prime}}\rpar }}{{\rm e}^{ - 2{\rm }g_{R}z^{\prime}}}\comma \;$$
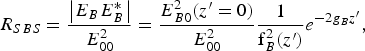$$R_{SBS} = \displaystyle{\left\vert E_B E_B^{\ast} \right\vert \over E_{00}^2} = \displaystyle{E_{B0}^2 \lpar z^{\prime} = 0\rpar \over E_{00}^2} \displaystyle{1 \over {\rm f}_B^2 \lpar z^{\prime}\rpar} e^{ - 2 g_B z^{\prime}}\comma \;$$
where 
$\nu_{gr} = (1 - {\rm \omega}_{pe}^2 / {\rm \omega}_R^2)^{1/2} \left(1 - {\rm \omega}_{pe}^2 / {\rm \omega}_0^2 \right)^{- 1/2}$, is ratio of the group velocity of the SRS beam to the group velocity of the pump beam. In the next section the numerical results are obtained.
3. RESULTS AND DISCUSSION
By solving the set of coupled Eqs (30), (31), and (32); we can obtain the dynamical evolution of the pump beam (
${\rm f}_0 $) and the scattered beams (
${\rm f}_{\rm R} \, {\rm and}\, \, {\rm f}_{\rm B} $). In these coupled equations; the first term (diffraction term) in the right-hand side leads to the divergence, while the second term (nonlinear coupling term) is responsible for the converging behavior of the respective beam. We have solved these coupled equations numerically by Runge-Kutta methods, for the parameter:
${{N_o} \over {N_{cr} }} = 0.01\comma \; $ λ = 1.053 μm, r 0 = r R,B = 12 μm, vth = 0.1c, I = 5 × 1019 W/cm2, Seed beam intesity = I × 10−4 W/cm2 by using the following boundary conditions:
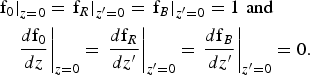$$\eqalign{& {\left. {{{\rm f}_0}} \right\vert _{z = 0}} = {\left. {{{\rm f}_R}} \right\vert _{{z^{\prime}} = 0} = {\left. {{{\rm f}_B}} \right\vert _{{z^{\prime}} = 0}} = 1\, \, {\rm and}\, \, } \cr & \quad {\left. {\displaystyle{{d{{\rm f}_0}} \over {dz}}} \right\vert _{z = 0}} = {\left. {\displaystyle{{d{{\rm f}_R}} \over {d{z^{\prime}}}}} \right\vert _{{z^{\prime}} = 0}} = {\left. {\displaystyle{{d{{\rm f}_B}} \over {d{z^{\prime}}}}} \right\vert _{{z^{\prime}} = 0}} = 0.}$$Figure 1 shows the variation of the dimensionless beam width parameters of the pump beam (f0) versus normalized distance of propagation for different cases. Dotdash curve corresponds to the undepleted pump case, dot and dash curve correspond to the pump depletion in isolated SBS and SRS, respectively, (3WI case) and solid curve depicts the pump depletion in 5WI case. Figure 2 represents the variation in the normalized intensity of the pump beam against the normalized distance of propagation for two cases: (1) corresponds to the undepleted pump case and; (2) corresponds to the pump depletion in 5WI case respectively. It is clear from the above figures that the relativistic filamentation process gets affected by the pump depletion significantly. Due to the pump depletion the relativistic Lorentz factor gets modified, which suppresses the filamentation. In the 5WI case, the pump depletion is more (in comparison to undepleted case and 3WI case) and hence results in lesser filamentation. Similarly, for the Raman and Brillouin back scattered beams, Figures 3a and 3b represents the normalized intensity variation respectively for the 5WI case. Intensities are normalized by the initial peak intensity of the pump beam.
Fig. 1. Variation of the dimensionless beam width parameters for the pump beam with the normalized distance of propagation.
Fig. 2. Normalized intensity plot of pump laser beam (a) without depletion, and (b) with depletion (5WI case).
Fig. 3. Normalized Intensity plot of back scattered beams in five wave interaction case (a) SRS and (b) SBS.
The variation in the back reflectivity against the normalized distance of propagation for SRS and SBS processes is shown in Figures 4 and 5, respectively. For each process, two cases are considered, dash and dot-dash curve corresponds to the without filamentation case (also referred as plane pump wave case) whereas dot and solid curve corresponds to the filamentation case (also referred as Gaussian pump wave case). Since the intensity of the scattered beams is proportional to the intensity of the pump, therefore enhancement in the back scattering is expected due to filamentation in contrast to the without filamentation case. Due to this filamentation effect, the intensity of the laser beam gets enhanced, which further modifies the gains (g R and g B) and consequently the back reflectivities (R SRS and R SBS) also get enhanced at the focused positions. In both the cases (filamentation and without filamentation), reflectivity for the 5WI case is always lower than 3WI case because the pump depletion in 5WI case is more than the 3WI case, which results in the lower reflectivity for the 5WI case.
Fig. 4. The variation of back reflectivity of SRS process with the normalized distance of propagation.
Fig. 5. The variation of back reflectivity of SBS process with the normalized distance of propagation.
Due to relativistic mass correction in the electron mass, modification in the back reflectivity for the SRS process (R SRS) is expected however the back reflectivity for the SBS process (R SBS) is not supposed to be changed. But from the Figure 5 it is clear that R SBS is greatly affected by relativistic self-focusing process, which can be understood as follows: from the set of coupled Eqs. (30), (31), and (32) the dimensionless beam width parameter of the SBS beam (fB) depends on coupling factor β, which further depends on the dimensionless beam width parameter (fR) and gain (g R) of the SRS beam along with the other parameters. In addition to this SBS gain factor g B also depends on relativistic factorγ, which is a function of fR and g R along with the other parameters. So any modification in the SRS process due to relativistic mass correction will further affect the fB and g B, hence the R SBS gets modified.
4. CONCLUSION
In summary, we have studied the two coexisting instabilities, SRS and SBS simultaneously, at relativistic laser power along with the relativistic filamentation of the pump and the scattered beams, within the paraxial ray approximations. We have examined that the pump depletion and relativistic filamentation affects the back-reflectivity of scattered beams significantly, for the 5WI case. Due to this filamentation effect, the intensity of the laser beam gets enhanced, which further modifies the gains (g R and g B) and consequently the back reflectivity (R SRS and R SBS) also gets enhanced. We have also demonstrated that the back reflectivities (R SRS and R SBS) get suppressed in the coexistence (5WI) case.
ACKNOWLEDGMENT
This work was partially supported by CSIR, India and DST, India.
