I. INTRODUCTION
“Silico-ferrite of calcium and aluminium” (SFCA) phases are the key bonding materials of industrial iron-ore sinter. Sinter is a major feedstock material of blast furnaces, utilised extensively worldwide in the production of steel from iron ore. During the iron ore sintering processes, iron-ore fines (the <6.3 mm fraction of iron ore) are mixed with flux (e.g. CaCO3) and coke and heated rapidly (~ 4 min) to temperatures of ~1300 °C followed by slower cooling in air (Dawson et al., Reference Dawson, Ostwald and Hayes1985). This results in partial melting of the mixture and the formation of a porous but physically strong composite material in which iron-bearing minerals (i.e. hematite, Fe2O3, and magnetite, Fe3O4, including relict ore particles) are bound by a complex matrix containing predominantly “SFCA” phases, as well as other Ca-rich ferrite phases, calcium silicates and glass (quenched liquid).
The “SFCA” in iron-ore sinter has been categorised on the basis of composition, morphology and crystal structure into two main types. The first is a low-Fe form called SFCA, which when found in industrial sinters typically contains 60–76 wt% Fe2O3, 13–16 wt% CaO, 3–10 wt% SiO2, and 4–10 wt% Al2O3. The second is a high-Fe, low-Si (e.g. 84 wt% Fe2O3, 13 wt% CaO, 1 wt% SiO2, and 2 wt% Al2O3) form called SFCA-I. A number of recent investigations have utilised in situ powder diffraction techniques, including laboratory-based X-ray diffraction (XRD), synchrotron XRD (S-XRD), and neutron diffraction (ND), with subsequent Rietveld refinement-based quantitative phase analysis (QPA) to determine the formation mechanisms of SFCA and SFCA-I under simulated sintering conditions (Scarlett et al., Reference Scarlett, Madsen, Pownceby and Christensen2004a, Reference Scarlett, Pownceby, Madsen and Christensen2004b; Webster et al., Reference Webster, Pownceby, Madsen and Kimpton2012, Reference Webster, Pownceby, Madsen and Kimpton2013a, Reference Webster, Pownceby and Madsen2013b, Reference Webster, Pownceby, Madsen, Studer, Manuel and Kimpton2014). In this paper, approaches to QPA and data collection strategies designed to minimise sample-related errors, and replicate industrial conditions more closely, are presented and discussed.
II. EXPERIMENTAL
A. Sample preparation
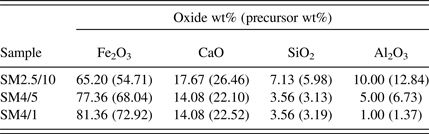
Table I shows the calculated oxide concentration (wt%) of each of the synthetic sinter mixtures examined in this study. The mixtures had compositions within the SFCA compositional stability domain established by Patrick and Pownceby (Reference Patrick and Pownceby2001) and were, therefore, designed to form SFCA. The mixtures were prepared from fine grained (<20 μm) synthetic Fe2O3 (Acros Organics, 99.999% purity), calcite (CaCO3, Thermo Fisher, 99.95%), quartz (SiO2, Sigma Aldrich, 99.995%), and gibbsite [Al(OH)3, Alcan OP25 Super White, 99.9%], which were mixed under acetone in a mortar and pestle with an intermediate drying and remixing stage to ensure homogenisation.
Table I. Compositions, in wt% oxides, of the sinter mixture samples. The numbers in parentheses show the actual wt% of each of the precursor materials [i.e. Fe2O3, CaCO3, SiO2, and Al(OH)3] in the room temperature mixture.

B. Data collection
Details of the in situ S-XRD, laboratory XRD, and ND experimentation have been described in detail previously (Webster et al., Reference Webster, Pownceby, Madsen and Kimpton2012, Reference Webster, Pownceby, Madsen and Kimpton2013a, Reference Webster, Pownceby and Madsen2013b, Reference Webster, Pownceby, Madsen, Studer, Manuel and Kimpton2014). Samples were heated over the range 25–1350 °C, at a heating rate of 20 °C min−1 from 25 to 600 °C as the decomposition temperature of CaCO3 was approached, and with individual datasets collected for 1 min continuously during heating. The rate was then reduced to 10 °C min−1 for the range 600–1350 °C which corresponded to the period of Ca-rich ferrite phase formation, reaction, and decomposition. This time–temperature profile is significantly slower than those encountered in industrial sintering – it was chosen so as to monitor phase formation with reasonable temperature resolution and to provide data with reasonable counting statistics. To simulate industrial heating rates more closely, a laboratory-based experiment was also performed using a heating rate of 175 °C min−1 with individual datasets collected for 0.1 min.
C. Quantitative phase analysis
Rietveld refinement-based QPA was performed using TOPAS (Bruker, 2009). Datasets were analysed sequentially, beginning with the dataset collected at room temperature. A parametric refinement approach, developed by Stinton and Evans (Reference Stinton and Evans2007) and shown to improve phase fractions in a number of cases, was beyond the scope of the current work. The crystal structure data of Blake et al. (Reference Blake, Hessevick, Zoltai and Finger1966), Maslen et al. (Reference Maslen, Strel'tsov, Strel'tsova and Ishizawa1995), Saalfeld and Wedde (Reference Saalfeld and Wedde1974), Lager et al. (Reference Lager, Jorgensen and Rotella1982), Schulz and Tscherry (Reference Schulz and Tscherry1972), Oftedal (Reference Oftedal1927), Berastegui et al. (Reference Berastegui, Eriksson and Hull1999), Decker and Kasper (Reference Decker and Kasper1957), Mumme et al. (Reference Mumme, Clout and Gable1998), Hamilton et al. (Reference Hamilton, Hoskins, Mumme, Borbidge and Montague1989), and Louisnathan (Reference Louisnathan1971), were used for the Fe2O3, CaCO3, Al(OH)3, α-SiO2, β-SiO2, CaO, C2(F1−xAx), CF, SFCA-I, SFCA, Ca2Al2SiO7, and Fe3O4 phases, respectively. The instrumental contribution to peak width and shape was determined from refinement of room-temperature data collected for a Y2O3 sample. The background was modelled using a Chebychev polynomial function. For the in situ S-XRD data, corrections to account for sample displacement and peak intensity variation in asymmetrical diffraction geometry were incorporated into the TOPAS refinement (Madsen et al., Reference Madsen, Grey and Mills2010). A March–Dollase preferred orientation correction ([002] direction) was applied to the Al(OH)3 reflections (Dollase, Reference Dollase1986).
The use of the QPA algorithm (Hill and Howard, Reference Hill and Howard1987) embodied in TOPAS returns relative, rather than absolute, concentrations for crystalline phases in a system if amorphous material, including melt phases, is present. The previous in situ work performed in this context (Scarlett et al., Reference Scarlett, Madsen, Pownceby and Christensen2004a, Reference Scarlett, Pownceby, Madsen and Christensen2004b; Webster et al., Reference Webster, Pownceby, Madsen and Kimpton2012, Reference Webster, Pownceby, Madsen and Kimpton2013a, Reference Webster, Pownceby and Madsen2013b, Reference Webster, Pownceby, Madsen, Studer, Manuel and Kimpton2014) has demonstrated that amorphous Al2O3 is present in these systems after the decomposition of Al(OH)3. Therefore, absolute phase concentrations as a function of temperature were determined using the “external standard” approach given by Webster et al. (Reference Webster, Madsen, Loan, Knott, Naim, Wallwork and Kimpton2010)
Here W i is the weight fraction of phase i, S i is the Rietveld scale factor, ZM is the unit-cell mass, V is the unit-cell volume, and μ m is the mass absorption coefficient of the entire mixture. I 0 and I i are the beam current values at the start of the first dataset and during dataset i, respectively. K is an experiment constant used to put W i on an absolute basis and was calculated for each sample using (i) the known concentrations of Fe2O3, CaCO3, SiO2, and Al(OH)3 in the starting mixture (the assumption is made that each of the materials in the starting sinter mixture are 100% crystalline), and (ii) the Rietveld-refined scale factor values for Fe2O3, CaCO3, SiO2, and Al(OH)3 in the first dataset collected at 25 °C according to
III. RESULTS AND DISCUSSION
A. QPA considerations
Figure 1 shows a plot of accumulated in situ S-XRD data, viewed down the intensity axis and with temperature plotted vs. 2θ, for the experiment performed on sample SM2.5/10. The first event during heating was the decomposition of Al(OH)3 to amorphous Al-oxide, which was complete by 315 °C. Then, the transformation of α-SiO2 to β-SiO2 occurred (complete by 583 °C) followed by decomposition of CaCO3 to CaO (complete by 671 °C). The first Ca-rich ferrite to form was alumina-substituted dicalcium ferrite [i.e. C2(F1−xAx), where C = CaO, F = Fe2O3 and A = Al2O3] at ~720 °C, followed by CF and CFA (average composition 71.7 wt% Fe2O3, 12.9 wt% CaO, 0.3 wt% SiO2, and 15.1 wt% Al2O3 and unknown crystal structure) together at ~970 °C. As the temperature increased further, SFCA-I, SFCA, and gehlenite (nominally Ca2Al2SiO7, but also likely to contain some Fe) formed, at ~1090, 1160, and 1230 °C, respectively. Incongruent melting (i.e. solid 1 → liquid + solid 2) of SFCA, which was complete by 1334 °C, produced an assemblage of Fe3O4 in a CaO–SiO2–Al2O3-rich melt.

Figure 1. In situ S-XRD data collected for sample SM2.5/10, viewed down the intensity axis and showing the phase decomposition, transformation, and formation events over the range 25–1350 °C.
Figure 2 shows the results of the Rietveld refinement-based QPA for the SM2.5/10 experiment. Focussing initially on the data collected at 25 °C, the K value was 37.7 and the QPA-determined concentrations of Fe2O3, CaCO3, α-SiO2, and Al(OH) in the starting mixture were 53.7, 27.3, 6.1, and 12.9 wt%, respectively, giving bias values from the values in Table I of −1.0, 0.9, 0.1, and 0.1 wt%, respectively. This provides an indication of the maximum accuracy of the QPA methodology embodied in Eqs (1) and (2) for these experiments, and QPA values should therefore be interpreted to the nearest integer only.

Figure 2. Results of QPA for the in situ synchrotron X-ray diffraction experiment performed for sample SM2.5/10, showing absolute phase concentrations as a function of temperature.
The rationale behind using each of the materials in the starting mixture in Eq. (2) to calculate K, rather than using the concentration and refined S value for the most abundant material (i.e. Fe2O3) only, was to minimise the effect of microabsorption on the QPA since there was significant absorption contrast between Fe2O3 (mass absorption coefficient = 101.3 cm2 g−1) and the other materials in the starting mixture [33.8, 15.8, and 10.6 cm2 g−1 for CaCO3, SiO2, and Al(OH)3, respectively] at 11.23 keV. This energy was chosen as a compromise to avoid fluorescence from the Pt and Fe in the heating strip and sample, respectively, and to ensure that the highest d-spacing reflections for the SFCA and SFCA-I phases (d = 8.19 and 10.72 Å, respectively) were within the observable 2θ range. For the sake of comparison, if the concentration and S value for Fe2O3 only were used to calculate K according to
then K = 37.0 and the QPA values for the starting sinter mixture would be 54.7, 27.8, 6.2, and 13.1 wt%. The bias values would then be 0.0, 1.4, 0.3, and 0.3 wt% and, importantly, the phase concentration values would sum to the unrealistic value of 101.9 wt%.
It is also apparent in Figure 2 that the concentration of Fe3O4 decreased significantly above ~1300 °C after melting of SFCA was complete; this decrease is considered to be an artefact of the experimental methodology. High-quality XRD data, with accurate relative peak intensities and positions, requires the exposure of a large number of randomly oriented crystallites to the X-ray beam. This was not the case for the Fe3O4 and melt phase assemblage, where, firstly, the sample/X-ray beam interaction volume was small (~2 mm3), secondly, there were only a relatively small number of Fe3O4 crystallites in a large amount of melt, and, finally, there was likely to be a flow of material away from the beam since the Pt strip was tilted at 4° from horizontal to achieve 4° incident beam-to-sample angle. Attempts to improve data quality by rocking and/or translating the sample stage did not alleviate these effects.
Owing to the highly penetrating nature of neutrons, powder ND provides the opportunity to achieve the volume diffraction necessary to reduce the effects of poor particle statistics observed in the S-XRD data at high temperature. To assess this, in situ ND data were collected for the sinter mixture SM4/1 (composition given in Table I) over the range 25–1300 °C. The data accumulated in the range 1055–1300 °C are plotted in Figure 3(a). SFCA was stable in the range 1181–1234 °C and decomposed to form the Fe3O4 and melt phase assemblage. Figure 3(b) shows plots of the refined Fe3O4 scale factors as a function of temperature for the in situ ND experiment and an in situ S-XRD experiment performed for SM4/1. The two plots are offset by ~40 °C in the temperature axis, which is attributed to pO2 differences between the ND (vacuum) and S-XRD (pO2 = 5 × 10−3 atm) experiments (Webster et al., Reference Webster, Pownceby, Madsen and Kimpton2013a).

Figure 3. (a) In situ ND data collected from sample SM4/1 over the range 1055–1300 °C; and (b) refined scale factor for Fe3O4 as a function of temperature for in situ S-XRD and ND experiments performed for SM4/1.
The ND-determined scale factor varied by 13% between 1234 and 1300°C, whereas the S-XRD-determined scale factor decreased by 57% in the range 1188–1259 °C and by 82% in the range 1188–1304 °C. Therefore, to assess the effect of process variables (e.g. Al2O3 content, CaO:SiO2 ratio, and pO2) on the amount of Fe3O4 formed in these iron ore sintering reactions, it is recommended to collect in situ ND data. ND data would also allow for QPA of phases crystallising during the cooling stage of the process. In situ ND and S-XRD experiments are, therefore, highly complementary in the iron ore sintering context, with the high angular resolution of S-XRD data crucial to unravelling the phase formation mechanisms of low-symmetry phases at lower temperatures.
B. Approaching industrial heating rates
Figure 4(a) shows a plot of the accumulated in situ laboratory XRD data collected for sample SM4/5, and Figure 4(b) is a stack plot of the data collected in the range 1159–1294 °C. Comparing these results with the S-XRD results for SM4/5 under the slower heating rate presented by Webster et al. (Reference Webster, Pownceby, Madsen and Kimpton2012), reflections for all of the characteristic phases including SFCA-I are clearly observed in the 6 s datasets with the exception, importantly, of SFCA. Given that this sinter mixture was designed to form SFCA (i.e. was within the equilibrium SFCA compositional domain established by Patrick and Pownceby, Reference Patrick and Pownceby2001), this provides significant insight into the effect of kinetics on phase formation in this system during heating. From an industrial sintering point of view, even if the reactive fines component of an industrial sinter mix has an SFCA composition, SFCA will not necessarily form during the rapid heating stage.

Figure 4. (a) In situ laboratory XRD data collected for the sample SM4/5 at a heating rate of 175 °C min−1; and (b) stack plot of datasets collected in the range 1159–1294 °C (datasets have been offset in the intensity axis for clarity).
IV. CONCLUSION
In situ S-XRD, ND, and laboratory XRD experimentation has been performed under simulated iron ore sintering conditions, and has been aimed at determining the formation mechanisms of SFCA and SFCA-I iron ore sinter bonding phases, and the effect of process variables on these mechanisms. It has been demonstrated that using an external standard approach to determine absolute phase concentrations via QPA, by including the entire starting sample in the determination of the experiment constant K, rather than considering the most abundant phase (i.e. Fe2O3) only, the errors in the QPA, induced largely by microabsorption, are reduced. The volume diffraction afforded by in situ ND was shown to be important for characterising the behaviour of Fe3O4 after melting of the SFCA phases was complete, and any QPA study attempting to determine the effect of process variables on the amount of Fe3O4 formed should involve ND. Finally, rapid data collection on a laboratory diffractometer has allowed for phase formation and decomposition to be characterised at a heating rate more closely approximating those encountered in industrial iron ore sintering. This demonstrates the power of such laboratory-based experimentation. Importantly, by the absence of clear SFCA reflections in the data it has given insight into the effect of kinetics in the formation of this phase.
ACKNOWLEDGEMENTS
The authors acknowledge the Australian Nuclear Science and Technology Organisation for financial support of this research. This research was partially undertaken on the powder diffraction beamline (10BM1) at the Australian Synchrotron, Victoria, Australia, under beamtime award AS132/PD6321. The Australian Institute of Nuclear Science and Engineering is acknowledged for travel and accommodation support under award P2275 for beamtime on the WOMBAT neutron powder diffractometer, New South Wales.