1. INTRODUCTION
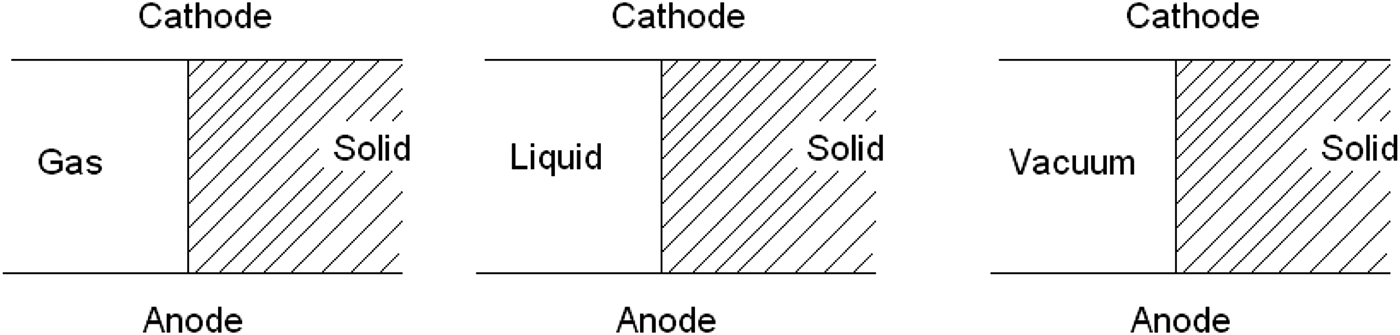
Composite insulation structures are widely used in high-voltage (HV) devices and pulsed power systems. Generally, there are three types of composite insulation structures: gas/solid insulators (Xiao et al., Reference Xiao, Zhang, Zhang, Li, Zhang, Song, Hu, Sun, Huo, Chen, Zhang and Liu2010; Peng et al., Reference Peng, Liu, Song and Su2011; Shao et al., Reference Shao, Tarasenko, Zhang, Baksht, Yan and Shut'Ko2012; Zhao et al., Reference Zhao, Pan, Su, Zhang, Wang, Fang, Sun and Li2013a), liquid/solid insulators (Wang et al., Reference Wang, Hu and Song2005; Cheng et al., Reference Cheng, Liu, Zhang, Hong and Qian2012; Liu et al., Reference Liu, Zhang, Fan, Hong and Feng2012; Zhang et al., Reference Zhang, Liu, Wang, Fan, Zhang and Feng2012; Zhao et al., Reference Zhao, Su, Zhang and Pan2012; Reference Zhao, Su, Zhang, Pan, Wang, Fang, Sun and Li2013b; Reference Zhao, Su, Zhang, Pan, Wang, Sun, Li, Zeng and Cheng2013c), and vacuum/solid insulators (Kiricov et al., Reference Kiricov, Belomyttsev, Ryzhov, Turchanovsky and Tarakanov2003; Milton, Reference Milton1972; Miller, Reference Miller1989; Reference Miller1993; Zhao et al., Reference Zhao, Peng, Pan, Zhang and Su2010; Wang et al., Reference Wang, Du and Hu2012; Zhang & Liu, Reference Zhang and Liu2012). These insulators play both the roles of separating a megavolt pulse voltage and presenting mechanical support. A reasonable design for the composite insulation structures can present a reliable and safe performance of the pulsed power systems. Figure 1 shows the typical composite insulators in pulsed power systems. For each type of composite insulator, the total insulation can be invalid due to different failure patterns. There are basically seven failure patterns for the three types of composite insulators according to where the failure occurs: gas breakdown, liquid breakdown, vacuum breakdown, solid breakdown, gas flashover, liquid flashover, and vacuum flashover. These failure patterns are listed in Table 1.
Fig. 1. Typical composite insulators in HV devices and pulsed power systems.
Table 1. Basic insulation failure patterns of composite insulators
For these failure patterns, a lot of insulation design formulas were suggested by different researches. In the 1960s, Martin (Reference Martin1992; Martin et al., Reference Martin, Guenther and Kristiansen1996) put forward a set of empirical insulation formula on the pulsed power systems, which includes the formula on the electric breakdown strength (E BD) of gas, liquid, solid, and electric surface flashover strength (E f) of vacuum. These formulas are well applied in practical insulation design. The specific expressions and the applied conditions of these formulas are summarized in Table 2. Aside from the Martin's formula, some other formulas were also put forward. Therein, Adler et al. (Reference Adler and Temple1978) presented an empirical formula for the pure vacuum breakdown, which was also listed in Table 2; Stygar et al. (Reference Stygar, Spielman, Anderson, Clark, Douglas, Gilliland, Horry, Hughes, Ives, Long, Martin, McDaniel, Milton, Mostrom, Seamen, Shoup, Smith, Struve, Vogtlin, Wagoner and Yamamoto1999) proposed a formula to describe the E f of vacuum insulator, which is as follows:
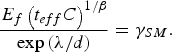$$\displaystyle{{E_f \left({t_{eff} C} \right)^{{1 / {\rm \beta} }} } \over {\exp \left({{{\rm \lambda} / d}} \right)}} = {\rm \gamma} _{SM}.$$where, E f corresponds to a flashover probability of 50% in kV/cm, t eff is the effective pulse width in μs, C is the mid perimeter of the insulator in cm; d is the thickness of the insulator in cm, β, λ and γSM are all constants. According to Wang (Reference Wang2006), for the condition of 0.5 ns < t eff < 10 µs and 0.5 < d < 4.32 cm, β = 10, λ = 0.24, and γ = 224 ± 15. A formula on the applied field of the vacuum insulators was also given, which is as follows (Vitkovitsky, Reference Vitkovitsky1987; Pai et al., Reference Pai and Zhang1995):
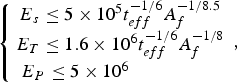$$\left\{{\matrix{ {E_s \le 5 \times 10^5 t_{eff}^{{{ - 1} / 6}} A_f^{{{ - 1} / {8.5}}} } \cr {E_T \le 1.6 \times 10^6 t_{eff}^{{{ - 1} / 6}} A_f^{{{ - 1} / 8}} } \cr \hskip-25pt{E_P \le 5 \times 10^6 \matrix{ {} & {} & {} \cr } } \cr } } \right.\comma \;$$where E S is the electric field (E-field) parallel with the insulator surface, E T is the total E-field, E p is the E-field on the cathode triple junction (CTJ), t eff is the effective pulse width as defined previously, and A f is the insulator surface area. Eq. (2) is usually applied on a nanosecond time scale, and the units for the parameters in Eq. (2) are using the MKS system. Even though Eqs. (1) and (2) are both for vacuum insulators, the application objects of them are different. For example, Eq. (1) is mainly for the multi-layer insulator stacks, whereas Eq. (2) is basically for the single low-inductance radial insulators. A formula for the gas breakdown on a nanosecond time scale was also reported, which is:
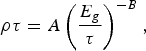$${\rm \rho} {\rm \tau} = A\left({\displaystyle{{E_g } \over {\rm \tau} }} \right)^{ - B}\comma \;$$where ρ is the gas density in g/cm3, τ is the time lag in s, E g is the gas breakdown strength as defined in Table 1 in kV/cm, A and B are both constants. The values for A and B were given by different researches, for example, Martin (Reference Martin1985; Reference Martin1989; Martin et al., Reference Martin, Seamen, Jobe and Pena1991) suggested that A = 97800 and B = 3.44; Mankowski (Reference Mankowski1997) suggested that A = 0.9 and B = 2.25; and Shao et al. (Reference Shao, Sun, Yan, Wang, Yuan, Sun and Zhang2006; Reference Shao, Sun, Yan and Zhang2007; Reference Shao, Tarasenko, Zhang, Baksht, Yan and Shut'Ko2012) obtained that A = 0.78 and B = 2.14. The fitting curves by the three groups of values are close to each other (Shao et al., Reference Shao, Sun, Yan, Wang, Yuan, Sun and Zhang2006). Recently, Zhao et al. (Reference Zhao, Liu, Su, Pan and Zhang2011) presented a formula to describe the thickness effect on E BD of different polymers, which is:
$$E_{BD} d_{}^{{1 / m}} = E_{BD1}\comma \;$$where d is the thickness of polymers, E BD1 is the E BD of polymers with unit thickness, which can be considered as a constant, for example, E BD1|d=1 mm of nylon is 1.58 MV/cm, m is also a constant, which is suggested to be 8 on a nanosecond time scale.
Table 2. Martin's empirical formula and other insulation formula for different types of insulation media
Formula of gas, liquid, solid breakdown can be seen in Martin (Reference Martin1992); formula of vacuum breakdown can be seen in Adler et al. (Reference Adler and Temple1978); formula of vacuum flashover can be seen in Martin et al. (Reference Martin, Guenther and Kristiansen1996).
Aside from these formulas, the general principles on composite insulation design are also concluded. Taking the vacuum/solid insulators as an example, researchers concluded the following key points (Xun et al., Reference Xun, Yang, Zhang, Liu, Wang and Zhao2008): (1) Uniform the E-field distribution on the insulator surface as much as possible, and avoid E-field peaks on the total distributions; (2) Design the angle between the E-field lines and the insulator surface near 45° and the insulator surface length, i.e., creepage length, as long as possible; (3) Decrease the E-field strength on CTJ to a level lower than 30 kV/cm in order to prevent electron emission from this region.
Based on the short review on the insulation design aforementioned, one can find that only one type of failure pattern is usually concentrated for a composite insulator. Also for the vacuum/solid insulators, the surface flashover is mostly paid attention to. This is probably because E f of vacuum is relatively lower than E BD of gas, liquid, solid as well as E f of liquid. In the point of the conventional insulation design, increasing E f means the enhancement of the total insulation performance of the vacuum/solid composite insulators. However, in practice, the breakdown of solid dielectrics in the vacuum/solid insulators can also cause the total insulation to fail (Roth et al., Reference Roth, Sincerny, Mandelcorn, Mendelsohn Smith, Engel, Schlitt and Cooke1997; Chantrenne et al., Reference Chantrenne and Sincerny1999; Zhao et al., Reference Zhao, Peng, Pan, Zhang and Su2010). These phenomena can be understood from the perspective of reliability. When a large number of pulses are imposed on a vacuum/solid insulator, the reliability of solid dielectric would obviously be decreased, which would be lower than that of the vacuum surface, and therefore the solid breakdown would take places. In view of this, the reliability of a composite insulator should be taken into account globally. Also consider the vacuum/solid insulators, the reliability of vacuum, solid, and vacuum/solid interface should be considered together, rather than only the interface being considered when conducting the insulation design.
In this paper, a uniform formula to describe the reliability of the insulation media like solid, liquid, gas, vacuum and vacuum surface is deduced and a method to design the composite insulation structures such as vacuum/solid insulators, gas/solid insulators, and liquid/solid insulators are presented. The theoretical bases for the formulas are presented in Section 2, which include the Weibull statistical distribution and the uniform insulation design formula. The method to design the composite insulation structures is described in Section 3. An example to design a specific high-voltage (HV) vacuum insulator with the proposed method is arranged in Section 4. The last section, i.e., Section 5, is for the conclusions and the remarks in this paper.
2. THEORETICAL BASES
2.1. Weibull Statistical Distribution
The Weibull statistical distribution was put forward by Wallodi and Weibull in 1939 when he researched the phenomenon of chain rupture (Dissado et al., Reference Dissado, Fothergill, Wolfe and Hill1984; Reference Dissado and Fothergill1992). This distribution is widely used in fields such as mechanical structure fatigue, HV insulation, and breakdown. Usually, the two-parameter Weibull distribution is expressed as follows:
$$F\left(x \right)= 1 - \exp \left({ - {{x^m } / {\rm \eta} }} \right)\comma \;$$where x is the arbitrary argument, F(x) is the Weibull probability, m is the shape parameter, and η is the dimension parameter. If x is equal to η1/m, F(x) = 0.6321, which is defined as the characteristic arbitrary argument, written as x 0. If the Weibull distribution is used to describe the HV breakdown phenomenon, F(x) is the breakdown probability or the failure probability. Taking into account that the sum of the breakdown probability (F) and the reliability (R) of an HV structure equals unit, which is:
$$R + F = 1\comma \;$$The arbitrary argument x at reliability R, labeled as x R, can be expressed as follows
$$x_R = x_0 \left[{\ln \left({1/R} \right)} \right]^{{1 / m}}.$$Since x 50% can be easily obtained by theoretical calculation or from experiments, Eq. (7) can further be transformed into the following form:
$$x_R = x_{50\%} \left[{{{\ln \left({1/R} \right)} / {\ln 2}}} \right]^{{1 / m}}.$$2.2. Uniform Insulation Design Formula
As mentioned above, J. C. Martin summarized the useful empirical formula for insulation design in pulsed power systems (Martin, Reference Martin1992; Martin et al., Reference Martin, Guenther and Kristiansen1996; Bluhm, Reference Bluhm2006). These formulas are listed in Table 2. The definitions of the key parameters and the application conditions of each formula are also summarized in this table. For the formula in Table 2, two points should be clarified. (1) The breakdown threshold or the surface flashover threshold corresponds to a failure probability of 50% (R = 50%). When R is increased, the applied field (E op) should be decreased. (2) Even though the physical meanings of these parameters are different, they basically conform to the following form:
$$Et^{{1 / a}} \Omega^{{1 / {\rm \beta} }} = k\comma \;$$where E is the breakdown or surface flashover threshold, t is the effective time or pulse width, Ω is the dimension representing thickness/length, area, or volume, α, β, and k are all constants. Letting x = Et 1/α, a uniform expression for these insulation formula can be obtained, which is:
$$x\Omega^{{1 / {\rm \beta} }} = k.$$If Eq. (10) is compared with the formula of the thickness effect on E BD in Eq. (4) (E BDd 1/m = E BD1), one can find that the two formula are basically with the same form.
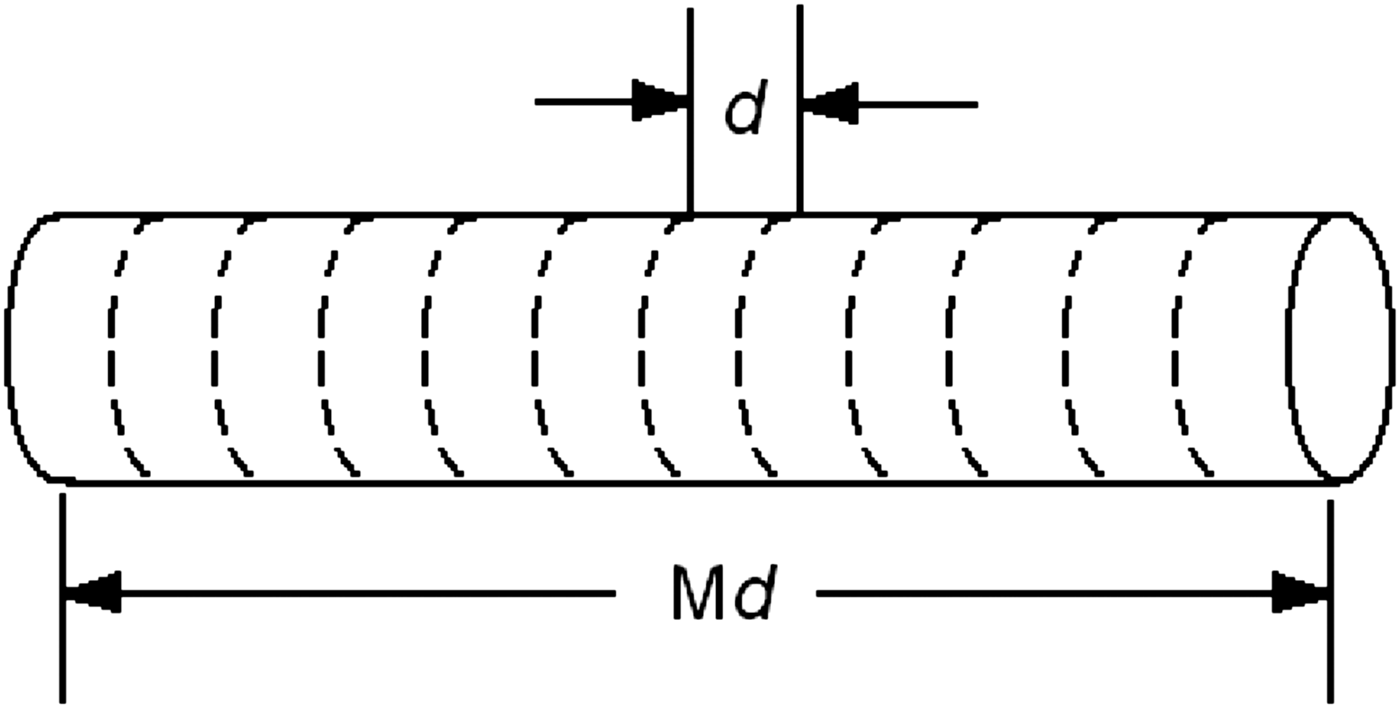
It is worth mentioning that the constant, m, in Eq. (4) is also the shape parameter of the Weibull distribution. The simple deduction process is as follows. Take into account two groups of polymer samples, the samples in the two groups are with the same cross-section, and the thickness of the samples in the second group is M times of that in the first group. Assume that the breakdown probability for the first group is as follows:
$$F_1 \left(E \right)= 1 - \exp \left({ - \displaystyle{{E^m } \over {\rm \eta} }} \right)\comma \;$$where F 1(E) is the breakdown probability, E is the applied field. Then, the characteristic electric breakdown strength, E BD1, corresponding to F 1(E) is η1/m. For the second group of samples, assume that each of them is stuck by M small samples in the first group, as shown in Figure 2, then the breakdown probability of the second group, F M(E), would conform to the following expression:
Fig. 2. Schematic diagram for deduction of the thickness effect on E BD of polymers.
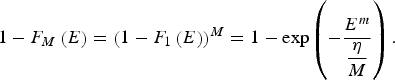$$1 - F_M \left(E \right)= \left({1 - F_1 \left(E \right)} \right)^M = 1 - \exp \left({ - \displaystyle{{E^m } \over {\displaystyle{{\rm \eta} \over M}}}} \right).$$Eq. (12) means that the characteristic electric breakdown strength for the second group, E BDM, would be:
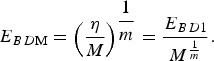$$E_{BD \rm M}= \left({\displaystyle{{\rm \eta} \over M}} \right)^{\displaystyle{1 \over m}} = {\displaystyle{E_{BD \rm 1}}\over {M^{{1 \over m}} }}.$$Furthermore, if the thickness of the first group of samples is unit, then E BD1 will be a constant and the thickness multiplied coefficient, M, will be the sample thickness of the second group, d. So, Eq. (13) can be transformed into:
$$E_{BD} \left(d \right)\cdot d^{{1 / m}} = E_{BD \rm 1} \comma \;$$Since Eq. (14) and Eq. (10) are with the same form, it is believed that a corresponding relation exists between the two formulas, that is, E BD(d) corresponds to x, E BD1 corresponds to k, and m corresponds to β. In addition, it is believed that the failure mechanisms between solid and gas, liquid, vacuum as well as surface flashover have some similarities to a certain degree. Based on these conjectures, it is assumed that β in Eq. (10) can represents the shape parameter of the Weibull distribution, that is, m = 6 for gas breakdown; m = 3.3 for vacuum breakdown; and m = 10 for liquid, solid breakdown and vacuum surface flashover. Eq. (10) can be considered as the uniform insulation design formula for different insulation media.
3. METHOD TO DEDIGN COMPOSITE INSULATION STRUCTURES
3.1. Reliability Curves for Different Insulation Media
By inserting the derived shape parameters into Eq. (8), the dependence curves of the normalized applied field (also labeled as x) on the reliability for different failure pattern can be obtained, which are shown in Figure 3. From this figure, it is seen that x decreases as R increases with different slopes for different types of insulation media and that x should be smaller than a certain value if R is required to be higher than a certain level.
Fig. 3. (Color online) Normalized applied field versus R for different insulation media.
It is noted that, owing to the fluidity, the E BD of gas, liquid, vacuum and E f of vacuum surface are affected little by the pulse numbers (N) effect; whereas E BD of solid dielectric breakdown obviously decreases as N increases. Zhao et al. (Reference Zhao, Su, Zhang, Pan, Wang, Sun and Li2013d) derived that the pulse number effect on reliability R of solid dielectrics can be expressed as follows:
$$R\left({N\comma \; E_{op} } \right)= \exp \left[{ - N\left({{{E_{op} } / {E_{BD} }}} \right)^8 } \right].$$Transforming Eq. (15) gives the following formula
$$E_{op} = E_{BD} \left[{{{\ln \left({1/R} \right)} / {N_L }}} \right]^{{1 / 8}}\comma \;$$where N is substituted with the lifetime, N L, of an insulator and E BD can be derived from Eq. (14). With Eq. (16), the dependence curves of normalized field of solid dielectrics, E op/E BD (x), on R can be plotted, as shown in Figure 4. This figure shows that x of solid dielectrics is relative smaller than those of gas, liquid, and vacuum. The reason lies in that solid dielectrics are usually required to be with a large N L, for example, N L > 105.
Fig. 4. (Color online) Normalized applied field versus R of different N L for solid dielectrics.
Only with the data in Figures 3 and 4, it is not enough to conduct the composite insulation design, since the “standard field,” which is the E BD or E f corresponding to a failure probability of 50%, is not known. As aforementioned, E BD|R=50% or E f|R=50% can be calculated theoretically with the formula in Table 2. For example, for water breakdown with a positive pulse polarity, E l|R=50% is calculated to be 257.5 kV/cm when t eff = 0.05 µs and Al = 105 cm2.
3.2. Procedure to Design a Composite Insulation Structure
Based on the above analysis, the general procedure to design a composite insulation structure with given N L and R can be concluded, which is as follows: (1) Identify the potential insulation failure patterns included in a composite insulation structure. For example, vacuum breakdown, solid breakdown, and vacuum surface flashover would cause the composite vacuum/solid insulators to fail; (2) Calculate the E BD|R=50% or E f|R=50% for each failure pattern with the empirical formula summarized in Table 2; (3) Find the normalized applied field at R and N L (x R) of each insulation medium, multiply E BD|R=50% or E f|R=50% with x R to get the maximum applied field E op_max; (4) Derive the common range of E op by comparing the E op_max of different failure patterns together and finish the composite insulation design in the common of E op.
4. EXAMPLE
Coaxial HV vacuum insulators are widely used in the Tesla-type pulsed power generators (Zhao et al., Reference Zhao, Peng, Pan, Zhang and Su2010; Reference Zhao, Pan, Su, Zhang, Wang, Fang, Sun and Li2013a; Peng et al., Reference Peng, Liu, Song and Su2011; Liu et al., Reference Liu, Zhang, Fan, Hong and Feng2012) and others types of generators (Xun et al., Reference Xun, Yang, Zhang, Liu, Wang and Zhao2008; Cheng et al., Reference Cheng, Liu, Zhang, Hong and Qian2012). With a coaxial HV vacuum insulator, the proposed method to design composite insulation structures is exemplified. This insulator is designed to sustain a pulse with width of 30 ns and amplitude of 1 MV. The general configuration of this insulator is shown in Figure 5. The key sizes of this insulator are that the outer radius R out = 175 mm, the inner radius R in = 79 mm, the insulator thickness d = 20 mm, the insulator angle θ = 45°, and the distance between the cathode shielding ring and the outer conductor d 2 = 60 mm. The insulator material is selected as nylon and the metal material is stainless steel. This insulator should work with a condition of R ≥ 90% and N L ≥ 107.
Fig. 5. (Color online) Configuration of a coaxial HV vacuum insulator.
Based on the procedure described in Section 3.2, the design on this insulator is formulated as follows. (1) This insulator probably suffers three types of insulation failure: insulator's bulk breakdown, vacuum surface flashover, and pure vacuum breakdown (the gap between the cathode shielding ring and the outer conductor). (2) As to vacuum surface flashover, with the key sizes above, the insulator's surface area, A v, is calculated to be 1149 cm2. Since t eff = 0.03 µs (30 ns), E vf|R=50% is calculated 98 kV/cm with the vacuum surface flashover formula. As to breakdown of the nylon insulator, E s|R=50% is calculated 1086 kV/cm with Eq. (14) for a thickness of 20 mm. As to vacuum breakdown, E vb|R=50% is calculated to be 204 kV/cm for a pair of stainless steel electrodes with a gap of 60 mm. (3) With Figure 3, x 90% of vacuum surface flashover is found to be 0.828, and x 90% of vacuum breakdown is 0.565. So, the E op_max of vacuum surface flashover is 81 kV/cm (E vf|R=50% = 0.828) and the E op_max of vacuum breakdown is 115 kV/cm (E vb|R=50% = 0.565). With Figure 4, it is found that x|R=90%, N=1E7 = 0.09. So, the E op_max of solid breakdown is 97 kV/cm (E s|R=50% = 0.09). (4) Since the insulator surface and the insulator itself suffer the same E-field, the common E op should be in a range smaller than the minimum (E vf = 0.828, E vb = 0.565) to ensure a global reliability of 90%. Min(E vf = 0.828, E vb = 0.565) equals to 81 kV/cm. In addition, the E op on the inner conductor surface should be smaller than 115 kV/cm. With these two criteria, simulation for this insulator is conducted, as shown in Figure 6. From Figure 6, the E-field distributions on both the inner and the out insulator surfaces are extracted, which are shown in Figure 7. From Figures 6 and 7 together, it is seen that the maximum E-field on the insulator surfaces is 63.5 kV/cm. This value is smaller than the first criterion, 81 kV/cm. So, design for the insulator is reasonable. However, the E-field on the inner conductor surface of the coaxial line is simulated to be 124 kV/cm. This value is larger than the second criterion, 115 kV/cm. So, the cathode shielding ring is still needed to be optimized so as to obtain a lower E-field.
Fig. 6. (Color online) Global E-field distribution of the HV insulator.
Fig. 7. (Color online) Outer and inner E-field distributions of the HV insulator.
5. CONCLUSIONS AND REMARKS
In conclusion, there are three types of composite insulation structures in pulsed power systems: vacuum/solid insulators, gas/solid insulators, and liquid/solid insulators. A method to design the composite insulators is proposed based on the Weibull statistical distribution and the empirical insulation formula. The design procedure includes: (1) Identify the potential failure patterns included in a composite insulation structure; (2) Calculate the E BD|R=50% and E f|R=50% of each failure pattern; (3) Find the normalized applied field x R at given R and N L in the x-R curves and obtain the E op_max by multiplying E BD|R=50% or E f|R=50% with x R; (4) Derive the common E op range of different failure patterns and optimize the insulation structures until the field requirement is met.
There are seven basic insulation failure patterns for these composite insulators: solid breakdown, liquid breakdown, gas breakdown, vacuum breakdown, vacuum surface flashover, liquid surface flashover, and gas surface flashover, as listed in Table 1. It is remarked that each failure pattern should be specially designed and the empirical insulation formula of these failure patterns should be known in advance. However, only the empirical formulas for the former five types have been developed, which are listed in Table 2; the empirical formula for liquid surface flashover and gas surface flashover are not known by far. In future, the question should be focused on. In addition, the suggested method is mainly developed from the perspective of electrical insulation. As a matter of fact, an ideal design for the insulation structures should comprise of the following factors: the type of the insulation material, the general configuration of the insulator, the mechanical stress, and the environment condition (gas pressure, temperature, and radiation), etc. All these factors may have influences on the safe performance of the insulator. It is suggested that these factors should be taken into account in advance. That is, before using this method, the material should be selected, the general configuration should be fixed, the mechanical stress should be eliminated and the disadvantageous environment effects should be prevented. After doing so, the method based on reliability can be employed.
ACKNOWLEDGMENTS
This work is supported by the National Natural Science Foundation of China under Grant No.51377135. The author wishes to express thanks to Prof. Weihua Jiang, Dr. Tao Shao, and Dr. Tao Xun due to the original ideas acquired from their papers.
