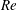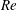1. Introduction
The study of coherent structures in small periodic domains, often referred to as ‘minimal flow units’, has provided considerable insight into the phase-space structure and the transition dynamics of shear flows without linear instabilities of the laminar state, such as pipe flow or plane Couette flow and various boundary layers (e.g. Kreilos & Eckhardt Reference Kreilos and Eckhardt2012 and references therein). For an understanding of the fascinating spatio-temporal dynamics in the transition region, where intriguing patterns of alternating laminar and turbulent dynamics (Barkley & Tuckerman Reference Barkley and Tuckerman2005; Duguet, Schlatter & Henningson Reference Duguet, Schlatter and Henningson2010) and a complicated evolution that has been linked to directed percolation (Manneville Reference Manneville2009; Moxey & Barkley Reference Moxey and Barkley2010; Avila et al. Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011) can be observed, it is necessary to investigate spatially extended domains and localised states. The interest in localised solutions also arises from the possibility of using them as building blocks for more complicated spatial patterns, such as the turbulent spots observed in plane Couette or plane Poiseuille flow in various experimental (e.g. Carlson, Widnall & Peeters Reference Carlson, Widnall and Peeters1982; Dauchot & Daviaud Reference Dauchot and Daviaud1995; Hegseth Reference Hegseth1996; Lemoult, Aider & Wesfreid Reference Lemoult, Aider and Wesfreid2013) and numerical (e.g. Henningson, Spalart & Kim Reference Henningson, Spalart and Kim1987; Lundbladh & Johansson Reference Lundbladh and Johansson1991; Schumacher & Eckhardt Reference Schumacher and Eckhardt2001) studies.
The spatially extended exact coherent structures arise in the form of stationary states without any time-dependence, travelling waves where a pattern moves downstream with a fixed speed, or relative periodic orbits that return to the initial pattern except for a displacement (Nagata Reference Nagata1990, Reference Nagata1997; Ehrenstein & Koch Reference Ehrenstein and Koch1991; Schmiegel Reference Schmiegel1999; Wang, Gibson & Waleffe Reference Wang, Gibson and Waleffe2007; Gibson, Halcrow & Cvitanović Reference Gibson, Halcrow and Cvitanović2009). Spanwise localised exact states have been identified by Schneider, Gibson & Burke (Reference Schneider, Gibson and Burke2010a ), Schneider, Marinc & Eckhardt (Reference Schneider, Marinc and Eckhardt2010b ), Gibson & Brand (Reference Gibson and Brand2014) and Zammert & Eckhardt (Reference Zammert and Eckhardt2014a ) for plane Couette and plane Poiseuille flow. Streamwise localised exact solutions have been described for the case of two-dimensional plane Poiseuille flow (Price, Brachet & Pomeau Reference Price, Brachet and Pomeau1993) and for pipe flow (Avila et al. Reference Avila, Mellibovsky, Roland and Hof2013; Chantry, Willis & Kerswell Reference Chantry, Willis and Kerswell2013). Spanwise localised states in plane Poiseuille flow show a complicated temporal dynamics (Zammert & Eckhardt Reference Zammert and Eckhardt2014a ) that has also been documented for the asymptotic suction boundary layer by Khapko et al. (Reference Khapko, Kreilos, Schlatter, Duguet, Eckhardt and Henningson2013, Reference Khapko, Duguet, Kreilos, Schlatter, Eckhardt and Henningson2014). A state in plane Couette flow that is localised in both the spanwise and streamwise directions has been identified recently by Brand & Gibson (Reference Brand and Gibson2014).
In this paper we present coherent structures for plane Poiseuille flow that are localised in the streamwise direction and in streamwise and spanwise direction. We find them using the method of edge tracking (Skufca, Yorke & Eckhardt Reference Skufca, Yorke and Eckhardt2006) in small periodic domains, and then continue them first to longer and then also to wider domains. We begin with a discussion of the extended states in narrow domains in § 2, followed by studies of streamwise localised states in § 3 and spanwise and streamwise localised structures in § 4. Conclusions are given in § 5.
2. The edge state in short domains: a travelling wave
We study the incompressible plane Poiseuille flow, the pressure-driven flow between two infinitely extended parallel plates. With the
![]() $x$
-axis along the flow direction, the plates are parallel to the
$x$
-axis along the flow direction, the plates are parallel to the
![]() $x$
–
$x$
–
![]() $z$
plane at
$z$
plane at
![]() $y=\pm h$
. The Reynolds number is based on
$y=\pm h$
. The Reynolds number is based on
![]() $h$
, the laminar centreline velocity
$h$
, the laminar centreline velocity
![]() $U_{0}$
and the kinematic viscosity
$U_{0}$
and the kinematic viscosity
![]() ${\it\nu}$
, so that
${\it\nu}$
, so that
![]() $\mathit{Re}=U_{0}h/{\it\nu}$
and the laminar non-dimensional profile becomes
$\mathit{Re}=U_{0}h/{\it\nu}$
and the laminar non-dimensional profile becomes
![]() $U(y)=(1-y^{2})$
. In all our simulations constant mass flux is imposed. The velocity fields used in the following are the deviations from the laminar profile, denoted
$U(y)=(1-y^{2})$
. In all our simulations constant mass flux is imposed. The velocity fields used in the following are the deviations from the laminar profile, denoted
![]() $\boldsymbol{u}=(u,v,w)$
, where
$\boldsymbol{u}=(u,v,w)$
, where
![]() $u$
,
$u$
,
![]() $v$
and
$v$
and
![]() $w$
are the streamwise, wall-normal and spanwise velocity components, respectively.
$w$
are the streamwise, wall-normal and spanwise velocity components, respectively.
The numerical simulations are based on the spectral code channelflow, developed and maintained by Gibson (Reference Gibson2012). The package provides a Newton method (Viswanath Reference Viswanath2007) for searching for exact solutions as well as tools for continuation and stability analysis. We adapted the channelflow-code to work with parallel FFTW (OpenMP) and replaced the Octave-library used for the linear algebra routines in the Newton method and the eigenvalue calculations by the Eigen-package (Guennebaud et al. Reference Guennebaud and Jacob2010). The method of the edge tracking algorithm is described e.g. by Toh & Itano (Reference Toh and Itano2003), Skufca et al. (Reference Skufca, Yorke and Eckhardt2006), Schneider et al. (Reference Schneider, Gibson, Lagha, De Lillo and Eckhardt2008) and Dijkstra et al. (Reference Dijkstra, Wubs, Cliffe, Doedel, Dragomirescu, Eckhardt, Gelfgat, Hazel, Lucarini, Salinger, Phipps, Sanchez-Umbria, Schuttelaars, Tuckerman and Thiele2014).
We started off with edge tracking from a random initial condition in a small periodic domain with streamwise length
![]() $L_{x}$
of
$L_{x}$
of
![]() $2{\rm\pi}$
and spanwise width
$2{\rm\pi}$
and spanwise width
![]() $L_{z}$
of
$L_{z}$
of
![]() $2{\rm\pi}$
with a numerical resolution of
$2{\rm\pi}$
with a numerical resolution of
![]() $N_{x}\times N_{y}\times N_{z}=32\times 65\times 48$
and a Reynolds number of 1400. We checked our resolution by comparison to a higher one of
$N_{x}\times N_{y}\times N_{z}=32\times 65\times 48$
and a Reynolds number of 1400. We checked our resolution by comparison to a higher one of
![]() $N_{x}\times N_{y}\times N_{z}=80\times 97\times 112$
. For this Re plane Poiseuille flow shows persistent turbulence although it is far below the critical Reynolds number of 5772 (Orszag Reference Orszag1971) that follows from linear stability theory. Note that on account of the domain length of
$N_{x}\times N_{y}\times N_{z}=80\times 97\times 112$
. For this Re plane Poiseuille flow shows persistent turbulence although it is far below the critical Reynolds number of 5772 (Orszag Reference Orszag1971) that follows from linear stability theory. Note that on account of the domain length of
![]() $2{\rm\pi}$
the actual critical Reynolds number in this domain is 5815. Edge tracking usually converges quickly to one travelling wave, referred to as
$2{\rm\pi}$
the actual critical Reynolds number in this domain is 5815. Edge tracking usually converges quickly to one travelling wave, referred to as
![]() $TW_{E}$
in the following. This state has two symmetries: a mirror symmetry with respect to the mid-plane, and a shift-and-reflect symmetry in the spanwise direction,
$TW_{E}$
in the following. This state has two symmetries: a mirror symmetry with respect to the mid-plane, and a shift-and-reflect symmetry in the spanwise direction,
Stability analysis of the travelling wave in the full space without any symmetry restriction shows that it has one unstable eigenvalue for
![]() $510<\mathit{Re}<5850$
so that its stable manifold is of co-dimension one. A stability analysis of this periodic state in longer domains shows that for
$510<\mathit{Re}<5850$
so that its stable manifold is of co-dimension one. A stability analysis of this periodic state in longer domains shows that for
![]() $L_{x}=4{\rm\pi}$
the state already has an additional pair of unstable complex-conjugated eigenvalues for
$L_{x}=4{\rm\pi}$
the state already has an additional pair of unstable complex-conjugated eigenvalues for
![]() $\mathit{Re}<1785$
. Further doubling of the domain size adds more unstable directions, so that, e.g. for
$\mathit{Re}<1785$
. Further doubling of the domain size adds more unstable directions, so that, e.g. for
![]() $L_{x}=8{\rm\pi}$
and
$L_{x}=8{\rm\pi}$
and
![]() $\mathit{Re}=1400$
, the wave has five unstable eigenvalues. The long-wavelength instabilities in the larger domains are precursors to localisation in the spanwise (Melnikov, Kreilos & Eckhardt Reference Melnikov, Kreilos and Eckhardt2014) and streamwise directions (Chantry et al.
Reference Chantry, Willis and Kerswell2013).
$\mathit{Re}=1400$
, the wave has five unstable eigenvalues. The long-wavelength instabilities in the larger domains are precursors to localisation in the spanwise (Melnikov, Kreilos & Eckhardt Reference Melnikov, Kreilos and Eckhardt2014) and streamwise directions (Chantry et al.
Reference Chantry, Willis and Kerswell2013).
3. Streamwise localised periodic orbits in long domains
In a longer domain of length
![]() $32{\rm\pi}$
but with the same width of
$32{\rm\pi}$
but with the same width of
![]() $2{\rm\pi}$
and at Reynolds number
$2{\rm\pi}$
and at Reynolds number
![]() $\mathit{Re}=1400$
, edge tracking converges to a state that at first glance looks like a state of constant energy density,
$\mathit{Re}=1400$
, edge tracking converges to a state that at first glance looks like a state of constant energy density,
However, closer inspection of the time trace in figure 1 reveals that it is not constant but shows a regular oscillation with an amplitude of order
![]() $10^{-8}$
. This oscillation is not a numerical artefact but reflects properties of the edge state, as we now show.
$10^{-8}$
. This oscillation is not a numerical artefact but reflects properties of the edge state, as we now show.

Figure 1. Edge tracking in a computational domain of length
![]() $L_{x}=32{\rm\pi}$
and width
$L_{x}=32{\rm\pi}$
and width
![]() $L_{z}=2{\rm\pi}$
for
$L_{z}=2{\rm\pi}$
for
![]() $\mathit{Re}=1400$
. Shown are the energy densities of trajectories that turn turbulent (thick grey, red online) and laminar (thin black), respectively. The edge state bracketed by these trajectories oscillates periodically in energy.
$\mathit{Re}=1400$
. Shown are the energy densities of trajectories that turn turbulent (thick grey, red online) and laminar (thin black), respectively. The edge state bracketed by these trajectories oscillates periodically in energy.
Although the initial velocity field is spatially non-localised, the flow state obtained by edge tracking is localised in the streamwise direction. Using this state as an initial condition in a Newton method, there is a quick convergence to a streamwise localised relative periodic orbit, referred to as
![]() $PO_{E}$
in the following. For further study we transfer the state to a computational domain of length
$PO_{E}$
in the following. For further study we transfer the state to a computational domain of length
![]() $64{\rm\pi}$
, which is possible because of its streamwise localisation. We use a resolution of
$64{\rm\pi}$
, which is possible because of its streamwise localisation. We use a resolution of
![]() $768\times 65\times 48$
and check our results with a higher spanwise resolution of
$768\times 65\times 48$
and check our results with a higher spanwise resolution of
![]() $N_{z}=80$
. The streamwise and spanwise velocity components in the mid-plane are shown in figure 2. Cross-sections for
$N_{z}=80$
. The streamwise and spanwise velocity components in the mid-plane are shown in figure 2. Cross-sections for
![]() $\mathit{Re}=1400$
for different streamwise positions are shown in figure 3(a–d) and the streamwise averaged velocity is shown in figure 3(e). The images reveal that the orbit has a mirror symmetry (
$\mathit{Re}=1400$
for different streamwise positions are shown in figure 3(a–d) and the streamwise averaged velocity is shown in figure 3(e). The images reveal that the orbit has a mirror symmetry (
![]() $s_{y}$
) but no
$s_{y}$
) but no
![]() $s_{z}{\it\tau}_{x}$
-symmetry and is dominated by a strong narrow low-speed streak and a weak and extended high-speed streak. It is therefore very similar to the travelling wave
$s_{z}{\it\tau}_{x}$
-symmetry and is dominated by a strong narrow low-speed streak and a weak and extended high-speed streak. It is therefore very similar to the travelling wave
![]() $TW_{E}$
. In particular, the streamwise-averaged flow for
$TW_{E}$
. In particular, the streamwise-averaged flow for
![]() $TW_{E}$
is close to the one shown in figure 3(e).
$TW_{E}$
is close to the one shown in figure 3(e).

Figure 2. Instantaneous velocities in the mid-plane for the edge state
![]() $PO_{E}$
at
$PO_{E}$
at
![]() $\mathit{Re}=1400$
at the time of minimal energy: (a) streamwise and (b) spanwise velocities. The dashed black lines in (a) mark the positions of the spanwise wall-normal cross-sections in figure 3(a–d). The solid and dashed lines in (b) are iso-contours of the Q-vortex criterion (Jeong & Hussain Reference Jeong and Hussain1995) at levels of 0.001 and 0.0001, respectively. The direction of the flow is from left to right.
$\mathit{Re}=1400$
at the time of minimal energy: (a) streamwise and (b) spanwise velocities. The dashed black lines in (a) mark the positions of the spanwise wall-normal cross-sections in figure 3(a–d). The solid and dashed lines in (b) are iso-contours of the Q-vortex criterion (Jeong & Hussain Reference Jeong and Hussain1995) at levels of 0.001 and 0.0001, respectively. The direction of the flow is from left to right.

Figure 3. (a–d) Instantaneous cross-sections of the edge state
![]() $PO_{E}$
at
$PO_{E}$
at
![]() $\mathit{Re}=1400$
at the streamwise positions indicated in figure 2(a). The in-plane components of the velocity are indicated by arrows and the streamwise component is colour coded. (e, f) The streamwise-averages of
$\mathit{Re}=1400$
at the streamwise positions indicated in figure 2(a). The in-plane components of the velocity are indicated by arrows and the streamwise component is colour coded. (e, f) The streamwise-averages of
![]() $PO_{E}$
at
$PO_{E}$
at
![]() $\mathit{Re}=1400$
and of the orbit that bifurcates from it,
$\mathit{Re}=1400$
and of the orbit that bifurcates from it,
![]() $PO_{asy}$
, at
$PO_{asy}$
, at
![]() $\mathit{Re}=1625$
, respectively.
$\mathit{Re}=1625$
, respectively.
The complex spatial propagation pattern of the wave can be seen in figure 4 where the spanwise velocity in the mid-plane at
![]() $z=0$
is plotted versus time for
$z=0$
is plotted versus time for
![]() $\mathit{Re}=1400$
. The total energy of the state is periodic with a period
$\mathit{Re}=1400$
. The total energy of the state is periodic with a period
![]() $T=45.402$
, but the state needs twice this time to return in shape, apart from a downstream shift. After a time
$T=45.402$
, but the state needs twice this time to return in shape, apart from a downstream shift. After a time
![]() $T$
it returns apart from a symmetry operation
$T$
it returns apart from a symmetry operation
![]() $s_{z}:[u,v,w](x,y,z)=[u,v,-w](x,y,-z)$
and a downstream shift that is half the one after
$s_{z}:[u,v,w](x,y,z)=[u,v,-w](x,y,-z)$
and a downstream shift that is half the one after
![]() $2T$
. The figure clearly shows a group velocity
$2T$
. The figure clearly shows a group velocity
![]() $v_{g}$
for the envelope of the state, and a phase velocity
$v_{g}$
for the envelope of the state, and a phase velocity
![]() $v_{ph}$
for the underlying structures. The group velocity
$v_{ph}$
for the underlying structures. The group velocity
![]() $v_{g}$
can be calculated by dividing the distance travelled over two periods by
$v_{g}$
can be calculated by dividing the distance travelled over two periods by
![]() $2T$
. For
$2T$
. For
![]() $\mathit{Re}=1400$
one obtains
$\mathit{Re}=1400$
one obtains
![]() $v_{g}=0.8753$
, indicated by the line at the upstream end of the state in figure 4. The structures underneath the envelope move with a different velocity
$v_{g}=0.8753$
, indicated by the line at the upstream end of the state in figure 4. The structures underneath the envelope move with a different velocity
![]() $v_{ph}$
, which can be read off from the slope of the maxima. However, the wavelength
$v_{ph}$
, which can be read off from the slope of the maxima. However, the wavelength
![]() ${\it\lambda}$
of the spanwise modulations varies slightly with position and is slightly larger at the front than in the centre and towards the end of the state. Therefore, the velocity of each maximum also varies slightly, so that the phase velocity depends on the position within the state.
${\it\lambda}$
of the spanwise modulations varies slightly with position and is slightly larger at the front than in the centre and towards the end of the state. Therefore, the velocity of each maximum also varies slightly, so that the phase velocity depends on the position within the state.

Figure 4. Space–time-display of the spanwise velocity of the periodic orbit
![]() $PO_{E}$
in the mid-plane
$PO_{E}$
in the mid-plane
![]() $y=0$
at
$y=0$
at
![]() $z=0$
for
$z=0$
for
![]() $\mathit{Re}=1400$
. The solid black lines indicate the group velocity
$\mathit{Re}=1400$
. The solid black lines indicate the group velocity
![]() $v_{g}$
and the phase velocity
$v_{g}$
and the phase velocity
![]() $v_{ph}$
for one of the maxima. The wavelength
$v_{ph}$
for one of the maxima. The wavelength
![]() ${\it\lambda}$
of the internal modulations varies along the state. The dashed black line marks one period
${\it\lambda}$
of the internal modulations varies along the state. The dashed black line marks one period
![]() $T$
in energy.
$T$
in energy.
Using a continuation method (see e.g. Dijkstra et al.
Reference Dijkstra, Wubs, Cliffe, Doedel, Dragomirescu, Eckhardt, Gelfgat, Hazel, Lucarini, Salinger, Phipps, Sanchez-Umbria, Schuttelaars, Tuckerman and Thiele2014) it is easy to track the state in
![]() $\mathit{Re}$
. It turns out that the periodic orbit exists down to
$\mathit{Re}$
. It turns out that the periodic orbit exists down to
![]() $\mathit{Re}\approx 1038$
, where it is created in a saddle–node bifurcation. Furthermore, it is also possible to identify the upper branch of the periodic orbit. This upper branch is also localised and has multiple unstable directions.
$\mathit{Re}\approx 1038$
, where it is created in a saddle–node bifurcation. Furthermore, it is also possible to identify the upper branch of the periodic orbit. This upper branch is also localised and has multiple unstable directions.
A stability analysis of the lower branch state shows that for
![]() $\mathit{Re}>1100$
it has one unstable direction. Therefore, for these Reynolds numbers the state is an edge state whose stable manifold can separate the state space into two parts. For lower values of
$\mathit{Re}>1100$
it has one unstable direction. Therefore, for these Reynolds numbers the state is an edge state whose stable manifold can separate the state space into two parts. For lower values of
![]() $\mathit{Re}$
the periodic orbit has more than one unstable direction. The bifurcation near
$\mathit{Re}$
the periodic orbit has more than one unstable direction. The bifurcation near
![]() $\mathit{Re}\approx 1100$
is a Sacker–Neimark bifurcation (Kuznetsov Reference Kuznetsov1998) that breaks the
$\mathit{Re}\approx 1100$
is a Sacker–Neimark bifurcation (Kuznetsov Reference Kuznetsov1998) that breaks the
![]() $s_{y}$
symmetry. This bifurcation is followed by further bifurcations resulting in eight unstable directions for the lower branch. One of the bifurcations of the lower branch is a pitchfork bifurcation that breaks the
$s_{y}$
symmetry. This bifurcation is followed by further bifurcations resulting in eight unstable directions for the lower branch. One of the bifurcations of the lower branch is a pitchfork bifurcation that breaks the
![]() $s_{y}$
symmetry and creates an asymmetric periodic orbit (
$s_{y}$
symmetry and creates an asymmetric periodic orbit (
![]() $PO_{asy}$
). The image of the state in figure 3( f) shows that its internal dynamics is more complex than that of
$PO_{asy}$
). The image of the state in figure 3( f) shows that its internal dynamics is more complex than that of
![]() $PO_{E}$
. The bifurcations and some properties of the states are summarised in figure 5.
$PO_{E}$
. The bifurcations and some properties of the states are summarised in figure 5.

Figure 5. Bifurcation diagram for the coherent structures. (a) Minimum energy of the localised periodic orbit
![]() $PO_{E}$
(grey, red online) and the asymmetric orbit
$PO_{E}$
(grey, red online) and the asymmetric orbit
![]() $PO_{asy}$
(black) versus
$PO_{asy}$
(black) versus
![]() $\mathit{Re}$
. In both cases the minimum in energy over the period
$\mathit{Re}$
. In both cases the minimum in energy over the period
![]() $T$
is shown. The stability of the orbit is indicated by the line type: solid for a single unstable direction, and dashed for more than one. (b) Variation of the periods in energy with
$T$
is shown. The stability of the orbit is indicated by the line type: solid for a single unstable direction, and dashed for more than one. (b) Variation of the periods in energy with
![]() $\mathit{Re}$
.
$\mathit{Re}$
.
Information about the localisation properties can be extracted from the streamwise variation of the energy density of the deviation from the laminar flow,
and the density of the cross-flow energy
The energy densities for the periodic orbit at
![]() $\mathit{Re}=2010$
(at times of minimal energy) are shown in figure 6(a). One can identify a small region with relatively high cross-flow energy at the front of the state. In this region the cross-flow draws energy from the laminar profile and transfers it into streamwise velocity, which then drives streaks and causes a steep increase of the total energy density at the front of the state. The energy in the streamwise components has its maximum at a position in the tail where the cross-flow energy is already very low again. In the absence of cross-flow motion the streaks are dampened by viscosity only, which results in the long tail of the state.
$\mathit{Re}=2010$
(at times of minimal energy) are shown in figure 6(a). One can identify a small region with relatively high cross-flow energy at the front of the state. In this region the cross-flow draws energy from the laminar profile and transfers it into streamwise velocity, which then drives streaks and causes a steep increase of the total energy density at the front of the state. The energy in the streamwise components has its maximum at a position in the tail where the cross-flow energy is already very low again. In the absence of cross-flow motion the streaks are dampened by viscosity only, which results in the long tail of the state.

Figure 6. Energy profiles of the localised state. (a) Densities of the total (light grey, red online) and cross-flow (dark grey, blue online) energy for the periodic orbit at
![]() $\mathit{Re}=2010$
along the flow direction, which is from left to right. The cross-flow energy density is multiplied by a factor of 10. (b) Downstream
$\mathit{Re}=2010$
along the flow direction, which is from left to right. The cross-flow energy density is multiplied by a factor of 10. (b) Downstream
![]() $l_{h}$
(light grey, orange online) and upstream
$l_{h}$
(light grey, orange online) and upstream
![]() $l_{t}$
(dark grey, green online) distances from the maximum to half the maximal values in energy.
$l_{t}$
(dark grey, green online) distances from the maximum to half the maximal values in energy.
Based on the energy density
![]() $E_{\bot }(x)$
one can introduce two characteristic length scales for
$E_{\bot }(x)$
one can introduce two characteristic length scales for
![]() $PO_{E}$
, associated with the extension in the downstream and upstream direction. Starting from the maximum in energy, one can determine the distances to the locations where the energy density has dropped to half its maximum. They are denoted
$PO_{E}$
, associated with the extension in the downstream and upstream direction. Starting from the maximum in energy, one can determine the distances to the locations where the energy density has dropped to half its maximum. They are denoted
![]() $l_{t}$
and
$l_{t}$
and
![]() $l_{h}$
for the upstream (tail) and downstream (head) sides, respectively, and are shown in figure 6(b). On the downstream side, the energy drops off quickly, on a length scale that varies very little with
$l_{h}$
for the upstream (tail) and downstream (head) sides, respectively, and are shown in figure 6(b). On the downstream side, the energy drops off quickly, on a length scale that varies very little with
![]() $\mathit{Re}$
. On the upstream side, the energy drops off more slowly, on a length scale that increases linearly with
$\mathit{Re}$
. On the upstream side, the energy drops off more slowly, on a length scale that increases linearly with
![]() $\mathit{Re}$
. The origin of this scaling is the viscous decay of the streaks on a time scale proportional to
$\mathit{Re}$
. The origin of this scaling is the viscous decay of the streaks on a time scale proportional to
![]() $\mathit{Re}$
, which then is translated into a spatial scale proportional to
$\mathit{Re}$
, which then is translated into a spatial scale proportional to
![]() $\mathit{Re}$
by the essentially constant advection velocity. In the case of plane Couette flow, Brand & Gibson (Reference Brand and Gibson2014) have been able to determine the slopes from a linear stability analysis that confirms this scaling. The case of plane Poiseuille flow is more complicated because the state is not stationary, and an analytical calculation of the decay rates has not been possible, yet.
$\mathit{Re}$
by the essentially constant advection velocity. In the case of plane Couette flow, Brand & Gibson (Reference Brand and Gibson2014) have been able to determine the slopes from a linear stability analysis that confirms this scaling. The case of plane Poiseuille flow is more complicated because the state is not stationary, and an analytical calculation of the decay rates has not been possible, yet.
Although the structure becomes longer with increasing
![]() $\mathit{Re}$
, the total energy and also the maximum of the energy density decrease with increasing
$\mathit{Re}$
, the total energy and also the maximum of the energy density decrease with increasing
![]() $\mathit{Re}$
(see figure 5). In finite domains the increasing length of the structures will then cause interference between head and tail and a loss of localisation. For instance, continuation of
$\mathit{Re}$
(see figure 5). In finite domains the increasing length of the structures will then cause interference between head and tail and a loss of localisation. For instance, continuation of
![]() $PO_{E}$
to high
$PO_{E}$
to high
![]() $\mathit{Re}$
in a box of length
$\mathit{Re}$
in a box of length
![]() $32{\rm\pi}$
shows that the orbit connects to the streamwise extended travelling wave
$32{\rm\pi}$
shows that the orbit connects to the streamwise extended travelling wave
![]() $TW_{E}$
at
$TW_{E}$
at
![]() $\mathit{Re}\approx 5385$
with a wavelength of
$\mathit{Re}\approx 5385$
with a wavelength of
![]() $2.66{\rm\pi}$
. This is documented in figure 7 in a plot of the energy densities versus
$2.66{\rm\pi}$
. This is documented in figure 7 in a plot of the energy densities versus
![]() $\mathit{Re}$
. For low
$\mathit{Re}$
. For low
![]() $\mathit{Re}$
there is a pronounced maximum in the densities, but for increasing
$\mathit{Re}$
there is a pronounced maximum in the densities, but for increasing
![]() $\mathit{Re}$
the differences decrease and finally at
$\mathit{Re}$
the differences decrease and finally at
![]() $\mathit{Re}\approx 5380$
the uniform energy density corresponding to the travelling wave is obtained. Turned the other way round, the localised state arises out of a streamwise long-wavelength instability of a travelling wave, very much like the long-wavelength instabilities discussed for plane Couette flow (Melnikov et al.
Reference Melnikov, Kreilos and Eckhardt2014) or pipe flow (Chantry et al.
Reference Chantry, Willis and Kerswell2013).
$\mathit{Re}\approx 5380$
the uniform energy density corresponding to the travelling wave is obtained. Turned the other way round, the localised state arises out of a streamwise long-wavelength instability of a travelling wave, very much like the long-wavelength instabilities discussed for plane Couette flow (Melnikov et al.
Reference Melnikov, Kreilos and Eckhardt2014) or pipe flow (Chantry et al.
Reference Chantry, Willis and Kerswell2013).

Figure 7. Profiles of
![]() $PO_{E}$
for increasing Reynolds numbers. The solid lines show the total and the dashed lines the cross-flow energy densities. Consistent with the increase in
$PO_{E}$
for increasing Reynolds numbers. The solid lines show the total and the dashed lines the cross-flow energy densities. Consistent with the increase in
![]() $l_{h}$
, the states become more and more delocalised with increasing Reynolds number, until they merge into a spatially extended state near
$l_{h}$
, the states become more and more delocalised with increasing Reynolds number, until they merge into a spatially extended state near
![]() $\mathit{Re}=5385$
. The streamwise length of the computational domain is
$\mathit{Re}=5385$
. The streamwise length of the computational domain is
![]() $32{\rm\pi}$
.
$32{\rm\pi}$
.
4. A streamwise and spanwise localised periodic orbit
The periodic orbits found in the domain with
![]() $L_{z}=2{\rm\pi}$
are localised in the streamwise direction. They show early signs of localisation in the spanwise direction in that the energy density close to the strong low-speed streak is much higher than in the region of the high-speed streak. To obtain periodic orbits that are also localised in the spanwise direction we continue the periodic orbit in box width. For the continuation in
$L_{z}=2{\rm\pi}$
are localised in the streamwise direction. They show early signs of localisation in the spanwise direction in that the energy density close to the strong low-speed streak is much higher than in the region of the high-speed streak. To obtain periodic orbits that are also localised in the spanwise direction we continue the periodic orbit in box width. For the continuation in
![]() $L_{z}$
we fix
$L_{z}$
we fix
![]() $\mathit{Re}=2180$
and a length of
$\mathit{Re}=2180$
and a length of
![]() $64{\rm\pi}$
. As a measure of the state we consider the energy density obtained by averaging over the streamwise and normal directions,
$64{\rm\pi}$
. As a measure of the state we consider the energy density obtained by averaging over the streamwise and normal directions,
This partially averaged energy density depends on the spanwise coordinate only, and is shown in figure 8 for various widths
![]() $L_{z}$
. The maximum at
$L_{z}$
. The maximum at
![]() $z=0$
corresponds to the position of the low-speed streak. For
$z=0$
corresponds to the position of the low-speed streak. For
![]() $L_{z}=2{\rm\pi}$
the second smaller maximum is the position of the weak high-speed streak. Slightly above
$L_{z}=2{\rm\pi}$
the second smaller maximum is the position of the weak high-speed streak. Slightly above
![]() $L_{z}=2{\rm\pi}$
the lower maximum splits into two. For
$L_{z}=2{\rm\pi}$
the lower maximum splits into two. For
![]() $L_{z}>5{\rm\pi}$
the energy density has a very low value over most of the domain, indicating a spanwise localised flow structure. The largest value of
$L_{z}>5{\rm\pi}$
the energy density has a very low value over most of the domain, indicating a spanwise localised flow structure. The largest value of
![]() $L_{z}$
which we studied is
$L_{z}$
which we studied is
![]() $72{\rm\pi}$
. For this domain we use a resolution of
$72{\rm\pi}$
. For this domain we use a resolution of
![]() $N_{x}\times N_{y}\times N_{z}=384\times 49\times 1728$
. The doubly-localised solution in this domain keeps the
$N_{x}\times N_{y}\times N_{z}=384\times 49\times 1728$
. The doubly-localised solution in this domain keeps the
![]() $s_{y}$
symmetry of the state that is localised in the streamwise direction only. The period
$s_{y}$
symmetry of the state that is localised in the streamwise direction only. The period
![]() $T$
of the orbit is 53.578. After this time the state returns in shape apart from a downstream shift and the symmetry operation
$T$
of the orbit is 53.578. After this time the state returns in shape apart from a downstream shift and the symmetry operation
![]() $s_{z}$
. The group speed of the orbit is
$s_{z}$
. The group speed of the orbit is
![]() $v_{g}=0.8803$
.
$v_{g}=0.8803$
.

Figure 8. Spanwise profiles of the total energy of the localised states
![]() $PO_{E}$
for various spanwise widths
$PO_{E}$
for various spanwise widths
![]() $L_{z}$
.
$L_{z}$
.
The logarithmic scale in figure 8 shows that
![]() $E_{\Vert }(z)$
does not drop off exponentially in the spanwise direction. Since the integrated density increases with the length of the turbulent region, a much better measure is the maximum in velocities along
$E_{\Vert }(z)$
does not drop off exponentially in the spanwise direction. Since the integrated density increases with the length of the turbulent region, a much better measure is the maximum in velocities along
![]() $x$
and
$x$
and
![]() $y$
for a fixed spanwise position, i.e. the
$y$
for a fixed spanwise position, i.e. the
![]() $\infty$
-norm
$\infty$
-norm
![]() $\mathscr{L}^{\infty }(u)=\max _{x,y}|u(x,y,z)|$
, here given for the streamwise component
$\mathscr{L}^{\infty }(u)=\max _{x,y}|u(x,y,z)|$
, here given for the streamwise component
![]() $u$
(Brand & Gibson Reference Brand and Gibson2014). Its values for the streamwise and spanwise component are shown in figure 9(a). The decay of
$u$
(Brand & Gibson Reference Brand and Gibson2014). Its values for the streamwise and spanwise component are shown in figure 9(a). The decay of
![]() $\mathscr{L}^{\infty }(u)$
is slower than exponential while
$\mathscr{L}^{\infty }(u)$
is slower than exponential while
![]() $\mathscr{L}^{\infty }(w)$
drops off faster. The second part is hidden in
$\mathscr{L}^{\infty }(w)$
drops off faster. The second part is hidden in
![]() $E_{\Vert }(z)$
because it is swamped by the higher values of the streamwise component. The behaviour near
$E_{\Vert }(z)$
because it is swamped by the higher values of the streamwise component. The behaviour near
![]() $z=L_{z}$
is clearly influenced by the boundary conditions: the streamwise component is symmetric under reflection at the boundary, whereas the spanwise component is antisymmetric and vanishes at the boundary. Taking this into account, the figure also shows fits to an algebraic decay with the correct symmetries: the agreement between the fit and the numerical data indicates that the velocity fields fall off like
$z=L_{z}$
is clearly influenced by the boundary conditions: the streamwise component is symmetric under reflection at the boundary, whereas the spanwise component is antisymmetric and vanishes at the boundary. Taking this into account, the figure also shows fits to an algebraic decay with the correct symmetries: the agreement between the fit and the numerical data indicates that the velocity fields fall off like
![]() $1/z^{2}$
over the width of the domain.
$1/z^{2}$
over the width of the domain.

Figure 9. (a) The
![]() $\mathscr{L}^{\infty }$
-norm (maximum over
$\mathscr{L}^{\infty }$
-norm (maximum over
![]() $y$
and
$y$
and
![]() $x$
) of the streamwise
$x$
) of the streamwise
![]() $u$
(solid red) and spanwise
$u$
(solid red) and spanwise
![]() $w$
(solid black) velocity components versus spanwise coordinate
$w$
(solid black) velocity components versus spanwise coordinate
![]() $z$
. The yellow lines show fits
$z$
. The yellow lines show fits
![]() $A(z^{-2}+(L_{z}-z)^{-2})$
(dotted) and
$A(z^{-2}+(L_{z}-z)^{-2})$
(dotted) and
![]() $A(z^{-2}-(L_{z}-z)^{-2})$
(dashed). (b) The
$A(z^{-2}-(L_{z}-z)^{-2})$
(dashed). (b) The
![]() $\mathscr{L}^{\infty }$
-norms (maximum over
$\mathscr{L}^{\infty }$
-norms (maximum over
![]() $y$
and
$y$
and
![]() $z$
) of the streamwise (solid red), spanwise (black) and wall-normal (dashed red) velocity components versus streamwise coordinate
$z$
) of the streamwise (solid red), spanwise (black) and wall-normal (dashed red) velocity components versus streamwise coordinate
![]() $x$
.
$x$
.
In the streamwise direction, as documented in figure 9(b), the decay is exponential for the domain sizes studied here. This agrees with the observations on the partially localised states in § 3, including the asymmetry in the decays in the upstream and downstream direction.
Images of the streamwise and spanwise velocity fields in the mid-plane are shown in figure 10. The visualisation of the spanwise velocity reveals a large-scale, quadrupolar-like flow field, where the centres of the left and the right pairs of lobes coincide with intensity maxima of
![]() $E_{\bot ,c}(x)$
. The quadrupolar shape of the spanwise velocity also exists away from the mid-plane, but becomes less distinct close to the walls. Given the observation of similar large-scale quadrupole flows in turbulent spots in plane Couette (e.g. Schumacher & Eckhardt Reference Schumacher and Eckhardt2001; Lagha & Manneville Reference Lagha and Manneville2007; Duguet & Schlatter Reference Duguet and Schlatter2013; Gibson & Brand Reference Gibson and Brand2014) and plane Poiseuille flow (Lemoult et al.
Reference Lemoult, Aider and Wesfreid2013, Reference Lemoult, Gumowski, Aider and Wesfreid2014), one can anticipate that they appear for all structures that are localised in all directions.
$E_{\bot ,c}(x)$
. The quadrupolar shape of the spanwise velocity also exists away from the mid-plane, but becomes less distinct close to the walls. Given the observation of similar large-scale quadrupole flows in turbulent spots in plane Couette (e.g. Schumacher & Eckhardt Reference Schumacher and Eckhardt2001; Lagha & Manneville Reference Lagha and Manneville2007; Duguet & Schlatter Reference Duguet and Schlatter2013; Gibson & Brand Reference Gibson and Brand2014) and plane Poiseuille flow (Lemoult et al.
Reference Lemoult, Aider and Wesfreid2013, Reference Lemoult, Gumowski, Aider and Wesfreid2014), one can anticipate that they appear for all structures that are localised in all directions.

Figure 10. Instantaneous (a) streamwise and (b) spanwise velocity in the mid-plane for the doubly-localised periodic orbit at
![]() $\mathit{Re}=2180$
in a domain with
$\mathit{Re}=2180$
in a domain with
![]() $L_{x}=64{\rm\pi}$
and
$L_{x}=64{\rm\pi}$
and
![]() $L_{z}=72{\rm\pi}$
. The snapshot is for the time of minimal energy during one period. Only the part of the domain that contains the localised flow structure is shown. The dashed lines in (b) mark the downstream positions of the maxima in the energy density
$L_{z}=72{\rm\pi}$
. The snapshot is for the time of minimal energy during one period. Only the part of the domain that contains the localised flow structure is shown. The dashed lines in (b) mark the downstream positions of the maxima in the energy density
![]() $E_{\bot ,c}(x)$
.
$E_{\bot ,c}(x)$
.
We verified that we can trace the doubly-localised solution in the domain with
![]() $L_{x}=64{\rm\pi}$
and
$L_{x}=64{\rm\pi}$
and
![]() $L_{z}=72{\rm\pi}$
also to lower and higher values of
$L_{z}=72{\rm\pi}$
also to lower and higher values of
![]() $\mathit{Re}$
, but because applying the Newton method to this large domain is computationally very expensive, we did not perform a complete continuation in Reynolds number.
$\mathit{Re}$
, but because applying the Newton method to this large domain is computationally very expensive, we did not perform a complete continuation in Reynolds number.
A stability analysis of the localised state as a function of
![]() $L_{z}$
at
$L_{z}$
at
![]() $\mathit{Re}=2180$
shows that is has two unstable eigenvalues for
$\mathit{Re}=2180$
shows that is has two unstable eigenvalues for
![]() $L_{z}\geqslant 6{\rm\pi}$
. Therefore, it is not an attracting state at the laminar–turbulent boundary. Edge tracking calculations starting from the disturbed localised periodic orbit do not result in a simple attractor. Instead, the time evolution of the state is chaotic, but it remains localised (Zammert & Eckhardt Reference Zammert and Eckhardt2014b
). This behaviour is similar to what has been seen in large plane Couette domains (Duguet, Schlatter & Henningson Reference Duguet, Schlatter and Henningson2009; Marinc, Schneider & Eckhardt Reference Marinc, Schneider, Eckhardt, Schlatter and Henningson2010; Schneider et al.
Reference Schneider, Marinc and Eckhardt2010b
), long pipes (Mellibovsky et al.
Reference Mellibovsky, Meseguer, Schneider and Eckhardt2009), or wide domains in the asymptotic suction boundary layer (Khapko et al.
Reference Khapko, Duguet, Kreilos, Schlatter, Eckhardt and Henningson2014).
$L_{z}\geqslant 6{\rm\pi}$
. Therefore, it is not an attracting state at the laminar–turbulent boundary. Edge tracking calculations starting from the disturbed localised periodic orbit do not result in a simple attractor. Instead, the time evolution of the state is chaotic, but it remains localised (Zammert & Eckhardt Reference Zammert and Eckhardt2014b
). This behaviour is similar to what has been seen in large plane Couette domains (Duguet, Schlatter & Henningson Reference Duguet, Schlatter and Henningson2009; Marinc, Schneider & Eckhardt Reference Marinc, Schneider, Eckhardt, Schlatter and Henningson2010; Schneider et al.
Reference Schneider, Marinc and Eckhardt2010b
), long pipes (Mellibovsky et al.
Reference Mellibovsky, Meseguer, Schneider and Eckhardt2009), or wide domains in the asymptotic suction boundary layer (Khapko et al.
Reference Khapko, Duguet, Kreilos, Schlatter, Eckhardt and Henningson2014).
5. Conclusions and outlook
We were able to identify a doubly-localised periodic orbit in plane Poiseuille flow. The orbit was shown to bifurcate from a streamwise extended travelling wave. Together with the other current examples of long-wavelength instabilities (Chantry et al. Reference Chantry, Willis and Kerswell2013; Melnikov et al. Reference Melnikov, Kreilos and Eckhardt2014) we anticipate that many more localised states can be found in bifurcations of the spatially extended states that have been identified already (Schmiegel Reference Schmiegel1999; Gibson et al. Reference Gibson, Halcrow and Cvitanović2009). Homotopies between plane Poiseuille flow and other flows, including plane Couette or the asymptotic suction boundary layer, can then reveal connections between these states (Waleffe Reference Waleffe2003; Kreilos et al. Reference Kreilos, Veble, Schneider and Eckhardt2013). More generally, the presence of localised states opens up the path to spatial delocalisation and the development of spatio-temporal patterns (see e.g. Barkley & Tuckerman Reference Barkley and Tuckerman2005; Avila et al. Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011; Tuckerman et al. Reference Tuckerman, Kreilos, Schrobsdorff, Schneider and Gibson2014).
Acknowledgements
We thank J. Gibson for providing channelflow and stimulating exchanges on localisation properties. We also thank Y. Duguet and T. Kreilos for discussions. This work was supported by the Deutsche Forschungsgemeinschaft within FOR 1182.