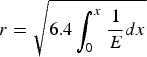1. INTRODUCTION
In recent years, with the development of the pulsed power technology, kinds of applications of pulsed discharge plasmas have attracted much attention because of the high-power density and high reduced electric field (Yatom et al., Reference Yatom, Gleizer, Levko, Vekselman, Gurovich, Hupf, Hadas and Krasik2011; Shao et al., Reference Shao, Tarasenko, Zhang, Baksht, Zhang, Erofeev, Ren, Shutko and Yan2013; Shkurenkov et al., Reference Shkurenkov, Burnette, Lempert and Adamovich2014; Zhao et al., Reference Zhao, Zhua, Zhang, Luo, Zou and Wang2014). Compared with the general discharges driven by AC and DC power supply, there are some particular phenomena in pulsed discharges, such as high breakdown voltage, high-energy electrons, and overlapped plasma channels (Naidis, Reference Naidis2011; Levko et al., Reference Levko, Tarasenko and Krasik2012c; Babaeva, Reference Babaeva2015; Zhang et al., Reference Zhang, Tarasenko, Shao, Beloplotov, Lomaev, Wang, Sorokin and Yan2015). These phenomena could no longer be interpreted by the traditional Townsend and Streamer mechanisms. Based on the runaway breakdown of high-energy electrons, different hypotheses are proposed to describe nanosecond pulse discharge. However, all these hypotheses admit that the runaway electrons with high energy play an important role in the avalanche development in nanosecond pulse discharge (Levko et al., Reference Levko, Krasik and Tarasenko2012a, Reference Levko, Yatom, Vekselman, Gleizer, Gurovich and Krasik2012b). Wilson firstly proposed the concept of the runaway electrons in 1925 (Wilson, Reference Wilson1925). However, such concept was still in a theoretical stage for the subsequent decades. Until 1970s, the detection of X rays provided an indirect evidence of the existence of high-energy electrons in nanosecond pulse discharge. Tarasova et al. detected the X rays by a scintillation detector in air and helium at different pressures. In their experiments, the voltage pulse was 180 kV, and the pulse duration was approximately 1.5 ns (Tarasova et al., Reference Tarasova, Khudyakova, Loiko and Tsukerman1974). The experimental results showed that the energy of X rays reached 15 keV. Byszewski et al. detected the X-ray dose in nitrogen and helium, and the detector consisted of a NaI(Tl) scintillation, a Be filter, and a photomultiplier tube (Byszewski & Reinhold, Reference Byszewski and Reinhold1982). The voltage pulse was 30 kV and the pulse duration was 45 ns. The results showed that the maximum of electron energy was 3 keV, which was consistent with the model of the fast and slow electrons. The high-energy electrons were responsible for the development of the electron avalanche. Since then, many studies aimed at the generation of X rays in nanosecond pulse discharge to investigate the behavior of runaway electrons (Bratchikov et al., Reference Bratchikov, Gagarinov, Kostyrya, Tarasenko, Tkachev and Yakovlenko2007; Mao et al., Reference Mao, Zou, Wang, Liu and Jiang2009; Kostyrya & Tarasenko, Reference Kostyrya and Tarasenko2015). However, the direct measurement of runaway electrons is still an ongoing topic. Since 2004, with the development of high-speed oscilloscopes and ultra-fast pulsed generator, runaway electron beams by different ways have been obtained, which confirms Wilson's hypothesis (Tarasenko et al., Reference Tarasenko, Skakun, Kostyrya, Alekseev and Orlovskii2004, Reference Tarasenko, Shpak, Shunailov and Kostyrya2005, Reference Tarasenko, Baksht, Burachenko, Kostyrya, Lomaev and Rybka2008a; Baksht et al., Reference Baksht, Burachenko, Kozhevnikov, Kozyrev, Kostyrya and Tarasenko2010; Alekseev et al., Reference Alekseev, Lomaev, Rybka, Tarasenko, Shao, Zhang and Yan2013; Erofeev et al., Reference Erofeev, Baksht, Tarasenko and Shut'ko2013; Ivanov, Reference Ivanov2013). Mesyats et al. measured the runaway electron beam of a picosecond resolution over a wide-range downstream of the absorbing foil filters by time-of-flight measurement (Mesyats et al., Reference Mesyats, Reutova, Sharypov, Shpak, Shunailov and Yalandin2011; Gurevich et al., Reference Gurevich, Mesyats, Zybin, Yalandin, Reutova, Shpak and Shunailov2012). The energy of the runaway electron beam reached 470 keV in a 19-cm gap. Furthermore, the avalanche generation of runaway electrons was demonstrated, and two flows of runaway electrons were observed in an extended air gap at the delay stage of a pulsed breakdown. Baksht et al. measured the runaway electrons in a nanosecond pulse discharge in SF6 (Baksht et al., Reference Baksht, Lomaev, Rybka, Sorokin and Tarasenko2008). The results showed that the pulse duration of the runaway electron beams deceased with the applied voltage, and the pulse duration increased with the gas pressure. From the aforementioned studies, measurement of runaway electron beams has been carried out in many experiments.
Due to different obstacles of the experimental investigation on the propagation of runaway electrons of the order of nanoseconds or sub-nanoseconds, a numerical simulation is an efficient method to investigate the above process. More exact results could be obtained in the case of a picosecond scale. Yakovlenko and co-workers built a one-dimensional (1D) particle-in-cell (PIC) model to study the generation of runaway electrons in SF6 (Boichenko et al., Reference Boichenko, Tkachev and Yakovlenko2003). In his model, the electric potential difference between the anode and cathode was fixed, and the secondary electron and the discharge between positive and negative ions were ignored. The simulation results showed that the electrons were mainly attached to the SF6 molecules when the E/p (E is the electric field strength, and p is the gas pressure) was less than 0.63 V/(cm Pa). Otherwise, the Townsend theory could account for the discharge when the E/p exceeded 0.63 V/(cm Pa). Under this condition, the maximum of the electron energy could reach eψC (ψC was the electric potential at the cathode). Levko et al. also simulated the runaway electrons in SF6 by a 1D PIC model (Levko et al., Reference Levko, Yatom, Vekselman, Gleizer, Gurovich and Krasik2012b, Reference Levko, Krasik, Tarasenko, Rybka and Burachenko2013). This model neglected the process of electrons’ detachment for the negative ion of SF6. The electron emission from the cathode was described by the Fowler–Nordheim (F–N) Law. The simulation results showed that the generation of the runaway electrons was significantly influenced by the virtual cathode, which was formed by the attachment of the low-energy electrons with the SF6 molecules. Both applied voltage and rise time affected the generation of the runaway electrons. In addition, the increase of SF6 gas pressure caused the decrease of the runaway electron number. Tarasenko and Yakovlenko used the friction force [F(ε)] caused by the collisions of electrons with gas atoms based on the Bethe approximation (Raether, Reference Raether1964; Tarasenko & Yakovlenko, Reference Tarasenko and Yakovlenko2008b)
where ε is the electron energy, z is the number of electrons in the atom or molecule of neutral gas, N is the particle number density in the neutral gas, and I is the mean inelastic energy loss. As ε increases, F(ε) increases at first, and then decreases. It is calculated that when ε is equal to 2.72I/2, F(ε) reaches the maximum. Therefore, the electrons can accelerate the energy from electric field when ε exceeds 2.72I/2. Finally, these electrons are likely to enter a runaway status when the critical electric field is reached. Note that in the above numerical work, behavior of runaway electrons is simulated in a single gas component at low pressure. However, because of the complicated types of particles and frequent impact ionizations in air, numerical simulations of runaway electrons under such condition require complex physical models and a lot of calculations. Instead of developing complicated physical models, Wang et al. developed a simple numerical model to simulate the avalanche propagation in dielectric barrier discharge in atmospheric air, and the avalanche length was used to determine the streamer formation (Wang et al., Reference Wang, Lu and Pu2002). The results showed that it was possible to obtain glow discharge with a gas length below 2 mm. This model can well describe the propagation of the electron avalanches in atmospheric pressure. It provides a good reference for simulating the avalanche propagation in nanosecond pulse discharges. From the aforementioned studies, the simulation on runaway electrons is complicated and is far from full understanding.
In our previous work, the detection of runaway electron beams and X rays in nanosecond pulse discharges was conducted (Shao et al., Reference Shao, Tarasenko, Zhang, Baksht, Yan and Shut'ko2012, Reference Shao, Tarasenko, Yang, Beloplotov, Zhang, Lomaev, Yan and Sorokin2014; Zhang et al., Reference Zhang, Tarasenko, Shao, Baksht, Burachenko, Yan and Kostyray2013, Reference Zhang, Tarasenko, Shao, Beloplotov, Lomaev, Sorokin and Yan2014). The experimental results showed that X rays mainly resulted from the bremsstrahlung at the anode, and these X rays were produced by the high-energy electrons. Moreover, the effect of anode and cathode materials on the generation of X rays was investigated. The runaway electron beams were measured in air and SF6 at the pressures ranged from 0.05 to 0.1 MPa. The aim of this work is to investigate the behavior of runaway electrons by simulation for better understanding nanosecond pulse discharge. A simple physical model is established to simulate the electron avalanche in nanosecond pulse discharge. Furthermore, the effect of pulse polarity and amplitude of applied voltage, and gas pressure on the generation of runaway electrons is studied.
2. NUMERICAL MODEL
In general, when nanosecond pulse with high overvoltage is applied on the gap, initial electrons will be generated due to field emissions in nanosecond pulse discharge. These electrons move toward the anode, and impact ionizations occur between the electrons and the gas atoms or molecules. As a result, positive ions are produced by the collisions. The electrons in the local area will enhance the electric field of the avalanche head, which leads to the acceleration of the electrons in the avalanche head. Under this condition, when the energy of the electrons gained from the electric field exceeds the collision energy loss, these electrons tend to run away from the avalanche head and to result in secondary avalanche, which is essential to the formation of the streamers. The distribution of the electric flied is an important parameter for determining the behavior of the runaway electrons. It is well known that electrons acquire energy from the electric field when they move along the electric field line in the gap, and the critical electric field strength for runaway breakdown is 450 kV/cm in atmospheric air (Tarasenko & Yakovlenko, Reference Tarasenko and Yakovlenko2008b; Zhang et al., Reference Zhang, Tarasenko, Shao, Baksht, Burachenko, Yan and Kostyray2013). In this paper, the static electric field is calculated by COMSOL Multiphysics software. The static electric field should comply with the charge conservation, as shown in Eqs. (2) and (3):
The discharge parameters are as follows: A 2 mm-diameter copper tube is used as the cathode and a 10 mm-length square copper plane is fixed as the anode. The distance between the cathode and anode is 12 mm. For the simulated parameters of the cathode and the anode, the relative magnetic permeability is 1, the conductivity is 5.998 × 107 S/m, the relative permittivity is 1 and the density is 8.7 × 103 kg/m3. The gap is filled with air. Figure 1 shows the distribution of electric field in the simulation. The simulation area is rectangular with a region of 32 × 24 mm2, whose dimension is much larger than that of the tube-to-plane electrodes, as shown in Figure 1a. The boundary of the rectangular region is considered as the position of zero potential. Figure 1b presents the enlarged electric field distribution at the edge of the tube electrode. It could be seen that the high electric field appeared in the region near the cathode, where the small curvature radius results in electric field amplification. Note that the maximal electric field is along the axis of the gap. The maximum electric field is approximately 600 kV/cm, which is higher than the critical electric field for runaway breakdown (450 kV/cm). It indicates that the electric field in our case is able to generate runaway electrons. Therefore, it can develop a physical model to simulate runaway electron inception and breakdown under our conditions.

Fig. 1. Distribution of the electric field in a tube-to-plane gap: (a) arrangement of the electrodes in the simulation; (b) detailed static electric field near the edge of the cathode (red dashed-line region in Fig. 1a).
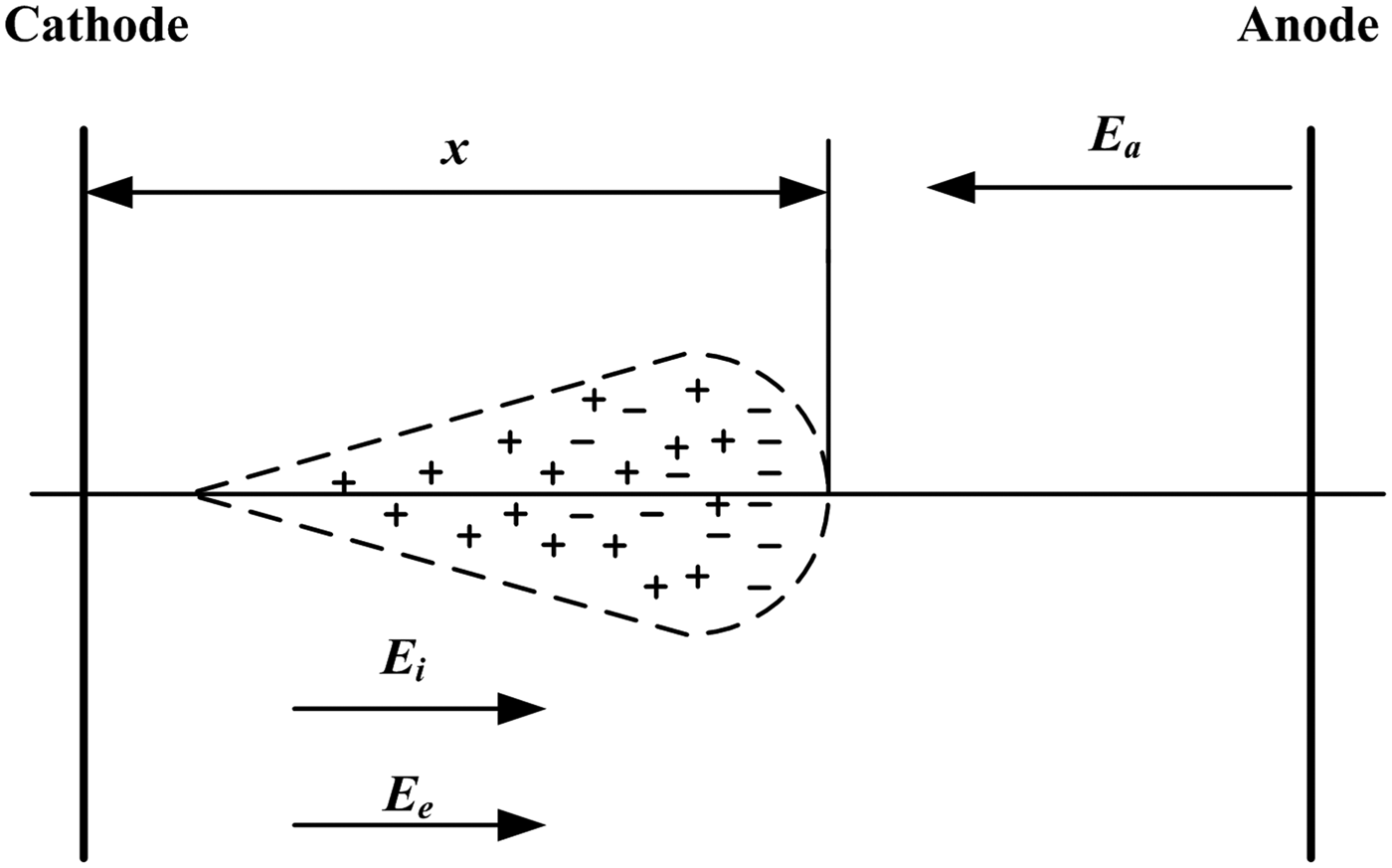
Because the velocity for electrons is much higher than that for positive ions, the avalanche behaves in a cone shape. At the front of the core, there are many electrons, while the positive ions are at the tail of the core. Thus, the combined electric field (E c) in the gap consists of external electric field (E a), electric field of electrons (E e), and electric field of the ions (E i). Figure 2 shows a schematic diagram of the avalanche propagation in our simulation. In order to simplify the simulation, it is considered that the ions are only generated along the x-axis and their distribution is discrete (Wang et al., Reference Wang, Lu and Pu2002). The diffusion of the electrons is spherical, and their distribution is uniform in the sphere. The above process can be described as follows: an electron moves toward the anode by gaining energy from the electric field, much more electrons appear due to the impact ionization and form the main avalanche, and then secondary avalanches appear due to the runaway behavior of high-energy electrons. Finally, the further development of the main avalanche and secondary avalanches forms the streamer. Therefore, several parameters including the electron velocity, the electron energy, and the combined electric field, are important in the numerical simulation.

Fig. 2. Schematic picture of the model for avalanche propagation.
The flow diagram of the simulation is shown in Figure 3. The simulation is a cyclic process, and can be achieved using the iteration method. The detailed cyclic process is as follows: when t = 0, E c = E a. The electron velocity, avalanche length, radius of electron sphere, ions number, and electrons number are calculated based on E c. When t = dt, electrons and ions appear in the gap. E e and E i are calculated according to Eqs. (2) and (3), and E c = E a + E e + E i. Then, the electron velocity, avalanche length, radius of electron sphere, ions number, and electrons number at t = 2dt can be calculated based on the E a at t = dt. Finally, the cyclic iteration is repeated until the avalanche length reaches the distance between the electrodes, and the cycle ended. It should be pointed out that the model uses the ideal conditions. Only the drift velocity of electrons is considered, but the thermal velocity is not considered in nanosecond pulse discharge. Also, the direction of the elastic scattering is not considered.

Fig. 3. Overview of the flow diagram in the simulation.
The parameters in Figure 3 are calculated as follows:
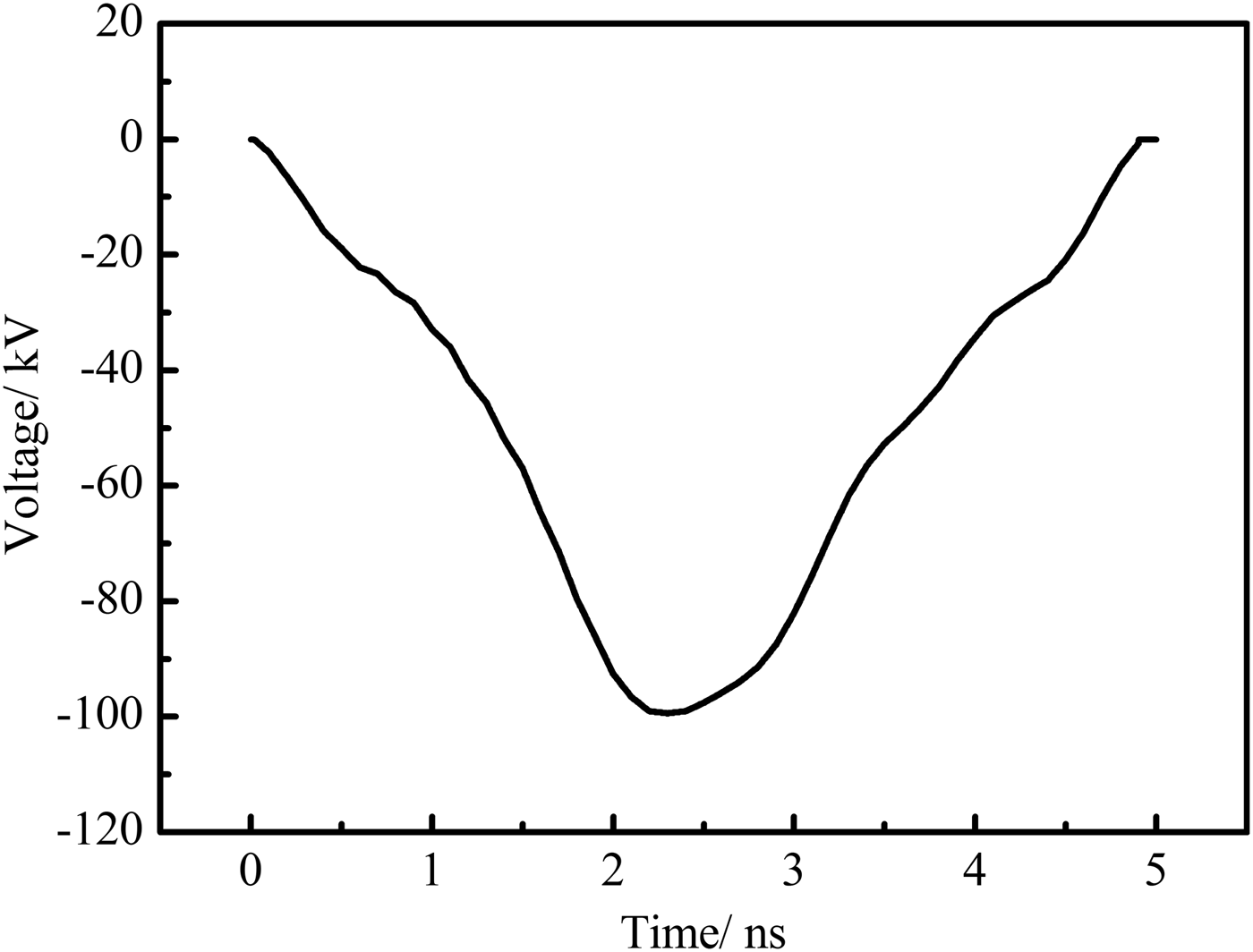
(1) E a: Although some empirical equations can be adapted to calculate the electric field in the tube-to-plane gap, they are inconsistent with the experimental conditions in our case. A fitted curve according to our experimental voltage pulse is used in the simulation (Zhang et al., Reference Zhang, Tarasenko, Shao, Beloplotov, Lomaev, Sorokin and Yan2014). Figure 4 presents the simulation waveform of the voltage pulse. It can show the variation of the electric field with time.
Fig. 4. The waveform of the voltage pulse in the simulation.
(2) E i: The electric field is two-dimensional, and the ions are considered as stationary. Thus, the avalanche in the model is approximately core-shaped. The electrons are in the head of the core, and the positive ions are in the tail of the core. The ions are simplified to distribute discretely along the x-axis. E i can be calculated by the electric charge equation:
(4)where Q is the quantity of electric charge of the ions, x d is the distance between the measured position and point charge. $${E_{\rm i}} = \displaystyle{Q \over {4{\rm \pi \varepsilon} {x_{\rm d}}^2}} $$
$${E_{\rm i}} = \displaystyle{Q \over {4{\rm \pi \varepsilon} {x_{\rm d}}^2}} $$(3) E e: Because electrons are uniformly distributed in the sphere, E e can be calculated by Eq. (5) (Korolev & Mesyats, Reference Korolev and Mesyats1991)
(5)where ρ is the charge density, R e is the radius of the electron sphere, r d is the distance between the electron and the center of the sphere. $${E_{\rm e}} = \displaystyle{{{\rm \rho} {r_{\rm d}}} \over {3{\rm \varepsilon}}} \left( {{r_{\rm d}} \le {R_{\rm e}}} \right),\quad {E_{\rm e}} = \displaystyle{{{\rm \rho} {R_{\rm e}}^3} \over {3{\rm \varepsilon} {r_{\rm d}}^2}} \left( {{r_{\rm d}} \gt {R_{\rm e}}} \right)$$
$${E_{\rm e}} = \displaystyle{{{\rm \rho} {r_{\rm d}}} \over {3{\rm \varepsilon}}} \left( {{r_{\rm d}} \le {R_{\rm e}}} \right),\quad {E_{\rm e}} = \displaystyle{{{\rm \rho} {R_{\rm e}}^3} \over {3{\rm \varepsilon} {r_{\rm d}}^2}} \left( {{r_{\rm d}} \gt {R_{\rm e}}} \right)$$(4) E c is the combination of E a, E i, and E e.
(5) Electrons drift velocity (v) (cm/s) under nanosecond pulse condition is calculated as follows (Kawada & Hosokawa, Reference Kawada and Hosokawa1989):
(6)where E (V/cm) is the electric field, p (Pa) is the pressure. It is valid when E ranges from 30 400 to 106 400 V/cm at atmospheric pressure. $$v = 1.25 \times {10^7} \times \sqrt {\displaystyle{E \over {40p}}} $$
$$v = 1.25 \times {10^7} \times \sqrt {\displaystyle{E \over {40p}}} $$(6) The avalanche length (x de) (cm) can be calculated by iterating the result of the previous cycle according to Eq. (7):
(7)where dt is the time step. $${x_{{\rm de}}}(n + 1) = {x_{{\rm de}}}(n) + {v_{{\rm de}}} \bullet dt$$
$${x_{{\rm de}}}(n + 1) = {x_{{\rm de}}}(n) + {v_{{\rm de}}} \bullet dt$$(7) Radius of the electron sphere [r(cm)] is calculated as follows:
(8)where x is the current position of the electrons. $$r = \sqrt {6.4\int_0^x {\displaystyle{1 \over E}} dx} $$
$$r = \sqrt {6.4\int_0^x {\displaystyle{1 \over E}} dx} $$(8) The electrons number (N e) and ions number (N i) are calculated as follows:
(9) $${N_{\rm e}}(t) = \exp \left( {\int_0^t {{\rm \alpha} {v_{{\rm de}}}dt}} \right)$$(10)
$${N_{\rm e}}(t) = \exp \left( {\int_0^t {{\rm \alpha} {v_{{\rm de}}}dt}} \right)$$(10) $${N_{\rm i}}(x) = {N_{\rm e}}(x){\rm \alpha} dx$$
$${N_{\rm i}}(x) = {N_{\rm e}}(x){\rm \alpha} dx$$
where α (cm−1) is the impact ionization coefficient, which can be calculated as follows (Raether, Reference Raether1964):
Equation (11) is valid when E = 15–110 kV/cm. A and B are the constant related to gas pressure, gas type, and electric field. In the simulation, A is 0.646 (cm Pa)−1, and B is 1.9 V/(cm Pa) (Raether, Reference Raether1964; Tarasenko & Yakovlenko, Reference Tarasenko and Yakovlenko2008b).
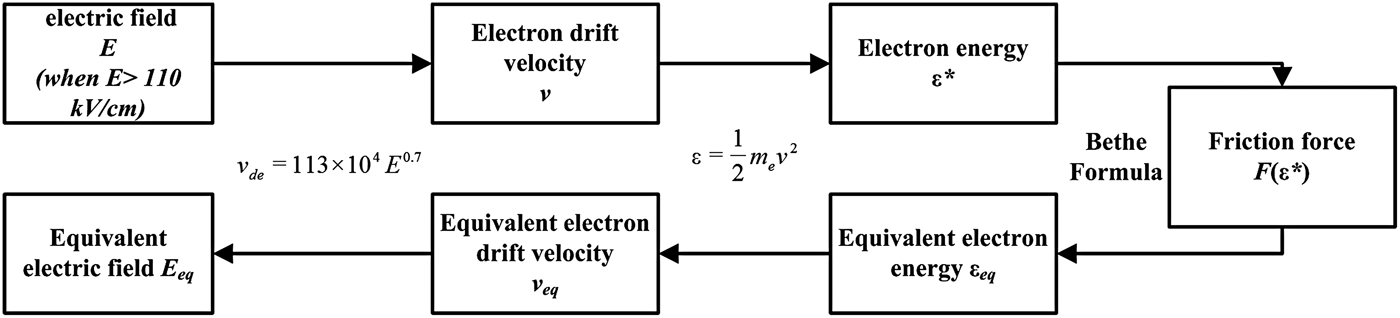
It should be pointed out that electric field may exceed 110 kV/cm under our conditions, which falls outside the valid range of formula (11). Therefore a procedure for deducing electric fields is developed, and the process can be described as follows: because the dependence of the friction force on the electron energy is parabolic (formula 1), which has a maximum value as the electron energy increases. Thus, there are two values of the electron energy according to the same friction force. When the electric field exceeds 110 kV/cm, electrons drift velocity can be deduced from Eq. (6) in accordance with the electric field. Then a corresponding electron energy (ε*) is obtained based on work–energy theorem. According to formula (1), there is an equivalent energy (εeq) whose friction force equals to that resulted from ε*. Thus, ε*can be used to deduce an equivalent electric field (E eq), which falls in the valid range of formula (11). The above process is described as the flow diagram shown in Figure 5.

Fig. 5. Flow diagram for calculating the equivalent electric field.
3. SIMULATION RESULTS
Typical simulation results of avalanche propagation in nanosecond pulse discharge, including the electrons number, avalanche length, electric field of the avalanche head, velocity of the avalanche, and the distribution of the electric field, are shown in Figure 6. In the simulation, the voltage pulse was applied on the tube electrode, and the plane electrode was grounded. Such electrode arrangement is the negative case. The time step in the simulation was 10 ps. It could be seen that all the electrons number, avalanche length, electric field of the avalanche head, and velocity of the avalanche increased after the voltage pulse was applied on the cathode. The electrons number steadily increased in the first 1.71 ns, and then it rapidly increased, as shown in Figure 6a. Both the length and velocity of the avalanche significantly increased after 1.71 ns, which indicated that runaway breakdown occurred during the rising edge of the applied voltage. Furthermore, the avalanche length of the last iteration was 3.23 mm, which was much smaller than the gap of 10 mm, as shown in Figure 6c. It was because the avalanche length in the next iteration exceeded 10 mm, the detailed results between 3.23 and 10 mm could not be obtained due to the limitation of the time step. However, the rapid increase of the avalanche length indicated that part of the electrons was in a runaway electron mode. Thus, in the paper, we considered 1.71 ns as inception of the runaway breakdown. Furthermore, the electrons number and the electric field of the avalanche head could also reflect the rapid increase in the last several iterations, as shown in Figures 6a and 6d. The distribution of the electric field showed the distortion of the electric field before the iteration finished, as shown in Figure 6f. Such distortion revealed the effect of the space charge on the electric field.

Fig. 6. Simulation results of: (a, b) the electrons number, (c) avalanche length, (d) electric field of the avalanche head, (e) velocity of the avalanche, and (f) the distribution of the electric field.
The polarity effect of applied voltage is an important parameter which could affect the behavior of runaway electrons in nanosecond pulse discharge. The simulation conditions were as follows: the voltage pulse was applied on the plane, and the tube was grounded. Such electrode arrangement was the positive polarity case in our simulation. Figure 7 shows the simulation results in the positive polarity case. It could be observed that the inception of the runaway breakdown was 1.68 ns. Moreover, the electric field of the avalanche head for positive polarity was much lower than that for negative polarity at the very beginning, as shown in Figure 7d. Such phenomenon could be explained with the reason that the electric field near the plane electrode was lower than that near the tube with a small radius of curvature, resulting in the low electric field of the avalanche head. Note that runaway electron beams were measured only under negative condition in our previous work (Zhang et al. Reference Zhang, Tarasenko, Shao, Baksht, Burachenko, Yan and Kostyray2013, Reference Zhang, Tarasenko, Shao, Beloplotov, Lomaev, Sorokin and Yan2014). Although the runaway electrons appeared earlier in the positive polarity case than in the negative polarity case, the electrons number was small because of the recombination between the electrons and positive ions near the plane electrode; thus, it was difficult to measure the runaway electron beams in the positive polarity case.

Fig. 7. Simulation results of: (a, b) the electrons number, (c) avalanche length, (d) electric field of the avalanche head, (e) velocity of the avalanche, and (f) the distribution of the electric field for positive polarity.
Figure 8 shows the simulated avalanche lengths at different amplitudes of the applied voltage. The simulation conditions were the same as those in Figure 6. The amplitudes of the applied voltage were 25, 50, 100, and 150 kV, respectively. It could be seen that the runaway breakdown occurred when the applied voltages were 50, 100, and 150 kV. The inception of the runaway breakdown increased with the decrease of the amplitude of the applied voltage, which indicated the runaway breakdown was closely related to the electric field. However, the avalanche length was about 0.145 mm when the applied voltage was 25 kV, which indicated that the avalanche could not arrive at the anode. It was because that low amplitude of the applied voltage could not provide sufficient energy for accelerating the electrons; the electrons generated near the cathode were not able to arrive at the anode. In addition, the simulation results showed that the threshold voltage of runaway breakdown was 33 kV in our case.

Fig. 8. Simulation results of the avalanche length at different applied voltages.
The impact ionization changes with the pressure, which may affect the multiplication of the electrons. Figure 9 shows the dependence of both the threshold voltage of runaway breakdown and the electrons number on air pressure. The simulation conditions were the same as those in Figure 6. The pressures ranged from 2.5 to 100 kPa in air. It was observed that the threshold voltage of runaway breakdown decreased with the increase of the pressure until it reached approximately 15 kV, for which the pressure was 10 kPa. Then, the threshold voltage of runaway breakdown was slightly changed until the pressure increased to 20 kPa. Further increasing the pressure gave a rise of the threshold voltage. On the contrary, the electrons number increased from 1 × 1011 to 5 × 1011 at first, and then it decreased to 2 × 108 when the pressure increased to 100 kPa. The maximum of the electrons number appeared when the pressure was approximately 10 kPa. Such results were similar to the simulation results obtained in SF6 (Levko et al., Reference Levko, Yatom, Vekselman, Gleizer, Gurovich and Krasik2012b). The variation of the electrons number could be explained by the change of the impact ionization. When the electric field was fixed, the impact ionization coefficient reached a maximum, as shown in Eq. (11). The larger the impact ionization was, the more the electrons were. Therefore, the electrons number and the pressure had a similar relationship with the impact ionization coefficient and the pressure. As to the threshold voltage of the runaway breakdown, the increase of the pressure led to the increase of the gas density when the gap was fixed, thus the mean free path of the electron decreased. Electrons could not accelerate sufficient energy between the two collisions. Therefore, more energy was required from the external electric field and the threshold voltage was high. However, when the pressure decreased to a certain value, the gas density was small, the mean free path of the electron was too long to make efficient impact ionization, and electrons also could not accelerate the energy to turn to runaway mode (Burachenko & Tarasenko, Reference Burachenko and Tarasenko2010). The threshold voltage was higher in the case of low pressure. To sum up, the threshold voltage of runaway breakdown had a minimum as the pressure increased.

Fig. 9. Dependence of the threshold voltage of runaway breakdown and the electrons number on the air pressure.
4. DISCUSSION
The investigations of nanosecond pulse discharge has been focused on the generation of runaway electrons with high energies (Tarasenko & Yakovlenko, Reference Tarasenko and Yakovlenko2008b; Baksht et al., Reference Baksht, Burachenko, Kozhevnikov, Kozyrev, Kostyrya and Tarasenko2010; Shao et al., Reference Shao, Tarasenko, Zhang, Baksht, Yan and Shut'ko2012; Zhang et al., Reference Zhang, Tarasenko, Shao, Baksht, Burachenko, Yan and Kostyray2013). In an inhomogeneous electric field with a tube-to-plane gap, the small radius of curvature is located at the tube, where the electric flied amplification appears. When nanosecond pulses are applied on the tube electrode, the field emission process produces initial electrons for the avalanche propagation near the tube. Simultaneously, large quantities of the positive ions leave behind the electrons and enhance the local electric field near the tube. These initial electrons continuously accelerate energy when they move toward the plane electrode, and can reach an extremely high-energy rank. When the energy of the electrons exceeds a threshold value, some electrons will turn to runaway mode. The runaway electrons play an important role in the avalanche propagation of nanosecond pulse discharges. According to the static electric field in Figure 1, the electric field could reach approximately 600 kV/cm near the cathode where the radius of curvature is small. The electrons in this area are most likely to become runaway electrons, and they form the main avalanche in the gap. Because the velocity of the electrons is much larger than that of the positive ions, runaway electrons often concentrate at the head of the main avalanche. Under such condition, these electrons are the source of the secondary electrons and avalanche. The secondary avalanches overlap with the main avalanche, and they will assist the gas breakdown. Furthermore, increasing the applied voltage and decreasing the gas pressure will enhance the field emission near the tube electrode, which is beneficial to the generation of the runaway electrons, as shown in Figure 5. The effect of the gas pressure on the nanosecond pulse is more complicated. The gas density decreases with the pressure and the corresponding mean free path of the electrons increases. Thus, electrons are able to gain sufficient energy for running away. The lowering of the gas pressure is, however, not necessarily suitable. Further decreasing the gas pressure will lead to a long mean free path. If the mean free path is too long, then impact ionization cannot occur and the electrons will not be able to accelerate sufficient energy for running away. Therefore, there is a minimum pressure for the generation of runaway breakdown, as shown in Figure 9.
5. CONCLUSION
The conducted simulation of the runaway electrons in nanosecond pulse discharges allows the following conclusions.
• In the case of applied voltage with a negative polarity, when the applied voltage is 100 kV, the electrons number, avalanche length, electric field of the avalanche head, and velocity of the avalanche increase with the time. The moment for runaway breakdown is 1.71 ns.
• The inception of the runaway breakdown advances 0.03 ns in the positive polarity case than that in the negative polarity case.
• The inception of the runaway breakdown and the avalanche length increase with the applied voltage when the amplitude of the applied voltage exceeds a threshold voltage. The simulated threshold voltage of runaway electrons is about 33 kV.
• Gas pressure has a significant influence on the behavior of runaway electrons. There is a minimum pressure (10 kPa) for generating runaway electrons.
ACKNOWLEDGEMENTS
The work was supported by the National Natural Science Foundation of China under Grants 51222701 and 51207154; and the National Basic Research Program of China under Grant 2014CB239505-3.