Introduction
The study of laser driven plasma-based accelerators for producing ultrahigh-energy electrons is an active area of research in laser–plasma interactions (Bingham, Reference Bingham2006; Joshi, Reference Joshi2007; Malka et al., Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc2008; Esarey et al., Reference Esarey, Schroeder and Leemans2009). Laser-driven plasma accelerators provide extremely large acceleration gradients that is, thousands of times stronger acceleration fields (100 GV/m) than conventional particle accelerators (100 MV/m). They are useful tools in various fields such as particle physics, materials science, medical diagnostics and treatment, manufacturing industry and to produce extremely short electron bunches. Various schemes are operative for particle acceleration such as laser wakefield accelerator (Tajima & Dawson, Reference Tajima and Dawson1979; Gorbunov & Kirsanov, Reference Gorbunov and Kirsanov1987; Sprangle et al., Reference Sprangle, Esarey, Ting and Joyce1988), plasma beat wave accelerator (Rosenbluth & Liu, Reference Rosenbluth and Liu1972; Tajima & Dawson, Reference Tajima and Dawson1979), multiple laser pulses (Nakajima, Reference Nakajima1992; Umstadter et al., Reference Umstadter, Esarey and Kim1994), self-modulated laser wakefield accelerator (Leemans et al., Reference Leemans, Catravas, Esarey, Geddes, Toth, Trines, Schroeder, Shadwick, Van Tilborg and Faure2002; Chen et al., Reference Chen, Chien, Lee, Lin, Wang and Chen2004), and so on in which very high intense laser beams are used. The yield of these schemes highly depends on the long propagation distance (over several Rayleigh lengths) of intense laser pulses in the plasmas without loss of the energy. A large amplitude plasma wave (with phase velocity near the speed of light) is driven by an intense laser pulse in which plasma electrons can be trapped and accelerated to relativistic energies. An extensive review on laser-driven plasma-based particle accelerators has been found in the literature (Esarey et al., Reference Esarey, Sprangle, Krall and Ting1996, Reference Esarey, Schroeder and Leemans2009; Malka et al., Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc2008).
Self-focusing of an intense laser pulse in plasmas plays an important role in laser-based charged particle accelerators and occurs due to increase of the on-axis index of refraction relative to the edges of the wavefront of the laser beam. When two intense laser beams with slightly different frequencies simultaneously propagate in plasma, self-focusing of one laser beam is affected by the self-focusing of another laser beam. This behavior is known as a cross-focusing of the laser beams (Gupta et al., Reference Gupta, Sharma and Gupta2005; Purohit et al., Reference Purohit, Chauhan, Pandey and Sharma2005). This method is used to generate large amplitude electron plasma wave (EPW) for ultrahigh gradient electron acceleration in plasma beat wave accelerator (PBWA) scheme. It is found that beat plasma waves are very efficient for electron acceleration up to ultra-relativistic energies (Walton et al., Reference Walton, Najmudin, Wei, Marle, Kingham, Krushelnick, Dangor, Clarke, Poulter, Hernandez-Gomez, Hawkes, Neely, Collier, Danson, Fritzler and Malka2006; Malka et al., Reference Malka, Faure, Gauduel, Lefebvre, Rousse and Phuoc2008; Esarey et al., Reference Esarey, Schroeder and Leemans2009; Malka Reference Malka2014). In this scheme, a large amplitude plasma wave with phase velocity close to the velocity of light is excited by beating of two intense laser beams in plasma to accelerate charged particles that is, two laser beams with slightly different frequencies ω1 and ω2 and corresponding wave numbers k 1 and k 2 beat together to generate a plasma wave at the difference frequency Δω (=ω1 − ω2) with wave vector Δ k (=k 1 − k 2). If the beat frequency Δω is close to the plasma frequency ωp, a very large amplitude relativistic EPW can be generated, which can be used to accelerate electrons efficiently to high energies in short distances. In this process, focusing on the lasers beams is essential to avoid an unacceptable loss of laser energy from the acceleration region.
The generation of EPW by beat wave process and particle acceleration has been theoretically and experimentally studied in the past, which reflect that the beat-wave scheme is a reliable and reproducible method for generating plasma waves having relativistic phase velocities (Tang et al., Reference Tang, Sprangle and Sudan1985; Gibbon & Bell, Reference Gibbon and Bell1988; Mori et al., Reference Mori, Joshi, Dawson, Forslund and Kindel1988; Clayton et al., Reference Clayton, Everett, Lal, Gordon, Marsh and Joshi1994; Everett et al., Reference Everett, Lal, Gordon, Clayton, Marsh and Joshi1994; Dyson et al., Reference Dyson, Dangor, Dymoke-Bradshaw, Ashfar-Rad, Gibbon, Bell, Danson, Edwards, Amiranoff, Matthieusent, Karttunen and Salomaa1996; Walton et al., Reference Walton, Najmudin, Wei, Marle, Kingham, Krushelnick, Dangor, Clarke, Poulter, Hernandez-Gomez, Hawkes, Neely, Collier, Danson, Fritzler and Malka2002; Walton et al., Reference Walton, Najmudin, Wei, Marle, Kingham, Krushelnick, Dangor, Clarke, Poulter, Hernandez-Gomez, Hawkes, Neely, Collier, Danson, Fritzler and Malka2006). The concept of PBWA was first proposed by Tajima and Dawson in 1979. However, Rosenbluth & Liu (Reference Rosenbluth and Liu1972) have previously analyzed resonant excitation of a plasma wave using two laser pulses for plasma heating applications. Plasma wave excitation by a resonant laser beat wave was observed initially by Clayton et al. (Reference Clayton, Joshi, Darrow and Umstadter1985) and this was extended in the form of beat wave accelerated electrons by Ebrahim et al. (Reference Ebrahim, Lavigne and Aithal1985). The main emphasis in the beat wave experiments was to demonstrate particle acceleration by the relativistic plasma wave. The first evidence of accelerated electrons using a laser-driven plasma wave was reported by Kitagawa et al. (Reference Kitagawa, Matsumoto, Minamihata, Sawai, Matsuo, Mima, Nishihara, Azechi, Tanaka, Takabe and Nakai1992) and shown that plasma electrons were trapped and accelerated to energy in excess of 10 MeV. Clayton et al. (Reference Clayton, Marsh, Dyson, Everett, Lal, Leemans, Williams and Joshi1993) and Everett et al. (Reference Everett, Lal, Gordon, Clayton, Marsh and Joshi1994) showed that high energy injected electrons could be trapped and accelerated to significant energies by relativistic plasma waves. Electron acceleration by relativistic EPWs driven by the optical mixing of laser light in a plasma has been reported by Ebrahim (Reference Ebrahim1994) and shown that electrons injected at 12.5 MeV accelerated to 29 MeV over a plasma length of approximately 1 cm corresponding to accelerating electric field gradient of approximately 1.7 GeV/m. Amiranoff et al. (Reference Amiranoff, Bernard, Cros, Jacquet, Matthieussent, Miné, Mora, Morillo, Moulin, Specka and Stenz1995) observed acceleration in beat wave experiments with Nd:Glass lasers of about 1 µm wavelengths by an electric field of 0.6 GV/m. Ghizzo et al. (Reference Ghizzo, Bertrand, Begue, Johnston and Shoucri1996) developed a Hilbert–Vlasov code for the study of high-frequency PBWA. Enhanced energy gain of externally injected electrons in a plasma has been demonstrated by a combined effect of ponderomotive forces of the laser beam and a high-gradient relativistic plasma wave (Tochitsky et al., Reference Tochitsky, Narang, Filip, Musumeci, Clayton, Yoder, Marsh, Rosenzweig, Pellegrini and Joshi2004). This work employed a laser beat wave induced plasma channel to extend the length of the accelerator, allowing acceleration of electrons up to 50 MeV. Walton et al. (Reference Walton, Najmudin, Wei, Marle, Kingham, Krushelnick, Dangor, Clarke, Poulter, Hernandez-Gomez, Hawkes, Neely, Collier, Danson, Fritzler and Malka2006) have observed the generation of relativistic plasma waves by a high-intensity short-pulse beat-wave and shown that large-amplitude plasma waves have been created by the beat wave interaction. Filip et al. (Reference Filip, Narang, Tochitsky, Clayton, Musumeci, Yoder, Marsh, Rosenzweig, Pellegrini and Joshi2004) studied nonresonant beat-wave excitation of relativistic plasma waves using both simulations and experiments for charged particle acceleration. The results show that, as opposed to the resonant case, the accelerating electric fields associated with the nonresonant plasmons are always in phase with the beat-pattern of the laser pulse. All-optical control of nonlinear focusing of laser beams in PBWA has been studied by Kalmykov et al. (Reference Kalmykov, Yi and Shvets2009) and reported that nonresonant plasma beat wave (ωp0 ≠ ω1 − ω2) can accelerate pre-injected electrons above 100 MeV with low energy spread. Recently, Gupta et al. (Reference Gupta, Singh and Suk2015) studied the effect of amplitude saturation of laser-driven plasma beat wave on electron acceleration and shown that the saturated amplitude of the plasma beat-wave traps the electrons more effectively to accelerate them to higher energy.
When an ultra-intense laser beam propagates through the collisionless plasmas, the combined effect of the ponderomotive–relativistic nonlinearity takes place at different time scales (Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin and Prokhorov1992; Brandi et al., Reference Brandi, Manus and Mainfray1993). The combined effect of both nonlinearities modifies the density perturbation in plasma/plasma refractive index, which results in further enhancement of self-focusing of the laser beams in plasma. Many earlier theoretical investigations on the excitation of EPW and particle acceleration have been carried out to the uniform laser beams or laser beams having Gaussian irradiance distribution along their wave fronts (Sodha et al., Reference Sodha, Govind, Tiwari, Sharma and Kaushik1979; Mahmoud et al., Reference Mahmoud, Pandey and Sharma2003; Purohit et al., Reference Purohit, Chauhan and Sharma2008; Sharma & Chauhan, Reference Sharma and Chauhan2008). In these studies, the effect of relativistic and ponderomotive nonlinearity has been taken separately. The dynamics of the propagation of laser beams in plasma is expected to be drastically affected by cumulative effects of relativistic–ponderomotive nonlinearity in comparison with only relativistic or ponderomotive nonlinearity. Only a few investigations have been reported on the excitation of EPW and particle acceleration by cross-focusing of two laser beams in plasmas incorporating the combined effect of relativistic and ponderomotive nonlinearities (Gupta et al., Reference Gupta, Sharma and Gupta2005; Rawat et al., Reference Rawat, Singh, Sharma and Purohit2014). Moreover, the yield of beat wave scheme strongly depends on the spatial intensity profile of laser beams. Specifically, the cosh-Gaussian beams (decentred Gaussian beams) have raised considerable current interest on account of their higher efficient power with a flat-top beam shape in comparison with that of a Gaussian laser beam (Konar et al., Reference Konar, Mishra and Jana2007; Patil & Takale, Reference Patil and Takale2013). Such type of beams can be produced by the superposition of two decentred Gaussian laser beams with same spot size and are in phase with each other (Lu et al., Reference Lu, Ma and Zhang1999). The literature review reveals that the propagation characteristics of cosh-Gaussian laser beams in plasma have not been investigated significantly under relativistic–ponderomotive regime; except that the recent study of beat wave excitation of EPW by relativistic cross-focusing of cosh-Gaussian laser beams in plasma (Singh & Gupta, Reference Singh and Gupta2015).
The present work is the extension of our previous work (Purohit et al., Reference Purohit, Gaur and Rawat2016), where authors investigated the propagation of two intense CGL beams in collisionless plasma with dominant relativistic–ponderomotive nonlinearity. These two intense beams interact with each other and generate relativistic EPW, which further accelerates electrons to relativistic energies. In this work, the effect of the beating of two cross-focused intense cosh-Gaussian laser beams in plasmas on the excitation of the EPW at difference frequency Δω (=ω1 − ω2) has been investigated. This excited EPW by the beat wave process can be used to accelerate electrons efficiently to high energies in short distances. The energy of the electron accelerated by the EPW has also been calculated, when relativistic and ponderomotive nonlinearities are operative. The results are compared with taking only relativistic nonlinearity and Gaussian profile of laser beams. In the section ‘Cross-focusing of cosh-Gaussian laser beams in plasma’, we have given the dimensionless beam width parameters of the two co-propagating CGL beams in plasma. A paraxial-ray approximation has been used in the present analysis (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976). The effect of the cross-focusing of the laser beams on the excitation of the EPW and electron acceleration is studied in sections ‘Beat wave excitation of EPW’ and ‘Charged particle acceleration’, respectively. The important results and conclusions based on the present investigation are presented in the section ‘Numerical results and discussion’. The conclusions are given in the section ‘Conclusion’.
Analytical formulation
Cross-focusing of cosh-Gaussian laser beams in plasma
Consider two linearly polarized intense CGL beams propagating along the z-direction with different frequencies ω1 and ω2, wave numbers k 1 and k 2, respectively, in the collisional plasma. The initial electric field distribution of the beams are given by (Singh et al., Reference Singh, Singh and Sharma2013)
$$\eqalign{(\mathop {E_1}\limits^{\to} \cdot \mathop {E_1^{\ast}} \limits^{\to})_{z = 0} & = \displaystyle{E_{10}^2 \over 4f_1^2 (z)}\exp \left(\displaystyle{b^2 \over 2} \right) \left[ \exp \left\{ - \left(\displaystyle{r \over r_{10} f_1^2 (z)} + \displaystyle{b^2 \over 2} \right)^2 \right\} \right. \cr & \quad \left. + \exp \left\{ - \left(\displaystyle{r \over r_{10} f_1^2 (z)} - \displaystyle{b^2 \over 2} \right)^2 \right\} \right]^2,}$$
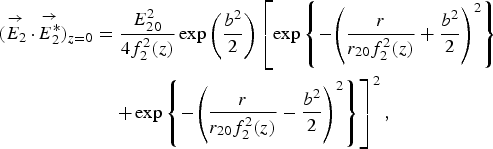$$\eqalign{(\mathop {E_2}\limits^{\to} \cdot \mathop {E_2^{\ast}} \limits^{\to})_{z = 0} & = \displaystyle{{E_{20}^2} \over {4f_2^2 (z)}}\exp \left({\displaystyle{{b^2} \over 2}} \right) \left[ {\exp \left\{ { - {\left( {\displaystyle{r \over {r_{20}f_2^2 (z)}} + \displaystyle{{b^2} \over 2}} \right)}^2} \right\}} \right. \cr &\left. \quad + \exp \left\{ { - {\left( {\displaystyle{r \over {r_{20}f_2^2 (z)}} - \displaystyle{{b^2} \over 2}} \right)}^2} \right\} \right]^2,}$$where r is the radial coordinate of the cylindrical coordinate system, r 10 and r 20 are the initial spot size of the laser beams, E 10 and E 20 are the amplitude of CGL beams for the central position at r = z = 0; b is the decentred parameter and f 1,2 are the dimensionless beamwidth parameters for beam 1 and 2, respectively.
The effective dielectric constant of the plasma can be written as
$${\rm \varepsilon} _{1,2} = {\rm \varepsilon} _{01,02} + {\rm \phi} _{1,2}(\mathop {E_1}\limits^{\to} \cdot \mathop {E_1^*} \limits^{\to}, \;\mathop {E_2}\limits^{\to} \cdot \mathop {E_2^*} \limits^{\to} ),$$
where ε01,02 = 1 − Ω2 
$(\Omega ^2 = {\rm \omega} _{{\rm p}0}^2 /{\rm \omega} _{1,2}^2 )$ and ϕ1,2 are the linear and nonlinear parts of the dielectric constant, respectively. The nonlinear parts of the dielectric constant are given by
$${\rm \phi} _{1,2}(\mathop {E_1}\limits^{\to} \cdot \mathop {E_1^*} \limits^{\to}, \mathop {E_2}\limits^{\to} \cdot \mathop {E_2^*} \limits^{\to}) = \Omega ^2\left( {1 - \displaystyle{{n} \over {n{}_0{\rm \gamma}}}} \right),$$
where n 0 is the density of plasma electrons in the absence of laser beam, γ is the relativistic factor given by γ = 
$(1 + {\rm \alpha} _1\mathop {E_1}\limits^ {\to} \cdot \mathop {E_1^*} \limits^{\to} + {\rm \alpha} _2\mathop {E_2}\limits^ {\to} \cdot \mathop {E_2^*} \limits^{\to} )^{1/2}$, 
${\rm \alpha} _{1,2} = (e{}^2/m_0^2 c{}^2{\rm \omega} _{1,2}^2 )$, and n is the total modified electron density due to relativistic-ponder motive force (Borisov et al., Reference Borisov, Borovskiy, Shiryaev, Korobkin and Prokhorov1992; Brandi et al., Reference Brandi, Manus and Mainfray1993). The spatial profile of intensity distribution of laser beams can be written as (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968)
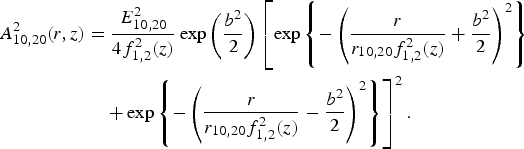$$\eqalign{ A_{10,20}^2 (r,z) & = \displaystyle{E_{10,20}^2 \over 4f_{1,2}^2 (z)} \exp \left(\displaystyle{b^2 \over 2} \right) \left[ \exp \left\{ - \left( \displaystyle{r \over r_{10,20}f_{1,2}^2 (z)} + \displaystyle{b^2 \over 2} \right)^2 \right\} \right. \cr &\left. \quad + \exp \left\{ - \left( \displaystyle{r \over r_{10,20}f_{1,2}^2 (z)} - \displaystyle{b^2 \over 2} \right)^2 \right\} \right]^2.}$$The dimensionless beam width parameters f 1,2 of two laser beams is given by (Purohit et al., Reference Purohit, Gaur and Rawat2016)
$$\eqalign{& \displaystyle{d^2f_{1,2} \over d{\rm \xi} ^2} = \displaystyle{{\rm \delta}_{1,2} \over {\rm \varepsilon}_{\,f1,2}}, \left[\displaystyle{\left(12 - 12b^2 - b^4 \right) \over 3f_{1,2}^3} - f_{1,2}\left(\displaystyle{{\rm \omega}_{\rm p0}^2 r_{1,2}^4 \over c^2} \right) \right. \cr &\quad \left\{\displaystyle{1 \over {\rm \gamma}_0^3} \left(\displaystyle{a_1 \over f_1^4 r_1^2} + \displaystyle{a_2 \over f_2^4 r_2^2} \right) + \displaystyle{c^2 \over {\rm \omega}_{\rm p0}^2} \left\{\displaystyle{\left(16 - 4b^2 \right) \over {\rm \gamma}_0^2} \left(\displaystyle{a_1 \over f_1^6 r_1^4} + \displaystyle{a_2 \over f_2^6 r_2^4} \right) \right. \right. \cr &\quad \left. \left. \quad + \displaystyle{\left(2b^2 - 16 \right) \over {\rm \gamma}_0^4} \left(\displaystyle{a_1^2 \over r_1^4 f_1^8} + \displaystyle{a_2^2 \over f_2^8 r_2^4} \right) - \displaystyle{8a_1 a_2 \over {\rm \gamma}_0^4 f_1^4 f_2^4 r_1^2 r_2^2} \right\} \right]}$$where ξ (=zc/ω1r 12) is normalized distance, δ1,2 = (ω1r 12/ω1,2(r 1,2)2)2, a 1 = (α1E 102), and a 2 (=α2E 202) are the intensity parameters of the beams. Equation (5) describes the cross-focusing of a CGL beams in a plasma with relativistic–ponderomotive nonlinearity, which determines the focusing/defocusing of the laser beams along with the distance of propagation in the plasma. The first term on the right-hand side shows the diffraction behavior of laser beams, whereas remaining terms on the right-hand side show the converging behavior that arises due to the relativistic–ponderomotive nonlinearity.
Beat wave excitation of EPW
The EPW is excited due to modification in plasma density via relativistic–ponderomotive force. The amplitude of EPW (which depends on the background electron density) gets strongly coupled to the laser beams.To study the effect of relativistic and ponderomotive nonlinearities on the generation of the plasma wave by the beat wave process in the paraxial region, we start with the following equations:
The continuity equation
$$\displaystyle{{\partial N_{\rm e}} \over {\partial t}} + \mathop \nabla \limits^{\to} (N_{\rm e} \cdot \mathop V\limits^{\to}) = 0.$$The momentum equation
$$\eqalign{m\left[ {\displaystyle{{\partial \mathop V\limits^{\to}} \over {\partial t}} + (\mathop V\limits^{\to} \cdot \mathop \nabla \limits^{\to})\mathop V\limits^{\to}} \right] & = - e\mathop E\limits^{\to} - \displaystyle{e \over c}\mathop V\limits^{\to} \times \mathop B\limits^{\to} - 2\Gamma _{\rm e}m_0\mathop V\limits^{\to} \cr &\,\quad- \displaystyle{{3k_0} \over {N_{\rm e}}}T_{\rm e}\mathop \nabla \limits^{\to} N_{\rm e}.}$$Poisson's equation
$$\nabla \cdot \mathop E\limits^{\to} = - 4{\rm \pi} eN_{\rm e}$$
where N e is the total electron density, 
$\mathop V\limits^{\to}$ is the sum of the drift velocities of the electron in the electromagnetic (EM) field and self-consistent field, 2Γe is the Landau damping factor (Krall & Trivelpiece, Reference Krall and Trivelpiece1973), 
$\mathop E\limits^{\to} $ and 
$\mathop B\limits^{\to} $ are the self-consistent electric and magnetic fields of laser beams corresponding to the EPW; and other symbols have their usual meaning.
Using Eqs. (6)–(8), following equation have been obtained for generated EPW in plasma (Sharma & Chauhan, Reference Sharma and Chauhan2008)
$$\eqalign{& \displaystyle{{\partial ^2N_{\rm e}} \over {\partial t^2}} + 2\Gamma _{\rm e}\displaystyle{{\partial N_{\rm e}} \over {\partial t}} - {\rm \upsilon} _{{\rm th}}^2 \nabla ^2N_{\rm e} - \displaystyle{e \over {m_0}}\nabla \cdot (N_{\rm e}E) \cr&= \nabla \cdot \left[ {\displaystyle{{N_{\rm e}} \over 2}\nabla (V \cdot V) - V\displaystyle{{\partial N_{\rm e}} \over {\partial t}}} \right],}$$where υ th is the square of the electron thermal speed. Therefore, the equation for generated EPW at frequency difference Δω (= ω1 − ω2) reduced to
$$\eqalign{& - ({\rm \omega} _1 - {\rm \omega} _2)^2N_1 + 2i\Gamma _{\rm e}({\rm \omega} _1 - {\rm \omega} _2)N_1 - {\rm \upsilon} _{{\rm th}}^2 \nabla ^2N_1 \cr & + \displaystyle{{{\rm \omega} _{{\rm p0}}^2} \over {\rm \gamma}} \displaystyle{n \over {n_0}}N_1 \approx \displaystyle{1 \over 4}N_0\nabla ^2(V_1 \cdot V_2^* ),}$$where N 1 is the component of electron density oscillating at a frequency Δω.
The drift velocities of electrons in the pump field at frequency ω1,2 are
$$V_{1,2} = \displaystyle{{eE_{1,2}} \over {m_0i{\rm \omega} _{1,2}{\rm \gamma}}}. $$Therefore, one can write
$$V_1 \cdot V_2^* = H\displaystyle{{C_1C_2} \over {{\rm \gamma} ^2}}e^{ - i\left\{ {(k_1 - k_2)Z + (k_1S_1 - k_2S_2)} \right\}},$$where
$$H = \displaystyle{{e^2} \over {m_0^2 {\rm \omega} _1{\rm \omega} _2}}\displaystyle{{E_{10}E_{20}} \over {4f_1f_2}},$$
$$C_1 = \exp \left[ { - \left( {\displaystyle{{r^2} \over {r_1^2 f_1^2}} + \displaystyle{{br} \over {r_1f_1}}} \right)} \right] + \exp \left[ { - \left( {\displaystyle{{r^2} \over {r_1^2 f_1^2}} - \displaystyle{{br} \over {r_1 f_1}}} \right)} \right],$$
$$C_2 = \exp \left[ { - \left( {\displaystyle{{r^2} \over {r_2^2 f_2^2}} + \displaystyle{{br} \over {r_2f_2}}} \right)} \right] + \exp \left[ { - \left( {\displaystyle{{r^2} \over {r_2^2 f_2^2}} - \displaystyle{{br} \over {r_2f_2}}} \right)} \right].$$Equation (10) contains two plasma waves (both have different frequencies). The first one is supported by hot plasma and the second by the source term at the different frequency. If, ωp0/Δω ≤ 1 , the phase velocity is almost equal to the thermal velocity of the electron and Landau damping occurs. But as ωp0/Δω ≈ 1, the phase velocity is very large as compared with the electron thermal velocity and Landau damping is negligible. The solution of Eq. (10) within the Wentzel–Kramers–Brillouin (WKB) approximation can be expressed as (Sodha et al., Reference Sodha, Govind, Tiwari, Sharma and Kaushik1979)
$$\eqalign{N_1& = N_{10}(r,z)\exp \left[ { - i(kz + S)} \right] + N_{20} \cr & \quad\exp \left[ { - i\left( {(k_1 - k_2)z + (k_1S_1 - k_2S_2)} \right)} \right],}$$
where N 10 and N 20 are the slowly varying real function of the space coordinate and 
$k^2 = ([({\rm \omega} _1 - {\rm \omega} _2)^2 - {\rm \omega} _{\rm p}^2 ]/{\rm \upsilon} _{{\rm th}}^2 )$. Substituting N 1 from Eq. (12) into Eq. (10) the equation for N 10 and N 20 can be obtained by equating the coefficient of exp[ −i(kz + S)] and exp[ −i((k 1 − k 2)z + (k 1S 1 − k 2S 2))] in the resulting equation
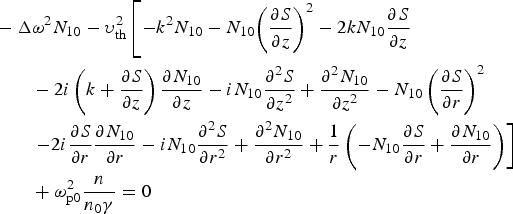$$\eqalign{& - \Delta {\rm \omega} ^2N_{10} - {\rm \upsilon} _{{\rm th}}^2 \left[ { - k^2N_{10} - N_{10}{\left( {\displaystyle{{\partial S} \over {\partial z}}} \right)}^2 - 2kN_{10}\displaystyle{{\partial S} \over {\partial z}}} \right. \cr & \quad \quad - 2i\left( {k + \displaystyle{{\partial S} \over {\partial z}}} \right)\displaystyle{{\partial N_{10}} \over {\partial z}} - iN_{10}\displaystyle{{\partial ^2S} \over {\partial z^2}} + \displaystyle{{\partial ^2N_{10}} \over {\partial z^2}} - N_{10}\left( {\displaystyle{{\partial S} \over {\partial r}}} \right)^2 \cr & \quad \quad \left. { - 2i\displaystyle{{\partial S} \over {\partial r}}\displaystyle{{\partial N_{10}} \over {\partial r}} - iN_{10}\displaystyle{{\partial ^2S} \over {\partial r^2}} + \displaystyle{{\partial ^2N_{10}} \over {\partial r^2}} + \displaystyle{1 \over r}\left( { - N_{10}\displaystyle{{\partial S} \over {\partial r}} + \displaystyle{{\partial N_{10}} \over {\partial r}}} \right)} \right] \cr &\qquad + {\rm \omega} _{{\rm p0}}^2 \displaystyle{n \over {n_0{\rm \gamma}}} = 0}$$and
$$\eqalign{& - ({\rm \omega} _1 - {\rm \omega} _2)^2N_{20} + 2i({\rm \omega} _1 - {\rm \omega} _2)\Gamma _{\rm e}N_{20} - \Delta k^2{\rm \upsilon} _{{\rm th}}^2. \cr & + {\rm \upsilon} _{{\rm th}}^2 \left( {\displaystyle{{\partial ^2N_{20}} \over {\partial z^2}} + \displaystyle{1 \over r}\displaystyle{{\partial N_{20}} \over {\partial r}} + \displaystyle{{\partial ^2N_{20}} \over {\partial r^2}}} \right) + {\rm \omega} _{{\rm p0}}^2 \displaystyle{n \over {n_0{\rm \gamma}}} = \displaystyle{1 \over 4}N_0\nabla ^2(V_1 \cdot V_2^{\ast} ).}$$After separating the real and imaginary parts of Eq. (13a), once obtain
$$\eqalign{& \left( {\displaystyle{{\partial S} \over {\partial r}}} \right)^2 +\; 2k\displaystyle{{\partial S} \over {\partial z}} = \displaystyle{1 \over {N_{10}}}\left[ {\displaystyle{{\partial ^2N_{10}} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial N_{10}} \over {\partial r}}} \right] \cr & \quad \quad + \displaystyle{1 \over {{\rm \upsilon} _{{\rm th}}^2}} \left[ {\Delta {\rm \omega} ^2 - k^2v_{{\rm th}}^2 - {\rm \omega} _{{\rm p0}}^2 \displaystyle{n \over {n_0{\rm \gamma}}}} \right]}$$and
$$\eqalign{& \displaystyle{{\partial N_{10}^2} \over {\partial z}} + N_{10}^2 \left( {\displaystyle{{\partial ^2S} \over {\partial r^2}} + \displaystyle{1 \over r}\displaystyle{{\partial S} \over {\partial r}}} \right) + \displaystyle{{\partial S} \over {\partial r}}\displaystyle{{\partial N_{10}^2} \over {\partial r}} \cr & \quad \quad + \displaystyle{{2\Gamma _{\rm e}({\rm \omega} _1 - {\rm \omega} _2)} \over {{\rm \upsilon} _{{\rm th}}^2}} N_{10}^2 = 0.}$$From Eq. (13b), N 20 is given by
$$\eqalign{\displaystyle{{N_{20}} \over {N_0}} & = \displaystyle{{HC_1C_2} \over {4{\rm \gamma} ^2\left( {\Delta {\rm \omega} ^2 - \Delta k^2{\rm \upsilon} _{{\rm th}}^2 - ({\rm \omega} _{{\rm p}0}^2 /{\rm \gamma} )(n/n_0)} \right)}} \cr & \quad \times \left[ {\Delta k^2 + \displaystyle{1 \over {r{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}} - \displaystyle{{2C^{\prime}_1C^{\prime}_2} \over {C_1C_2}} - \displaystyle{1 \over {C_1}}} \right. \left( {C^{ \prime \prime} _1 + \displaystyle{{C^{\prime}_1} \over r} - \displaystyle{{2C^{\prime}_1} \over {{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}}} \right) \cr & \quad \left. {- \displaystyle{1 \over {C_2}}\left( {C^{\prime \prime} _2 + \displaystyle{{C^{\prime}_2} \over r} - \displaystyle{{2C^{\prime}_2} \over {{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}}} \right)} \right]}$$where
$$\eqalign{C{\rm ^{\prime}}_{1,2} = & \exp \left[ { - \left( {\displaystyle{{r^2} \over {r_{1,2}^2 f_{1,2}^2}} + \displaystyle{{br} \over {r_{1,2}f_{1,2}}}} \right)} \right]\left[ { - \left( {\displaystyle{{2r} \over {r_{1,2}^2 f_{1,2}^2}} + \displaystyle{b \over {r_{1,2}f_{1,2}}}} \right)} \right] \cr & + \exp \left[ { - \left( {\displaystyle{{r^2} \over {r_{1,2}^2 f_{1,2}^2}} - \displaystyle{{br} \over {r_{1,2}f_{1,2}}}} \right)} \right]\left[ { - \left( {\displaystyle{{2r} \over {r_{1,2}^2 f_{1,2}^2}} - \displaystyle{b \over {r_{1,2}f_{1,2}}}} \right)} \right],} $$
$$\eqalign{C_{1,2}^{\prime\prime} & = \left[ {{\left( {\displaystyle{{2r} \over {r_{1,2}^2 f_{1,2}^2}} + \displaystyle{b \over {r_{1,2}f_{1,2}}}} \right)}^2 - \displaystyle{2 \over {r_{1,2}^2 f_{1,2}^2}}} \right]\exp \left[ { - \left( {\displaystyle{{r^2} \over {r_{1,2}^2 f_{1,2}^2}} + \displaystyle{{br} \over {r_{1,2}f_{1,2}}}} \right)} \right] \cr & \quad + \left[ {{\left( {\displaystyle{{2r} \over {r_{1,2}^2 f_{1,2}^2}} - \displaystyle{b \over {r_{1,2}f_{1,2}}}} \right)}^2 - \displaystyle{2 \over {r_{1,2}^2 f_{1,2}^2}}} \right]\exp \left[ { - \left( {\displaystyle{{r^2} \over {r_{1,2}^2 f_{1,2}^2}} - \displaystyle{{br} \over {r_{1,2}f_{1,2}}}} \right)} \right],} $$
$$\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}} = \displaystyle{1 \over 2}\left( {\displaystyle{{a_1} \over {\,f_1^2}} C_1C^{\prime}_1 + \displaystyle{{a_2} \over {\,f_2^2}} C_2C^{\prime}_2} \right).$$The solution of Eqs. (14a) and (14b) within the paraxial ray approximation can be written as (Akhmanov et al., Reference Akhmanov, Sukhorukov and Khokhlov1968; Sodha et al., Reference Sodha, Ghatak and Tripathi1976)
$$S = \displaystyle{{r^2} \over 2}{\rm \beta} (z) + {\rm \phi} (z),$$
$${\rm \beta} (z) = \displaystyle{k \over {\,f_{\rm e}}}\displaystyle{{df_{\rm e}} \over {dz}},$$
$$\eqalign{N_{10}^2 & = \displaystyle{{B^2} \over {4f_{\rm e}^2}} \exp \left( {\displaystyle{{b^2} \over 2}} \right) \left\{\exp \left[ { - {\left( {\displaystyle{r \over {a_0f_{\rm e}}} + \displaystyle{b \over 2}} \right)}^2} \right] \right. \cr &\left. \quad+ \exp \left[ { - {\left( {\displaystyle{r \over {a_0f_{\rm e}}} - \displaystyle{b \over 2}} \right)}^2} \right] \right\}^2\exp ( - 2k_iz),}$$
where 
$k_i = \Gamma _{\rm e}({\rm \omega} _1 - {\rm \omega} _2)/k{\rm \upsilon} _{{\rm th}}^2, $ a 0 and B are constants to be determined by the boundary condition that the magnitude of the generated plasma wave at z = 0 is zero. This gives
$$B = \displaystyle{{ - 2{\left[ {N_{20}} \right]}_{\,f_{1,2} = 1}} \over \matrix{\exp \left( {(b^2/4)} \right)\left\{ {\exp \left[ { - {\left( {(r/a_0) + (b/2)} \right)}^2} \right]} \right. \hfill \cr \left. { + \exp \left[ { - {\left( {(r/a_0) - (b/2)} \right)}^2} \right]} \right\} \hfill}} $$and
$$a_0 = \displaystyle{{r_{10}^2 r_{20}^2} \over {r_{10}^2 + r_{20}^2}}. $$In Eq. (16), f e is the dimensionless beam width of the EPW given by
$$\eqalign{\displaystyle{{d^2f_{\rm e}} \over {d{\rm \xi} ^2}} &= \displaystyle{{(12 - 12b^2 - b^4)r_{1,2}^4} \over {3f_{\rm e}^3 a_0^4}} - \displaystyle{{{\rm \omega} _{{\rm p0}}^2 r_{1,2}^4 f_{\rm e}} \over {{\rm \upsilon} _{{\rm th}}^2}} \cr &\quad \left\{ {\displaystyle{1 \over {{\rm \gamma} _{r = 0}^3}} \left( {\displaystyle{{a_1} \over {\,f_1^4 r_1^2}} + \displaystyle{{a_2} \over {\,f_2^4 r_2^2}}} \right) + \displaystyle{{c^2} \over {{\rm \omega} _{{\rm p0}}^2}}} \times \left[ {\displaystyle{{(16 - 4b^2)} \over {{\rm \gamma} _{r = 0}^4}} \left( {\displaystyle{{a_1} \over {\,f_1^6 r_1^4}} + \displaystyle{{a_2} \over {\,f_2^6 r_2^4}}} \right)} \right. \right. \cr &\quad \left. \left. + \displaystyle{(2b^2 - 16) \over {\rm \gamma}_{r = 0}^4} \left(\displaystyle{a_1^2 \over f_1^8 r_1^4} + \displaystyle{a_2^2 \over f_2^8 r_2^4} \right) \right] - \displaystyle{8a_1 a_2 \over {\rm \gamma}_{r = 0}^4 f_1^4 f_2^4 r_1^2 r_2^2} \right\}}$$with the boundary condition f e = 1 and df e/dz = 0 at z = 0. By using Poisson's equation one can obtain the electric vector E(Δω) of the plasma wave excited at the difference frequency
$$\eqalign{E(\Delta {\rm \omega} ) & = \displaystyle{{im_0c^2{\rm \omega} _{{\rm p0}}^2 \sqrt {a_1a_2}} \over {16e\Delta k{\rm \gamma} ^2}} \cr & \quad \left\{ {G_1\left[ {\exp \left( { - {\left( {\displaystyle{r \over {a_0f_{\rm e}}} + \displaystyle{b \over 2}} \right)}^2} \right) + \exp \left( { - {\left( {\displaystyle{r \over {a_0f_{\rm e}}} - \displaystyle{b \over 2}} \right)}^2} \right)} \right]} \right. \cr & \quad \times \exp ( - k_iz)\exp [ - i(kz + z)] - G_2{\rm} {\rm C}_{\rm 1}C_2 \cr & \quad\;\quad \left. {\exp \left[ { - i\left( {(k_1 - k_2)z + (k_1S_1 - k_2S_2)} \right)} \right]} \right\},}$$where
$$G_1 = \displaystyle{\matrix{\left( {{\rm C}_{\rm 1}{\rm C}_{\rm 2}} \right)_{\,f_{1,2} = 1}\left[ {{(\Delta k)}^2 + \displaystyle{1 \over {r{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}} - {2C{\rm ^{\prime}_1C^{\prime}_2} \over {C_1C_2}} - \displaystyle{1 \over {C_1}}} \right. \hfill \cr \left. {\left( {C^{\rm \prime \prime} _1 + \displaystyle{{C^{\prime}_1} \over r} - \displaystyle{{2C^{\prime}_1} \over {{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}}} \right) - \displaystyle{1 \over {C_2}}\left( {C^{\rm \prime \prime} _2 + \displaystyle{{C^{\prime}_2} \over r} - \displaystyle{{2C^{\prime}_2} \over {{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}}} \right)} \right]_{\,f_{1,2} = 1} \hfill} \over {\,f_{\rm e}(\Delta {\rm \omega} ^2 - \Delta k^2{\rm \upsilon} _{{\rm th}}^2 - {\rm \omega} _{{\rm p0}}^2 {\left( {(n/n_0{\rm \gamma} )} \right)}_{\,f_{1,2} = 1})}},$$
$$G_2 = \displaystyle{\matrix{\left[ {{(\Delta k)}^2 + \displaystyle{1 \over {r{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}} - \displaystyle{{2C^{\prime}_1C^{\prime}_2} \over {C_1C_2}} - \displaystyle{1 \over {C_1}}\left( {C^{\rm \prime \prime} _1 + \displaystyle{{C^{\prime}_1} \over r} - \displaystyle{{2C^{\prime}_1} \over {{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}}} \right)} \right. \hfill \cr \left. { - \displaystyle{1 \over {C_2}}\left( {C^{\rm \prime \prime} _2 + \displaystyle{{C^{\prime}_2} \over r} - \displaystyle{{2C^{\prime}_2} \over {{\rm \gamma} ^2}}\displaystyle{{\partial {\rm \gamma} ^2} \over {\partial r}}} \right)} \right] \hfill} \over {\,f_1f_2\left( {\Delta {\rm \omega} ^2 - \Delta k^2{\rm \upsilon} _{{\rm th}}^2 - {\rm \omega} _{{\rm p0}}^2 (n/n_0{\rm \gamma} )} \right)}}.$$This is the expression for the electric vector of the excited plasma wave at the difference frequency (Δω) by the two CGL beams in the paraxial region when the effect of relativistic–ponderomotive cross-focusing of the two laser beams and self-focusing of the plasma wave is taken into account.
The power associated with EPW is (Gupta et al., Reference Gupta, Sharma and Gupta2005)
$$P_{{\rm EPW}} = \left( {\displaystyle{{V_{\rm g}k^2m^2c^4} \over {16{\rm \pi} e^2}}} \right)\int_0^\infty {E(\Delta {\rm \omega} )E^*(\Delta {\rm \omega} )2{\rm \pi} rdr},$$
where 
$V_{\rm g} = {\rm \upsilon} _{{\rm th}} ( {1 - ({\rm \omega} _{{\rm p0}}^2 /{\rm \omega} _{1,2}^2 )} )^{1/2}$ is the group velocity. Equation (19) has been solved numerically with the help of Eqs. (5), (17) and (18).
Charged particle acceleration
The excited EPW transfers its energy to accelerate the electrons at the difference frequency of laser beams. The equation governing electron momentum and energy are
$$\displaystyle{{dp} \over {dt}} = - eE(\Delta {\rm \omega} )$$and the electron energy is given by
$$\displaystyle{{d{\rm \gamma}} \over {dt}} = - \displaystyle{{eE(\Delta {\rm \omega} ) \cdot V} \over {m_0c^2}}$$
where 
${\rm \gamma} = \sqrt {1 + P^2/m^2c^2} $ is the electron energy.
Equation (21) can be written as
$$\displaystyle{{d{\rm \gamma}} \over {dt}} = - \displaystyle{{eE(\Delta {\rm \omega} )} \over {m_0c^2}},$$where E (∆ω) is given by Eq. (18).
Numerical results and discussion
In order to describe the generation of EPW and particle acceleration by the beating of two cross-focused intense CGL beams in collisionless plasma under relativistic–ponderomotive regime, we have performed a numerical computation of Eqs (4), (19) and (22), respectively, using MATLAB Software. The results are compared with taking only relativistic nonlinearity and fundamental Gaussian profile of laser beams (b = 0). The following set of the parameters has been used in the numerical calculation: r 1 = 15 µm, r 2 = 20 µm, ω1 = 1.778 × 1015, ω2 = 1.716 × 1015, ωp0 = 0.04ω2, b = 0, 0.5 and 1, and a 1 = 2 and a 2 = 1.5 are the intensity of first and second laser beam, respectively. For initial plane wave fronts of the beams, the initial conditions for f 1,2 are f 1,2 = 1 and df 1,2/dz = 0 at z = 0.
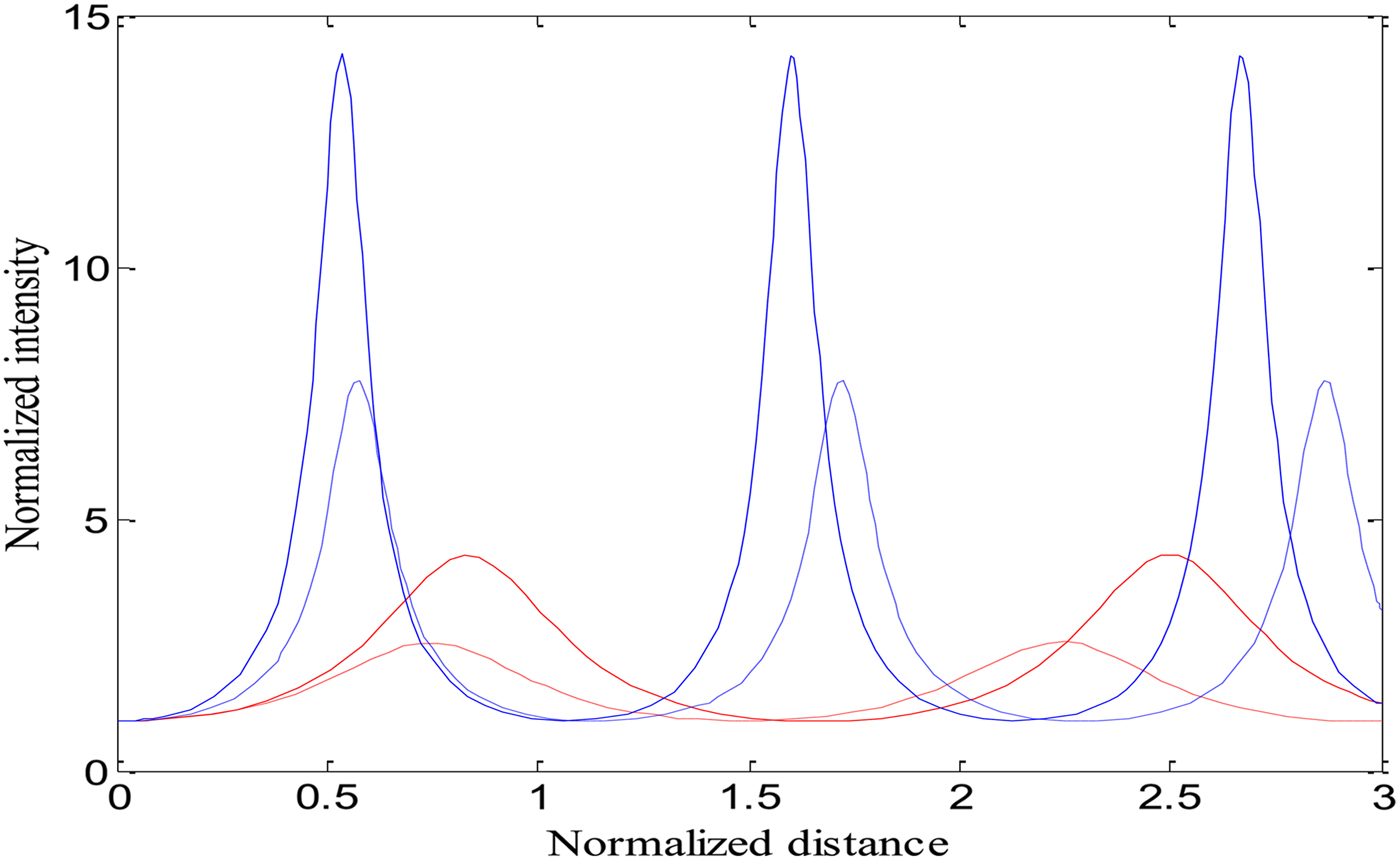
Equation (4) describes the intensity profile of the laser beams in the plasma along the radial direction, while Eq. (5) represents the focusing/defocusing of the laser beam along the distance of propagation in plasma with relativistic and ponderomotive nonlinearities. It is clear from Eq. (4) that the intensity profile of both laser beams depends on the beam width parameters f 1,2. Figure 1 depicts the variation of the normalized intensity of laser beams along with the normalized distance of propagation when only relativistic and relativistic–ponderomotive nonlinearities are operatives. It is observed that the intensity and focusing of both laser beams in plasma are higher when both nonlinearities (relativistic and ponderomotive) are present. This is due to the fact that the nonlinearity in the dielectric constant of the plasma depends on the total intensity of the beams (electron mass variation due to laser intensities) and the change in electron density due to ponderomotive force; therefore, the intensity patterns in the case of only relativistic nonlinearity are different from the relativistic–ponderomotive nonlinearity. The effects of various laser and plasma parameters such as decentred parameter (b), plasma density (ωp0) and the initial intensity of laser beams on cross-focusing process of two intense CGLBs in plasma is found in our earlier work (Purohit et al., Reference Purohit, Gaur and Rawat2016). This study indicates that the decentred parameter (b) plays a significant role to decide the early and strong focusing ability of intense cosh-Gaussian beams in plasma.
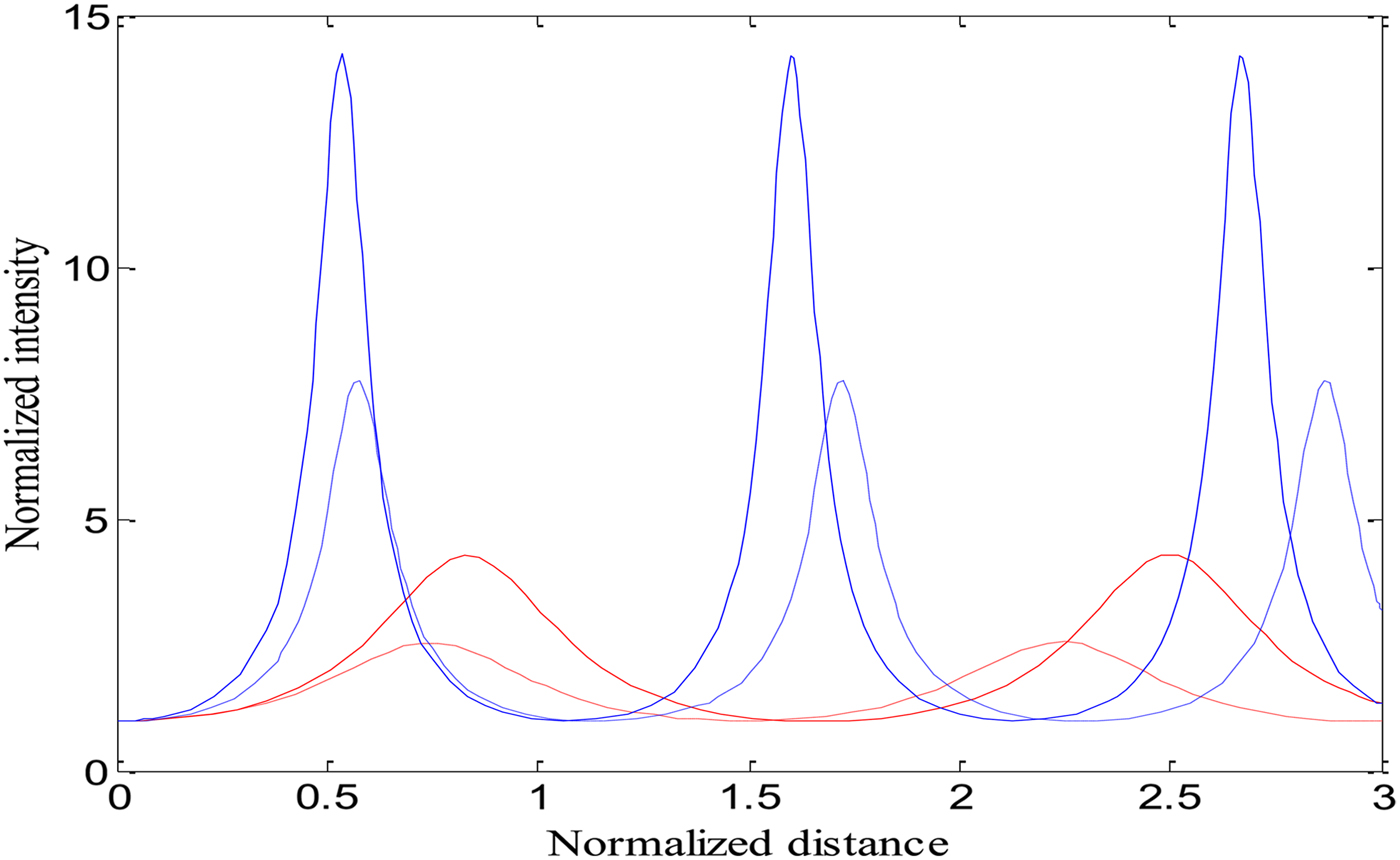
Fig. 1. Variation of laser beam intensity in plasma with normalized distance of propagation (ξ) of the first and second laser beams, when only relativistic (red colour) and relativistic–ponderomotive (blue colour) nonlinearities are operatives, keeping a 1 = 2, a 2 = 1.5, b = 0.5, and ωp0 = 0.04ω2. The solid line represents f 1 and dotted line represents f 2.
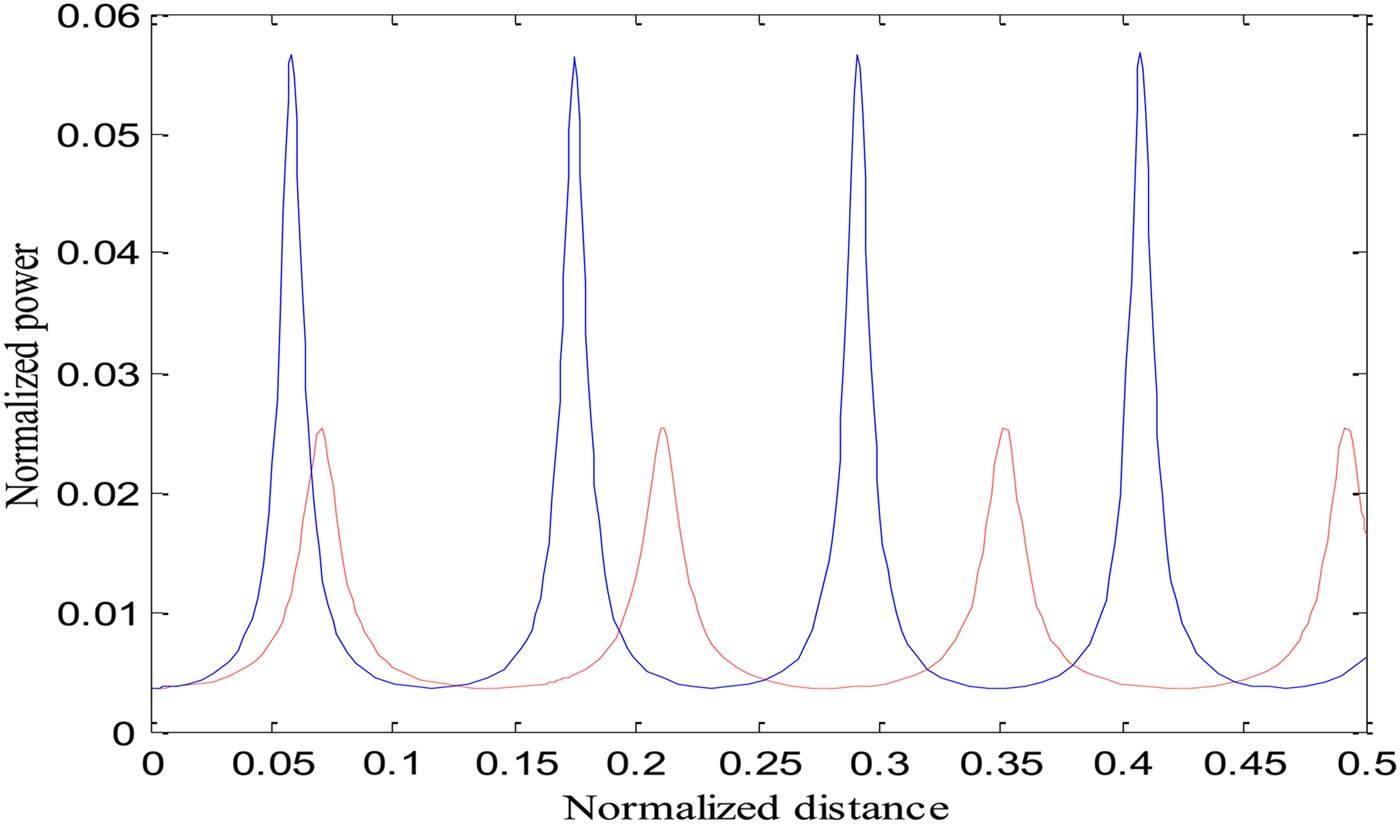
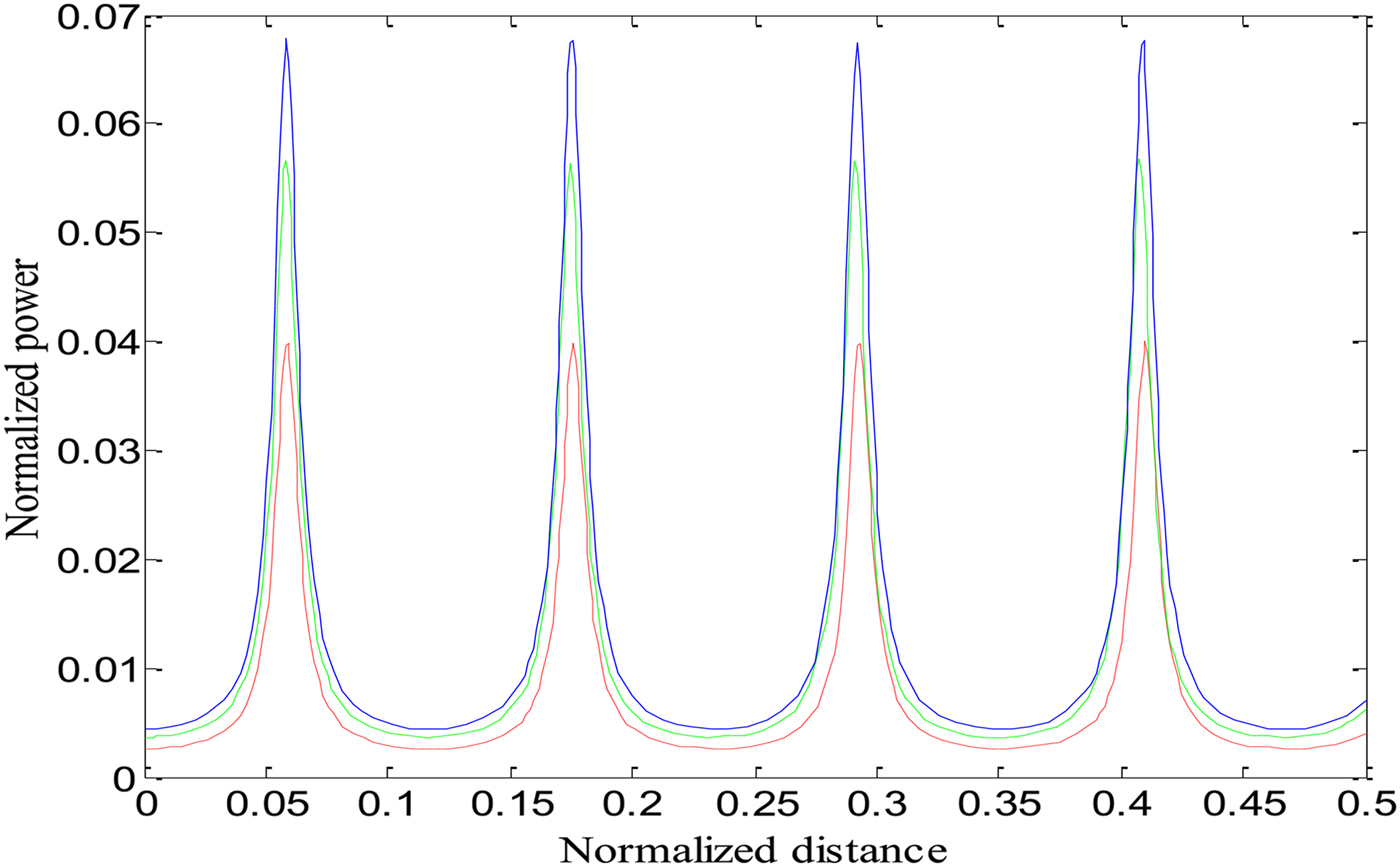
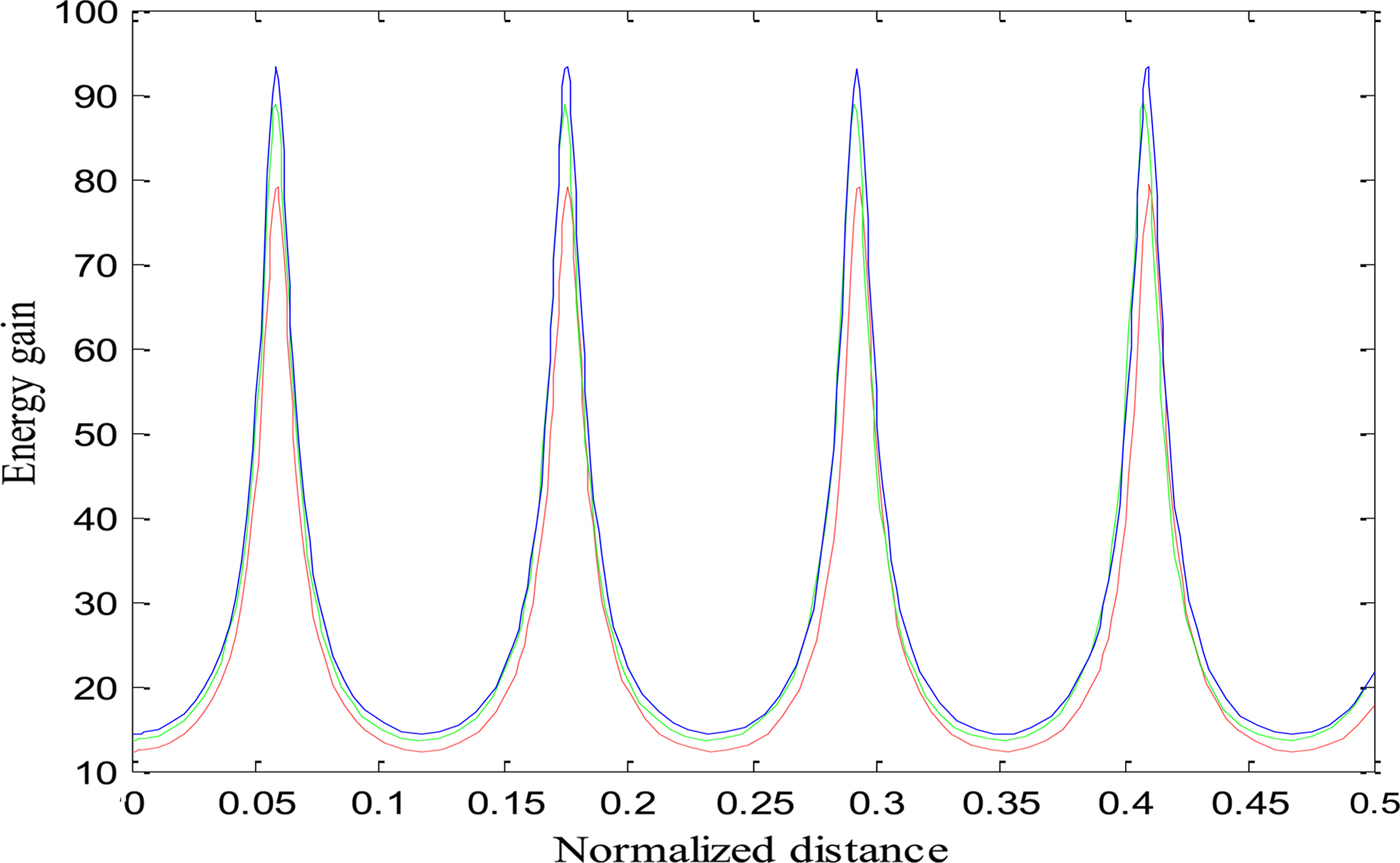
To see the effect of two cross-focused intense CGL beams on the excitation of the EPW, we have studied the excitation of the EPW by the beat wave process. It is important to mention here that beating between two co-propagating intense laser beams in plasma can generate a longitudinal EPW with a high-electric field and a relativistic phase velocity. At ωp0 ≈ ω1 − ω2, an effectively resonant EPW is generated, which accelerates the electrons to high energies. Equation (18) gives the normalized power of EPW generated as a result of the beating of the two laser beams when both relativistic and ponderomotive nonlinearities are operative. We have solved Eq. (18) numerically along with the numerical computation of Eqs. (4), (16) and (17) to obtain the power of generated EPW. The same set of parameters has been used for numerical calculations as in Eq. (3). Figure 2 illustrates the variation of the power of generated plasma wave with the distance of propagation in the presence of only relativistic and relativistic–ponderomotive nonlinearities. It is evident from the figure that the power of generated plasma wave is higher when both nonlinearities are present. Figure 3 depicts the effect of the decentred parameter (b) and relativistic–ponderomotive nonlinearity on the power of generated EPW. It is observed that with an increase in the value of b there is an increase in the power of generated plasma wave. The effect of changing the intensity of second laser beam with relativistic–ponderomotive non-linearity on the power of generated plasma wave is shown in Figure 4. When the intensity of second laser beam in increased, the power of EPW is also increased. Figures 2–4 reflects that the power of generated EPW is increased by increasing various laser and plasma parameters when both relativistic and relativistic–ponderomotive non-linearities are operatives. This is because of the fact that the power of EPW depends on the focusing behaviour of laser beams in plasma (f 1,2) at different values of b and laser intensities (a 1 and a 2), beamwidth of EPW (f e) and the electric field associated with EPW E(Δω). Strong focusing of both laser beams has been observed in a relativistic–ponderomotive regime with increasing the values of b and laser intensity (Purohit et al., Reference Purohit, Gaur and Rawat2016). However, the extent of self-focusing of both laser beams and the power of EPW has been decreased when only relativistic non-linearity is taken into account (Singh & Gupta, Reference Singh and Gupta2015).
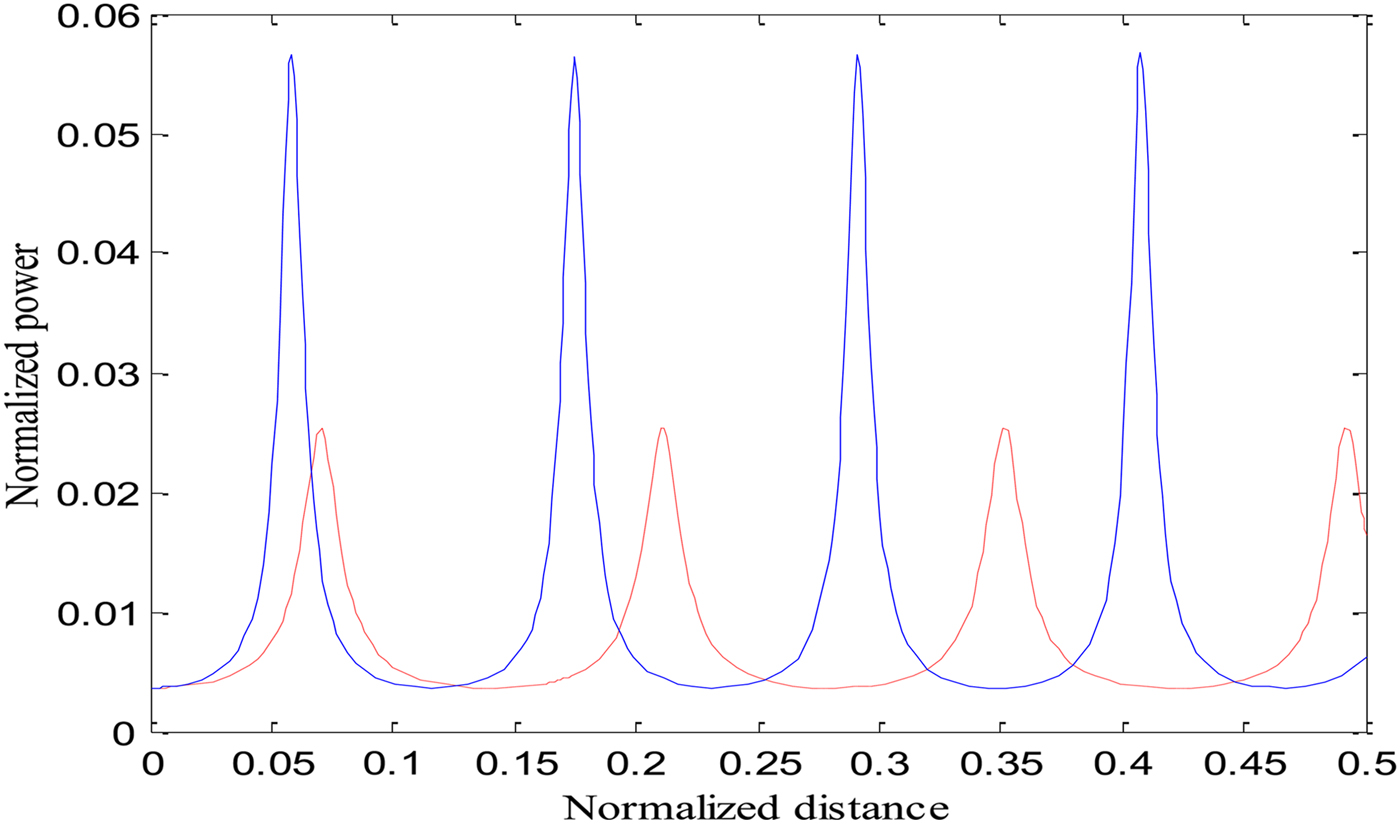
Fig. 2. Variation of normalized power of electron plasma wave (beat wave) with normalized distance of propagation ξ, keeping a 1 = 2, a 2 = 1.5, b = 0.5, and ωp0 = 0.04ω2. Red and blue lines represent the cases for only relativistic nonlinearity and relativistic and ponderomotive nonlinearities, respectively.
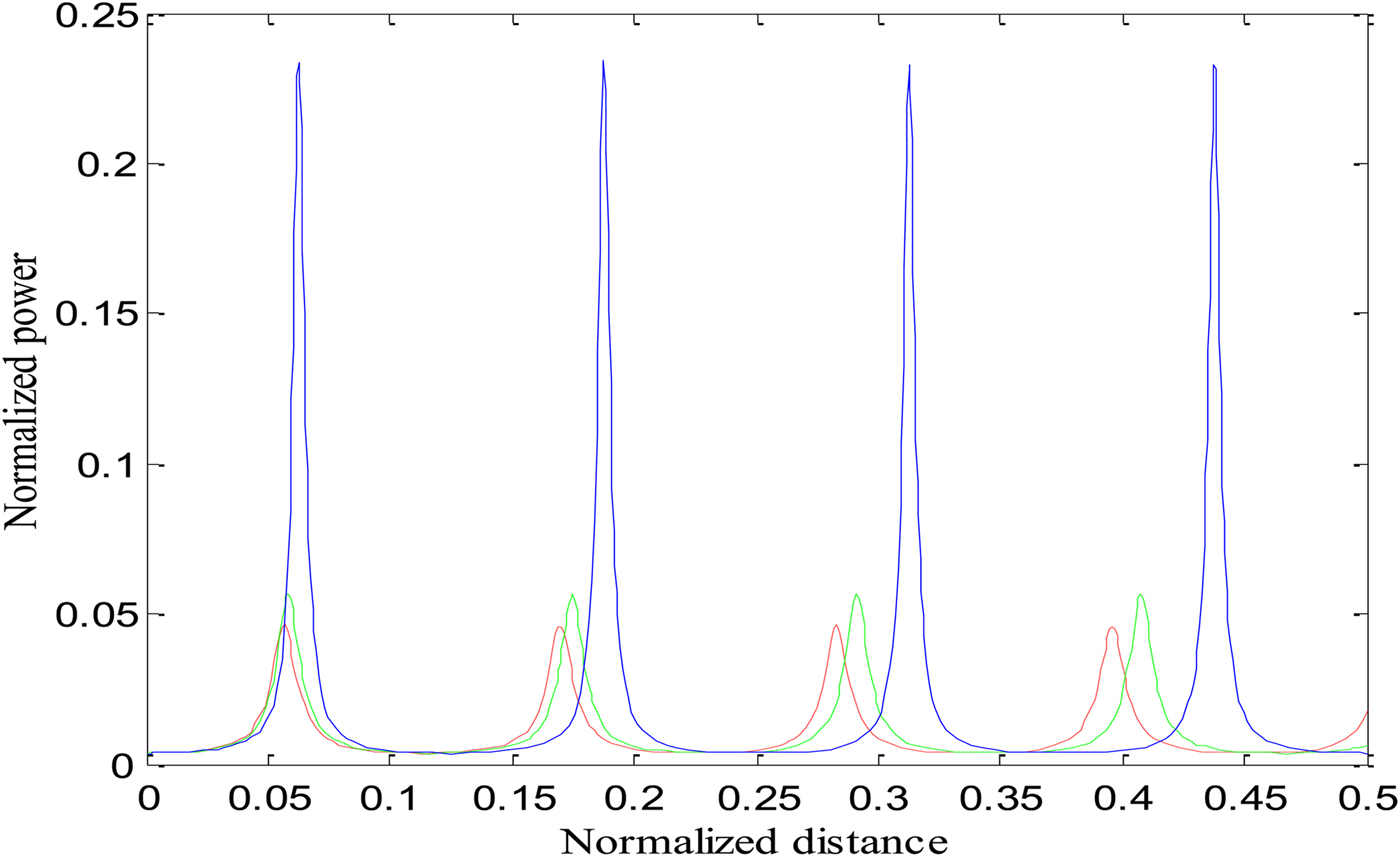
Fig. 3. Variation of normalized power of beat wave with normalized distance of propagation ξ, at different values of decentred parameter (b) when relativistic and ponderomotive nonlinearities are operative. Keeping a 1 = 2, a 2 = 1.5, and ωp0 = 0.04ω2. Red Line represents (b = 0), green line represents (b = 0.5), and blue line represents (b = 1), respectively.
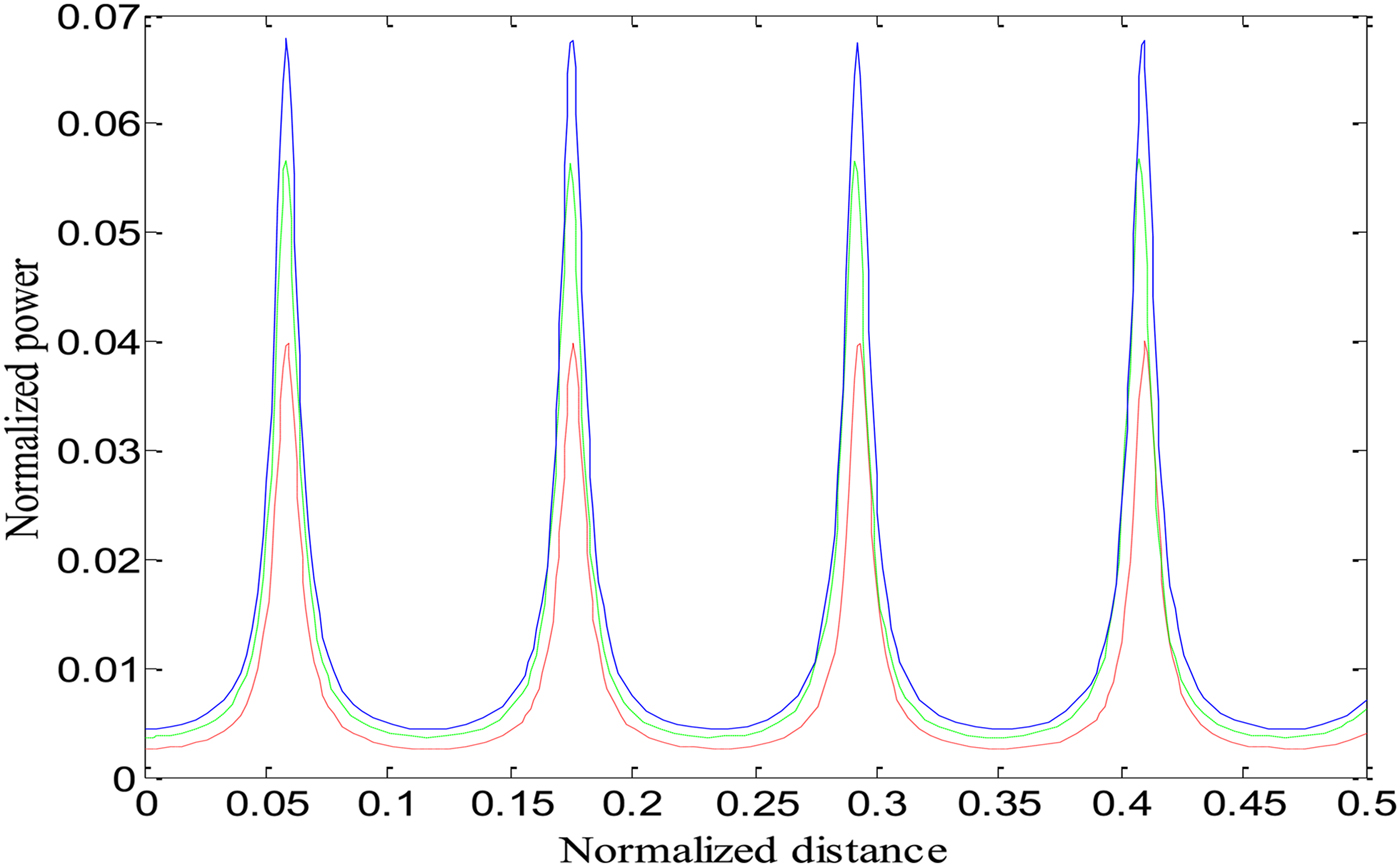
Fig. 4. Variation of normalized power of beat wave with normalized distance of propagation ξ, when relativistic and ponderomotive nonlinearities are operative. Keeping a 1 = 2, b = 0.5, ωp0 = 0.04ω2 and at different intensities of second laser beam. Red Line represents (a 2 = 1), green line represents (a 2 = 1.5), and blue line represents (a 2 = 1.9), respectively.
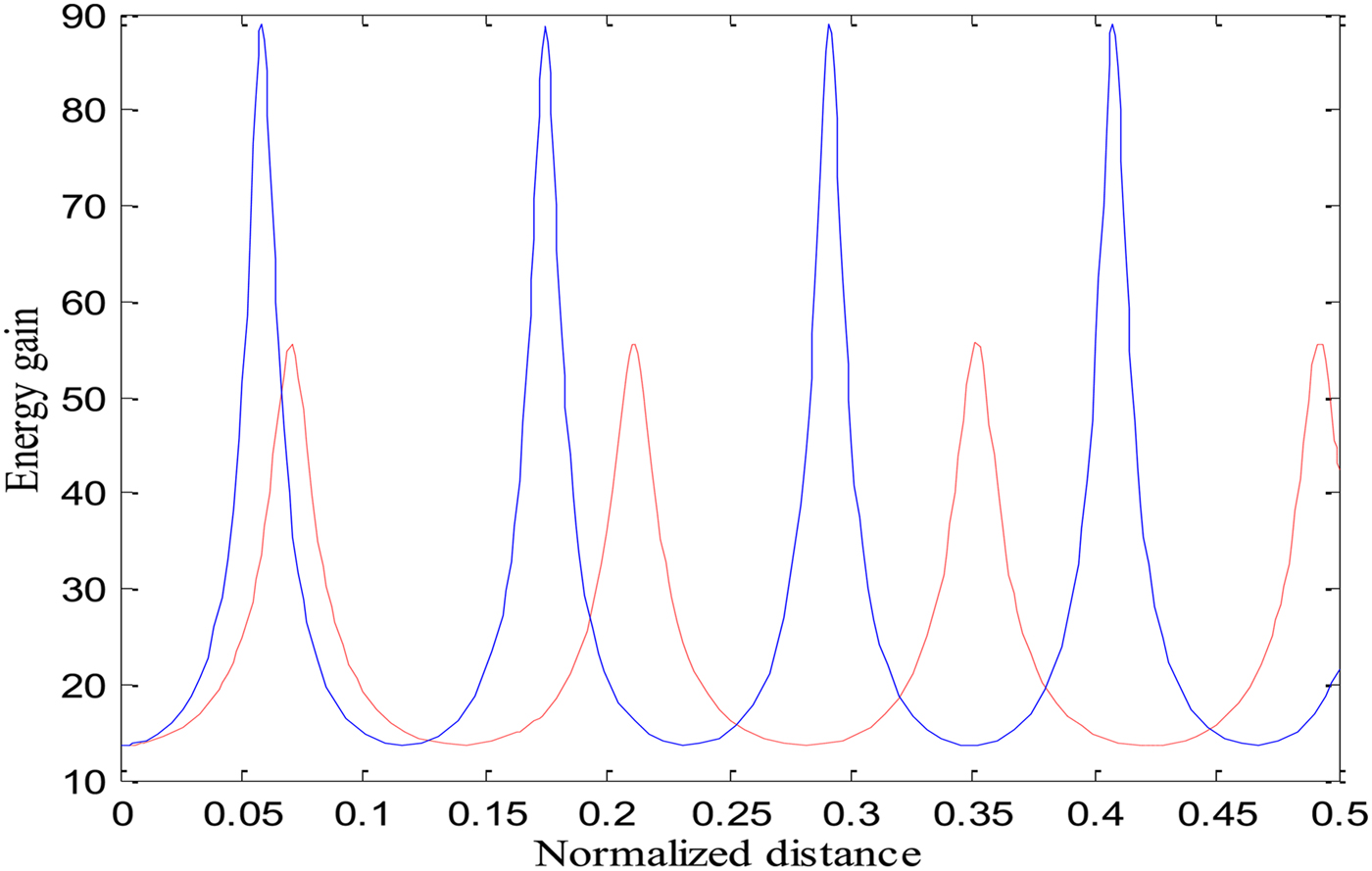
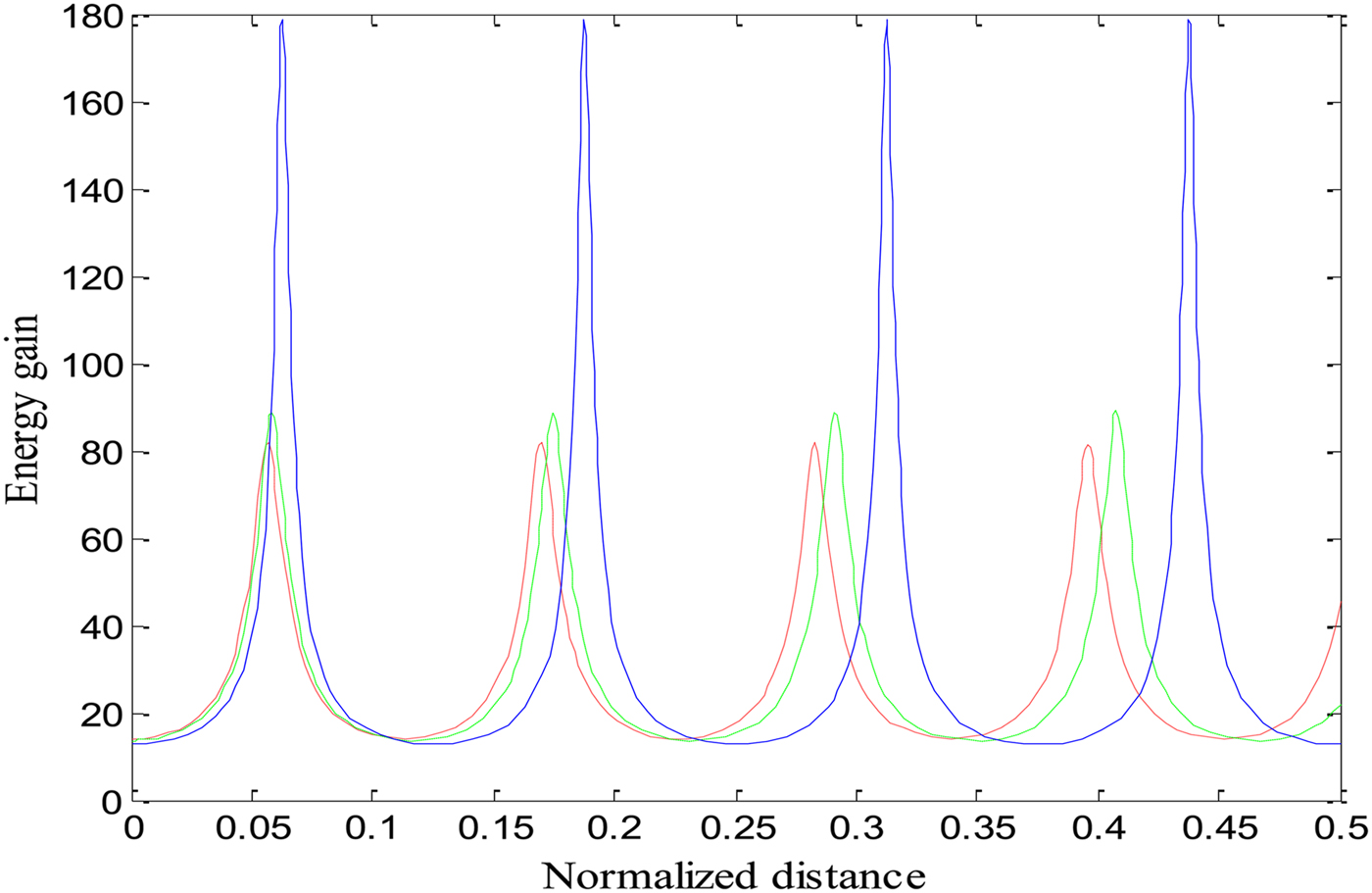
Electrons trapped in the plasma wave can be accelerated to high energy. The high electric field associated with excited EPW at a beat frequency can be used to accelerate the electrons through PBWA scheme. Equation (22) gives the expression for electron energy, which has been numerically solved with the help of Eqs. (5) and (18). Figure 5 represents the variation of the electron energy (γ) with the normalized distance of propagation when only relativistic and relativistic–ponderomotive non-linearities are operatives. It is obvious that energy gain is reduced when only relativistic non-linearity is taken into account. Figures 6 and 7 illustrate the effects of changing the value of b and the intensity of second laser beam (a 2) with relativistic–ponderomotive nonlinearity on energy gain by the electrons. These results show that the maximum energy gain by electrons is significantly increased by increasing the value of b and a 2. Although, the nature of these results are similar to those obtained in the case of the power of excited EPW due to the same reasons as discussed above.
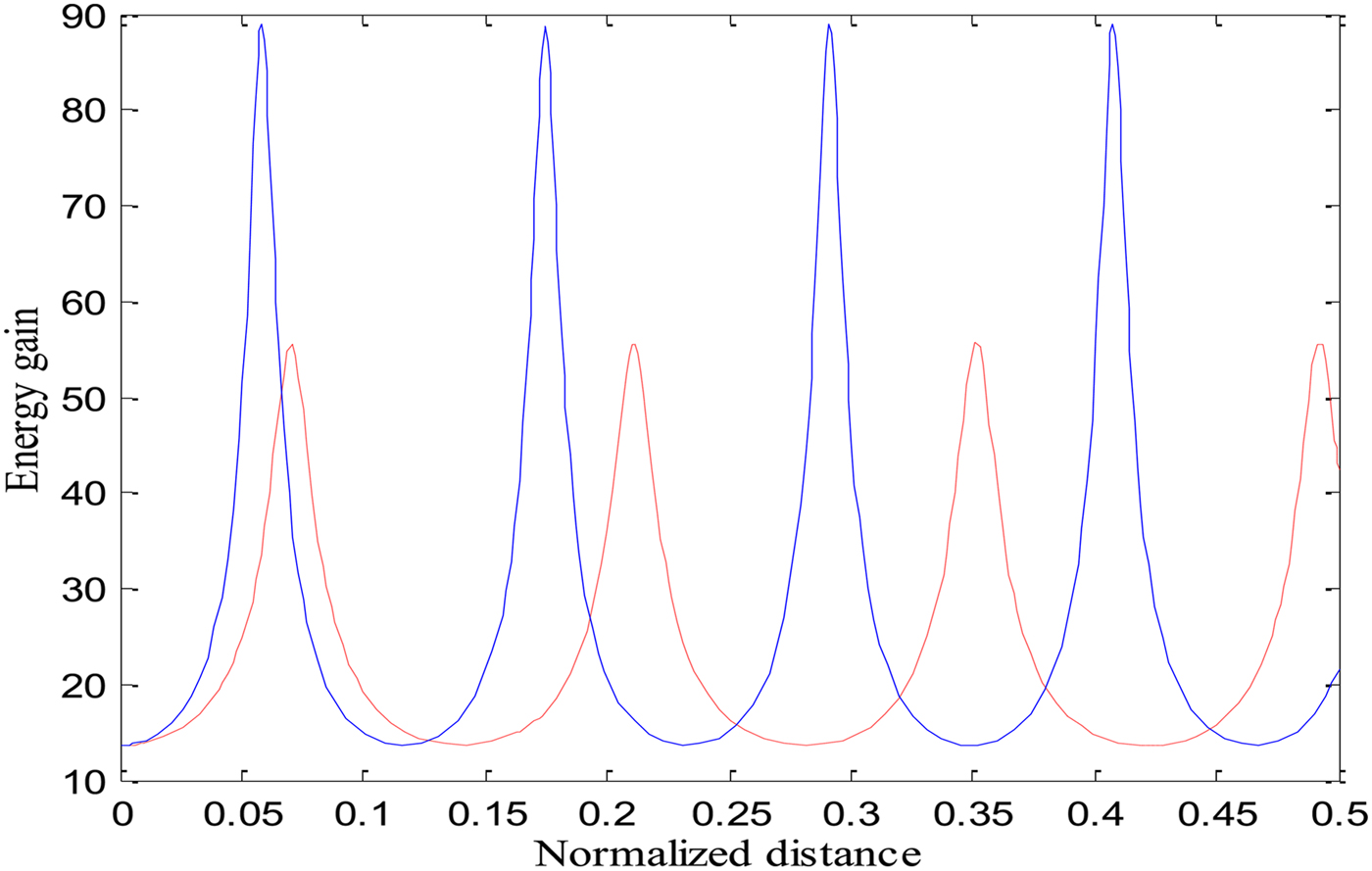
Fig. 5. Variation of energy gain of electrons (γ) with a normalized distance of propagation ξ. Red and blue lines represent the cases for the only relativistic nonlinearity and the relativistic and ponderomotive nonlinearities, respectively, for the same set of parameters as used for Figure 2.
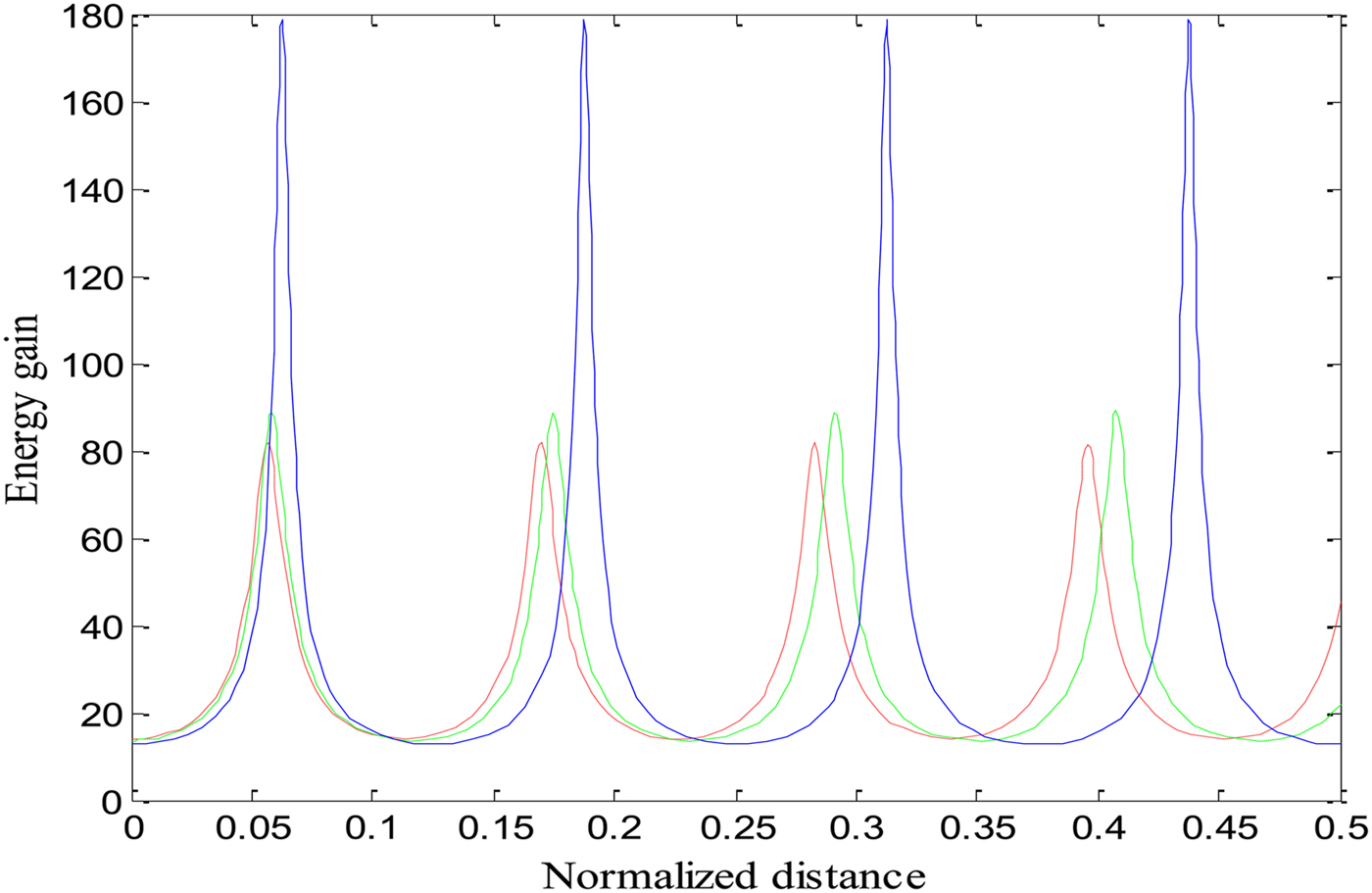
Fig. 6. Variation of energy gain of electrons (γ) with a normalized distance of propagation ξ, at different values of the decentred parameter (b) and for the same set of parameters as used for Figure 3, when relativistic and ponderomotive nonlinearities are operative. Red, green, and blue lines represent b = 0, 0.5, and 1, respectively.
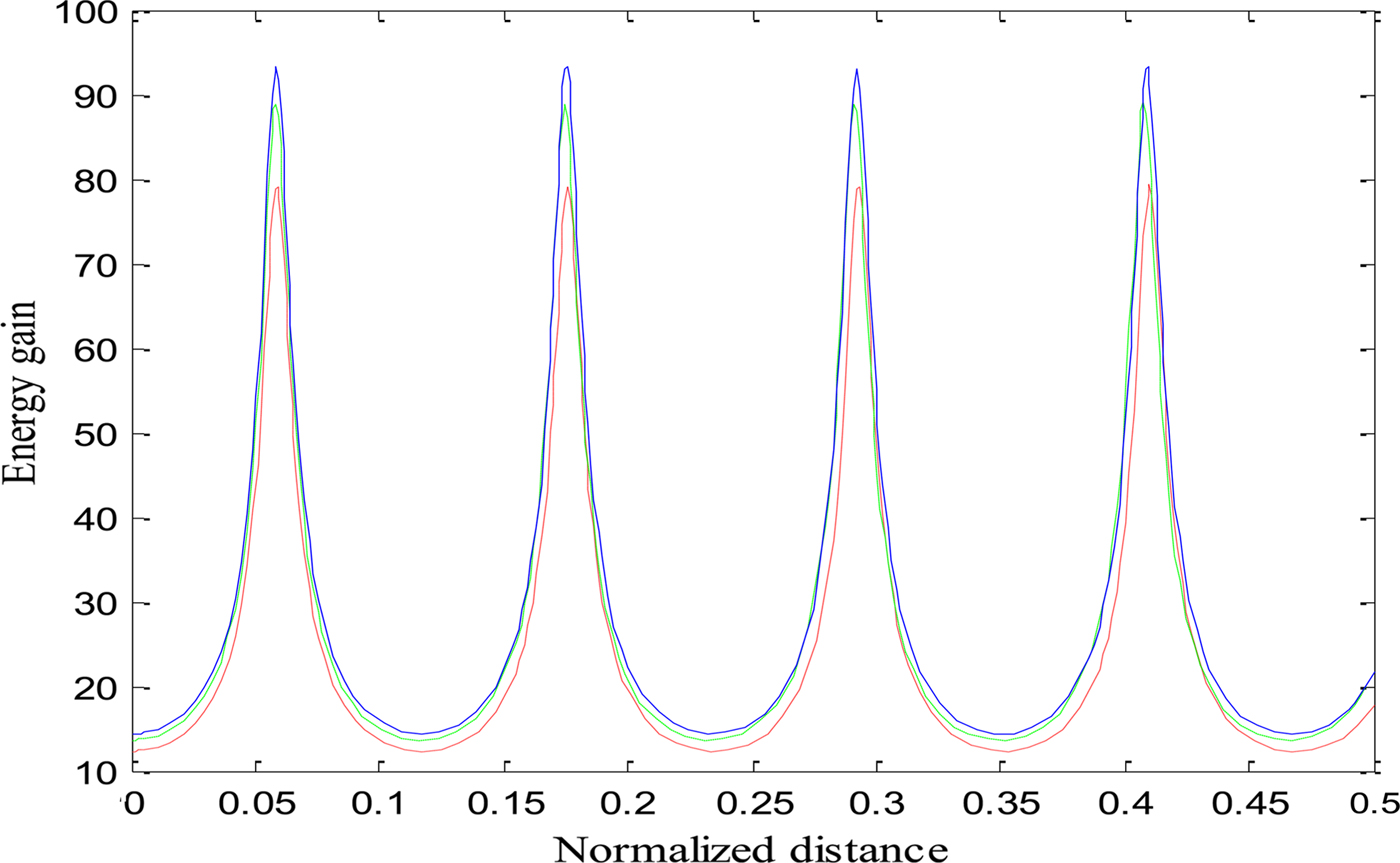
Fig. 7. Variation of energy gain of electrons (γ) with a normalized distance of propagation ξ for a fixed power of first laser beam and different powers of the second laser beam, and for the same set of parameters as used for Figure 4, when relativistic and ponderomotive nonlinearities are operative. Red, green, and blue lines represent a 2 = 1, 1.5, and 1.9, respectively.
Conclusion
In conclusion, we have studied beat wave generation of EPW by two cross-focused intense cosh-Gaussian laser beams in a plasma and the acceleration of electrons using the WKB and paraxial approximations, when relativistic and ponderomotive nonlinearities are operative. The results are compared with only relativistic nonlinearity and Gaussian profile of laser beams. It is found that the power of excited EPW and energy gain is increased in the relativistic ponderomotive case as compared with the only relativistic case. The power of plasma wave/energy gain is minimum at b = 0, and increased by increasing the value of b and the intensity of first/second laser beams. The results show that maximum power of the generated plasma wave and energy gain depends on the strong self-focusing of cosh-Gaussian laser beams with relativistic–ponderomotive nonlinearity. These results are relevant to laser beat wave based particle accelerators and in other applications requiring multiple laser beams.
Acknowledgments
The authors are thankful to the Science & Engineering Research Board (SERB), Department of Science & Technology, Government of India for providing financial assistance for carrying out this research work vide project file No. EMR/2016/000112.
