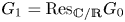Let ![]() $G$ be a connected semisimple algebraic group defined over a number field
$G$ be a connected semisimple algebraic group defined over a number field ![]() $k$. Consider the Lie group
$k$. Consider the Lie group ![]() $\textbf {G}=G(k\otimes \mathbb {R})$ and let us denote by
$\textbf {G}=G(k\otimes \mathbb {R})$ and let us denote by ![]() $\boldsymbol {\theta }$ a Cartan involution. A
$\boldsymbol {\theta }$ a Cartan involution. A ![]() $k$-automorphism
$k$-automorphism ![]() $\phi$ of
$\phi$ of ![]() $G$ is said to be of Cartan type if the automorphism
$G$ is said to be of Cartan type if the automorphism ![]() $\Phi$ induced by
$\Phi$ induced by ![]() $\phi$ on
$\phi$ on ![]() $\textbf {G}$ can be written as
$\textbf {G}$ can be written as ![]() $\Phi =\mathrm {Int}(x)\circ \boldsymbol {\theta }$ where
$\Phi =\mathrm {Int}(x)\circ \boldsymbol {\theta }$ where ![]() $\mathrm {Int}(x)$ is the inner automorphism defined by some
$\mathrm {Int}(x)$ is the inner automorphism defined by some ![]() $x\in \textbf {G}$. Theorem 10.6 of [Reference Borel, Labesse and SchwermerBLS96] establishes the following result regarding the existence of non-trivial cuspidal cohomology classes for
$x\in \textbf {G}$. Theorem 10.6 of [Reference Borel, Labesse and SchwermerBLS96] establishes the following result regarding the existence of non-trivial cuspidal cohomology classes for ![]() $S$-arithmetic subgroups of
$S$-arithmetic subgroups of ![]() $G$.
$G$.
Theorem 1 Let ![]() $G$ be an absolutely almost simple algebraic group defined over
$G$ be an absolutely almost simple algebraic group defined over ![]() $k$ that admits a Cartan-type automorphism. When the coefficient system is trivial, the cuspidal cohomology of
$k$ that admits a Cartan-type automorphism. When the coefficient system is trivial, the cuspidal cohomology of ![]() $G$ over
$G$ over ![]() $S$ does not vanish, that is, every
$S$ does not vanish, that is, every ![]() $S$-arithmetic subgroup of
$S$-arithmetic subgroup of ![]() $G$ has a subgroup of finite index with non-zero cuspidal cohomology with respect to the trivial coefficient system.
$G$ has a subgroup of finite index with non-zero cuspidal cohomology with respect to the trivial coefficient system.
The following assertion appears as Corollary 10.7 in [Reference Borel, Labesse and SchwermerBLS96]. Assume that ![]() $G$ is
$G$ is ![]() $k$-split and
$k$-split and ![]() $k$ totally real or
$k$ totally real or ![]() $G = {\mathrm {Res}}_{k'/k}G'$ where
$G = {\mathrm {Res}}_{k'/k}G'$ where ![]() $k'$ is a CM-field. Then the cuspidal cohomology of
$k'$ is a CM-field. Then the cuspidal cohomology of ![]() $G$ over
$G$ over ![]() $S$ with respect to the trivial coefficient system does not vanish.
$S$ with respect to the trivial coefficient system does not vanish.
The proof of Corollary 10.7 amounts to exhibiting, in each case, a Cartan-type automorphism. In the first case, dealing with split groups, the proof is correct. As regards the second case where ![]() $G = {\mathrm {Res}}_{k'/k}G'$ with
$G = {\mathrm {Res}}_{k'/k}G'$ with ![]() $k'$ a CM-field, it was observed by Rohlfs and Clozel independently that the assertion (and the proof) must be corrected since, to make sense, the argument implicitly uses strong extra assumptions. First of all,
$k'$ a CM-field, it was observed by Rohlfs and Clozel independently that the assertion (and the proof) must be corrected since, to make sense, the argument implicitly uses strong extra assumptions. First of all, ![]() $G'$ has to be defined over
$G'$ has to be defined over ![]() $k$ so that the complex conjugation
$k$ so that the complex conjugation ![]() $c$ induced by the non-trivial element
$c$ induced by the non-trivial element ![]() $\sigma$ in
$\sigma$ in ![]() $\mathrm {Gal}(k'/k)$ acts as a
$\mathrm {Gal}(k'/k)$ acts as a ![]() $k$-rational automorphism of
$k$-rational automorphism of ![]() $G$. Observe that, strictly speaking, one has to extend the scalars from
$G$. Observe that, strictly speaking, one has to extend the scalars from ![]() $k$ to
$k$ to ![]() $k'$ before applying the restriction functor. Further assumptions are necessary so that Corollary 10.7 in [Reference Borel, Labesse and SchwermerBLS96] should be replaced by the following statement.
$k'$ before applying the restriction functor. Further assumptions are necessary so that Corollary 10.7 in [Reference Borel, Labesse and SchwermerBLS96] should be replaced by the following statement.
Theorem 2 Let ![]() $k$ be a totally real number field and
$k$ be a totally real number field and ![]() $G$ be an absolutely almost simple algebraic group defined over
$G$ be an absolutely almost simple algebraic group defined over ![]() $k$. Consider the following cases:
$k$. Consider the following cases:
(1)
 $G$ is
$G$ is  $k$-split.
$k$-split.(2)
 $G = {\mathrm {Res}}_{k'/k}G'$ where
$G = {\mathrm {Res}}_{k'/k}G'$ where  $k'$ is a CM-field with
$k'$ is a CM-field with  $G'$ defined over
$G'$ defined over  $k$ totally real, satisfying one of the following hypotheses:
$k$ totally real, satisfying one of the following hypotheses:
(2a)
 $\mathbf{H}=G'(k\otimes \mathbb {R})$ has a compact Cartan subgroup;
$\mathbf{H}=G'(k\otimes \mathbb {R})$ has a compact Cartan subgroup;(2b)
 $G'$ is split over
$G'$ is split over  $k$ and simply connected.
$k$ and simply connected.
Then the cuspidal cohomology of ![]() $G$ over
$G$ over ![]() $S$ with respect to the trivial coefficient system does not vanish.
$S$ with respect to the trivial coefficient system does not vanish.
Proof. In case (1), when ![]() $G$ is
$G$ is ![]() $k$-split, the proof is given in [Reference Borel, Labesse and SchwermerBLS96]: it relies on the first case of [Reference Borel, Labesse and SchwermerBLS96, Corollary 10.7] and Theorem 1. In case (2a) the result follows from Proposition 3 below and Theorem 1. In case (2b) the assertion is a particular case of [Reference LabesseLab99, Theorem 4.7.1], which in turn relies on case (1) above.
$k$-split, the proof is given in [Reference Borel, Labesse and SchwermerBLS96]: it relies on the first case of [Reference Borel, Labesse and SchwermerBLS96, Corollary 10.7] and Theorem 1. In case (2a) the result follows from Proposition 3 below and Theorem 1. In case (2b) the assertion is a particular case of [Reference LabesseLab99, Theorem 4.7.1], which in turn relies on case (1) above.
Most of the following proposition is well known (see, in particular, [Reference ShelstadShe79, Corollary 2.9], [Reference LanglandsLan89, Lemma 3.1] and [Reference AdamsAda14, p. 2132]) but, not knowing of a convenient reference, we sketch a proof.
Consider a connected semisimple algebraic group ![]() $G_0$ defined over
$G_0$ defined over ![]() $\mathbb {R}$. We denote by
$\mathbb {R}$. We denote by ![]() $\textbf {G}=G_0(\mathbb {C})$ the group of its complex points and by
$\textbf {G}=G_0(\mathbb {C})$ the group of its complex points and by ![]() $\textbf {c}$ the complex conjugation on
$\textbf {c}$ the complex conjugation on ![]() $\textbf {G}$. Then
$\textbf {G}$. Then ![]() $\textbf {H}=G_0(\mathbb {R})$ is the group of fixed points under
$\textbf {H}=G_0(\mathbb {R})$ is the group of fixed points under ![]() $\textbf {c}$. This anti-holomorphic involution is induced by an
$\textbf {c}$. This anti-holomorphic involution is induced by an ![]() $\mathbb {R}$-automorphism
$\mathbb {R}$-automorphism ![]() $c$ of
$c$ of ![]() $G_1=\mathrm {Res}_{\mathbb {C}/\mathbb {R}}G_0$. Let
$G_1=\mathrm {Res}_{\mathbb {C}/\mathbb {R}}G_0$. Let ![]() $\boldsymbol {\theta }$ be a Cartan involution of
$\boldsymbol {\theta }$ be a Cartan involution of ![]() $\textbf {G}$. The group
$\textbf {G}$. The group ![]() $\textbf {U}$ of fixed points of
$\textbf {U}$ of fixed points of ![]() $\boldsymbol {\theta }$ in
$\boldsymbol {\theta }$ in ![]() $\textbf {G}$ is a compact real form:
$\textbf {G}$ is a compact real form: ![]() $\textbf {U}=U(\mathbb {R})$ where
$\textbf {U}=U(\mathbb {R})$ where ![]() $U$ is a form of
$U$ is a form of ![]() $G_0$ but not necessarily inner. Let
$G_0$ but not necessarily inner. Let ![]() $G^{**}$ be the split outer form of
$G^{**}$ be the split outer form of ![]() $G_0$. Choose a splitting
$G_0$. Choose a splitting ![]() $(B^*,T^*, \{X_\alpha \}_{\alpha \in \Delta })$ for
$(B^*,T^*, \{X_\alpha \}_{\alpha \in \Delta })$ for ![]() $G^{**}$ over
$G^{**}$ over ![]() $\mathbb {R}$ where
$\mathbb {R}$ where ![]() $T^*$ is a torus in a Borel subgroup
$T^*$ is a torus in a Borel subgroup ![]() $B^*$ and for each
$B^*$ and for each ![]() $\alpha \in \Delta$, the set of simple roots,
$\alpha \in \Delta$, the set of simple roots, ![]() $X_\alpha$ is a root vector. Let
$X_\alpha$ is a root vector. Let ![]() $\psi ^*$ be the automorphism of
$\psi ^*$ be the automorphism of ![]() $G^{**}$ that preserves the splitting and whose action defines
$G^{**}$ that preserves the splitting and whose action defines ![]() $G^*$, the quasi-split inner form of
$G^*$, the quasi-split inner form of ![]() $G_0$. Let
$G_0$. Let ![]() $w$ be the element of maximal length in the Weyl group for
$w$ be the element of maximal length in the Weyl group for ![]() $T^*$.
$T^*$.
Proposition 3 The following assertions are equivalent.
(i) The automorphism
 $c$ is of Cartan type.
$c$ is of Cartan type.(ii) The group
 $\mathbf{U}$ is an inner compact real form.
$\mathbf{U}$ is an inner compact real form.(iii) The group
 $\mathbf{H}$ has a compact Cartan subgroup.
$\mathbf{H}$ has a compact Cartan subgroup.(iv) The group
 $\mathbf{H}$ admits discrete series.
$\mathbf{H}$ admits discrete series.(v) The involution
 $w\circ \psi ^*$ acts by
$w\circ \psi ^*$ acts by  $-1$ on the root system of
$-1$ on the root system of  $T^*$.
$T^*$.
Proof. The automorphism ![]() $c$ is of Cartan type if, by definition,
$c$ is of Cartan type if, by definition, ![]() $\textbf {c}=\mathrm {Int}(x)\circ \boldsymbol {\theta }$ for some
$\textbf {c}=\mathrm {Int}(x)\circ \boldsymbol {\theta }$ for some ![]() $x\in \textbf {G}$, that is, if and only if
$x\in \textbf {G}$, that is, if and only if ![]() $U$ is an inner form of
$U$ is an inner form of ![]() $G_0$ or equivalently of
$G_0$ or equivalently of ![]() $G^*$. This proves the equivalence of (i) and (ii). Assume now that
$G^*$. This proves the equivalence of (i) and (ii). Assume now that ![]() $U$ is an inner form of
$U$ is an inner form of ![]() $G_0$. Up to conjugation under
$G_0$. Up to conjugation under ![]() $\textbf {G}$, we may assume that
$\textbf {G}$, we may assume that ![]() $\boldsymbol {\theta }$ is of the form
$\boldsymbol {\theta }$ is of the form ![]() $\boldsymbol {\theta }=\mathrm {Int}(x)\circ \textbf {c}$ with
$\boldsymbol {\theta }=\mathrm {Int}(x)\circ \textbf {c}$ with ![]() $x$ in the normalizer of a maximal torus
$x$ in the normalizer of a maximal torus ![]() $T$ in
$T$ in ![]() $G_0$ defined over
$G_0$ defined over ![]() $\mathbb {R}$. In particular,
$\mathbb {R}$. In particular, ![]() $x$ is semisimple and its centralizer
$x$ is semisimple and its centralizer ![]() $\textbf {L}$ in
$\textbf {L}$ in ![]() $\textbf {G}$ is a complex reductive subgroup of maximal rank. The cocycle relation
$\textbf {G}$ is a complex reductive subgroup of maximal rank. The cocycle relation ![]() $\mathrm {Int}(x\,\textbf {c}(x))=1$ implies that
$\mathrm {Int}(x\,\textbf {c}(x))=1$ implies that ![]() $\textbf {L}$ is stable under
$\textbf {L}$ is stable under ![]() $\textbf {c}$. Then
$\textbf {c}$. Then ![]() $\textbf {c}$ induces an anti-holomorphic involution on
$\textbf {c}$ induces an anti-holomorphic involution on ![]() $\textbf {L}$ whose fixed points
$\textbf {L}$ whose fixed points ![]() $\textbf {M}=\textbf {L}\cap \textbf {H}=\textbf {U}\cap \textbf {H}$ are a compact real form of
$\textbf {M}=\textbf {L}\cap \textbf {H}=\textbf {U}\cap \textbf {H}$ are a compact real form of ![]() $\textbf {L}$. A Cartan subgroup
$\textbf {L}$. A Cartan subgroup ![]() $\textbf {C}$ of
$\textbf {C}$ of ![]() $\textbf {M}$ is a compact Cartan subgroup in
$\textbf {M}$ is a compact Cartan subgroup in ![]() $\textbf {H}$. Hence (ii) implies (iii). Now, consider a torus
$\textbf {H}$. Hence (ii) implies (iii). Now, consider a torus ![]() $T$ in
$T$ in ![]() $G_0$ such that
$G_0$ such that ![]() $\textbf {C}=T(\mathbb {R})$ is compact. Then the complex conjugation
$\textbf {C}=T(\mathbb {R})$ is compact. Then the complex conjugation ![]() $\textbf {c}$ acts by
$\textbf {c}$ acts by ![]() $-1$ on the weights of
$-1$ on the weights of ![]() $T$. Hence there is
$T$. Hence there is ![]() $n\in \textbf {G}$ which belongs to the normalizer of
$n\in \textbf {G}$ which belongs to the normalizer of ![]() $T^*\subset G^*$ such that
$T^*\subset G^*$ such that ![]() $\mathrm {Int}(n)\circ \psi ^*$ acts as
$\mathrm {Int}(n)\circ \psi ^*$ acts as ![]() $-1$ on the root system of
$-1$ on the root system of ![]() $T^*$. Now, since
$T^*$. Now, since ![]() $\psi ^*$ preserves the set of positive roots,
$\psi ^*$ preserves the set of positive roots, ![]() $w=\mathrm {Int}(n)|_{T^*}$ is the element of maximal length in the Weyl group. This shows that (iii) implies (v). The equivalence of (iii) and (iv) is a well-known theorem [Reference Harish-ChandraHar66, Theorem 13] due to Harish-Chandra. Finally, Lemma 4 below shows that (v) implies (ii).
$w=\mathrm {Int}(n)|_{T^*}$ is the element of maximal length in the Weyl group. This shows that (iii) implies (v). The equivalence of (iii) and (iv) is a well-known theorem [Reference Harish-ChandraHar66, Theorem 13] due to Harish-Chandra. Finally, Lemma 4 below shows that (v) implies (ii).
Lemma 4 Assume ![]() $w\circ \psi ^*$ acts by
$w\circ \psi ^*$ acts by ![]() $-1$ on the root system. Then
$-1$ on the root system. Then ![]() $G^*$ has an inner form
$G^*$ has an inner form ![]() $U$ such that
$U$ such that ![]() $\mathbf{U}=U(\mathbb {R})$ is compact.
$\mathbf{U}=U(\mathbb {R})$ is compact.
Proof. Consider the complex Lie algebra ![]() $\mathfrak {g}=\mathrm {Lie}(\textbf {G})$. Let
$\mathfrak {g}=\mathrm {Lie}(\textbf {G})$. Let ![]() $\Sigma$ be the set of roots,
$\Sigma$ be the set of roots, ![]() $\Sigma ^+$ the set of positive roots and
$\Sigma ^+$ the set of positive roots and ![]() $\mathfrak {g}_\alpha$ the vector space attached to
$\mathfrak {g}_\alpha$ the vector space attached to ![]() $\alpha \in \Sigma$ with respect to the torus
$\alpha \in \Sigma$ with respect to the torus ![]() $T^*(\mathbb {C})$. Following Weyl [Reference WeylWey26], Chevalley [Reference ChevalleyChe55] and Tits [Reference TitsTit66], one may choose elements
$T^*(\mathbb {C})$. Following Weyl [Reference WeylWey26], Chevalley [Reference ChevalleyChe55] and Tits [Reference TitsTit66], one may choose elements ![]() $X_\alpha \in \mathfrak {g}_\alpha$ for
$X_\alpha \in \mathfrak {g}_\alpha$ for ![]() ${\alpha \in \Sigma }$ such that, if we define
${\alpha \in \Sigma }$ such that, if we define ![]() $H_\alpha \in \mathrm {Lie}(T^*(\mathbb {C}))$ by
$H_\alpha \in \mathrm {Lie}(T^*(\mathbb {C}))$ by ![]() $H_\alpha =[X_\alpha ,X_{-\alpha }]$, we have
$H_\alpha =[X_\alpha ,X_{-\alpha }]$, we have
We assume the splitting compatible with this choice. Now let
The elements ![]() $Y_\alpha$ and
$Y_\alpha$ and ![]() $Z_\alpha$ for
$Z_\alpha$ for ![]() $\alpha \in \Sigma ^+$ together with the
$\alpha \in \Sigma ^+$ together with the ![]() $W_\alpha$ for
$W_\alpha$ for ![]() $\alpha \in \Delta$ build a basis for a real Lie algebra
$\alpha \in \Delta$ build a basis for a real Lie algebra ![]() $\mathfrak {u}$. As in the proof of [Reference HelgasonHel62, Chapter III, Theorem 6.3], we see that the Killing form is negative definite on
$\mathfrak {u}$. As in the proof of [Reference HelgasonHel62, Chapter III, Theorem 6.3], we see that the Killing form is negative definite on ![]() $\mathfrak {u}$ and hence the Lie subgroup
$\mathfrak {u}$ and hence the Lie subgroup ![]() $\textbf {U}\subset \textbf {G}$ with Lie algebra
$\textbf {U}\subset \textbf {G}$ with Lie algebra ![]() $\mathfrak {u}$ is compact. Since
$\mathfrak {u}$ is compact. Since ![]() $\psi ^*$ preserves the splitting,
$\psi ^*$ preserves the splitting, ![]() $\psi ^*(X_\alpha )=X_{\psi ^*(\alpha )}$ for
$\psi ^*(X_\alpha )=X_{\psi ^*(\alpha )}$ for ![]() $\alpha \in \Delta$. Let
$\alpha \in \Delta$. Let ![]() $w$ be the element of maximal length in the Weyl group for
$w$ be the element of maximal length in the Weyl group for ![]() $T^*$. There is an
$T^*$. There is an ![]() $n^*\in \textbf {G}$, uniquely determined modulo the center, such that the inner automorphism
$n^*\in \textbf {G}$, uniquely determined modulo the center, such that the inner automorphism ![]() $w^*=\mathrm {Int}(n^*)$ acts as
$w^*=\mathrm {Int}(n^*)$ acts as ![]() $w$ on
$w$ on ![]() $T^*$ and such that
$T^*$ and such that ![]() $w^*(X_\alpha )=-X_{w\alpha }$ for
$w^*(X_\alpha )=-X_{w\alpha }$ for ![]() $\alpha \in \Delta$. This automorphism is of order 2 and commutes with
$\alpha \in \Delta$. This automorphism is of order 2 and commutes with ![]() $\psi ^*$. Now let
$\psi ^*$. Now let ![]() $\phi =w^*\circ \psi ^*$. Since
$\phi =w^*\circ \psi ^*$. Since ![]() $w\circ \psi ^*$ acts by
$w\circ \psi ^*$ acts by ![]() $-1$ on
$-1$ on ![]() $\Sigma$ this implies
$\Sigma$ this implies ![]() $\phi (X_\alpha )=-X_{\phi (\alpha )}=-X_{-\alpha }$ for
$\phi (X_\alpha )=-X_{\phi (\alpha )}=-X_{-\alpha }$ for ![]() $\alpha \in \Delta$. It follows from the commutation relations and the relations
$\alpha \in \Delta$. It follows from the commutation relations and the relations ![]() $N_{\alpha ,\beta }=-N_{-\alpha ,-\beta }$ that
$N_{\alpha ,\beta }=-N_{-\alpha ,-\beta }$ that ![]() $\phi (X_\alpha )=-X_{-\alpha }$ and
$\phi (X_\alpha )=-X_{-\alpha }$ and ![]() $\phi (H_\alpha )=-H_{\alpha }$ for all
$\phi (H_\alpha )=-H_{\alpha }$ for all ![]() $\alpha \in \Sigma$. Now
$\alpha \in \Sigma$. Now ![]() $\phi$, which acts as an automorphism of the real Lie algebras
$\phi$, which acts as an automorphism of the real Lie algebras ![]() $\mathfrak {g}^{**}$ generated by the
$\mathfrak {g}^{**}$ generated by the ![]() $X_\alpha$ for
$X_\alpha$ for ![]() $\alpha \in \Sigma$, can be extended to an antilinear involution of
$\alpha \in \Sigma$, can be extended to an antilinear involution of ![]() $\mathfrak {g}^{**}\otimes \mathbb {C}=\mathfrak {g}=\mathfrak {u}+i\mathfrak {u}$. This, in turn, induces a Cartan involution
$\mathfrak {g}^{**}\otimes \mathbb {C}=\mathfrak {g}=\mathfrak {u}+i\mathfrak {u}$. This, in turn, induces a Cartan involution ![]() $\boldsymbol {\theta }$ on
$\boldsymbol {\theta }$ on ![]() $\textbf {G}$: its fixed point set is the compact group
$\textbf {G}$: its fixed point set is the compact group ![]() $\textbf {U}=U(\mathbb {R})$ with Lie algebra
$\textbf {U}=U(\mathbb {R})$ with Lie algebra ![]() $\mathfrak {u}$, and
$\mathfrak {u}$, and ![]() $U$ is the inner form of
$U$ is the inner form of ![]() $G^*$ defined by the Galois cocycle
$G^*$ defined by the Galois cocycle ![]() $a_1=1$ and
$a_1=1$ and ![]() $a_\sigma =w^*$.
$a_\sigma =w^*$.
We observe that when, moreover, ![]() $G^*$ is almost simple, which means that the root system of
$G^*$ is almost simple, which means that the root system of ![]() $G^*$ is irreducible, the classification shows that condition (v) holds except when
$G^*$ is irreducible, the classification shows that condition (v) holds except when ![]() $G^*$ is split of type
$G^*$ is split of type ![]() $A_n$ with
$A_n$ with ![]() $n\geqslant 2$, or
$n\geqslant 2$, or ![]() $D_n$ with
$D_n$ with ![]() $n\geqslant 3$ odd, or
$n\geqslant 3$ odd, or ![]() $E_6$ or when
$E_6$ or when ![]() $G^*$ is quasi-split but non-split of type
$G^*$ is quasi-split but non-split of type ![]() $D_n$ with
$D_n$ with ![]() $n\ge 4$ even.
$n\ge 4$ even.
Acknowledgements
We thank Laurent Clozel and Raphaël Beuzart-Plessis for very useful discussions as well as the referee for pertinent remarks.