Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-11T18:44:21.828Z Has data issue: false hasContentIssue false
  • English
  • Français

A Matter of Representation: Spatial Voting and Inconsistent Policy Preferences

Published online by Cambridge University Press:  12 July 2017

Lukas F. Stoetzer
Rights & Permissions [Opens in a new window]

Abstract

The application of spatial voting theories to popular elections presupposes an electorate that chooses political representatives on the basis of their well-structured policy preferences. Behavioral researchers have long contended that parts of the electorate instead hold unstructured and inconsistent policy beliefs. This article proposes an extension to spatial voting theories to analyze the effect of varying consistency in policy preferences on electoral behavior. The model results in the expectation that voters with less consistent policy preferences will put less weight on policy distance when learning about candidates who should represent their political positions. The study tests this expectation for the 2008 US presidential election, and finds that for respondents with less consistent self-placements on the liberal–conservative scale, policy distance less strongly affects their voting decision. The results have implications for the quality of political representation, as certain parts of the electorate are expected to be less closely represented.

Keywords

voting behaviorspatial votingmass belief systemsrepresentation
Type
Articles
Information
British Journal of Political Science , Volume 49 , Issue 3 , July 2019 , pp. 941 - 956
Copyright
© Cambridge University Press 2017 

The crucial stage at which the democratic representation of citizens’ preferences can go wrong is at the ballot box. If citizens do not elect candidates who match their preference for a particular political outcome, governments are unlikely to be responsive, and political representation could end up being mismatched. For a dominant perspective in political theory, however, this fear has been regarded as irrelevant, as it builds on the idea that all citizens know exactly what kind of policies they would like to see implemented. Those who are opposed to minimum wages, who want increased taxation for higher incomes and who are in favor of gay marriage would simply vote for candidates or parties with political platforms that aim to implement these goals. In political science, spatial theories of voting and empirical tests thereof promote the idea that policy distance is indeed an essential factor in citizens’ voting decisions.Footnote 1

But what if ordinary voters are not equipped with policy views that easily permit them to select matching representatives? Critiques have long asserted that such a model of democratic representation is based on an unrealistic portrayal of citizens’ policy views. Researchers stress that citizens base their political behavior on unstructured beliefs and attitudes rather than well-defined preferences over political outcomes. From Converse’s early ‘non-attitude model’,Footnote 2 through studies of preference formation,Footnote 3 to the impact of ideological thinking,Footnote 4 the bottom line of this area of research is that it doubts whether well-defined preference is a sensible assumption for explaining voters’ behavior. Instead, it is argued that citizens differ in the degree of consistency in their policy views: some citizens express opinions that are more constrained by underlying political dimensions than others. While it is often presupposed that this hinders citizens’ ability to find matching representatives, political science has acquired relatively little theoretical insight into the mechanisms of how this affects voting.

In this article, I offer an extension to spatial voting that integrates a behavioral conceptualization of policy views and propose to model inconsistent, unconstrained preferences as a belief over different policy platforms. Those beliefs can signify that citizens might be uncertain about their ideal political outcome, building on the idea that ‘people do not know how much they will like an outcome if and when it does occur’.Footnote 5 I argue that this conceptualization also makes allowance for varying consistency in preferences. As some citizens’ beliefs are less strongly constrained, policy preferences will also be less strongly aligned with political dimensions.

Studying how this influences voting shows that citizens with loosely structured beliefs will put considerably less weight on policy distance when deciding between candidates. For citizens with preferences that do not align with the ideological expectations, and who attempt to learn about the utility-difference between two candidates, policy platforms would prove less informative. This is because, for citizens, the information contained in the candidates’ platforms depends on their own policy beliefs. Therefore, citizens with wide beliefs will put considerably less weight on policy distance when learning about utility differences between candidates.

An empirical test confirms the moderating effect of inconsistency on spatial voting and its importance for electoral representation. In the 2008 US presidential elections, I find that for respondents with a higher inconsistency in self-placement on the liberal–conservative scale, policy distance is less important for explaining voting decisions. This finding supports the implications from the model and calls into question the degree to which the assumption that all voters possess the same structured preferences is a reasonable starting point for understanding representative democracies. There is considerable heterogeneity in citizens’ ability to choose politicians who best represent their interests based on policy platforms, which means that certain parts of the electorate are expected to be, on average, less closely represented than those parts that organize their opinions along ideological dimensions.

ABSTRACTING CITIZENS’ PREFERENCES IN TERMS OF POLICY PLATFORMS

Since Downs’s seminal contribution,Footnote 6 spatial voting theories have analyzed voting behavior based on the premise that citizens hold well-defined policy preferences about political outcomes. In the original formulation, political outcomes are described by policy platforms that are ordered along a liberal–conservative ideological dimension, and their platforms perfectly capture all citizens’ preferences. Building on this idea, spatial voting theories make the implicit homogeneity assumption that two voters with the same ideal policy platform possess the same policy views.Footnote 7 The same ideological platforms that organize parties’ and candidates’ programs are thus assumed to perfectly approximate voters’ policy preferences.

This assumption contrasts with results from studies on public opinion and mass belief systems. Authors of these studies take for granted that citizens most seldom ‘express consistently liberal, conservative, or centrist positions on government policy’.Footnote 8 The sociological model of belief systems is built on the idea that political attitudes ‘are organized into coherent structures by political elites for consumption by the public’.Footnote 9 This implies that political platforms do not exist along ideological dimensions per se, but are created by political elites to structure the political process. Citizens adapt these structures to varying degrees. This perspective is most famously associated with Phillip Converse’s chapter, ‘The nature of belief systems in mass publics’.Footnote 10 Based on the analysis of survey responses, he argued that ‘large portions of an electorate do not have meaningful beliefs even on the issues that have formed the basis for intense political controversy among elites for substantial periods of time’.Footnote 11 Instead, citizens most often hold unstructured and inconsistent preferences about political issues.Footnote 12 Overall, this school of thought claims that there is considerable heterogeneity between citizens. Although for some citizens ideal policy platforms may be a reliable abstraction of their opinions, for others they are not.Footnote 13

This article explores the electoral consequences of this conceptualization. The greatest worry for democratic theory is a general public whose political preferences do not equip them to elect representative leaders, because ‘without preferences [..] democratic theory – at least in its most liberal guise – loses its starting point’.Footnote 14 But what matters for representative democracy is not that some citizens show signs of potential inconsistency, but how this could affect the election of representatives. Although electoral researchers often pursue a political-sophistication argumentation, according to which sophisticated citizens with a more reliable understanding of the political space are also more likely to employ policy voting rationalities,Footnote 15 this does not provide theoretical answers to the key concerns inherent in these models: to what extent can voters with preferences that do not coincide with the spatial voting model make valid policy-orientated voting decisions? Contemporary spatial voting theories cannot address the concerns raised by behavioral researchers, as they assume that all citizens hold the same structure regarding policy preferences. To address this shortcoming, the next section outlines an extension to spatial voting theory to model variation in citizens’ preference structures, permitting the analysis of the electoral consequences of varying consistency.

A SPATIAL REPRESENTATION OF CITIZENS’ POLICY BELIEFS

Both formal theories of spatial voting, as well as behavioral researchers, agree that political elites structure their communication in terms of ideological policy platforms. However, in the behavioral conceptualizations discussed above, citizens differ in their ability to abstract their policy views in terms of these platforms. This perspective implies that citizens differ in how strongly ideology constrains their policy preferences. The origin of the theoretical argument presented here is to conceptualize this constraint in terms of variation in citizens’ policy beliefs about their ideal political platform.

Policy beliefs can be integrated into the general utility framework of spatial voting. Instead of supposing that citizens’ preferences are homogeneously approximated by policy platforms, researchers can assume that citizens are – to a specific degree – uncertain which platform is in their own best interest. This uncertainty about the ideal platform can be embodied in terms of voter-specific belief distributions. The idea that preferences regarding outcomes are uncertain is well integrated into general choice theory.Footnote 16

The belief distribution about the different policy platforms is specified in terms of a voter’s state of mind ${\rm \Theta }_{i} $ . The specification extends models of spatial voting as, for example, discussed by Jessee,Footnote 17 in which each voter has a fixed ideal point on a one-dimensional spectrum.Footnote 18 Instead it is assumed that voter $i$ ’s policy belief follows a normal distribution, defined along a one-dimensional policy space.

(1) $$\Theta _{i} \,\sim\,N(x_{i} ,\sigma _{{\Theta _{i} }}^{2} )$$

This distribution represents the idea that each voter has a mean belief about her ideal policy platform (x i ), but is uncertain whether her most-preferred position might be slightly to the left or right of it. The extent of uncertainty depends on the variance in beliefs ( $\sigma _{{{\rm \Theta }_{i} }}^{2} $ ). With increasing belief variance, voters become less certain about their ideal policy outcome. Figure 1 exemplifies the beliefs of two different voters with different mean beliefs. The first voter’s mean belief x 1 is to the left of voter two’s mean belief x 2. The voters also differ in their belief variance. While the first voter is quite certain that her platform yields the most beneficial outcome, the second voter has a wider belief variance and therefore is clearly less certain that a specific platform is in her best interest.

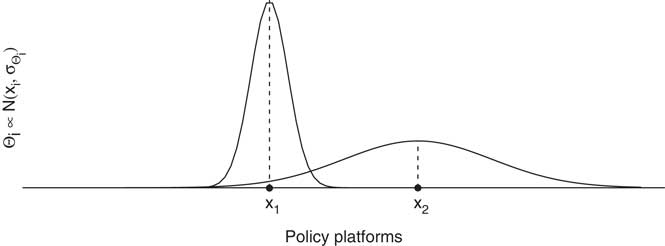
Fig. 1 A spatial representation of citizens’ policy beliefs Note: the figure shows policy beliefs of two voters about their ideal policy platform. The voters differ in their mean belief $x_{i} $ , but also in their belief variance $\sigma _{{{\rm \Theta }_{i} }}^{2} $ . The second voter holds a wider belief variance, compared to the first, and is thereby less certain about the ideal policy platform.

For the argumentation, it is central that the belief variance can be linked to the consistency of policy preferences. The starting point is the assertion that policy beliefs are related to preferences, attitudes and opinions for concrete policy proposals – for example, whether a respondent is opposed to or in favor of gay marriage. Within the spatial voting literature, this link is commonly conceptualized in terms of item response models or factor analytical models.Footnote 19 Basically, a widening of policy belief variance loosens the systematic relationship between ideological platforms and policy preferences, making the latter appear less consistent. For instance, the inconsistency that a self-indicated ideologically liberal voter is in favor of gay marriage but opposed to abortion rights is an irregularity that is often insufficiently explained by variance-constant measurement error, but can straightforwardly be attributed to varying belief variances.Footnote 20 Belief variance adds an additional source of randomness to answering patterns on different policy issues – and an increasing variance causes them to be inconsistent with political platforms.Footnote 21 This line of thought is picked up in the empirical section to derive an operationalization of inconsistency that reflects the theoretical conceptualization of policy beliefs and verifies the theoretical connection between the two.

In contrast to this approach, models of spatial voting rely on the assumption that beliefs about policy platforms are fixed. The implicit assumption is that all voters have the same types of constraints, which – from an adaptive utility perspective – means they would all be equally certain with respect to which platform best represents their interests. Formally, in these theories, voters’ beliefs are fixed to a specific value ${\rm \Theta }_{i} {\equals}x_{i} $ , where x i represents the most preferred policy platform.Footnote 22 Essentially, this assumption permits spatial theorists to simplify citizens’ overall preferences via their ideal platform. One virtue of this conceptualization is that the standard spatial preference model is nested within the spatial representation of policy beliefs: assuming that all voters possess a belief variance of zero recovers the standard model. The key difference is that the extension allows us to relax the fixed preference assumption and thereby generates leverage to study the consequences of varying inconsistency on voting behavior.

THE INFLUENCE OF POLICY BELIEFS ON VOTING DECISIONS

Policy beliefs can be included in the spatial model of probabilistic voting,Footnote 23 allowing us to analyze the consequences of varying inconsistency for voting decisions. In the following section, I analyze a voter’s decision between two candidates. A voter’s evaluation of a candidate is usually expressed in terms of expected utility and additional unobserved factors. A voter will vote for the first candidate if her overall utility is larger for this candidate, and for the second candidate if the utility is larger for this candidate. This overall utility will be determined by the expected utility and additional, randomly distributed, factors.Footnote 24

Of theoretical concern, then, is how voters form their expected utility based on the candidate’s communicated platform. In spatial voting, utility is derived from the closeness of a candidate’s policy platform to a voter. Each voter receives utility given her policy beliefs about the closeness of a candidate’s platform. In order to model the closeness of a candidate’s platform, I employ a quadratic loss function.Footnote 25 Utility in this specification is a random variable, as a voter’s preferences over the platforms follow the policy beliefs, rather than fixed ideal platforms. Put differently, voters are uncertain about the utility they will receive from a candidate because they are uncertain which platform they most prefer.Footnote 26

An approach that highlights the interaction between candidates and voters might suppose that candidates send certain information about themselves and voters process these signals to learn what they can expect from the candidates.Footnote 27 This learning model focuses on how the communicated policy platforms alter difference in expected utility. The expections from this model are relatively straightforward: for voters with wider policy belief variance, information contained in platform signals is less informative than for voters with consistent policy beliefs. This holds because the information contained in the candidate’s signal depends on the degree of uncertainty a voter possesses about her ideal platform. Expected utility is less strongly affected by policy distance for voters with a wide policy belief variance who are uncertain about their ideal policy platform compared to those with a low belief variance. Formally, this idea can be derived from a Bayesian updating model about the difference in expected utility.Footnote 28 The condensed idea is that voters start off with a prior belief about the utility difference between the candidates and employ the candidate platform signals to learn about this utility difference. The expected utility from the posteriori beliefs results in choice probabilities:

(2) $$Pr\left[ {V_{{i1}} \,\gt\,V_{{i2}} } \right]\,{\equals}\,\Phi \left[ {{\minus}w_{i} \beta \left[ {(x_{i} {\minus}C_{1} )^{2} {\minus}(x_{i} {\minus}C_{2} )^{2} } \right]} \right],$$

where the derived weight w i depends on a voter’s variance in policy beliefs $\sigma _{{{\rm \Theta }_{i} }}^{2} $ and thereby on the inconsistency in policy preferences.Footnote 29 The resulting voting probabilities deviate from homogeneous effect models in the literature. If the belief variance increases, the weight on policy distance decreases. It shows that the voting probabilities are less strongly affected when comparing voters with same mean positions but different belief variances. The marginal effect of distance on expected utility decreases with higher levels of variance. In the most extreme case, policy distance has no effect at all, because the platform signals are not informative to these voters.Footnote 30

To sum up, the analysis of a learning model results in the hypothesis that the importance of policy distance is affected by policy inconsistency: policy distance should be more important for voters with consistent policy preferences, and less important for those with inconsistent preferences. The next section outlines an empirical test that closely follows the conceptualization of the theoretical model.

A POLICY-WEIGHTED MODEL FOR SPATIAL VOTING DECISIONS

The US presidential election of 4 November 2008 constitutes an ideal case in which to obtain estimates for the outlined model. The expectations are derived for a situation in which two candidates compete for votes by signaling their policy platforms, and those platform signals are equally well observed by the electorate. The vast amount of campaign spending and media coverage in presidential elections make this a plausible assumption.Footnote 31 I mostly rely on Wave 10 of the 2008–2009 American National Election Panel Study, as the interviews were conducted in the weeks prior to the election.Footnote 32

The expectations can be tested using an empirical specification similar to the theoretical model. According to this model, respondents should put different weights on policy distance when forming the expected utility difference between two candidates. The specific weight that each respondent assigns to policy distance is a function of the variance in policy beliefs. This function can be approximated to be linear, which naturally results in an interaction effect model to test for the mediating effect. The direct effect represents the effect of policy distance for voters with zero belief variance, and an interaction term estimates if respondents with increasing belief variance put less, more or equal weight on policy when forming expected utility. Thus, under the theoretical model, one would expect a negative interaction effect parameter. The empirical specification is completed by further adding an intercept, a set of socio-demographic and political controls, and a direct effect of inconsistency. Given that vote choice is a binary indicator if a respondent intends to vote for the first or second candidate, and the difference in unobserved factors is assumed to be standardized normal, the model results in a standard probit specification.Footnote 33 The next section describes the operationalization of respondents’ inconsistency, candidates’ policy platforms, respondents’ policy beliefs, voting intentions and a set of controls in more detail.

MEASUREMENT OF INCONSISTENCY AND POLICY PLATFORMS IN THE AMERICAN NATIONAL ELECTION STUDIES 2008

To estimate the outlined model, reliable measurements of voters’ policy beliefs and candidate platforms are needed. The basis of the measurements is a battery of eight policy questions included in the American National Election Studies (ANES) 2008, concerning gay marriage, taxation, health care, terrorism and immigration.Footnote 34 Respondents are first asked whether they favor, are opposed to, or neither favor nor oppose a certain preposition – for example, ‘Do you favor or oppose illegal immigrants becoming citizens?’ Afterwards they are asked about the strength of their expressed attitudes on a three-point scale (‘a great deal’, ‘moderately’, ‘a little’). This creates seven-point scales that represent voters’ preferences for the different policy proposals.

Voters’ mean policy beliefs are estimated using a one-dimensional factor model.Footnote 35 Based on these answering patterns, factor loadings are extracted based on an explanatory factor analysis. The one-dimensional factor model has reasonable fit (RMSE of 0.09) and the factor loadings correlate highly with self-placements in this wave.Footnote 36 Additionally, voters are asked to locate the presidential candidates on the same seven-point scales. Using the factor loadings from the model, these placements can be employed to project candidates on the same dimension.Footnote 37 I use this to construct two measurements of difference in quadratic policy distance: the policy distance to the mean perceived political platform and the individual perceived political platform.Footnote 38

Crucial to the empirical analysis is the measurement of the policy belief variance that is linked to inconsistent policy preferences. In order to directly test the theoretical expectations, the analysis opts for a close connection between the theoretical specification and the empirical measurement of inconsistency.Footnote 39 The starting point is the connection between policy preferences and ideological orientation as discussed in the theory section. Given that respondents’ attitudes towards the specific proposals can be expressed as a linear function of their beliefs about policy platforms, increased belief variance should result in more randomness when relating answering patterns for concrete policy proposals to policy platforms. This is because it adds an additional stochastic element to the model. Formally, after considering the mean platform, the variance in responses to the policy proposal is not only a function of measurement error, but also of the belief variance. Based on this, it is possible to derive an estimator that approximates the belief variance as the average sum of squared residuals when regressing the mean platform belief on the attitude towards the policy proposal. Following this, I estimate separate regressions of a respondent’s average liberal–conservative self-placement on the battery of policy issues. Based on the regression residuals for each individual I then calculate the average sum of squared errors and use them to measure variation in consistency with underlying platforms.Footnote 40

The inconsistency measurement can generally be understood as the average deviation from the ideologically expected answering pattern. This mimics the original conceptualization found in Converse’s chapter,Footnote 41 in which ideological belief systems are argued to impose a structure that generates certain expectations about policy views.Footnote 42 The set of expectations here is approximated using different regressions, confirming, for example, that self-indicated ideological liberal respondents is expected to be in favor of gay marriage and high income taxation. Strongly deviating from this rule creates an inconsistency that is then reflected in the estimator. A liberal respondent who confirms with both expectations has a smaller average residual than a liberal respondent who is unexpectedly opposed to high income taxation. In this, the measurement creates variation between respondents who align their attitudes fairly closely to their ideological platform and those who reveal inconsistent policy preferences. The analysis further includes a set of controls in the full specification: a respondent’s party identification, age, gender, race (African-American), education, home ownership and income. All are based on fairly common survey questions from the ANES.Footnote 43

MAIN RESULTS: THE DECREASING IMPORTANCE OF POLICY DISTANCE

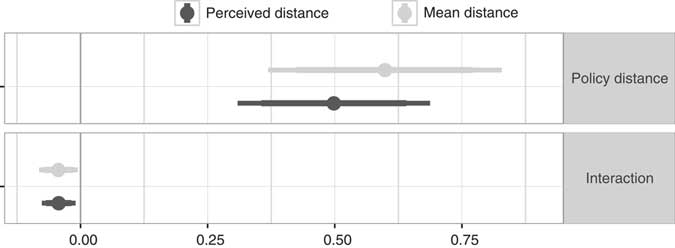
The estimates for the direct effect of policy distance and the interaction effect are plotted in Figure 2. The model relies once on the negative quadratic distance to the mean candidate platform, and once on the perceived candidate platform. In both cases, the estimate of the direct effect is positive, implying that the closer a respondent is to Obama than to McCain, the higher the respondent’s chances of voting for Obama. The estimate of the interaction effect that affects the weight voters put on policy distance is negative. Both parameter estimates are statistically distinguishable from zero, as the 95 per cent confidence intervals do not include zero.Footnote 44

Fig. 2 Parameter estimates for policy-weighted model using perceived (black) and mean distance (grey) to candidate platform Note: the figure shows point estimates as well as 95 per cent and 99 per cent confidence intervals for the direct effect of policy distance and interaction effect with inconsistency.

The parameter estimates imply a decreasing marginal effect of policy distance on expected utility with increasing inconsistency. Figure 3 shows the marginal effect on expected utility calculated from both models. For both, the marginal effect decreases from around 0.5/0.6 to below zero. The resulting empirical pattern is in line with the expectations from the learning model and recovers an important implication of this model. Policy distance affects the voting decisions of (almost) all voters. The marginal effect fails to reach signifcance only for the 2 per cent of respondents with the weakest constraint. Thus distance to candidate’s signaled platform is informative to all, but the results clearly highlight that it is less informative for voters who do not structure their preferences in line with ideological platforms. Those citizens put less weight on policy distance when deciding which candidate generates higher expected utility.

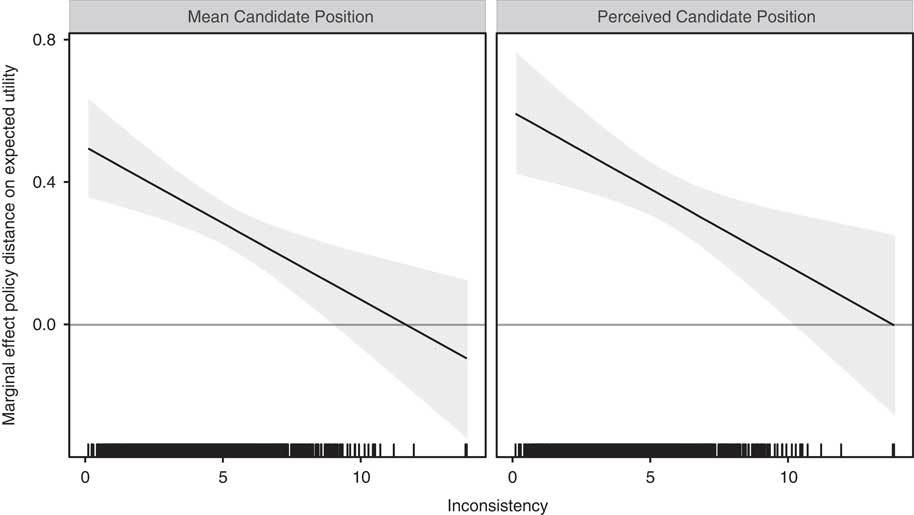
Fig. 3 Marginal effect of policy distance on difference in expected utility for varying levels of inconsistency Note: the left panel shows the marginal effect for mean candidate positions, the right panel for perceived candidate distance. The lines on the x-axis show the distribution of inconsistency in the sample.

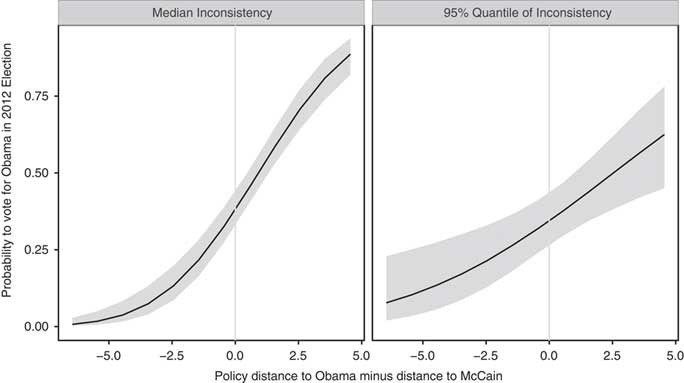
Although this confirms the expectation regarding the decreasing marginal effect on expected utility, the extent to which this also influences the marginal effect of policy distance on voting intention needs further investigation.Footnote 45 This effect becomes apparent when comparing the voting probabilities of a median inconsistency respondent with a respondent from the 95 per cent quantile of inconsistency. Figure 4 shows the simulated predicted probabilities at different values of policy distances.Footnote 46 While policy distance has a strong effect for a respondent with medium consistency, this effect is weaker for a respondent with strong inconsistency. It is important to note that the effect of policy distance at the 95 per cent quantile is still present, as the probability of voting for Obama still increases from 0.4 (with the same distance to both Obama and McCain) to over 0.75 (for voters who are close to Obama and furthest away from McCain’s platform). This again supports the implication that policy distance affects the voting decisions of all citizens, but less so for those with inconsistent policy preferences. I conduct a series of robustness checks, and find support that the main results hold with other measurements, are robust when taking into account measurement uncertainty in inconsistency, and are further evident when applied to another set of policy issues for voting decisions in the 2012 presidential elections.Footnote 47

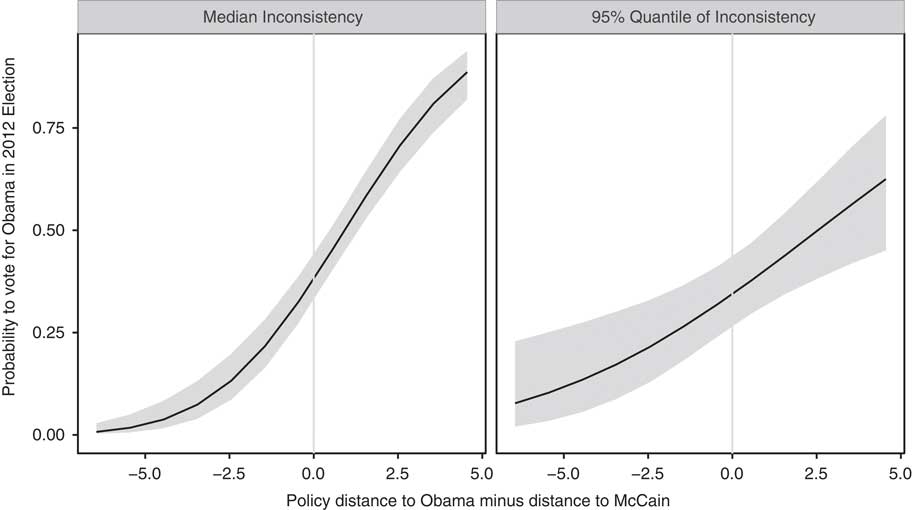
Fig. 4 Probability to vote for Obama by policy distance to obama minus distance to McCain simulated from mean platform model Note: the left panel shows the voting probabilities for a respondent with consistent policy preferences (value correspondent to the median value in the sample). The right panel shows the voting probabilities for respondent with inconsistent policy preferences (value correspondent to the 95 per cent quantile in the sample).

Taken together, the evidence presented in this analysis supports the expectation from the learning perspective. Voters with inconsistent, unconstrained policy preferences put less weight on policy distance. The theoretical foundation tells us something important about the mechanisms of this relationship. Rather than understanding voting decisions as the static formation of expected utilities, voters seem to use platform signals to learn about the expected benefit of their decisions for themselves. For some parts of the electorate, the signals are meaningful and helpful in choosing candidates; for others they are not. This has far-reaching implications for political representation, as will be discussed below.

IMPLICATIONS: EXPECTED REPRESENTATIONAL CLOSENESS

The systematically varying effect of policy distance influences the representation of citizens’ political interests. If citizens with inconsistent policy preferences rely less on policy platforms when deciding which candidate to vote for, they can be expected to be further away from their representatives. The variation in representational closeness can be depicted in terms of the expected distance to the candidate for whom a citizen intends to vote.Footnote 48

Figure 5 shows the expected representational closeness for the 2008 presidential election. The figure plots the simulated sampling distribution of the average expected distance for different levels of inconsistency.Footnote 49 Respondents with consistent policy preferences (10 per cent percentile of inconsistency measurement) are expected to be closer to the candidate they intend to vote for compared to voters with inconsistent policy preferences (90 per cent percentile of inconsistency measurement). Voters at median values are found in between the two. The values are meaningful on the original scale. A zero indicates that voters are expected to share the same platform as the candidate they intend to vote for. Of course, given that candidates only offer one platform and voter positions diverge from this, on average, voters will be expected to be at some distance from their representative. Still, voters with consistent policy preferences are expected to be relatively close to their representative (average of −0.45 on scale with range around 3.5). For voters with inconsistent preferences, this increase of around 35 per cent highlights the looser connection to their representatives.

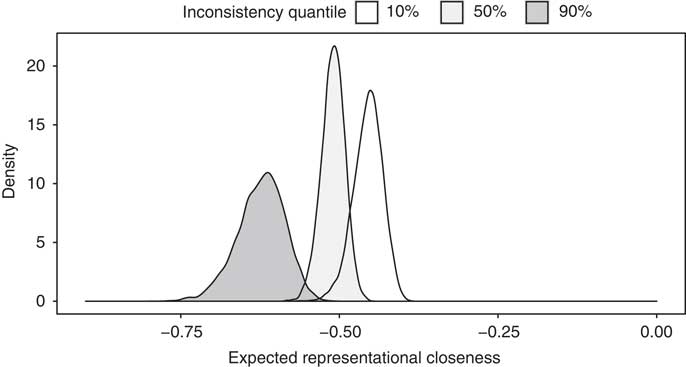
Fig. 5 Average expected distance for varying degrees of inconsistency Note: the x-axis shows the expected distance to a respondent's representative. Values of zero imply that a voter is expected to share the same position with the candidate she intends to vote for. Decreasing values indicate a stronger expected distance.

The analysis underscores the importance of the theoretical extensions to spatial voting models for our understanding of political representation. Parts of the electorate that do not structure their policy preferences in terms of the underlying dimensions of politics are expected to be less closely represented.

DISCUSSION

Citizens with views on different issues that are not organized in liberal vs. conservative terms rely less on distance when deciding which candidate to vote for, compared to citizens with well-defined policy preferences. This article offers a comprehensive theoretical explanation for this hypothesis. The way that citizens form expected utility about political programs depends on each citizen’s own policy belief regarding what political outcomes they would like to see. Because these beliefs exhibit varying constraints, candidates’ communicated platforms are informative to a different degree to citizens. This means that in learning about their representative match, citizens place different levels of emphasis on policy considerations. The empirical results on the basis of the 2008 presidential elections underscore that this extension to spatial models of vote choice has important implications for political representation. While citizens who structure their preferences in line with the underlying dimension of politics are expected to find closely matching candidates, citizens who do not are expected to be further away from their representatives.

While previous empirical studies tested a related political sophistication hypothesis about heterogeneity in spatial voting decisions,Footnote 50 in which less informed or aware voters rely less on policy distance, this article is the first to put these suppositions on a solid theoretical basis. The argumentation highlights that those prior findings might work through differences in ideological structures that are potentially interrelated with political awareness and the motivation to acquire necessary political information. The theoretical model then investigates a concrete mechanism through which those concepts affect voters’ decision making. The ongoing interaction between candidates and voters, and how voters learn what they can expect from different candidates, is argued to be one key to understanding heterogeneity in a voter’s decision calculus. In this, the theoretical model extends on prior empirical studies on the matter, but also imposes a perspective on how those models can be integrated into widely applied spatial models of vote choice.

The theoretical formulation also clearly speaks to directional theories of spatial voting that tried to integrate doubts about citizens’ ideological competence into a general policy-based voting theory. Directional theories of vote choice argue that citizens have a less concrete notion of policy preferences than the classic model assumes. The basic claim is that citizens’ preferences are actually directional: they prefer parties that are on their side of the ideological spectrum and those that take on more intense positions.Footnote 51 Essentially, directional models make the same homogeneity assumption as the classic models do, but formulate them in the ‘opposite’ direction: all individuals possess a vague directional policy preference. This is in contrast to the homogeneity assumption in the classic model, in which all citizens possess the same consistency in policy preferences. The developed spatial representation of citizen’s policy beliefs offers a powerful theory to uncover empirically evident – but under-theorized – ‘heterogeneous decision rules’.Footnote 52

There is a well-known assertion in the literature that two broad ideological dimensions structure political conflict – economic and cultural.Footnote 53 To acknowledge these findings, the policy belief conceptualization can be extended to multiple dimensions by defining multivariate belief distributions. This task will involve further conceptual clarifications and offer an enriched representation of the ideological structure of the general public. For instance, the supposition that the electorate holds defined positions on cultural but not on economic issues, and how this matters, can be approached with this extension. Developing a more fine-grained two-dimensional inconsistency measurement might also be important for capturing central heterogeneity. In its current form, the inconsistency measurement picks up two groups of respondents: those who posses weak, essentially random, attitudes and those who have a crystallized mix of strong liberal and strong conservative attitudes. While Appendix Section E.4 shows that this does not affect the results in the main text, a two-dimensional extension could potentiality differentiate between those two groups, providing a more accurate estimate of the moderating effect.

In general, the argumentation attempts to alleviate tensions between opposing positions in political science research by showing that political behaviorists’ sentiments about spatial theorists’ depictions of policy preferences can be integrated using an extension of the theory. The model extension grants spatial theorists the leverage to study political concepts that were hitherto only integrated into models of political behavior. Up-to-date findings from political psychology and public opinion are seldom integrated into spatial voting models, as these models build on a strong axiomatic assumption that voters have exogenous and fixed preferences. This assumption, for example, makes it impossible to study how preferences change over time and can be influenced by environmental circumstances. For many political scientists the important part of the political process is why citizens hold specific beliefs in the first place, and how they can be influenced.Footnote 54 Further research can build on the model’s reciprocal interaction between voters and parties including persuasion and campaigning.

Returning to the starting point, we should ask what all of this implies for democratic representation. If ordinary voters are not equipped with rigorous policy preferences, does this distort the simple model of representative democracy? The findings indicate that it does to a certain degree. For citizens who do not live up to the axiomatic preference portrayal adopted in simple models of representation, the ideal of equal political representation is somewhat hampered. Those parts of the electorate will find it considerably harder to identify ideologically similiar politicians. The theoretical considerations, however, reveal the conditions under which voters are able to use policy platforms to make informed, considered decisions and find matching representatives. If all citizens have policy beliefs with only a small belief variance (which implies that they can exactly identify their ideal policy platform), the model presented shows convergence with the classic perspective: voters will find it easy to find the closest match. This implies that citizens need to be able to learn about their expected benefit from different policy platforms.

Footnotes

*

University of Zurich (email: lukas.stoetzer@uzh.ch). I thank Thomas Gschwend, Adam Berinsky, Devin Caughey, Daniel Stegmueller, Eric Dickson, Laron Williams, Steffen Zittlau, Tilko Swalve, Anita Gohdes, participants of different workshops at the University of Mannheim and three anonymous reviewers for helpful comments on the article. Support for this research was provided by the Fritz-Thyssen Foundation, financing a post-doc scholarship at the Massachusetts Institute of Technology during which most of the work was conducted. Data replication sets are available in Harvard Dataverse at: doi:10.7910/DVN/J0G6K3 Stoetzer (2017) and online appendices are available at https://doi.org/10.1017/S0007123417000102

1 See, e.g., Jessee Reference Jessee2009; RePass Reference RePass1971; Westholm Reference Westholm1997.

2 Converse Reference Converse1964.

3 Gerber and Jackson Reference Gerber and Jackson1993, 640.

4 Jacoby Reference Jacoby1991.

5 Gerber and Jackson Reference Gerber and Jackson1993, 640.

6 Downs Reference Downs1957.

7 See, e.g., Adams, Merrill, and Grofman Reference Adams, Merrill and Grofman2005; Ansolabehere, Rodden, and Snyder Reference Ansolabehere, Rodden and Snyder2008; Jessee Reference Jessee2009; Kedar Reference Kedar2005.

8 Kinder Reference Kinder1998, 768.

9 Feldman Reference Feldman1988, 417.

10 Converse Reference Converse1964.

11 Converse Reference Converse1964, 245.

12 Further research in this area highlights the role of ‘core values’ and ‘predispositions’, as well as the varying degree of ideological thinking about political matters, and stresses varying attention to public debate about politics as a factor that explains unstable and inconsistent views (see Feldman Reference Feldman1988; Jacoby Reference Jacoby1991; Jacoby Reference Jacoby1995; Zaller Reference Zaller1992).

13 Studies reject these concerns by attributing such conclusions to falsely specified empirical models that do not sufficiently account for measurement error. Articles relying on structural equation models or other approaches show that latent policy preferences are actually consistent and stable enough to reject the notion of an unsophisticated public with no meaningful preferences about policies (see Achen Reference Achen1975; Ansolabehere, Rodden, and Snyder Reference Ansolabehere, Rodden and Snyder2008; Jackson Reference Jackson1983; Moskowitz and Jenkins Reference Moskowitz and Jenkins2004).

14 Bartels Reference Bartels2003, 50.

15 See, e.g., Jessee Reference Jessee2010; Knight Reference Knight1985; Lavine and Gschwend Reference Lavine and Gschwend2006; Wyckoff Reference Wyckoff1980.

16 Adaptive utility theory studies situations in which the decision maker is uncertain how much she benefits from a specific outcome (see Axelrod and Cohen Reference Axelrod and Cohen1984; Calvert Reference Calvert1985; Cyert and DeGroot Reference Cyert and DeGroot1987). Because spatial voting theories are also formulated in terms of a utility-maximizing framework, this makes adapting policy beliefs to spatial voting straightforward. Moreover, adaptive utility has been argued to be a useful model for spatial voting, as it is reasonable to assume that the rewards from a certain policy platform are never directly observed, but are to some degree always dependent on political beliefs about how much better the implementation of the policy will be for a voter (see Gerber and Jackson Reference Gerber and Jackson1993).

17 Jessee Reference Jessee2009.

18 See the discussion for a possible extension to multiple dimensions.

19 See, e.g., Jessee Reference Jessee2009; Schofield et al. Reference Schofield, Martin, Quinn and Whitford1998.

20 This works very similar to Lauderdale’s analysis of unpredictable voters in ideal point analysis, in that some actors systematically deviate from the ideological expected behavior due to increasing variance (see Lauderdale Reference Lauderdale2010).

21 In order to illustrate this further, one might employ a simplified version of an item-response model. Consider two liberal policies $j\in(1,2)$ and two different citizens $i\in(1,2)$ . Suppose that citizens’ attitudes towards proposals p ij can be expressed as a linear function of their beliefs ${\rm \Theta }_{i} $ over policy platforms: $p_{{ij}} \,{\equals}\,{\rm \Theta }_{i} {\plus}{\epsilon}_{{ij}} $ , where ε ij is random measurement error $\left( {Var[{\epsilon}_{{ij}} ]\,{\equals}\,1} \right)$ . Values of p ij below 0 indicate opposition to a policy, and values above indicate the favoring of a policy. Although both voters can have the same liberal position (x i =1), unequal belief variances ( $\sigma _{{\Theta _{1} }}^{2} \,{\equals}\,0.1$ and $\sigma _{{{\rm \Theta }_{2} }}^{2} \,{\equals}\,1$ ) might make the policy preferences of one voter seem consistent (as the probability that both preferences are liberal is quite high $Pr(p_{{11}} \,\gt\,0 \, {\cap} \,p_{{12}} \,\gt\,0)\,{\equals}\,0.99$ ), while the other voters’ preferences are likely to be inconsistent (there is a high probability that one preference is conservative and the other is liberal $1{\minus}Pr(p_{{21}} \,\gt\,0 \, {\cap}\, p_{{22}} \,\gt\,0)\,{\equals}\,0.33$ ).

22 In the simplified answering model described in the footnote above, this implies that two respondents with the same ideal platform are expected to have the same policy preferences because, whenever x 1=x 2, it follows that Pr(p 1j )=Pr(p 2j ).

23 See Adams, Merrill, and Grofman (Reference Adams, Merrill and Grofman2005).

24 Formally, the utility model for voter $i\in(1,\,\ldots\,,N)$ and party $k\in(1,2)$ can be defined as $V_{{ik}} \,{\equals}\,{\Bbb E}[U_{{ik}} ]{\plus}{\epsilon}_{{ik}} $ , where V ik is the overall utility, ${\Bbb E}[U_{{ik}} ]$ the expected utility and ε ik captures additionally randomly distributed aspects.

25 This is written as $U_{{ik}} \,{\equals}\,{\minus}\beta \left( {C_{k} {\minus}{\rm \Theta }_{i} } \right)^{2} $ , where C k is the candidate’s platform and β depicts the importance of policy distance on a voter’s utility evaluation. This functional form implies that voters are risk averse in policy distance (see Berinsky and Lewis Reference Berinsky and Lewis2007; Ye, Li, and Leiker Reference Ye, Li and Leiker2011), which has the important implication that variance in policy beliefs negatively affects expected utility. Assuming other commonly employed norms (e.g., Euclidean or city block norm) makes a conclusion later on analytically intractable, but does not change the intuition of the analysis.

26 Within the spatial voting theory, uncertainty has so far only been formalized as originating from the candidate’s platform (see, e.g., Bartels Reference Bartels1986; Enelow and Hinich Reference Enelow and Hinich1981). While individuals’ varying ability to pin down exactly what programs candidates will put into place if elected can be a powerful source of variation in policy-directed voting, analyzing the interplay between uncertainty about a candidate’s position and variance in policy beliefs is unfortunately beyond the scope of this article.

27 The standard way to deal with uncertainty in a spatial voting model is to set up the utility function and form the expectation over the whole utility term, in order to understand how uncertainty enters utility (see Enelow and Hinich Reference Enelow and Hinich1981). For a discussion of expectations from this approach, please see Appendix Section A.1. It offers an alternative mechanism to the learning model: as the uncertainty that arises from the inconsistencies concerns both candidates equally, it cancels out when voters make decisions. The expectations are, thus, that inconsistencies should not effect voting.

28 For a description of this model, see the Appendix Section A.2.

29 The weight is the result of the mixture of normal distributions: $w_{i} \,{\equals}\,{\tau \over {4\beta ^{2} (C_{1} {\minus}C_{2} )^{2} \sigma _{{\Theta _{i} }}^{2} {\plus}\tau }}$ , where τ is the variance of the prior distribution that is centered around zero.

30 The marginal effect of policy distance on utility is equal to the homogeneous effect with decreasing uncertainty $${\rm lim}\,_{{\sigma _{{\Theta _{i} }}^{2} \to0}} w_{i} \beta \,{\equals}\,\beta $$ and equal to zero if uncertainty increases ${\rm lim}\,_{{\sigma _{{\Theta _{i} }}^{2} \to{\plus}\infty}} w_{i} \beta \,{\equals}\,0$ .

31 Additionally, the model supposes that prior to the signaling, voters should possess limited knowledge about the positions, as otherwise campaign signals describe candidates’ platform movements rather than platform taking. Hence, in order to study a case that closely mimics the line of argumentation, an open-seat election appears especially well suited.

32 The American National Election Studies (2008).

33 The formal specification is:

$Pr\left[ {y_{i} \,{\equals}\,1} \right]\,{\equals}\,\Phi \big[ {{\minus}[\delta _{1} {\plus}\delta _{2} \sigma _{{\Theta _{i} }} ]\big[ {(x_{i} {\minus}C_{1} )^{2} {\minus}(x_{i} {\minus}C_{2} )^{2} } \big]{\plus}X_{i} \gamma } \big],$

where y i is the observed voting intention, δ 1 the direct effect of policy distance, δ 2 the interaction effect, $\big[ {(x_{i} {\minus}C_{1} )^{2} {\minus}(x_{i} {\minus}C_{2} )^{2} } \big]$ the difference in quadratic distance and X i a matrix of controls, and γ is a vector of effect parameters.

34 The exact wording of the question and descriptions are available in the Appendix.

35 Factor-analytic techniques to estimate policy platforms from these concrete issue item batteries have been used in various articles concerned with spatial voting decisions (see Schofield et al. Reference Schofield, Martin, Quinn and Whitford1998; Schofield and Zakharov Reference Schofield and Zakharov2009; Stoetzer and Zittlau Reference Stoetzer and Zittlau2015; Quinn, Martin, and Whitford Reference Quinn, Martin and Whitford1999).

36 A more detailed description of the results is provided in the Appendix.

37 This allows the calculation of perceived as well as average factor scores for both Obama and McCain. While the average score for Obama is 0.32, the average score for McCain is −0.91.

38 The first employs each respondent’s negative quadratic distance to Obama’s mean platform score minus the distance to McCain’s mean platform score. In line with the theoretical model, this perspective supposes that each candidate offers a single, unambiguous policy platform. The second uses perceived candidate platforms instead, and presumes that voters potentially possess different perceptions of the signaled platforms that do not necessarily need to be correct. As there are no good reasons to prefer one over the other, the model is then separately estimated for both measurements of policy distance.

39 Different measurements of inconsistency have been proposed. Barton and Parson use a respondent’s standard deviation over different issues (Wyckoff Reference Wyckoff1980; Barton and Parsons Reference Barton and Parsons1977). Higher standard deviations are taken as an indication of unconstrained, inconsistent policy preferences. Jacoby relies on a different measurement, employing Mokken scaling of answering patterns to measure the degree of ideological thinking about political stimuli (see Jacoby Reference Jacoby1995; Lavine and Gschwend Reference Lavine and Gschwend2006). Converse and researchers from the measurement-error tradition rely on correlations in answering patterns at different time points to gauge citizens’ inconsistency and (especially) instability in policy preferences (Converse Reference Converse1964; Hill and Kriesi Reference Hill and Kriesi2001). These measurements lack a direct connection between policy preferences and underlying political platforms, and thus do not sufficiently match the theoretical specification of belief variance.

40 For a formal description and derivation of this estimator, please refer to the Appendix. The results of the separate regressions, as well as a figure of the resulting distribution in the sample, can be found in the Appendix. Values vary strongly between respondents, ranging from (0.11), which implies almost perfect prediction on policy issues, to above 9. For the latter, an average error of three on a seven-point scale highlights the inconsistent connection between policy attitudes and ideological placements.

41 Converse Reference Converse1964.

42 In line with expectations of the idea that the ideological constraints are particularly strong among politically sophisticated voters, the measurement is also related to political sophistication, as Appendix Section C.3 outlines.

43 For descriptive statistics, please consult Appendix Section D.1.

44 The other parameter estimates are reported in Appendix Section D.2. Party identification and race have a statistically significant effect on probability of voting for Obama. There is no direct effect of inconsistency.

45 It is well known that in probit models this marginal effect also depends on the predicted probabilities (see Ai and Norton Reference Ai and Norton2003; Berry, DeMeritt, and Esarey Reference Berry, DeMeritt and Esarey2010). Following Ai and Norton, I calculate the marginal interaction effect and find that it is strongest for observation with average predicted probability to vote for Obama (see Appendix D.2).

46 I use simulation techniques as described by King, Tomz, and Wittenberg (Reference King, Tomz and Wittenberg2000), setting all other covariates to their median value for the average platform measurement.

47 The results and a detailed description are reported in Appendix Section E.

48 For the two-candidate case, this concept is formalized by:

${\Bbb E}[\left( {C_{{y_{i} }} {\minus}x_{i} } \right)^{2} ]\,{\equals}\,Pr\left( {y_{i} \,{\equals}\,1} \right)\left( {C_{1} {\minus}x_{i} } \right)^{2} {\plus}Pr\left( {y_{i} \,{\equals}\,2} \right)\left( {C_{2} {\minus}x_{i} } \right)^{2} $ .

The equation describes the expected distance to the elected candidate C yi . This term is equal to a weighted average between the distance to the first candidate (C 1–x i )2 and the second candidate (C 2–x 1)2, where the weights correspond to the predicted probabilities. If a voter is predicted to vote for the first candidate, such that the predicted probabilities are Pr(y i =1)=1, the expected distance to the representative will be equal to the distance to the first candidate. If the predicted probabilities are equal Pr (y i =1)=Pr (y i =2)=0.5, the expected distance accords to the average of the distances to the two candidates.

49 For this plot, I simulated expected probabilities from the candidate position model, taking into account estimation uncertainty according to King, Tomz, and Wittenberg (Reference King, Tomz and Wittenberg2000). Using an observed case approach (Hanmer and Ozan Reference Hanmer and K2013), I set inconsistency for all respondents to a specific value and calculate the average predicted probabilities. For each draw from the sampling distribution I then calculate the expected distance.

50 Carmines and Stimson Reference Carmines and Stimson1980; Jessee Reference Jessee2010; Knight Reference Knight1985; Lavine and Gschwend Reference Lavine and Gschwend2006; Wyckoff (Reference Wyckoff1980).

51 Matthews Reference Matthews1979; Rabinowitz and Macdonald Reference Rabinowitz and Macdonald1989.

52 Rivers Reference Rivers1988, 738.

53 Benoit and Laver Reference Benoit and Laver2006; Klar Reference Klar2014; Shafer and Claggett Reference Shafer and Claggett1995; Treier and Hillygus Reference Treier and Hillygus2009.

54 See, e.g., Mutz, Brody, and Sniderman Reference Mutz, Brody and Sniderman1996.

References

Achen, Christopher H. 1975. Mass Political Attitudes and the Survey Response. The American Political Science Review 69 (4):1219–1231.Google Scholar
Adams, James, Merrill, Samuel, and Grofman, Bernard. 2005. A Unified Theory of Party Competition: A Cross-National Analysis Integrating Spatial and Behavioral Factors. New York and Cambridge: Cambridge University Press.Google Scholar
Ai, Chunrong, and Norton, Edward C.. 2003. Interaction Terms in Logit and Probit Models. Economics Letters 80 (1):123–129.Google Scholar
Ansolabehere, Stephen, Rodden, Jonathan, and Snyder, James M.. 2008. The Strength of Issues: Using Multiple Measures to Gauge Preference Stability, Ideological Constraint, and Issue Voting. American Political Science Review 102 (2):215–232.Google Scholar
Axelrod, Robert, and Cohen, Michael. 1984. Harnessing Complexity: Organizational Implications of a Scientific Frontier. New York: Free Press.Google Scholar
Bartels, Larry M. 1986. Issue Voting Under Uncertainty: An Empirical Test. American Journal of Political Science 30 (4):709–728.Google Scholar
Bartels, Larry M.. 2003. Democracy with Attitudes. In Electoral Democracy, edited by Michael B. MacKuen and George Rabinowitz, 48–82. Ann Arbor: University of Michigan Press.Google Scholar
Barton, Allen H., and Parsons, R. Wayne. 1977. Measuring Belief System Structure. Public Opinion Quarterly 41 (2):159–180.Google Scholar
Benoit, Kenneth, and Laver, Michael. 2006. Party Policy in Modern Democracies. London: Routledge.Google Scholar
Berinsky, Adam J., and Lewis, Jeffrey. 2007. An Estimate of Risk Aversion in the US Electorate. Quarterly Journal of Political Science 2 (2):139–154.Google Scholar
Berry, William D., DeMeritt, Jacqueline H., and Esarey, Justin. 2010. Testing for Interaction in Binary Logit and Probit Models: Is a Product Term Essential? American Journal of Political Science 54 (1):248–266.Google Scholar
Calvert, Randall L. 1985. The Value of Biased Information: A Rational Choice Model of Political Advice. The Journal of Politics 47 (2):530–555.Google Scholar
Carmines, Edward G., and Stimson, James A.. 1980. The Two Faces of Issue Voting. The American Political Science Review 74 (1):78–91.Google Scholar
Converse, Philip E. 1964. The Nature of Belief Systems in the Mass Public. In Ideology and Discontent, edited by D. E. Apter, 206–261. New York: Free Press.Google Scholar
Cyert, Richard M., and DeGroot, Morris H.. 1987. Bayesian Analysis and Uncertainty in Economic Theory. Rowman & Littlefield.Google Scholar
Downs, Anthony. 1957. An Economic Theory of Political Action in a Democracy. New York: Harper and Row.Google Scholar
Enelow, James, and Hinich, Melvin J.. 1981. A New Approach to Voter Uncertainty in the Downsian Spatial Model. American Journal of Political Science 25 (3):483–493.Google Scholar
Feldman, Stanley. 1988. Structure and Consistency in Public Opinion: The Role of Core Beliefs and Values. American Journal of Political Science 32 (2):416–440.Google Scholar
Gerber, Elisabeth R., and Jackson, John E.. 1993. Endogenous Preferences and the Study of Institutions. American Political Science Review 87 (3):639–656.Google Scholar
Hanmer, Michael J., and K, Kerem Ozan. 2013. Behind the Curve: Clarifying the Best Approach to Calculating Predicted Probabilities and Marginal Effects from Limited Dependent Variable Models. American Journal of Political Science 57 (1):263–277.Google Scholar
Hill, Jennifer L., and Kriesi, Hanspeter. 2001. An Extension and Test of Converse’s Black-and-White Model of Response Stability. The American Political Science Review 95 (2):397–413.Google Scholar
Jackson, John E. 1983. The Systematic Beliefs of the Mass Public: Estimating Policy Preferences with Survey Data. The Journal of Politics 45 (4):840–865.Google Scholar
Jacoby, William G. 1991. Ideological Identification and Issue Attitudes. American Journal of Political Science 35 (1):178–205.Google Scholar
Jacoby, William G. 1995. The Structure of Ideological Thinking in the American Electorate. American Journal of Political Science 39 (2):314–335.Google Scholar
Jessee, Stephen A. 2009. Spatial Voting in the 2004 Presidential Election. American Political Science Review 103 (01):59–81.Google Scholar
Jessee, Stephen A. 2010. Partisan Bias, Political Information and Spatial Voting in the 2008 Presidential Election. The Journal of Politics 72 (2):327.Google Scholar
Kedar, Orit. 2005. When Moderate Voters Prefer Extreme Parties: Policy Balancing in Parliamentary Elections. American Political Science Review 99 (2):185–199.Google Scholar
Kinder, Donald R. 1998. Communication and Opinion. Annual Review of Political Science 1 (1):167–197.Google Scholar
King, Gary, Tomz, Michael, and Wittenberg, Jason. 2000. Making the Most of Statistical Analyses: Improving Interpretation and Presentation. American Journal of Political Science 44 (2):347–361.Google Scholar
Klar, Samara. 2014. A Multidimensional Study of Ideological Preferences and Priorities among the American Public. Public Opinion Quarterly 78 (S1):344–359.Google Scholar
Knight, Kathleen. 1985. Ideology in the 1980 Election: Ideological Sophistication Does Matter. Journal of Politics 47 (3):828–853.Google Scholar
Lauderdale, Benjamin E. 2010. Unpredictable Voters in Ideal Point Estimation. Political Analysis 18 (2):151–171.Google Scholar
Lavine, Howard, and Gschwend, Thomas. 2006. Issues, Party and Character: The Moderating Role of Ideological Thinking on Candidate Evaluation. British Journal of Political Science 37 (01):139.Google Scholar
Matthews, Steven A. 1979. A Simple Direction Model of Electoral Competition. Public Choice 34 (2):141–156.Google Scholar
Moskowitz, Adam N., and Jenkins, J. Craig. 2004. Structuring Political Opinions: Attitude Consistency and Democratic Competence among the US Mass. The Sociological Quarterly 45 (3):395–419.Google Scholar
Mutz, Diana C., Brody, Richard A, and Sniderman, Paul M. 1996. Political persuasion and attitude change. Ann Arbor: University of Michigan Press.Google Scholar
Quinn, Kevin M, Martin, Andrew D., and Whitford, Andrew B.. 1999. Voter Choice in Multi-Party Democracies: A Test of Competing Theories and Models. American Journal of Political Science 43 (4):1231–1247.Google Scholar
Rabinowitz, George, and Macdonald, Stuart E.. 1989. A Directional Theory of Issue Voting. The American Political Science Review 83 (1):93–121.Google Scholar
RePass, David E. 1971. Issue Salience and Party Choice. The American Political Science Review 65 (2):389–400.Google Scholar
Rivers, Douglas. 1988. Heterogeneity in Models of Electoral Choice. American Journal of Political Science 32 (3):737–757.Google Scholar
Schofield, Norman, and Zakharov, Alexei. 2009. A Stochastic Model of the 2007 Russian Duma Election. Public Choice 142 (1–2):177–194.Google Scholar
Schofield, Norman, Martin, Andrew D., Quinn, Kevin M., and Whitford, Andrew B.. 1998. Multiparty Electoral Competition in the Netherlands and Germany: A Model Based on Multinomial Probit. Public Choice 97 (2):257–293.Google Scholar
Shafer, Byron E., and Claggett, William J.. 1995. The Two Majorities: The Issue Context of American Politics. Baltimore, MD: Johns Hopkins University Press.Google Scholar
Stoetzer, Lukas F., and Zittlau, Steffen. 2015. Multidimensional Spatial Voting with Non-Separable Preferences. Political Analysis 23:415–428.Google Scholar
Stoetzer, Lukas. 2017. Replication Data for: A matter of representation: spatial voting and inconsistent policy preferences, doi:10.7910/DVN/J0G6K3, Harvard Dataverse, V1.Google Scholar
The American National Election Studies (ANES). 2008. 2008-2009 Panel Study [dataset]. Stanford, CA and Ann Arbor, MI: Stanford University and the University of Michigan.Google Scholar
Treier, Shawn, and Hillygus, Sunshine D.. 2009. The Nature of Political Ideology in the Contemporary Electorate. Public Opinion Quarterly 73 (4):679–703.Google Scholar
Westholm, Anders. 1997. Distance Versus Direction: The Illusory Defeat of the Proximity Theory of Electoral Choice. The American Policital Science Review 91 (4):865–883.Google Scholar
Wyckoff, Mikel L. 1980. Belief System Constraint and Policy Voting: A Test of the Unidimensional Consistency Model. Political Behavior 2 (2):115–146.Google Scholar
Ye, Min, Li, Quan, and Leiker, Kyle W.. 2011. Evaluating Voter–Candidate Proximity in a Non-Euclidean Space. Journal of Elections, Public Opinion & Parties 21 (4):497–521.Google Scholar
Zaller, John R. 1992. The Nature and Origins of Mass Opinion. Cambridge University Press.Google Scholar
Figure 0

Fig. 1 A spatial representation of citizens’ policy beliefs Note: the figure shows policy beliefs of two voters about their ideal policy platform. The voters differ in their mean belief $x_{i} $, but also in their belief variance $\sigma _{{{\rm \Theta }_{i} }}^{2} $. The second voter holds a wider belief variance, compared to the first, and is thereby less certain about the ideal policy platform.

Figure 1

Fig. 2 Parameter estimates for policy-weighted model using perceived (black) and mean distance (grey) to candidate platform Note: the figure shows point estimates as well as 95 per cent and 99 per cent confidence intervals for the direct effect of policy distance and interaction effect with inconsistency.

Figure 2

Fig. 3 Marginal effect of policy distance on difference in expected utility for varying levels of inconsistency Note: the left panel shows the marginal effect for mean candidate positions, the right panel for perceived candidate distance. The lines on the x-axis show the distribution of inconsistency in the sample.

Figure 3

Fig. 4 Probability to vote for Obama by policy distance to obama minus distance to McCain simulated from mean platform model Note: the left panel shows the voting probabilities for a respondent with consistent policy preferences (value correspondent to the median value in the sample). The right panel shows the voting probabilities for respondent with inconsistent policy preferences (value correspondent to the 95 per cent quantile in the sample).

Figure 4

Fig. 5 Average expected distance for varying degrees of inconsistency Note: the x-axis shows the expected distance to a respondent's representative. Values of zero imply that a voter is expected to share the same position with the candidate she intends to vote for. Decreasing values indicate a stronger expected distance.

Supplementary material: Link

Stoetzer Dataset

Datasets

http://dx.doi.org/10.7910/DVN/J0G6K3
Link
Supplementary material: PDF

Stoetzer supplementary material

Appendix

Download Stoetzer supplementary material(PDF)
PDF 284.7 KB