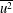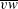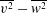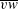1 Introduction
Three-dimensional wall jets are formed when a fluid flows from a finite width opening tangentially along a wall, as shown in figure 1. Wall jets have a diverse range of engineering applications, among which are included the cooling of gas turbine combustor walls, ventilation systems, and flow under dam sluice gates and over spillways. The three-dimensional wall jet is normally characterized by taking profiles along the jet centreline and across the jet at
![]() $y_{max}$
, the height of the maximum velocity point,
$y_{max}$
, the height of the maximum velocity point,
![]() $U_{max}$
(as shown in figure 1
a). One of the most noteworthy features of a three-dimensional wall jet is that the growth of the lateral half-width is five to eight times greater than the vertical half-width in the far field (e.g. Davis & Winarto Reference Davis and Winarto1980; Launder & Rodi Reference Launder and Rodi1983; Padmanabham & Gowda Reference Padmanabham and Gowda1991a
,Reference Padmanabham and Gowda
b
; Abrahamsson, Johansson & Lofdahl Reference Abrahamsson, Johansson and Lofdahl1997b
; Venas et al.
Reference Venas, Abrahamsson, Krogsad and Lofdahl1999; Craft & Launder Reference Craft and Launder2001; Sun Reference Sun2002; Sun & Ewing Reference Sun and Ewing2002b
; Hall & Ewing Reference Hall and Ewing2007b
; Agelinchaab & Tachie Reference Agelinchaab and Tachie2011; Namgyal Reference Namgyal2012).
$U_{max}$
(as shown in figure 1
a). One of the most noteworthy features of a three-dimensional wall jet is that the growth of the lateral half-width is five to eight times greater than the vertical half-width in the far field (e.g. Davis & Winarto Reference Davis and Winarto1980; Launder & Rodi Reference Launder and Rodi1983; Padmanabham & Gowda Reference Padmanabham and Gowda1991a
,Reference Padmanabham and Gowda
b
; Abrahamsson, Johansson & Lofdahl Reference Abrahamsson, Johansson and Lofdahl1997b
; Venas et al.
Reference Venas, Abrahamsson, Krogsad and Lofdahl1999; Craft & Launder Reference Craft and Launder2001; Sun Reference Sun2002; Sun & Ewing Reference Sun and Ewing2002b
; Hall & Ewing Reference Hall and Ewing2007b
; Agelinchaab & Tachie Reference Agelinchaab and Tachie2011; Namgyal Reference Namgyal2012).

Figure 1. (a) Schematic and nomenclature for a three-dimensional wall and (b) experimental set-up showing the laser and PIV camera arrangement.
The cause of the large lateral growth of turbulent three-dimensional wall jets is not fully understood; Launder & Rodi (Reference Launder and Rodi1983) noted that the large lateral growth had to be related to mean secondary flows in the jet, and examined the governing equations for the transport of mean streamwise vorticity for steady incompressible flow:
 $$\begin{eqnarray}\displaystyle \underbrace{\frac{\text{D}\overline{{\it\Omega}}_{x}}{\text{D}t}}_{A} & = & \displaystyle \underbrace{\overline{{\it\Omega}}_{x}\frac{\partial \overline{U}}{\partial x}}_{B}+\underbrace{\overline{{\it\Omega}}_{y}\frac{\partial \overline{U}}{\partial y}+\overline{{\it\Omega}}_{z}\frac{\partial \overline{U}}{\partial z}}_{C}+\underbrace{\frac{\partial ^{2}}{\partial y\partial z}(\overline{v^{2}}-\overline{w^{2}})}_{D}+\underbrace{\left(\frac{\partial ^{2}}{\partial z^{2}}-\frac{\partial ^{2}}{\partial y^{2}}\right)\overline{vw}}_{E}\nonumber\\ \displaystyle & & \displaystyle +\,\underbrace{v\left(\frac{\partial ^{2}{\it\Omega}_{x}}{\partial x^{2}}+\frac{\partial ^{2}\overline{{\it\Omega}}_{x}}{\partial y^{2}}+\frac{\partial ^{2}\overline{{\it\Omega}}_{x}}{\partial z^{2}}\right)}_{F},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \underbrace{\frac{\text{D}\overline{{\it\Omega}}_{x}}{\text{D}t}}_{A} & = & \displaystyle \underbrace{\overline{{\it\Omega}}_{x}\frac{\partial \overline{U}}{\partial x}}_{B}+\underbrace{\overline{{\it\Omega}}_{y}\frac{\partial \overline{U}}{\partial y}+\overline{{\it\Omega}}_{z}\frac{\partial \overline{U}}{\partial z}}_{C}+\underbrace{\frac{\partial ^{2}}{\partial y\partial z}(\overline{v^{2}}-\overline{w^{2}})}_{D}+\underbrace{\left(\frac{\partial ^{2}}{\partial z^{2}}-\frac{\partial ^{2}}{\partial y^{2}}\right)\overline{vw}}_{E}\nonumber\\ \displaystyle & & \displaystyle +\,\underbrace{v\left(\frac{\partial ^{2}{\it\Omega}_{x}}{\partial x^{2}}+\frac{\partial ^{2}\overline{{\it\Omega}}_{x}}{\partial y^{2}}+\frac{\partial ^{2}\overline{{\it\Omega}}_{x}}{\partial z^{2}}\right)}_{F},\end{eqnarray}$$
where
![]() $A$
is the transport of streamwise vorticity;
$A$
is the transport of streamwise vorticity;
![]() $B$
is the streamwise amplification of mean vorticity by vortex stretching;
$B$
is the streamwise amplification of mean vorticity by vortex stretching;
![]() $C$
is the vorticity production by vortex-line bending;
$C$
is the vorticity production by vortex-line bending;
![]() $D$
is the vorticity production by gradients in the cross-flow Reynolds normal stresses;
$D$
is the vorticity production by gradients in the cross-flow Reynolds normal stresses;
![]() $E$
is the vorticity production by gradients in the cross-flow Reynolds shear stress;
$E$
is the vorticity production by gradients in the cross-flow Reynolds shear stress;
![]() $F$
is the viscous diffusion of vorticity;
$F$
is the viscous diffusion of vorticity;
![]() $\overline{{\it\Omega}_{x}}$
is the mean streamwise vorticity;
$\overline{{\it\Omega}_{x}}$
is the mean streamwise vorticity;
![]() $\overline{{\it\Omega}_{y}}$
is the mean normal vorticity;
$\overline{{\it\Omega}_{y}}$
is the mean normal vorticity;
![]() $\overline{{\it\Omega}_{z}}$
is the mean lateral vorticity;
$\overline{{\it\Omega}_{z}}$
is the mean lateral vorticity;
![]() $\overline{u^{2}}$
,
$\overline{u^{2}}$
,
![]() $\overline{v^{2}}$
and
$\overline{v^{2}}$
and
![]() $\overline{w^{2}}$
are the Reynolds normal stress;
$\overline{w^{2}}$
are the Reynolds normal stress;
![]() $\overline{vw}$
is the Reynolds shear stress;
$\overline{vw}$
is the Reynolds shear stress;
![]() $\overline{U}$
is the mean streamwise velocity;
$\overline{U}$
is the mean streamwise velocity;
![]() $v$
is the kinematic viscosity;
$v$
is the kinematic viscosity;
![]() $x$
is the streamwise coordinate;
$x$
is the streamwise coordinate;
![]() $y$
is the vertical coordinate; and
$y$
is the vertical coordinate; and
![]() $z$
is the lateral coordinate.
$z$
is the lateral coordinate.
Launder & Rodi (Reference Launder and Rodi1983) stated that one possible source of streamwise vorticity in the three-dimensional wall jet was due to the vortex-line bending (term
![]() $C$
). They suggested that this causes the formation of the two counter-rotating regions of mean streamwise vorticity on either side of the jet centreline in the far field. These regions were thought to drive the mean flow down towards the wall and eject it laterally outward, thereby causing the large lateral spreading. Many experimental studies have found evidence of mean streamwise vorticity like that proposed by Launder & Rodi (Reference Launder and Rodi1983), although, in general, the oppositely signed regions of mean streamwise vorticity on either side of the jet centreline have tended to be side by side, as opposed to on top of one another (Matsuda, Iida & Hayakawa Reference Matsuda, Iida and Hayakawa1990; Sun & Ewing Reference Sun and Ewing2002a
; Hall & Ewing Reference Hall and Ewing2005a
,Reference Hall and Ewing
b
, Reference Hall and Ewing2006, Reference Hall and Ewing2007a
, Reference Hall and Ewing2010; Namgyal & Hall Reference Namgyal and Hall2011). These regions of mean streamwise vorticity have also tended to be closer to the wall than
$C$
). They suggested that this causes the formation of the two counter-rotating regions of mean streamwise vorticity on either side of the jet centreline in the far field. These regions were thought to drive the mean flow down towards the wall and eject it laterally outward, thereby causing the large lateral spreading. Many experimental studies have found evidence of mean streamwise vorticity like that proposed by Launder & Rodi (Reference Launder and Rodi1983), although, in general, the oppositely signed regions of mean streamwise vorticity on either side of the jet centreline have tended to be side by side, as opposed to on top of one another (Matsuda, Iida & Hayakawa Reference Matsuda, Iida and Hayakawa1990; Sun & Ewing Reference Sun and Ewing2002a
; Hall & Ewing Reference Hall and Ewing2005a
,Reference Hall and Ewing
b
, Reference Hall and Ewing2006, Reference Hall and Ewing2007a
, Reference Hall and Ewing2010; Namgyal & Hall Reference Namgyal and Hall2011). These regions of mean streamwise vorticity have also tended to be closer to the wall than
![]() $U_{max}$
, so the profiles measured across the jet at
$U_{max}$
, so the profiles measured across the jet at
![]() $y_{max}$
, as typically done, would offer little information about the secondary flow.
$y_{max}$
, as typically done, would offer little information about the secondary flow.
Launder & Rodi (Reference Launder and Rodi1983) also suggested that the mean streamwise vorticity could be generated because of gradients in the Reynolds stresses (terms
![]() $D$
and
$D$
and
![]() $E$
). They argued that the production of mean streamwise vorticity due to gradients in the normal stresses (term
$E$
). They argued that the production of mean streamwise vorticity due to gradients in the normal stresses (term
![]() $D$
) should be of the same order as the vortex-tilting terms and should act to reinforce the secondary flow due to vortex tilting in the far field. Later, Craft & Launder (Reference Craft and Launder2001) numerically examined the three-dimensional wall jet and noted that a similar vortex-tilting process should occur in the laminar jet to that in the turbulent case. They modelled the laminar jet and found that the lateral growth was significantly less than in the turbulent case. From this, they argued that the vortex-tilting process alone was not sufficient to cause the large lateral spreading that occurs in the turbulent wall jet, and thus it must be due to gradients in the Reynolds stresses.
$D$
) should be of the same order as the vortex-tilting terms and should act to reinforce the secondary flow due to vortex tilting in the far field. Later, Craft & Launder (Reference Craft and Launder2001) numerically examined the three-dimensional wall jet and noted that a similar vortex-tilting process should occur in the laminar jet to that in the turbulent case. They modelled the laminar jet and found that the lateral growth was significantly less than in the turbulent case. From this, they argued that the vortex-tilting process alone was not sufficient to cause the large lateral spreading that occurs in the turbulent wall jet, and thus it must be due to gradients in the Reynolds stresses.
Unfortunately, little information exists about the Reynolds stress distribution in the three-dimensional wall jet, in particular
![]() $\overline{vw}$
,
$\overline{vw}$
,
![]() $\overline{v^{2}}$
and
$\overline{v^{2}}$
and
![]() $\overline{w^{2}}$
. Despite the widespread attention paid to the three-dimensional wall jet, there have been no previous investigations that have measured the full Reynolds stress tensor throughout the wall jet. Many studies have used hot-wire anemometry to examine the turbulent profiles on the jet centreline and at
$\overline{w^{2}}$
. Despite the widespread attention paid to the three-dimensional wall jet, there have been no previous investigations that have measured the full Reynolds stress tensor throughout the wall jet. Many studies have used hot-wire anemometry to examine the turbulent profiles on the jet centreline and at
![]() $y_{max}$
(e.g. Davis & Winarto Reference Davis and Winarto1980; Padmanabham & Gowda Reference Padmanabham and Gowda1991a
,Reference Padmanabham and Gowda
b
; Abrahamsson et al.
Reference Abrahamsson, Johansson and Lofdahl1997b
; Venas et al.
Reference Venas, Abrahamsson, Krogsad and Lofdahl1999; Sun Reference Sun2002; Sun & Ewing Reference Sun and Ewing2002b
; Hall & Ewing Reference Hall and Ewing2007b
); however, these studies did not measure all of the components of the Reynolds stress tensor. Particle image velocimetry has been used in the three-dimensional wall jet by Agelinchaab & Tachie (Reference Agelinchaab and Tachie2011), although the measurements they presented were confined to the jet centreline or profiles at
$y_{max}$
(e.g. Davis & Winarto Reference Davis and Winarto1980; Padmanabham & Gowda Reference Padmanabham and Gowda1991a
,Reference Padmanabham and Gowda
b
; Abrahamsson et al.
Reference Abrahamsson, Johansson and Lofdahl1997b
; Venas et al.
Reference Venas, Abrahamsson, Krogsad and Lofdahl1999; Sun Reference Sun2002; Sun & Ewing Reference Sun and Ewing2002b
; Hall & Ewing Reference Hall and Ewing2007b
); however, these studies did not measure all of the components of the Reynolds stress tensor. Particle image velocimetry has been used in the three-dimensional wall jet by Agelinchaab & Tachie (Reference Agelinchaab and Tachie2011), although the measurements they presented were confined to the jet centreline or profiles at
![]() $y_{max}$
. Full flow field measurements have been performed in the full cross-flow plane using hot-wire anemometry (Matsuda et al.
Reference Matsuda, Iida and Hayakawa1990; Sun & Ewing Reference Sun and Ewing2002b
; Hall & Ewing Reference Hall and Ewing2007a
,Reference Hall and Ewing
b
), but these measurements only measured the mean streamwise velocity or a few components of the Reynolds stress tensor.
$y_{max}$
. Full flow field measurements have been performed in the full cross-flow plane using hot-wire anemometry (Matsuda et al.
Reference Matsuda, Iida and Hayakawa1990; Sun & Ewing Reference Sun and Ewing2002b
; Hall & Ewing Reference Hall and Ewing2007a
,Reference Hall and Ewing
b
), but these measurements only measured the mean streamwise velocity or a few components of the Reynolds stress tensor.
In the present paper, stereoscopic PIV is used for computing these stresses to improve our understanding of the distribution of the Reynolds stresses and in turn the secondary flow in the three-dimensional wall jet.
2 Experimental set-up
The air flow to the jet was supplied by a 4.5 kW single-stage centrifugal blower. The flow was conditioned using a
![]() $0.9~\text{m}\times 0.9~\text{m}\times 0.9~\text{m}$
settling chamber which had three 10 mm screens. The flow from the settling chamber then passed through a flow straightener placed inside a 0.20 m diameter pipe. Finally, the air flowed through a contoured nozzle with an area ratio of 28 : 1 and a diameter of 38.1 mm. The nozzle had a fifth-order polynomial profile so as to yield a top-hat exit velocity profile with less than 0.25 % turbulence intensity. For all measurements, the jet Reynolds number at the outlet was set to 250 000. Upon exiting the nozzle the air flowed tangentially along a
$0.9~\text{m}\times 0.9~\text{m}\times 0.9~\text{m}$
settling chamber which had three 10 mm screens. The flow from the settling chamber then passed through a flow straightener placed inside a 0.20 m diameter pipe. Finally, the air flowed through a contoured nozzle with an area ratio of 28 : 1 and a diameter of 38.1 mm. The nozzle had a fifth-order polynomial profile so as to yield a top-hat exit velocity profile with less than 0.25 % turbulence intensity. For all measurements, the jet Reynolds number at the outlet was set to 250 000. Upon exiting the nozzle the air flowed tangentially along a
![]() $2.49~\text{m}\times 2.08~\text{m}$
horizontal wall forming the three-dimensional wall jet.
$2.49~\text{m}\times 2.08~\text{m}$
horizontal wall forming the three-dimensional wall jet.
The velocity field was acquired using a LaVision Stereoscopic PIV system. Both the laser and the cameras were arranged as shown in figure 1(b). The flow and surrounding air were seeded using olive oil droplets generated by a Laskin type atomizer. This produced a mean particle diameter of
![]() $3~{\rm\mu}\text{m}$
. A Solo 120XT Nd–Yag laser having a pulse energy of 120 mJ was used to illuminate the flow. The images from the tracer particles were acquired by a pair of 12 bit CCD cameras (LaVision Imager Intense) with a resolution of
$3~{\rm\mu}\text{m}$
. A Solo 120XT Nd–Yag laser having a pulse energy of 120 mJ was used to illuminate the flow. The images from the tracer particles were acquired by a pair of 12 bit CCD cameras (LaVision Imager Intense) with a resolution of
![]() $1376\times 1040$
pixels. The double frame instantaneous images were processed using LaVision Flow Manager (DaVis 7.2 version). In the data processing, multi-pass decreasing interrogation window sizes from
$1376\times 1040$
pixels. The double frame instantaneous images were processed using LaVision Flow Manager (DaVis 7.2 version). In the data processing, multi-pass decreasing interrogation window sizes from
![]() $64\times 64$
pixels to
$64\times 64$
pixels to
![]() $32\times 32$
pixels with 75 % overlap were adopted and a normalized correlation function was used, and then the processed data were reconstructed using the Whittaker algorithm (Whittaker Reference Whittaker1915; LaVision 2007).
$32\times 32$
pixels with 75 % overlap were adopted and a normalized correlation function was used, and then the processed data were reconstructed using the Whittaker algorithm (Whittaker Reference Whittaker1915; LaVision 2007).
In order to have statistically converged data, the following number of independent pairs of images were taken at various downstream locations; 3000 image pairs up to
![]() $x/D=15$
, 4500 at
$x/D=15$
, 4500 at
![]() $x/D=20$
, 5100 at
$x/D=20$
, 5100 at
![]() $x/D=30$
and 6000 at
$x/D=30$
and 6000 at
![]() $x/D=40$
. Only one half of the jet could be measured at
$x/D=40$
. Only one half of the jet could be measured at
![]() $x/D=40$
due to limitations in the laser source, so statistics for one half of the jet were computed at this position. Since every vector field could be considered as an independent event due to the time lag between the image pairs, the uncertainties at 95 % confidence level associated with the mean streamwise velocity at the centre of the jet at
$x/D=40$
due to limitations in the laser source, so statistics for one half of the jet were computed at this position. Since every vector field could be considered as an independent event due to the time lag between the image pairs, the uncertainties at 95 % confidence level associated with the mean streamwise velocity at the centre of the jet at
![]() $y_{max}$
and at
$y_{max}$
and at
![]() $y_{1/2}$
were determined to be within 0.14–0.76 % and 1.04–1.55 % respectively. The uncertainties in estimating
$y_{1/2}$
were determined to be within 0.14–0.76 % and 1.04–1.55 % respectively. The uncertainties in estimating
![]() $\overline{U}$
and some of the quantities of interest are also included in table 1.
$\overline{U}$
and some of the quantities of interest are also included in table 1.
Table 1. Uncertainty in the estimators of
![]() $\overline{U}$
,
$\overline{U}$
,
![]() $u$
,
$u$
,
![]() $\overline{vw}$
and
$\overline{vw}$
and
![]() $(\overline{v^{2}}-\overline{w^{2}})$
at 95 % confidence level (due to sampling time) at
$(\overline{v^{2}}-\overline{w^{2}})$
at 95 % confidence level (due to sampling time) at
![]() $y_{max}$
.
$y_{max}$
.

3 Experimental results
The jet development can be characterized by examining the decay of the local maximum mean streamwise velocity, as shown in figure 2. The measurements are compared with those of Sun (Reference Sun2002) (contoured nozzle) and Hall & Ewing (Reference Hall and Ewing2007b
) (long channel). Here,
![]() $U_{max}$
is normalized by the mean outlet velocity for the contoured nozzle jets and by the bulk velocity at the jet outlet for the channel jets. The
$U_{max}$
is normalized by the mean outlet velocity for the contoured nozzle jets and by the bulk velocity at the jet outlet for the channel jets. The
![]() $x$
coordinate is normalized by
$x$
coordinate is normalized by
![]() $D$
for the circular jets and
$D$
for the circular jets and
![]() $\sqrt{A}$
for the channel jets; this parameter was shown by Rajaratnam & Pani (Reference Rajaratnam and Pani1974) and Hall & Ewing (Reference Hall and Ewing2007b
) to collapse the streamwise development of three-dimensional wall jets issuing from non-circular channels.
$\sqrt{A}$
for the channel jets; this parameter was shown by Rajaratnam & Pani (Reference Rajaratnam and Pani1974) and Hall & Ewing (Reference Hall and Ewing2007b
) to collapse the streamwise development of three-dimensional wall jets issuing from non-circular channels.

Figure 2. The decay of the local maximum streamwise velocity of the wall jet: (●) present investigation,
![]() $(+)$
$(+)$
![]() $A_{r}=1$
and (▵)
$A_{r}=1$
and (▵)
![]() $A_{r}=4$
channel jets by Hall & Ewing (Reference Hall and Ewing2007b
), and (*) contoured nozzle by Sun (Reference Sun2002).
$A_{r}=4$
channel jets by Hall & Ewing (Reference Hall and Ewing2007b
), and (*) contoured nozzle by Sun (Reference Sun2002).
At
![]() $x/D=5$
, the local maximum velocity is still equal to the exit velocity. This indicates the persistence of the jet potential core at this location. Downstream at
$x/D=5$
, the local maximum velocity is still equal to the exit velocity. This indicates the persistence of the jet potential core at this location. Downstream at
![]() $x/D=10$
, the mean velocity drops off considerably, showing that the collapse of the potential core has occurred by this point, which signifies the onset of the intermediate field. Further downstream, the jet velocity continues to decay due to the entrainment of ambient air, as expected. The present investigation shows reasonable agreement with Sun (Reference Sun2002), and the minor differences here can probably be attributed to the different jet Reynolds numbers. The local maximum streamwise velocity measured by Hall & Ewing (Reference Hall and Ewing2007b
) decays slightly faster than for the current results, in particular in the near-field region. This behaviour is due to the long channel exit condition used by Hall and Ewing, and the known slower development of channel jets compared with contoured nozzles (Hall & Ewing Reference Hall and Ewing2007b
).
$x/D=10$
, the mean velocity drops off considerably, showing that the collapse of the potential core has occurred by this point, which signifies the onset of the intermediate field. Further downstream, the jet velocity continues to decay due to the entrainment of ambient air, as expected. The present investigation shows reasonable agreement with Sun (Reference Sun2002), and the minor differences here can probably be attributed to the different jet Reynolds numbers. The local maximum streamwise velocity measured by Hall & Ewing (Reference Hall and Ewing2007b
) decays slightly faster than for the current results, in particular in the near-field region. This behaviour is due to the long channel exit condition used by Hall and Ewing, and the known slower development of channel jets compared with contoured nozzles (Hall & Ewing Reference Hall and Ewing2007b
).
The development of the three-dimensional wall jet is next characterized by examining the streamwise variation of the vertical and lateral half-widths, as shown in figures 3(a) and 3(b) respectively. These results are compared with the half-widths measured by Sun & Ewing (Reference Sun and Ewing2002b
). The variations in the vertical half-width agree well with the data of Sun & Ewing (Reference Sun and Ewing2002b
), but the lateral half-widths measured here are slightly lower, particularly in the far-field region. A least-square linear fit of the vertical half-width yields a vertical growth rate of 0.041, which is close to the consensus value determined by Launder & Rodi (Reference Launder and Rodi1983) (0.048). The streamwise variation of the normalized lateral half-width was not linear, so a fourth-order polynomial function was fitted to the data, as shown in figure 3(b). The lateral half-width determined in the region
![]() $30\leqslant x/D\leqslant 40$
was 5.6 times the vertical half-width, agreeing with the value of 5.5 determined by Hall & Ewing (Reference Hall and Ewing2007b
) but slightly higher than the value reported by Sun & Ewing (Reference Sun and Ewing2002b
).
$30\leqslant x/D\leqslant 40$
was 5.6 times the vertical half-width, agreeing with the value of 5.5 determined by Hall & Ewing (Reference Hall and Ewing2007b
) but slightly higher than the value reported by Sun & Ewing (Reference Sun and Ewing2002b
).

Figure 3. (a) The streamwise development of the vertical half-width in a three-dimensional wall jet: (○) present investigation, (●) Sun (Reference Sun2002) and (—) least-square linear fit. (b) The streamwise development of the lateral half-width in a three-dimensional wall jet: (○) present investigation, (●) Sun (Reference Sun2002) and (—) fourth-order polynomial fit.
To set the context for the secondary flow and Reynolds stress results, all three components of the mean velocity field are examined in figures 4–6. All of the mean velocity contours are normalized by the local maximum streamwise velocity,
![]() $U_{max}$
, and the respective jet half-width. A comparison of the streamwise evolution of the normalized mean streamwise velocity is shown at all downstream locations in figure 4. The contours indicate that the jet starts off round and that the lateral growth of the jet is observed to start near the wall. As the flow evolves downstream, the contours of the mean streamwise velocity begin to bulge more at the wall and begin to take on the characteristic wall jet shape, loosely approaching a self-similar shape at
$U_{max}$
, and the respective jet half-width. A comparison of the streamwise evolution of the normalized mean streamwise velocity is shown at all downstream locations in figure 4. The contours indicate that the jet starts off round and that the lateral growth of the jet is observed to start near the wall. As the flow evolves downstream, the contours of the mean streamwise velocity begin to bulge more at the wall and begin to take on the characteristic wall jet shape, loosely approaching a self-similar shape at
![]() $x/D=30$
. These results are quite similar to contours of the mean flow acquired by Matsuda et al. (Reference Matsuda, Iida and Hayakawa1990), Sun & Ewing (Reference Sun and Ewing2002b
) and Hall & Ewing (Reference Hall and Ewing2007a
).
$x/D=30$
. These results are quite similar to contours of the mean flow acquired by Matsuda et al. (Reference Matsuda, Iida and Hayakawa1990), Sun & Ewing (Reference Sun and Ewing2002b
) and Hall & Ewing (Reference Hall and Ewing2007a
).
As shown in figure 6, the bulging in the mean streamwise velocity near the wall is accompanied by large lateral velocities that persist near the wall on either side of the jet centreline (figure 6). Near the wall, these lateral velocities are oriented to eject flow laterally outward. The strength of the lateral flow relative to
![]() $U_{max}$
increases as the jet evolves downstream, reaching approximately 14 % of
$U_{max}$
increases as the jet evolves downstream, reaching approximately 14 % of
![]() $U_{max}$
, which is consistent with the known increase in lateral growth as the jet develops from the near field to the far field (e.g. Sun Reference Sun2002). It should also be noted that these large lateral velocities tend to be strongest below
$U_{max}$
, which is consistent with the known increase in lateral growth as the jet develops from the near field to the far field (e.g. Sun Reference Sun2002). It should also be noted that these large lateral velocities tend to be strongest below
![]() $y_{max}$
, traversing in the
$y_{max}$
, traversing in the
![]() $z$
direction, and at this height would underestimate the mean lateral velocities.
$z$
direction, and at this height would underestimate the mean lateral velocities.
The normalized contours of
![]() $\overline{V}$
, shown in figure 5, also vary significantly as the jet evolves downstream. In the near field, at
$\overline{V}$
, shown in figure 5, also vary significantly as the jet evolves downstream. In the near field, at
![]() $x/D=5$
, the velocity at the centre of the jet is positive, indicating that the jet is on average growing away from the wall, whereas in the shear layers around the jet, the velocities are negative, indicating that the flow is directed downward. The negative velocities are probably associated with the downward entrainment of ambient air. The region of large negative velocity tends to grow and surround the small region of positive
$x/D=5$
, the velocity at the centre of the jet is positive, indicating that the jet is on average growing away from the wall, whereas in the shear layers around the jet, the velocities are negative, indicating that the flow is directed downward. The negative velocities are probably associated with the downward entrainment of ambient air. The region of large negative velocity tends to grow and surround the small region of positive
![]() $\overline{V}$
as the flow evolves downstream, suggesting that as the jet develops downstream, the flow is overwhelmingly drawing the surrounding fluid down towards the wall. Taken together, the contours of
$\overline{V}$
as the flow evolves downstream, suggesting that as the jet develops downstream, the flow is overwhelmingly drawing the surrounding fluid down towards the wall. Taken together, the contours of
![]() $\overline{V}$
and
$\overline{V}$
and
![]() $\overline{W}$
suggest that this downward mean flow probably supplies the strongly lateral outward mean flow.
$\overline{W}$
suggest that this downward mean flow probably supplies the strongly lateral outward mean flow.

Figure 4. The normalized mean streamwise velocity,
![]() $\overline{U}/U_{max}$
, at various downstream locations: (a)
$\overline{U}/U_{max}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.

Figure 5. The normalized mean velocity normal to the wall,
![]() $\overline{V}/U_{max}$
, at various downstream locations: (a)
$\overline{V}/U_{max}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.

Figure 6. The normalized mean lateral velocity,
![]() $\overline{W}/U_{max}$
, at various downstream locations: (a)
$\overline{W}/U_{max}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.
Jet development is often characterized by examining the mass flow rate,
and momentum flux of the jet,
These values have been determined in free jets by Panchapakesan & Lumley (Reference Panchapakesan and Lumley1993), Hussein, Capp & George (Reference Hussein, Capp and George1994) and Tinney, Glauser & Ukeiley (Reference Tinney, Glauser and Ukeiley2008) but have never been used in the three-dimensional wall jet, mostly due to a lack of high-density full flow field measurements like those here. The streamwise variation of the mass entrainment ratio,
![]() $(Q-Q_{o})/Q_{o}$
, is shown in figure 7(a), where
$(Q-Q_{o})/Q_{o}$
, is shown in figure 7(a), where
![]() $Q_{o}$
is the mass flow rate at the nozzle outlet. The current results are compared with those in a free jet exiting from a round sharp-edged orifice (Quinn Reference Quinn2005). In both cases, the entrainment of air increases linearly with the downstream distance; however, the entrainment values for the wall jet are approximately one half of those for the free jet. This reduced entrainment is not unexpected because the presence of the wall reduces the surface area for which the jet can entrain ambient fluid.
$Q_{o}$
is the mass flow rate at the nozzle outlet. The current results are compared with those in a free jet exiting from a round sharp-edged orifice (Quinn Reference Quinn2005). In both cases, the entrainment of air increases linearly with the downstream distance; however, the entrainment values for the wall jet are approximately one half of those for the free jet. This reduced entrainment is not unexpected because the presence of the wall reduces the surface area for which the jet can entrain ambient fluid.
The variation of the momentum flux ratio,
![]() $M/M_{o}$
, where
$M/M_{o}$
, where
![]() $M_{o}$
is the outlet momentum flux, is shown in figure 7(b). For a free jet, it is well known that mean momentum is conserved throughout the jet (Capp, Hussien & George Reference Capp, Hussien and George1990; Hussein et al.
Reference Hussein, Capp and George1994; Tinney et al.
Reference Tinney, Glauser and Ukeiley2008), while here the momentum flux decreases as the jet evolves downstream. This is due to momentum being lost to the wall. This decrease is significantly larger than the momentum flux variation observed in a two-dimensional plane wall jet by Eriksson, Karlsson & Persson (Reference Eriksson, Karlsson and Persson1998). This can probably be attributed to the (obvious) enhanced three-dimensionality (and associated near-wall turbulence) of the present flow over a two-dimensional wall jet.
$M_{o}$
is the outlet momentum flux, is shown in figure 7(b). For a free jet, it is well known that mean momentum is conserved throughout the jet (Capp, Hussien & George Reference Capp, Hussien and George1990; Hussein et al.
Reference Hussein, Capp and George1994; Tinney et al.
Reference Tinney, Glauser and Ukeiley2008), while here the momentum flux decreases as the jet evolves downstream. This is due to momentum being lost to the wall. This decrease is significantly larger than the momentum flux variation observed in a two-dimensional plane wall jet by Eriksson, Karlsson & Persson (Reference Eriksson, Karlsson and Persson1998). This can probably be attributed to the (obvious) enhanced three-dimensionality (and associated near-wall turbulence) of the present flow over a two-dimensional wall jet.

Figure 7. (a) Mass entrainment into the jet: (●) present investigation (contoured nozzle) and (*) sharp-edged slot round jet by Quinn (Reference Quinn2005). (b) Momentum flux of the jet: (●) present investigation and (▵) two-dimensional plane wall jet by Eriksson et al. (Reference Eriksson, Karlsson and Persson1998).
Profiles of the Reynolds stresses measured on the jet centreline are shown in figure 8. The results have been normalized by the square of the local maximum streamwise velocity,
![]() $U_{max}^{2}$
, and
$U_{max}^{2}$
, and
![]() $y_{1/2}$
. At
$y_{1/2}$
. At
![]() $x/D=40$
, the current Reynolds stress measurements,
$x/D=40$
, the current Reynolds stress measurements,
![]() $\overline{vv}$
and
$\overline{vv}$
and
![]() $\overline{uv}$
, are compared with the results of Abrahamsson et al. (Reference Abrahamsson, Johansson and Lofdahl1997b
) (
$\overline{uv}$
, are compared with the results of Abrahamsson et al. (Reference Abrahamsson, Johansson and Lofdahl1997b
) (
![]() $\overline{vv}$
and
$\overline{vv}$
and
![]() $\overline{uv}$
) and Venas et al. (Reference Venas, Abrahamsson, Krogsad and Lofdahl1999) (
$\overline{uv}$
) and Venas et al. (Reference Venas, Abrahamsson, Krogsad and Lofdahl1999) (
![]() $\overline{uv}$
). The results indicate good agreement with the present measurement near the wall, but show some differences in the outer regions. This is probably due to the known underprediction of conventional hot-wire measurements when the local turbulence intensity is high, like in the outer region of the wall jet. This underprediction of conventional hot-wire measurements in the outer region of both two- and three-dimensional wall jets has been previously discussed by Venas et al. (Reference Venas, Abrahamsson, Krogsad and Lofdahl1999) and was also discussed by Namgyal & Hall (Reference Namgyal and Hall2010) in the three-dimensional wall jet measured using two-dimensional PIV.
$\overline{uv}$
). The results indicate good agreement with the present measurement near the wall, but show some differences in the outer regions. This is probably due to the known underprediction of conventional hot-wire measurements when the local turbulence intensity is high, like in the outer region of the wall jet. This underprediction of conventional hot-wire measurements in the outer region of both two- and three-dimensional wall jets has been previously discussed by Venas et al. (Reference Venas, Abrahamsson, Krogsad and Lofdahl1999) and was also discussed by Namgyal & Hall (Reference Namgyal and Hall2010) in the three-dimensional wall jet measured using two-dimensional PIV.

Figure 8. Profiles of the normalized Reynolds stresses measured at the jet centreline for various streamwise locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
,(e)
$x/D=20$
,(e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
; (●)
$x/D=40$
; (●)
![]() $\overline{uu}$
, (▪)
$\overline{uu}$
, (▪)
![]() $\overline{vv}$
, (▫)
$\overline{vv}$
, (▫)
![]() $\overline{vv}$
(Abrahamsson et al.
Reference Abrahamsson, Johansson and Lofdahl1997b
),
$\overline{vv}$
(Abrahamsson et al.
Reference Abrahamsson, Johansson and Lofdahl1997b
),
![]() $(+)$
$(+)$
![]() $\overline{ww}$
, (▴)
$\overline{ww}$
, (▴)
![]() $\overline{uv}$
, (▵)
$\overline{uv}$
, (▵)
![]() $\overline{uv}$
(Abrahamsson et al.
Reference Abrahamsson, Johansson and Lofdahl1997b
), (♢)
$\overline{uv}$
(Abrahamsson et al.
Reference Abrahamsson, Johansson and Lofdahl1997b
), (♢)
![]() $\overline{uv}$
(Venas et al.
Reference Venas, Abrahamsson, Krogsad and Lofdahl1999), (○)
$\overline{uv}$
(Venas et al.
Reference Venas, Abrahamsson, Krogsad and Lofdahl1999), (○)
![]() $\overline{uw}$
and
$\overline{uw}$
and
![]() $(\times )$
$(\times )$
![]() $\overline{vw}$
.
$\overline{vw}$
.
Throughout the jet,
![]() $\overline{u^{2}}$
makes the largest contribution to the Reynolds stresses at all downstream positions; this is again due to the much larger value of
$\overline{u^{2}}$
makes the largest contribution to the Reynolds stresses at all downstream positions; this is again due to the much larger value of
![]() $\overline{U}$
than
$\overline{U}$
than
![]() $\overline{V}$
or
$\overline{V}$
or
![]() $\overline{W}$
(Namgyal Reference Namgyal2012). More details on the mean and fluctuating velocities can be found in Namgyal (Reference Namgyal2012). The profiles of the normal stresses,
$\overline{W}$
(Namgyal Reference Namgyal2012). More details on the mean and fluctuating velocities can be found in Namgyal (Reference Namgyal2012). The profiles of the normal stresses,
![]() $\overline{v^{2}}$
and
$\overline{v^{2}}$
and
![]() $\overline{w^{2}}$
, at the jet centreline indicate that initially in the near-field region at
$\overline{w^{2}}$
, at the jet centreline indicate that initially in the near-field region at
![]() $x/D=5$
,
$x/D=5$
,
![]() $\overline{w^{2}}$
is dominant over
$\overline{w^{2}}$
is dominant over
![]() $\overline{v^{2}}$
, both near the wall and in the outer region around
$\overline{v^{2}}$
, both near the wall and in the outer region around
![]() $y/y_{1/2}=0.8$
to 1.3 (figure 8
a). However, as the flow progresses downstream, the magnitudes of both
$y/y_{1/2}=0.8$
to 1.3 (figure 8
a). However, as the flow progresses downstream, the magnitudes of both
![]() $\overline{v^{2}}$
and
$\overline{v^{2}}$
and
![]() $\overline{w^{2}}$
become nearly equal in the outer region, while
$\overline{w^{2}}$
become nearly equal in the outer region, while
![]() $\overline{w^{2}}$
still remains dominant over
$\overline{w^{2}}$
still remains dominant over
![]() $\overline{v^{2}}$
in the region close to the wall (figure 8
e,f). These results suggest that the near-wall anisotropy of the turbulence is not an artefact of the potential core, and seems to be characteristic of intermediate and far-field jet development.
$\overline{v^{2}}$
in the region close to the wall (figure 8
e,f). These results suggest that the near-wall anisotropy of the turbulence is not an artefact of the potential core, and seems to be characteristic of intermediate and far-field jet development.

Figure 9. Profiles of the normalized Reynolds stresses measured across the jet at
![]() $y_{max}$
for various streamwise locations: (a)
$y_{max}$
for various streamwise locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
; (●)
$x/D=40$
; (●)
![]() $\overline{uu}$
, (▪)
$\overline{uu}$
, (▪)
![]() $\overline{vv}$
,
$\overline{vv}$
,
![]() $(+)$
$(+)$
![]() $\overline{ww}$
, ( ▲ )
$\overline{ww}$
, ( ▲ )
![]() $\overline{uv}$
, (○)
$\overline{uv}$
, (○)
![]() $\overline{uw}$
and
$\overline{uw}$
and
![]() $(\times )$
$(\times )$
![]() $\overline{vw}$
.
$\overline{vw}$
.
At
![]() $x/D=5$
, the values of
$x/D=5$
, the values of
![]() $\overline{uv}$
in the outer shear layer are comparable to
$\overline{uv}$
in the outer shear layer are comparable to
![]() $\overline{v^{2}}$
but are much larger than
$\overline{v^{2}}$
but are much larger than
![]() $\overline{vw}$
or
$\overline{vw}$
or
![]() $\overline{uw}$
, whereas the values of
$\overline{uw}$
, whereas the values of
![]() $\overline{uv}$
are negative close to the wall in the inner shear layer. By
$\overline{uv}$
are negative close to the wall in the inner shear layer. By
![]() $x/D=15$
, the negative near-wall peak in
$x/D=15$
, the negative near-wall peak in
![]() $\overline{uv}$
dissipates and the largest values of
$\overline{uv}$
dissipates and the largest values of
![]() $\overline{uv}$
tend to occur in the outer shear layer at approximately
$\overline{uv}$
tend to occur in the outer shear layer at approximately
![]() $y/y_{1/2}=0.8$
but get slightly lower as the jet evolves downstream to approximately
$y/y_{1/2}=0.8$
but get slightly lower as the jet evolves downstream to approximately
![]() $y/y_{1/2}=0.75$
. This is in reasonable agreement with Sun (Reference Sun2002), who found that
$y/y_{1/2}=0.75$
. This is in reasonable agreement with Sun (Reference Sun2002), who found that
![]() $\overline{uv}$
peaked at a height of approximately
$\overline{uv}$
peaked at a height of approximately
![]() $y/y_{1/2}=0.7$
by
$y/y_{1/2}=0.7$
by
![]() $x/D=90$
. Both the shear stresses,
$x/D=90$
. Both the shear stresses,
![]() $\overline{uw}$
and
$\overline{uw}$
and
![]() $\overline{vw}$
, are quite small compared with the other Reynolds stresses at the jet centreline at all streamwise locations. This is probably related to the negligible
$\overline{vw}$
, are quite small compared with the other Reynolds stresses at the jet centreline at all streamwise locations. This is probably related to the negligible
![]() $\overline{W}$
values on the jet centreline.
$\overline{W}$
values on the jet centreline.
The Reynolds stress profiles measured across the jet at
![]() $y_{max}$
are shown in figure 9, normalized by
$y_{max}$
are shown in figure 9, normalized by
![]() $z_{1/2}$
and
$z_{1/2}$
and
![]() $U_{max}^{2}$
. Initially, at
$U_{max}^{2}$
. Initially, at
![]() $x/D=5$
, the Reynolds stresses are the largest at
$x/D=5$
, the Reynolds stresses are the largest at
![]() $z_{1/2}$
in the lateral shear layers. The relative magnitudes of
$z_{1/2}$
in the lateral shear layers. The relative magnitudes of
![]() $\overline{u^{2}}$
are the largest, followed by
$\overline{u^{2}}$
are the largest, followed by
![]() $\overline{v^{2}}$
then
$\overline{v^{2}}$
then
![]() $\overline{w^{2}}$
. Unlike on the jet centreline, the
$\overline{w^{2}}$
. Unlike on the jet centreline, the
![]() $\overline{uw}$
shear stresses are now comparable to
$\overline{uw}$
shear stresses are now comparable to
![]() $\overline{w^{2}}$
, whereas the magnitudes of
$\overline{w^{2}}$
, whereas the magnitudes of
![]() $\overline{uv}$
and
$\overline{uv}$
and
![]() $\overline{vw}$
are small. By
$\overline{vw}$
are small. By
![]() $x/D=10$
, the
$x/D=10$
, the
![]() $\overline{w^{2}}$
values begin to become comparable to
$\overline{w^{2}}$
values begin to become comparable to
![]() $\overline{v^{2}}$
, and eventually overtake the
$\overline{v^{2}}$
, and eventually overtake the
![]() $\overline{v^{2}}$
values at the middle of the jet at
$\overline{v^{2}}$
values at the middle of the jet at
![]() $x/D=15$
. This behaviour is probably due to the establishment of relatively larger lateral mean velocities in the jet at this point (Namgyal Reference Namgyal2012). The values of
$x/D=15$
. This behaviour is probably due to the establishment of relatively larger lateral mean velocities in the jet at this point (Namgyal Reference Namgyal2012). The values of
![]() $\overline{uv}$
are small and positive but are significantly larger than the
$\overline{uv}$
are small and positive but are significantly larger than the
![]() $\overline{vw}$
shear stress across the jet.
$\overline{vw}$
shear stress across the jet.
The profiles of the Reynolds stresses point to a fairly complicated spatial variation in the Reynolds stresses. The physics of the flow and the relationship between the Reynolds stresses can be better understood by examining contours of the full flow field. Contours of the Reynolds stresses measured in the
![]() $y{-}z$
plane are shown in figures 10–15. All of the stress contours are normalized by
$y{-}z$
plane are shown in figures 10–15. All of the stress contours are normalized by
![]() $U_{max}^{2}$
and the respective jet half-widths.
$U_{max}^{2}$
and the respective jet half-widths.

Figure 10. The normalized Reynolds normal stress,
![]() $\overline{u^{2}}/U_{max}^{2}$
, at various downstream locations: (a)
$\overline{u^{2}}/U_{max}^{2}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.
The normal stress contours at
![]() $x/D=5$
have a prominent low-intensity circular region at the centre of the jet, indicating the existence of a potential core region at this location (i.e. figures 10
a, 11
a and 12
a). As expected, the largest Reynolds normal stresses occur around the periphery of the jet in the outer shear layer, but by
$x/D=5$
have a prominent low-intensity circular region at the centre of the jet, indicating the existence of a potential core region at this location (i.e. figures 10
a, 11
a and 12
a). As expected, the largest Reynolds normal stresses occur around the periphery of the jet in the outer shear layer, but by
![]() $x/D=10$
, the largest normal stresses tend to be located at the centre of the jet. The magnitudes of the normalized normal stresses are still increasing at
$x/D=10$
, the largest normal stresses tend to be located at the centre of the jet. The magnitudes of the normalized normal stresses are still increasing at
![]() $x/D=40$
, indicating that the flow is not self-similar by this point, consistent with the discussion of Craft & Launder (Reference Craft and Launder2001), who suggested that the turbulent three-dimensional wall jet may not truly become self-similar until
$x/D=40$
, indicating that the flow is not self-similar by this point, consistent with the discussion of Craft & Launder (Reference Craft and Launder2001), who suggested that the turbulent three-dimensional wall jet may not truly become self-similar until
![]() $x/D>100$
.
$x/D>100$
.

Figure 11. The normalized Reynolds normal stress,
![]() $\overline{v^{2}}/U_{max}^{2}$
, at various downstream locations: (a)
$\overline{v^{2}}/U_{max}^{2}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.

Figure 12. The normalized Reynolds normal stress,
![]() $\overline{w^{2}}/U_{max}^{2}$
, at various downstream locations: (a)
$\overline{w^{2}}/U_{max}^{2}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.

Figure 13. The normalized Reynolds shear stress,
![]() $\overline{uv}/U_{max}^{2}$
, at various downstream locations: (a)
$\overline{uv}/U_{max}^{2}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.
The downstream evolution of the turbulent shear stresses,
![]() $\overline{uv}$
, is shown in figure 13. Initially, there is a negative region near the wall and a positive region associated with the outer shear layer. Positive
$\overline{uv}$
, is shown in figure 13. Initially, there is a negative region near the wall and a positive region associated with the outer shear layer. Positive
![]() $\overline{uv}$
terms commonly occur in the free shear layers of jets and have been observed by several authors in the three-dimensional wall jet (Padmanabham & Gowda Reference Padmanabham and Gowda1991b
; Abrahamsson, Johansson & Lofdahl Reference Abrahamsson, Johansson and Lofdahl1997a
; Sun Reference Sun2002). This outer positive region may be associated with the passage of a spanwise vorticity,
$\overline{uv}$
terms commonly occur in the free shear layers of jets and have been observed by several authors in the three-dimensional wall jet (Padmanabham & Gowda Reference Padmanabham and Gowda1991b
; Abrahamsson, Johansson & Lofdahl Reference Abrahamsson, Johansson and Lofdahl1997a
; Sun Reference Sun2002). This outer positive region may be associated with the passage of a spanwise vorticity,
![]() $\overline{{\it\Omega}}_{z}$
, which causes an event that drives the flow down and downstream (or up and upstream). The negative region is associated with the inner wall layer, consistent with the sign of
$\overline{{\it\Omega}}_{z}$
, which causes an event that drives the flow down and downstream (or up and upstream). The negative region is associated with the inner wall layer, consistent with the sign of
![]() $\overline{uv}$
observed in a boundary layer (Tachie Reference Tachie2000), near the wall in an impinging jet (Cooper et al.
Reference Cooper, Jackson, Launder and Liau1993) and in a plane wall jet (Eriksson et al.
Reference Eriksson, Karlsson and Persson1998; Rostamy et al.
Reference Rostamy, Bergstrom, Sumner and Bugg2011). The negative near-wall region may be related to an event that causes a streamwise backflow and an ejection of fluid away from the wall, like the passage of a spanwise oriented vortex structure (
$\overline{uv}$
observed in a boundary layer (Tachie Reference Tachie2000), near the wall in an impinging jet (Cooper et al.
Reference Cooper, Jackson, Launder and Liau1993) and in a plane wall jet (Eriksson et al.
Reference Eriksson, Karlsson and Persson1998; Rostamy et al.
Reference Rostamy, Bergstrom, Sumner and Bugg2011). The negative near-wall region may be related to an event that causes a streamwise backflow and an ejection of fluid away from the wall, like the passage of a spanwise oriented vortex structure (
![]() $\overline{{\it\Omega}}_{z}$
). As the flow evolves downstream, the outer positive region grows and suppresses the small negative region towards the jet centreline and down to the wall. This is consistent with the decrease of
$\overline{{\it\Omega}}_{z}$
). As the flow evolves downstream, the outer positive region grows and suppresses the small negative region towards the jet centreline and down to the wall. This is consistent with the decrease of
![]() $y_{max}$
noted at this point. By
$y_{max}$
noted at this point. By
![]() $x/D=30$
, there is no evidence of the negative region in the measurements; however, it is unclear whether this region has disappeared or has simply moved closer to the wall. Eriksson & Karlsson (Reference Eriksson and Karlsson2000) performed near-wall laser doppler anemometry measurements for the plane turbulent wall jet and showed that a large negative value of
$x/D=30$
, there is no evidence of the negative region in the measurements; however, it is unclear whether this region has disappeared or has simply moved closer to the wall. Eriksson & Karlsson (Reference Eriksson and Karlsson2000) performed near-wall laser doppler anemometry measurements for the plane turbulent wall jet and showed that a large negative value of
![]() $\overline{uv}$
persists near the wall and has a local minima at
$\overline{uv}$
persists near the wall and has a local minima at
![]() $y^{+}=10$
. Of course, we cannot resolve this close to the wall with our PIV measurements, so this suggests that there is probably an unresolved region of strong
$y^{+}=10$
. Of course, we cannot resolve this close to the wall with our PIV measurements, so this suggests that there is probably an unresolved region of strong
![]() $\overline{uv}$
near the wall.
$\overline{uv}$
near the wall.
The contours of the turbulent shear stress,
![]() $\overline{uw}$
, shown in figure 14, initially start out concentrated on either side of the jet centreline with opposite sign. These regions may be associated with a turbulent event that drives the flow into the streamwise direction and laterally outward, like a vertically oriented vortex (
$\overline{uw}$
, shown in figure 14, initially start out concentrated on either side of the jet centreline with opposite sign. These regions may be associated with a turbulent event that drives the flow into the streamwise direction and laterally outward, like a vertically oriented vortex (
![]() $\overline{{\it\Omega}}_{y}$
) (consistent with coherent structure models in the jet (Namgyal Reference Namgyal2012)). As the flow evolves downstream to
$\overline{{\it\Omega}}_{y}$
) (consistent with coherent structure models in the jet (Namgyal Reference Namgyal2012)). As the flow evolves downstream to
![]() $x/D=10$
and then 15, these regions become wider, but by
$x/D=10$
and then 15, these regions become wider, but by
![]() $x/D=30$
, they start to evolve downward towards the wall. This may be tied to the increasing large mean lateral velocities that persist near the wall in the jet.
$x/D=30$
, they start to evolve downward towards the wall. This may be tied to the increasing large mean lateral velocities that persist near the wall in the jet.

Figure 14. The normalized Reynolds shear stress,
![]() $\overline{uw}/U_{max}^{2}$
, at various downstream locations: (a)
$\overline{uw}/U_{max}^{2}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.
The downstream variation of the
![]() $\overline{vw}$
contours is shown in figure 15. Initially, these regions are organized in four oppositely signed regions at
$\overline{vw}$
contours is shown in figure 15. Initially, these regions are organized in four oppositely signed regions at
![]() $x/D=5$
. The reason for this behaviour is unclear, although this term has been linked with the presence of streamwise vortices in free jets (Bradshaw Reference Bradshaw1987). As the flow evolves downstream, for example to
$x/D=5$
. The reason for this behaviour is unclear, although this term has been linked with the presence of streamwise vortices in free jets (Bradshaw Reference Bradshaw1987). As the flow evolves downstream, for example to
![]() $x/D=15$
and 20, the upper two regions tend to diffuse outward and the lower two regions tend to get pushed down towards the wall. However, the relative magnitude of
$x/D=15$
and 20, the upper two regions tend to diffuse outward and the lower two regions tend to get pushed down towards the wall. However, the relative magnitude of
![]() $\overline{vw}$
tends to decrease rapidly as the jet develops downstream. By
$\overline{vw}$
tends to decrease rapidly as the jet develops downstream. By
![]() $x/D=30$
and 40, these regions become hard to distinguish due to the low magnitudes. These results suggests that
$x/D=30$
and 40, these regions become hard to distinguish due to the low magnitudes. These results suggests that
![]() $\overline{vw}$
plays only a minor role in the far-field development of the three-dimensional wall jet.
$\overline{vw}$
plays only a minor role in the far-field development of the three-dimensional wall jet.

Figure 15. The normalized Reynolds shear stress,
![]() $\overline{vw}/U_{max}^{2}$
, at various downstream locations: (a)
$\overline{vw}/U_{max}^{2}$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.
In order to understand the behaviour of the mean secondary flow in the three-dimensional turbulent wall jet, the distribution of the mean streamwise vorticity,
![]() $\overline{{\it\Omega}}_{x}$
, is examined for various streamwise locations in figure 16. At
$\overline{{\it\Omega}}_{x}$
, is examined for various streamwise locations in figure 16. At
![]() $x/D=5$
, the contours of
$x/D=5$
, the contours of
![]() $\overline{{\it\Omega}}_{x}$
are dominated by a pair of oppositely signed regions located on either side of the jet centreline in the lateral shear layers (i.e. figure 16
a). These regions correspond to the location of the near-wall bulging of the mean streamwise velocity contours, indicating that the streamwise vorticity is directly tied to the lateral growth of the flow, as expected. As the jet evolves further downstream, the outer regions of streamwise vorticity become more diffuse and begin to move away from the wall, consistent with the finding previously reported by Matsuda et al. (Reference Matsuda, Iida and Hayakawa1990), Sun & Ewing (Reference Sun and Ewing2002b
) and Hall & Ewing (Reference Hall and Ewing2007a
). These regions are oriented to drive the flow down towards the wall and laterally outward. The inner regions of near-wall vorticity tend to spread outward along the wall, for example at
$\overline{{\it\Omega}}_{x}$
are dominated by a pair of oppositely signed regions located on either side of the jet centreline in the lateral shear layers (i.e. figure 16
a). These regions correspond to the location of the near-wall bulging of the mean streamwise velocity contours, indicating that the streamwise vorticity is directly tied to the lateral growth of the flow, as expected. As the jet evolves further downstream, the outer regions of streamwise vorticity become more diffuse and begin to move away from the wall, consistent with the finding previously reported by Matsuda et al. (Reference Matsuda, Iida and Hayakawa1990), Sun & Ewing (Reference Sun and Ewing2002b
) and Hall & Ewing (Reference Hall and Ewing2007a
). These regions are oriented to drive the flow down towards the wall and laterally outward. The inner regions of near-wall vorticity tend to spread outward along the wall, for example at
![]() $x/D=20$
to 40; this behaviour has been attributed to the vortex tilting in the outer leg of the large-scale structures by Sun & Ewing (Reference Sun and Ewing2002b
).
$x/D=20$
to 40; this behaviour has been attributed to the vortex tilting in the outer leg of the large-scale structures by Sun & Ewing (Reference Sun and Ewing2002b
).

Figure 16. The mean streamwise vorticity,
![]() $\overline{{\it\Omega}}_{x}~(1~\text{s}^{-1})$
, at various downstream locations: (a)
$\overline{{\it\Omega}}_{x}~(1~\text{s}^{-1})$
, at various downstream locations: (a)
![]() $x/D=5$
, (b)
$x/D=5$
, (b)
![]() $x/D=10$
, (c)
$x/D=10$
, (c)
![]() $x/D=15$
, (d)
$x/D=15$
, (d)
![]() $x/D=20$
, (e)
$x/D=20$
, (e)
![]() $x/D=30$
and (f)
$x/D=30$
and (f)
![]() $x/D=40$
.
$x/D=40$
.
In order to improve our understanding of the sources of the turbulence generated secondary flow in the jet and the relative size of terms
![]() $D$
and
$D$
and
![]() $E$
in (1.1), profiles of the difference in the Reynolds normal stresses, (
$E$
in (1.1), profiles of the difference in the Reynolds normal stresses, (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) are compared with the Reynolds shear stress,
$\overline{v^{2}}-\overline{w^{2}}$
) are compared with the Reynolds shear stress,
![]() $\overline{vw}$
, on the jet centreline in figure 17. At
$\overline{vw}$
, on the jet centreline in figure 17. At
![]() $x/D=5$
and 10, the profiles of (
$x/D=5$
and 10, the profiles of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) have two peaks located in the inner and outer shear-layer regions (figure 17
a), and the contribution is significantly larger than
$\overline{v^{2}}-\overline{w^{2}}$
) have two peaks located in the inner and outer shear-layer regions (figure 17
a), and the contribution is significantly larger than
![]() $\overline{vw}$
. The peak in (
$\overline{vw}$
. The peak in (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) associated with the outer shear layers decreases, and by
$\overline{v^{2}}-\overline{w^{2}}$
) associated with the outer shear layers decreases, and by
![]() $x/D=40$
, (
$x/D=40$
, (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) becomes negligible and comparable in magnitude to
$\overline{v^{2}}-\overline{w^{2}}$
) becomes negligible and comparable in magnitude to
![]() $\overline{vw}$
away from the wall. However, near the wall (
$\overline{vw}$
away from the wall. However, near the wall (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) continues to dominate at all downstream locations. It is apparent that the
$\overline{v^{2}}-\overline{w^{2}}$
) continues to dominate at all downstream locations. It is apparent that the
![]() $y$
gradient of (
$y$
gradient of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) is much steeper near the wall.
$\overline{v^{2}}-\overline{w^{2}}$
) is much steeper near the wall.

Figure 17. Profiles of the cross-flow Reynolds stresses, (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) and
$\overline{v^{2}}-\overline{w^{2}}$
) and
![]() $\overline{vw}$
$\overline{vw}$
![]() $(\text{m}^{2}~\text{s}^{-2})$
, measured at the jet centreline for various streamwise locations: (a)
$(\text{m}^{2}~\text{s}^{-2})$
, measured at the jet centreline for various streamwise locations: (a)
![]() $x/D=5$
to 15 and (b)
$x/D=5$
to 15 and (b)
![]() $x/D=20$
to 40. The filled symbols represent
$x/D=20$
to 40. The filled symbols represent
![]() $(\overline{v^{2}}-\overline{w^{2}})$
and the empty symbols represent
$(\overline{v^{2}}-\overline{w^{2}})$
and the empty symbols represent
![]() $\overline{vw}$
: (▸) and (▹)
$\overline{vw}$
: (▸) and (▹)
![]() $x/D=5$
, (●) and (○)
$x/D=5$
, (●) and (○)
![]() $x/D=10$
, (▪) and (▫)
$x/D=10$
, (▪) and (▫)
![]() $x/D=15$
, (▵) and (▴)
$x/D=15$
, (▵) and (▴)
![]() $x/D=20$
, (▿) and (▾)
$x/D=20$
, (▿) and (▾)
![]() $x/D=30$
, and (♢) and (♦)
$x/D=30$
, and (♢) and (♦)
![]() $x/D=40$
.
$x/D=40$
.
A similar comparison is made for the Reynolds stresses, (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) and
$\overline{v^{2}}-\overline{w^{2}}$
) and
![]() $\overline{vw}$
, measured across one half of the jet at
$\overline{vw}$
, measured across one half of the jet at
![]() $y_{max}$
, as shown in figure 18. Initially, the profiles of (
$y_{max}$
, as shown in figure 18. Initially, the profiles of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) have large peaks at
$\overline{v^{2}}-\overline{w^{2}}$
) have large peaks at
![]() $z/z_{1/2}=1$
in the lateral shear layers. As the jet develops downstream to
$z/z_{1/2}=1$
in the lateral shear layers. As the jet develops downstream to
![]() $x/D=40$
, this peak becomes negligible. Moreover, at all locations, (
$x/D=40$
, this peak becomes negligible. Moreover, at all locations, (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) is significantly larger than
$\overline{v^{2}}-\overline{w^{2}}$
) is significantly larger than
![]() $\overline{vw}$
. Although the turbulence secondary flow is strictly tied to the spatial gradients of these terms, these results suggest that the difference in the normal stresses makes a much larger contribution than
$\overline{vw}$
. Although the turbulence secondary flow is strictly tied to the spatial gradients of these terms, these results suggest that the difference in the normal stresses makes a much larger contribution than
![]() $\overline{vw}$
.
$\overline{vw}$
.

Figure 18. Profiles of the cross-flow Reynolds stresses, (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) and
$\overline{v^{2}}-\overline{w^{2}}$
) and
![]() $\overline{vw}$
$\overline{vw}$
![]() $(\text{m}^{2}~\text{s}^{-2})$
, measured parallel across the wall at
$(\text{m}^{2}~\text{s}^{-2})$
, measured parallel across the wall at
![]() $y_{max}$
: (a)
$y_{max}$
: (a)
![]() $x/D=5$
to 15 and (b)
$x/D=5$
to 15 and (b)
![]() $x/D=20$
to 40. The filled symbols represent
$x/D=20$
to 40. The filled symbols represent
![]() $(\overline{v^{2}}-\overline{w^{2}})$
and the empty symbols represent
$(\overline{v^{2}}-\overline{w^{2}})$
and the empty symbols represent
![]() $\overline{vw}$
: (▸) and (▹)
$\overline{vw}$
: (▸) and (▹)
![]() $x/D=5$
, (●) and (○)
$x/D=5$
, (●) and (○)
![]() $x/D=10$
, (▪) and (▫)
$x/D=10$
, (▪) and (▫)
![]() $x/D=15$
, (▵) and (▴)
$x/D=15$
, (▵) and (▴)
![]() $x/D=20$
, (▿) and (▾)
$x/D=20$
, (▿) and (▾)
![]() $x/D=30$
, and (♢) and (♦)
$x/D=30$
, and (♢) and (♦)
![]() $x/D=40$
.
$x/D=40$
.

Figure 19. Comparison of the normalized cross-flow Reynolds stresses,
![]() $\overline{vw}//U_{max}^{2}$
and
$\overline{vw}//U_{max}^{2}$
and
![]() $(\overline{v^{2}}-\overline{w^{2}})/U_{max}^{2}$
, at various streamwise locations: (a,b)
$(\overline{v^{2}}-\overline{w^{2}})/U_{max}^{2}$
, at various streamwise locations: (a,b)
![]() $x/D=5$
, (c,d)
$x/D=5$
, (c,d)
![]() $x/D=10$
, (e,f)
$x/D=10$
, (e,f)
![]() $x/D=15$
, (g,h)
$x/D=15$
, (g,h)
![]() $x/D=20$
, (i,j)
$x/D=20$
, (i,j)
![]() $x/D=30$
and (k,l)
$x/D=30$
and (k,l)
![]() $x/D=40$
.
$x/D=40$
.
Profiles of these two terms are useful to get a feel for the magnitude and trend associated with these terms, but a better representation of the size and total distribution of these terms can be gained by examining the contours of the full flow field. Contours of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) and
$\overline{v^{2}}-\overline{w^{2}}$
) and
![]() $\overline{vw}$
are shown in figure 19. For the purpose of comparing the relative magnitudes, both terms are plotted on the same contour level and are normalized by the square of the local maximum streamwise velocity,
$\overline{vw}$
are shown in figure 19. For the purpose of comparing the relative magnitudes, both terms are plotted on the same contour level and are normalized by the square of the local maximum streamwise velocity,
![]() $U_{max}^{2}$
. Initially, at
$U_{max}^{2}$
. Initially, at
![]() $x/D=5$
, the contours of (
$x/D=5$
, the contours of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) have local maxima in the lateral shear layers and minima near the wall and in the outer shear layers. By
$\overline{v^{2}}-\overline{w^{2}}$
) have local maxima in the lateral shear layers and minima near the wall and in the outer shear layers. By
![]() $x/D=15$
, the large negative region of (
$x/D=15$
, the large negative region of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) spans the wall and persists as the jet evolves downstream, suggesting that its contribution does not decrease into the far field. At all downstream measurement locations, the contours indicate that the magnitude of (
$\overline{v^{2}}-\overline{w^{2}}$
) spans the wall and persists as the jet evolves downstream, suggesting that its contribution does not decrease into the far field. At all downstream measurement locations, the contours indicate that the magnitude of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) is much larger than that of
$\overline{v^{2}}-\overline{w^{2}}$
) is much larger than that of
![]() $\overline{vw}$
, particularly near the wall, although the magnitudes of (
$\overline{vw}$
, particularly near the wall, although the magnitudes of (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) and
$\overline{v^{2}}-\overline{w^{2}}$
) and
![]() $\overline{vw}$
are comparable away from the wall. This finding is also consistent with the findings of Brundrett & Baines (Reference Brundrett and Baines1964), who examined the turbulent generated mean secondary flows that persist in a square duct due to the corners, and with Xu (Reference Xu2009), who examined the mean secondary flows in a square annular duct flow. (It should be noted that the turbulent generated secondary flow in a square or rectangular duct causes a flow that is directed into the corners of a square duct. Unlike a square duct flow, the three-dimensional wall jet is unconfined, so the mean secondary flows influence the growth of the jet.) Both found that differences in the normal stresses were dominant near the wall. In fact, the relative magnitude of
$\overline{vw}$
are comparable away from the wall. This finding is also consistent with the findings of Brundrett & Baines (Reference Brundrett and Baines1964), who examined the turbulent generated mean secondary flows that persist in a square duct due to the corners, and with Xu (Reference Xu2009), who examined the mean secondary flows in a square annular duct flow. (It should be noted that the turbulent generated secondary flow in a square or rectangular duct causes a flow that is directed into the corners of a square duct. Unlike a square duct flow, the three-dimensional wall jet is unconfined, so the mean secondary flows influence the growth of the jet.) Both found that differences in the normal stresses were dominant near the wall. In fact, the relative magnitude of
![]() $\overline{vw}$
here seems to decrease as the jet evolves downstream, which suggests from a magnitude perspective only and not a gradient perspective that the relative importance of this term in the production of the turbulence generated secondary flow decreases into the far field. This again indicates that the differences in the cross-flow normal stresses are (from a magnitude perspective only) likely to be primarily responsible for the production of streamwise vorticity. The magnitude of the term is, by far, the highest near the wall.
$\overline{vw}$
here seems to decrease as the jet evolves downstream, which suggests from a magnitude perspective only and not a gradient perspective that the relative importance of this term in the production of the turbulence generated secondary flow decreases into the far field. This again indicates that the differences in the cross-flow normal stresses are (from a magnitude perspective only) likely to be primarily responsible for the production of streamwise vorticity. The magnitude of the term is, by far, the highest near the wall.
To truly quantify the actual sources of the turbulence generated secondary flow, information is required about the double spatial gradients of each of these terms. Every attempt was made at quantifying these sources, but as differentiation is a process that amplifies any noise in the measurements, the measurements were not resolved enough to yield satisfactory results. This is despite the fact that 3000 (near field) to 6000 (far field) statistically independent images were taken, many more than in any previous PIV study of the wall jet (Adane & Tachie Reference Adane and Tachie2010). Nevertheless, the measurements indicate that the difference in the cross-flow normal stresses is significantly larger than the cross-flow shear stress, and, thus, prior to taking the spatial derivatives term,
![]() $D$
should make the largest contribution to the turbulence generated secondary flow.
$D$
should make the largest contribution to the turbulence generated secondary flow.

Figure 20. Contours of turbulent kinetic energy
![]() $(\text{m}^{2}~\text{s}^{-2})$
and turbulent production terms
$(\text{m}^{2}~\text{s}^{-2})$
and turbulent production terms
![]() $(\text{m}^{2}~\text{s}^{-3})$
at
$(\text{m}^{2}~\text{s}^{-3})$
at
![]() $x/D=5$
: (a)
$x/D=5$
: (a)
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
, (b)
$-\overline{uv}(\partial \overline{U}/\partial y)$
, (b)
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
, (c)
$-\overline{uw}(\partial \overline{U}/\partial z)$
, (c)
![]() $-\overline{vv}(\partial \overline{V}/\partial y)$
, (d)
$-\overline{vv}(\partial \overline{V}/\partial y)$
, (d)
![]() $-\overline{vw}(\partial \overline{V}/\partial z)$
, (e)
$-\overline{vw}(\partial \overline{V}/\partial z)$
, (e)
![]() $-\overline{vw}(\partial \overline{W}/\partial y)$
, (f)
$-\overline{vw}(\partial \overline{W}/\partial y)$
, (f)
![]() $-\overline{ww}(\partial \overline{W}/\partial z)$
, (g)
$-\overline{ww}(\partial \overline{W}/\partial z)$
, (g)
![]() $P$
and (h)
$P$
and (h)
![]() $\overline{q}$
.
$\overline{q}$
.

Figure 21. Contours of turbulent kinetic energy
![]() $(\text{m}^{2}~\text{s}^{-2})$
and turbulent production terms
$(\text{m}^{2}~\text{s}^{-2})$
and turbulent production terms
![]() $(\text{m}^{2}~\text{s}^{-3})$
at
$(\text{m}^{2}~\text{s}^{-3})$
at
![]() $x/D=20$
: (a)
$x/D=20$
: (a)
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
, (b)
$-\overline{uv}(\partial \overline{U}/\partial y)$
, (b)
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
, (c)
$-\overline{uw}(\partial \overline{U}/\partial z)$
, (c)
![]() $-\overline{vv}(\partial \overline{V}/\partial y)$
, (d)
$-\overline{vv}(\partial \overline{V}/\partial y)$
, (d)
![]() $-\overline{vw}(\partial \overline{V}/\partial z)$
, (e)
$-\overline{vw}(\partial \overline{V}/\partial z)$
, (e)
![]() $-\overline{vw}(\partial \overline{W}/\partial y)$
, (f)
$-\overline{vw}(\partial \overline{W}/\partial y)$
, (f)
![]() $-\overline{ww}(\partial \overline{W}/\partial z)$
, (g)
$-\overline{ww}(\partial \overline{W}/\partial z)$
, (g)
![]() $P$
and (h)
$P$
and (h)
![]() $\overline{q}$
.
$\overline{q}$
.

Figure 22. Contours of turbulent kinetic energy
![]() $(\text{m}^{2}~\text{s}^{-2})$
and turbulent production terms
$(\text{m}^{2}~\text{s}^{-2})$
and turbulent production terms
![]() $(\text{m}^{2}~\text{s}^{-3})$
at
$(\text{m}^{2}~\text{s}^{-3})$
at
![]() $x/D=30$
: (a)
$x/D=30$
: (a)
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
, (b)
$-\overline{uv}(\partial \overline{U}/\partial y)$
, (b)
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
, (c)
$-\overline{uw}(\partial \overline{U}/\partial z)$
, (c)
![]() $-\overline{vv}(\partial \overline{V}/\partial y)$
, (d)
$-\overline{vv}(\partial \overline{V}/\partial y)$
, (d)
![]() $-\overline{vw}(\partial \overline{V}/\partial z)$
, (e)
$-\overline{vw}(\partial \overline{V}/\partial z)$
, (e)
![]() $-\overline{vw}(\partial \overline{W}/\partial y)$
, (f)
$-\overline{vw}(\partial \overline{W}/\partial y)$
, (f)
![]() $-\overline{ww}(\partial \overline{W}/\partial z)$
, (g)
$-\overline{ww}(\partial \overline{W}/\partial z)$
, (g)
![]() $P$
and (h)
$P$
and (h)
![]() $\overline{q}$
.
$\overline{q}$
.
The current results can also be used to determine whether the vorticity produced by the differences in the Reynolds normal stresses acts to reinforce or counteract the existing streamwise vorticity in the jet. Inspection of figure 19 (along with figures 17 and 18) reveals a rapid increase in the differences in the normal stresses in the
![]() $y$
direction oriented to produce a positive gradient in the first quadrant. Similarly, inspection of the near-wall region of large negative (
$y$
direction oriented to produce a positive gradient in the first quadrant. Similarly, inspection of the near-wall region of large negative (
![]() $\overline{v^{2}}-\overline{w^{2}}$
) also reveals that the
$\overline{v^{2}}-\overline{w^{2}}$
) also reveals that the
![]() $z$
gradient should be positive on the right side of the jet. Taken together, these results indicate that the differences in the Reynolds normal stresses near the wall are oriented to produce positive streamwise vorticity on the right side of the jet. On the left side of the jet centreline, the
$z$
gradient should be positive on the right side of the jet. Taken together, these results indicate that the differences in the Reynolds normal stresses near the wall are oriented to produce positive streamwise vorticity on the right side of the jet. On the left side of the jet centreline, the
![]() $z$
gradient is negative, so negative streamwise vorticity is then produced. Both of these sources are oriented to reinforce the mean near-wall streamwise vorticity in the jet, which, in turn, helps to sustain the large lateral development of this flow.
$z$
gradient is negative, so negative streamwise vorticity is then produced. Both of these sources are oriented to reinforce the mean near-wall streamwise vorticity in the jet, which, in turn, helps to sustain the large lateral development of this flow.
To help in understanding the underlying mechanism that sustains the turbulence, it is useful to examine the turbulent kinetic energy,
![]() $\overline{u_{i}u_{i}}$
, and its associated distribution throughout the jet. The kinetic energy of the turbulent fluctuations for a Cartesian coordinate system is given by, for example, Mathieu & Scott (Reference Mathieu and Scott2000):
$\overline{u_{i}u_{i}}$
, and its associated distribution throughout the jet. The kinetic energy of the turbulent fluctuations for a Cartesian coordinate system is given by, for example, Mathieu & Scott (Reference Mathieu and Scott2000):
 $$\begin{eqnarray}\underbrace{\frac{\partial \overline{q}}{\partial t}}_{\text{I}}+\underbrace{\overline{U_{k}}\frac{\partial \overline{q}}{\partial x_{k}}}_{\text{II}}=-\underbrace{\overline{u_{i}u_{k}}\frac{\partial \overline{U_{i}}}{\partial x_{k}}}_{\text{III}}-\underbrace{\frac{\partial \overline{qu_{k}}}{\partial x_{k}}}_{\text{IV}}-\underbrace{\frac{1}{{\it\rho}}\overline{u_{i}\frac{\partial p}{\partial x_{i}}}}_{\text{V}}+\underbrace{{\it\nu}\overline{u_{i}\frac{\partial ^{2}u_{i}}{\partial x_{k}\partial x_{k}}}}_{\text{VI}},\end{eqnarray}$$
$$\begin{eqnarray}\underbrace{\frac{\partial \overline{q}}{\partial t}}_{\text{I}}+\underbrace{\overline{U_{k}}\frac{\partial \overline{q}}{\partial x_{k}}}_{\text{II}}=-\underbrace{\overline{u_{i}u_{k}}\frac{\partial \overline{U_{i}}}{\partial x_{k}}}_{\text{III}}-\underbrace{\frac{\partial \overline{qu_{k}}}{\partial x_{k}}}_{\text{IV}}-\underbrace{\frac{1}{{\it\rho}}\overline{u_{i}\frac{\partial p}{\partial x_{i}}}}_{\text{V}}+\underbrace{{\it\nu}\overline{u_{i}\frac{\partial ^{2}u_{i}}{\partial x_{k}\partial x_{k}}}}_{\text{VI}},\end{eqnarray}$$
where
-
 $\overline{q}=(1/2)\overline{u_{i}u_{i}}$
;
$\overline{q}=(1/2)\overline{u_{i}u_{i}}$
; -
I – rate of increase of turbulent energy at a fixed point;
-
II – convection of turbulent energy by the mean flow;
-
III – production of turbulent energy by interaction between the mean flow and turbulence;
-
IV – convective transport of turbulent energy by the fluctuating motion (turbulent mixing);
-
V – transfer of turbulent energy by pressure effects;
-
VI – viscous effects (dissipation, diffusion).
Determination of the kinetic energy budget in the three-dimensional wall jet has only received limited attention in the literature. For example, Abrahamsson et al. (Reference Abrahamsson, Johansson and Lofdahl1997a
) measured all three components of the kinetic energy and four of nine turbulent production terms at the jet centreline for the three-dimensional wall jet at
![]() $x/D=80$
. Padmanabham & Gowda (Reference Padmanabham and Gowda1991b
) measured three turbulent production terms for the wall jet, again at the jet centreline, for the inlet nozzle configuration
$x/D=80$
. Padmanabham & Gowda (Reference Padmanabham and Gowda1991b
) measured three turbulent production terms for the wall jet, again at the jet centreline, for the inlet nozzle configuration
![]() $h/D=0.8$
at
$h/D=0.8$
at
![]() $x/D=60$
. However, until now, there is no information about the kinetic energy and production terms off the centreline of the jet. Having this information off the centreline is crucial to improving our understanding of this flow, as a number of the Reynolds stresses are the largest away from the jet centreline.
$x/D=60$
. However, until now, there is no information about the kinetic energy and production terms off the centreline of the jet. Having this information off the centreline is crucial to improving our understanding of this flow, as a number of the Reynolds stresses are the largest away from the jet centreline.
In order to better understand the turbulent mechanisms that sustain the flow, the production of turbulent kinetic energy by the interaction of mean flow and turbulence,
![]() $-\overline{u_{i}u_{k}}(\partial \overline{U_{i}}/\partial x_{k})$
, is examined. Expanding the term
$-\overline{u_{i}u_{k}}(\partial \overline{U_{i}}/\partial x_{k})$
, is examined. Expanding the term
![]() $-\overline{u_{i}u_{k}}(\partial \overline{U_{i}}/\partial x_{k})$
yields
$-\overline{u_{i}u_{k}}(\partial \overline{U_{i}}/\partial x_{k})$
yields
 $$\begin{eqnarray}\displaystyle -\overline{u_{i}u_{k}}\frac{\partial \overline{U_{i}}}{\partial x_{k}} & = & \displaystyle -\overline{uu}\frac{\partial \overline{U}}{\partial x}-\overline{uv}\frac{\partial \overline{U}}{\partial y}-\overline{uw}\frac{\partial \overline{U}}{\partial z}-\overline{uv}\frac{\partial \overline{V}}{\partial x}-\overline{vv}\frac{\partial \overline{V}}{\partial y}-\overline{vw}\frac{\partial \overline{V}}{\partial z}-\overline{uw}\frac{\partial \overline{W}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle -\,\overline{vw}\frac{\partial \overline{W}}{\partial y}-\overline{ww}\frac{\partial \overline{W}}{\partial z}.\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\overline{u_{i}u_{k}}\frac{\partial \overline{U_{i}}}{\partial x_{k}} & = & \displaystyle -\overline{uu}\frac{\partial \overline{U}}{\partial x}-\overline{uv}\frac{\partial \overline{U}}{\partial y}-\overline{uw}\frac{\partial \overline{U}}{\partial z}-\overline{uv}\frac{\partial \overline{V}}{\partial x}-\overline{vv}\frac{\partial \overline{V}}{\partial y}-\overline{vw}\frac{\partial \overline{V}}{\partial z}-\overline{uw}\frac{\partial \overline{W}}{\partial x}\nonumber\\ \displaystyle & & \displaystyle -\,\overline{vw}\frac{\partial \overline{W}}{\partial y}-\overline{ww}\frac{\partial \overline{W}}{\partial z}.\end{eqnarray}$$
Of the nine production terms, only the six production terms that are associated with the spatial derivatives with respect to
![]() $y$
and
$y$
and
![]() $z$
can be computed here as there is no information about the streamwise spatial gradients. However, in the intermediate field and on towards the far field it is likely that the jet only changes slowly in the
$z$
can be computed here as there is no information about the streamwise spatial gradients. However, in the intermediate field and on towards the far field it is likely that the jet only changes slowly in the
![]() $x$
direction, and thus the contribution from these terms will be assumed to be negligible. This assumption was also used by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1969) in their study of the turbulent kinetic energy budget of a turbulent free jet. However, some care should be taken in interpreting these terms in the three-dimensional wall jet, as Abrahamsson et al. (Reference Abrahamsson, Johansson and Lofdahl1997a
) have shown that
$x$
direction, and thus the contribution from these terms will be assumed to be negligible. This assumption was also used by Wygnanski & Fiedler (Reference Wygnanski and Fiedler1969) in their study of the turbulent kinetic energy budget of a turbulent free jet. However, some care should be taken in interpreting these terms in the three-dimensional wall jet, as Abrahamsson et al. (Reference Abrahamsson, Johansson and Lofdahl1997a
) have shown that
![]() $-\overline{uu}(\partial \overline{U}/\partial x)$
makes a significant contribution to the production close to the wall on the jet centreline.
$-\overline{uu}(\partial \overline{U}/\partial x)$
makes a significant contribution to the production close to the wall on the jet centreline.
Contours of each of the production terms are compared at
![]() $x/D=5$
, 20 and 30 in figures 20–22. These contours are compared with the turbulent kinetic energy,
$x/D=5$
, 20 and 30 in figures 20–22. These contours are compared with the turbulent kinetic energy,
![]() $q$
, and the sum of all of the production terms that could be measured here:
$q$
, and the sum of all of the production terms that could be measured here:
In the near field at
![]() $x/D=5$
, by far the largest contributions to the production come from the shear stress terms
$x/D=5$
, by far the largest contributions to the production come from the shear stress terms
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
and
$-\overline{uv}(\partial \overline{U}/\partial y)$
and
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
, with the contribution from each of the terms being similar in magnitude and being roughly an order of magnitude larger than all of the other production terms. The
$-\overline{uw}(\partial \overline{U}/\partial z)$
, with the contribution from each of the terms being similar in magnitude and being roughly an order of magnitude larger than all of the other production terms. The
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
production term is largest in the upper shear layer of the jet, principally due to the large values of
$-\overline{uv}(\partial \overline{U}/\partial y)$
production term is largest in the upper shear layer of the jet, principally due to the large values of
![]() $\overline{uv}$
here and the large mean streamwise velocity, although there is a relatively strong region of production near the wall associated with this term at the jet centreline. Similarly, the large streamwise flow velocity and the large value of
$\overline{uv}$
here and the large mean streamwise velocity, although there is a relatively strong region of production near the wall associated with this term at the jet centreline. Similarly, the large streamwise flow velocity and the large value of
![]() $\overline{uw}$
associated with the lateral shear layers also cause the
$\overline{uw}$
associated with the lateral shear layers also cause the
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
term to be large. All of the other production terms are much smaller and occur in much smaller localized regions. When all of the contributions to the production are summed, the contours of
$-\overline{uw}(\partial \overline{U}/\partial z)$
term to be large. All of the other production terms are much smaller and occur in much smaller localized regions. When all of the contributions to the production are summed, the contours of
![]() $P$
indicate that the turbulent kinetic energy is produced in the shear layers of the jet. The contours of turbulent kinetic energy look very much like the production contours at this position.
$P$
indicate that the turbulent kinetic energy is produced in the shear layers of the jet. The contours of turbulent kinetic energy look very much like the production contours at this position.
Further downstream, at
![]() $x/D=20$
, it is apparent that the shear stress terms
$x/D=20$
, it is apparent that the shear stress terms
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
and
$-\overline{uv}(\partial \overline{U}/\partial y)$
and
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
still make the largest contributions to the turbulent production; however, the term
$-\overline{uw}(\partial \overline{U}/\partial z)$
still make the largest contributions to the turbulent production; however, the term
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
is making a proportionally larger contribution. The contours associated with
$-\overline{uv}(\partial \overline{U}/\partial y)$
is making a proportionally larger contribution. The contours associated with
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
are still the largest near the centre of the jet and are spreading upwards and laterally, but are still probably associated with the turbulence in the upper shear layer. The contours associated with
$-\overline{uv}(\partial \overline{U}/\partial y)$
are still the largest near the centre of the jet and are spreading upwards and laterally, but are still probably associated with the turbulence in the upper shear layer. The contours associated with
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
are still large, but are smaller primarily because the large lateral width of the jet is causing
$-\overline{uw}(\partial \overline{U}/\partial z)$
are still large, but are smaller primarily because the large lateral width of the jet is causing
![]() $\partial \overline{U}/\partial z$
to become smaller. The other production terms are again much smaller. The contours of
$\partial \overline{U}/\partial z$
to become smaller. The other production terms are again much smaller. The contours of
![]() $P$
are much more diffuse than at
$P$
are much more diffuse than at
![]() $x/D=5$
and are primarily associated with the nominal position of the outer shear layers in the jet. The
$x/D=5$
and are primarily associated with the nominal position of the outer shear layers in the jet. The
![]() $P$
contours still do loosely resemble the contours of turbulent kinetic energy, but the turbulent kinetic energy is the highest in the centre of the jet and down towards the wall. It should be noted that near the wall at the jet centreline the turbulent kinetic energy is large and there is low production at this point; this could be due to the transport or diffusion or to a production term that we cannot measure.
$P$
contours still do loosely resemble the contours of turbulent kinetic energy, but the turbulent kinetic energy is the highest in the centre of the jet and down towards the wall. It should be noted that near the wall at the jet centreline the turbulent kinetic energy is large and there is low production at this point; this could be due to the transport or diffusion or to a production term that we cannot measure.
At
![]() $x/D=30$
, although the contributions from
$x/D=30$
, although the contributions from
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
, and
$-\overline{uv}(\partial \overline{U}/\partial y)$
, and
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
are still dominant, the contribution from
$-\overline{uw}(\partial \overline{U}/\partial z)$
are still dominant, the contribution from
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
continues to decrease and is now approximately half the size of
$-\overline{uw}(\partial \overline{U}/\partial z)$
continues to decrease and is now approximately half the size of
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
. The contours of
$-\overline{uv}(\partial \overline{U}/\partial y)$
. The contours of
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
are much larger and broader with the largest values occurring in the outer shear layers at the jet centreline. The contours of
$-\overline{uv}(\partial \overline{U}/\partial y)$
are much larger and broader with the largest values occurring in the outer shear layers at the jet centreline. The contours of
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
are tending down towards the wall and are getting much more localized, consistent with the downward trend for
$-\overline{uw}(\partial \overline{U}/\partial z)$
are tending down towards the wall and are getting much more localized, consistent with the downward trend for
![]() $\overline{uw}$
with increasing downstream distance shown earlier. The contours of
$\overline{uw}$
with increasing downstream distance shown earlier. The contours of
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
for
$-\overline{uw}(\partial \overline{U}/\partial z)$
for
![]() $x/D=40$
, not shown here for the sake of brevity, indicate that the largest region of production gets still closer to the wall and the magnitude gets smaller with respect to
$x/D=40$
, not shown here for the sake of brevity, indicate that the largest region of production gets still closer to the wall and the magnitude gets smaller with respect to
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
. The contours of total production,
$-\overline{uv}(\partial \overline{U}/\partial y)$
. The contours of total production,
![]() $P$
, strongly resemble the term
$P$
, strongly resemble the term
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
, and both strongly resemble the contours of turbulent kinetic energy. It should be noted that even though the contours of
$-\overline{uv}(\partial \overline{U}/\partial y)$
, and both strongly resemble the contours of turbulent kinetic energy. It should be noted that even though the contours of
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
are large near the wall, they seem to be negated by the negative near-wall contributions by
$-\overline{uw}(\partial \overline{U}/\partial z)$
are large near the wall, they seem to be negated by the negative near-wall contributions by
![]() $-\overline{ww}(\partial \overline{W}/\partial z)$
, so that the near-wall contribution is negligible in
$-\overline{ww}(\partial \overline{W}/\partial z)$
, so that the near-wall contribution is negligible in
![]() $P$
.
$P$
.
It is unexpected that, in a flow with such strong lateral velocities and large lateral growth, the contribution of the lateral shear stresses plays a diminishing role in the production of turbulence as the jet evolves into the far field. It has been suggested by Craft & Launder (Reference Craft and Launder2001) that the large lateral growth of the three-dimensional wall jet indicates that the jet is not yet fully developed and that it may not reach the far field until 100 diameters downstream. Perhaps this change in the turbulent production mechanism is also related to the slow development of this flow.
The convection of turbulent kinetic energy by the turbulent motions (the mixing term IV in (3.3)) is also examined. This term can be expanded to yield
 $$\begin{eqnarray}\displaystyle -\frac{\partial \overline{qu_{k}}}{\partial x_{k}} & = & \displaystyle -\frac{\partial }{\partial x_{k}}\left(\frac{1}{2}\overline{u_{i}u_{i}u_{k}}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{\partial }{\partial x}\left(\frac{1}{2}\overline{u^{2}u}\right)-\frac{\partial }{\partial y}\left(\frac{1}{2}\overline{u^{2}v}\right)-\frac{\partial }{\partial z}\left(\frac{1}{2}\overline{u^{2}w}\right)-\frac{\partial }{\partial x}\left(\frac{1}{2}\overline{v^{2}u}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\partial }{\partial y}\left(\frac{1}{2}\overline{v^{2}v}\right)-\frac{\partial }{\partial z}\left(\frac{1}{2}\overline{v^{2}w}\right)-\frac{\partial }{\partial x}\left(\frac{1}{2}\overline{w^{2}u}\right)-\frac{\partial }{\partial y}\left(\frac{1}{2}\overline{w^{2}v}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\partial }{\partial z}\left(\frac{1}{2}\overline{w^{2}w}\right).\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle -\frac{\partial \overline{qu_{k}}}{\partial x_{k}} & = & \displaystyle -\frac{\partial }{\partial x_{k}}\left(\frac{1}{2}\overline{u_{i}u_{i}u_{k}}\right)\nonumber\\ \displaystyle & = & \displaystyle -\frac{\partial }{\partial x}\left(\frac{1}{2}\overline{u^{2}u}\right)-\frac{\partial }{\partial y}\left(\frac{1}{2}\overline{u^{2}v}\right)-\frac{\partial }{\partial z}\left(\frac{1}{2}\overline{u^{2}w}\right)-\frac{\partial }{\partial x}\left(\frac{1}{2}\overline{v^{2}u}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\partial }{\partial y}\left(\frac{1}{2}\overline{v^{2}v}\right)-\frac{\partial }{\partial z}\left(\frac{1}{2}\overline{v^{2}w}\right)-\frac{\partial }{\partial x}\left(\frac{1}{2}\overline{w^{2}u}\right)-\frac{\partial }{\partial y}\left(\frac{1}{2}\overline{w^{2}v}\right)\nonumber\\ \displaystyle & & \displaystyle -\,\frac{\partial }{\partial z}\left(\frac{1}{2}\overline{w^{2}w}\right).\end{eqnarray}$$
Again,
![]() $x$
derivatives could not be computed here, but as the jet develops slowly in the intermediate and far field, although not shown here, the results indicate that the second and third terms make the largest contributions to the mixing term. Contours of the turbulent mixing term at
$x$
derivatives could not be computed here, but as the jet develops slowly in the intermediate and far field, although not shown here, the results indicate that the second and third terms make the largest contributions to the mixing term. Contours of the turbulent mixing term at
![]() $x/D=5$
, 20 and 30 are included in the Appendix for comparison.
$x/D=5$
, 20 and 30 are included in the Appendix for comparison.
The convection of turbulent kinetic energy by the mean flow, term II in (3.3), is also examined. When expanded, the full convection term is represented by
The first term could not be computed here as there is no information about the streamwise variation of
![]() $\overline{q}$
, and the total convection of turbulent kinetic energy by the mean flow is approximated by the second two terms. It should be noted that this approximation is probably not as good as for the earlier mixing or production terms, as even though
$\overline{q}$
, and the total convection of turbulent kinetic energy by the mean flow is approximated by the second two terms. It should be noted that this approximation is probably not as good as for the earlier mixing or production terms, as even though
![]() $\partial \overline{q}/\partial x$
can be expected to be small in the intermediate and far field,
$\partial \overline{q}/\partial x$
can be expected to be small in the intermediate and far field,
![]() $\overline{U}$
is by far the largest mean velocity component. Nevertheless, some insight into the turbulent kinetic energy can be gained by examining these contours. Contours of the turbulent mixing term at
$\overline{U}$
is by far the largest mean velocity component. Nevertheless, some insight into the turbulent kinetic energy can be gained by examining these contours. Contours of the turbulent mixing term at
![]() $x/D=5$
, 20 and 30 are also included in the Appendix for comparison.
$x/D=5$
, 20 and 30 are also included in the Appendix for comparison.

Figure 23. Contours of the turbulent kinetic energy budget at
![]() $x/D=5$
: (a) turbulent production,
$x/D=5$
: (a) turbulent production,
![]() $P~(\text{m}^{2}~\text{s}^{-3})$
, (b) convection of turbulent energy by turbulence,
$P~(\text{m}^{2}~\text{s}^{-3})$
, (b) convection of turbulent energy by turbulence,
![]() $-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
$-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), (c) convection of turbulent energy by mean,
$\text{m}^{2}~\text{s}^{-3}$
), (c) convection of turbulent energy by mean,
![]() $(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
$(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), and (d) turbulent kinetic energy,
$\text{m}^{2}~\text{s}^{-3}$
), and (d) turbulent kinetic energy,
![]() $(\overline{q})$
(
$(\overline{q})$
(
![]() $\text{m}^{2}~\text{s}^{-2}$
).
$\text{m}^{2}~\text{s}^{-2}$
).

Figure 24. Contours of the turbulent kinetic energy budget at
![]() $x/D=20$
: (a) turbulent production,
$x/D=20$
: (a) turbulent production,
![]() $P$
(
$P$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), (b) convection of turbulent energy by turbulence,
$\text{m}^{2}~\text{s}^{-3}$
), (b) convection of turbulent energy by turbulence,
![]() $-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
$-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), (c) convection of turbulent energy by mean,
$\text{m}^{2}~\text{s}^{-3}$
), (c) convection of turbulent energy by mean,
![]() $(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
$(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), and (d) turbulent kinetic energy,
$\text{m}^{2}~\text{s}^{-3}$
), and (d) turbulent kinetic energy,
![]() $(\overline{q})$
(
$(\overline{q})$
(
![]() $\text{m}^{2}~\text{s}^{-2}$
).
$\text{m}^{2}~\text{s}^{-2}$
).

Figure 25. Contours of the turbulent kinetic energy budget at
![]() $x/D=30$
: (a) turbulent production,
$x/D=30$
: (a) turbulent production,
![]() $P$
(
$P$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), (b) convection of turbulent energy by turbulence,
$\text{m}^{2}~\text{s}^{-3}$
), (b) convection of turbulent energy by turbulence,
![]() $-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
$-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), (c) convection of turbulent energy by mean,
$\text{m}^{2}~\text{s}^{-3}$
), (c) convection of turbulent energy by mean,
![]() $(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
$(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), and (d) turbulent kinetic energy,
$\text{m}^{2}~\text{s}^{-3}$
), and (d) turbulent kinetic energy,
![]() $(\overline{q})$
(
$(\overline{q})$
(
![]() $\text{m}^{2}~\text{s}^{-2}$
).
$\text{m}^{2}~\text{s}^{-2}$
).
The production, mixing and convection of turbulent kinetic energy are plotted on the same contour levels and compared at
![]() $x/D=5$
, 20 and 30 in figures 23–25 to allow for an examination of the turbulent energy budget in the three-dimensional wall jet. Here, contours of the turbulent kinetic energy,
$x/D=5$
, 20 and 30 in figures 23–25 to allow for an examination of the turbulent energy budget in the three-dimensional wall jet. Here, contours of the turbulent kinetic energy,
![]() $\overline{q}$
, are also included for the purpose of comparison.
$\overline{q}$
, are also included for the purpose of comparison.
At
![]() $x/D=5$
, the production is largest in the shear layer and makes by far the largest contribution to the turbulent energy budget. This production is balanced by the turbulent transport of energy out of the shear-layer region, and a corresponding increase in turbulent transport in the potential core region and outside of the shear layers (particularly in the lateral shear layers). (More information can be gained by examining this term and the mean term plotted on different contours levels in figure 26 in the Appendix.) The convection of turbulent kinetic energy by the mean (the in-plane term) is quite small but is positive inside the shear layers and negative outside of the shear layers.
$x/D=5$
, the production is largest in the shear layer and makes by far the largest contribution to the turbulent energy budget. This production is balanced by the turbulent transport of energy out of the shear-layer region, and a corresponding increase in turbulent transport in the potential core region and outside of the shear layers (particularly in the lateral shear layers). (More information can be gained by examining this term and the mean term plotted on different contours levels in figure 26 in the Appendix.) The convection of turbulent kinetic energy by the mean (the in-plane term) is quite small but is positive inside the shear layers and negative outside of the shear layers.
Further downstream at
![]() $x/D=20$
, as shown in figure 24, the production again makes the largest contribution to the turbulent kinetic energy budget and resembles the contours of turbulent kinetic energy except near the wall at the jet centreline. This region corresponds to a large positive region of turbulent diffusion. Again, there is a large region of negative turbulent diffusion where the production is the highest, and this is offset by positive diffusion outside of the outer shear layers and the aforementioned large positive region. This near-wall region of positive turbulent diffusion at the centreline is also apparent at
$x/D=20$
, as shown in figure 24, the production again makes the largest contribution to the turbulent kinetic energy budget and resembles the contours of turbulent kinetic energy except near the wall at the jet centreline. This region corresponds to a large positive region of turbulent diffusion. Again, there is a large region of negative turbulent diffusion where the production is the highest, and this is offset by positive diffusion outside of the outer shear layers and the aforementioned large positive region. This near-wall region of positive turbulent diffusion at the centreline is also apparent at
![]() $x/D=30$
and again offsets the region of low production in this area. At both
$x/D=30$
and again offsets the region of low production in this area. At both
![]() $x/D=20$
and 30 the mean convective term is again quite small in relation to the other terms but indicates that there is a negative region that persists near the wall and is probably tied to the large lateral velocities in the jet at this location. Most importantly, it should be noted that examining the terms in the turbulent energy budget along the jet centreline only would give a very different turbulent energy budget than on either side of the jet centreline.
$x/D=20$
and 30 the mean convective term is again quite small in relation to the other terms but indicates that there is a negative region that persists near the wall and is probably tied to the large lateral velocities in the jet at this location. Most importantly, it should be noted that examining the terms in the turbulent energy budget along the jet centreline only would give a very different turbulent energy budget than on either side of the jet centreline.
4 Concluding remarks
Three-component velocity measurements were performed in the cross-flow plane of the turbulent three-dimensional wall jet. The results indicate that on average, the jet entrains air down towards the wall and ejects it laterally outward. The measurements were of sufficient resolution so that mass and momentum flux could be computed for the first time in the three-dimensional wall jet. The mass flux measurements indicate that the entrainment of ambient fluid increases linearly in the wall jet at one half of the rate of a round free jet. The momentum flux decreases fairly linearly in the three-dimensional wall jet due to the momentum lost to the wall, but at a significantly faster rate than for a two-dimensional wall jet.
For the first time, measurements of all six components of the Reynolds stresses were performed in the cross-flow plane of the three-dimensional wall jet. The distribution of the Reynolds stress field in the three-dimensional wall jet was compared at the jet centreline and across the jet at
![]() $y_{max}$
for various streamwise locations. Throughout the jet,
$y_{max}$
for various streamwise locations. Throughout the jet,
![]() $\overline{u^{2}}$
makes the largest contribution to the Reynolds stress field. The measurement at the jet centreline indicates that both
$\overline{u^{2}}$
makes the largest contribution to the Reynolds stress field. The measurement at the jet centreline indicates that both
![]() $\overline{uw}$
and
$\overline{uw}$
and
![]() $\overline{vw}$
are quite small compared with other Reynolds stresses; however, across the jet,
$\overline{vw}$
are quite small compared with other Reynolds stresses; however, across the jet,
![]() $\overline{uw}$
is significantly larger than
$\overline{uw}$
is significantly larger than
![]() $\overline{vw}$
. Typically, the magnitude of
$\overline{vw}$
. Typically, the magnitude of
![]() $\overline{w^{2}}$
is larger than that of
$\overline{w^{2}}$
is larger than that of
![]() $\overline{v^{2}}$
, particularly near the wall in the far-field region, again illustrating that the turbulent anisotropy is an important feature of this flow, even far from the jet outlet.
$\overline{v^{2}}$
, particularly near the wall in the far-field region, again illustrating that the turbulent anisotropy is an important feature of this flow, even far from the jet outlet.
The contours of
![]() $\overline{uv}$
show a large positive region with a maximum located around the vertical half-width and a smaller negative region close to the wall. As the flow evolved downstream, the negative region was suppressed down towards the wall and the outer positive region grew and diffused throughout the jet. The contours of
$\overline{uv}$
show a large positive region with a maximum located around the vertical half-width and a smaller negative region close to the wall. As the flow evolved downstream, the negative region was suppressed down towards the wall and the outer positive region grew and diffused throughout the jet. The contours of
![]() $\overline{uw}$
have two regions with opposite sign, located on either side of the jet centreline, whereas the contours of
$\overline{uw}$
have two regions with opposite sign, located on either side of the jet centreline, whereas the contours of
![]() $\overline{vw}$
indicate a pair of oppositely signed regions, one above the other, that are placed on either side of the jet centreline. However, the magnitude of
$\overline{vw}$
indicate a pair of oppositely signed regions, one above the other, that are placed on either side of the jet centreline. However, the magnitude of
![]() $\overline{vw}$
was found to be quite small compared with other Reynolds stresses and, in fact, the relative contribution of this term decreases rapidly as the flow evolves downstream, and becomes difficult to distinguish in the far-field region because it is so small.
$\overline{vw}$
was found to be quite small compared with other Reynolds stresses and, in fact, the relative contribution of this term decreases rapidly as the flow evolves downstream, and becomes difficult to distinguish in the far-field region because it is so small.
The distribution of the mean streamwise vorticity in the turbulent three-dimensional wall jet was examined at various streamwise locations. The contours of
![]() $\overline{{\it\Omega}}_{x}$
in the near field have a pair of counter-rotating regions that are located near the wall in the lateral shear layers. As the flow evolves downstream, these regions begin to reorient themselves until the outer regions move above the inner regions. This causes the mean flow to be driven into the wall and laterally outward, thereby causing the large lateral growth of the three-dimensional wall jet.
$\overline{{\it\Omega}}_{x}$
in the near field have a pair of counter-rotating regions that are located near the wall in the lateral shear layers. As the flow evolves downstream, these regions begin to reorient themselves until the outer regions move above the inner regions. This causes the mean flow to be driven into the wall and laterally outward, thereby causing the large lateral growth of the three-dimensional wall jet.
The relative contributions from the difference in the Reynolds normal stresses,
![]() $(\overline{v^{2}}-\overline{w^{2}})$
, and the Reynolds shear stress,
$(\overline{v^{2}}-\overline{w^{2}})$
, and the Reynolds shear stress,
![]() $\overline{vw}$
, were calculated and compared at each downstream location. At all locations, the magnitude of
$\overline{vw}$
, were calculated and compared at each downstream location. At all locations, the magnitude of
![]() $(\overline{v^{2}}-\overline{w^{2}})$
is significantly larger than that of
$(\overline{v^{2}}-\overline{w^{2}})$
is significantly larger than that of
![]() $\overline{vw}$
, particularly near the wall. Furthermore, the gradients associated with the near-wall regions of
$\overline{vw}$
, particularly near the wall. Furthermore, the gradients associated with the near-wall regions of
![]() $(\overline{v^{2}}-\overline{w^{2}})$
are oriented to reinforce the near-wall streamwise vorticity. Together, these results suggest that the anisotropy in the Reynolds normal stresses (term
$(\overline{v^{2}}-\overline{w^{2}})$
are oriented to reinforce the near-wall streamwise vorticity. Together, these results suggest that the anisotropy in the Reynolds normal stresses (term
![]() $D$
) caused by the presence of the wall reinforces any vortex-line bending mechanism and contributes to the large lateral growth of the wall jet. Any turbulence model that hopes to capture the large lateral growth of the three-dimensional wall jet should be capable of capturing the anisotropy of the cross-flow normal stresses near the wall (experimental data can be found at supplementary data section).
$D$
) caused by the presence of the wall reinforces any vortex-line bending mechanism and contributes to the large lateral growth of the wall jet. Any turbulence model that hopes to capture the large lateral growth of the three-dimensional wall jet should be capable of capturing the anisotropy of the cross-flow normal stresses near the wall (experimental data can be found at supplementary data section).
Of the six turbulent kinetic energy production terms that could be computed here, the turbulent production terms corresponding to
![]() $-\overline{uv}(\partial \overline{U}/\partial y)$
and
$-\overline{uv}(\partial \overline{U}/\partial y)$
and
![]() $-\overline{uw}(\partial \overline{U}/\partial z)$
were, by far, the largest contributors to the total production in the turbulent kinetic energy budget at all locations in the three-dimensional wall jet. As the jet evolved downstream, the contribution from the latter term diminished in proportion to the former. The results indicate that the majority of the turbulent energy is produced in the jet shear layers and near the wall. The turbulent transport term was negative in the outer shear-layer region, indicating that energy is diffusing from the shear layers; the regions inside and outside of the shear layers were positive, indicating that turbulent kinetic energy diffuses into these regions. Even well downstream of the jet exit at
$-\overline{uw}(\partial \overline{U}/\partial z)$
were, by far, the largest contributors to the total production in the turbulent kinetic energy budget at all locations in the three-dimensional wall jet. As the jet evolved downstream, the contribution from the latter term diminished in proportion to the former. The results indicate that the majority of the turbulent energy is produced in the jet shear layers and near the wall. The turbulent transport term was negative in the outer shear-layer region, indicating that energy is diffusing from the shear layers; the regions inside and outside of the shear layers were positive, indicating that turbulent kinetic energy diffuses into these regions. Even well downstream of the jet exit at
![]() $x/D=20$
and 30, the results indicate that the turbulent energy budget obtained on the jet centreline is not fully indicative of the energy budgets off of the centreline.
$x/D=20$
and 30, the results indicate that the turbulent energy budget obtained on the jet centreline is not fully indicative of the energy budgets off of the centreline.
Acknowledgements
The authors are grateful for the financial support of the Natural Sciences and Engineering Research Council of Canada, and Druk Green Power Corporation Limited of Bhutan.
Supplementary data
Supplementary data is available at https://www.researchgate.net/publication/303552765_Dataset_corresponding_to_Reynolds_Stress_Distribution_and_Turbulence_Generated_Secondary_Flow_in_the_Turbulent_Three-Dimensional_Wall_Jet_by_L_Namgyal_and_JW_Hall_Journal_of_Fluid_Mechanics_Accepted_2).
Appendix. Convection of turbulent kinetic energy by mean and fluctuating velocities

Figure 26. (a,c,e) Convection of turbulent energy by the fluctuating flow,
![]() $-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
$-((\partial \overline{qv}/\partial y)+(\partial \overline{qw}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), and (b,d,f) convection of turbulent energy by the mean flow,
$\text{m}^{2}~\text{s}^{-3}$
), and (b,d,f) convection of turbulent energy by the mean flow,
![]() $(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
$(\overline{V}(\partial \overline{q}/\partial y)+\overline{W}(\partial \overline{q}/\partial z))$
(
![]() $\text{m}^{2}~\text{s}^{-3}$
), at (a,b)
$\text{m}^{2}~\text{s}^{-3}$
), at (a,b)
![]() $x/D=5$
, (c,d)
$x/D=5$
, (c,d)
![]() $x/D=20$
, (e,f)
$x/D=20$
, (e,f)
![]() $x/D=30$
.
$x/D=30$
.