1. INTRODUCTION
In the Z-pinch system, the plasma is produced by applying a high voltage pulse across an anode-cathode gap that is either pre-filled with an annular and hollow gas shell or bridged by an array of wires. The plasma is imploded by the azimuthal magnetic field produced by the axially flowing pulsed discharge current. During compression and stagnation, the kinetic energy is converted to thermal energy and radiation, and a hot and dense core is formed at the center. Highly stripped ions are formed during the thermalization phase, and the plasma emits mostly in the X-ray regime. The X-ray radiation could account for more than 10% of the total electromagnetic energy. This pulsed X-ray emission has many important future applications among which is thermonuclear fusion, being the main reason for current worldwide interest in Z-pinch plasmas (Wu et al., Reference Wu, Wang, Qiu, Han, Li, Lei, Cong, Qiu, Yang and Lv2011; Kuai et al., Reference Kuai, Wu, Qiu, Wang, Cong and Wang2009).
In 1997, the Sandia Laboratories in its PBFA-Z project made a breakthrough in Z-pinch research. They got the promising parameters of 1.8 MJ X-ray energy with an efficiency of 16% from electrical energy to X-ray and 290 TW X-ray pulsed power (Deeney et al., Reference Deeney, Douglas, Spielman, Nash, Peterson, Eplattenier, Chandler, Seamen and Struve1998). The breakthrough has sparked the interest in Z-pinch-driven nuclear fusion (Ramirez, Reference Ramirez1997). One of the reasons for this breakthrough was thought to be the use of PBFA accelerator (20 MA, 100 ns) as Z-pinch driver. Recently, a number of architectures have been proposed in the literatures for the design of future pulsed power Z-pinch drivers (Stygar et al., Reference Stygar, Cuneo, Headley, Ives, Leeper, Mazarakis, Olson, Porter, Wagoner and Woodworth2007). In the design, the monolithic radial transmission lines (MRTLs) were used to combine the outputs of several-hundred terawatt-level pulse generators to produce a petawatt-level pulse in Z-pinch load. An important aspect of the previous studies is that the researchers had dealt usually with the MRTLs by circuit simulation on the assumption that the voltage wave transmits in quasi-TEM mode (Hu et al., Reference Hu, Qiu, Huang, Sun, Cong, Zeng, Zhang and Lei2011; Zhang et al., Reference Zhang, Mao, Huang, Zou and Wang2012; Mao, et al., Reference Mao, Zou and Wang2014). In the circuit simulation, it was shown that the MRTL with an exponential impedance profile has higher transmitted power efficiency than those with Gaussian profiles. From two-dimensional fully electromagnetic simulation of MRTL it was also found that as Γ → 0 (where Γ is the ratio of the pulse width to the one-way transit time of the MRTL), the transmitted power efficiency is maximized when the impedance profile is exponential (Welch et al., Reference Welch, Genoni, Rose, Bruner and Stygar2008).
In this paper, the quasi-TEM mode approximation was thoroughly tested by performing three-dimensional (3D) electromagnetic simulation of the MRTLs with a code called CST microwave studio. Focusing on the difference in the transmitted power efficiency between the 3D electromagnetic simulation and the circuit simulation, we compared the MRTLs with different impedance profiles (exponential, Gaussian, hyperbolic). Being comparable in the power efficiency to the exponential line and easy in fabrication, the hyperbolic line was found to be the best choice.
2. MODEL FOR ELECTROMAGNETIC SIMULATION
We investigated the future pulsed power Z-pinch driver proposed by Stygar et al. (Reference Stygar, Cuneo, Headley, Ives, Leeper, Mazarakis, Olson, Porter, Wagoner and Woodworth2007). A 3D model of the driver is shown in Figure 1. The MRTLs were used to combine the outputs from several-hundred terawatt pulsed generators to produce a petawatt pulse at the center of the driver. Being put around the circumference of the MRTLs, all the pulsed generators were installed on three stacked levels that drive three stacked levels (one per generator level) of the MRTLs. There are six MRTLs in total since each level is made of monolithic triplets.
Fig. 1. Three-dimensional model of the future pulsed power Z-pinch driver.
The parameters designed for each MRTL are Z in = 0.203 Ω at r 2 = 36.88 m and Z out = 2.16 Ω at r 1 = 3.05 m, which means the length of the MRTL is l = 33.83 m, corresponding to a one-way transit time τ = 1009 ns for the electromagnetic wave to propagate through the water-insulated line. The input voltage is half-sine shape with an angular frequency of ω0 = 14 MRad/s, corresponding to a pulse width (FWHM) of T = 150 ns, which is close to the pulse shape for Z-pinch.
The impedance profiles of the MRTLs considered in this paper are exponential, hyperbolic and Gaussian. They are expressed with equations (1), (2), and (3), respectively.
For exponential line:
$$Z\left(r \right)= Z_{in} \cdot \exp \left[{\rm \beta} \cdot \left(r_2 - r \right)\right]\comma \;$$
where β is a constant and determined by 
${\rm \beta} = \displaystyle{\ln \left(Z_{out}/Z_{in} \right)\over r_2 - r_1}$. For the hyperbolic line:
$${\rm Z}\left(r \right)= \displaystyle{1 \over r_2 - r_1} \cdot \left[\displaystyle{Z_{in} \cdot r_2 \left(r - r_1 \right)- Z_{out} \cdot r_1 \left(r - r_2 \right)\over r} \right].$$For the Gaussian line:
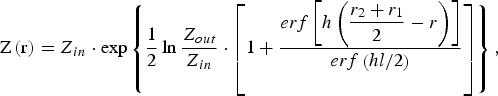$${\rm Z}\left({\rm r} \right)= Z_{in} \cdot \exp \left\{\displaystyle{1 \over 2} \ln \displaystyle{Z_{out} \over Z_{in}} \cdot \left[1 + \displaystyle{erf \left[h \left(\displaystyle{r_2 + r_1 \over 2} - r \right)\right]\over erf \left(hl/2 \right)} \right]\right\}\comma \;$$where h is a constant and erf(y) is the error function defined by Eq. (4).
$$erf \left(y \right)= \displaystyle{2 \over \sqrt{{\rm \pi}}} \int_0^y e^{ - u^2} du.$$For any MRTL, the impedance as a function of radius can be calculated with Eq. (5).
$${\rm Z}\left(r \right)= \sqrt{\displaystyle{{\rm \mu} \over {\rm \varepsilon}}} \cdot \displaystyle{G\left(r \right)\over 2{\rm \pi} r}\comma \;$$where G(r) is the gap of the MRTL; μ and ε are the permeability, and the permittivity of the insulated water that is used as the medium of the MRTL.
Combining Eq. (5), respectively, with (1), (2), and (3), as shown in Figure 2, we obtained the gap profiles for the exponential line, the hyperbolic line, and the Gaussian line. The 3D electromagnetic simulation of the MRTL was performed with a code called CST microwave studio. Based on Figure 2 the geometry of the MRTL used in the 3D simulation was obtained and shown in Figure 3.
Fig. 2. Gap profiles G(r) as a function of radius.
Fig. 3. Geometry of the MRTL used in the 3D simulation.
In the simulation, the MRTL was considered as n pieces of fan-shaped radial transmission lines in parallel and it was shown in Figure 4. In order to compare the results with those obtained from the circuit simulation; each fan-shaped line was made impedance matching at the input end and the output end. For each fan-shaped line, a pulsed generator was connected to the input end through a long uniform transmission line with an impedance of n·Z in and a matching resistor of n·Z out was connected at the output end. In this case, n is also the total number of the pulsed generators to drive one MRTL.
Fig. 4. A MRTL equivalent to n pieces of fan-shaped radial transmission lines in parallel.
3. RESULTS AND DISCUSSIONS
For the MRTLs to be used in Z-pinch, researchers normally focus on the maximum transmitted power efficiency that is defined by Eq. (6).
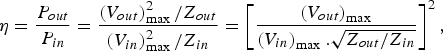$${\rm \eta} = \displaystyle{P_{out} \over P_{in}} = \displaystyle{\left(V_{out} \right)_{\max}^2 /Z_{out} \over \left(V_{in} \right)_{\max}^2 /Z_{in}} = \left[\displaystyle{\left(V_{out} \right)_{\max} \over \left(V_{in} \right)_{\max}. \sqrt{Z_{out}/Z_{in}}} \right]^2\comma \; $$where P in and P out are the maximum power input to and output from the MRTL, respectively. (V in)max and (V out)max are the amplitude of the voltage input to and output from the MRTL, respectively.
As we know, the MRTL was also considered as an impedance transformer with an ideal output voltage of 
$V_{in} \cdot \sqrt{Z_{out}/Z_{in}}$. Therefore, Eq. (6) can be rewritten as Eq. (7).
$${\rm \eta} = \left({\rm \eta}_V \right)^2\comma \;$$where ηV is the maximum transmitted voltage efficiency.
In order to be conveniently compared with the results from 3D electromagnetic simulation, the results from the circuit simulation were listed in Table 1. The results from 3D electromagnetic simulation for exponential line and Gaussian lines were shown in Figure 5. It was found that the maximum transmitted power efficiency increases as the total number of the pulsed generators driving one MRTL increases, but this increase shows a saturated value of 76% for the exponential line and 72–75% for the Gaussian lines when n is larger than 128. η for the exponential line is higher than that for the Gaussian lines, which is similar to that from the circuit simulation. However, all the η from the electromagnetic simulation are about 15% lower than those shown in Table 1 from the circuit simulation, indicating the existence of considerable non-TEM modes. In this case, the circuit simulation based on the quasi-TEM mode approximation will cause non-ignorable error.
Fig. 5. Maximum transmitted power efficiencies obtained with 3D electromagnetic simulation.
Table 1. Maximum transmitted power efficiencies for different radial transmission lines obtained with circuit simulation (Z in = 0.203 Ω, Z out = 2.16 Ω, r 2 = 36.88 m, r 1 = 3.05 m)
The results of Figure 5 were obtained using the geometry of the exponential line and Gaussian line shown in Figure 3. It can be seen from Figure 3 that the electrodes for the exponential line and Gaussian line are made of the curved plates rather than the flat plates. Obviously, the exponential lines or the Gaussian lines with the curved electrodes cannot be stacked together in the way shown in Figure 1. There may be three methods to solve this problem.
The first method is to make the pulse generator much smaller in size so as to put all the pulse generators around the circumference of one MRTL. In this case, only one MRTL is used and no stacked MRTLs are needed. Since six stacked and paralleled MRTLs are replaced by one MRTL, Z in and Z out for the MRTL should be reduced by a factor of 1/6 and changed from 0.203 Ω and 2.16 Ω to 0.034 Ω and 0.36 Ω, respectively.
It was found from the 3D electromagnetic simulation that no matter what the impedance profile is the maximum transmitted power efficiency is significantly increased when Z in and Z out for the MRTL are reduced by a factor of 1/6. Figure 6 shows the results for the exponential lines. It can be seen from Figure 6 that η is increased from 76% to 89% when Z in and Z out for the exponential line are reduced by a factor of 1/6. The reason for this increase may be given below.
Fig. 6. An increased η from 76% to 89% when Z in and Z out for the exponential line are reduced by a factor of 1/6.
According to Eqs. (1)–(3), if Z in and Z out of a MRTL are reduced by a factor of 1/6, the impedance of the whole line will be also reduced by the same factor no matter what an impedance profile of the MRTL is. From the point of view of the electric circuit, η should keep unchanged since the reflection coefficient and transmission coefficient at any point of the MRTL will not change if the impedance of the whole line is reduced by the same factor. Indeed, the circuit simulation yields the same η of 90.8% for the two exponential lines with Z in and Z out as shown in Figure 6. Thus, the increase of η should be caused by the change in the size rather than the impedance of the MRTL. From Eq. (5) we know that the gap of the MRTL will be reduced by a factor of 1/6 if the impedance of the whole line is reduced by a factor of 1/6 under the condition that the radial dimension of the line is kept unchanged. According to the wave guide theory (Pozar, Reference Pozar2005), it may be deduced that the non-TEM modes supported in the MRTL will be significantly reduced by greatly reducing the gap of the line, leading to a transmitted electromagnetic field closer to quasi-TEM mode and an increased η of 89% that is close to the η of 90.8% obtained by the circuit simulation based on the quasi-TEM mode approximation.
The first method mentioned above seems perfect. However, making a terawatt-level pulse generator much smaller in size is a very difficult job. Therefore, the second method was proposed. It was shown in Figure 1 that there are several wide radial slots cut in the cathode electrodes to achieve the desired exponential impedance profiles with flat electrodes so as all the MRTLs being stacked together. Figure 7 shows the comparison of η between two exponential lines, one with the curved electrodes, and the other with the flat electrodes on which 16 wide radial slots are cut. From Figure 7 it can be seen that η of the exponential line using the flat electrodes with 16 radial slots is a little bit lower than that without the wide radial slots, which may be due to the electromagnetic-radiation losses from the wide radial slots.
Fig. 7. Comparison of η between two exponential lines.
We proposed a third method of using the MRTLs with a hyperbolic impedance profile. As shown in Figure 3, the hyperbolic lines are with flat electrodes and easily to be stacked together. Figure 8 shows the comparison of η between the exponential line with 16 radial slots and the hyperbolic line. In contrast to the results from the circuit simulation shown in Table 1 in which η for the hyperbolic line is 5% lower than that for the exponential line, the results from the 3D electromagnetic simulation indicate that η for the hyperbolic line is almost the same as that for the exponential line of the flat electrodes with 16 wide radial slots. The reasons for the almost equal η for these two lines were discussed below. In comparison with the hyperbolic line, the exponential line of the flat electrodes with wide radial slots has an advantage and a disadvantage in the power transmission. Although both lines have the same gap profile and radial dimension, the exponential line suffers from the electromagnetic-radiation losses due to the wide radial slots, which is the disadvantage of the exponential line. However, the exponential impedance profile is superior in less reflection to the hyperbolic impedance profile, which is the advantage of the exponential line. The advantage is compensated by the disadvantage. Therefore, η for these two lines are almost equal.
Fig. 8. Comparison of η between the exponential line with 16 radial slots and the hyperbolic line.
4. CONCLUSIONS
For the MRTLs, the maximum transmitted power efficiency from the electromagnetic simulation is about 15% lower than that from the circuit simulation, indicating the existence of considerable non-TEM modes. In this case, the circuit simulation based on the quasi-TEM mode approximation will cause non-ignorable error. As far as the stacked MRTLs are concerned, the hyperbolic line may be the best choice. While the hyperbolic line has a little bit lower transmitted power efficiency than that of the exponential line with several wide radial slots cut on the flat electrodes, it is much easier in fabrication.
ACKNOWLEDGEMENT
The research was supported by the National Science Foundation of China under Contract 51277109.
