I. Introduction
A substantial oenological literature exists on the opinions of experts and neophytes as they rate the quality of wines (Ashenfelter, Reference Ashenfelter and Quandt1998; Cicchetti, Reference Cicchetti2004; Lindley, Reference Lindley2006). In distinct contrast, the purpose of this article is to present a new methodology for examining the extent of agreement between wine tasters in their binary judgments of wine characteristics—that is, in providing answers to the following types of questions: Is a wine oaked? Does it contain sulfites? What is the grape varietal? Cabernet Sauvignon or Cabernet Franc? Grenache or Syrah? Pinot Noir or Gamay? When comparing this hypothetical example to an actual oenological research investigation, a number of other factors would, per force, need to be experimentally controlled, such as the type of oak, previous barrel use, the duration of exposure to oak, and other relevant factors. Similar reasoning would also apply to any binary variable that is of oenological interest. The reviewer's recognition of this caveat is appreciated.
The motivation for this research derives from several sources: participation in wine-tasting studies focusing on differentiating various wine varietals (e.g., at annual meetings of the New York and New World Wine Experiences, empirical studies in the science of wine (Goode, Reference Goode2014), and some of the recent research undertaken by the author (Cicchetti and Cicchetti Reference Cicchetti and Cicchetti2009; Reference Cicchetti and Cicchetti2014).
An anonymous reviewer notes that some oenological research with a focus upon factual variables has been published, citing several relevant investigations. For example, Frøst and Noble (Reference Frøst and Noble2002) study the influence of a taster's factual knowledge and level of expertise on preferences for certain characteristics of red wines, such as typical aromas and tastes. A second oenological investigation compares support vector machines (SVMs)—“supervised learning methods used for classification”—and three types of neural networks (NNs) for predicting the quality of wine based upon physiochemical data that include such variables as levels of alcohol, sulfates, citric acid, and fixed acidity (Nachev and Hogan, Reference Nachev and Hogan2013, p. 310). The authors find that SVMs outperform each of three versions of NNs. In a third oenological investigation, Cortez et al. (Reference Cortez, Cerdeira, Almeida, Matos and Reis2009) compare SVM to NN methods using a multiple-regression methodology to predict wine-taster preferences, including such variables as measures of acidity, residual sugar, chlorides, sulfates, and other physicochemical properties in red and white wines. Once again, SVMs outperform their methodological competitors.
These results are comparable to the findings of non-oenological biobehavioral diagnostic studies that have been reported earlier by the author and colleagues (Cicchetti et al., Reference Cicchetti, Volkmar, Klin and Showalter1995). The results of this investigation show that NN is outperformed by Logistic Regression (LR), Linear Discriminant Function Analysis (LDFA), and Quadratic Discriminant Function Analysis (QDFA) in the diagnosis of the presence or absence of autism by 15 International Classification of Diseases (ICD-10) criteria. This result is consistent with the author's initial critique of NN research (Cicchetti, Reference Cicchetti1992) and with the results of an earlier study by Fletcher et al. (Reference Fletcher, Rice and Ray1978). These latter investigations reveal that a critical factor in applying NN and competing methodologies is not the sample size, per se, but rather the ratio of the number of subjects to the number of predictor variables, also known as the S/V ratio. Additionally, shrinkage is defined as the percentage loss in classification accuracy between the training set and the cross-validation results. If the training-set level of accuracy is 90% and the cross-validation level is 80%, this would indicate a 10% level of shrinkage. Thus, Fletcher and colleagues show that when LDFA is applied to classification studies in neuropsychology research, the S/V ratio is of critical importance: With an S/V of 1:1, the shrinkage estimates from test to cross-validation fell within a very narrow range of 34% to 36%, whether the sample sizes were 10, 25, or 50. For an S/V of 2:1, with sample sizes of 20, 50, and 100, shrinkage estimates vary from 21% to 23%; for a 3:1 ratio, with sample sizes of 30, 75, and 150, the shrinkages were all 17%; when the S/V was 4:1, with sample sizes of 40, 100, and 200, the corresponding levels of shrinkage ranged between 13% and 15%; and, finally, for S/V ratios of 5:1, with sample sizes of 50, 125, and 250, the cross-validation shrinkages ranged between 9% and 12%. These data clearly indicate that sample sizes are of negligible importance in comparison to the size of the S/V in the design of classification research, whether in the arena of oenology research or more broadly. It should be noted that the S/V ratios in the Cicchetti et al. (Reference Cicchetti, Volkmar, Klin and Showalter1995) investigation are 15:1 for the autistic subjects and 17:1 for the non-autistic subjects. The S/V ratios in the Nachev and Hogan (Reference Nachev and Hogan2013) and Cortez et al. (Reference Cortez, Cerdeira, Almeida, Matos and Reis2009) investigations are in excess of 50:1; one therefore assumes that the resulting shrinkage levels from the training to the cross-validation sets are very low.
In addition to the relative dearth of research on oenophiles’ judgments in the factual realm, there is a second serious problem in the literature: the absence of a defensible biostatistical strategy to apply to this neglected realm of important oenological research. This second area of focus defines the main thrust of this report, with the resulting approach best understood as it applies to the accuracy of assessing oenological facts. The next section focuses on recommended biostatistical methods for providing answers in the study of oenological binary variables.
II. Hypothetical Oenophiles Distinguish between Oaked and Unoaked Wines
Consider that 10 apocryphal wine lovers consent to participate in a tasting with the objective of differentiating between five oaked and five unoaked wines of the same vintage year from around the globe. How accurate are their judgments? Here, we have a binary judgment to answer the research question: Are the wines classified as oaked, yes or no? Borrowing from the broader fields of biomedical science, physics, and chemistry, the components of wine judgment would be Overall Accuracy (OA), Sensitivity (Se), Specificity (Sp), Predicted Positive Accuracy (PPA), and Predicted Negative Accuracy (PNA).
III. Defining the Five Components of Judgmental Accuracy
Overall Accuracy (OA) refers to the total percentage of correct judgments. Applying the criteria of Cicchetti et al. (Reference Cicchetti, Volkmar, Klin and Showalter1995) to judgmental accuracy, less than 70% rates as poor, 70% to 79% is fair, 80% to 89% is good, and 90% to 100% is excellent. (These criteria also apply to each of the remaining four measures of judgmental accuracy.) Sensitivity (Se) refers to the percentage of oaked wines that are correctly judged as such. Specificity (Sp) refers to the percentage of unoaked wines that are correctly judged as such. Predicted Positive Accuracy (PPA) refers to the percentage of wines judged as oaked that are actually oaked. Finally, Predicted Negative Accuracy (PNA) refers to the percentage of wines judged as unoaked that are actually unoaked.
The simulated summary data across the 10 wine judges appear in contingency table format, as shown in Table 1.
Table 1 10 Tasters Classify 100 Wines as Oaked or Unoaked—Summary Data*

* Applying the criteria of Cicchetti et al. (Reference Cicchetti, Volkmar, Klin and Showalter1995) to levels of judged accuracy: < 70% = Poor; 70%–79% = Fair; 80%–89% = Good; and 90%–100% = Excellent; the figures in parentheses refer to the proportion of accurately judged wines expected on the basis of chance alone (PC); the method used to obtain the four figures in parentheses is the same one used in the chi-square (d) test. To obtain the overall taster agreement with the correct classification, one simply adds the two figures in parentheses that appear on the main diagonal and then divides the result by 100; PC then becomes (22.5 + 27.5)/100 = .50, or 50%.
In binary classification data, such as in Table 1, the off-diagonal cases represent two types of errors, classified as Type I and Type II. The Type I errors can also be conceptualized as false positives, or the extent to which a true negative result (i.e., the wine is unoaked (–)) is misjudged as a positive one (i.e., the wine is oaked (+)). In distinct contrast, the Type II error occurs when the wine is incorrectly judged as oaked (+) (i.e., the wine is actually unoaked (– –)). This type can also be referred to as a false negative.
Applying this reasoning to the hypothetical summary data in Table 1, five unoaked wines (negative for oak) are misclassified as oaked (positive for oak). These results represent the tasters’ false-positive judgments (Type I errors); correspondingly, 10 oaked (+) wines have been misclassified as unoaked (–). These results represent false-negative judgments (Type II errors).
These hypothetical wine data can also be expressed separately for each of the judges; see Tables 2 and 3. Again, less than 70% rates as poor, 70% to 79% is fair, 80% to 89% is good, and 90% to 100% is excellent in terms of wine-judging accuracy (Cicchetti et al., Reference Cicchetti, Volkmar, Klin and Showalter1995).
Table 2 Each of 10 Tasters Classifies 10 Wines as Oaked or Unoaked
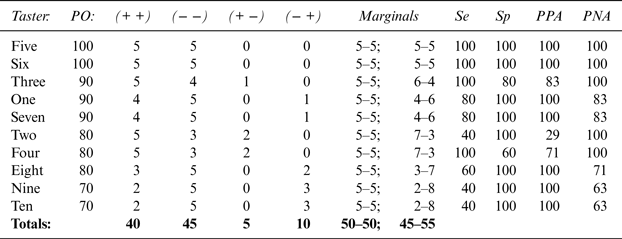
Table 3 Eight Faces of Overall Accuracy in Judging Oaked and Unoaked Wines
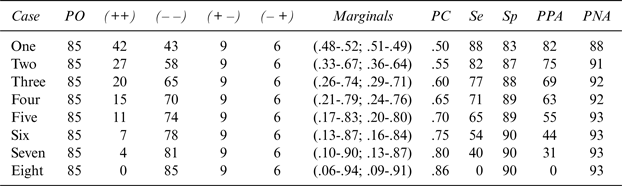
*The clinical or practical significance of Se, Sp, PPA, and PNA values can be interpreted according to the criteria of Cicchetti et al. (Reference Cicchetti, Volkmar, Klin and Showalter1995) regarding levels of accuracy in differentiating between oaked and unoaked wine, wherein < 70% = Poor; 70%–79% = Fair, 80%–89% = Good; and 90%–100% = Excellent.
The notations presented in Table 3 are defined as follows:
-
(++) means the taster judges the wine as oaked (+), and the correct judgment is oaked (+).
-
(− −) means that the taster judges the wine as unoaked (– –), and the correct judgment is unoaked (– –).
-
(+ −) means the taster judges the wine as oaked (+), but the correct judgment is unoaked (–).
-
(− +) means the taster judges the wine as unoaked (–), but the correct judgment is oaked (+).
Marginals occur in two sets, as they appear in Tables 2 and 3. The first set for each case refers to the numbers of oaked (+) and unoaked (–) wines. For Case 1, 48 of the wines are oaked (+), and 52 are unoaked (–). The second set for each case refers to the wine tasters’ judgments as to whether a wine is oaked (+) or unoaked (–). For Case 1, 51 wines are judged to be oaked (+), and 49 are judged to be unoaked (–). The same design holds for Cases 2 through 8.
PC refers to the extent of agreement between a given taster and the correct classification concerning whether a wine is oaked. The calculation is the same as for the familiar and venerable chi-square (d) test; the PC calculation method is illustrated in Table 1.
IV. Why Overall Accuracy Is an Invalid Indicator of Judges’ Evaluations
OA is not an adequate measure of wine judges’ accuracy for several key reasons. Because it is an omnibus measure, a high level of OA (>80%) can be associated with a wide range of levels of the remaining four components of judged accuracy. The simulated data in Table 2 strongly support this caveat. The OA level of 85% is considered good; the OA across the 10 apocryphal wine judges ranges between 70% (barely acceptable or fair) and 100% (perfect). For Wine Judges 5 and 6, Se varies between 40% and 100%, Sp between 60% and 100%, PPA between 29% and 100%, and PNA between 63% and 100%. The simulated data in Table 3 support the same argument: Depending on how the results distribute themselves to produce the same level of OA (here again, a value of 85%), Se values vary between 0% and 88%, and PPA values range similarly from 0% to 82%. The distribution across the four accuracy indices (Se, Sp, PPA, and PNA) is best for Case 1 (88%, 83%, 82%, and 88%, respectively) and worst for Case 8 (0%, 90%, 0%, and 93%, respectively).
V. Implications for Future Research Investigations of Factual Binary Variables
The hypothetical data in Table 1 provide important information for future research studies designed to test wine judges’ ability to correctly answer binary questions, such as whether a wine is oaked, whether one can distinguish Grenache from Syrah or filtered from unfiltered wines, and so forth. The simulated data in Table 3 indicate that the best design includes each binary variable with approximately 50% frequency. This advice also has implications across diverse fields of the behavioral and biomedical sciences and biostatistics—in fact, wherever a gold standard is available. The methodology and caveats also apply to diagnostic areas in which proxy gold standards are used, such as best clinical judgment in lieu of an unavailable gold standard (e.g., in judging the validity or accuracy of the binary diagnosis of autism (Cicchetti et al., Reference Cicchetti, Volkmar, Klin and Showalter1995) and other biomedical disorders (Feinstein, Reference Feinstein1987)). The term gold standard can be defined in relative or absolute terms. Perusing the literature, the more accurate definition, in this author's opinion, is more in accord with a relative concept. In this important regard, the definition offered by Versi (Reference Versi1992) in a letter to the editor of British Medical Journal makes eminently good sense. Versi regards the gold standard as not the perfect test but the best available at a given moment in time, which means it can and will be replaced by a better test once one becomes available.
If one examines the hypothetical data in Table 3, two phenomena become apparent: First, the driving force behind the varying levels of PC, Se, Sp, PPA, and PNA is the extent of maldistribution among the proportions of cases that are correctly judged as positive (oaked) or negative (unoaked); and second, as the level of the maldistribution increases, so does the dissimilarity in the values of PC, Se, Sp, PPA, and PN. It is also clear that the distribution of positive and negative cases produces the best results when their apportionment is as close to 50% as possible, as when the correct classification is 48% (+) and 52% (–).
As shown in Table 4, the Pearson correlation between the maldistribution of positive and negative cases and PC is nearly perfect, at 0.96; the Pearson correlation between PC and the range of percentages across Se, Sp, PPA, and PNA is also nearly perfect, at 0.97.
Table 4 Correlating 85% Agreement Levels for Oaked/Unoaked Wines with: Chance Agreement Levels (PC) and Ranges of Se, Sp, PPA and PNA Values.
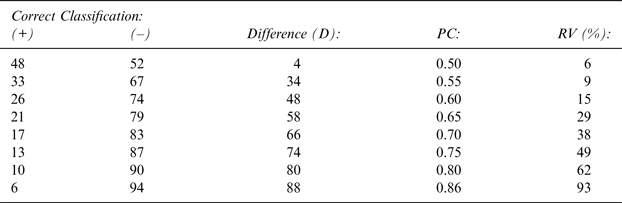
Note: The Pearson correlation between D and PC is + 0.96, and that between PC and RV is 0.97. These nearly perfect correlations represent very large Effect Sizes (ES) according to Cicchetti's (Reference Cicchetti2008) extended ES categories of Cohen (Reference Cohen1988).
These findings provide strong support for designing any oenological investigation based upon binary factual variables such that 50% of the wines represent each of the two sides of the binary/winery coin—namely, positive (+) and negative (–).
VI. Conclusions
The purpose of this report is to utilize methodology from the fields of biobehavioral medical and physical sciences to compare wine judgments to binary wine facts. In a hypothetical example, wine judges’ classifications of wines as oaked or unoaked are analyzed for their degree of accuracy. The biostatistics of the problem have broad applications in future oenological research investigations as well as in other scientific disciplines; the results are in distinct contrast to the wider area of research in which two or more judges’ opinions about the quality of wine are compared. As the anonymous reviewer notes, the sample size is import in the design of oenological research. Three variables that loom large are palate fatigue/dead palate, the scheduled time of day for the tastings, and the known taster variations in recognition threshold levels for the perceived levels of sugar in any given wine (Cicchetti and Cicchetti, Reference Cicchetti and Cicchetti2008). Once these factors are controlled, a valid and simple test allows one to accurately estimate appropriate sample sizes (Kraemer and Thiemann, Reference Kraemer and Thiemann1987). Finally, a more comprehensive report on the reliability and accuracy of binary diagnoses has recently been published by the author and colleagues (Cicchetti, Klin and Volkmar, Reference Cicchetti, Klin and Volkmar2017); these findings are currently under evaluation for their relevance to oenological research.
Acknowledgment
This is to acknowledge the valuable suggestions of an anonymous reviewer concerning the often unrecognized complexity of oenological binary variables, sample-size considerations, and references to additional oenological research for its relevance to this investigation. These comments are appreciated and have, along with other related issues, been woven into the fabric of the current version of the revised text.






