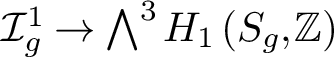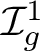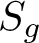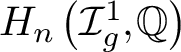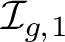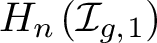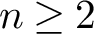1 Introduction
1.1 The Torelli group
Let
![]() $S_{g,r}^{s}$
denote a connected and oriented surface of genus g, with r marked points and s boundary components. If either of r or s is zero, we simply omit the corresponding index.
$S_{g,r}^{s}$
denote a connected and oriented surface of genus g, with r marked points and s boundary components. If either of r or s is zero, we simply omit the corresponding index.
Recall that the mapping-class group of
![]() $S_{g,r}^s$
is the group
$S_{g,r}^s$
is the group
 $$ \begin{align*} \Gamma_{g,r}^s:=\pi_0\text{Diff}^+\left(S_{g,r}^s\right) \end{align*} $$
$$ \begin{align*} \Gamma_{g,r}^s:=\pi_0\text{Diff}^+\left(S_{g,r}^s\right) \end{align*} $$
of isotopy classes of orientation-preserving diffeomorphisms of
![]() $S_{g,r}^s$
that fix the marked points and boundary components. We define
$S_{g,r}^s$
that fix the marked points and boundary components. We define
![]() $H:=H_1\left (S_{g},\mathbb {Q}\right )$
and
$H:=H_1\left (S_{g},\mathbb {Q}\right )$
and
![]() $H_{\mathbb {Z}}:=H_1\left (S_{g},\mathbb {Z}\right )$
. Since
$H_{\mathbb {Z}}:=H_1\left (S_{g},\mathbb {Z}\right )$
. Since
 $\text {Diff}^+\left (S_{g,r}^s\right )$
acts on
$\text {Diff}^+\left (S_{g,r}^s\right )$
acts on
![]() $S_g$
,
$S_g$
,
![]() $\Gamma _{g,r}^s$
acts on H, which is a symplectic vector space. The
$\Gamma _{g,r}^s$
acts on H, which is a symplectic vector space. The
![]() $\Gamma _{g,r}^s$
-action preserves the corresponding symplectic form
$\Gamma _{g,r}^s$
-action preserves the corresponding symplectic form
 $$ \begin{align*} \omega:=\sum_{i=1}^g a_i\wedge b_i\in\bigwedge ^2 H, \end{align*} $$
$$ \begin{align*} \omega:=\sum_{i=1}^g a_i\wedge b_i\in\bigwedge ^2 H, \end{align*} $$
where
![]() $a_1,b_1$
,
$a_1,b_1$
,
![]() $\dots $
c,
$\dots $
c,
![]() $a_{g},b_g$
is any symplectic basis of H, and this gives us a group homomorphism
$a_{g},b_g$
is any symplectic basis of H, and this gives us a group homomorphism
where
![]() $\text {Sp}(H)$
denotes the symplectic group of H. We define the Torelli group of
$\text {Sp}(H)$
denotes the symplectic group of H. We define the Torelli group of
![]() $S_{g,r}^s$
, denoted
$S_{g,r}^s$
, denoted
![]() $\mathcal {I}_{g,r}^s$
, to be the kernel of this homomorphism. The Torelli group is thus the subgroup of
$\mathcal {I}_{g,r}^s$
, to be the kernel of this homomorphism. The Torelli group is thus the subgroup of
![]() $\Gamma _{g,r}^s$
consisting of those isotopy classes of diffeomorphisms that act trivially on H. It is a classic result that the image of
$\Gamma _{g,r}^s$
consisting of those isotopy classes of diffeomorphisms that act trivially on H. It is a classic result that the image of
![]() $\Gamma _{g,r}^s\to \text {Sp}(H)$
is precisely the arithmetic subgroup
$\Gamma _{g,r}^s\to \text {Sp}(H)$
is precisely the arithmetic subgroup
![]() $\text {Sp}(H_{\mathbb {Z}})$
, so we get a short exact sequence
$\text {Sp}(H_{\mathbb {Z}})$
, so we get a short exact sequence
The conjugation action of
![]() $\Gamma _{g,r}^s$
on
$\Gamma _{g,r}^s$
on
![]() $\mathcal {I}_{g,r}^s$
gives us an action by
$\mathcal {I}_{g,r}^s$
gives us an action by
![]() $\text {Sp}(H_{\mathbb {Z}})$
on
$\text {Sp}(H_{\mathbb {Z}})$
on
![]() $\mathcal {I}_{g,r}^s$
by outer automorphisms, which makes
$\mathcal {I}_{g,r}^s$
by outer automorphisms, which makes
 $H_n\left (\mathcal {I}_{g,r}^s,\mathbb {Q}\right )$
into an
$H_n\left (\mathcal {I}_{g,r}^s,\mathbb {Q}\right )$
into an
![]() $\text {Sp}(H_{\mathbb {Z}})$
-representation, for all
$\text {Sp}(H_{\mathbb {Z}})$
-representation, for all
![]() $n\ge 0$
. Unless explicitly stated, all homology is taken with rational coefficients from now on.
$n\ge 0$
. Unless explicitly stated, all homology is taken with rational coefficients from now on.
1.2 The Johnson homomorphism
Many basic questions about the groups
 $H_n\left (\mathcal {I}_{g,r}^s\right )$
are unanswered for
$H_n\left (\mathcal {I}_{g,r}^s\right )$
are unanswered for
![]() $n\ge 2$
. By contrast, the case
$n\ge 2$
. By contrast, the case
![]() $n=1$
is completely understood, due to work by Johnson in the early 1980s [Reference Johnson7]. Among other things, Johnson contructed a group homomorphism
$n=1$
is completely understood, due to work by Johnson in the early 1980s [Reference Johnson7]. Among other things, Johnson contructed a group homomorphism
 $$ \begin{align*} \tau_J:\mathcal{I}_{g}^1\to\bigwedge^3 H_{\mathbb{Z}}, \end{align*} $$
$$ \begin{align*} \tau_J:\mathcal{I}_{g}^1\to\bigwedge^3 H_{\mathbb{Z}}, \end{align*} $$
which is known as the Johnson homomorphism. For
![]() $g\ge 3$
, he proved that the induced
$g\ge 3$
, he proved that the induced
![]() $\text {Sp}(H_{\mathbb {Z}})$
-equivariant map
$\text {Sp}(H_{\mathbb {Z}})$
-equivariant map
 $$ \begin{align*} \tau:H_1\left(\mathcal{I}_{g}^1\right)\to \bigwedge^3 H \end{align*} $$
$$ \begin{align*} \tau:H_1\left(\mathcal{I}_{g}^1\right)\to \bigwedge^3 H \end{align*} $$
is an isomorphism. In particular, this proves that
 $H_1\left (\mathcal {I}_{g}^1\right )$
is finite-dimensional and algebraic as a representation of
$H_1\left (\mathcal {I}_{g}^1\right )$
is finite-dimensional and algebraic as a representation of
![]() $\text {Sp}(H_{\mathbb {Z}})$
for
$\text {Sp}(H_{\mathbb {Z}})$
for
![]() $g\ge 3$
. Two important open questions about the higher homology groups are thus as follows:
$g\ge 3$
. Two important open questions about the higher homology groups are thus as follows:
Question 1. Are the homology groups
 $H_n\left (\mathcal {I}_{g,r}^s\right )$
finite-dimensional, for
$H_n\left (\mathcal {I}_{g,r}^s\right )$
finite-dimensional, for
![]() $n\ge 1$
and g sufficiently large?
$n\ge 1$
and g sufficiently large?
Question 2. Are the homology groups
 $H_n\left (\mathcal {I}_{g,r}^s\right )$
algebraic
$H_n\left (\mathcal {I}_{g,r}^s\right )$
algebraic
![]() $\text {Sp}(H_{\mathbb {Z}})$
-representations, for
$\text {Sp}(H_{\mathbb {Z}})$
-representations, for
![]() $n\ge 1$
and g sufficiently large?
$n\ge 1$
and g sufficiently large?
In low genera, we know that the answer to both questions is generally no. In genus
![]() $2$
, it was proven by Mess [Reference Mess12] that for a certain permutation matrix
$2$
, it was proven by Mess [Reference Mess12] that for a certain permutation matrix
![]() $e\in \text {Sp}(2,\mathbb {Z})$
, we have
$e\in \text {Sp}(2,\mathbb {Z})$
, we have
He also showed that
![]() $H_3(\mathcal {I}_3)$
contains a subrepresentation isomorphic to
$H_3(\mathcal {I}_3)$
contains a subrepresentation isomorphic to
![]() $\mathbb {Q}[\text {Sp}(3,\mathbb {Z})/(\text {Sp}(1,\mathbb {Z})\times \text {Sp}(2,\mathbb {Z}))]$
. It was recently proven by Gaifullin [Reference Gaifullin5] that for
$\mathbb {Q}[\text {Sp}(3,\mathbb {Z})/(\text {Sp}(1,\mathbb {Z})\times \text {Sp}(2,\mathbb {Z}))]$
. It was recently proven by Gaifullin [Reference Gaifullin5] that for
![]() $g\ge 3$
and
$g\ge 3$
and
![]() $2g-3\le n\le 3g-6$
,
$2g-3\le n\le 3g-6$
,
![]() $H_n\left (\mathcal {I}_g,\mathbb {Z}\right )$
contains a free abelian subgroup of infinite rank. This means that
$H_n\left (\mathcal {I}_g,\mathbb {Z}\right )$
contains a free abelian subgroup of infinite rank. This means that
![]() $H_n\left (\mathcal {I}_g\right )$
is neither algebraic nor finite-dimensional in either of these cases.
$H_n\left (\mathcal {I}_g\right )$
is neither algebraic nor finite-dimensional in either of these cases.
For
![]() $n\ge 1$
,
$n\ge 1$
,
![]() $\tau _J$
induces a map
$\tau _J$
induces a map
 $$ \begin{align*} (\tau_J)_*:H_n\left(\mathcal{I}_{g}^1\right)\to H_n\left(\bigwedge^3 H\right)\cong\bigwedge^n\left(\bigwedge^3 H\right), \end{align*} $$
$$ \begin{align*} (\tau_J)_*:H_n\left(\mathcal{I}_{g}^1\right)\to H_n\left(\bigwedge^3 H\right)\cong\bigwedge^n\left(\bigwedge^3 H\right), \end{align*} $$
which we will denote by
![]() $\psi _n$
. An equivalent definition of
$\psi _n$
. An equivalent definition of
![]() $\psi _n$
is as the composition of the comultiplication
$\psi _n$
is as the composition of the comultiplication
 $H_n\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^n H_1\left (\mathcal {I}_{g}^1\right )$
with
$H_n\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^n H_1\left (\mathcal {I}_{g}^1\right )$
with
![]() $\wedge ^n \tau $
. For
$\wedge ^n \tau $
. For
![]() $n\ge 2$
, it follows from results by Hain that the map
$n\ge 2$
, it follows from results by Hain that the map
![]() $\psi _n$
is not surjective [Reference Hain6], but it is natural to ask the question:
$\psi _n$
is not surjective [Reference Hain6], but it is natural to ask the question:
Question 3. Is
![]() $\psi _n$
injective for all
$\psi _n$
injective for all
![]() $n\ge 1$
and g sufficiently large?
$n\ge 1$
and g sufficiently large?
It is not clear whether to expect this to be true. A positive answer would of course imply positive answers to Questions 1 and 2 in the corresponding case. It was proven by Kupers and Randal-Williams that the converse is also true [Reference Kupers and Randal-Williams11]. They also gave an explicit description of the kernel of the dual map of
![]() $\psi _n$
, under these assumptions.
$\psi _n$
, under these assumptions.
Remark 1.1. In the case of a surface without a boundary component, Johnson instead defined a homomorphism
 $\mathcal {I}_g\to \left (\bigwedge ^3 H_{\mathbb {Z}}\right )/H_{\mathbb {Z}}$
, where
$\mathcal {I}_g\to \left (\bigwedge ^3 H_{\mathbb {Z}}\right )/H_{\mathbb {Z}}$
, where
![]() $H_{\mathbb {Z}}$
is embedded as a subspace of
$H_{\mathbb {Z}}$
is embedded as a subspace of
 $\bigwedge ^3H_{\mathbb {Z}}$
by inserting the symplectic form. This is also known as the Johnson homomorphism. This homomorphism induces an
$\bigwedge ^3H_{\mathbb {Z}}$
by inserting the symplectic form. This is also known as the Johnson homomorphism. This homomorphism induces an
![]() $\text {Sp}(H_{\mathbb {Z}})$
-equivariant isomorphism
$\text {Sp}(H_{\mathbb {Z}})$
-equivariant isomorphism
 $H_1\left (\mathcal {I}_g\right )\to \left (\bigwedge ^3 H\right )/H$
.
$H_1\left (\mathcal {I}_g\right )\to \left (\bigwedge ^3 H\right )/H$
.
Remark 1.2. Hain [Reference Hain6] has studied the dual of the map
![]() $\psi _n$
in the unpointed case and determined its image completely for
$\psi _n$
in the unpointed case and determined its image completely for
![]() $n=2$
. For
$n=2$
. For
![]() $n=3$
, its image was determined by Sakasai, up to one irreducible subrepresentation [Reference Sakasai14], the presence of which was settled by Kupers and Randal-Williams [Reference Kupers and Randal-Williams11].
$n=3$
, its image was determined by Sakasai, up to one irreducible subrepresentation [Reference Sakasai14], the presence of which was settled by Kupers and Randal-Williams [Reference Kupers and Randal-Williams11].
The Johnson homomorphisms are closely related to homomorphisms
 $\Gamma _{g,1}\to \frac {1}{2}\bigwedge ^3 H_{\mathbb {Z}}\rtimes \text {Sp}(H_{\mathbb {Z}})$
and
$\Gamma _{g,1}\to \frac {1}{2}\bigwedge ^3 H_{\mathbb {Z}}\rtimes \text {Sp}(H_{\mathbb {Z}})$
and
 $\Gamma _g\to \frac {1}{2}\left (\bigwedge ^3 H_{\mathbb {Z}}\right )/H_{\mathbb {Z}}\rtimes \text {Sp}(H_{\mathbb {Z}})$
defined by Morita [Reference Morita13], which were used by Kawazumi and Morita to give a description of the tautological subalgebra of
$\Gamma _g\to \frac {1}{2}\left (\bigwedge ^3 H_{\mathbb {Z}}\right )/H_{\mathbb {Z}}\rtimes \text {Sp}(H_{\mathbb {Z}})$
defined by Morita [Reference Morita13], which were used by Kawazumi and Morita to give a description of the tautological subalgebra of
![]() $H^*\left (\Gamma _{g,1}\right )$
in terms of trivalent graphs [Reference Kawazumi and Morita10].
$H^*\left (\Gamma _{g,1}\right )$
in terms of trivalent graphs [Reference Kawazumi and Morita10].
We will study how the image of
![]() $\psi _n$
decomposes into irreducible
$\psi _n$
decomposes into irreducible
![]() $\text {Sp}(H_{\mathbb {Z}})$
-representations and determine a lower bound on this image in the stable range. The representation
$\text {Sp}(H_{\mathbb {Z}})$
-representations and determine a lower bound on this image in the stable range. The representation
 $\bigwedge ^n\left (\bigwedge ^3 H\right )$
is algebraic, and this implies that its irreducible subrepresentations viewed as an
$\bigwedge ^n\left (\bigwedge ^3 H\right )$
is algebraic, and this implies that its irreducible subrepresentations viewed as an
![]() $\text {Sp}(H)$
- and an
$\text {Sp}(H)$
- and an
![]() $\text {Sp}(H_{\mathbb {Z}})$
-representation agree. Therefore, we will work with the image of
$\text {Sp}(H_{\mathbb {Z}})$
-representation agree. Therefore, we will work with the image of
![]() $\psi _n$
as an
$\psi _n$
as an
![]() $\text {Sp}(H)$
-representation.
$\text {Sp}(H)$
-representation.
1.3 Irreducible representations of symplectic groups
In order to state our results, we need to recall some basics from the representation theory of symplectic groups. The isomorphism classes of irreducible representations of
![]() $\text {Sp}(H)$
are indexed by partitions. A partition is a decreasing sequence
$\text {Sp}(H)$
are indexed by partitions. A partition is a decreasing sequence
![]() $(\lambda _1\ge \lambda _2\ge \dotsb \ge 0\ge 0\ge \dotsb )$
of nonnegative integers that eventually reaches zero. For example, the standard representation H corresponds to the partition
$(\lambda _1\ge \lambda _2\ge \dotsb \ge 0\ge 0\ge \dotsb )$
of nonnegative integers that eventually reaches zero. For example, the standard representation H corresponds to the partition
![]() $(1\ge 0\ge 0\ge \dotsb )$
. We will write
$(1\ge 0\ge 0\ge \dotsb )$
. We will write
![]() $(\lambda _1\ge \lambda _2\ge \dotsb \ge \lambda _k)$
for the partition, where all following entries in the sequence are zero. The sum
$(\lambda _1\ge \lambda _2\ge \dotsb \ge \lambda _k)$
for the partition, where all following entries in the sequence are zero. The sum
 $\sum _{n\ge 1}\lambda _n$
is called the weight of the partition. If
$\sum _{n\ge 1}\lambda _n$
is called the weight of the partition. If
![]() $\lambda _{i-1}>\lambda _{i}=\dotsb =\lambda _{i+l-1}>\lambda _{i+l}$
, we will often write
$\lambda _{i-1}>\lambda _{i}=\dotsb =\lambda _{i+l-1}>\lambda _{i+l}$
, we will often write
 $\left (\lambda _1\ge \dotsb>\lambda _i^l>\dotsb \ge \lambda _k\right )$
, for brevity, and use the convention that if
$\left (\lambda _1\ge \dotsb>\lambda _i^l>\dotsb \ge \lambda _k\right )$
, for brevity, and use the convention that if
![]() $l=0$
, then
$l=0$
, then
![]() $\lambda _i$
does not occur in the partition.
$\lambda _i$
does not occur in the partition.
We will write
![]() $V_\lambda =V_{\lambda _1,\dotsc ,\lambda _k}$
for the irreducible representation corresponding to the partition
$V_\lambda =V_{\lambda _1,\dotsc ,\lambda _k}$
for the irreducible representation corresponding to the partition
![]() $\lambda =(\lambda _1\ge \lambda _2\ge \dotsb \ge \lambda _k)$
. In particular, we have
$\lambda =(\lambda _1\ge \lambda _2\ge \dotsb \ge \lambda _k)$
. In particular, we have
![]() $V_1\cong H$
. We define the weight of
$V_1\cong H$
. We define the weight of
![]() $V_{\lambda }$
to be the weight of
$V_{\lambda }$
to be the weight of
![]() $\lambda $
. For
$\lambda $
. For
![]() $k\ge 1$
, the representation
$k\ge 1$
, the representation
![]() $H^{\otimes k}$
contains irreducible subrepresentations of weight at most k, which means that the top weight irreducible subrepresentations of
$H^{\otimes k}$
contains irreducible subrepresentations of weight at most k, which means that the top weight irreducible subrepresentations of
 $\bigwedge ^n\left (\bigwedge ^3 H\right )$
have weight
$\bigwedge ^n\left (\bigwedge ^3 H\right )$
have weight
![]() $3n$
. For more details on the irreducible representations of symplectic groups, see, for example, [Reference Fulton and Harris4, Chapter 17].
$3n$
. For more details on the irreducible representations of symplectic groups, see, for example, [Reference Fulton and Harris4, Chapter 17].
1.4 Results
Our first main result is the following:
Theorem 1.3. For
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $g\ge 3n$
, the image of
$g\ge 3n$
, the image of
 $\psi _n:H_n\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
contains the
$\psi _n:H_n\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
contains the
![]() $\text {Sp}(H)$
-subrepresentation of
$\text {Sp}(H)$
-subrepresentation of
 $\bigwedge ^n\left (\bigwedge ^3 H\right )$
spanned by all irreducible subrepresentations of weight
$\bigwedge ^n\left (\bigwedge ^3 H\right )$
spanned by all irreducible subrepresentations of weight
![]() $3n$
.
$3n$
.
Remark 1.4. The kernel of the dual map described by Kupers and Randal-Williams contains no irreducible subrepresentations of top weight, which means that if Questions 1 and 2 have positive answers, Theorem 1.3 follows immediately.
To get a feeling for what Theorem 1.3 means in practice, let us list the irreducible subrepresentations of
 $\bigwedge ^n\left (\bigwedge ^3 H\right )$
of top weight for
$\bigwedge ^n\left (\bigwedge ^3 H\right )$
of top weight for
![]() $n\le 4$
in a table, together with their dimension for
$n\le 4$
in a table, together with their dimension for
![]() $g=3n$
. These can be computed using, for example, SAGE.
$g=3n$
. These can be computed using, for example, SAGE.

Contrary to what the table might suggest, the irreducible subrepresentations are generally not of multiplicity
![]() $1$
for higher n.
$1$
for higher n.
Theorem 1.3 is actually a special case of our second main theorem. This second theorem requires a bit more work to prove, which is why we list and prove the theorems separately. In order to state this result a bit more clearly, we will consider the irreducible
![]() $\text {Sp}(H)$
-representation
$\text {Sp}(H)$
-representation
![]() $V_{1^k}$
as a
$V_{1^k}$
as a
![]() $\mathbb {Z}$
-graded vector space concentrated in degree k, and use the Koszul sign convention. Note that in particular, H is concentrated in degree
$\mathbb {Z}$
-graded vector space concentrated in degree k, and use the Koszul sign convention. Note that in particular, H is concentrated in degree
![]() $1$
. From now on, we will therefore use
$1$
. From now on, we will therefore use
![]() $\bigwedge $
to denote the free graded commutative algebra functor, rather than the exterior algebra functor of ungraded vector spaces.
$\bigwedge $
to denote the free graded commutative algebra functor, rather than the exterior algebra functor of ungraded vector spaces.
Theorem 1.5. Set
![]() $n\ge 1$
and let
$n\ge 1$
and let
 $\lambda =(\lambda _1^{k_1}>\dotsb > \lambda _m^{k_m}>0)$
and
$\lambda =(\lambda _1^{k_1}>\dotsb > \lambda _m^{k_m}>0)$
and
 $\mu =(\mu _1^{l_1}>\dotsb >\mu _{m+2}^{l_{m+2}}>0)$
be partitions such that
$\mu =(\mu _1^{l_1}>\dotsb >\mu _{m+2}^{l_{m+2}}>0)$
be partitions such that
![]() $\mu _{i}=\lambda _i+2$
for
$\mu _{i}=\lambda _i+2$
for
![]() $i=1,\dotsc ,m$
and
$i=1,\dotsc ,m$
and
![]() $\lvert \lambda \rvert +\lvert \mu \rvert =n$
. Let
$\lvert \lambda \rvert +\lvert \mu \rvert =n$
. Let
![]() $k_{m+1}=k_{m+2}=0$
,
$k_{m+1}=k_{m+2}=0$
,
![]() $k=\sum _{i=1}^{m} k_i$
, and
$k=\sum _{i=1}^{m} k_i$
, and
 $l=\sum _{i=1}^{m+2}l_i$
, and suppose that
$l=\sum _{i=1}^{m+2}l_i$
, and suppose that
![]() $g\ge n+2k+l$
. Then the subrepresentation of
$g\ge n+2k+l$
. Then the subrepresentation of
 $$ \begin{align*} \bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}V_{1^{\mu_i}} \end{align*} $$
$$ \begin{align*} \bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}V_{1^{\mu_i}} \end{align*} $$
spanned by all irreducible subrepresentations of weight
![]() $n+2k$
is contained in
$n+2k$
is contained in
![]() $\text {Im}(\psi _n)$
.
$\text {Im}(\psi _n)$
.
In particular, we see that the case
![]() $m=1$
,
$m=1$
,
![]() $\lambda _1=1$
,
$\lambda _1=1$
,
![]() $k_1=n$
gives us back Theorem 1.3, since
$k_1=n$
gives us back Theorem 1.3, since
 $\bigwedge ^3 H\cong V_{1^3}\oplus V_1$
.
$\bigwedge ^3 H\cong V_{1^3}\oplus V_1$
.
Remark 1.6. The Johnson homomorphism
 $\tau _J:\mathcal {I}_{g}^1\to \bigwedge ^3 H_{\mathbb {Z}}$
actually factors as
$\tau _J:\mathcal {I}_{g}^1\to \bigwedge ^3 H_{\mathbb {Z}}$
actually factors as
 $\mathcal {I}_{g}^1\to \mathcal {I}_{g,1}\to \bigwedge ^3 H_{\mathbb {Z}}$
, where the first map is induced by sewing a disk with a marked point into the boundary component and extending diffeomorphisms by the identity. Thus the analogous results to Theorems 1.3 and 1.5 also hold in the pointed case.
$\mathcal {I}_{g}^1\to \mathcal {I}_{g,1}\to \bigwedge ^3 H_{\mathbb {Z}}$
, where the first map is induced by sewing a disk with a marked point into the boundary component and extending diffeomorphisms by the identity. Thus the analogous results to Theorems 1.3 and 1.5 also hold in the pointed case.
Our strategy is to consider abelian cycles in
 $H_n\left (\mathcal {I}_{g}^1\right )$
determined by n-tuples of pairwise disjoint bounding-pair maps. These notions will be defined in §3. What makes this strategy work is that the coproduct of an abelian cycle has a simple expression in terms of abelian cycles of lower degree (Lemma 3.2), which makes the map
$H_n\left (\mathcal {I}_{g}^1\right )$
determined by n-tuples of pairwise disjoint bounding-pair maps. These notions will be defined in §3. What makes this strategy work is that the coproduct of an abelian cycle has a simple expression in terms of abelian cycles of lower degree (Lemma 3.2), which makes the map
![]() $\psi _n$
easy to evaluate.
$\psi _n$
easy to evaluate.
Remark 1.7. The main inspiration for using abelian cycles is papers by Church and Farb [Reference Church, Ellenberg and Farb1] and Sakasai [Reference Sakasai14]. In the former, these are used to study the images of certain homomorphisms
 $\tau _n:H_n\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^{n+2} H$
that generalize
$\tau _n:H_n\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^{n+2} H$
that generalize
![]() $\tau $
to higher degree (see [Reference Johnson7, pp. 172--173]). Church and Farb prove, among other things, that for
$\tau $
to higher degree (see [Reference Johnson7, pp. 172--173]). Church and Farb prove, among other things, that for
![]() $n\ge 1$
and
$n\ge 1$
and
![]() $g\ge n+2$
, the homomorphism
$g\ge n+2$
, the homomorphism
![]() $\tau _n$
gives a surjection
$\tau _n$
gives a surjection
![]() $H_n\left (\mathcal {I}_{g,1}\right )\twoheadrightarrow V_{1^{n+2}}\oplus V_{1^n}$
. This means that the dimension of
$H_n\left (\mathcal {I}_{g,1}\right )\twoheadrightarrow V_{1^{n+2}}\oplus V_{1^n}$
. This means that the dimension of
![]() $H_n\left (\mathcal {I}_{g,1}\right )$
has a lower bound of order
$H_n\left (\mathcal {I}_{g,1}\right )$
has a lower bound of order
![]() $\sim g^{n+2}$
for all
$\sim g^{n+2}$
for all
![]() $n\ge 1$
. We can note that by Theorem 1.3 and Remark 1.6 we get a lower bound on the dimensions of
$n\ge 1$
. We can note that by Theorem 1.3 and Remark 1.6 we get a lower bound on the dimensions of
 $H_n\left (\mathcal {I}_{g}^1\right )$
and
$H_n\left (\mathcal {I}_{g}^1\right )$
and
![]() $H_n\left (\mathcal {I}_{g,1}\right )$
of order
$H_n\left (\mathcal {I}_{g,1}\right )$
of order
![]() $\sim g^{3n}$
for
$\sim g^{3n}$
for
![]() $g\ge 3n$
.
$g\ge 3n$
.
Remark 1.8. Church, Ellenberg, and Farb have used representation stability [Reference Church and Farb2, §7.2] to prove the following theorem:
Theorem 1.9. Church, Ellenberg, Farb
For each
![]() $n\ge 0$
there exists a polynomial
$n\ge 0$
there exists a polynomial
![]() $P_n(T)$
of degree at most
$P_n(T)$
of degree at most
![]() $3n$
such that
$3n$
such that
 $$ \begin{align*} \dim\left(\text{Im}\left(\bigwedge^n H^1\left(\mathcal{I}_{g}^1\right)\to H^n\left(\mathcal{I}_{g}^1\right)\right)\right)=P_n(g) \end{align*} $$
$$ \begin{align*} \dim\left(\text{Im}\left(\bigwedge^n H^1\left(\mathcal{I}_{g}^1\right)\to H^n\left(\mathcal{I}_{g}^1\right)\right)\right)=P_n(g) \end{align*} $$
for
![]() $g\gg n$
.
$g\gg n$
.
Since
 $H^n\left (\mathcal {I}_{g}^1\right )\cong H_n\left (\mathcal {I}_{g}^1\right )^*$
as
$H^n\left (\mathcal {I}_{g}^1\right )\cong H_n\left (\mathcal {I}_{g}^1\right )^*$
as
![]() $\text {Sp}(H)$
-representations for all
$\text {Sp}(H)$
-representations for all
![]() $n\ge 0$
, it follows that the dimension of the image in Theorem 1.9 is bounded from below by the dimension of the image of
$n\ge 0$
, it follows that the dimension of the image in Theorem 1.9 is bounded from below by the dimension of the image of
 $\psi _n:H_n\left (\mathcal {I}_g^1\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
, so the following corollary follows from Theorems 1.3 and 1.9:
$\psi _n:H_n\left (\mathcal {I}_g^1\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
, so the following corollary follows from Theorems 1.3 and 1.9:
Corollary 1.10. The polynomial
![]() $P_n(T)$
in Theorem 1.9 has degree
$P_n(T)$
in Theorem 1.9 has degree
![]() $3n$
.
$3n$
.
For the final result of the paper, we will work with a marked point instead of a boundary component, since this gives us something a bit more general. Abusing notation, we will use
![]() $\psi _n$
to denote the map
$\psi _n$
to denote the map
 $H_n\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
as well. Which
$H_n\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
as well. Which
![]() $\psi _n$
is intended will be clear from context. The last main result concerns the limitations of using abelian cycles of the type we consider. More specifically:
$\psi _n$
is intended will be clear from context. The last main result concerns the limitations of using abelian cycles of the type we consider. More specifically:
Theorem 1.11. Set
![]() $n\ge 2$
and let
$n\ge 2$
and let
![]() $A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
be the subrepresentation generated by abelian cycles determined by pairwise disjoint bounding-pair maps. Then
$A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
be the subrepresentation generated by abelian cycles determined by pairwise disjoint bounding-pair maps. Then
![]() $\psi _n\left (A_n\left (\mathcal {I}_{g,1}\right )\right )$
is concentrated in weights
$\psi _n\left (A_n\left (\mathcal {I}_{g,1}\right )\right )$
is concentrated in weights
![]() $n, n+2,\dotsc ,3n$
. However,
$n, n+2,\dotsc ,3n$
. However,
![]() $\psi _n\left (H_n\left (\mathcal {I}_{g,1}\right )\right )$
also contains a subrepresentation of weight
$\psi _n\left (H_n\left (\mathcal {I}_{g,1}\right )\right )$
also contains a subrepresentation of weight
![]() $n-2$
for all
$n-2$
for all
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $g\gg 0$
. In particular,
$g\gg 0$
. In particular,
![]() $A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
is a proper subrepresentation for
$A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
is a proper subrepresentation for
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $g\gg 0$
.
$g\gg 0$
.
Remark 1.12. We will see that the map induced on homology by
 $\mathcal {I}_g^1\to \mathcal {I}_{g,1}$
maps
$\mathcal {I}_g^1\to \mathcal {I}_{g,1}$
maps
 $A_n\left (\mathcal {I}_g^1\right )\to A_n\left (\mathcal {I}_{g,1}\right )$
. From this it follows that the first claim of Theorem 1.11 holds for
$A_n\left (\mathcal {I}_g^1\right )\to A_n\left (\mathcal {I}_{g,1}\right )$
. From this it follows that the first claim of Theorem 1.11 holds for
 $\psi _n\left (A_n\left (\mathcal {I}_g^1\right )\right )$
as well. To prove the second claim, however, we construct a homology class that requires a marked point rather than a boundary component, and it is not clear how to construct something analogous using a boundary component. However, it follows from results by Kupers and Randal-Williams [Reference Kupers and Randal-Williams11] that
$\psi _n\left (A_n\left (\mathcal {I}_g^1\right )\right )$
as well. To prove the second claim, however, we construct a homology class that requires a marked point rather than a boundary component, and it is not clear how to construct something analogous using a boundary component. However, it follows from results by Kupers and Randal-Williams [Reference Kupers and Randal-Williams11] that
 $H_3\left (\mathcal {I}_g^1\right )$
contains an irreducible subrepresentation of weight
$H_3\left (\mathcal {I}_g^1\right )$
contains an irreducible subrepresentation of weight
![]() $1$
, so it seems reasonable to expect Theorem 1.11 to hold in its entirety for
$1$
, so it seems reasonable to expect Theorem 1.11 to hold in its entirety for
 $A_n\left (\mathcal {I}_g^1\right )$
as well. If we also believe that Questions 1–3 have positive answers, it follows from the results by Kupers and Randal-Williams that for large n there are many classes in
$A_n\left (\mathcal {I}_g^1\right )$
as well. If we also believe that Questions 1–3 have positive answers, it follows from the results by Kupers and Randal-Williams that for large n there are many classes in
 $H_n\left (\mathcal {I}_{g}^1\right )$
that are of lower weight than n and thus cannot lie in
$H_n\left (\mathcal {I}_{g}^1\right )$
that are of lower weight than n and thus cannot lie in
 $A_n\left (\mathcal {I}_{g}^1\right )$
.
$A_n\left (\mathcal {I}_{g}^1\right )$
.
1.5 Structure of the paper
In §2 we give a brief description of Schur–Weyl duality for symplectic groups, which is a fundamental result in the representation theory of symplectic groups. We then describe some simple but useful consequences of this theorem.
In §3 we recall some basics from the theory of mapping-class groups in order to define bounding-pair maps. We then introduce abelian cycles and show how
![]() $\psi _n$
can be easily evaluated on these. This allows us to give a simple proof of Theorem 1.3.
$\psi _n$
can be easily evaluated on these. This allows us to give a simple proof of Theorem 1.3.
In §4 we prove Theorem 1.5. Here we see how considering surfaces with a boundary component allows us to define a ‘multiplication’ of abelian cycles and thereby prove the theorem in a systematic way.
2 Schur–Weyl duality for symplectic groups
We want to investigate how the image of
 $\psi _n:H_n\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
decomposes into irreducible representations of
$\psi _n:H_n\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^n\left (\bigwedge ^3 H\right )$
decomposes into irreducible representations of
![]() $\text {Sp}(H)$
, and to this end we first need to understand how
$\text {Sp}(H)$
, and to this end we first need to understand how
![]() $H^{\otimes k}$
decomposes into irreducible subrepresentations for any
$H^{\otimes k}$
decomposes into irreducible subrepresentations for any
![]() $k\ge 1$
. This decomposition is well understood, by so-called Schur–Weyl duality for symplectic groups. The representation
$k\ge 1$
. This decomposition is well understood, by so-called Schur–Weyl duality for symplectic groups. The representation
![]() $H^{\otimes k}$
contains irreducible subrepresentation of weight at most k (see §1.3), and the irreducibles of top weight form a subrepresentation which we denote by
$H^{\otimes k}$
contains irreducible subrepresentation of weight at most k (see §1.3), and the irreducibles of top weight form a subrepresentation which we denote by
![]() $H^{\langle k\rangle }$
. We call the tensors in
$H^{\langle k\rangle }$
. We call the tensors in
![]() $H^{\langle k\rangle }$
traceless, since these are precisely those tensors in
$H^{\langle k\rangle }$
traceless, since these are precisely those tensors in
![]() $H^{\otimes k}$
that are mapped to zero by all of the contraction maps
$H^{\otimes k}$
that are mapped to zero by all of the contraction maps
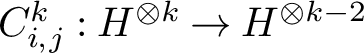 $C^k_{i,j}:H^{\otimes k}\to H^{\otimes k-2}$
, given by contracting with the ith and jth factors with the symplectic form. The space
$C^k_{i,j}:H^{\otimes k}\to H^{\otimes k-2}$
, given by contracting with the ith and jth factors with the symplectic form. The space
![]() $H^{\langle k\rangle }$
has both a left action by
$H^{\langle k\rangle }$
has both a left action by
![]() $\text {Sp}(H)$
and a commuting right action by the symmetric group
$\text {Sp}(H)$
and a commuting right action by the symmetric group
![]() $\Sigma _k$
, by permuting the tensor factors. Schur–Weyl dualityFootnote
1
describes how
$\Sigma _k$
, by permuting the tensor factors. Schur–Weyl dualityFootnote
1
describes how
![]() $H^{\langle k\rangle }$
decomposes as a representation of
$H^{\langle k\rangle }$
decomposes as a representation of
![]() $\text {Sp}(H)\times \Sigma _k$
. The irreducible representations of
$\text {Sp}(H)\times \Sigma _k$
. The irreducible representations of
![]() $\Sigma _k$
are classified by partitions of weight k, as described in [Reference Fulton and Harris4, Chapter 4], and for such a partition
$\Sigma _k$
are classified by partitions of weight k, as described in [Reference Fulton and Harris4, Chapter 4], and for such a partition
![]() $\lambda $
we denote the corresponding irreducible representation of
$\lambda $
we denote the corresponding irreducible representation of
![]() $\Sigma _k$
by
$\Sigma _k$
by
![]() $\sigma _\lambda $
. Schur–Weyl duality for symplectic groups, which is described for example in [Reference Fulton and Harris4, Chapter 17.3], then states that
$\sigma _\lambda $
. Schur–Weyl duality for symplectic groups, which is described for example in [Reference Fulton and Harris4, Chapter 17.3], then states that
 $$ \begin{align*} H^{\langle k\rangle}\cong\bigoplus_{\lvert\lambda\rvert=k}V_\lambda\otimes\sigma_\lambda. \end{align*} $$
$$ \begin{align*} H^{\langle k\rangle}\cong\bigoplus_{\lvert\lambda\rvert=k}V_\lambda\otimes\sigma_\lambda. \end{align*} $$
Up to isomorphism, each
![]() $V_\lambda $
can be constructed as the image of a certain Young symmetrizer
$V_\lambda $
can be constructed as the image of a certain Young symmetrizer
![]() $\mathbf {c}_\lambda :H^{\langle k\rangle }\to H^{\langle k\rangle }$
, which is an element of
$\mathbf {c}_\lambda :H^{\langle k\rangle }\to H^{\langle k\rangle }$
, which is an element of
![]() $\mathbb {Q}[\Sigma _k]$
. For a proof of this fact, once again see [Reference Fulton and Harris4, Chapters 6 and 17.3]. Young symmetrizers are defined using Young diagrams, which are diagrams that represent partitions, as illustrated in Figure 1. A Young tableau is a Young diagram with a choice of numbering of the boxes.
$\mathbb {Q}[\Sigma _k]$
. For a proof of this fact, once again see [Reference Fulton and Harris4, Chapters 6 and 17.3]. Young symmetrizers are defined using Young diagrams, which are diagrams that represent partitions, as illustrated in Figure 1. A Young tableau is a Young diagram with a choice of numbering of the boxes.

Figure 1 The Young diagram representing the partition
![]() $(5\ge 3\ge 1)$
and a corresponding Young tableau.
$(5\ge 3\ge 1)$
and a corresponding Young tableau.
To define
![]() $\mathbf {c}_\lambda $
, for
$\mathbf {c}_\lambda $
, for
![]() $\lvert \lambda \rvert =k$
, we first need to pick a Young tableau with an underlying Young diagram representing
$\lvert \lambda \rvert =k$
, we first need to pick a Young tableau with an underlying Young diagram representing
![]() $\lambda $
. We denote this tableau by T and let
$\lambda $
. We denote this tableau by T and let
![]() $P_\lambda =\{\sigma \in \Sigma _k\mid \sigma \text { preserves each row of }T\}$
and
$P_\lambda =\{\sigma \in \Sigma _k\mid \sigma \text { preserves each row of }T\}$
and
![]() $Q_\lambda =\{\sigma \in \Sigma _k\mid \sigma \text { preserves each column of }T\}$
. We now define
$Q_\lambda =\{\sigma \in \Sigma _k\mid \sigma \text { preserves each column of }T\}$
. We now define
![]() $\mathbf {c}_\lambda :=\mathbf {a}_\lambda \mathbf {b}_\lambda \in \mathbb {Q}[\Sigma _k],$
where
$\mathbf {c}_\lambda :=\mathbf {a}_\lambda \mathbf {b}_\lambda \in \mathbb {Q}[\Sigma _k],$
where
 $$ \begin{align*} \mathbf{a}_\lambda:=\sum_{\sigma\in P_\lambda}\sigma,\qquad \mathbf{b}_\lambda:=\sum_{\sigma\in Q_\lambda}\text{sgn}(\sigma)\sigma. \end{align*} $$
$$ \begin{align*} \mathbf{a}_\lambda:=\sum_{\sigma\in P_\lambda}\sigma,\qquad \mathbf{b}_\lambda:=\sum_{\sigma\in Q_\lambda}\text{sgn}(\sigma)\sigma. \end{align*} $$
If we take the Young tableau of
![]() $\lambda $
that is numbered analogously to the tableau in Figure 1 and let
$\lambda $
that is numbered analogously to the tableau in Figure 1 and let
![]() $\mu =(\mu _1\ge \dotsb \ge \mu _l)$
denote the partition we get by transposing the rows and columns of the Young diagram representing
$\mu =(\mu _1\ge \dotsb \ge \mu _l)$
denote the partition we get by transposing the rows and columns of the Young diagram representing
![]() $\lambda $
, it follows that the image of the corresponding Young symmetrizer
$\lambda $
, it follows that the image of the corresponding Young symmetrizer
![]() $\mathbf {c}_\lambda :H^{\langle k\rangle }\to H^{\langle k\rangle }$
is the subrepresentation of
$\mathbf {c}_\lambda :H^{\langle k\rangle }\to H^{\langle k\rangle }$
is the subrepresentation of
 $$ \begin{align*} \bigwedge^{\mu_1}H\otimes\dotsb\otimes\bigwedge^{\mu_l} H \end{align*} $$
$$ \begin{align*} \bigwedge^{\mu_1}H\otimes\dotsb\otimes\bigwedge^{\mu_l} H \end{align*} $$
generated by the tensor
for any choice of symplectic basis
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of H. From this, it follows that as an
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of H. From this, it follows that as an
![]() $\text {Sp}(H)$
-representation,
$\text {Sp}(H)$
-representation,
![]() $V_\lambda \otimes \sigma _{\lambda }$
is generated by tensors of the form
$V_\lambda \otimes \sigma _{\lambda }$
is generated by tensors of the form
for
![]() $\sigma \in \Sigma _k$
. Here the action is defined by viewing
$\sigma \in \Sigma _k$
. Here the action is defined by viewing
![]() $\bigwedge ^{\mu _1}H\otimes \dotsb \otimes \bigwedge ^{\mu _l} H$
as a subspace of
$\bigwedge ^{\mu _1}H\otimes \dotsb \otimes \bigwedge ^{\mu _l} H$
as a subspace of
![]() $H^{\otimes k}$
– that is, as the composite map
$H^{\otimes k}$
– that is, as the composite map
 $$ \begin{align*} \bigwedge^{\mu_1}H\otimes\dotsb\otimes\bigwedge^{\mu_l} H\hookrightarrow H^{\otimes k}\overset{\cdot\sigma}{\longrightarrow} H^{\otimes k}, \end{align*} $$
$$ \begin{align*} \bigwedge^{\mu_1}H\otimes\dotsb\otimes\bigwedge^{\mu_l} H\hookrightarrow H^{\otimes k}\overset{\cdot\sigma}{\longrightarrow} H^{\otimes k}, \end{align*} $$
where the first map is the standard inclusion. This allows us to prove the following lemma:
Lemma 2.1. For all
![]() $g\ge k\ge 1$
, the
$g\ge k\ge 1$
, the
![]() $\text {Sp}(H)$
-representation
$\text {Sp}(H)$
-representation
![]() $H^{\langle k\rangle }$
is generated by the tensor
$H^{\langle k\rangle }$
is generated by the tensor
for any fixed symplectic basis
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of H.
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of H.
Proof. By the foregoing discussion, it suffices to prove that every tensor A of the form
for
![]() $i_1,\dotsc ,i_j\in \{1,\dotsc ,g\}$
, lies in the
$i_1,\dotsc ,i_j\in \{1,\dotsc ,g\}$
, lies in the
![]() $\mathbb {Q}[\text {Sp}(H)]$
-span of the tensor
$\mathbb {Q}[\text {Sp}(H)]$
-span of the tensor
![]() $a_1\otimes \dotsb \otimes a_{k}$
. We may reorder the symplectic basis in such a way that for each
$a_1\otimes \dotsb \otimes a_{k}$
. We may reorder the symplectic basis in such a way that for each
![]() $1\le j\le k$
, we have
$1\le j\le k$
, we have
![]() $a_{i_j}=a_j$
, unless
$a_{i_j}=a_j$
, unless
![]() $a_{i_j}=a_{i_l}$
for some
$a_{i_j}=a_{i_l}$
for some
![]() $l<j$
. In other words, we may assume that A agrees with
$l<j$
. In other words, we may assume that A agrees with
![]() $a_1\otimes \dotsb \otimes a_k$
in every tensor factor except for in those where A has a repeating element.
$a_1\otimes \dotsb \otimes a_k$
in every tensor factor except for in those where A has a repeating element.
For
![]() $p,q\in \{1,\dotsc ,g\}$
such that
$p,q\in \{1,\dotsc ,g\}$
such that
![]() $p\neq q$
, let
$p\neq q$
, let
![]() $S_{p,q}\in \text {Sp}(H)$
denote the linear map defined by mapping
$S_{p,q}\in \text {Sp}(H)$
denote the linear map defined by mapping
![]() $a_p\mapsto a_p+a_q$
and
$a_p\mapsto a_p+a_q$
and
![]() $b_q\mapsto b_q-b_p$
and mapping all other basis vectors to themselves. If
$b_q\mapsto b_q-b_p$
and mapping all other basis vectors to themselves. If
![]() $a_{i_j}=a_l$
for some
$a_{i_j}=a_l$
for some
![]() $l<j$
, we can act on
$l<j$
, we can act on
![]() $a_1\otimes \dotsb \otimes a_k$
with
$a_1\otimes \dotsb \otimes a_k$
with
![]() $S_{j,l}-\mathbf {1}$
and get
$S_{j,l}-\mathbf {1}$
and get
We can do this for every repeated tensor factor of A and thus see that A does indeed lie in the
![]() $\mathbb {Q}[\text {Sp}(H)]$
-span of
$\mathbb {Q}[\text {Sp}(H)]$
-span of
![]() $a_1\otimes \dotsb \otimes a_k$
.
$a_1\otimes \dotsb \otimes a_k$
.
This has the following immediate corollary:
Corollary 2.2. Let V be a direct summand of
![]() $H^{\otimes k}$
for
$H^{\otimes k}$
for
![]() $g\ge k\ge 1$
, as a representation of
$g\ge k\ge 1$
, as a representation of
![]() $\text {Sp}(H)$
. Let
$\text {Sp}(H)$
. Let
![]() $p:H^{\otimes k}\to V$
be the projection map and fix a symplectic basis
$p:H^{\otimes k}\to V$
be the projection map and fix a symplectic basis
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of H. Then the subspace of V spanned by irreducible subrepresentations of weight k lies in the
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of H. Then the subspace of V spanned by irreducible subrepresentations of weight k lies in the
![]() $\mathbb {Q}[\text {Sp}(H)]$
-span of the tensor
$\mathbb {Q}[\text {Sp}(H)]$
-span of the tensor
3 Abelian cycles and bounding-pair maps
Computing the n-fold coproduct of a general class
 $\alpha \in H_n\left (\mathcal {I}_{g}^1\right )$
is difficult, but we will restrict our interest to a simple class of homology classes, called abelian cycles, for which we can give an explicit expression. For a group G, abelian cycles in
$\alpha \in H_n\left (\mathcal {I}_{g}^1\right )$
is difficult, but we will restrict our interest to a simple class of homology classes, called abelian cycles, for which we can give an explicit expression. For a group G, abelian cycles in
![]() $H_n(G)$
are constructed from commuting elements in the group itself, so in order to construct such classes for
$H_n(G)$
are constructed from commuting elements in the group itself, so in order to construct such classes for
![]() $\mathcal {I}_{g}^1$
in particular, we will first recall some basic notions from the theory of mapping-class groups.
$\mathcal {I}_{g}^1$
in particular, we will first recall some basic notions from the theory of mapping-class groups.
3.1 Dehn twists and bounding-pair maps
First, recall that if
![]() $\alpha $
is a simple, closed curve in
$\alpha $
is a simple, closed curve in
![]() $S_{g,r}^s$
, then a Dehn twist along
$S_{g,r}^s$
, then a Dehn twist along
![]() $\alpha $
is a diffeomorphism of
$\alpha $
is a diffeomorphism of
![]() $S_{g,r}^s$
that is obtained as follows: start with some tubular neighborhood N around
$S_{g,r}^s$
that is obtained as follows: start with some tubular neighborhood N around
![]() $\alpha $
, with a diffeomorphism
$\alpha $
, with a diffeomorphism
![]() $N\cong S^1\times I$
. The corresponding Dehn twist is then given by the identity outside of N, and on
$N\cong S^1\times I$
. The corresponding Dehn twist is then given by the identity outside of N, and on
![]() $N\cong S^1\times I$
by
$N\cong S^1\times I$
by
 $(s,t)\mapsto \left (se^{i2\pi t},t\right )$
. Pictorially, we can illustrate this as in Figure 2.
$(s,t)\mapsto \left (se^{i2\pi t},t\right )$
. Pictorially, we can illustrate this as in Figure 2.

Figure 2 A Dehn twist.
Up to isotopy, the choice of tubular neighborhood does not matter, and if
![]() $\alpha $
and
$\alpha $
and
![]() $\alpha '$
are homotopic, the corresponding Dehn twists are isotopic. Given a homotopy class
$\alpha '$
are homotopic, the corresponding Dehn twists are isotopic. Given a homotopy class
![]() $\alpha $
of simple, closed curves in
$\alpha $
of simple, closed curves in
![]() $S_{g,r}^s$
, it is thus well defined to talk about the Dehn twist along
$S_{g,r}^s$
, it is thus well defined to talk about the Dehn twist along
![]() $\alpha $
as an element of
$\alpha $
as an element of
![]() $\Gamma _{g,r}^s$
. We will denote this element by
$\Gamma _{g,r}^s$
. We will denote this element by
![]() $T_{\alpha }$
. It is a classic result by Dehn, and later independently by Lickorish, that
$T_{\alpha }$
. It is a classic result by Dehn, and later independently by Lickorish, that
![]() $\Gamma _{g,r}^s$
is generated by Dehn twists.
$\Gamma _{g,r}^s$
is generated by Dehn twists.
Dehn twists themselves are generally not elements of
![]() $\mathcal {I}_{g,r}^s$
, but it is easy to find compositions of Dehn twists which are. A bounding pair in
$\mathcal {I}_{g,r}^s$
, but it is easy to find compositions of Dehn twists which are. A bounding pair in
![]() $S_{g,r}^s$
is a pair of simple, closed, nonseparating, and homologous curves. If
$S_{g,r}^s$
is a pair of simple, closed, nonseparating, and homologous curves. If
![]() $(\alpha ,\beta )$
is a bounding pair, we call the composition
$(\alpha ,\beta )$
is a bounding pair, we call the composition
![]() $T_\alpha T_{\beta ^{-1}}$
the bounding-pair map corresponding to this bounding pair. The typical form of a bounding pair is illustrated in Figure 3.
$T_\alpha T_{\beta ^{-1}}$
the bounding-pair map corresponding to this bounding pair. The typical form of a bounding pair is illustrated in Figure 3.

Figure 3 A typical bounding pair.
Bounding-pair maps are elements of
![]() $\mathcal {I}_{g,r}^s$
, and in fact, Johnson [Reference Johnson9] proved that
$\mathcal {I}_{g,r}^s$
, and in fact, Johnson [Reference Johnson9] proved that
![]() $\mathcal {I}_{g}$
is generated by a finite number of bounding-pair maps for
$\mathcal {I}_{g}$
is generated by a finite number of bounding-pair maps for
![]() $g\ge 3$
. This was also used to prove that
$g\ge 3$
. This was also used to prove that
 $\tau :H_1\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^3 H$
is an isomorphism in this range.
$\tau :H_1\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^3 H$
is an isomorphism in this range.
Any bounding pair
![]() $(\alpha ,\beta )$
separates
$(\alpha ,\beta )$
separates
![]() $S_{g}^1$
into two connected components. Let
$S_{g}^1$
into two connected components. Let
![]() $S'$
denote the connected component not containing the original boundary component and let
$S'$
denote the connected component not containing the original boundary component and let
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
be a symplectic basis of H such that for some
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
be a symplectic basis of H such that for some
![]() $1\le k\le g$
,
$1\le k\le g$
,
![]() $\{a_1,b_1,\dotsc ,a_{k},b_{k},[\alpha ]\}$
descends to a basis for
$\{a_1,b_1,\dotsc ,a_{k},b_{k},[\alpha ]\}$
descends to a basis for
![]() $H_1(S')$
, where
$H_1(S')$
, where
![]() $[\alpha ]$
denotes the homology class of
$[\alpha ]$
denotes the homology class of
![]() $\alpha $
.
$\alpha $
.
Proposition 3.1. [Reference Johnson8, Lemma 4B]
Let
![]() $(\alpha ,\beta )$
be a bounding pair and let
$(\alpha ,\beta )$
be a bounding pair and let
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
be a symplectic basis of H as in the previous paragraph. If f denotes the bounding-pair map corresponding to
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
be a symplectic basis of H as in the previous paragraph. If f denotes the bounding-pair map corresponding to
![]() $(\alpha ,\beta )$
, we have
$(\alpha ,\beta )$
, we have
 $$ \begin{align*} \tau(f)=\sum_{i=1}^{k}(a_i\wedge b_i)\wedge [\alpha]\in\bigwedge^3 H. \end{align*} $$
$$ \begin{align*} \tau(f)=\sum_{i=1}^{k}(a_i\wedge b_i)\wedge [\alpha]\in\bigwedge^3 H. \end{align*} $$
Note that since
![]() $\alpha $
and
$\alpha $
and
![]() $\beta $
belong to the same homology class, this formula is well defined.
$\beta $
belong to the same homology class, this formula is well defined.
3.2 Abelian cycles
If two bounding pairs are disjoint, the corresponding bounding-pair maps commute. This gives us a good way to construct elements in
 $H_n\left (\mathcal {I}_{g}^1\right )$
. If G is a group and
$H_n\left (\mathcal {I}_{g}^1\right )$
. If G is a group and
![]() $(f_1,\dotsc ,f_n)$
is an n-tuple of pairwise commuting elements in G, this determines a map
$(f_1,\dotsc ,f_n)$
is an n-tuple of pairwise commuting elements in G, this determines a map
![]() $\mathbb {Z}^n\to G$
, which induces a map
$\mathbb {Z}^n\to G$
, which induces a map
![]() $H_n(\mathbb {Z}^n)\to H_n(G)$
. We have
$H_n(\mathbb {Z}^n)\to H_n(G)$
. We have
![]() $H_n(\mathbb {Z}^n)\cong H_n(T^n)$
, where
$H_n(\mathbb {Z}^n)\cong H_n(T^n)$
, where
![]() $T^n$
denotes the n-torus, and hence
$T^n$
denotes the n-torus, and hence
![]() $H_n(\mathbb {Z}^n)$
is generated by its fundamental class. We call the image of this class under the map to
$H_n(\mathbb {Z}^n)$
is generated by its fundamental class. We call the image of this class under the map to
![]() $H_n(G)$
the abelian cycle determined by
$H_n(G)$
the abelian cycle determined by
![]() $(f_1,\dotsc ,f_n)$
and denote it by
$(f_1,\dotsc ,f_n)$
and denote it by
![]() $A(f_1,\dotsc ,f_n)$
.
$A(f_1,\dotsc ,f_n)$
.
Lemma 3.2. If
![]() $\Delta ^{n-1}:H_n(G)\to \bigwedge ^n H_1(G)$
is the comultiplication map, then
$\Delta ^{n-1}:H_n(G)\to \bigwedge ^n H_1(G)$
is the comultiplication map, then
where
![]() $[f]\in H_1(G)$
denotes the homology class of
$[f]\in H_1(G)$
denotes the homology class of
![]() $f\in G$
.
$f\in G$
.
Proof. The homology
![]() $H_*(\mathbb {Z}^n)$
is a bialgebra, and if
$H_*(\mathbb {Z}^n)$
is a bialgebra, and if
![]() $\{a_1,\dotsc ,a_n\}$
is a basis for
$\{a_1,\dotsc ,a_n\}$
is a basis for
![]() $H_1(\mathbb {Z}^n)$
, the fundamental class of
$H_1(\mathbb {Z}^n)$
, the fundamental class of
![]() $H_n(\mathbb {Z}^n)$
is
$H_n(\mathbb {Z}^n)$
is
![]() $a_1\dotsm a_n$
. Thus
$a_1\dotsm a_n$
. Thus
Furthermore, the map
![]() $H_1(\mathbb {Z}^n)\to H_1(G)$
maps
$H_1(\mathbb {Z}^n)\to H_1(G)$
maps
![]() $a_i\mapsto [f_i]$
, for
$a_i\mapsto [f_i]$
, for
![]() $1\le i\le n$
. By functoriality of homology, we have a commutative diagram
$1\le i\le n$
. By functoriality of homology, we have a commutative diagram

which means that
If
![]() $(f_1,\dotsc ,f_n)$
is an n-tuple of bounding pairs corresponding to pairwise disjoint bounding pairs, we will simply call this an n-tuple of disjoint bounding-pair maps. We will consider abelian cycles in
$(f_1,\dotsc ,f_n)$
is an n-tuple of bounding pairs corresponding to pairwise disjoint bounding pairs, we will simply call this an n-tuple of disjoint bounding-pair maps. We will consider abelian cycles in
 $H_n\left (\mathcal {I}_{g,r}^s\right )$
that are determined by such n-tuples and denote by
$H_n\left (\mathcal {I}_{g,r}^s\right )$
that are determined by such n-tuples and denote by
 $A_n\left (\mathcal {I}_{g,r}^s\right )$
the subrepresentation of
$A_n\left (\mathcal {I}_{g,r}^s\right )$
the subrepresentation of
 $H_n\left (\mathcal {I}_{g,r}^s\right )$
generated by these.
$H_n\left (\mathcal {I}_{g,r}^s\right )$
generated by these.
Remark 3.3. It is clear from the definition of a bounding-pair map that the map
 $\mathcal {I}_g^1\to \mathcal {I}_{g,1}$
induces a map
$\mathcal {I}_g^1\to \mathcal {I}_{g,1}$
induces a map
 $A_n\left (\mathcal {I}_g^1\right )\to A_n\left (\mathcal {I}_{g,1}\right )$
.
$A_n\left (\mathcal {I}_g^1\right )\to A_n\left (\mathcal {I}_{g,1}\right )$
.
If
 $A(f_1,\dotsc ,f_n)\in H_n\left (\mathcal {I}_g^1\right )$
is an abelian cycle, it follows by Lemma 3.2 that
$A(f_1,\dotsc ,f_n)\in H_n\left (\mathcal {I}_g^1\right )$
is an abelian cycle, it follows by Lemma 3.2 that
To evaluate
![]() $\psi _n$
on an abelian cycle, this means that we only need Johnson’s original result on the image of
$\psi _n$
on an abelian cycle, this means that we only need Johnson’s original result on the image of
![]() $\tau $
.
$\tau $
.
Example 3.4. Consider the abelian cycle A determined by the bounding pairs in Figure 4. With an appropriate choice of symplectic basis of H, we see that the image of this abelian cycle is

Figure 4 Bounding pairs determining an abelian cycle in
 $H_n\left (\mathcal {I}_{g}^1\right )$
, for
$H_n\left (\mathcal {I}_{g}^1\right )$
, for
![]() $g\ge 3n$
.
$g\ge 3n$
.
We can now use this to prove Theorem 1.3:
Proof of Theorem 1.3. Since
 $\bigwedge ^n\left (\bigwedge ^3 H\right )$
is a direct summand of
$\bigwedge ^n\left (\bigwedge ^3 H\right )$
is a direct summand of
![]() $H^{\otimes 3n}$
, it follows by Corollary 2.2 that it suffices to show that the tensor
$H^{\otimes 3n}$
, it follows by Corollary 2.2 that it suffices to show that the tensor
lies in the image of
![]() $\psi _n$
. To this end, we consider the abelian cycle from Example 3.4. For
$\psi _n$
. To this end, we consider the abelian cycle from Example 3.4. For
![]() $i\neq j\in \{1,\dotsc ,g\}$
let
$i\neq j\in \{1,\dotsc ,g\}$
let
![]() $T_{i,j}:H\to H$
denote the linear map defined by mapping
$T_{i,j}:H\to H$
denote the linear map defined by mapping
![]() $b_i\mapsto b_i+a_j$
and
$b_i\mapsto b_i+a_j$
and
![]() $b_j\mapsto b_j+a_i$
and mapping all other basis vectors to themselves. Each such map lies in
$b_j\mapsto b_j+a_i$
and mapping all other basis vectors to themselves. Each such map lies in
![]() $\text {Sp}(H)$
, and we see that if we act with
$\text {Sp}(H)$
, and we see that if we act with
![]() $\prod _{i=1}^{n}\left (T_{3i-2,3i-1}-\mathbf {1}\right )\in \mathbb {Q}[\text {Sp}(H)]$
on
$\prod _{i=1}^{n}\left (T_{3i-2,3i-1}-\mathbf {1}\right )\in \mathbb {Q}[\text {Sp}(H)]$
on
we get
□
4 Proof of Theorem 1.5
Let us start by restating Theorem 1.5:
Theorem 1.5. Set
![]() $n\ge 1$
and let
$n\ge 1$
and let
 $\lambda =(\lambda _1^{k_1}>\dotsb > \lambda _m^{k_m}>0)$
and
$\lambda =(\lambda _1^{k_1}>\dotsb > \lambda _m^{k_m}>0)$
and
 $\mu =(\mu _1^{l_1}>\dotsb >\mu _{m+2}^{l_{m+2}}>0)$
be partitions such that
$\mu =(\mu _1^{l_1}>\dotsb >\mu _{m+2}^{l_{m+2}}>0)$
be partitions such that
![]() $\mu _{i}=\lambda _i+2$
for
$\mu _{i}=\lambda _i+2$
for
![]() $i=1,\dotsc ,m$
and
$i=1,\dotsc ,m$
and
![]() $\lvert \lambda \rvert +\lvert \mu \rvert =n$
. Let
$\lvert \lambda \rvert +\lvert \mu \rvert =n$
. Let
![]() $k_{m+1}=k_{m+2}=0$
,
$k_{m+1}=k_{m+2}=0$
,
![]() $k=\sum _{i=1}^{m} k_i$
, and
$k=\sum _{i=1}^{m} k_i$
, and
 $l=\sum _{i=1}^{m+2}l_i$
, and suppose that
$l=\sum _{i=1}^{m+2}l_i$
, and suppose that
![]() $g\ge n+2k+l$
. Then the subrepresentation of
$g\ge n+2k+l$
. Then the subrepresentation of
 $$ \begin{align*} \bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}V_{1^{\mu_i}} \end{align*} $$
$$ \begin{align*} \bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}V_{1^{\mu_i}} \end{align*} $$
spanned by all irreducible subrepresentations of weight
![]() $n+2k$
is contained in
$n+2k$
is contained in
![]() $\text {Im}(\psi _n)$
.
$\text {Im}(\psi _n)$
.
The idea for proving this is essentially to consider two simple kinds of abelian cycles in
![]() $H_n\left (\mathcal {I}_{g,1}\right )$
, whose respective images have components in
$H_n\left (\mathcal {I}_{g,1}\right )$
, whose respective images have components in
![]() $V_{1^{n+2}}$
and
$V_{1^{n+2}}$
and
![]() $V_{1^{n}}$
, and then taking products of such cycles, for a range of ns corresponding to the partitions. The special case of Theorem 1.3 is given by taking the nth power of a bounding pair in
$V_{1^{n}}$
, and then taking products of such cycles, for a range of ns corresponding to the partitions. The special case of Theorem 1.3 is given by taking the nth power of a bounding pair in
 $H_1\left (\mathcal {I}_{3}^1\right )$
whose image has a component in
$H_1\left (\mathcal {I}_{3}^1\right )$
whose image has a component in
![]() $V_{1^3}$
(see Example 4.2).
$V_{1^3}$
(see Example 4.2).
4.1 Products of abelian cycles
Given mapping classes
 $f_1\in \mathcal {I}_{g_1}^1$
and
$f_1\in \mathcal {I}_{g_1}^1$
and
 $f_2\in \mathcal {I}_{g_2}^1$
, we may glue the surfaces
$f_2\in \mathcal {I}_{g_2}^1$
, we may glue the surfaces
 $S_{g_1}^1$
and
$S_{g_1}^1$
and
 $S_{g_2}^1$
along the dashed segments illustrated in Figure 5, and since both mapping classes fix the boundaries, this naturally gives us a mapping class in
$S_{g_2}^1$
along the dashed segments illustrated in Figure 5, and since both mapping classes fix the boundaries, this naturally gives us a mapping class in
 $\mathcal {I}_{g_1+g_2}^1$
. Thus we get a map
$\mathcal {I}_{g_1+g_2}^1$
. Thus we get a map
 $\mathcal {I}_{g_1}^1\times \mathcal {I}_{g_2}^1\to \mathcal {I}_{g_1+g_2}^1$
, which induces a multiplication
$\mathcal {I}_{g_1}^1\times \mathcal {I}_{g_2}^1\to \mathcal {I}_{g_1+g_2}^1$
, which induces a multiplication
 $$ \begin{align*} H_i\left(\mathcal{I}_{g_1}^1\right)\otimes H_j\left(\mathcal{I}_{g_2}^1\right)\to H_{i+j}\left(\mathcal{I}_{g_1+g_2}^1\right) \end{align*} $$
$$ \begin{align*} H_i\left(\mathcal{I}_{g_1}^1\right)\otimes H_j\left(\mathcal{I}_{g_2}^1\right)\to H_{i+j}\left(\mathcal{I}_{g_1+g_2}^1\right) \end{align*} $$
by precomposing with the Künneth map. This makes the space
 $\bigoplus _{g,n\ge 0} H_n\left (\mathcal {I}_{g}^1\right )$
into a bigraded associative and commutative algebra.
$\bigoplus _{g,n\ge 0} H_n\left (\mathcal {I}_{g}^1\right )$
into a bigraded associative and commutative algebra.

Figure 5 Gluing the surfaces along the dashed segments induces the map
 $H_i(\mathcal{I}_{g_1}^1)\times H_j(\mathcal{I}_{g_1}^1)\to H_{i+j}(\mathcal{I}_{g_1+g_2}^1)$
.
$H_i(\mathcal{I}_{g_1}^1)\times H_j(\mathcal{I}_{g_1}^1)\to H_{i+j}(\mathcal{I}_{g_1+g_2}^1)$
.
In
 $H_{i+j}\left (\mathbb {Z}^{i+j}\right )\cong H_{i}\left (\mathbb {Z}^i\right )\otimes H_j\left (\mathbb {Z}^j\right )$
, the fundamental class is the tensor product of the fundamental classes in
$H_{i+j}\left (\mathbb {Z}^{i+j}\right )\cong H_{i}\left (\mathbb {Z}^i\right )\otimes H_j\left (\mathbb {Z}^j\right )$
, the fundamental class is the tensor product of the fundamental classes in
 $H_{i}\left (\mathbb {Z}^i\right )$
and
$H_{i}\left (\mathbb {Z}^i\right )$
and
 $H_{j}\left (\mathbb {Z}^j\right )$
. This proves the following proposition:
$H_{j}\left (\mathbb {Z}^j\right )$
. This proves the following proposition:
Proposition 4.1. If
![]() $A(f_1,\dotsc ,f_i)$
and
$A(f_1,\dotsc ,f_i)$
and
![]() $A\left (f_{i+1},\dotsc ,f_{i+j}\right )$
are abelian cycles in
$A\left (f_{i+1},\dotsc ,f_{i+j}\right )$
are abelian cycles in
 $H_i\left (\mathcal {I}_{g_1}^1\right )$
and
$H_i\left (\mathcal {I}_{g_1}^1\right )$
and
 $H_j\left (\mathcal {I}_{g_2}^1\right )$
, respectively, their product is the abelian cycle
$H_j\left (\mathcal {I}_{g_2}^1\right )$
, respectively, their product is the abelian cycle
 $A\left (f_1,\dotsc ,f_{i+j}\right )\in H_{i+j}\left (\mathcal {I}_{g_1+g_2}^1\right )$
.
$A\left (f_1,\dotsc ,f_{i+j}\right )\in H_{i+j}\left (\mathcal {I}_{g_1+g_2}^1\right )$
.
Example 4.2. With this in mind, we see that the abelian cycle depicted in Figure 4 is simply the product
![]() $\sigma _1^n\cdot 1_{g-3n}$
, where
$\sigma _1^n\cdot 1_{g-3n}$
, where
![]() $\sigma _1$
is the class in
$\sigma _1$
is the class in
 $H_1\left (\mathcal {I}_{3}^1\right )$
determined by the bounding pair in Figure 6, and
$H_1\left (\mathcal {I}_{3}^1\right )$
determined by the bounding pair in Figure 6, and
 $1_{g-3n}\in H_0\left (\mathcal {I}_{g-3n}^1\right )$
is the generator.
$1_{g-3n}\in H_0\left (\mathcal {I}_{g-3n}^1\right )$
is the generator.

Figure 6 The cycle
![]() $\sigma _1$
.
$\sigma _1$
.
4.2 Families of truly nested bounding pairs
With Example 4.2 in mind, we will consider abelian cycles determined by families of bounding pairs of the form depicted in Figure 7 and then their products. We call these families of bounding pairs truly nested, a terminology that we borrow from [Reference Church, Ellenberg and Farb1].

Figure 7 Truly nested families of bounding pairs defining the abelian cycles
 $\sigma _n\in H_n\left (\mathcal {I}_{n+2}^1\right )$
and
$\sigma _n\in H_n\left (\mathcal {I}_{n+2}^1\right )$
and
 $\rho _n\in H_n\left (\mathcal {I}_{n+1}^1\right )$
considered in Example 4.5.
$\rho _n\in H_n\left (\mathcal {I}_{n+1}^1\right )$
considered in Example 4.5.
Definition 4.3. A family
![]() $(\alpha _1,\beta _1),\dotsc ,(\alpha _n,\beta _n)$
of bounding pairs is truly nested if
$(\alpha _1,\beta _1),\dotsc ,(\alpha _n,\beta _n)$
of bounding pairs is truly nested if
-
(1) the curves
 $\alpha _i$
are pairwise nonhomologous and
$\alpha _i$
are pairwise nonhomologous and -
(2) after possibly reordering the bounding pairs, cutting the surface along
 $\left (\alpha _j,\beta _j\right )$
separates the bounding pair
$\left (\alpha _j,\beta _j\right )$
separates the bounding pair
 $(\alpha _i,\beta _i)$
from the original boundary component whenever
$(\alpha _i,\beta _i)$
from the original boundary component whenever
 $i<j$
.
$i<j$
.
We will always assume that the bounding pairs in such a family are numbered so that Definition 4.3(2) is met. By induction it can be seen that a truly nested family of bounding pairs is always of the form depicted in Figure 7, but possibly with holes between each adjacent couple of bounding pairs.
If we are given a truly nested family of bounding pairs
![]() $(\alpha _1,\beta _1),\dotsc ,(\alpha _n,\beta _n)$
and we cut the surface along a bounding pair, we can talk about the resulting connected component that is ‘furthest’ from the original boundary component. If the surface is cut along
$(\alpha _1,\beta _1),\dotsc ,(\alpha _n,\beta _n)$
and we cut the surface along a bounding pair, we can talk about the resulting connected component that is ‘furthest’ from the original boundary component. If the surface is cut along
![]() $(\alpha _1,\beta _1)$
, consider that component and let
$(\alpha _1,\beta _1)$
, consider that component and let
![]() $\omega _0$
denote the symplectic form of a maximal subsurface with only one boundary component. In order to prove Theorem 1.5, we will need the following lemma:
$\omega _0$
denote the symplectic form of a maximal subsurface with only one boundary component. In order to prove Theorem 1.5, we will need the following lemma:
Lemma 4.4. Let
![]() $A(f_1,\dotsc ,f_n)$
be an abelian cycle determined by a truly nested family of bounding-pair maps. Then there exists an
$A(f_1,\dotsc ,f_n)$
be an abelian cycle determined by a truly nested family of bounding-pair maps. Then there exists an
![]() $\text {Sp}(H)$
-equivariant map
$\text {Sp}(H)$
-equivariant map
 $\Phi _n:\bigwedge ^n\left (\bigwedge ^3 H\right )\to \bigwedge ^{n+2} H$
, defined by a sequence of
$\Phi _n:\bigwedge ^n\left (\bigwedge ^3 H\right )\to \bigwedge ^{n+2} H$
, defined by a sequence of
![]() $n-1$
contractions, such that
$n-1$
contractions, such that
for some nonzero integer
![]() $\lambda _n$
, where
$\lambda _n$
, where
![]() $c_i$
is the homology class of the bounding pair corresponding to
$c_i$
is the homology class of the bounding pair corresponding to
![]() $f_i$
and
$f_i$
and
![]() $\omega _0$
is as already defined.
$\omega _0$
is as already defined.
We construct the map
![]() $\Phi _n$
as follows: for
$\Phi _n$
as follows: for
![]() $n=1$
we set
$n=1$
we set
![]() $\Phi _1=\text {id}_{\bigwedge ^3 H}$
. For
$\Phi _1=\text {id}_{\bigwedge ^3 H}$
. For
![]() $n\ge 2$
, we have a map
$n\ge 2$
, we have a map
 $\phi _1^n:\bigwedge ^n\left (\bigwedge ^3 H\right )\to \bigwedge ^4 H\otimes \bigwedge ^{n-2}\left (\bigwedge ^3 H\right )$
, given by contracting ‘diagonally’ with the symplectic form and composing with the multiplication map
$\phi _1^n:\bigwedge ^n\left (\bigwedge ^3 H\right )\to \bigwedge ^4 H\otimes \bigwedge ^{n-2}\left (\bigwedge ^3 H\right )$
, given by contracting ‘diagonally’ with the symplectic form and composing with the multiplication map
 $\bigwedge ^2\left (\bigwedge ^2 H\right )\to \bigwedge ^4 H$
. For any
$\bigwedge ^2\left (\bigwedge ^2 H\right )\to \bigwedge ^4 H$
. For any
![]() $2\le k\le n-1$
, we similarly have a composite map
$2\le k\le n-1$
, we similarly have a composite map
 $$ \begin{align*} \bigwedge^{k+2} H\otimes \bigwedge^{n-k}\left(\bigwedge^3 H\right)\to\bigwedge^{k+1} H\otimes \bigwedge^2 H\otimes\bigwedge^{n-k-1}\left(\bigwedge^3 H\right)\to\bigwedge^{k+3} H\otimes\bigwedge^{n-k-1}\left(\bigwedge^3 H\right), \end{align*} $$
$$ \begin{align*} \bigwedge^{k+2} H\otimes \bigwedge^{n-k}\left(\bigwedge^3 H\right)\to\bigwedge^{k+1} H\otimes \bigwedge^2 H\otimes\bigwedge^{n-k-1}\left(\bigwedge^3 H\right)\to\bigwedge^{k+3} H\otimes\bigwedge^{n-k-1}\left(\bigwedge^3 H\right), \end{align*} $$
which we denote by
![]() $\phi _k^n$
. We define
$\phi _k^n$
. We define
 $\Phi _n:\bigwedge ^{n}\left (\bigwedge ^3 H\right )\to \bigwedge ^{n+2} H$
as the composition
$\Phi _n:\bigwedge ^{n}\left (\bigwedge ^3 H\right )\to \bigwedge ^{n+2} H$
as the composition
![]() $\phi _{n-1}^n\circ \dotsb \circ \phi _1^n$
.
$\phi _{n-1}^n\circ \dotsb \circ \phi _1^n$
.
The calculations needed to prove the formula in Lemma 4.4 are simple but tedious and not very enlightening, and we will therefore leave them until the end of this section. Before proving the theorem, let us consider the following example, which illustrates the idea of the proof:
Example 4.5. Let
 $\sigma _n\in H_n\left (\mathcal {I}_{n+2}^1\right )$
denote the abelian cycle determined by the bounding pairs in Figure 7(a). With an appropriate choice of symplectic basis, it follows from Lemma 4.4 that
$\sigma _n\in H_n\left (\mathcal {I}_{n+2}^1\right )$
denote the abelian cycle determined by the bounding pairs in Figure 7(a). With an appropriate choice of symplectic basis, it follows from Lemma 4.4 that
for some nonzero integer
![]() $\lambda _n$
. As in the proof of Theorem 1.3, we can now act by
$\lambda _n$
. As in the proof of Theorem 1.3, we can now act by
![]() $T_{1,2}-\mathbf {1}$
, which gives us
$T_{1,2}-\mathbf {1}$
, which gives us
From Corollary 2.2, we can now draw the conclusion that
![]() $V_{1^{n+2}}$
lies in the image, since this is the top weight representation of
$V_{1^{n+2}}$
lies in the image, since this is the top weight representation of
 $\bigwedge ^{n+2} H$
.
$\bigwedge ^{n+2} H$
.
Similarly, let
 $\rho _n\in H_n\left (\mathcal {I}_{n+1}^1\right )$
denote the cycle determined by bounding pairs as in Figure 7(b). Let
$\rho _n\in H_n\left (\mathcal {I}_{n+1}^1\right )$
denote the cycle determined by bounding pairs as in Figure 7(b). Let
![]() $\Psi _n$
denote the composition of
$\Psi _n$
denote the composition of
![]() $\Phi _n$
with the contraction map
$\Phi _n$
with the contraction map
 $\bigwedge ^{n+2} H\to \bigwedge ^n H$
. If we once again order the basis appropriately, we see that
$\bigwedge ^{n+2} H\to \bigwedge ^n H$
. If we once again order the basis appropriately, we see that
and hence
![]() $V_{1^n}$
lies in the image. We can thus draw the conclusion that if
$V_{1^n}$
lies in the image. We can thus draw the conclusion that if
![]() $g\ge n+2$
, then
$g\ge n+2$
, then
![]() $V_{1^{n+2}}\oplus V_{1^n}$
are contained in the image of
$V_{1^{n+2}}\oplus V_{1^n}$
are contained in the image of
![]() $\psi _n$
, whereas if
$\psi _n$
, whereas if
![]() $g\ge n$
,
$g\ge n$
,
![]() $V_{1^n}$
is contained in the image.
$V_{1^n}$
is contained in the image.
With
![]() $\lambda $
and
$\lambda $
and
![]() $\mu $
as in Theorem 1.5, we see that for
$\mu $
as in Theorem 1.5, we see that for
![]() $i=1,\dotsc ,m$
, each of
$i=1,\dotsc ,m$
, each of
![]() $\sigma _{\lambda _i}$
and
$\sigma _{\lambda _i}$
and
![]() $\rho _{\mu _i}$
gives us a copy of
$\rho _{\mu _i}$
gives us a copy of
![]() $V_{1^{\lambda _i+2}}=V_{1^{\mu _i}}$
in
$V_{1^{\lambda _i+2}}=V_{1^{\mu _i}}$
in
 $\psi _{\lambda _i}\left (H_{\lambda _i}\left (\mathcal {I}_{\lambda _i+2}^1\right )\right )$
and
$\psi _{\lambda _i}\left (H_{\lambda _i}\left (\mathcal {I}_{\lambda _i+2}^1\right )\right )$
and
 $\psi _{\mu _i}\left (H_{\mu _i}\left (\mathcal {I}_{\mu _i+1}^1\right )\right )$
, respectively. The weight of these irreducibles is at least
$\psi _{\mu _i}\left (H_{\mu _i}\left (\mathcal {I}_{\mu _i+1}^1\right )\right )$
, respectively. The weight of these irreducibles is at least
![]() $3$
. Meanwhile,
$3$
. Meanwhile,
![]() $\rho _{\mu _{m+1}}$
and
$\rho _{\mu _{m+1}}$
and
![]() $\rho _{\mu _{m+2}}$
give us copies of
$\rho _{\mu _{m+2}}$
give us copies of
![]() $V_{1^{\mu _{m+1}}}$
and
$V_{1^{\mu _{m+1}}}$
and
![]() $V_{1^{\mu _{m+2}}}$
in
$V_{1^{\mu _{m+2}}}$
in
 $\psi _{\mu _{m+1}}\left (H_{\mu _{m+1}}\left (\mathcal {I}_{\mu _{m+1}+1}^1\right )\right )$
and
$\psi _{\mu _{m+1}}\left (H_{\mu _{m+1}}\left (\mathcal {I}_{\mu _{m+1}+1}^1\right )\right )$
and
 $\psi _{\mu _{m+2}}\left (H_{\mu _{m+2}}\left (\mathcal {I}_{\mu _{m+2}+1}^1\right )\right )$
, respectively, and here the weight may be lower.
$\psi _{\mu _{m+2}}\left (H_{\mu _{m+2}}\left (\mathcal {I}_{\mu _{m+2}+1}^1\right )\right )$
, respectively, and here the weight may be lower.
The idea for Theorem 1.5 is therefore to consider the product
 $\sigma _{\lambda _1}^{k_1}\rho _{\mu _1}^{l_1}\dotsm \sigma _{\lambda _{m}}^{k_{m}}\rho _{\mu _{m}}^{l_{m}}\rho _{\mu _{m+1}}^{l_{m+1}}\rho _{\mu _{m+2}}^{l_{m+1}}\cdot \mathbf {1}_{g-n-2k-l}$
. This is what gives us the condition that
$\sigma _{\lambda _1}^{k_1}\rho _{\mu _1}^{l_1}\dotsm \sigma _{\lambda _{m}}^{k_{m}}\rho _{\mu _{m}}^{l_{m}}\rho _{\mu _{m+1}}^{l_{m+1}}\rho _{\mu _{m+2}}^{l_{m+1}}\cdot \mathbf {1}_{g-n-2k-l}$
. This is what gives us the condition that
 $$ \begin{align*} g\ge \sum_{i=1}^{m+2}( k_i(\lambda_i+2)+l_i(\mu_i+1))=\lvert\lambda\rvert+\lvert\mu\rvert+2k+l=n+2k+l. \end{align*} $$
$$ \begin{align*} g\ge \sum_{i=1}^{m+2}( k_i(\lambda_i+2)+l_i(\mu_i+1))=\lvert\lambda\rvert+\lvert\mu\rvert+2k+l=n+2k+l. \end{align*} $$
4.3 Proof of the theorem
Using the foregoing, we may now prove the theorem:
Proof of Theorem 1.5, assuming Lemma 4.4. As stated previously, we will use the abelian cycle
 $$ \begin{align*} \sigma:=\sigma_{\lambda_1}^{k_1}\rho_{\mu_1}^{l_1}\dotsm\sigma_{\lambda_{m}}^{k_{m}}\rho_{\mu_{m}}^{l_{m}}\rho_{\mu_{m+1}}^{l_{m+1}}\rho_{\mu_{m+2}}^{l_{m+1}}\cdot\mathbf{1}_{g-n-2k-l}, \end{align*} $$
$$ \begin{align*} \sigma:=\sigma_{\lambda_1}^{k_1}\rho_{\mu_1}^{l_1}\dotsm\sigma_{\lambda_{m}}^{k_{m}}\rho_{\mu_{m}}^{l_{m}}\rho_{\mu_{m+1}}^{l_{m+1}}\rho_{\mu_{m+2}}^{l_{m+1}}\cdot\mathbf{1}_{g-n-2k-l}, \end{align*} $$
where
![]() $\sigma _{\lambda _i}$
and
$\sigma _{\lambda _i}$
and
![]() $\rho _{\mu _i}$
are defined as in Example 4.5. For
$\rho _{\mu _i}$
are defined as in Example 4.5. For
![]() $1\le i\le m+2$
and
$1\le i\le m+2$
and
![]() $1\le p\le k_i$
, we let
$1\le p\le k_i$
, we let
 $H_{\sigma _{\lambda _i}}^{(p)}$
denote the first homology of the subsurface corresponding to the pth
$H_{\sigma _{\lambda _i}}^{(p)}$
denote the first homology of the subsurface corresponding to the pth
![]() $\sigma _{\lambda _i}$
-factor, with
$\sigma _{\lambda _i}$
-factor, with
 $H_{\sigma _{\lambda _{m+1}}}^{(p)}$
and
$H_{\sigma _{\lambda _{m+1}}}^{(p)}$
and
 $H_{\sigma _{\lambda _{m+2}}}^{(p)}$
defined as 0 for all p. We define
$H_{\sigma _{\lambda _{m+2}}}^{(p)}$
defined as 0 for all p. We define
 $H_{\rho _{\mu _i}}^{(q)}$
similarly, so that
$H_{\rho _{\mu _i}}^{(q)}$
similarly, so that
 $$ \begin{align*} H=\bigoplus_{i=1}^{m+2}\left(\left(\bigoplus_{p=1}^{k_i} H_{\sigma_{\lambda_i}}^{(p)}\right)\oplus\left(\bigoplus_{q=1}^{l_i} H_{\rho_{\mu_i}}^{(q)}\right)\right)\oplus H_1\left(S_{g-n-2k-l}\right). \end{align*} $$
$$ \begin{align*} H=\bigoplus_{i=1}^{m+2}\left(\left(\bigoplus_{p=1}^{k_i} H_{\sigma_{\lambda_i}}^{(p)}\right)\oplus\left(\bigoplus_{q=1}^{l_i} H_{\rho_{\mu_i}}^{(q)}\right)\right)\oplus H_1\left(S_{g-n-2k-l}\right). \end{align*} $$
By Proposition 3.1 we have
 $$ \begin{align*} \psi_{n}(\sigma)\in \bigotimes_{i=1}^{m+2}\left(\left(\bigotimes_{p=1}^{k_i}\bigwedge^{\lambda_i}\bigwedge^3 H_{\sigma_{\lambda_i}}^{(p)}\right)\otimes\left(\bigotimes_{q=1}^{l_i}\bigwedge^{\mu_i}\bigwedge^3 H_{\rho_{\mu_i}}^{(q)}\right)\right)\subseteq \bigwedge^{n}\bigwedge^3 H. \end{align*} $$
$$ \begin{align*} \psi_{n}(\sigma)\in \bigotimes_{i=1}^{m+2}\left(\left(\bigotimes_{p=1}^{k_i}\bigwedge^{\lambda_i}\bigwedge^3 H_{\sigma_{\lambda_i}}^{(p)}\right)\otimes\left(\bigotimes_{q=1}^{l_i}\bigwedge^{\mu_i}\bigwedge^3 H_{\rho_{\mu_i}}^{(q)}\right)\right)\subseteq \bigwedge^{n}\bigwedge^3 H. \end{align*} $$
Define
 $F:=\Phi _{\lambda _1}^{\wedge k_1}\wedge \Psi _{\mu _1}^{\wedge l_1}\wedge \dotsb \wedge \Phi _{\lambda _{m}}^{\wedge k_{m}}\wedge \Psi _{\mu _{m}}^{\wedge l_{m}}\wedge \Psi _{\mu _{m+1}}^{\wedge l_{m+1}}\wedge \Psi _{\mu _{m+2}}^{\wedge l_{m+2}}$
. Since the direct summands
$F:=\Phi _{\lambda _1}^{\wedge k_1}\wedge \Psi _{\mu _1}^{\wedge l_1}\wedge \dotsb \wedge \Phi _{\lambda _{m}}^{\wedge k_{m}}\wedge \Psi _{\mu _{m}}^{\wedge l_{m}}\wedge \Psi _{\mu _{m+1}}^{\wedge l_{m+1}}\wedge \Psi _{\mu _{m+2}}^{\wedge l_{m+2}}$
. Since the direct summands
 $H_{\sigma _{\lambda _i}}^{(p)}$
and
$H_{\sigma _{\lambda _i}}^{(p)}$
and
 $H_{\rho _{\mu _i}}^{(q)}$
of H are pairwise orthogonal with respect to the symplectic form
$H_{\rho _{\mu _i}}^{(q)}$
of H are pairwise orthogonal with respect to the symplectic form
![]() $\omega $
, it follows from the definitions of
$\omega $
, it follows from the definitions of
![]() $\Phi _{\lambda _i}$
and
$\Phi _{\lambda _i}$
and
![]() $\Psi _{\lambda _i}$
that
$\Psi _{\lambda _i}$
that
 $$ \begin{align*} F(\psi_n(\sigma))\in\bigotimes_{i=1}^{m+2}\left(\left(\bigotimes_{p=1}^{k_i}\bigwedge^{\mu_i} H_{\sigma_{\lambda_i}}^{(p)}\right)\otimes\left(\bigotimes_{q=1}^{l_i}\bigwedge^{\mu_i}H_{\rho_{\mu_i}}^{(q)}\right)\right)\subseteq\bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}\left(\bigwedge^{\mu_{i}} H\right). \end{align*} $$
$$ \begin{align*} F(\psi_n(\sigma))\in\bigotimes_{i=1}^{m+2}\left(\left(\bigotimes_{p=1}^{k_i}\bigwedge^{\mu_i} H_{\sigma_{\lambda_i}}^{(p)}\right)\otimes\left(\bigotimes_{q=1}^{l_i}\bigwedge^{\mu_i}H_{\rho_{\mu_i}}^{(q)}\right)\right)\subseteq\bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}\left(\bigwedge^{\mu_{i}} H\right). \end{align*} $$
Since the top weight irreducibles of
 $\bigotimes _{i=1}^{m+2}\bigwedge ^{k_i+l_i}\left (\bigwedge ^{\mu _{i}} H\right )$
are precisely the top weight irreducibles of
$\bigotimes _{i=1}^{m+2}\bigwedge ^{k_i+l_i}\left (\bigwedge ^{\mu _{i}} H\right )$
are precisely the top weight irreducibles of
 $\bigotimes _{i=1}^{m+2}\bigwedge ^{k_i+l_i} V_{1^{\mu _i}}$
, we now want to apply Corollary 2.2. The representation
$\bigotimes _{i=1}^{m+2}\bigwedge ^{k_i+l_i} V_{1^{\mu _i}}$
, we now want to apply Corollary 2.2. The representation
 $\bigotimes _{i=1}^{m+2}\bigwedge ^{k_i+l_i}\left (\bigwedge ^{\mu _{i}} H\right )$
is a direct summand of
$\bigotimes _{i=1}^{m+2}\bigwedge ^{k_i+l_i}\left (\bigwedge ^{\mu _{i}} H\right )$
is a direct summand of
![]() $H^{\otimes (n+2k)}$
. Let us denote the projection map by
$H^{\otimes (n+2k)}$
. Let us denote the projection map by
![]() $\pi $
. If we choose a symplectic basis for each
$\pi $
. If we choose a symplectic basis for each
 $H_{\sigma _{\lambda _i}}^{(p)}$
and each
$H_{\sigma _{\lambda _i}}^{(p)}$
and each
 $H_{\sigma _{\mu _i}}^{(q)}$
, extend the union of these to a symplectic basis
$H_{\sigma _{\mu _i}}^{(q)}$
, extend the union of these to a symplectic basis
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
for H, and order this basis appropriately, we have
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
for H, and order this basis appropriately, we have
 $$ \begin{align*} \pi(a_1\otimes\dotsb\otimes a_{n+2k})\in\bigotimes_{i=1}^{m+2}\left(\left(\bigotimes_{p=1}^{k_i}\bigwedge^{\mu_i} H_{\sigma_{\lambda_i}}^{(p)}\right)\otimes\left(\bigotimes_{q=1}^{l_i}\bigwedge^{\mu_i}H_{\rho_{\mu_i}}^{(q)}\right)\right)\subseteq\bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}\left(\bigwedge^{\mu_{i}} H\right). \end{align*} $$
$$ \begin{align*} \pi(a_1\otimes\dotsb\otimes a_{n+2k})\in\bigotimes_{i=1}^{m+2}\left(\left(\bigotimes_{p=1}^{k_i}\bigwedge^{\mu_i} H_{\sigma_{\lambda_i}}^{(p)}\right)\otimes\left(\bigotimes_{q=1}^{l_i}\bigwedge^{\mu_i}H_{\rho_{\mu_i}}^{(q)}\right)\right)\subseteq\bigotimes_{i=1}^{m+2}\bigwedge^{k_i+l_i}\left(\bigwedge^{\mu_{i}} H\right). \end{align*} $$
From what we saw in Example 4.5, there is an element
 $$ \begin{align*} T\in\mathbb{Q}\left[\left(\prod_{i=1}^{m+2}\left(\prod_{p=1}^{k_i}\text{Sp}\left(H_{\sigma_{\lambda_i}}^{(p)}\right)\right)\times\left(\prod_{q=1}^{l_i}\text{Sp}\left(H_{\rho_{\mu_i}}^{(q)}\right)\right)\right)\times \text{Sp}\left(H_1\left(S_{g-n-2k-l}\right)\right)\right]\subseteq \mathbb{Q}[\text{Sp}(H)] \end{align*} $$
$$ \begin{align*} T\in\mathbb{Q}\left[\left(\prod_{i=1}^{m+2}\left(\prod_{p=1}^{k_i}\text{Sp}\left(H_{\sigma_{\lambda_i}}^{(p)}\right)\right)\times\left(\prod_{q=1}^{l_i}\text{Sp}\left(H_{\rho_{\mu_i}}^{(q)}\right)\right)\right)\times \text{Sp}\left(H_1\left(S_{g-n-2k-l}\right)\right)\right]\subseteq \mathbb{Q}[\text{Sp}(H)] \end{align*} $$
such that
□
4.4 Proof of Lemma 4.4
Now let us prove the lemma.
Proof of Lemma 4.4. We prove equation (2) by induction on n. For
![]() $n=1$
we have
$n=1$
we have
![]() $\psi _1=\tau $
and
$\psi _1=\tau $
and
![]() $\Phi _1=\text {Id}_{\bigwedge ^3 H}$
, so the identity holds with
$\Phi _1=\text {Id}_{\bigwedge ^3 H}$
, so the identity holds with
![]() $\lambda _1=1$
, by Proposition 3.1.
$\lambda _1=1$
, by Proposition 3.1.
Now suppose
![]() $n\ge 2$
and that
$n\ge 2$
and that
![]() $f_1,\dotsc ,f_n$
are bounding-pair maps that correspond to truly nested bounding pairs
$f_1,\dotsc ,f_n$
are bounding-pair maps that correspond to truly nested bounding pairs
![]() $(\alpha _1,\beta _1),\dotsc ,(\alpha _n,\beta _n)$
. We may pick a symplectic basis
$(\alpha _1,\beta _1),\dotsc ,(\alpha _n,\beta _n)$
. We may pick a symplectic basis
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
such that
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
such that
![]() $[\alpha _k]=a_{i_k}$
for
$[\alpha _k]=a_{i_k}$
for
![]() $1\le k\le n$
, where
$1\le k\le n$
, where
![]() $i_1\le \dotsb \le i_n$
and such that
$i_1\le \dotsb \le i_n$
and such that
![]() $a_1\wedge b_1+\dotsb +a_{i_k-1}\wedge b_{i_k-1}$
descends to a symplectic form of the homology of the surface not containing the original boundary component that we get by cutting along
$a_1\wedge b_1+\dotsb +a_{i_k-1}\wedge b_{i_k-1}$
descends to a symplectic form of the homology of the surface not containing the original boundary component that we get by cutting along
![]() $(\alpha _k,\beta _k)$
. For
$(\alpha _k,\beta _k)$
. For
![]() $n=2$
, a simple calculation shows that
$n=2$
, a simple calculation shows that
 $$ \begin{align*} & \Phi_2\circ\psi_2(A(f_1,f_2)) \\ &\quad =\phi_{1}^2\Big(\big(\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\big)\wedge\big(\left(a_1\wedge b_1+\dotsb+a_{i_2-1}\wedge b_{i_2-1}\right)\wedge a_{i_2}\big)\Big)\\ &\quad =-3\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge a_{i_2}. \end{align*} $$
$$ \begin{align*} & \Phi_2\circ\psi_2(A(f_1,f_2)) \\ &\quad =\phi_{1}^2\Big(\big(\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\big)\wedge\big(\left(a_1\wedge b_1+\dotsb+a_{i_2-1}\wedge b_{i_2-1}\right)\wedge a_{i_2}\big)\Big)\\ &\quad =-3\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge a_{i_2}. \end{align*} $$
Now we let
![]() $n\ge 3$
and assume that
$n\ge 3$
and assume that
 $$ \begin{align*} & \Phi_{n-1}\circ\psi_{n-1}\left(A\left(f_1,\dotsc,\hat{f_i},\dotsc ,f_{n}\right)\right) \\ &\quad =\lambda_{n-1}\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge\hat{a}_{i_k}\wedge \dotsb\wedge a_{i_n} \end{align*} $$
$$ \begin{align*} & \Phi_{n-1}\circ\psi_{n-1}\left(A\left(f_1,\dotsc,\hat{f_i},\dotsc ,f_{n}\right)\right) \\ &\quad =\lambda_{n-1}\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge\hat{a}_{i_k}\wedge \dotsb\wedge a_{i_n} \end{align*} $$
and
for some nonzero
![]() $\lambda _{n-1}\in \mathbb {Z}$
. Since
$\lambda _{n-1}\in \mathbb {Z}$
. Since
 $$ \begin{align*} \Phi_n=\phi_{n-1}^n\circ\left(\Phi_{n-1}\wedge\text{Id}_{\bigwedge^3 H}\right) \end{align*} $$
$$ \begin{align*} \Phi_n=\phi_{n-1}^n\circ\left(\Phi_{n-1}\wedge\text{Id}_{\bigwedge^3 H}\right) \end{align*} $$
and
 $$ \begin{align*} \psi_n(A(f_1,\dotsc,f_n))=(-1)^{n-k}\psi_{n-1}\left(A\left(f_1,\dotsc,\hat{f}_k,\dotsc,f_n\right)\right.\wedge \tau([f_k]) \end{align*} $$
$$ \begin{align*} \psi_n(A(f_1,\dotsc,f_n))=(-1)^{n-k}\psi_{n-1}\left(A\left(f_1,\dotsc,\hat{f}_k,\dotsc,f_n\right)\right.\wedge \tau([f_k]) \end{align*} $$
for each
![]() $k=1,\ldots ,n$
, it follows that
$k=1,\ldots ,n$
, it follows that
 $$ \begin{align*} & \Phi_{n}\circ\psi_n(A(f_1,\dotsc,f_n))=\lambda_{n-1}\cdot \phi_{n-1}^n \\ &\qquad \times \bigg((-1)^{n-1}\left(a_1\wedge b_1+\dotsb+a_{i_2-1}\wedge b_{i_2-1}\right)\wedge a_{i_2}\wedge \dotsb\wedge a_{i_n} \\ &\qquad \otimes \left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\\ &\qquad +\sum_{k=2}^n (-1)^{n-k}\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge\hat{a}_{i_k}\wedge \dotsb\wedge a_{i_n} \\ &\qquad \otimes \left(a_1\wedge b_1+\dotsb+a_{i_k-1}\wedge b_{i_k-1}\right)\wedge a_{i_k}\bigg). \end{align*} $$
$$ \begin{align*} & \Phi_{n}\circ\psi_n(A(f_1,\dotsc,f_n))=\lambda_{n-1}\cdot \phi_{n-1}^n \\ &\qquad \times \bigg((-1)^{n-1}\left(a_1\wedge b_1+\dotsb+a_{i_2-1}\wedge b_{i_2-1}\right)\wedge a_{i_2}\wedge \dotsb\wedge a_{i_n} \\ &\qquad \otimes \left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\\ &\qquad +\sum_{k=2}^n (-1)^{n-k}\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge\hat{a}_{i_k}\wedge \dotsb\wedge a_{i_n} \\ &\qquad \otimes \left(a_1\wedge b_1+\dotsb+a_{i_k-1}\wedge b_{i_k-1}\right)\wedge a_{i_k}\bigg). \end{align*} $$
A simple calculation shows that
 $$ \begin{align*} & \phi_{n-1}^n \left(\left(a_1\wedge b_1+\dotsb+a_{i_2-1}\wedge b_{i_2-1}\right)\wedge a_{i_2} \wedge \dotsb\wedge a_{i_n}\otimes\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\right) \\ &\quad =3(-1)^{n}\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge a_{i_n}, \end{align*} $$
$$ \begin{align*} & \phi_{n-1}^n \left(\left(a_1\wedge b_1+\dotsb+a_{i_2-1}\wedge b_{i_2-1}\right)\wedge a_{i_2} \wedge \dotsb\wedge a_{i_n}\otimes\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\right) \\ &\quad =3(-1)^{n}\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge a_{i_n}, \end{align*} $$
and similarly
 $$ \begin{align*} & \phi_{n-1}^n ((a_1\wedge b_1+\dotsb+a_{i_1-1} \wedge b_{i_1-1})\wedge a_{i_1}\wedge\dotsb\wedge\hat{a}_{i_k}\wedge \dotsb\wedge a_{i_n} \\ &\qquad \otimes (a_1\wedge b_1+\dotsb+a_{i_k-1}\wedge b_{i_k-1})\wedge a_{i_k}) \\ &\quad =(-1)^{n-k-1}(k+1)(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1})\wedge a_{i_1}\wedge\dotsb\wedge a_{i_n}. \end{align*} $$
$$ \begin{align*} & \phi_{n-1}^n ((a_1\wedge b_1+\dotsb+a_{i_1-1} \wedge b_{i_1-1})\wedge a_{i_1}\wedge\dotsb\wedge\hat{a}_{i_k}\wedge \dotsb\wedge a_{i_n} \\ &\qquad \otimes (a_1\wedge b_1+\dotsb+a_{i_k-1}\wedge b_{i_k-1})\wedge a_{i_k}) \\ &\quad =(-1)^{n-k-1}(k+1)(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1})\wedge a_{i_1}\wedge\dotsb\wedge a_{i_n}. \end{align*} $$
Thus we have
 $$ \begin{align*} \Phi_n\circ\psi_n(A(f_1,\dotsc,f_n))&= -\lambda_{n-1}\sum_{k=0}^{n}(k+1)\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge a_{i_n}\\ &=-\lambda_{n-1}\frac{(n+1)(n+2)}{2}\tau_n(A(f_1,\dotsc,f_n)), \end{align*} $$
$$ \begin{align*} \Phi_n\circ\psi_n(A(f_1,\dotsc,f_n))&= -\lambda_{n-1}\sum_{k=0}^{n}(k+1)\left(a_1\wedge b_1+\dotsb+a_{i_1-1}\wedge b_{i_1-1}\right)\wedge a_{i_1}\wedge\dotsb\wedge a_{i_n}\\ &=-\lambda_{n-1}\frac{(n+1)(n+2)}{2}\tau_n(A(f_1,\dotsc,f_n)), \end{align*} $$
which proves the formula.□
Remark 4.6. The idea to consider truly nested families of bounding pairs is taken from [Reference Church, Ellenberg and Farb1]. There the authors consider a family of
![]() $\text {Sp}(H_{\mathbb {Z}})$
-equivariant maps
$\text {Sp}(H_{\mathbb {Z}})$
-equivariant maps
 $\tau _n:H_n\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^{n+2} H$
that generalize the map
$\tau _n:H_n\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^{n+2} H$
that generalize the map
 $\tau :H_1\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^3 H$
to higher degree. We can note that
$\tau :H_1\left (\mathcal {I}_{g,1}\right )\to \bigwedge ^3 H$
to higher degree. We can note that
![]() $\tau _n$
and
$\tau _n$
and
![]() $\Phi _n\circ \psi _n$
have the same codomain. In [Reference Church, Ellenberg and Farb1, §3], the image of
$\Phi _n\circ \psi _n$
have the same codomain. In [Reference Church, Ellenberg and Farb1, §3], the image of
![]() $\tau _n$
on abelian cycles determined by truly nested families of bounding-pair maps is proven to satisfy
$\tau _n$
on abelian cycles determined by truly nested families of bounding-pair maps is proven to satisfy
with the notation being the same as in our Lemma 4.4. We can thus see that on such abelian cycles, the two maps agree, up to multiplication by a nonzero scalar. An interesting question is whether these maps agree on all of
![]() $H_n\left (\mathcal {I}_{g,1}\right )$
, so that the image of
$H_n\left (\mathcal {I}_{g,1}\right )$
, so that the image of
![]() $\tau _n$
is simply a subrepresentation of the image of
$\tau _n$
is simply a subrepresentation of the image of
![]() $\psi _n$
, or whether there is some other way to explicitly relate
$\psi _n$
, or whether there is some other way to explicitly relate
![]() $\psi _n$
and
$\psi _n$
and
![]() $\tau _n$
.
$\tau _n$
.
5 Proof of Theorem 1.11
As we have seen, abelian cycles determined by disjoint bounding-pair maps are a useful and simple tool for computing big parts of the image of
![]() $\psi _n$
. In this section we will give an explicit limitation on the images of such cycles. More specifically, we will prove the following theorem:
$\psi _n$
. In this section we will give an explicit limitation on the images of such cycles. More specifically, we will prove the following theorem:
Theorem 1.11. Set
![]() $n\ge 2$
and let
$n\ge 2$
and let
![]() $A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
be the subrepresentation generated by abelian cycles determined by pairwise disjoint bounding-pair maps. Then
$A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
be the subrepresentation generated by abelian cycles determined by pairwise disjoint bounding-pair maps. Then
![]() $\psi _n\left (A_n\left (\mathcal {I}_{g,1}\right )\right )$
is concentrated in weights
$\psi _n\left (A_n\left (\mathcal {I}_{g,1}\right )\right )$
is concentrated in weights
![]() $n, n+2,\dotsc ,3n$
. However,
$n, n+2,\dotsc ,3n$
. However,
![]() $\psi _n\left (H_n\left (\mathcal {I}_{g,1}\right )\right )$
also contains a subrepresentation of weight
$\psi _n\left (H_n\left (\mathcal {I}_{g,1}\right )\right )$
also contains a subrepresentation of weight
![]() $n-2$
for all
$n-2$
for all
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $g\gg 0$
. In particular,
$g\gg 0$
. In particular,
![]() $A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
is a proper subrepresentation for
$A_n\left (\mathcal {I}_{g,1}\right )\subset H_n\left (\mathcal {I}_{g,1}\right )$
is a proper subrepresentation for
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $g\gg 0$
.
$g\gg 0$
.
We will prove the following two claims of the theorem separately:
Claim 5.1.
The image
![]() $\psi _n\left (A_n\left (\mathcal {I}_{g,1}\right )\right )$
is concentrated in weights
$\psi _n\left (A_n\left (\mathcal {I}_{g,1}\right )\right )$
is concentrated in weights
![]() $n,n+2,\dotsc ,3n$
.
$n,n+2,\dotsc ,3n$
.
Claim 5.2.
For
![]() $n\ge 2$
and
$n\ge 2$
and
![]() $g\gg 0$
, the image of
$g\gg 0$
, the image of
![]() $\psi _n\left (H_n\left (\mathcal {I}_{g,1}\right )\right )$
contains an irreducible subrepresentation of weight
$\psi _n\left (H_n\left (\mathcal {I}_{g,1}\right )\right )$
contains an irreducible subrepresentation of weight
![]() $n-2$
.
$n-2$
.
To prove Claim 5.1, we will need to find a description of the tensor
![]() $\psi _n(A(f_1,\dotsc ,f_n))$
that we can work with, for any
$\psi _n(A(f_1,\dotsc ,f_n))$
that we can work with, for any
![]() $A(f_1,\dotsc ,f_n)\in A_n\left (\mathcal {I}_{g,1}\right )$
. This will be done using the following lemma:
$A(f_1,\dotsc ,f_n)\in A_n\left (\mathcal {I}_{g,1}\right )$
. This will be done using the following lemma:
Lemma 5.3. Set
![]() $A(f_1,\dotsc , f_n)\in A_n\left (\mathcal {I}_{g,1}\right )$
. Then there exists a Lagrangian subspace
$A(f_1,\dotsc , f_n)\in A_n\left (\mathcal {I}_{g,1}\right )$
. Then there exists a Lagrangian subspace
![]() $L\subset H$
, such that for
$L\subset H$
, such that for
![]() $k=1,\dotsc ,n$
, we have
$k=1,\dotsc ,n$
, we have
 $$ \begin{align*} \tau([f_k])\in\text{Im}\left(\bigwedge^2 L\otimes H\to \bigwedge^3 H\right). \end{align*} $$
$$ \begin{align*} \tau([f_k])\in\text{Im}\left(\bigwedge^2 L\otimes H\to \bigwedge^3 H\right). \end{align*} $$
Proof. Let us denote the bounding pair corresponding to
![]() $f_k$
by
$f_k$
by
![]() $(\alpha _k,\beta _k)$
, for
$(\alpha _k,\beta _k)$
, for
![]() $k=1,\dotsc , n$
. Note that since the bounding pairs are pairwise disjoint, the span of
$k=1,\dotsc , n$
. Note that since the bounding pairs are pairwise disjoint, the span of
![]() $\{[\alpha _1],\dotsc ,[\alpha _n]\}$
is an isotropic subspace of H, which we may denote by I. Recalling Proposition 3.1, we want to extend this to a Lagrangian subspace L in such a way that after the surface is cut by
$\{[\alpha _1],\dotsc ,[\alpha _n]\}$
is an isotropic subspace of H, which we may denote by I. Recalling Proposition 3.1, we want to extend this to a Lagrangian subspace L in such a way that after the surface is cut by
![]() $(\alpha _k,\beta _k)$
, for any k, L restricts to a Langrangian subspace of the first homologies of both of the closed surfaces obtained by filling in the boundary components with open disks.
$(\alpha _k,\beta _k)$
, for any k, L restricts to a Langrangian subspace of the first homologies of both of the closed surfaces obtained by filling in the boundary components with open disks.
Now let us cut the surface along all the bounding pairs and sew in open disks in all resulting boundary components, in order to get
![]() $n+1$
closed surfaces. For each such closed surface we may pick curves whose homology classes span a Lagrangian subspace of its first homology. These curves can be chosen so that they do not intersect the sewn-in disks or their boundaries and thus, viewed as curves in
$n+1$
closed surfaces. For each such closed surface we may pick curves whose homology classes span a Lagrangian subspace of its first homology. These curves can be chosen so that they do not intersect the sewn-in disks or their boundaries and thus, viewed as curves in
![]() $S_g$
they do not intersect any of our bounding pairs. This means that taking the span of the homology classes of these curves and all bounding pairs will still be an isotropic subspace of H. Let us denote this subspace by L. To see that L is Lagrangian, it suffices to note that the total genus of the subsurfaces we get by cutting along all bounding pairs is
$S_g$
they do not intersect any of our bounding pairs. This means that taking the span of the homology classes of these curves and all bounding pairs will still be an isotropic subspace of H. Let us denote this subspace by L. To see that L is Lagrangian, it suffices to note that the total genus of the subsurfaces we get by cutting along all bounding pairs is
![]() $g-\dim I$
, which means that this is also the dimension of the subspace of H spanned by the chosen curves. Since their classes are linearly independent of the classes in I, it follows that
$g-\dim I$
, which means that this is also the dimension of the subspace of H spanned by the chosen curves. Since their classes are linearly independent of the classes in I, it follows that
![]() $\dim L=g$
.
$\dim L=g$
.
By the construction of L through a selection of pairwise nonintersecting curves, it is clear that if the surface is cut along one bounding pair, the remaining curves all end up in only one of the connected components and are still pairwise nonintersecting. Since the genera of the resulting two subsurfaces add to
![]() $g-1$
, it follows that the span of the homology classes of the curves in either boundary component still form Lagrangian subspaces in their respective components, and hence L has the sought-after property.
$g-1$
, it follows that the span of the homology classes of the curves in either boundary component still form Lagrangian subspaces in their respective components, and hence L has the sought-after property.
This means that when the surface is cut along the bounding pair
![]() $(\alpha _k,\beta _k)$
, for any
$(\alpha _k,\beta _k)$
, for any
![]() $k=1,\dotsc ,n$
, we can find a symplectic basis for the first homology of the closed surface corresponding to the connected component not containing the original boundary component, such that its symplectic forms can be written
$k=1,\dotsc ,n$
, we can find a symplectic basis for the first homology of the closed surface corresponding to the connected component not containing the original boundary component, such that its symplectic forms can be written
 $$ \begin{align*} \omega_1=\sum_{i=1}^{g_1} a_i\wedge b_i, \end{align*} $$
$$ \begin{align*} \omega_1=\sum_{i=1}^{g_1} a_i\wedge b_i, \end{align*} $$
with
![]() $a_i\in L$
. It follows by Proposition 3.1 that
$a_i\in L$
. It follows by Proposition 3.1 that
which lies in
 $\text {Im}\left (\bigwedge ^2 L\otimes H\to \bigwedge ^3 H\right )$
, since
$\text {Im}\left (\bigwedge ^2 L\otimes H\to \bigwedge ^3 H\right )$
, since
![]() $[\alpha _k]\in L$
.
$[\alpha _k]\in L$
.
Using this we may now prove the claim:
Proof of Claim 5.1. By Lemma 5.3, we can find a Lagrangian
![]() $L\in H$
such that
$L\in H$
such that
 $$ \begin{align*} \psi_n(A(f_1,\dotsc,f_n))\in\text{Im}\left(\bigwedge^n\left(\bigwedge^2 L\otimes H\right)\to\bigwedge^n\left(\bigwedge^3 H\right)\right). \end{align*} $$
$$ \begin{align*} \psi_n(A(f_1,\dotsc,f_n))\in\text{Im}\left(\bigwedge^n\left(\bigwedge^2 L\otimes H\right)\to\bigwedge^n\left(\bigwedge^3 H\right)\right). \end{align*} $$
This means that if we apply the standard inclusion
 $\iota :\bigwedge ^n\left (\bigwedge ^3 H\right )\hookrightarrow H^{\otimes 3n}$
, each term of
$\iota :\bigwedge ^n\left (\bigwedge ^3 H\right )\hookrightarrow H^{\otimes 3n}$
, each term of
![]() $\psi _n(A(f_1,\dotsc ,f_n))$
lies in the subspace
$\psi _n(A(f_1,\dotsc ,f_n))$
lies in the subspace
up to a permutation of the factors. From this it follows that
![]() $\iota (\psi _n(A(f_1,\dotsc ,f_n)))$
must be mapped to zero by any composition of more than n contractions, and thus it cannot have a component in an irreducible subrepresentation of weight less than n.□
$\iota (\psi _n(A(f_1,\dotsc ,f_n)))$
must be mapped to zero by any composition of more than n contractions, and thus it cannot have a component in an irreducible subrepresentation of weight less than n.□
Remark 5.4. We have stated Claim 5.1 in the pointed case, but it holds in the unpointed case as well. To see this, define
 $U:=\left (\bigwedge ^3 H\right )/H$
, let
$U:=\left (\bigwedge ^3 H\right )/H$
, let
![]() $A_n\left (\mathcal {I}_{g}\right )\subseteq H_n\left (\mathcal {I}_g\right )$
be defined similarly as
$A_n\left (\mathcal {I}_{g}\right )\subseteq H_n\left (\mathcal {I}_g\right )$
be defined similarly as
![]() $A_n\left (\mathcal {I}_{g,1}\right )$
, and let
$A_n\left (\mathcal {I}_{g,1}\right )$
, and let
![]() $\psi _n':H_n\left (\mathcal {I}_g\right )\to \bigwedge ^n U$
be defined similarly as
$\psi _n':H_n\left (\mathcal {I}_g\right )\to \bigwedge ^n U$
be defined similarly as
![]() $\psi _n$
. We then have the commutative diagram
$\psi _n$
. We then have the commutative diagram

which proves that
![]() $\psi _n'\left (A_n\left (\mathcal {I}_{g}\right )\right )$
cannot contain any irreducibles of weight less than n. In [Reference Sakasai14], Sakasai uses elements of
$\psi _n'\left (A_n\left (\mathcal {I}_{g}\right )\right )$
cannot contain any irreducibles of weight less than n. In [Reference Sakasai14], Sakasai uses elements of
![]() $A_3\left (\mathcal {I}_{g}\right )$
to determine the stable image of (the dual map of)
$A_3\left (\mathcal {I}_{g}\right )$
to determine the stable image of (the dual map of)
![]() $\psi _3'$
, but his result leaves open whether or not the image contains a copy of
$\psi _3'$
, but his result leaves open whether or not the image contains a copy of
![]() $V_1$
.Footnote
2
Claim 5.1 illustrates why this could not be determined using Sakasai’s method.
$V_1$
.Footnote
2
Claim 5.1 illustrates why this could not be determined using Sakasai’s method.
Now it only remains to prove Claim 5.2. Before proving this, we need some additional background. Let
![]() $\mathcal {T}_g$
denote the Torelli space, the moduli space of Riemann surfaces of genus g endowed with a homology marking – that is, a choice of basis for the first homology group. This is the quotient of the Teichmüller space
$\mathcal {T}_g$
denote the Torelli space, the moduli space of Riemann surfaces of genus g endowed with a homology marking – that is, a choice of basis for the first homology group. This is the quotient of the Teichmüller space
![]() $\text {Teich}_g$
by the free action of
$\text {Teich}_g$
by the free action of
![]() $\mathcal {I}_g$
, which means that
$\mathcal {I}_g$
, which means that
![]() $H_*\left (\mathcal {I}_g\right )\cong H_*\left (\mathcal {T}_g\right )$
. In a similar way, we can construct the Torelli space
$H_*\left (\mathcal {I}_g\right )\cong H_*\left (\mathcal {T}_g\right )$
. In a similar way, we can construct the Torelli space
![]() $\mathcal {T}_{g,1}$
of pointed Riemann surfaces. The map given by forgetting the marked point, which we will denote by
$\mathcal {T}_{g,1}$
of pointed Riemann surfaces. The map given by forgetting the marked point, which we will denote by
![]() $\pi $
, makes
$\pi $
, makes
into a universal
![]() $S_g$
-bundle over
$S_g$
-bundle over
![]() $\mathcal {T}_g$
. We will use this to prove the claim.
$\mathcal {T}_g$
. We will use this to prove the claim.
Proof of Claim 5.2. First we consider the case
![]() $n=2$
. Let
$n=2$
. Let
![]() $[*]\in H_0\left (\mathcal {T}_g\right )$
be the class given by choosing a point
$[*]\in H_0\left (\mathcal {T}_g\right )$
be the class given by choosing a point
![]() $*\hookrightarrow \mathcal {T}_g$
. Pulling this map back along the universal bundle, we get the trivial bundle
$*\hookrightarrow \mathcal {T}_g$
. Pulling this map back along the universal bundle, we get the trivial bundle

which by integration over the fibers gives us a class
![]() $\pi ^!([*])$
in
$\pi ^!([*])$
in
![]() $H_2\left (S_g\right )$
, which is just the fundamental class
$H_2\left (S_g\right )$
, which is just the fundamental class
![]() $\left [S_g\right ]$
. By abuse of notation, we will use
$\left [S_g\right ]$
. By abuse of notation, we will use
![]() $\left [S_g\right ]$
to denote the corresponding class
$\left [S_g\right ]$
to denote the corresponding class
![]() $\pi ^!([*])\in H_2\left (\mathcal {T}_{g,1}\right )\cong H_2\left (\mathcal {I}_{g,1}\right )$
as well.
$\pi ^!([*])\in H_2\left (\mathcal {T}_{g,1}\right )\cong H_2\left (\mathcal {I}_{g,1}\right )$
as well.
To compute
![]() $\psi _2\left (\left [S_g\right ]\right )$
, we may compute its coproduct in
$\psi _2\left (\left [S_g\right ]\right )$
, we may compute its coproduct in
![]() $H_2\left (S_g\right )$
and then use functoriality. The coproduct can be computed using the diagram
$H_2\left (S_g\right )$
and then use functoriality. The coproduct can be computed using the diagram

where Z is the wedge of tori in Figure 8, that we get from
![]() $S_g$
by collapsing a subsurface of genus
$S_g$
by collapsing a subsurface of genus
![]() $0$
with g boundary components to a point.
$0$
with g boundary components to a point.

Figure 8 The quotient surface obtained from
![]() $S_g$
by collapsing a subsurface of genus
$S_g$
by collapsing a subsurface of genus
![]() $0$
with g boundary components to a point.
$0$
with g boundary components to a point.
The horizontal arrow on the second row of the diagram is an isomorphism, so we only need to compute the coproduct of the fundamental class
![]() $[Z]$
, which is equal to the sum
$[Z]$
, which is equal to the sum
![]() $[Z_1]+\dotsb +\left [Z_g\right ]\in H_2(Z)\cong H_2(Z_1)\oplus \dotsb \oplus H_2\left (Z_g\right )$
of the fundamental classes of the g tori. Since the homology of each torus is a bialgebra, we get
$[Z_1]+\dotsb +\left [Z_g\right ]\in H_2(Z)\cong H_2(Z_1)\oplus \dotsb \oplus H_2\left (Z_g\right )$
of the fundamental classes of the g tori. Since the homology of each torus is a bialgebra, we get
![]() $\Delta ([Z_k])=a_k\wedge b_k$
, where
$\Delta ([Z_k])=a_k\wedge b_k$
, where
![]() $\{a_k,b_k\}$
is a symplectic basis for
$\{a_k,b_k\}$
is a symplectic basis for
![]() $H_1(Z_k)$
. The union of these bases corresponds in a natural way to a symplectic basis
$H_1(Z_k)$
. The union of these bases corresponds in a natural way to a symplectic basis
![]() $\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of
$\left \{a_1,b_1,\dotsc ,a_g,b_g\right \}$
of
![]() $H_1\left (S_g\right )$
, so we get that
$H_1\left (S_g\right )$
, so we get that
![]() $\Delta \left (\left [S_g\right ]\right )=\omega $
, where
$\Delta \left (\left [S_g\right ]\right )=\omega $
, where
![]() $\omega $
is the symplectic form of
$\omega $
is the symplectic form of
![]() $H_1\left (S_g\right )$
.
$H_1\left (S_g\right )$
.
The map
![]() $S_g\to \mathcal {T}_{g,1}$
induces the so called ‘point-pushing’ map
$S_g\to \mathcal {T}_{g,1}$
induces the so called ‘point-pushing’ map
![]() $\pi _1\left (S_g\right )\to \mathcal {I}_{g,1}$
[Reference Farb and Margalit3, Chapters 4.2 and 6.4.2], and using this it follows that if
$\pi _1\left (S_g\right )\to \mathcal {I}_{g,1}$
[Reference Farb and Margalit3, Chapters 4.2 and 6.4.2], and using this it follows that if
![]() $c\in H_1\left (S_g\right )$
and we denote its image by
$c\in H_1\left (S_g\right )$
and we denote its image by
![]() $[c]\in H_1\left (\mathcal {I}_{g,1}\right )$
, then
$[c]\in H_1\left (\mathcal {I}_{g,1}\right )$
, then
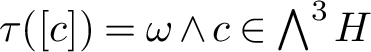 $\tau ([c])=\omega \wedge c\in \bigwedge ^3 H$
. Thus it follows by functoriality that
$\tau ([c])=\omega \wedge c\in \bigwedge ^3 H$
. Thus it follows by functoriality that
![]() $\psi _2\left (\left [S_g\right ]\right )$
is the image of
$\psi _2\left (\left [S_g\right ]\right )$
is the image of
![]() $\omega $
by the map
$\omega $
by the map
 $\bigwedge ^2 H\to \bigwedge ^2\left (\bigwedge ^3 H\right )$
, given by inserting the symplectic form in each factor. The class
$\bigwedge ^2 H\to \bigwedge ^2\left (\bigwedge ^3 H\right )$
, given by inserting the symplectic form in each factor. The class
 $\omega \in \bigwedge ^2 H$
generates the trivial representation, which means that
$\omega \in \bigwedge ^2 H$
generates the trivial representation, which means that
![]() $\psi _2\left (\left [S_g\right ]\right )$
has weight
$\psi _2\left (\left [S_g\right ]\right )$
has weight
![]() $0$
. This proves the claim in the case
$0$
. This proves the claim in the case
![]() $n=2$
.
$n=2$
.
The case
![]() $n=3$
has already been treated by Kupers and Randal-Williams [Reference Kupers and Randal-Williams11, §8], who proved that for
$n=3$
has already been treated by Kupers and Randal-Williams [Reference Kupers and Randal-Williams11, §8], who proved that for
![]() $g\gg 0$
, the image of the dual of the map
$g\gg 0$
, the image of the dual of the map
 $\psi _3:H_3\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^3\left (\bigwedge ^3 H\right )$
contains
$\psi _3:H_3\left (\mathcal {I}_{g}^1\right )\to \bigwedge ^3\left (\bigwedge ^3 H\right )$
contains
![]() $V_1$
, which implies that
$V_1$
, which implies that
![]() $V_1$
is also contained in the image of
$V_1$
is also contained in the image of
![]() $\psi _3:H_3\left (\mathcal {I}_{g,1}\right )$
, by the factorization
$\psi _3:H_3\left (\mathcal {I}_{g,1}\right )$
, by the factorization
 $\mathcal {I}_{g}^1\to \mathcal {I}_{g,1}\to \bigwedge ^3 H_{\mathbb {Z}}$
.
$\mathcal {I}_{g}^1\to \mathcal {I}_{g,1}\to \bigwedge ^3 H_{\mathbb {Z}}$
.
To prove the result for
![]() $n\ge 4$
, we will use the result for
$n\ge 4$
, we will use the result for
![]() $n=2$
. Let us suppose that
$n=2$
. Let us suppose that
![]() $n\ge 4$
and
$n\ge 4$
and
![]() $g\ge 2n-4$
. If we once again define
$g\ge 2n-4$
. If we once again define
 $U:=\left (\bigwedge ^3 H\right )/H$
, we have a commutative diagram
$U:=\left (\bigwedge ^3 H\right )/H$
, we have a commutative diagram

where the leftmost square commutes by the projection formula and the middle square commutes by functoriality of homology.
The composition of the arrows in the upper row is
![]() $\psi _n$
. Since the rightmost vertical arrow is surjective, and since we now know that the image of the composition
$\psi _n$
. Since the rightmost vertical arrow is surjective, and since we now know that the image of the composition
 $\psi _2\circ \pi ^!:H_0\left (\mathcal {T}_g\right )\to \bigwedge ^2\bigwedge ^3 H$
lies in weight
$\psi _2\circ \pi ^!:H_0\left (\mathcal {T}_g\right )\to \bigwedge ^2\bigwedge ^3 H$
lies in weight
![]() $0$
, it now suffices to find a class in
$0$
, it now suffices to find a class in
![]() $H_{n-2}\left (\mathcal {T}_g\right )$
whose image in
$H_{n-2}\left (\mathcal {T}_g\right )$
whose image in
 $\bigwedge ^{n-2} U$
has a nonzero component in weight
$\bigwedge ^{n-2} U$
has a nonzero component in weight
![]() $n-2$
. Note that this is impossible for
$n-2$
. Note that this is impossible for
![]() $n=3$
, since
$n=3$
, since
![]() $H_1\left (\mathcal {T}_g\right )\cong U\cong V_{1^3}$
, which is why this case had to be treated separately.
$H_1\left (\mathcal {T}_g\right )\cong U\cong V_{1^3}$
, which is why this case had to be treated separately.
For
![]() $m=n-2\ge 2$
, let us consider the image of the cycle
$m=n-2\ge 2$
, let us consider the image of the cycle
![]() $\rho _1^m$
, with
$\rho _1^m$
, with
![]() $\rho _1$
defined as in Example 4.5, under the map
$\rho _1$
defined as in Example 4.5, under the map
 $H_m\left (\mathcal {I}_{g}^1\right )\to H_m\left (\mathcal {I}_{g,1}\right )$
. We also get a corresponding abelian cycle in
$H_m\left (\mathcal {I}_{g}^1\right )\to H_m\left (\mathcal {I}_{g,1}\right )$
. We also get a corresponding abelian cycle in
![]() $H_m\left (\mathcal {I}_g\right )$
by forgetting the marked point. Abusing notation, we will use
$H_m\left (\mathcal {I}_g\right )$
by forgetting the marked point. Abusing notation, we will use
![]() $\rho _1^m$
to denote this class in either of these homology groups. Let
$\rho _1^m$
to denote this class in either of these homology groups. Let
 $\psi _m':H_m\left (\mathcal {I}_g\right )\to \bigwedge ^3 U$
be defined as in Remark 5.4. Then we have a commutative diagram
$\psi _m':H_m\left (\mathcal {I}_g\right )\to \bigwedge ^3 U$
be defined as in Remark 5.4. Then we have a commutative diagram

which means that we may work with the image of
![]() $\psi _m\left (\rho _1^m\right )$
in
$\psi _m\left (\rho _1^m\right )$
in
![]() $\bigwedge ^m U$
. The map
$\bigwedge ^m U$
. The map
 $\bigwedge ^3 H\to U$
can be described explicitly, by identifying U with the image of the map
$\bigwedge ^3 H\to U$
can be described explicitly, by identifying U with the image of the map
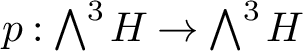 $p:\bigwedge ^3 H\to \bigwedge ^3 H$
defined by
$p:\bigwedge ^3 H\to \bigwedge ^3 H$
defined by
 $$ \begin{align*} p(x\wedge y\wedge z)=x\wedge y\wedge z -\frac{1}{g-1}C_3(x\wedge y\wedge z)\wedge\omega, \end{align*} $$
$$ \begin{align*} p(x\wedge y\wedge z)=x\wedge y\wedge z -\frac{1}{g-1}C_3(x\wedge y\wedge z)\wedge\omega, \end{align*} $$
where
 $C_3:\bigwedge ^3 H\to H$
is the contraction map. Note that this image is precisely the subrepresentation of traceless tensors in
$C_3:\bigwedge ^3 H\to H$
is the contraction map. Note that this image is precisely the subrepresentation of traceless tensors in
 $\bigwedge ^3 H$
. With a suitable choice of basis of H, we get
$\bigwedge ^3 H$
. With a suitable choice of basis of H, we get
 $$ \begin{align*} & (p^{\wedge m}\circ\psi_m)\left(\rho_1^m\right) \\ &\quad =\left(a_1\wedge b_1\wedge a_{m+1}-\frac{1}{g-1}\omega\wedge a_{m+1}\right)\wedge\dotsb\wedge \left(a_{m}\wedge b_m\wedge a_{2m}-\frac{1}{g-1}\omega\wedge a_{2m}\right). \end{align*} $$
$$ \begin{align*} & (p^{\wedge m}\circ\psi_m)\left(\rho_1^m\right) \\ &\quad =\left(a_1\wedge b_1\wedge a_{m+1}-\frac{1}{g-1}\omega\wedge a_{m+1}\right)\wedge\dotsb\wedge \left(a_{m}\wedge b_m\wedge a_{2m}-\frac{1}{g-1}\omega\wedge a_{2m}\right). \end{align*} $$
We want to show that this has a nonzero component in an irreducible subrepresentation of weight m, so we apply the map
 $\bigwedge ^m\left (\bigwedge ^3 H\right )\to \bigwedge ^{3m} H$
and then contract m times. If we let
$\bigwedge ^m\left (\bigwedge ^3 H\right )\to \bigwedge ^{3m} H$
and then contract m times. If we let
![]() $[m]=\{1,\dotsc ,n\}$
, the image in
$[m]=\{1,\dotsc ,n\}$
, the image in
 $\bigwedge ^{3m} H$
can be written as
$\bigwedge ^{3m} H$
can be written as
 $$ \begin{align*} &\left(\sum_{k=0}^m\frac{(-1)^{k}}{(g-1)^k}\sum_{\left\{i_1,\dotsc,i_k\right\}\subset [m]}\omega^{\wedge k}\wedge a_1\wedge b_1\wedge \dotsb\wedge\widehat{a_{i_1}\wedge b_{i_1}}\wedge\dotsb\wedge\widehat{a_{i_k}\wedge b_{i_k}}\wedge\dotsb\wedge a_m\wedge b_m\right)\\ &\quad \wedge a_{m+1}\wedge\dotsb\wedge a_{2m}. \end{align*} $$
$$ \begin{align*} &\left(\sum_{k=0}^m\frac{(-1)^{k}}{(g-1)^k}\sum_{\left\{i_1,\dotsc,i_k\right\}\subset [m]}\omega^{\wedge k}\wedge a_1\wedge b_1\wedge \dotsb\wedge\widehat{a_{i_1}\wedge b_{i_1}}\wedge\dotsb\wedge\widehat{a_{i_k}\wedge b_{i_k}}\wedge\dotsb\wedge a_m\wedge b_m\right)\\ &\quad \wedge a_{m+1}\wedge\dotsb\wedge a_{2m}. \end{align*} $$
By contracting each term m times, we get
 $$ \begin{align*} &\frac{1}{(g-1)^m}\sum_{k=0}^m(-1)^k\binom{m}{k}(g-1)^{m-k}(g-2m+1)^k a_{m+1}\wedge\dotsb\wedge a_{2m} \\ &\quad=\frac{(2m-2)^m}{(g-1)^m}a_{m+1}\wedge\dotsb\wedge a_{2m}, \end{align*} $$
$$ \begin{align*} &\frac{1}{(g-1)^m}\sum_{k=0}^m(-1)^k\binom{m}{k}(g-1)^{m-k}(g-2m+1)^k a_{m+1}\wedge\dotsb\wedge a_{2m} \\ &\quad=\frac{(2m-2)^m}{(g-1)^m}a_{m+1}\wedge\dotsb\wedge a_{2m}, \end{align*} $$
which is nonzero, since
![]() $m=n-2\ge 2$
, and which contracts to zero and thus lies in
$m=n-2\ge 2$
, and which contracts to zero and thus lies in
![]() $V_{1^m}\subset \bigwedge ^m H$
. This proves the claim for
$V_{1^m}\subset \bigwedge ^m H$
. This proves the claim for
![]() $n\ge 4$
.□
$n\ge 4$
.□
Remark 5.5. The proof of Claim 5.2 is heavily inspired by [Reference Church, Ellenberg and Farb1, §4], where the authors compute the image of
![]() $\tau _n\circ \pi ^!$
for truly nested families of bounding-pair maps. In our situation, it would be reasonable to expect the formula
$\tau _n\circ \pi ^!$
for truly nested families of bounding-pair maps. In our situation, it would be reasonable to expect the formula
 $$ \begin{align*} \psi_{n}\left(\pi^!\pi_*A(f_1,\dotsc,f_{n-2})\right)=\tau([f_1])\wedge\dotsb\wedge\tau([f_{n-2}])\wedge\psi_2\left(\left[S_g\right]\right) \end{align*} $$
$$ \begin{align*} \psi_{n}\left(\pi^!\pi_*A(f_1,\dotsc,f_{n-2})\right)=\tau([f_1])\wedge\dotsb\wedge\tau([f_{n-2}])\wedge\psi_2\left(\left[S_g\right]\right) \end{align*} $$
to hold for any abelian cycle
![]() $A(f_1,\dotsc ,f_{n-2})\in H_{n-2}\left (\mathcal {I}_{g,1}\right )$
, which would prove Claim 5.2 for
$A(f_1,\dotsc ,f_{n-2})\in H_{n-2}\left (\mathcal {I}_{g,1}\right )$
, which would prove Claim 5.2 for
![]() $n\ge 3$
directly from the case
$n\ge 3$
directly from the case
![]() $n=2$
. We have not, however, been able to verify or disprove this.
$n=2$
. We have not, however, been able to verify or disprove this.
Acknowledgment
I would like to thank my PhD supervisor, Dan Petersen, whose suggestions led me to investigate the topics of this paper and whose supervision and support have been invaluable throughout the project.
Competing Interest
None.