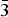II. EXPERIMENTAL

The ternary Pd₂HgSe₃ phase was prepared using silica glass tube technique. Stoichiometric amounts of palladium (Aldrich 99.99%), mercury (Lachema, 99.999%), and selenium (Aldrich, 99.999%) were used as starting materials for synthesis. The following amounts of reagents were used for synthesis: 0.0658 g of palladium (0.6180 mmol), 0.0620 g of mercury (0.3090 mmol), and 0.0732 g of selenium (0.9270 mmol). The evacuated tube with the carefully weighted charge was at first heated at 800 °C for 24 h. After cooling in a cold-water bath, the charge was removed from the tube and gently ground to powder in acetone using a pestle and an agate mortar. Afterwards, the pulverized charge was again sealed in an evacuated silica glass tube and heated at 400 °C for 41 days. After heating, the sample was quenched in a cold-water bath.

Chemical analyses (EMPA) of Pd₂HgSe₃ phase were performed with a Cameca SX-100 electron microprobe using the wavelength-dispersion mode. Accelerating voltage was set to 15 kV, and the beam current was 10 nA. X-ray lines and standards were as follows: SeLα (pure Se), PdLα (pure Pd), and HgMα (HgS). Data were acquired (11 analyses) from different spots on several grains and then averaged. The chemical data yielded an overall composition Pd 32.53 wt.%, Hg 30.19 wt.%, Se 36.52 wt.%, and total 99.24 wt.% with empirical formula Pd_2.00Hg_0.98Se_3.02 calculated on six atoms per formula unit.

Ideally, the experimental product should consist only of title phase Pd₂HgSe₃. The subsequent phase and Rietveld analysis of diffraction data revealed small admixture of Pd₈Hg₃Se₉ (~12 wt.%) and HgSe (~2 wt.%) in the experimental product. These admixtures have very likely occurred because of possible presence of small amounts of selenium and mercury in a vapour phase during the initial stages of solid-state reactions.

III. STRUCTURE REFINEMENT

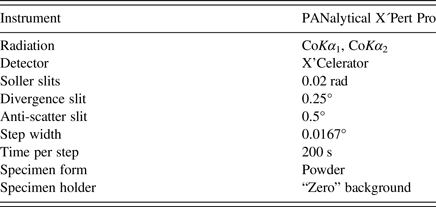
The powder X-ray diffraction pattern of the sample was collected in the Bragg–Brentano geometry on an X'Pert Pro PANalytical diffractometer, equipped with an X'Celerator detector using CoKα radiation. An iron filter, placed in a diffracted beam, was used to produce pseudo-monochromatic radiation. To minimize background, a flat low-background silicon wafer was used as the specimen holder. The data were collected in the range from 6 to 130° 2θ. A full-width at half maximum of 0.106° 2θ was obtained at 19.497° 2θ indicating well-crystalized sample of Pd₂HgSe₃. The experimental details are summarized in Table I. With the exception of a few peaks attributable to Pd₈Hg₃Se₉ (~12 wt.%) and HgSe (~2 wt.%), the diffraction pattern of Pd₂HgSe₃ was indexed using the DICVOL06 programme (Louër and Boultif, Reference Louër and Boultif2007) on the basis of a trigonal cell listed in Table II. The unit cell suggested by Drábek et al. (Reference Drábek, Vymazalová and Laufek2014) was confirmed. The crystal structure of Pd₂HgSe₃ was subsequently refined by the Rietveld method for powder X-ray diffraction data using the FullProf programme (Rodriguez-Carvajal, Reference Rodriguez-Carvajal1990). The starting structural model for Pd₂HgSe₃ was derived from the structural data of Pt₂HgSe₃ phase, which is known as a mineral jacutingaite (Vymazalová et al., Reference Vymazalová, Laufek, Drábek, Cabral, Haloda, Sidorinová, Lehmnn, Galbiatti and Drahokoupil2012). This mineral phase has very similar unit-cell parameters [a = 7.3477(2), c = 5.2955(1) Å] and analogous stoichiometry. Only the Pt atoms were replaced by Pd atoms and the structure was subsequently refined. The structure data for Pd₈Hg₃Se₉ and HgSe were taken from the papers of Laufek et al. (Reference Laufek, Vymazalová, Drábek, Navrátil and Drahokoupil2014) and Earley (Reference Earley1950), respectively. During the Rietveld refinement, the scale factors and unit-cell parameters of these two phases were refined, while their fractional coordinates and displacement parameters were fixed.

Table I. Experimental conditions.

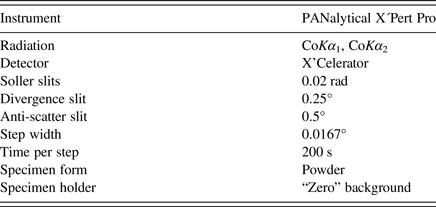
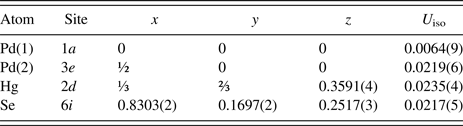
Table II. Refined parameters for Pd₂HgSe₃ [room temperature, space group P $\bar 3$ m1. a = 7.3096(2) Å, c = 5.2829(1) Å, V = 244.45(1) Å³, D _c =  8.84 g/cm³, Z = 2, R _p = 1.53%, R _wp = 2.21%, and R _B = 4.37%, F(000) = 502, μ = 206.3 mm⁻¹].

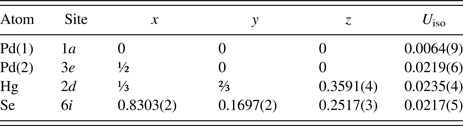
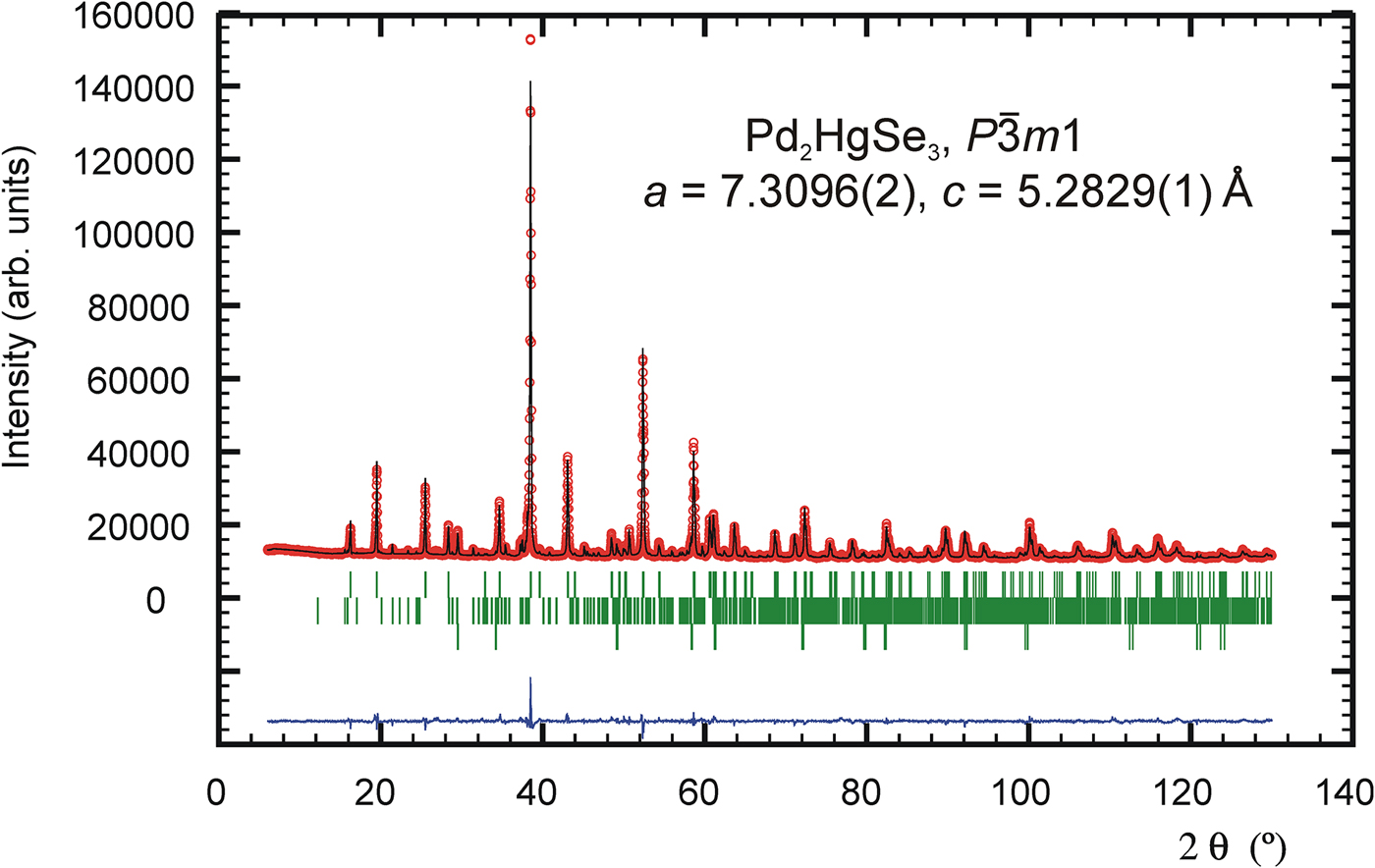
The pseudo-Voigt function was used to generate the shape of the diffraction peaks in the subsequent Rietveld refinement. The background was modelled by the linear interpolation between consecutive breakpoints in the pattern. The refined parameters of Pd₂HgSe₃ include those describing the peak shape and width, peak asymmetry, unit-cell parameters, fractional coordinates, March–Dollase model of preferred orientation along [001] and isotropic displacement parameters for all atoms. Peak asymmetry was modelled using the correction of Bérar and Baldinozzi (Reference Bérar and Baldinozzi1993); two parameters were refined. In total, 24 parameters were refined; 138 reflections were observed. The refinement of preferred orientation correction significantly improved the Rietveld fit; the R _wp factor decreased from 4.78 to 2.21%. The G ₁ parameter of the March–Dollase correction model was refined to 0.761(1). The final cycles of refinement converged to the residual factors: R _B = 4.37%, R _wp = 2.21%, and R _p = 1.53%. The refined atomic coordinates are given in Table II. Figure 1 shows the final Rietveld plot.

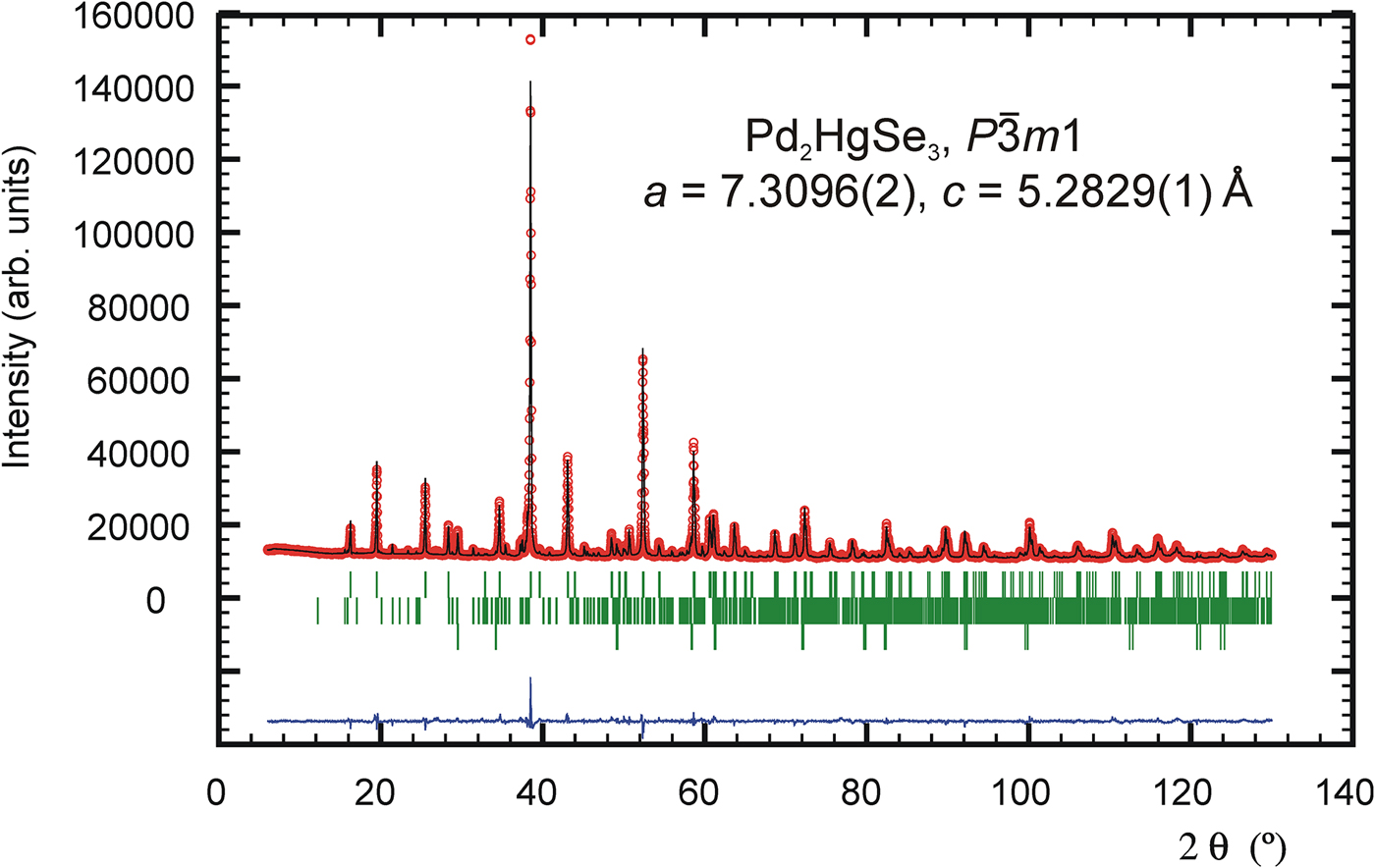
Figure 1. (Color online) The observed (circles), calculated (solid line), and difference Rietveld profiles for Pd₂HgSe₃. The upper reflections bars correspond to Pd₂HgSe₃; the middle and lower bars to 12 and 2 wt.% of Pd₈Hg₃Se₉ and HgSe impurities, respectively.

IV. RESULTS AND DISCUSSION

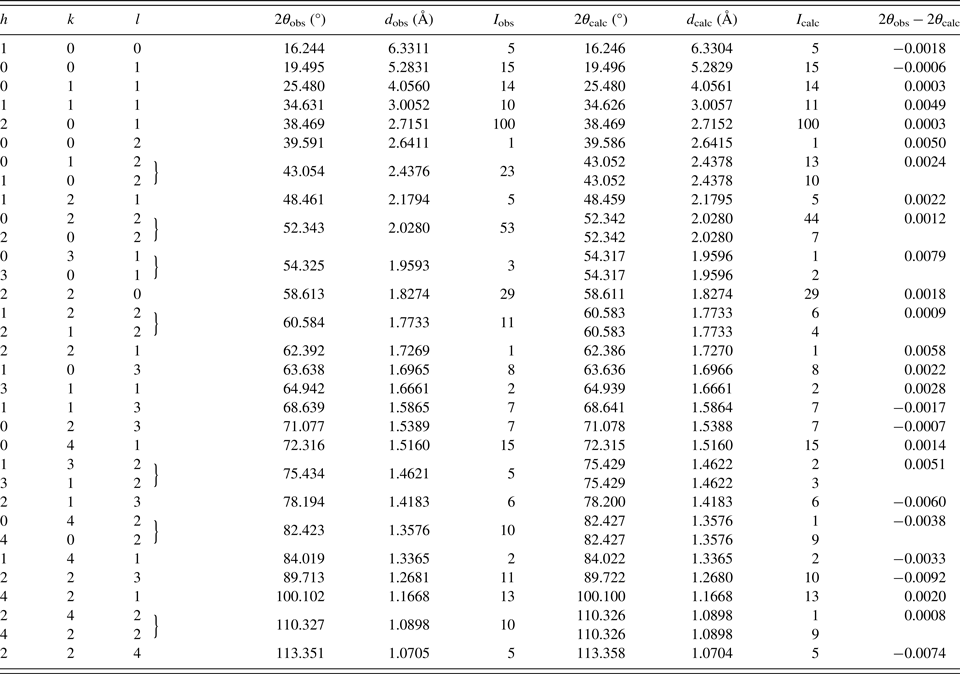
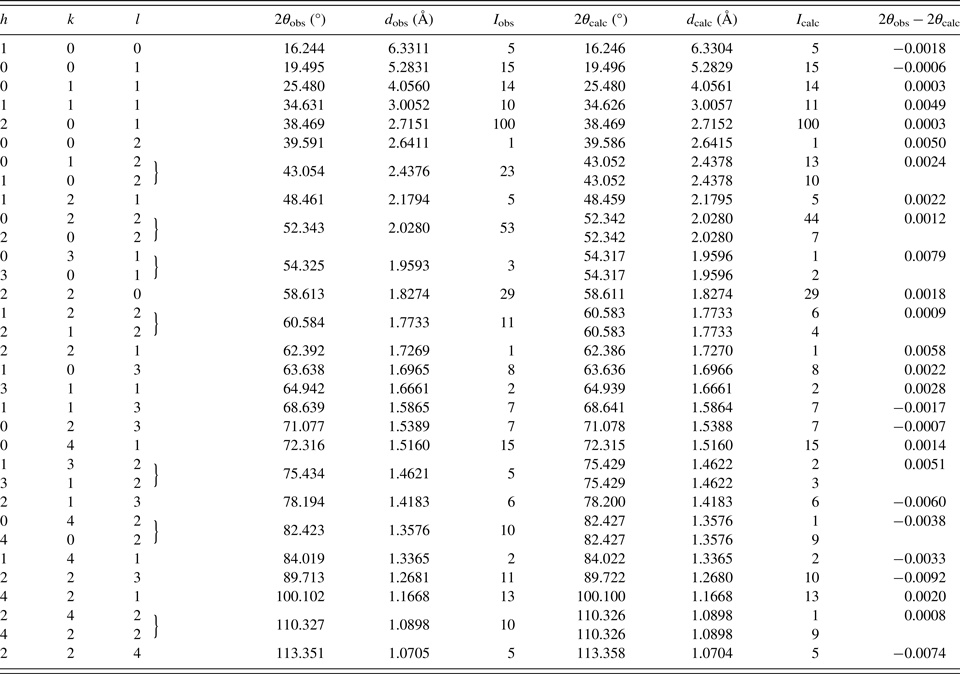
The powder diffraction data are listed in Table III. The observed values of diffraction positions, d-spacing, and intensities were extracted by the Topas programme (Bruker AXS, 2014) using the split Pearson VII profile function. The 2θ _obs and d _obs were corrected for the refined sample displacement correction. No significant diffraction overlap between diffraction patterns of Pd₂HgSe₃ and HgSe occurs. The phase Pd₈Hg₃Se₉ (Pmmn, V = 782.5 Å) shows relatively complex diffraction pattern. Consequently, roughly above 60° of 2θ, there is a noticeable diffraction overlap between patterns of Pd₂HgSe₃ and Pd₈Hg₃Se₉. However, considering the low content of Pd₈Hg₃Se₉ in a sample and its complex diffraction pattern, its intensity contribution to the diffraction pattern of Pd₂HgSe₃ above 60° of 2θ is negligible.

Table III. Powder diffraction data for Pd₂HgSe₃ (CoKα radiation) (reflections with I _obs and I _calc < 1 are not shown in the table).

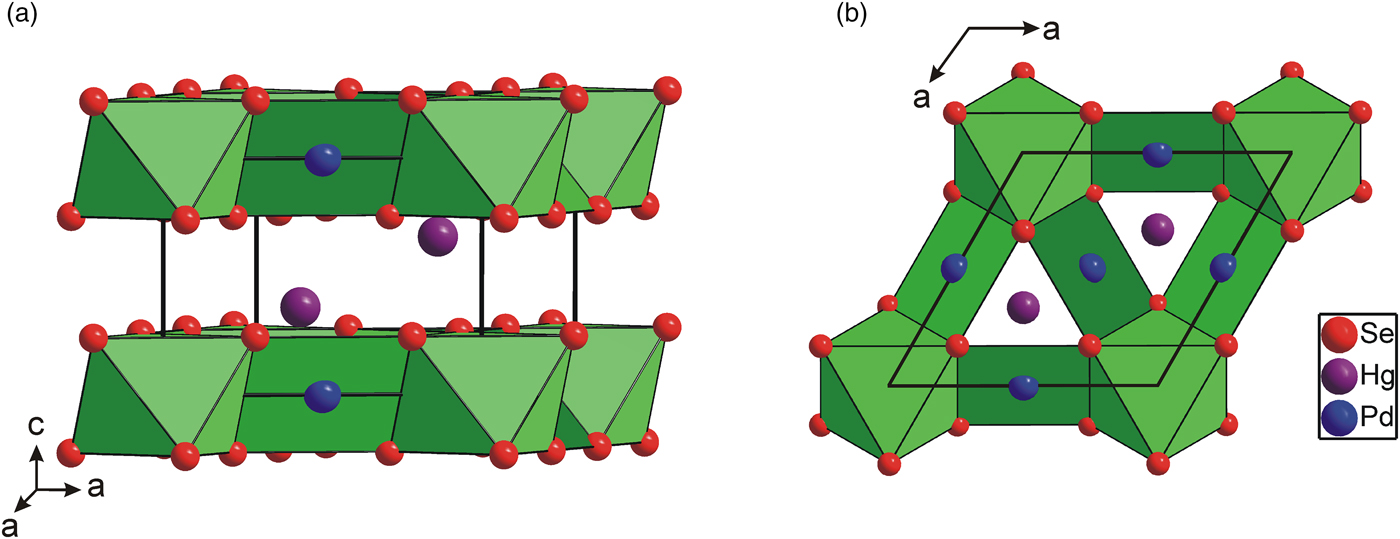
The crystal structure of Pd₂HgSe₃ is isostructural with mineral jacutingaite, Pt₂HgSe₃ (Vymazalová et al., Reference Vymazalová, Laufek, Drábek, Cabral, Haloda, Sidorinová, Lehmnn, Galbiatti and Drahokoupil2012), and synthetic phases Pt₄Tl₂S₆, Pt₄Tl₂Se₆, Pt₄Tl₂Te₆, and Pd₄Tl₂Se₆ (Bronger and Bonsmann, Reference Bronger and Bonsmann1995). The structure contains two independent Pd positions, one Hg and one Se position. The Pd(1) atom is surrounded by six Se atoms at 2.526(2) Å forming a slightly distorted octahedron with intra-octahedral Se–Pd(1)–Se angles 85.14(5)° and 94.85(5)° instead of 90° being for a regular octahedron. Unlike the Pd(1) atom, the Pd(2) atom forms a square planar configuration with four Se atoms at a distance of 2.478(2) Å. The coordination of the Pd(2) atom is further completed by two Hg atoms at 2.837(1) Å. The vector of Pd–Hg bonds is almost perpendicular to the [PdSe₄] squares. This Pd–Hg distance is comparable to 2.82 Å found in PdHg (Terada and Cagle, Reference Terada and Cagle1960) indicating significant Pd–Hg bonding interactions.

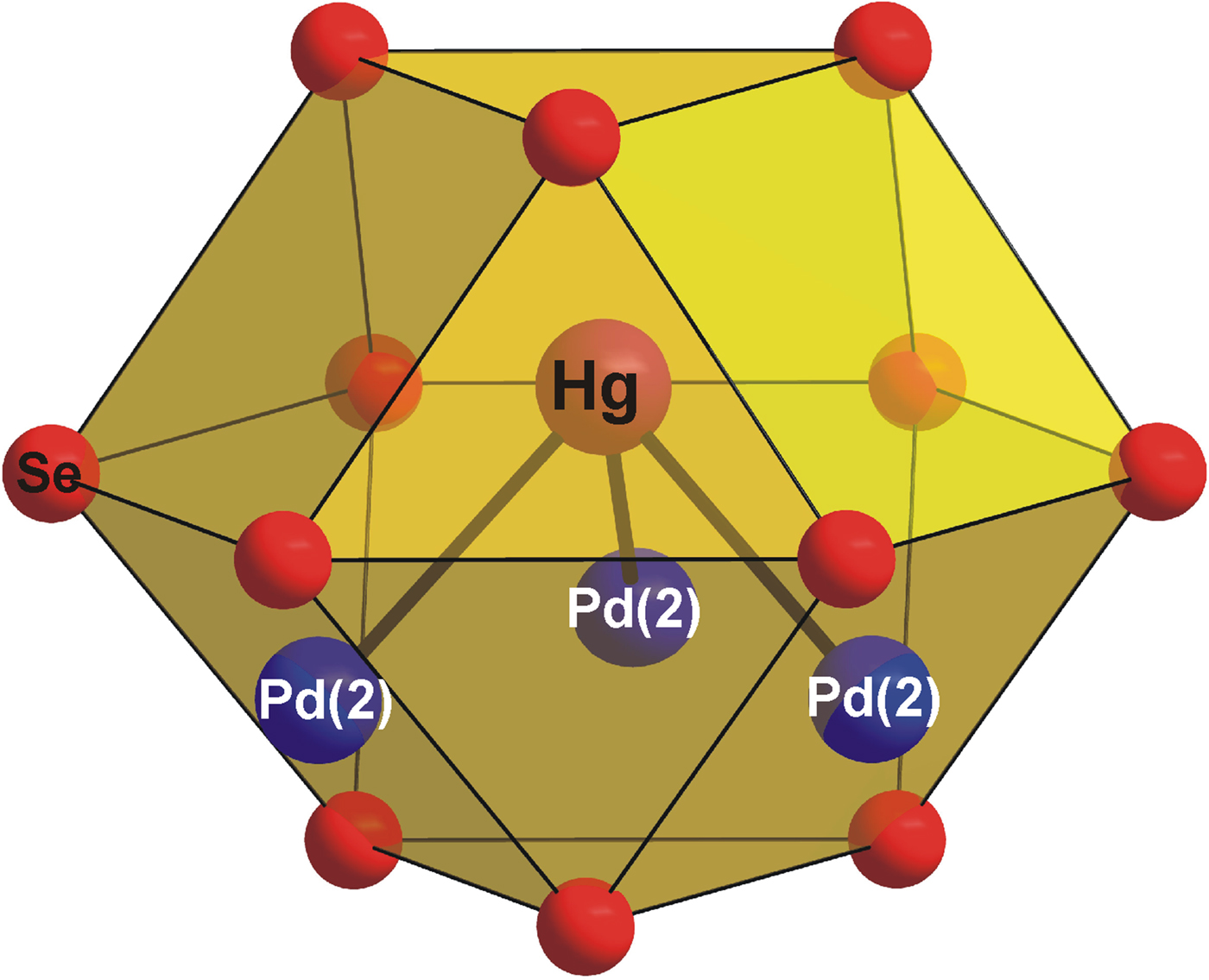
As is shown in Figure 2, the [PdSe₆] octahedra shares six Se–Se edges with adjacent [PdSe₄] squares forming layers parallel to the (001) plane. The layers are stacked along the c-axis and show the AA type of stacking. It is interesting to note that the [PdSe₆] octahedra have a shared edge length [d _Se–Se = 3.419(2) Å] considerably shorter than its unshared edge [d _Se–Se = 3.721(2) Å], which is in agreement with the Pauling third rule (Pauling, Reference Pauling1929). The [PdSe₄] squares also show two different Se–Se edge lengths: 3.419(2) and 3.588(2) Å for the shared and unshared edges, respectively. This brings the Pd–Pd separation to 3.655(1) Å and consequently reduces the Coulombic repulsion between cations. Hg atoms show three short Pd and Se contacts at 2.837(1) and 2.918(2) Å. For the sake of convenient structure description, Hg atoms can be considered to occupy the anti-cubooctahedral voids formed by Se atoms with the 3 + 6 + 3 bonding scheme. However, the next six and three Se atoms are at distances of 3.698(2) and 3.834(2) Å, respectively, and thus represent only weak Hg–Se bonds. In addition, Hg atom has three Pd contacts at 2.837(1) Å forming [HgPd₃] trigonal pyramid (Figure 3). Selected interatomic distances compared with those found in isostructural Pt₂HgSe₃ are summarized in Table IV. The relatively high values of displacement parameters (U _iso) of Pd(2), Hg, and Se atoms (see Table II) might be an indirect indication of possible structural disorder; however, no broad peaks or apparent peak asymmetry have been observed in powder diffraction pattern of Pd₂HgSe₃.

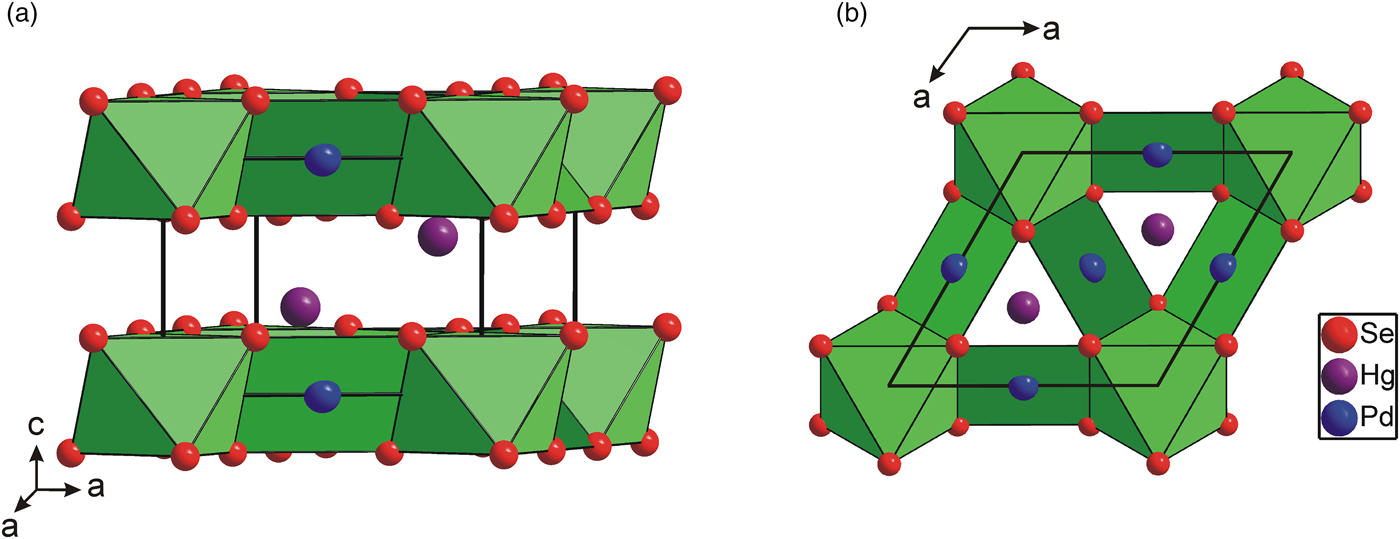
Figure 2. (Color online) Polyhedral representation of Pd₂HgSe₃ crystal structure showing the [Pd(1)Se₆] octahedra and [Pd(2)Se₄] squares. (a) Perspective view, (b) view along the c-axis.

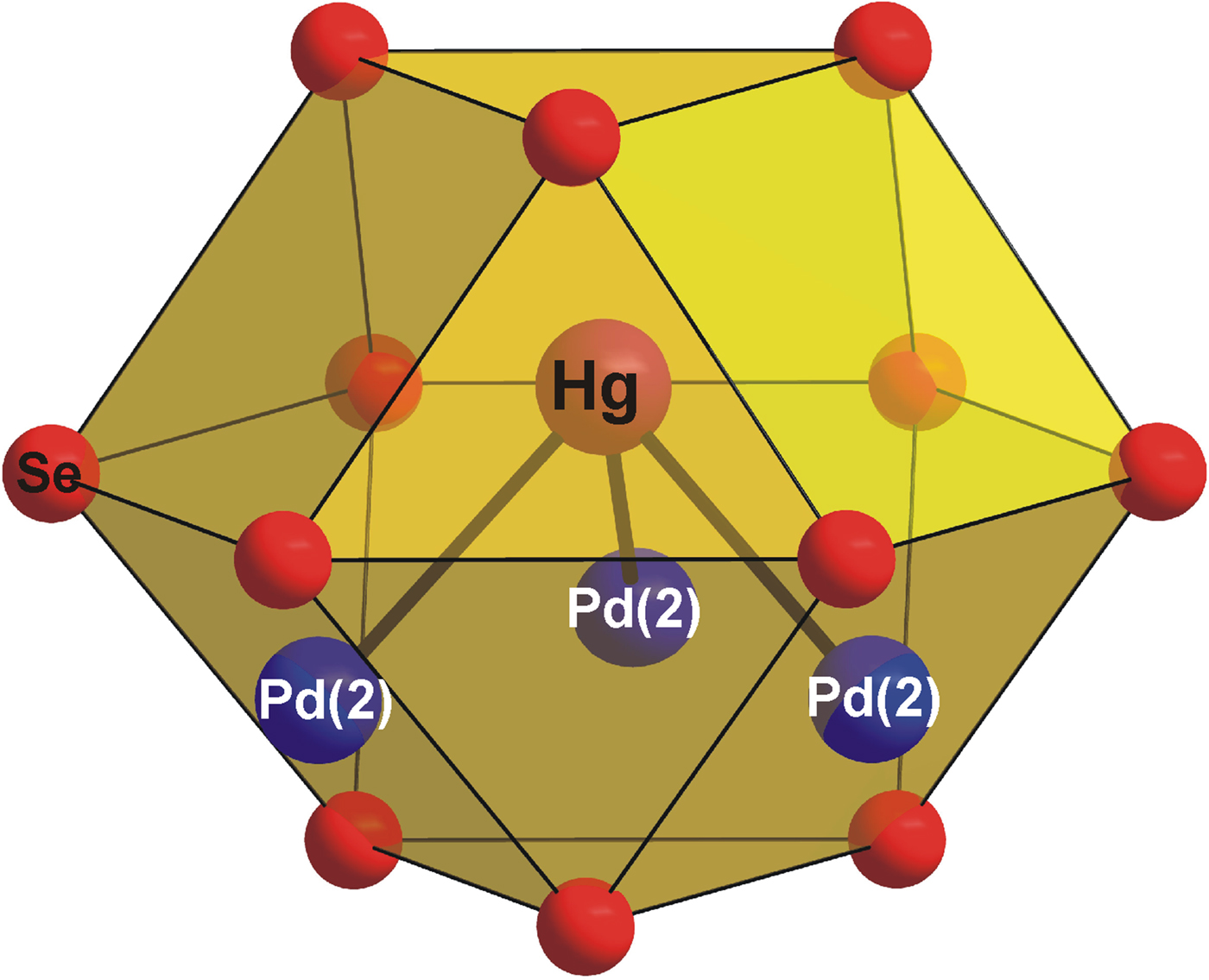
Figure 3. (Color online) The coordination polyhedra of Hg in the Pd₂HgSe₃ crystal structure.

Table IV. Selected interatomic distances (Å) in isostructural compounds Pd₂HgSe₃ and Pt₂HgSe₃.

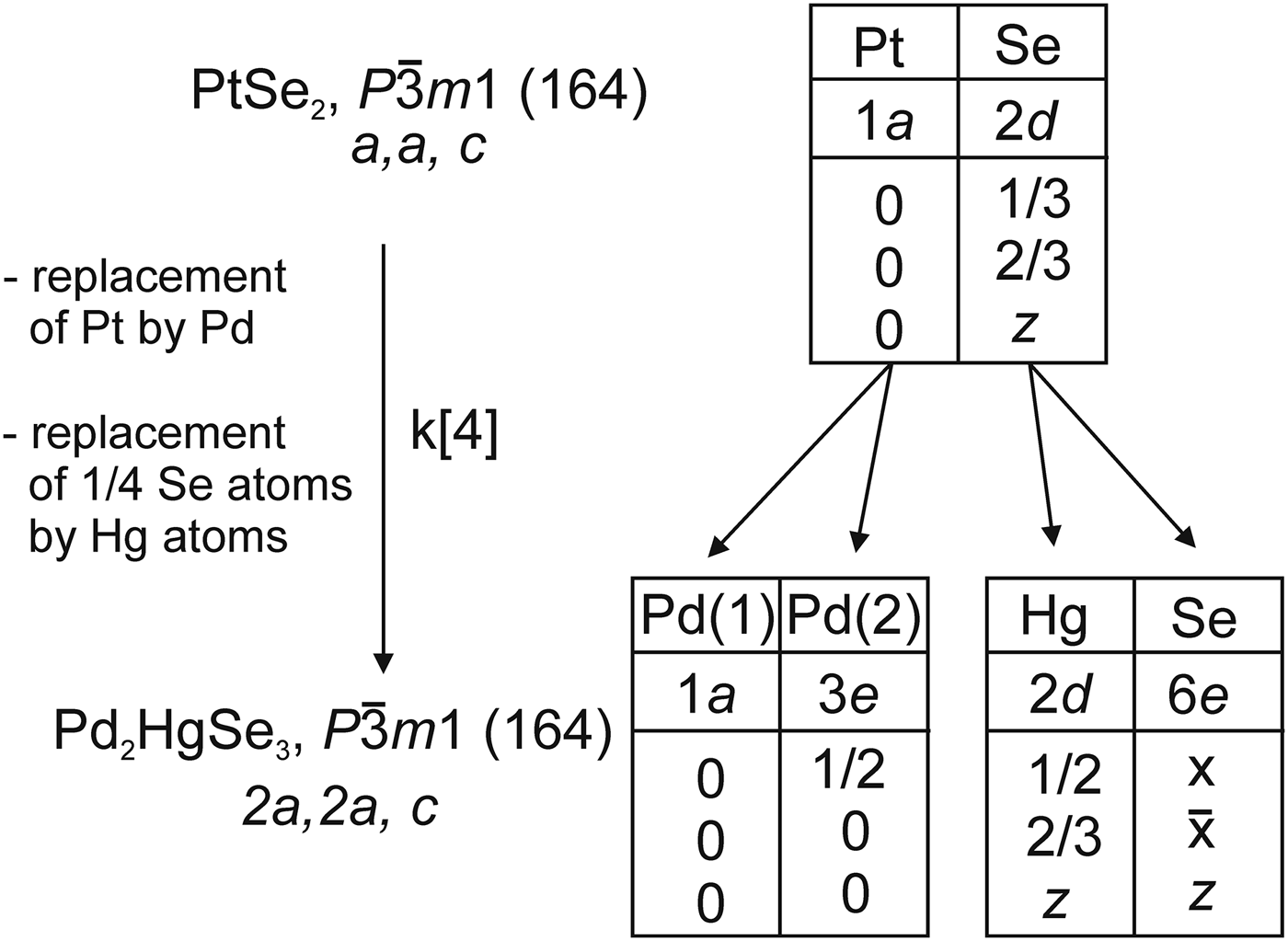
The crystal structure of Pd₂HgSe₃ can also be described as a 2a.2a.c superstructure of PtSe₂ structure, where Pt atoms and one-quarter of Se atoms have been replaced by Pd and Hg atoms, respectively. PtSe₂, which is also known as a mineral sudovikovite, adopts a layered structure of the CdI₂-structure type (Furuseth et al., Reference Furuseth, Selte and Kjekshus1965). The corresponding group–subgroup relation is $P\bar 3m1(k4/2a.2a.c)P\bar 3m1$ and is shown in Figure 4. The splitting of Wyckoff position in the space group $P\bar 3m1$ was constructed using the programme Wycksplit (Kroumova et al., Reference Kroumova, Perez-Mato and Aroyo1998).

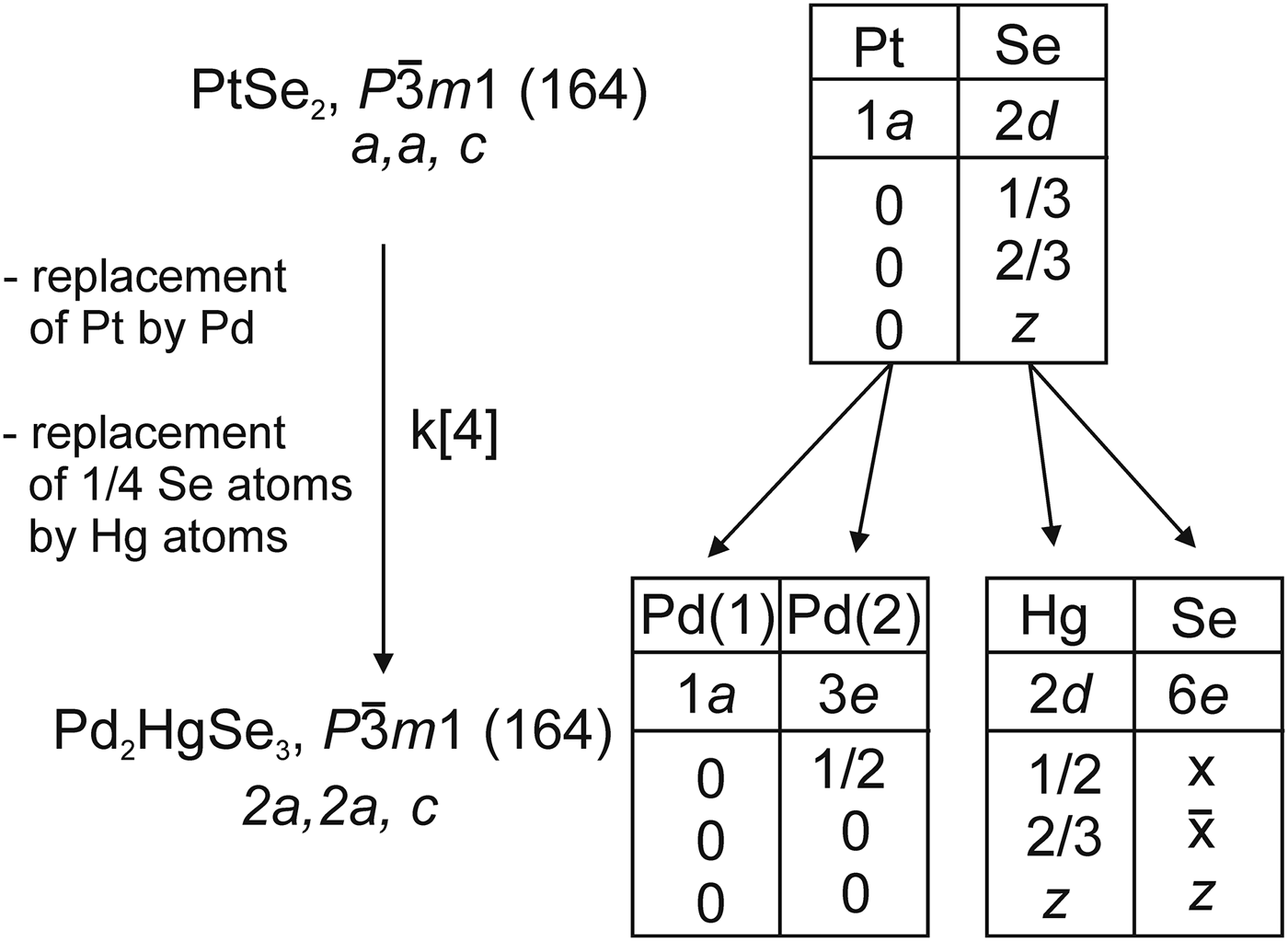
Figure 4. The group–subgroup relation between the PtSe₂ and Pd₂HgSe₃ structures including splitting of the Wyckoff positions.

Apart from its isostructural compounds (see above), the most closely structural related phase to Pd₂HgSe₃ is the mineral temagamite, Pd₃HgTe₃ (Laufek et al., Reference Laufek, Vymazalová, Drábek, Dušek, Navrátil and Černošková2016). Both crystal structures show trigonal symmetry and Pd₃HgTe₃ shows approximately similar unit-cell parameter a [7.8211(6) Å]. The crystal structure of Pd₃HgTe₃ was described as being composed of layered modules (denoted as A through F) stacked along the c-axis. The modules B and F in temagamite structure show the same bond topology of Pd and Te atoms as Pd and Se atoms in Pd₂HgSe₃. Hg atoms occupy the anti-cubooctahedral voids in both compounds. The crystal structure of another Pd–Hg selenide, the mineral tischendorfite Pd₈Hg₃Se₉ (Laufek et al., Reference Laufek, Vymazalová, Drábek, Navrátil and Drahokoupil2014), differs from Pd₂HgSe₃ to a certain extent. On one hand, Pd and Se atoms in Pd₈Hg₃Se₉ show different bond topology. On the other hand, Hg atoms have essentially identical coordination in both compounds. The crystal structure of a third known Pd–Hg selenide, the phase Pd₅HgSe (Laufek et al., Reference Laufek, Vymazalová, Drábek, Navrátil, Plecháček and Drahokoupil2012), is based on [HgPd₁₂] cubooctahedra and [SePd₈] rectangular prism, and hence deviates significantly from the structure of Pd₃HgSe₂.