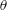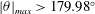1 Introduction
We shall study two-dimensional irrotational periodic waves propagating under the influence of gravity
![]() $g$
without change of form at the interface between two ideal unbounded fluids of different densities
$g$
without change of form at the interface between two ideal unbounded fluids of different densities
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
when
$\unicode[STIX]{x1D70C}_{2}$
when
![]() $\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}$
and
$\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
is the density of the lower fluid. For
$\unicode[STIX]{x1D70C}_{2}$
is the density of the lower fluid. For
![]() $\unicode[STIX]{x1D70C}_{1}=0$
, these waves are the well-known surface Stokes waves. It was conjectured by Stokes that the surface waves achieve their maximum amplitude when the maximum velocity of the fluid in the
$\unicode[STIX]{x1D70C}_{1}=0$
, these waves are the well-known surface Stokes waves. It was conjectured by Stokes that the surface waves achieve their maximum amplitude when the maximum velocity of the fluid in the
![]() $x$
-direction equals the phase speed of the wave. Then, in the frame of reference moving with the phase speed, the highest surface waves would have stagnation points at the crests, and from a local analysis of the equations of motion, Stokes showed that the crests would be sharp and enclose an angle of
$x$
-direction equals the phase speed of the wave. Then, in the frame of reference moving with the phase speed, the highest surface waves would have stagnation points at the crests, and from a local analysis of the equations of motion, Stokes showed that the crests would be sharp and enclose an angle of
![]() $120^{\circ }$
. A rigorous mathematical confirmation of the Stokes conjecture was given by Amick, Fraenkel & Toland (Reference Amick, Fraenkel and Toland1982).
$120^{\circ }$
. A rigorous mathematical confirmation of the Stokes conjecture was given by Amick, Fraenkel & Toland (Reference Amick, Fraenkel and Toland1982).
It is clear that for
![]() $\unicode[STIX]{x1D70C}_{1}>0$
, Stokes’ limiting configuration is no longer possible, because the stagnation angular point in the lower fluid would result in an infinite velocity at the same point but in the upper fluid, and hence satisfying the condition of continuous pressure across the interface becomes impossible.
$\unicode[STIX]{x1D70C}_{1}>0$
, Stokes’ limiting configuration is no longer possible, because the stagnation angular point in the lower fluid would result in an infinite velocity at the same point but in the upper fluid, and hence satisfying the condition of continuous pressure across the interface becomes impossible.
Let
![]() $\unicode[STIX]{x1D703}$
be the angle between the tangent line to the interfacial curve and the horizontal direction. Holyer (Reference Holyer1979) proposed that the limiting configurations of interfacial waves are those with a vertical slope of the interface (
$\unicode[STIX]{x1D703}$
be the angle between the tangent line to the interfacial curve and the horizontal direction. Holyer (Reference Holyer1979) proposed that the limiting configurations of interfacial waves are those with a vertical slope of the interface (
![]() $|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
). This conjecture generalizes Stokes’ conjecture, because the vertical slope means that, at the point of the interface where this slope is achieved, the horizontal particle velocity equals the phase speed.
$|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
). This conjecture generalizes Stokes’ conjecture, because the vertical slope means that, at the point of the interface where this slope is achieved, the horizontal particle velocity equals the phase speed.
It is evident that, if at a point of the interface
![]() $|\unicode[STIX]{x1D703}|>\unicode[STIX]{x03C0}/2$
, then at this point the horizontal velocities on both sides of the interface will be greater than the phase speed. Saffman & Yuen (Reference Saffman and Yuen1982) pointed out that there are no dynamical or kinematical reasons to reject interfacial waves for which the horizontal velocity exceeds the phase velocity at some points. Numerical evidence of the existence of such waves was demonstrated by Meiron & Saffman (Reference Meiron and Saffman1983). For these S-shaped waves, some portions of heavier fluid lie above lighter fluid, and Meiron & Saffman (Reference Meiron and Saffman1983) called them ‘overhanging waves’.
$|\unicode[STIX]{x1D703}|>\unicode[STIX]{x03C0}/2$
, then at this point the horizontal velocities on both sides of the interface will be greater than the phase speed. Saffman & Yuen (Reference Saffman and Yuen1982) pointed out that there are no dynamical or kinematical reasons to reject interfacial waves for which the horizontal velocity exceeds the phase velocity at some points. Numerical evidence of the existence of such waves was demonstrated by Meiron & Saffman (Reference Meiron and Saffman1983). For these S-shaped waves, some portions of heavier fluid lie above lighter fluid, and Meiron & Saffman (Reference Meiron and Saffman1983) called them ‘overhanging waves’.
Thus, the computations of Meiron & Saffman (Reference Meiron and Saffman1983) showed that the appearance of the vertical slope on the interface does not correspond to a limiting configuration. Saffman & Yuen (Reference Saffman and Yuen1982) proposed that the overhanging S-shaped waves continue to exist until the interface intersects itself. However, the calculations of Meiron & Saffman (Reference Meiron and Saffman1983) were stopped well before any such limiting configurations, and hence do not confirm the conjecture of Saffman & Yuen (Reference Saffman and Yuen1982).
Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986) confirmed the existence of overhanging waves as computed by Meiron & Saffman (Reference Meiron and Saffman1983) and extended their calculations. Computing along a continuous branch of solutions, Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986) found that there is a return from the overhanging configuration to one in which the interface is a single-valued function of the horizontal variable. The authors conjectured that an alternation between non-overhanging and overhanging waves continues indefinitely as one proceeds along the continuous solution branch. The authors considered such oscillatory behaviour to be analogous to the oscillations by Longuet-Higgins & Fox (Reference Longuet-Higgins and Fox1977, Reference Longuet-Higgins and Fox1978) of surface wave properties (see also Maklakov Reference Maklakov2002).
In the works by Pullin & Grimshaw (Reference Pullin and Grimshaw1983a
,Reference Pullin and Grimshaw
b
) and Grimshaw & Pullin (Reference Grimshaw and Pullin1986), the interfacial waves were studied for the Boussinesq limit in which the density difference is neglected in all but the buoyancy terms of the equations of motion. The most extensive computations of overhanging waves were carried out in Grimshaw & Pullin (Reference Grimshaw and Pullin1986), where the authors investigated the case when the lower fluid is infinitely deep, but the upper fluid has a mean depth
![]() $d_{1}$
, and may also contain a basic current with constant vorticity
$d_{1}$
, and may also contain a basic current with constant vorticity
![]() $\unicode[STIX]{x1D714}_{1}$
. On the basis of computations for
$\unicode[STIX]{x1D714}_{1}$
. On the basis of computations for
![]() $d_{1}\rightarrow \infty$
and
$d_{1}\rightarrow \infty$
and
![]() $\unicode[STIX]{x1D714}_{1}=0$
, Grimshaw & Pullin (Reference Grimshaw and Pullin1986, figure 9) conjectured that the limiting configuration contains a periodic stagnation zone formed by both the upper and lower fluid. The zone is bounded from above and below by the two free surfaces of the highest Stokes waves with the angular crests that are oppositely directed and shifted by a half-period with respect to each other. Almost limiting configurations have a mushroom shape with an almost flat underside of the mushroom cap. Similar mushroom shapes were obtained by Grimshaw & Pullin (Reference Grimshaw and Pullin1986) when the upper fluid has constant vorticity (
$\unicode[STIX]{x1D714}_{1}=0$
, Grimshaw & Pullin (Reference Grimshaw and Pullin1986, figure 9) conjectured that the limiting configuration contains a periodic stagnation zone formed by both the upper and lower fluid. The zone is bounded from above and below by the two free surfaces of the highest Stokes waves with the angular crests that are oppositely directed and shifted by a half-period with respect to each other. Almost limiting configurations have a mushroom shape with an almost flat underside of the mushroom cap. Similar mushroom shapes were obtained by Grimshaw & Pullin (Reference Grimshaw and Pullin1986) when the upper fluid has constant vorticity (
![]() $\unicode[STIX]{x1D714}_{1}\neq 0$
), but in this case the mushroom caps (almost stagnation zones) consist only of the points of the lower fluid.
$\unicode[STIX]{x1D714}_{1}\neq 0$
), but in this case the mushroom caps (almost stagnation zones) consist only of the points of the lower fluid.
Generally speaking, the computations of Grimshaw & Pullin (Reference Grimshaw and Pullin1986), carried out for the Boussinesq limit, confirm the conjecture of Saffman & Yuen (Reference Saffman and Yuen1982) that the overhanging S-shaped waves continue to exist until the interface starts to touch itself.
The recent paper by Akers et al. (Reference Akers, Ambrose, Pond and Wright2016) was especially devoted to the numerical analysis of overturned internal gravity–capillary waves. It is well known that the limiting configurations of pure capillary surface waves have a point of self-intersection (see Crapper Reference Crapper1957). The problem formulation by Akers et al. (Reference Akers, Ambrose, Pond and Wright2016) uses the presence of surface tension in a fundamental way. So, these authors did not consider the cases of dominant gravity forces, and the limiting configurations that they found are not mushroom-shaped as in Grimshaw & Pullin (Reference Grimshaw and Pullin1986) (see also figure 7) but similar to that of Crapper (Reference Crapper1957).
In the present paper, by making use of the Hopf lemma, we rigorously prove that, if
![]() $\unicode[STIX]{x1D703}$
is the angle between the tangent line to the interfacial curve and the horizontal direction, then
$\unicode[STIX]{x1D703}$
is the angle between the tangent line to the interfacial curve and the horizontal direction, then
![]() $-\unicode[STIX]{x03C0}<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}$
. This inequality allows us to put forward a criterion of proximity of the interface to the limiting configuration, namely, the angle
$-\unicode[STIX]{x03C0}<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}$
. This inequality allows us to put forward a criterion of proximity of the interface to the limiting configuration, namely, the angle
![]() $|\unicode[STIX]{x1D703}|_{max}$
must be close to but may not exceed
$|\unicode[STIX]{x1D703}|_{max}$
must be close to but may not exceed
![]() $\unicode[STIX]{x03C0}$
. We develop a new numerical method of computing interfacial waves based on the representation of a piecewise-analytic function to be found in such a manner that only the shape of the interface is unknown. All other hydrodynamic quantities, for example, the velocity field, can be expressed analytically through only one Cauchy-type integral whose density and path of integration depend on the functions describing the interfacial shape. Using this method, we compute the almost limiting configurations of overhanging interfacial waves with
$\unicode[STIX]{x03C0}$
. We develop a new numerical method of computing interfacial waves based on the representation of a piecewise-analytic function to be found in such a manner that only the shape of the interface is unknown. All other hydrodynamic quantities, for example, the velocity field, can be expressed analytically through only one Cauchy-type integral whose density and path of integration depend on the functions describing the interfacial shape. Using this method, we compute the almost limiting configurations of overhanging interfacial waves with
![]() $|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
.
$|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
.
Analysing the results of computations for overhanging waves, we introduce two new concepts: an inner crest, and an inner solution near the inner crest. These concepts allow us to make a well-grounded prediction for the limiting interfacial configurations. Our computations demonstrate that, for any ratios
![]() $0<\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{2}<1$
, almost limiting configurations are analogous to those obtained by Grimshaw & Pullin (Reference Grimshaw and Pullin1986) for the Boussinesq limit (
$0<\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{2}<1$
, almost limiting configurations are analogous to those obtained by Grimshaw & Pullin (Reference Grimshaw and Pullin1986) for the Boussinesq limit (
![]() $\unicode[STIX]{x1D70C}_{1}\rightarrow \unicode[STIX]{x1D70C}_{2}$
) with the vorticity
$\unicode[STIX]{x1D70C}_{1}\rightarrow \unicode[STIX]{x1D70C}_{2}$
) with the vorticity
![]() $\unicode[STIX]{x1D714}_{1}\neq 0$
. The configurations have a mushroom shape with an almost flat (
$\unicode[STIX]{x1D714}_{1}\neq 0$
. The configurations have a mushroom shape with an almost flat (
![]() $|\unicode[STIX]{x1D703}|_{max}\rightarrow \unicode[STIX]{x03C0}$
) underside of the mushroom cap (see figure 7), and, again, the mushroom caps (almost stagnation zones) consist only of the points of the lower fluid. So our computations also confirm the conjecture by Saffman & Yuen (Reference Saffman and Yuen1982) that, for the almost limiting configurations, the interface has a ‘nearly touching’ shape.
$|\unicode[STIX]{x1D703}|_{max}\rightarrow \unicode[STIX]{x03C0}$
) underside of the mushroom cap (see figure 7), and, again, the mushroom caps (almost stagnation zones) consist only of the points of the lower fluid. So our computations also confirm the conjecture by Saffman & Yuen (Reference Saffman and Yuen1982) that, for the almost limiting configurations, the interface has a ‘nearly touching’ shape.
2 Formulation of the problem
Consider a system of two-dimensional irrotational periodic waves of wavelength
![]() $\unicode[STIX]{x1D706}$
propagating with phase velocity
$\unicode[STIX]{x1D706}$
propagating with phase velocity
![]() $c$
under the influence of gravity
$c$
under the influence of gravity
![]() $g$
without change of form from right to left at the interface
$g$
without change of form from right to left at the interface
![]() $L$
between two ideal unbounded fluids of different densities
$L$
between two ideal unbounded fluids of different densities
![]() $\unicode[STIX]{x1D70C}_{1}$
and
$\unicode[STIX]{x1D70C}_{1}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
. We suppose that
$\unicode[STIX]{x1D70C}_{2}$
. We suppose that
![]() $\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}$
, where
$\unicode[STIX]{x1D70C}_{1}<\unicode[STIX]{x1D70C}_{2}$
, where
![]() $\unicode[STIX]{x1D70C}_{2}$
is the density of the lower fluid. In the wave-fixed frame of reference, the flow appears to be steady. Let us assume that the waves are symmetric, the ordinate axis
$\unicode[STIX]{x1D70C}_{2}$
is the density of the lower fluid. In the wave-fixed frame of reference, the flow appears to be steady. Let us assume that the waves are symmetric, the ordinate axis
![]() $y$
is that of symmetry which goes through one of the wave crests and the abscissa axis
$y$
is that of symmetry which goes through one of the wave crests and the abscissa axis
![]() $x$
is located on the mean line of the waves. One period of the flow region is shown in figure 1.
$x$
is located on the mean line of the waves. One period of the flow region is shown in figure 1.

Figure 1. One period of waves.
Let us introduce the ratio
![]() $\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{2}$
, which changes in the range
$\unicode[STIX]{x1D70C}=\unicode[STIX]{x1D70C}_{1}/\unicode[STIX]{x1D70C}_{2}$
, which changes in the range
![]() $0\leqslant \unicode[STIX]{x1D70C}\leqslant 1$
. We non-dimensionalize all flow parameters by choosing
$0\leqslant \unicode[STIX]{x1D70C}\leqslant 1$
. We non-dimensionalize all flow parameters by choosing
![]() $\unicode[STIX]{x1D706}/(2\unicode[STIX]{x03C0})$
,
$\unicode[STIX]{x1D706}/(2\unicode[STIX]{x03C0})$
,
![]() $\sqrt{g\unicode[STIX]{x1D706}/(2\unicode[STIX]{x03C0})}$
and
$\sqrt{g\unicode[STIX]{x1D706}/(2\unicode[STIX]{x03C0})}$
and
![]() $\unicode[STIX]{x1D70C}_{2}$
as the scales for length, velocity and density, respectively. In what follows, all physical quantities will be dimensionless in accordance with the chosen scales. Now, the dimensionless wavelength is
$\unicode[STIX]{x1D70C}_{2}$
as the scales for length, velocity and density, respectively. In what follows, all physical quantities will be dimensionless in accordance with the chosen scales. Now, the dimensionless wavelength is
![]() $2\unicode[STIX]{x03C0}$
,
$2\unicode[STIX]{x03C0}$
,
![]() $\unicode[STIX]{x1D70C}_{2}=g=1$
and
$\unicode[STIX]{x1D70C}_{2}=g=1$
and
![]() $\unicode[STIX]{x1D70C}_{1}=\unicode[STIX]{x1D70C}$
.
$\unicode[STIX]{x1D70C}_{1}=\unicode[STIX]{x1D70C}$
.
The interface
![]() $L$
divides the flow region into two parts. We designate the upper part as
$L$
divides the flow region into two parts. We designate the upper part as
![]() $D_{1}$
and the lower one as
$D_{1}$
and the lower one as
![]() $D_{2}$
. The upper and lower parts of the interface we designate as
$D_{2}$
. The upper and lower parts of the interface we designate as
![]() $L^{+}$
and
$L^{+}$
and
![]() $L^{-}$
, respectively.
$L^{-}$
, respectively.
Let
![]() $z=x+\text{i}y$
be the complex variable and
$z=x+\text{i}y$
be the complex variable and
![]() $F(z)$
be any piecewise continuous function (real or complex-valued) with the jump curve
$F(z)$
be any piecewise continuous function (real or complex-valued) with the jump curve
![]() $L$
. We shall use the following notation:
$L$
. We shall use the following notation:
Thus
![]() $\langle F\rangle (z)$
is the mean value of the boundary values
$\langle F\rangle (z)$
is the mean value of the boundary values
![]() $F^{+}(z)$
and
$F^{+}(z)$
and
![]() $F^{-}(z)$
on the sides of the interface
$F^{-}(z)$
on the sides of the interface
![]() $L$
.
$L$
.
We introduce the complex potential
![]() $w=\unicode[STIX]{x1D719}+\text{i}\unicode[STIX]{x1D713}$
and the complex conjugate velocity
$w=\unicode[STIX]{x1D719}+\text{i}\unicode[STIX]{x1D713}$
and the complex conjugate velocity
where
![]() $q$
and
$q$
and
![]() $\unicode[STIX]{x1D70F}$
are the modulus and inclination of the velocity vector
$\unicode[STIX]{x1D70F}$
are the modulus and inclination of the velocity vector
![]() $\boldsymbol{q}$
, respectively.
$\boldsymbol{q}$
, respectively.
First, we formulate a boundary-value problem for the piecewise-analytic function (2.3). The interface is defined by two conditions:
(i) the interface is a streamline both for the upper and lower flow; and
(ii) the pressure
 $p$
has no jump across the interface.
$p$
has no jump across the interface.
Condition (i) can be written as
where
![]() $z\in L$
and
$z\in L$
and
![]() $\unicode[STIX]{x1D703}$
is the angle between the tangent line to the interfacial curve and the horizontal direction.
$\unicode[STIX]{x1D703}$
is the angle between the tangent line to the interfacial curve and the horizontal direction.
To rewrite condition (ii) in terms of
![]() $q$
, we use the Bernoulli equation on the sides
$q$
, we use the Bernoulli equation on the sides
![]() $L^{+}$
and
$L^{+}$
and
![]() $L^{-}$
of the interface:
$L^{-}$
of the interface:
where
![]() $z=x+\text{i}y\in L$
and
$z=x+\text{i}y\in L$
and
![]() $R_{1}$
,
$R_{1}$
,
![]() $R_{2}$
are the Bernoulli constants in the domains
$R_{2}$
are the Bernoulli constants in the domains
![]() $D_{1}$
,
$D_{1}$
,
![]() $D_{2}$
, respectively. The pressure
$D_{2}$
, respectively. The pressure
![]() $p$
has no jump across
$p$
has no jump across
![]() $L$
; therefore
$L$
; therefore
![]() $p^{+}=p^{-}$
, and we can exclude
$p^{+}=p^{-}$
, and we can exclude
![]() $p$
from (2.5) to give
$p$
from (2.5) to give
Let us denote one period
![]() $A^{\prime }BA$
of the interface line by
$A^{\prime }BA$
of the interface line by
![]() $L_{2\unicode[STIX]{x03C0}}$
(figure 1). Using the identity of Levi-Civita (Reference Levi-Civita1925, p. 277), we obtain
$L_{2\unicode[STIX]{x03C0}}$
(figure 1). Using the identity of Levi-Civita (Reference Levi-Civita1925, p. 277), we obtain
Since the
![]() $x$
-axis is located on the mean line of the waves, we have
$x$
-axis is located on the mean line of the waves, we have
With allowance for (2.7) and (2.8), we integrate (2.6) along
![]() $L_{2\unicode[STIX]{x03C0}}$
with respect to the variable
$L_{2\unicode[STIX]{x03C0}}$
with respect to the variable
![]() $x$
to get
$x$
to get
The boundary condition (2.6) of continuous pressure across the interface takes the form
or
where
![]() $z=x+\text{i}y\in L$
, and
$z=x+\text{i}y\in L$
, and
![]() $k$
is a parameter which, at fixed
$k$
is a parameter which, at fixed
![]() $\unicode[STIX]{x1D70C}$
, is uniquely connected with the phase speed
$\unicode[STIX]{x1D70C}$
, is uniquely connected with the phase speed
![]() $c$
by the relationships
$c$
by the relationships
We should also add to the conditions (2.4) and (2.11) at the interface the conditions at infinity:
To complete the formulation, we need to specify a parameter that is responsible for the wave steepness
where
![]() $y_{B}$
and
$y_{B}$
and
![]() $y_{A}$
are the ordinates of the crest and trough. We may specify, for example, the parameter
$y_{A}$
are the ordinates of the crest and trough. We may specify, for example, the parameter
![]() $k$
, which is equivalent to specifying the phase speed
$k$
, which is equivalent to specifying the phase speed
![]() $c$
, as follows from (2.12). Or, we may include (2.14) in the boundary conditions to find the unknown
$c$
, as follows from (2.12). Or, we may include (2.14) in the boundary conditions to find the unknown
![]() $k$
. However, the results of Grimshaw & Pullin (Reference Grimshaw and Pullin1986) and Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986) demonstrate that neither
$k$
. However, the results of Grimshaw & Pullin (Reference Grimshaw and Pullin1986) and Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986) demonstrate that neither
![]() $c$
nor
$c$
nor
![]() $H$
label the overhanging interfacial waves uniquely. This is opposite to surface waves, for which, as was shown by Schwartz (Reference Schwartz1974) and confirmed in numerous further works, the wave steepness
$H$
label the overhanging interfacial waves uniquely. This is opposite to surface waves, for which, as was shown by Schwartz (Reference Schwartz1974) and confirmed in numerous further works, the wave steepness
![]() $H$
provides the uniqueness. In the present paper, we introduce the parameter
$H$
provides the uniqueness. In the present paper, we introduce the parameter
![]() $P$
, which is the ratio of the arclength of the curve
$P$
, which is the ratio of the arclength of the curve
![]() $L_{2\unicode[STIX]{x03C0}}$
to the wavelength
$L_{2\unicode[STIX]{x03C0}}$
to the wavelength
![]() $2\unicode[STIX]{x03C0}$
:
$2\unicode[STIX]{x03C0}$
:
It is evident that
![]() $P>1$
. On the basis of numerical computations in § 6 below, we demonstrate that, at a given
$P>1$
. On the basis of numerical computations in § 6 below, we demonstrate that, at a given
![]() $\unicode[STIX]{x1D70C}$
, the parameter
$\unicode[STIX]{x1D70C}$
, the parameter
![]() $P$
defines uniquely the periodic progressive surface waves as well as the waves at the interface between two fluids of infinite extent.
$P$
defines uniquely the periodic progressive surface waves as well as the waves at the interface between two fluids of infinite extent.
So, the problem is to find a piecewise-analytic,
![]() $2\unicode[STIX]{x03C0}$
-periodic function
$2\unicode[STIX]{x03C0}$
-periodic function
![]() $\text{d}w/\text{d}z$
, the jump curve
$\text{d}w/\text{d}z$
, the jump curve
![]() $L$
and the parameter
$L$
and the parameter
![]() $k$
which satisfy the conditions (2.4), (2.8), (2.11), (2.13) and (2.15).
$k$
which satisfy the conditions (2.4), (2.8), (2.11), (2.13) and (2.15).
3 On the maximum and minimum inclination angle of the interface
According to the theory of infinitesimal interfacial waves (see Lamb Reference Lamb1932, § 231), the shape of the interface
![]() $y=y(x)$
and the phase speed
$y=y(x)$
and the phase speed
![]() $c$
are given by
$c$
are given by
where
![]() $a=\unicode[STIX]{x03C0}H$
is the wave amplitude (one-half the vertical distance from the crest to the trough). For small values of
$a=\unicode[STIX]{x03C0}H$
is the wave amplitude (one-half the vertical distance from the crest to the trough). For small values of
![]() $P-1>0$
, it can be easily demonstrated that
$P-1>0$
, it can be easily demonstrated that
Proposition 1. If the interface is a smooth curve, then, for any continuous branch of solutions to the problem of interfacial waves branching off from the infinitesimal waves defined by (
3.1
), the angle
![]() $\unicode[STIX]{x1D703}$
between the tangent line to the interfacial curve and the horizontal direction satisfies the two-sided inequality
$\unicode[STIX]{x1D703}$
between the tangent line to the interfacial curve and the horizontal direction satisfies the two-sided inequality
Proof. Let
![]() $\unicode[STIX]{x1D703}_{max}$
be the maximum angle of inclination of the interface and
$\unicode[STIX]{x1D703}_{max}$
be the maximum angle of inclination of the interface and
![]() $M$
be the point at which this maximum is achieved. We denote by
$M$
be the point at which this maximum is achieved. We denote by
![]() $s$
the arclength of the interface, where
$s$
the arclength of the interface, where
![]() $s$
increases in the direction of the vectors
$s$
increases in the direction of the vectors
![]() $\boldsymbol{q}^{+}$
and
$\boldsymbol{q}^{+}$
and
![]() $\boldsymbol{q}^{-}$
. At the point
$\boldsymbol{q}^{-}$
. At the point
![]() $M$
, we draw the normal to the interface in the direction to the domain
$M$
, we draw the normal to the interface in the direction to the domain
![]() $D_{1}$
(figure 2).
$D_{1}$
(figure 2).

Figure 2. Illustration for the proof of proposition 1.
Let us introduce the Levi-Civita function
By virtue of (2.4), the function
![]() $\unicode[STIX]{x1D70F}(x,y)$
is continuous in the whole flow domain; moreover, by virtue of (3.4),
$\unicode[STIX]{x1D70F}(x,y)$
is continuous in the whole flow domain; moreover, by virtue of (3.4),
![]() $\unicode[STIX]{x1D70F}(x,y)$
is harmonic in each of the domains
$\unicode[STIX]{x1D70F}(x,y)$
is harmonic in each of the domains
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
. Therefore,
$D_{2}$
. Therefore,
![]() $\unicode[STIX]{x1D70F}(x,y)$
cannot take its maximum inside the domains
$\unicode[STIX]{x1D70F}(x,y)$
cannot take its maximum inside the domains
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
; hence the maximum is achieved at the interface
$D_{2}$
; hence the maximum is achieved at the interface
![]() $L$
. Then, according to (2.4),
$L$
. Then, according to (2.4),
![]() $\unicode[STIX]{x1D70F}(x,y)$
takes its maximum at the point
$\unicode[STIX]{x1D70F}(x,y)$
takes its maximum at the point
![]() $M$
, and
$M$
, and
![]() $\unicode[STIX]{x1D70F}_{max}=\unicode[STIX]{x1D703}_{max}$
.
$\unicode[STIX]{x1D70F}_{max}=\unicode[STIX]{x1D703}_{max}$
.
The functions
![]() $\unicode[STIX]{x1D70F}(x,y)$
and
$\unicode[STIX]{x1D70F}(x,y)$
and
![]() $\log q(x,y)$
are conjugate harmonic functions, which satisfy the Cauchy–Riemann conditions. Then, at the point
$\log q(x,y)$
are conjugate harmonic functions, which satisfy the Cauchy–Riemann conditions. Then, at the point
![]() $M$
, we have
$M$
, we have
By making use of Hopf’s boundary-point lemma (see Gilbarg & Trudinger Reference Gilbarg and Trudinger2001, p. 35, Lemma 3.4), we obtain
The relationships (3.5) and (3.6) lead to the inequalities
Now, we differentiate the boundary condition (2.11) with respect to
![]() $s$
:
$s$
:
Then, as follows from (3.7) and (3.8),
![]() $\sin \unicode[STIX]{x1D703}_{max}>0$
at the point
$\sin \unicode[STIX]{x1D703}_{max}>0$
at the point
![]() $M$
.
$M$
.
It is clear that, for infinitesimal waves (3.1), the values of
![]() $\unicode[STIX]{x1D703}_{max}<\unicode[STIX]{x03C0}$
. Now, let us assume that for a solution which branches off from the infinitesimal waves the value of
$\unicode[STIX]{x1D703}_{max}<\unicode[STIX]{x03C0}$
. Now, let us assume that for a solution which branches off from the infinitesimal waves the value of
![]() $\unicode[STIX]{x1D703}_{max}>\unicode[STIX]{x03C0}$
. Since we consider the continuous branch, there exists a solution with
$\unicode[STIX]{x1D703}_{max}>\unicode[STIX]{x03C0}$
. Since we consider the continuous branch, there exists a solution with
![]() $\unicode[STIX]{x1D703}_{max}=\unicode[STIX]{x03C0}$
, but this is impossible, because
$\unicode[STIX]{x1D703}_{max}=\unicode[STIX]{x03C0}$
, but this is impossible, because
![]() $\sin \unicode[STIX]{x1D703}_{max}>0$
. Thus, we have proved that
$\sin \unicode[STIX]{x1D703}_{max}>0$
. Thus, we have proved that
![]() $\unicode[STIX]{x1D703}_{max}<\unicode[STIX]{x03C0}$
. The proof of the inequality
$\unicode[STIX]{x1D703}_{max}<\unicode[STIX]{x03C0}$
. The proof of the inequality
![]() $\unicode[STIX]{x1D703}_{min}>-\unicode[STIX]{x03C0}$
is analogous, so the two-sided inequality (3.3) is true. ☐
$\unicode[STIX]{x1D703}_{min}>-\unicode[STIX]{x03C0}$
is analogous, so the two-sided inequality (3.3) is true. ☐
It is worth noting that the above proof can be easily generalized for the case when the upper and lower fluids are bounded by horizontal lids.
The inequality (3.3) of proposition 1 allows us to put forward a criterion of proximity of the interface to the limiting configuration, namely, the angle
![]() $|\unicode[STIX]{x1D703}|_{max}$
must be close to
$|\unicode[STIX]{x1D703}|_{max}$
must be close to
![]() $\unicode[STIX]{x03C0}$
but may not exceed
$\unicode[STIX]{x03C0}$
but may not exceed
![]() $\unicode[STIX]{x03C0}$
.
$\unicode[STIX]{x03C0}$
.
4 Jump problem for a piecewise-analytic function with an unknown jump line
Let us introduce the piecewise-analytic function
 $$\begin{eqnarray}\displaystyle F(z)=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D70C}\left(\frac{\text{d}w}{c\,\text{d}z}\right)^{2}-1, & z\in D_{1},\\ \displaystyle \left(\frac{\text{d}w}{c\,\text{d}z}\right)^{2}-1, & z\in D_{2},\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle F(z)=\left\{\begin{array}{@{}ll@{}}\displaystyle \unicode[STIX]{x1D70C}\left(\frac{\text{d}w}{c\,\text{d}z}\right)^{2}-1, & z\in D_{1},\\ \displaystyle \left(\frac{\text{d}w}{c\,\text{d}z}\right)^{2}-1, & z\in D_{2},\end{array}\right. & & \displaystyle\end{eqnarray}$$
and formulate the boundary-value problem for
![]() $F(z)$
. To do so, we multiply the boundary condition (2.11) by
$F(z)$
. To do so, we multiply the boundary condition (2.11) by
![]() $\text{e}^{-2\text{i}\unicode[STIX]{x1D703}}$
. Noting that, by virtue of (2.4),
$\text{e}^{-2\text{i}\unicode[STIX]{x1D703}}$
. Noting that, by virtue of (2.4),
we obtain
where
and
![]() $z=x+\text{i}y\in L$
. The condition (4.3) is that of the jump problem for the piecewise-analytic function
$z=x+\text{i}y\in L$
. The condition (4.3) is that of the jump problem for the piecewise-analytic function
![]() $F(z)$
(see e.g. Muskheleshvili Reference Muskheleshvili1972; Lu Reference Lu1993), and as one can see from (4.4), the jump function
$F(z)$
(see e.g. Muskheleshvili Reference Muskheleshvili1972; Lu Reference Lu1993), and as one can see from (4.4), the jump function
![]() $\unicode[STIX]{x1D706}(z)$
depends only on the parameter
$\unicode[STIX]{x1D706}(z)$
depends only on the parameter
![]() $k$
and the shape of the interface.
$k$
and the shape of the interface.
At the interface, the conditions (2.4) and (2.11) contain three real-valued equations, but in the complex-valued jump condition (4.3), which has been obtained by making use of both (2.4) and (2.11), we have only two real-valued equations. To get the third equation, we rewrite (2.4) in the form
In principle, either of equations (4.5) can be used as the third one, but it is more convenient to deduce from them the following relationship:
Here
![]() $\langle F\rangle (z)$
is defined by (2.2), and we have used the fact that, if two complex values have the same argument, the argument of their simple average is also the same.
$\langle F\rangle (z)$
is defined by (2.2), and we have used the fact that, if two complex values have the same argument, the argument of their simple average is also the same.
Taking into account that
![]() $\arg z=\text{Im}\log z$
, we rewrite the third real-valued equation in the form
$\arg z=\text{Im}\log z$
, we rewrite the third real-valued equation in the form
Besides (4.3), (4.4) and (4.7), the function
![]() $F(z)$
must satisfy the boundary conditions at the upper (
$F(z)$
must satisfy the boundary conditions at the upper (
![]() $I_{1}$
) and lower (
$I_{1}$
) and lower (
![]() $I_{2}$
) infinities:
$I_{2}$
) infinities:
which follow from formulae (2.13) and (4.1).
To provide the symmetry of the waves with respect to the
![]() $y$
-axis, we should impose on
$y$
-axis, we should impose on
![]() $F(z)$
the complementary condition
$F(z)$
the complementary condition
It follows from the Riemann–Schwarz symmetry principle that, if
![]() $F(z)$
satisfies (4.9), then
$F(z)$
satisfies (4.9), then
where the overbar indicates a complex conjugate value.
Thus, we formulate the following boundary-value problem.
Problem 1. Find the piecewise-analytic
![]() $2\unicode[STIX]{x03C0}$
-periodic function
$2\unicode[STIX]{x03C0}$
-periodic function
![]() $F(z)$
, jump curve
$F(z)$
, jump curve
![]() $L$
and parameter
$L$
and parameter
![]() $k>0$
which satisfy the boundary conditions (2.8), (2.15), (4.3), (4.4), (4.7), (4.8a
) and (4.9).
$k>0$
which satisfy the boundary conditions (2.8), (2.15), (4.3), (4.4), (4.7), (4.8a
) and (4.9).
It is clear that, if
![]() $F(z)$
is
$F(z)$
is
![]() $2\unicode[STIX]{x03C0}$
-periodic and satisfies (4.10), then the jump curve
$2\unicode[STIX]{x03C0}$
-periodic and satisfies (4.10), then the jump curve
![]() $L$
is also
$L$
is also
![]() $2\unicode[STIX]{x03C0}$
-periodic and symmetric with respect to the
$2\unicode[STIX]{x03C0}$
-periodic and symmetric with respect to the
![]() $y$
-axis. The
$y$
-axis. The
![]() $2\unicode[STIX]{x03C0}$
-periodicity of
$2\unicode[STIX]{x03C0}$
-periodicity of
![]() $L$
means that
$L$
means that
and its symmetry means that
For any
![]() $2\unicode[STIX]{x03C0}$
-periodic line
$2\unicode[STIX]{x03C0}$
-periodic line
![]() $L$
and any
$L$
and any
![]() $2\unicode[STIX]{x03C0}$
-periodic complex-valued function
$2\unicode[STIX]{x03C0}$
-periodic complex-valued function
![]() $\unicode[STIX]{x1D706}(z)$
, the jump problem (4.3) and (4.8a
) has a simple analytical solution
$\unicode[STIX]{x1D706}(z)$
, the jump problem (4.3) and (4.8a
) has a simple analytical solution
where
![]() $\unicode[STIX]{x1D701}\in L$
. If
$\unicode[STIX]{x1D701}\in L$
. If
![]() $L$
is symmetric and
$L$
is symmetric and
![]() $\unicode[STIX]{x1D706}(z)$
is also symmetric in the sense that
$\unicode[STIX]{x1D706}(z)$
is also symmetric in the sense that
then
![]() $F(z)$
in the form (4.13) satisfies the symmetry condition (4.9).
$F(z)$
in the form (4.13) satisfies the symmetry condition (4.9).
We should remark that formulating problem 1, we do not include in the consideration the condition (4.8b
) at the upper infinity. This is because conditions (2.8) and (4.8b
) are equivalent. Indeed, consider the function
![]() $F(z)$
which satisfies (2.8), (4.3), (4.4) and (4.8a
). Then
$F(z)$
which satisfies (2.8), (4.3), (4.4) and (4.8a
). Then
![]() $F(z)$
can be determined by formula (4.13). Since
$F(z)$
can be determined by formula (4.13). Since
we have
where in (4.16b
)
![]() $\unicode[STIX]{x1D701}=x+\text{i}y\in L_{2\unicode[STIX]{x03C0}}$
and
$\unicode[STIX]{x1D701}=x+\text{i}y\in L_{2\unicode[STIX]{x03C0}}$
and
![]() $\unicode[STIX]{x1D706}(\unicode[STIX]{x1D701})=(ky+\unicode[STIX]{x1D70C}-1)\text{e}^{-2\text{i}\unicode[STIX]{x1D703}}$
. Taking into account that
$\unicode[STIX]{x1D706}(\unicode[STIX]{x1D701})=(ky+\unicode[STIX]{x1D70C}-1)\text{e}^{-2\text{i}\unicode[STIX]{x1D703}}$
. Taking into account that
![]() $\text{e}^{-2\text{i}\unicode[STIX]{x1D703}}\,\text{d}\unicode[STIX]{x1D701}=\text{d}x-\text{i}\,\text{d}y$
, we deduce that, by virtue of (2.8) and the
$\text{e}^{-2\text{i}\unicode[STIX]{x1D703}}\,\text{d}\unicode[STIX]{x1D701}=\text{d}x-\text{i}\,\text{d}y$
, we deduce that, by virtue of (2.8) and the
![]() $2\unicode[STIX]{x03C0}$
-periodicity of the line
$2\unicode[STIX]{x03C0}$
-periodicity of the line
![]() $L$
,
$L$
,
It follows from (4.16b ) and (4.17) that, at upper infinity, the condition (4.8b ) is fulfilled.
Problem 1 can be called the jump problem with an unknown jump line. We should emphasize that in problem 1 the jump
![]() $\unicode[STIX]{x1D706}(z)$
of the function
$\unicode[STIX]{x1D706}(z)$
of the function
![]() $F(z)$
is fully determined by the shape of the interface
$F(z)$
is fully determined by the shape of the interface
![]() $L$
and the value of the parameter
$L$
and the value of the parameter
![]() $k$
. So, solving problem 1, one needs to find only the shape of the interface and
$k$
. So, solving problem 1, one needs to find only the shape of the interface and
![]() $k$
, the function
$k$
, the function
![]() $F(z)$
itself being found by (4.13). This is not the case for the formulation with respect to the complex conjugate velocity
$F(z)$
itself being found by (4.13). This is not the case for the formulation with respect to the complex conjugate velocity
![]() $\text{d}w/\text{d}z$
, which has been presented in § 2 and used in the works by Pullin & Grimshaw (Reference Pullin and Grimshaw1983a
,Reference Pullin and Grimshaw
b
) and Grimshaw & Pullin (Reference Grimshaw and Pullin1986). For such a formulation, the jump of
$\text{d}w/\text{d}z$
, which has been presented in § 2 and used in the works by Pullin & Grimshaw (Reference Pullin and Grimshaw1983a
,Reference Pullin and Grimshaw
b
) and Grimshaw & Pullin (Reference Grimshaw and Pullin1986). For such a formulation, the jump of
![]() $\text{d}w/\text{d}z$
is also an unknown function which is to be found as part of the solution together with the shape of the interface.
$\text{d}w/\text{d}z$
is also an unknown function which is to be found as part of the solution together with the shape of the interface.
Problem 1 can be easily reduced to an integral equation. Indeed, let
![]() $s$
be the arc-abscissa of the line
$s$
be the arc-abscissa of the line
![]() $L$
counted from the point
$L$
counted from the point
![]() $B$
, and
$B$
, and
![]() $\unicode[STIX]{x1D703}(s)$
be an unknown function. It is clear that
$\unicode[STIX]{x1D703}(s)$
be an unknown function. It is clear that
![]() $\unicode[STIX]{x1D703}(s)$
is an odd and
$\unicode[STIX]{x1D703}(s)$
is an odd and
![]() $2\unicode[STIX]{x03C0}P$
-periodic function:
$2\unicode[STIX]{x03C0}P$
-periodic function:
In terms of
![]() $\unicode[STIX]{x1D703}(s)$
, the shape of the interface is expressed by the formulae
$\unicode[STIX]{x1D703}(s)$
, the shape of the interface is expressed by the formulae
where
![]() $y_{B}$
is the ordinate of the wave crest. Since the line
$y_{B}$
is the ordinate of the wave crest. Since the line
![]() $L$
is
$L$
is
![]() $2\unicode[STIX]{x03C0}$
-periodic, the function
$2\unicode[STIX]{x03C0}$
-periodic, the function
![]() $\unicode[STIX]{x1D703}(s)$
must satisfy the condition
$\unicode[STIX]{x1D703}(s)$
must satisfy the condition
Using the condition (2.8), we can express
![]() $y_{B}$
in terms of
$y_{B}$
in terms of
![]() $\unicode[STIX]{x1D703}(s)$
:
$\unicode[STIX]{x1D703}(s)$
:
The integral in (4.13) is that of Cauchy type; therefore, with allowance for (4.17), the mean value
‘p.v.’ denoting the principal value.
Making use of (4.4), (4.19) and (4.22), we deduce from (4.7) the equation
where
and
![]() $y_{B}$
being defined by (4.21).
$y_{B}$
being defined by (4.21).
The system (4.20) and (4.23) is possibly the most compact mathematical formulation for the interfacial gravity wave problems. Indeed, at a given
![]() $P>1$
, we have here only one nonlinear singular integral equation, (4.23), and only one
$P>1$
, we have here only one nonlinear singular integral equation, (4.23), and only one
![]() $2\unicode[STIX]{x03C0}P$
-periodic odd unknown function,
$2\unicode[STIX]{x03C0}P$
-periodic odd unknown function,
![]() $\unicode[STIX]{x1D703}(s)$
, with the known domain of definition,
$\unicode[STIX]{x1D703}(s)$
, with the known domain of definition,
![]() $-\unicode[STIX]{x03C0}P\leqslant s\leqslant \unicode[STIX]{x03C0}P$
. To find the unknown parameter
$-\unicode[STIX]{x03C0}P\leqslant s\leqslant \unicode[STIX]{x03C0}P$
. To find the unknown parameter
![]() $k$
, we have the complementary integral relationship (4.20). The system allows a generalization for the case of finite depths. This system can be discretized and reduced to a system of nonlinear equations, which in turn can be solved by the Newton method. It is worth noting that, if one discretizes the system (4.20) and (4.23) using
$k$
, we have the complementary integral relationship (4.20). The system allows a generalization for the case of finite depths. This system can be discretized and reduced to a system of nonlinear equations, which in turn can be solved by the Newton method. It is worth noting that, if one discretizes the system (4.20) and (4.23) using
![]() $N$
points, one will get a system of
$N$
points, one will get a system of
![]() $N+1$
nonlinear equations with
$N+1$
nonlinear equations with
![]() $N+1$
unknowns, whereas in the mathematical formulation of Meiron & Saffman (Reference Meiron and Saffman1983), the number of unknowns is
$N+1$
unknowns, whereas in the mathematical formulation of Meiron & Saffman (Reference Meiron and Saffman1983), the number of unknowns is
![]() $3N-1$
, and in that of Grimshaw & Pullin (Reference Grimshaw and Pullin1986), this number is
$3N-1$
, and in that of Grimshaw & Pullin (Reference Grimshaw and Pullin1986), this number is
![]() $3N+3$
. So, our formulation allows us to reduce by a factor of three times the number of nonlinear equations to be solved.
$3N+3$
. So, our formulation allows us to reduce by a factor of three times the number of nonlinear equations to be solved.
It is well known that one of most time-consuming operations in the Newton’s iteration steps is computing the Jacobian matrix. Studying almost highest surface waves and applying the method of conformal mappings, Maklakov (Reference Maklakov2002) succeeded in carrying out this operation analytically. For the discrete analogues of the system (4.20) and (4.23), such analytical calculations of the Jacobian seem to be impossible. So, to reduce the time of computations, we will not directly solve the system (4.20) and (4.23) but apply a method which can be characterized as Newton’s method for boundary-value problems with unknown boundaries. Indeed, Newton’s method replaces solving nonlinear equations by a series of linear ones. In our method, we replace solving the nonlinear boundary-value problems with unknown boundaries by a series of linear boundary-value problems with known boundaries. For these linear boundary-value problems, we will carry out the discretization. The method is general and can be applied to many two-dimensional hydrodynamic problems with unknown boundaries. In a sense, such a method is equivalent to the analytical calculations of the Jacobian.
5 Newton’s method for solving boundary-value problems with unknown boundaries
5.1 Variations of boundary values in the jump problems when the jump line and the jump itself are varied
Consider a
![]() $2\unicode[STIX]{x03C0}$
-periodic line
$2\unicode[STIX]{x03C0}$
-periodic line
![]() $L$
and the jump problem for the piecewise-analytic function
$L$
and the jump problem for the piecewise-analytic function
![]() $F(z)$
:
$F(z)$
:
where
![]() $z\in L$
and
$z\in L$
and
![]() $\unicode[STIX]{x1D706}(z)$
is a
$\unicode[STIX]{x1D706}(z)$
is a
![]() $2\unicode[STIX]{x03C0}$
-periodic function of the points
$2\unicode[STIX]{x03C0}$
-periodic function of the points
![]() $z$
.
$z$
.
Let us shift the points of the line
![]() $L$
by means of a
$L$
by means of a
![]() $2\unicode[STIX]{x03C0}$
-periodic, complex-valued function
$2\unicode[STIX]{x03C0}$
-periodic, complex-valued function
![]() $\unicode[STIX]{x1D6FF}(z)$
, so that the points
$\unicode[STIX]{x1D6FF}(z)$
, so that the points
![]() $z+\unicode[STIX]{x1D6FF}(z)$
lie on a new
$z+\unicode[STIX]{x1D6FF}(z)$
lie on a new
![]() $2\unicode[STIX]{x03C0}$
-periodic line
$2\unicode[STIX]{x03C0}$
-periodic line
![]() $\unicode[STIX]{x1D6EC}$
. For the line
$\unicode[STIX]{x1D6EC}$
. For the line
![]() $\unicode[STIX]{x1D6EC}$
, we formulate the following new jump problem for the function
$\unicode[STIX]{x1D6EC}$
, we formulate the following new jump problem for the function
![]() $F_{\unicode[STIX]{x1D6EC}}(z)$
:
$F_{\unicode[STIX]{x1D6EC}}(z)$
:
where again
![]() $z\in L$
, and
$z\in L$
, and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(z)$
is a
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(z)$
is a
![]() $2\unicode[STIX]{x03C0}$
-periodic, complex-valued function of the points
$2\unicode[STIX]{x03C0}$
-periodic, complex-valued function of the points
![]() $z$
lying on
$z$
lying on
![]() $L$
. Both problems (5.1) and (5.2) can be solved exactly by formula (4.13).
$L$
. Both problems (5.1) and (5.2) can be solved exactly by formula (4.13).
Let us assume now that the functions
![]() $\unicode[STIX]{x1D6FF}(z)$
and
$\unicode[STIX]{x1D6FF}(z)$
and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(z)$
are infinitely small functions of order
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D706}(z)$
are infinitely small functions of order
![]() $\unicode[STIX]{x1D700}$
. Consider the variation
$\unicode[STIX]{x1D700}$
. Consider the variation
It is clear that this variation is a piecewise-analytic function of order
![]() $\unicode[STIX]{x1D700}$
, which vanishes at the lower infinity and has a jump across
$\unicode[STIX]{x1D700}$
, which vanishes at the lower infinity and has a jump across
![]() $L$
. To deduce the jump conditions for
$L$
. To deduce the jump conditions for
![]() $\unicode[STIX]{x1D6FF}F(z)$
, we write
$\unicode[STIX]{x1D6FF}F(z)$
, we write
Subtracting (5.6) from (5.5) and taking into account (5.1) and (5.2), we come to the following jump problem for
![]() $\unicode[STIX]{x1D6FF}F(z)$
:
$\unicode[STIX]{x1D6FF}F(z)$
:
where the derivative
![]() $\text{d}\unicode[STIX]{x1D706}/\text{d}z$
is computed along the jump curve
$\text{d}\unicode[STIX]{x1D706}/\text{d}z$
is computed along the jump curve
![]() $L$
.
$L$
.
Let us denote by
![]() $\unicode[STIX]{x1D6FF}\langle F\rangle (z)$
the variation of the mean values of the function
$\unicode[STIX]{x1D6FF}\langle F\rangle (z)$
the variation of the mean values of the function
![]() $F(z)$
:
$F(z)$
:
Adding (5.5) and (5.6), we obtain
where again the derivative
![]() $\text{d}\langle F\rangle /\text{d}z$
is computed along the jump curve
$\text{d}\langle F\rangle /\text{d}z$
is computed along the jump curve
![]() $L$
.
$L$
.
Equations (5.7) and (5.9) form the basis for constricting Newton’s algorithm for solving problem 1.
5.2 Linearization of problem 1 in a neighbourhood of an approximate solution (one step of Newton’s iterative method)
Let us assume that we know an approximate solution to problem 1. This means that we know a value of the parameter
![]() $k>0$
and the shape of a certain line
$k>0$
and the shape of a certain line
![]() $L$
which satisfies the conditions of
$L$
which satisfies the conditions of
![]() $2\unicode[STIX]{x03C0}$
-periodicity (4.11) and symmetry (4.12). The corresponding approximation for
$2\unicode[STIX]{x03C0}$
-periodicity (4.11) and symmetry (4.12). The corresponding approximation for
![]() $F(z)$
can be found by formula (4.13). We designate as
$F(z)$
can be found by formula (4.13). We designate as
![]() $s$
the arc-abscissa of the line
$s$
the arc-abscissa of the line
![]() $L$
counted from the point
$L$
counted from the point
![]() $B$
and use the arc-coordinate
$B$
and use the arc-coordinate
![]() $s$
to label the points
$s$
to label the points
![]() $z$
on this line. Thus,
$z$
on this line. Thus,
all the above functions being assumed to be known. By virtue of
![]() $2\unicode[STIX]{x03C0}$
-periodicity and symmetry of
$2\unicode[STIX]{x03C0}$
-periodicity and symmetry of
![]() $L$
, the functions
$L$
, the functions
![]() $x(s)$
and
$x(s)$
and
![]() $y(s)$
possess the following properties:
$y(s)$
possess the following properties:
where
![]() $2l_{s}$
is the arclength of one period of the line
$2l_{s}$
is the arclength of one period of the line
![]() $L$
. By making use of (4.13), we can compute
$L$
. By making use of (4.13), we can compute
and
The piecewise-analytic function
![]() $F(z)$
in the form (5.12) automatically satisfies the boundary conditions (4.3), (4.4), (4.8a
) and (4.9) of problem 1. The remaining unfulfilled conditions are (2.8), (2.15) and (4.7). Let us compute the left-hand sides of the remaining conditions, namely,
$F(z)$
in the form (5.12) automatically satisfies the boundary conditions (4.3), (4.4), (4.8a
) and (4.9) of problem 1. The remaining unfulfilled conditions are (2.8), (2.15) and (4.7). Let us compute the left-hand sides of the remaining conditions, namely,
and assume that the values of
![]() $S_{L}$
,
$S_{L}$
,
![]() $P_{L}-P$
and the function
$P_{L}-P$
and the function
![]() $R(s)$
are of order
$R(s)$
are of order
![]() $\unicode[STIX]{x1D700}$
, where
$\unicode[STIX]{x1D700}$
, where
![]() $\unicode[STIX]{x1D700}$
is a small parameter. This assumption is natural, because
$\unicode[STIX]{x1D700}$
is a small parameter. This assumption is natural, because
![]() $k$
,
$k$
,
![]() $L$
and
$L$
and
![]() $F(z)$
are supposed to be an approximate solution to problem 1. We should remark that
$F(z)$
are supposed to be an approximate solution to problem 1. We should remark that
![]() $R(s)$
coincides with the left-hand side of (4.23). Our aim now is to define the shift function
$R(s)$
coincides with the left-hand side of (4.23). Our aim now is to define the shift function
![]() $\unicode[STIX]{x1D6FF}(z)$
so that, on the new line
$\unicode[STIX]{x1D6FF}(z)$
so that, on the new line
![]() $\unicode[STIX]{x1D6EC}$
, the boundary conditions (2.8), (2.15) and (4.7) would be fulfilled with an asymptotic accuracy of order
$\unicode[STIX]{x1D6EC}$
, the boundary conditions (2.8), (2.15) and (4.7) would be fulfilled with an asymptotic accuracy of order
![]() $\unicode[STIX]{x1D700}$
(all terms of order
$\unicode[STIX]{x1D700}$
(all terms of order
![]() $\unicode[STIX]{x1D700}^{2}$
should be neglected). We shall seek the shift function
$\unicode[STIX]{x1D700}^{2}$
should be neglected). We shall seek the shift function
![]() $\unicode[STIX]{x1D6FF}(z)$
in the form
$\unicode[STIX]{x1D6FF}(z)$
in the form
where
![]() $h$
is the shift of the point
$h$
is the shift of the point
![]() $z\in L$
to the point
$z\in L$
to the point
![]() $z_{1}\in \unicode[STIX]{x1D6EC}$
in the direction of the normal to
$z_{1}\in \unicode[STIX]{x1D6EC}$
in the direction of the normal to
![]() $L$
(
$L$
(
![]() $h>0$
if
$h>0$
if
![]() $z_{1}\in D_{1}$
).
$z_{1}\in D_{1}$
).
In fact, by defining the shift
![]() $\unicode[STIX]{x1D6FF}(z)$
in the form (5.15), we have introduced the curvilinear ‘boundary layer’ coordinate system (see figure 3
a) in which the location of a point
$\unicode[STIX]{x1D6FF}(z)$
in the form (5.15), we have introduced the curvilinear ‘boundary layer’ coordinate system (see figure 3
a) in which the location of a point
![]() $M$
is defined by the pair
$M$
is defined by the pair
![]() $(s,h)$
, where
$(s,h)$
, where
![]() $h$
is the distance from
$h$
is the distance from
![]() $M$
to
$M$
to
![]() $L$
. In this system, the equation of the line
$L$
. In this system, the equation of the line
![]() $\unicode[STIX]{x1D6EC}$
is
$\unicode[STIX]{x1D6EC}$
is
![]() $h=h(s)$
with
$h=h(s)$
with
![]() $h(s)$
being an even and
$h(s)$
being an even and
![]() $2l_{s}$
-periodic function of
$2l_{s}$
-periodic function of
![]() $s$
.
$s$
.

Figure 3. ‘Boundary layer’ coordinate system.
Let
![]() $s_{1}$
be the arc-abscissa of the line
$s_{1}$
be the arc-abscissa of the line
![]() $\unicode[STIX]{x1D6EC}$
counted from the point
$\unicode[STIX]{x1D6EC}$
counted from the point
![]() $B_{1}$
, which has been obtained by the shift
$B_{1}$
, which has been obtained by the shift
![]() $h(0)$
of the point
$h(0)$
of the point
![]() $B$
, and
$B$
, and
![]() $\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
be the increment of the angle
$\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}$
be the increment of the angle
![]() $\unicode[STIX]{x1D703}$
due to the shift
$\unicode[STIX]{x1D703}$
due to the shift
![]() $h(s)$
(see figure 3
a,b). The parametric equation of the line
$h(s)$
(see figure 3
a,b). The parametric equation of the line
![]() $\unicode[STIX]{x1D6EC}$
is
$\unicode[STIX]{x1D6EC}$
is
Differentiating this equation with respect to
![]() $s$
results in
$s$
results in
where
![]() $K=K(s)=\unicode[STIX]{x1D703}^{\prime }(s)$
is the curvature of the line
$K=K(s)=\unicode[STIX]{x1D703}^{\prime }(s)$
is the curvature of the line
![]() $L$
. It follows from (5.17) that
$L$
. It follows from (5.17) that
From here on, we suppose that
![]() $h(s)$
and its derivative are of order
$h(s)$
and its derivative are of order
![]() $\unicode[STIX]{x1D700}$
. Then neglecting the terms of order
$\unicode[STIX]{x1D700}$
. Then neglecting the terms of order
![]() $\unicode[STIX]{x1D700}^{2}$
, we get
$\unicode[STIX]{x1D700}^{2}$
, we get
Let us denote by
![]() $\unicode[STIX]{x1D6EC}_{2\unicode[STIX]{x03C0}}$
one period of the line
$\unicode[STIX]{x1D6EC}_{2\unicode[STIX]{x03C0}}$
one period of the line
![]() $\unicode[STIX]{x1D6EC}$
. Consider condition (2.8). It can be easily demonstrated that
$\unicode[STIX]{x1D6EC}$
. Consider condition (2.8). It can be easily demonstrated that
Neglecting the terms of order
![]() $\unicode[STIX]{x1D700}^{2}$
and equating the right-hand side of (5.20) to zero yields
$\unicode[STIX]{x1D700}^{2}$
and equating the right-hand side of (5.20) to zero yields
where the evenness of the function
![]() $h(s)$
has been taken into account. Consider condition (2.15). With allowance for (5.19a
) and (5.14b
) we get
$h(s)$
has been taken into account. Consider condition (2.15). With allowance for (5.19a
) and (5.14b
) we get
Equating (5.22) to
![]() $P$
, we obtain
$P$
, we obtain
Thus, we have represented the boundary conditions (2.8) and (2.15) in the form of linear integral equations with respect to the unknown function
![]() $h(s)$
.
$h(s)$
.
Now, let us transform the main boundary condition (4.7), which provides that the line
![]() $\unicode[STIX]{x1D6EC}$
is a streamline. To do so, we use formulae (5.7a
) and (5.9). It follows from (4.7) and (5.9) that
$\unicode[STIX]{x1D6EC}$
is a streamline. To do so, we use formulae (5.7a
) and (5.9). It follows from (4.7) and (5.9) that
 $$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(s)+\frac{1}{2}\,\text{Im}\log [\langle F\rangle (s)+1]+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}(s)+\frac{1}{2}\,\text{Im}\frac{\displaystyle \frac{\text{d}\langle F\rangle (z)}{\text{d}z}\unicode[STIX]{x1D6FF}(z)+\langle \unicode[STIX]{x1D6FF}F\rangle (s)}{\langle F\rangle (s)+1}=0, & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle \unicode[STIX]{x1D703}(s)+\frac{1}{2}\,\text{Im}\log [\langle F\rangle (s)+1]+\unicode[STIX]{x1D6FF}\unicode[STIX]{x1D703}(s)+\frac{1}{2}\,\text{Im}\frac{\displaystyle \frac{\text{d}\langle F\rangle (z)}{\text{d}z}\unicode[STIX]{x1D6FF}(z)+\langle \unicode[STIX]{x1D6FF}F\rangle (s)}{\langle F\rangle (s)+1}=0, & & \displaystyle\end{eqnarray}$$
where
![]() $\unicode[STIX]{x1D6FF}F(z)$
is a piecewise-analytic function satisfying the boundary conditions (5.7) on
$\unicode[STIX]{x1D6FF}F(z)$
is a piecewise-analytic function satisfying the boundary conditions (5.7) on
![]() $L$
. Taking into account (5.14c
), (5.15), (5.19b
) and the equalities
$L$
. Taking into account (5.14c
), (5.15), (5.19b
) and the equalities
we rewrite the boundary conditions (4.7) and (5.7) in the form
where in (5.26) we have introduced the notation
In this notation,
![]() $\langle F\rangle _{z}^{\prime }[z(s)]=\langle F\rangle ^{\prime }(s)\text{e}^{-\text{i}\unicode[STIX]{x1D703}(s)}$
, with the function
$\langle F\rangle _{z}^{\prime }[z(s)]=\langle F\rangle ^{\prime }(s)\text{e}^{-\text{i}\unicode[STIX]{x1D703}(s)}$
, with the function
![]() $\langle F\rangle (s)$
being defined by (5.13).
$\langle F\rangle (s)$
being defined by (5.13).
Now, we need to express the right-hand side of condition (5.27a
) in terms of
![]() $h(s)$
. By making use of (4.4), we find
$h(s)$
. By making use of (4.4), we find
From (5.19b
) and the equality
![]() $\unicode[STIX]{x1D6FF}y(s)=h(s)\cos [\unicode[STIX]{x1D703}(s)]$
we deduce
$\unicode[STIX]{x1D6FF}y(s)=h(s)\cos [\unicode[STIX]{x1D703}(s)]$
we deduce
with
![]() $\unicode[STIX]{x1D6FF}k$
being the increment of the parameter
$\unicode[STIX]{x1D6FF}k$
being the increment of the parameter
![]() $k$
. The boundary conditions (5.27) for the function
$k$
. The boundary conditions (5.27) for the function
![]() $\unicode[STIX]{x1D6FF}F(z)$
take the form
$\unicode[STIX]{x1D6FF}F(z)$
take the form
where
Thus we come to the following linear boundary-value problem: find the piecewise-analytic function
![]() $\unicode[STIX]{x1D6FF}F(z)$
, which has a jump along the known curve
$\unicode[STIX]{x1D6FF}F(z)$
, which has a jump along the known curve
![]() $L$
, and the even,
$L$
, and the even,
![]() $2l_{s}$
-periodic, real-valued function
$2l_{s}$
-periodic, real-valued function
![]() $h(s)$
which satisfy the conditions (5.21), (5.23), (5.26) and (5.31).
$h(s)$
which satisfy the conditions (5.21), (5.23), (5.26) and (5.31).
In this problem, the function
![]() $\unicode[STIX]{x1D6FF}F(z)$
is auxiliary and can be excluded from consideration. Indeed, the boundary conditions (5.26) and (5.31a
) can be represented in the form of an integro-differential equation. To do so, we use (4.13) to write
$\unicode[STIX]{x1D6FF}F(z)$
is auxiliary and can be excluded from consideration. Indeed, the boundary conditions (5.26) and (5.31a
) can be represented in the form of an integro-differential equation. To do so, we use (4.13) to write
and
![]() $D[\unicode[STIX]{x1D714}](s)$
is a linear integral operator with respect to the
$D[\unicode[STIX]{x1D714}](s)$
is a linear integral operator with respect to the
![]() $2l_{s}$
-periodic, complex-valued and symmetric function
$2l_{s}$
-periodic, complex-valued and symmetric function
![]() $\unicode[STIX]{x1D714}(s)$
:
$\unicode[STIX]{x1D714}(s)$
:
The symmetry of the function
![]() $\unicode[STIX]{x1D714}(s)$
is understood in the sense that
$\unicode[STIX]{x1D714}(s)$
is understood in the sense that
![]() $\unicode[STIX]{x1D714}(-s)=\overline{\unicode[STIX]{x1D714}(s)}$
.
$\unicode[STIX]{x1D714}(-s)=\overline{\unicode[STIX]{x1D714}(s)}$
.
Since (5.33) involves the derivative
![]() $h^{\prime }(s)$
, it is convenient to express (5.21) and (5.23) in terms of
$h^{\prime }(s)$
, it is convenient to express (5.21) and (5.23) in terms of
![]() $h^{\prime }(s)$
. Integrating by parts their right-hand sides yields
$h^{\prime }(s)$
. Integrating by parts their right-hand sides yields
where
is the initial condition for the function
![]() $h(s)$
. Thus, we can formulate the following problem.
$h(s)$
. Thus, we can formulate the following problem.
Problem 2. Find the
![]() $2l_{s}$
-periodic, even function
$2l_{s}$
-periodic, even function
![]() $h(s)$
and the parameters
$h(s)$
and the parameters
![]() $\unicode[STIX]{x1D6FF}k$
and
$\unicode[STIX]{x1D6FF}k$
and
![]() $h_{0}$
such that the function and the parameters satisfy the system of integro-differential equations (5.33)–(5.36), in which
$h_{0}$
such that the function and the parameters satisfy the system of integro-differential equations (5.33)–(5.36), in which
![]() $a(s)$
,
$a(s)$
,
![]() $b(s)$
,
$b(s)$
,
![]() $c(s)$
,
$c(s)$
,
![]() $d(s)$
,
$d(s)$
,
![]() $U(s)$
,
$U(s)$
,
![]() $S_{L}$
,
$S_{L}$
,
![]() $P_{L}$
and
$P_{L}$
and
![]() $R(s)$
are defined by formulae (5.32), (5.28) and (5.14), respectively.
$R(s)$
are defined by formulae (5.32), (5.28) and (5.14), respectively.
So, to make one step of Newton’s iteration method, one needs to solve problem 2 and after that to determine the new approximation for the line
![]() $L$
by means of equation (5.16). The details of the numerical method for discretizing and solving problem 2 are presented in the appendix A.
$L$
by means of equation (5.16). The details of the numerical method for discretizing and solving problem 2 are presented in the appendix A.
6 Numerical computations
All the numerical computations have been carried out by locating 800 points on the right half of the interface
![]() $L_{2\unicode[STIX]{x03C0}}$
. At a fixed value of
$L_{2\unicode[STIX]{x03C0}}$
. At a fixed value of
![]() $\unicode[STIX]{x1D70C}\in [0,1]$
, we have gradually increased the parameter
$\unicode[STIX]{x1D70C}\in [0,1]$
, we have gradually increased the parameter
![]() $P$
from
$P$
from
![]() $P=1.0002$
either up to the value of
$P=1.0002$
either up to the value of
![]() $P$
at which
$P$
at which
![]() $|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
(for interfacial waves) or up to the moment when the Newton iteration process starts to diverge (for surface waves). At
$|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
(for interfacial waves) or up to the moment when the Newton iteration process starts to diverge (for surface waves). At
![]() $P=1.0002$
, to determine an initial approximation, we have used the formulae
$P=1.0002$
, to determine an initial approximation, we have used the formulae
which follow from (2.12a
), (3.1a
) and (3.2). The gradual increase of
![]() $P$
is carried out with a small step
$P$
is carried out with a small step
![]() $\unicode[STIX]{x0394}P$
which can be changed in the case of divergence of the Newton iterations, i.e.
$\unicode[STIX]{x0394}P$
which can be changed in the case of divergence of the Newton iterations, i.e.
![]() $\unicode[STIX]{x0394}P$
depends on
$\unicode[STIX]{x0394}P$
depends on
![]() $P$
. At
$P$
. At
![]() $P>1.0002$
, as an initial approximation, we have taken the solution for the previous
$P>1.0002$
, as an initial approximation, we have taken the solution for the previous
![]() $P$
. The Newton iterations have been stopped when the magnitudes of the right-hand sides in (5.33)–(5.36) become less than
$P$
. The Newton iterations have been stopped when the magnitudes of the right-hand sides in (5.33)–(5.36) become less than
![]() $10^{-8}$
. Usually, to get the desired accuracy, four or five iterations are enough. All our computations demonstrate that the pair
$10^{-8}$
. Usually, to get the desired accuracy, four or five iterations are enough. All our computations demonstrate that the pair
![]() $(\unicode[STIX]{x1D70C},P)$
defines uniquely the interfacial waves.
$(\unicode[STIX]{x1D70C},P)$
defines uniquely the interfacial waves.
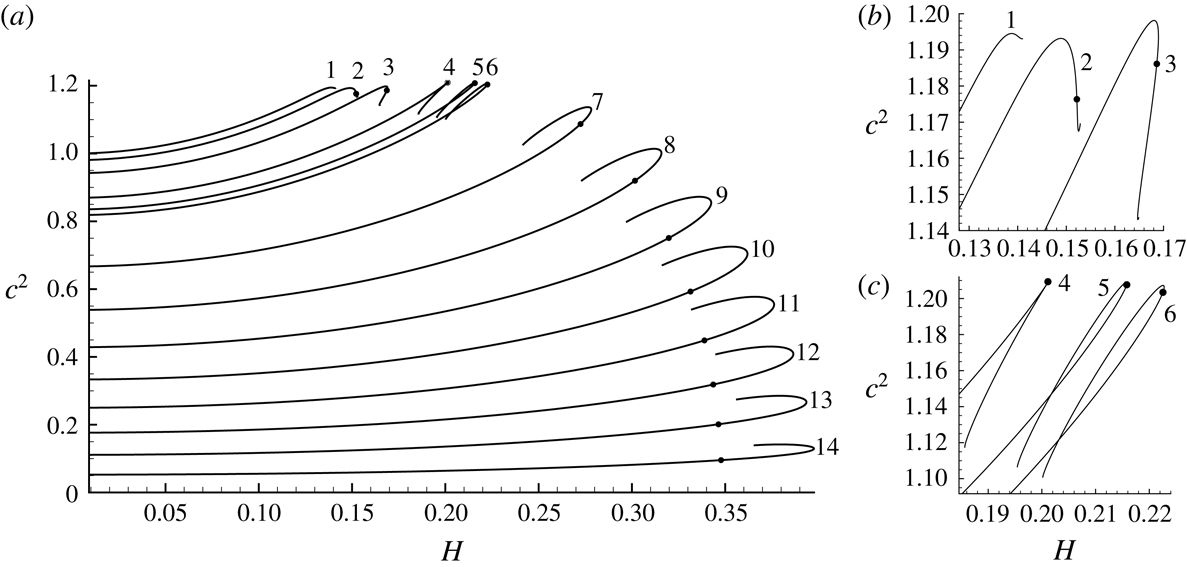
6.1 Test computations for surface waves
For surface waves, the parameter
![]() $\unicode[STIX]{x1D70C}=0$
, and according to the work by Maklakov (Reference Maklakov2002), the maximum inclination angle of the free surfaces is
$\unicode[STIX]{x1D70C}=0$
, and according to the work by Maklakov (Reference Maklakov2002), the maximum inclination angle of the free surfaces is
![]() $\unicode[STIX]{x1D703}_{max}=30.3787^{\circ }$
. Starting with
$\unicode[STIX]{x1D703}_{max}=30.3787^{\circ }$
. Starting with
![]() $P=1.0002$
, by means of the gradual increase of
$P=1.0002$
, by means of the gradual increase of
![]() $P$
, we have achieved
$P$
, we have achieved
![]() $P_{max}=1.0516537$
. At
$P_{max}=1.0516537$
. At
![]() $P=P_{max}$
, the value of
$P=P_{max}$
, the value of
![]() $\unicode[STIX]{x1D703}_{max}=30.3780^{\circ }$
. The further increase of
$\unicode[STIX]{x1D703}_{max}=30.3780^{\circ }$
. The further increase of
![]() $P$
is time-consuming and requires a greater accuracy.
$P$
is time-consuming and requires a greater accuracy.
For surface waves, a convenient way of checking the computational accuracy is to reproduce numerically the oscillations by Longuet-Higgins & Fox (Reference Longuet-Higgins and Fox1977, Reference Longuet-Higgins and Fox1978, Reference Longuet-Higgins and Fox1996) for some wave property. Let us introduce the parameter
where
![]() $q_{A}$
and
$q_{A}$
and
![]() $q_{B}$
are the velocities at the trough and crest of the wave, respectively. The parameter
$q_{B}$
are the velocities at the trough and crest of the wave, respectively. The parameter
![]() $A$
is responsible for the wave steepness and ranges from 0 to
$A$
is responsible for the wave steepness and ranges from 0 to
![]() $+\infty$
. When
$+\infty$
. When
![]() $A=+\infty$
(
$A=+\infty$
(
![]() $q_{B}=0$
), the wave is of limiting height with a
$q_{B}=0$
), the wave is of limiting height with a
![]() $120^{\circ }$
angular crest; when
$120^{\circ }$
angular crest; when
![]() $A\rightarrow 0$
, the waves are infinitesimal. For surface waves, the parameter
$A\rightarrow 0$
, the waves are infinitesimal. For surface waves, the parameter
![]() $A$
, as well as the wave steepness
$A$
, as well as the wave steepness
![]() $H$
, defines the wave uniquely.
$H$
, defines the wave uniquely.
As an example, consider the squared phase speed
![]() $c^{2}$
, which oscillates by the law (see Maklakov Reference Maklakov2002)
$c^{2}$
, which oscillates by the law (see Maklakov Reference Maklakov2002)
where
and
![]() $c_{\ast }^{2}$
being the value of
$c_{\ast }^{2}$
being the value of
![]() $c^{2}$
for the highest surface wave. It follows from (6.3) that the function
$c^{2}$
for the highest surface wave. It follows from (6.3) that the function
must be close to the cosine curve
![]() $\unicode[STIX]{x1D6FA}=\cos (kA-b_{M})$
for
$\unicode[STIX]{x1D6FA}=\cos (kA-b_{M})$
for
![]() $A\gg 1$
. At
$A\gg 1$
. At
![]() $P=P_{max}=1.0516537$
, we get
$P=P_{max}=1.0516537$
, we get
![]() $A_{max}=4.848442$
and the factor
$A_{max}=4.848442$
and the factor
![]() $\text{e}^{3A_{max}}/a_{M}\approx 2.5\times 10^{6}$
in (6.5). So, to force the point
$\text{e}^{3A_{max}}/a_{M}\approx 2.5\times 10^{6}$
in (6.5). So, to force the point
![]() $\unicode[STIX]{x1D6FA}(A_{max})$
to lie on the cosine curve, the computed value of the phase speed
$\unicode[STIX]{x1D6FA}(A_{max})$
to lie on the cosine curve, the computed value of the phase speed
![]() $c$
at
$c$
at
![]() $A=A_{max}$
must have at least eight correct decimals.
$A=A_{max}$
must have at least eight correct decimals.
In figure 4, the points are plotted for the computed values of
![]() $\unicode[STIX]{x1D6FA}(A)$
, and the solid line is the cosine curve
$\unicode[STIX]{x1D6FA}(A)$
, and the solid line is the cosine curve
![]() $\unicode[STIX]{x1D6FA}=\cos (kA-b_{M})$
. As one can see, the coincidence is excellent, which means that we have really achieved the desired accuracy of
$\unicode[STIX]{x1D6FA}=\cos (kA-b_{M})$
. As one can see, the coincidence is excellent, which means that we have really achieved the desired accuracy of
![]() $10^{-8}$
.
$10^{-8}$
.

Figure 4. The computed values of
![]() $\unicode[STIX]{x1D6FA}(A)$
(points) and the cosine curve
$\unicode[STIX]{x1D6FA}(A)$
(points) and the cosine curve
![]() $\unicode[STIX]{x1D6FA}=\cos (kA-b_{M})$
(solid line) for surface waves.
$\unicode[STIX]{x1D6FA}=\cos (kA-b_{M})$
(solid line) for surface waves.

Figure 5. (a) The shape of the almost highest surface wave of infinite depth at
![]() $A=4.848442$
. (b) The shape of its rounded crest scaled by the length
$A=4.848442$
. (b) The shape of its rounded crest scaled by the length
![]() $l=5.44869\times 10^{-5}$
, equal to the distance between the crest and the Bernoulli zero-velocity level.
$l=5.44869\times 10^{-5}$
, equal to the distance between the crest and the Bernoulli zero-velocity level.

Figure 6. The scaled local curvature
![]() $\hat{K}=K\times l$
versus the scaled arc-abscissa
$\hat{K}=K\times l$
versus the scaled arc-abscissa
![]() ${\hat{s}}$
for surface (a) and interfacial (b) waves.
${\hat{s}}$
for surface (a) and interfacial (b) waves.
Figure 5(a) shows the shape of the almost highest surface wave of infinite depth at
![]() $A=A_{max}$
. The crest of the wave looks angular, but figure 5(b) demonstrates that it is rounded. In fact, the shape shown in figure 5(b) is very close to the so-called inner solution in the vicinity of the crest (see Longuet-Higgins & Fox Reference Longuet-Higgins and Fox1977). The natural scale for this solution is the length
$A=A_{max}$
. The crest of the wave looks angular, but figure 5(b) demonstrates that it is rounded. In fact, the shape shown in figure 5(b) is very close to the so-called inner solution in the vicinity of the crest (see Longuet-Higgins & Fox Reference Longuet-Higgins and Fox1977). The natural scale for this solution is the length
![]() $l=q_{B}^{2}/2$
, which equals the distance between the crest and the Bernoulli zero-velocity level. For surface waves of infinite depth, the Bernoulli equation on the free surface takes the form
$l=q_{B}^{2}/2$
, which equals the distance between the crest and the Bernoulli zero-velocity level. For surface waves of infinite depth, the Bernoulli equation on the free surface takes the form
It follows from (6.6) that the Bernoulli zero-velocity level is
![]() $h_{0}=c^{2}/2$
, and
$h_{0}=c^{2}/2$
, and
where
![]() $H$
is the wave steepness. Figure 5(b) is plotted in the stretched coordinates
$H$
is the wave steepness. Figure 5(b) is plotted in the stretched coordinates
and in these coordinates, the Bernoulli equation is
where the velocity
![]() $q$
is scaled by
$q$
is scaled by
![]() $q_{B}/\sqrt{2}$
, i.e.
$q_{B}/\sqrt{2}$
, i.e.
![]() $\hat{q}=\sqrt{2}q/q_{B}$
. The dashed line in figure 5(b) is the asymptote
$\hat{q}=\sqrt{2}q/q_{B}$
. The dashed line in figure 5(b) is the asymptote
![]() $y=-\tan (\unicode[STIX]{x03C0}/6)|x|$
to which the shape of the free surface tends as
$y=-\tan (\unicode[STIX]{x03C0}/6)|x|$
to which the shape of the free surface tends as
![]() $\hat{x}\rightarrow \infty$
(see Longuet-Higgins & Fox Reference Longuet-Higgins and Fox1977). The two points in figure 5(b) indicate the location of the maximum slope of the free surface. For figure 5(b), this maximum slope
$\hat{x}\rightarrow \infty$
(see Longuet-Higgins & Fox Reference Longuet-Higgins and Fox1977). The two points in figure 5(b) indicate the location of the maximum slope of the free surface. For figure 5(b), this maximum slope
![]() $\unicode[STIX]{x1D703}_{max}=30.3780^{\circ }$
, which is very close to the maximum value
$\unicode[STIX]{x1D703}_{max}=30.3780^{\circ }$
, which is very close to the maximum value
![]() $\unicode[STIX]{x1D703}_{max}=30.3787^{\circ }$
achieved by Maklakov (Reference Maklakov2002) for
$\unicode[STIX]{x1D703}_{max}=30.3787^{\circ }$
achieved by Maklakov (Reference Maklakov2002) for
![]() $A>6$
.
$A>6$
.
It should be noted that, if the natural scale
![]() $l$
is small enough (the parameter
$l$
is small enough (the parameter
![]() $A$
is large enough), then all near-crest free-surface shapes scaled by
$A$
is large enough), then all near-crest free-surface shapes scaled by
![]() $l$
become identical. To confirm this fact, we have plotted in figure 6(a) the dependences of the scaled local curvature
$l$
become identical. To confirm this fact, we have plotted in figure 6(a) the dependences of the scaled local curvature
![]() $\hat{K}=K\times l$
versus the scaled arc-abscissa
$\hat{K}=K\times l$
versus the scaled arc-abscissa
![]() ${\hat{s}}=s/l$
for five values of
${\hat{s}}=s/l$
for five values of
![]() $A>2$
. The corresponding values of
$A>2$
. The corresponding values of
![]() $A$
and
$A$
and
![]() $l$
are demonstrated in table 1. As one can see in figure 6(a), all five graphs coincide, which again corroborates the accuracy of our computations. From table 1, one can conclude that the fully developed inner solution occurs if the natural scale
$l$
are demonstrated in table 1. As one can see in figure 6(a), all five graphs coincide, which again corroborates the accuracy of our computations. From table 1, one can conclude that the fully developed inner solution occurs if the natural scale
![]() $l$
is of order 0.01 or less.
$l$
is of order 0.01 or less.
Table 1. The values of
![]() $A$
and
$A$
and
![]() $l$
for the graphs of figure 6(a).
$l$
for the graphs of figure 6(a).
6.2 Almost limiting configurations
In figure 7, we have plotted 15 wave configurations. The first configuration corresponds to the steepest surface wave (
![]() $\unicode[STIX]{x1D70C}=0$
) that we have obtained. The remaining 14 configurations (
$\unicode[STIX]{x1D70C}=0$
) that we have obtained. The remaining 14 configurations (
![]() $0<\unicode[STIX]{x1D70C}\leqslant 1$
) we consider as almost limiting because for all of them
$0<\unicode[STIX]{x1D70C}\leqslant 1$
) we consider as almost limiting because for all of them
![]() $|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
. All these configurations have a mushroom shape and the sizes of their mushroom caps depend on
$|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
. All these configurations have a mushroom shape and the sizes of their mushroom caps depend on
![]() $\unicode[STIX]{x1D70C}$
. For a small
$\unicode[STIX]{x1D70C}$
. For a small
![]() $\unicode[STIX]{x1D70C}$
of 0.01 the cap is very small, but nevertheless it exists. Some properties of the waves shown in figure 7 are presented in table 2. Each configuration in figure 7 corresponds to one of the values of
$\unicode[STIX]{x1D70C}$
of 0.01 the cap is very small, but nevertheless it exists. Some properties of the waves shown in figure 7 are presented in table 2. Each configuration in figure 7 corresponds to one of the values of
![]() $\unicode[STIX]{x1D70C}$
in table 2, and the correspondence can be easily discerned, because, as follows from the table, the width of the mushroom cap,
$\unicode[STIX]{x1D70C}$
in table 2, and the correspondence can be easily discerned, because, as follows from the table, the width of the mushroom cap,
![]() $w_{cap}$
, increases monotonically as
$w_{cap}$
, increases monotonically as
![]() $\unicode[STIX]{x1D70C}$
increases.
$\unicode[STIX]{x1D70C}$
increases.

Figure 7. Almost limiting configurations of interfacial waves.
Table 2. Properties of waves shown in figure 7.


Figure 8. (a) The dependences of
![]() $|F^{+}+1|$
(solid line) and
$|F^{+}+1|$
(solid line) and
![]() $|F^{-}+1|$
(dashed line) on the arc-abscissa
$|F^{-}+1|$
(dashed line) on the arc-abscissa
![]() $s$
for the almost limiting configuration at
$s$
for the almost limiting configuration at
![]() $\unicode[STIX]{x1D70C}=0.3$
. (b) The ordinates
$\unicode[STIX]{x1D70C}=0.3$
. (b) The ordinates
![]() $y_{D}$
versus
$y_{D}$
versus
![]() $c^{2}$
(solid lines); the dashed line is the function
$c^{2}$
(solid lines); the dashed line is the function
![]() $y=c^{2}/2$
.
$y=c^{2}/2$
.
As one can see from figure 7, a characteristic feature of the almost limiting interfacial configurations is an almost flat underside of the mushroom caps. In figure 8(a), we demonstrate the functions
![]() $|F^{+}(s)+1|$
and
$|F^{+}(s)+1|$
and
![]() $|F^{-}(s)+1|$
along the right half of the almost limiting interface at
$|F^{-}(s)+1|$
along the right half of the almost limiting interface at
![]() $\unicode[STIX]{x1D70C}=0.3$
. According to (4.1) and (4.2), the functions
$\unicode[STIX]{x1D70C}=0.3$
. According to (4.1) and (4.2), the functions
![]() $F^{+}(s)$
and
$F^{+}(s)$
and
![]() $F^{-}(s)$
are connected with the squared velocities
$F^{-}(s)$
are connected with the squared velocities
![]() $(q^{+})^{2}$
and
$(q^{+})^{2}$
and
![]() $(q^{-})^{2}$
by the formulae
$(q^{-})^{2}$
by the formulae
Figure 8(a) shows that there exists a section of the interface along which the values of
![]() $|F^{+}(s)+1|$
and
$|F^{+}(s)+1|$
and
![]() $|F^{-}(s)+1|$
are both almost exactly equal to zero. For other values of
$|F^{-}(s)+1|$
are both almost exactly equal to zero. For other values of
![]() $\unicode[STIX]{x1D70C}$
, the situation is analogous, namely, there always exists a section of the almost limiting interface along which
$\unicode[STIX]{x1D70C}$
, the situation is analogous, namely, there always exists a section of the almost limiting interface along which
![]() $F^{+}(s)\approx F^{-}(s)\approx -1$
. Such sections just correspond to the almost flat undersides of the mushroom caps. Indeed, one can set on the sections that
$F^{+}(s)\approx F^{-}(s)\approx -1$
. Such sections just correspond to the almost flat undersides of the mushroom caps. Indeed, one can set on the sections that
![]() $(q^{+}/c)^{2}=(q^{-}/c)^{2}=0$
and
$(q^{+}/c)^{2}=(q^{-}/c)^{2}=0$
and
![]() $F^{+}(z)=F^{-}(z)=-1$
. Then, according to (4.3) and (4.4), along the section
$F^{+}(z)=F^{-}(z)=-1$
. Then, according to (4.3) and (4.4), along the section

Figure 9. Sketches of the almost limiting (a) and limiting (b) interfacial configurations with characteristic points and lengths.
Taking into account equation (2.12), we conclude that the ordinate of the flat section of the interface is
For surface waves, the ordinate
![]() $h_{0}=c^{2}/2$
is the Bernoulli zero-velocity level, which is always higher than any wave surface. For interfacial waves, the line
$h_{0}=c^{2}/2$
is the Bernoulli zero-velocity level, which is always higher than any wave surface. For interfacial waves, the line
![]() $y=c^{2}/2$
can intersect the interface even for waves of moderate steepness. However, for the almost limiting configurations, the level
$y=c^{2}/2$
can intersect the interface even for waves of moderate steepness. However, for the almost limiting configurations, the level
![]() $c^{2}/2$
plays an important role, namely, this is the height of the almost flat undersides of the mushroom caps.
$c^{2}/2$
plays an important role, namely, this is the height of the almost flat undersides of the mushroom caps.
In figure 9(a), we have plotted the sketch of an almost limiting configuration and indicated its characteristic points and lengths. Consider the point
![]() $D$
on the interface at which the slope
$D$
on the interface at which the slope
![]() $\unicode[STIX]{x1D703}$
achieves its negative minimum, i.e. at this point
$\unicode[STIX]{x1D703}$
achieves its negative minimum, i.e. at this point
![]() $\unicode[STIX]{x1D703}=-|\unicode[STIX]{x1D703}|_{max}$
. To confirm the above-mentioned conclusion about the level
$\unicode[STIX]{x1D703}=-|\unicode[STIX]{x1D703}|_{max}$
. To confirm the above-mentioned conclusion about the level
![]() $h_{0}=c^{2}/2$
, we have plotted figure 8(b), where solid lines show the ordinates
$h_{0}=c^{2}/2$
, we have plotted figure 8(b), where solid lines show the ordinates
![]() $y_{D}$
of the points
$y_{D}$
of the points
![]() $D$
versus
$D$
versus
![]() $c^{2}$
for several values of
$c^{2}$
for several values of
![]() $\unicode[STIX]{x1D70C}$
. The dashed line is the function
$\unicode[STIX]{x1D70C}$
. The dashed line is the function
![]() $y=c^{2}/2$
. The plots demonstrate explicitly that the ends of all solid lines tend to the coincidence with the dashed line, and, in the scales of the figure, this coincidence seems to be full.
$y=c^{2}/2$
. The plots demonstrate explicitly that the ends of all solid lines tend to the coincidence with the dashed line, and, in the scales of the figure, this coincidence seems to be full.
6.3 Inner crest and the inner solution near the inner crest
Let us denote by
![]() $C$
the point which indicates the location of the narrowest width of the mushroom stem for the almost limiting interfacial configurations (see figure 9
a). This point we shall call the inner crest. Consider the solid line in figure 8(a), which shows the dependence of
$C$
the point which indicates the location of the narrowest width of the mushroom stem for the almost limiting interfacial configurations (see figure 9
a). This point we shall call the inner crest. Consider the solid line in figure 8(a), which shows the dependence of
![]() $|F^{+}(s)+1|$
on
$|F^{+}(s)+1|$
on
![]() $s$
. On this line, there exists a section where
$s$
. On this line, there exists a section where
![]() $|F^{+}(s)+1|$
almost vanishes, and the length of this section is twice as long as that where
$|F^{+}(s)+1|$
almost vanishes, and the length of this section is twice as long as that where
![]() $F^{+}(s)\approx F^{-}(s)\approx -1$
. Let us set on the section that
$F^{+}(s)\approx F^{-}(s)\approx -1$
. Let us set on the section that
![]() $|F^{+}(s)+1|=0$
. Then, according to (6.10a
), we have
$|F^{+}(s)+1|=0$
. Then, according to (6.10a
), we have
![]() $\unicode[STIX]{x1D70C}(q^{+}/c)^{2}=0$
, and according to (2.11), we have
$\unicode[STIX]{x1D70C}(q^{+}/c)^{2}=0$
, and according to (2.11), we have
Taking into account formula (2.12a ), equation (6.13) can be rewritten as
where
![]() $h_{0}=c^{2}/2$
,
$h_{0}=c^{2}/2$
,
![]() $q_{C}^{-}$
is the velocity of the lower fluid at the inner crest
$q_{C}^{-}$
is the velocity of the lower fluid at the inner crest
![]() $C$
, and
$C$
, and
In (6.15),
![]() $s_{C}$
is the arc-abscissa of the point
$s_{C}$
is the arc-abscissa of the point
![]() $C$
, and the last equality follows from (2.12a
) and (6.10b
).
$C$
, and the last equality follows from (2.12a
) and (6.10b
).
Setting in equation (6.14) that
![]() $q^{-}=q_{C}^{-}$
, we deduce that the length
$q^{-}=q_{C}^{-}$
, we deduce that the length
![]() $l$
is the vertical distance between the inner crest
$l$
is the vertical distance between the inner crest
![]() $C$
and the level
$C$
and the level
![]() $h_{0}=c^{2}/2$
(see figure 9
a). Recall that, for surface waves,
$h_{0}=c^{2}/2$
(see figure 9
a). Recall that, for surface waves,
![]() $l$
is the distance between the crest
$l$
is the distance between the crest
![]() $B$
and the same level
$B$
and the same level
![]() $h_{0}=c^{2}/2$
. Now we proceed in the same manner as for surface waves. We introduce the stretched coordinates
$h_{0}=c^{2}/2$
. Now we proceed in the same manner as for surface waves. We introduce the stretched coordinates
![]() $\hat{x}$
and
$\hat{x}$
and
![]() ${\hat{y}}$
by formulae (6.8) and the scaled velocity
${\hat{y}}$
by formulae (6.8) and the scaled velocity
![]() $\hat{q}=\sqrt{2}q^{-}/q_{C}^{-}$
(for surface waves the scaled velocity is
$\hat{q}=\sqrt{2}q^{-}/q_{C}^{-}$
(for surface waves the scaled velocity is
![]() $\hat{q}=\sqrt{2}q/q_{B}$
). In these coordinates and with such a velocity scaling, equation (6.14) transforms to the ordinary boundary condition (6.9) of constant pressure on the free surface.
$\hat{q}=\sqrt{2}q/q_{B}$
). In these coordinates and with such a velocity scaling, equation (6.14) transforms to the ordinary boundary condition (6.9) of constant pressure on the free surface.
Thus, analogously to surface waves, if the length
![]() $l$
is small enough, all interfacial shapes must be identical in the coordinates
$l$
is small enough, all interfacial shapes must be identical in the coordinates
![]() $\hat{x}$
and
$\hat{x}$
and
![]() ${\hat{y}}$
independently of the density ratio
${\hat{y}}$
independently of the density ratio
![]() $\unicode[STIX]{x1D70C}$
. For the interfacial configurations presented in figure 7, the values of
$\unicode[STIX]{x1D70C}$
. For the interfacial configurations presented in figure 7, the values of
![]() $l$
computed by formula (6.15) are shown in the ninth column of table 2. For surface waves when
$l$
computed by formula (6.15) are shown in the ninth column of table 2. For surface waves when
![]() $\unicode[STIX]{x1D70C}=0$
, the parameter
$\unicode[STIX]{x1D70C}=0$
, the parameter
![]() $l$
has been computed by formula (6.7).
$l$
has been computed by formula (6.7).

Figure 10. The boundaries of flows in the vicinity of the inner crest for interfacial waves in the stretched coordinates
![]() $\hat{x}$
and
$\hat{x}$
and
![]() ${\hat{y}}$
.
${\hat{y}}$
.
Let us take the configurations from 2 to 9. According to table 2, for these configurations,
![]() $l<0.05$
. In figure 10 we have plotted the configurations in the coordinates
$l<0.05$
. In figure 10 we have plotted the configurations in the coordinates
![]() $\hat{x}$
and
$\hat{x}$
and
![]() ${\hat{y}}$
. As one can see from figure 10 and table 2, if
${\hat{y}}$
. As one can see from figure 10 and table 2, if
![]() $l<0.02$
(configurations 2–6) all curves practically coincide. The difference becomes noticeable only for
$l<0.02$
(configurations 2–6) all curves practically coincide. The difference becomes noticeable only for
![]() $l>0.02$
(configurations 7–9).
$l>0.02$
(configurations 7–9).
Let us introduce the scaled arc-abscissa
![]() ${\hat{s}}$
counted from the inner crest
${\hat{s}}$
counted from the inner crest
![]() $C$
: i.e.
$C$
: i.e.
![]() ${\hat{s}}=(s-s_{C})/l$
. In figure 6(b), we have plotted the graphs analogous to those of figure 6(a), namely, the scaled local curvature
${\hat{s}}=(s-s_{C})/l$
. In figure 6(b), we have plotted the graphs analogous to those of figure 6(a), namely, the scaled local curvature
![]() $\hat{K}=K\times l$
versus
$\hat{K}=K\times l$
versus
![]() ${\hat{s}}$
for all interfacial configurations 2–15 of figure 7. Here the coincidence is even more evident than in figure 10. The worst result we have is for the Boussinesq limit, when
${\hat{s}}$
for all interfacial configurations 2–15 of figure 7. Here the coincidence is even more evident than in figure 10. The worst result we have is for the Boussinesq limit, when
![]() $\unicode[STIX]{x1D70C}=1$
and the value of
$\unicode[STIX]{x1D70C}=1$
and the value of
![]() $l\approx 0.184$
. The latter, certainly, cannot be considered to be small enough.
$l\approx 0.184$
. The latter, certainly, cannot be considered to be small enough.
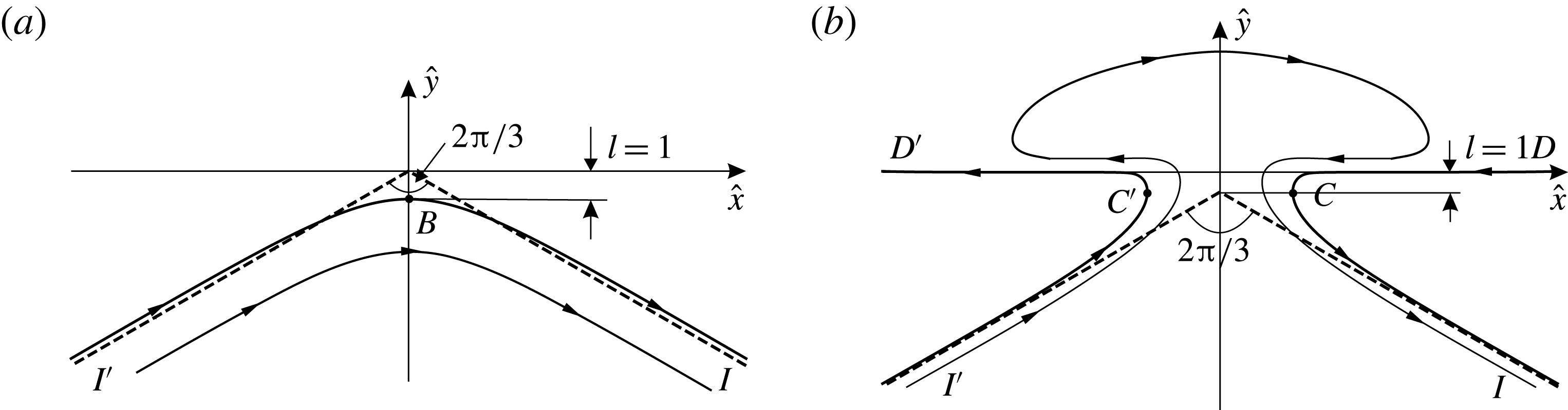
Figure 11. Sketches of inner solutions: surface waves (a) and interfacial waves (b).
The sketches of the inner solutions for surface and interfacial waves are shown in figure 11. As one can see, these inner solutions are qualitatively different. For surface waves, the flow is similar to that in the angle of
![]() $120^{\circ }$
with a rounded apex. For the interfacial wave, the streamlines enter into the slot
$120^{\circ }$
with a rounded apex. For the interfacial wave, the streamlines enter into the slot
![]() $C^{\prime }C$
between the inner crests and go out through the same slot; the points
$C^{\prime }C$
between the inner crests and go out through the same slot; the points
![]() $D^{\prime }$
and
$D^{\prime }$
and
![]() $D$
at infinity are the stagnation ones with
$D$
at infinity are the stagnation ones with
![]() $\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
and
$\unicode[STIX]{x1D703}=\unicode[STIX]{x03C0}$
and
![]() $\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}$
, respectively. On the streamlines
$\unicode[STIX]{x1D703}=-\unicode[STIX]{x03C0}$
, respectively. On the streamlines
![]() $D^{\prime }C^{\prime }I^{\prime }$
and
$D^{\prime }C^{\prime }I^{\prime }$
and
![]() $DCI$
, the ordinate
$DCI$
, the ordinate
![]() $y$
decreases monotonically from zero to
$y$
decreases monotonically from zero to
![]() $-\infty$
. For surface waves, the inner solution forms near the upper crest
$-\infty$
. For surface waves, the inner solution forms near the upper crest
![]() $B$
; for interfacial waves, the inner solution does so near the inner crests
$B$
; for interfacial waves, the inner solution does so near the inner crests
![]() $C$
and
$C$
and
![]() $C^{\prime }$
. It is also worthwhile to mention the difference between the asymptotes:
$C^{\prime }$
. It is also worthwhile to mention the difference between the asymptotes:
For surface waves, the asymptote (6.16a
) was established by Longuet-Higgins & Fox (Reference Longuet-Higgins and Fox1977). For interfacial waves, according to figure 10, the asymptote (6.16a
) seems to be shifted by one unit downwards from the vertical benchmark
![]() $h_{0}=c^{2}/2$
. For surface waves, the asymptote always intersects the boundary close to the almost limiting configuration; for interfacial waves, according to figure 10, this seems not to be the case.
$h_{0}=c^{2}/2$
. For surface waves, the asymptote always intersects the boundary close to the almost limiting configuration; for interfacial waves, according to figure 10, this seems not to be the case.
However, there exist some general features, namely, the vertical benchmarks for both flows are the same,
![]() $h_{0}=c^{2}/2$
; the formulae for the natural scales are similar. In the dimensional form, they are as follows:
$h_{0}=c^{2}/2$
; the formulae for the natural scales are similar. In the dimensional form, they are as follows:
In addition, the boundary conditions on the free surfaces
![]() $I^{\prime }BI$
and
$I^{\prime }BI$
and
![]() $I^{\prime }C^{\prime }D^{\prime }DCI$
are absolutely identical: both free surfaces are streamlines on which equation (6.9) of constant pressure is fulfilled.
$I^{\prime }C^{\prime }D^{\prime }DCI$
are absolutely identical: both free surfaces are streamlines on which equation (6.9) of constant pressure is fulfilled.
6.4 Limiting configurations
The results obtained in §§ 6.2 and 6.3 allow us to predict easily the sketch of the limiting interfacial configuration. Indeed, it is evident that, for a fixed
![]() $\unicode[STIX]{x1D70C}$
, the limiting configuration takes place when the length
$\unicode[STIX]{x1D70C}$
, the limiting configuration takes place when the length
![]() $l$
defined by (6.15) is zero. Let
$l$
defined by (6.15) is zero. Let
![]() $x_{C}$
be the abscissa of the inner crest
$x_{C}$
be the abscissa of the inner crest
![]() $C$
. According to the last column of table 2, for the almost limiting interfacial waves
$C$
. According to the last column of table 2, for the almost limiting interfacial waves
![]() $x_{C}\approx 3.7\times l$
. Hence if
$x_{C}\approx 3.7\times l$
. Hence if
![]() $l=0$
, then
$l=0$
, then
![]() $x_{C}=0$
too. This means that the points
$x_{C}=0$
too. This means that the points
![]() $C$
and
$C$
and
![]() $C^{\prime }$
in figure 9(a) coincide. Moreover, at
$C^{\prime }$
in figure 9(a) coincide. Moreover, at
![]() $l=0$
, the inner flow, whose sketch is shown in figure 11(b), shrinks to the point
$l=0$
, the inner flow, whose sketch is shown in figure 11(b), shrinks to the point
![]() $C$
coinciding with
$C$
coinciding with
![]() $C^{\prime }$
. However, this shrinking conserves the directions of the slope
$C^{\prime }$
. However, this shrinking conserves the directions of the slope
![]() $\unicode[STIX]{x1D703}$
at the infinitely remote points
$\unicode[STIX]{x1D703}$
at the infinitely remote points
![]() $D^{\prime }$
,
$D^{\prime }$
,
![]() $D$
and
$D$
and
![]() $I^{\prime }$
,
$I^{\prime }$
,
![]() $I$
. This reasoning naturally leads to the conclusion that the sketch of the limiting configuration is as shown in figure 9(b). The mushroom caps of the limiting interfacial configurations are stagnation zones consisting of the particles of the lower fluid.
$I$
. This reasoning naturally leads to the conclusion that the sketch of the limiting configuration is as shown in figure 9(b). The mushroom caps of the limiting interfacial configurations are stagnation zones consisting of the particles of the lower fluid.
Evidently, if
![]() $s_{C}$
is the arc-abscissa of point
$s_{C}$
is the arc-abscissa of point
![]() $C$
, then for the limiting configurations,
$C$
, then for the limiting configurations,
Thus for the limiting interfacial configurations, the function
![]() $\unicode[STIX]{x1D703}(s)$
is not continuous but has jumps at the points
$\unicode[STIX]{x1D703}(s)$
is not continuous but has jumps at the points
![]() $\pm s_{C}$
. Therefore, the interface is not a smooth curve, proposition 1 is not true any more, and as follows from equations (6.18a,c
),
$\pm s_{C}$
. Therefore, the interface is not a smooth curve, proposition 1 is not true any more, and as follows from equations (6.18a,c
),
![]() $|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}$
for the limiting case.
$|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}$
for the limiting case.
If the density ratio
![]() $\unicode[STIX]{x1D70C}=1$
(Boussinesq limit), then the points
$\unicode[STIX]{x1D70C}=1$
(Boussinesq limit), then the points
![]() $(-\unicode[STIX]{x03C0}/2,0)$
and
$(-\unicode[STIX]{x03C0}/2,0)$
and
![]() $(\unicode[STIX]{x03C0}/2,0)$
are those of central symmetry for the left and right half of the interface, respectively. The limiting configuration in this case must be as predicted by Grimshaw & Pullin (Reference Grimshaw and Pullin1986, figure 9). The configuration contains a periodic stagnation zone formed by both the upper and lower fluids. The zone is bounded from above and below by the two free surfaces of the highest Stokes waves with angular crests that are oppositely directed and shifted by a half-period with respect to each other.
$(\unicode[STIX]{x03C0}/2,0)$
are those of central symmetry for the left and right half of the interface, respectively. The limiting configuration in this case must be as predicted by Grimshaw & Pullin (Reference Grimshaw and Pullin1986, figure 9). The configuration contains a periodic stagnation zone formed by both the upper and lower fluids. The zone is bounded from above and below by the two free surfaces of the highest Stokes waves with angular crests that are oppositely directed and shifted by a half-period with respect to each other.

Figure 12. (a) The dependences of
![]() $c^{2}$
on
$c^{2}$
on
![]() $H$
for different values of
$H$
for different values of
![]() $\unicode[STIX]{x1D70C}$
from table 2. The upper parts of curves 1–3 (b) and 4–6 (c). The points indicate the pairs
$\unicode[STIX]{x1D70C}$
from table 2. The upper parts of curves 1–3 (b) and 4–6 (c). The points indicate the pairs
![]() $(H,c^{2})$
for Holyer’s limiting configurations with
$(H,c^{2})$
for Holyer’s limiting configurations with
![]() $|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
(Holyer Reference Holyer1979).
$|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
(Holyer Reference Holyer1979).
6.5 The dependences of the phase speed on the wave steepness for interfacial waves
It is well known that, for surface waves, the wave steepness
![]() $H$
is one of the parameters that define the wave uniquely. As was shown by Grimshaw & Pullin (Reference Grimshaw and Pullin1986) and Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986), for interfacial waves this is not the case. In figure 12(a), we demonstrate the dependences of
$H$
is one of the parameters that define the wave uniquely. As was shown by Grimshaw & Pullin (Reference Grimshaw and Pullin1986) and Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986), for interfacial waves this is not the case. In figure 12(a), we demonstrate the dependences of
![]() $c^{2}$
on
$c^{2}$
on
![]() $H$
for different density ratios
$H$
for different density ratios
![]() $\unicode[STIX]{x1D70C}$
. The correspondence between the numbered curves and the density ratios
$\unicode[STIX]{x1D70C}$
. The correspondence between the numbered curves and the density ratios
![]() $\unicode[STIX]{x1D70C}$
can be found in table 2. For interfacial waves (numbers 2–14), the end points of all curves correspond to the almost limiting configurations with
$\unicode[STIX]{x1D70C}$
can be found in table 2. For interfacial waves (numbers 2–14), the end points of all curves correspond to the almost limiting configurations with
![]() $\unicode[STIX]{x1D703}_{max}>179.98^{\circ }$
. As one can see, for
$\unicode[STIX]{x1D703}_{max}>179.98^{\circ }$
. As one can see, for
![]() $\unicode[STIX]{x1D70C}\geqslant 0.03$
, the wave steepness
$\unicode[STIX]{x1D70C}\geqslant 0.03$
, the wave steepness
![]() $H$
really does not define the wave uniquely. Another conclusion that can be drawn from figure 12(a) is that, generally, the phase speed
$H$
really does not define the wave uniquely. Another conclusion that can be drawn from figure 12(a) is that, generally, the phase speed
![]() $c$
decreases as the parameter
$c$
decreases as the parameter
![]() $\unicode[STIX]{x1D70C}$
increases, but the fastest waves occur at
$\unicode[STIX]{x1D70C}$
increases, but the fastest waves occur at
![]() $0.07\leqslant \unicode[STIX]{x1D70C}\leqslant 0.1$
. For the Boussinesq limit when
$0.07\leqslant \unicode[STIX]{x1D70C}\leqslant 0.1$
. For the Boussinesq limit when
![]() $\unicode[STIX]{x1D70C}\rightarrow 1$
, the phase speed
$\unicode[STIX]{x1D70C}\rightarrow 1$
, the phase speed
![]() $c\rightarrow 0$
, and we do not number this graph.
$c\rightarrow 0$
, and we do not number this graph.
The points in figure 12 correspond to the Holyer (Reference Holyer1979) limiting configurations (
![]() $|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
). Accurate values of the pairs
$|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
). Accurate values of the pairs
![]() $(H,c^{2})$
for the Holyer limit are presented in table 3.
$(H,c^{2})$
for the Holyer limit are presented in table 3.
Let us consider the case of small
![]() $\unicode[STIX]{x1D70C}$
in more detail. The upper parts of curves 1–3 of figure 12(a) are shown in figure 12(b). Curve 2 demonstrates that at
$\unicode[STIX]{x1D70C}$
in more detail. The upper parts of curves 1–3 of figure 12(a) are shown in figure 12(b). Curve 2 demonstrates that at
![]() $\unicode[STIX]{x1D70C}=0.01$
the pair
$\unicode[STIX]{x1D70C}=0.01$
the pair
![]() $(H,c^{2})$
defines the wave uniquely, but already at
$(H,c^{2})$
defines the wave uniquely, but already at
![]() $\unicode[STIX]{x1D70C}=0.03$
(curve 3) the uniqueness disappears. Curves 4–6 of figure 12(c) prove that, for
$\unicode[STIX]{x1D70C}=0.03$
(curve 3) the uniqueness disappears. Curves 4–6 of figure 12(c) prove that, for
![]() $0.07<\unicode[STIX]{x1D70C}\leqslant 0.1$
, the dependences
$0.07<\unicode[STIX]{x1D70C}\leqslant 0.1$
, the dependences
![]() $c^{2}$
versus
$c^{2}$
versus
![]() $H$
have points of self-intersection, which means that in this range of
$H$
have points of self-intersection, which means that in this range of
![]() $\unicode[STIX]{x1D70C}$
there exist waves which have identical values of the wave steepness
$\unicode[STIX]{x1D70C}$
there exist waves which have identical values of the wave steepness
![]() $H$
and the phase velocity
$H$
and the phase velocity
![]() $c$
but different shapes. Two such waves at
$c$
but different shapes. Two such waves at
![]() $\unicode[STIX]{x1D70C}=0.1$
are displayed in figure 13. For the sake of comparison, the
$\unicode[STIX]{x1D70C}=0.1$
are displayed in figure 13. For the sake of comparison, the
![]() $x$
-axis here is located at equal vertical distances from the crest and trough (
$x$
-axis here is located at equal vertical distances from the crest and trough (
![]() $y_{B}=-y_{A}$
). The values of the parameters
$y_{B}=-y_{A}$
). The values of the parameters
![]() $P$
,
$P$
,
![]() $|\unicode[STIX]{x1D703}|_{max}$
,
$|\unicode[STIX]{x1D703}|_{max}$
,
![]() $H$
and
$H$
and
![]() $c^{2}$
for these two waves are shown in table 4.
$c^{2}$
for these two waves are shown in table 4.

Figure 13. Two waves with the same
![]() $H$
and
$H$
and
![]() $c^{2}$
at
$c^{2}$
at
![]() $\unicode[STIX]{x1D70C}=0.1$
.
$\unicode[STIX]{x1D70C}=0.1$
.
Table 3. The pairs
![]() $(H,c^{2})$
for Holyer’s limiting configurations with
$(H,c^{2})$
for Holyer’s limiting configurations with
![]() $|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
(Holyer Reference Holyer1979).
$|\unicode[STIX]{x1D703}|_{max}=\unicode[STIX]{x03C0}/2$
(Holyer Reference Holyer1979).

Table 4. The parameters
![]() $P$
,
$P$
,
![]() $|\unicode[STIX]{x1D703}|_{max}$
,
$|\unicode[STIX]{x1D703}|_{max}$
,
![]() $H$
and
$H$
and
![]() $c^{2}$
for two waves of figure 13.
$c^{2}$
for two waves of figure 13.
7 Discussion of results and conclusions
7.1 Comparison with the work by Saffman & Yuen (Reference Saffman and Yuen1982)
Accurate computations of interfacial waves of moderate steepness were carried out by Saffman & Yuen (Reference Saffman and Yuen1982). In table 2 of their paper, these authors presented the values of the phase speed
versus
![]() $2\unicode[STIX]{x03C0}H$
for the density ratio
$2\unicode[STIX]{x03C0}H$
for the density ratio
![]() $\unicode[STIX]{x1D70C}=0.1$
. As follows from (3.1),
$\unicode[STIX]{x1D70C}=0.1$
. As follows from (3.1),
![]() $C$
is the dimensionless phase speed non-dimensionalized with respect to the phase speed of infinitesimal waves. In table 5 (second column), we have reproduced the results by Saffman & Yuen (Reference Saffman and Yuen1982). The third to fifth columns present our computations of
$C$
is the dimensionless phase speed non-dimensionalized with respect to the phase speed of infinitesimal waves. In table 5 (second column), we have reproduced the results by Saffman & Yuen (Reference Saffman and Yuen1982). The third to fifth columns present our computations of
![]() $C$
at
$C$
at
![]() $N=800$
, 1600 and 3200, where
$N=800$
, 1600 and 3200, where
![]() $N$
is the number of points which approximate the right half of the interface
$N$
is the number of points which approximate the right half of the interface
![]() $L_{2\unicode[STIX]{x03C0}}$
.
$L_{2\unicode[STIX]{x03C0}}$
.
Generating the data of table 2, Saffman & Yuen (Reference Saffman and Yuen1982) thoroughly checked their decimals, and as one can see from table 5, their check turns out to be very efficient because all these decimals are correct. In our computations, we consider
![]() $N=800$
as a working point number which allows us to compute the interfacial waves for any
$N=800$
as a working point number which allows us to compute the interfacial waves for any
![]() $0<\unicode[STIX]{x1D70C}\leqslant 1$
in the range
$0<\unicode[STIX]{x1D70C}\leqslant 1$
in the range
![]() $0<|\unicode[STIX]{x1D703}|_{max}\leqslant 179.98^{\circ }$
with an error less than
$0<|\unicode[STIX]{x1D703}|_{max}\leqslant 179.98^{\circ }$
with an error less than
![]() $10^{-8}$
. Table 5 confirms that at
$10^{-8}$
. Table 5 confirms that at
![]() $N=800$
we have at least eight correct decimals and at the same time demonstrates an explicit convergence of the algorithm as
$N=800$
we have at least eight correct decimals and at the same time demonstrates an explicit convergence of the algorithm as
![]() $N$
increases. The last column of table 5 shows the values of
$N$
increases. The last column of table 5 shows the values of
![]() $|\unicode[STIX]{x1D703}|_{max}$
in order to give the reader a representation about the closeness of the waves to the limiting configuration.
$|\unicode[STIX]{x1D703}|_{max}$
in order to give the reader a representation about the closeness of the waves to the limiting configuration.
At
![]() $N=800$
, the time for computing one wave is only several seconds but certainly the time increases with increase of
$N=800$
, the time for computing one wave is only several seconds but certainly the time increases with increase of
![]() $N$
. Nevertheless, all data of table 5 have been generated for approximately one hour on the notebook HP G1 EliteBook Folio 1040.
$N$
. Nevertheless, all data of table 5 have been generated for approximately one hour on the notebook HP G1 EliteBook Folio 1040.
Table 5. Continuation of table 2 from the paper by Saffman & Yuen (Reference Saffman and Yuen1982, S&Y) (
![]() $\unicode[STIX]{x1D70C}=0.1$
).
$\unicode[STIX]{x1D70C}=0.1$
).

7.2 Comparison with the work by Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986)
In the paper by Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986), the most extensive numerical data were obtained for the case
![]() $\unicode[STIX]{x1D70C}=0.1$
. The results were displayed in figure 2 (p. 374) of their paper and a copy of this figure is shown in figure 14(a). In the notation used by Turner & Vanden-Broeck,
$\unicode[STIX]{x1D70C}=0.1$
. The results were displayed in figure 2 (p. 374) of their paper and a copy of this figure is shown in figure 14(a). In the notation used by Turner & Vanden-Broeck,
![]() $s$
is the wave steepness
$s$
is the wave steepness
![]() $H$
, and
$H$
, and
![]() $\unicode[STIX]{x1D707}$
is the squared phase velocity
$\unicode[STIX]{x1D707}$
is the squared phase velocity
![]() $c^{2}$
. As one can see from figure 14(a), the authors indicate on the curve five characteristic points:
$c^{2}$
. As one can see from figure 14(a), the authors indicate on the curve five characteristic points:
(i) a non-overhanging wave;
(ii) the wave for the Holyer limit;
(iii) the wave with the greatest overhang;
(iv) a wave with a slight overhang; and
(v) a non-overhanging wave similar to the wave (ii).
On the basis of these computations, the authors conjectured (p. 371) that ‘an alternation between non-overhanging and overhanging waves continues indefinitely as one proceeds along the solution branch’. We have digitized the graph of figure 14(a) and plotted it together with our results in figure 14(b). As one can see, our computations do not confirm the conjecture by Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986), but as was demonstrated in § 6.4, they confirm the conjecture by Saffman & Yuen (Reference Saffman and Yuen1982) that the overhanging waves continue to exist until the interface starts to touch itself.

Figure 14. (a) A copy of figure 2 from the paper by Turner & Vanden-Broeck (Reference Turner and Vanden-Broeck1986). (b) Comparison of our results with those in (a): the point indicates the Holyer limit; squares correspond to the data of table 5.
7.3 Conclusions
In this paper, we have studied progressive gravity waves at the interface between two unbounded fluids of different densities. The main concern is to determine the structure of the almost limiting configurations for overhanging waves and to make a correct prediction about limiting configurations. New results of the paper are as follows.
(i) A rigorous proof that the inclination angle
 $\unicode[STIX]{x1D703}$
of the interface is in the range
$\unicode[STIX]{x1D703}$
of the interface is in the range
 $-\unicode[STIX]{x03C0}<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}$
(proposition 1 in § 3).
$-\unicode[STIX]{x03C0}<\unicode[STIX]{x1D703}<\unicode[STIX]{x03C0}$
(proposition 1 in § 3).(ii) A compact mathematical formulation for the problems of interfacial waves (§ 4, equation (4.23)).
(iii) A new method of solving nonlinear boundary-value problems based on solving a series of corresponding linear boundary-value problems (§ 5 and appendix A).
(iv) Computations of the almost limiting mushroom-shaped waves with
 $|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
(§ 6.2, figure 7).
$|\unicode[STIX]{x1D703}|_{max}>179.98^{\circ }$
(§ 6.2, figure 7).(v) Numerical evidence that, for any
 $\unicode[STIX]{x1D70C}\in (0,1]$
, the level
$\unicode[STIX]{x1D70C}\in (0,1]$
, the level
 $h_{0}=c^{2}/2$
is the height of the almost flat undersides of the mushroom caps (§ 6.2, figures 8 and 9
a).
$h_{0}=c^{2}/2$
is the height of the almost flat undersides of the mushroom caps (§ 6.2, figures 8 and 9
a).(vi) The concepts of the inner crest and the inner solution near the inner crest. Numerical evidence that the vertical distance,
 $l$
, from the level
$l$
, from the level
 $h_{0}=c^{2}/2$
to the inner crest is a natural scale for the inner solutions (§ 6.3, figures 6
b and 10).
$h_{0}=c^{2}/2$
to the inner crest is a natural scale for the inner solutions (§ 6.3, figures 6
b and 10).(vii) The structure of the inner solutions (§ 6.3, figure 11 b).
(viii) A well-grounded conjecture about the structure of limiting configurations for any
 $\unicode[STIX]{x1D70C}\in (0,1]$
(§ 6.4, figure 9
b). The structure is characterized by the formation of a stagnation zone bounded by a part of the interface, whereas for limiting surface waves (
$\unicode[STIX]{x1D70C}\in (0,1]$
(§ 6.4, figure 9
b). The structure is characterized by the formation of a stagnation zone bounded by a part of the interface, whereas for limiting surface waves (
 $\unicode[STIX]{x1D70C}=0$
), only one stagnation point appears at the free surface.
$\unicode[STIX]{x1D70C}=0$
), only one stagnation point appears at the free surface.(ix) Numerical evidence that there exist overhanging and non-overhanging interfacial waves which have the same wavelength
 $\unicode[STIX]{x1D706}$
, phase speed
$\unicode[STIX]{x1D706}$
, phase speed
 $c$
and wave steepness
$c$
and wave steepness
 $H$
(§ 6.5, figure 13).
$H$
(§ 6.5, figure 13).(x) Confirmation of the conjectures by Saffman & Yuen (Reference Saffman and Yuen1982) and Grimshaw & Pullin (Reference Grimshaw and Pullin1986, figure 10) that the overhanging waves continue to exist until the interface starts to touch itself.
Acknowledgement
The work was supported by the Russian Science Foundation, project number 14-19-01633.
Appendix A. Details of the numerical algorithm for discretizing and solving problem 2
A.1 Computation of the integrals of Cauchy type by the method of complex splines
In the complex plane
![]() $t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
, consider a closed smooth contour
$t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
, consider a closed smooth contour
![]() $C$
without self-intersections and a complex-valued function
$C$
without self-intersections and a complex-valued function
![]() $\unicode[STIX]{x1D714}(u)$
(
$\unicode[STIX]{x1D714}(u)$
(
![]() $u\in C$
) of the points
$u\in C$
) of the points
![]() $u$
of this contour. We need to compute the integral of Cauchy type
$u$
of this contour. We need to compute the integral of Cauchy type
for any point
![]() $t$
of the complex plane.
$t$
of the complex plane.
Let
![]() $t_{1},t_{2},\ldots ,t_{N}=t_{1}$
be points on
$t_{1},t_{2},\ldots ,t_{N}=t_{1}$
be points on
![]() $C$
arranged in anticlockwise order, separating
$C$
arranged in anticlockwise order, separating
![]() $C$
into arcs
$C$
into arcs
![]() $C_{n}$
, with
$C_{n}$
, with
![]() $C_{n}$
being the arc from
$C_{n}$
being the arc from
![]() $t_{n}$
to
$t_{n}$
to
![]() $t_{n+1}$
$t_{n+1}$
![]() $(n=\overline{1,N-1})$
. The notation in parentheses means that
$(n=\overline{1,N-1})$
. The notation in parentheses means that
![]() $n$
changes from 1 to
$n$
changes from 1 to
![]() $N-1$
with step 1. Since
$N-1$
with step 1. Since
![]() $t_{N}=t_{1}$
, the general number of different points on
$t_{N}=t_{1}$
, the general number of different points on
![]() $C$
is
$C$
is
![]() $N-1$
. For this subdivision
$N-1$
. For this subdivision
![]() $\unicode[STIX]{x1D6E5}$
of
$\unicode[STIX]{x1D6E5}$
of
![]() $C$
, we form a complex spline
$C$
, we form a complex spline
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
on
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
on
![]() $C$
of order
$C$
of order
![]() $r$
composed of complex
$r$
composed of complex
![]() $r$
-degree polynomials in powers of
$r$
-degree polynomials in powers of
![]() $u$
. These polynomials we denote by
$u$
. These polynomials we denote by
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5},n}(u)$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5},n}(u)$
,
![]() $n=\overline{1,N-1}$
. The polynomials contain
$n=\overline{1,N-1}$
. The polynomials contain
![]() $(N-1)(r+1)$
complex unknown coefficients which are chosen so that the interpolation function
$(N-1)(r+1)$
complex unknown coefficients which are chosen so that the interpolation function
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
is continuous and has continuous derivatives up to order
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
is continuous and has continuous derivatives up to order
![]() $r-1$
on
$r-1$
on
![]() $C$
. In this paper, we shall use the cubic spline interpolation
$C$
. In this paper, we shall use the cubic spline interpolation
![]() $(r=3)$
and the linear interpolation
$(r=3)$
and the linear interpolation
![]() $(r=1)$
. We should note that the algorithms for constructing the complex cubic splines on a closed contour and periodic cubic splines on a line segment are absolutely identical (see Ahlberg, Nilson & Walsh Reference Ahlberg, Nilson and Walsh1967). For the complex cubic splines, one needs only to consider the values
$(r=1)$
. We should note that the algorithms for constructing the complex cubic splines on a closed contour and periodic cubic splines on a line segment are absolutely identical (see Ahlberg, Nilson & Walsh Reference Ahlberg, Nilson and Walsh1967). For the complex cubic splines, one needs only to consider the values
![]() $t_{n}$
and
$t_{n}$
and
![]() $\unicode[STIX]{x1D714}_{n}=\unicode[STIX]{x1D714}(t_{n})$
(
$\unicode[STIX]{x1D714}_{n}=\unicode[STIX]{x1D714}(t_{n})$
(
![]() $n=\overline{1,N}$
) as complex numbers (
$n=\overline{1,N}$
) as complex numbers (
![]() $t_{N}=t_{1}$
is included in the set of knots). For the linear splines, we have an explicit representation of the polynomials:
$t_{N}=t_{1}$
is included in the set of knots). For the linear splines, we have an explicit representation of the polynomials:
In the paper by Ahlberg, Nilson & Walsh (Reference Ahlberg, Nilson and Walsh1969), a compact formula (14) was deduced for computing the integral (A 1):
which is correct for the complex splines of any order. Formula (A 3) from Ahlberg et al. (Reference Ahlberg, Nilson and Walsh1969) is a convenient tool for calculating the integrals of Cauchy type over closed contours.
Estimates of errors of the representations
![]() $\unicode[STIX]{x1D714}(u)=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
and
$\unicode[STIX]{x1D714}(u)=\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
and
![]() $\unicode[STIX]{x1D6F7}(t)=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(t)$
can be found in Ahlberg et al. (Reference Ahlberg, Nilson and Walsh1967) (for complex cubic splines) and in Atkinson (Reference Atkinson1972) (for complex linear splines). In this paper, we do not dwell on these estimates, but an obvious remark that the interpolation by cubic spline is much more accurate than that by linear splines is yet necessary.
$\unicode[STIX]{x1D6F7}(t)=\unicode[STIX]{x1D6F7}_{\unicode[STIX]{x1D6E5}}(t)$
can be found in Ahlberg et al. (Reference Ahlberg, Nilson and Walsh1967) (for complex cubic splines) and in Atkinson (Reference Atkinson1972) (for complex linear splines). In this paper, we do not dwell on these estimates, but an obvious remark that the interpolation by cubic spline is much more accurate than that by linear splines is yet necessary.
To discretize problem 2, we should be able to compute the principal values
![]() $\langle \unicode[STIX]{x1D6F7}\rangle (t)$
of the Cauchy-type integrals directly at the knots
$\langle \unicode[STIX]{x1D6F7}\rangle (t)$
of the Cauchy-type integrals directly at the knots
![]() $t_{n}$
,
$t_{n}$
,
![]() $n=\overline{1,N-1}$
. Let
$n=\overline{1,N-1}$
. Let
![]() $\unicode[STIX]{x1D6FE}_{n}$
be the angles between the tangent line at the knots
$\unicode[STIX]{x1D6FE}_{n}$
be the angles between the tangent line at the knots
![]() $t_{n}$
of the contour
$t_{n}$
of the contour
![]() $C$
and the
$C$
and the
![]() $\unicode[STIX]{x1D709}$
-axis. It is clear that
$\unicode[STIX]{x1D709}$
-axis. It is clear that
Now, we introduce the functions
![]() $E_{n}(t)$
, which are defined for any
$E_{n}(t)$
, which are defined for any
![]() $t$
of the complex plane
$t$
of the complex plane
![]() $t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
:
$t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
:
 $$\begin{eqnarray}\displaystyle E_{n}(t)=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{2\unicode[STIX]{x03C0}\text{i}}\log \frac{t-t_{n+1}}{t-t_{n}} & \text{if}~t\neq t_{n}\cup t\neq t_{n+1},\\ \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\text{i}}\left(\log \frac{t-t_{n+1}}{\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n}}}+\log \frac{t-t_{n+1}}{-\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n}}}\right) & \text{if}~t=t_{n},\\ \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\text{i}}\left(\log \frac{\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n+1}}}{t-t_{n}}+\log \frac{-\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n+1}}}{t-t_{n}}\right) & \text{if}~t=t_{n+1},\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle E_{n}(t)=\left\{\begin{array}{@{}ll@{}}\displaystyle \frac{1}{2\unicode[STIX]{x03C0}\text{i}}\log \frac{t-t_{n+1}}{t-t_{n}} & \text{if}~t\neq t_{n}\cup t\neq t_{n+1},\\ \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\text{i}}\left(\log \frac{t-t_{n+1}}{\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n}}}+\log \frac{t-t_{n+1}}{-\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n}}}\right) & \text{if}~t=t_{n},\\ \displaystyle \frac{1}{4\unicode[STIX]{x03C0}\text{i}}\left(\log \frac{\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n+1}}}{t-t_{n}}+\log \frac{-\text{i}\text{e}^{\text{i}\unicode[STIX]{x1D6FE}_{n+1}}}{t-t_{n}}\right) & \text{if}~t=t_{n+1},\end{array}\right. & & \displaystyle\end{eqnarray}$$
where
![]() $n=\overline{1,N-1}$
and the standard branch of the logarithm with the cut along the negative part of the
$n=\overline{1,N-1}$
and the standard branch of the logarithm with the cut along the negative part of the
![]() $\unicode[STIX]{x1D709}$
-axis is chosen, i.e.
$\unicode[STIX]{x1D709}$
-axis is chosen, i.e.
Taking into account the continuity of the approximation
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
on the contour
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
on the contour
![]() $C$
, one can easily demonstrate that
$C$
, one can easily demonstrate that
these representations being correct for the complex spline approximation
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
of any order. For the linear complex spline approximation (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D6E5}}(u)$
of any order. For the linear complex spline approximation (
![]() $r=1$
), by making use of (A 2), formula (A 7) can be rewritten in the following manner:
$r=1$
), by making use of (A 2), formula (A 7) can be rewritten in the following manner:
where
 $$\begin{eqnarray}\displaystyle G_{n}(t)=\left\{\begin{array}{@{}ll@{}}\displaystyle -\frac{t-t_{2}}{t_{2}-t_{1}}E_{1}(t) & \text{for}~n=1,\\ \displaystyle \frac{t-t_{n-1}}{t_{n}-t_{n-1}}E_{n-1}(t)-\frac{t-t_{n+1}}{t_{n+1}-t_{n}}E_{n}(t) & \text{for}~2\leqslant n\leqslant N-1,\\ \displaystyle \frac{t-t_{N-1}}{t_{N}-t_{N-1}}E_{N-1}(t) & \text{for}~n=N.\end{array}\right. & & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle G_{n}(t)=\left\{\begin{array}{@{}ll@{}}\displaystyle -\frac{t-t_{2}}{t_{2}-t_{1}}E_{1}(t) & \text{for}~n=1,\\ \displaystyle \frac{t-t_{n-1}}{t_{n}-t_{n-1}}E_{n-1}(t)-\frac{t-t_{n+1}}{t_{n+1}-t_{n}}E_{n}(t) & \text{for}~2\leqslant n\leqslant N-1,\\ \displaystyle \frac{t-t_{N-1}}{t_{N}-t_{N-1}}E_{N-1}(t) & \text{for}~n=N.\end{array}\right. & & \displaystyle\end{eqnarray}$$
A.2 Discretization of functions included in the formulation of problem 2
Let the right half of the line
![]() $L_{2\unicode[STIX]{x03C0}}$
be approximated by a system of points
$L_{2\unicode[STIX]{x03C0}}$
be approximated by a system of points
![]() $z_{n}=x_{n}+\text{i}y_{n}$
(
$z_{n}=x_{n}+\text{i}y_{n}$
(
![]() $n=\overline{1,N}$
) arranged from
$n=\overline{1,N}$
) arranged from
![]() $B$
to
$B$
to
![]() $A$
. The point
$A$
. The point
![]() $z_{1}$
coincides with
$z_{1}$
coincides with
![]() $B$
, and the point
$B$
, and the point
![]() $z_{N}$
coincides with
$z_{N}$
coincides with
![]() $A$
. This means that
$A$
. This means that
![]() $\text{Re}\,z_{1}=x_{1}=0$
and
$\text{Re}\,z_{1}=x_{1}=0$
and
![]() $\text{Re}\,z_{N}=x_{N}=\unicode[STIX]{x03C0}$
.
$\text{Re}\,z_{N}=x_{N}=\unicode[STIX]{x03C0}$
.
To draw a smooth line through the system, we use the chord parametrization by introducing the mesh of knots
and constructing on this mesh the cubic splines
![]() $x(\unicode[STIX]{x1D6FC})$
and
$x(\unicode[STIX]{x1D6FC})$
and
![]() $y(\unicode[STIX]{x1D6FC})$
with the values
$y(\unicode[STIX]{x1D6FC})$
with the values
![]() $x_{n}$
and
$x_{n}$
and
![]() $y_{n}$
at the knots
$y_{n}$
at the knots
![]() $\unicode[STIX]{x1D6FC}_{n}$
(
$\unicode[STIX]{x1D6FC}_{n}$
(
![]() $n=\overline{1,N}$
), respectively. The boundary conditions for these splines are
$n=\overline{1,N}$
), respectively. The boundary conditions for these splines are
As a result, we have the functions
![]() $x(\unicode[STIX]{x1D6FC})$
and
$x(\unicode[STIX]{x1D6FC})$
and
![]() $y(\unicode[STIX]{x1D6FC})$
, which are defined on the interval
$y(\unicode[STIX]{x1D6FC})$
, which are defined on the interval
![]() $[\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{N}]$
. Extending these functions onto the whole
$[\unicode[STIX]{x1D6FC}_{1},\unicode[STIX]{x1D6FC}_{N}]$
. Extending these functions onto the whole
![]() $\unicode[STIX]{x1D6FC}$
-axis by the rules
$\unicode[STIX]{x1D6FC}$
-axis by the rules
we obtain a parametric representation of a smooth,
![]() $2\unicode[STIX]{x03C0}$
-periodic and symmetric line
$2\unicode[STIX]{x03C0}$
-periodic and symmetric line
![]() $L$
with continuous curvature.
$L$
with continuous curvature.
Assume now that the line
![]() $L$
, the parameter
$L$
, the parameter
![]() $k$
and the function
$k$
and the function
![]() $F(z)$
determined from (4.13) are an approximate solution to problem 1. To discretize problem 2, one needs to construct discrete analogues of the functions and to find the values of the parameters included in the formulation of the problem, namely,
$F(z)$
determined from (4.13) are an approximate solution to problem 1. To discretize problem 2, one needs to construct discrete analogues of the functions and to find the values of the parameters included in the formulation of the problem, namely,
![]() $a(s)$
,
$a(s)$
,
![]() $b(s)$
,
$b(s)$
,
![]() $c(s)$
,
$c(s)$
,
![]() $d(s)$
,
$d(s)$
,
![]() $U(s)$
,
$U(s)$
,
![]() $S_{L}$
,
$S_{L}$
,
![]() $P_{L}$
and
$P_{L}$
and
![]() $R(s)$
, where
$R(s)$
, where
![]() $s$
is the arc-coordinate which labels the point
$s$
is the arc-coordinate which labels the point
![]() $z$
on
$z$
on
![]() $L$
. The coordinate
$L$
. The coordinate
![]() $s$
can be easily replaced by
$s$
can be easily replaced by
![]() $\unicode[STIX]{x1D6FC}$
, but, making the discretization, we take as an argument the number
$\unicode[STIX]{x1D6FC}$
, but, making the discretization, we take as an argument the number
![]() $n$
of the point
$n$
of the point
![]() $z_{n}$
,
$z_{n}$
,
![]() $n=\overline{1,N}$
. For example,
$n=\overline{1,N}$
. For example,
![]() $\unicode[STIX]{x1D703}(s)$
is replaced by the set of values
$\unicode[STIX]{x1D703}(s)$
is replaced by the set of values
![]() $\unicode[STIX]{x1D703}_{n}$
, which are the angles between the tangent line at the knots
$\unicode[STIX]{x1D703}_{n}$
, which are the angles between the tangent line at the knots
![]() $z_{n}$
of the line
$z_{n}$
of the line
![]() $L$
and the
$L$
and the
![]() $x$
-axis. Thus, we compute
$x$
-axis. Thus, we compute
and the curvatures
After determining these values, we calculate
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
and
$b_{n}$
and
![]() $c_{n}$
by formulae (5.32). We find also the arc-coordinates
$c_{n}$
by formulae (5.32). We find also the arc-coordinates
![]() $s_{n}$
:
$s_{n}$
:
To calculate accurately the integrals in (A 15b
), we subdivide the intervals
![]() $[\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FC}_{n+1}]$
uniformly into 10 parts and use Simpson’s rule. The half-perimeter of the line
$[\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FC}_{n+1}]$
uniformly into 10 parts and use Simpson’s rule. The half-perimeter of the line
![]() $L$
is evidently
$L$
is evidently
![]() $l_{s}=s_{N}$
; then the parameter
$l_{s}=s_{N}$
; then the parameter
![]() $P_{L}$
on the right-hand side of (5.35b
) is
$P_{L}$
on the right-hand side of (5.35b
) is
![]() $P_{L}=l_{s}/\unicode[STIX]{x03C0}$
. The values
$P_{L}=l_{s}/\unicode[STIX]{x03C0}$
. The values
![]() $s_{n}$
and
$s_{n}$
and
![]() $l_{s}$
are necessary to discretize (5.35a
). The parameter
$l_{s}$
are necessary to discretize (5.35a
). The parameter
![]() $S_{L}$
on the right-hand side of (5.35a
) can be found from the formula
$S_{L}$
on the right-hand side of (5.35a
) can be found from the formula
On each interval
![]() $[\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FC}_{n+1}]$
, the integrand in (A 16) is a polynomial of fifth degree, which allows the analytical computation of
$[\unicode[STIX]{x1D6FC}_{n},\unicode[STIX]{x1D6FC}_{n+1}]$
, the integrand in (A 16) is a polynomial of fifth degree, which allows the analytical computation of
![]() $S_{L}$
to be carried out.
$S_{L}$
to be carried out.
To find the discrete analogues of the functions
![]() $d(s)$
,
$d(s)$
,
![]() $U(s)$
and
$U(s)$
and
![]() $R(s)$
, i.e the values
$R(s)$
, i.e the values
![]() $d_{n}$
,
$d_{n}$
,
![]() $U_{n}$
and
$U_{n}$
and
![]() $R_{n}$
, one needs to determine
$R_{n}$
, one needs to determine
![]() $\langle F\rangle _{n}$
, i.e. the principal values of the integral (4.13) at the points
$\langle F\rangle _{n}$
, i.e. the principal values of the integral (4.13) at the points
![]() $z_{n}$
. To evaluate
$z_{n}$
. To evaluate
![]() $\langle F\rangle _{n}$
, we map conformally one period of the flow domain, shown in figure 1, onto the plane
$\langle F\rangle _{n}$
, we map conformally one period of the flow domain, shown in figure 1, onto the plane
![]() $t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
by means of the function
$t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
by means of the function
![]() $t=\text{e}^{\text{i}z}$
. Under this mapping, the image of the interfacial line
$t=\text{e}^{\text{i}z}$
. Under this mapping, the image of the interfacial line
![]() $L_{2\unicode[STIX]{x03C0}}$
is a closed contour
$L_{2\unicode[STIX]{x03C0}}$
is a closed contour
![]() $C$
, which is symmetric with respect to the
$C$
, which is symmetric with respect to the
![]() $\unicode[STIX]{x1D709}$
-axis. The upper and lower flow domains
$\unicode[STIX]{x1D709}$
-axis. The upper and lower flow domains
![]() $D_{1}$
and
$D_{1}$
and
![]() $D_{2}$
transform into the interior and exterior of the contour
$D_{2}$
transform into the interior and exterior of the contour
![]() $C$
, respectively. The upper and lower infinities
$C$
, respectively. The upper and lower infinities
![]() $I_{1}$
and
$I_{1}$
and
![]() $I_{2}$
in the
$I_{2}$
in the
![]() $z$
-plane correspond to the points
$z$
-plane correspond to the points
![]() $t=0$
and
$t=0$
and
![]() $t=\infty$
in the
$t=\infty$
in the
![]() $t$
-plane. The images of the points
$t$
-plane. The images of the points
![]() $z_{n}$
are the points
$z_{n}$
are the points
![]() $t_{n}=\exp (\text{i}z_{n})$
(
$t_{n}=\exp (\text{i}z_{n})$
(
![]() $n=\overline{1,N}$
), located on the upper half of the contour
$n=\overline{1,N}$
), located on the upper half of the contour
![]() $C$
(compare figure 1 of the main text and figure 15).
$C$
(compare figure 1 of the main text and figure 15).

Figure 15. The plane
![]() $t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
for computing the integrals of Cauchy type.
$t=\unicode[STIX]{x1D709}+\text{i}\unicode[STIX]{x1D702}$
for computing the integrals of Cauchy type.
The change of variable
![]() $z=-\text{i}\log t$
converts the integral (4.13) into the integral of Cauchy type:
$z=-\text{i}\log t$
converts the integral (4.13) into the integral of Cauchy type:
where
![]() $\unicode[STIX]{x1D706}(u)$
satisfies the symmetry condition
$\unicode[STIX]{x1D706}(u)$
satisfies the symmetry condition
which follows from (4.14). It is to be noted that the condition (A 18) implies that
So, to compute
![]() $\langle F\rangle _{n}$
, we can use the technique described in § A.1. It can be easily demonstrated that the angle
$\langle F\rangle _{n}$
, we can use the technique described in § A.1. It can be easily demonstrated that the angle
![]() $\unicode[STIX]{x1D6FE}$
between the tangent line to the contour
$\unicode[STIX]{x1D6FE}$
between the tangent line to the contour
![]() $C$
and the
$C$
and the
![]() $\unicode[STIX]{x1D709}$
-axis is
$\unicode[STIX]{x1D709}$
-axis is
![]() $\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D703}+x+\unicode[STIX]{x03C0}/2$
,
$\unicode[STIX]{x1D6FE}=\unicode[STIX]{x1D703}+x+\unicode[STIX]{x03C0}/2$
,
![]() $x+\text{i}y\in L_{2\unicode[STIX]{x03C0}}$
.
$x+\text{i}y\in L_{2\unicode[STIX]{x03C0}}$
.
First, we find
![]() $\unicode[STIX]{x1D6FE}_{n}=\unicode[STIX]{x1D703}_{n}+x_{n}+\unicode[STIX]{x03C0}/2$
and determine the functions
$\unicode[STIX]{x1D6FE}_{n}=\unicode[STIX]{x1D703}_{n}+x_{n}+\unicode[STIX]{x03C0}/2$
and determine the functions
![]() $E_{n}(t)$
by formulae (A 5). Second, on the mesh of knots
$E_{n}(t)$
by formulae (A 5). Second, on the mesh of knots
![]() $t_{n}$
,
$t_{n}$
,
![]() $n=\overline{1,N}$
, we construct the complex cubic spline
$n=\overline{1,N}$
, we construct the complex cubic spline
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
with the values
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
with the values
![]() $\unicode[STIX]{x1D706}_{n}$
at the knots
$\unicode[STIX]{x1D706}_{n}$
at the knots
![]() $t_{n}$
. The boundary conditions for this spline are
$t_{n}$
. The boundary conditions for this spline are
To construct such a cubic spline, we proceed in the following manner. We compute three complex cubic splines
![]() $\unicode[STIX]{x1D706}_{0\unicode[STIX]{x1D6E5}}(u)$
,
$\unicode[STIX]{x1D706}_{0\unicode[STIX]{x1D6E5}}(u)$
,
![]() $\unicode[STIX]{x1D706}_{1\unicode[STIX]{x1D6E5}}(u)$
and
$\unicode[STIX]{x1D706}_{1\unicode[STIX]{x1D6E5}}(u)$
and
![]() $\unicode[STIX]{x1D706}_{2\unicode[STIX]{x1D6E5}}(u)$
which satisfy the conditions
$\unicode[STIX]{x1D706}_{2\unicode[STIX]{x1D6E5}}(u)$
which satisfy the conditions
The algorithm for computing the complex cubic splines with specified second derivatives at the end points is absolutely analogous to that for the ordinary cubic splines on a line segment. After finding
![]() $\unicode[STIX]{x1D706}_{0\unicode[STIX]{x1D6E5}}(u)$
,
$\unicode[STIX]{x1D706}_{0\unicode[STIX]{x1D6E5}}(u)$
,
![]() $\unicode[STIX]{x1D706}_{1\unicode[STIX]{x1D6E5}}(u)$
and
$\unicode[STIX]{x1D706}_{1\unicode[STIX]{x1D6E5}}(u)$
and
![]() $\unicode[STIX]{x1D706}_{2\unicode[STIX]{x1D6E5}}(u)$
, we seek
$\unicode[STIX]{x1D706}_{2\unicode[STIX]{x1D6E5}}(u)$
, we seek
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
in the form
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
in the form
where
![]() $\unicode[STIX]{x1D6FD}_{1}$
and
$\unicode[STIX]{x1D6FD}_{1}$
and
![]() $\unicode[STIX]{x1D6FD}_{2}$
are unknown real parameters. It is clear that
$\unicode[STIX]{x1D6FD}_{2}$
are unknown real parameters. It is clear that
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
satisfies the boundary conditions (A 20b
). The remaining operation is to determine
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
satisfies the boundary conditions (A 20b
). The remaining operation is to determine
![]() $\unicode[STIX]{x1D6FD}_{1}$
and
$\unicode[STIX]{x1D6FD}_{1}$
and
![]() $\unicode[STIX]{x1D6FD}_{2}$
from the boundary conditions (A 20a
).
$\unicode[STIX]{x1D6FD}_{2}$
from the boundary conditions (A 20a
).
The function
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
is defined on the upper half of the contour
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
is defined on the upper half of the contour
![]() $C$
. The relation (A 19) and the boundary conditions (A 20) provide that the extension of the function
$C$
. The relation (A 19) and the boundary conditions (A 20) provide that the extension of the function
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
onto the whole contour
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
onto the whole contour
![]() $C$
by the rule (A 18) is continuous and has continuous derivatives up to second order at the break points
$C$
by the rule (A 18) is continuous and has continuous derivatives up to second order at the break points
![]() $t_{n}$
and at their symmetric counterparts
$t_{n}$
and at their symmetric counterparts
![]() $\overline{t_{n}}$
.
$\overline{t_{n}}$
.
Now, using (A 7) and taking into account the symmetry conditions (A 18), we calculate
After that, with the help of (5.14c
) and (5.28b
), we compute
![]() $R_{n}$
and
$R_{n}$
and
![]() $U_{n}$
.
$U_{n}$
.
To calculate
![]() $d_{n}$
by (5.28a
), we construct the complex cubic spline
$d_{n}$
by (5.28a
), we construct the complex cubic spline
![]() $\langle F\rangle _{\unicode[STIX]{x1D6E5}}(u)$
with the values
$\langle F\rangle _{\unicode[STIX]{x1D6E5}}(u)$
with the values
![]() $\langle F\rangle _{n}$
at the knots
$\langle F\rangle _{n}$
at the knots
![]() $t_{n}$
and with the same boundary conditions (A 20) as for
$t_{n}$
and with the same boundary conditions (A 20) as for
![]() $\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
. Computing analytically the derivatives
$\unicode[STIX]{x1D706}_{\unicode[STIX]{x1D6E5}}(u)$
. Computing analytically the derivatives
![]() $\langle F\rangle _{\unicode[STIX]{x1D6E5}}^{\prime }(t_{n})$
and using the chain rule, we find
$\langle F\rangle _{\unicode[STIX]{x1D6E5}}^{\prime }(t_{n})$
and using the chain rule, we find
At this stage, we have found the values of
![]() $a_{n}$
,
$a_{n}$
,
![]() $b_{n}$
,
$b_{n}$
,
![]() $c_{n}$
,
$c_{n}$
,
![]() $d_{n}$
,
$d_{n}$
,
![]() $U_{n}$
and
$U_{n}$
and
![]() $R_{n}$
, which are the discrete analogues of the functions
$R_{n}$
, which are the discrete analogues of the functions
![]() $a(s)$
,
$a(s)$
,
![]() $b(s)$
,
$b(s)$
,
![]() $c(s)$
,
$c(s)$
,
![]() $d(s)$
,
$d(s)$
,
![]() $U(s)$
and
$U(s)$
and
![]() $R(s)$
included in the formulation of problem 2. The parameters
$R(s)$
included in the formulation of problem 2. The parameters
![]() $S_{L}$
and
$S_{L}$
and
![]() $P_{L}$
have been found too. It is to be noted that making use of the cubic splines technique provides a high accuracy of computing the right-hand sides of equations (5.33) and (5.35). For exact solutions to problem 1, these right-hand sides are exactly zero, and their difference from zero defines the general accuracy of the solution to problem 1.
$P_{L}$
have been found too. It is to be noted that making use of the cubic splines technique provides a high accuracy of computing the right-hand sides of equations (5.33) and (5.35). For exact solutions to problem 1, these right-hand sides are exactly zero, and their difference from zero defines the general accuracy of the solution to problem 1.
A.3 Discretization of equations (5.33) and (5.35)
Now we should discretize the left-hand sides of (5.33) and (5.35). In discretizing the left-hand side of (5.33), the accuracy is of less importance, but the computer time is of higher priority. So, discretizing the operator
![]() $D[\unicode[STIX]{x1D714}](s)$
, defined by (5.34), we shall use the complex linear spline interpolation (A 8). With the help of (A 9), we compute the functions
$D[\unicode[STIX]{x1D714}](s)$
, defined by (5.34), we shall use the complex linear spline interpolation (A 8). With the help of (A 9), we compute the functions
![]() $G_{n}(t)$
(
$G_{n}(t)$
(
![]() $n=\overline{1,N}$
). Taking into account (A 8) and the symmetry condition
$n=\overline{1,N}$
). Taking into account (A 8) and the symmetry condition
![]() $\unicode[STIX]{x1D714}(\bar{u})=\overline{\unicode[STIX]{x1D714}(u)}$
, we write
$\unicode[STIX]{x1D714}(\bar{u})=\overline{\unicode[STIX]{x1D714}(u)}$
, we write
The discrete analogue of the operator
![]() $D[\unicode[STIX]{x1D714}](s)$
takes the form
$D[\unicode[STIX]{x1D714}](s)$
takes the form
where
![]() $A_{m,n}$
and
$A_{m,n}$
and
![]() $A_{m,n}$
are real-valued squared matrices defined as
$A_{m,n}$
are real-valued squared matrices defined as
and in the last formula we have taken into account the symmetry condition
![]() $\unicode[STIX]{x1D714}(\bar{u})=\overline{\unicode[STIX]{x1D714}(u)}$
, which implies that
$\unicode[STIX]{x1D714}(\bar{u})=\overline{\unicode[STIX]{x1D714}(u)}$
, which implies that
![]() $\text{Im}\,\unicode[STIX]{x1D714}_{1}=\text{Im}\,\unicode[STIX]{x1D714}_{N}=0$
.
$\text{Im}\,\unicode[STIX]{x1D714}_{1}=\text{Im}\,\unicode[STIX]{x1D714}_{N}=0$
.
Solving system (5.33) and (5.35), we shall seek the function
![]() $\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})=h^{\prime }(\unicode[STIX]{x1D6FC})$
, which we approximate on the segment
$\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})=h^{\prime }(\unicode[STIX]{x1D6FC})$
, which we approximate on the segment
![]() $[0,\unicode[STIX]{x1D6FC}_{N}]$
by a cubic spline with the not-a-knot condition (see de Boor Reference de Boor1978). The unknowns in this interpolation are the values
$[0,\unicode[STIX]{x1D6FC}_{N}]$
by a cubic spline with the not-a-knot condition (see de Boor Reference de Boor1978). The unknowns in this interpolation are the values
![]() $\unicode[STIX]{x1D708}_{n}=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC}_{n})$
. It is evident that
$\unicode[STIX]{x1D708}_{n}=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC}_{n})$
. It is evident that
The discrete analogue of the integral operator in (A 32) is
where
![]() $S_{m,n}$
is a squared matrix whose columns can be found by integrating in sequence the so-called fundamental splines
$S_{m,n}$
is a squared matrix whose columns can be found by integrating in sequence the so-called fundamental splines
![]() $S_{n}(\unicode[STIX]{x1D6FC})$
(
$S_{n}(\unicode[STIX]{x1D6FC})$
(
![]() $n=\overline{1,N}$
), which take zero values at all knots except the knot with number
$n=\overline{1,N}$
), which take zero values at all knots except the knot with number
![]() $n$
where
$n$
where
![]() $S_{n}(\unicode[STIX]{x1D6FC}_{n})=1$
. The formulae for
$S_{n}(\unicode[STIX]{x1D6FC}_{n})=1$
. The formulae for
![]() $S_{m,n}$
are as follows:
$S_{m,n}$
are as follows:
the integral being computed analytically in (A 34b ).
Taking into account that
![]() $h^{\prime }(s)=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})/\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FC})$
, where
$h^{\prime }(s)=\unicode[STIX]{x1D708}(\unicode[STIX]{x1D6FC})/\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FC})$
, where
![]() $\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FC})=\sqrt{[x^{\prime }(\unicode[STIX]{x1D6FC})]^{2}+[y^{\prime }(\unicode[STIX]{x1D6FC})]^{2}}$
, and introducing the notation
$\unicode[STIX]{x1D707}(\unicode[STIX]{x1D6FC})=\sqrt{[x^{\prime }(\unicode[STIX]{x1D6FC})]^{2}+[y^{\prime }(\unicode[STIX]{x1D6FC})]^{2}}$
, and introducing the notation
we come to the following system of
![]() $N+2$
linear equations with
$N+2$
linear equations with
![]() $N+2$
unknowns:
$N+2$
unknowns:
where
 $$\begin{eqnarray}\displaystyle Q_{m,n} & = & \displaystyle \unicode[STIX]{x1D6FF}_{m,n}/\unicode[STIX]{x1D707}_{m}+d_{m}S_{m,n}+A_{m,n}\,\text{Re}(a_{n}/\unicode[STIX]{x1D707}_{n})+B_{m,n}\,\text{Im}(b_{n}/\unicode[STIX]{x1D707}_{n})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=1}^{N}(A_{m,j}\,\text{Re}\,b_{j}+B_{m,j}\,\text{Im}\,b_{j})S_{j,n},\quad m,n=\overline{1,N},\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle Q_{m,n} & = & \displaystyle \unicode[STIX]{x1D6FF}_{m,n}/\unicode[STIX]{x1D707}_{m}+d_{m}S_{m,n}+A_{m,n}\,\text{Re}(a_{n}/\unicode[STIX]{x1D707}_{n})+B_{m,n}\,\text{Im}(b_{n}/\unicode[STIX]{x1D707}_{n})\nonumber\\ \displaystyle & & \displaystyle +\,\mathop{\sum }_{j=1}^{N}(A_{m,j}\,\text{Re}\,b_{j}+B_{m,j}\,\text{Im}\,b_{j})S_{j,n},\quad m,n=\overline{1,N},\end{eqnarray}$$
![]() $\unicode[STIX]{x1D6FF}_{m,n}$
is the Kronecker delta,
$\unicode[STIX]{x1D6FF}_{m,n}$
is the Kronecker delta,
After solving system (A 36), we determine
New approximations for the parameter
![]() $k$
and line
$k$
and line
![]() $L$
are
$L$
are