1. Introduction
Maritime transport has made a significant contribution to the development of the global economy. Meanwhile, numerous tragic accidents continue to remind us of the high risk of shipping, among which ship collision is one major threat to navigation safety at sea (Chen et al., Reference Chen, Huang, Mou and van Gelder2018). An effective measure to prevent collision is to assess the potential collision risk around a ship as early as possible and to provide collision-avoidance decisions.
Researchers in this field have been dedicated to finding various methods to assess potential collision risk of ships, which can be divided into three main categories generally: distance-based methods, velocity-based methods and domain-based methods. As far as the distance-based methods are concerned, the concept of closest point of approach (CPA) is widely used. By calculating the time to the closest point of approach (TCPA) and the distance at closest point of approach (DCPA) and determining whether it is within the given threshold, collision candidate can be detected (Chin and Debnath, Reference Chin and Debnath2009). The collision candidates are defined as the pair of ships in an encounter process where their spatiotemporal relationships satisfy certain criteria that has the potential for collision (Chen et al., Reference Chen, Huang, Mou and van Gelder2018). By weighting the DCPA and the TCPA, the collision risk index (CRI) model that can quantify the potential collision risk was proposed (Kearon, Reference Kearon1977; Zhen et al., Reference Zhen, Riveiro and Jin2017). In subsequent research, the CRI model was improved by introducing other factors, such as ship distance, the relative bearing and the hydrometeorological condition based on the DCPA and the TCPA (Ren et al., Reference Ren, Mou, Yan and Zhang2011; Li and Pang, Reference Li and Pang2013; Zhang et al., Reference Zhang, Montewka, Manderbacka, Kujala and Hirdaris2021).
Regarding the velocity-based methods, the collision threat parameter area (CTPA) algorithm and the velocity obstacle (VO) algorithm are two typical and widely used methods. Among them, CTPA has been proved to be identical to the linear-VO algorithm (Huang et al., Reference Huang, van Gelder and Wen2018). By calculating the velocity obstacle set and judging whether a ship's velocity is in the set, the potential collision risk can be detected. Compared with the CPA method, the VO algorithms have a greater advantage in dealing with nonlinear trajectories of target ships (Chen et al., Reference Chen, Huang, Mou and van Gelder2018). However, it is difficult to achieve the quantification of the potential collision risk with velocity-based methods.
In addition, many studies have focused on the ship domain theory. A ship domain is an invisible water area around a ship under way which most navigators of target ships would avoid entering. It reflects the subjective risk pressure that other ships are kept away from the potential collision area of the observer's own ship (Pietrzykowski, Reference Pietrzykowski2008). The collision risk model combining the existing ship domain with the CPA is proposed according to the navigator's awareness of the ship encounter situations (Yoo and Lee, Reference Yoo and Lee2019). Moreover, the ship domain has been adopted to quantify the potential collision risk, by which the level of collision candidate could be identified. For example, the potential risk ship domain (PRSD) model that consists of continuously risk levels has been proposed and verified (Im and Luong, Reference Im and Luong2019).
Traditional distance-based methods are more suitable for early warning while velocity-based methods are more appropriate for the collision-avoidance decisions. However, papers are rarely found to combine the two kinds of methods to establish a hierarchical prewarning model. Considering the ship domain has demonstrated an excellent assessment performance of risk pressure around a ship, this paper presents a risk hierarchy prewarning (RHP) model based on the violation detection of the own ship domain. The proposed model can assess the potential collision risk and provide a two-level alarm scheme under different risk pressures for ships sailing at sea.
The rest of the paper is organised as follows. Section 2 presents a literature review on the research of ship domains and introduces the reason an eccentric ellipse ship domain is adopted in this study. Section 3 proposes the RHP model wherein three main parameters of the risk measurement based on the violation detection of the ship domain are calculated. All parameters on the risk measurement including the DCPA and the TCPA used in different encounter situations are analysed, and a novel guard zone based on the RHP model is established in Section 4, followed by paper's conclusions and suggestions for future work in Section 5.
2. Ship domain model
This section introduces the development of the domain theory, especially on different domain shapes and their features. Then, an eccentric ellipse ship domain is adopted on which the RHP model will be established.
2.1 Overview of ship domain
The ship domain is one of important concepts of the marine traffic safety theory, which was initiated by combining the ship traffic survey with mathematical statistics in narrow waterways (Fujii and Tanaka, Reference Fujii and Tanaka1971). The domain proposed by Fujii is an ellipse centred on a ship whose size is determined by the ship's length. A ship domain is not a real physical distance but is an expected clearance area in a perfect and imagined situation (Zhang et al., Reference Zhang, Wang and Meng2015).
After decades of development, ship's domain is widely used in the marine field, including the ship's collision avoidance (Szlapczynski et al., Reference Szlapczynski, Krata and Szlapczynska2018; Mou et al., Reference Mou, Li, Hu, Zhang, Gong, Chen and He2020), the risk assessment of ship's traffic (Chai et al., Reference Chai, Weng and Li2020; Zheng et al., Reference Zheng, Chen, Jiang and Qiao2020; Rawson and Brito, Reference Rawson and Brito2021) and the waterway traffic capacity (Zhang et al., Reference Zhang, Mou, Zhu and Chen2017; Weng et al., Reference Weng, Liao and Yang2020). More importantly, different domain theories have been proposed continuously. In the early stage, empirical methods were adopted to find shapes and sizes, including a regular geometric figure such as a circle (Davis et al., Reference Davis, Dove and Stockel1980), an ellipse (Fujii and Tanaka, Reference Fujii and Tanaka1971; Tak and Spaans, Reference Tak and Spaans1997) and an irregular geometric figure (Goodwin, Reference Goodwin1973; Pietrzykowski, Reference Pietrzykowski2008). Data in their papers are obtained from the sea traffic observation and radar simulator test, or probability statistics (Goodwin, Reference Goodwin1973; Coldwell, Reference Coldwell1983).
Based on various shapes and sizes, different models were established accordingly. However, it is hard to determine which shape is more reasonable since it is not a physical area. Thus, some additional methods were introduced into the different models to enhance their availability, including the fuzzy mathematics method (Wang, Reference Wang2010, Reference Wang2013), AIS technology (Hansen et al., Reference Hansen, Jensen, Lehn-Schioler, Melchild, Rasmussen and Ennemark2013; Zhou and Zheng, Reference Zhou and Zheng2019) and artificial intelligence (Zhu et al., Reference Zhu, Xu and Lin2001; Pietrzykowski and Uriasz, Reference Pietrzykowski and Uriasz2009). Furthermore, a variable ship domain whose shape and size can change with the ship's speed or the traffic flow was proposed (Wang, Reference Wang2013; Pietrzykowski and Wielgosz, Reference Pietrzykowski and Wielgosz2021). The variable ship domain can solve the inconsistency of risk in different scenarios, though its accuracy needs further confirmation in practice.
Obviously, the shape and its size are the core part of the ship domain theory. However, the effective area around a ship which a navigator would like to keep free with respect to other ships and stationary objects (Coldwell, Reference Coldwell1983) was still not fixed exclusively. Despite its diversities, the theory has been used successfully to measure the potential collision risk by calculating the degree of domain violation. There are three types of domain violation. Firstly, the target ship's domain is violated (Fujii and Tanaka, Reference Fujii and Tanaka1971; Dinh and Im, Reference Dinh and Im2016; Szlapczynski and Szlapczynska, Reference Szlapczynski and Szlapczynska2016). Secondly, our own ship's domain is violated (Davis et al., Reference Davis, Dove and Stockel1980, Reference Davis, Dove and Stockel1982; Coldwell, Reference Coldwell1983; Pietrzykowski, Reference Pietrzykowski2008; Wang, Reference Wang2010; Wang, Reference Wang2013) and thirdly, two ship's domains overlap (Rawson et al., Reference Rawson, Rogers, Foster and Philips2014; Liu et al., Reference Liu, Zhou, Li, Wang and Liu2016; Wang and Chin, Reference Wang and Chin2016). This paper focuses on the second violation: our own ship's domain being violated.
2.2 Eccentric ellipse ship domain
Despite the emergence of various shapes and sizes in different domain models, two trends have become more definite. On the one hand, in many studies the area ahead of a ship on the starboard side is evaluated as a dangerous part. Thus, an eccentric domain is more commonly adopted. On the other hand, a ship domain is just an expected clearance area, so a domain violation does not mean a physical collision between two ships. Therefore, it is more important to establish a possible collision domain based on the physical collision.
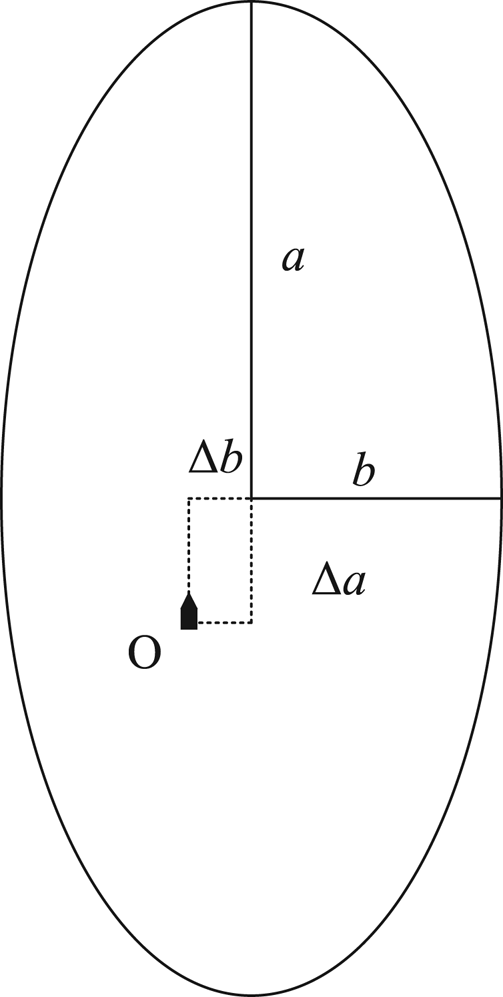
To achieve the goal, the model adopted in this study is similar to the Coldwell model, which has more buffer space on our own ship's bow and starboard side. In other words, our own ship, if regarded as a point, will be shifted to the left-rear part of its domain. A classical ellipse will be chosen as the shape of the ship domain in the RHP model, shown in Figure 1. The values of a and b indicate the length of the semi-major axis and semi-minor axis, respectively, and the values of $\Delta a$
and $\Delta b$
are offsets.
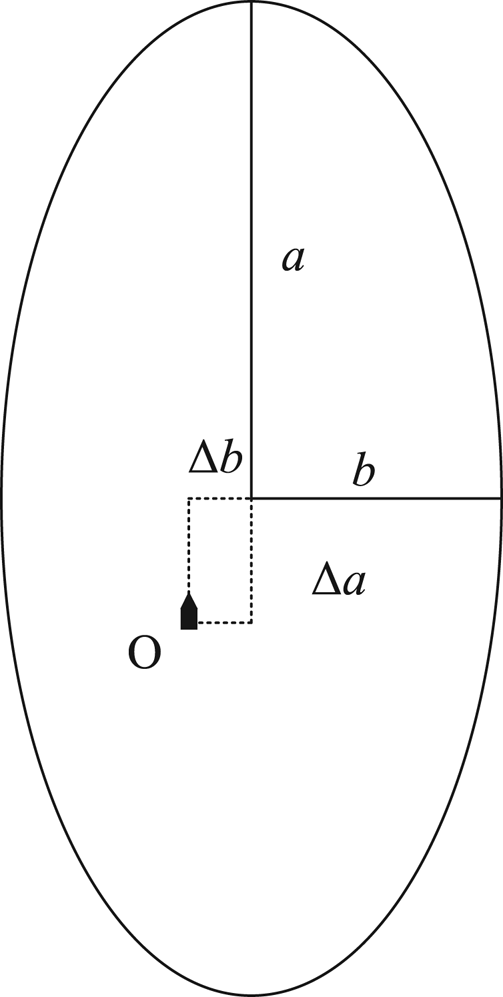
Figure 1. Eccentric ellipse ship domain
3. Risk hierarchy prewarning model
In this section, a hierarchical prewarning model based on the eccentric ellipse ship domain, the RHP model, will be proposed. The model includes several key indicators of the risk measurement on which the two-level prewarning scheme will be established.
3.1 Risk measurement
Three indicators including the approach factor, the time to domain violation, and the possible collision domain will be discussed respectively. The indicators imply the degree of danger to which the own ship is exposed.
3.1.1 Minimum approach factor
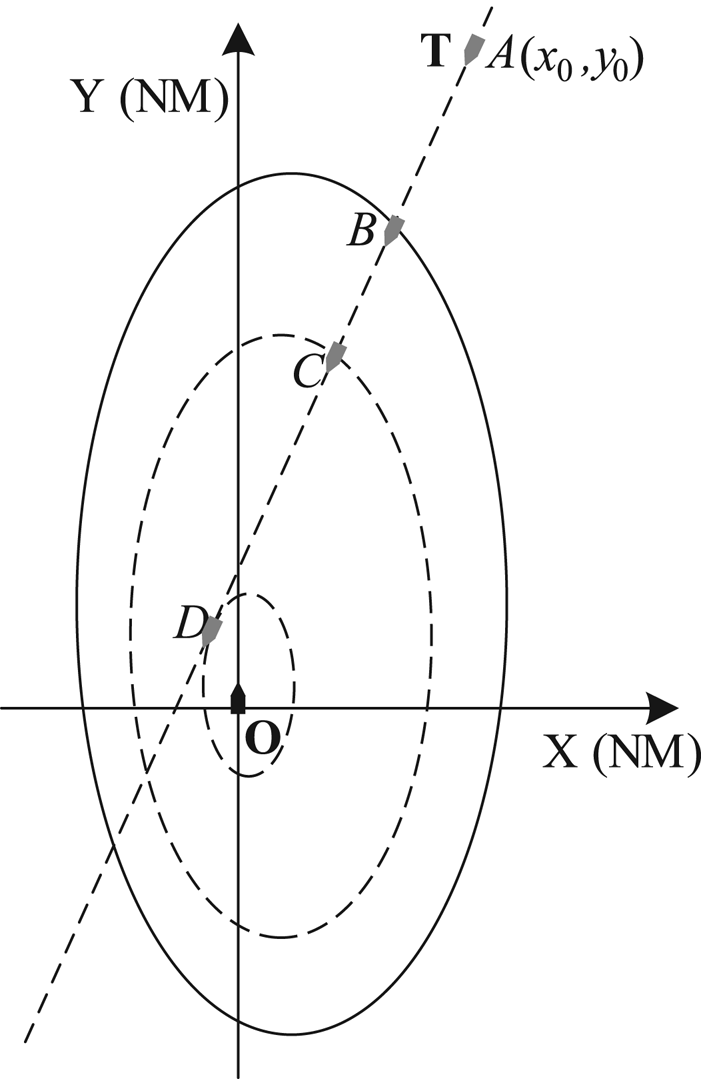
With the domain-oriented collision risk measure (Szlapczynski, Reference Szlapczynski2006; Szlapczynski and Szlapczynska, Reference Szlapczynski and Szlapczynska2016), the approach factor f is adopted in this paper to judge whether the target ship is likely to invade the own ship domain and to measure the degree of violation. It is known that there exists a characteristic triangle coming from two foci and a vertex of a given ellipse, and two ellipses with similar characteristic triangles are called ‘similar ellipses’. The similarity ratio of triangles is the same as the similarity ratio of the two ellipses, which is defined as the approach factor f. So, the approach factor means a scale factor of a zooming domain of our own ship, which can be illustrated by Figure 2.
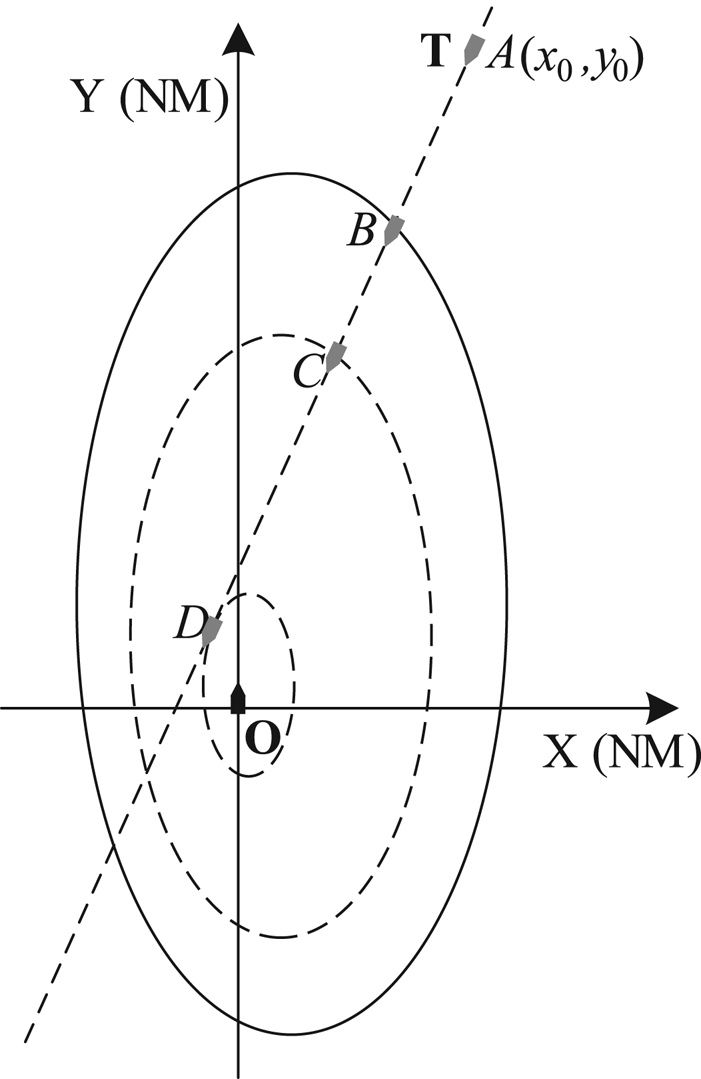
Figure 2. Approach factor illustration
Taking our own ship as a reference, the target ship will sail along the dotted route as shown in Figure 2, and the approach factor can be determined when the own ship domain is reduced to make sure that the target ship is located on the boundary of the domain. In this case, the values of f gradually decrease with the target ship approaching the domain from the point A to the point B and reaches its minimum at the point D when the scaled domain is tangent to the dotted route. After that, the values of f gradually increase and leaves the own ship domain in the end.
For a given plane rectangular coordinate system with the own ship as the centre, the ship's track direction as the y-axis and its starboard beam direction as the x-axis, our scaled ship domain equation can be expressed as
where $[{x(t ),y(t )} ]$
= coordinate position of the target ship, which changes over time.
Let the initial position of the target ship be $({{x_0},{y_0}} )$
at time ${t_0}$
, the relative velocity to the own ship be ${V_R}$
whose components along the x-axis and y-axis are ${V_x}$
and ${V_y}$
, respectively. Then, $x(t )$
and $y(t )$
can be expressed by
Substituting Equations (3.2) and (3.3) for $x(t )$
and $y(t )$
in Equation (3.1), f can be expressed by time t, denoted as $f(t )$
. Obviously, ${f_{min}}$
can be obtained by Equations (3.4) and (3.1):
${f_{min}}$
means the maximum violation of our ship. When ${f_{min}} > 1$
, our ship's domain will not be invaded by the target ship. When ${f_{min}} = 1$
, the target ship will be on the boundary of our ship's domain. However, when ${f_{min}} < 1$
, our own ship's domain will be invaded inevitably.
3.1.2 Time to domain violation
If a target ships is out of our ship's domain with ${f_{min}} < 1$
, the time remaining to entering our ship's domain, denoted as time to domain violation (TDV), is a very important index which implies the time urgency of the potential collision risk from the target ship. The TDV can be obtained by Equation (3.5), which means the target ship is on the boundary of our ship's domain:
Solving Equation (3.5), we get two positive solutions. A small number means the time remaining that the target ship will intersect with the boundary of our ship's domain for the first time, and the large one means the time remaining that the target ship will leave the domain. Apparently, the small solution is the TDV we want.
If Equation (3.5) has no solution, it means the target ship will not invade our ship's domain and ${f_{min}} > 1$
; if one of solutions is negative, it means the target ship has entered our ship's domain and will leave our domain at the time of the positive solution. Two negative solutions mean the target ship has run out of our domain.
Moreover, when the target ship is on the boundary of our ship's domain for the first time, the distance from the point of domain violation to our own ship, denoted as distance between the target ship and our own ship (DTO), can also be calculated after the TDV has been determined.
3.1.3 Possible collision domain
The risk pressure of our ship can be indicated by the TDV and the DTO, while the possible physical collision risk is still uncertain. A ship domain reflects the risk distribution which is different from the real physical collision between two ships. Therefore, it is essential to find a possible collision domain (PCD) based on the physical collision region. The PCD can be used as a red line that cannot be crossed by any ship if collisions is to be avoided.
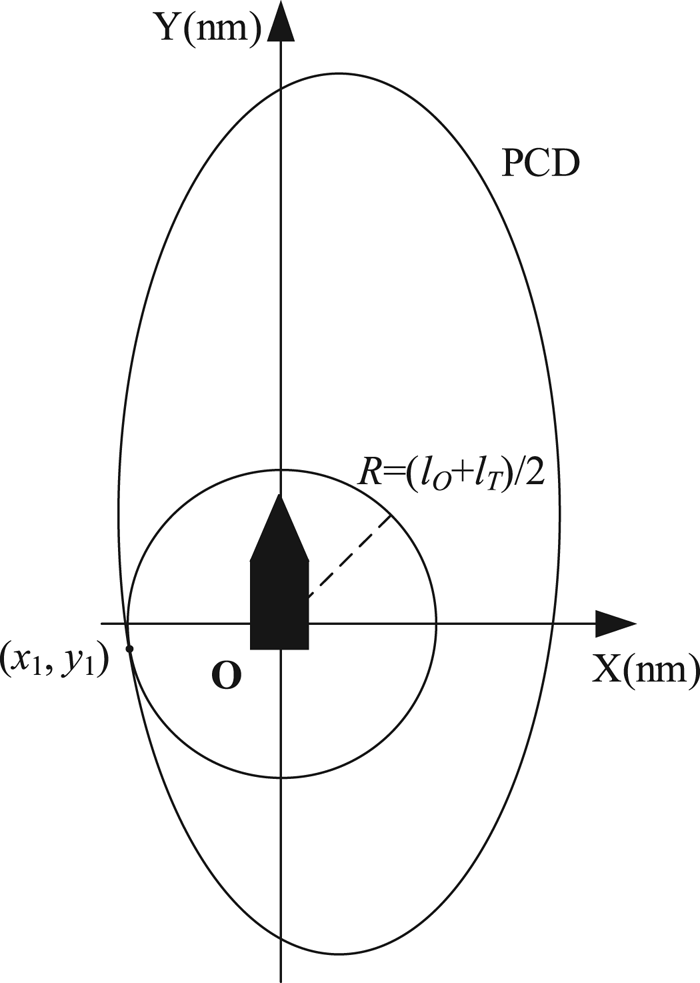
To find the PCD, the length of a target ship is reduced to a point while our own ship was expanded into a circular area with radius R. This area, written in Equation (3.6), describes all the possible position of the target ship when a collision happens (Chen et al., Reference Chen, Huang, Mou and van Gelder2018; Huang et al., Reference Huang, van Gelder and Wen2018):
The value of R strongly depends on the length of our own ship (${l_O}$
) and the target ship (${l_T}$
). In this paper, the possible collision domain is defined as the minimum eccentric ellipse domain containing the stated circular area, as shown in Figure 3.
Figure 3. PCD factor illustration
The PCD can be regarded as a special scale factor, denoted as ${f_{pcd}}$
, that the ship domain is reduced to be tangent to the circle. Let the coordinate position of the tangent point be (x 1, y 1), our ship domain be an eccentric ellipse with the semi-major axis $a = \alpha {l_o}$
and the semi-minor axis $b = \beta {l_o}$
, offsets $\Delta a = \gamma {l_o}$
and $\Delta b = \delta {l_o}$
, Equation (3.1) can be rewritten as
The equation of a circle can be rewritten as
Another equation is established according to the equal slopes at the tangent point between the equations of the eccentric ellipse and the circle, as
Obviously, ${f_{pcd}}$
can be determined by Equations (3.7)–(3.9) with three unknown quantities ${x_1}$
,$\; {y_1}$
and ${f_{pcd}}$
.
The possible collision domain can reflect not only the risk pressure around our ship but also the approximate physical collision she may suffer. As far as the area of a ship domain is concerned, the PCD is about the size of the circular area with radius R in Equation (3.6), but is safer since it covers the collision circle.
3.2 Prewarning model
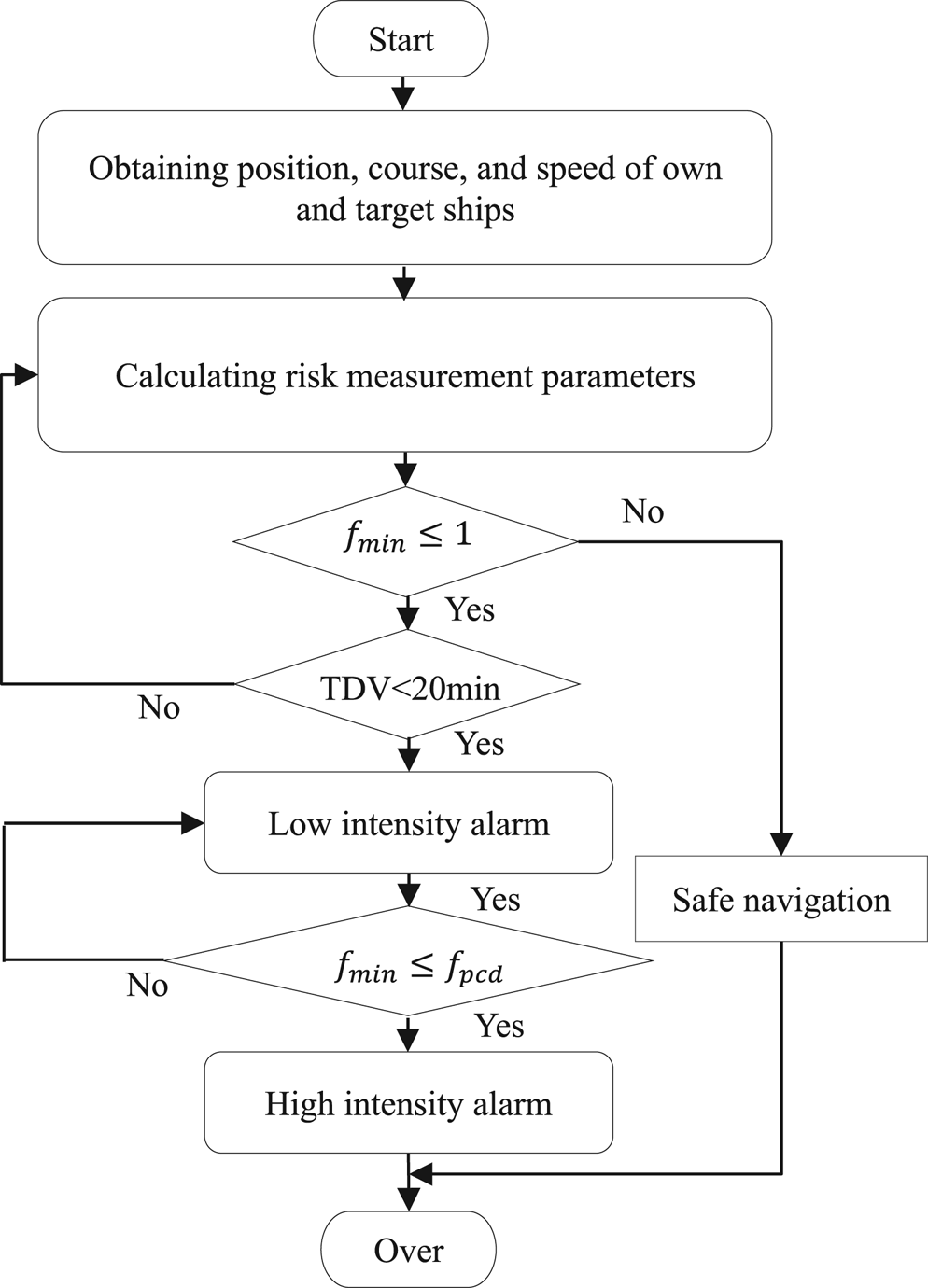
After the factor of the possible collision domain is determined, a risk assessment model for a ship's potential collision based on the ship domain, the RHP model, can be established, as shown in Figure 4.
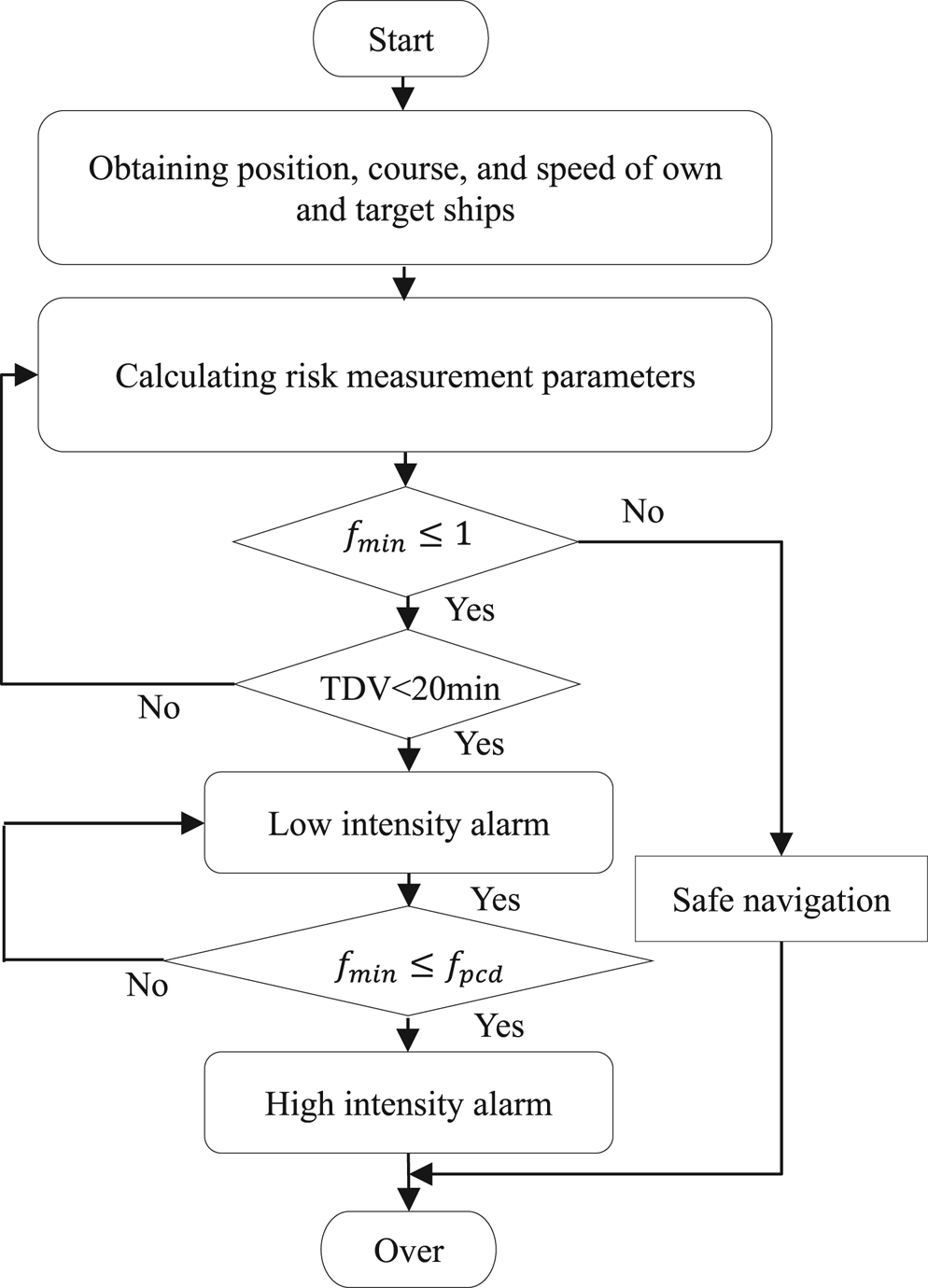
Figure 4. Risk hierarchy prewarning model
The two-level prewarning scheme proposed in the model will be activated if the thresholds of the approach factor, the TDV, and the PCD are met. The low-intensity alarm (LIA) will be sounded if our ship's domain will be violated within 20 min. Furthermore, the high-intensity alarm (HIA) will be sounded if our possible collision domain will be violated within 20 min.
The size of a possible collision domain depends on the LOAs of the target ship and ours. Table 1 gives some values of ${f_{pcd}}$
calculated by several typical LOAs.
Table 1. Values of fpcd calculated by several typical ship lengths
Note: a = 10lO, b = 5lO, $\Delta a$
= 2⋅5lO, and $\Delta b$
= 1⋅25lO.
S.D. stands for the standard deviation, which is the measure of speed most frequently used. The sign Δ means the maximum difference between values and the average. Table 1 shows that fpcd is sensitive to the length of our own ship. When the length of the own ship is 400 m, the average value of fpcd is 0⋅23, and its S.D. is only 0⋅05. However, when the length of the own ship is 100 m, the average value and the S.D. reach 0⋅49 and 0⋅18, respectively.
4. Scenario analysis and application
In this section, risk measurement parameters in the model are calculated based on a certain ship's length, and the results are discussed further under different ship-to-ship encounter situations to test their effects. After that, a new guard zone operation mode in radar based on the RHP model will be discussed to replace our traditional DCPA/TCPA working mode, when a ship is sailing at sea.
4.1 Encounter situation analysis
To further explain the advantages of the ship domain, 16 scenarios belonging to three typical situations (head-on, overtaking and crossing) are analysed, respectively. The risk difference around our ship is shown by the 16 encounter situations.
4.1.1 Multiple encounter situations
For consistency with the paper (Szlapczynski and Szlapczynska, Reference Szlapczynski and Szlapczynska2016), the domain's dimensions used in this work is set as a = 10 L, b = 5 L, $\Delta a$
= 2⋅5 L, and $\Delta b$
= 1⋅25 L. Our ship's length, L, is assumed 370 m. After calculation, the approximate size of our ship's domain is shown as Figure 5. In addition, for the convenience of comparison, initial positions, velocities and courses of the target ship are purposefully designated so that she will pass our bow and stern half by half in the 16 scenarios with the same DCPAs (one nautical mile) and TCPAs (20 minutes), as shown in Figure 6.
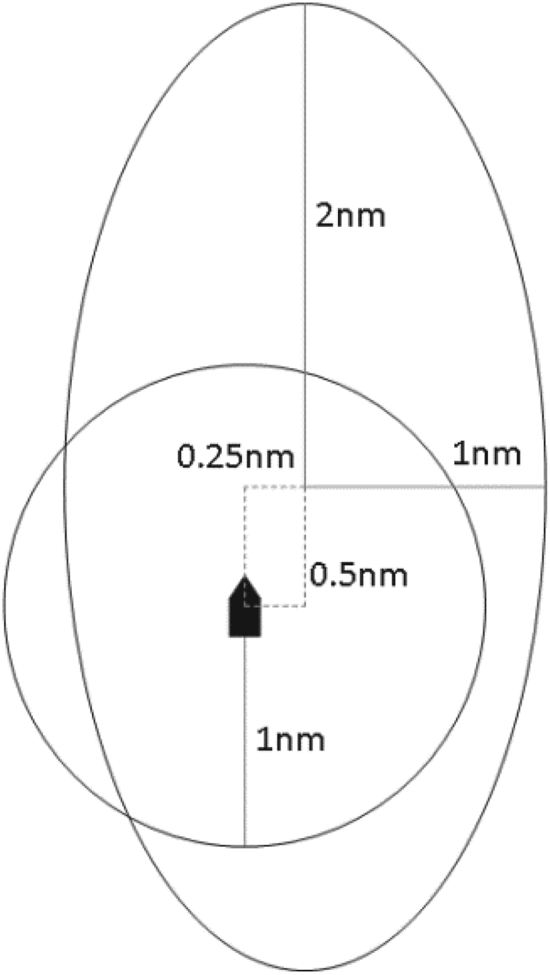
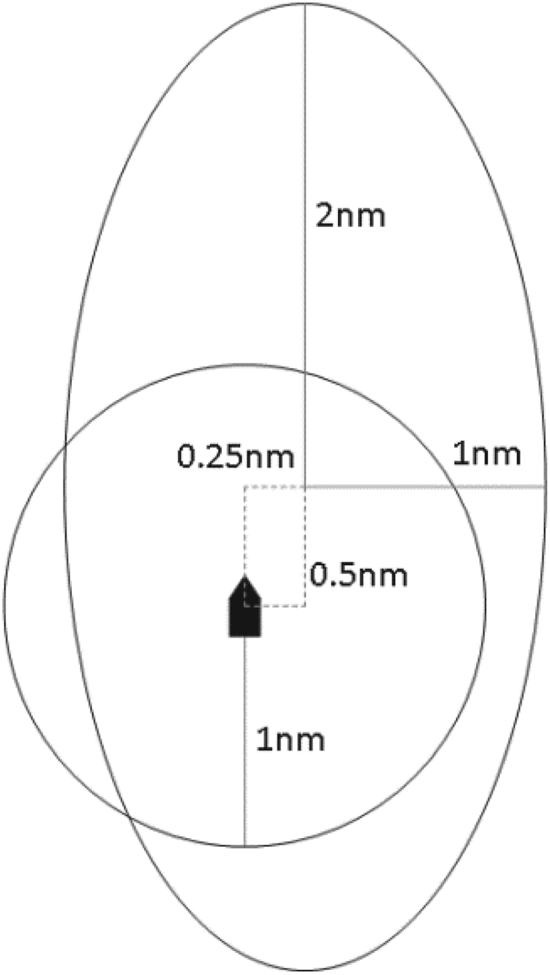
Figure 5. Approximate size of domain
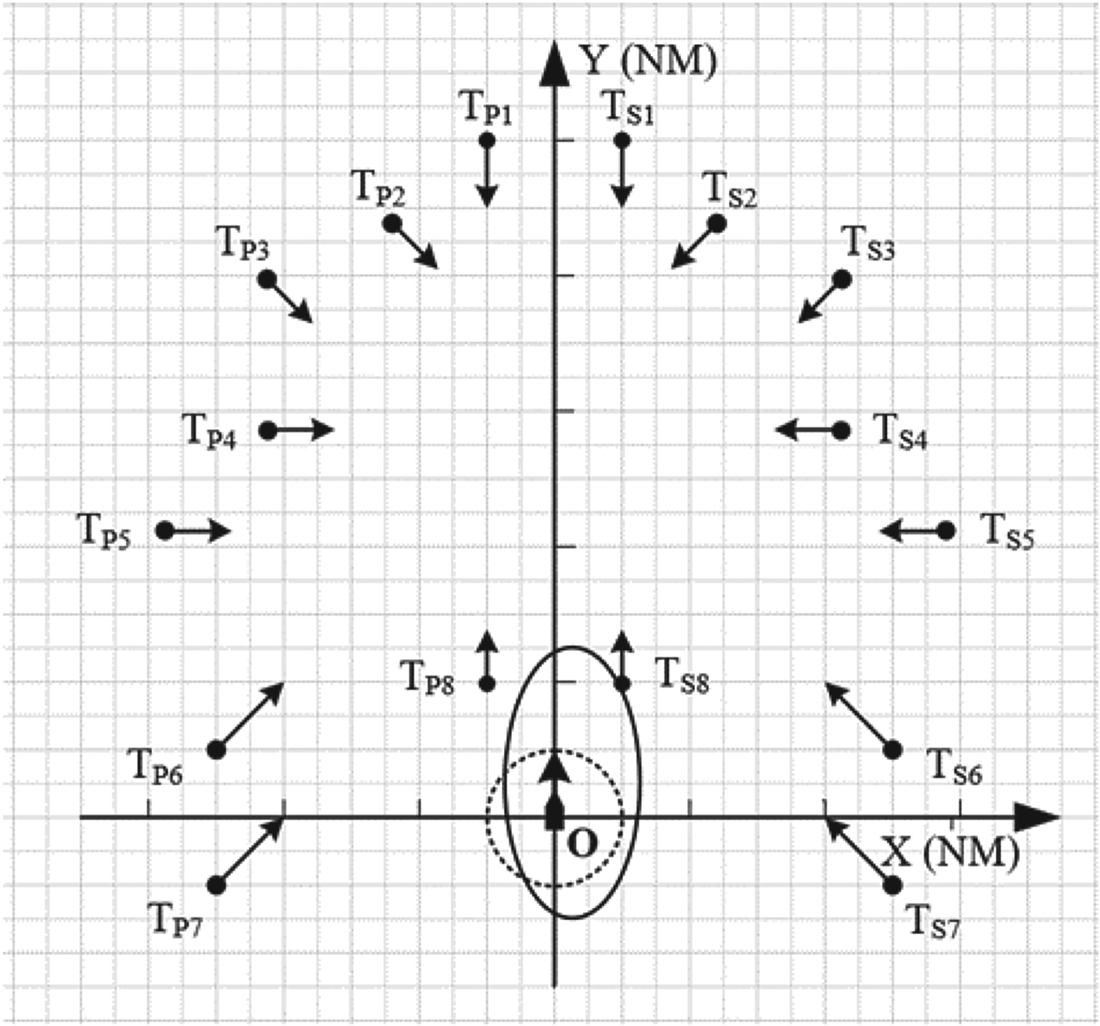
Figure 6. Sixteen ship-to-ship encounter situations
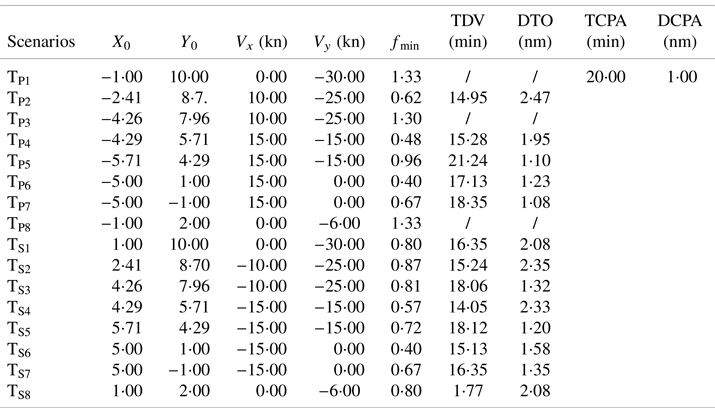
TP means a target ship is on our port side, and TS means a target ship on our starboard side in Figure 6. The side length of a square lattice is 0⋅5 nautical miles. The radius of the dotted circle is 1 nautical mile, and our ship is at the centre of a rectangular coordinate system. Then all key parameters can be determined by equations previously mentioned, which are shown in Table 2.
Table 2. Key parameters in RHP model in 16 scenarios
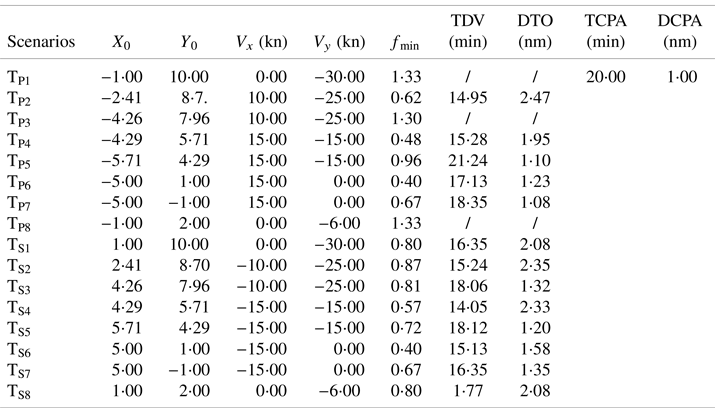
In Table 2, X 0 and Y 0 means the initial position. In the fourth and fifth column, Vx and Vy are components of the relative velocity of the target ship to our ship along the x-axis and y-axis, respectively, and the minus sign means the speed of the target ship is slower than that of our ship.
4.1.2 Model advantage analysis
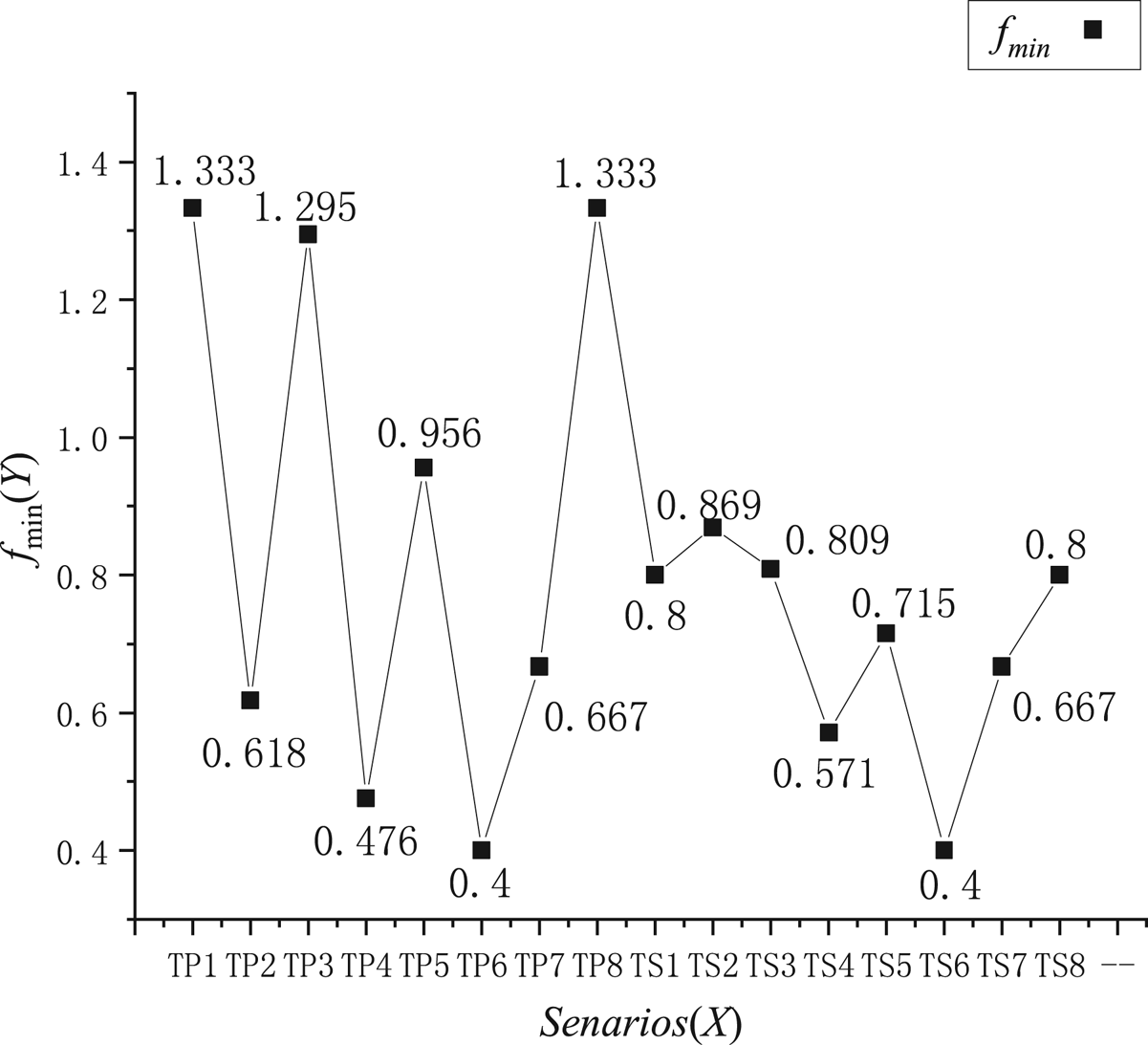
The superiority of the RHP model can be shown by some key parameters, which can be illustrated by Figures 7 and 8. The scenario TP1, TP3 and TP8 are not included in Figure 8 because their values of ${f_{min}}$
are greater than 1.
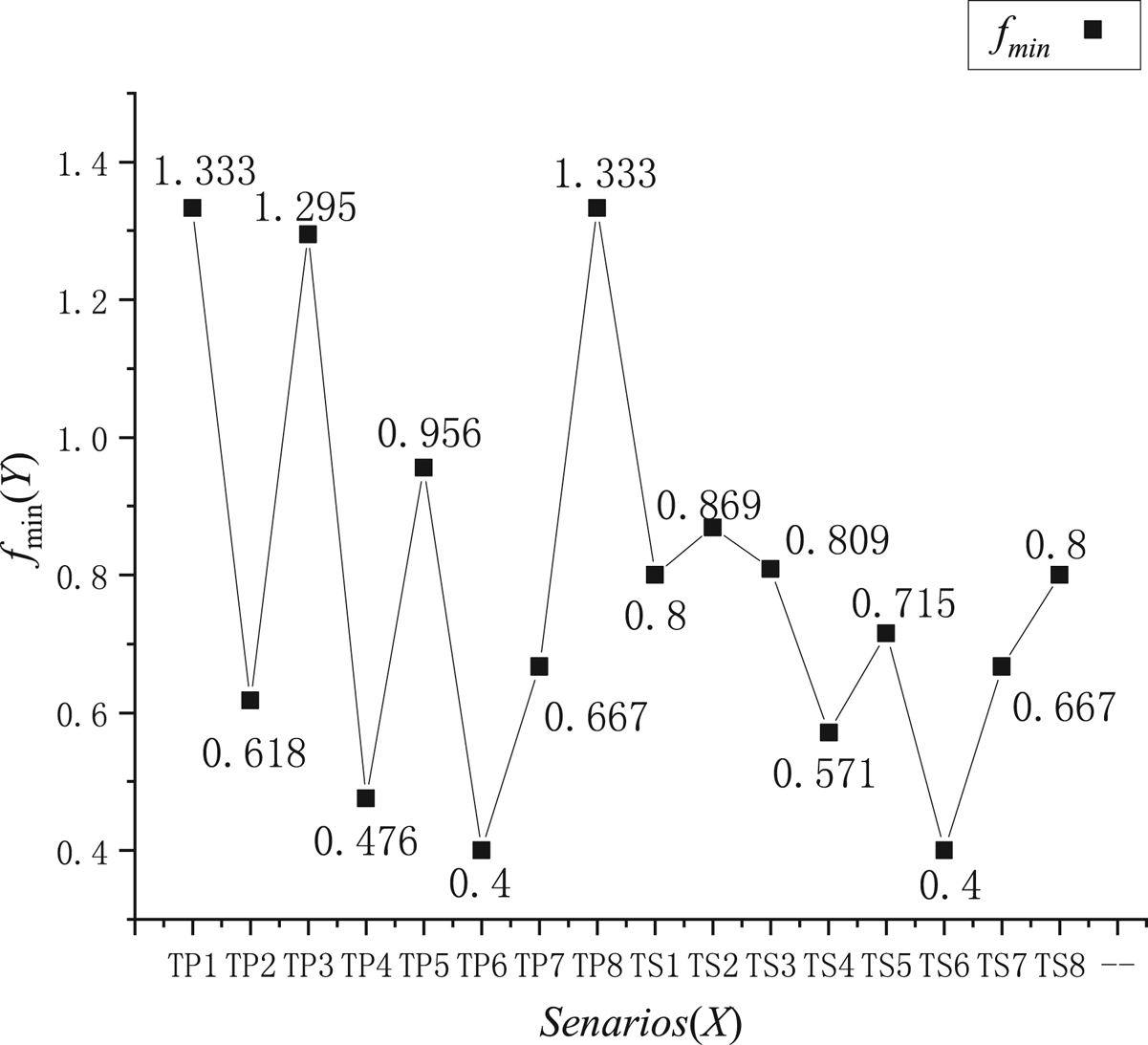
Figure 7. Values of ${f_{min}}$
in 16 scenarios
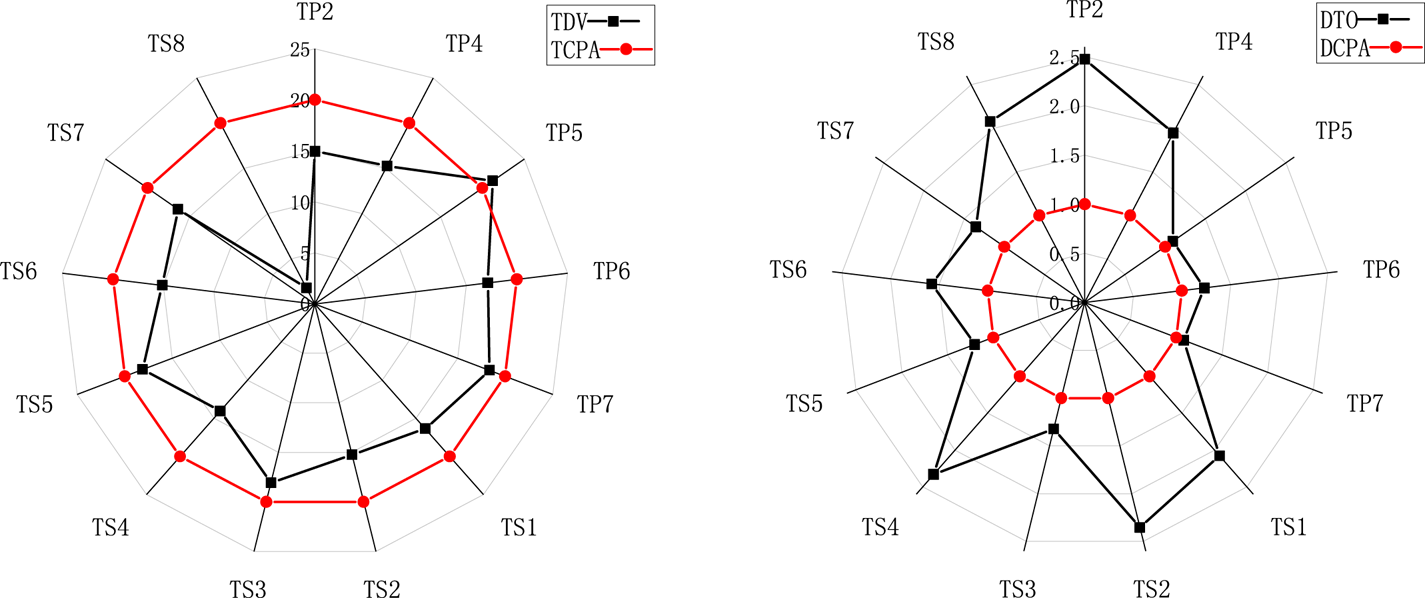
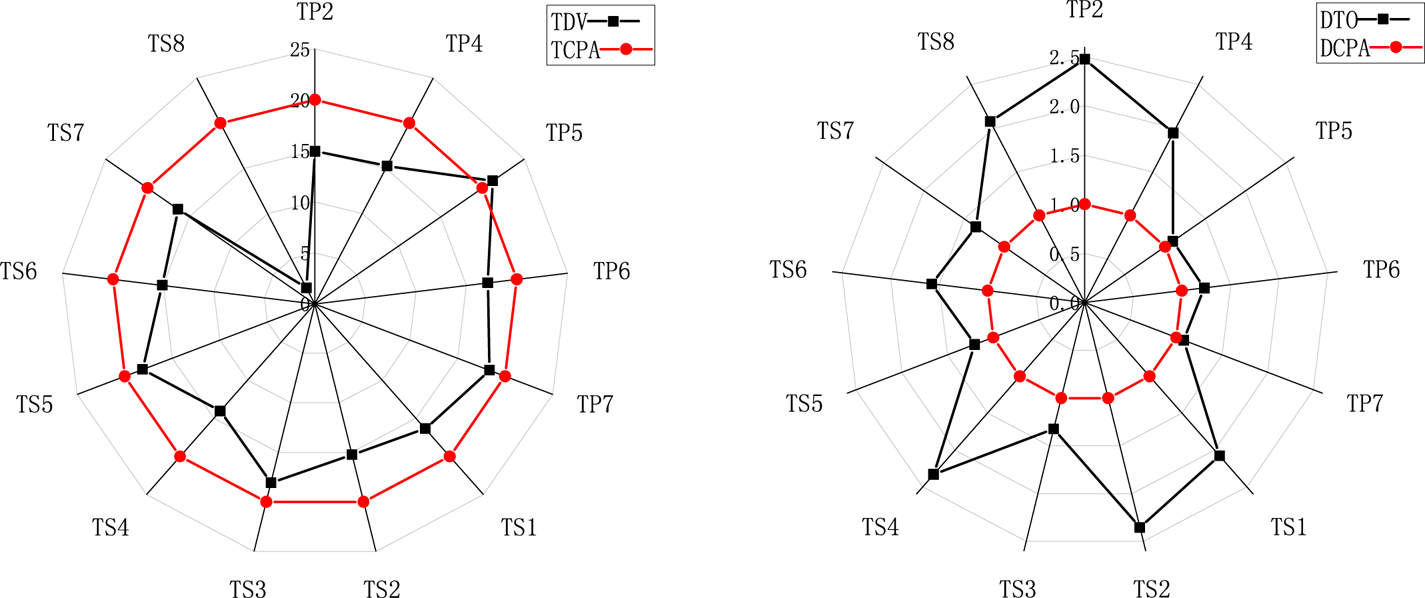
Figure 8. Comparison of TDV and TCPA, DTO and DCPA
Figure 7 shows values of f min are totally different in 16 scenarios, which means a target ship from different bearings poses different risks to our ship, although two ships have the same DCPA and DCPA. Figure 8 shows comparisons between the TDV and the TCPA, the DTO and the DCPA. Most TDV values are less than 20 minutes, which means the LIA time in the RHP model is earlier than that in the traditional TCPA warning pattern. In addition, most DTO values are greater than 1 nautical mile, which means when the LIA is triggered, the distance between two ship is further and safer than that in the traditional DCPA warning pattern. Furthermore, the time and the distances from different bearings vary considerably, so the model based on the ship domain can describe the risk pressure around a ship more accurately and reasonably.
The RHP model is derived from the eccentric ellipse ship domain, which shows that the right side of the ship (starboard) is more dangerous than the left side (port), and the front side (forward) is more dangerous than the rear side (aft). Therefore, it is more accurate to be used to predict the potential collision risk of ships. Moreover, the model can leave more reaction time and avoidance distance in encounter situations which can make navigation safer.
4.2 Model application
Considering its many excellent properties, the RHP model can be used in many aspects, such as in a decision-making support system for collision avoidance, in an early warning system at sea or even in an autonomous navigation system in the future. For example, the model can be adopted as an early warning pattern in an ECDIS system, among which ship's positions are obtained from GPS and courses are reckoned by track directions. All real-time dynamic data from the own ship and target ship will be calculated continually to find the related risk parameters: ${f_{min}}$
, TDV, and ${f_{pcd}}$
.
Moreover, the model can also be applied in the radar watchkeeping system, in which the parameters are determined by relative positions, relative velocities, etc. To further explain the application of the model, a novel guard zone based on the ship domain in radar system are described in detail.
4.2.1 New guard zone
Traditionally, the purpose of a guard zone set in ARPA radar is to alert the watch officer that a target ship is approaching the preset TCPA and DCPA limit. The DCPA threshold is usually set to 1 nautical mile, and the TCPA threshold 20 min on the coastal voyage, while they are 2 nautical miles and 20 min, respectively, on the oceangoing voyage. Since a domain-based risk measurement can assess ship potential collision risk more accurately and reasonably, a new guard zone in ARPA radar based on the ship domain can be proposed accordingly.
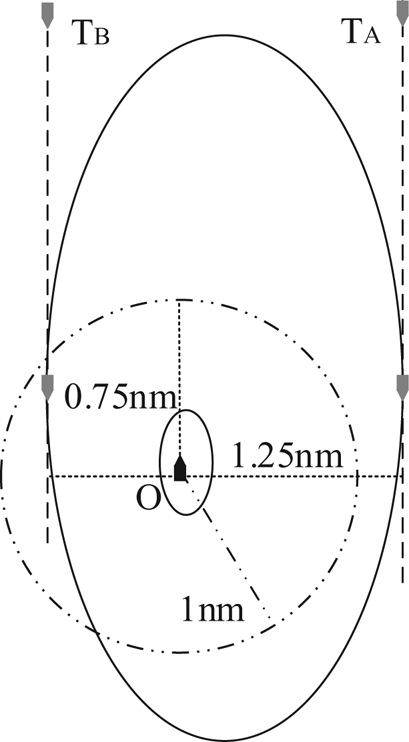
In the new guard zone, an eccentric ellipse ship domain with a semi-major axis of 2 nautical miles, a semi-minor axis of 1 nautical mile is adopted analogically on the coastal voyage, as shown in Figure 9. Likewise, the domain with a semi-major axis of 4 nautical miles, and a semi-minor axis of 2 nautical miles is set on the oceangoing voyage. The RHP model has still been used as a two-level alarm scheme. Table 3 shows related parameters in guard zones based on the RHP model and on the TCPA/DCPA comparatively.
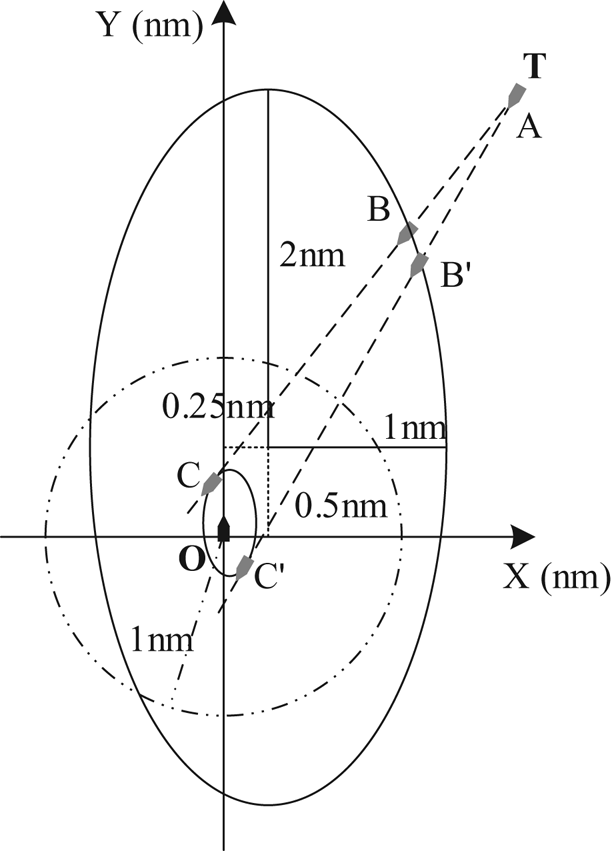
Figure 9. Domain-based alarm mode
Table 3. Guard zones based on RHP model and on TCPA/DCPA
As shown in Table 3, the traditional guard zone mode relies on the DCPA and TCPA thresholds. The ARPA radar system will alarm automatically when two thresholds are met simultaneously. However, the RHP-based guard zone relies on the eccentric ellipse ship domain, and its shape, size and eccentricity will be set in accordance with the coastal or oceangoing voyage. The ARPA radar system in new guard zone mode will sound low intensity alarm automatically when the real-time approach factor and the TDV meet thresholds. Furthermore, it will sound a high-intensity alarm when the real-time approach factor is less than or equal to the factor of the possible collision domain.
Furthermore, ${f_{pcd}}$
is determined by the length of the own ship (l0) and the length of the target ship (lt), so in multi-ship encounter situations, n target ships will form n different factors of the possible collision domain due to their different lengths of target ships. Apparently, each ${f_{pcd}}$
contains a significant pairing tag which implies a particular target ship and our ship. If the high-intensity alarm is activated by two or more target ships at the same time, all ships involved will be shown clearly to attract the attention of duty officers.
4.2.2 Comparison and analysis
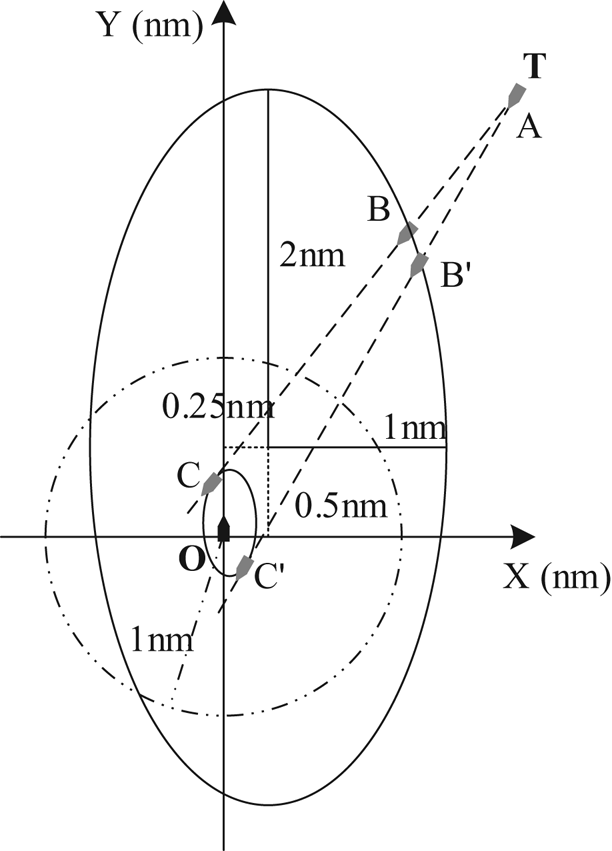
Compared with the traditional DCPA method which is illustrated by the dotted circle with a radius of 1 nautical mile in Figure 9, domain-based method can show the risk pressure around a ship more accurately. For example, the ellipse is not tangent to the circle due to its eccentricity although the semi-minor axis is equal to the radius. As far as coastal voyages are concerned, if a target ship navigates parallel to our ship in the opposite direction which is a near head-on situation, the domain-based guard zone can treat them differently when the target ship approaches us from the port side or starboard side. Figure 10 shows the typical situation which always confused duty officers.
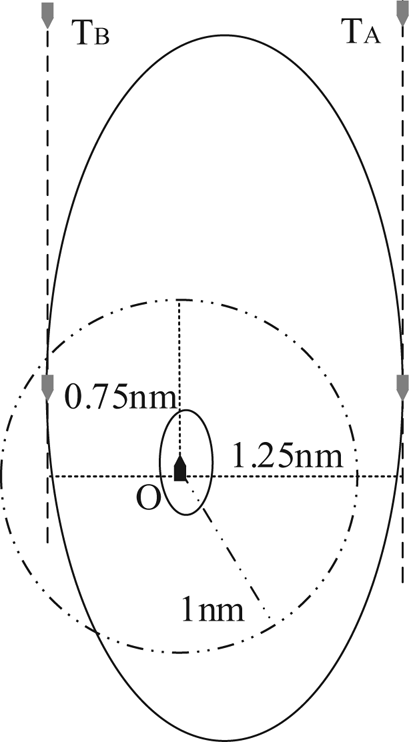
Figure 10. Comparison for near head-on situation
The alarm will sound with the vertical distance of parallel courses less than or equal to 0⋅75 nautical miles on our port side, and 1⋅25 nautical miles on the starboard side. Apparently, asymmetric distance parameters are more reasonable and acceptable because it is a common encounter situation for ships to pass red to red, as shown by ship TB in Figure 10. Course can be altered to starboard if two ships are found too close due to winds or currents. However, it is a vexed situation if the target ship navigates on our starboard side, as shown by ship TA in Figure 10. Altering course to starboard side is obviously dangerous due to the location of the target ship. However, primary responsibilities shall be borne if we alter course to port side which leads to the collision accidentally. Therefore, it is seaman's practices to keep enough safe clearance from a ship located on our starboard side, which is consistent with the domain-based RHP model.
Furthermore, the guard zone proposed in this paper could be used in restricted waters, such as in narrow channels, traffic separation schemes (TSSs) or channels for entering or leaving a port. The risk pressure is higher when ships navigate in those waters than at sea, and it is common that the low intensity alarm always sounds in congested waters. In such a situation, great attention should be paid to the high intensity alarm which may cause an accident possibly.
To summarise, the domain-based guard zone can be used in different scenarios, including ship entering or leaving the port, sailing along the coast or on the oceangoing voyage. The guard zone can reflect the risk distribution around the ship reasonably, and sound different intensity alarms with the increase of the risk pressure. Moreover, it has a more accurate risk description for the confused near head-on situation.
5. Conclusions and future work
Different shapes of the ship domain are discussed, and the eccentric ellipse ship domain is adopted to assess the degree of domain violation in this paper. Related risk measurement parameters, including the approach factor, the TDV and the DTO, are calculated accordingly, among which the approach factor f is the key indicator that determine the minimum factor ${f_{min}}$
and the possible collision factor ${f_{pcd}}$
. ${f_{min}}$
can not only imply whether the target ship will invade our ship's domain but also give the maximum degree of domain violation if that happens, while ${f_{pcd}}$
represents two ships will probably collide each other if ${f_{min}}$
is less than or equal to ${f_{pcd}}$
.
Based on the risk parameters mentioned, the RHP model with the function of risk perception is proposed, on which the flexibility of a ship domain as a risk measurement is fully reflected. First, our ship's risk pressure will be determined once the shape of our ship's domain and its eccentric degree are selected properly. Target ships from different bearings will produce different risk levels to our ship. Second, a high-intensity alarm is the last line of defence, which means a target ship will pass the possible collision domain of our ship and the collision becomes a very real possibility.
Subsequently, the RHP model has been used as a key module of the guard zone in ARPA radar to establish a ship's risk perception system. New guard zones based on eccentric ellipses of different sizes are proposed in two main application scenarios, respectively, including the coastal voyage and the oceangoing voyage. Compared with our traditional guard zone mode, the new one can perceive the risk pressure of the target ship coming from different bearings even if collision candidates have the same TCPA and DCPA. It can not only improve the accuracy of risk identification around our ship, but also be used as a decision support system for collision avoidance. Obviously, it will fundamentally relieve duty officers of the burden at sea.
By far, ship domain models are still developing. It is difficult to conclude which shape performs overall the best. In this paper, the classic eccentric ellipse ship domain is introduced for computation. For future research, other shapes of domain shall be adopted to improve the RHP model. For example, a variable ship domain whose shape and size change dynamically with our ship's speed and the density of traffic flow could be introduced to increase the adaptability of the model in narrow channels, TSSs and channels for entering or leaving a port.
Funding statement
This work is supported by the National Science Foundation of China (NSFC) through Grant No. 51709168. We wish to thank Prof. Hu for his kind advice and assistance with the English revision in this manuscript.
