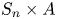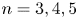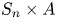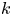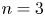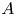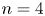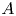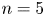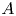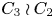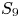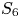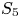1. Introduction
There are only finitely many number fields with bounded discriminant, therefore it makes sense to ask how many there are. Malle's conjecture aims to answer the asymptotic question for number fields with prescribed Galois group. Let 
$k$ be a number field and 
$K/k$ be a degree 
$n$ extension with Galois closure 
$\tilde {K}/k$; we define 
$\operatorname {Gal}(K/k)$ to be 
$\operatorname {Gal}(\tilde {K}/k)$ as a transitive permutation subgroup of 
$S_n$ where the permutation action is defined by its action on the 
$n$ embeddings of 
$K$ into 
$\bar {k}$. Let 
$N_k(G, X)$ be the number of isomorphism classes of extensions of 
$k$ with Galois group isomorphic to 
$G$ as a permutation subgroup of 
$S_n$ and absolute discriminant bounded by 
$X$. Malle's conjecture states that 
$N_k(G,X) \sim C X^{1/a(G)} \ln ^{b(k,G)-1} X$ where 
$a(G)$ depends on the permutation representation of 
$G$ and 
$b(k,G)$ depends on both the permutation representation and the base field 
$k$. See § 2.3 for explanations on the constants.
Malle's conjecture has been proven for abelian extensions over 
$\mathbb {Q}$ [Reference MäkiMäk85] and over arbitrary bases [Reference WrightWri89]. However, for non-abelian groups, there are only a few cases known. The first case is 
$S_3$ cubic fields proved by Davenport and Heilbronn [Reference Davenport and HeilbronnDH71] over 
$\mathbb {Q}$ and later proved by Datskovsky and Wright [Reference Datskovsky and WrightDW88] over any 
$k$. Bhargava and Wood [Reference Bhargava and WoodBW08] and Belabas and Fouvry [Reference Belabas and FouvryBF10] independently proved the conjecture for 
$S_3$ sextic fields. The cases of 
$S_4$ quartic fields [Reference BhargavaBha05] and 
$S_5$ quintic fields [Reference BhargavaBha10] over 
$\mathbb {Q}$ were also proved by Bhargava. In [Reference Bhargava, Shankar and WangBSW15], these cases are generalized to arbitrary 
$k$ by Bhargava, Shankar and Wang. The case of 
$D_4$ quartic fields over 
$\mathbb {Q}$ was proved by Cohen, Diaz y Diaz and Olivier [Reference Cohen, Diaz y Diaz and OlivierCDO02]. It was generalized by Klüners to groups of the form 
$C_2\wr H$ [Reference KlünersKlü12] under mild conditions on 
$H$.
The main result of this paper is to prove Malle's conjecture for 
$S_n\times A$ in its 
$S_{n|A|}$ representation for 
$n=3,4,5$ with certain families of abelian groups 
$A$.
Theorem 1.1 Let 
$A$ be an abelian group and let 
$k$ be any number field. Then there exists 
$C$ such that the asymptotic distribution of 
$S_n\times A$ number fields over 
$k$ by absolute discriminant is
\[ N_k(S_n\times A, X) \sim C X^{1/|A|} \]in the following cases:
(1)
$n=3$, if $2\nmid |A|$;(2)
$n=4$, if $2,3 \nmid |A|$;(3)
$n=5$, if $2,3,5\nmid |A|$.
See § 2.5 for the explanation that this agrees with Malle's conjecture. We can write out the constant 
$C$ explicitly given the generating series of 
$A$ extensions by discriminant; see, for example, [Reference MäkiMäk85, Reference WoodWoo10, Reference WrightWri89] for where these generating series are explicitly given. The constant 
$C$ could be written as a finite sum of Euler products when the generating series of 
$A$ extensions is a finite sum of Euler products.
For example, if we count all homomorphisms 
$G_{\mathbb {Q}}\to S_3\times C_3$ that surject onto the 
$S_3$ factor, the asymptotic count of these homomorphisms by discriminant is
\begin{equation} 2\prod_{p}c_p X^{1/3}, \end{equation}
where 
$c_p = (1+ p^{-1}+ 5p^{-2}+ 2p^{-7/3})(1-p^{-1})$ for 
$p\equiv 1 \mod 3$ and 
$c_p = (1+p^{-1}+ p^{-2})(1-p^{-1})$ for 
$p\equiv 2\mod 3$. For 
$p=3$, we use the database of local fields [LMF13] to compute that 
$c_3 = 3058\cdot 3^{-5}+ 4\cdot 3^{4/3}\approx 29.8914$. If we count the actual number of isomorphism classes of 
$S_3\times C_3$ extensions (i.e. all surjections 
$G_{\mathbb {Q}} \to S_3\times C_3$ up to an automorphism), the asymptotic constant is naturally a difference of two Euler products simply by inclusion-exclusion. More explicitly, one Euler product is counting the number of 
$\rho : G_{\mathbb {Q}}\to S_3\times C_3$ that surject onto the 
$S_3$ factor, but do not necessarily surject onto the 
$C_3$ factor, and it is exactly the Euler product given above. The second one counts 
$\rho : G_{\mathbb {Q}} \to S_3\times C_3$ that surject onto the 
$S_3$ factor, but do not surject onto the 
$C_3$ factor (which has to be trivial), and it is simply counting all 
$S_3$ extensions bounded by 
$X^{1/3}$ with a multiplicity of 
$|\text {Aut}(S_3)|=6$, that is, 
$6 N_{\mathbb {Q}}(S_3, X^{1/3})$. Then it suffices to take the difference between the two Euler products and divide it by 
$|\text {Aut}(S_3\times C_3)| = 12$.
However, Malle's conjecture has been shown generally not to be correct. Klüners [Reference KlünersKlü05a] shows that the conjecture does not hold for 
$C_3\wr C_2$ number fields over 
$\mathbb {Q}$ in its 
$S_6$ representation, where Malle's conjecture predicts a smaller power for 
$\ln X$ in the main term. See [Reference KlünersKlü05a] and [Reference TurkelliTur08] for suggestions on how to fix the conjecture. And by relaxing the precise description of the power for 
$\ln X$, the weak form of Malle's conjecture states that for arbitrary given small 
$\epsilon >0$, the distribution satisfies 
$C_1 X^{1/a(G)} \le N_k(G,X) \le _{\epsilon } C_2(\epsilon ) X^{1/a(G)+\epsilon }$ when 
$X$ is large enough. Klüners and Malle proved this weak form of Malle's conjecture for all nilpotent groups [Reference Klüners and MalleKM04].
Notice that for Klüners’ counter-example, 
$C_3\wr C_2\simeq S_3\times C_3$, we have the following corollary.
Corollary 1.2 Malle's conjecture holds for 
$C_3\wr C_2$ in its 
$S_9$ representation over any number field 
$k$.
Counting non-Galois number fields could be considered as counting Galois number fields by discriminant of certain subfields. A natural question thus will be: what kind of subfields provide the discriminant as an invariant by which the asymptotic estimate is as predicted by Malle?
Malle considers the compatibility of the conjecture under taking compositum in his original paper [Reference MalleMal02] and estimates both the lower bound and upper bound of asymptotic distribution for compositum when the two Galois groups have no common quotient. Klüners also considered counting direct product in his thesis [Reference KlünersKlü05b]. Assuming some condition on counting 
$H$ extensions which is known when 
$H = S_n$ with degree 
$n=3,4,5$, he proves an upper bound of 
$N(G, X)$ in the order of 
$O_{\epsilon }(X^{1/a(G)+\epsilon })$ for 
$G = C_l\times H$ where 
$C_l$ is a prime order cyclic group. By working out a product argument, we show a better lower bound for general direct product; see Corollary 3.3. And by analyzing the behavior of the discriminant carefully and applying good local uniformity results on ramified extensions, we show a better upper bound for our cases 
$S_n\times A$; see Theorem 1.1. It gives the same order of main term and actually matches Malle's prediction. The local uniformity results will be a key input for our proof of Theorem 1.1. For example, we prove the following new local uniformity estimates for ramified 
$S_5$ quintic extensions.
Theorem 1.3 The number of 
$S_5$ quintic extensions over a number field 
$K$ which are totally ramified at a product of finite places 
$q = \prod {p_i}$ is
\[ N_q(S_5,X) = O_{\epsilon}\bigg(\frac{X}{|q|^{4-\epsilon}}\bigg) + O_{\epsilon}(X^{36/40+\epsilon}|q|^{\epsilon}), \]
for any square-free integral ideal 
$q$ of 
$K$. The implied constant is independent of 
$q$, and only depends on 
$K$ and 
$\epsilon$. In particular,
\[ N_q(S_5,X) = O_{\epsilon}\bigg(\frac{X}{|q|^{2/5-\epsilon}}\bigg). \] The proof combines an adaptation of Bhargava's geometric sieve in [Reference BhargavaBha14] and the averaging technique first introduced by Bhargava in [Reference BhargavaBha05]. The averaging technique is especially useful for counting low-rank (
$n= 3,4,5$) irreducible orders with a power-saving error. Aside from counting the total number of irreducible orders, it could also be used to count the number of irreducible orders satisfying certain local conditions. In this paper we apply the averaging technique to count the number of irreducible orders that are ramified at finitely many places. As an input to apply the averaging technique, we will need to count the number of irreducible ramified lattice points inside an inhomogeneous expanding compact region. We use the key observation in [Reference BhargavaBha14] that ramified lattice points are rational points of a certain closed subscheme and the lattice counting question could be therefore translated to a geometric setting. In order to prove Theorem 1.3, we first adapt Bhargava's geometric sieve to give an upper bound on the number of integral points that are within an expanding compact region and are 
$O_K/qO_K$-rational points of a closed scheme 
$Y$ where 
$q$ is a square-free ideal. See Theorems 4.4–4.6 for explicit statements with increasing complexity. This generalizes and improves on a corollary of [Reference BhargavaBha14, Theorem 3.3] which gives an upper bound on the number of integral points that are ramified at a single prime 
$p$. We generalize the number of closed schemes from one to finitely many, the modulus from a prime ideal to a square-free ideal, and the base field from 
$\mathbb {Q}$ to a general number field 
$K$. When the local condition on ramification is only at finitely many places, we slightly improve on the power-saving error. The observation of this geometric structure in [Reference BhargavaBha14] enables us to get a power-saving error that is uniform in 
$q$ and reserved by the averaging technique, which is crucial to our the proof. The explicit computation for the averaging technique is carried out in the proof of Theorem 1.3.
This paper is organized as follows. In § 2 we analyze the discriminant of a compositum in terms of each individual discriminant and give the algorithm to compute the discriminant of the compositum precisely in general. Then, by applying the algorithm, we compute the discriminant explicitly for the case 
$S_n\times A$. Finally we check that Theorem 1.1 agrees with Malle's prediction. In § 3 we prove a product argument in two different cases. In § 4 we include and prove some necessary local uniformity results. For 
$S_n$ extensions with 
$n=3,4$, the local uniformity estimates mainly follow from [Reference Datskovsky and WrightDW88] and [Reference Bhargava, Shankar and WangBSW15] by class field theory. For 
$S_5$ extensions, we adapt Bhargava's geometric sieve and then apply an averaging technique. For all abelian extensions we prove perfect uniformity estimates by class field theory. In § 5, in order to prove our main theorem, Theorem 1.1, we first count by a family of new invariants, which are approximations of the discriminant. With the input of uniformity results we have developed in § 4, we show that counting functions of this family of invariants will finally converge to the counting function of the discriminant.
Notation
Throughout the paper, unless stated otherwise, we will use 
$k$ to denote a fixed number field as the base field. In this list, we will assume 
$K/k$ is a finite extension.
$p$: a finite place in base field 
$k$
$K_{\mathfrak {p}}$: the completion of 
$K$ with respect to the valuation at 
$\mathfrak {p}$ where 
$\mathfrak {p}\in O_K$ is a prime ideal
$(K)_p$: the local étale algebra 
$K \otimes _k k_p = \oplus _{\mathfrak {p}|p} K_{\mathfrak {p}}$ where the sum is over ideals 
$\mathfrak {p}$ of 
$K$ above 
$p$
$|\cdot |$: absolute norm 
$\operatorname {Nm}_{k/\mathbb {Q}}$
$\operatorname {disc}(K/k)$ : relative discriminant ideal in base field 
$k$
$\operatorname {disc}_p(K/k)$: an ideal 
$p^{\text {val}_p(\operatorname {disc}(K/k))}$ for a prime ideal 
$p$ of 
$k$
$\operatorname {Disc}(K)$: absolute norm of 
$\operatorname {disc}(K/k)$ to 
$\mathbb {Q}$
$\operatorname {Disc}_p(K)$: absolute norm of 
$\operatorname {disc}_p(K/k)$
$\tilde {K}$: Galois closure of 
$K$ over base field 
$k$
$\large \langle g\large \rangle$: the subgroup of 
$G$ generated by 
$g\in G$
$\operatorname {ind}(g)$: 
$n - \sharp \{\text {orbits}\}$ for a permutation element 
$g\in S_n$; we define it to be the index of 
$g$
$\operatorname {ind}(G)$: 
$\min _{g\ne e \in G } \operatorname {ind}(g)$ for a permutation group 
$G\subset S_n$; we define it to be the index of 
$G$
$G_{k_p}$: the Galois group of the separable closure 
$\overline {k_p}$ over 
$k_p$
$G_k$: the Galois group of the separable closure 
$\bar {k}$ over 
$k$
$N_k(G,X)$: the number of isomorphism classes of 
$G$ extensions over 
$k$ with 
$\operatorname {Disc}$ bounded by 
$X$
$f(x)\sim g(x)$: 
$\lim _{x\to \infty } ({f(x)}/{g(x)}) = 1$
$A\asymp B$: there exists absolute constants 
$C_1$ and 
$C_2$ such that 
$C_1 B\le A\le C_2 B$
2. Discriminant of compositum
Throughout this section we will fix the number field 
$k$ as the base field, and denote by 
$K/k$ and 
$L/k$ two extensions over 
$k$ such that 
$\tilde {K}\cap \tilde {L}= k$ with 
$m= [K:k]$ and 
$n = [L:k]$. Therefore the Galois groups can be given the permutation structure 
$\operatorname {Gal}(K/k)\subset S_m$ and 
$\operatorname {Gal}(L/k)\subset S_n$. Under the condition that 
$\tilde {K}\cap \tilde {L} = k$, we have 
$\operatorname {Gal}(KL/k) \simeq \operatorname {Gal}(K/k) \times \operatorname {Gal}(L/k) \subset S_{mn}$, where the isomorphism is a product of the restrictions to 
$K$ and 
$L$.
2.1 General bound
In this section, we will give a general upper bound on 
$\operatorname {Disc}(KL)$ in terms of 
$\operatorname {Disc}(K)$ and 
$\operatorname {Disc}(L)$ when 
$\tilde {K}$ and 
$\tilde {L}$ have trivial intersection. Notice that, given 
$\tilde {K}\cap \tilde {L} = k$, we have 
$[KL:k] = [K:k] [L:k]$. It suffices to prove the following theorem.
Theorem 2.1 Let 
$K/k$ and 
$L/k$ be extensions over 
$k$ with 
$[KL:k] = [K:k][L:k]$. Then 
$\operatorname {Disc}(KL) \le \operatorname {Disc}(K)^{n} \operatorname {Disc}(L)^{m}$, where 
$n = [L:k]$ and 
$m = [K: k]$.
Proof. If 
$k = \mathbb {Q}$, then the rings of integers 
$O_K$ and 
$O_L$ are free 
$\mathbb {Z}$-modules with rank 
$m$ and 
$n$, therefore we could find an integral basis 
$\{ e_i \mid 1\le i \le m \}$ and 
$\{ d_j\mid 1\le j\le n \}$ for 
$O_K$ and 
$O_L$. Then 
$\{ e_id_j \mid 1\le i\le m, 1\le j\le n \}$ will be an integral basis for 
$O_KO_L$ as a free 
$\mathbb {Z}$-module with rank 
$mn$. By using the definition of discriminant to be the determinant of trace form, we can compute and see that 
$\operatorname {Disc}(O_KO_L) = \operatorname {Disc}(K)^{n} \operatorname {Disc}(L)^{m}$. Since 
$O_KO_L\subset O_{KL}$, we get an upper bound for 
$\operatorname {Disc}(O_{KL})$. Over an arbitrary number field 
$k$, the ring of integers 
$O_K$ may not admit an integral basis (i.e. may not be a free 
$O_k$-module) but it is locally free. Therefore we could look at the discriminant ideal 
$\operatorname {disc}(K/k)$ at each place 
$p$ of 
$O_k$. Given a prime ideal 
$p$, let 
$S$ be the subset 
$O_k\backslash p$ of 
$O_k$ that is closed under multiplication. To understand the 
$p$-part of the relative discriminant, we have 
$\operatorname {disc}(S^{-1}O_K/S^{-1}O_k) = S^{-1}\operatorname {disc}(O_K/O_k)$ as an 
$S^{-1}O_k$-module; see, for example, [Reference NeukirchNeu99, Chapter III, Theorem 
$(2.9)$]. Now 
$S^{-1}O_k$ is a discrete valuation ring with the unique maximal ideal 
$S^{-1}p$, and 
$S^{-1}O_K$ is a finitely generated 
$S^{-1}O_k$-module, which therefore admits an integral basis. Similarly for 
$S^{-1}O_L$. Notice that by assumption 
$S^{-1}O_K$ intersects trivially with 
$S^{-1}O_L$, and again by working with the integral basis as before, but over 
$S^{-1}O_k$, we get that 
$S^{-1}\operatorname {disc}(O_KO_L/O_k) = \operatorname {disc}(S^{-1}O_K\cdot S^{-1}O_L) =\operatorname {disc}(S^{-1}O_K)^{n}\operatorname {disc}(S^{-1}O_L)^{m}$. And 
$S^{-1}\operatorname {disc}(K/k)$ as an ideal of 
$S^{-1}O_k$ has the same valuation at 
$S^{-1}p$ as the valuation of 
$\operatorname {disc}(K/k)$ at 
$p$. So the valuation of 
$\operatorname {disc}(O_{KL}/O_k)$ at 
$p$ is at most the valuation of 
$\operatorname {disc}(O_KO_L/O_k)$, which is the valuation of 
$\operatorname {disc}(O_K)^{n}\operatorname {disc}(O_L)^{m}$ for every 
$p$. By taking the absolute norm, we get the theorem.
2.2 Tamely ramified places
In this section we will give a precise description of 
$\operatorname {disc}_p(KL)$ in terms of 
$\operatorname {disc}_p(K)$ and 
$\operatorname {disc}_p(L)$ at a prime 
$p$ where both 
$K$ and 
$L$ are tamely ramified. We will always assume 
$\tilde {K}\cap \tilde {L} = k$. This enables us to compute explicitly 
$\operatorname {disc}_p(KL)$ when 
$KL/k$ is tamely ramified at 
$p$, thus determining 
$\operatorname {Disc}(KL/k)$ completely in this situation.
We recall some standard properties of tamely ramified extensions. Firstly, given a general field extension 
$M/k$ with degree 
$n$ that is tamely ramified at a prime 
$p$ in 
$k$, the inertia group at 
$p$ is always a cyclic group. Therefore the inertia group could be described by a generator. Notice that the inertia group at 
$p$ can only be defined up to conjugacy subgroups, so the generator can only be specified up to conjugacy classes. Secondly, the inertia group at 
$p$ for a tamely ramified extension 
$M/k$ completely determines 
$\operatorname {disc}_p(M/k)$. Suppose the inertia group at 
$p$ is the subgroup generated by 
$g_M$ (i.e. 
$I_p =\large \langle g_M\large \rangle$), then recall the definition of index 
$\operatorname {ind}(g): = n - \sharp \{ \text {orbits of }g\}$ of 
$g\in G\subset S_n$. We have that
\[ \operatorname{ind}(g_M) = n - \sharp\{ \text{orbits of }g_M\} = \sum (e_i-1) \,f_i \]
is exactly the exponent of 
$p$ in 
$\operatorname {disc}(M/k)$, or equivalently
\[ \operatorname{disc}_p(M/k) = p^{\operatorname{ind}(g_M)}. \]
Here by the number of orbits we mean the number of cycles of 
$g$ as a permutation element inside 
$S_n$. So we can determine 
$\operatorname {disc}_p(M/k)$ just by looking at the cycle structure of 
$g \in S_n$. For example, if the inertia group 
$I_p =\large \langle (12)(34)\large \rangle \subset S_4$ for a 
$S_4$ quartic extension 
$M/k$, then 
$\operatorname {Disc}_p(M/k) = p^{2}$ since 
$\operatorname {ind}((12)(34)) = 4-2 = 2$.
We are now ready to consider 
$\operatorname {disc}_p(KL)$. Recall that if 
$\tilde {K}\cap \tilde {L} = k$, then 
$\operatorname {Gal}(KL/k) \simeq \operatorname {Gal}(K/k) \times \operatorname {Gal}(L/k) \subset S_{mn}$. Suppose 
$\tilde {K}$ and 
$\tilde {L}$ are both tamely ramified at 
$p$ with inertia groups 
$I_K = \large \langle g_1\large \rangle \subset \operatorname {Gal}(K/k) \subset S_m$ for 
$K/k$ and 
$I_L = \large \langle g_2\large \rangle \subset \operatorname {Gal}(L/k) \subset S_n$ for 
$L/k$. Then 
$\widetilde {KL}/k$ is also tamely ramified since tamely ramified extensions are closed under taking compositum. Notice that for an arbitrary tower of extensions 
$L/K/F$ where every relative extension is Galois, the inertia group of the subfield is naturally the quotient of the inertia group, that is, 
$I_p(K/F) = I_p(L/F)\operatorname {Gal}(L/K)/\operatorname {Gal}(L/K)$. Therefore the inertia group at 
$p$ for 
$\widetilde {KL}/k$ is 
$I = \large \langle (g_1, g_2)\large \rangle \in \operatorname {Gal}(K/k) \times \operatorname {Gal}(L/k) \subset S_{mn}$.
Theorem 2.2 Given 
$K/k$ and 
$L/k$ with 
$\tilde {K}\cap \tilde {L}= k$, are both tamely ramified at 
$p$, let 
$e_K$ and 
$e_L$ be the ramification indices of 
$\tilde {K}$ and 
$\tilde {L}$ at 
$p$ with 
$(e_K, e_L) = 1$. Then denote a generator of an inertia group of 
$K$, 
$L$ and 
$KL$ at 
$p$ by 
$g_K$, 
$g_L$ and 
$g_{KL}$. We have
\[ \operatorname{ind}(g_{KL}) = \operatorname{ind}(g_K)\cdot n + \operatorname{ind}(g_L)\cdot m - \operatorname{ind}(g_K)\cdot \operatorname{ind}(g_L), \]
where 
$m = [K:k]$ and 
$n= [L:k]$.
Proof. Suppose 
$g_K\in \operatorname {Gal}(K/k) \subset S_m$ is a product of disjoint cycles 
$\prod _k c_k$. Then 
$e_K$ will be the least common multiple of 
$|c_k|$, the length of the cycle 
$c_k$, for all 
$k$. Similarly, suppose 
$g_L$ is a product of disjoint cycles 
$\prod _l d_l$. Now consider the image of 
$g_{KL} = (g_K,g_L)$ as embedded in 
$S_{mn}$; the permutation action is naturally defined to be mapping 
$a_{i,j}$ to 
$a_{g_K(i), g_K(j)}$ for 
$1\le i\le m$, 
$1\le j\le n$. If 
$(e_K,e_L) = 1$, then for any pair of cycles 
$c_k$ and 
$d_l$, we have 
$(|c_k|,|d_l|) = 1$ and therefore 
$(c_k,d_l)$ forms a single cycle of length 
$|c_k||d_l|$ in 
$S_{mn}$. So the number of orbits in 
$g_{KL}$ is the product of the number of orbits in 
$g_K$ and 
$g_L$. Therefore 
$\operatorname {ind}(g_{KL}) = mn - (m-\operatorname {ind}(g_K))(n-\operatorname {ind}(g_L)) = \operatorname {ind}(g_K)\cdot n + \operatorname {ind}(g_L)\cdot m - \operatorname {ind}(g_K)\cdot \operatorname {ind}(g_L)$.
This gives a nice description of 
$\operatorname {disc}_p(KL)$ in terms of 
$\operatorname {disc}_p(K)$ and 
$\operatorname {disc}_p(L)$ that only depends on the ramification indices 
$e_K$ and 
$e_L$, and is independent of the cycle structure of 
$g_K$ and 
$g_L$ when the ramification indices are relatively prime. In general, to compute 
$\operatorname {ind}(g_{KL})$ requires more knowledge on the cycle type of 
$g_K$ and 
$g_L$.
Theorem 2.3 Given 
$K/k$ and 
$L/k$ with 
$\tilde {K}\cap \tilde {L}= k$, are both tamely ramified at 
$p$, let the generator of an inertia group of 
$K$ at 
$p$ be 
$g_K = \prod _k c_k$, and the generator of an inertia group of 
$L$ at 
$p$ be 
$g_L =\prod _l d_l$. Then the generator 
$g_{KL}$ of an inertia group of 
$KL$ at 
$p$ satisfies
\[ \operatorname{ind}(g_{KL}) = mn - \sum_{k,l} \gcd(|c_k|, |d_l|), \]
where 
$m = [K:k]$ and 
$n= [L:k]$.
Proof. In general, the product of cycles 
$(c_k, d_l)$ in 
$S_{mn}$ is no longer a single orbit. Instead, it splits into 
$\gcd (|c_k|, |d_l|)$ many orbits. So by taking the summation over all pairs of cycles, we have 
$\operatorname {ind}(g_{KL}) = \sum _{k,l} (|c_k||d_l| - \gcd (|c_k|, |d_l|)) = mn - \sum _{k,l} \gcd (|c_k|, |d_l|)$.
2.3 Wildly ramified places
In this section we will give a general theorem that 
$\operatorname {disc}_p(KL)$ could be completely determined by the local étale algebras 
$(K)_p$ and 
$(L)_p$. This will hold for every prime 
$p$ in 
$k$. Although we do not give an explicit way to compute the number, it will be good enough for our application.
Theorem 2.4 Let 
$K/k$ and 
$L/k$ with 
$\tilde {K}\cap \tilde {L}= k$ be given. The local étale algebra of the compositum 
$(KL)_p$ at a prime 
$p$ could be determined by the local étale algebras 
$(K)_p$ and 
$(L)_p$. In particular, the relative discriminant ideal 
$\operatorname {disc}_p(KL)$ as an invariant of 
$(KL)_p$ could be determined by 
$(K)_p$ and 
$(L)_p$.
Proof. There is a bijection between degree 
$n$ étale extension over a field 
$F$ and continuous morphisms from 
$\operatorname {Gal}(\bar {F}/F)$ to 
$S_n$ up to conjugation inside 
$S_n$ (here 
$\bar {F}$ is the separable closure of 
$F$); see, for example, [Reference WoodWoo16, Proposition 6.1]. The property we use from the bijection is the explicit description of the bijective map; that is, when the étale extension is an actual field extension, the kernel of the defining map 
$G_{\mathbb {Q}} \to G$ fixes the field extensions. Therefore we can find the maps
\[ \rho_{K,p}: G_{k_p} \to S_n, \quad \rho_{L,p}: G_{k_p}\to S_m, \]
that correspond to 
$(K)_p$ and 
$(L)_p$. Similarly, for 
$K$ and 
$L$, we get
\[ \rho_K: G_k\to S_n, \quad \rho_L : G_k \to S_m. \]
Moreover, the map 
$\rho _{K,p}$ could be taken as the composition of 
$G_{k_p}\hookrightarrow G_k$ and 
$\rho _K$.
Given 
$\tilde {K}\cap \tilde {L} = k$, we get a representative of the map corresponding to 
$KL$,
\[ \rho_K\times \rho_L: G_k\to S_n\times S_m\subset S_{mn}. \]
The local map corresponding to 
$(KL)_p$ is therefore the composition of 
$G_{k_p}\to G_k$ and 
$\rho _K\times \rho _L$, which is exactly 
$\rho _{K,p}\times \rho _{L,p}$ and is completely determined by 
$(K)_p$ and 
$(L)_p$. By finding a representative of maps 
$\rho _{KL, p}: G_{k_p} \to S_{mn}$ corresponding to 
$(KL)_p$, we completely determine the structure 
$(KL)_p$ from 
$(K)_p$ and 
$(L)_p$. If 
$(KL)_p = \oplus _{\mathfrak {p}|p} KL_{\mathfrak {p}}$ where 
$\mathfrak {p}$ are primes in 
$KL$ above 
$p$ and 
$KL_{\mathfrak {p}}$ are field extensions of 
$k_p$, then by definition the discriminant of the local étale algebra 
$\operatorname {disc}((KL)_p/k_p)= \prod _{\mathfrak {p}|p } \operatorname {disc}(KL_{\mathfrak {p}}/k_p) = \operatorname {disc}_p(KL/k)$, so 
$\operatorname {disc}_p(KL/k)$ is an invariant of 
$(KL)_p$.
2.4 Discriminant for $S_n\times A$
In this section we will apply the theorems developed in § 2.2 to compute explicitly 
$\operatorname {disc}_p(KL)$ for an 
$S_n$ (
$n= 3,4,5$) degree 
$n$ extension 
$K/k$ and an odd abelian 
$A$ extension 
$L$ with 
$\tilde {K}\cap \tilde {L} = k$ at tamely ramified 
$p$. Firstly, in order to demonstrate how Theorems 2.2 and 2.3 can be used to carry out such computations, we give an explicit computation for the example of 
$S_3\times C_{l^{k}}$ extensions with 
$l^{k}$ a prime power. Secondly, we will use this approach to prove Lemmas 2.5–2.7, which compute 
$\operatorname {disc}_p(KL)$ for all cases of 
$S_n\times A$ extensions with 
$n=3,4,5$ and 
$A$ an odd-order abelian group. The key results from this section that will be crucial for the proof of Theorem 1.1 are the statements of Lemmas 2.5–2.7, which essentially give lower bounds on 
$\operatorname {disc}_p(KL)$ in terms of 
$\operatorname {disc}_p(K)$ and 
$\operatorname {disc}_p(L)$. See the end of this section for more explanation on Lemmas 2.5–2.7.
Firstly, in order to demonstrate our approach to the computation of the discriminant, we consider the special example of 
$S_3\times A$ where 
$A = C_{l^{k}}$ is cyclic with odd prime power order 
$l^{k}$. Possible tame inertia generators in 
$S_3$ are 
$(12)$ and 
$(123)$. For 
$A\subset S_{|A|}$, possible generators are of the form 
$g = (123\cdots l^{k})$ or powers of 
$g$, that is, a product of 
$l^{r}$ cycles where each cycle has length 
$l^{k-r}$. So among all 
$g\in A$, the index 
$\operatorname {ind}(g)$ is minimal when 
$g$ is product of 
$l^{k-1}$ cycles of length 
$l$. Therefore we see that 
$\operatorname {ind}(A)= l^{k}-l^{k-1}$, and 
${|A|}/{\operatorname {ind}(A)} = {l}/({l-1})$.
If 
$l\ne 3$, then the ramification index 
$e_L$ for 
$L$ is always relatively prime to 
$2$ and 
$3$, so we can apply Theorem 2.2 to get Table 1. The first column is the conjugacy class of the inertia generator 
$g_K\in S_3$ of 
$K$ at 
$p$, and the second column is the index 
$\operatorname {ind}(g_L) = \text {val}_p(\operatorname {disc}(L/k))$ of the inertia generator 
$g_L\in A\subset S_{|A|}$ of 
$L$ at 
$p$. The last column is 
$\text {val}_p (\operatorname {disc}(KL/k))$ when 
$K$ and 
$L$ are specified to have property in previous columns at 
$p$.
Table 1. Table of 
$\operatorname {disc}_p(KL/k)$ for 
$S_3\times C_{l^{k}}$, 
$l\ne 3$.
If 
$l = 3$, we need to be more careful and apply Theorem 2.3 to get Table 2.
Table 2. Table of 
$\operatorname {disc}_p(KL/k)$ for 
$S_3\times C_{l^{k}}$, 
$l=3$.
If one of the generators 
$g_K$ and 
$g_L$ is the identity at 
$p$, then by Theorem 2.2 we get that 
$\operatorname {disc}_p(KL) = \operatorname {disc}_p(K)^{n}\operatorname {disc}_p(L)^{m}$.
We will now prove the general case of 
$S_n\times A$ with 
$n =3,4,5$ and 
$A$ an odd-order abelian group. The idea is to consider 
$A = \prod _l A_l$ as a direct product of Sylow subgroups 
$A_l$ over all prime numbers 
$l$. To simplify the notation, for 
$g \in S_n$ and 
$c\in A$, we will denote the index of 
$(g, c) \in S_n\times A \subset S_{n|A|}$ by 
$\operatorname {ind}(g, c)$.
Lemma 2.5 Let 
$A$ be an abelian group of odd order 
$m$ and 
$(12)$, 
$(123)$ be elements in 
$S_3$. Then for all 
$c\in A$, the index 
$\operatorname {ind}((12),c)/m > 2$ and 
$\operatorname {ind}((123),c)/m>1$.
Proof. One can compute that for any abelian group 
$A$, the quotient 
${|A|}/{\operatorname {ind}(A)}$ equals 
${p}/({p-1})$ where 
$p$ is the minimal prime divisor of 
$|A|$. This can be seen by combining the Sylow subgroups 
$A_l$ of 
$A$ inductively. Notice that if 
$p\ne 2$, then 
${p}/({p-1})<2$. Now by Theorem 2.2, we compute 
$\operatorname {ind}((12),c) = m+3\cdot \operatorname {ind}(c) - \operatorname {ind}(c) = m+2\cdot \operatorname {ind}(c)\ge m+ 2 \cdot \operatorname {ind}(A) > 2m$ since 
${|A|}/{\operatorname {ind}(A)}<2$.
For 
$\operatorname {ind}((123),c)$, if 
$3\nmid |A|$, then 
$\operatorname {ind}((123), c) = 2m + 3\cdot \operatorname {ind}(c)\!-\!2\cdot \operatorname {ind}(c) \!=\! 2m+\operatorname {ind}(c)\!>\!m$. If 
$3| |A|$, we separate the 
$3$-Sylow subgroup 
$A_3$ of 
$A$ to compute 
$\operatorname {ind}((123), c)$. Let 
$A = A_3\times A_{>3}$ where 
$A_3$ is the 
$3$-Sylow subgroup of 
$A$ and 
$A_{>3}:= \prod _{l>3} A_l$ is the direct product of all 
$l$-Sylow subgroups with 
$l>3$. Let 
$c = (c_3, c_{>3})$ be any element in 
$A$. We consider the element 
$((123), c) = ((123), c_3, c_{>3})\in S_3\times A_3\times A_{>3}$. We can compute 
$\operatorname {ind}((123),c)= \operatorname {ind}((123),(c_3,c_{>3})) = \operatorname {ind}(((123),c_3),c_{>3})$ where 
$((123),c_3)$ is an element in 
$S_3\times A_3 \subset S_{3|A_3|}$. Suppose 
$\operatorname {ind}((123),c_3) = i$. Then since 
$|S_3\times A_3|$ is relatively prime to 
$|A_{>3}|$, we could apply Theorem 2.2 first:
\begin{align} \operatorname{ind}((123), c_3, c_{>3}) &= i|A_{>3}|+ (3|A_3| - i)\cdot \operatorname{ind}(c_{>3}) \nonumber\\ &= i(|A_{>3}| - \operatorname{ind}(c_{>3})) + 3|A_3|\cdot \operatorname{ind}(c_{>3}). \end{align}
Therefore among all possible 
$c\in A$, the minimal value of 
$\operatorname {ind}((123),c)$ is obtained when both 
$i$ and 
$\operatorname {ind}(c_{>3})$ are as small as possible. The smallest possible 
$\operatorname {ind}(c_{>3})$ is 
$\operatorname {ind}(A_{>3})$ by definition. The smallest 
$i = \operatorname {ind}((123), c_3)$ is 
$\operatorname {ind}((123), e) = 2|A_3|$. Therefore, if 
$A = A_3$, then 
$2|A_3|/m = 2>1$. If 
$A_{>3}$ is non-trivial, then by (2.1), the index 
$\operatorname {ind}((123),c) \ge 2m+|A_3|\cdot \operatorname {ind}(A_{>3}) > m$.
Lemma 2.6 Let 
$A$ be an abelian group with 
$2,3\nmid |A|=m$ and let 
$(12)$, 
$(123)$, 
$(1234)$, 
$(12)(34)$ be elements in 
$S_4$. Then, for all 
$c\in A$, we have
\[ \operatorname{ind}((12), c)/m > 2, \quad \operatorname{ind}((12)(34), c)/m>1, \quad \operatorname{ind}((123), c)/m>3, \quad\operatorname{ind}((1234), c)/m>2. \]Proof. We can apply Theorem 2.2 since 
$2,3\nmid m$. Then 
$\operatorname {ind}((12), c) = m + 3\cdot \operatorname {ind}(c) \ge m+ 3\cdot \operatorname {ind}(A) > 2m$, 
$\operatorname {ind}((12)(34), c) = 2m+2\cdot \operatorname {ind}(c) > m$, 
$\operatorname {ind}((1234), c) = 3m+ \operatorname {ind}(c)>2m$, and 
$\operatorname {ind}((123),c) = 2m+2\cdot \operatorname {ind}(c) \ge 2m+ 2\cdot \operatorname {ind}(A) \ge 2m+ 2\cdot \frac {4}{5}m > 3m$.
Lemma 2.7 Let 
$A$ be an abelian group with 
$2,3, 5\nmid |A|=m$. Then for all 
$c\in A$ and 
$d\in S_5$, 
$\operatorname {ind}(d, c) /m\ge 1 + \operatorname {ind}(d)-1/7$.
Proof. We can apply Theorem 2.2 since 
$2,3\nmid m$. Then 
$\operatorname {ind}(d, c) = m\operatorname {ind}(d)+ 5\operatorname {ind}(c) - \operatorname {ind}(d)\operatorname {ind}(c)$ 
$=m\operatorname {ind}(d) + (5-\operatorname {ind}(d))\operatorname {ind}(c) = (m-\operatorname {ind}(c))\operatorname {ind}(d) + 5\operatorname {ind}(c)$. So for a certain 
$d$, the value is smallest when 
$\operatorname {ind}(c) = \operatorname {ind}(A)$. When 
$\operatorname {ind}(c) = \operatorname {ind}(A)$, we have 
$\operatorname {ind}(d,c)/m = \operatorname {ind}(d) + (5-\operatorname {ind}(d))({\operatorname {ind}(A)}/{m}) = \operatorname {ind}(d) + (5-\operatorname {ind}(d))(({p-1})/{p})$ where 
$p$ is the smallest divisor of 
$m$ and 
$p\ge 7$. So 
$\operatorname {ind}(d)/m - \operatorname {ind}(d) = (5-\operatorname {ind}(d))(({p-1})/{p})\ge (5 - 4) \frac {6}{7} = \frac {1}{7}$.
Remark 2.8 Lemmas 2.5–2.7 are one of the two sides of Lemma 5.1. We could compute 
$\operatorname {disc}_p(KL/k)$ precisely in terms of 
$\operatorname {disc}_p(K/k)$ and 
$\operatorname {disc}_p(L/k)$ for all tamely ramified 
$p$. What is enough for the proof of the main theorem is a good lower bound on 
$\operatorname {Disc}_p(KL)$. The other side of Lemma 5.1 will be how good uniformity estimates we can prove, which is measured by the number 
$r_d$ (see definition in the statement of Lemma 5.1). As long as the comparison between the two sides satisfies the inequality in Lemma 5.1, our main proof proceeds with no problem.
2.5 Malle's prediction for $S_n\times A$
In this section we compute the value of 
$a(G)$ and 
$b(k, G)$ for 
$S_n\times A$. A similar discussion on 
$a(G)$ when 
$G$ is a direct product of two groups in general can be found in [Reference MalleMal02]. We include the computation here for the convenience of the reader. Recall that, given a permutation group 
$G\subset S_n$, for each element 
$g\in G$, we have the index 
$\operatorname {ind}(g)= n - \sharp \{ \text {orbits of } g\}$. We define 
$a(G)$ to be the minimum value of 
$\operatorname {ind}(g)$ among all 
$g\neq e$. The absolute Galois group 
$G_k$ acts on the conjugacy classes of 
$G$ via its action on the character table of 
$G$. We define 
$b(k,G)$ to be the number of orbits under 
$G_k$ action within all conjugacy classes with minimal index.
Let 
$G_i\subset S_{n_i}$, for 
$i = 1,2$, be two permutation groups. Consider 
$G = G_1\times G_2\subset S_{n_1n_2}$. Suppose that 
$\operatorname {ind}(g_i) = \operatorname {ind}(G_i)$ gives the minimal index. Then for 
$G\subset S_{n_1n_2}$, the minimal index will come from either 
$g_1\times e$ or 
$e\times g_2$ since 
$\operatorname {ind}(g_1, e)\le \operatorname {ind}(g_1, g)$ for any 
$g\in G_2$ (and similarly the symmetric statement). One can compute 
$\operatorname {ind}(g_1\times e) = n_2\operatorname {ind}(g_1)$. Therefore 
$a(G) = \min \{ n_2\cdot a(G_1), n_1\cdot a(G_2)\} = n_1n_2\min \{ {a(G_1)}/{n_1}, {a(G_2)}/{n_2} \}$.
If 
${a(G_1)}/{n_1} < {a(G_2)}/{n_2}$, then 
$\{ g\times e \in G \mid \operatorname {ind}(g) = a(G_1)\}$ contains exactly the elements with minimal index in 
$G$. Irreducible representations of 
$G_1\times G_2$ are 
$\rho _1\otimes \rho _2$ where 
$\rho _i$ is one irreducible representation of 
$G_i$ with character 
$\chi _i$. The corresponding character for 
$\rho _1\otimes \rho _2$ is 
$\chi _1\cdot \chi _2$. Therefore the 
$G_k$ action on 
$g\times e$ has the same orbit as its action on 
$g$. So 
$b(k, G) = b(k, G_1)$.
Our case 
$S_n\times A \subset S_{n|A|}$ satisfies the above condition, therefore 
$a (S_n\times A) = nm\min\{ {1}/{n,} ({p-1})/{p}\} = m$ where 
$p$ is the smallest prime divisor of 
$|A| = m$ and 
$n=3, 4, 5$. And 
$b(k, S_n\times A) = b(k, S_n) = 1$.
3. Product lemma
This section answers the question: given two distributions 
$F_i$, for 
$i = 1, 2$, each describing the asymptotic distribution of some multi-set 
$S_i$ containing a sequence of positive real numbers (i.e. let 
$F_i(X) = \sharp \{ s\in S_i \mid s\le X\}$, say 
$F_i(X) \sim A_i X^{n_i}\ln ^{r_i} X$ where 
$n_i>0$ and 
$r_i\in \mathbb {Z}_{\ge 0}$), what is the product distribution 
$P(X) = \sharp \{ (s_1,s_2)\mid s_i\in S_i, s_1s_2\le X\}$?
We will split the discussion into two cases: if 
$n_1 = n_2$ we have Lemma 3.1, and if 
$n_1\neq n_2$ we apply Lemma 3.2. The magnitude of the main term for this question can be answered by the Tauberian theorem; see, for example, [Reference Montgomery and VaughanMV06, Reference NarkiewiczNar83]. By integration by parts we can deduce the analytic continuation for the generating series 
$f_i(s) = \sum _{\mu \in S_i} \mu ^{-s}$ from the distribution function 
$F_i(X)$, and then by applying the Tauberian theorem, we can deduce the product distribution from the analytic continuation of the generating series 
$f_1(s)\cdot \,f_2(s)$ for the product. This helps us to see the difference between the two cases: if 
$n_1 = n_2=n$, then 
$f_i(s)$ has the rightmost pole at 
$s = n$ with order 
$r_i+1$, therefore 
$f_1(s)\cdot \,f_2(s)$ has the rightmost pole still at 
$s = n$ but with order 
$r_1+r_2+2$; if 
$n_1\neq n_2$, say 
$n_1> n_2$, then 
$f_1(s)\cdot \,f_2(s)$ has the rightmost pole at 
$s= n_1$ with order 
$r_1+1$. In the following we include a proof for both cases via elementary methods mainly for two reasons: firstly, for self-consistency and convenience of the reader; and secondly, the exact statements in Lemma 3.2 are convenient for us to use since we determine an upper bound of the product distribution where the constant for the leading term is given explicitly in terms of the constants 
$A_i$, which is not obvious from applying the Tauberian theorem directly.
Lemma 3.1 Let 
$F_i(X) = \sharp \{ s\in S_i \mid s\le X\}$ be the asymptotic distribution of some multi-set 
$S_i$ containing a sequence of positive real numbers that are greater than or equal to 
$1$ for 
$i=1,2$. Let 
$F_i(X) \sim A_i X^{n_i}\ln ^{r_i} X$ be given, where 
$n_i>0$ and 
$r_i\in \mathbb {Z}_{\ge 0}$. If 
$n_1=n_2=n$, then
\[ P(X)\sim A_1A_2\frac{r_1 !r_2!}{(r_1+r_2+1)!}nX^{n}\ln^{r_1+r_2+1} X. \]Proof. We will prove this in two steps. We first explain why we can reduce to the case 
$n=1$. For general 
$n$, it suffices to consider the modified multi-sets 
$S'_i = \{ s^{n}\mid s\in S_i \}$. Then for the modified multi-sets 
$S'_i$ we have the distribution function 
$F'_i(X) = F_i(X^{1/n}) \sim ({A_i}/{ n^{r_i}}) X\ln ^{r_i} X$. If we determine the product distribution 
$P'(X)$ for 
$F'_i(X)$, then we get 
$P(X) = P'(X^{n})$ since 
$s_1^{n} s_2^{n}\le X^{n}$ if and only if 
$s_1 s_2\le X$.
Case 1: 
$F_1(X) = A_1 X\ln ^{r_1} X + o(X\ln ^{r_1}X)$, 
$F_2(X) = A_2 X\ln ^{r_2}X+ O(1)$. Define 
$a_{\mu }$ to be the number of copies of 
$\mu$ in 
$S_1$; then
\[ F_1(X) = \sum_{\mu\le X} a_{\mu}. \]
To simplify, we denote the main term of 
$F_i(X)$ by 
$M_i(X)$. Then
\begin{align} P(X) &= \sum_{s_1\in S_1} F_2\bigg(\frac{X}{s_1}\bigg) = \sum_{\mu\le X} a_{\mu} F_2 \bigg(\frac{X}{\mu}\bigg)\nonumber\\ &= \sum_{\mu\le X} a_{\mu} M_2\bigg(\frac{X}{\mu}\bigg) + \sum_{\mu\le X} a_{\mu} O(1). \end{align}The last term is easily shown to be small:
\begin{equation} \sum_{\mu\le X} a_{\mu} O(1) \le O\bigg( \sum_{\mu\le X} a_{\mu}\bigg) = O(X\ln^{r_1} X). \end{equation}
For 
$X>0$, define 
$\underline {X}$ to be the largest real number less than or equal to 
$X$ such that 
$a_{\underline {X}}>0$. Therefore 
$F_1(X) = F_1(\underline {X})$, so 
$M_1(X)- M_1(\underline {X}) = o(X\ln ^{r_1} X)$, therefore
\[ \lim_{X\to \infty} \frac{\underline{X}\ln^{r_1} \underline{X}}{ X\ln^{r_1} X} = 1, \]which implies that
\[ \lim_{X\to \infty} \frac{\underline{X}}{X} = 1. \]We now apply summation by parts to compute the first sum:
\begin{equation} \sum_{\mu\le X} a_{\mu} M_2\bigg(\frac{X}{\mu}\bigg) = F_1(\underline{X}) M_2(1) - \int_{1}^{\underline{X}} F_1(t)\frac{d}{d t} \bigg(M_2 \bigg(\frac{X}{t}\bigg)\bigg)\, d t. \end{equation}
If 
$r_2 = 0$, the boundary term 
$F_1(\underline {X}) M_2(1)$ is
\begin{equation} A_1A_2\underline{X}\ln^{r_1} \underline{X} + o(X\ln^{r_1} X), \end{equation}
otherwise it is 
$0$. In either case it will be less than the expected main term that we are going to show. The derivative in the integral is
\begin{align} \frac{d}{d t}\bigg(M_2\bigg(\frac{X}{t}\bigg)\bigg) & = -A_2 X \frac{1}{t^{2}} \bigg(\ln^{r_2}\frac{X}{t} + r_2 \ln^{r_2-1} \frac{X}{t}\bigg)\nonumber\\ & = X \bigg(\sum_{0\le i\le r_2} P_i(t) \ln^{i}X\bigg). \end{align}So the integral is
\begin{equation} \sum_{0\le i\le r_2} X\ln^{i}X \int_{1}^{\underline{X}} F_1(t)P_i(t) \, d t. \end{equation}
We will show that we can replace the 
$\underline {X}$ in (3.6) with 
$X$. Indeed, from the first equality in (3.5), it suffices to show the following integral is negligible:
\begin{equation} X \int_{\underline{X}}^{X} \frac{F_1(t)}{t}\cdot \ln^{r_2} \frac{X}{t}\cdot \frac{1}{t}\, d t \le X \frac{F_1(\underline{X})}{\underline{X}} \ln^{r_2} \frac{X}{\underline{X}} \int_{\underline{X}}^{X} \frac{1}{t}\, d t = o(X \ln^{r_1} X). \end{equation}
Similarly, we could plug in the second term in (3.5) and show it is also negligible. So from now on, we will consider (3.6) with 
$\underline {X}$ replaced with 
$X$.
It is standard in analysis that if 
$f$ and 
$g$ are positive and 
$\lim _{X\to \infty }\int _1^{X}f(t)g(t) \, d t= \infty$, then 
$\int _{1}^{X} o(\,f(t))g(t) \, d t = o(\int _{1}^{X} f(t)g(t)\, d t)$. Therefore we can replace 
$F_1(t)$ with 
$M_1(t)$ to estimate each integral in (3.6) up to a small error because 
$F_1(t) - M_1(t) = o(M_1(t))$. By an explicit computation that we do not include here, one can check that in (3.6), each integral of 
$M_1(t) P_i(t)$ together with 
$X\ln ^{i} X$ gives a precise main term in the order 
$X\ln ^{r_1+r_2+1} X$. So replacing 
$F_1(t)$ with 
$M_1(t)$ in (3.6) will only result in an error in the order of 
$o(X\ln X^{r_1+r_2+1})$ for each 
$i$. So we have shown that it suffices to compute the following integral 
$I$:
\begin{align} I & = \int_{1}^{X} M_1(t) \frac{d}{d t}\bigg(M_2\bigg(\frac{X}{t}\bigg)\bigg)\, d t \nonumber\\ & = -A_1A_2X\int_{1}^{X}\ln^{r_1} t \cdot \bigg(\ln^{r_2}\frac{X}{t} + r_2\ln ^{r_2-1} \frac{X}{t}\bigg) \frac{d t}{t}. \end{align}
Using the substitution 
$u = {\ln t}/{\ln X}$, we reduce the integral
\begin{equation} \int_{1}^{X}\ln^{r_1} t \cdot \ln^{r_2}\frac{X}{t}\frac{d t}{t} = \ln^{r_1+r_2+1} X\int_{0}^{1} u^{r_1}(1-u)^{r_2}\, d u \end{equation}
to the beta function [Reference Whittaker and WatsonWW96] 
$B(r_1+1,r_2+1)$, therefore
\begin{equation} -I =A_1A_2 B(r_1+1,r_2+1)X\ln^{r_1+r_2+1} X + o (X(\ln X)^{r_1+r_2+1}). \end{equation}This is of greater order than the boundary term (3.4), and hence completes the proof of the first case.
Case 2: 
$F_i(X) = A_i X \ln ^{r_i} X + o(X\ln ^{r_i}X)$. For any 
$\epsilon$, we can bound 
$F_i(X)$ by 
$A_iX\ln ^{r_i}X(1+\epsilon ) + O_{\epsilon }(1).$ By a similar argument to Case 
$1$, we can give a upper bound on 
$P(X)$ as
\[ \limsup_{X\to \infty} \frac{P(X)}{X\ln^{r_1+r_2+1}X} \le (1+\epsilon)A_1A_2 B(r_1+1,r_2+1). \]
Notice that by plugging in an upper bound 
$\tilde {F}_2(X)$ of 
$F_2(X)$ with a precise main term 
$\tilde {M}_2(X)$ in (3.1) and (3.3), we could also give an upper bound for 
$P(X)$. All other computations then remain the same after (3.3). Here our upper bound is 
$A_2X\ln ^{r_i}X(1+\epsilon ) + O_{\epsilon }(1)$ with 
$M_2(X)= A_2(1+\epsilon )X\ln ^{r_i}X$, and 
$O_{\epsilon }(1)$ is an absolute constant depending on 
$\epsilon$. We get an upper bound for each 
$\epsilon$, and then take the limit as 
$\epsilon \to 0$. We can give a lower bound in exactly the same way:
\[ \liminf_{X\to \infty} \frac{P(X)}{X\ln^{r_1+r_2+1}X} \ge (1-\epsilon)A_1A_2B(r_1+1,r_2+1). \]
So the limit exists and has to be 
$A_1A_2B(r_1+1,r_2+1)$. In the case where some 
$A_i = 0$, we only need the upper bound to show the limit is 
$0$.
Lemma 3.2 Let 
$F_i(X) = \sharp \{ s\in S_i \mid s\le X\}$ be the asymptotic distribution of some multi-set 
$S_i$ containing a sequence of positive real numbers that are greater than or equal to 
$1$ for 
$i=1,2$. Let 
$F_i(X) \sim A_i X^{n_i}\ln ^{r_i} X$ be given, where 
$n_i>0$ and 
$r_i\in \mathbb {Z}_{\ge 0}$. If 
$n_1>n_2$, then there exists a constant 
$C$ such that
\[ P(X)\sim C X^{n_1}\ln^{r_1} X. \]
Furthermore, if 
$F_i(X) \le A_i X^{n_i}\ln ^{r_i} X$, then we have
\[ P(X)\le A_1A_2 r_2! \frac{1}{(n_1-n_2)^{r_2+1}}n_1X^{n_1} \ln^{r_1} X. \]Proof. For similar reasons as in the proof of Lemma 3.1, we could reduce to the case 
$n_1 =1>n_2$. Given general 
$n_1>n_2$, it suffices to consider the modified multi-sets 
$S'_i = \{ s^{n_1}\mid s\in S_i \}$. Then for the modified multi-sets 
$S'_i$ we have the distribution functions 
$F'_1(X) = F_1(X^{1/n_1}) \sim ({A_1}/{ n_1^{r_1}}) X\ln ^{r_1} X$ and 
$F'_2(X) = F_2(X^{1/n_1}) \sim ({A_2}/{ n_1^{r_2}}) X^{n_2/n_1}\ln ^{r_2} X$ with 
$0 < n_2/n_1 < 1$. If we determine the product distribution 
$P'(X)$ for 
$F'_i(X)$, then we get 
$P(X) = P'(X^{n})$ since 
$s_1^{n} s_2^{n}\le X^{n}$ if and only if 
$s_1 s_2\le X$.
From now on we will assume 
$n_1 = 1>n_2>0$. We first prove the existence of 
$C$ in two steps.
Case 1: 
$F_1(X) = A_1 X\ln ^{r_1} X + O(1)$, 
$F_2(X) = A_2 X^{n_2}\ln ^{r_2}X+ o(X^{n_2}\ln ^{r_2}X)$. As in Lemma 3.1, we need to bound the sum
\begin{align} P(X)&= \sum_{\mu\lambda\le X} a_{\mu} b_{\lambda} = \sum_{\lambda\le X} b_{\lambda} F_1\bigg(\frac{X}{\lambda}\bigg)\nonumber\\ &= \sum_{\lambda\le X} b_{\lambda} A_1\cdot \frac{X}{\lambda} \cdot \ln^{r_1}\bigg(\frac{X}{\lambda}\bigg) + \sum_{\lambda\le X} b_{\lambda} O(1)\nonumber\\ &=A_1X\ln^{r_1} X \sum_{\lambda\le X} \frac{b_{\lambda}}{\lambda}\bigg(1-\frac{\ln \lambda}{\ln X}\bigg)^{r_1} + O(X^{n_2}\ln^{r_2} X). \end{align}It suffices to show that the sum
\[ C(X) = \sum_{\lambda\le X} \frac{b_{\lambda}}{\lambda} \bigg(1-\frac{\ln \lambda}{\ln X}\bigg)^{r_1} \]
converges to a constant 
$C'$ (i.e. 
$C(X) = C' + o(1)$). Notice that 
$C(X)$ is monotonically increasing, so it suffices to show 
$C(X)$ is bounded above from some constant. For a given 
$X>0$, we will denote by 
$\underline {X}$ the largest real number less than or equal to 
$X$ such that 
$b_{\underline {X}}>0$. By summation by parts,
\begin{align} C(X) & \le \sum_{\lambda\le X} \frac{b_\lambda}{\lambda} = \frac{F_2(\underline{X})}{\underline{X}} + \int_1^{\underline{X}} F_2(t) t^{-2}\, d t \nonumber\\ & \le O(X^{n_2-1}) + \int_1^{X} (M t^{n_2}\ln^{r_2} t + M)t^{-2}\, d t \end{align}
is bounded by a constant. The first term is 
$o(1)$ since 
$1-n_2 > 0$. For the second term, we can always find 
$M$ such that 
$F_2(t) \le Mt^{n_2}\ln ^{r_2}t + M$, where the constant term 
$M$ is a technical modification for 
$t=1$ when 
$r_2>0$. One can compute the integral to see that it is bounded by a constant. Therefore, we have proved that 
$C(X) = C' + o(1)$ and
\begin{equation} P(X) \sim A_1C'X \ln^{r_1} X. \end{equation} Case 2: 
$F_1(X) = A_i X\ln ^{r_1} X + o(X\ln ^{r_1}X)$, 
$F_2(X) = A_2 X^{n_2}\ln ^{r_2} X + o(X^{n_2}\ln ^{r_2}X)$. Notice that 
$C(X)$ is purely dependent on 
$F_2(X)$ and 
$r_1$, therefore the limit 
$C'$ only depends on 
$F_2(X)$ and 
$r_1$. Therefore the coefficient of 
$P$ is linearly dependent on 
$A_1$ from (3.13).
Now to get the upper bound on 
$P(X)$ in this case, we can bound 
$F_1(X)\le A_1(1+\epsilon )X\ln ^{r_1} X + O_{\epsilon }(1)$ from the assumption and compute the upper bound
\[ \limsup_{X\to \infty} \frac{P(X)}{X\ln^{r_1}X} \le (1+\epsilon) A_1C', \]by reducing to Case 1. We can get the lower bound similarly. Therefore,
\[ \lim_{X\to \infty} \frac{P(X)}{X\ln^{r_1}X} = A_1C'. \]
Bound on 
$C$. We assume further that 
$F_i(X) \le M_i(X) = A_i X^{n_i}\ln ^{r_i} X$ for all 
$X\ge 1$. We want to show the constant 
$C$ can be bounded by 
$O(A_1A_2)$. We can still assume 
$n_1 = 1$ without loss of generality. By summation by parts,
\begin{align} P(X) & \le \sum_{\mu\le X} a_{\mu} M_2\bigg(\frac{X}{\mu}\bigg)\nonumber\\ & \le F_1(X) M_2(1) - \int_{1}^{X} M_1(t) \frac{d}{d t}\bigg(M_2\bigg(\frac{X}{t}\bigg)\bigg)\, d t. \end{align}
Here notice that in order to get the second inequality, we do not need to worry about taking 
$\underline {X}$ in 
$S_1$ because (3.5) is negative. If 
$r_2 = 0$, the boundary term 
$F_1(X) M_2(1)$ is bounded by
\[ A_1A_2X \ln^{r_1} X, \]
otherwise it is 
$0$. Next, we consider the integral
\begin{align} -I & = -\int_{1}^{ X} M_1(t) \frac{d}{d t}\bigg(M_2\bigg(\frac{X}{t}\bigg)\bigg)\, d t \nonumber\\ & = A_1A_2X^{n_2} \int_{1}^{X}t^{1- n_2 }\ln^{r_1} t \cdot \bigg(n_2\ln^{r_2}\frac{X}{t} + r_2\ln ^{r_2-1} \frac{X}{t}\bigg) \frac{d t}{t}. \end{align}This integral is a sum of multiple pieces of the form
\[ I_{n,r_1,r_2} = \int_{1}^{X} t^{n}\ln^{r_1}t \ln^{r_2} \frac{X}{t} \frac{d t}{t}. \]
Via integration by parts (first integrate against 
$t^{n} ({dt}/{t})$), it satisfies an induction formula
\begin{equation} I_{n,r_1,r_2} = -\frac{r_1}{n} I_{n, r_1-1,r_2} + \frac{r_2}{n} I_{n,r_1, r_2 -1}, \end{equation}with initial data
\begin{equation} I_{n, r_1, 0} \le \frac{1}{n} X^{n} \ln^{r_1} X, \quad I_{n, 0, r_2} \le \frac{r_2!}{n^{r_2+1}} X^{n}. \end{equation}
Notice that 
$I_{n,r_1,r_2}$ is always positive; by the induction formula one can show
\begin{equation} I_{n,r_1,r_2} \le \frac{r_2!}{n^{r_2+1}} X^{n} \ln^{r_1}X. \end{equation}
If 
$r_2 = 0$, then by (3.17), we get 
$-I$ together with the boundary term 
$F_1(X) M_2(1)$ bounded,
\begin{equation} P(X) \le A_1A_2 \frac{1}{1- n_2} X\ln^{r_1} X. \end{equation}
When both 
$r_i \ne 0$, we have
\begin{equation} P(X) \le A_1A_2r_2! \frac{1}{(1-n_2)^{r_2+1}}X \ln^{r_1} X. \end{equation}
This formula is compatible with the special case where 
$r_2=0$.
Now combining with Theorem 2.1, we obtain the following corollary.
Corollary 3.3 Let 
$k$ be an arbitrary number field, and 
$G_1\subset S_n$ and 
$G_2\subset S_m$ be two Galois groups with no isomorphic non-trivial quotients. Suppose Malle's conjecture holds for both groups. Then there is a lower bound on 
$N_k(G_1\times G_2\subset S_{mn},X)$,
\[ N_k(G_1\times G_2\subset S_{mn},X) \ge CX^{a}\ln^{r} X + o(X^{a}\ln^{r} X), \]
where 
$a = \max \{ a(G_1)/m, a(G_2)/n\}$. If 
$a(G_1)/m= a(G_2)/n$, then 
$r = b(G_1, k)+ b(G_2,k)-1$; if 
$a(G_1)/m > a(G_2)/n$, then 
$r = b(G_1,k) -1$.
For the same value 
$a$, a lower bound 
$X^{a}$ is also obtained in [Reference MalleMal02, Proposition 4.2]. Here we improve on this general lower bound by adding a 
$\ln ^{r} X$ factor with a possibly positive 
$r$ that we describe explicitly.
4. Uniformity estimate for $S_n$ and $A$ number fields
In this section we will include and prove some necessary uniformity results we need for 
$S_3$ cubic, 
$S_4$ quartic, 
$S_5$ quintic and abelian number fields over arbitrary global field 
$k$. We will first treat the cases of 
$S_3$ cubic extensions and 
$S_4$ quartic extensions, since both cases take advantage of class field theory in a very similar fashion. Then we will treat 
$S_5$ quintic fields by applying an adaptation of Bhargava's geometric sieve. Finally, we will apply class field theory to deduce a perfect local uniformity result for all abelian extensions.
4.1 Local uniformity for $S_n$ extensions for $n = 3, 4$
We will include the uniformity estimates for 
$S_3$ and 
$S_4$ extensions with certain ramification behavior at finitely many places. Both results are deduced from class field theory after relating degree 
$n$ extensions with a certain ramification type to certain ray class fields.
We will say that a 
$S_3$ cubic extension 
$K/k$ is totally ramified at 
$q$ for a square-free ideal 
$q$ of 
$k$ if 
$K$ is totally ramified at every prime divisor of 
$q$. We have the following theorem.
Theorem 4.1 [Reference Datskovsky and WrightDW88, Proposition 6.2]
The number of non-cyclic cubic extensions over 
$k$ which are totally ramified at a product of finite places 
$q = \prod {p_i}$ is
\[ N_q(S_3,X) = O_{\epsilon}\bigg(\frac{X}{|q|^{2-\epsilon}}\bigg), \]
for any number field 
$k$ and any square-free integral ideal 
$q$. The implied constant is independent of 
$q$, and only depends on 
$k$ and 
$\epsilon$.
For discussions about 
$S_4$ quartic extensions, we will follow the definition in [Reference BhargavaBha05]. Given an 
$S_4$ quartic extension 
$K/k$, a prime ideal 
$p$ of 
$k$ is overramified in 
$K/k$: (1) if 
$p$ factors into 
$\mathfrak {P}^{4}$, 
$\mathfrak {P}^{2}$ or 
$\mathfrak {P}_1^{2}\mathfrak {P}_2^{2}$ for a finite place 
$p$; (2) if 
$p$ factors into a product of two ramified places for infinite place 
$p$. Equivalently, this means the inertia group at 
$p$ contains 
$\large \langle (12)(34) \large \rangle$ or 
$\large \langle (1234) \large \rangle$ up to conjugacy. We will say that 
$K/k$ is overramified at a square-free ideal 
$q$ if 
$K/k$ is overramified at all prime divisors of 
$q$. The uniformity estimate for overramified 
$S_4$ extensions over 
$\mathbb {Q}$ is given in [Reference BhargavaBha05, Proposition 23]. And we will prove the same uniformity over an arbitrary number field 
$k$, following the method in [Reference BhargavaBha05]. We will first state a lemma that is the analogue over 
$\mathbb {Q}$; for its analogue, see [Reference BhargavaBha05].
We fix the notation for this section. For every Galois 
$S_4$ extension 
$K_{24}/k$, we denote by 
$K_6$, 
$K_4$ and 
$K_3$ the subfields fixed by the subgroup 
$E = \{e, (12), (34), (12)(34)\}$, 
$F = \large \langle (12), (123)\large \rangle$ and 
$H=\large \langle E, (1324)\large \rangle$ respectively. Thus 
$[K_6:k] = 6$, 
$[K_4:k] = 4$ and 
$[K_3:k] = 3$, and 
$K_3\subset K_6$ and the Galois closure 
$\widetilde {K_4}/k= \widetilde {K_6}/k = K_{24}$.
Lemma 4.2 Given an arbitrary number field 
$k$ and 
$K_{24}/k$ a Galois 
$S_4$ extension over 
$k$, we have, for arbitrary 
$p\nmid 6$,
\[ {\rm val}_p(\operatorname{Nm}_{K_3/k}(\operatorname{disc}(K_6/K_3))) \equiv 0 \mod 2. \]Proof. Notice that
\[ \operatorname{Nm}_{K_3/k}(\operatorname{disc}(K_6/K_3)) =\operatorname{disc}(K_6/k)/\operatorname{disc}(K_3/k)^{2}, \]
therefore it suffices to show 
$\operatorname {Disc}(K_6)$ has even valuation at 
$p$. If 
$p\nmid 2, 3$, then it is always tamely ramified. In order to compute 
$\operatorname {disc}(K_6/k)$, we can compute the action of 
$G$ on 
$E$-cosets inside 
$G$, which gives the permutation structure of 
$S_4 \subset S_6$. Explicitly, in this permutation representation, we have cycle type 
$(1234)$ mapped to cycle type 
$(1235)(46)$, 
$(123)$ to 
$(124)(356)$, 
$(23)$ to 
$(14)(36)(2)(5)$, and 
$(13)(24)$ to 
$(13)(25)(4)(6)$. The valuation at 
$p$ will be 
$6-\sharp \{ \text {orbits of } g \}$ where 
$g\in S_4$ is one generator of one inertia group at 
$p$. So by the computation above of all possible cycle structures of 
$g\in S_4\subset S_6$, we can see the number of orbits can only be 
$2$ or 
$4$, which proves our claim that the valuation is always even at 
$p$. Moreover, we could also compute the valuation of 
$\operatorname {disc}(K_3/k)$ at such 
$p$. If one inertia group at 
$p$ is 
$\large \langle (12)(34) \large \rangle$ or 
$\large \langle (1324) \large \rangle$ up to conjugacy (i.e. the prime 
$p$ is overramified in 
$K_4/k$), then the valuation of 
$\operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3))$ at 
$p$ is 
$2$, and if one inertia group is 
$\large \langle (123) \large \rangle$ or 
$\large \langle e \large \rangle$ up to conjugacy, then the valuation is 
$0$ at 
$p$.
Theorem 4.3 The number of 
$S_4$ quartic extensions over 
$k$ which are overramified at a product of finite places 
$q = \prod {p_i}$ is
\[ N_q(S_4,X) = O_{\epsilon}\bigg(\frac{X}{|q|^{2-\epsilon}}\bigg), \]
for any number field 
$k$ and any square-free integral ideal 
$q$. The implied constant is independent of 
$q$, and only depends on 
$k$ and 
$\epsilon$.
Proof. We apply the class field theory argument in [Reference BhargavaBha05]. As proved in [Reference Bhargava, Shankar and WangBSW15], we have that the mean two-class number of non-cyclic cubic extensions over any number field 
$k$ is bounded, that is,
\[ \sum_{K \in \mathcal{F}(X) } h_2(K/k) = O(X), \]
where 
$\mathcal {F}(X) := \{ K/k\mid \operatorname {Gal}(K/k)= S_3, \operatorname {Disc}(K/k) < X \}$. This statement essentially follows from 
$N_k(S_4, X) = O(X)$.
We will first prove this theorem for a square-free ideal 
$q$ that is relatively prime to any prime ideal above 
$2$ and 
$3$. From the above discussion on the relation between the valuation of 
$\operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3))$ at 
$p$ and the 
$S_4$ quartic extensions being overramified at 
$p$, we can see that every 
$S_4$ quartic extension 
$K_4/k$ that are overramified at 
$q$ could be generated as a subfield of 
$K_{24}$ where: (1) there exists a non-cyclic cubic extension 
$K_3$ where 
$K_6/K_3$ is a quadratic extension over 
$K_3$ and 
$\widetilde {K_6}/k = K_{24}$; (2) the relative discriminant 
$\operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3))$ is a square (away from 
$2, 3$) with 
$q^{2}| \operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3))$. We will write 
$\operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3))_S$ to denote the product 
$\prod _{p\nmid 6} p^{\text {val}_p(\operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3)))}$ over all primes 
$p$ of 
$k$ that are relatively prime to 
$2$ and 
$3$. Given a fixed 
$K_3$ and an ideal 
$n$ of 
$k$, denote the number of quadratic extensions 
$K_6$ with 
$\operatorname {Nm}_{K_3/k}(\operatorname {disc}(K_6/K_3))_S = n^{2}$ by 
$g(K_3, n)$. By class field theory, at each 
$p| n$, the number of homomorphisms from 
$\prod _{\mathfrak {p}|p} (O_{K_3})^{*}_{\mathfrak {p}}$ to 
$\mathbb {Z}/2\mathbb {Z}$ with relative discriminant 
$p^{2}$ is bounded by 
$3$, therefore it follows from class field theory that 
$g(K_3, n)$ is bounded by
\[ g(K_3, n)\le \kappa h_2(K_3/k) 3^{\omega(n)}, \]
where 
$\kappa$ is some absolute constant only depending on 
$k$ and not depending on 
$K_3$ (see [Reference BhargavaBha10] for similar results over 
$\mathbb {Q}$). For such quadratic extensions 
$K_6/K_3$, the quartic field 
$K_4$ inside 
$\widetilde {K_6}/k$ satisfies that 
$\operatorname {disc}(K_3/k)n^{2} | \operatorname {disc}(K_4/k)$. Therefore for each fixed 
$K_3$, in order to bound the number of quartic fields 
$K_4/k$ that are overramified at 
$q$ and with 
$K_3$ a subfield of 
$\widetilde {K_4}/k$, it suffices to add up 
$g(K_3, n)$ over all 
$n$ with 
$q|n$ and 
$\operatorname {Disc}(K_3/k) \operatorname {Nm}_{k/\mathbb {Q}}(n)^{2}\le X$. We will write 
$|n|$ for 
$\operatorname {Nm}_{k/\mathbb {Q}}(n)$. Now denote
\[ S(q, X):=\{ n\subset O_k \mid n \text{ square-free}, q|n , |n|^{2}\le X \}. \]
Then the number of 
$S_4$ quartic extensions 
$K_4/k$ with 
$q^{2} | \operatorname {disc}(K_4/k)$ and 
$\operatorname {Disc}(K_4/k) < X$ is bounded by
\begin{align} N_q(S_4,X) &= \sum_{K_3/k} \sum_{n \in S(q, X/\operatorname{Disc}(K_3/k))} \kappa h_2(K_3/k)3^{\omega(n)}\nonumber\\ &\le \kappa\sum_{K_3/k} 3^{\omega(q)} \sum_{m\in S(1, X/\operatorname{Disc}(K_3/k)|q|^{2})} \kappa h_2(K_3/k) 3^{\omega(m)}\nonumber\\ &\le \kappa 3^{\omega(q)} \sum_{m\in S(1, X/|q|^{2})} 3^{\omega(m)} \sum_{K_3\in \mathcal{F}(X/|m|^{2}|q|^{2})} \kappa h_2(K_3/k)\nonumber\\ &\le \kappa 3^{\omega(q)} \sum_{m\in S(1, X/|q|^{2})} 3^{\omega(m)} O(X/|m|^{2}|q|^{2})\nonumber\\ &\le O_{\epsilon}\bigg(\frac{X}{|q|^{2-\epsilon}}\bigg) \sum_{m} \frac{1}{|m|^{2-\epsilon}} = O_{\epsilon}\bigg(\frac{X}{|q|^{2-\epsilon}}\bigg). \end{align}
This finishes the proof for 
$q$ relatively prime to 
$2$ and 
$3$. For general square-free ideal 
$q$ of 
$k$, we can write 
$q = q_1q_2$ where 
$q_1 = \prod _{p|6} p^{\text {val}_p(q)}$. Therefore
\begin{equation} N_q(S_4, X) \le N_{q_2} (S_4, X) = O_{\epsilon} \bigg(\frac{X}{|q_2|^{2-\epsilon}}\bigg) \le \bigg(\prod_{p|6} |p|^{2}\bigg) O_{\epsilon}\bigg( \frac{X}{|q|^{2-\epsilon}}\bigg). \end{equation}4.2 Local uniformity for $S_n$ extensions for $n=5$
In this section we will prove the uniformity of 
$S_5$ quintic extensions by geometry of numbers based on previous works [Reference BhargavaBha10, Reference BhargavaBha14, Reference Bhargava, Shankar and WangBSW15]. The goal is to prove Theorem 1.3.
We will use slightly different notation just for this section. Let 
$K$ be an arbitrary number field that will be our base field through out this section with degree 
$d = \deg (K)$. (Warning: the base field is denoted by 
$k$ in every other section, but exactly in this subsection we save 
$k$ for codimension to follow the notation in [Reference BhargavaBha14].) Let 
$Y$ be a closed subscheme in 
$\mathbb {A}^{n}_{O_K}$. Given a prime 
$p$ of 
$K$, we will say that an 
$S_5$ quintic extension 
$L/K$ is totally ramified at 
$p$ if 
$p = \mathfrak {P}^{5}$ in 
$L$. Given a square-free ideal 
$q$ of 
$K$, we will say that an 
$S_5$ quintic extension 
$L/K$ is totally ramified at 
$q$ if 
$L/K$ is totally ramified at all prime divisors of 
$q$.
The proof is an adaptation of Bhargava's geometric sieve method [Reference BhargavaBha14]. By [Reference BhargavaBha14], in the prehomogeneous space, those lattice points that parametrize orders with certain ramification type at a finite place 
$p$ correspond to 
$O_K/pO_K$-points of 
$Y$, where 
$Y$ is a certain closed subscheme cut out by partial derivatives of the discriminant polynomial. The key theorem is [Reference BhargavaBha14, Theorem 3.3]. Here for our application, instead of considering lattice points that, after mod 
$p$, lie in 
$Y(O_K/pO_K)$ for some prime 
$p>M$, we need to count the number of points that lie in 
$Y(O_K/pO_K)$ for finitely many specified primes 
$\{ p_i \}$. So the first step of the proof is to prove an upper bound on counting lattice points lying in 
$Y(O_K/qO_K)$ with 
$q = \prod p_i$ and within bounded compact region; see Theorems 4.4–4.6.
The second step of the proof is to count the number of lattice points in the fundamental domain of the prehomogeneous space (the parametrization space for quintic orders) that lie in 
$Y(O_K/qO_K)$. In order to get a power-saving error for our estimate, which is crucial for our application, we apply the averaging technique, introduced in [Reference BhargavaBha05] and applied in [Reference BhargavaBha10, Reference Belabas, Bhargava and PomeranceBBP10, Reference Bhargava, Shankar and TsimermanBST13, Reference Shankar and TsimermanST14], as suggested in [Reference BhargavaBha14, Remark 4.2]. In order to apply the averaging technique, we will need to solve the question in the first step with a compact region of the form 
$mrB$ where 
$B\subset {\mathbb {R}^{n}}$ is a fixed compact region, the factor 
$m$ is a unipotent matrix in 
${\rm GL} _n(\mathbb {R})$, and 
$r = (r_1, \ldots , r_n)$ is a tuple of scaling factors with possibly different scaling factors in different directions. Here 
$n=40$ is the dimension of the parametrization space for quintic orders. Finally, the proof of Theorem 1.3 carefully carries out the full computation inside the parametrization space. All theorems and conclusions in this section are also proved over arbitrary number fields.
Theorem 4.4 Let 
$B$ be a compact region in 
$\mathbb {R}^{n}$ having finite measure. Let 
$Y_i$, for 
$1\le i\le N$, be any closed subschemes of 
$\mathbb {A}^{n}_{\mathbb {Z}}$ of codimension 
$k_i$, say 
$k= \max \{k_i \mid 1\le i\le N\}$. Let 
$q= \prod _{i=1}^{N} p_i$ be a square-free integer. Then we have
\begin{align} &\sharp \{ a\in rB\cap \mathbb{Z}^{n} \mid \forall 1\le i\le N, a(\mathrm{mod }\,p_i) \in Y_i(\mathbb{Z}/p_i\mathbb{Z}) \} \nonumber\\ &\quad = O( r^{n-k} ) \cdot C^{\sum k_i} \cdot \max \bigg\{ 1, \ldots, \frac{r^{s}}{\prod_{i, s-k+k_i \ge 0} p_i^{s-k+k_i}} \ldots, \frac{r^{k}}{\prod_i p_i^{k_i}} \bigg\}, \end{align}
where the maximum is taken among 
$0\le s\le k$. The implied constant depends only on 
$B$ and 
$Y_i$, and 
$C$ only depends on the maximal degree of 
$Y_i$ and 
$k$. In particular, by letting 
$Y_i = Y$ with codimension 
$k$, and 
$q = \prod _i p_i$, we get
\begin{equation} \sharp \{ a\in rB\cap \mathbb{Z}^{n} \mid a(\mathrm{mod }\,q) \in Y(\mathbb{Z}/q\mathbb{Z})\} = O( r^{n-k} ) \cdot C^{k\omega(q)} \cdot \max \bigg\{ 1, \bigg(\frac{r}{q}\bigg)^{k} \bigg\}, \end{equation}
where the implied constant depends only on 
$B$ and 
$Y$, and 
$C$ only depends on 
$Y$ and 
$k$.
Proof. Although (4.4) is our main goal for later application, to prove it in a convenient way we will use induction on 
$n$ and 
$k_i$ to prove the more general formula (4.3). We will focus on proving (4.3). The case when 
$k =0$ is trivial since the number of lattice points in the box is 
$O(r^{n})$. For questions with general 
$n$, 
$k_i$ and 
$p_i$, let us write the key parameters of the form 
$[(n, k_1)_{p_1}, \ldots , (n, k_N)_{p_N}]$ to denote the corresponding counting question with these parameters.
The initial case is 
$[(1, k_1)_{p_1}, \ldots , (1, k_N)_{p_N}]$ where there exists 
$i$ with 
$k_i = 1$. For example, we look at the case 
$[(1, 1)_{p_1}, (1, 0)_{p_2}, \ldots , (1, 0)_{p_N}]$ with only 
$k_1 = 1$. Let us say 
$Y_1$ is cut out by the polynomial 
$f(x)$. Let 
$S = S(Y_1)$ (which only depends on 
$Y_1$) be the set of primes 
$p$ at which 
$f(x) \equiv 0$ is a 
$0$ polynomial mod 
$p$. If 
$p_1$ is away from 
$S(Y_1)$, then the number of solutions in 
$\mathbb {Z}/p_1\mathbb {Z}$ is bounded by 
$C$, therefore the number of lattice points is 
$O(C\cdot \max \{ 1, {r}/{p_1}\})$, where 
$C$ could be taken to be the degree of 
$f$ and the implied constant only depends on 
$f$ and 
$B$. If 
$p_1\in S$, then we can get an upper bound
\[ O(r) \le \bigg(\prod_{p\in S}p\bigg) \cdot O\bigg( \max \bigg\{ 1, \frac{r}{p_1}\bigg\}\bigg) \le O\bigg(C\cdot \max \bigg\{ 1, \frac{r}{p_1}\bigg\}\bigg), \]
where the final implied constant depends only on 
$B$ and 
$Y_1$. For the general case where 
$n=1$ and 
$k=1$, let us say that 
$Y_i$ is cut out by the polynomial 
$f^{(i)}(x)$. Similarly, for each 
$i$ with 
$k_i= 1$, we could get that the number of solutions in 
$\mathbb {Z}/p_1\mathbb {Z}$ is bounded by 
$C$, so by the Chinese remainder theorem, the number of solutions in 
$\mathbb {Z}/q\mathbb {Z}$ with 
$q = \prod _{i} p_i^{k_i}$ is bounded by 
$\prod _{i, k_i = 1} C_i \le C^{\sum _i k_i}$. So we can get an upper bound
\[ O(1) \cdot C^{\sum_i k_i}\cdot \max \bigg\{ 1, \frac{r}{\prod_{i} p_i^{k_i}}\bigg\}, \]
where the implied constant depends on 
$Y_i$ and 
$B$ and 
$C$ could be taken to be the maximum degree of 
$Y_i$ for all 
$i$.
Next we apply induction on 
$n$ and 
$k_i$ to solve the general case 
$[(n, k_1)_{p_1}, \ldots , (n, k_N)_{p_N}]$. We will use an observation in [Reference PoonenPoo03, Lemma 5.1] for the induction. Let 
$\pi : \mathbb {A}^{n}_{\mathbb {Z}} \to \mathbb {A}^{n-1}_{\mathbb {Z}}$ be the projection onto the first 
$n-1$ coordinates. Given a variety 
$Y$, for 
$i= 0, 1$, let 
$Z_i$ be the set of 
$z \in \mathbb {A}^{n-1}_{\mathbb {Z}}$ such that the fiber 
$Y_z : = Y \cap \pi ^{-1}(z)$ has codimension 
$i$ in 
$\pi ^{-1}(z)$. Then, by the dimension formula, the subset 
$Z_i$ has codimension at least 
$k-i$ in 
$\mathbb {A}^{n-1}_{\mathbb {Z}}$. More explicitly, as argued in [Reference BhargavaBha14, Lemma 3.1], if 
$Y$ has codimension 
$k$, then without loss of generality we could assume 
$Y$ is cut out by 
$f_j$ for 
$j = 1, \ldots , k$, and by elimination theory, we could assume 
$f_j = \,f_j(x_1, \ldots , x_{n-1})$ for 
$j\le k-1$ and 
$f_k(x_1, \ldots , x_n) = \sum _{i\le d} h_i(x_1, \ldots , x_{n-1}) x_n^{i}$ where 
$d$ is the degree of 
$f_k$ as a polynomial in 
$x_n$. The subset 
$Z_1\subset \mathbb {A}^{n-1}_{\mathbb {Z}}$ is contained in the closed subscheme 
$Z'_1$ cut out by 
$f_1, \ldots , \,f_{k-1}$ with codimension 
$k-1$ in 
$\mathbb {A}^{n-1}_{\mathbb {Z}}$. The subset 
$Z_0$ is the closed subscheme cut out by 
$f_1, \ldots , \,f_{k-1}, h_0, \ldots , h_d$ with codimension at least 
$k$ in 
$\mathbb {A}^{n-1}_{\mathbb {Z}}$. Therefore in order to give an upper bound, we can assume 
$Z_1$ and 
$Z_0$ are subschemes of 
$\mathbb {A}^{n-1}_{\mathbb {Z}}$.
For 
$Y_i$, where 
$1\le i \le N$, let 
$Z_{i,j}$ denote the corresponding projection of 
$Y_i$ with codimension 
$j$ under 
$\pi$. If 
$a = (x_1, \ldots , x_{n-1})$ satisfies 
$a\ (\mathrm {mod}\, p_i) \in Z_{i,j_i}$, then the number of such 
$a$ in 
$\mathbb {A}^{n-1}_{\mathbb {Z}}$ is bounded by the answer to 
$[(n-1, k_i-j_i)_{p_i}]_1^{N}$, which by induction, is bounded by
\[ O( r^{n-1-k'} ) \cdot C^{\sum_i k_i-j_i} \cdot \max \bigg\{ 1, \ldots, \frac{r^{s}}{\prod_{i, s-k'+k_i-j_i \ge 0} p_i^{s-k'+k_i-j_i}} \ldots, \frac{r^{k'}}{\prod_i p_i^{k_i-j_i}}\bigg\}, \]
where 
$k' = \max \{ k_i-j_i\mid 1\le i\le N \}$ and the implied constant only depends on the finitely many schemes 
$Z_{i,j}$, for 
$1\le i\le N$ and 
$j = 0,1$. Now for any such given 
$a$, the number of integral 
$x_n$ such that 
$(a, x_n)$ satisfies the original question is bounded by
\[ O(1) \cdot C^{\sum_i j_i} \cdot \max \bigg\{1, \frac{r}{\prod_{i} p_i^{j_i}}\bigg\} . \]
Notice here we do not use the induction, instead we count the lattice points directly from the Chinese remainder theorem and geometry of numbers, as we did in the case 
$n=1$. The constant only depends on the degree of 
$f_k$ as a polynomial in 
$x_n$, therefore could be made uniform for all such 
$a$. By taking the product of the two parts, the total number of 
$(x_1, \ldots , x_n)$ with 
$(x_1, \ldots , x_{n-1})$ lying in the class of 
$[(n-1, k_i-j_i)_{p_i}]_1^{N}$ is bounded by
\begin{align} &O( r^{n-1-k'} ) \cdot C^{\sum_i k_i} \cdot \max \bigg\{ 1, \ldots, \frac{r^{s}}{\prod_{i, s-k'+k_i-j_i \ge 0} p_i^{s-k'+k_i-j_i}} \ldots, \frac{r^{k'}}{\prod_i p_i^{k_i-j_i}}\bigg\} \cdot \max \bigg\{1, \frac{r}{\prod_{i} p_i^{j_i}}\bigg\} \nonumber\\ &\quad \le O( r^{n-k} ) \cdot C^{\sum_i k_i} \cdot \max \bigg\{ 1, \ldots, \frac{r^{s}}{\prod_{i, s-k+k_i \ge 0} p_i^{s-k+k_i}} \ldots, \frac{r^{k}}{\prod_i p_i^{k_i}} \bigg\}. \end{align}
One could check the inequality by means of computations. One convenient one is to separate the discussions when 
$k' = k-1$ or 
$k' = k$. This gives an upper bound for all classes 
$[(n-1, k_i-j_i)_{p_i}]_1^{N}$ under the projection. There are altogether 
$2^{\sum _{i, k_i>0} 1}$ possible cases, so the same bound, after multiplication by 
$2^{\sum _{i, k_i>0} 1}$, holds for the total counting by adding up over all cases. Since we need to multiply by 
$2^{\sum _{i, k_i>0} 1}$, we will need to take 
$2C$ instead of 
$C$. The induction stops after at most 
$k$ steps, so it suffices to take 
$2^{k}D$ where 
$D$ is the maximal degree of 
$Y_i$, among all 
$i$, for the constant 
$C$ in the theorem.
It is very important that for every step in induction, the dependence of the implied constant all comes from the finitely many schemes 
$Z_{i,j}$ under 
$\pi$ and 
$B$. Therefore after finitely many induction steps, we prove the main statement (4.3).
Notice that although [Reference BhargavaBha14, Theorem 3.3] focuses on counting lattice points where there exists 
$p> M$ such that the points lie in 
$Y(\mathbb {Z}/p\mathbb {Z})$, it also gives an upper bound for counting at a single prime 
$p$ by letting 
$M = p$. On the one hand, our statement includes the cases where residue conditions are specified at finitely many primes for finitely many schemes, instead of at a single prime for a single scheme. On the other hand, as suggested by Bhargava, we can get a slightly better error in the order of 
$r^{n-k}$ instead of 
$r^{n-k+1}$.
In order to apply the averaging technique, we also need to consider the number of lattice points in the box 
$mrB$ that is not necessarily expanding homogeneously in each direction. Here 
$m$ is a lower triangular unipotent transformation in 
${\rm GL} _n(\mathbb {R})$, 
$r = (r_1, \dots , r_n)$ is the scaling factors, and the estimate will depend on 
$r_i$. We will see in the proof that the introduction of 
$m$ here does not change the estimate much; however, it is crucial to deal with different 
$r_i$ in different directions.
Theorem 4.5 Let 
$B$ be a compact region in 
$\mathbb {R}^{n}$ having finite measure. Let 
$Y_t$, for 
$1\le t\le N$, be any closed subschemes of 
$\mathbb {A}^{n}_{\mathbb {Z}}$ of codimension 
$k_t$, say 
$k= \max \{k_t \mid 1\le t\le N\}$. Let 
$r = (r_1, \dots , r_n)$ be a diagonal matrix of positive real numbers where 
$r_i \ge \kappa$ for a certain absolute constant 
$\kappa >0$. Let 
$q= \prod _{t=1}^{N} p_t$ be a square-free integer, and 
$m$ be a lower triangular unipotent transformation in 
${\rm GL} _n(\mathbb {R})$. Then we have
\begin{align} &\sharp \{ a\in mrB\cap \mathbb{Z}^{n} \mid \forall 1\le t\le N, a(\mathrm{mod }\,p_t) \in Y_t(\mathbb{Z}/p_t\mathbb{Z}) \} \nonumber\\ &\quad = O\bigg(\prod_{i=1}^{n} r_i\bigg) \cdot C^{\sum_t k_t} \cdot \max \bigg\{\prod_{i= i_1}^{i_{k}}r_i^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k-s}}r_i^{-1}}{\prod_{t,s-k+k_t\ge 0} p_t^{s-k+k_t} }, \ldots, \frac{1}{\prod_t p_t^{k_t}} \bigg\},\end{align}
where the maximum is taken among 
$0\le s\le k$ and all possible choices 
$\{i_1,i_2, \ldots , i_{k-s} \} \subset \{ 1, 2, \ldots , N\}$ for each 
$s$.The implied constant depends only on 
$B$ and 
$Y_t$, and 
$C$ only depends on the maximal degree of 
$Y_t$ for all 
$t$ and 
$k$. In particular, by letting 
$Y_t= Y$ and 
$q = \prod _i p_i$, we get
\begin{align} &\sharp \{ a\in mrB\cap \mathbb{Z}^{n} \mid a(\mathrm{mod }\,q) \in Y(\mathbb{Z}/q\mathbb{Z})\} \nonumber\\ &\quad = O\bigg(\prod_{i=1}^{n} r_i\bigg) \cdot C^{k\omega(q)} \cdot \max\bigg\{ \prod_{i= i_1}^{i_{k}}r_i^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k-s}}r_i^{-1}}{ q^{s} }, \ldots, \frac{1}{q^{k}}\bigg\}, \end{align}
where the maximum is taken among 
$0\le s\le k$ and all possible choices 
$\{i_1,i_2, \ldots , i_{k-s} \} \subset \{ 1, 2, \ldots , N\}$ for each 
$s$. The implied constant depends only on 
$B$, 
$Y$ and 
$\kappa$, and 
$C$ only depends on the degree of 
$Y$ and 
$k$.
Proof. Similarly to the proof of Theorem 4.4, we prove the theorem by induction.
For case 
$k =0$, we can get the result 
$O(\prod _{i=1}^{n} r_i)$ directly because the total count of lattice points in 
$mrB$ only differs from those in 
$rB$ by lower dimension projections of 
$rB$, which is 
$O(\prod _{ i\in I} r_i)$ with 
$|I| < n$. Notice that we have assumed 
$r_i > \kappa$ where 
$\kappa$ is some absolute constant, so all lower dimension projections could be bounded by 
$O(\prod _{i=1}^{n} r_i)$ where the implied constant only depends on 
$\kappa$.
The initial case when 
$k=1$, 
$n= 1$ with type
$[(1,k_t)_{p_t}]_1^{N}$ is estimated to be
\[ O(1) \cdot \prod_{t, k_t = 1} C^{\sum_t k_t}\cdot \max \bigg\{ 1, \frac{r_1}{\prod_t p_t^{k_t}}\bigg\}. \]It is the same as in Theorem 4.4 since there is no non-trivial unipotent action.
For general 
$n$ and 
$k$, we will still consider the projection 
$\pi$ as introduced in Theorem 4.4. By induction, the number of points 
$a = (x_1, \ldots , x_{n-1})$ with 
$a\ (\mathrm {mod}\, p_t)$ lying in 
$Z_{t, j_t}(\mathbb {Z}/p_t\mathbb {Z})$ for all 
$t$ is bounded by
\[ O\bigg(\prod_{i=1}^{n-1} r_i\bigg) \cdot C^{\sum_t k_t-j_t} \cdot \max \bigg\{\prod_{i= i_1}^{i_{k'}}r_i^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k'-s}}r_i^{-1}}{ \prod_{t,s-k'+k_t-j_t\ge 0} p_t^{s-k'+k_t-j_t} }, \ldots, \frac{1}{\prod_t p_t^{k_t-j_t}} \bigg\}, \]
where 
$k' = \max \{ k_t-j_t\mid 1\le t\le N \}$ and the implied constant only depends on the finitely many schemes 
$Z_{t,j}$ for 
$1\le t\le N$ and 
$j = 0,1$, and 
$B$ and 
$\kappa$. Now for such a given 
$a = (x_1, \ldots , x_{n-1})$, the number of integrals 
$x_n$ such that 
$(x_1, \ldots , x_n)$ satisfies the original question is bounded by
\[ O(1)\cdot C^{\sum_t j_t} \cdot \max \bigg\{1, \frac{r_n}{\prod_{t} p_t^{j_t}} \bigg\}, \]
since the action of 
$m$ only translates the range of 
$x_n$, but keeps the length as big as 
$r_n$. Therefore the total number of 
$(x_1, \ldots , x_n)$ with 
$(x_1, \ldots , x_{n-1})$ lying in this class is bounded by
\begin{align} &O\bigg(\prod_{i=1}^{n-1} r_i\bigg) \cdot C^{\sum_t k_t} \cdot \max \bigg\{\prod_{i= i_1}^{i_{k'}}r_i^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k'-s}}r_i^{-1}}{\prod_{t,s-k'+k_t-j_t\ge 0} p_t^{s-k'+k_t-j_t} }, \ldots, \frac{1}{\prod_t p_t^{k_t-j_t}} \bigg\}\nonumber\\ &\qquad \cdot \max \bigg\{1, \frac{r_n}{\prod_t p_t^{j_t}}\bigg\}\nonumber\\ &\quad \le O\bigg(\prod_{i=1}^{n} r_i\bigg) \cdot C^{\sum_t k_t} \cdot \max \bigg\{\prod_{i= i_1}^{i_{k}}r_i^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k-s}}r_i^{-1}}{ \prod_{t,s-k+k_t\ge 0} p_t^{s-k+k_t} }, \ldots, \frac{1}{\prod_t p_t^{k_t}} \bigg\}, \end{align}
where the implied constant only depends on 
$Z_{t, j_t}$, 
$B$ and 
$\kappa$. We can similarly get the same bound for every class depending on 
$j_t$ for every 
$1\le t\le N$. So after finitely many induction steps, we prove the main theorem.
Proof Proof of Theorem 1.3 over 
$\mathbb {Q}$
We will first prove this statement over 
$\mathbb {Q}$ and then show that the computation over arbitrary number field 
$K$ should give the same answer. Recall that by the work of Bhargava [Reference BhargavaBha10], the set of quintic orders together with its sextic resolvent is parametrized by 
$G(\mathbb {Z})$-orbits in 
$V(\mathbb {Z})$ where 
$G = {\rm GL} _4\times {\rm GL} _5$ and 
$V$ is the space of quadruples of skew symmetric 
$5\times 5$ matrices. In order to give an upper bound on quintic fields, it suffices to give an upper bound on the set the of all quintic orders with sextic resolvent. Denote the fundamental domain of 
$G(\mathbb {R})/ G(\mathbb {Z})$ by 
$\mathcal {F}$, and 
$B$ is a compact region in 
$V(\mathbb {R})$. Let 
$S$ be any 
$G(\mathbb {Z})$-invariant subset of 
$V^{(i)}_{\mathbb {Z}}$ which specifies a certain property of quintic orders, denote by 
$S^{\mathrm {irr}}$ the subset of irreducible points in 
$S$, and denote by 
$N(S; X)$ the number of irreducible-
$G(\mathbb {Z})$ orbits in 
$S$ with discriminant less than 
$X$. Then by formula 
$(11)$ in [Reference BhargavaBha10], the averaging integral for a certain signature 
$i$ is in the following:Footnote 1
\begin{equation} N(S; X) = \frac{1}{M_i}\int_{g\in \mathcal{F}} \sharp \{x \in S^{\mathrm{irr}} \cap gB\cap V_{\mathbb{R}}^{(i)}: |\text{Disc}(x)| < X \}\,dg, \end{equation}
where 
$M_i$ is a constant depending on 
$B$.
Here, for our purpose, 
$S = S_q$ should be the set of maximal orders that are totally ramified at all primes 
$p| q$. We can replace the condition 
$x\in S^{\mathrm {irr}}$ by 
$x\in Y(\mathbb {Z}/q\mathbb {Z})$ to get an upper bound, where 
$Y$ is a codimension 
$k = 4$ variety in an 
$n=40$ dimensional space defined by 
$f^{(j)} =0$ for all partial derivatives of the discriminant polynomial with order 
$j<4$. See [Reference BhargavaBha14] for more discussion on definition of 
$Y$.
For 
$g\in G(\mathbb {R})$, we have 
$g= mak\lambda \in NA\mathcal {K}\Lambda$ as the Iwasawa decomposition [Reference BhargavaBha10]. Here 
$m$ is a lower triangular unipotent transformation, 
$a = (t_1, \dots , t_n)$ is a diagonal element with determinant 1, 
$k$ is an orthogonal transformation in 
$G(\mathbb {R})$ and 
$\lambda = \lambda I$ is the scaling factor. We will choose 
$B$ such that 
$\mathcal {K}B = B$, so 
$gB = ma\lambda B = mrB$, where we denote 
$r = \lambda (t_1, \dots , t_n)$ with 
$\prod ^{n}_1 t_i =1$. Lastly, the requirement 
$|\text {Disc}(x)| < X$ could be dropped as long as we take 
$\lambda \le O(X^{1/n})$ where this implied constant depends only on 
$B$. So we have
\[ \sharp \{x \in S^{\mathrm{irr}} \cap gB\cap V_{\mathbb{R}}^{(i)}: |\text{Disc}(x)| < X \}\le \sharp \{ x \in mrB\cap \mathbb{Z}^{n} \mid a(\mathrm{mod }\,q) \in Y(\mathbb{Z}/q\mathbb{Z})\}. \] We will apply Theorem 4.5 to estimate the integral in (4.9). By [Reference BhargavaBha10], all 
$S_5$ orders are parametrized by quadruples of skew symmetric 
$5\times 5$ matrices. So there are 
$40$ variables and therefore the dimension for the whole space is 
$n=40$. Let us call those variables 
$a^{l}_{ij}$ where 
$1\le l \le 4$ means the 
$m$th matrix, 
$1\le i \le 4$ is the row index of a skew-symmetric 
$5\times 5$ matrix, and 
$2\le j\le 5$ is the column index. We can define the partial order among all 
$40$ entries: 
$a^{i}_{jk}$ is smaller than 
$a^{l}_{mn}$ if 
$i\le l$, 
$j\le m$ and 
$k\le n$. The scaling factor 
$t_i$ in our situation could be described by a pair of diagonal matrices 
$(A , B)$ where
\[ A = \text{diag} (s_1^{-3}s_2^{-1}s_3^{-1}, s_1s_2^{-1}s_3^{-1}, s_1s_2s_3^{-1}, s_1s_2s_3^{3} ) \]and
\[ B =\text{diag} (s_4^{-4}s_5^{-3}s_6^{-2}s_7^{-1}, s_4s_5^{-3}s_6^{-2}s_7^{-1}, s_4s_5^{2}s_6^{-2}s_7^{-1} , s_4s_5^{2}s_6^{3}s_7^{-1}, s_4s_5^{2}s_6^{3}s_7^{4} ). \]
Then 
$t_{lij} = A_l B_i B_j$ is the scaling factor for the 
$a^{l}_{ij}$ entry. Since the fundamental domain requires that all 
$s_i \ge C$, this partial order also gives the partial order on the magnitude of 
$r_{lij}= \lambda t_{lij}$.
There are many regions in the fundamental domain that provide irreducible 
$S_5$ orders. We will consider the biggest region first: the points with 
$a^{1}_{12} \ne 0$. This region requires that 
$\lambda s_1^{-3}s_2^{-1}s_3^{-1}s_4^{-3}s_5^{-6}s_6^{-4}s_7^{-2} \ge \kappa$, therefore 
$r_{lij} \ge C\kappa$ for all 
$l, i,j$ where 
$C$ is some constant. Let us denote this region in 
$\mathcal {F}$ by 
$D_\lambda = \{ s_i\ge C_i\mid s_1^{3}s_2s_3s_4^{3}s_5^{6}s_6^{4}s_7^{2}\le \lambda /\kappa \}$. So we could apply Theorem 4.5 directly. Let us call this count 
$N^{1}( Y ; X)$. The corresponding integrand (i.e. the number of lattice points in the expanding ball 
$gB$ where 
$g\in D_{\lambda }$) is bounded by
\begin{align} L^{1} &= \sharp \{x \in mrB\cap V^{(i)}_{\mathbb{Z}} \mid x (\mathrm{mod } \,q) \in Y(\mathbb{Z}/ q\mathbb{Z})\}\nonumber\\ &= O\bigg(\frac{\lambda^{n}}{q^{k}}\bigg) \cdot C^{\omega(q)} \cdot \max\bigg\{1, \frac{q}{\lambda t_i}, \frac{q^{2}}{\lambda ^{2}t_i t_j} , \dots, \frac{q^{k}}{\lambda ^{k} \prod_{i= i_1}^{i_k} t_i}\bigg\}\nonumber\\ &= O\bigg(\frac{\lambda^{40}}{q^{4}}\bigg) \cdot C^{\omega(q)} \cdot \max\bigg\{1, \frac{q}{\lambda t_{112}}, \frac{q^{2}}{\lambda^{2} t_{112} t_{113}}, \frac{q^{2}}{\lambda^{2} t_{112} t_{212}}, \frac{q^{3}}{\lambda^{3} t_{112} t_{113} t_{123}} , \frac{q^{3}}{\lambda^{3} t_{112} t_{113} t_{114}}, \nonumber\\ &\quad \frac{q^{3}}{\lambda^{3} t_{112} t_{113} t_{212}}, \frac{q^{3}}{\lambda^{3} t_{112} t_{212} t_{312}}, \frac{q^{4}}{\lambda^{4} t_{112} t_{113} t_{114}t_{115}}, \frac{q^{4}}{\lambda^{4} t_{112} t_{113} t_{114}t_{123}}, \frac{q^{4}}{\lambda^{4} t_{112} t_{113} t_{114}t_{212}},\nonumber\\ &\quad \frac{q^{4}}{\lambda^{4} t_{112} t_{113} t_{123}t_{212}},\frac{q^{4}}{\lambda^{4} t_{112} t_{113}t_{212}t_{213}}, \frac{q^{4}}{\lambda^{4} t_{112} t_{113}t_{212}t_{312}} , \frac{q^{4}}{\lambda^{4} t_{112} t_{212}t_{312}t_{412}} \bigg\}. \end{align}
To integrate 
$L^{1}$ over 
$D_\lambda$ and then against 
$\lambda$, we just need to focus on the inner integral over 
$D_\lambda$, and see whether the integral of those products of 
$t_{lij}$ over 
$D_\lambda$ produces 
$O(1)$ or 
$\lambda ^{r}$ for some 
$r> 0$ as the result. If it is 
$O(1)$, then we just need to integrate against 
$\lambda$ and get the expected estimate (i.e. 
${X^{40-i}}/{q^{4-i}}$ for 
$0\le i\le 4$ where 
$i$ is the number of 
$t_{lij}$ factors in the product); if it is 
$\lambda ^{r}$ for some power 
$r>0$, then we will get a bigger power of 
$X$ than the expected counting 
${X^{40-i}}/{q^{4-i}}$.
For example, 
$t^{-1}_{112} = s_1^{3}s_2s_3s_4^{3}s_5^{6}s_6^{4}s_7^{2}$ and 
$dg = \delta _5 ds^{\times } = s_1^{-12}s_2^{-8}s_3^{-12}s_4^{-20}s_5^{-30}s_6^{-30}s_7^{-20} ds^{\times }$, therefore 
$t^{-1}_{112} \delta _5$ contains 
$s_i$ with negative power for each 
$i$. So after integrating over 
$D_\lambda$, it is 
$O(1)$. Notice that all these products have at most four 
$t_{lij}$ factors, so the biggest power we could get for 
$s_4$, 
$s_5$, 
$s_6$ and 
$s_7$ should be 
$(B_1B_2)^{4} = s_4^{-12}s_5^{-24}s_6^{-16}s_7^{-8}$, so those later 
$s_i$ would not be a problem. Therefore we will focus on 
$s_i$ for 
$i = 1,2,3$, especially on those terms with large numbers of factors of the form 
$t_{1**}$. By comparing the exponent in the integrand, the integration over 
$D_{\lambda }$ is 
$O(1)$, except for 
$t_{112} t_{113}t_{114}t_{115}$, 
$t_{112} t_{113}t_{114}t_{123}$. Equivalently, these terms are the product of four 
$t_{lij}$ where 
$l=1$ for all of them. These terms have a factor 
$s_1^{-12}s_2^{-4}s_3^{-4}$ whose integral over 
$D_{\lambda }$ ends up being bounded by 
$\lambda ^{\epsilon }$ by the following computation:
\begin{equation} \int_{s_1, s_2, s_3 \ge O(1), s_1^{3}s_2s_3\le \lambda} s_1^{-12+12}s_2^{-8+4}s_3^{-12+4} \text{d}s^{\times} \le O(1) \cdot \int_{O(1) \le s_1\le \lambda^{1/3}} \text{d} s_1^{\times} \le O(\lambda^{\epsilon}). \end{equation}So the whole result is:
\begin{align} N^{1}(Y; X) & \le \frac{1}{M_i} \int^{O(X^{1/40})}_{\lambda = O(1)} \int_{D_{\lambda}} L^{1} s_1^{-12}s_2^{-8}s_3^{-12}s_4^{-20}s_5^{-30}s_6^{-30}s_7^{-20}\text{d}s^{\times} \text{d}\lambda^{\times} \nonumber\\ & = O(C^{\omega(q)} )\cdot \max \bigg\{ \frac{X}{q^{4}}, \frac{X^{39/40}}{q^{4-1}}, \frac{X^{38/40}}{q^{4-2}}, \frac{X^{37/40}}{q^{4-3}} ,\frac{X^{36/40+\epsilon}}{q^{4-4}} \bigg\}\nonumber\\ & = O(C^{\omega(q)} )\cdot \max \bigg\{ \frac{X}{q^{4}}, X^{36/40+\epsilon} \bigg\}. \end{align} We know that there are a lot of regions containing irreducible points for 
$S_5$ extensions. Notice, however, that the last term above is 
$X^{36/40+\epsilon }$, therefore we will not compute for those regions with a total counting smaller than this; these regions must contribute an even smaller counting when we impose this restriction on ramification in those regions. By in [Reference BhargavaBha10, Table 1], there are still a lot of regions left to be considered when 
$a^{1}_{12} =0$, namely, 
$1$, 
$2a$, 
$2b$, 
$3a$, 
$3b$, 
$3c$, 
$3d$, 
$4a$, 
$4b$, 
$5a$, 
$5c$, 
$6a$, 
$13$.
We will work on region 
$1$ as an example. Region 
$1$ contains the points 
$a^{1}_{12}=0$, 
$a^{1}_{13}\ne 0$, 
$a^{2}_{12} \ne 0$. The corresponding domain of integration therefore is
\[ D_{\lambda} = \{ s_i\ge C_i \mid s_1^{3}s_2s_3s_4^{3}s_5s_6^{4}s_7^{2}\le \lambda /\kappa, s_1^{-1}s_2s_3s_4^{3}s_5^{6}s_6^{4}s_7^{2}\le \lambda /\kappa \}. \]
Since we only want to count integral points with 
$a^{1}_{12}=0$, we can apply Theorem 4.5 with 
$\lambda t_{112} = \kappa$, where 
$\kappa$ is a small absolute number, to get an upper bound. By Theorem 4.5, we again need to evaluate the same integrand 
$L^{1}$ in (4.10) but with a different domain 
$D_{\lambda }$. As considered before, we only need to focus on those difficult terms and it suffices to see that we still have 
$s_1 \le O(\lambda ^{1/3})$ again in this 
$D_{\lambda }$. Starting from now, we can reduce to the computation (4.11), and all the terms we see here are included in (4.12).
For all other regions, we will always reduce to the same integral and see the same terms. The only thing we need to simplify the computation and reduce to (4.11) and (4.12) is to show an upper bound for 
$s_1$ in the corresponding domain 
$D_{\lambda }$. We list the factors we use to deduce such a bound:
1.
$2a$: use $a^{1}_{14} a^{1}_{23} \gg \kappa$,2.
$2b$: use $a^{1}_{13} \gg \kappa$,3.
$3a$: use $a^{1}_{15} a^{1}_{23} \gg \kappa$,4.
$3b$: use $a^{1}_{14} a^{2}_{12} \gg \kappa$,5.
$3c$: use $a^{1}_{14} a^{1}_{23} \gg \kappa$,6.
$3d$: use $a^{1}_{13} \gg \kappa$,7.
$4a$: use $a^{1}_{23} a^{2}_{12}\gg \kappa$,8.
$4b$: use $a^{1}_{24} a^{2}_{12} \gg \kappa$,9.
$5a$: use $a^{1}_{24} a^{2}_{12} \gg \kappa$,10.
$5c$: use $a^{1}_{34} a^{2}_{12} \gg \kappa$,11.
$6a$: use $a^{1}_{34} a^{2}_{12} \gg \kappa$,12.
$13$: use $(a^{1}_{25})^{4} a^{1}_{34} (a^{2}_{24})^{2} (a^{3}_{14})^{2} (a^{4}_{13})^{3} \gg \kappa$.
Therefore, we get the uniformity result for
\begin{equation} N_q(S_5, X) = O\bigg( \frac{X}{q^{4-\epsilon}}\bigg) + O(X^{36/40+\epsilon} q^{\epsilon}). \end{equation}
Finally, notice that 
$q^{4}\le X$, and we get an upper bound of the form
\[ N_q(S_5, X)\le O\bigg(\frac{X}{q^{2/5-\epsilon}}\bigg), \]which will be convenient for our application later.
In order to prove Theorem 1.3 over arbitrary number field 
$K$, we will need to prove the analogue of Theorem 4.5 over an arbitrary number field 
$K$. The setup is a bit more complex than the case over 
$\mathbb {Q}$. The variety that describes points with extra ramification is defined over 
$O_K$. Since 
$\rho :O_K\hookrightarrow \mathbb {R}^{r}\bigoplus \mathbb {C} ^{s}$ is a full lattice, an 
$O_K$-point on the variety corresponds to a lattice point in 
$\mathbb {R}^{dn} \simeq (\mathbb {R}^{r}\bigoplus \mathbb {C} ^{s})^{n}$ where 
$d$ is the degree of 
$K/\mathbb {Q}$ and 
$n$ is the dimension of the ambient space. Denote 
$\mathbb {R}^{r}\bigoplus \mathbb {C}^{s}$ by 
$F$. The scaling vector is 
$r = (r_1, \dots , r_n)$ where 
$r_i\in F$ for each 
$i$. Define 
$|\cdot |_{\infty }$ to be the norm in 
$F$: 
$|v|_{\infty } = \prod _{1\le i\le r} |v_i|_i \prod _{1\le j\le s} |v_j|_j$ where 
$|\cdot |_i$ denotes the standard norm in 
$\mathbb {R}$ at real places and the square of the standard norm in 
$\mathbb {C}$ at complex places.
Theorem 4.6 Let 
$B$ be a compact region in 
$F^{n} \simeq \mathbb {R}^{nd}$ with finite measure. Let 
$Y_t$, for 
$1\le t\le N$, be any closed subschemes of 
$\mathbb {A}^{n}_{O_K}$ of codimension 
$k_t$, say 
$k= \max \{k_t \mid 1\le t\le N\}$. Let 
$r = (r_1, \dots , r_n)$ be a diagonal matrix of non-zero elements where 
$|r_i|_{\infty } \ge \kappa$ for a certain absolute constant 
$\kappa >0$. Let 
$q$ be a square-free integral ideal in 
$O_K$ and 
$m$ be a lower triangular unipotent transformation in 
${\rm GL} _n(F)$. Then we have
\begin{align} &\sharp \{ a\in mrB\cap (O_K)^{n} \mid \forall 1\le t\le N, a(\mathrm{mod }\,p_t) \in Y_t(O_K/p_tO_K) \} \nonumber\\ &\quad = O\bigg(\prod_{i=1}^{n} |r_i|_{\infty}\bigg) \cdot C^{\sum_t k_t} \cdot \max \bigg\{\prod_{i= i_1}^{i_{k}}|r_i|_{\infty}^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k-s}}|r_i|_{\infty}^{-1}}{ \prod_{t,s-k+k_t\ge 0} p_t^{s-k+k_t} }, \ldots, \frac{1}{\prod_t p_t^{k_t}} \bigg\}, \end{align}
where the maximum is taken among 
$0\le s\le k$ and all possible choices 
$\{i_1,i_2, \ldots , i_{k-s} \} \subset \{ 1, 2, \ldots , N\}$ for each 
$s$. Here the implied constant depends only on 
$B$, 
$Y$ and 
$\kappa$, and 
$C$ depends on the degree of 
$Y_t$ for all 
$t$ and 
$k$. In particular, by letting 
$Y_t = Y$ and 
$q = \prod _{t} p_t$, we get
\begin{align} &\sharp \{ a\in mrB\cap (O_K)^{n}\mid a (\mathrm{mod } \,q)\in Y(O_K/qO_K) \} \nonumber\\ &\quad =O\bigg(\prod_{i=1}^{n} |r_i|_{\infty}\bigg) \cdot C^{k\omega(q)} \cdot \max\bigg\{ \prod_{i= i_1}^{i_{k}}|r_i|_{\infty}^{-1},\ldots,\frac{\prod_{i= i_1}^{i_{k-s}}|r_i|_{\infty}^{-1}}{ q^{s} }, \ldots, \frac{1}{q^{k}}\bigg\}, \end{align}
where the maximum is taken among 
$0\le s\le k$ and all possible choices 
$\{i_1,i_2, \ldots , i_{k-s} \} \subset \{ 1, 2, \ldots , N\}$ for each 
$s$. Here the implied constant depends only on 
$B$, 
$Y$ and 
$\kappa$, and 
$C$ depends on the degree of 
$Y$ and 
$k$.
In order to prove this analogue, we need the following lemma on the regularity of shapes of the ideal lattices for a fixed number field 
$K$. Given an integral ideal 
$I\subset O_K$, we can embed it in 
$F$ as a full lattice, with its relative covolume with respect to 
$O_K$ (i.e. covolume of 
$I$ over covolume of 
$O_K$) to be the absolute norm 
$[O_K : I] = \operatorname {Nm}_{K/\mathbb {Q}}(I)$, which we will write as 
$|I|$.
Lemma 4.7 Let 
$K$ be a number field and 
$I\subset O_K$ be an arbitrary ideal. Given 
$\lambda = (\lambda _i) \in F = \mathbb {R}^{r}\bigoplus \mathbb {C} ^{s}$, then
\[ \sharp \{ a \in I \mid \forall i, |\sigma_i(a)|_i \le |\lambda_i|_i \} = O\bigg(\frac{|\lambda|_{\infty}}{|I|}\bigg) + 1, \]
where 
$\sigma _i$, for 
$i =1, \dots , r+s$, are the Archimedean valuations of 
$K$ and 
$|\cdot |_i$ is the usual norm in 
$\mathbb {R}$ for real embeddings and the square of the usual norm in 
$\mathbb {C}$ for complex embeddings. The implied constant depends only on 
$K$.
Proof. Given 
$I$ in the ideal class 
$R$ in the class group of 
$K$, denote by 
$[a]$ the equivalence class of non-zero 
$a$ in 
$I$ where 
$a\sim a'$ if 
$a = ua'$ for some unit 
$u$. Then we have [Reference LangLan94]
\begin{equation} \sharp \{ [a] \in I \mid |[a]|_{\infty} \le |I|X \} = \sharp \{\alpha \subset O_K \mid \alpha\in R^{-1}, |\alpha| < X \} = O(X). \end{equation}
To take advantage of the equality above, we cover the set 
$W: = \{ a \in I \mid \forall i, |\sigma _i(a)|_i \le |\lambda _i|_i \} \backslash \{ 0 \}$ by a disjoint union of subsets 
$W_k$:
\begin{equation} W = \bigcup_{k\ge 1} \bigg\{ a \in I \biggm| \forall i, |\sigma_i(a)|_i \le |\lambda_i|_i , \frac{|\lambda|_{\infty}}{2^{k}} \le |a|_{\infty} \le \frac{|\lambda|_{\infty}}{2^{k-1}} \bigg\} = \bigcup_k W_k. \end{equation}
For 
$a\in W_k$, we have that
\[ \frac{|\lambda_i|_i}{2^{k}}\le |\sigma_i(a)|_i \le |\lambda_i|_i, \]
and if 
$ua$ is also in 
$W$, it must also be in the same 
$W_k$ since 
$|ua|_{\infty } = |a|_{\infty }$. So the magnitude of 
$u$ is bounded by 
$2^{-k}\le |\sigma _i(u)|_i \le 2^{k}$ by the above inequality. By Dirichlet's unit theorem, the units of 
$K$, aside from roots of unity after taking the logarithm, form a lattice of rank 
$r+s-1$ satisfying 
$\sum _i \ln |\sigma _i(u)|_i = 0$, therefore
\[ \sharp \{ u\in O_K^{\times} \mid |\ln |\sigma_i(u)|_i|\le k \} = O (k^{r+s-1}). \]
So for each 
$[a]\in W_k$, the multiplicity is bounded by 
$O(k^{r+s-1})$, and the number of equivalence classes in 
$W_k$ is bounded by
\begin{equation} \sharp \bigg\{ [a] \in I \biggm| |a|_{\infty} < \frac{|\lambda|_{\infty}}{2^{k-1}}\bigg\} \le O \bigg(\frac{|\lambda|_{\infty}}{|I|}\cdot \frac{1}{2^{k-1}}\bigg). \end{equation}Therefore
\begin{equation} |W_k| \le O \bigg(\frac{|\lambda|_{\infty}}{|I|}\bigg) \cdot \frac{k^{r+s-1}}{2^{k-1}}. \end{equation}
The total counting by summation over all 
$k$ is
\[ \sharp \{ a \in I \mid \,\forall i, |\sigma_i(a)|_i \le |\lambda_i|_i \}\backslash \{0\} = \sum_k |W_k|\le O\bigg(\frac{|\lambda|_{\infty}}{|I|}\bigg) \sum_k \frac{k^{r+s-1}}{2^{k-1}} \le O\bigg(\frac{|\lambda|_{\infty}}{|I|}\bigg). \]So the total counting after including the origin is
\[ \sharp \{ a \in I \mid \forall i, |\sigma_i(a)|_i \le |\lambda_i|_i \} = O\bigg(\frac{|\lambda|_{\infty}}{|I|}\bigg) + 1. \] A corollary of this lemma is that the shape of the ideal lattices inside 
$O_K$ cannot be too skew. We will make this precise in the following lemma and prove it by a more direct approach.
Lemma 4.8 Given a number field 
$K$ with degree 
$d$, for any integral ideal 
$I \subset O_K$, denote by 
$\mu _i$, 
$1\le i\le d$, the 
$i$th successive minimum for the Minkowski reduced basis for 
$I$ as a lattice in 
$\mathbb {R}^{d}$. Then 
$\mu _i$ is bounded by
\[ \mu_i \le O(|I|^{1/d}), \]
for all 
$1\le i \le d$. The implied constant only depends on the degree of 
$K$, the number of complex embeddings of 
$K$ and the absolute discriminant of 
$K$.
Proof. Given an integral ideal 
$I$, and an arbitrary non-zero element 
$\alpha \in I$, we have 
$(\alpha ) \subset I$, so 
$|(\alpha )| \ge |I|$. The length of 
$\alpha$ in 
$\mathbb {R}^{d}$ is
\begin{align} \sqrt{|\alpha|_1^{2} + \cdots + |\alpha|_r^{2} + |\alpha|_{r+1} + \cdots + |\alpha|_{r+s} } &\ge \sqrt{ d \bigg(\prod_{1\le i\le r} |\alpha_i|^{2}\prod_{r+1\le i\le r+s} \frac{|\alpha|_i^{2}}{4}\bigg)^{1/d}}\nonumber\\ &\ge \sqrt{d} 2^{-s/d} |(\alpha)|^{1/d}\nonumber\\ &\ge \sqrt{d} 2^{-s/d} |I|^{1/d}. \end{align}
The first inequality comes from the fact that the arithmetic mean is greater than the geometric mean. While Minkowski's first theorem guarantees that 
$\mu _1 \le O(|I|^{1/d})$, we have also shown that 
$\mu _1$ could be bounded from below by 
$O(|I|^{1/d})$. This amounts to saying that the first minimum 
$\mu _1$ of Minkowski's reduced basis is exactly at the order of the diameter 
$O(|I|^{1/d})$. Moreover, Minkowski's second theorem states that
\begin{equation} \prod_{1\le i\le d} \mu_i \le 2^{d} \operatorname{Disc}(K)^{1/2}|I|, \end{equation}
therefore for all 
$i\le d$,
\[ \mu_i \le O(|I|^{1/d}), \]
where the implied constant could be written explicitly in the degree 
$d$ of 
$K/\mathbb {Q}$, the number of complex embeddings 
$s$ and the absolute discriminant 
$\operatorname {Disc}(K)$, by combining (4.20) and (4.21).
Remark 4.9 By Lemma 4.7, if we pick 
$\lambda$ with 
$|\lambda |_{\infty } = O(|I|)$ and 
$|\lambda _i|_i = O(|I|^{1/d})$ for real places and 
$|\lambda _i|_i = O(|I|^{2/d})$ for complex places, we get a square box with side length 
$O(|I|^{1/d})$ in 
$\mathbb {R}^{d}$. The first term in Lemma 4.7 could be bounded by 
$O({|\lambda |_{\infty }}/{|I|}) = O(1)$, therefore among all square boxes with identical side length, we can see that the largest such box containing only one lattice point (i.e. the origin) has side length as large as 
$C|I|^{1/d}$ for some constant 
$C$. Indeed, if Lemma 4.8 did not hold (i.e. if the first minimum 
$\mu _1$ is too small), then by taking the square box just described, we would get many more points than 
$O(1)$, which contradicts Lemma 4.7. Therefore we can also see from Lemma 4.7 that 
$\mu _1$ cannot be too small, which also implies Lemma 4.8.
On the other hand, Minkowski's reduced basis generates the whole lattice with covolume 
$|I|D_K^{1/2}$, so the angle among the vectors in the basis is away from zero. This basically means that Minkowski's reduced basis, among the family of all integral ideals of 
$K$, all look like square boxes, and we can find a fundamental domain within the square box. This proves the following corollary.
Corollary 4.10 Given a number field 
$K$ with degree 
$d$, for any integral ideal 
$I \subset O_K$ and any residue class 
$\bar {c}\in O_K/IO_K$, we can find a representative 
$c\in O_K$ such that each
\[ |c_i| \le O(|I|^{1/d}), \]
where 
$c_i$ is the 
$i$th coordinate in 
$\mathbb {R}^{d}$ for all 
$1\le i \le d$. The implied constant depends only on 
$K$.
Proof of Theorem 4.6 The case where 
$k =0$ is trivial since the number of lattice points in the box is 
$O(\prod _{i=1}^{n} |r_i|_{\infty })$. It suffices to prove the statement for the initial case when 
$k = 1$ and 
$n=1$. The induction procedure works similarly to Theorem 4.5.
Let us look at an initial case 
$[(1,k_t)_{p_t}]_1^{N}$, for example. Suppose that, for those 
$t$ with 
$k_t = 1$, the scheme 
$Y_t$ is cut out by 
$f_t(x)$. For each 
$f_t(x)$, the number of solutions for 
$f_t (\mathrm {mod }\, p_t)$ is bounded by 
$C = \deg (\,f)$. Denote 
$q= \prod _t p_t^{k_t}$. Therefore inside 
$O_K/ qO_K$, the number of residue classes that satisfy each 
$t$th condition is bounded by 
$C^{\sum _t k_t}$. To answer the counting question, the set of such lattice points 
$a\in O_K$ is a union of 
$C^{\sum _t k_t}$ translations of lattices: translation of the lattice 
$q$ by 
$c$ (the new lattice is 
$q+c$) where 
$c$ is a certain lift of 
$\bar {c}\in O_K/ qO_K$ and 
$\bar {c}$ is one solution of 
$f_t (\mathrm {mod }\,p_t)$ for all 
$t$ with 
$p_t| q$.
Lemma 4.7 states that for arbitrary 
$r\in F$,
\[ \sharp \{ a \in rB \cap O_K \mid a\in 0+q \} = O \bigg(\max \bigg\{ \frac{|r|_{\infty}}{|q|}, 1 \bigg\}\bigg), \]
when 
$B$ is the unit square in 
$F$. It follows that the equality is true for any general compact set 
$B$, since we could cover the new set 
$B$ by a bigger square, and the effect on the implied constant of doing this will only depend on 
$B$. For other non-trivial translations by a root 
$c$, we have
\begin{equation} \sharp \{ a \in rB \cap O_K \mid a\in c+q \} = \sharp \{ a\in (rB-c) \cap O_K \mid a\in q \}. \end{equation}
So it is equivalent to consider the number of lattice points in a translation of a square box 
$rB$ centered at the origin. We could cover 
$B$ by 
$2^{n}$ sub-boxes 
$B_s$ which are defined by sign in each 
$\mathbb {R}$ space (consider complex embeddings as two copies of 
$\mathbb {R}$). Then 
$rB-c$ could be covered by 
$rB_s -c$. It suffices to count lattice points in each 
$rB_s-c$ and add them up. For each 
$s$, if there exists one lattice point 
$P \in rB_s-c$, then we can cover 
$rB_s-c$ by 
$P+2rB_s$, and the number of lattice points in 
$2rB_s+P$ is equivalent to that in 
$2rB_s$, which is
\[ \sharp \{ (P+2rB_s) \cap q \} = \sharp \{ 2rB_s\cap q \} \le O \bigg(\max \bigg\{ \frac{|r|_{\infty}}{|q|}, 1 \bigg\}\bigg). \]
If there are no lattice points in 
$B_s$, then there is nothing to add. Altogether we have that for any residue class 
$\bar {c}$ and any compact set 
$B$,
\[ \sharp \{ a \in rB \cap O_K \mid a\in c+q \}\le O \bigg( 2^{n} \max \bigg\{ \frac{|r|_{\infty}}{|q|}, 1 \bigg\}\bigg) = O \bigg( \max \bigg\{ \frac{|r|_{\infty}}{|q|}, 1 \bigg\}\bigg). \]
Here the implied constant depends only on 
$B$ and 
$K$. Therefore by adding up counting for all 
$\bar {c}$, we get an upper bound
\[ O(1) \cdot C^{\sum_t k_t}\cdot \max \bigg\{ 1, \frac{|r_1|_{\infty}}{\prod_{t} p_t^{k_t}}\bigg\}. \]
This completes the proof for the case 
$k = 1$, 
$n=1$.
Finally, based on Theorem 4.6, we can prove Theorem 1.3 over a number field 
$K$.
Proof Proof of Theorem 1.3 over 
$K$
We will follow the notation of [Reference Bhargava, Shankar and WangBSW15] in this proof. Counting 
$S_n$ number fields for 
$n= 3,4,5$ over a number field 
$K$ is different from that over 
$\mathbb {Q}$ mostly in two respects.
Firstly, the structure of finitely generated 
$O_K$-modules is more complicated than that of 
$\mathbb {Z}$, therefore the parametrization of 
$S_n$ number fields over 
$K$ will involve other orbits aside from 
$G(O_K)$-orbits of 
$V(O_K)$ points. More precisely, finitely generated 
$O_K$-modules with rank 
$n$ are classified in correspondence to the ideal class group 
$\text {Cl}(K)$ of 
$K$. So for each ideal class 
$\beta$, we get a lattice 
$\mathcal {L}_\beta$ corresponding to 
$S_n$ extensions 
$L$ with 
$O_L$ corresponding to 
$\beta$ (i.e. the Steinitz class of 
$L$ is 
$\beta$). More explicitly, by formula 
$(12)$ in [Reference Bhargava, Shankar and WangBSW15], we have
\[ \mathcal{L}_{\beta}:=V_n(F)\cap \beta^{-1} \prod_{\mathfrak{p}\notin S} V_n(\mathcal{O}_{\mathfrak{p}})\prod_{\mathfrak{p}\in S} V_n(F_{\mathfrak{p}}). \]
In order to give an upper bound on the number of cubic extensions of 
$K$ with Steinitz class 
$\beta$, we just need to count the number of orbits in 
$\mathcal {L}_\beta$ under the action of 
$\Gamma _\beta$ where, by 
$(13)$ in [Reference Bhargava, Shankar and WangBSW15],
\[ \Gamma_\beta:= G_n(F)\cap \beta^{-1} \prod_{\mathfrak{p}\notin S} G_n(\mathcal{O}_{\mathfrak{p}})\prod_{\mathfrak{p}\in S} G_n(F_{\mathfrak{p}}) \beta, \]
is commensurable with 
$G(O_K)$ and 
$\mathcal {L}_\beta$ is commensurable with 
$V(O_K)$. See [Reference Bhargava, Shankar and WangBSW15, § 3] for more details.
Secondly, the reduction theory over a number field 
$K$ is slightly different in that the description of fundamental domains requires the introduction of units, and this effect of units is especially beneficial for summation over fundamental domains. The most significant difference is in the description of the torus. Over 
$\mathbb {Q}$, we have 
$G(\mathbb {R})\backslash G(\mathbb {Z}) = NA\mathcal {K}\Lambda$ [Reference BhargavaBha10] where 
$A$ is an 
$l$-dimensional torus (
$l=7$ for 
$S_5$) embedded into 
${\rm GL} _n(\mathbb {R})$ (
$n=40$ for 
$S_5$) as diagonal elements
\[ T(c) = \{ t(s_1,\dots, s_l)\in T(\mathbb{R}) = \mathbb{G}^{l}_m(\mathbb{R})\mid \forall i, s_i\ge c\}. \]
Given a number field 
$K$, recall that 
$\rho :O_K\hookrightarrow F = \mathbb {R}^{r}\bigoplus \mathbb {C}^{s}$ is the embedding of 
$O_K$ as a full lattice in 
$\mathbb {R}^{d}$. Then 
$A$ could be described as a subset of
\[ T(c,c') = \bigg\{ t = t(s_1,\dots, s_l)\in T(F) = \mathbb{G}^{l}_m(F)\biggm| \forall i, |s_i|_{\infty} \ge c , \forall j,k, \ln \frac{|s_i|_{j}}{|s_i|_{k}} \le c' \bigg\}. \]
Here 
$|s_i|_j \le O(|s_i|_{k})$, for all 
$j, k$, guarantees that 
$|s_i|_k \asymp |s_i|_j$, that is, 
$|s_i|_k$ and 
$|s_i|_j$ are of comparable size for any 
$j$, 
$k$. Thus 
$|s_i|_v \asymp |s_i|_{\infty }^{1/(r+s)}$. Therefore, if we have a bound that 
$|s_i|_{\infty } \le C$ for some number 
$C$, then we can get the bound 
$|s_i|_v\le O(C^{1/(r+s)})$. See [Reference Bhargava, Shankar and WangBSW15, § 4] for more details.
Now over 
$K$, the signature 
$i$ is a collection of degree 
$n$ étale algebras over 
$\mathbb {R}$ for every real embedding of 
$K$ (in [Reference Bhargava, Shankar and WangBSW15] this corresponds to an 
$S$-specification with 
$S = S_{\infty}$ being the set of infinite places). There are only finitely many signatures; again we will ignore the dependence on 
$i$ in our discussion. Recall that, for each 
$\beta$, we need to compute
\begin{equation} N(S; X) = \frac{1}{M_i}\int_{g\in \mathcal{F}_{\beta}} \sharp \{x \in S^{\mathrm{irr}} \cap gB\cap V^{(i)}_{F}: |\text{Disc}(x)|_{\infty} < X \}\,dg. \end{equation}
Here 
$\mathcal {F}_{\beta }$ is the fundamental domain 
$\Gamma _{\beta }\backslash G(F)$, 
$V_F^{(i)}$ is a subspace of 
$V_F$ with a certain signature, and 
$B$ is a compact ball in the space 
$V_F$ that is invariant under the action of the orthogonal group 
$\mathcal {K}$, 
$S = S_q$ is the set of maximal orders that are totally ramified at all primes 
$p|q$, 
$S^{\mathrm {irr}}$ is the subset of irreducible points in 
$S$, 
$dg$ is the same Haar measure as over 
$\mathbb {Q}$ as long as we interpret 
$s_i$ to be 
$|s_i|_{\infty }$, and we denote 
$\text {d}^{\times } s = \text {d}^{\times } s_1 \cdots \text {d}^{\times } s_7$ where 
$\text {d}^{\times } s_i = \prod _{v|\infty } \text {d}^{\times } (s_i)_v$. By Theorem 4.6, the integrand is
\begin{align} \sharp \{x &\in S^{\mathrm{irr}} \cap gB\cap V^{(i)}_{F}: |\text{Disc}(x)|_{\infty} < X \}\nonumber\\ &\quad \le \sharp \{x \in m\lambda t B\cap \mathcal{L} \mid x (\mathrm{mod } \,q) \in Y(\mathbb{Z}/ q\mathbb{Z})\}\nonumber\\ &\quad = O\bigg(\frac{|\lambda|_{\infty}^{n}}{|q|^{k}}\bigg) \cdot C^{\omega(q)} \cdot \max\bigg\{1, \frac{|q|}{|\lambda t_i|_{\infty}}, \frac{|q|^{2}}{|\lambda ^{2}t_it_j|_{\infty}} , \dots, \frac{|q|^{k}}{|\lambda ^{k} \prod_{i= i_1}^{i_k} t_i|_{\infty}}\bigg\}. \end{align}
Here, in order to present the result in a similar form to that over 
$\mathbb {Q}$, for each 
$\lambda \in \mathbb {R}^{+}$ we denote by 
$\lambda$ the scalar diagonal matrix such that 
$|\text {Disc}(\lambda v)|_{\infty } = |\lambda |^{n}_{\infty } |\text {Disc}(v)|_{\infty }$ where 
$n= 40$ for 
$S_5$.
The first case is to evaluate the integral in (4.23) for 
$\beta = e$, i.e. to compute the number of 
$G(O_K)$-orbits in 
$V(O_K)$ with the given ramification condition. For this case, the fundamental domain in 
$\mathcal {F}$ is 
$G(O_K)\backslash G(F)$. Denote by 
$\mathcal {L}$ the image of 
$V(O_K)$ in 
$V(F)$. We first look at the case where 
$a^{1}_{12}\ne 0$. Since 
$\mathcal {L}$ is a lattice, 
$x$ with non-zero 
$a^{1}_{12}$ is away from zero and 
$|a|_{\infty }$ could be bounded from below by 
$\kappa$, so we would only integrate over
\[ D_\lambda = \{ t= t(s_i)\in T(c,c')\mid |s_1^{3}s_2s_3s_4^{3}s_5^{6}s_6^{4}s_7^{2}|_{\infty}\le \lambda /\kappa\}. \]
The integral over 
$F= \mathbb {R}^{d}$ gives the same result as over 
$\mathbb {Q}$ since, for arbitrary bound 
$C$, we see that the integration of 
$|s|^{u}_{\infty }$ satisfies the same law for integrating polynomials over 
$\mathbb {Q}$:
\begin{equation} \int_{O(1)}^{C} |s|^{u}_{\infty}\text{d}s^{\times} \le \prod_{1\le i\le r} \int_{O(1)}^{O(C^{1/(r+s)})} s_i^{u}\text{d}s_i^{\times} \prod_{r+1\le i\le r+s} \int_{O(1)}^{O(C^{1/2(r+s)})} r_i^{2(u-1)}r_i\text{d}r_i = O(C^{u}). \end{equation}
The equation above implies that in order to transit from integration (see (4.10)) over 
$\mathbb {Q}$ to integration over 
$K$ (see (4.24)), we can simply replace the number 
$s$ by the tuple 
$|s|$ in every formula. Then the integration proceeds in an identical way. So we will end up with the same result over 
$K$.
For fields corresponding to other ideal classes 
$\beta \in \text {Cl}(K)$, we can similarly compute the average number of lattice points in 
$\mathcal {F}v$ for 
$v\in B$ with bounded discriminant. Denote 
$\mathcal {F}_\beta = \Gamma _\beta \backslash G(F)$. By [Reference Bhargava, Shankar and WangBSW15], we can cover 
$\mathcal {F}_\beta$ by finitely many 
$g_i\mathcal {F}$ where 
$g_i \in G(O_K)$ are representatives of 
$(G(O_K)\cap \Gamma _\beta ) \backslash G(O_K)$. Writing 
$\mathcal {D}_i = \mathcal {F}_\beta \cap g_i\mathcal {F}$, we just need to sum up over 
$\mathcal {D}_i$ to get an upper bound for 
$N(S;X)$:
\begin{align} N(S; X) &= \frac{1}{M_i}\int_{g\in \mathcal{D}_i} \sharp \{x \in S^{\mathrm{irr}} \cap gB\cap V^{(i)}_{F}: |\text{Disc}(x)|_{\infty} < X \}\,dg\nonumber\\ &\le \frac{1}{M_i}\int_{g\in g_i\mathcal{F}} \sharp \{x \in S^{\mathrm{irr}} \cap gB\cap V^{(i)}_{F}: |\text{Disc}(x)|_{\infty} < X \}\,dg\nonumber\\ &\le \frac{1}{M_i}\int_{g\in \mathcal{F}} \sharp \{x \in g_i^{-1}S^{\mathrm{irr}} \cap gB\cap V^{(i)}_{F} \}\,dg. \end{align} Recall that 
$\mathcal {L}_{\beta }:= V_n(K) \cap \beta ^{-1} \prod _{p\nmid \infty } V(O_p) \prod _{p|\infty } V(F_p)$, where 
$\beta$ is a representative of the double coset 
$\text {cl}_S = ( \prod _{p\nmid \infty } G(O_p))\backslash G(\mathbb {A}_f) /G(K)$. Here 
$\mathbb {A}_f$ is the restricted product of 
$K_p^{\times }$ for all finite places 
$p$. Given the representative 
$\beta \in (\prod _{p\nmid \infty } G(O_p))\backslash G(\mathbb {A}_f) /G(K)$, due to the definition of restricted product, aside from a finite set of places that we denote by 
$S_{\beta }$, the component 
$\beta _p$ at a prime 
$p$ is in 
$G(O_p)$. Taking the action of 
$\prod _{p\nmid \infty } G(O_p)$ into consideration, we could further assume 
$\beta _p$ is the identity element in 
$G(O_p)$ for 
$p\notin S_{\beta }$. At 
$p \in S_{\beta }$, the component 
$\beta _p$ is not necessarily in 
$G(O_p)$, but is in 
$G(K_p)$. We will show that by multiplication with some 
$a\in O_K$, the lattice 
$a\mathcal {L}_{\beta }$ is integral. Since 
$\beta _p^{-1}$ is a linear action on 
$V(K_p)$, there must exist 
$r_0$ such that
\[ \beta_p^{-1} \pi^{r} V(O_p) \subset V(O_p), \]
for every 
$r\ge r_0$ where 
$\pi$ is a uniformizer for 
$O_p$. If the ideal 
$p$ has order 
$r_1$ in the class group of 
$K$, then 
$p^{r_1} = (a_p)\subset O_K$ for some 
$a_p\in O_K$, and 
$\text {val}_p(a_p)= \text {val}_p(\pi ^{r_1})$. By choosing 
$r\ge r_0$ that is also a multiple of 
$r_1$, we can see that
\[ \beta_p^{-1} a_p V(O_p) \subset V(O_p). \]
Define 
$a = \prod _{p\in S_{\beta }} a_p \in O_K$ that is the finite product of elements 
$a_p\in O_K$. By the way 
$a$ and 
$a_p$ are defined, we see that 
$a\mathcal {L}_\beta \subset V(O_K)$ and 
$a\in O_p^{\times }$ at 
$p\notin S_{\beta }$. So for 
$p\notin S_{\beta }$, an element 
$v\in \mathcal {L}_\beta$ is in 
$Y(O_K/p)$ if and only if 
$av \in O_K$ is in 
$Y(O_K/p)$. Therefore aside from finitely many places, we can instead count lattice points in 
$a\mathcal {L}_{\beta }$ that are ramified at 
$q$. Since there are only finitely many ideal classes, and thus finitely many 
$\beta$ and finitely many 
$S_{\beta }$, the union 
$S= \bigcup _{\beta } S_{\beta }$ contains only finitely many primes. Therefore it will not affect the form of the uniformity estimate but only the implied constant. From now on, we will assume 
$\mathcal {L}_{\beta }$ to be in 
$O_K$.
In (4.26), recall that the set 
$S^{\mathrm {irr}}$ is the set of irreducible points that are totally ramified points at 
$q$ in 
$\mathcal {L}_{\beta }$. Firstly, we assume 
$q$ is a square-free integral ideal away from 
$S$. In the integrand in (4.26) we need to bound the number of 
$x \in g_i^{-1} S^{\mathrm {irr}}$. Denoting 
$g_i^{-1} Y = Y_i$, then 
$x\in g_i^{-1} S^{\mathrm {irr}}$ implies that 
$x\in Y_i(O_K/q)$, then it suffices to give an upper bound on
\begin{equation} \sharp \{x \in g_i^{-1}\mathcal{L}_{\beta}\cap gB \cap Y_i(O_K/q) \}, \end{equation}
and integrate. Since 
$g_i^{-1}Y$ differs from 
$Y$ only by a linear transformation of coordinates, 
$Y_i$ has the same codimension. We apply Theorem 4.6 to 
$Y_i$ to get the upper bound.
To consider arbitrary square-free ideal 
$q = q_1q_2$ with 
$q_2$ containing the involved factors in 
$S$, we can consider the number of orbits that are ramified at 
$q_1$ as an upper bound, and get the estimate in (4.13):
\[ O\bigg( \frac{X}{q_1^{4-\epsilon}}\bigg) + O(X^{36/40} q_1^{\epsilon}) \le \bigg(\prod_{p\in S}|p|^{4}\bigg) \cdot\bigg(O\bigg( \frac{X}{q^{4-\epsilon}}\bigg) + O(X^{36/40} q^{\epsilon})\bigg). \]
The extra product over 
$S$ only depends on 
$k$, so we also get the expected upper bound for arbitrary square-free ideal 
$q$.
4.3 Local uniformity for abelian extensions
In this subsection, we will prove perfect local uniformity estimates on ramified abelian extensions for all abelian groups 
$A$ over arbitrary number field 
$k$ with arbitrary ramification type.
It has been proved [Reference WrightWri89] that Malle's conjecture is true for all abelian groups over any number field 
$k$.
Theorem 4.11 Let 
$A$ be a finite abelian group and 
$k$ be a number field. The number of 
$A$ extensions over 
$k$ with the absolute discriminant bounded by 
$X$ is
\[ N(A,X) \sim C X^{1/a(A)}(\ln X)^{b(k,A)-1}. \] We will need to prove a uniformity estimate for 
$A$ extensions with certain local conditions. For an arbitrary integral ideal 
$q$ in 
$O_k$, define 
$N_q(A,X) = \sharp \{ K\mid \operatorname {Disc}(K/k)\le X, \operatorname {Gal}(K/k) = A, q| \operatorname {disc}(K/k) \}$.
Theorem 4.12 Let 
$A$ be a finite abelian group and 
$k$ be a number field. Then
\[ N_q(A,X) \le O(C^{\omega(q)})\left(\frac{X}{|q|}\right)^{1/a(A)} (\ln X)^{b(k, A)-1}, \]
for an arbitrary integral ideal 
$q$ in 
$O_k$, where 
$C$ and the implied constant depend only on 
$k$.
Proof. We will employ the notation and language of [Reference WoodWoo10] to describe abelian extensions. By class field theory, there is a bijection between the set of 
$A$ extensions and the set of continuous surjective homomorphisms from the idèle class group 
$C_k$ to 
$A$ (up to composition with 
$\sigma \in \text {Aut}(A)$). Therefore in order to get an upper bound on 
$A$ extensions, it suffices to bound on the number of continuous homomorphisms 
$C_k\to A$. Similarly, for 
$A$ extensions with certain local conditions, it suffices to bound on the number of continuous homomorphisms from the idèle class group 
$C_k\to A$ satisfying certain local conditions.
Let 
$S$ be a finite set of primes such that: (1) primes in 
$S$ generate the class group of 
$k$; (2) primes at infinity are in 
$S$; (3) primes 
$p| |A|$ are in 
$S$. Denote by 
$J_k$ the idèle group of 
$k$, and by 
$J_S$ the idèle group with component 
$O_v^{\times }$ for all 
$v\notin S$, and write 
$O_S^{*}$ for 
$k^{*}\cap J_S$. By [Reference WoodWoo10, Lemma 2.8], the idèle class group 
$C_k = J_k/k^{\times }\simeq J_S/O_S^{\times }$. Therefore to bound the number of continuous homomorphisms 
$C_k\simeq J_S/O_S^{\times } \to A$, it suffices to bound the number of continuous homomorphisms 
$J_S\to A$. The Dirichlet series for 
$J_S\to A$ with respect to absolute discriminant is an Euler product (see [Reference WoodWoo10, § 2.4])
\begin{align} F_{S, A} (s) =\sum_{\rho: J_S\to A} \frac{1}{\operatorname{Disc}(\rho)^{s}} =\prod_{p\in S} \bigg(\sum_{\rho_p: k_p^{*}\to A} |p|^{-d(\rho_p)s}\bigg) \prod_{p\notin S}\bigg(\sum_{\rho_p: O_p^{*}\to A} |p|^{-d(\rho_p)s}\bigg) = \sum_{n\subset O_k} \frac{a_n}{|n|^{s}}, \end{align}
where 
$d(\rho _p)$ is the exponent of 
$p$ in the relative discriminant and can be determined by 
$\rho _p$ in general. For 
$p\notin S$, the exponent 
$d(\rho _p)$ could be determined by the inertia group at 
$p$, which is the image of 
$O_p^{*}$ in 
$A$. [Reference WoodWoo10, Lemma 2.10] shows that 
$F_{S,A}(s)$ has exactly the rightmost pole at 
$s = {1}/{a(A)}$ with order 
$b(k,A)$, the same as the Dirichlet series for 
$A$ extensions.
The generating series 
$F_{S,A}(s)$ is a nice Euler product: for all 
$p$-factors, there is a uniform bound 
$M$ on the magnitude of coefficient 
$a_{p^{r}}$ and a uniform bound 
$R$ on 
$r$ such that 
$a_{p^{r}}$ is zero for 
$r>R$. Denote the partial sum of 
$F_{S,A}(s)$ by 
$B(X) = \sum _{n \le X} a_n$, and there exists 
$C_0$ such that 
$B(X) \le C_0 X^{1/a(A)} \ln ^{b(A)-1} X$. Then, for an arbitrary integral ideal 
$q = \prod _i p_i^{r_i}$, we define 
$B_q(X) = \sum _{q|n, |n| < X} a_n$. It is clear that 
$N_q(A, X) \le B_q(X)$, so it suffices to bound on 
$B_q(X)$. Let 
$q_0 = \prod _i p_i^{R}$. Then
\begin{align} B_q(X) & = \sum_{q|d|q_0} a_d \sum_{k, (d,k)= 1, |dk| < X} a_k \le \sum_{q|d|q_0} a_d \cdot B\bigg(\frac{X}{d}\bigg) \le \sum_{q|d|q_0} M^{\omega(q)} \cdot C_0 \bigg(\frac{X}{d}\bigg)^{1/a(A)} \ln^{b(A)-1}X\nonumber\\ & = C_0 M^{\omega(q)} X^{1/a(A)}\ln ^{b(A)-1}X \sum_{q|d|q_0} \frac{1}{d^{1/a(A)}}\nonumber\\ & \le C_0 (MR)^{\omega(q)} X^{1/a(A)}\ln^{b(A)-1} X \frac{1}{q^{1/a(A)}} = O(C^{\omega(q)})\bigg(\frac{X}{q}\bigg)^{1/a(A)} \ln^{b(A)-1} X, \end{align}
where the implied constant and 
$C$ are determined by 
$M, R, C_0$. The theorem then follows from 
$N_q(A,X)\le B_{q}(X)$ for an arbitrary integral ideal 
$q$.
5. Proof of the main theorem
In this section we prove our main result, Theorem 1.1. The idea of this proof is similar to that in [Reference Bhargava and WoodBW08]. Basically we expect that 
$\operatorname {Disc}(KL)$ is approximately the product 
$\operatorname {Disc}(K)^{m}\operatorname {Disc}(L)^{3}$, with differences only at places where both 
$K$ and 
$L$ are ramified. So we define a new invariant 
$\operatorname {Disc}_Y(KL)$ which only considers those differences at small primes, and aim to prove that counting by 
$\operatorname {Disc}_Y(KL)$ will finally converge to the true counting. Before we start the proof, we give the following lemma that states exactly the inequality we need in the proof. This inequality includes all useful data we have developed before. It measures how good the local uniformity we proved is in comparison to how much we need. The latter is derived by group-theoretic computation in § 2.4.
Lemma 5.1 For 
$n=3,4,5$, let 
$A$ be an abelian group satisfying the corresponding condition on 
$m = |A|$ in Theorem 1.1. Then for all 
$c\in A$ and 
$d\in S_n$,
\begin{equation} \operatorname{ind}(d, c) /m -\operatorname{ind}(d) + r_d \ge 1 , \end{equation}
where the local uniformity 
$O(X/|q|^{r_d-\epsilon })$ with exponent 
$r_d$ holds for 
$S_n$ degree 
$n$ extensions with the tame inertia generator at 
$p|q$ equal to 
$d$ up to conjugacy.
We conclude this paper by proving our main result.
Proof of Theorem 1.1 We will describe 
$S_n\times A$ extensions by pairs of 
$S_n$ degree 
$n$ field 
$K$ and 
$A$ extensions 
$L$,
\[ N(S_n\times A, X) = \sharp \{ (K,L)| \operatorname{Gal}(K/k) \simeq S_n, \operatorname{Gal}(L/k) \simeq A, \operatorname{Disc}(KL) < X\}. \]
We will write 
$N(X)$ for short and omit the conditions 
$\operatorname {Gal}(K/k) \simeq S_n$ and 
$\operatorname {Gal}(L/k) \simeq A$ when there is no confusion. The equality holds since 
$S_n$ and odd abelian groups have no isomorphic quotient.
We will prove this result in three steps.
Step 1: estimate pairs by 
$\operatorname {Disc}(O_K O_L)$. By Theorem 2.1, we can get a lower bound for 
$N(S_n\times A, X)$ by counting the number of pairs by 
$\operatorname {Disc}(O_KO_L)$. Denote 
$|A| = m$, then there exists 
$C_0$ such that
\begin{align} &N(S_n\times A, X)\nonumber\\ &\quad \ge \sharp \{ (K,L)\mid \operatorname{Gal}(K/k) \simeq S_n, \operatorname{Gal}(L/k) \simeq A, \operatorname{Disc}(O_KO_L) = \operatorname{Disc}(K)^{m} \operatorname{Disc}(L)^{n} < X\}\nonumber\\ &\quad\sim C_0 X^{1/m}. \end{align}
The last line follows from Lemma 3.2. We can get a better understanding of the constant 
$C_0$ by means of Dirichlet series. Let 
$f(s)$ be the Dirichlet series of 
$S_n$ degree 
$n$ extensions with absolute discriminant, and 
$g(s)$ be the Dirichlet series of 
$A$ extensions with absolute discriminant. Then the Dirichlet series for pairs 
$\{(K,L)\}$ with respect to 
$\operatorname {Disc}(K)^{m}\operatorname {Disc}(L)^{n}$ is 
$f(ms) g(ns)$. The analytic continuation and pole behavior of 
$f$ and 
$g$ have both been well studied [Reference Taniguchi and ThorneTT13, Reference WrightWri89, Reference WoodWoo10]. It has been shown that 
$f(s)$ has the rightmost pole at 
$s = {1}/{\operatorname {ind}(S_n)}= 1$ and 
$g(s)$ has the rightmost pole at 
$s = {1}/{\operatorname {ind}(A)}$. Recall that for arbitrary abelian group 
$A$, the quantity 
${m}/{\operatorname {ind}(A)} = {p}/({p-1})$ where 
$p$ is the minimal prime divisor of 
$|A|$, so 
${1}/{m} > {1}/{n\operatorname {ind}(A)}$. Therefore the rightmost pole of 
$f(ms)g(ns)$ is at 
$s={1}/{m}$, and the order of the pole is exactly the order of the pole of 
$f(s)$ at 
$s=1$, which is 
$1$. By the Tauberian theorem [Reference NarkiewiczNar83],
\begin{equation} \liminf_{X\to \infty} \frac{N(S_n\times A, X)}{X^{1/m}} \ge (\text{Res}_{s=1}f)\cdot g\bigg(\frac{n}{\operatorname{ind}(S_n)\cdot m}\bigg) = (\text{Res}_{s=1}f)\cdot g\bigg(\frac{n}{m}\bigg). \end{equation} Step 2: estimate pairs by 
$\operatorname {Disc}_Y(KL)$. Define 
$\operatorname {Disc}_Y$ to approximate 
$\operatorname {Disc}$ as follows:
\begin{equation} \operatorname{Disc}_{Y,p}(KL) = \begin{cases} \operatorname{Disc}_p(KL) & |p|\le Y \\ \operatorname{Disc}_p(K)^{m} \operatorname{Disc}_p(L)^{n} & |p|>Y, \end{cases} \end{equation}
and 
$\operatorname {Disc}_{Y}(KL) = \prod _{p} \operatorname {Disc}_{Y,p}(KL)$ where the product is over all primes 
$p$ in 
$k$. Recall that 
$\operatorname {Disc}_p(\cdot )$ means the absolute norm of the 
$p$-factor in the relative discriminant, while 
$\operatorname {Disc}_Y$, as described above, is an approximation of 
$\operatorname {Disc}$. The notation would be distinguished by whether the lower index is an upper- or lower-case letter.
Define 
$N_Y(X) = \sharp \{(K,L)\mid \operatorname {Disc}_Y(KL) < X \}$. Since 
$\operatorname {Disc}_Y(KL) \ge \operatorname {Disc}(KL)$, as 
$Y$ gets larger, we get 
$N_Y(X) \le N(X)$ which is an increasingly better lower bound for 
$N(X)$.
We explain here the notation we will use. Let 
$\Sigma _1$ be a set containing, for each 
$|p|\le Y$, a local étale extension over 
$k_{p}$ of degree 
$n$. Let 
$\Sigma _2$ be a set containing, for each 
$|p|\le Y$, a local étale extension of degree 
$m$. We can think of 
$\Sigma _1$ as a specification of local conditions for 
$S_n$ extensions at all 
$|p|\le Y$, and 
$\Sigma _2$ as the specification of local conditions for 
$A$ extensions at all 
$|p|\le Y$. Then let 
$\Sigma = (\Sigma _1, \Sigma _2)$ contain a pair of specification for each 
$p$ with 
$|p|\le Y$. There are finitely many local étale extensions of degree 
$n$ and 
$m$, so there are finitely many different 
$\Sigma _i$ and thus finitely many 
$\Sigma$s for a fixed 
$Y$. We will write 
$K\in \Sigma _1$ if, for each 
$|p|\le Y$, the local étale algebra 
$(K)_p$ is in 
$\Sigma _1$. Similarly, we will write 
$L\in \Sigma _2$ if, for each 
$|p|\le Y$, the local étale algebra 
$(L)_p$ is in 
$\Sigma _2$. We will write 
$(K, L)\in \Sigma$ if 
$K\in \Sigma _1$ and 
$L\in \Sigma _2$.
For each 
$\Sigma _1$, we know the counting result of 
$S_n$ degree 
$n$ extensions [Reference Bhargava, Shankar and WangBSW15] with finitely many local conditions
\[ N_{\Sigma_1}(S_n, X) = \sharp \{ K \mid \operatorname{Gal}(K/k) \simeq S_n, K\in \Sigma_1\}, \]
and similarly for abelian extensions with 
$\Sigma _2$ as the specification [Reference MäkiMäk85, Reference WrightWri89, Reference WoodWoo10].
Given a fixed 
$Y$, we can relate 
$\operatorname {Disc}_Y(KL)$ and 
$\operatorname {Disc}(KL)$ for pairs 
$(K,L)\in \Sigma$ as follows:
\begin{align} \operatorname{Disc}_Y(KL) & = \prod_{|p|\le Y} \operatorname{Disc}_p(KL) \prod_{|p|>Y} \operatorname{Disc}_p(K)^{m} \operatorname{Disc}_p(L)^{n}\nonumber\\ & = \operatorname{Disc}(K)^{m} \operatorname{Disc}(L)^{n} \prod_{|p|\le Y} \operatorname{Disc}_p(KL) \operatorname{Disc}_p(K)^{-m}\operatorname{Disc}_p(L)^{-n}\nonumber\\ & = \frac{\operatorname{Disc}(K)^{m} \operatorname{Disc}(L)^{n} }{d_\Sigma}, \end{align}
where 
$d_{\Sigma }$ is a factor only depending on 
$\Sigma$ (see § 2 for full discussion). Therefore for a fixed 
$Y$ and 
$\Sigma$, the relation 
$\operatorname {Disc}_Y(KL)\le X$ is equivalent to 
$\operatorname {Disc}(K)^{m} \operatorname {Disc}(L)^{n}\le d_\Sigma X$ for 
$(K,L)\in \Sigma$. Applying Lemma 3.2 to 
$N_{\Sigma _1}(S_n, X^{1/m})$ and 
$N_{\Sigma _2}(A, X^{1/n})$, we show that there exists a constant 
$C_Y$ such that
\begin{equation} \lim_{X\to\infty} \frac{N_Y(X)}{X^{1/m}} = C_Y. \end{equation}
For each 
$Y$, the counting 
$N_Y(X) \le N(X)$ gives a lower bound, therefore
\begin{equation} \lim_{Y\to \infty} \lim_{X\to\infty} \frac{N_Y(X)}{X^{1/m}} = \lim_{Y\to\infty} C_Y \le \liminf_{X \to \infty} \frac{N(X)}{X^{1/m}}. \end{equation}
By definition of 
$N_Y$, the constant 
$C_Y$ is monotonically increasing as 
$Y$ increases and will be shown to be uniformly bounded in the next step. So the middle limit in (5.7) does exist and gives a lower bound on 
$N(X)$.
Step 3: bound 
$N(X) - N_Y(X)$. Our goal is to prove the other direction of the inequality (5.7), that is, to prove
\begin{equation} \lim_{Y\to\infty} C_Y \ge \limsup_{X \to \infty} \frac{N(X)}{X^{1/m}}, \end{equation}and thus
\begin{equation} \lim_{X\to\infty} \frac{N(X)}{X^{1/m}} = \lim_{Y\to \infty} \lim_{X\to \infty}\frac{N_Y(X)}{X^{1/m}} = \lim_{Y\to\infty}C_Y . \end{equation}
To get an upper bound of 
$N(X)$ via 
$N_Y(X)$, we need to bound on 
$N(X)-N_Y(X)$. It suffices to show the difference is 
$o(X^{1/m})$.
By definition, the difference is exactly
\begin{align} N(X) - N_Y(X) & = \sharp \{(K,L)\mid \operatorname{Disc}(KL) < X < \operatorname{Disc}_Y(KL)\}\nonumber\\ & = \sum_{\Sigma'} \sharp\{ (K,L)\in \Sigma'\mid \operatorname{Disc}(KL) < X < \operatorname{Disc}_Y(KL) \}, \end{align}
where we explain the local condition 
$\Sigma '$ as following.
Each 
$\Sigma '$ specifies: (1) a finite set of primes 
$S$; (2) for each 
$p\in S$ and 
$p| n!m$ (meaning 
$p$ is possibly wildly ramified in either 
$K$ or 
$L$), a pair of ramified local étale algebras 
$(h_p, g_p)$ over 
$k_p$ at 
$p$ of degree 
$n$ and 
$m$, respectively; (3) for each 
$p\in S$ and 
$p\nmid n!m$, a pair of inertia generators 
$(h_p, g_p)$ with 
$h_p\in S_n$ and 
$g_p\in A$ up to conjugacy. We will write 
$(K,L)\in \Sigma '$ if: (1) for each 
$p\in S$, the local étale algebras 
$(K)_{p} = h_p$ (or 
$I_p(K)= \large \langle h_p \large \rangle$) and 
$(L)_{p} = g_p$ (or 
$I_p(L) = \large \langle g_p \large \rangle$) for 
$K$ and 
$L$; (2) for each 
$p\notin S$, 
$K$ and 
$L$ are not simultaneously ramified at 
$p$ (i.e. the set 
$S$ contains exactly the primes where both 
$K$ and 
$L$ are ramified). So 
$\Sigma '$ gives a specification of local conditions for 
$(K, L)$ at infinitely many places. By only remembering the local specification 
$\{ h_p \mid p\in S \}$ on 
$S_n$ extensions, we will write 
$K\in \Sigma '$ if 
$(K)_p = h_p$(or 
$I_p(K)= \large \langle h_p \large \rangle$) for all 
$p\in S$. Similarly, for abelian extension 
$L$, we will write 
$L\in \Sigma '$ if 
$(L)_p = g_p$ (or 
$I_p(L)= \large \langle g_p \large \rangle$) for all 
$p\in S$. Denote by 
$\operatorname {exp}(\cdot )$ the corresponding exponent of 
$p$ in the relative discriminant. By § 2, at tame places, 
$\operatorname {exp}(\cdot )$ is equal to 
$\operatorname {ind}(g)$ where 
$g$ is the generator of the inertia group 
$I_p$; at possibly wildly ramified places, the exponent 
$\operatorname {exp}(\cdot )$ could be determined by 
$(K)_p$ or 
$(L)_p$. We will write 
$\operatorname {exp}(h_p, g_p)$ to denote the exponent of 
$\operatorname {Disc}_p(KL)$ where 
$(K)_p= h_p$ (or 
$I_p(K)= \large \langle h_p \large \rangle$) and 
$(L)_p = g_p$(or 
$I_p(L)= \large \langle g_p \large \rangle$). This quantity is completely determined by 
$h_p$ and 
$g_p$ by Theorem 2.4. Given a fixed 
$\Sigma '$, by definition of 
$\operatorname {exp}(h_p, g_p)$, we can relate 
$\operatorname {Disc}(KL)$ for 
$(K, L) \in \Sigma '$ to the product as follows:
\begin{align} \operatorname{Disc}(KL) &= \operatorname{Disc}(K)^{m} \operatorname{Disc}(L)^{n} \prod_{p\in S} |p|^{\operatorname{exp}(h_p, g_p) - m\cdot \operatorname{exp}(h_p)-n\cdot \operatorname{exp}(g_p)}\nonumber\\ &= \frac{\operatorname{Disc}(K)^{m} \operatorname{Disc}(L)^{n} }{d_{\Sigma'}}. \end{align}
So the summand indexed by 
$\Sigma '$ in (5.10) is
\begin{align} & \sharp\{ (K,L)\in \Sigma'\mid\operatorname{Disc}(KL) < X < \operatorname{Disc}_Y(KL) \}\nonumber\\ &\quad \le \sharp\{ (K,L)\in \Sigma'\mid\operatorname{Disc}(KL) < X\}\nonumber\\ &\quad = \sharp\{ (K,L)\in \Sigma'\mid\operatorname{Disc}(K)^{m} \operatorname{Disc}(L)^{n} < Xd_{\Sigma'}\}\nonumber\\ &\quad = \sharp\bigg\{ (K,L)\in \Sigma'\biggm|\prod_{p\notin S} \operatorname{Disc}_p(K)^{m} \operatorname{Disc}_p(L)^{n}< \frac{X}{\prod_{p\in S} |p|^{\operatorname{exp}(h_p,g_p)} }\bigg\}. \end{align}
If all primes in 
$S$ are smaller than 
$Y$, then 
$\operatorname {Disc}(KL) = \operatorname {Disc}_Y(KL)$, therefore only 
$\Sigma '$ with 
$\prod _{p\in S} |p|>Y$ is non-zero. Denote 
$\prod _{p\notin S}\operatorname {Disc}_p(K)$ by 
$\operatorname {Disc}_{\mathrm {res}}(K)$. Given 
$\Sigma '$ and a conjugacy class 
$d$ in 
$S_n$, define 
$q_d = \prod _{p\in S, h_p= d}' p$ where 
$\prod '$ means the product is taken only over tamely ramified 
$p$ in 
$S$. Then we can bound the number of 
$K\in \Sigma '$ with bounded 
$\operatorname {Disc}_{\mathrm {res}}(K)$ as follows:
\begin{align} \sharp \{ K \mid K\in \Sigma', \operatorname{Disc}_{\mathrm{res}}(K) \le X\} &= \sharp \bigg\{ K \biggm| K \in \Sigma' , \operatorname{Disc}(K)\le X \prod_{p\in S} |p|^{\operatorname{exp}(h_p)}\bigg\}\nonumber\\ &= O_{\epsilon}\bigg(\prod_{d}|q_d|^{-r_d} \prod_{p\in S} |p|^{\operatorname{exp}(h_p)}\bigg) X \nonumber\\ &= O_{\epsilon}\bigg(\prod_{d}|q_d|^{-r_d+\operatorname{ind}(d)}\bigg) X, \end{align}
where we apply Lemma 5.1 for the second equality. We will show why we could ignore wildly ramified primes at this step. There are only finitely many primes that could possibly become wildly ramified and there are finitely many local étale algebras over 
$k_p$ with bounded degree at each 
$p$, therefore the constant 
$|p|^{\operatorname {exp}(h_p)}$ is uniformly bounded at all possibly wildly ramified primes 
$p$. Thus the product of 
$|p|^{\operatorname {exp}(h_p)}$ over all possibly wildly ramified primes 
$p$ is also uniformly bounded by an absolute constant, say by 
$C$. So we could get an upper bound of the second line by considering 
$\operatorname {Disc}(K)\le CX \prod _d |q_d|^{\operatorname {ind}(d)}$. Similarly, we could bound the number of 
$A$ extension with bounded 
$\operatorname {Disc}_{\mathrm {res}}(L)$ as follows:
\begin{align} \sharp \{ L \mid L\in \Sigma', \operatorname{Disc}_{\mathrm{res}}(L) \le X\} &= \sharp \bigg\{ L \biggm| L \in \Sigma' , \operatorname{Disc}(L)\le X \prod_{p\in S} |p|^{\operatorname{exp}(g_p)}\bigg\}\nonumber\\ & = O_{\epsilon}\bigg( \bigg(\prod_{p\in S} |p|^{\operatorname{exp}(g_p)} \bigg)^{\epsilon}\bigg) X^{1/a(A)}\ln^{b(A)} X\nonumber\\ & = O_{\epsilon}\bigg( \prod_{p\in S} |p|^{\epsilon} \bigg) X^{1/a(A)}\ln^{b(A)} X, \end{align}
where for the second equality we apply Theorem 4.12 since 
$(L)_p = g_p$ (or 
$I_p(L)= \large \langle g_p \large \rangle$) implies that 
$p^{\operatorname {exp}(g_p)} |\operatorname {disc}_p(L)$. Now applying Lemma 3.2 to distribution functions of 
$\operatorname {Disc}_{\mathrm {res}}(K)^{m}$ (obtained by (5.13)) and 
$\operatorname {Disc}_{\mathrm {res}}(L)^{n}$ (obtained by (5.14) ) in (5.12), we get
\begin{align} & \sharp\bigg\{ (K,L)\in \Sigma'\biggm|\operatorname{Disc}_{\mathrm{res}}(K)^{m} \operatorname{Disc}_{\mathrm{res}}(L)^{n}< \frac{X}{\prod_{p\in S} |p|^{\operatorname{exp}(h_p,g_p)} }\bigg\}\nonumber\\ &\quad \le O_{\epsilon} \bigg(\prod_{d}|q_d|^{-r_d+\operatorname{ind}(d) +\epsilon}\bigg) \bigg(\frac{X}{\prod_{p\in S} |p|^{\operatorname{exp}(h_p,g_p)}}\bigg)^{1/m}\nonumber\\ &\quad \le O_{\epsilon} \bigg(\prod_{d}|q_d|^{-r_d+\operatorname{ind}(d) +\epsilon} \prod_{p|q_d} |p|^{-\operatorname{ind}(d, g_p)/m}\bigg)X^{1/m}\nonumber\\ &\quad \le O_{\epsilon} \bigg(\prod_d |q_d|^{\delta+\epsilon}\bigg)X^{1/m}, \end{align}
where for the last second inequality we plug in 
$\operatorname {exp}(h_p, g_p) = \operatorname {ind}(d, g_p)$, and for the last inequality we apply Lemma 5.1 and get 
$\delta = \max _{d\in S_n, c\in A} (-r_d+ \operatorname {ind}(d) - \operatorname {ind}(d,c)/m ) <-1$.
For each fixed 
$\Sigma '$, a list of 
$(q_d)$ of relatively prime ideals of 
$k$, over all conjugacy classes 
$d$ in 
$S_n$, is determined by 
$\Sigma '$. Conversely, for each list 
$(q_d)$, we will show that there are at most 
$O_{\epsilon }(\prod _d q_d)^{\epsilon }$ many 
$\Sigma '$s giving the list 
$(q_d)$. Let 
$M_p$ be the upper bound on the number of pairs 
$(h_p, g_p)$ of ramified local étale algebra over 
$k_p$ with degree 
$n$ and 
$m$ respectively, and let 
$M$ be 
$\prod _p M_p$ over all 
$p$ with 
$p|n!m$. For each 
$q_d$, the number of options for 
$\Sigma '$ at 
$p|q_d$ is bounded by 
$(n!m)^{\omega (q_d)}$, therefore the total number of options for 
$\Sigma '$ is bounded by 
$M (n!m)^{\omega (\prod _d q_d)} = O_{\epsilon }(\prod _d q_d)^{\epsilon }$.
Finally, we can bound the difference (5.10) as follows:
\begin{align} N(X) - N_Y(X) & \le \sum_{\Sigma'} \sharp\bigg\{ (K,L)\in \Sigma'\biggm|\operatorname{Disc}_{\mathrm{res}}(K)^{m} \operatorname{Disc}_{\mathrm{res}}(L)^{n} \le \frac{X}{\prod_{p\in S}|p|^{\operatorname{exp}(h_p, g_p)}}\bigg\}\nonumber\\ & \le X^{1/m} O_{\epsilon} \bigg(\sum_{(q_d), \prod_d |q_d|> Y} \prod_d |q_d|^{\delta+\epsilon} \bigg)\nonumber\\ & \le X^{1/m} O_{\epsilon} \bigg(\sum_{|q|>Y} |q|^{\delta+\epsilon}\bigg). \end{align}
Therefore the summation in the last line is convergent since 
$\delta <-1$ and 
$N(X) - N_Y(X)$ is uniformly bounded as 
$O(X^{1/m})$. By taking 
$Y = Y_0$ for some 
$Y_0>0$, we get that
\[ C_Y \le \limsup_{X\to \infty} \frac{N(X)}{X^{1/m}} \le C_{Y_0} + O(1), \]
which shows the uniform boundedness of 
$C_Y$ for all 
$Y>0$ and the convergence of 
$C_Y$ as 
$Y$ approaches to infinity. Moreover, the difference
\begin{equation} \lim_{Y\to \infty}\limsup_{X\to\infty}\frac{N(X) - N_Y(X)}{X^{1/m}} \le \lim_{Y\to \infty} \sum_{|q|>Y} O_{\epsilon} (|q|^{\delta+\epsilon} )= 0, \end{equation}therefore proving that
\begin{align} \limsup_{X\to\infty} \frac{N(X)}{X^{1/m}} & \le \lim_{Y\to \infty}\bigg( \lim_{X\to\infty} \frac{N_Y(X)}{X^{1/m}} + \limsup_{X\to\infty}\frac{N(X) - N_Y(X)}{X^{1/m}}\bigg)\nonumber\\ & = \lim_{Y\to \infty}C_Y. \end{align}Acknowledgements
I am extremely grateful to my advisor M. M. Wood for constant encouragement and many helpful discussions. I would like to thank M. Bhargava, J. Klüners, A. Shankar, T. Taniguchi, F. Thorne and J. Tsimerman for helpful conversations. I would like to thank, in particular, M. Bhargava for a suggestion to improve the uniformity estimate, and F. Thorne for a suggestion to improve the product lemma. I would also like to thank M. Bhargava, E. Dummit, G. Malle, A. Shankar, T. Taniguchi, T. Yasuda, and the anonymous referee for suggestions on an earlier draft. I thank the anonymous referee for pointing out a mistake in the computation in Section 4 in an earlier draft and for many helpful comments. This work is partially supported by National Science Foundation grant DMS-1301690.
