As one of the inventors of the twelve-tone technique and the first well-known composer of twelve-tone music, it makes eminent sense that Arnold Schoenberg would be understood by scholars and musicians as a traditionalist, in both the positive and negative senses. Much fruitful work has been done that shows ways in which Schoenberg carried over elements of classical and Romantic form and harmony into his twelve-tone compositions. To mention a few examples, one thinks of Richard Kurth’s illustrations of analogies to classical phrase types and tonic-dominant harmonic progressions in the opening of the Menuett from the Suite op. 25, or Ethan Haimo’s demonstration of how Schoenberg preserves the typical modulation schemes of sonata form using regions of twelve-tone rows in the opening movement of the Fourth Quartet op. 37 (Reference KurthKurth 1996: 105; Reference HaimoHaimo 2002: 225–6). On the other hand, it was Schoenberg’s obstinate tendency to hold on to classical and Romantic conventions of rhythm, form, and texture that caused Pierre Boulez the irritation he so vehemently expressed in ‘Schoenberg Is Dead’ (Reference BoulezBoulez 1952). But there is one way in which Schoenberg’s music preserved musical tradition that previous commentators and critics have hardly mentioned, perhaps the one with the most significance for long-range coherence in his twelve-tone music: what he called ‘musical idea’.
What exactly is a musical idea? Schoenberg’s explications of it in his writings were less than systematic, and, unfortunately, he never illustrated the concept with one of his own pieces, tonal, atonal, or twelve-tone, so there is room for disagreement on how to understand the term. The closest thing he provided to a textbook definition is found in the essay ‘New Music, Outmoded Music, Style and Idea’ (Reference Schoenberg, Black and SteinSchoenberg 1975c):
In its most common meaning, the term idea is used as a synonym for theme, melody, phrase or motive. I myself consider the totality of a piece as the idea: the idea which its creator wanted to present. But because of the lack of better terms I am forced to define the term idea in the following manner: Every tone which is added to a beginning tone makes the meaning of that tone doubtful. If for instance, G follows after C, the ear may not be sure whether this expresses C major or G major, or even F major or E minor, and the addition of other tones may or may not clarify this problem. In this manner there is produced a state of unrest, of imbalance which grows throughout most of the piece, and is enforced further by similar functions of the rhythm. The method by which balance is restored seems to me the real idea of the composition.
Note that here a musical idea is defined as a tonal piece: the initial problem which causes imbalance that grows through the course of the piece, and is eventually resolved at or near the end, is defined as an uncertainty regarding the tonal context of pitch classes C and G. And, not surprisingly, the literature that attempts to illustrate ‘musical idea’ through analysis, primarily by Schoenberg’s student Patricia Carpenter and her own students, deals almost exclusively with tonal music: Carpenter’s article ‘Grundgestalt as Tonal Function’, an insightful study of tonal problems, elaborations, and solutions in the first movement of Beethoven’s op. 57 piano sonata, is the first and one of the best examples of analytic work in this vein (Reference CarpenterCarpenter 1983).
Since the notions of ‘tonal context’ or ‘tonal problem’ are not possible in twelve-tone music, however, it is more difficult to grasp how a musical idea might serve as the framework for a twelve-tone piece. Since, in the twelve-tone style, no note should be considered any more central than any other, how can one perceive a note as foreign or distant from the centre? In my Schoenberg’s Twelve-Tone Music, I explored a number of ways in which pitch classes, intervals, and set classes can participate in narratives that involve creating an ideal state, setting another state in opposition to it, allowing that opposition to elaborate itself and branch out in various ways through the piece, and finally resolving it. Some of my analyses highlighted problems and elaborations that stem from the differences between a symmetrical pitch-class or interval pattern (presented or implied at the beginning) and various close or distant approximations of it. The symmetrical pattern is then reasserted at or near the end, and the approximations are connected to it in significant ways, as a solution. In other cases, the initial opposition and elaboration involve different partitions of different rows that create what seem like irreconcilable pitch-class or set-class elements. The solution will then consist of demonstrating how the conflicting partitions and their clashing consequences can be traced back to the original source row. Finally, a number of Schoenberg’s twelve-tone pieces, particularly later ones, include a struggle between various source row forms for primacy, which is resolved in favour of one of the potential sources at piece’s end.
The bulk of this chapter will be devoted to illustrating how musical idea is manifested in two of Schoenberg’s twelve-tone piano pieces: the Prelude from the Suite for Piano op. 25, written right at the beginning of his twelve-tone period in 1921–3, and the Piano Piece op. 33a, written in 1928–9 after Schoenberg had gained some facility at working with row pairs related by combinatoriality; ‘hexachordal inversional combinatoriality’ refers to a property between inversionally related row forms in which the corresponding hexachords have no notes in common and may be combined vertically into other orderings of the twelve-note universe. Both the Prelude and the Piano Piece express their musical idea by elaborating and resolving an opposition between a symmetrical ideal and close or distant approximations of it: the symmetrical pattern consists of pitch classes in the Prelude, and of pitch intervals in op. 33a. Given the limits of this chapter, I will not be able to give these pieces thorough section-by-section analyses, as I do in chapters 2 and 5 of Schoenberg’s Twelve-Tone Music, but instead will highlight how their problems are posed, elaborated, and resolved with a few snapshots.
Suite for Piano Op. 25, Prelude
The Prelude was the first piece by Schoenberg to be written in the twelve-tone style throughout, and a number of scholars have claimed that it does not use the row according to the conventional notion, as a single, consistent linear ordering of all twelve pitch classes. Ethan Haimo argues for what he calls a ‘tetrachordal polyphonic complex’, a division of the row into its three discrete tetrachords, which are then ordered freely between themselves (but usually preserve ordering within themselves) and often appear simultaneously (Reference HaimoHaimo 1990: 85–6). In what follows, I will sometimes count twelve-tone rows using ‘order positions’ (meaning first, second, third, etc., notes in the row), starting with 0 and ending with 11, and will highlight them in bold, so that tetrachords ordered within themselves but not between themselves might read: 4–5–6–7, 0–1–2–3, 8–9–10–11; or 8–9–10–11, 0–1–2–3, 4–5–6–7; or other such combinations. However, when these same twelve numbers (0–11) are not in bold, they represent the different pitches of the chromatic scale, regardless of octave. Therefore, C is represented as 0, C♯/D♭ as 1, D as 2, and so on. Hence, a C major triad could be represented as [047].
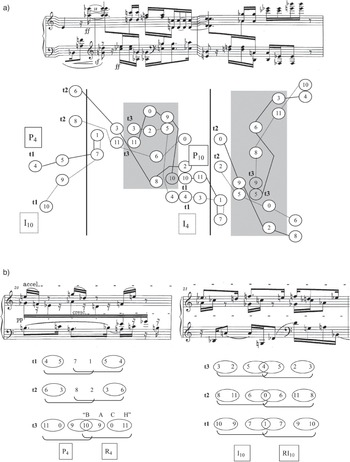
Part of Schoenberg’s set table for the piece, in the transcription provided by Reinhold Brinkmann for the collected edition of Schoenberg’s works, is reproduced in Figure 4.1, to which I have added a pitch-class map (Reference 396Schoenberg and BrinkmannSchoenberg 1975d: 77), while the autograph version of the table appears earlier in this volume as Figure 1.2. Haimo also reproduces this same set table, to provide evidence that Schoenberg had not yet conceived of the source row of the Prelude as a linearly ordered twelve-tone row – but I am interested in it for a completely different reason. Namely, it sets the discrete tetrachords of P4 (the prime form beginning on pitch class 4) and R4 (the retrograde of that same form) against one another, tetrachord by tetrachord, so that each line of the configuration creates a palindrome, and the whole also creates a symmetrical pitch-class structure. This structure then becomes the ‘ideal state’ in the piece, which is only approximated at the beginning (creating a problem), approached more closely but then completely abandoned for a different symmetrical structure in the middle (the elaboration of the problem), and finally realised in its perfect form near the end as a solution.
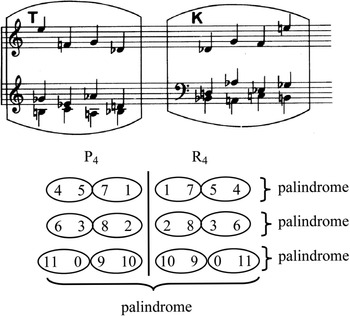
Figure 4.1 Part of Schoenberg’s set tables for the Suite, op. 25, with a pitch-class map
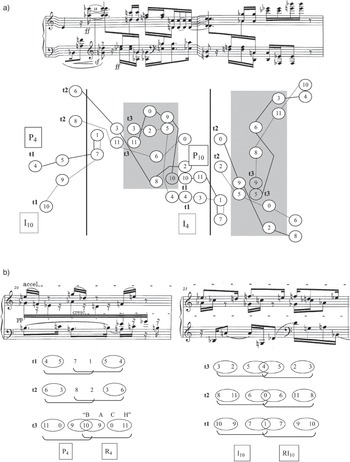
Figure 4.2 illustrates the opening of the piece, in which the ideal symmetrical shape is hinted at but not realised. The pitch-class map at the top of the example shows that when P4 and P10 are divided into discrete tetrachords and the corresponding tetrachords placed against one another, instead of the full collection of six contiguous dyad palindromes that P4 and R4 had created, only two are realised contiguously (<7, 1> – <1, 7> and <8, 2> – <2, 8>), while two are realised by a contiguous dyad and a non-contiguous one: <4, 5> – <5, 4> and <11, 10> – <10, 11>. In this way, the combination of P4 and P10 can only hint at the perfect symmetry that P4 and R4 would have created. Looking now at how these four palindromic dyads are projected in the score itself, it seems that Schoenberg has in fact attempted to highlight the available symmetries in a variety of ways: <7, 1> – <1, 7> through proximity and similar contours and articulations (accents), <8, 2> – <2, 8> through similar contours and articulations, <4, 5> – <5, 4> by means of similar dynamics and articulations, and finally <11, 10> – <10, 11> with similar articulations. These dyads account for much of the ‘balance’ that Kurth celebrates in this opening phrase’s ‘mosaic polyphony’ (Reference KurthKurth 1992: 190–6). But they still fall short of a completely symmetrical state, and that creates a problem – with its associated opportunities for elaboration and solution.

Figure 4.2 Schoenberg, Prelude op. 25, bb. 1–3
As the Prelude continues, it breaks up into subsections of the overall binary form’s A section (bb. 1–16a) that contain pairs and sometimes trios of row forms, in bb. 3b–5a, 5b–7a, 7b–9a, 9b–11a, and 11b–13a. These early sections fluctuate between pairings that yield fewer palindromic dyads and those that yield more, and also vary the number of potential two-note palindromes that are emphasised as audible motives within the texture. With b. 13, however, comes a passage that approximates the ideal more closely than anything heard before – but falls just short. It is shown in Figure 4.3.
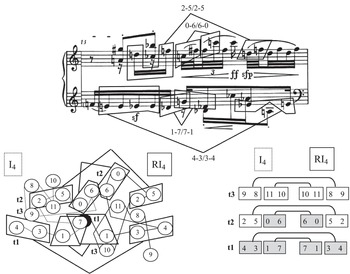
Figure 4.3 Schoenberg, Prelude op. 25, b. 13
The lower right-hand corner of the example shows that I4 (the inversion of the prime form that starts on pitch class 4, around that pitch class) and RI4 (the retrograde of I4), the row pair featured in this passage, have the potential for six palindromic dyads because they are retrogrades of one another. But only three of these dyads are highlighted in the music itself (shaded in the example): <0, 6> – <6, 0>, <4, 3> – <3, 4>, and <1, 7> – <7, 1>, the last of which is realised by using an overlap to create a three-note horizontal mirror in the middle of the left-hand part. As the registrally sensitive pitch-class map in the lower left-hand corner and the marked score at the top of the example show, the other three potential dyad palindromes are all obscured in some way. <9, 8> and <11, 10> are given as verticals in the right hand of b. 13a and answered in the left hand of b. 13b by horizontal renditions of <10, 11> and <8, 9> that have parts of other dyads interleaved between them. And the second dyad in <2, 5> – <5, 2> is reversed within the tremolo figure (marked in the score, together with the three highlighted palindromes). This is not a solution quite yet, though it comes close.
Before finding its eventual solution, however, the Prelude wanders off into one more subsection that elaborates the problem more radically than anything heard before, the climactic passage near the beginning of the large A′ section at bb. 17b–19. It is portrayed, with its rather complex pitch-class map, in Figure 4.4a. As the pitch-class map shows (once it is untangled), there are a number of contiguous and non-contiguous dyad invariances between P4, I10, P10, and I4 that enable Schoenberg to assign various pitch pairs to more than one tetrachord, and, in addition, within both row pairs the second and third tetrachords routinely begin before the first and second finish, creating multiple overlaps. All four rows contain pitch classes 1 and 7 in order positions 2 and 3, and the first tetrachords of P4 and I10 link to one another on the downbeat of b. 18 through this invariance, as do the first tetrachords of P10 and I4 on the downbeat of b. 19. The non-contiguous dyad invariances begin with pitch classes 3 and 11, which appear in order position 5 of P4 and I10, and then swap places in order position 8 of the same rows. Schoenberg uses this to create a link (expressed as repeating notes Cb5 and Eb5 in the left hand of b. 18a) between the second and third tetrachords of P4 and I10. Other tetrachords that are linked in similar ways are the third tetrachords of P4 and I10 with the first tetrachords of P10 and I4, through {4, 10} (left hand of b. 18b), the second tetrachords of P4 and I10 with the second tetrachords of P10 and I4, through {0, 2} (right hand of bb. 18b–19a), and the second and third tetrachords of P10 and I4, through {5, 9} (left hand of b. 19a).
Figures 4.4a and b Schoenberg, Prelude op. 25, bb. 17b–21
The ensuing tangle of tetrachords and pitch classes with dual meanings, so much more complicated than the simple palindromic ideal of Figure 4.1, nevertheless creates its own symmetrical shape. It is highlighted within Figure 4.4a’s pitch-class map by the white circles inside the two shaded boxes: the verticals {3, 11}, {0, 2}, {6, 8}, and {5, 9} in b. 18, balanced by {5, 9}, {6, 8}, {0, 2}, and {3, 11} in b. 19. Kurth calls this the ‘gamma palindrome’ and highlights it as the most important and perceptible of three pitch palindromes in the passage, which do not synchronise with each other and together ‘motivate [a] drive toward some greater stability’ (the loud dynamics and registral extremes also mark this passage as unsettled) (Reference KurthKurth 1992: 200–6). But in the larger context of the subsections that have preceded it, we can also understand Kurth’s ‘gamma’ as the ultimate elaboration of the work’s problem, which follows all the approaches to and departures from complete horizontal symmetry of all twelve contiguous dyads in bb. 1–17 with a completely different approach to dyad symmetry involving non-contiguous verticals. It is almost as if the piece is saying: ‘I’ve tried to attain this piece’s ideal pitch-class palindrome for seventeen bars and failed. I’m going to try a completely different kind of palindrome.’
This ultimate elaboration of the problem, this high point of instability, is followed immediately by a passage that Kurth claims to bring ‘desired stability’ (Reference KurthKurth 1992: 205), and that I understand as the solution to the work’s problem: bb. 20–21, portrayed in Figure 4.4b. In each of these measures, since retrograde-related rows are again pushed up against one another, tetrachord by tetrachord, P4/R4 and I10/RI10, there is the potential for six dyad palindromes – the ideal shape. In b. 20, this potential is not fully realised, because <7, 1> and <8, 2> do not reverse themselves. But the other four dyads in the configuration not only reverse their pitch classes, but also their pitches, so that the music takes a large step closer to perfect symmetry. In b. 21, it gets all the way to perfect pitch-class symmetry, as the middle dyad pairs overlap in a single note, <5, 4, 5>, <6, 0, 6>, and <7, 1, 7>. The one detail preventing complete pitch symmetry is Schoenberg’s transposition of A and B♭ in the left hand at the end of the measure down one octave. The passage’s function as a solution following bb. 17–19’s ultimate elaboration is made clearer, I think, by Schoenberg’s drastic reduction in dynamics from ff to pp and narrowing of the register.
Piano Piece Op. 33a
I have shown how, at the very beginning of Schoenberg’s twelve-tone period, he created a narrative spanning the op. 25 Prelude which manifests the ‘musical idea’, by suggesting a symmetrical pitch-class pattern, obscuring it further, and bringing it back into closer focus, then presenting an alternative symmetry that is nothing like the first in a climax, and, finally, realising the symmetry that was originally only suggested in a denouement. Five years later, after discovering and developing the hexachordal-combinatorial relationship between rows, he would return to the same sort of idea presentation in the op. 33a Piano Piece, expressing an old narrative in a new way. Op. 33a’s initial problem has to do with an incompatibility it presents between intervallic symmetry and row order, as shown in Figure 4.5a.

Figures 4.5a and b Schoenberg, Piano Piece op. 33a, bb. 1–9
As the example shows, the two principal (and combinatorial) rows of the piece, P10 and I3, are first presented out of order as a series of six discrete tetrachord sonorities (with the second row’s tetrachords in retrograde) in bb. 1–2, then both of them in linear order, but reversed with RI3 above R10, in bb. 3–5. The extensive reordering of notes in bb. 1–2 enables a pattern between the unordered pitch intervals of the six chords that is both horizontally and vertically symmetrical. (Schoenberg associated simultaneous horizontal and vertical symmetry with perfection in a number of his other pieces, and it even portrayed God’s perfection in Moses und Aron (cf. Reference BossBoss 2014: 332–41).) Counting intervals up from the bottom produces <1, 5, 5>, <4, 2, 3>, <6, 2, 3>, followed by a sequence of chords that reverses the previous elements and simultaneously flips them upside down: <3, 2, 6>, <3, 2, 4>, <5, 5, 1>. I call this the ‘palindromic ideal’ in Figure 4.5a. Once row order regains control in bb. 3–5, however, the pitch-interval symmetry of the opening measures disappears and is replaced by a less immediately audible symmetry, that caused by set classes: 4–23 (0257), 4–1 (0123), 4–10 (0235), 4–10, 4–1, 4–23. I call this the more abstract ‘echo’ of the ‘palindromic ideal’. The problem that op. 33a poses in its opening measures has to do with the seeming incompatibility of vertical and horizontal symmetry on the one hand and row order on the other: can both coexist? Or must row order necessarily weaken perfect intervallic symmetry?
Before answers to these questions are produced near the end of the piece, the first step in the realisation of the musical idea in op. 33a is progressively to obscure both the palindromic idea and the echo, similar to the way the Prelude op. 25 blurred its palindromic pitch-class pattern in its opening measures. Figure 4.5b shows how bb. 6–9 obfuscate the symmetries of the previous example through rhythmic displacement, as well as moving certain notes up or down by octave. (In the larger sonata form that spans op. 33a, bb. 6–9 constitute the first variation of bb. 1–5’s first theme.) In b. 6’s variation of the first chord of the palindromic ideal, C3, F3, and B♭3 rise an octave and B2 is delayed an eighth note, forming unordered pitch-interval stack <5, 5> followed by −13 (rather than <1, 5, 5>). The second chord delays its top three notes by an eighth, changing <4, 2, 3> to <+4, 2, 3>. And the rhythmic displacements and octave transfers carry on through the remaining four chords, changing what had been six horizontally and vertically symmetrical tetrachords into six conglomerations of chords and melodic intervals, all of which are unique and some of which are not even tetrachords (at the end of b. 7).
Bars 8–9 perform the same kind of obfuscation through rhythmic displacement of the set-class symmetrical ‘echo’ of bb. 3–5. To produce something like the original passage’s palindrome (4–23, 4–1, 4–10, 4–10, 4–1, 4–23), I had to group notes from different parts of the measure and from overlapping parts of the texture, creating a pitch-class segmentation that calls to mind the gerrymander – that is, manipulating the boundary line of a legislative district to favour a particular party – from partisan politics. Even with the gerrymanders, though, the sequence of set classes does not form a pure horizontal mirror: the initial pair (4–23 and 4–1) repeats. Through rhythmic and registral changes, but also through repeating parts of the row out of order, Schoenberg begins to obscure the perfect and imperfect symmetries of his opening.
After a second variation of the P theme in bb. 10–13 that continues the process of obfuscation, the subsidiary theme enters in bb. 14–18, shown in Figure 4.6a. This passage and the one that immediately follows (Figure 4.6b) play an elaborating role within op. 33a’s ‘musical idea’ that is closely analogous to the part bb. 17–19 (Figure 4.4a) played in the Prelude – after the initial symmetry is progressively obscured, the S theme casts it aside and tries to attain symmetrical perfection in a completely different way (but still using the main pair of combinatorial rows, P10 and I3). Namely, the subsidiary theme abandons the intervallic and set-class symmetry of the opening measures in favour of horizontal pitch symmetry, particularly in the right hand of the piano. Bars 14 and 15 present the first hexachord of P10 as the complete palindrome <B♭4, F4, C4, B3, A3, F♯4, A3, B3, C4, F4, B♭4> (some pairs of notes are grouped vertically) followed by an incomplete version of the same. Bars 16–18 then supply the second hexachord of P10, split into two pitch palindromes: <D♭5, E♭4, G5, A♭4, G5, E♭4, D♭5> and <D5, E4, G5, A♭4, G5, E4, D5>. The left hand accompanies with the corresponding hexachords of I3 mostly in linear arrangements, forming aggregates between the hands in bb. 14–16a and 16b–18.

Figures 4.6a and b Schoenberg, Piano Piece op. 33a, bb. 14–22
This attempt to create horizontal pitch symmetry does a certain amount of violence to the ordered presentation of P10 in bb. 14–18. In the following closing section, shown in Figure 4.6b, the same incentive results in even more confusion with respect to the linearity of the row form. Not only are parts of rows taken forward and backward, but also notes of the complete linear presentations of R10, RI3, and the second hexachords of P10 and I3 are missing. Bars 19–20 set R10 in the right hand against RI3 in the left, using rhythms and textures reminiscent of first theme material (this abbreviation of thematic material is my main justification for calling this section ‘closing’). R10 progresses as far as order position 9, pitch class 0, and then that pitch class with its predecessors, <9, 6, 11, 0>, gets caught up in another pitch palindrome, <A6, F♯6, B5, C5, B5, F♯6, A6>, which repeats. Meanwhile, RI3 also only progresses as far as its order position 9, pitch class 1, which likewise takes part in a smaller pitch palindrome, <D3, C♯2, D3>. In both cases, it is the emergence of the pitch palindromes that causes the row to be incomplete. Likewise, the second hexachord of I3 that counterpoints with the second hexachord of P10 in bb. 20–23a, using the rhythms and textures of the S theme, stops one note short, not reaching all the way to pitch class 9, because it gets entangled in a small palindrome, <B♭3, F3, B2, F3, B♭3>. The C theme elaborates the problem within the Piano Piece’s musical idea by showing, repeatedly and forcefully, that the alternative way of making palindromes proposed by the S theme is not an acceptable substitute, because it destroys the integrity of the ordered row. The violence it does in the pitch-class realm is made much more tangible by the forte dynamic marking and ‘martellato’ of bb. 19–20.
So now that it has become clear that pitch palindromes cannot reconcile the piece’s initial conflict between symmetry and row order, but in fact have the completely opposite effect, it remains for Schoenberg to show how those two properties can coexist within the same texture. After a fairly long development section (bb. 25–32a) where he gradually rebuilds the palindromic ideal of bb. 1–2, interval by interval, bb. 32b–34 presents the recapitulation of the P theme – portrayed in Figure 4.7. Instructors of undergraduate core theory who use op. 33a as an introduction to twelve-tone music will certainly recognise the right hand in bb. 32–33a as that place to which they send their students to find the source row of the piece in its pure, unadulterated form, presented without order changes, missing notes, or verticals to confuse the analytic process. RI3 follows it in bb. 33b–34, but with several verticals and a short palindrome involving the third discrete tetrachord in b. 34b. The left hand in this section accompanies with the combinatorial forms I3, followed by R10 – in order between the tetrachords, but with the order within the tetrachords compromised by verticals.
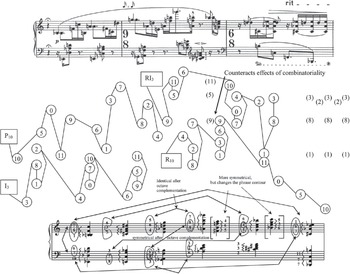
Figure 4.7 Schoenberg, Piano Piece op. 33a, bb. 32b–34
Still, these measures present one of their row forms in proper order, and the other three in something relatively close to proper order. It is remarkable, then, that at the same time they are able to preserve some (but not all) of the palindromic ideal, the horizontally and vertically symmetrical pattern, of bb. 1–2. At the bottom of Figure 4.7, the discrete tetrachords of P10 and RI3 in the right hand as well as I3 and R10 in the left are stacked vertically so as to preserve the register of each note, and unordered pitch intervals between the pitches are listed. The intervals of P10 and RI3 (from the bottom up) are: <1, 6, 7>, <5, 3, 6>, <4, 6, 5>, <8, 6, 7>, <5, 4, 6>, and <7, 6, 1> – different intervals from bb. 1–2, but preserving some of the same symmetries. Most salient is the inverted relationship between verticals 1 and 6, which replicates the outside chords of the palindromic ideal in a different form. But verticals 2 and 5 also share pitch intervals 5 and 6 in corresponding locations (not inverted), preserving some of their horizontal symmetry; as do verticals 3 and 5, which preserve interval 6 in the middle position and octave-complement the intervals on the outside: 4 and 5 become 8 and 7. Finally, there are also a few vertical symmetries between the hands, marked at the bottom of Figure 4.7 with circles and arrows.
This passage constitutes the solution to op. 33a’s problem, the demonstration that vertical and horizontal symmetry and row order can indeed coexist. It is certainly true that it could have done a more thorough job of mirroring its interval stacks in the right hand. The bracketed chords after verticals 4 and 5 at the bottom of Figure 4.7 show what those verticals would have looked like had Schoenberg created an exact horizontal and vertical palindrome like the one in bb. 1–2. It would indeed have been possible for the right hand to play through these bracketed verticals in the order prescribed by RI3, <A5, B4, F5, F♯4> and <B♭4, C6, G5, E5>, forming a perfect union of intervallic symmetry and row order. But that would have made the arch contour in the right hand less clear, obscuring an important feature that makes a connection between this passage and the opening measures.
Not every twelve-tone piece Schoenberg wrote expresses a complete musical idea – problem, elaborations, and solution – as the two examples I have discussed in this chapter do. Moses und Aron, because of its subject – Moses’s failed attempt to communicate God to his people – organises itself around an incomplete musical idea: an initial problem, representing the conflict between Moses’s words and Aron’s images, which continues to elaborate itself without ever coming to resolution (see Reference BossBoss 2014, 330–94). Other pieces with texts – for example ‘Tot’ from the Drei Lieder op. 48 – abstract a ‘basic image’ from the text and use that as an organising principle rather than an idea (Stephen Peles explains quite well how the image of a unitary entity with two opposite sides controls the partitions and intervallic and pitch-class patterns of that song) (Reference PelesPeles 2004). But, in general, the ‘musical idea’, adapted for use as an analytic framework, is an invaluable tool for understanding how Schoenberg’s music coheres and exactly how he carried on the tradition of his German and Austrian predecessors.