When steep density or temperature gradients exist in a plasma, the condition of validity of the Spitzer–Härm transport theory (Spitzer & Härm, 1953) is broken, that is, λ_e /L < 2 × 10⁻³, where λ_e is the mean free path and L is the temperature scale length. This implies that the electron transport and its effect on the plasma characteristics cannot be considered local anymore (Luciani et al., 1983, 1985; Epperlein & Short, 1990, 1992; Bychenkov et al., 1995; Alouani Bibi & Matte, 2002). Moreover, in such situations, as will be shown later, the electrons that carry the most heat flux have velocities below the Spitzer value, that is, 3.7 v_th, where v_th is the thermal velocity

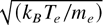
, which also induces a decrease of the thermal conduction in plasma (Mora & Yahi, 1982). Such steep gradients occur in many plasma physics situations, and particularly for laser-heated plasmas in contexts such as inertial confinement fusion (ICF). Moreover, in addition to the noted transport anomaly, there is also another aspect that was not fully taken into account yet, related to the fact that the laser energy absorption in underdense plasmas is mainly due to inverse bremsstrahlung, which is known to cause a deformation of the electron velocity distribution function (EVDF; Langdon, 1980) from a Maxwellian to a super-Gaussian, exp(−(v/v_m)^m), 2 < m ≤ 5, which causes additional changes to the plasma characteristics, that is, temperature and heat flux and electron–ion energy exchange, as shown below.

In this work, we present our approach to take into account both the nonlocal character of electron transport and the effect of the strong collisional heating mechanism on the population of electrons that cause the nonlocality. As first shown in several works (Langdon, 1980; Matte et al., 1988), in an underdense plasma interacting with a high-intensity laser beam, the important parameter that can be used to estimate the deviation from the Maxwellian shape of the electron velocity distribution function is the ratio α = Z(v_osc /v_th)², which is often referred to in the literature as Langdon parameter, where Z is the ion charge state, v_osc = |eE|/mω₀ is the velocity of oscillation of the electrons under the effect of the laser beam's electric field E, ω₀ is the laser angular frequency, and v_th = (k_BT/m_e)^1/2 is the electron thermal velocity. The Maxwellian limit corresponds to α << 1, which means that thermal processes are dominant in plasma, or, in other words, the rate of relaxation of the distribution function is higher than the heating rate. This is particularly true for low-Z plasmas, where electron–electron collisions are important. When α is of order 1 or more, and v_osc < v_th, which can be the case for high-Z plasma even at intermediate intensities, laser energy absorption is reduced by a factor R = 1 − 0.553/(1 + (0.27/α)^0.75) (Langdon, 1980). This results from the fact that laser energy absorption by means of inverse bremsstrahlung causes a shift in the low-energy part of the electron distribution function in the velocity space to intermediate energies, because these electrons are more effectively heated due to the (1/v³) dependence of the Inverse Bremsstrahlung (IB) operator. Thus, after some time, which depends on α and density and temperature, the EVDF will have a deficit of low energy electrons that causes a decrease of the laser energy absorption in the plasma (Langdon, 1980). The decrease of the low-energy part of the distribution function also modifies the energy exchange between electron and ions. The high energy part of the electron distribution function is also reduced: As these electrons are nearly collisionless, they are less heated than the others. As these electrons are the main cause of the nonlocality of heat flux in plasma, one would expect considerable modifications to the nonlocal electron transport in plasma.

The main idea behind the nonlocal electron transport is that the heat flux is no longer described by the local Spitzer–Härm value, which actually greatly exaggerates it, but in each spatial point of the plasma the heat flux is changed by the nonlocal contribution of electrons for which the free path length is comparable with the temperature scale length.

This has been expressed at first by Luciani et al. (1983) in the following form, which will be adopted in this work:

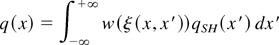
with

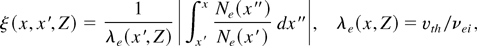
q_SH is the Spitzer–Härm heat flux, w is the nonlocal kernel, λ_e is the electron mean free path, and ν_ei is the mean electron–ion collision frequency at velocity v_th.

The main task for us is to develop a new nonlocal kernel taking into account the effects of both nonlocal electron transport and the modification of the distribution function by the collisional heating. To do so, we performed a series of simulations in perturbation mode using our electron kinetic code “FPI” (Matte et al., 1988; Ethier & Matte, 2001). An initially uniform plasma is heated by a uniform laser field with a small intensity modulation. Such an approach was first used by Epperlein and Short (1994). Assuming the form given by Eq. (1), the Fourier transform of the nonlocal kernel is then the ratio of the computed heat flux to the Spitzer–Härm one in Fourier space, that is,

The α dependence is obtained by increasing the laser intensity and keeping the percent of the modulation constant. Sets of the nonlocal kernels are therefore obtained for different α, Z, and kλ_e. An example of such a kernel is presented in Figure 1 for Z = 11. The inverse Fourier transform of these propagators (Alouani Bibi & Matte, 2002) has been incorporated in our hydrodynamic code Hydro+, in which the following hydrodynamic equations are solved:

n_e,i are the particle densities, taking into account the quasineutral assumption (n_e = Zn_i), m_i is the ion mass, P is the thermal pressure (n_eT_e or n_iT_i), F_p is the laser ponderomotive force, P_v is the ion viscosity, q is the heat flux, Q_ei is the term for the energy exchange between electrons and ions, and S is the external electron energy source term, which is here the collisional laser heating. The reduction of S due to the Langdon effect (Langdon, 1980) is taken into account.

The Fourier transform of the nonlocal propagator, that is, corrected thermal conductivity obtained by our Fokker–Planck code for Z = 11, as a function of kλe at different values of the Langdon parameter α(α = Z(vos /vth)2).

The energy equation has been improved by adding a new modification to the electrons–ions energy exchange term, accounting for the effect of non-Maxwellian electron distribution function (Alouani Bibi & Matte, 2003), that is,

where

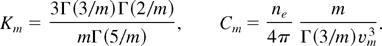
Here m represents the index of the super-Gaussian electron distribution index m, which in turn depends on the Langdon parameter α according to the formula given by Matte et al. (1988), m = 2 + 3/(1 + 1.66/α^0.724). This correction is important, and the value of K_m varies from 1—the traditional value (NRL Plasma Formulary, 2000)—in the Maxwellian case to 1.98 when the deformation is strongest, that is, for m = 5. This shows a considerable change to the temperature equilibrium between electrons and ions when the electron distribution function is not a Maxwellian. On the other hand, as the variation of C_m with m is almost as 1/K_m, there is little effect if T_i << T_e.

Using Hydro+, we performed simulations of a hot spot (actually a hot line, as the geometry is planar) interacting with an initially uniform plasma. The range of the laser beam intensity was varied from 10¹⁴ to 10¹⁶ W/cm² at different wave lengths. Here we present results for λ₀ = 0.53 μm and I₀ = 2 × 10¹⁵ W/cm². The laser pulse is considered Gaussian, with a temporal full width at half maximum (FWHM) of 200 ps in time and size of 19 μm in space. The plasma is considered initially uniform with undercritical electron density and Z = 11. In all the results presented here, the initial electron density and temperature were n_e = 2 × 10²⁰ cm⁻³ and T_e = 0.5 keV. Before the illustration of the characteristics of the plasma such as temperature or heat flux, let us first show some results concerning the kinetic aspect of the plasma in such situations. In Figure 2, the isotropic component of the electron distribution function is plotted as a function of energy at the laser pulse maximum and at different spatial points in plasma. The point x = 0 corresponds to the center of the hot spot region; we clearly see that as we move from the cold to the hot region of the plasma, the distribution function becomes less Maxwellian and we note the reductions in the low- and high-energy parts with an increase in the intermediate energies. In Figure 3 we plot f₁ v⁵, the maximum of which gives an immediate indication of the heat flux carriers, (as q ∼ ∫f₁ v⁵ dv). We can clearly see that the heat flux carriers have an energy much lower that the one assumed by the Spitzer–Härm theory.

The isotropic component of the electron velocity distribution function at different spatial points in the plasma. The point x = 0 corresponds to the hot spot region. I0 = 2 × 1015 W/cm2, Z = 11, FWHM (temporal) 200 ps, and FWHM (spatial) 19 μm. The profiles are presented at the laser pulse maximum (200 ps).

The quantity f1 v5 illustrating the contribution to the heat flux. I0 = 2 × 1015 W/cm2, Z = 11, FWHM (temporal) 200 ps, and FWHM (spatial) 19 μm. The profile is presented at the laser pulse maximum (200 ps).

The temperature and heat flux profiles are presented in Figures 4 and 5, and are compared with the results obtained by our electron kinetic code FPI, and with two other nonlocal heat flow formulas from the literature (Luciani et al., 1983; Epperlein & Short, 1992). In these figures, the ions are considered cold and immobile. From Figures 4 and 5, it can be clearly seen that the new proposed nonlocal model gives a good agreement with the Fokker–Planck results, in particular near the hot region where the distribution function is strongly non-Maxwellian (see Fig. 2).

Temperature profiles: [bull ]: Fokker–Planck results (FPI), *: our newly developed model (AM), □: Luciani–Mora–Virmont, Δ: Epperlein–Short. I0 = 2 × 1015 W/cm2, Z = 11, FWHM (temporal) 200 ps, and FWHM (spatial) 19 μm. The profiles are presented at the laser pulse maximum (200 ps).

Heat flux: [bull ]: Fokker–Planck results (FPI), *: our newly developed model (AM), □: Luciani–Mora–Virmont, Δ: Epperlein–Short. I0 = 2 × 1015 W/cm2, Z = 11, FWHM (temporal) 200 ps, and FWHM (spatial) 19 μm. The profiles are presented at the laser pulse maximum (200 ps).

The temperature profiles for ions for the same physical situation as mentioned above with both a traditional and a modified energy exchange term (Eq. (4)) are illustrated in Figure 6. Because of the correction to the electron–ion exchange term, the ions are more heated than predicted by the traditional formula. The difference in the ion temperature with and without the correction is about 100 eV in the case presented; however, as noted by Alouani Bibi and Matte (2003), this is principally related to the initial temperature conditions of electrons and ions. Taking this effect into account can be helpful in modeling with better accuracy the energy transfer between the components of the plasma.

The ion temperature profiles, with and without the correction to the energy exchange term. The electron heat transport is computed with our nonlocal model. I0 = 2 × 1015 W/cm2, Z = 11, FWHM (temporal) 200 ps, and FWHM (spatial) 19 μm. The profiles are presented at the laser pulse maximum (200 ps). Initial temperatures: Te = Ti = 0.5 keV.