2. A framework for understanding reference-dependence effects

The example that will be used here to illustrate the role of reference-dependence effects is that in which the two dimensions are a monetary cost and the probability of an adverse health outcome. The lessons that will be derived are quite general, although this format differs from the usual discussions of WTA–WTP. In the conventional framework that draws its inspiration from the prospect theory model, the reference dependence is in terms of the arguments of the utility function, such as money or valued goods. In my example, there is a reference effect not only for money, but also for risk. In particular, I also incorporate the role of reference risk effects introduced in Viscusi, Magat and Huber (Reference Viscusi, Magat and Huber1987), in which the reference effect is with respect to the probability of a particular outcome. The model structure consequently will illustrate the role of reference-dependence effects both with respect to monetary values as well as probabilities. Encompassing both kinds of reference effects is of considerable practical importance for policy in that many policies involve the reduction in the probability of injury or illness from risk and environmental regulations or the increased likelihood of survival from the availability of new drugs.

The analysis is in terms of the marginal tradeoff rates between health risks and money. This formulation highlights the nature and direction of the reference-dependence effects and may be better suited to analyzing the role of different reference point effects than focusing on the compensating variation needed to maintain the individual’s current utility level or, in this instance, the expected utility level.Footnote ² Thus, the analysis will consider the implications for all the four possible combinations of increases and decreases in the values of the two matters of concern, cost and risk.

Figure 1 presents the four possible quadrants of the tradeoff relationships, where the risk of the adverse outcome is on the horizontal axis and the cost of the policy is on the vertical axis. Higher cost levels and higher risk levels are each undesirable. Quadrant 1 is the standard WTP amount in which the individual incurs an increase in costs in order to reduce the risk from its current reference level. For simplicity, I assume that all reference-dependence effects are with respect to the individual’s current situation. In Quadrant 1 there will be no reference risk effect as the risk is decreasing, but there will be a reference-dependent effect due to the increase in costs, consistent with the original prospect theory formulation. The existence of the reference-dependence effect for costs will tend to depress the WTP values. Quadrant 2 involves a cost increase and a risk increase, each of which are undesirable and will generate pertinent reference effects. This quadrant focuses on the tradeoff among losses (TL). A priori there is no way to ascertain which effect is more consequential, as the risk reference effect will boost valuations and the cost reference effect will depress the tradeoff rate. Quadrant 3 is the WTA situation in which there is a risk increase, which has an associated reference risk effect, and a cost decrease in which there is no reference-dependence effect. The final quadrant 4 is the tradeoff among gains (TG) quadrant in which both cost and risk have declined and have no associated reference point effects.

Figure 1 Categorization of reference-dependence effects.

It is instructive to illustrate the role of reference-dependence effects using simple models in which there is some linear reference point effect with respect to adverse departures from the reference point. Actual reference-dependence effects could be much more complex. There could be reference point effects with respect to gains as well as losses.Footnote ³ The reference effects also could be nonlinear functions of the extent of the departure from the reference point. Or they could involve interactions among the different reference point influences. The simple model below does, however, indicate the importance of accounting for the potential role of reference points on multiple dimensions.

Consider a choice situation in which there is both a monetary cost and an associated probability of some adverse health impact $h$ . The individual has a utility function $v$ for costs, where $v^{\prime }<0$ . Let the initial cost level be $c_{0}$ . If the new policy has an associated cost of $c_{1}\leqslant c_{0}$ , then the utility of this cost is $v(c_{1})$ . If, however, costs have increased so that $c_{1}>c_{0}$ and there is a reference point effect with respect to the initial cost level $c_{0}$ , then there is some additional loss ${\it\mu}[v(c_{1})-v(c_{0})]$ , where ${\it\mu}>1$ . This type of reference dependence is in the spirit of Kahneman and Tversky’s (Reference Kahneman and Tversky1979) analysis as well as all subsequent studies in which the reference dependence is with respect to the argument of the utility function, whether it be money, a mug in an experiment, or an environmental amenity in a stated preference survey.

A second class of reference-dependence effects is with respect to the probability of some outcome, in this example the health loss $h$ . This type of reference-dependence effect, which was first identified by Viscusi et al. (Reference Viscusi, Magat and Huber1987), pertains to the probability of the particular risk involved rather than a change in some payoff state reference point. The initial risk of the adverse health outcome is $p_{0}$ . The subsequent risk value is $p_{1}$ . If $p_{1}\leqslant p$ then there is no reference point effect, and the expected health loss is given by $p_{1}h$ . If, however, $p_{1}>p_{0}$ so that the probability of the health risk has increased, the expected health loss is given by $p_{1}h+{\it\lambda}(p_{1}-p_{0})h$ . Using this formulation, it is possible to develop an analysis of how the tradeoff rates between cost $c$ , and risk $p_{1}$ differ in the different situations in Figure 1.

Quadrant 1: WTP

In this quadrant the individual has incurred an increase in costs or a financial loss relative to the reference state $c_{0}$ . However, the risk has declined from $p_{0}$ to $p_{1}$ , so there is no reference point effect with respect to the probabilities based on this formulation. The expected utility $u(c_{1}\mid c_{0};p_{1}\mid p_{0})$ consequently simplifies to $u(c_{1}\mid c_{0};p_{1})$ since there is no dependence on $p_{0}$ . The expected utility is consequently

(1) $$\begin{eqnarray}u(c_{1}\mid c_{0};p_{1})=v(c_{1})+{\it\mu}[v(c_{1})-v(c_{0})]+p_{1}h.\end{eqnarray}$$

The tradeoff rate between cost and the health risk probability is

(2) $$\begin{eqnarray}\displaystyle \frac{-\partial c_{1}}{\partial p_{1}}=\displaystyle \frac{h}{(1+{\it\mu})v^{\prime }}.\end{eqnarray}$$

The reference-dependence term ${\it\mu}$ in the denominator reduces the tradeoff rate as the loss in money associated with the WTP value triggers a reference-dependence loss.

Quadrant 2: TL

Matters become more complicated for situations when there are losses with respect to both reference points. If costs have increased from $c_{0}$ to $c_{1}$ , $c_{1}>c_{0}$ , and risks have increased from $p_{0}$ to $p_{1}$ , $p_{1}>p_{0}$ , then there is a loss with respect to both reference points. In this instance, the expected utility $u(c_{1}\mid c_{0};p_{1}\mid p_{0})$ is a function of both the initial and final costs and risks. Thus,

(3) $$\begin{eqnarray}u(c_{1}\mid c_{0};p_{1}\mid p_{0})=v(c_{1})+{\it\mu}[v(c_{1})-v(c_{0})]+p_{1}h+{\it\lambda}[p_{1}-p_{0}]h.\end{eqnarray}$$

The cost–risk tradeoff rate is given by

(4) $$\begin{eqnarray}\displaystyle \frac{-\partial c_{1}}{\partial p_{1}}=\displaystyle \frac{(1+{\it\lambda})h}{(1+{\it\mu})v^{\prime }}.\end{eqnarray}$$

Whether the presence of reference-dependence effects boosts the tradeoff rate (if ${\it\lambda}>{\it\mu}$ ), lowers the tradeoff rate (if ${\it\lambda}<{\it\mu}$ ), or has no effect on the tradeoff rate (if ${\it\lambda}={\it\mu}$ ) depends on the relative magnitude of the two reference point effects. Which is more influential, the financial loss associated with the increased costs or the expected health loss associated with the increased probability of an adverse health effect? These relationships will vary substantially depending on the context and magnitude of the effects.

Quadrant 3: WTA

In the WTA Quadrant 3, there is no cost reference point effect because the person is being compensated when $c_{1}<c_{0}$ , but there is a probability of reference point effect since $p_{1}>p_{0}$ . The expected utility $u(c_{1};p_{1}\mid p_{0})$ consequently is dependent on $p_{0}$ but not on $c_{0}$ , or

(5) $$\begin{eqnarray}u(c_{1};p_{1}\mid p_{0})=v(c_{1})+p_{1}h+{\it\lambda}(p_{1}-p_{0}),\end{eqnarray}$$

so that

(6) $$\begin{eqnarray}\displaystyle \frac{-\partial c_{1}}{\partial p_{1}}=\displaystyle \frac{(1+{\it\lambda})h}{v^{\prime }}.\end{eqnarray}$$

Because ${\it\lambda}>0$ when there are reference-dependence effects with respect to the risk probability, the WTA is increased by the presence of such influences.

Quadrant 4: TG

The simplest case is that in which costs are reduced, as is the risk probability. Because there are gains in both dimensions, there are no reference-dependence effects. The expected utility $u(c_{1},p_{1})$ is not dependent on either $c_{0}$ or $p_{0}$ , so that $u(c_{1},p_{1})=v(c_{1})+p_{1}h$ , so that the cost–risk tradeoff rate is

(7) $$\begin{eqnarray}\displaystyle \frac{-\partial c_{1}}{\partial p_{1}}=\displaystyle \frac{h}{v^{\prime }}.\end{eqnarray}$$

Ordering the tradeoff values

While there is no way to rank order all the different tradeoff rates in general, three of the possibilities in the four quadrants always can be ordered. For the rankings that include the situation in Quadrant 4 in which there are no reference point effects, the following relationships hold:

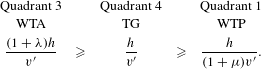(8) $$\begin{eqnarray}\begin{array}{@{}ccccc@{}}\text{Quadrant 3} & & \text{Quadrant 4} & & \text{Quadrant 1}\\ \text{WTA} & & \text{TG} & & \text{WTP}\\ \displaystyle \frac{(1+{\it\lambda})h}{v^{\prime }} & {\geqslant} & \displaystyle \frac{h}{v^{\prime }} & {\geqslant} & \displaystyle \frac{h}{(1+{\it\mu})v^{\prime }}.\end{array}\end{eqnarray}$$

Similarly, when the intermediate case is from Quadrant 2 involving both reference-dependence effects, the relationships follow the ordering:

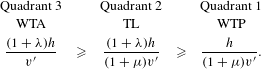(9) $$\begin{eqnarray}\begin{array}{@{}ccccc@{}}\text{Quadrant 3} & & \text{Quadrant 2} & & \text{Quadrant 1}\\ \text{WTA} & & \text{TL} & & \text{WTP}\\ \displaystyle \frac{(1+{\it\lambda})h}{v^{\prime }} & {\geqslant} & \displaystyle \frac{(1+{\it\lambda})h}{(1+{\it\mu})v^{\prime }} & {\geqslant} & \displaystyle \frac{h}{(1+{\it\mu})v^{\prime }}.\end{array}\end{eqnarray}$$

In each of these comparisons, WTA is always the largest value, WTP is the smallest value, and the other values are in the intermediate range. Thus, if there are any reference-dependence effects that should be taken into account, the use of WTP always understates benefits.

The ordering of the two intermediate tradeoff rates for quadrants 2 and 4 depends on the relative magnitude of the reference-dependence effects. The value of

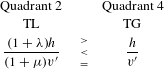(10) $$\begin{eqnarray}\begin{array}{@{}ccc@{}}\text{Quadrant 2}~~~~\ & & \text{Quadrant 4}\\ \text{TL}~~~~\ & & \text{TG}\\ \displaystyle \frac{(1+{\it\lambda})h}{(1+{\it\mu})v^{\prime }}~~~~\ & \begin{array}{@{}c@{}}{>}\\ {<}\\ =\end{array} & \displaystyle \frac{h}{v^{\prime }}\end{array}\end{eqnarray}$$

as

(11) $$\begin{eqnarray}\begin{array}{@{}ccc@{}}{\it\lambda} & \begin{array}{@{}c@{}}{>}\\ {<}\\ =\end{array} & {\it\mu}.\end{array}\end{eqnarray}$$

3. Empirical evidence on the four quadrants

The first study of reference risk effects in Viscusi et al. (Reference Viscusi, Magat and Huber1987) employed a stated preference study of a large sample of consumers who were asked their willingness to purchase reformulated insecticide and toilet bowl cleaner products that in some instances were made safer and in one instance was made riskier. The health risks involved inhalation, skin poisoning, and child poisoning for the insecticide and chloramine gassing, eyeburns, and child poisoning for the toilet bowl cleaner. For the different risk combinations, 62%–77% of the consumers were unwilling to purchase the products at all for any discount if the risk of these injuries increased by 1/10,000. For those consumers willing to purchase the products after receiving a discount, the required discount was several times greater than the extra amount that they would be willing to pay for a much greater 5/10,000 reduction in the current risk level. The substantial WTA–WTP gap found in this stated preference study of risk levels is also mirrored by a large disparity in experimental valuations of lottery tickets in Kachelmeier and Shehata (Reference Kachelmeier and Shehata1992).

To go beyond the WTA–WTP dichotomy, consider the stated preference results reported by Viscusi and Huber (Reference Viscusi and Huber2012) for all four quadrants. Their study used a nationally representative sample of 4,745 households. The focus of the study was on gastrointestinal (GI) risks associated with drinking water. The monthly water bill was the cost component in the study, so both the payment mechanism and the good were familiar to the consumers. Each respondent was told the actual baseline national GI risk, which was 5/100 annually. Thus, the survey conveyed a truthful risk reference point to consumers. All changes in risk in the surveys were with respect to their current risk level, enhancing the credibility of departures from the reference point. Figure 2 provides a capsule summary of the four different scenarios in which changes in the water treatment facility generated the situations involving changes in risk levels and changes in cost.

Figure 2 Possible reference-dependence effects for water treatment policy.

The means, standard errors of the means, and median valuations per 1/1,000 change in the GI risk are summarized in Table 1. The top panel presents the raw actual tradeoff rates, and the bottom panel presents the estimated tradeoff rates derived from the experimental variations alone, controlling for differences across demographic characteristics of respondents. The estimated values are sometime larger, but the ordering among quadrants is similar in each case. Consistent with theoretical predictions in equation (8), the Quadrant 3 WTA value in which there is a reference risk effect is significantly greater than the Quadrant 4 TG value for which there are no reference effects, which in turn significantly exceed the Quadrant 1 value for which there is a cost reference effect. Also following theoretical predictions of equation (9) is that the Quadrant 3 WTA value is significantly greater than the Quadrant 2 TL value. The failure of the Quadrant 2 value to exceed the Quadrant 1 value indicates that the reference risk effect is not strong, at least in the presence of a cost increase as this becomes the dominant concern. That Quadrant 4 values are significantly higher than the Quadrant 2 values is consistent with a theoretical model summarized in equation (10) in which ${\it\mu}<{\it\lambda}$ , or the cost reference point effect is greater than the risk reference point effect.

Table 1 Water quality valuations per 1/1,000 GI risk.

The experimental results also permit an estimation of the role of income effects, which theoretically could contribute to a WTA–WTP disparity. For this sample and for the levels of expenditures considered, the income effects on the total amounts that respondents were willing to pay for safer water or to accept for riskier water are always under a penny. Income effects are consequently negligible and do not account for the WTA–WTP disparity or any other differences in Table 1.

The study by Zong and Knetsch (Reference Zong and Knetsch2013) also analyzed the four cost–risk quadrants using a sample of 206 Chinese students who considered policies offering different combinations of bicycle theft risk and cost. Unlike the water quality study above, the format of the bicycle risk study did not maintain a consistent reference point across treatments. The normal theft rates and the theft rates for the past year were varied across different treatments. The strength of the results consequently hinges on whether the stated values were credible as opposed to respondents bringing to bear their own probabilistic beliefs regarding local bicycle theft risks. In many other experimental contexts prior beliefs combine with the influence of stated probabilities and may account for many purported anomalies in choices involving risk (Viscusi, Reference Viscusi1989). The Zong and Knetsch (Reference Zong and Knetsch2013) study finds, as predicted, that there was a substantial WTA–WTP gap. However, they also found that the values for Quadrant 4 (mean of 46, median of 30) were perhaps somewhat larger than the WTA values in Quadrant 3 (mean of 42, median of 30), but the differences are not statistically significant. The theoretical framework above would have predicted either a higher value for Quadrant 3 or equality if there is no risk reference point effect. The smallest values were for Quadrant 2 (mean of 17, median of 12) and Quadrant 1 (mean of 20 and median of 12), which were also fairly similar in magnitude. The cost reference-dependence effects in Quadrants 1 and 2 were the dominant influence in depressing the valuations as compared to Quadrants 3 and 4. The risk reference effects in Quadrants 2 and 3 were less evident as these estimates are similar to the values in Quadrants 1 and 4. This pattern is similar to that in the Viscusi and Huber (Reference Viscusi and Huber2012) study. However, the role of risk reference effects or other reference point influences could become more prominent in other choice situations such as that in Viscusi et al. (Reference Viscusi, Magat and Huber1987).

The strong cost reference point effects in these studies raise broader considerations. There is not simply a WTA–WTP gap. Rather, the presence of a cost increase tends to depress tradeoff rate for the quadrants involving both directions of changes in risk, including the WTP value. An alternative interpretation is that it is not a cost reference point effect that boosts the values in Quadrants 1 and 2 but rather that people do not fully internalize the financial costs, particularly in experimental contexts when costs are decreasing. Thus, the cost decrease domains may involve a “house money” effect in which the absence of actual financial impacts makes the costs less tangible matters of concern.

4. Implications for estimates of the value of a statistical life

Adjustments for the influence of a WTA–WTP gap based on a benefits transfer approach using current estimates of the average WTA/WTP ratio could have a dramatic effect on benefit assessments involving the value of a statistical life (VSL) if one interprets the VSL estimates as WTA values. Horowitz and McConnell (Reference Horowitz and McConnell2002) found an average WTA/WTP ratio of 7.2, while Tuncel and Hammitt (Reference Tuncel and Hammitt2014) found a ratio of 5.1 for studies involving health and safety. The U.S. Department of Transportation (Reference U.S. Department of Transportation2013) currently uses a VSL of $9.1 million based on a review of the most credible labor market studies, which employ the Census of Fatal Occupational Injury fatality data. Suppose one were to treat the labor market estimates of the VSL as a WTA measure. Adjusting for the average WTA/WTP ratio to convert these values into a WTP value using the meta-analysis WTA/WTP estimates above would lead to a corrected VSL range from $1.3 million to $1.8 million, producing an 80–86% decrease in risk-related benefits. Since these benefits constitute the largest component of recent regulatory benefits, making this adjustment could have substantial policy ramifications. Whether one should adopt a WTP, WTA, or some other tradeoff measure affects whether any adjustment is pertinent. One might argue, as do Knetsch, Riyanto and Zong (Reference Knetsch, Riyanto and Zong2012), that a WTA measure is often the appropriate policy value. In this case, no adjustment is needed if in fact the VSL is a WTA measure.

Setting aside the choice of the appropriate reference point for policy analysis until Section 5, consider the narrower question of whether labor market estimates of VSL are actually generating WTA values or WTP values. In simple theoretical models for which the inspiration can be traced back to Adam Smith, a worker considering a choice between a risk-free job and a risky job requires a compensating differential to take the hazardous job. Contemporary single-period analyses generally frame the job choice as being broader than a pairwise comparison of a risky job and a completely safe job. Instead, the worker is choosing from an opportunities locus of wage–risk combinations. In practice, workers are not starting from ground zero with completely safe employment but instead are making a series of potentially risky job choices throughout their careers. As a result, the pertinent reference point with respect to the risk level and subsequent job decisions is the worker’s reference risk value, which one would expect to be a value that changes over the worker’s career and reflects the risk level of the worker’s current job.

This formulation of the reference risk level for potentially dangerous jobs was the approach adopted by Kniesner, Viscusi and Ziliak (Reference Kniesner, Viscusi and Ziliak2014). Using employment data from the Panel Study of Dynamics in conjunction with annual measures of the fatality rate for different industry-occupational groups, the authors focused on workers who changed jobs in any series of years or over the course of the survey. The job risk associated with the worker’s initial job served as the reference risk level. The article estimated the positive wage premium workers receive for moving to riskier jobs as a measure of WTA as these jobs involve an increase from the worker’s baseline risk level. Workers who move to safer positions incur a loss in terms of the wage premium for risk. The VSL implied by job choices involving moves to safer jobs are WTP amounts. The average annual fatality risk for the sample was 6.3 fatal injuries per 100,000 workers. Workers who switched jobs and moved to riskier positions faced an average job risk of 8.7 per 100,000 workers, while workers who moved to safer positions faced an annual risk of 3.4 per 100,000. A priori one would not expect movements within this fairly narrow range of fatality rates to generate substantial reference point effects. Note as well that while all these risks are relatively small, even the workers who moved to safer positions did not move to risk-free jobs. Indeed, while some jobs are quite safe, there are very few major occupational groups that are completely risk-free.Footnote ⁴ As a result, using the worker’s current job risk is a more appropriate reference point than hypothesizing that the worker has a risk-free reference point. Such a hypothetical job does not characterize the worker’s current position or any other jobs the worker may have held.

The theoretical model that formulates the role of reference-dependence effects in the context of estimating the VSL using labor market data on job changers has a structure that is the wage counterpart to the cost analysis of consumer choice reference points involving changes in risk. The analysis of job changers and their associated compensating differentials gives rise to two quadrants in Figure 3. In Quadrant 1, which is the WTP value, the worker incurs a wage cut in order to obtain a decrease in risk. The operative reference point in this quadrant is that for wages. A reference-dependent effect for wage levels will make the worker reluctant to make any sacrifices from the current wage level, thus reducing the wage cut below what the worker would be willing to sacrifice in the absence of reference-dependence effects. The WTA value is in Quadrant 3, as the worker receives additional compensation to move to the riskier job. In this instance, the reference point effect is with respect to the risk level, as increases in the risk loom larger than they otherwise would in the absence of such effects.

Figure 3 Reference-dependence effects analyzed for labor market valuations of risk.

The empirical results did not indicate any statistically significant gap between the WTA VSL estimates and the WTP estimates of VSL. All differences were within the bounds of error. Based on the point estimates, there is some evidence of a modest, but not statistically significant WTA–WTP discrepancy. In seven of the ten sets of estimates reported, the WTA estimate of VSL exceeded the WTP value. On average across all estimates, the WTA was 17% higher than the WTP.

While there may be some small WTA–WTP gap, it is certainly not consistent with adopting a benefits transfer approach of simply dividing the VSL estimates in the literature by a meta-analysis estimate of the WTA/WTP ratio. As discussed above, labor market estimates of VSL embody both WTP and WTA values depending on the nature of the worker’s pattern of job changing so that it is not correct to assume that they reflect only WTP values. In addition, the generalizability of the average meta-analysis estimates of WTA/WTP is doubtful given the much narrower estimated values in the labor market. Before undertaking adjustments based on other evidence of WTA/WTP ratios, the analyst should ensure that these studies are in fact pertinent to the particular benefit context.

Kniesner et al. (Reference Kniesner, Viscusi and Ziliak2014) suggest that there are several reasons why there were not large WTA–WTP differences. Because the job risks involve small probabilities rather than goods for which the probability of ownership drops from 1 to 0 when it is given up, the role of the reference point may be less salient. The results also are consistent with other findings in some experimental studies, such as Plott and Zeiler (Reference Plott and Zeiler2005) with respect to subjects’ experience with the good and the ability to both buy and sell the good. The risky job choice involves a familiar context with which most workers have substantial experience. It is also a context in which there are both buying and selling opportunities for risk as the worker, in effect, can buy or sell safety by moving to a safer or riskier job. The role of reference points may be less prominent in such situations.

5. Guidelines for choosing the pertinent benefit measure

Selecting the appropriate reference point framing for the benefit value is the most important component of the policy analysis decision. This framing also can be quite controversial as different economic commentators have very different perspectives on whether WTP values, WTA values, or other measures should be used. Much of the controversy can be traced to disagreement with respect to what should be the appropriate reference point for considering whether some outcome constitutes a loss or a gain. As I indicate below, proper application of the analytical framework outlined above should clarify the choice of the benefit measure.

How one should approach this decision depends on the particular context. In the case of government policies, the decisions are prospective in nature. Forex ante policy assessment such as this, the reference point is the baseline situation rather than the outcomes after the policy has been implemented. For that reason, the WTP measure is usually the most logical benefit approach, but as I indicate below it is not always the most pertinent. In contrast, judicial decisions are ex post in nature. The amount that a person should be compensated for property damage or a property taking is generally a WTA value. While one could suggest, as do Cooter and Ulen (Reference Cooter and Ulen1997), that the value of “the harm caused by imposing the bad equals the victim’s WTP to be free from it,” adopting the WTP value would only be pertinent if there is equality between WTP and WTA. In the case of property takings, there may be quite legitimate economic reasons why the person’s WTA greatly exceeds the WTP value, wholly apart from strategic considerations and the well-known hold-up problem in the provision of public goods. The WTA measure is a much more pertinent compensation measure in such instances than is WTP. The focus below will be on benefit–cost analysis of government policies rather than compensation in judicial proceedings.

The four quadrants in Figure 1 provide a useful framework for categorizing the policy choice situation. The WTP value in Quadrant 1 involves the imposition of some cost in return for some benefit that represents an improvement from one’s reference state, such as a decrease in the risk of cancer or the provision of a valued public good. This WTP framing consequently is directly applicable across a broad range of policies. In the case of publicly provided goods that did not previously exist, such as a neighborhood recreation center or a new interstate highway bypass, the cost imposed on the taxpayer is for the provision of new valued goods. Policies reducing risk levels likewise often take the form of valued improvements. Flood control efforts, highway safety measures, occupational safety and health regulations, and reductions in current crime rates all involve pre-existing risks that are included in the range of situations in Quadrant 1. Thus, the reference state for evaluating such policies is not a world with no floods, no traffic accidents, no job injuries, and no crime.

Quadrant 2 of Figure 1 involves costs imposed to advance the policy, as does Quadrant 1. These are typically the quadrants involving the most frequently encountered policy situations. However, in the case of Quadrant 2 the cost is accompanied by the experience of a loss from one’s reference state. If there has been an oil spill for which there is no private responsible party that can be identified, then the cleanup cost would be borne by the public and the policy is operating in a realm in which the risk has increased from the reference value as have costs. Similarly, if there is debris on the road that the public must pay to clean up or if there has been a crime surge from the normal rate, then those situations as well would be Quadrant 2 contexts.Footnote ⁵

Certainly the most prominent policy example where Quadrant 2 is applicable is with respect to climate change policies. The scientific consensus is that the earth is getting warmer, which will have adverse effects relative to our current situation. Economic analyses have documented the considerable policy costs that will be needed to slow down the pace of climate change. Consequently, there will be both reference cost effects and reference risk effects. The reference risk effect from our deteriorating climate should boost society’s valuations compared to a situation in which there are no reference point effects, but there is a competing reference cost effect that is operative as well since climate change policies will entail cost increases. Climate change critics who suggest that the future climate trajectory is a normal fluctuation consequently are questioning both the risk level and whether there is a departure from current reference points. If the critics can succeed in leading the public to believe that climate change policies generate policy improvements as opposed to averting a prospective loss, doing so would move the situation from Quadrant 2 to Quadrant 1, lowering the public’s benefit value.

The Quadrant 3 WTA amount is most pertinent in situations in which there is some kind of compensation provided for incurring a loss. The most natural example is that of liability contexts in which an injurer is seeking to make the victim whole, such as legally required damages after a major oil spill. Also fitting this situation are budgetary cutbacks that will save the citizenry money but will sacrifice some valued programs, such as a reduction in police protection or decreased services at national parks. The Quadrant 3 examples involve a reference risk effect but no cost reference effect so the tradeoff rate between cost and risk should reflect the public’s strong aversion to losing valued services. The WTA values in empirical studies are often quite high, and figure prominently in discussions of benefit measure choices. However, the circumstances in which the WTA values are applicable in evaluating a loss may be much more limited than those encompassed by Quadrant 2 in which there is an accompanying increase in costs as well as a loss.

The final Quadrant 4 involves no reference-dependence effects. Unfortunately, it pertains to the likely infrequent situation in which both costs and risks are decreasing. In some instances, improving overall economic conditions may make it possible to reap gains on both dimensions. For example, reduced societal unemployment rates or demographic shifts that decrease the population share of the high crime-age population each may lead to reduced risks as well as to reduced taxpayer costs for police protection.

Even after identifying the pertinent quadrant and associated empirical estimates, it is worthwhile to assess whether the reference-dependence effects should be taken into account in a policy evaluation. Reference risk effects could arise from considerations that some might view as irrational. The high risk beliefs may stem from a fundamental misunderstanding of the risk change. Consumers may believe that a company’s admission that a reformulation of the product will increase the risk by a very small amount really means that the product will be exceedingly dangerous. One could allay this excessive response to the risk with additional, credible information provision. People also may have exaggerated perceptions of risks, particularly with respect to low probability events called to their attention. Or the mention of a particular class of hazards, such as the risk of cancer, may provoke generalized dread and fears that are not warranted by the actual level and severity of the particular risks involved. Consequently, in the Quadrant 2 and Quadrant 3 situations in which the risk has increased, it is often worthwhile to explore the impetus for the reference risk effect and whether it is based on a sound understanding of the risk.

One might undertake similar explorations with respect to the cost reference effects in Quadrants 1 and 2, and their contrast with Quadrants 3 and 4. Are the reference cost effects reasonable given the individuals’ income levels and other choices? Or are the reference cost effects due to a misunderstanding of the payment mechanism in which, for example, they fear that any one time policy levy will in fact become a permanent tax? The relatively high tradeoff values displayed in Quadrants 3 and 4 also may merit scrutiny, as the presence of “house money” effects may generate an overstatement of the tradeoff values.

Even once purported irrationalities been identified, there will remain the issue of whether the policy values should institutionalize the irrationalities or seek to overcome them. Observers advocating citizen sovereignty and respect for the revealed preferences of consumers might choose to incorporate private valuations in the analysis irrespective of whether they arise from erroneous beliefs and irrational choices. An alternative view, which I advocate, is that the policies should be based on the decisions consumers would make if they were accurately informed and acted rationally, which may include reference-dependence effects. Addressing the choice of the benefit measure ultimately may become intertwined with an assessment of the source of the benefit measure discrepancies and what constitutes irrational behavior.