2. INDUCTIVE SWITCHING SCHEME

Consider configuration shown in Figure 1 for cylindrical geometry. Two inductances, L_z of the load and L₀ of the additional volume are connected electrically in parallel through the convolute 3. Both inductances are powered by a low-impedance microsecond capacitor bank 1 (C, L_g). The connector 5 is open during the capacitor discharge. The current through the conductor 4 with the initial mass M reaches its maximum value I₀. The conductor is accelerated axially by the j × B force up to high velocity. This results in variation of the associated conductor inductance L_p from its initial value L₀. When the conductor reaches the end of the axial acceleration region and goes beyond, the mass of the conductor starts to expand to the large vacuum cavity 6. This may results in interruption of electrical contact of this mass with the electrodes. Or, a small current-carrying portion of the conductor mass m is formed, and it is further magnetically accelerated toward the axis. In both cases, inductive voltage I₀ × dL_p /dt is generated across the load 2. At this moment, the closing switch 5 connects the load to the rest of the circuit and the magnetic energy is transferred into the inductance L_z.

Inductive switch arrangement in the considered electrical circuit. 1—capacitor bank, 2—inductive load, 3—convolute, 4—initial position of a conductor, 5—closing switch, 6—conductor expanding into vacuum, its inductance Lp changes from L0 to L1. M—the main conductor mass, m—possible residual conducting mass.

One should address two important issues here. First, the electrode geometry in Figure 1 is chosen to provide L_p << L_g and dL_p /dt << (L_g/C)^1/2 at the axial stage of the conductor motion. This must ensure efficient current transfer from a low-impedance generator to the conductor volume. Second, consider the motion of possible residual conductor mass m. The impedance dL_p /dt associated with radial acceleration of this small mass is higher than that appearing during the axial acceleration of the whole mass M. In contrast with the other type of fuses or opening switches mentioned above, the impedance dL_p /dt arising during radial acceleration may be proportional to the maximum current I₀ or, at least, remains constant. This scaling is typical for radially imploded fast z-pinches (Matzen, 1997 and the references therein) and suggests potential applicability of the scheme at mega-Ampere currents.

The staged axial-to-radial acceleration is typical for plasma flow switch geometries (Turchi et al., 1987). In the plasma flow switch, however, a part of the conductor mass is supposed to bring the current to the load. The configuration of Figure 1 suggests a different scenario: the moving conductor operates as an opening switch in parallel to the load and does not penetrate into the load region.

3. EXPERIMENT ON STAGED ACCELERATION

Therefore, a critical assumption for efficient operation of the scheme of Figure 1 is that the electrode geometry provides L_p ≈ L₀ << L_g during the magnetic energy storage time (typically of the order of 1 μs for modern low-impedance capacitor banks) and that the conductor inductance subsequently increases to the value L₁ >> L₀. Also, an inductive voltage must be generated by the accelerating and expanding conductor in order to allow power multiplication and further current transfer to a load if the latter is connected.

Validation of these criteria for the geometry of Figure 1 was performed on GIT12 generator (Kovalchuk et al., 1997) at the current level of 2–3 MA. The terminal part of GIT12 was modified as shown in Figure 2. Moderate level of the available generator current and hence limited maximum mass of the conductor 4 in Figure 1 did not allow usage of azimuthally homogeneous shells. The conductor in Figure 2 is organized by 12 tungsten 11 μ-diameter wires tighten horizontally at the initial position 4 between the cathode, R_c = 10 cm, and the anode, R_a = 13 cm. The acceleration distance between the wires and the exit to the large volume 6 is 4 cm.

Experimental arrangement on GIT12. C—cathode, A—anode, D1, Dc, D2—dI/dt probes for measurements of the currents I1, Ic, and I2, respectively. Other notations are the same as in Figure 1.

The GIT12 generator 1 is equivalent to a capacitor, C = 14.4 μF, an active resistance of 0.04 Ohm and a storage inductance (up to the D₁ probe position), L_g = 89 nH. Geometrical inductance between D₁ and the convolute 3 is L_v = 11.3 nH. Corresponding value for the part between the convolute and the initial wire position 4 is L₀ = 7.8 nH. The voltage U_s is measured at the bottom of a 424 nH mechanical support (not shown in Fig. 2) and then inductively corrected. Therefore, the voltage values corresponding to the convolute, U_c, and to the initial wire position, U_p, as well as the varying wire array inductance during the shot, L_p, can be evaluated as follows:

Figure 3 shows experimental result on the temporal profiling of the inductance L_p. The convolute current I_c becomes negative indicating intense (> 1 MA) current losses, presumably under the form of electron beams provoked by the plasma radiation. The convolute current is measured as the average of three D_c probe signals and it is sensitive to the vacuum current. The convolute leakages effectively act as a vacuum diode load in parallel to the inductive part and they lead to the I₂ current drop.

Measured currents upstream, I1, and downstream, I2, of the convolute in a wire array shot. Ic—convolute current. Measured, Us and inductively corrected, Uc and Up, voltages in the same shot, as well as the inductance evaluated from experimental results with the help of Eq. (1). Is.c.—current of all the probes in a calibration shot with a short circuit at the position 4 in Figure 2.

The results of Figure 2 confirm that the chosen geometry of electrodes allows maintaining low values of L_p ≈ L₀ during the microsecond magnetic energy storage time. Later in time, a voltage pulse is generated having amplitude at the convolute of ∼130 kV. The conductor inductance, evaluated by Eq. (1), increases by approximately 20 nH during 300 ns, and reaches the value of ∼25 nH. Therefore, the chosen geometry of electrodes allows efficient coupling with a low-impedance capacitor bank and further generation of the voltage of inductive origin.

An undesirable but predictable effect in the described setup is that the conductor mass is limited by the limited number of wires. The inter-wire distance appears to be almost twice larger than the anode-cathode gap. This may not allow formation of a compact conducting shell and can lead to relatively slow plasma precursor formation (Lebedev et al., 1997; Aleksandrov et al., 2003, 2004; Sinars et al., 2004) instead of acceleration of the whole mass. However, apparently successful L_p(t) staging in Figure 3 and appearance of the voltage multiplication in the experiment suggest that the scheme is further improvable. Usage of very high number of wires (Mazarakis et al., 2004) or of thin foils (Nash et al., 2004) at higher energies may allow either keeping the conductor thickness close to the initial thickness of a solid-state foil (as in the explosively driven magnetic flux compression experiments, Megagauss, 1990), or reaching theoretical limit for a plasma shell thickness, Δz ∼ δ_sk, where δ_sk is the magnetic field skin-depth (Rudakov et al., 2003). Higher shell compactness would provide higher dL_p /dt values to be reachable.

4. IDEAL SCHEME EFFICIENCY

Let us perform a simple analysis on the scheme shown in Figure 1. As shown the experiment, motion of the conductor 4 in Figures 1 and 2 can be presented by variable inductance L_p(t) changing from its initial value L₀ to the final value L₁. This inductance is almost constant at the inductive storage stage. This allows the energy stored in the capacitor C to be converted into magnetic energy in the inductance L_g + L₀. Full energy conversion occurs at the time moment equal to the quarter-period τ of the capacitor discharge in LC circuit:

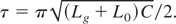
Consider further rapid change of the inductance L_p and simultaneous connection of the load 2 in Figure 2. For the sake of simplicity, we consider an inductive load with constant inductance L_z = const. The load is connected at the moment when the inductance L_p starts to rise. Neglecting the energy dissipation, the magnetic flux in the circuit at this moment is further conserved, and it is equal to the magnetic flux at the moment when L_p = L₁ and when the load current is equal to I_z. This provides us with the following current transfer coefficient:

Here I₀ is the generator current at L_p = L₀, I_z is the load current at L_p = L₁. The energy efficiency coefficient is therefore defined as

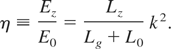
Here E₀ is the initial stored energy and E_z is the magnetic energy in the load inductance. For L_z = L_g, L₀ → 0 and L₁ → ∞ we have η = 0.25 (25 % efficiency) and k = 0.5 (half of the stored current is transferred into the load).

The further logic is the following. The circuit parameters defining feasibility of a pulse power system using the configuration of Figure 1 are L₁ (defining the efficiency of inductive switching), the capacitor bank erecting voltage V, and the duration of the inductive storage phase τ, Eq. (2). To optimize the system, let us consider the function η(L_g). Its maximum occurs at

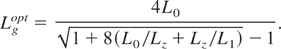
The other important characteristic is the Vτ product, which should be preferably minimized (smaller charging voltages reduce the risk of electric breakdowns and smaller generator current rise-times result in smaller subsequent load current rise-times):

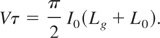
Therefore, for a fixed load inductance and for fixed inductive switch inductances L₀ and L₁, Eqs. (5) and (6) define the maximum energy transfer efficiency η(L_g^opt) and the parameter Vτ.

5. EXAMPLE OF A MEGA-AMPERE GENERATOR

Consider parameters of a pulse power system with inductive load. For example, one could estimate L_z = 5–7 nH as the mean load inductance of a fast z-pinch (Davis et al., 1996; Matzen, 1997). Figure 4 shows calculated values of η(L_g^opt) and Vτ(L_g^opt) for the load with L_z = 7 nH, I_z = 60 MA and for different values of ΔL = L₂ − L₁.

Efficiency η and the parameter Vτ (in MV × μs) for L0 = 2 nH (triangles), L0 = 4 nH (squares) and L0 = 6 nH (circles). The load inductance is Lz = 7 nH.

One can see that the increase of L₀ considerably decreases the maximum efficiency η and increases Vτ. For example, the value L₀ = 4 nH (corresponds to the inductance of electrical connections with the initial conductor position 4 in Fig. 1) yields to η > 10% for ΔL > 30 nH. From the results of Figure 4 and for the case of L₁ = 40 nH, one could derive generator characteristics shown in Table 1.

Generator parameters calculated from Figure 4 for the scheme shown in Figure 1

For a microsecond capacitor bank discharge, the primary generator voltage can be maintained at the level of 2–3 MV, i.e., at the values acceptable for existing technologies of microsecond capacitor banks.

The scheme of Figure 1 allows parallel connection of inductive volumes as schematically shown in Figure 5. This relaxes the requirement on the output voltage of the primary generator. For example, at unchanged performance of the scheme (i.e., same I_z,τ,L₀, and L₁), each capacitor bank is characterized by the parameters shown in Table 2.

Parallel connection to a common load. 1—to two capacitor bank, 2—load, 3—convolute, 4—accelerated conductor, 5—closing switches (dielectric flashover), 6—mechanical support.

Generator parameters calculated from Figure 4 for parallel connection of two inductive switches shown in Figure 5

6. ELECTRICAL CIRCUIT MODEL

Modeling of the electrical circuit of Figure 1 was performed for a z-pinch-type load. Equivalent circuit corresponding to the scheme of Figure 1 can be represented by the following set of equations:

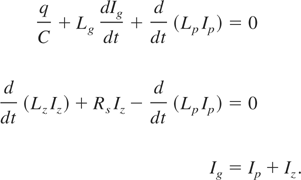
Here C and L_g are the parameters of the capacitive primary storage taken from Table 1. I_g is the generator current; L_p and I_p correspond to the varying inductance and current of the conductor; L_z and I_z are the time-dependent inductance and the current of the load shell. R_s is the resistance of an ideal closing switch connecting L_p and L_z parts (R_s = ∞ during the magnetic energy storage time and then R_s = 0).

The load was assumed to be a perfectly conducting cylindrical shell accelerated by the magnetic field of the load current I_z and having the mass m_z = 0.1 g, the height h_z = 2 cm, and the initial radius r_ini = 2.2 cm.

The conductor 4 in Figure 1 was assumed to be a perfectly conducting foil accelerated by the current I_p and having the mass M = 0.2 g. The axial acceleration occurs at the distance h = 5 cm in the space between a cathode, R_c = 50 cm, and an anode, R_a = 55 cm. In order to model the motion of a small current-carrying portion of the conductor mass m shown in Figure 1, the whole conductor mass is divided into two parts at the end of axial acceleration. The mass M − m continues its axial motion. The small mass m is considered as a perfectly conducting cylindrical shell with the height varying in time and equal to z_M − h, where z_M(t) is the current position of the main conductor mass. This mass is further radially accelerated by the current I_p.

All the moving parts (load shell and the conductor) participating to the whole scheme operation is described by simple equations of motion

Here ξ_i, M_i, and I_i represent accordingly the coordinate, the mass and the current in the described motion, i.e., z, M, and I_p for the main conductor mass; r, m, and I_p for the residual conductor mass compressed radially; r, m_z, and I_z for the load shell. L_i are the varying inductances in corresponding geometries. We also assume a 10-fold radial compression ratio for the masses m and m_z, i.e., their motion is stopped when the masses reach r = R_c/10 and r = r_ini/10 accordingly.

Figures 6 and 7 show the results of numerical solution of the Eqs. (7) and (8) describing the scheme of Figure 1. In the beginning of the capacitor discharge, the current flows through L_g and through the axially accelerated conductor with the mass M. When the conductor passes the length h, the load is connected (R_s = 0) and the current starts to flow simultaneously through the shell of residual mass m and through the load shell with the mass m_z. Both masses are imploded radially towards the axis of the system, Figure 1.

Circuit modeling result for m/M = 0.01. Generator parameters are taken from Table 1. Parameters of the load and of the inductive switch are defined in the text. (a) Currents Ig (dotted), Ip (solid), and Iz (bold); (b) inductance Lp (solid) and the load liner kinetic energy (bold).

The same modeling result as for Figure 6 with m/M = 0.1.

The voltage generated during compression of the mass m allows the power flow into the load. There is an uncertainty in quantifying the residual mass value m. This value could be obtained only from more realistic, multi-dimensional numerical modeling. Figures 6 and 7 show the general trend in influence of this parameter on the scheme efficiency. For example, consider m = 0.01 M and m = 0.1 M. In both cases the load current I_z reaches the maximum value predicted in Section 5 and the generator-to-load energy transfer efficiency is about 10%. However, the higher is the residual mass m, the slower is its compression, the lower is the voltage across the load inductance and the greater is the load current rise-time.