1. Hobbes's State of Nature: State of War
An important cornerstone of Hobbes's political philosophy is his justification for the existence of governments. Hobbes's justification for the existence of government relies on the purported fact that without a government people's lives would be not simply much worse, but utterly unbearable. This is because without a government that has sufficient power to enforce criminal laws and effectively regulate people's behaviors, the state of nature (which is a state where there is no government) will, according to Hobbes, inevitably dissolve into a state of universal war of all against all. Hobbes writes:
Hereby it is manifest that during the time men live without a common power to keep them all in awe, they are in that condition which is called war, and such a war as is of every man against every man. (Leviathan, ch. 13, section 8)
Hobbes has famously summarized the life in the state of nature as ‘the life of man, solitary, poor, nasty, brutish, and short’ (Leviathan, ch. 13, section 9).
2. The Five Conditions of Hobbes's State of Nature
What are the specific conditions of the state of nature that make Hobbes conclude that this state will inevitably result in universal war? Based on textual evidence, the characteristic conditions that, according to Hobbes, would inevitably lead the state of nature to universal war can be summarized in five conditions as follows (I will refer to these as the ‘five conditions of Hobbes's state of nature’)
C1 (Equality): People's physical and mental capabilities are roughly equal.
The most important implication of this condition is that, in the state of nature, even the weakest human being has enough power (either physical or mental) to kill the strongest human being. As Hobbes writes,
For as to the strength of body, the weakest has strength enough to kill the strongest, . . . . As to the faculties of the mind . . . I find yet a greater equality amongst men than that of strength. (Leviathan, ch 13, sections 1, 2)
This means that in the state of nature all others can be a (potential) threat to one's own self-preservation.
C2 (Competition Due To Scarce Resources): In the state of nature, resources are scarce in such a way that there will inevitably arise situations where two people would want to obtain the same object.
Coupled with the condition of equality (i.e., C1), this condition implies that, in the state of nature, one would inevitably face situations where one is in direct competition for a given resource with another person who has the potential to kill. This is what Hobbes predicts in the following passage:
But the most frequent cause why men want to hurt each other arises when many want the same thing at the same time, without being able to enjoy it in common or to divide it. The consequence is that it must go to the stronger. But who is the stronger? Fighting must decide. (On the Citizen, ch. 1, section 6)
And therefore, if any two men desire the same thing, which nevertheless they cannot both enjoy, they become enemies; and in the way to their end, which is principally their own conservation, and sometimes their delectation only, endeavour to destroy or subdue one another. (Leviathan, ch. 13, section 3)
Note that, for Hobbes, there is a resource that is guaranteed to be scarce: power. One of the most significant characteristics of power (over other people) is that it is a zero-sum resource; that is, one person's gain is necessarily coupled with another person's loss. This makes power a scarce resource that not everybody can fully enjoy. And, according to Hobbes, not only do people need power to secure their own self-preservation, but there is a certain proportion of the human population that values power extremely highly and therefore pursues power (not simply as a means for one's self-preservation, but) for its own sake. This leads us to the next two important conditions of the state of nature.
C3 (Two Types of Men): In the state of nature, there exist two types of people: the modest type and the vainglorious type. Furthermore, it is common knowledge that there is a certain proportion of the entire human population that is vainglorious—these are people who enjoy having power over others and who pursue power, not as a means to secure their self-preservation, but for its own sake.
C4 (Non-Universal Egoism): Not everybody seeks to maximize his/her own self-interest (i.e., power.). The modest types, who compose the majority of the entire population, would strictly prefer to cooperate with other people if these other people cooperate in return. By contrast, the vainglorious people are those for whom maximizing self-interest is the primary aim; hence, they would gladly enjoy taking advantage of other people's good intentions whenever it is to their advantage and thus increase their power.
Many scholars have thought that Hobbes was committed to psychological egoism (i.e., a view of human psychology that claims that human beings are solely motivated by self-interest or that human beings are beings who universally maximize their self-interest), and, even more, that universal egoism is absolutely needed for Hobbes to derive his desired conclusion (see Butler Reference Butler and Darwall1983; Hume Reference Hume1975; Broad Reference Broad1950; Kavka Reference Kavka1986; McNeilly Reference McNeilly1966; and Hampton Reference Hampton1986). Conditions C3 and C4 directly defy this standard interpretation, and therefore I feel the need to justify them.
The textual ground for these two conditions comes from the following passages:
Also, because there be some that taking pleasure in contemplating their own power in the acts of conquest, which they pursue farther than their security requires, if others (that otherwise would be glad to be at ease within modest bounds) should not by invasion increase their power, they would not be able, long time, by standing only on their defence, to subsist. (Leviathan, ch. 13, section 4, emphasis added)
In the state of nature there is in all men a will to do harm, but not for the same reason or with equal culpability. One man practices the equality of nature . . . this is the mark of modest man . . . . Another, supposing himself superior to others, wants to be allowed everything . . . that is the sign of an aggressive character. In his case, the will to do harm derives from vainglory. (On the Citizen, ch. 1, section 4, emphasis added)
Clearly, Hobbes is not assuming that everybody is inclined to maximize his/her self-interest (i.e., power). He explicitly distinguishes two types of people: the modest and the vainglorious. And he claims that the modest type “would be glad to be at ease within modest bounds.” In other words, the modest types will stop short of maximizing their self-interest or power once they reach a reasonable threshold. The fact that the modest types will not pursue their interest any further once they reach a reasonable threshold (even when gaining more is possible by exploiting others’ cooperation) implies that they are not the types who are solely motivated by self-interest. The existence of this modest type of people contradicts psychological egoism.
By contrast, the vainglorious type of people are those who will always try to maximize their self-interest/power simply because they enjoy the conquest and having power over other people. However, Hobbes makes it clear that only ‘some’—and not all—human beings fit into this category.
If the state of nature consisted only of the first type, the modest type of people, it might not have been so hard to achieve mutual cooperation without external enforcement. In such situations, people might be able to live in a peaceful anarchy, and establishing a government might not be necessary. However, this is not the case for Hobbes's state of nature. As we have seen, in Hobbes's state of nature, it is a known fact that there are vainglorious people who will try to maximize their self-interest/power at the expense of others by attacking. The major problem is that, in the state of nature, there is no reliable way to identify these vainglorious people in advance. This leads us to our final condition of Hobbes’ state of nature.
C5 (Uncertainty): In the state of nature, people cannot reliably know other people's types.
For the modest type, such uncertainty causes fear that the other party may attack while one is unprepared.
In men's mutual fear . . . I mean by that word any anticipation of future evil. . . . Even the strongest armies fully ready for battle, open negotiations from time to time about peace, because they fear each other's forces and the risk of being beaten. Men take precautions because they are afraid. (On the Citizen, ch. 1, 25)
From this fear of not knowing whether or not one's opponent will attack, the modest type sees launching a preemptive attack as the best way to avoid the worst-case scenario—which is for the modest person to get killed by in an attack by his/her opponent while being unprepared.
And from this diffidence of one another, there is no way for any man to secure himself so reasonable as anticipation, that is, by force or wiles to master the persons of all men he can, so long till he see no other power great enough to endanger him. (Leviathan, ch. 13, section 4)
Note that it is not the lust for power or the desire to conquer, but fear and diffidence that motivate the modest type to attack. In other words, the modest types will attack mainly as a defensive measure. By contrast, the vainglorious types will attack simply for the enjoyment of conquest and of having power over others. Despite the different motivations of the modest and vainglorious types, this means that launching a preemptive attack is a dominant strategy for everybody in the state of nature. This establishes the following lemma:
LEMMA (Preemptive Attack as a Dominant Strategy): In the state of nature, launching a preemptive attack is the dominant strategy for everybody regardless of his/her type.
Remember that, according to Hobbes, it is mainly fear of not knowing whether or not the other party will attack (rather than a lust for power) that motivates the modest types to attack. Absent such fear, the modest types would gladly cooperate and seek peace with other people in the state of nature, as they are the type of people who would be “glad to be at ease within modest bounds.” The reason why this is not possible is that the modest types cannot tell whether their opponents are modest or vainglorious. Thus, for the modest types, it is not egoism, but uncertainty that compels them to attack.
With launching a preemptive attack being a strictly dominant strategy for everybody in the state of nature, Hobbes's pessimistic conclusion, which may be stated as the following theorem, easily follows:
THEOREM (War of Every Man against Every Man): The state of nature results in a state of war of every man against every man.
Hobbes's justification for the existence of governments is widely known; the gist is that a central authority that monopolizes power is necessary, because without it life in the state of nature will inevitably lead to a state of universal war, which everybody finds miserable. However, I think that many people have generally misunderstood the specific mechanism that Hobbes presented in his original text to explain how the state of nature leads to a state of universal war. The most familiar understanding is that it is Hobbes's particular assumption concerning human psychology—universal egoism—that leads him to conclude that the state of nature descends into a state of universal war. I argue that the specific mechanism that drives Hobbes's pessimistic conclusion of the state of nature is not universal egoism, but rather, uncertainty.
As a matter of fact, we have seen specific passages that show Hobbes had explicitly denied universal egoism. This is not to say that Hobbes had completely denied the existence of such egoistic individuals. In fact, it is crucial for Hobbes's argument for there to be people who try to maximize their self-interest/power at the expense of others. However, he says that only some (and not all) human beings fit into this category. ‘Some’ is a vague word, but in everyday usage the word does not seem to imply the majority. If that is so, then it might be more faithful to Hobbes's original text to assume that the majority of the inhabitants living in Hobbes's state of nature are what he calls the modest type, the ones who would gladly cooperate with other people to secure universal peace.
Critics might claim that this would be insufficient to generate universal warfare in Hobbes's state of nature and thus would defeat Hobbes's very purpose of justifying the existence of governments. I claim that it is sufficient under quite general circumstances—whenever the modest types value their lives sufficiently highly.
Such a dispute cannot be settled by mere philosophical reflection. I believe that this is where a little formal modeling could help; a formal model could provide a specific mechanism that shows the process under which the state of nature inhabited by mostly modest peace lovers could dissolve into a state of universal war when people are faced with uncertainty. Of course, there have been many scholars who have presented game-theoretic models to give insights into Hobbes's state of nature. However, most of these models have neglected the most important ingredient of Hobbes's argument for the state of nature: uncertainty. This deficiency is what I intend to supplement in this paper.
3. The Three Desiderata of Hobbes's State of Nature
Based on the discussion of the five conditions of the state of nature we have seen so far, we can see that any game-theoretic model that attempts to represent Hobbes's state of nature correctly must try to meet the following set of desiderata:
-
1. It must meet all of the five conditions (C1 through C5) of Hobbes's state of nature.
-
2. It must show that universal warfare is the unique equilibrium of the state of nature.
-
3. It must show that universal war is suboptimal (i.e., Pareto-inferior): that is, it must show that there is a social state (i.e., universal peace) that everybody would strictly prefer to the state of universal war.
Why any formal model should meet the first desideratum is obvious; in order to represent Hobbes's state of nature formally, the formal model must at the very least incorporate all of the characteristic conditions of the state of nature that Hobbes assumes. The formal model should also meet desiderata 2 and 3: if it fails to meet desideratum 2, then it contradicts Hobbes's main claim that the state of nature will necessarily lead to state of universal war; if the model fails to meet desideratum 3, then it is unclear why establishing a government would be universally preferable.
4. Previous Models of Hobbes's State of Nature
Many contemporary Hobbes scholars have attempted to show why universal conflict inevitably arises in Hobbes's state of nature by modeling Hobbes's state of nature in light of contemporary game theory. The most widely used game is the Prisoner's Dilemma (PD Game). Other attempts include the Stag Hunt, the Assurance Dilemma as well as the iterated PD Game. In this section, I will explain why I think all of these games are inadequate models of Hobbes's state of nature.
4.1 Why Hobbes's State of Nature is Not a PD Game
Many people have tried to model Hobbes's state of nature as a PD game (Rawls Reference Rawls1971, Reference Rawls1999: 269; Taylor Reference Taylor1976, Reference Taylor1987: ch. 6; Barry Reference Barry1965: 253–54; Gauthier Reference Gauthier1969: 76–89). The main structure of the PD game can be summarized by the following matrix.
The PD Game
The left-most column corresponds to the actions available to player 1, while the first row corresponds to the actions available to player 2. As we can see, both players have two actions—cooperate and defect—available to them. The combination of two actions played by each player results in an outcome. The adjective written on the left-hand side of the comma describes the place of the outcome in player 1's preference ordering (from best to good to bad to worst), while the adjective written on the right-hand side of the comma describes the place of the outcome in player 2's preference ordering.
It is understandable why so many people have been attracted to the idea of modeling Hobbes's state of nature as a PD game. First of all, in a PD game, the act of defection strictly dominates the act of cooperation and, thereby, universal defection is the unique Nash equilibrium of the game. (I have indicated the Nash equilibrium of the game in bold.) If the state of nature is seen as a PD game, and if we interpret the act of cooperation as ‘Seeking Mutual Peace’ and the act of defection as ‘Initiating a Preemptive Attack’, then this implies that initiating a preemptive attack will be the dominant strategy for everybody living in Hobbes's state of nature. This explains very well why the state of nature, according to Hobbes, inevitably results in a state of universal war. So, modeling Hobbes's state of nature as a PD game meets the second desideratum that we have seen in the beginning of the previous section.
Second, the unique Nash equilibrium of a PD game (namely, the state where both players defect) is suboptimal; that is, there is a state (namely, the state where both players cooperate) that both players in the game would strictly prefer over the equilibrium. The sub-optimality of the unique Nash equilibrium of the PD game can be understood as representing the misery and the insecurity that Hobbes associates with life in the state of nature and supports Hobbes's own justification for establishing a government that has the power to enforce peace. This shows that modeling Hobbes's state of nature as a PD game meets the third desideratum as well.
What all this shows is that the PD game is an attractive game to model Hobbes's state of nature. However, modeling Hobbes's state of nature in this way has the problem of misrepresenting what Hobbes deems to be the major cause of conflict in the state of nature.
It is true that Hobbes thinks that everybody in the state of nature has a tendency to initiate a preemptive attack and start a war of all against all. However, as we have already seen in section 2, Hobbes explicitly states that not everybody is inclined to initiate a preemptive attack for the same reason. As already noted, according to Hobbes, the state of nature consists of two different types of people: (a) the modest person and (b) the vainglorious person. Hobbes makes it clear that, for the modest person, it is mainly fear, rather than a lust for power, that prompts him/her to attack. The fact that, unlike the vainglorious person, the modest person is motivated by fear or diffidence rather than a lust for power suggests that, without such fear of the other party attacking, the modest person would gladly cooperate and seek peace with other people in the state of nature. In other words, the vainglorious person and the modest person each has a completely different preference ordering.
However, this is not the situation that is described in the PD game. In the PD game, both players have exactly the same preference orderings; both players strictly prefer to defect even when there is a guarantee that the other player is going to cooperate. If we translate this to Hobbes's the state of nature, this would imply that everybody in Hobbes's state of nature would prefer to initiate a preemptive attack even when there is guarantee that the other party will cooperate and seek mutual peace. In other words, modeling Hobbes's state of nature as a PD game implies that everybody in the state of nature is vainglorious.
This directly conflicts with what Hobbes says in the passages that we have just seen previously, which explicitly distinguishes between two types (i.e., the modest type and the vainglorious type) of people. This means that modeling Hobbes's state of nature as a PD game fails to meet conditions C3 (Two Types of Men) and C4 (Non-Universal Egoism).
Furthermore, the primary reason why the modest people dwelling in Hobbes's state of nature lack assurance that the other party will not initiate a preemptive attack is, as we have seen, because they are uncertain about the other party's type. This means that the game theoretic model that aims to represent Hobbes's state of nature should include aspects of uncertainty.
However, one should note that there are no aspects of uncertainty involved in the PD game. The PD game (using the terminology of game theorists) is a complete information game; that is, each player is completely aware of the other player's preferences, payoffs, what type of strategies are available to each player, how many times the game will be played in what sequence, and so on. As we have seen, this is not how Hobbes describes the situation in the state of nature where uncertainty is one of its most characteristic features as well as the main cause of conflict. In short, the PD game fails to meet condition C5 (Uncertainty).
What all this shows is that, despite having some notable features that could be used to explain the universal conflict in Hobbes's state of nature, the PD game fails to meet the first desideratum of Hobbes's state of nature. By doing so, it underrepresents some of the key features (i.e., different types of people and uncertainty) that Hobbes deems to be the main source of conflict in the state of nature.
However, independent of whether the PD game fits with Hobbes's original text well or not, it should be noted that modeling the state of nature as a PD game has an additional problem of significantly weakening the major purpose of Hobbes's political philosophy; which is to justify the existence of governments. It is well-known that many experiments that have been led by contemporary behavior economists show that people tend to cooperate much more often than they defect in psychological experiments designed to mimic the structure of the Prisoner's Dilemma (see Dawes and Thaler Reference Dawes and Thaler1988; Cooper et al. Reference Cooper, Douglas, Dejong and Ross1996). This suggests that people might not actually be playing the PD game even if they were in situations like Hobbes's state of nature where there is no government to enforce laws. In other words, if we consider the frequent cooperation displayed in experiments that were designed to mimic the structure of the PD game, the argument that people will engage in universal warfare in the state of nature because they will be playing the PD game is quite likely to be at odds with empirical human psychology (that is, in these experiments people cooperate more often than they defect, which goes against the mathematical prediction of the PD game that people will universally defect). The more one's justification for the existence of governments is based on a premise that is at odds with empirical data, the more it loses practical force and plausibility.
This last point suggests that even if Hobbes's own text really did suggest that the state of nature is a PD game, it might have been advisable for contemporary scholars to find alternative models simply to boost the plausibility of Hobbes's justification for the existence of governments by modeling Hobbes's state of nature in a different way. However, as we have seen, we do not even need to go that far, since there is more than enough textual evidence showing that Hobbes did not think that the primary cause of universal warfare in the state of nature was that everybody was dominated by a basic passion for vainglory, something that is required for the state of nature to be a PD game.
4.2 Why Hobbes's State of Nature is Not a Game of Stag Hunt
Some scholars have argued that Hobbes's state of nature could be better represented as a game of Stag Hunt rather than a one-shot PD game.Footnote 1 The game of Stag Hunt can be summarized by the following matrix:
The Stag Hunt
The game of Stag Hunt has two pure strategy (Nash) equilibria (which, again, are indicated in bold), namely, mutual cooperation and mutual defection, and it has one mixed strategy (Nash) equilibrium, which will depend on the specific utilities assigned to each outcome.
We can see here that the game of Stag Hunt violates the second desideratum of Hobbes's state of nature. Of course, mutual defection is a Nash equilibrium of the game. Furthermore, such a Nash equilibrium is suboptimal. However, the problem is that mutual defection is not the unique Nash equilibrium of the game. Unlike in the PD game, here mutual cooperation, along with mutual defection, is also an equilibrium. This basically is what distinguishes the Stag Hunt from the PD game. Accordingly, if Hobbes's state of nature is truly a game of Stag Hunt, it is quite unclear why the state of nature should inevitably descend into a state of universal war, as Hobbes himself claims, rather than turn out to be a state of mutual peace and harmony.
In The Strategy of Conflict, Thomas Schelling has argued that when there is more than one equilibrium in a game, the actual equilibrium will turn out to be the one that is salient based on cultural, historical, conventional factors. Schelling has called such an equilibrium a focal point of a game (see Schelling 1981). This means that if Hobbes's state of nature is a game of Stag Hunt, then individuals will be able to achieve peaceful harmony without government enforcement in some states of nature in which there has historically been an ethos of mutual cooperation. As a result, in such situations, there would be no need for a government. This completely defies one of the main purposes of Hobbes's political philosophy, namely, the purpose of justifying the existence of governments.
Furthermore, just like the PD game, the game of Stag Hunt does not incorporate one of Hobbes's major assumptions—namely, C3—that in the state of nature there are two types of people (i.e., the modest type and the vainglorious type) who respectively have distinct preference orderings. As we can see in the matrix above, in the game of Stag Hunt, the players are of one type only, and the preferences of the two players are symmetric.
Like the PD game, the game of Stag Hunt is a complete information game that incorporates no aspects of uncertainty and, hence, fails to meet condition C5. In short, modeling Hobbes's state of nature as a game of Stag Hunt not only completely defies one of the major aims of Hobbes's political philosophy, but it fails to meet the first desideratum we have discussed above.
4.3 Why Hobbes's State of Nature is Not an Assurance Dilemma
Some scholars have thought that Hobbes's state of nature can best be modeled as what people, following Kavka (Reference Kavka1989), call the Assurance Dilemma (see Kavka Reference Kavka1989 and Dodds and Shoemaker Reference Dodds and Shoemaker2002). The Assurance Dilemma is a two-player game in which one player has prisoner's dilemma preferences, while the other player has stag hunt preferences. The Assurance Dilemma can be represented by the following matrix:
The Assurance Dilemma
Compared to the PD game and the Stag Hunt, the Assurance Dilemma is an advancement in the sense that it at least distinguishes the two different types of people in Hobbes's state of nature. In other words, the Assurance Dilemma satisfies condition C3 of Hobbes's state of nature.
However, the Assurance Dilemma still fails to satisfy condition C5, which requires any model of Hobbes's state of nature to incorporate uncertainty. The Assurance Dilemma, just like the PD game and the game of Stag Hunt, is a complete information game. It essentially says that, in Hobbes's state of nature, every person of the modest type will necessarily be paired with a vainglorious type and that both modest types and vainglorious types will know this fact with certainty.
Not only is this implausible, but it was also not Hobbes's explanation of why the state of nature inevitably descends into a state of universal war. Remember that for the modest types the main motivation for deciding to initiate a preemptive attack stems from ‘diffidence’—that is, from the fear caused by not knowing whether or not the other party will attack. If the modest types knew with certainty that they will always encounter a vainglorious type, then they will know for sure that their counterparts will attack, and as a result, the type of diffidence Hobbes describes will not arise for the modest types. In short, uncertainty was a key to Hobbes's model. The fact that the Assurance Dilemma does not incorporate uncertainty renders it an unsatisfactory model for Hobbes's state of nature.
4.4 Why Hobbes's State of Nature is Not an Iterated PD Game
Some scholars have thought that the state of nature described by Hobbes should be represented as a repeated PD game (see Kavka Reference Kavka1986: ch. 4; Hampton Reference Hampton1986: ch. 3 Taylor Reference Taylor1987). A repeated PD game is a game in which the two players play the PD game multiple times. When the PD game is played multiple times, it is possible for each player to either reward (by cooperating in the next round) or punish (by defecting in the next round) his/her opponent's behavior in the previous round. This changes the dynamics of the game significantly.
If the game is played only a finite number of times, then the game has only one equilibrium, namely, mutual defection in every period of the game (which can be proved by backward induction). However, if the game is played infinitely many times, there are other equilibria besides the one in which both players defect in every period of the game. One such equilibrium is where both players play a strategy known as tit for tat. The rule of tit for tat is simple: cooperate in your first move and then copy what your opponent did in the previous round. Tit for tat can be characterized as a strategy of both punishment and forgiveness: it punishes one's opponent by defecting in the current round if one's opponent defected in the previous round; however, it forgives and rewards one's opponent by cooperating in the next round if one's opponent cooperates in the current round.
There are a number of other equilibrium strategy pairs (in addition to tit for tat and unconditional defection) in the infinitely repeated PD game. These other equilibrium strategy pairs can be distinguished by the severity of the punishment that each strategy prescribes when one first encounters defection by the other player. The grim trigger strategy (i.e., the strategy of no forgiveness) prescribes that a player cooperate until first encountering defection by the other player; in that case, the strategy prescribes the player consistently to defect afterward. The strategy of limited punishment prescribes that the player initially cooperates, and when first encountering defection by the other player, the player is to punish the other player by defecting for a given number (n) of periods. With an adequate discount rate, it can be shown that both players playing either the grim trigger strategy or the strategy of limited punishment can create equilibria in a PD game repeated an infinite number of times.
What's important is that, unlike in a one-shot PD game, in an infinitely repeated PD game it is possible for both players to reap the benefits of mutual cooperation for infinite number of periods by mutually employing the right kind of strategies. Just like the Stag Hunt, the infinitely repeated PD game fails to meet the second desideratum of Hobbes's state of nature: universal defection is not the unique Nash equilibrium of the game.
However, modeling Hobbes's state of nature as an iterated PD game has its own merits. The most significant merit is that it seems to explain the universal warfare that is characteristic of the state of nature while showing how people can escape the state of nature and successfully establish a government by themselves. As I have briefly explained, although it is true that both players defecting in every period of the game creates an equilibrium, there are other equilibria where both players are able to mutually cooperate throughout the game. These latter equilibria open possibilities for people to escape the predicament they face in the state of nature.
However, the solution is not that simple. One problem is whether it is really plausible to think of the interaction among the people living in the state of nature as a repeated PD game. The iterated PD game requires each player to play the PD game with the same opponent repeatedly. I doubt that this would be the case for people living in the state of nature. In the state of nature, it would be far more likely for each person to randomly encounter a different opponent every time the individual happens to interact with somebody. If this is so, then it might be more plausible to model Hobbes's state of nature as a one-shot game, rather than some repeated game.
Even if one happens to interact with the same person more than once, such interaction cannot be repeated an infinite number of times in the state of nature. This is because in the state of nature interaction with other people can, in many cases, result in the death of one of the parties. This means that Hobbes's state of nature can, at best, be modeled as a PD game that is repeated a finite number of times. However, as I have explained, in a finitely repeated PD game, mutual defection for all periods of the game is the only equilibrium of the game. This takes away a major attraction of modeling Hobbes's state of nature as an iterated PD game; namely, the fact that it shows how people can escape the state of nature and successfully establish a government by themselves.
Even if we concede that an interaction in the state of nature can be repeated with the same person an infinite number of times, modeling Hobbes's state of nature as an infinitely repeated PD game has exactly the same problems as the Stag Hunt game. That is, since there exist multiple equilibria where both parties can naturally achieve mutual cooperation in an infinitely repeated PD game, modeling Hobbes's state of nature as an infinitely repeated PD game significantly weakens Hobbes's major argument for the necessity of government. Furthermore, modeling Hobbes's state of nature as an infinitely repeated PD game fails to meet conditions C3 and C5 by not incorporating the distinction between the two types of people (i.e., the modest type and the vainglorious type) as well as aspects of uncertainty, which Hobbes clearly assumes to exist in the state of nature.
In short, although many people have been attracted to the idea of modeling Hobbes's state of nature as an infinitely repeated PD game, this model fails to be an ideal game theoretic-model that is both faithful to Hobbes's original text and that could serve Hobbes's original intentions well.
5. Modeling Hobbes's State of Nature
We have just seen that most game-theoretic models that have been hitherto used to represent Hobbes's state of nature failed to provide an adequate representation by neglecting one or more characteristic conditions or desiderata we have discussed above. Most notably, all the game-theoretic models seen up to now do not incorporate condition C5, uncertainty, and thereby fail to meet desideratum 1. Again, if one is faithful to Hobbes's original text, it is not hard to realize that it was not, strictly speaking, egoism, but rather uncertainty that led Hobbes to conclude that the state of nature will deteriorate into a state of universal war. Therefore, any game-theoretic model that does not model uncertainty is, I claim, an incorrect model of Hobbes's state of nature. And in order to model uncertainty, one would have to utilize what is known as Bayesian game theory. Here, I present a model of Hobbes's state of nature that directly models uncertainty by utilizing the tools of Bayesian game theory.
The model that is most similar in spirit to the one presented here is Vanderschraaf's (2006); Peter Vanderschraaf presents a remarkable incomplete-information Bayesian game-theoretic model he calls, the ‘variable anticipation threshold model’ and later uses it in various computer simulations. Although Vanderschraaf's model and the model that I will soon present here are completely different—the former is dynamic, while the latter is static—both are similar in spirit in the sense that both models regard uncertainty concerning one's counterpart's type as the primary reason why Hobbes's state of nature inevitably descends into a state of universal war.
What we can gain by studying the model I present here in relation to Vanderschraaf's model is to learn that, once we represent all of the major characteristics of Hobbes's state of nature accurately, the specific nature of the interaction—whether it is static or dynamic—is peripheral to the derivation of Hobbes's main conclusion. It is important to see that Hobbes's main insight is retained under different structural settings of the model; we might think of this as showing the robustness of Hobbes's main conclusion. Furthermore, the model presented here reveals a central mechanism that drives Hobbes's pessimistic conclusion, a mechanism that has been previously unnoticed in modeling Hobbes's state of nature: namely, that the necessity of the state of nature descending into a state of universal war depends on how much the modest types value their own lives. What this means will become apparent once we present and analyze our model of Hobbes's state of nature.
5.1 The Model
The formal construction of the model as well as how the model incorporates all of the five conditions of Hobbes's state of nature is described in Supplementary Appendix 1 (available online). Here, I will mostly rely on informal discussion to convey the main intuitions of the model. I first present the model in extensive game form (see Figure 1).
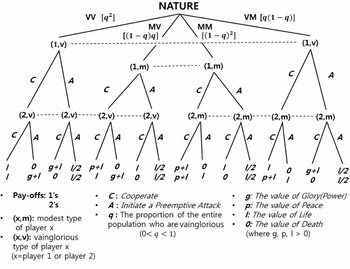
Figure 1: Our Model
Let me briefly explain what the model is saying. At first, NATURE makes the first move and determines the proportion q of the entire population that are vainglorious. That is, q is a probability that is known to all types of players. One may think that people living in the state of nature know the value of q by their collective past experiences; that is, if many people on average had encountered m vainglorious persons among n people they had interacted with in the past, then people living in the state of nature will believe that
${\rm q} = \frac{{\rm m}}{{\rm n}}$
. Let's assume that the proportion q of the entire population that is vainglorious is common knowledge.
Based on the value of q, NATURE assigns a probability distribution to the four possible states of affairs: VV, VM, MV, MM. The four branches that ramify from NATURE each corresponds to these four possible states of affairs. The left-most branch corresponds to the state where both player 1 and player 2 are vainglorious, (1, v) and (2, v); the second branch corresponds to the state where player 1 is modest, (1, m), while player 2 is vainglorious, (2, v). The third branch corresponds to the state where both player 1 and player 2 are modest—that is, (1, m) and (2, m). And the fourth branch corresponds to the state where player 1 is vainglorious while player 2 is modest—that is, (1, v) and (2, m).
After a specific state of affairs is realized, player 1, without knowing with which type of player 2 he/she is interacting chooses an action either to cooperate (C) or attack (A), and then, without knowing the type or the action of player 1, player 2 chooses an action either to cooperate (C) or attack (A), and the game ends.
There are four possible outcomes of the game: Power—when one attacks while the other unilaterally cooperates; Peace—when both cooperate; War—when both attack; and Death—when one unilaterally cooperates when the other attacks. The default payoff for staying alive is: l. The vainglorious types receive an additional payoff of g when the outcome is Power, and the modest types receive an additional payoff of p when the outcome is Peace. All types of players receive a payoff of l/2 (i.e., each has one-half chance of surviving, which basically incorporates condition C1 [Equality]) when the outcome is War, and all types of players receive a zero payoff when the outcome is Death.
The nodes that are connected with a dotted line denote a given information set; where the player, given the information he/she has received, knows that he/she is located at one of the nodes in the information set, but does not completely know at which particular node that he/she is located. For example, the first information at the very top signifies that player 1 knows that he/she is a vainglorious type but does not know whether he/she is dealing with a modest player 2 or a vainglorious player 2. In the bottom-left information set, player 2 knows that he/she is a vainglorious type, but does not know whether he/she is interacting with a modest player 1 or a vainglorious player 1, and also does not know what action each type of player 1 had performed.
5.2 Formal Results of Our Model
The main results of our model will be formally stated and proved in Supplementary Appendix 2. Here I present and explain the main results of our model with minimum use of formal language.
Result 1 (Corresponding to Proposition 1 in Supplementary Appendix 2): The vainglorious types will attack for sure.
In other words, all vainglorious types in the state of nature will initiate a preemptive attack regardless of their opponent's type or behavior. The main reason why this is so is that the vainglorious types, unlike the modest types, value glory (i.e., g > 0), which is attained by having power over other people. Therefore, even when one knows that one's opponent will cooperate, a vainglorious type will initiate a preemptive attack in order to conquer the opponent. As it is obvious that the vainglorious types will want to attack when his/her counterpart attacks, this makes initiating a preemptive attack a strictly dominant strategy for the vainglorious types.
Thus, the vainglorious types will attack for sure. This is not a surprise. Given that the vainglorious types attack for sure, how would the modest types react? Analyzing the behaviors of the modest types is slightly more complicated. It turns out that the optimal behavior of the modest types depends on two parameters: (a) the proportion of glory seekers in the state of nature (i.e., q), and (b) the probability that other modest types will attack (i.e., β and δ).
Result 2 (Corresponding to Proposition 2 in Supplementary Appendix 2): There exists a threshold of attack, T, (defined by
${\rm T} = \frac{{2\beta p + \beta l - l}}{{2\beta p + \beta l}}$
for (2, m); and
${\rm T} = \frac{{2\delta p + \delta l - l}}{{2\delta p + \delta l}}$
for (1, m)) such that the modest types will choose to attack if and only if the proportion of vainglorious types exceeds T.
Let's consider the situation of modest type of player 2, i.e., (2,m). (The situation of (1,m) is symmetric.) For (2,m), the threshold of attack T can be written as:
${\rm T} = \frac{{2{\rm \beta p} + {\rm \beta l} - {\rm l}}}{{2{\rm \beta p} + {\rm \beta l}}} = 1 - \frac{l}{{2\beta p + \beta l}} = 1 - \frac{l}{{\beta \left( {2p + l} \right)}}$
. Seeing T as a function of β means the graph of T is a hyperbola. Since β and q are probabilities, their values range from 0 to 1: Therefore, the graph of T can be represented inside the square box of unit length on the βq − plane as follows:
Figure 2: The graph of T: The threshold of attack
Note that the graph of T (i.e., the threshold of attack) demarcates the βq-box into two separate regions—the region of cooperation and the region of attack. For any given value of β ∈ [0, 1], (2,m) will choose to initiate a preemptive attack whenever the known proportion of vainglorious people in the state of nature exceeds the threshold of attack T: The threshold of attack T depends on β; that is, this threshold depends on (2,m)'s belief concerning the probability that player 1 will cooperate given that player 1 is a modest type.
The more (2,m) believes it likely for (1,m) to cooperate, the higher the proportion of vainglorious people will it require for (2,m) to initiate a preemptive attack. This makes intuitive sense. Note that when β falls below
$\frac{{\rm l}}{{2{\rm p} + {\rm l}}} > 0$
, (2,m) will initiate a preemptive attack regardless of the proportion of vainglorious people in the state of nature. Also, even when β = 1 (i.e., (2,m) believes that (1,m) will cooperative for sure), (2,m) will still choose to initiate a preemptive attack whenever the proportion of vainglorious people in the state of nature exceeds
$\frac{{2p}}{{2p + l}} < 1$
.
Now let's do some simple comparative statics. Consider the β -intercept,
$\frac{l}{{2p + l}}$
, and the value of T when
$\beta = 1,\frac{{2p}}{{2p + l}}{\rm }$
. What would happen to these two values if people in the state of nature start to value their lives relatively more highly? That is, what would happen to these values if we increase the value of l?
Result 3 (Corresponding to Proposition 3 in Supplementary Appendix 2): As people in the state of nature start to value their own lives more highly, ‘the region of attack’ expands and ‘the region of cooperation’ shrinks.
To understand this graphically, let l increase to l′ (where l > l), and see how this change will affect the graph of T qualitatively:
Figure 3: Graph of T (when l increases to l′)
We can see that as the value of life increases from l to l′, the region of cooperation shrinks. The qualitative interpretation of this is as follows: the more the modest types value their own lives, the smaller the proportion of vainglorious people in the state of nature will be required for the modest types to initiate a preemptive attack. In other words, the modest types are likelier to initiate a preemptive attack the more they value their own lives. And, since we know, by Proposition 1, that the vainglorious types will initiate a preemptive attack for sure, this implies that the more value the modest types attach to their own lives, the likelier it is for the state of nature to descend into a state of war of all against all!
This is a rather surprising result. However, there is an intuitive explanation for this: The more the modest types value their own lives, the more they would be afraid of even the slightest chance of encountering a vainglorious type, because in such an encounter, any unilateral cooperative behavior on the part of the modest types will be taken advantage of and result in their death. Thus, the more the modest types value their own lives, the more they would try to avoid such a situation, which means that they would be more likely to execute the first strike mainly as a defensive measure. In other words, for the modest types, initiating a preemptive attack actually stems from a rather conservative motivation. As Hobbes himself explains, it stems from fear and diffidence rather than aggression or a lust for power (see On the Citizen, ch. 1: 25).
What would happen if this conservative motivation on part of the modest types went to the very extreme? The result can be summarized by the following asymptotic result:
Result 4 (Corresponding to Proposition 4 in Supplementary Appendix 2): As people in the state of nature start to value their own lives arbitrarily highly, the region of cooperation disappears.
In other words, as people in the state of nature start to value their own lives arbitrarily highly, the entire βq-box turns into the region of attack. This means that as the value of life goes arbitrarily up, even the modest types will attack for sure regardless of how few vainglorious types they believe are in the state of nature. This leads us to the following important result:
Result 5 (Corresponding to Proposition 5 in Supplementary Appendix 2): For any arbitrarily small proportion q ∈ (0, 1] of of vainglorious types in the state of nature, there exists a threshold of life,
$L_q = \frac{{2{\rm p}\left( {1 - {\rm q}} \right)}}{{\rm q}}$
, such that whenever the modest types value their own lives more than this threshold, they will attack for sure.
By result 1, we know that the vainglorious types will attack for sure. Result 5 tells us that, for any proportion of vainglorious types in the state of nature, the modest types will also attack for sure whenever they value their own lives sufficiently highly, namely, when they value their lives more than the ‘threshold of life.’ In other words, our model has just shown our previous lemma of Hobbes's state of nature.
LEMMA (Preemptive Attack as a Dominant Strategy): In the state of nature, initiating a preemptive attack is the dominant strategy for everybody regardless of his/her type.
We are now in a position to state our final result:
Result 6 (Corresponding to Proposition 6 in Supplementary Appendix 2): Let q ∈ (0, 1) be any arbitrarily small proportion of vainglorious types in the state of nature. Then, whenever the modest types value their own lives more than the threshold of life (i.e.,
$L_q = \frac{{2{\rm p}\left( {1 - {\rm q}} \right)}}{{\rm q}}$
), the state of nature will necessarily descend into a state of universal war.
Note that result 6 states a sufficient condition for Hobbes's state of nature to descend into a state of universal war; that is, there may be other situations that may lead Hobbes's state of nature to a state of universal war. However, this result is enough to establish Hobbes's main theorem, namely,
THEOREM (War of Every Man against Every Man): The state of nature results in a state of war of every man against every man.
Figure 4 summarizes the equilibrium path of our model.
Figure 4: Equilibrium Path of Our Model
In our model, one of the central mechanisms (besides uncertainty) that drives our main results and thereby establishes Hobbes's main theorem of war of all against all is the modest types’ valuation of their own lives. It is true that, for whatever proportion of vainglorious types in the state of nature, there will exist a threshold of life over which the modest types will attack for sure. However, this threshold of life is dependent on context; it depends on the proportion of vainglorious types in that particular state of nature. As the proportion q of vainglorious types in the state of nature gets smaller and smaller, the threshold of life
$L_q = \frac{{2{\rm p}\left( {1 - {\rm q}} \right)}}{{\rm q}}$
becomes higher and higher. In other words, for a very small proportion of vainglorious types in the state of nature, the modest types would have to value their own lives quite highly in order for Hobbes's state of nature to descend necessarily into a state of universal war of all against all. One natural question to ask at this point is how highly had Hobbes actually thought the modest types would value their own lives. The short answer is: ‘very’. Consider the following passage:
Moreover, the greatest of goods for each is his own preservation. For nature is so arranged that all desire good for themselves. Insofar as it is within their capacities, it is necessary to desire life, health, and further, insofar as it can be done, security of future time. (De Homine, ch. 11, section 6, emphasis added)
Hobbes claims that the greatest good for every human being is his/her own preservation, and that it is necessary for people to desire life and health (the two major components of self-preservation) as much as they possibly can. It is quite ironic to discover that when Hobbes was emphasizing the importance of one's self-preservation and was urging people to value their own lives as much as they could, he was actually reinforcing one of the central mechanisms of the state of nature that makes universal war unavoidable.
6. Contribution and Concluding Remarks
We can see that our current model meets all three desiderata that I have introduced in section 3.
First, given that the modest types value their lives sufficiently highly (i.e., l >
$L_q = \frac{{2{\rm p}\left( {1 - {\rm q}} \right)}}{{\rm q}}$
), our model shows that universal warfare is the unique equilibrium of Hobbes's state of nature for any proportion q ∈ (0, 1] of the vainglorious types. We have also seen textual evidence that supports the requirement l >
Lq
.
Second, we can see that the unique equilibrium of our model is suboptimal. Notice that in our model, every combination of player types receives a payoff of
$\frac{l}{2}$
in the ‘war equilibrium’. If every type of player were to cooperate, this would generate a payoff of l for every player. That is, universal peace is a social state in which everybody (including the vainglorious types) would prefer to be. This means that if there happens to be a powerful authority, such as a government, that has the power to enforce universal peace among people living in the state of nature, then such social institution would improve the situation of everybody without worsening the situation of anybody. This is Hobbes's justification for the existence of governments, and we can see that our model nicely captures Hobbes's original intentions in this respect.
However, even the one-shot PD game meets these two desiderata (i.e., desiderata 2 and 3.) The major contribution of our model over the PD game is that, unlike the PD game or any other game-theoretic model we have discussed, our model nicely meets all of the five conditions of the state of nature. That is, the distinction between the modest type and the vainglorious type, a distinction that Hobbes himself explicitly makes in his original text, and the characteristic uncertainty Hobbes deems to be the primary cause of conflict are directly incorporated into our model. Therefore, our model (unlike the one-shot PD game or any of the other game-theoretic models discussed in section 4) meets the very first desideratum of Hobbes's state of nature.
I believe that this is a significant contribution to contemporary Hobbes scholarship, and, by extension, social contract theory in the following ways. First, this model properly respects what Hobbes wrote and thus does not distort Hobbes's original intentions. Careful reading shows that Hobbes did not think that it is part of our universal human nature to maximize power and self-interest. Nor did Hobbes think that everybody being obsessed with maximizing his/her self-interest is what causes universal conflict in the state of nature.
The one-shot PD game distorts this fact. Saying that Hobbes's state of nature inevitably deteriorates into a state of war because everybody, by his/her very nature, seeks to maximize his/her own power and self-interest is a different explanation from saying that Hobbes's state of nature inevitably deteriorates into a state of war because, although most people would like to cooperate with other people to achieve universal peace, there is a small proportion of glory-obsessed war-prone individuals that the peace-loving majority cannot reliably identify. Hobbes had presented the latter explanation. Thinking of Hobbes's state of nature as a one-shot PD game forces us to adopt the first explanation.
The second advantage that our current model has over the one-shot PD game is that it allows us to free Hobbes from psychological egoism—a contestable doctrine of human psychology that many people reject, with good reason. Psychological egoism claims that all human beings are solely motivated by self-interest. When people first hear about the parable of Hobbes's state of nature, many wonder why Hobbes did not think that it is possible to achieve universal peace through people's spontaneous efforts and cooperation. The standard answer is: because Hobbes thought that everybody is selfish by nature. That is, the standard answer is that Hobbes is committed to psychological egoism, and it is this that prevents Hobbes from thinking that it is possible for people to cooperate with one another without external enforcement.
However, some people might not think that human beings in general are selfish in the way that psychological egoism describes. Potentially, this could prevent people from taking Hobbes's argument seriously. We must remember that the primary role the state of nature plays in Hobbes's political philosophy is to justify the existence of governments by illustrating the misery people would face if they did not have one. However, if the universal conflict as well as the misery accompanying it can only be explained by assuming a theory of human psychology many people think to be implausible, Hobbes's justification for the existence of governments would, to that very extent, be weakened.
Our model has the advantage of explaining the universal conflict in the state of nature without assuming that everybody has a strictly egoistic psychology. It shows that even when the vast majority of the entire population in Hobbes's state of nature are peace-loving people—who, more than anything else, prefer universal peace—universal warfare could still break out if there is no reliable way for people in the peace-loving majority to distinguish themselves from and properly identify a small number of war-prone power seekers that everybody in Hobbes's state of nature knows to exist. In other words, our model shows that even when the majority of people strictly favor mutual peace and cooperation, universal conflict can still emerge primarily because of uncertainty. This explanation is free of any contestable psychological assumptions and is, therefore, more plausible and widely applicable to many actual human situations. This means that our model provides a much firmer foundation on which Hobbes's entire political philosophy can rest and can thus provide a more plausible justification for the existence of governments.
Lastly, our model has revealed one of the central mechanisms (in addition to uncertainty) that drives Hobbes's pessimistic conclusion (namely, that the state of nature will necessarily deteriorate into a state of universal war) that has been previously neglected in the literature. This mechanism consists in the modest types’ high valuation of their own lives. Such high valuation of their own lives leads the modest types to attack for the sake of self-protection, leading the state of nature necessarily to deteriorate into a state of war of all against all. In other words, out of an extremely conservative motivation simply to protect themselves, the modest types will prefer going to war to taking a chance to cooperate with the other party—because they fear that the other party might be a vainglorious type who would take advantage of their cooperation, and this could ultimately result in their death.
I think that Hobbes presented a very convincing argument for the existence of governments. Showing that having no government results in a Pareto-inferior equilibrium is a powerful justification for the existence of governments that could be accepted even today. However, the plausibility of Hobbes's original argument wanes when one oversimplifies some of the major features of Hobbes's original text and represents the state of nature as, say, a one-shot PD game. Such simplistic models keep us from properly appreciating Hobbes's argument. I believe that this is part of the reason why there are still many political theorists/philosophers who think applying game theory to interpreting Hobbes is fundamentally misguided. However, I argue that applying game theory to political theory is misguided only when one tries to apply the wrong model; not all game-theoretic models are wrong. This is why I believe conserving the details of Hobbes's logic is important. I believe that the model provided in this paper is the correct game-theoretic model that represents Hobbes's state of nature in a way that Hobbes had originally intended it to be.
Supplementary Material
For supplementary appendices accompanying this paper, please visit http://dx.doi.org/10.1017/apa.2015.12.
