1. INTRODUCTION
The Global Positioning System (GPS) is widely used in land, aviation, marine and space navigation applications due to its high accuracy of position and simple user requirements. GPS is not only used in position navigation but also in velocity and acceleration sensors, such as Inertial Measurement Unit (IMU) sensors (Serrano, Kim et al., Reference Serrano and Kim2004). Position determination algorithms that use GPS signals typically use a GPS satellite's position and pseudorange, which is the distance measurement from the GPS satellite to a receiver using a radio frequency signal, and the velocity determination algorithm uses the GPS satellite's velocity and Doppler measurement (Xu, Reference Xu2007). The accuracy of the receiver's position and velocity is directly affected by the GPS satellite's position and velocity (Warren and Raquet, Reference Warren and Raquet2003). The GPS satellite's position can be obtained from the GPS broadcast ephemeris data, which are modulated on the L1 C/A signal, but the ephemeris algorithm in publication IS-GPS-200F provides GPS satellite position only. To obtain the GPS satellite's velocity and acceleration, Zhang et al. (Reference Zhang and Zhang2006) provide a closed form of GPS satellite's velocity and acceleration.
The GPS modernization program was started by the US government, which comprises launching new GPS satellites and broadcasting new civil signals: L2C, L5 and L1C. The new civil signal is modulated using a new method using new civil navigation (CNAV) messages that contain new ephemeris and Earth Orientation Parameters (EOP) (GPS.GOV, 2012; GPSD, 2011). In the CNAV ephemeris, the data bits and the number of parameters are increased; therefore, the CNAV ephemeris can provide more accurate GPS satellite position, which is the real-time prediction of the GPS satellite a few hours into the future, and the prediction accuracy has increased. The EOP is required when transforming Earth Centred Earth Fixed (ECEF) data into Earth Centred Inertial (ECI) data; the ECI vector data are needed for space-based users such as the International Space Station (ISS), or satellites in Low Earth Orbit (LEO), for orbit determination (Yunck, Reference Yunck1996).
In this paper we propose a closed form of the velocity and acceleration determination algorithm using the CNAV ephemeris, because IS-GPS-200F does not provide velocity and acceleration determination. The results of the proposed algorithm are compared with the National Geospatial-Intelligence Agency (NGA)'s precise ephemeris data. When testing the proposed algorithm, a virtual CNAV ephemeris is used that was created using the precise ephemeris and Legacy Navigation (LNAV) ephemeris. The EOP transformation algorithm and result are also compared. The result shows that the maximum error of the calculated GPS satellite's velocity using CNAV is within 0·00025 m/s, and the maximum error of the acceleration is within 0·0001 m/s2. This accuracy is improved compared with using LNAV.
2. KEPLERIAN ORBIT ELEMENTS AND FRAME TRANSFORMATION
Classical orbit position and velocity determination algorithms use Keplerian orbit elements. The position and velocity of a satellite are first calculated in an orbital plane, and the state vector is then transformed into ECI coordinates. To obtain the position and the velocity of the satellite in the ECEF coordinates, the ECI-to-ECEF coordinates transform must be applied. The GPS broadcast ephemeris is somewhat different in calculation procedure compared with the classical Keplerian orbit elements. The difference is that the x-axis of the GPS orbital plane is different compared with the classical orbital plane, and the calculated state vector is expressed in ECEF coordinates immediately; this method does not produce a state vector in ECI coordinates. To aid in a better understanding of the GPS satellite state vector determination algorithm, the classical orbital plane and the GPS orbital plane are described below.
2.1. Satellite State Vector in ECI Using Keplerian Orbit Elements
Keplerian orbit elements are determined using the equatorial and orbital plane. Figure 1 shows the Keplerian orbit elements in the ECI and the perifocal coordinate frame. The elements are the following:
a is the semi major axis;
 $\vec e$ is the eccentricity vector;
$\vec e$ is the eccentricity vector;i is the inclination angle;
Ω is the right ascension of ascending node (RAAN);
ω is the argument of perigee;
ν is the true anomaly;
E is the eccentricity anomaly; and
U is the argument of latitude.

Figure 1. Classical orbit elements in the ECI and the perifocal coordinate frame.
There are two main parts to determining the satellite position and velocity. The first part is the calculation of the position and velocity in the orbital plane (perifocal coordinate frame), and the second part is to transform the position and velocity from the orbital plane to the ECI coordinate frame. The position determination of the satellite in the orbital plane can be expressed as Equation (1) (Montenbruck and Gill, Reference Montenbruck and Gill2005; Misra and Enge, Reference Misra and Enge2006).
 $$\vec r_{orb} = \left[ \matrix{x_{orb} \cr y_{orb} \cr 0 } \right] = \left[ {\matrix{ {r\cos \nu} \cr {r\sin \nu} \cr 0 \cr}} \right] = \left[ {\matrix{ {a\cos E - ae} \cr {a\sqrt {1 - e^2} \sin E} \cr 0 \cr}} \right]$$
$$\vec r_{orb} = \left[ \matrix{x_{orb} \cr y_{orb} \cr 0 } \right] = \left[ {\matrix{ {r\cos \nu} \cr {r\sin \nu} \cr 0 \cr}} \right] = \left[ {\matrix{ {a\cos E - ae} \cr {a\sqrt {1 - e^2} \sin E} \cr 0 \cr}} \right]$$The velocity of the satellite in the orbital plane can be derived as:
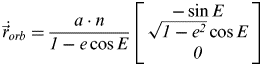 $$ \dot {\vec r}_{orb} = \displaystyle{{a \cdot n} \over {1 - e\cos E}}\left[ {\matrix{ { - \sin E} \cr {\sqrt {1 - e^2} \cos E} \cr 0 \cr}} \right]$$
$$ \dot {\vec r}_{orb} = \displaystyle{{a \cdot n} \over {1 - e\cos E}}\left[ {\matrix{ { - \sin E} \cr {\sqrt {1 - e^2} \cos E} \cr 0 \cr}} \right]$$where n is the mean motion of the satellite and is expressed as:
G is the gravitational constant and M is mass of the Earth.
The acceleration of the satellite in the orbital plane can be expressed as:
The state vector of the satellite in the orbital coordinate can be transformed to the ECI coordinate frame using the rotation matrix. The transform matrix from the orbital plane to the ECI coordinate frame is:
The R1, R2 and, R3 rotation matrices are:
 $$ \eqalign{R_1 (\theta ) & = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {\cos \theta } & {\sin \theta } \cr 0 & { - \sin \theta } & {\cos \theta } \cr } } \right],R_2 (\theta ) = \left[ {\matrix{ {\cos \theta } & 0 & { - \sin \theta } \cr 0 & 1 & 0 \cr {\sin \theta } & 0 & {\cos \theta } \cr } } \right], \cr R_3 (\theta ) & = \left[ {\matrix{ {\cos \theta } & {\sin \theta } & 0 \cr { - \sin \theta } & {\cos \theta } & 0 \cr 0 & 0 & 1 \cr } } \right]} $$
$$ \eqalign{R_1 (\theta ) & = \left[ {\matrix{ 1 & 0 & 0 \cr 0 & {\cos \theta } & {\sin \theta } \cr 0 & { - \sin \theta } & {\cos \theta } \cr } } \right],R_2 (\theta ) = \left[ {\matrix{ {\cos \theta } & 0 & { - \sin \theta } \cr 0 & 1 & 0 \cr {\sin \theta } & 0 & {\cos \theta } \cr } } \right], \cr R_3 (\theta ) & = \left[ {\matrix{ {\cos \theta } & {\sin \theta } & 0 \cr { - \sin \theta } & {\cos \theta } & 0 \cr 0 & 0 & 1 \cr } } \right]} $$where θ is the arbitrary angle that you want to rotate. The position of the satellite in the ECEF coordinate frame can be transformed using Equation (7).
W, R, N, P and B are the polar motion, the rotation, the nutation, the precession and the bias transformational matrices (Vallado and McClain, Reference Vallado and McClain2001; IERS, 2010; Bradley, Vallado et al., Reference Bradley and Vallado2011). A detailed description of the ECEF to the ECI transformation algorithm will be discussed in Section 4.
2.2. GPS Satellite State Vector in the GPS Orbital Plane
The orbital coordinate system described in IS-GSP-200F is different from the natural (or classical) orbital coordinate system. In the natural orbital coordinate system, the direction of the x-axis is defined by the direction of the perigee, but the direction of the x-axis in the IS-GPS-200F orbital coordinate system is defined by the direction of ascending node (Zhang, Zhang et al., Reference Zhang and Zhang2006). In IS-GPS-200F, the position of the GPS satellite is calculated in the GPS orbital plane and is then transformed into the ECEF coordinate frame by applying two rotation matrices; however, the position in the classical orbital plane is first transformed into the ECI and is then transformed into the ECEF if needed.
The reason that the IS-GPS-200F system produces a position in the ECEF coordinates is because, in most cases, ground-based users want the position only in the ECEF coordinate frame. The ECEF-to-ECI coordinate transform algorithm requires Earth Orientation Parameters (EOP) and additional complicated numerical calculations. Therefore, this orbital plane to ECEF direct transformation method reduces the computational burdens to the ground-based user who does not need positional data in the ECI coordinate frame.
However, this method is a weak point for the space-based user who wants the positional data in both the ECI and the ECEF frames. The user that wants the position in the ECI frame using the LNAV message must have additional EOP data, which are provided by other agencies. This requirement means that position in the ECI frame cannot be calculated using the LNAV message alone and EOP data must be obtained from other sources through an external data link. To improve this burdensome process, the EOP data will be included in the CNAV message type 32.
There are two main procedures in the position calculation algorithm described in IS-GSP-200F. The first step is calculating the position in the CNAV orbital plane, and the second step is rotating the position from the GPS (or CNAV) orbital plane to the ECEF frame using equation (8). ![]() $\vec r_{CNAVorb} $ is the position vector of the GPS satellite in the CNAV orbital plane, and
$\vec r_{CNAVorb} $ is the position vector of the GPS satellite in the CNAV orbital plane, and ![]() $\vec r_{ECEF} $ is the position vector in the ECEF coordinate frame. R l(−i k) and R 3(−Ωk) are the rotation matrices that rotate the position vector by the CNAV angle of inclination and the CNAV longitude of ascending node. It is important to note that the CNAV longitude of the ascending node is completely different from the classical orbit element. The inclination angle of the CNAV is slightly different from the inclination of the classical orbit elements in the ECI coordinate frame.
$\vec r_{ECEF} $ is the position vector in the ECEF coordinate frame. R l(−i k) and R 3(−Ωk) are the rotation matrices that rotate the position vector by the CNAV angle of inclination and the CNAV longitude of ascending node. It is important to note that the CNAV longitude of the ascending node is completely different from the classical orbit element. The inclination angle of the CNAV is slightly different from the inclination of the classical orbit elements in the ECI coordinate frame.
 $$R_i^e = \left[ {\matrix{ {\cos \Omega _k} & { - \sin \Omega _k \cos i_k} & {\sin \Omega _k \sin i_k} \cr {\sin \Omega _k} & {\cos \Omega _k \cos i_k} & { - \cos \Omega _k \sin i_k} \cr 0 & {\sin i_k} & {\cos i_k} \cr}} \right]$$
$$R_i^e = \left[ {\matrix{ {\cos \Omega _k} & { - \sin \Omega _k \cos i_k} & {\sin \Omega _k \sin i_k} \cr {\sin \Omega _k} & {\cos \Omega _k \cos i_k} & { - \cos \Omega _k \sin i_k} \cr 0 & {\sin i_k} & {\cos i_k} \cr}} \right]$$The velocity determination equation is not described in IS-GPS-200F, but the velocity can be calculated by differentiating the position determination equation analytically. The simple format of the analytical velocity determination equation is represented as:
The acceleration determination algorithm can be calculated by differentiating the velocity equation. The simple format of the analytical acceleration equation is represented as:
2.3. GPS SATELLITE POSITION IN ECEF
The position determination algorithm described in IS-GPS-200F is divided into the position calculation part and the rotation from the CNAV orbital coordinate frame to the ECEF coordinate frame. The position determination equation in the CNAV orbital coordinate frame is:
 $$\vec r_{CNAVorb} = \left[ {\matrix{ {X_{CNAVorb}} \cr {Y_{CNAVorb}} \cr 0 \cr}} \right] = \left[ {\matrix{ {r_k \cos u_k} \cr {r_k \sin u_k} \cr 0 \cr}} \right]$$
$$\vec r_{CNAVorb} = \left[ {\matrix{ {X_{CNAVorb}} \cr {Y_{CNAVorb}} \cr 0 \cr}} \right] = \left[ {\matrix{ {r_k \cos u_k} \cr {r_k \sin u_k} \cr 0 \cr}} \right]$$where r k is the radius of the satellite in the CNAV orbital plane, which is calculated using A k, en and Ek. The value of e n is a constant value that is broadcast in the CNAV ephemeris message. The equation to calculate the radius:
where A k is determined by:
A REF is predefined in IS-GPS-200F, ![]() $\dot A$ and ΔA are broadcast parameters in the CNAV ephemeris and are new parameters that were not included in the LNAV. In equation (13), E k is an eccentricity anomaly at epoch time t k that is determined by M k and e n. The relationship of M k, Ek and e n is:
$\dot A$ and ΔA are broadcast parameters in the CNAV ephemeris and are new parameters that were not included in the LNAV. In equation (13), E k is an eccentricity anomaly at epoch time t k that is determined by M k and e n. The relationship of M k, Ek and e n is:
where M k is the mean anomaly that changes in time, n A is the rate of M k, and the relationship between M k and n A is defined in Equation (16), where M 0, Δn 0 and ![]() $\Delta \dot n_0 $ are broadcast in the CNAV ephemeris.
$\Delta \dot n_0 $ are broadcast in the CNAV ephemeris.
 $$\eqalign{n_0 & = \sqrt {\displaystyle{\mu \over {A_0^3 }}} \cr \Delta n_A & = \Delta n_0 + \displaystyle{1 \over 2}\Delta \dot n_0 \cdot t_k \cr n_A & = n_0 + \Delta n_A {\rm } \cr M_k & = M_0 + n_A \cdot t_k } $$
$$\eqalign{n_0 & = \sqrt {\displaystyle{\mu \over {A_0^3 }}} \cr \Delta n_A & = \Delta n_0 + \displaystyle{1 \over 2}\Delta \dot n_0 \cdot t_k \cr n_A & = n_0 + \Delta n_A {\rm } \cr M_k & = M_0 + n_A \cdot t_k } $$δr k in Equation (13) is the argument of latitude correction term for the radius in the CNAV orbital plane. δr k is determined by the following algorithm:
where C rs−n and C rc−n are the harmonic perturbation correction coefficients that are broadcast in CNAV ephemeris. Φk is the argument of the latitude and is determined by:
 $$\eqalign{\Phi _k & = \nu _k + \omega _n \cr \nu _k & = \tan ^{ - 1} \left( {\displaystyle{{\sqrt {1 - e_n^2 } \sin E_k } \over {\cos E_k - e}}} \right)} $$
$$\eqalign{\Phi _k & = \nu _k + \omega _n \cr \nu _k & = \tan ^{ - 1} \left( {\displaystyle{{\sqrt {1 - e_n^2 } \sin E_k } \over {\cos E_k - e}}} \right)} $$where ν k is the true anomaly, and ω n is the argument of the perigee in CNAV orbital plane. The value of ν k changes in time, and ω n is a broadcast value in the CNAV ephemeris.
In Equation (12), μ k is the corrected argument of the latitude given by:
where C us−n and C uc−n are the amplitude of the harmonic correction terms for the argument of latitude and are broadcasted in the CNAV ephemeris.
In Equation (9), ![]() $R_i^e $ is the rotation matrix from the CNAV orbital plane to the ECEF coordinate frame. The rotation matrix
$R_i^e $ is the rotation matrix from the CNAV orbital plane to the ECEF coordinate frame. The rotation matrix![]() $R_i^e $ is:
$R_i^e $ is:
where:
Ω0 is the reference of the right ascension;
Ω is the rate of right ascension;
ΩREF is the predefined reference rate of right ascension; and
ΔΩ is the correction of the rate of right ascension.
The i k term and its related terms in Equation (9) have had their notation changed for clarity because ![]() $\dot i_k $ (the rate of inclination angle) can be misread as i k (the inclination angle). The modified notations are:
$\dot i_k $ (the rate of inclination angle) can be misread as i k (the inclination angle). The modified notations are:
 $$\eqalign{I_k & = i_k \cr I_{0 - n} & = i_{0 - n} \cr \dot I_{0 - n} & = i_{0 - n} - DOT \cr \delta I_k & = \delta i_k } $$
$$\eqalign{I_k & = i_k \cr I_{0 - n} & = i_{0 - n} \cr \dot I_{0 - n} & = i_{0 - n} - DOT \cr \delta I_k & = \delta i_k } $$ The inclination angle I k is calculated using the rate of inclination angle ![]() $\dot I_{0 - n} $ and the inclination correction δI k that is given in Equation (22). In Equation (22), C is−n and C ic−n are the amplitudes of the harmonic correction term to the inclination and are broadcasted in the CNAV ephemeris.
$\dot I_{0 - n} $ and the inclination correction δI k that is given in Equation (22). In Equation (22), C is−n and C ic−n are the amplitudes of the harmonic correction term to the inclination and are broadcasted in the CNAV ephemeris.
2.4. GPS SATELLITE VELOCITY IN ECEF
The GPS satellite velocity ![]() $\dot \vec {r}_{CNAVorb} $ can be determined using Equation (23). In Equation (23),
$\dot \vec {r}_{CNAVorb} $ can be determined using Equation (23). In Equation (23), ![]() $\dot \vec {r}_{CNAVorb} $ and
$\dot \vec {r}_{CNAVorb} $ and ![]() $\dot R_i^e $ are needed to calculate the velocity.
$\dot R_i^e $ are needed to calculate the velocity.
 $$ \dot {\vec r}_{CNAVorb} = \left[ {\matrix{ { \dot X_{CNAVorb}} \cr { \dot Y_{CNAVorb}} \cr 0 \cr}} \right] = \left[ {\matrix{ { \dot r_k \cos u_k - r_k \sin u_k \cdot \dot u_k} \cr { \dot r_k \sin u_k + r_k \cos u_k \cdot \dot u_k} \cr 0 \cr}} \right]$$
$$ \dot {\vec r}_{CNAVorb} = \left[ {\matrix{ { \dot X_{CNAVorb}} \cr { \dot Y_{CNAVorb}} \cr 0 \cr}} \right] = \left[ {\matrix{ { \dot r_k \cos u_k - r_k \sin u_k \cdot \dot u_k} \cr { \dot r_k \sin u_k + r_k \cos u_k \cdot \dot u_k} \cr 0 \cr}} \right]$$where ![]() $\dot r_k $ is the differential of the radius in the CNAV orbital plane and is calculated by:
$\dot r_k $ is the differential of the radius in the CNAV orbital plane and is calculated by:
In Equation (24), ![]() $\dot A_k $,
$\dot A_k $, ![]() $\dot E_k $ and
$\dot E_k $ and ![]() $\left[ {\delta r_k} \right]\prime $ are needed to calculate derivative of radius
$\left[ {\delta r_k} \right]\prime $ are needed to calculate derivative of radius ![]() $\dot r_k $.
$\dot r_k $. ![]() $\dot A_k $ can be set to broadcast CNAV ephemeris term
$\dot A_k $ can be set to broadcast CNAV ephemeris term ![]() $\dot A$ as:
$\dot A$ as:
![]() $\dot E_k $ can be obtained by differentiating Equation (15) and the differential of the eccentricity anomaly equation is:
$\dot E_k $ can be obtained by differentiating Equation (15) and the differential of the eccentricity anomaly equation is:
 $$\eqalign{& \dot E_k = \displaystyle{{n_A} \over {1 - e_n \cos E_k}} \cr & n_A = n_0 + \Delta n_0 + \displaystyle{1 \over 2}\Delta \dot n_0 \cdot t_k} $$
$$\eqalign{& \dot E_k = \displaystyle{{n_A} \over {1 - e_n \cos E_k}} \cr & n_A = n_0 + \Delta n_0 + \displaystyle{1 \over 2}\Delta \dot n_0 \cdot t_k} $$The mean anomaly value in Equation (26) is different from that of the LNAV, as the rate of the mean motion is added in the CNAV.
In Equation (24), the derivative of the radial correction is:
where ![]() $\dot \nu _k $ is the derivative of the true anomaly. The derivative of the true anomaly can be defined by:
$\dot \nu _k $ is the derivative of the true anomaly. The derivative of the true anomaly can be defined by:
 $$ \dot \nu _k = \displaystyle{{A_k ^2 \sqrt {1 - e_n^2} \cdot n_A} \over {r_k^2}} $$
$$ \dot \nu _k = \displaystyle{{A_k ^2 \sqrt {1 - e_n^2} \cdot n_A} \over {r_k^2}} $$The derivative of the corrected argument of latitude ![]() $\dot u_k $ is:
$\dot u_k $ is:
![]() ${\rm \dot \Phi} _k $ can be obtained by differentiating Equation (18) under the condition that ω n is a constant value.
${\rm \dot \Phi} _k $ can be obtained by differentiating Equation (18) under the condition that ω n is a constant value.
![]() $\dot R_i^e $ in Equation (10), can be obtained by differentiating the rotation matrix
$\dot R_i^e $ in Equation (10), can be obtained by differentiating the rotation matrix ![]() $R_i^e $. This is a simple process that only requires the derivative of each component and the result is:
$R_i^e $. This is a simple process that only requires the derivative of each component and the result is:
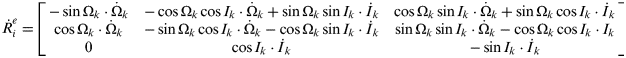 $$ \dot R_i^e = \! \left[ {\matrix{ { - \sin \Omega _k \cdot {\rm \dot \Omega} _k } & { - \cos \Omega _k \cos I_k \cdot {\rm \dot \Omega} _k + \sin \Omega _k \sin I_k\cdot \dot I_k } & {\cos \Omega _k \sin I_k \cdot {\rm \dot \Omega} _k + \sin \Omega _k \cos I_k \cdot \dot I_k } \cr {\cos \Omega _k \cdot {\rm \dot \Omega} _k } & { - \sin \Omega _k \cos I_k \cdot {\rm \dot \Omega} _k - \cos \Omega _k \sin I_k \cdot \dot I_k } & {\sin \Omega _k \sin I_k \cdot {\rm \dot \Omega} _k - \cos \Omega _k \cos I_k \cdot I_k } \cr 0 & {\cos I_k \cdot \dot I_k } & { - \sin I_k \cdot \dot I_k } \cr } } \right]$$
$$ \dot R_i^e = \! \left[ {\matrix{ { - \sin \Omega _k \cdot {\rm \dot \Omega} _k } & { - \cos \Omega _k \cos I_k \cdot {\rm \dot \Omega} _k + \sin \Omega _k \sin I_k\cdot \dot I_k } & {\cos \Omega _k \sin I_k \cdot {\rm \dot \Omega} _k + \sin \Omega _k \cos I_k \cdot \dot I_k } \cr {\cos \Omega _k \cdot {\rm \dot \Omega} _k } & { - \sin \Omega _k \cos I_k \cdot {\rm \dot \Omega} _k - \cos \Omega _k \sin I_k \cdot \dot I_k } & {\sin \Omega _k \sin I_k \cdot {\rm \dot \Omega} _k - \cos \Omega _k \cos I_k \cdot I_k } \cr 0 & {\cos I_k \cdot \dot I_k } & { - \sin I_k \cdot \dot I_k } \cr } } \right]$$where ![]() ${\rm \dot \Omega} _k $ and
${\rm \dot \Omega} _k $ and ![]() $\dot I_k $ are:
$\dot I_k $ are:
2.5. GPS Satellite Acceleration in ECEF
To obtain the GPS satellite acceleration, two additional variables are needed: the second order differential of the rotation matrix ![]() $ \ddot R_i^e $ and the second order differential of the radius
$ \ddot R_i^e $ and the second order differential of the radius ![]() $ \ddot \vec r_{ECEF} $ in the CNAV orbital plane. To obtain the second order differential of the rotation matrix
$ \ddot \vec r_{ECEF} $ in the CNAV orbital plane. To obtain the second order differential of the rotation matrix ![]() $ \ddot R_i^e $, each component of the first order derivative of the rotation matrix
$ \ddot R_i^e $, each component of the first order derivative of the rotation matrix ![]() $\dot R_i^e $ is simply differentiated. In this differential calculation,
$\dot R_i^e $ is simply differentiated. In this differential calculation, ![]() $\ddot I_k $ and
$\ddot I_k $ and ![]() $\ddot \Omega _k $ are set to zero, because these values have only first differential values in the CNAV ephemeris. The second order of differential of the rotation matrix is:
$\ddot \Omega _k $ are set to zero, because these values have only first differential values in the CNAV ephemeris. The second order of differential of the rotation matrix is:
 $$ \ddot R_i^e = \left[ {\matrix{ { - \cos \Omega _k \cdot {\rm \dot \Omega} _k^2} & {\sin \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \cos I_k} & { - \sin \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \sin I_k} \cr { - \sin \Omega _k \cdot {\rm \dot \Omega} _k^2} & { - \cos \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \cos I_k} & {\cos \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \sin I_k} \cr 0 & 0 & 0 \cr}} \right]$$
$$ \ddot R_i^e = \left[ {\matrix{ { - \cos \Omega _k \cdot {\rm \dot \Omega} _k^2} & {\sin \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \cos I_k} & { - \sin \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \sin I_k} \cr { - \sin \Omega _k \cdot {\rm \dot \Omega} _k^2} & { - \cos \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \cos I_k} & {\cos \Omega _k \cdot {\rm \dot \Omega} _k^2 \cdot \sin I_k} \cr 0 & 0 & 0 \cr}} \right]$$ The second order differential of the radius ![]() $\ddot \vec {r}_{CNAVorb} $ in the CNAV orbital plane is defined in Equation (4). The acceleration of the GPS satellite is:
$\ddot \vec {r}_{CNAVorb} $ in the CNAV orbital plane is defined in Equation (4). The acceleration of the GPS satellite is:
3. ECEF-TO-ECI COORDINATE TRANSFORMATION
The space-based user that is using a GPS receiver, such as a LEO satellite or the International Space Station (ISS), needs navigation data not only in the ECEF coordinate frame but also in the ECI coordinate frame for satellite propagation and estimation applications. The calculated position using the LNAV or the CNAV ephemeris is represented in the ECEF coordinate frame (WGS-84). The GPS receiver user, who is using LNAV, can obtain an inaccurate state vector in the ECI frame by rotating the state vector in the ECEF frame about the z-axis by the angle of the Greenwich Apparent Sidereal Time (GAST) (IS-GPS-200F). The accuracy of the rotation about the z-axis alone is very low, such that the result is not appropriate for use in orbit propagation or estimation. To obtain the correct transformed state vector, the EOP data are needed. Accordingly, the EOP data will be loaded in the CNAV in message type 32. The parameters are listed in Table 1.
Table 1. CNAV EOP Parameters.
To use EOP data correctly, a rotation matrices calculation algorithm is needed. IS-GPS-200F recommends using the frame transform algorithms described in Circular-179, which is published by the United States Naval Observatory (USNO). There are three different algorithms explained in Circular-179, and two algorithms are implemented in the C and Fortran programming languages known as the Naval Observatory Vector Astrometry Subroutines (NOVAS) (USNO, 2009). These three frame transform algorithms have different notations and implementation procedures. We choose one of them to use in the frame transformation, which is the equinox-based transformation that is based on IAU-2000A theory. The equinox-based transformation algorithm transforms the ITRF to the GCRF and vice versa. The ITRF is one type of ECEF frame and GCRF is one type of ECI frame that are adopted by the IAU. The ECEF and the ECI are not specifically implemented frames; hence, several ECI and ECEF frames exist. The equinox-based transformation takes the ITRF and the GCRF frames in its implementation. The ITRF is consistent with the WGS-84 to within 2 cm, so the ITRF can be considered the WGS-84 frame. In other words, one can assume that the GPS (WGS-84) is a good approximation of the ITRS. [Circular 176] The GCRS is an implementation of IAU 2000 resolution B1.3 and the GCRF is a realization of Geocentric Celestial Reference System (GCRS). The equinox-based transformation consists of five sequential rotation matrices. The rotation matrix equations are:
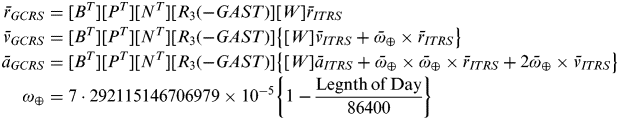 $$\eqalign{\bar r_{GCRS} & = [B^T ][P^T ][N^T ][R_3 ( - GAST)][W]\bar r_{ITRS} \cr \bar v_{GCRS} & = [B^T ][P^T ][N^T ][R_3 ( - GAST)]\left\{ {[W]\bar v_{ITRS} + \bar \omega _ \oplus \times \bar r_{ITRS} } \right\} \cr \bar a_{GCRS} & = [B^T ][P^T ][N^T ][R_3 ( - GAST)]\left\{ {[W]\bar a_{ITRS} + \bar \omega _ \oplus \times \bar \omega _ \oplus \times \bar r_{ITRS} + 2\bar \omega _ \oplus \times \bar v_{ITRS} } \right\} \cr \omega _ \oplus & = 7\cdot292115146706979 \times 10^{ - 5} \left\{ {1 - \displaystyle{{{\rm Legnth}\,{\rm of}\,{\rm Day}} \over {86400}}} \right\}} $$
$$\eqalign{\bar r_{GCRS} & = [B^T ][P^T ][N^T ][R_3 ( - GAST)][W]\bar r_{ITRS} \cr \bar v_{GCRS} & = [B^T ][P^T ][N^T ][R_3 ( - GAST)]\left\{ {[W]\bar v_{ITRS} + \bar \omega _ \oplus \times \bar r_{ITRS} } \right\} \cr \bar a_{GCRS} & = [B^T ][P^T ][N^T ][R_3 ( - GAST)]\left\{ {[W]\bar a_{ITRS} + \bar \omega _ \oplus \times \bar \omega _ \oplus \times \bar r_{ITRS} + 2\bar \omega _ \oplus \times \bar v_{ITRS} } \right\} \cr \omega _ \oplus & = 7\cdot292115146706979 \times 10^{ - 5} \left\{ {1 - \displaystyle{{{\rm Legnth}\,{\rm of}\,{\rm Day}} \over {86400}}} \right\}} $$where:
B is the frame bias matrix;
P is the precession matrix;
N is the nutation matrix;
R 3(−GAST) is the sidereal rotation matrix; and
W is the polar motion matrix.
Equation (33) is the summary of the equinox-based transformation algorithm. The details of the equinox-based transformation algorithm are described in Circular-179 and by Vallado (Reference Vallado and McClain2001).
4. SIMULATION PROCEDURE AND RESULTS
Three different simulations were performed to verify the algorithm proposed in this paper. The first simulation compared the analytical and the numerical results of the velocity and the acceleration to verify the correctness of the proposed algorithm, which uses the CNAV. The second simulation tested improvement of the CNAV ephemeris accuracy in terms of position, velocity and acceleration determination. Virtual CNAV ephemeris data were generated, using the GPS LNAV ephemeris and the NGA precise GPS position and velocity data, to test the accuracy improvement when using the CNAV, because CNAV was not broadcasting at that time (1 October 2012) [USNO data]. The third simulation was the state vector coordinate transform using the EOP data that were taken from the USNO.
4.1. Virtual CNAV Message
To test the proposed algorithm, the virtual CNAV ephemeris data were constructed using the precise GPS position and velocity data from the NGA and the LNAV ephemeris data from International GNSS Service (IGS). The procedure of generating the virtual CNAV is described in Figure 2. The main difference between LNAV and CNAV is that CNAV has two new additional terms: the rate of mean motion and the rate of semi-major axis motion. These two terms are generated using the NGA precise GPS data and the LNAV ephemeris correction terms. In this paper, we used data from 1 March 2011 from time 04:00:00 to 06:00:00.

Figure 2. Virtual CNAV generation procedure using the LNAV ephemeris and the precise GPS ephemeris
4.2. Correctness Test
To check the correctness of the proposed position, velocity and acceleration determination algorithm, we compared these values to the numerical velocity and acceleration. The analytical velocity ![]() $\dot \bar {r}_{ECEF} $ was determined using Equation (10), and the numerical velocity
$\dot \bar {r}_{ECEF} $ was determined using Equation (10), and the numerical velocity ![]() $\dot \bar {r}_{Num\_ECEF} $ was generated using Equation (34). The same procedure was performed for the correctness test on the acceleration. The analytical acceleration
$\dot \bar {r}_{Num\_ECEF} $ was generated using Equation (34). The same procedure was performed for the correctness test on the acceleration. The analytical acceleration ![]() $ \ddot \bar {r}_{ECEF} $ and the numerical acceleration
$ \ddot \bar {r}_{ECEF} $ and the numerical acceleration ![]() $ \ddot \bar {r}_{Num\_ECEF} $ were compared using the virtual CNAV. The analytical acceleration was generated using Equation (11), and the numerical acceleration
$ \ddot \bar {r}_{Num\_ECEF} $ were compared using the virtual CNAV. The analytical acceleration was generated using Equation (11), and the numerical acceleration ![]() $\ddot \bar r_{Num\_ECEF} $ was generated using Equation (35).
$\ddot \bar r_{Num\_ECEF} $ was generated using Equation (35).
where Δt was set to 1 second.
The comparison of the analytical and the numerical position and velocity is presented in Figure 3 and Figure 4. The difference between the analytical and the numerical velocity is less than 0·00001 m/s for each axis, and the difference in the acceleration is less than 0·00008 m/s2. With these results, we conclude that the proposed algorithm has continuity and correctness in terms of GPS satellite position, velocity and acceleration determination.

Figure 3. Velocity difference between the analytical and the numerical methods.

Figure 4. Acceleration difference between the analytical and numerical methods.
4.3. Accuracy of GPS Satellite State Vector Using CNAV
The position, velocity and acceleration of the PRN5 GPS satellite were calculated using the virtual CNAV ephemeris, and these results were compared to the NGA precise position, velocity and acceleration of the PRN5 GPS satellite. The simulation start time was set as 1 March 2011 04:00:00 and the simulation had a duration of two hours and step intervals of 15 minutes. The NGA precise GPS position and velocity data were assumed to be the true data, and the numerically calculated acceleration data using the NGA precise GPS velocity were also assumed to be the true acceleration data.
During the same time and PRN conditions, the GPS satellite position was calculated using the LNAV and the CNAV. The residual of the position is shown in Figure 5. Over the two hours of the simulation, we observed that the calculated position data using the virtual CNAV is more accurate than using the LNAV. The maximum error of the position calculated using the virtual CNAV is 0·34 m and that of the position calculated using LNAV is 0·69 m. By considering the maximum value of the residual at each epoch, the virtual CNAV shows more accurate results than the LNAV.

Figure 5. Position residuals of the LNAV and CNAV ephemerides.
Next, we checked the accuracy of the calculated velocity using the LNAV and the virtual CNAV. The residuals of the velocity, which are the differences between the true and calculated velocity of the satellite are shown in Figure 6. During the two hours of the simulation, the residual of the velocity using the virtual CNAV is less than that of the LNAV except for three epochs. This result is caused by the limited accuracy of the virtual CNAV ephemeris.

Figure 6. Velocity residuals of the LNAV and CNAV ephemerides.
The residuals of the acceleration calculated using the LNAV and the virtual CNAV are shown in Figure 7. The result shows that the acceleration error residuals of the LNAV and the virtual CNAV are almost the same. This result is caused by the fact that the virtual CNAV is not a complete CNAV; for instance, the inclination and the right ascension of ascending node are adapted from the LNAV and the LNAV derivation value as well. These terms are used when determining the acceleration in Equations (29) and (31); as a result, the accelerations of these two values are approximately the same when using the virtual CNAV ephemeris. The residual of the calculated acceleration is less than 0·0001 m/s2.

Figure 7. Acceleration residuals of the LNAV and CNAV ephemerides.
Note that the CNAV in each figure is the virtual CNAV that was constructed using the LNAV data and the NGA precise GPS data. The accuracy of the calculated position, velocity and acceleration data is not exactly the expected value that is generated using the broadcast CNAV; however, the accuracy of the virtual CNAV is greater than that of LNAV, and we expect that the accuracy of the broadcast CNAV will be better than that of the virtual CNAV.
4.4. COORDINATE TRANSFORMATION SIMULATION
IAU-2000 Resolution, which is the equinox-based ITRF-to-GCRF transformation, is the standard reference algorithm; therefore, we assumed that the transformed result using the equinox-based transformation is true. If not using EOP parameters, the ECEF to the ECI transformation can be performed by a simple rotation about the z-axis neglecting effects due to wobble, precession and nutation. When applying simple rotation, the rotation angle is set as the Greenwich Apparent Sidereal Time (GAST) (GPSD, 2011). This simple rotation method was compared to the IAU-2000 equinox-based transformation to evaluate the accuracy improvement when using the EOP data. The EOP and UT1 data from the International Earth Rotation and Reference Systems Service (IERS) are used in this simulation (IERS, 2012). The position, velocity and acceleration transformation results are shown in Figures 8 to 10. The maximum position transformation error using the simple rotation is approximately 70 km in the x-axis and several tens of kilometres along each axis. The maximum velocity transformation error is approximately 9 m/s in x-axis, and the maximum acceleration transformation error is 0·015 m/s in x-axis. Therefore, we concluded that when not using EOP data and the IAU-2000 resolution transformation algorithm, the accuracy of the frame transformation result will be degraded.
5. CONCLUSION
The US government has a plan to broadcast new Global Positioning System (GPS) civil signals and Civil Navigation (CNAV) messages. The CNAV message contains new ephemeris and Earth Orientation Parameter (EOP) data, which provide more accurate GPS satellite ephemeris and Earth Centred Earth Fixed (ECEF)-to-Earth Centred Inertial (ECI) transformation data. To obtain the receiver's velocity and acceleration data, the GPS satellite's velocity and acceleration are needed, but the CNAV ephemeris provides only the position data. In this paper we propose an analytical velocity and acceleration determination algorithm that is more efficient in computation compared with the numerical method. To verify the correctness of our proposed algorithm, we fabricated a virtual CNAV message using the Legacy Navigation (LNAV) and the National Geospatial-Intelligence Agency's (NGA) precise GPS satellite position and velocity data, and we used this virtual CNAV to calculate the GPS satellite's position, velocity and acceleration. The results showed that the proposed algorithm is correct, and that the position and the velocity data using the virtual CNAV are more accurate than LNAV. Therefore, we concluded that the position and velocity data will be more accurate if using an actual broadcast CNAV. The equinox-based ECEF-to-ECI transformation algorithm along with the EOP data produced more correct results than the simple rotation method about the x-axis. As a result, we concluded that the proposed velocity and acceleration determination algorithm and equinox-based transformation can provide accurate GPS satellite position, velocity and acceleration data for a GPS user.

Figure 8. Position difference between the simple rotation and the equinox-based transformation.

Figure 9. Velocity difference between the simple rotation and the equinox-based transformation.

Figure 10. Acceleration difference between simple rotation and equinox-based transformation.
ACKNOWLEDGEMENT
This work was supported by Korea Aerospace Research Institute through KARI's University Partnership Program contracted through the Institute of Advanced Aerospace Technology at Seoul National University.













