Published online by Cambridge University Press: 05 December 2005
In this paper the results of numerical computations of rippling smoothing basing on the broad-band laser irradiation method for the laser intensity range 1016−1017 W/cm2 and short-pulse (<10 ps) interaction with plasma are described.
In order to use a high-energy and short-pulse laser-plasma interaction for direct-drive laser fusion, we are obliged to reduce a number of setbacks received from the experimental observation. Such a problem was caused by non-linear and anomalous phenomena and was mentioned in the 1960s and 1970s.
The major obstacles to achieving a direct-drive fusion are Rayleigh–Taylor instability and stochastic pulsation. For the last year, a lot of efforts were made by many research groups all over the world in order to reduce the second effect. For example, in the paper of Boreham et al. (1997), basing on genuine two-fluid model, it investigated interaction between three wave-set with plasma, leading to reduction of rippling amplitude for long pulses with τL > 20 ps and for beam intensity in the range 1015 W/cm2 to 1016 W/cm2.
The stochastic pulsation was recognized from numerical studies in 1974 at the University of Rochester (Hora, 1991: Figs. 10.10 and 10.11; Hoffmann et al., 1990) and measured most convincingly by Maddever et al. (1990). The theory (Hora & Aydin, 1992) confirmed this mechanism and how this could be overcome by laser beam smoothing, especially by broad band irradiation (Hora & Aydin, 1999; Osman & Hora, 2004). The following approach is specifically directed to analyze new developments of the plasma block generation (Hora et al., 2002; Badziak et al., 2004a, 2004b) as an alternative scheme for laser fusion (Hora, 2004) as one option of fast ignition (Bauer, 2003; Deutsch, 2004; Mulser & Schneider, 2004; Mulser & Bauer, 2004; Osman & Hora, 2004; Ramirez et al., 2004; Hoffmann et al., 2005; Badziak et al., 2005).
Due to fast progress in laser technology, there are in use now laser systems generating pico and sub-pico second pulses with intensities above 1016 W/cm2. In this paper the results of numerical computations of rippling smoothing for the laser intensity range 1016–1018 W/cm2 and short-pulse (<10 ps) interaction with plasma are described.
The mechanism of stochastic pulsation was first explained in 1974 when the mentioned phenomena were bound with interaction between laser field and plasma. Due to a big value of ponderomotive force, it is possible to observe rippling of electrons and ions density profiles. Such a self-generated von-Laue grating prevents the propagation of laser radiation through the plasma and prevents energy deposition to the critical region of plasma. Due to a thermal relaxation, gratings disappear after some time and all the phenomenon can repeat again if the interaction time is sufficiently long.
In order to interrupt this pulsation for long laser pulses smoothing methods are usually used. The most popular of them are:
In this paper, the last method of smoothing is investigated. Broad-band irradiation was simulated by analyzing the interaction between three or five wave-sets with plasma. The difference between frequencies of waves in wave-set was in the range 0.5–2.0% of ω0.
The interaction of a short laser pulse with an inhomogeneous plasma layer was investigated by Glowacz et al. (2004) with the use of the computation code of the advanced two-fluid plasma model. This model is based on the nontermalized direct electromagnetic interaction between the laser light and the fully ionized plasma. In this model, electrons and ions are treated as separate conductive fluids which interact between each other by collisions (momentum exchange) and the Coulomb interaction. The electron and ion fluids are described by six quantities which are mass densities (ρe, ρi), temperatures (Te, Ti), and velocities of electrons and ions (υe, υi). The equations of the model were solved in one dimension which means that all just mentioned quantities depend on one spatial coordinate (x) and time (t). The velocities υe and υi are in the x-direction.
To obtain these six quantities we solved six equations and particularly: the equations of continuity for electrons and ions
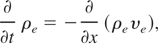
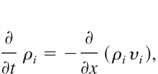
the equations describing conservation of momentum for electrons and ions

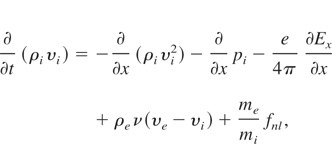
and the equations which allow us to take into account changes of the temperature of ions and electrons (conservation of energy)
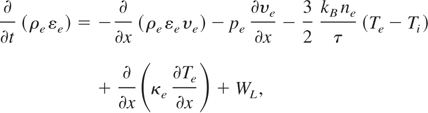
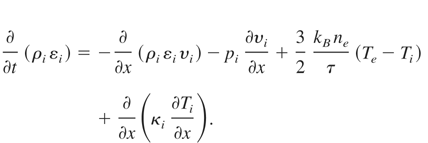
It was assumed that equations of state for these two fluids are pe = kBTe ρe /me,pi = kBTi ρi /mi (ideal gas), where kB is the Boltzman constant and electron and ion mass are me and mi, respectively. As εe is internal energy of electrons and εi is energy of ions, we can replace these quantities with temperatures using εe = 3/2kBTe /me for electrons, and εI = 3/2kBTi /mi for ions. The quantities ν, t, and WL are the collision frequency, the temperature equipartition time, and the density of electron heating power by laser absorption in plasma. The formulas for κe and κi which are thermal conductivities for the electron and ion fluids, respectively, must be known.
To describe the Coulomb interaction between the two charged fluids, which play the most crucial role in the ion current appearance, Poisson equation was solved
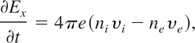
where Ex is the electric field in the x-direction, ni and ne are the electron and ion number densities, respectively.
To find non-linear ponderomotive force (fNL = 1/cj × H) in the x-direction (fNL) and the density of electron heating power (WL), the electromagnetic wave equations in plasma were solved
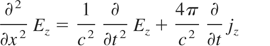
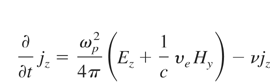
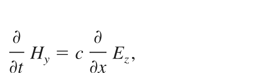
where Ez and Hy, are electric and magnetic fields of laser light and jz is a current in the z-direction. The impact of electron motion in electric field of light wave on the collision frequency ν, was taken into account. The equations of the model were solved basing on the Lax method.
In order to estimate level of rippling effect and results of smoothing an especial numerical tool based on the multilayers stack theory was created.
The main idea of the method is simple:
For the derivation of main equations for multilayers method phase relationship between electric E, and magnetic H fields on the layer's border was taken into consideration (Fig. 1).

The idea of multilayers method of rippling evaluation.
The values for E and H evaluated on the first border were used for evaluating such values on the next border and so on.
The main relations used in the method are described below:

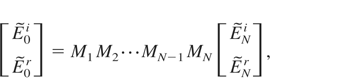
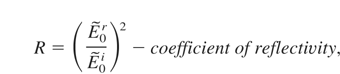
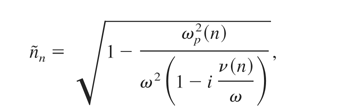
where

The example of correlation between plasma profile and refractive coefficient is shown in Figure 2. Analyzing the data in Figure 2, we can see that for plasma block width of 2.5 μm reflectivity coefficient is equal to about 18%, but for the width of 5 μm this value reach 62%. For ion density profile without rippling, reflectivity coefficients are equal about 0% for the width of 2.5 μm and 5 μm (Fig. 3).

Reflection of laser beam from plasma region as a function of the distance and ion density profile. T = 1.2 ps, I = 1016 W/cm2, τ1/2 = 1 ps, λ = 1.06 μm.

Reflection of laser beam from plasma region as a function of the distance and ion density profile for time t = 0.6 ps since start of interaction. I = 1016 W/cm2, τ1/2 = 1 ps, λ = 1.06 μm.
A characteristic 100% reflection for plasma 13.5 μm wide is a result of reflection from critical density region ncr.
The numerical calculations were performed for 20 μm hydrogen, inhomogeneous plasma layer of initial density increasing in the direction of the laser beam propagation. Linear plasma density profile described by the function n(x) = (0.04x + 0.5)ncr, where ncr—critical density, x—distance from plasma face in μm was taken into consideration. The mentioned density profile was preceded by short 1 μm plasma layer with a steeper density profile in order to improve numerical stability (Fig. 3). The computations were made for two laser intensities 1016 W/cm2 and 1017 W/cm2. For each intensity one wave, three waves, and five waves cases of interaction with plasma were analyzed (Table 1). In the case of multi waves, the total maximum amplitude of electric E and magnetic H components for waves was equal to the maximum amplitude E and H for one wave case. The parameter “relative intensity of laser beam” describes the relation between total intensity (not maximum intensity) of the laser pulse used during computations, relatively to the total intensity of one wave case. It should be noticed that this relation is constant and independent of shift Δω, see Figure 4. The decrease in the total intensity in the function of the wave's quantity is a result of interference between multi wave's elements in laser pulse. Results for intensity 1016 W/cm2 are presented in Figure 5, Figure 6, Figure 7, and Figure 8.
Parameters of laser beams used during computations


Shapes of the laser pulse intensity for frequency shift between waves: 1.0% of ω0 (left figure) and 2% of ω0 (right figure).

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for one wave. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for three waves of Δω = 0.5% ω0. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for five waves of Δω = 1.0% ω0. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of the ion velocity profile for three waves (left figure) and for five waves (right figure), results for 2 ps after the start of interaction. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.
Basing on the figures presented above we observed that for maximum of laser pulse intensity 1016 W/cm2, differences between interaction with plasma for one wave and multi-waves beams gives, for maximum ion velocity, very similar results in both directions of the plasma block propagation. Such an effect may be a surprise when we remember the fact that total intensity of the pulse in the cases of three and five waves is much smaller than in the case of one wave Figure 4. The main reason for the observed phenomena is only one, the smoothing of rippling effect. The most reduction of rippling amplitude was observed for frequency shift Δω = 0.5% ω0 (three waves) and for Δω = 1.0% ω0 (five waves). The mentioned amplitudes were decreased 3 times and 5 times, respectively. This fact was theoretically proved by Glowacz et al. (2006).
Similar relations were observed for higher pulse intensity I = 1017 W/cm2, Figure 9, Figure 10, Figure 11, and Figure 12, but for this example, an advantageous influence of smoothing was much more distinct and maximum values of ion velocities were about 2.5–3.0 times greater than for the case without smoothing.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for one wave. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for three waves of Δω = 0.5% ω0. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for five waves of Δω = 1.0% ω0. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of the ion velocity profile for three waves (left figure) and for five waves (right figure), results for 1.5 ps after the start of interaction. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm
It must be necessarily said that the method analyzed in the paper, which is well known for longer pulses can be successfully used to improve of the interaction between short (<1 ps) laser pulses and plasma.
This work was supported in part by the State Committee for Scientific Research (KBN), Poland under Grant No. 1 PO3B 043 26 and by a grant for a Visiting Scientist by the University of Western Sydney, Australia.

The idea of multilayers method of rippling evaluation.

Reflection of laser beam from plasma region as a function of the distance and ion density profile. T = 1.2 ps, I = 1016 W/cm2, τ1/2 = 1 ps, λ = 1.06 μm.

Reflection of laser beam from plasma region as a function of the distance and ion density profile for time t = 0.6 ps since start of interaction. I = 1016 W/cm2, τ1/2 = 1 ps, λ = 1.06 μm.

Parameters of laser beams used during computations

Shapes of the laser pulse intensity for frequency shift between waves: 1.0% of ω0 (left figure) and 2% of ω0 (right figure).

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for one wave. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for three waves of Δω = 0.5% ω0. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for five waves of Δω = 1.0% ω0. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of the ion velocity profile for three waves (left figure) and for five waves (right figure), results for 2 ps after the start of interaction. I = 1016 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for one wave. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for three waves of Δω = 0.5% ω0. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of ion density profile (left figure) and reflection of laser beam from plasma region (right figure) as a function of distance and interaction time for five waves of Δω = 1.0% ω0. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm.

Evolution of the ion velocity profile for three waves (left figure) and for five waves (right figure), results for 1.5 ps after the start of interaction. I = 1017 W/cm2, τL = 1 ps, λ = 1.06 μm