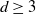1. Introduction and main result
Consider a branching random walk (BRW) on a graph G, beginning with one particle at some vertex, where each particle branches into a random number of offspring (independently and according to some fixed distribution), each of which jumps to a uniformly chosen neighbour. The behaviour of BRW when
![]() $G=\mathbb{Z}$
is a well-studied subject starting with Hammersley [Reference Hammersley12], Kingman [Reference Kingman14], and several papers by Biggins; see for example [Reference Biggins4], [Reference Biggins5], and [Reference Biggins6]. We also highlight an early paper of Bramson [Reference Bramson8], which contrasts with more recent results of Aidekon [Reference Aidekon1] and Bramson, Ding, and Zeitouni [Reference Bramson, Ding and Zeitouni9].
$G=\mathbb{Z}$
is a well-studied subject starting with Hammersley [Reference Hammersley12], Kingman [Reference Kingman14], and several papers by Biggins; see for example [Reference Biggins4], [Reference Biggins5], and [Reference Biggins6]. We also highlight an early paper of Bramson [Reference Bramson8], which contrasts with more recent results of Aidekon [Reference Aidekon1] and Bramson, Ding, and Zeitouni [Reference Bramson, Ding and Zeitouni9].
In this article we consider instead the case when the underlying graph G is the regular tree in which every vertex has exactly
![]() $d\ge 3$
neighbours (of course,
$d\ge 3$
neighbours (of course,
![]() $G=\mathbb{Z}$
can be viewed as the case
$G=\mathbb{Z}$
can be viewed as the case
![]() $d=2$
). We suppose that the expected number of offspring of each particle in the branching random walk is also d; this is critical in the geometric sense that the expected number of offspring moving to each neighbouring site has mean 1. We start with one particle at the root (an arbitrary vertex) of the tree, and ask for the cover time of a ball of radius r. That is, how long does it take before every site within distance r of the root has been visited by a particle of the BRW?
$d=2$
). We suppose that the expected number of offspring of each particle in the branching random walk is also d; this is critical in the geometric sense that the expected number of offspring moving to each neighbouring site has mean 1. We start with one particle at the root (an arbitrary vertex) of the tree, and ask for the cover time of a ball of radius r. That is, how long does it take before every site within distance r of the root has been visited by a particle of the BRW?
Tostate our result precisely, let T be the infinite d-ary tree in which every vertex has d neighbours, and fix a vertex which we label 0 and refer to as the root or origin. Suppose that
![]() $\mu$
is a probability measure on
$\mu$
is a probability measure on
![]() $\mathbb{Z}_+$
such that
$\mathbb{Z}_+$
such that
![]() $\sum_{j\ge 0}j\mu(j)=d$
and
$\sum_{j\ge 0}j\mu(j)=d$
and
![]() $\sum_{j\ge 0}j^2\mu(j)<\infty$
. Consider a branching random walk on T, starting with one particle at the root, in which at everytime step:
$\sum_{j\ge 0}j^2\mu(j)<\infty$
. Consider a branching random walk on T, starting with one particle at the root, in which at everytime step:
-
(a) each particle at any site
 $x\in T$
dies and gives birth to a random number of children independently and with distribution
$x\in T$
dies and gives birth to a random number of children independently and with distribution
 $\mu$
;
$\mu$
; -
(b) each of these offspring independently jumps to a neighbour of x, uniformly at random.
For each vertex
![]() $x\in T$
, let H(x) be the first time at which there is a particle at x. For
$x\in T$
, let H(x) be the first time at which there is a particle at x. For
![]() $r\ge 0$
, let
$r\ge 0$
, let
![]() $B(r) = \{x\in T \colon d(0,x)\le r\}$
and
$B(r) = \{x\in T \colon d(0,x)\le r\}$
and
![]() $\partial B(r) = \{x\in T \colon d(0,x)=\lfloor r\rfloor\}$
. We are interested in the cover time of B(r), defined to be
$\partial B(r) = \{x\in T \colon d(0,x)=\lfloor r\rfloor\}$
. We are interested in the cover time of B(r), defined to be
when r is large. Of course, if
![]() $\mu(0)>0$
, there is a positive probability that the process will die out in finite time; however, since
$\mu(0)>0$
, there is a positive probability that the process will die out in finite time; however, since
![]() $\mu$
has mean larger than one and finite variance, there is strictly positive probability that the process does not die out in finite time [Reference Kesten and Stigum13]. In this case we say that the process survives.
$\mu$
has mean larger than one and finite variance, there is strictly positive probability that the process does not die out in finite time [Reference Kesten and Stigum13]. In this case we say that the process survives.
Theorem 1.1. For any
![]() $d\ge 3$
, given that the process survives,
$d\ge 3$
, given that the process survives,
This result is initially surprising for two reasons. The first is that the cover time is so close (within a constant times
![]() $\log\log r$
) to its trivial lower bound of r. However, upon reading Bramson’s article [Reference Bramson8], one can see the reason for the
$\log\log r$
) to its trivial lower bound of r. However, upon reading Bramson’s article [Reference Bramson8], one can see the reason for the
![]() $\log\log r$
term, and might guess convergence of the quantity in our theorem to
$\log\log r$
term, and might guess convergence of the quantity in our theorem to
![]() $2/\log 2$
. Indeed, in the case
$2/\log 2$
. Indeed, in the case
![]() $d=2$
, this is the correct answer. The appearance of
$d=2$
, this is the correct answer. The appearance of
![]() $2/\log(3/2)$
instead comes from the fact that there are exponentially many vertices in
$2/\log(3/2)$
instead comes from the fact that there are exponentially many vertices in
![]() $\partial B(r)$
, some of which are hit unusually late; although it is interesting then that the answer does not depend on the value of
$\partial B(r)$
, some of which are hit unusually late; although it is interesting then that the answer does not depend on the value of
![]() $d\ge 3$
. We give a short heuristic in Section 2.
$d\ge 3$
. We give a short heuristic in Section 2.
The article is set out as follows. In Section 2 we give some background to Theorem 1.1 as well as a heuristic walkthrough of the proof; we also state some related open problems. In Section 3 we introduce the key ingredient for our proof of Theorem 1.1, which is a variant of our BRW in which we freeze particles that do not move in a particular direction. We then prove the lower bound for Theorem 1.1 in Section 4 and the upper bound in Section 5.
2. Notation, background, heuristics and open problems
We write
![]() $f(n)\asymp g(n)$
to mean that there exist constants
$f(n)\asymp g(n)$
to mean that there exist constants
![]() $0<c\le C<\infty$
such that
$0<c\le C<\infty$
such that
![]() $c\le f(n)/g(n) \le C$
for all large n. We write
$c\le f(n)/g(n) \le C$
for all large n. We write
![]() $\mathbb{P}_{n,x}$
for the probability measure under which we start with n particles at the vertex x. More generally, for a collection
$\mathbb{P}_{n,x}$
for the probability measure under which we start with n particles at the vertex x. More generally, for a collection
![]() $\Gamma = (x_1,\ldots,x_n)$
of vertices, we write
$\Gamma = (x_1,\ldots,x_n)$
of vertices, we write
![]() $\mathbb{P}_\Gamma$
for the probability measure under which we start with a particle at each of the vertices
$\mathbb{P}_\Gamma$
for the probability measure under which we start with a particle at each of the vertices
![]() $x_1,\ldots,x_n$
. For example,
$x_1,\ldots,x_n$
. For example,
![]() $\mathbb{P}_{(x,x,x)} = \mathbb{P}_{3,x}$
and
$\mathbb{P}_{(x,x,x)} = \mathbb{P}_{3,x}$
and
![]() $\mathbb{P} = \mathbb{P}_{(0)} = \mathbb{P}_{1,0}$
.
$\mathbb{P} = \mathbb{P}_{(0)} = \mathbb{P}_{1,0}$
.
2.1. Background
The problem of how fast a branching random walk spreads first appeared in the mid-1970s, with papers by Hammersley [Reference Hammersley12], Kingman [Reference Kingman14], and Biggins [Reference Biggins4–Reference Biggins6] giving – amongst other results – the first-order behaviour of the particle at maximal (or minimal) distance from the origin after n steps. In 1978, Bramson [Reference Bramson8] described a branching random walk on
![]() $\mathbb{Z}_+$
, beginning with one particle at 0, in which at each time step each particle branched into an average of
$\mathbb{Z}_+$
, beginning with one particle at 0, in which at each time step each particle branched into an average of
![]() $m>1$
new particles, each of which stayed at its previous location with probability
$m>1$
new particles, each of which stayed at its previous location with probability
![]() $1/m$
and moved one step to the right with probability
$1/m$
and moved one step to the right with probability
![]() $1-1/m$
. Letting
$1-1/m$
. Letting
![]() $M_n$
be the position of the minimal particle after n steps, he showed that
$M_n$
be the position of the minimal particle after n steps, he showed that
almost surely, where V is some non-trivial random variable. One of the purposes of looking at this model was that it showed significantly different behaviour from Bramson’s concurrent work on branching Brownian motion (BBM) [Reference Bramson7], demonstrating that giving a result on the detailed behaviour of
![]() $M_n$
was much harder in general for BRW than for BBM. In fact, results in the spirit of [Reference Bramson7] were not given for BRW in
$M_n$
was much harder in general for BRW than for BBM. In fact, results in the spirit of [Reference Bramson7] were not given for BRW in
![]() $\mathbb{R}$
until relatively recently, by Aidekon [Reference Aidekon1] and then Bramson, Ding, and Zeitouni [Reference Bramson, Ding and Zeitouni9]. Bramson’s result (2.1) is very closely related to the cover time problem in the case
$\mathbb{R}$
until relatively recently, by Aidekon [Reference Aidekon1] and then Bramson, Ding, and Zeitouni [Reference Bramson, Ding and Zeitouni9]. Bramson’s result (2.1) is very closely related to the cover time problem in the case
![]() $d=2$
, and we will use elements of Bramson’s proof in this article.
$d=2$
, and we will use elements of Bramson’s proof in this article.
For branching random walks on other graphs, particularly trees, much of the existing literature is concerned with recurrence and transience and related questions: see for example [Reference Gantert and Müller11], [Reference Liggett16], [Reference Madras and Schinazi18], and [Reference Pemantle and Stacey20]. The ‘maximal particle’ question mentioned above for BRW on
![]() $\mathbb{R}$
has no direct analogue on trees. One could ask for the maximal distance from the origin over all particles after n steps; it is easy to see that with our choice of parameters (d-ary tree and offspring distribution mean d), conditionally on survival, this is
$\mathbb{R}$
has no direct analogue on trees. One could ask for the maximal distance from the origin over all particles after n steps; it is easy to see that with our choice of parameters (d-ary tree and offspring distribution mean d), conditionally on survival, this is
![]() $n-{\mathrm{O}} (1)$
almost surely. Studying the cover time, or equivalently the largest ball that has been covered in n steps, is an equally natural alternative, and with our choice of parameters it is a much more delicate and interesting question.
$n-{\mathrm{O}} (1)$
almost surely. Studying the cover time, or equivalently the largest ball that has been covered in n steps, is an equally natural alternative, and with our choice of parameters it is a much more delicate and interesting question.
For our proof we will need the following well-known result on critical Galton–Watson processes, which is originally due to Kolmogorov [Reference Kolmogorov15] under a third moment assumption. See for example [Reference Lyons and Peres17, Theorem 12.7] for a modern proof.
Lemma 2.1. (Kolmogorov.)Suppose that
![]() $(Z_n, n\ge 0)$
is a Galton–Watson process started from
$(Z_n, n\ge 0)$
is a Galton–Watson process started from
![]() $Z_0=1$
satisfying
$Z_0=1$
satisfying
![]() $\mathbb{E}[Z_1]=1$
and
$\mathbb{E}[Z_1]=1$
and
![]() $\sigma^2 \,{:\!=}\, \mathbb{E}[Z_1^2]-1 <\infty$
. Then
$\sigma^2 \,{:\!=}\, \mathbb{E}[Z_1^2]-1 <\infty$
. Then
Key to our argument will be a result on the total progeny of a Galton–Watson process up to generation n due to Pakes [Reference Pakes19].
Lemma 2.2. (Pakes.)Suppose that
![]() $(Z_n, n\ge 0)$
is a Galton–Watson process started from
$(Z_n, n\ge 0)$
is a Galton–Watson process started from
![]() $Z_0=1$
satisfying
$Z_0=1$
satisfying
![]() $\mathbb{E}[Z_1]=1$
and
$\mathbb{E}[Z_1]=1$
and
![]() $\sigma^2 \,{:\!=}\, \mathbb{E}[Z_1^2]-1 <\infty$
. Let
$\sigma^2 \,{:\!=}\, \mathbb{E}[Z_1^2]-1 <\infty$
. Let
![]() $S_n = \sum_{i=0}^n Z_i$
. Then, for any
$S_n = \sum_{i=0}^n Z_i$
. Then, for any
![]() $\gamma\in(0,\infty)$
,
$\gamma\in(0,\infty)$
,
where F satisfies
We will not need the precise form of F, only that
![]() $F(\gamma)$
is strictly smaller than 1 for each finite
$F(\gamma)$
is strictly smaller than 1 for each finite
![]() $\gamma$
. As a result, combining Lemmas 2.1 and 2.2 (using the same notation), and noting that
$\gamma$
. As a result, combining Lemmas 2.1 and 2.2 (using the same notation), and noting that
we obtain that for each
![]() $\gamma\in[0,\infty)$
there exists a constant
$\gamma\in[0,\infty)$
there exists a constant
![]() $q(\gamma)>0$
depending only on
$q(\gamma)>0$
depending only on
![]() $\gamma$
and
$\gamma$
and
![]() $\sigma^2$
such that
$\sigma^2$
such that
We will also use the following simple and well-known Chernoff bound. Suppose that X is a finite sum of independent Bernoulli random variables. Then
2.2. Heuristics
We now give a heuristic for Theorem 1.1. We hope that it will provide useful intuition for our proof.
Fix a vertex y in
![]() $\partial B(r)$
for large r. In order to hit y by time close to r, some particles must make long ‘runs’ of consecutive steps towards y without taking any steps away from y. (We associate each particle with all its ancestors, so that although technically a particle only lives for one unit of time, when we talk about it making a run of length
$\partial B(r)$
for large r. In order to hit y by time close to r, some particles must make long ‘runs’ of consecutive steps towards y without taking any steps away from y. (We associate each particle with all its ancestors, so that although technically a particle only lives for one unit of time, when we talk about it making a run of length
![]() $\ell$
towards y, we mean that it and its last
$\ell$
towards y, we mean that it and its last
![]() $\ell-1$
ancestors all stepped towards y.)
$\ell-1$
ancestors all stepped towards y.)
Start from one particle at 0, and let
![]() $Z_i$
be the number of particles at time i that have taken i steps towards y. Then
$Z_i$
be the number of particles at time i that have taken i steps towards y. Then
![]() $(Z_i, i\ge0)$
forms a critical Galton–Watson process. Although this process will eventually die out (likely before any particle hits y), its total progeny has infinite mean. This gives rise to a potentially large number of particles that have taken exactly one step away from y. Suppose this number is A. Each of these A particles starts another critical Galton–Watson tree of particles that have taken
$(Z_i, i\ge0)$
forms a critical Galton–Watson process. Although this process will eventually die out (likely before any particle hits y), its total progeny has infinite mean. This gives rise to a potentially large number of particles that have taken exactly one step away from y. Suppose this number is A. Each of these A particles starts another critical Galton–Watson tree of particles that have taken
![]() $i-1$
steps towards y at time i. It is known that if we run A independent critical Galton–Watson processes, or equivalently one critical Galton–Watson process starting with A initial particles, then with probability of order 1 it will survive for of order A generations, with a total progeny of order
$i-1$
steps towards y at time i. It is known that if we run A independent critical Galton–Watson processes, or equivalently one critical Galton–Watson process starting with A initial particles, then with probability of order 1 it will survive for of order A generations, with a total progeny of order
![]() $A^2$
. This gives rise to of order
$A^2$
. This gives rise to of order
![]() $A^2$
particles that have taken exactly two steps away from y. Repeating this argument k times suggests that we should expect (very roughly)
$A^2$
particles that have taken exactly two steps away from y. Repeating this argument k times suggests that we should expect (very roughly)
![]() $A^{2^{k-1}}$
particles that have taken exactly k steps away from y, giving rise to another critical Galton–Watson process starting with (very roughly)
$A^{2^{k-1}}$
particles that have taken exactly k steps away from y, giving rise to another critical Galton–Watson process starting with (very roughly)
![]() $A^{2^{k-1}}$
initial particles, which survives for (very roughly)
$A^{2^{k-1}}$
initial particles, which survives for (very roughly)
![]() $A^{2^{k-1}}$
generations.
$A^{2^{k-1}}$
generations.
As soon as one of these processes – say the kth – survives for
![]() $d(0,y)+k$
generations, then y must have been hit by a particle. At the moment it hits y, this particle will have taken k steps in the wrong direction, and therefore
$d(0,y)+k$
generations, then y must have been hit by a particle. At the moment it hits y, this particle will have taken k steps in the wrong direction, and therefore
![]() $d(0,y)+2k$
steps in total. In other words, if
$d(0,y)+2k$
steps in total. In other words, if
![]() $A^{2^{k-1}} > d(0,y)+k$
, then
$A^{2^{k-1}} > d(0,y)+k$
, then
![]() $H(y)\le d(0,y)+2k$
. The converse is not quite true, but the fact that
$H(y)\le d(0,y)+2k$
. The converse is not quite true, but the fact that
![]() $A^{2^{k-1}}$
grows so quickly means that it is almost true, in that the correction is of smaller order. This implies that
$A^{2^{k-1}}$
grows so quickly means that it is almost true, in that the correction is of smaller order. This implies that
![]() $H(y) \approx d(0,y) + (2/\log 2)\log\log d(0,y)$
, which can be made rigorous and holds with high probability for each y.
$H(y) \approx d(0,y) + (2/\log 2)\log\log d(0,y)$
, which can be made rigorous and holds with high probability for each y.
We might thus expect the cover time of the ball of radius r to be roughly
![]() $r + (2/\log 2)$
$r + (2/\log 2)$
![]() $\log\log r$
. Indeed, this is essentially the explanation for the
$\log\log r$
. Indeed, this is essentially the explanation for the
![]() $(1/\log2)\log\log n$
term in (2.1) (the extra factor of 2 accounts for the fact that our particles cannot stay still but must either move towards or away from y at each step), and gives the correct answer to the cover time problem when
$(1/\log2)\log\log n$
term in (2.1) (the extra factor of 2 accounts for the fact that our particles cannot stay still but must either move towards or away from y at each step), and gives the correct answer to the cover time problem when
![]() $d=2$
. The fact that we instead see
$d=2$
. The fact that we instead see
![]() $r+({2}/{\log(3/2)})\log\log r$
when
$r+({2}/{\log(3/2)})\log\log r$
when
![]() $d\ge 3$
boils down to the fact that while most vertices
$d\ge 3$
boils down to the fact that while most vertices
![]() $y\in \partial B(r)$
are hit by time
$y\in \partial B(r)$
are hit by time
![]() $r+(2/\log 2)\log\log r$
, there are many vertices in
$r+(2/\log 2)\log\log r$
, there are many vertices in
![]() $\partial B(r)$
, and some are not hit until later.
$\partial B(r)$
, and some are not hit until later.
To see how this happens, again suppose that we have A particles that have taken exactly one step away from y. The probability that the resulting critical Galton–Watson process starting with A initial particles survives for fewer than
![]() $A^{1/2+\varepsilon}$
generations (for some small
$A^{1/2+\varepsilon}$
generations (for some small
![]() $\varepsilon>0$
) is roughly
$\varepsilon>0$
) is roughly
![]() $(1-c/A^{1/2+\varepsilon})^A \approx \exp(-cA^{1/2-\varepsilon})$
. In doing so the particles cover distance roughly
$(1-c/A^{1/2+\varepsilon})^A \approx \exp(-cA^{1/2-\varepsilon})$
. In doing so the particles cover distance roughly
![]() $A^{1/2+\varepsilon}$
, and therefore the number of possible vertices y at this distance from the origin that could see such behaviour is of order
$A^{1/2+\varepsilon}$
, and therefore the number of possible vertices y at this distance from the origin that could see such behaviour is of order
![]() $(d-1)^{A^{1/2+\varepsilon}}$
. Since, for A large and
$(d-1)^{A^{1/2+\varepsilon}}$
. Since, for A large and
![]() $d>3$
, we have
$d>3$
, we have
![]() $(d-1)^{A^{1/2+\varepsilon}} \gg \exp(cA^{1/2-\varepsilon})$
, we might expect that some vertices do see such behaviour. The total number of particles seen if this occurs is of order
$(d-1)^{A^{1/2+\varepsilon}} \gg \exp(cA^{1/2-\varepsilon})$
, we might expect that some vertices do see such behaviour. The total number of particles seen if this occurs is of order
![]() $A\cdot A^{1/2+\varepsilon} = A^{3/2+\varepsilon}$
.
$A\cdot A^{1/2+\varepsilon} = A^{3/2+\varepsilon}$
.
Continuing recursively, we might expect that some vertices y see only
![]() $A^{(3/2+\varepsilon)^k}$
particles that have taken k steps away from y. Following the same argument as above, we deduce that these vertices have hitting times satisfying
$A^{(3/2+\varepsilon)^k}$
particles that have taken k steps away from y. Following the same argument as above, we deduce that these vertices have hitting times satisfying
and since
![]() $\varepsilon>0$
was arbitrarily small, this agrees with our desired result.
$\varepsilon>0$
was arbitrarily small, this agrees with our desired result.
This argument gives us essentially a first moment estimate on the number of vertices whose hitting times are of the order stated in Theorem 1.1. Unfortunately a naive second moment bound does not work, since the processes seen from two different vertices in the tree are highly dependent, especially if the two vertices are near each other. To get around this we use the tree structure of the graph strongly. We fix
![]() $r'<r$
and show that many vertices in
$r'<r$
and show that many vertices in
![]() $\partial B(r')$
behave ‘normally’, in that they are not hit too early and the number of particles moving towards them is not too large. For each of these ‘normal’ vertices x we fix a vertex
$\partial B(r')$
behave ‘normally’, in that they are not hit too early and the number of particles moving towards them is not too large. For each of these ‘normal’ vertices x we fix a vertex
![]() $z(x)\in \partial B(r)$
that is in the subtree rooted at x, by which we mean that any path from 0 to z must pass through x. Using the argument above, we estimate the probability that z(x) is hit later than usual and has a relatively small number of particles moving towards it (given that x is normal), and use the tree structure to get independence of these events for different vertices x. In fact, rather than just carrying out this procedure for the desired choice of r, we carry out a multi-scale argument using the scales dictated by the argument above: very roughly,
$z(x)\in \partial B(r)$
that is in the subtree rooted at x, by which we mean that any path from 0 to z must pass through x. Using the argument above, we estimate the probability that z(x) is hit later than usual and has a relatively small number of particles moving towards it (given that x is normal), and use the tree structure to get independence of these events for different vertices x. In fact, rather than just carrying out this procedure for the desired choice of r, we carry out a multi-scale argument using the scales dictated by the argument above: very roughly,
![]() $r_k\approx A^{(1/2+\varepsilon)(3/2+\varepsilon)^k}$
for each k.
$r_k\approx A^{(1/2+\varepsilon)(3/2+\varepsilon)^k}$
for each k.
2.3. Criticality of
 $\mu$
$\mu$
We mentioned in Section 1 that our model is critical in a certain geometric sense. To explain more thoroughly, we consider a branching random walk on T where the offspring distribution
![]() $\mu$
has mean m not necessarily equal to d. It is well known that the Galton–Watson tree underlying our BRW becomes extinct almost surely when
$\mu$
has mean m not necessarily equal to d. It is well known that the Galton–Watson tree underlying our BRW becomes extinct almost surely when
![]() $\mu\le 1$
, and survives with positive probability when
$\mu\le 1$
, and survives with positive probability when
![]() $\mu>1$
. When
$\mu>1$
. When
![]() $\mu>1$
we may condition on survival and ask whether the whole of T is eventually covered by particles of the BRW. A standard calculation shows that the spectral radius of the d-ary tree is
$\mu>1$
we may condition on survival and ask whether the whole of T is eventually covered by particles of the BRW. A standard calculation shows that the spectral radius of the d-ary tree is
![]() $\rho = {(2\sqrt{d-1})}/{d}$
, and a (much more general) result of Gantert and Müller [Reference Gantert and Müller11, Theorem 3.2] implies that when
$\rho = {(2\sqrt{d-1})}/{d}$
, and a (much more general) result of Gantert and Müller [Reference Gantert and Müller11, Theorem 3.2] implies that when
![]() $m\le 1/\rho$
there is local extinction and some vertices in T are never hit by particles of the BRW, whereas when
$m\le 1/\rho$
there is local extinction and some vertices in T are never hit by particles of the BRW, whereas when
![]() $m>1/\rho$
the system is recurrent on survival. In the latter case the cover time
$m>1/\rho$
the system is recurrent on survival. In the latter case the cover time
![]() $T_{\textrm{cov}}(r)$
is finite for all r. Since we consider simple random walk in discrete time,
$T_{\textrm{cov}}(r)$
is finite for all r. Since we consider simple random walk in discrete time,
![]() $T_{\textrm{cov}}(r)$
is at least r, and when
$T_{\textrm{cov}}(r)$
is at least r, and when
![]() $m>d$
it is easy to see – for example via a simple second moment calculation – that
$m>d$
it is easy to see – for example via a simple second moment calculation – that
![]() $T_{\textrm{cov}}(r) = r+{\mathrm{O}} (1)$
almost surely given survival. We expect that for
$T_{\textrm{cov}}(r) = r+{\mathrm{O}} (1)$
almost surely given survival. We expect that for
![]() $m\in(1/\rho,d)$
, conditionally on survival,
$m\in(1/\rho,d)$
, conditionally on survival,
![]() $T_{\textrm{cov}}$
satisfies
$T_{\textrm{cov}}$
satisfies
for some constants
![]() $c_1$
and
$c_1$
and
![]() $c_2$
; in fact,
$c_2$
; in fact,
![]() $c_1=c_1(m,d)>1$
should satisfy
$c_1=c_1(m,d)>1$
should satisfy
Determining the value of
![]() $c_2$
may be possible using techniques related to those in this paper, together with tail estimates for the maximal particle in a random walk on a one-dimensional lattice available from [Reference Bramson, Ding and Zeitouni9, Proposition 3.1]; see also [Reference Bramson, Ding and Zeitouni9, Section 5] for discussion of lattice branching random walks.
$c_2$
may be possible using techniques related to those in this paper, together with tail estimates for the maximal particle in a random walk on a one-dimensional lattice available from [Reference Bramson, Ding and Zeitouni9, Proposition 3.1]; see also [Reference Bramson, Ding and Zeitouni9, Section 5] for discussion of lattice branching random walks.
We therefore have the following categorisation.
-
 $m\le 1$
: global extinction.
$m\le 1$
: global extinction. -
 $m\in(1,{d}/{(2\sqrt{d-1})}]$
: global survival with positive probability, but local extinction and
$m\in(1,{d}/{(2\sqrt{d-1})}]$
: global survival with positive probability, but local extinction and
 $T_{\textrm{cov}}(r)=\infty$
for all large r, almost surely.
$T_{\textrm{cov}}(r)=\infty$
for all large r, almost surely. -
 $m\in({d}/{(2\sqrt{d-1})}, d)$
: conjecture that on survival, for
$m\in({d}/{(2\sqrt{d-1})}, d)$
: conjecture that on survival, for \begin{equation*}\lim_{r\to\infty} \dfrac{T_{\textrm{cov}}(r)-c_1 r}{\log r} = c_2 \quad \text{almost surely}\end{equation*}
\begin{equation*}\lim_{r\to\infty} \dfrac{T_{\textrm{cov}}(r)-c_1 r}{\log r} = c_2 \quad \text{almost surely}\end{equation*}
 $c_1=c_1(m,d)>1$
satisfying (2.4) and some as yet unknown
$c_1=c_1(m,d)>1$
satisfying (2.4) and some as yet unknown
 $c_2$
.
$c_2$
.
-
 $m=d$
: Theorem 1.1 states that for
$m=d$
: Theorem 1.1 states that for
 $d\ge 3$
, on survival, and it follows from (2.1) that when
$d\ge 3$
, on survival, and it follows from (2.1) that when \begin{equation*}\lim_{r\to\infty} \dfrac{T_{\textrm{cov}}(r)-r}{\log\log r} = \dfrac{2}{\log(3/2)} \quad \text{almost surely,}\end{equation*}
\begin{equation*}\lim_{r\to\infty} \dfrac{T_{\textrm{cov}}(r)-r}{\log\log r} = \dfrac{2}{\log(3/2)} \quad \text{almost surely,}\end{equation*}
 $d=2$
, on survival
$d=2$
, on survival  \begin{equation*}\lim_{r\to\infty} \dfrac{T_{\textrm{cov}}(r)-r}{\log\log r} = \dfrac{2}{\log 2} \quad \text{almost surely.}\end{equation*}
\begin{equation*}\lim_{r\to\infty} \dfrac{T_{\textrm{cov}}(r)-r}{\log\log r} = \dfrac{2}{\log 2} \quad \text{almost surely.}\end{equation*}
-
 $m>d$
:
$m>d$
:
 $T_{\textrm{cov}}(r) = r + {\mathrm{O}} (1)$
.
$T_{\textrm{cov}}(r) = r + {\mathrm{O}} (1)$
.
2.4. Open questions
One open question is whether our main result, Theorem 1.1, can be strengthened further, perhaps along the lines of the result (2.1) of Bramson [Reference Bramson8]. It would also be interesting to give results when the offspring distribution has mean
![]() $m\in ({d}/{(2\sqrt{d-1})}, d)$
, as discussed above.
$m\in ({d}/{(2\sqrt{d-1})}, d)$
, as discussed above.
Our model considers only the simple random walk in discrete time, and one could consider other random walks, either in discrete or continuous time. One important observation in continuous time is that the random walk is no longer restricted to any finite set by a fixed time t, and therefore we will not have
![]() $T_{\textrm{cov}}(r) = r - {\mathrm{O}} (1)$
when the offspring mean is larger than d; instead we expect that
$T_{\textrm{cov}}(r) = r - {\mathrm{O}} (1)$
when the offspring mean is larger than d; instead we expect that
![]() $\lim_{r\to\infty}T_{\textrm{cov}}(r)/r > 1$
, with corrections of order
$\lim_{r\to\infty}T_{\textrm{cov}}(r)/r > 1$
, with corrections of order
![]() $\log r$
, as in the (geometrically) subcritical case. The critical case when the offspring mean equals d should also show a correction of order
$\log r$
, as in the (geometrically) subcritical case. The critical case when the offspring mean equals d should also show a correction of order
![]() $\log r$
in this setting, unlike the behaviour identified in Theorem 1.1. This is more ‘typical’ behaviour, in that only branching random walks with carefully chosen parameters will see a correction of order
$\log r$
in this setting, unlike the behaviour identified in Theorem 1.1. This is more ‘typical’ behaviour, in that only branching random walks with carefully chosen parameters will see a correction of order
![]() $\log\log r$
. One example that can be expected to demonstrate a delay of order
$\log\log r$
. One example that can be expected to demonstrate a delay of order
![]() $\log\log r$
is the (discrete-time) lazy branching random walk with offspring distribution mean 2d, where particles remain at their parent’s location with probability
$\log\log r$
is the (discrete-time) lazy branching random walk with offspring distribution mean 2d, where particles remain at their parent’s location with probability
![]() $1/2$
, or jump to each neighbour with probability
$1/2$
, or jump to each neighbour with probability
![]() $1/(2d)$
. In this case we should have (for
$1/(2d)$
. In this case we should have (for
![]() $d\ge 3$
)
$d\ge 3$
)
since the ‘mis-steps’ that break up long runs are able to remain in place, rather than stepping in the wrong direction. Alternatively one may consider a system where particles give birth to on average d children who each jump independently to a uniformly chosen neighbour, but the original particle remains in place and gives birth to another family at each subsequent time step. Again, since particles are able to remain in place rather than either jumping towards or away from their target, we expect (2.5) to hold for
![]() $d\ge 3$
. A proof of (2.5) in either of these cases would require a relatively minor alteration to the strategy used in this paper.
$d\ge 3$
. A proof of (2.5) in either of these cases would require a relatively minor alteration to the strategy used in this paper.
Another option is to extend our results to other trees. For example, what is the cover time when the underlying graph G is itself a non-trivial Galton–Watson tree? This is a much more delicate question than the one in this paper. The speed of simple random walk on (non-trivial) Galton–Watson trees with mean offspring distribution
![]() $d-1$
is slower than on regular d-ary trees, and our proof techniques no longer apply. Work is underway to at least partially address this question.
$d-1$
is slower than on regular d-ary trees, and our proof techniques no longer apply. Work is underway to at least partially address this question.
Further, one may ask for the cover time of tree-indexed random walk on trees, where the time tree has branching number d, and the space tree has branching number
![]() $d'$
. See [Reference Benjamini and Peres2] for the study of tree-indexed random walks and the book [Reference Lyons and Peres17] for background. Variants of BRW and tree-indexed random walks were used in [Reference Benjamini and Schramm3] and [Reference Sudakov and Vondrák21] to study the embedding of trees into graphs.
$d'$
. See [Reference Benjamini and Peres2] for the study of tree-indexed random walks and the book [Reference Lyons and Peres17] for background. Variants of BRW and tree-indexed random walks were used in [Reference Benjamini and Schramm3] and [Reference Sudakov and Vondrák21] to study the embedding of trees into graphs.
Finally, this paper relies heavily on the fact that the underlying graph G is a tree, so that there is only one path between any two vertices. It seems natural to expect qualitatively similar behaviour in more general settings, for example on planar hyperbolic lattices.
3. Freezing particles
3.1. Freezing particles after one step in the wrong direction
Fix a vertex x in our d-ary tree T. Consider our usual BRW (with offspring mean d) on T, but freeze any particle (i.e. prevent it from moving or branching) as soon as it either (a) takes a step away from x, or (b) reaches x, whichever happens first. In this picture, let
![]() $Y_x$
be the number of particles that hit x, let
$Y_x$
be the number of particles that hit x, let
![]() $F_x$
be the number of particles that are frozen as they step away from x, and let
$F_x$
be the number of particles that are frozen as they step away from x, and let
![]() $S_x$
be the total number of particles ever seen (until the time that all particles have become frozen). If we start with any finite collection of particles, then
$S_x$
be the total number of particles ever seen (until the time that all particles have become frozen). If we start with any finite collection of particles, then
![]() $S_x$
is finite since at each step any non-frozen particle must step either towards or away from x and particles are frozen as soon as they step away from x or reach x.
$S_x$
is finite since at each step any non-frozen particle must step either towards or away from x and particles are frozen as soon as they step away from x or reach x.
For
![]() $x\in T$
and
$x\in T$
and
![]() $r\ge 0$
, let T(x, r) be the set of vertices at distance
$r\ge 0$
, let T(x, r) be the set of vertices at distance
![]() $\lfloor r \rfloor$
from x in the subtree rooted at x; that is, those vertices at distance
$\lfloor r \rfloor$
from x in the subtree rooted at x; that is, those vertices at distance
![]() $\lfloor r\rfloor$
from x and
$\lfloor r\rfloor$
from x and
![]() $\lfloor r\rfloor +d(0,x)$
from 0. We aim to provide upper and lower bounds on the number of particles in the freezing process outlined above. First we give an upper bound in the form of the following simple expectation calculation.
$\lfloor r\rfloor +d(0,x)$
from 0. We aim to provide upper and lower bounds on the number of particles in the freezing process outlined above. First we give an upper bound in the form of the following simple expectation calculation.
Lemma 3.1. Fix
![]() $n\in \mathbb{N}$
,
$n\in \mathbb{N}$
,
![]() $R\ge 1$
, and
$R\ge 1$
, and
![]() $x\in T$
. Suppose that
$x\in T$
. Suppose that
![]() $\Gamma$
consists of vertices that are at distance at most R from x. Then
$\Gamma$
consists of vertices that are at distance at most R from x. Then
Proof. Fix a vertex
![]() $v\in\Gamma$
and label the vertices in the path from v to x as
$v\in\Gamma$
and label the vertices in the path from v to x as
![]() $v=v_0, v_1,\ldots, v_k=x$
. Let
$v=v_0, v_1,\ldots, v_k=x$
. Let
![]() $Z_j$
be the number of particles that reach
$Z_j$
be the number of particles that reach
![]() $v_j$
after j steps, for each
$v_j$
after j steps, for each
![]() $j\le k$
. For
$j\le k$
. For
![]() $j< k$
, each particle at
$j< k$
, each particle at
![]() $v_j$
independently has a random number of children with distribution
$v_j$
independently has a random number of children with distribution
![]() $\mu$
, which has mean d and finite variance, each of which moves to
$\mu$
, which has mean d and finite variance, each of which moves to
![]() $v_{j+1}$
with probability
$v_{j+1}$
with probability
![]() $1/d$
. Thus the sequence
$1/d$
. Thus the sequence
![]() $(Z_j, j=0,\ldots,k)$
forms a critical Galton–Watson process with finite variance, stopped at generation k. As a result,
$(Z_j, j=0,\ldots,k)$
forms a critical Galton–Watson process with finite variance, stopped at generation k. As a result,
Now, the total number of particles seen is exactly those that contribute to
![]() $Z_j$
for
$Z_j$
for
![]() $0\le j\le k-1$
, together with their frozen children. Thus
$0\le j\le k-1$
, together with their frozen children. Thus
 \begin{equation*}\mathbb{E}_{1,v}[S_x] \le (d+1) \mathbb{E}_{1,v}\left[\sum_{j=0}^{k-1} Z_j\right] = (d+1)k , \end{equation*}
\begin{equation*}\mathbb{E}_{1,v}[S_x] \le (d+1) \mathbb{E}_{1,v}\left[\sum_{j=0}^{k-1} Z_j\right] = (d+1)k , \end{equation*}
and since
![]() $v\in\Gamma$
we have
$v\in\Gamma$
we have
![]() $k=d(v,x)\le R$
so
$k=d(v,x)\le R$
so
![]() $\mathbb{E}_{1,v}[S_x]\le (d+1)R$
. To complete the proof of the lemma we simply sum over
$\mathbb{E}_{1,v}[S_x]\le (d+1)R$
. To complete the proof of the lemma we simply sum over
![]() $v\in\Gamma$
.
$v\in\Gamma$
.
For a lower bound it is easier to bound the number of unfrozen particles than the number of frozen particles. However, we will eventually need to bound the number of frozen particles, so we will need the following lemma, which checks that if the number of unfrozen particles is large then the number of frozen particles should be large.
Lemma 3.2. There exists a constant
![]() $\nu\in(0,1/2)$
such that, for any
$\nu\in(0,1/2)$
such that, for any
![]() $R,M\in\mathbb{N}$
and
$R,M\in\mathbb{N}$
and
![]() $v,x\in T$
with
$v,x\in T$
with
![]() $d(v,x)\le R$
,
$d(v,x)\le R$
,
Proof. As in the proof of Lemma 3.1, label the vertices in the path from v to x as
![]() $v=v_0, v_1,\ldots, v_k=x$
. For each
$v=v_0, v_1,\ldots, v_k=x$
. For each
![]() $j\le k-1$
, let
$j\le k-1$
, let
![]() $Z_j$
be the number of (non-frozen) particles that reach
$Z_j$
be the number of (non-frozen) particles that reach
![]() $v_j$
after j steps, and let
$v_j$
after j steps, and let
![]() $W_j$
be the number of these particles that have at least one child that is frozen as it steps away from x.
$W_j$
be the number of these particles that have at least one child that is frozen as it steps away from x.
Note that for each non-frozen particle at
![]() $v_j$
, the event that it has no children that step away from x is independent of other non-frozen particles at
$v_j$
, the event that it has no children that step away from x is independent of other non-frozen particles at
![]() $v_j$
, and has probability
$v_j$
, and has probability
where L is a random variable with distribution
![]() $\mu$
. Therefore, for each
$\mu$
. Therefore, for each
![]() $j\le k-1$
,
$j\le k-1$
,
Given the value of
![]() $Z_j$
,
$Z_j$
,
![]() $W_j$
is the sum of
$W_j$
is the sum of
![]() $Z_j$
independent Bernoulli random variables. Thus we can apply the Chernoff bound (2.3), giving
$Z_j$
independent Bernoulli random variables. Thus we can apply the Chernoff bound (2.3), giving
Setting
![]() $\kappa= 1-\mathbb{E}\big[1/d^L\big] \in(0,1)$
and combining the two equations above, we have
$\kappa= 1-\mathbb{E}\big[1/d^L\big] \in(0,1)$
and combining the two equations above, we have
and so
By a union bound, since
![]() $k = d(v,x)\le R$
,
$k = d(v,x)\le R$
,
Since
![]() $S_x = \sum_{j=0}^{k-1} Z_j + F_x + Y_x$
, we have
$S_x = \sum_{j=0}^{k-1} Z_j + F_x + Y_x$
, we have
 \begin{align*}\mathbb{P}_{1,v}(F_x + Y_x \le \nu S_x - R M) &= \mathbb{P}_{1,v}\left(F_x + Y_x \le \nu\sum_{j=0}^{k-1}Z_j + \nu F_x +\nu Y_x - R M\right)\\&= \mathbb{P}_{1,v}\left( (1-\nu)(F_x+Y_x) \le \nu \sum_{j=0}^{k-1}Z_j - RM\right)\\&\le \mathbb{P}_{1,v}\left( (1-\nu)F_x \le \nu \sum_{j=0}^{k-1}Z_j - (1-\nu)kM\right)\!,\end{align*}
\begin{align*}\mathbb{P}_{1,v}(F_x + Y_x \le \nu S_x - R M) &= \mathbb{P}_{1,v}\left(F_x + Y_x \le \nu\sum_{j=0}^{k-1}Z_j + \nu F_x +\nu Y_x - R M\right)\\&= \mathbb{P}_{1,v}\left( (1-\nu)(F_x+Y_x) \le \nu \sum_{j=0}^{k-1}Z_j - RM\right)\\&\le \mathbb{P}_{1,v}\left( (1-\nu)F_x \le \nu \sum_{j=0}^{k-1}Z_j - (1-\nu)kM\right)\!,\end{align*}
where the last line follows trivially since
![]() $Y_x\ge 0$
and
$Y_x\ge 0$
and
![]() $RM\ge kM\ge (1-\nu)kM$
. Now note that
$RM\ge kM\ge (1-\nu)kM$
. Now note that
![]() $F_x \ge \sum_{j=0}^{k-1} W_j$
, so following on from the above,
$F_x \ge \sum_{j=0}^{k-1} W_j$
, so following on from the above,
 \begin{align*}\mathbb{P}_{1,v}(F_x+Y_x \le \nu S_x - R M) &\le \mathbb{P}_{1,v}\left( (1-\nu)\sum_{j=0}^{k-1} W_j \le \nu \sum_{j=0}^{k-1}Z_j - (1-\nu)kM\right)\\&= \mathbb{P}_{1,v}\left( \sum_{j=0}^{k-1} (W_j+M) \le \dfrac{\nu}{1-\nu} \sum_{j=0}^{k-1}Z_j \right)\\&\le \mathbb{P}_{1,v}\left(\exists j\le k-1 \colon W_j + M \le \dfrac{\nu}{1-\nu} Z_j \right)\!.\end{align*}
\begin{align*}\mathbb{P}_{1,v}(F_x+Y_x \le \nu S_x - R M) &\le \mathbb{P}_{1,v}\left( (1-\nu)\sum_{j=0}^{k-1} W_j \le \nu \sum_{j=0}^{k-1}Z_j - (1-\nu)kM\right)\\&= \mathbb{P}_{1,v}\left( \sum_{j=0}^{k-1} (W_j+M) \le \dfrac{\nu}{1-\nu} \sum_{j=0}^{k-1}Z_j \right)\\&\le \mathbb{P}_{1,v}\left(\exists j\le k-1 \colon W_j + M \le \dfrac{\nu}{1-\nu} Z_j \right)\!.\end{align*}
Choosing
![]() $\nu\in(0,1/2)$
such that
$\nu\in(0,1/2)$
such that
![]() $\nu/(1-\nu)\le \kappa/2$
and
$\nu/(1-\nu)\le \kappa/2$
and
![]() $\nu\le\kappa/8$
, the result follows from (3.1).
$\nu\le\kappa/8$
, the result follows from (3.1).
We can now give our lower bound on the number of frozen particles.
Lemma 3.3. Suppose that
![]() $A,n\in\mathbb{N}$
,
$A,n\in\mathbb{N}$
,
![]() $x\in T$
, and
$x\in T$
, and
![]() $y\in T(x,A)$
. Suppose also that
$y\in T(x,A)$
. Suppose also that
![]() $\Gamma$
consists of at least n vertices, none of which is in the subtree rooted at x except possibly at x itself, and all of which are at distance at most 2A from y. Then, provided that A is sufficiently large, we have
$\Gamma$
consists of at least n vertices, none of which is in the subtree rooted at x except possibly at x itself, and all of which are at distance at most 2A from y. Then, provided that A is sufficiently large, we have
for some constant
![]() $\delta\in(0,1]$
depending only on d and the variance of
$\delta\in(0,1]$
depending only on d and the variance of
![]() $\mu$
.
$\mu$
.
Proof of Lemma 3.3. Without loss of generality we may assume that
![]() $|\Gamma|=n$
. Label the initial n particles from 1 to n and say that particle i starts from vertex
$|\Gamma|=n$
. Label the initial n particles from 1 to n and say that particle i starts from vertex
![]() $v_i$
. Run the y-freezing process and set
$v_i$
. Run the y-freezing process and set
![]() $X_i$
equal to 1 if particle i has at least
$X_i$
equal to 1 if particle i has at least
![]() $A^2$
descendants in total, and
$A^2$
descendants in total, and
![]() $X_i=0$
otherwise. Fix
$X_i=0$
otherwise. Fix
![]() $\nu>0$
as in Lemma 3.2 and let
$\nu>0$
as in Lemma 3.2 and let
![]() $X'_i$
equal 1 if particle i has at least
$X'_i$
equal 1 if particle i has at least
![]() $\nu A^2 / 2$
frozen descendants (i.e. descendants that contribute to either
$\nu A^2 / 2$
frozen descendants (i.e. descendants that contribute to either
![]() $F_y$
or
$F_y$
or
![]() $Y_y$
), and
$Y_y$
), and
![]() $X'_i=0$
otherwise.
$X'_i=0$
otherwise.
By the argument in the proof of Lemma 3.1, the number of non-frozen descendants of particle i after
![]() $0,1,2,\ldots,d(v_i,y)-1$
steps forms a critical Galton–Watson process with finite variance, stopped at generation
$0,1,2,\ldots,d(v_i,y)-1$
steps forms a critical Galton–Watson process with finite variance, stopped at generation
![]() $d(v_i,y)-1$
. Thus the total number of non-frozen descendants of particle i is distributed as the total progeny up to generation
$d(v_i,y)-1$
. Thus the total number of non-frozen descendants of particle i is distributed as the total progeny up to generation
![]() $d(v_i,y)-1 \ge A-1$
of a Galton–Watson process with mean offspring number 1 and finite variance. By (2.2), the probability that a critical Galton–Watson process with finite variance has total progeny up to generation
$d(v_i,y)-1 \ge A-1$
of a Galton–Watson process with mean offspring number 1 and finite variance. By (2.2), the probability that a critical Galton–Watson process with finite variance has total progeny up to generation
![]() $A-1$
of at least
$A-1$
of at least
![]() $A^2$
is at least
$A^2$
is at least
![]() $c/A$
, for some constant
$c/A$
, for some constant
![]() $c>0$
depending on the variance. Thus, foreach i,
$c>0$
depending on the variance. Thus, foreach i,
Also, by Lemma 3.2, choosing
![]() $M=\nu A/4$
and
$M=\nu A/4$
and
![]() $R=2A$
,
$R=2A$
,
which for A sufficiently large is at most
![]() $c/(2A)$
. Therefore, for A sufficiently large,
$c/(2A)$
. Therefore, for A sufficiently large,
Letting
![]() $X=\sum_{i=1}^n X'_i$
, we have
$X=\sum_{i=1}^n X'_i$
, we have
Since X is a sum of independent Bernoulli random variables we can apply the Chernoff bound (2.3), obtaining
But if
![]() $X>cn/(4A)$
, then
$X>cn/(4A)$
, then
![]() $F_y+Y_y$
must be at least
$F_y+Y_y$
must be at least
Since
![]() $\nu<1/2$
, choosing
$\nu<1/2$
, choosing
![]() $\delta = \min\{c\nu/8,1\}$
gives the result.
$\delta = \min\{c\nu/8,1\}$
gives the result.
3.2. Ulam–Harris notation and the FKG inequality
For our next lemma we will need to introduce the Fortuin–Kasteleyn–Ginibre (FKG) inequality in the context of a certain class of marked forests. To make our discussion precise, we need to introduce some more notation, which will also be useful in the next section. We introduce the Ulam–Harris set
The particles (we talk about particles to avoid confusion with the vertices in our spatial tree T) in our forest will be elements of
![]() $\Omega$
, with (3,2,7), for example, representing the 7th child of the 2nd child of the 3rd root. For
$\Omega$
, with (3,2,7), for example, representing the 7th child of the 2nd child of the 3rd root. For
![]() $u,v\in\Omega$
, we write
$u,v\in\Omega$
, we write
![]() $u\circ v$
for the concatenation of u and v, so for example
$u\circ v$
for the concatenation of u and v, so for example
![]() $(3,2,7)\circ(1,5) = (3,2,7,1,5)$
. We write
$(3,2,7)\circ(1,5) = (3,2,7,1,5)$
. We write
![]() $u\le v$
and say that u is an ancestor of v if there exists
$u\le v$
and say that u is an ancestor of v if there exists
![]() $w\in\Omega$
such that
$w\in\Omega$
such that
![]() $u\circ w = v$
, and say that u is in generation j if it has j ancestors, or equivalently if
$u\circ w = v$
, and say that u is in generation j if it has j ancestors, or equivalently if
![]() $u\in\mathbb{N}^{j+1}$
.
$u\in\mathbb{N}^{j+1}$
.
A forest is a subset
![]() $f\subset\Omega$
such that the following hold.
$f\subset\Omega$
such that the following hold.
-
There exists
 $k\in\mathbb{N}$
such that
$k\in\mathbb{N}$
such that
 $(1),(2),\ldots,(k)\in f$
, but
$(1),(2),\ldots,(k)\in f$
, but
 $(\ell)\not\in f$
for
$(\ell)\not\in f$
for
 $\ell>k$
. That is, there are
$\ell>k$
. That is, there are
 $k\ge 1$
roots.
$k\ge 1$
roots. -
For any
 $u,v\in\Omega$
, if
$u,v\in\Omega$
, if
 $u\circ v\in f$
then
$u\circ v\in f$
then
 $u\in f$
. That is, if f contains a particle then it contains all ancestors of that particle.
$u\in f$
. That is, if f contains a particle then it contains all ancestors of that particle. -
For any
 $u\in f$
, there exists
$u\in f$
, there exists
 $A_u\in\{0,1,2,\ldots\}$
such that
$A_u\in\{0,1,2,\ldots\}$
such that
 $u\circ(1), u\circ(2), \ldots, u\circ(A_u) \in f$
but
$u\circ(1), u\circ(2), \ldots, u\circ(A_u) \in f$
but
 $u\circ(\ell)\not\in f$
for
$u\circ(\ell)\not\in f$
for
 $\ell> A_u$
. That is, every particle in f has a finite number of children.
$\ell> A_u$
. That is, every particle in f has a finite number of children.
Say that an up–down k-forest of height at most r is a forest with k roots and no vertices of generation greater than r, in which every particle except the root in each tree is marked either ‘up’ or ‘down’, and internal particles (i.e. those with at least one child) can only be marked ‘up’. In the freezing process outlined above, if we start with k particles at
![]() $y\in T$
, we can think of r as d(y, x), the number of roots in the forest being k, with particles that step towards x being marked as ‘up’, and particles that step away from x being marked as ‘down’.
$y\in T$
, we can think of r as d(y, x), the number of roots in the forest being k, with particles that step towards x being marked as ‘up’, and particles that step away from x being marked as ‘down’.
Indeed, we define a probability measure
![]() $P_{k,r}$
on the set of up–down k-forests of height at most r, under which each root independently has j children in generation 1 with probability
$P_{k,r}$
on the set of up–down k-forests of height at most r, under which each root independently has j children in generation 1 with probability
![]() $\mu(j)$
, and each child is independently marked ‘up’ with probability
$\mu(j)$
, and each child is independently marked ‘up’ with probability
![]() $1/d$
and ‘down’ otherwise. Then each of the generation 1 particles marked ‘up’ independently has j children in generation 2 with probability
$1/d$
and ‘down’ otherwise. Then each of the generation 1 particles marked ‘up’ independently has j children in generation 2 with probability
![]() $\mu(j)$
, each of which is independently marked ‘up’ with probability
$\mu(j)$
, each of which is independently marked ‘up’ with probability
![]() $1/d$
and ‘down’ otherwise. (Particles marked ‘down’ do not have any children.) This continues until we reach generation r, when all particles have 0 children.
$1/d$
and ‘down’ otherwise. (Particles marked ‘down’ do not have any children.) This continues until we reach generation r, when all particles have 0 children.
For two up–down k-forests of height at most r, say
![]() $F_1$
and
$F_1$
and
![]() $F_2$
, we define
$F_2$
, we define
![]() $F_1\wedge F_2$
to be the up–down k-forest of height at most r given by taking the intersection of the two forests (as subsets of
$F_1\wedge F_2$
to be the up–down k-forest of height at most r given by taking the intersection of the two forests (as subsets of
![]() $\Omega$
), and marking each non-root vertex ‘up’ only if it is marked ‘up’ in both
$\Omega$
), and marking each non-root vertex ‘up’ only if it is marked ‘up’ in both
![]() $F_1$
and
$F_1$
and
![]() $F_2$
. Also define
$F_2$
. Also define
![]() $F_1\vee F_2$
to be the up–down k-forest of height at most r given by taking the union of the two forests (as subsets of
$F_1\vee F_2$
to be the up–down k-forest of height at most r given by taking the union of the two forests (as subsets of
![]() $\Omega$
) and marking a vertex ‘up’ if it is marked ‘up’ in either
$\Omega$
) and marking a vertex ‘up’ if it is marked ‘up’ in either
![]() $F_1$
or
$F_1$
or
![]() $F_2$
. Moreover, introduce the partial order
$F_2$
. Moreover, introduce the partial order
![]() $\preceq$
by setting
$\preceq$
by setting
![]() $F_1\preceq F_2$
if
$F_1\preceq F_2$
if
![]() $F_1\wedge F_2 = F_1$
.
$F_1\wedge F_2 = F_1$
.
Say that an event A is decreasing if
![]() $\unicode{x1d7d9}_A(F_1) \ge \unicode{x1d7d9}_A(F_2)$
whenever
$\unicode{x1d7d9}_A(F_1) \ge \unicode{x1d7d9}_A(F_2)$
whenever
![]() $F_1\preceq F_2$
. The FKG inequality [Reference Fortuin, Kasteleyn and Ginibre10] says that if A and B are both decreasing events, then
$F_1\preceq F_2$
. The FKG inequality [Reference Fortuin, Kasteleyn and Ginibre10] says that if A and B are both decreasing events, then
It is easy to check that
![]() $P_{k,r}$
satisfies the FKG lattice condition with equality, since
$P_{k,r}$
satisfies the FKG lattice condition with equality, since
![]() $P_{k,r}(F)$
can be written as a product over the particles in F of the probability that that particle has the required number of children and the required mark. Indeed, the collection of offspring numbers and marks of
$P_{k,r}(F)$
can be written as a product over the particles in F of the probability that that particle has the required number of children and the required mark. Indeed, the collection of offspring numbers and marks of
![]() $F_1$
and
$F_1$
and
![]() $F_2$
together equals the collection of offspring numbers and marks of
$F_2$
together equals the collection of offspring numbers and marks of
![]() $F_1\vee F_2$
and
$F_1\vee F_2$
and
![]() $F_1\wedge F_2$
together, so
$F_1\wedge F_2$
together, so
![]() $P_{k,r}(F_1)P_{k,r}(F_2) = P_{k,r}(F_1\vee F_2)P_{k,r}(F_1\wedge F_2)$
.
$P_{k,r}(F_1)P_{k,r}(F_2) = P_{k,r}(F_1\vee F_2)P_{k,r}(F_1\wedge F_2)$
.
We deduce the following lemma, which will be needed in the next section.
Lemma 3.4. Suppose that
![]() $y\in T$
and
$y\in T$
and
![]() $x\in T(y,r)$
. Then, for any
$x\in T(y,r)$
. Then, for any
![]() $k,N\in\mathbb{N}$
,
$k,N\in\mathbb{N}$
,
Proof. As mentioned above, the freezing process started with k particles at y corresponds to an up–down k-forest of height at most
![]() $d(y,x)=r$
, where particles that step towards x are marked ‘up’ and particles that step away from x are marked ‘down’. For F an up–down k-forest of height at most r, let
$d(y,x)=r$
, where particles that step towards x are marked ‘up’ and particles that step away from x are marked ‘down’. For F an up–down k-forest of height at most r, let
![]() $\tilde Y(F)$
be the number of ‘up’ particles in generation r and
$\tilde Y(F)$
be the number of ‘up’ particles in generation r and
![]() $\tilde S(F)$
the total number of particles in F.
$\tilde S(F)$
the total number of particles in F.
Then
![]() $Y_x$
, the number of particles frozen at x, has the same distribution as
$Y_x$
, the number of particles frozen at x, has the same distribution as
![]() $\tilde Y(F)$
under
$\tilde Y(F)$
under
![]() $P_{k,r}$
, and
$P_{k,r}$
, and
![]() $S_x$
, the total number of particles seen until all particles are frozen, has the same distribution as
$S_x$
, the total number of particles seen until all particles are frozen, has the same distribution as
![]() $\tilde S(F)$
under
$\tilde S(F)$
under
![]() $P_{k,r}$
. Thus
$P_{k,r}$
. Thus
and since the events
![]() $\{\tilde Y(F) = 0\}$
and
$\{\tilde Y(F) = 0\}$
and
![]() $\{\tilde S(F)\le N\}$
are decreasing, by (3.2) we have
$\{\tilde S(F)\le N\}$
are decreasing, by (3.2) we have
 \begin{align*}P_{k,r}(\tilde Y(F) = 0 \ \text{and}\ \tilde S(F) \le N) &\ge P_{k,r}(\tilde Y(F) = 0)P_{k,r}(\tilde S(F) \le N)\\[3pt] &= \mathbb{P}_{k,y}(Y_{x} = 0)\mathbb{P}_{k,y}(S_{x} \le N),\end{align*}
\begin{align*}P_{k,r}(\tilde Y(F) = 0 \ \text{and}\ \tilde S(F) \le N) &\ge P_{k,r}(\tilde Y(F) = 0)P_{k,r}(\tilde S(F) \le N)\\[3pt] &= \mathbb{P}_{k,y}(Y_{x} = 0)\mathbb{P}_{k,y}(S_{x} \le N),\end{align*}
which completes the proof.
3.3. Freezing particles after k steps in the wrong direction
Fix a vertex
![]() $x\in T$
and
$x\in T$
and
![]() $k\in\mathbb{N}$
, and consider our original branching random walk. We would like to generalise the discussion in the previous section, allowing ourselves to freeze any particle (i.e. prevent it from moving or branching) as soon as it either (a) takes its kth step away from x, or (b) hits x, whichever happens first; we call this the (x, k)-freezing process. However, we would like to do this in a consistent way for all vertices x, and for all k, so that the analogues of
$k\in\mathbb{N}$
, and consider our original branching random walk. We would like to generalise the discussion in the previous section, allowing ourselves to freeze any particle (i.e. prevent it from moving or branching) as soon as it either (a) takes its kth step away from x, or (b) hits x, whichever happens first; we call this the (x, k)-freezing process. However, we would like to do this in a consistent way for all vertices x, and for all k, so that the analogues of
![]() $Y_x$
,
$Y_x$
,
![]() $F_x$
, and
$F_x$
, and
![]() $S_x$
are coupled in a natural way.
$S_x$
are coupled in a natural way.
To do this we will use the Ulam–Harris labels
![]() $\Omega = \bigcup_{j\in\mathbb{N}}\mathbb{N}^j$
and the definition of a forest given in the previous section, recalling that each particle is an element of
$\Omega = \bigcup_{j\in\mathbb{N}}\mathbb{N}^j$
and the definition of a forest given in the previous section, recalling that each particle is an element of
![]() $\Omega$
, and (3,2,7), for example, represents the 7th child of the 2nd child of the 3rd initial particle. Recall also that
$\Omega$
, and (3,2,7), for example, represents the 7th child of the 2nd child of the 3rd initial particle. Recall also that
![]() $A_u$
is the number of children of particle u. We can then interpret our original (i.e. unfrozen) branching random walk as a labelled forest, where every particle has a label
$A_u$
is the number of children of particle u. We can then interpret our original (i.e. unfrozen) branching random walk as a labelled forest, where every particle has a label
![]() $X(u)\in T$
corresponding to its position (recall that T is our d-ary tree).
$X(u)\in T$
corresponding to its position (recall that T is our d-ary tree).
Let
![]() $\tau$
be the (random) forest generated by our branching random walk. For each particle
$\tau$
be the (random) forest generated by our branching random walk. For each particle
![]() $u\in\tau$
, let
$u\in\tau$
, let
![]() $\overset{\leftarrow}{u}$
be the parent of u. To each particle
$\overset{\leftarrow}{u}$
be the parent of u. To each particle
![]() $u\in\tau$
and vertex
$u\in\tau$
and vertex
![]() $x\in T$
we associate the following additional labels:
$x\in T$
we associate the following additional labels:
![]() $J_x(u)$
counts the number of steps that u has taken away from x, and
$J_x(u)$
counts the number of steps that u has taken away from x, and
![]() $H_x(u)$
counts the number of times that u has hit x. We note that these are functions of X(w) for the ancestors w of u; they do not include any new information. Then define
$H_x(u)$
counts the number of times that u has hit x. We note that these are functions of X(w) for the ancestors w of u; they do not include any new information. Then define
 \begin{align*}Y^{(k)}_x &= \#\{u\in\tau \colon X(u)=x,\, J_x(u)\le k-1\},\\[3pt] F^{(k)}_x &= \#\{u\in\tau \colon J_x(u) = k,\, J_x(\overset{\leftarrow}{u})=k-1,\, H_x(u)=0\}, \end{align*}
\begin{align*}Y^{(k)}_x &= \#\{u\in\tau \colon X(u)=x,\, J_x(u)\le k-1\},\\[3pt] F^{(k)}_x &= \#\{u\in\tau \colon J_x(u) = k,\, J_x(\overset{\leftarrow}{u})=k-1,\, H_x(u)=0\}, \end{align*}
and
In the (x, k)-freezing process described above,
![]() $Y^{(k)}_x$
corresponds to the number of particles that are frozen at x,
$Y^{(k)}_x$
corresponds to the number of particles that are frozen at x,
![]() $F^{(k)}_x$
the number of particles that are frozen as they take their kth step away from x, and
$F^{(k)}_x$
the number of particles that are frozen as they take their kth step away from x, and
![]() $S^{(k)}_x$
the total number of particles ever seen (until all particles are frozen). In particular,
$S^{(k)}_x$
the total number of particles ever seen (until all particles are frozen). In particular,
![]() $Y^{(1)}_x$
,
$Y^{(1)}_x$
,
![]() $F^{(1)}_x$
, and
$F^{(1)}_x$
, and
![]() $S^{(1)}_x$
have the same distributions as the quantities
$S^{(1)}_x$
have the same distributions as the quantities
![]() $Y_x$
,
$Y_x$
,
![]() $F_x$
, and
$F_x$
, and
![]() $S_x$
described in the previous section.
$S_x$
described in the previous section.
We also let
![]() $\mathcal{F}_x^k$
be the
$\mathcal{F}_x^k$
be the
![]() $\sigma$
-algebra generated by the (x, k)-freezing process. More precisely,
$\sigma$
-algebra generated by the (x, k)-freezing process. More precisely,
In words,
![]() $\mathcal{F}_x^k$
knows everything about particles that have taken strictly fewer than k steps away from x and have not hit x, and it knows the position of particles that have just taken their kth step away from x, or just hit x for the first time (after taking fewer than k steps away from x).
$\mathcal{F}_x^k$
knows everything about particles that have taken strictly fewer than k steps away from x and have not hit x, and it knows the position of particles that have just taken their kth step away from x, or just hit x for the first time (after taking fewer than k steps away from x).
We will use freezing processes in both the lower and upper bounds for Theorem 1.1. In the remainder of this section we aim to prove the following proposition, which uses Lemma 3.1 and will be used in the lower bound for Theorem 1.1.
Proposition 3.1. Suppose that
![]() $k,n\in\mathbb{N}$
,
$k,n\in\mathbb{N}$
,
![]() $k\le n^{1/2}$
, and
$k\le n^{1/2}$
, and
![]() $x\in T(0,n^{1/2})$
. Then, on the event
$x\in T(0,n^{1/2})$
. Then, on the event
we have
for some constant c (depending only on d and the variance of
![]() $\mu$
) and all large A and n.
$\mu$
) and all large A and n.
We now aim to prove this result. Take
![]() $a\ge 5d$
. We will use a two-stage argument, first showing that there are, with high probability, many vertices y in
$a\ge 5d$
. We will use a two-stage argument, first showing that there are, with high probability, many vertices y in
![]() $T(x, a n^{1/2})$
that satisfy
$T(x, a n^{1/2})$
that satisfy
![]() $Y_y^{(k-1)} = 0$
,
$Y_y^{(k-1)} = 0$
,
![]() $Y_y^{(k)} < a n$
, and
$Y_y^{(k)} < a n$
, and
![]() $F_y^{(k)} < 3a^2 n^{3/2}$
. We call such vertices ‘good’. Then, in the second stage, we will show that with high probability there is a vertex z in
$F_y^{(k)} < 3a^2 n^{3/2}$
. We call such vertices ‘good’. Then, in the second stage, we will show that with high probability there is a vertex z in
![]() $T(y,an^{1/2})$
with our desired properties for at least one of the good vertices y.
$T(y,an^{1/2})$
with our desired properties for at least one of the good vertices y.
To make this argument rigorous, define
and
That is,
![]() $M_n(x)$
is the set of good vertices and
$M_n(x)$
is the set of good vertices and
![]() $\bar M_n(x)$
is its complement in
$\bar M_n(x)$
is its complement in
![]() $T(x,a n^{1/2})$
.
$T(x,a n^{1/2})$
.
Our first aim is to show that
![]() $M_n(x)$
is large with high probability, on the event that
$M_n(x)$
is large with high probability, on the event that
![]() $F^{(k-1)}_x\le n$
and
$F^{(k-1)}_x\le n$
and
![]() $Y^{(k-1)}_x=0$
.
$Y^{(k-1)}_x=0$
.
Lemma 3.5. Suppose that
![]() $k,n\in\mathbb{N}$
,
$k,n\in\mathbb{N}$
,
![]() $k\le n^{1/2}$
,
$k\le n^{1/2}$
,
![]() $a\ge 4d$
, and
$a\ge 4d$
, and
![]() $x\in T(0,n^{1/2})$
. Then, on the event
$x\in T(0,n^{1/2})$
. Then, on the event
we have
Proof. Fix
![]() $y\in T(x,a n^{1/2})$
. Note that if we start from one particle at 0, then in order to be (y, k)-frozen, a particle must first be
$y\in T(x,a n^{1/2})$
. Note that if we start from one particle at 0, then in order to be (y, k)-frozen, a particle must first be
![]() $(x,k-1)$
frozen. If furthermore
$(x,k-1)$
frozen. If furthermore
![]() $Y^{(k-1)}_x=0$
, then all
$Y^{(k-1)}_x=0$
, then all
![]() $(x,k-1)$
-frozen particles may take exactly one more step away from y before they are (y, k)-frozen. Thus, if
$(x,k-1)$
-frozen particles may take exactly one more step away from y before they are (y, k)-frozen. Thus, if
![]() $Y^{(k-1)}_x=0$
, running the (y,1)-freezing process from the starting configuration consisting of the
$Y^{(k-1)}_x=0$
, running the (y,1)-freezing process from the starting configuration consisting of the
![]() $(x,k-1)$
-frozen particles is equivalent to running the (y, k)-freezing process. Thus, letting
$(x,k-1)$
-frozen particles is equivalent to running the (y, k)-freezing process. Thus, letting
![]() $\Gamma=(v_1,\ldots,v_m)$
consist of the locations of the
$\Gamma=(v_1,\ldots,v_m)$
consist of the locations of the
![]() $(x,k-1)$
-frozen particles, we have
$(x,k-1)$
-frozen particles, we have
Since the
![]() $(x,k-1)$
-frozen particles have taken at most
$(x,k-1)$
-frozen particles have taken at most
![]() $k-1$
steps away from x (in fact, if
$k-1$
steps away from x (in fact, if
![]() $Y^{(k-1)}_x=0$
, then they have taken exactly
$Y^{(k-1)}_x=0$
, then they have taken exactly
![]() $k-1$
steps away from x), we know that
$k-1$
steps away from x), we know that
![]() $d(v_i,y)\le k+d(0,x)+d(x,y) \le (1+1+a)n^{1/2} \le 3an^{1/2}$
. By Lemma 3.1, we have
$d(v_i,y)\le k+d(0,x)+d(x,y) \le (1+1+a)n^{1/2} \le 3an^{1/2}$
. By Lemma 3.1, we have
and therefore, by Markov’s inequality,
Note that on the event
we have
![]() $|\Gamma|=m\le n$
, so combining the above with (3.3), we have
$|\Gamma|=m\le n$
, so combining the above with (3.3), we have
Then, since
![]() $Y^{(k-1)}_x=0$
implies that
$Y^{(k-1)}_x=0$
implies that
![]() $Y^{(k-1)}_y=0$
, we have
$Y^{(k-1)}_y=0$
, we have
 \begin{align*}&\mathbb{E}\bigl[|\bar M_n(x)|\big| \mathcal{F}_x^{k-1}\bigr]\unicode{x1d7d9}_{\big\{F^{(k-1)}_x \le n \ \text{and}\ Y^{(k-1)}_x=0\big\}}\\[3pt] &\quad = \big|T\big(x,a n^{1/2}\big)\big|\cdot \mathbb{P}\bigl( Y^{(k)}_y \ge a n \ \text{or}\ F^{(k)}_y \ge 3a^2 n^{3/2} \big| \mathcal{F}_x^{k-1} \bigr)\unicode{x1d7d9}_{\big\{F^{(k-1)}_x \le n \ \text{and}\ Y^{(k-1)}_x=0\big\}}\\[3pt] &\quad \le \dfrac{2d}{a} |T(x,a n^{1/2})|.\end{align*}
\begin{align*}&\mathbb{E}\bigl[|\bar M_n(x)|\big| \mathcal{F}_x^{k-1}\bigr]\unicode{x1d7d9}_{\big\{F^{(k-1)}_x \le n \ \text{and}\ Y^{(k-1)}_x=0\big\}}\\[3pt] &\quad = \big|T\big(x,a n^{1/2}\big)\big|\cdot \mathbb{P}\bigl( Y^{(k)}_y \ge a n \ \text{or}\ F^{(k)}_y \ge 3a^2 n^{3/2} \big| \mathcal{F}_x^{k-1} \bigr)\unicode{x1d7d9}_{\big\{F^{(k-1)}_x \le n \ \text{and}\ Y^{(k-1)}_x=0\big\}}\\[3pt] &\quad \le \dfrac{2d}{a} |T(x,a n^{1/2})|.\end{align*}
Thus, applying Markov’s inequality again,
and therefore, since
![]() $|M_n(x)| + |\bar M_n(x)| = \big|T\big(x,a n^{1/2}\big)\big|$
, we have
$|M_n(x)| + |\bar M_n(x)| = \big|T\big(x,a n^{1/2}\big)\big|$
, we have
as required.
Next we aim to bound from below the probability that, if y is a good vertex, then there is a vertex z in
![]() $T(y,a n^{1/2})$
such that
$T(y,a n^{1/2})$
such that
![]() $Y_z=0$
.
$Y_z=0$
.
Lemma 3.6. Suppose that
![]() $k,n\in\mathbb{N}$
,
$k,n\in\mathbb{N}$
,
![]() $k\le n^{1/2}$
,
$k\le n^{1/2}$
,
![]() $a\ge 4d$
, and
$a\ge 4d$
, and
![]() $x\in T(0,n^{1/2})$
. There exists
$x\in T(0,n^{1/2})$
. There exists
![]() $c>0$
such that if
$c>0$
such that if
![]() $y\in M_n(x)$
and n is large, then for any
$y\in M_n(x)$
and n is large, then for any
![]() $z\in T(y,an^{1/2})$
we have
$z\in T(y,an^{1/2})$
we have
Proof. Fix
![]() $z\in T(y,an^{1/2})$
. Note that if we start with one particle at 0, then in order for a particle to be (z, k)-frozen, it must also be (y, k)-frozen. In fact, to contribute to either
$z\in T(y,an^{1/2})$
. Note that if we start with one particle at 0, then in order for a particle to be (z, k)-frozen, it must also be (y, k)-frozen. In fact, to contribute to either
![]() $Y^{(k)}_{z}$
or
$Y^{(k)}_{z}$
or
![]() $F^{(k)}_{z}-F^{(k)}_y$
, a particle must be (y, k)-frozen at y specifically. Also, if
$F^{(k)}_{z}-F^{(k)}_y$
, a particle must be (y, k)-frozen at y specifically. Also, if
![]() $y\in M_n(x)$
, then all particles that are (y, k)-frozen at y have taken exactly
$y\in M_n(x)$
, then all particles that are (y, k)-frozen at y have taken exactly
![]() $k-1$
steps away from y, since
$k-1$
steps away from y, since
![]() $Y^{(k-1)}_y=0$
. Thus, if
$Y^{(k-1)}_y=0$
. Thus, if
![]() $y\in M_n(x)$
, then
$y\in M_n(x)$
, then
 \begin{align*}&\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \big| \mathcal{F}_y^k\bigr) \\[3pt] &\quad \ge \mathbb{P}_{\lfloor a n\rfloor,y}(Y_{z} = 0 \ \text{and}\ F_{z} \le 2(d+1) a^2 n^{3/2}).\end{align*}
\begin{align*}&\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \big| \mathcal{F}_y^k\bigr) \\[3pt] &\quad \ge \mathbb{P}_{\lfloor a n\rfloor,y}(Y_{z} = 0 \ \text{and}\ F_{z} \le 2(d+1) a^2 n^{3/2}).\end{align*}
Of course
![]() $F_{z} \le S_{z}$
, so for
$F_{z} \le S_{z}$
, so for
![]() $y\in M_n(x)$
we have
$y\in M_n(x)$
we have
 \begin{align*}&\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \big| \mathcal{F}_y^k\bigr) \\[3pt] &\quad \ge \mathbb{P}_{\lfloor a n\rfloor,y}(Y_{z} = 0 \ \text{and}\ S_{z} \le 2(d+1) a^2 n^{3/2}).\end{align*}
\begin{align*}&\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \big| \mathcal{F}_y^k\bigr) \\[3pt] &\quad \ge \mathbb{P}_{\lfloor a n\rfloor,y}(Y_{z} = 0 \ \text{and}\ S_{z} \le 2(d+1) a^2 n^{3/2}).\end{align*}
Applying Lemma 3.4, we deduce that for
![]() $y\in M_n(x)$
,
$y\in M_n(x)$
,
 \begin{align}&\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \big| \mathcal{F}_y^k\bigr) \notag \\[3pt] &\quad \ge \mathbb{P}_{\lfloor a n\rfloor,y}(Y_{z} = 0) \mathbb{P}_{\lfloor a n\rfloor,y}(S_{z} \le 2(d+1) a^2 n^{3/2}).\end{align}
\begin{align}&\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \big| \mathcal{F}_y^k\bigr) \notag \\[3pt] &\quad \ge \mathbb{P}_{\lfloor a n\rfloor,y}(Y_{z} = 0) \mathbb{P}_{\lfloor a n\rfloor,y}(S_{z} \le 2(d+1) a^2 n^{3/2}).\end{align}
Note that, starting with any number
![]() $j\in\mathbb{N}$
of particles at y,
$j\in\mathbb{N}$
of particles at y,
Recall from the proof of Lemma 3.3 that under
![]() $\mathbb{P}_{1,y}$
, the event that
$\mathbb{P}_{1,y}$
, the event that
![]() $Y_{z}$
equals zero is the event that a critical Galton–Watson tree (with finite variance) survives for fewer than
$Y_{z}$
equals zero is the event that a critical Galton–Watson tree (with finite variance) survives for fewer than
![]() $\lfloor a n^{1/2}\rfloor$
generations; this has probability at least
$\lfloor a n^{1/2}\rfloor$
generations; this has probability at least
![]() $1-c/(a n^{1/2})$
for some finite constant c by Lemma 2.1. Thus, for large n,
$1-c/(a n^{1/2})$
for some finite constant c by Lemma 2.1. Thus, for large n,
where for the second inequality we used the fact that
![]() $1-u \ge {\mathrm{e}}^{-2u}$
for
$1-u \ge {\mathrm{e}}^{-2u}$
for
![]() $0\le u\le 1/2$
. Also
$0\le u\le 1/2$
. Also
so applying Lemma 3.1,
Substituting these bounds back into (3.4), we get that for
![]() $y\in M_n(x)$
,
$y\in M_n(x)$
,
 \begin{align*}\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \mid \mathcal{F}_y^k \bigr) &\ge \exp\left(-\dfrac{2c an}{a n^{1/2}}\right) \cdot \biggl(1 - \dfrac{an}{2an}\biggr)\\[3pt] & = \dfrac12 {\mathrm{e}}^{-2 c n^{1/2}},\end{align*}
\begin{align*}\mathbb{P}\bigl(Y^{(k)}_{z} = 0 \ \text{and}\ F^{(k)}_{z}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2} \mid \mathcal{F}_y^k \bigr) &\ge \exp\left(-\dfrac{2c an}{a n^{1/2}}\right) \cdot \biggl(1 - \dfrac{an}{2an}\biggr)\\[3pt] & = \dfrac12 {\mathrm{e}}^{-2 c n^{1/2}},\end{align*}
which completes the proof.
We now state a simple lemma that will be used in the proof of Proposition 3.1. Recall that
![]() $\overset{\leftarrow}{u}$
denotes the parent of particle u.
$\overset{\leftarrow}{u}$
denotes the parent of particle u.
Lemma 3.7. Suppose that
![]() $x,y\in T$
and x is not in the subtree rooted at y. If
$x,y\in T$
and x is not in the subtree rooted at y. If
![]() $X(u)=y$
and
$X(u)=y$
and
![]() $H_y(\overset{\leftarrow}{u})=0$
, then
$H_y(\overset{\leftarrow}{u})=0$
, then
![]() $J_x(u)\ge J_y(u)+1$
.
$J_x(u)\ge J_y(u)+1$
.
Proof. Let
![]() $u_0\le u_1\le \cdots \le u_k = u$
be the ancestors of u. Take any
$u_0\le u_1\le \cdots \le u_k = u$
be the ancestors of u. Take any
![]() $j\in\{1,\ldots,k-1\}$
such that
$j\in\{1,\ldots,k-1\}$
such that
![]() $J_y(u_j) = J_y(u_{j-1}) + 1$
, i.e. such that
$J_y(u_j) = J_y(u_{j-1}) + 1$
, i.e. such that
![]() $u_j$
jumps away from y. Since T is a tree and
$u_j$
jumps away from y. Since T is a tree and
![]() $X(u)=y$
, every step along the path of u that moves away from y must later be retraced. That is, there must be
$X(u)=y$
, every step along the path of u that moves away from y must later be retraced. That is, there must be
![]() $\ell>j$
such that
$\ell>j$
such that
![]() $X(u_\ell)=X(u_{j-1})$
and
$X(u_\ell)=X(u_{j-1})$
and
![]() $X(u_{\ell-1})=X(u_j)$
, and of course this step is towards y, so
$X(u_{\ell-1})=X(u_j)$
, and of course this step is towards y, so
![]() $J_y(u_\ell) = J_y(u_{\ell-1})$
. But then one of the two steps identified, either from
$J_y(u_\ell) = J_y(u_{\ell-1})$
. But then one of the two steps identified, either from
![]() $X(u_{j-1})$
to
$X(u_{j-1})$
to
![]() $X(u_{j})$
or from
$X(u_{j})$
or from
![]() $X(u_{j})$
to
$X(u_{j})$
to
![]() $X(u_{j-1})$
, must be away from x. In other words, either
$X(u_{j-1})$
, must be away from x. In other words, either
![]() $J_x(u_j) = J_x(u_{j-1})+1$
or
$J_x(u_j) = J_x(u_{j-1})+1$
or
![]() $J_x(u_\ell) = J_x(u_{\ell-1}) + 1$
. We deduce that, over the jth and
$J_x(u_\ell) = J_x(u_{\ell-1}) + 1$
. We deduce that, over the jth and
![]() $\ell$
th steps together, the path of u makes one step towards y and one step away from y, and one step towards x and another away from x. That is,
$\ell$
th steps together, the path of u makes one step towards y and one step away from y, and one step towards x and another away from x. That is,
This is true for any step where
![]() $J_y(u_j)$
increases, and
$J_y(u_j)$
increases, and
![]() $J_x(u_j)$
is non-decreasing in j, so for other steps
$J_x(u_j)$
is non-decreasing in j, so for other steps
As a result,
 \begin{equation*}J_y(u_{k-1}) = \sum_{j=1}^{k-1} (J_y(u_j) - J_y(u_{j-1})) \le \sum_{j=1}^{k-1} (J_x(u_j)-J_x(u_j)) = J_x(u_{k-1}).\end{equation*}
\begin{equation*}J_y(u_{k-1}) = \sum_{j=1}^{k-1} (J_y(u_j) - J_y(u_{j-1})) \le \sum_{j=1}^{k-1} (J_x(u_j)-J_x(u_j)) = J_x(u_{k-1}).\end{equation*}
On the other hand, at the final step u steps towards y and away from x, so
This completes the proof.
Now we prove Proposition 3.1 by putting the estimates from Lemmas 3.5 and 3.6 together, and using Lemma 3.7 to ensure that there is enough independence between different freezing processes.
Proof of Proposition 3.1. Take
![]() $a\ge 5d$
. Let
$a\ge 5d$
. Let
 \begin{equation*}\mathcal{G}_x^{k,r} = \sigma\left(\bigcup_{y\in T(x,r)} \mathcal{F}_y^k\right)\!,\end{equation*}
\begin{equation*}\mathcal{G}_x^{k,r} = \sigma\left(\bigcup_{y\in T(x,r)} \mathcal{F}_y^k\right)\!,\end{equation*}
the
![]() $\sigma$
-algebra generated by the (y, k)-freezing processes for all
$\sigma$
-algebra generated by the (y, k)-freezing processes for all
![]() $y\in T(x,r)$
. For each
$y\in T(x,r)$
. For each
![]() $y\in T(x,a n^{1/2})$
, arbitrarily choose a vertex
$y\in T(x,a n^{1/2})$
, arbitrarily choose a vertex
![]() $z(y)\in T(y,an^{1/2})$
. Say that
$z(y)\in T(y,an^{1/2})$
. Say that
![]() $y\in T(x,an^{1/2})$
is ‘special’ if
$y\in T(x,an^{1/2})$
is ‘special’ if
![]() $Y^{(k)}_{z(y)} = 0$
and
$Y^{(k)}_{z(y)} = 0$
and
![]() $F^{(k)}_{z(y)}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2}$
.
$F^{(k)}_{z(y)}-F^{(k)}_{y} \le 2(d+1) a^2 n^{3/2}$
.
If
![]() $y\in M_n(x)$
, then since
$y\in M_n(x)$
, then since
![]() $Y^{(k-1)}_y = 0$
, any particle u that is (y, k)-frozen at y satisfies
$Y^{(k-1)}_y = 0$
, any particle u that is (y, k)-frozen at y satisfies
![]() $J_y(u)=k-1$
and (obviously)
$J_y(u)=k-1$
and (obviously)
![]() $X(u)=y$
. Thus, by Lemma 3.7, for any other
$X(u)=y$
. Thus, by Lemma 3.7, for any other
![]() $y'\in T(x,\lfloor an^{1/2}\rfloor)$
, we must have
$y'\in T(x,\lfloor an^{1/2}\rfloor)$
, we must have
![]() $J_{y'}(u)\ge k$
. This means that no information about descendants of u is included in
$J_{y'}(u)\ge k$
. This means that no information about descendants of u is included in
![]() $\mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor}$
. Since only particles that are (y, k)-frozen at y can contribute to either
$\mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor}$
. Since only particles that are (y, k)-frozen at y can contribute to either
![]() $Y^{(k)}_{z(y)}$
or
$Y^{(k)}_{z(y)}$
or
![]() $F^{(k)}_{z(y)}-F^{(k)}_{y}$
, we deduce that
$F^{(k)}_{z(y)}-F^{(k)}_{y}$
, we deduce that
-
(a) the events
 $\{\{y \text{ is special}\} \colon y\in M_n(x)\}$
are independent given
$\{\{y \text{ is special}\} \colon y\in M_n(x)\}$
are independent given
 $\mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor}$
, and
$\mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor}$
, and -
(b)
 $\mathbb{P}\bigl(y \text{ is special} \mid \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \bigr) = \mathbb{P}\big(y \text{ is special} \big| \mathcal{F}_y^k \big)$
for all
$\mathbb{P}\bigl(y \text{ is special} \mid \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \bigr) = \mathbb{P}\big(y \text{ is special} \big| \mathcal{F}_y^k \big)$
for all
 $y\in M_n(x)$
.
$y\in M_n(x)$
.
We note next that if y is both good and special, then
![]() $Y^{(k)}_{z(y)} = 0$
and
$Y^{(k)}_{z(y)} = 0$
and
![]() $F^{(k)}_{z(y)} \le (2d+5)a^2 n^{3/2}$
. Thus, using also that
$F^{(k)}_{z(y)} \le (2d+5)a^2 n^{3/2}$
. Thus, using also that
![]() $\mathcal{F}_x^{k-1} \subset \mathcal{G}_x^{k,r}$
for any
$\mathcal{F}_x^{k-1} \subset \mathcal{G}_x^{k,r}$
for any
![]() $r\ge0$
,
$r\ge0$
,
 \begin{align*}&\mathbb{P}\big(\exists z\in T\big(x,2an^{1/2}\big) \colon Y^{(k)}_z = 0 \ \text{and}\ F^{(k)}_z \le (2d+5)a^2 n^{3/2} \big| \mathcal{F}_x^{k-1} \big)\\[3pt] &\quad \ge \mathbb{P}\left( |M_n(x)| \ge \dfrac12 |T\big(x,an^{1/2}\big)|,\,\exists y\in M_n(x) \colon y \text{ is special} \Big| \mathcal{F}_x^{k-1} \right)\\[3pt] &\quad =\mathbb{E}\Big[ \unicode{x1d7d9}_{\big\{|M_n(x)| \ge \frac12 |T(x,an^{1/2})|\big\}} \mathbb{P}\big(\exists y\in M_n(x) \colon y \text{ is special} \mid \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \big) \big| \mathcal{F}_x^{k-1}\Big].\end{align*}
\begin{align*}&\mathbb{P}\big(\exists z\in T\big(x,2an^{1/2}\big) \colon Y^{(k)}_z = 0 \ \text{and}\ F^{(k)}_z \le (2d+5)a^2 n^{3/2} \big| \mathcal{F}_x^{k-1} \big)\\[3pt] &\quad \ge \mathbb{P}\left( |M_n(x)| \ge \dfrac12 |T\big(x,an^{1/2}\big)|,\,\exists y\in M_n(x) \colon y \text{ is special} \Big| \mathcal{F}_x^{k-1} \right)\\[3pt] &\quad =\mathbb{E}\Big[ \unicode{x1d7d9}_{\big\{|M_n(x)| \ge \frac12 |T(x,an^{1/2})|\big\}} \mathbb{P}\big(\exists y\in M_n(x) \colon y \text{ is special} \mid \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \big) \big| \mathcal{F}_x^{k-1}\Big].\end{align*}
By (a) the above is at least
 \begin{equation*}\mathbb{E}\left[ \unicode{x1d7d9}_{\big\{|M_n(x)\big| \ge \frac12 \big|T(x,an^{1/2})\big|\big\}}\left(1- \prod_{y\in M_n(x)}\mathbb{P}\Big(y \text{ is not special} \mid \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \Big)\right) \Biggm| \mathcal{F}_x^{k-1}\right].\end{equation*}
\begin{equation*}\mathbb{E}\left[ \unicode{x1d7d9}_{\big\{|M_n(x)\big| \ge \frac12 \big|T(x,an^{1/2})\big|\big\}}\left(1- \prod_{y\in M_n(x)}\mathbb{P}\Big(y \text{ is not special} \mid \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \Big)\right) \Biggm| \mathcal{F}_x^{k-1}\right].\end{equation*}
By (b) and Lemma 3.6, for any
![]() $y\in M_n(x)$
we have
$y\in M_n(x)$
we have
 \begin{align*} \mathbb{P}\Big(y \text{ is not special} \Big| \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \Big) & = \mathbb{P}\bigl(y \text{ is not special} \mid \mathcal{F}_y^k \bigr)\\[3pt] & \le 1-{\mathrm{e}}^{-2c n^{1/2}}/2 \le \exp\bigl(- {\mathrm{e}}^{-2c n^{1/2}}/2\bigr).\end{align*}
\begin{align*} \mathbb{P}\Big(y \text{ is not special} \Big| \mathcal{G}_x^{k,\lfloor an^{1/2}\rfloor} \Big) & = \mathbb{P}\bigl(y \text{ is not special} \mid \mathcal{F}_y^k \bigr)\\[3pt] & \le 1-{\mathrm{e}}^{-2c n^{1/2}}/2 \le \exp\bigl(- {\mathrm{e}}^{-2c n^{1/2}}/2\bigr).\end{align*}
Putting all this together we have shown that
 \begin{align*}&\mathbb{P}\big(\exists z\in T(x,2an^{1/2}) \colon Y^{(k)}_z = 0 \ \text{and}\ F^{(k)}_z \le (2d+5)a^2 n^{3/2} \big| \mathcal{F}_x^{k-1} \big)\\[3pt] &\quad \ge \mathbb{E}\left[ \unicode{x1d7d9}_{\big\{|M_n(x)\big| \ge \frac12 \big|T(x,an^{1/2})\big|\big\}}\left(1- \prod_{y\in M_n(x)}\exp\Big(- {\mathrm{e}}^{-2c n^{1/2}}/2\Big)\right) \Biggm| \mathcal{F}_x^{k-1}\right]\\[3pt] &\quad \ge \mathbb{P}\left( |M_n(x)| \ge \dfrac12 |T(x,an^{1/2})| \Big| \mathcal{F}_x^{k-1}\right) \big(1- \exp\big(- |T(x,an^{1/2})|{\mathrm{e}}^{-2c n^{1/2}}/4\big)\big)\end{align*}
\begin{align*}&\mathbb{P}\big(\exists z\in T(x,2an^{1/2}) \colon Y^{(k)}_z = 0 \ \text{and}\ F^{(k)}_z \le (2d+5)a^2 n^{3/2} \big| \mathcal{F}_x^{k-1} \big)\\[3pt] &\quad \ge \mathbb{E}\left[ \unicode{x1d7d9}_{\big\{|M_n(x)\big| \ge \frac12 \big|T(x,an^{1/2})\big|\big\}}\left(1- \prod_{y\in M_n(x)}\exp\Big(- {\mathrm{e}}^{-2c n^{1/2}}/2\Big)\right) \Biggm| \mathcal{F}_x^{k-1}\right]\\[3pt] &\quad \ge \mathbb{P}\left( |M_n(x)| \ge \dfrac12 |T(x,an^{1/2})| \Big| \mathcal{F}_x^{k-1}\right) \big(1- \exp\big(- |T(x,an^{1/2})|{\mathrm{e}}^{-2c n^{1/2}}/4\big)\big)\end{align*}
By Lemma 3.5, on the event
this is at least
Since
![]() $|T(y,a n^{1/2})| \ge (d-1)^{a n^{1/2}}$
, we have
$|T(y,a n^{1/2})| \ge (d-1)^{a n^{1/2}}$
, we have
![]() $\exp\bigl(-{\mathrm{e}}^{-2cn^{1/2}}|T(y,a n^{1/2})|/4 \bigr) \le 1/a$
provided that a and n are large, so the above is at least
$\exp\bigl(-{\mathrm{e}}^{-2cn^{1/2}}|T(y,a n^{1/2})|/4 \bigr) \le 1/a$
provided that a and n are large, so the above is at least
![]() $1-5d/a$
. And of course if
$1-5d/a$
. And of course if
![]() $Y^{(k)}_z=0$
and
$Y^{(k)}_z=0$
and
![]() $F^{(k)}_z\le (2d+5)a^2 n^{3/2}$
, then for any
$F^{(k)}_z\le (2d+5)a^2 n^{3/2}$
, then for any
![]() $j\ge0$
, any vertex
$j\ge0$
, any vertex
![]() $v\in T(z,j) \subset T(x, 2an^{1/2}+j)$
also has
$v\in T(z,j) \subset T(x, 2an^{1/2}+j)$
also has
![]() $Y^{(k)}_v=0$
and
$Y^{(k)}_v=0$
and
![]() $F^{(k)}_v\le (2d+5)a^2 n^{3/2}$
. Thus
$F^{(k)}_v\le (2d+5)a^2 n^{3/2}$
. Thus
Writing
![]() $A=(2d+5)a^2$
completes the proof.
$A=(2d+5)a^2$
completes the proof.
4. Proof of the lower bound in Theorem 1.1
We aim to prove that, for any
![]() $\eta>0$
,
$\eta>0$
,
Take
![]() $\delta\in(0,1/4)$
small and M large, both to be fixed later. For
$\delta\in(0,1/4)$
small and M large, both to be fixed later. For
![]() $k\ge1$
, let
$k\ge1$
, let
 \begin{equation*}n_k = M^{(3/2+\delta)^k}, \quad p_k = M^{-\delta(3/2+\delta)^{k-1}/2}, \quad R_k = \sum_{j=0}^{k-1} M^{(1/2+\delta)(3/2+\delta)^j}.\end{equation*}
\begin{equation*}n_k = M^{(3/2+\delta)^k}, \quad p_k = M^{-\delta(3/2+\delta)^{k-1}/2}, \quad R_k = \sum_{j=0}^{k-1} M^{(1/2+\delta)(3/2+\delta)^j}.\end{equation*}
Say that
![]() $x\in \partial B(R_{k})$
is slow if
$x\in \partial B(R_{k})$
is slow if
![]() $Y_x^{(k)}=0$
and
$Y_x^{(k)}=0$
and
![]() $F_x^{(k)}\le n_k$
. Define
$F_x^{(k)}\le n_k$
. Define
![]() $\mathcal A_k$
to be the event that there is at least one slow vertex in
$\mathcal A_k$
to be the event that there is at least one slow vertex in
![]() $\partial B(R_k)$
, that is,
$\partial B(R_k)$
, that is,
Let
![]() $X_k$
be a uniformly chosen slow vertex in
$X_k$
be a uniformly chosen slow vertex in
![]() $\partial B(R_k)$
, or
$\partial B(R_k)$
, or
![]() $X_k=0$
if there are no such vertices.
$X_k=0$
if there are no such vertices.
Note that when M is large,
![]() $R_{k-1}\le n_{k-1}^{1/2}$
and
$R_{k-1}\le n_{k-1}^{1/2}$
and
![]() $k\le n_k^{1/2}$
. Thus, setting
$k\le n_k^{1/2}$
. Thus, setting
![]() $A=n_{k-1}^\delta$
so that
$A=n_{k-1}^\delta$
so that
![]() $n_k = An_{k-1}^{3/2}$
,
$n_k = An_{k-1}^{3/2}$
,
![]() $R_k-R_{k-1}= An_{k-1}^{1/2}$
, and
$R_k-R_{k-1}= An_{k-1}^{1/2}$
, and
![]() $p_k=A^{-1/2}$
, Proposition 3.1 tells us that, for any slow
$p_k=A^{-1/2}$
, Proposition 3.1 tells us that, for any slow
![]() $x\in \partial B(R_{k-1})$
, we have
$x\in \partial B(R_{k-1})$
, we have
In particular,
and therefore
Since
 \begin{equation*}\mathbb{P}\left(\bigcup_{j=1}^k \mathcal A_j^c \right) \le \mathbb{P}\left(\bigcup_{j=1}^{k-1} \mathcal A_j^c \right) + \mathbb{P}(\mathcal A_k^c, \mathcal A_{k-1}) \le \mathbb{P}\left(\bigcup_{j=1}^{k-1} \mathcal A_j^c \right) + cp_k,\end{equation*}
\begin{equation*}\mathbb{P}\left(\bigcup_{j=1}^k \mathcal A_j^c \right) \le \mathbb{P}\left(\bigcup_{j=1}^{k-1} \mathcal A_j^c \right) + \mathbb{P}(\mathcal A_k^c, \mathcal A_{k-1}) \le \mathbb{P}\left(\bigcup_{j=1}^{k-1} \mathcal A_j^c \right) + cp_k,\end{equation*}
by induction we have
 \begin{equation*}\mathbb{P}\left(\bigcup_{j=1}^k \mathcal A_j^c \right) \le c\sum_{j=2}^k p_j + \mathbb{P}(\mathcal A_1^c) \le c\sum_{j=2}^\infty p_j + \mathbb{P}(\mathcal A_1^c).\end{equation*}
\begin{equation*}\mathbb{P}\left(\bigcup_{j=1}^k \mathcal A_j^c \right) \le c\sum_{j=2}^k p_j + \mathbb{P}(\mathcal A_1^c) \le c\sum_{j=2}^\infty p_j + \mathbb{P}(\mathcal A_1^c).\end{equation*}
Note that we can make
![]() $\mathbb{P}(\mathcal A_1^c)$
arbitrarily small by choosing M sufficiently large, since for large enough r any vertex
$\mathbb{P}(\mathcal A_1^c)$
arbitrarily small by choosing M sufficiently large, since for large enough r any vertex
![]() $z\in\partial B(r)$
satisfies
$z\in\partial B(r)$
satisfies
![]() $Y_z=0$
and
$Y_z=0$
and
![]() $F_z\le r$
with probability at least
$F_z\le r$
with probability at least
![]() $1-\varepsilon$
.
$1-\varepsilon$
.
Choose
![]() $\varepsilon>0$
and
$\varepsilon>0$
and
![]() $\delta>0$
arbitrarily small, and M large enough that
$\delta>0$
arbitrarily small, and M large enough that
![]() $c\sum_{j=2}^\infty p_j + \mathbb{P}(\mathcal A_1^c) < \varepsilon$
. Then
$c\sum_{j=2}^\infty p_j + \mathbb{P}(\mathcal A_1^c) < \varepsilon$
. Then
![]() $\mathbb{P}(\bigcup_k \mathcal A_k^c)<\varepsilon$
. On the event
$\mathbb{P}(\bigcup_k \mathcal A_k^c)<\varepsilon$
. On the event
![]() $\mathcal A_k$
, there is a vertex
$\mathcal A_k$
, there is a vertex
![]() $z\in \partial B(R_k)$
such that no particles hit z without first taking at least k steps away from z. In this case the first hitting time of z (and all its descendants in the tree) must be at least
$z\in \partial B(R_k)$
such that no particles hit z without first taking at least k steps away from z. In this case the first hitting time of z (and all its descendants in the tree) must be at least
![]() $R_k + 2k$
. We deduce that
$R_k + 2k$
. We deduce that
All that remains now is to invert
![]() $R_k$
. Note that if
$R_k$
. Note that if
then
![]() $\exp((3/2+3\delta)^k)\le n$
, so if n is large then
$\exp((3/2+3\delta)^k)\le n$
, so if n is large then
![]() $M^{(3/2+2\delta)^k}\le n$
and indeed
$M^{(3/2+2\delta)^k}\le n$
and indeed
![]() $R_k \le n$
. Therefore
$R_k \le n$
. Therefore
and since
![]() $\delta$
and
$\delta$
and
![]() $\varepsilon$
were arbitrary, this completes the proof of the lower bound in Theorem 1.1.
$\varepsilon$
were arbitrary, this completes the proof of the lower bound in Theorem 1.1.
5. Proof of the upper bound in Theorem 1.1
We want to show that for any
![]() $\eta>0$
$\eta>0$
Suppose that
![]() $x\in T$
and
$x\in T$
and
![]() $y\in T(x,A)$
, for some large
$y\in T(x,A)$
, for some large
![]() $A\in\mathbb{N}$
. Lemma 3.3 tells us that if
$A\in\mathbb{N}$
. Lemma 3.3 tells us that if
![]() $\Gamma$
consists of at least n particles, none of which is in the subtree rooted at x except possibly at x itself, and none of which have distance greater than 2A from y, then
$\Gamma$
consists of at least n particles, none of which is in the subtree rooted at x except possibly at x itself, and none of which have distance greater than 2A from y, then
where
![]() $\delta\in(0,1]$
is some fixed constant.
$\delta\in(0,1]$
is some fixed constant.
Now fix
![]() $N\in\mathbb{N}$
. If we start with N particles all at 0, then (for any
$N\in\mathbb{N}$
. If we start with N particles all at 0, then (for any
![]() $k\ge 2$
) none of the
$k\ge 2$
) none of the
![]() $(x,k{-}1)$
-frozen particles are within the subtree rooted at x except possibly at x itself, and all have distance at most
$(x,k{-}1)$
-frozen particles are within the subtree rooted at x except possibly at x itself, and all have distance at most
![]() $d(0,y)+k$
from y. Thus, if
$d(0,y)+k$
from y. Thus, if
![]() $d(0,y)+k\le 2A$
, then recalling that
$d(0,y)+k\le 2A$
, then recalling that
![]() $\mathcal{F}_x^{k-1}$
is the
$\mathcal{F}_x^{k-1}$
is the
![]() $\sigma$
-algebra generated by the
$\sigma$
-algebra generated by the
![]() $(x,k-1)$
-freezing process, on the event
$(x,k-1)$
-freezing process, on the event
we have
For each
![]() $k\in\mathbb{N}$
, set
$k\in\mathbb{N}$
, set
 \begin{equation*}N_k = \dfrac{{\mathrm{e}}^{(3/2)^k}}{\delta^2 a^2} \quad \text{and} \quad R_k = \sum_{j=1}^{k-1} a N_j^{1/2}\end{equation*}
\begin{equation*}N_k = \dfrac{{\mathrm{e}}^{(3/2)^k}}{\delta^2 a^2} \quad \text{and} \quad R_k = \sum_{j=1}^{k-1} a N_j^{1/2}\end{equation*}
for some small
![]() $a>0$
to be chosen later, and for
$a>0$
to be chosen later, and for
![]() $z\in T$
define the event
$z\in T$
define the event
Note that provided a is sufficiently small, we have
![]() $R_k+k\le 2 aN_{k-1}^{1/2}$
for all
$R_k+k\le 2 aN_{k-1}^{1/2}$
for all
![]() $k\in\mathbb{N}$
. Thus, by the argument above, if
$k\in\mathbb{N}$
. Thus, by the argument above, if
![]() $k\ge 2$
,
$k\ge 2$
,
![]() $x\in \partial B(R_{k-1})$
and
$x\in \partial B(R_{k-1})$
and
![]() $y\in T(x, a N_{k-1}^{1/2})$
, then on the event
$y\in T(x, a N_{k-1}^{1/2})$
, then on the event
![]() $\mathcal B^{k-1}_x$
we have
$\mathcal B^{k-1}_x$
we have
Since
![]() $\delta a N_{k-1}^{3/2} = N_k$
, we deduce that
$\delta a N_{k-1}^{3/2} = N_k$
, we deduce that
Let
![]() $\mathcal B_k = \bigcap_{x\in \partial B(R_k)} \mathcal B^k_x$
. There are
$\mathcal B_k = \bigcap_{x\in \partial B(R_k)} \mathcal B^k_x$
. There are
![]() $d(d-1)^{R_k-1}$
vertices in
$d(d-1)^{R_k-1}$
vertices in
![]() $\partial B(R_k)$
, so a union bound gives
$\partial B(R_k)$
, so a union bound gives
Since
 \begin{equation*}\mathbb{P}_{N,0}\left(\bigcup_{j=1}^k \mathcal B_j^c \right) \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^{k-1} \mathcal B_j^c \right) + \mathbb{P}_{N,0}(\mathcal B_k^c, \mathcal B_{k-1}) ,\end{equation*}
\begin{equation*}\mathbb{P}_{N,0}\left(\bigcup_{j=1}^k \mathcal B_j^c \right) \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^{k-1} \mathcal B_j^c \right) + \mathbb{P}_{N,0}(\mathcal B_k^c, \mathcal B_{k-1}) ,\end{equation*}
by induction we have
 \begin{equation}\mathbb{P}_{N,0}\left(\bigcup_{j=1}^k \mathcal B_j^c \right) \le \sum_{j=2}^k d(d-1)^{R_j-1}\exp\bigl(-\delta N_{j-1}^{1/2} / a\bigr) + \mathbb{P}_{N,0}(\mathcal B_1^c).\end{equation}
\begin{equation}\mathbb{P}_{N,0}\left(\bigcup_{j=1}^k \mathcal B_j^c \right) \le \sum_{j=2}^k d(d-1)^{R_j-1}\exp\bigl(-\delta N_{j-1}^{1/2} / a\bigr) + \mathbb{P}_{N,0}(\mathcal B_1^c).\end{equation}
Now fix
![]() $k\ge1$
and suppose that
$k\ge1$
and suppose that
![]() $\mathcal B_k$
occurs, so for each
$\mathcal B_k$
occurs, so for each
![]() $z\in \partial B(R_k)$
, there are at least
$z\in \partial B(R_k)$
, there are at least
![]() $N_k$
particles that are (z, k)-frozen. All such particles have taken at most k steps away from z when they are frozen. Each of these particles has distance at most
$N_k$
particles that are (z, k)-frozen. All such particles have taken at most k steps away from z when they are frozen. Each of these particles has distance at most
![]() $R_k+k$
from z, and therefore the probability that it has a descendant that hits z without taking any more steps away from z is bounded from below by the probability that a critical Galton–Watson process with finite variance survives for
$R_k+k$
from z, and therefore the probability that it has a descendant that hits z without taking any more steps away from z is bounded from below by the probability that a critical Galton–Watson process with finite variance survives for
![]() $R_k+k \le 2R_k$
generations. This is at least
$R_k+k \le 2R_k$
generations. This is at least
![]() $c/R_k$
for some constant c by Lemma 2.1. Thus the probability that none of the (z, k)-frozen particles has a descendant that hits z without taking any more steps away from z is at most
$c/R_k$
for some constant c by Lemma 2.1. Thus the probability that none of the (z, k)-frozen particles has a descendant that hits z without taking any more steps away from z is at most
![]() $(1-c/R_k)^{N_k}\le \exp(-cN_k/R_k)$
. Therefore, if H(z) is the first hitting time of z, we have
$(1-c/R_k)^{N_k}\le \exp(-cN_k/R_k)$
. Therefore, if H(z) is the first hitting time of z, we have
Now, if a particle hits z without taking more than k steps away from z, then for every x on the path from 0 to z, x is hit by time
![]() $d(0,x)+2k$
. Thus
$d(0,x)+2k$
. Thus
 \begin{align}&\mathbb{P}_{N,0}(\exists r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k \mid \mathcal B_k)\notag\\[3pt] &\quad = \mathbb{P}_{N,0}(\exists r\le R_k, \, x\in \partial B(r) \colon H(x) > r + 2k \mid \mathcal B_k)\notag\\[3pt] &\quad \le \mathbb{P}_{N,0}(\exists z\in \partial B(R_k) \colon H(z) > R_k + 2k \mid \mathcal B_k)\notag\\[3pt] &\quad \le d(d-1)^{R_k-1}\exp(-cN_k/R_k).\end{align}
\begin{align}&\mathbb{P}_{N,0}(\exists r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k \mid \mathcal B_k)\notag\\[3pt] &\quad = \mathbb{P}_{N,0}(\exists r\le R_k, \, x\in \partial B(r) \colon H(x) > r + 2k \mid \mathcal B_k)\notag\\[3pt] &\quad \le \mathbb{P}_{N,0}(\exists z\in \partial B(R_k) \colon H(z) > R_k + 2k \mid \mathcal B_k)\notag\\[3pt] &\quad \le d(d-1)^{R_k-1}\exp(-cN_k/R_k).\end{align}
Then
 \begin{align*}&\mathbb{P}_{N,0}\Bigl(\exists k \colon \max_{r\le R_k}(T_{\textrm{cov}}(r)-r) > 2k\Bigr)\\[3pt] &\quad \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^\infty \mathcal B_j^c\right) + \mathbb{P}_{N,0}\left(\{\exists k,\, r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k\}\cap \bigcap_{j=1}^\infty \mathcal B_j\right)\\[3pt] &\quad \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^\infty \mathcal B_j^c\right) + \sum_{k=1}^\infty \mathbb{P}_{N,0}(\{\exists r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k\}\cap \mathcal B_k)\\[3pt] &\quad \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^\infty \mathcal B_j^c\right) + \sum_{k=1}^\infty \mathbb{P}_{N,0}(\exists r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k \mid \mathcal B_k).\end{align*}
\begin{align*}&\mathbb{P}_{N,0}\Bigl(\exists k \colon \max_{r\le R_k}(T_{\textrm{cov}}(r)-r) > 2k\Bigr)\\[3pt] &\quad \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^\infty \mathcal B_j^c\right) + \mathbb{P}_{N,0}\left(\{\exists k,\, r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k\}\cap \bigcap_{j=1}^\infty \mathcal B_j\right)\\[3pt] &\quad \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^\infty \mathcal B_j^c\right) + \sum_{k=1}^\infty \mathbb{P}_{N,0}(\{\exists r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k\}\cap \mathcal B_k)\\[3pt] &\quad \le \mathbb{P}_{N,0}\left(\bigcup_{j=1}^\infty \mathcal B_j^c\right) + \sum_{k=1}^\infty \mathbb{P}_{N,0}(\exists r\le R_k \colon T_{\textrm{cov}}(r) > r + 2k \mid \mathcal B_k).\end{align*}
By (5.1) and (5.2), this is at most
 \begin{equation*}\sum_{j=2}^\infty d(d-1)^{R_j-1}{\mathrm{e}}^{-\delta N_{j-1}^{1/2} / a} + \mathbb{P}_{N,0}(\mathcal B_1^c) + \sum_{k=1}^\infty d(d-1)^{R_k-1}\exp(-cN_k/R_k).\end{equation*}
\begin{equation*}\sum_{j=2}^\infty d(d-1)^{R_j-1}{\mathrm{e}}^{-\delta N_{j-1}^{1/2} / a} + \mathbb{P}_{N,0}(\mathcal B_1^c) + \sum_{k=1}^\infty d(d-1)^{R_k-1}\exp(-cN_k/R_k).\end{equation*}
Recalling that for
![]() $k\ge1$
$k\ge1$
 \begin{equation*}N_k = \dfrac{{\mathrm{e}}^{(3/2)^k}}{\delta^2 a^2} \quad \text{and} \quad R_k = \sum_{j=1}^{k-1} a N_j^{1/2},\end{equation*}
\begin{equation*}N_k = \dfrac{{\mathrm{e}}^{(3/2)^k}}{\delta^2 a^2} \quad \text{and} \quad R_k = \sum_{j=1}^{k-1} a N_j^{1/2},\end{equation*}
we note that for any
![]() $\varepsilon>0$
, by choosing a sufficiently small, we can ensure that
$\varepsilon>0$
, by choosing a sufficiently small, we can ensure that
 \begin{equation*}\sum_{j=2}^\infty d(d-1)^{R_j-1}{\mathrm{e}}^{-\delta N_{j-1}^{1/2} / a} + \sum_{k=1}^\infty d(d-1)^{R_k-1}\exp(-cN_k/R_k) < \varepsilon\end{equation*}
\begin{equation*}\sum_{j=2}^\infty d(d-1)^{R_j-1}{\mathrm{e}}^{-\delta N_{j-1}^{1/2} / a} + \sum_{k=1}^\infty d(d-1)^{R_k-1}\exp(-cN_k/R_k) < \varepsilon\end{equation*}
and thus
Since
![]() $R_1=0$
and
$R_1=0$
and
![]() $N_1 = {\mathrm{e}}^{3/2}/\big(\delta^2 a^2\big)$
, we have
$N_1 = {\mathrm{e}}^{3/2}/\big(\delta^2 a^2\big)$
, we have
However, under
![]() $\mathbb{P}_{N,0}$
, we have
$\mathbb{P}_{N,0}$
, we have
![]() $F^{(1)}_0 = 0$
and
$F^{(1)}_0 = 0$
and
![]() $Y^{(1)}_0 = N$
, so for
$Y^{(1)}_0 = N$
, so for
![]() $N\ge {\mathrm{e}}^{3/2}/(\delta^2 a^2)$
we have
$N\ge {\mathrm{e}}^{3/2}/(\delta^2 a^2)$
we have
![]() $\mathbb{P}_{N,0}(\mathcal B_1)=1$
and therefore
$\mathbb{P}_{N,0}(\mathcal B_1)=1$
and therefore
In our original model we started with 1 particle (rather than N particles) at the origin, but by waiting until the first time at which the number of particles at 0 is at least
![]() ${\mathrm{e}}^{3/2}/(\delta^2a^2)$
, which is almost surely finite given that the process survives, we may choose t large enough such that
${\mathrm{e}}^{3/2}/(\delta^2a^2)$
, which is almost surely finite given that the process survives, we may choose t large enough such that
Since
![]() $\varepsilon>0$
was arbitrary, applying this with
$\varepsilon>0$
was arbitrary, applying this with
for arbitrarily small
![]() $\eta>0$
completes the proof of the upper bound in Theorem 1.1.
$\eta>0$
completes the proof of the upper bound in Theorem 1.1.
Acknowledgements
I wish to thank Itai Benjamini, who asked me this question, and sent me a short proof of a weaker bound on
![]() $T_{\textrm{cov}}(r)$
that he had written jointly with Gady Kozma. Thanks also to Alice Callegaro and two anonymous referees, each of whom suggested several corrections and improvements to the paper.
$T_{\textrm{cov}}(r)$
that he had written jointly with Gady Kozma. Thanks also to Alice Callegaro and two anonymous referees, each of whom suggested several corrections and improvements to the paper.
Funding information
This work was supported by a Royal Society University Research Fellowship.
Competing interests
There were no competing interests to declare which arose during the preparation or publication process of this article.