The Compact Network RTK Method: An Effective Solution to Reduce GNSS Temporal and Spatial Decorrelation Error

Byungwoon Park; Changdon Kee

doi:10.1017/S0373463309990440

The Compact Network RTK Method: An Effective Solution to Reduce GNSS Temporal and Spatial Decorrelation Error

Published online by Cambridge University Press: 23 February 2010

Byungwoon Park and

Changdon Kee

Show author details

Byungwoon Park: Affiliation:
(Seoul National University)
Changdon Kee*: Affiliation:
(Seoul National University)
*: (E-mail: coolguy4@snu.ac.kr)

Article contents

Abstract
INTRODUCTION
Existing Algorithms and protocols
Compact Network RTK
CORRECTION SCHEDULING ALGORITHM
DATA TEST CONSTRUCTION AND RESULTS
Advantages of compact rtk
Conclusions
References

Rights & Permissions

Abstract

This paper proposes a method that combines compact real-time kinematic (RTK) and reference station (RS) networking techniques, and shows that this approach can reduce both the temporal and spatial decorrelation error. The compact RTK method compatibility with all the conventional network RTK systems, i.e., Master-Auxiliary Concept (MAC), Virtual Reference Stations (VRS), and Flächen-Korrektur Parameter (FKP), is examined theoretically in this paper. To prove that the compact RTK approach is not only valid, but also helpful to the network RTK system, a field test was held using one hour of Receiver Independent Exchange Format (RINEX) data logged every second from Continuously Operating Reference Stations (CORS). No matter which network RTK method is applied, the Compact Network RTK approach resolves the ambiguity of the carrier phase in 10–40 s and determines position with 6–7 cm horizontal and 7–8 cm vertical error (95%) in a 100 by 100 km region. Moreover, the Compact Network RTK approach enables network RTK service providers to reduce the data-link bandwidth for correction messages to 5–700 bps (bit/s) down from several thousand bps, currently 9600 bps of GPRS/GSM, without a severe degradation of accuracy.

Keywords

Compact RTK Network RTK Time delay Distance-dependent error

Type: Research Article
Information: The Journal of Navigation , Volume 63 , Issue 2 , April 2010 , pp. 343 - 362

DOI: https://doi.org/10.1017/S0373463309990440 [Opens in a new window]
Copyright: Copyright © The Royal Institute of Navigation 2010

1. INTRODUCTION

Differential GPS (DGPS), with an accuracy of several metres, is used very widely and practically for navigation or non-precision aviation because of its wide and continuous coverage and low rate data-link for correction messages. Fields of geographical concern involving the design of highways, railways, harbour approaches, precision farming, and surveys that demand a high spatial accuracy to within several centimetres to decimetres can be achieved by real-time kinematic (RTK) performance. The use of the RTK approach however still remains experimental and is not yet practical because of its narrow coverage and the high data-link rates necessary.

The Global Navigation Satellite System (GNSS) common errors are highly correlated within a small time-latency and a short distance, so an RTK correction message generated from a reference station (RS) can easily cancel the error out. A decorrelation error, however, becomes larger when the correction age gets older or when the distance between the reference and a rover increases, so the single RS generally broadcasts an RTK correction message every second within a 10–20 km baseline. As summarized in Table 1, a 10 s latency error can make a 0·2 m error, and a user located 100 km away from the reference station may experience an error of several metres. This additional error is too large to cause a wrong ambiguity fixing and deteriorates the RTK performance (Park Reference Park2006, Reference Park2008).

Table 1. Error decorrelation due to the delay and distance.

To reduce the temporal decorrelation error, Seoul National University RTK (SNUR) has been suggested as an RTK compact correction (Kim, 2002). It has been shown that this protocol can deal with time-delay-induced error and that the accuracy degradation is negligible even under a low rate (500 bps) data-link. Many companies, governments, and international organizations such as Radio Technical Commission for Maritime Services (RTCM) are seeking a network RTK solution to reduce the distance-dependent error. There are currently several network RTK methods on the market including the Master–Auxiliary Concept (MAC), Virtual Reference Station (VRS), and the Flächen-Korrektur Parameter (FKP). Both compact and network RTK provide a proper solution to either temporal- or spatial-related issues, but neither one of them deals with both of the decorrelation errors. In this paper, we suggest a method to reduce both the temporal and the spatial decorrelation errors at the same time.

2. Existing Algorithms and protocols

Network RTK is a maturing technology that can reduce the spatial decorrelation error using a network of three or more reference stations. The concept of network RTK has been proven commercially and service providers use several competing solutions in the market, including MAC, VRS, or an FKP (Rizos Reference Rizos and Han2003, Dorota Reference Dorota2007).

In the case of network RTK, the observations of auxiliary reference stations are pre-processed in a computing centre. Network corrections made from the central facility are then applied to the rover in the RS network. The data format and content of the network correction cause differences in the network RTK solution.

2.1. Master–Auxiliary Concept (MAC)

A network RTK system based on the MAC consists of a master RS and several auxiliary RSs, as shown in Figure 1. According to this concept, each auxiliary RS sends its own measurements to the master, and the inter-station difference of the correction is used to estimate the adequate correction:

(1)

$\eqalign {MAC_{ri}^{i} \tab\equals {}_{A_{{ri}} }\rmDelta _{M} \lpar d^{i} \minus \hat{b}^{i} \plus \hat{B} \minus \phi ^{i} \rpar \plus {}_{A_{{ri}} }\rmDelta _{M} \hat{N}^{i} \lambda {\rm \ }\cr \tab {\rm \equals } \minus {}_{A_{{ri}} }\rmDelta _{M} \lpar \minus I^{i} \plus T^{i} \minus \delta b^{i} \plus \delta R^{i} \rpar \plus {}_{A_{{ri}} }\rmDelta _{M} \lpar \lambda \delta N^{i} \minus \delta B\rpar$

where MAC_riⁱ is the MAC correction between the ri-th auxiliary and the master RS for the i-th satellite; ${}_{A_{{ri}} }\rmDelta _{M}$ , inter RS difference operation between ri-th auxiliary and master RS; ∧, estimated value for each component; δ, estimation error for each component; φ, carrier phase observable; d, distance from a satellite; b, satellite clock offset; B, receiver clock bias; N, cycle ambiguity of the carrier phase measurement; λ, carrier wavelength for each frequency; I, ionosphere-induced error; and T, tropospheric delay error.

Figure 1. Overview of the MAC method.

This correction can be split into dispersive (MAC _disp) and non-dispersive (MAC _non–disp) corrections for broadcast efficiency (Euler Reference Euler2001). Recently this has been accepted as the basis of RTCM v.3 network messages (RTCM, 2006):

(2)

$MAC_{ri\comma disp}^{i} \equals {{f_{\setnum{2}}^{\setnum{2}} } \over {f_{\setnum{2}}^{\setnum{2}} \minus f_{\setnum{1}}^{\setnum{2}} }}MAC_{ri\comma f_{\setnum{1}} }^{i} \minus {{f_{\setnum{2}}^{\setnum{2}} } \over {f_{\setnum{2}}^{\setnum{2}} \minus f_{\setnum{1}}^{\setnum{2}} }}MAC_{ri\comma f_{\setnum{2}} }^{i}$

(3)

$MAC_{ri\comma non \minus disp}^{i} \equals {{f_{\setnum{1}}^{\setnum{2}} } \over {f_{\setnum{1}}^{\setnum{2}} \minus f_{\setnum{2}}^{\setnum{2}} }}MAC_{ri\comma f_{\setnum{1}} }^{i} \minus {{f_{\setnum{2}}^{\setnum{2}} } \over {f_{\setnum{1}}^{\setnum{2}} \minus f_{\setnum{2}}^{\setnum{2}} }}MAC_{ri\comma f_{\setnum{2}} }^{i}$

where f ₁ and f ₂ are L1 and L2 frequency.

This solution can be applied with one-way communication, so a user of a kinematic application can determine its position without any interruptions and discontinuities. The rover can decide whether to use the complete information of a single RS, or use part of, or the complete suite of transferred RS data to derive the best solution. However, more data is transmitted with the MAC correction, so the data bandwidth can increase with the number of RSs and the update rate.

2.2. Flächen-Korrektur Parameter (FKP)

The FKP (or Area Correction Parameter) method calculates the coefficients of a polynomial surface which models the correction difference referenced to the master station. These coefficients are horizontal gradients for the dispersive and non-dispersive error, and are used for evaluating the error polynomial at the desired location. The rover interpolates corrections and applies them with the master station observations or corrections (Wübbena Reference Wübbena2001). This method is currently under discussion by the RTCM Committee for use in standardization.

The MAC dispersive and non-dispersive corrections are represented by these equations:

(4)

$MAC_{ri\comma disp}^{i} \equals 6{\cdot}37H \lsqb {{\partial n_{disp}^{i} } \over {\partial \varphi }}{}_{ri}\rmDelta _{m} \varphi \plus {{\partial e_{disp}^{i} } \over {\partial \lambda }}{}_{ri}\rmDelta _{m} \lambda \cos \lpar \varphi _{m} \rpar \rsqb$

(5)

$MAC_{ri\comma non \minus disp}^{i} \equals 6{\cdot}37\lsqb {{\partial n_{non \minus disp}^{i} } \over {\partial \varphi }}{}_{ri}\rmDelta _{m} \varphi \plus {{\partial e_{non \minus disp}^{i} } \over {\partial \lambda }}{}_{ri}\rmDelta _{m} \lambda \cos \lpar \varphi _{m} \rpar \rsqb$

where $H \comma 1 \plus 16\lpar 0{\cdot}53 \minus {{el_{ri}^{i} } \over \pi }\rpar ^{\setnum{3}}$ ; ϕ,λ, latitude and longitude; ${{\partial n^{i} } \over {\partial \varphi }}\comma {{\partial e^{i} } \over {\partial \lambda }}$ , correction gradient in latitude and longitude directions; and el _riⁱ, elevation angle for i-th satellite from ri-th RS.

Protocol for the FKP correction includes information on the coefficients, ${{\partial n_{disp}^{i} } \over {\partial \varphi }}\comma {{\partial e_{disp}^{i} } \over {\partial \lambda }}\comma {{\partial n_{non \minus disp}^{i} } \over {\partial \varphi }}$ and ${{\partial e_{non \minus disp}^{i} } \over {\partial \lambda }}$ . It broadcasts coefficients that can express the error plane efficiently in the way described in Figure 2, so it is very suitable for broadcasting corrections. However, unlike the MAC approach, the provider's decision on the complexity of the model can influence the rover performance.

Figure 2. Overview of the FKP method.

2.3. Virtual Reference Station (VRS)

In the VRS case in Figure 3, the reference data are not from a permanent RS. Instead, they are computed and refer to a point within the network area from which it would be convenient for the user to obtain data. The network software in VRS implementation estimates the double-difference ambiguities and the corrections for each station and each satellite. The user sends his or her approximate position to the central computing facility; the corrections are then properly interpolated onto the position of the rover. The VRS corrections or observations used for baseline positioning are finally transmitted to the rover receiver following the generation of a virtual reference station (Dai Reference Dai, Han, Wang and Rizos2001).

Figure 3. Overview of the VRS method.

A VRS-based network RTK array transports the correction stream in a single RS-based correction message (RTCM 2.3 MT18, RTCM 3.0, MT1003/1004), so the rover receivers do not need any firmware change. In addition to its compatibility with conventional receivers, the VRS technique has the advantage that the server can continuously optimize the correction stream for each rover position.

To establish the optimal model for the continuous position of the rover, the VRS method requires bidirectional communication. Bidirectional communication cannot be free of the privacy problem. If the correction is generated based on the initial user position without a continuous position update, similar distance-dependent errors to those of single RS RTK will be present.

2.4. Relationship of conventional network RTK methods

Despite differences in their mode of operation, all the network RTK modes share a common goal, which is to improve the positioning performance of the rover when compared with the single RS-based RTK approach. Network RTK data are processed through several steps as shown in Figure 4. Different network RTK modes are defined by the amount of pre-processing applied by the network software, but all the solutions can be realized from the MAC approach (Takac Reference Takac2008). To see if the compact RTK method can work with all the conventional methods, we need to check the compatibility with the MAC only.

Figure 4. General processes involved in network RTK solutions (Takac Reference Takac2008).

3. Compact Network RTK

3.1. Compact RTK

To implement an RTK service, a user should receive GPS observables in real time from each RS. The observables to be transmitted are mainly pseudorange and carrier phase data. The measurements principally consist of the distance from a satellite to the user, the satellite offset, the receiver clock bias, and other error terms. Their variations, which are dominated by a change in the geometric range due to the orbital motion of the satellite and the rotation of the Earth, are very large and nonlinear. In this system, it is hard to predict the variation of observables in time delay, and the effect of time latency is critical to the performance. For continuous and reliable GPS-RTK results, the bandwidth of the data-link between the GPS-RTK RS and the user should be large to minimize the latency effect.

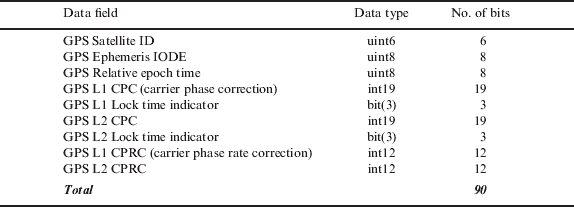
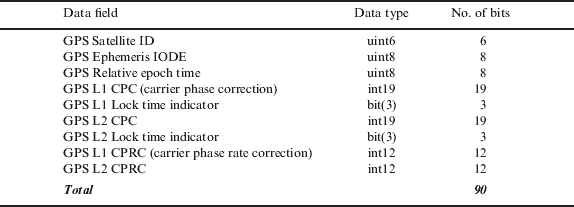
When GPS-RTK corrections are transmitted instead of raw GPS observables, a high-accuracy GPS-RTK result is guaranteed using only a linear latency compensator as shown in Figure 5. This is because corrections change slower and more linearly than the raw observables do. A compact RTK RS should generate GPS-RTK carrier phase corrections (CPC) which satisfy both continuity and linearity, and the protocol represented in Table 2 is suitable to contain the information and to compensate for the time delay (Kim and Kee Reference Kee and Kim2002).

Figure 5. Continuity and linearity of CPC variation.

Table 2. Compact RTK CPC protocol (MT 131).

To reduce the latency effect of CPC, a new asynchronous transmitting technique for CPC is proposed. By transmitting the CPC with a high latency error more frequently, the performance of the GPS-RTK method using a 500 bps data-link is almost identical to that derived via a high-bandwidth data-link.

The protocol that is suitable for the low rate data-link has been proposed in RTCM SC-104 v.3. In this paper we name the protocols of CPC and pseudorange correction (PRC) as MT 131 and 132, following temporary numbering in the RTCM draft documentation.

3.2. Compatibility of Compact RTK and Network RTK

The CPC for the i-th satellite, $\mathop \delta \limits_{C} \phi _{M}^{i}$ in compact RTK can be generated by using the estimated clock bias ( $\hat{B}_{M}$ ) and integer ambiguity ( $\hat{N}_{M}^{i}$ ), so it inevitably includes errors in clock bias and ambiguity. The error in clock bias, δB _M is common to all the channels, and the ambiguity error, λδN _Mⁱ still has the integer characteristics, so the user can determine his or her own double difference ambiguity without any problem. The true correction term, (−I _Mⁱ+T _Mⁱ−δb ⁱ+δR ⁱ) varies slowly, so it can endure a 2–5 s delay:

(6)

$\mathop \delta \limits_{C} \phi _{M}^{i} \equals d_{M}^{i} \minus \phi _{M}^{i} \minus \hat{b}^{i} \plus \hat{B}_{M} \plus \hat{N}_{M}^{i} \lambda \equals \minus \lpar \minus I_{M}^{i} \plus T_{M}^{\,i} \minus \delta b^{i} \plus \delta R^{i} \rpar \minus \delta B_{M} \minus \lambda \delta N_{M}^{i}$

(7)

$\mathop \delta \limits_{C} \phi _{M}^{j} \equals \minus \lpar \minus I_{M}^{j} \plus T_{M}^{\;j} \minus \delta b^{j} \plus \delta R^{j} \rpar \minus \delta B_{M} \minus \lambda \delta N_{M}^{j}$

Similarly, the MAC has some errors in its inter-station differences of ambiguity and clock bias between master (M) and ri-th auxiliary (A _ri) RS. These errors, ${}_{A_{{ri}} }\rmDelta _{M} \lambda \delta N^{i}$ and ${}_{A_{{ri}} }\rmDelta _{M} \delta B$ , are common to all the channels for each auxiliary station, so they do not cause user problems in the same way as compact RTK:

(8)

$\eqalign {MAC_{ri}^{i} \equals {}_{A_{{ri}} }\rmDelta _{M} \mathop \delta \limits_{R} \phi ^{i} \plus {}_{A_{{ri}} }\rmDelta _{M} \hat{N}^{i} \lambda {\rm \ \equals } \minus {}_{A_{{ri}} }\rmDelta _{M} \lpar \minus I^{i} \plus T^{\,i} \minus \delta b^{i} \plus \delta R^{i} \rpar \plus {}_{A_{{ri}} }\rmDelta _{M} \lpar \lambda \delta N^{i} \minus \delta B\rpar$

(9)

$\eqalign{ MAC_{ri}^{j} \tab \equals {}_{A_{{ri}} }\rmDelta _{M} \mathop \delta \limits_{R} \phi ^{i} \plus {}_{A_{{ri}} }\rmDelta _{M} {}^{j}\nabla ^{i} N\lambda \plus {}_{A_{{ri}} }\rmDelta _{M} \hat{N}^{i} \lambda \cr \tab \equals \minus {}_{A_{{ri}} }\rmDelta _{M} \lpar \minus I^{j} \plus T^{\;j} \minus \delta b^{j} \plus \delta R^{j} \rpar \plus {}_{A_{{ri}} }\rmDelta _{M} \lpar \lambda \delta N^{i} \minus \delta B\rpar \cr}$

After combining these two types of correction, the rover chooses the appropriate auxiliary RS and determines the weighting factor (ω_ri) for each correction. By using this method, the distance-dependent error can be mitigated as expressed in equations (10) and (11):

(10)

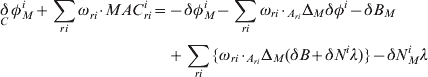
$\eqalign{\mathop \delta \limits_{C} \phi _{M}^{i} \plus \sum\limits_{ri} {\omega _{ri}^{} \cdot MAC_{ri}^{i} } \equals \tab\minus \delta \phi _{M}^{i} \minus \sum\limits_{ri}^{} {\omega _{ri} \cdot {}_{A_{{ri}} }\rmDelta _{M} \delta \phi ^{i} } \minus \delta B_{M} \cr \tab \plus \sum\limits_{ri}^{} {\lcub \omega _{ri} \cdot {}_{A_{{ri}} }\rmDelta _{M} \lpar \delta B \plus \delta N^{i} \lambda \rpar } \rcub \minus \delta N_{M}^{i} \lambda$

(11)

$\eqalign{\mathop \delta \limits_{C} \phi _{M}^{j} \plus \sum\limits_{ri} {\omega _{ri} \cdot MAC_{ri}^{j} } \equals \tab\minus \delta \phi_{M}^{\hskip2pt j} \minus \sum\limits {\omega _{ri} \cdot {}_{A_{{ri}} }\rmDelta _{M} \delta \phi ^{\hskip2pt j} \minus \delta B_{M}} \cr\tab\plus \sum\limits_{ri}^{} {\lcub \omega _{ri} \cdot {}_{A_{{ri}} }\rmDelta _{M} \lpar \delta B \plus \delta N^{i} \lambda \rpar \rcub } \minus \delta N_{M}^{\hskip1ptj} \lambda$

$\sum\limits_{ri}^{} {\lcub \omega _{ri} \cdot {}_{A_{{ri}} }\rmDelta _{M} \lpar \delta B \plus \delta N^{i} \lambda \rpar \rcub }$ in equations (10) and (11) is common to all the observables, and the ambiguity errors, δN _Mⁱ and δN _M^j, still hold their integer property. In spite of these error terms, which are included by combining the compact RTK and MAC systems, the network RTK method does not lose its original nature, nor does it damage the achievable performance. The compact RTK and MAC methods are therefore theoretically compatible.

3.3. Compatibility check using the Zero-baseline equivalent system

Our suggestion needs to be verified not only by mathematics but also in the real field. To make the system simple in order to check compatibility, we assumed a zero-baseline equivalent system in which a user is located at an RS as shown in Figure 6. The master station, which generates a compact RTK correction, has been assigned as Pittsburgh (PITT), and the inter-station difference between Raleigh (RALR) and PITT makes a MAC correction. The distance between the master and auxiliary stations is 49 km and Continuously Operating Reference Stations CORS RINEX data logged in 1-s intervals were used for this study.

Figure 6. Compatibility test between compact RTK and network RTK (zero-baseline equivalent).

The results when the user compensated the distance-dependent error and then applied this to its own observables are shown in Figure 7. The errors are smaller than 1 cm, which shows exactly the same performance as the zero-baseline test.

Figure 7. Zero-baseline compatibility test result between compact RTK and network RTK (left, horizontal; right, vertical).

Both from the theoretical approach and the zero-baseline data test, we conclude that the compact RTK and MAC approaches are perfectly compatible with each other. Other network RTK solutions can be derived from the MAC correction; we therefore conclude that all the network RTK methods are compatible to the compact RTK solution.

4. CORRECTION SCHEDULING ALGORITHM

Scheduling of the correction messages is a crucial procedure because the network RTK method needs various message types. The data broadcasting bandwidth is limited, so a scheduling scheme is helpful in maximizing efficiency.

According to the RTCM standard 10403.1 (RTCM, 2006), the RTCM guideline recommendations for scheduling are:

• raw observables (MT 1003 or 1004) containing master RS data at a high rate (0·5–2 Hz) immediately (no latency);
• the maximum interval for ionospheric (dispersive) and geometric (non-dispersive) correction difference message for all auxiliary RS (MT 1015 and 1016, or 1017) should not exceed 10 s; and
• the dissemination for a station information message (1014) for all master and auxiliary RSs should be completed after a maximum time span of 15 s (optimized for start-up time).

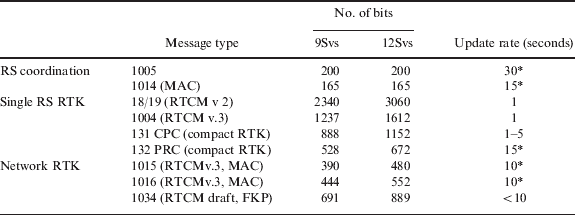
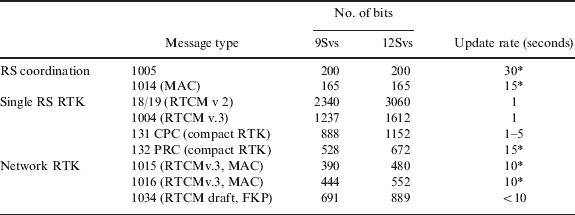
Based on the RTCM recommendation and protocol standard, we have summarized and compared the protocols, data size and update rate of RTK-related correction information in Table 3.

Table 3. RTK protocols, data size, and update rate (RTCM recommendation).

This scheduling scheme is very simple and easy to implement, but it does not sufficiently reflect the characteristics of each correction. It is difficult to predict the variation of the carrier phase observable that is included in the RTCM recommendation, so it should be broadcast at a high rate. Transmission of the RS information and the network RTK correction needs to be accompanied by the observable as expressed in Figure 8. As a result, a service provider should assign a bandwidth sufficiently large to contain all the messages in the same epoch because latency is detrimental to the performance.

Figure 8. Network RTK correction broadcasting algorithm.

If a provider wishes to broadcast the observables of nine satellites and MAC information from five auxiliary RSs and to broadcast MAC data at 0·1 Hz, the minimum bandwidth of this system should be 1900 bps. This is assigned 1237 bits for MT1004, 444/390 bits for MT 1016/1015 and 200/165 bits for MT1005/1014. Similarly, we need 1237 bits and 691/200 bits for MT1004 and MT1034/MT1005, respectively, so the bandwidth should accommodate at least 2000 bps in the FKP case. If the system is implemented based on the VRS approach, it needs to utilize 1500 bps.

According to the RTCM documentation recommendations, the RS coordinate information and networking correction do not need to be transmitted to a user every second, whereas raw observables from master RS data should be immediately broadcast at a high rate. During the epoch when messages other than the master RS correction are not being sent there is an inevitable surplus in the data bandwidth.

CPC in a compact RTK transmission can, however, endure several seconds of latency because of its linear variation which is expressed in Figure 9. Predictability deduction from the rate information is a key characteristic of compact RTK use, and it enables the provider to use its own bandwidth very effectively. If the difference between real correction and that predicted from CPRC for a specific satellite are known, the provider can distinguish urgent corrections from others. In this manner it transmits the CPC with a high latency error more frequently, and adaptively delays the broadcasting of other data.

Figure 9. Compact RTK CPC variation.

Compared to the CPC case, in the MAC case the value of the correction remains momentarily stationary in Figure 10, so there is no need to broadcast this information every epoch. It is difficult to recognize any obvious linear variation, so rate information is not used. RTCM recommends broadcasting each 10 s, but as with the compact RTK situation, some corrections are urgently required whereas others are not. Scheduling of the network RTK-related information would be helpful in improving efficiency.

Figure 10. MAC correction variation (left, non-dispersive; right, dispersive).

Based on these approaches, we can construct an adaptive, smart scheduler as in Figure 11. Master and auxiliary RS coordinates are broadcast most infrequently, consequently their message has the highest priority. After such a transmission, we check if any of the network RTK information needs to be transmitted by comparing the currently estimated correction with the last one. Thereafter, if there still remains available data space, we must check which correction needs to be urgently updated. If the MAC or FKP information needs a fast update, we can delay the compact RTK correction broadcast. However, if we do not need to broadcast the network RTK information, we should transmit the CPC as frequently as possible. Therefore we do not need to assign a wide bandwidth and we can make full use of it.

Figure 11. Compact Network RTK correction scheduling scheme.

5. DATA TEST CONSTRUCTION AND RESULTS

5.1. Field test construction

To determine if the suggested algorithm is applicable to real data within the existing protocols, we constructed a test system illustrated in Figure 12. In the same way as the zero-baseline test, PITT CORS RS is the master RS and we chose five auxiliary RSs: Hillsborough (HILB), Asheboro (NCAS), Lillington (NCLI), Fayetteville (NCFA), and RALR. The maximum distance from a master to an auxiliary station was 81 km, and the service area was about 100 km by 100 km. The user was located at Stanford (SNFD) 27 km away from the master RS. Using CORS RINEX data logged at intervals of 1 s we constructed an RS correction generator to encode messages based on the standard format, which were RTCM v.3 MT 1005 (RS information), RTCM v.3 MT 1015 and 1016 (MAC), RTCM v.3 draft MT 1034 (FKP), and MT 131 and 132 (compact RTK). The user decodes the logged correction to apply to its own RINEX observables, and it finally determines its own position. We also introduced a 1-second intentional time delay, so there was little difference from a real-time system.

Figure 12. Real-time data processing system array.

We assumed that the user in the MAC case uses a distance-based linear interpolation method, and that the FKP provider models distance-dependent error as a linear plane. We placed the VRS 500 m away from the user. This modelling is very basic and may be improved to give better performance if a more refined technique is applied to a conventional network RTK.

5.2. Compact RTK with MAC

To check the performance degradation due to a narrow data-bandwidth, we compared the result for our suggested width with that given by 1500 bps. The bandwidth should be broader than 1900 bps when the system utilizes RTCM MT 1004 for the master RS correction without delay, whereas 1500 bps is sufficiently broad for the compact RTK result not to suffer from any latency. In other words the result for 1500 bps compact RTK/1900 bps RTCM as shown in Figure 13 is almost equivalent to that for an unlimited data-link array such as 9600 bps in GSM or GPRS available on the market.

Figure 13. Field test result of compact RTK method+MAC (left, horizontal; right, vertical).

The 2DRMS error of the compact RTK with 700 bps is a horizontal 6·00 cm and a vertical 7·99 cm, and the degradation of position performance caused by the lesser bandwidth is only a horizontal 0·5 mm and a vertical 0·1 mm. It takes 41 s for a Compact Network RTK user to resolve its own measurement ambiguity, which is 11 s longer than a conventional algorithm. The reason why the process time difference in obtaining a fix between these two systems exists is because the system using the low data-link rate needs more time to get full network information. As expressed in Table 4, the ambiguities in both systems are resolved in 10 or 11 s after receiving all the MAC corrections, so we conclude that the compact RTK method with a narrow bandwidth does not detract from the MAC ambiguity resolution performance.

Table 4. Performance of compact RTK method with MAC with a 700 bps data-link.

We examined the latency for each correction, and Figure 14 with Table 5, shows the reason why the Compact Network RTK method can be made available at 700 bps. Most CPC message dissemination at 1500 bps is completed in just 1 s, but the average delay at 700 bps is more than 2 s. Similarly, the latency of the MAC approach at 700 bps is about 15 s on average, which is about three times as much as at 1500 bps with 5·6 s. Some satellite CPC is still useful even after a 7-s latency. The maximum available delay for the MAC application is 30 s or more.

Figure 14. Latency of CPC (1^st row), dispersive correction (2^nd row), and non-dispersive correction (3^rd row) in a compact-MAC RTK case (left, 1500 bps; right, 700 bps).

Table 5. Average and maximum delay of correction messages.

5.3. Compact RTK with FKP

Figures 15–16 and Tables 6–7 are the results from a combination of the compact RTK approach with FKP. The epoch by epoch result is not exactly the same as that derived through the MAC because the FKP had a plane model based on a MAC difference correction, but the total performance and general characteristics are very similar to those seen in the MAC result. The accuracy statistics, which are 5·48 cm (horizontal) and 6·80 cm (vertical), do not differ largely from the MAC case. It takes a shorter time to fix the user position than in the MAC case because the FKP method user needs only one data-set for the network RTK information, i.e., MT 1034, which includes error model coefficients.

Figure 15. Field test result of the compact RTK+FKP method (left, horizontal; right, vertical).

Figure 16. Latency of CPC (1^st row) and FKP correction (2^nd row) in compact RTK+FKP case (left, 1700 bps; right, 600 bps).

Table 6. Performance of compact RTK+FKP method with a 600 bps data-link.

Table 7. Correction delay statistics.

5.4. Compact RTK-based VRS

When considering the time-to-fix performance, the VRS result does not differ from that of the single RS case because it does not need any more information than the CPC. The user can get its own position within 5·43 cm (horizontally) and 6·76 cm (vertically) after 11 s of initialization in both the 500 and 1000 bps test, and there is no performance degradation with the reduced transmission rate. See Table 8.

Table 8. Performance of compact RTK-based VRS in a 500 bps data-link.

6. Advantages of compact rtk

The compact RTK correction can make the MAC technique available in a 700 bps data-link, whereas conventional use indicates at least 1900 bps. The FKP method using an RTCM message type 1004 needs a 2000 bps data rate, but 600 bps is sufficient for it to be operated with the compact RTK. Moreover, using VRS, we can reduce the baud rate from 1400 bps to 500 bps with a slight degradation of accuracy of less than 0·5 mm. The baud rate gain in this case is 59–70%. See Table 9. The temporal decorrelation error reduction when using the compact RTK approach is still useful in a network RTK method application.

Table 9. Baud rate gain by compact network RTK.

Figure 17 shows how the conventional network RTK method can help the compact RTK approach drawback in a single RS-based system. A single RS system requires 288 RSs to cover an area equivalent to that of South Korea. However, only 46 RSs would be sufficient to implement a continuous and homogeneous Compact Network RTK system.

Figure 17. Reduction in number of RSs using a compact network RTK system.

7. Conclusions

In this paper we propose that the compact RTK method suggested for the single RS RTK system is mathematically compatible to all the network RTK solutions such as MAC, VRS, and FKP, which are implemented in many countries. Although the combined correction includes some residual errors which are common or that retain the integer property, the combined method does not let the corrections lose the original character and does not detract from the achieved performance. This theoretical approach has been shown to work through zero-baseline equivalent data processing, and testing using CORS RINEX data.

Compact RTK and conventional network RTK solutions are complementary. Distance-dependent error in the compact RTK correction from a single RS can be reduced by the networking of additional RSs. The compact RTK method is useful in resolving the temporally decorrelated error problem encountered in the network RTK approach. To verify this compatibility, we processed 1 h of RINEX data from the CORS RSs in North Carolina State, with the scenario of a compact RTK correction message sent as alternative to a Type 1004 message with network RTK correction messages following the RTCM-recommended schedule. No matter which network RTK method is applied, the user, located 27 km away from the master RS in a 100 by 100 km region, is able to resolve the ambiguity of its own carrier phase measurement in 10–40 s. It also determines position with a 6–7 cm horizontal and 7–8 cm vertical error (95%) using a data link of only 500–700 bps. The compact RTK correction can make the MAC technique available with a small data link of 700 bps. Conventional methods use at least 1900 bps. The FKP method using an RTCM message type 1004 needs a 2000 bps data rate, but 600 bps is adequate for it to be operated with a compact RTK format. Moreover, we can reduce the baud rate from 1400 bps to 500 bps using a VRS method without severe degradation of accuracy.

Based on the Compact Network RTK protocols, several centimetres to one decimetre accuracy are achievable in a region covering several hundreds of square kilometres with a few RSs using a very small data bandwidth. The derived equations and test results indicate that the compact RTK approach is compatible with all the conventional network RTK solutions no matter which method is used. Furthermore, Compact Network RTK messaging can cut the data rate by 59–70% and the RSs may be reduced by 80%. This universality and efficiency are very important factors when considering which protocol standard, such as the RTCM version 3, should prevail. We consider that the demonstrated compatibility of the Compact Network RTK approach is a substantial basis for it to be considered for incorporation in forthcoming RTK services as a general and efficient standard correction data format.

ACKNOWLEDGMENTS

The study was supported by the second stage of the Brain Korea 21 Project in 2009, SNU-IAMD, Institute of Advanced Aerospace Technology at Seoul National University.

References

REFERENCES

RTCM (2001), Recommended Standards for Differential GNSS (Global Navigation Satellite Systems) Services – Version 2.3, RTCM Standard 10402.3.Google Scholar

RTCM (2006), Recommended Standards for Differential GNSS (Global Navigation Satellite Systems) Service, Version 3.1, RTCM Standard 10403.1.Google Scholar

TRIMBLE TERRASAT GMBH White Paper (2005). “Support of network formats by Trimble GPSNet network RTK solution.”Google Scholar

Dai, L., Han, S., Wang, J., and Rizos, C. (2001). “A study of GPS/GLONASS multiple reference station techniques for precise real-time carrier phase-based positioning.” 14th Int. Tech. Meeting of the Satellite Division of the United States ION, Salt Lake City, Utah, 392–403.Google Scholar

Dorota, A. G. et al. , (2007). Efficiency and reliability of ambiguity resolution in network-based real-time kinematic GPS, Journal of Surveying. Engineering 133(2): 56–65.Google Scholar

Euler, H. J., et al. (2001). “Study of a simplified approach in utilizing information from permanent reference station arrays.” Proceedings of the ION GPS 2001, Salt Lake City, UT, 379–391.Google Scholar

Gianniou, M. (2008). “HEPOS: Modern network-based GPS surveying.” GIS/GPS, 2008, 4–7.Google Scholar

Kee, C., and Kim, J. (2002). “Efficient transmission technique of compact RTK correction messages for low-rate RTK data-link, Proceedings of the ION GPS-2002, Portland Oregon, 1361–1371.Google Scholar

Kee, C., et al. (2004). “Test results of RTK-GPS using low-rate datalink.” Proceedings of the ION 2004 National Technical Meetings, San Diego CA, 462–468.Google Scholar

Kim, J., and Kee, C. (2002). “A proposal of new correction data format for real-time kinematic positioning.” Proceedings of the ION-2002 National Technical Meetings, San Diego CA, 854–862.Google Scholar

Kim, J., and Kee, C. (2004). “RTK-GPS correction generation technique for low-rate data-link.” The Journal of Navigation, 57, 465–477.CrossRef Google Scholar

Kim, J., et al. (2004). “Budget analysis and realization of precise RTK-GPS via compact correction messages applied to commercial GPS receivers.” Proceedings of the ION GNSS-2004, 1460–1467.Google Scholar

Park, B., et al. (2006). “RRC unnecessary for DGPS messages.” IEEE Transactions on Aerospace and Electronic Systems, 42(3), 1149–1160.CrossRef Google Scholar

Park, B. (2008). “A study on reducing temporal and spatial decorrelation effect in GNSS augmentation system: considering of the correction message standardization.” Ph.D. Thesis, Seoul National Univ., Seoul, Korea.Google Scholar

Rizos, C., and Han, S. (2003). Reference station network based RTK. systems–concepts & progress.” Proceedings of 4th International Symposium on GPS/GNSS (CD-ROM), Wuhan, P. R. China.Google Scholar

Takac, F. (2008). “The relationship between network RTK solutions MAC, VRS, PRS, FKP and i-MAX.” Proceedings of the ION GNSS 2008, 16–19 September 2008, Savannah, GA., 348–355.Google Scholar

Wübbena, G., et al. (2001). “RTK networks based on Geo++® GNSMART−concepts, implementation, results.” Proceedings of the ION GPS 2001, Salt Lake City, UT, 369–378.Google Scholar