Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-02-12T07:03:52.291Z Has data issue: false hasContentIssue false
  • English
  • Français

The taming of institutions in economics: the rise and methodology of the ‘new new institutionalism’

Published online by Cambridge University Press:  23 October 2009

PETER SPIEGLER  and
WILLIAM MILBERG
PETER SPIEGLER*
Affiliation:
University of Massachusetts, Boston, MA, USA
WILLIAM MILBERG
Affiliation:
New School for Social Research, New York, NY, USA
*
*Correspondence to: Peter Spiegler, University of Massachusetts-Boston, 100 Morrissey Blvd., Boston, MA 02125, USA. Email: peter.spiegler@umb.edu.
Rights & Permissions [Opens in a new window]

Abstract:

We examine the origin and methodology of a ‘New New Institutional Economics’ (NNIE) – an emerging research agenda distinguished by its attempt to account for the role of institutions in complex socio-economic change by formally modeling institutions as the background conditions to parameterized cost–benefit calculations. The NNIE expands the application of economic modeling tools to new areas of inquiry, models institutional outcomes with parsimony and mathematical rigor, and introduces political and economic power, thereby allowing for consideration of institutional change that is not Pareto improving. Using a four-part analytical framework, we find that the explanatory power of NNIE analysis derives not from its formal models, but from a more vague, nuanced, and narrative version of the formal models, which we call ‘Quasi-Models’. We find that the NNIE's formal models are too parsimonious to meaningfully illuminate the complex institutions they ostensibly represent.

Type
Research Article
Information
Journal of Institutional Economics , Volume 5 , Issue 3 , December 2009 , pp. 289 - 313
Copyright
Copyright © The JOIE Foundation 2009

1. Introduction

Economics has rediscovered the importance of ‘institutions’. Hodgson (Reference Hodgson2007: 7), for example, writing about the economics profession, notes that ‘evolutionary ideas and the study of institutions are now commonplace. Previously the longstanding preserve of mavericks and dissidents, such ideas are now fashionable.’ Rodrik et al. (Reference Rodrik, Subramanian and Trebbi2004) argue that ‘institutions rule’ over geography and trade openness in the determination of national income levels across a large sample of countries over a long period of time. In this paper we explore some implications of this new found interest in institutions for the economic theory of institutions.

Our focus is the ambitious new approach to institutional economics in the work of Daron Acemoglu, James Robinson, Andrei Shleifer, Edward Glaeser, and others.Footnote 1 They use highly parsimonious formal models to capture the central role of institutions in the explanation of various grand historical changes in power, politics, and long-term economic trends, including, among others, the success and failure of democratization, the rise of the American regulatory state, and the prospects for the realization of Immanuel Kant's state of perpetual peace. The work has appeared in the top journals of the profession and in the books of its top university presses, but has received little attention within the institutional economics literature for its achievements.Footnote 2 This lack of recognition should not be interpreted as evidence that the work is not properly categorized as ‘institutional economics’. Its practitioners are using economic methodology to investigate the role of socio-politico-economic institutions in economic activity and thus their work falls, undeniably, on the turf of institutional economics. It is important for institutional economists to become familiar with this work, assess its merits, and consider its relationship to existing strains of institutional economics.

This paper offers an overview and methodological assessment of this work, which we refer to as the ‘New New Institutional Economics’ or NNIE. We find that although the NNIE has built upon and extended the work of the old and new institutional economics in important ways, it has, at the same time, set back economists’ understanding of institutions by overstating the applicability of its models. Specifically, we find that the NNIE has contributed to institutional economics by: (1) expanding the application of economic modeling tools to new areas of inquiry; (2) insisting on parsimonious and rigorous formal models of institutional outcomes; and (3) introducing the role of (political and economic) power to the study of the determination of institutions, thereby allowing for consideration of institutional change that is not Pareto improving.

While making these important contributions to positive political economy and institutional economics, however, we find that the NNIE's formal models are too parsimonious to meaningfully illuminate the complex institutions they ostensibly represent. The explanatory power of NNIE analyses ultimately comes not from its formal models, then, but rather from more vague, nuanced, and narrative versions of the formal models which we call ‘Quasi-Models’ – essentially rough, ordinary-language articulations of what the pure model is meant to represent. The formal and Quasi-Models are meant to be different articulations of the same underlying model, but close examination shows that it is only the Quasi-Model that is used for analysis, interpretation, and testing. We present a framework for isolating the formal model from the Quasi-Model and show that the correspondence between the two is loose and that the untethered nature of the Quasi-Model renders it inadequate as a source of rigorous conjecture.

Perhaps most importantly, the claim that the formal models of the NNIE are its true analytic engine leads to unwarranted and erroneous conclusions about institutions. The formal models represent institutions as mere background conditions to decision making, whose effects on outcomes are determined by exogenously determined parameter values. This representation of institutions amounts not to investigating them but taming them – making them safe for economic analysis by converting them into something that fits into a world of constrained optimization problems. If it is the case, as we argue below, that the NNIE's formal models do not and cannot generate the insight contained in NNIE work, then this taming of institutions is an unhelpful distraction.

This paper has four sections. In Section 2, we discuss the theoretical conditions for the emergence of the NNIE, emphasizing the breakdown of general equilibrium economics and the abandonment of traditional criteria of robustness in the determination of advances in economic knowledge. In Section 3, we provide a close reading and critique of some NNIE work, using a four-part framework to assess the aptness and efficacy of the NNIE's modeling methodology. Section 4 concludes with a comparison of the NNIE conception of institutions with that found in the old and new institutionalism, showing that the NNIE offers greater precision of modeling but less descriptive power and greater ambiguity in its implied conjectures.

2. The re-emergence of institutions in economic thought

The 1970s saw the economics profession move away from its longstanding concern with the robustness of its model of a competitive, private enterprise economy. In part, this move was prompted by the inability to prove the uniqueness and stability of general equilibrium (GE). But more than this, it ultimately was the aridity of the GE approach – i.e., its insulation from institutional and historical detail – that brought a degree of self-questioning and rethinking.Footnote 3 As the limited applicability of GE was becoming more apparent to economists, a small, internal response began to form. A ‘New Economics’ arose in a series of sub-fields in the profession, including international economics, labor economics, industrial organization, and macroeconomics. These new approaches all sought greater relevance, and had some common features across sub-fields, including an emphasis on imperfect market competition (rather than perfect competition), on asymmetric information (rather than symmetric information), on increasing returns to scale technology (rather than constant returns to scale), or on strategic behavior by firms and governments (as opposed to optimization independent of rival behavior). This greater relevance, however, was bought at the expense of robustness and generality, with New Economics’ models generating results that were more contingent, explosive, and path dependent than those produced in the era of GE analysis. In fact, some complained that the models were ad hoc and could be used to model any pre-determined outcome (Solow, Reference Solow1997). Moreover, results were not only not unique – multiple equilibria were now the norm rather than the exception – they were not robust; that is, the results were highly sensitive to the choice of assumptions, parameter values, and functional forms.Footnote 4

In the era of competitive general equilibrium analysis, an economic model was understood to generate new knowledge if it provided a proof of a known result, but required weaker, i.e. more general, assumptions than did existing proofs of the same result. The great strength of this methodology was the clarity of its criterion for establishing the progress of knowledge – increased mathematical generality, or robustness, of its proofs. In the era of the New Economics, robustness was abandoned as a methodological ideal.Footnote 5

In the context of this New Economics, institutions emerged as a focus of research for at least two reasons. One was that the New Economics’ modeling methodology allowed more freedom in taking up a broad set of issues not traditionally considered within the scope of economic inquiry. Second, with the New Economics’ lack of consensus over the preferred model and model assumptions, and its abandonment of the traditional criteria (i.e. robustness and generality) for judging the progress of economic knowledge, ‘institutions’ were frequently called upon as the important missing explanatory factor of economic life.

This rediscovery of the importance of institutions is one of the most substantive ideas to emerge from the churning in economic thought over the past 25 years, in contrast to many other recent innovations in economics – such as complexity theory, agent-based modeling, experimentalism – which are largely technical advances rather than new conceptions of how an economy functions. Today it is standard practice in the study of economic growth and economic development to introduce institutions to the explanation of outcomes (see Barro, Reference Barro1997; Rodrik et al., Reference Rodrik, Subramanian and Trebbi2004). And with institutions now more squarely within the confines of economics, the scope of inquiry has broadened significantly to include such issues as culture (Guiso et al., Reference Guiso, Sapienza and Zingales2006), religion (McLeary and Barro, 2006), politics (Rodrik et al., Reference Rodrik, Subramanian and Trebbi2004), and the sociology of business (Langlois, Reference Langlois2003). This enhanced view of the importance of institutions in these contexts is recognized by both neoclassical and non-neoclassical economists (see, for example, Barro, Reference Barro1997; Chang, Reference Chang2007).

Perhaps the most ambitious effort to integrate institutions into contemporary economics is that of the New New Institutional Economists – a group that has sought, along the lines of much of the New Economics, to provide rational choice foundations for historical and market changes, with institutions as background conditions for rational, strategic decision-making.

While the NNIE, like any body of literature, is a varied set, its work shares some salient characteristics to an extent that we believe warrants grouping it as a new form of institutional economics. Specifically, work in the NNIE is characterized by two constitutive characteristics: (1) a stated concern with explaining the origin, dynamics, and/or economic implications of complex socio-politico-economic institutions; and (2) the use of hyper-reductive mathematical models to represent these institutions as a means of explaining them.Footnote 6 The NNIE authors are for the most part concerned with socially, politically, and historically significant institutions – the kinds of institutions that both the academic insider and the layperson would likely consider ‘important’ and not necessarily the kind of target generally associated with economic analysis. This, in fact, is the allure of this work: it aims to tackle big, important issues. The titles of its papers make a point of advertising this. They are short, ambitious, and often sound more like the titles of lengthy political economy treatises than of short economics’ journal articles: ‘The Rise of the Regulatory State’, ‘The Dynamics of Political Compromise’, ‘Persuasion in Politics’, ‘Social Culture and Economic Performance’, ‘The Politician and the Judge: Accountability in Government’, ‘War and Democracy’.Footnote 7 There is, also, at least one major book-length contribution to this literature: Acemoglu and Robinson's (Reference Acemoglu and Robinson2006) Economic Origins of Dictatorship and Democracy, which intentionally recalls Moore's (Reference Moore1966) influential sociological treatise.

It is the interaction of the two characteristics, though, that gives rise to both the promise and the peril of the NNIE approach. The prospect of adequately understanding highly complex social phenomena without needing to delve into all of their particularities and context-dependency has been a major (if not the major) selling point of economics since the marginalist revolution of the late nineteenth century.Footnote 8 The NNIE is perhaps the most audacious example of this approach. We turn now to a detailed examination of the methodology of the NNIE to determine how well it is able to overcome this peril and to deliver on its substantial promise.

3. NNIE methodology: a four-part framework of analysis

NNIE analyses seek to explain and understand institutions by representing those institutions with hyper-reductive mathematical models, and positing the dynamics of those models as the underlying dynamics driving the institutions as well. The attraction and promise of this approach is that it not only provides illumination of apparently puzzling and complex institutions, but also that it does so using models that are parsimonious and formal (and therefore simple and entirely devoid of vagueness). Because of this ideal combination of illumination and parsimony, the NNIE is presented by its practitioners as an advance over previous versions of institutional economics.

Although straightforward in conception, the precise workings of this explanatory methodology are complicated. In order to critically assess the methodology, we must first explicate it clearly. To do so, it will be helpful to present a methodological framework – which we call the ‘Four-Part Framework’ or ‘FPF’ – that clearly delineates the path taken by NNIE work. As noted above, NNIE work illuminates its subject matter using formal models. As such, whatever else they include in their analyses, NNIE practitioners will need to introduce their subject matter, introduce the model that will represent the subject matter, solve the model, and then explain the manner in which the model's solution dynamics address the initial research question. The FPF summarizes this process by breaking it into four distinct but related phases;Footnote 9 namely:

  1. 1. Delimiting, in which the set of social phenomena under study is specified and a research question is formed.

  2. 2. Naming, in which a mathematical construct meant to be analogous to the social phenomena is introduced, along with a ‘catalog of correspondences’ which links elements of the construct with elements of the phenomena under study.

  3. 3. Solution, in which the mathematical construct is brought to a solution.

  4. 4. Interpretation, in which the mathematical solution and its implications are interpreted with respect to the research question. Empirical testing of the interpretation is also a part of this phase.Footnote 10

In addition to delineating the four phases of the analysis, the FPF also highlights an important divide in the analysis – i.e. the divide between the realm of ordinary language descriptions (the language of ordinary usage and linguistic convention) and mathematical language descriptions. NNIE analyses must twice cross this divide. At the outset, their research question will be phrased in ordinary language. (And this is not arbitrary or incidental: NNIE analyses are meant to unravel complexities of the world-as-we-encounter-it, and description of that world must, in the first instance, be done on its own terms.) The mathematical model, however, will be articulated and manipulated using mathematical language. And in the final stage of the analysis, when the initial research question is answered, ordinary language will again be used. Figure 1 summarizes the FPF in graphical form.

Figure 1. The four-part framework

To illustrate this process at work in an NNIE analysis, we turn to a few exemplary works. We will focus primarily on Acemoglu and Robinson's book Economic Origins of Dictatorship and Democracy (Reference Acemoglu and Robinson2006), and secondarily on Glaeser and Shleifer's ‘The Rise of the Regulatory State’ (Reference Glaeser and Shleifer2003), and Maskin and Tirole's ‘The Politician and the Judge: Accountability in Government’ (Reference Maskin and Tirole2004).

Delimiting

The Delimiting phase of Acemoglu and Robinson (Reference Acemoglu and Robinson2006) includes statements in ordinary language about the authors’ target subject matter and the particular puzzles they will seek to illuminate. In keeping with the tenor of NNIE work, their research questions are broad and ambitious: ‘Why is it that some countries are democracies, where there are regular and free elections and politicians are accountable to citizens, whereas other countries are not?’ (Acemoglu and Robinson, Reference Acemoglu and Robinson2006: xi). Specific questions that the authors see as falling under this general rubric include: ‘What determines whether a country is a democracy? Which factors can explain the patterns of democratization we observe? Why did the United States attain universal male suffrage more than a century before many Latin American countries? Why, once created, did democracy persist and consolidate in some countries, such as Britain, Sweden, and the United States, and collapse in others, such as Argentina, Brazil, and Chile?’ (Acemoglu and Robinson, Reference Acemoglu and Robinson2006: xii) Again, these questions are phrased in ordinary language, and are meant to bring to mind the delimited social phenomena – countries, democracy, elections, citizens, etc. – as we actually encounter them, embedded in their social context.

We also find Delimiting phase statements, targeting large, complex institutions in ordinary language in Glaeser and Shleifer (Reference Glaeser and Shleifer2003) and Maskin and Tirole (Reference Maskin and Tirole2004). Glaeser and Shleifer (Reference Glaeser and Shleifer2003) delimit the set of phenomena associated with the various regulatory regimes and corporate liability laws before and during the Progressive Era in America as their target phenomena. Articulating the main aim of their paper, they state: ‘we attempt to understand why these changes occurred in the United States between 1887 and 1917’ (Glaeser and Shleifer, Reference Glaeser and Shleifer2003: 401). Maskin and Tirole (Reference Maskin and Tirole2004) delimit the set of phenomena associated with accountability in representative democratic government. ‘The premise behind democracy’, they write, ‘is that public decisions should reflect the will of the people. But in most democracies, comparatively few decisions are made directly by the public. More often, the power to decide is delegated to representatives. . . . But if representatives decide for the public, what induces them to act in the public interest?’ (Maskin and Tirole, Reference Maskin and Tirole2004: 1034–5).

Naming

The Naming phase of NNIE analysis involves connecting the delimited social phenomena to a formal model. This typically involves at least two stages. First, the structure of the model is described informally using the ordinary language names of the phenomena under study. The following passage from Acemoglu and Robinson (Reference Acemoglu and Robinson2006) is an example of this stage:

To starkly illustrate our framework, consider a society in which there are two groups: an elite and the citizens. Nondemocracy is rule by the elite; democracy is rule by the more numerous groups who constitute the majority – in this case the citizens. In nondemocracy, the elite get [sic] the policies it wants; in democracy, the citizens have more power to get what they want. Because the elite loses under democracy, it naturally has an incentive to oppose or subvert it; yet, most democracies arise when they are created by the elite. (Acemoglu and Robinson, Reference Acemoglu and Robinson2006: xii)

This statement combines elements of the formal model and the socially understood phenomena under study. The authors use terms that invoke social experience – for example society, democracy, non-democracy, elite, citizens, policies, power, etc. – but they also gesture toward a structure that belongs to the world of the formal model they will later introduce. Significantly, although the authors will ultimately want to claim that this structure also represents the causal dynamics underlying the delimited social phenomena, that claim is still conjectural in statements such as the one quoted above. Put succinctly: presentations of the structure of the model using ordinary language terms are necessarily conjectures until and unless an argument is made establishing the truth value of the conjecture.

We see such informal, ordinary-language descriptions of model structure in Glaeser and Shleifer (Reference Glaeser and Shleifer2003) and Maskin and Tirole (Reference Maskin and Tirole2004) as well. Glaeser and Shleifer (Reference Glaeser and Shleifer2003) offer the following description:

we develop a theory of law enforcement in which private litigation, government regulation, a combination of the two, and doing nothing are considered as alternative institutional arrangements to secure property rights. In our theory, whatever law enforcement strategy the society chooses, private individuals will seek to subvert its workings to benefit themselves. The efficiency of alternative institutional arrangements depends in part on their vulnerability to such subversion. (Glaeser and Shleifer, Reference Glaeser and Shleifer2003: 401)

And Maskin and Tirole (Reference Maskin and Tirole2004) offer the following informal description of (a portion of) their model's structure:

we set out a two-period model with a homogeneous electorate. In each period, there is a decision to be made between two possible actions. One action is ‘popular’ in the sense that the electorate believes it to be optimal with better than fair odds. The electorate will either decide for itself (direct democracy) or delegate the decision to an official, who knows which action is optimal. Each official is either congruent (i.e., she has the same preferences as the electorate) or noncongruent with society, although ex ante the electorate does not know which case holds. She also places some weight on holding office for its own sake. (Maskin and Tirole, Reference Maskin and Tirole2004: 1036)

As with the similar statement from Acemoglu and Robinson (Reference Acemoglu and Robinson2006) above, both of these statements are meant to (a) introduce the structure of the model, but (b) in a way that is intended to get the reader used to the idea that the model's structure is also a possible structure for the social phenomena described in the Delimiting phase, while (c) not yet submitting that conjecture to a test in order to support its validity.

In the second stage of the Naming phase, the structure of the model is formalized. Specifically, during this phase the authors provide mathematical analogues of the phenomena under study, formal definitions of these mathematical analogues, and a solution concept for the model described by this collection of new mathematical objects and rules. The full version of the model ultimately used in Acemoglu and Robinson (Reference Acemoglu and Robinson2006) has many parts – too many to present in full here. We can, though, provide a few illustrative elements of the model and the authors’ presentation of these elements as formal analogues of various elements of the delimited social phenomena. The following passage provides mathematical analogues to the social concepts of income, distribution, distributional conflict, and inequality:

Consider . . . a society consisting of two types of individuals: the rich with fixed income yr and the poor with income yp < yr. To economize on notation, total population is normalized to 1; a fraction 1 − δ > 1/2 of the agents is poor, with income yp; and the remaining fraction δ is rich with income yr. Mean income is denoted by $\bar y$. Our focus is on distributional conflict, so it is important to parameterize inequality. To do so, we introduce the notation θ as the share of income accruing to the rich; hence, we have:

\begin{equation} y^p = \frac{{({1 - \theta})\bar{y}}}{{1 - \delta}}\quad {\rm and}\quad y^r = \frac{{\theta \bar{y}}}{\delta}\end{equation}\kern-3pt

Notice that an increase in θ represents an increase in inequality. Of course, we need $y^p < \bar{y} < y^r $, which requires that:

\begin{equation} \frac{(1 - \theta)\bar{y}}{1-\delta} \textless \frac{{\theta \bar{y}}}{\delta}\quad {\rm or}\quad \theta \textgreater \delta .\, ({\rm Acemoglu}\,{\rm and}\,{\rm Robinson},\,2006:\,104)\end{equation}

By the end of the Naming phase, then, we have three articulations of the phenomena under study:

  1. (1) the ordinary language articulation: an articulation in ordinary language, whose referents are the phenomena of interest in their socially embedded context;

  2. (2) the pure model: an articulation in mathematical language, whose referents are mathematical objects whose nature and dynamics are formally defined (and therefore complete and unambiguous) – the claim that this articulation is a representation of the phenomena of interest is still a conjecture at this point;

  3. (3) a hybrid articulation, which we will call the ‘Quasi-Model’, that expresses the structure of the model informally, using the ordinary language names of the phenomena of interest – this articulation is an embodiment of the conjecture that the model's structure represents the phenomena of interest, as it places those phenomena within that structure. The referents of the Quasi-Model are ambiguous, with authors implying sometimes that its terms refer to the socially embedded phenomena and sometimes to the mathematical analogues. Table 1 summarizes the Naming phase elements of the statement quoted above in a ‘Catalog of correspondences’ between the social phenomena and the formal model.

Table 1. ‘Catalog of correspondences’ of Acemoglu and Robinson (Reference Acemoglu and Robinson2006)

This is just an example of a part of the ‘Catalog of correspondences’. The full version of the ‘Catalog of correspondences’ would also include the rules and relations that compose the solution concept. In this case, the model is solved using game theory, and the solution concept is Nash equilibrium (specifically, either subgame perfect Nash equilibrium or Markov perfect equilibrium, depending upon the version of the model). Appendix 1 depicts the simplest version of Acemoglu and Robinson's (Reference Acemoglu and Robinson2006) pure model of democratization.

Glaeser and Shleifer (Reference Glaeser and Shleifer2003) and Maskin and Tirole (Reference Maskin and Tirole2004) also introduce the formal version of their model in the manner reviewed above. For the sake of brevity, we will include here just a summary version of portions of their ‘Catalog of correspondences’ (see Table 2).

Table 2. ‘Catalog of correspondences’ of Glaeser and Shleifer (Reference Glaeser and Shleifer2003) and Maskin and Tirole (Reference Maskin and Tirole2004)

Solution

The Solution phase is the most straightforward of the phases, as it resides purely in the mathematical realm and involves only the working out of the mathematical model according to the formal definitions and solution concept specified in the Naming phase. As long as the model has been appropriately (mathematically speaking) articulated, then either a solution (or solutions) exists, a solution does not exist, or it is not possible to determine whether or not a solution exists. In the case of Acemoglu and Robinson (Reference Acemoglu and Robinson2006), the Solution phase consists of articulating subgame perfect Nash or Markov perfect equilibria for their extensive form game. For both Glaeser and Shleifer (Reference Glaeser and Shleifer2003) and Maskin and Tirole (Reference Maskin and Tirole2004) it involves solving objective-maximization problems under different parameter values, and ranking the desirability of each of these solutions according to formally defined criteria.

Rather than simply reporting the solution in purely mathematical terms – i.e. as a set of statements that is immediately either true, false, or undecidable, depending entirely and only on the formal definitions given in the paper and the relevant rules of mathematics – solutions may be reported with ordinary language names substituted for the mathematical names of the objects. This is a conflation of the Solution phase and the Interpretation phase. It amounts to reporting as a solution something that is a conjecture (i.e. the conjecture that the solution to the mathematical model also represents a solution to the social puzzle articulated in the Delimiting phase) rather than a true (i.e. internally consistent) mathematical statement.

Proposition 6.1 (from Acemoglu and Robinson, Reference Acemoglu and Robinson2006), is an example of such a hybrid form of solution presentation. We have added boldface to the ordinary language terms to emphasize this. (Note that μ is a parameter meant to measure ‘the material cost of revolution’, and that θ is the share of income going to the ‘rich’):Footnote 11

Proposition 6.1:There is a unique subgame perfect equilibrium $\left\{{\tilde \sigma ^r, \tilde \sigma ^p} \right\}$in the game described in Figure 6.1, and it is such that:

  • • If θ ≤ μ, then the revolution constraint does not bind and the elites can stay in power without democratizing or redistributing income.

  • • If θ > μ, then the revolution constraint binds. In addition, let μ* be defined by (6.6). Then:

    1. (1) If μ ≥ μ*, the elites do not democratize and set the tax rate $\hat \tau $to redistribute enough income to avoid a revolution.

    2. (2) If μ<μ* and (6.7) holds, concessions are insufficient to avoid a revolution and the elites democratize.

    3. (3) If μ < μ* and (6.7) does not hold, there is a revolution.

(Acemoglu and Robinson, Reference Acemoglu and Robinson2006: 185, emphasis added)

As noted above, this way of presenting the solution involves both mathematical and ordinary language terms. A purely mathematical presentation of the solution would look like this:

Proposition 6.1.1There is a unique subgame perfect equilibrium $\{{\tilde \sigma ^r, \tilde \sigma ^p} \}$in the game described in Figure 6.1, and it is such that:

  • • If θ ≤ μ, then the actions of Agent 1 include τ1, 1 = τ1, 2 = 0; φ = B

  • • If θ > μ, then, with μ* defined by (6.6):

    1. (1) If μ ≥ μ*, then the actions of Agent 1 include φ = B, $\tau _{1,1} = \hat \tau $. The actions of Agent 2 include ρ = β.

    2. (2) If μ < μ* and (6.7) holds, the actions of Agent 1 include φ = A.

    3. (3) If μ < μ* and (6.7) does not hold, the actions of Agent 2 include ρ = α.

Proposition 6.1.1, which does not appear in Acemoglu and Robinson (Reference Acemoglu and Robinson2006), can be assessed solely against the definitions of the model and the relevant rules of mathematics. On this basis, it is a true (i.e. internally consistent) statement, and one that has no necessary connection to the phenomena under study. Unlike Proposition 6.1, it is not a conjecture.Footnote 12

Glaeser and Shleifer (Reference Glaeser and Shleifer2003) also present their results in hybrid form. The following is an excerpt from their Solution phase (with emphasis added to ordinary language terms) demonstrating this hybrid form. (Supplementary definitions are provided in Appendix 2.)

Proposition 1. If Pα < P1, then:

for $\frac{X}{S} < \frac{C}{p}$, the only feasible option is laissez faire;

for $\frac{C}{p} < \frac{X}{S} < \frac{C}{{P_1}}$, regulation dominates laissez faire if $D > \frac{C}{{\left({1 - \pi _\&#x03B1;} \right)\left({P_1 - P_2} \right)}}$, and

vice versa if this condition does not hold;

for $\frac{C}{p} < \frac{X}{S} < \frac{C}{{P_1 - P_2}}$, negligence achieves first-best; and

for $\frac{X}{S} > \frac{C}{{P_1 - P_2}}$, both negligence and strict liability achieve first-best.

(Glaeser and Shleifer, Reference Glaeser and Shleifer2003: 410)

This is a hybrid statement because it reports a mathematical result using the ordinary language terms ‘laissez faire’, ‘regulation’, ‘negligence’, and ‘strict liability’ – terms that refer to actual social institutional arrangements, but also have mathematical representations in the paper (Glaeser and Shleifer, Reference Glaeser and Shleifer2003: 409–410). The statement above would be unobjectionably true (i.e. internally consistent) if it referred only to the purely mathematical elements of the ‘Catalog of correspondences’. As it is written, however, Proposition 1 (like Acemoglu and Robinson's, Reference Acemoglu and Robinson2006, Proposition 6.1) is a conjecture whose truth value has not yet been established or even probed.Footnote 13

Interpretation

The Interpretation phase of NNIE analysis involves interpreting the solution of the model as a solution to the puzzle articulated in the Delimiting phase, and, if there is an empirical element to the paper, providing empirical support for this interpretation. The interpretation is generally presented through hybrid statements that are very close to the explicit expression of the Pure Model solution – i.e. by articulating the solution to the Pure Model with ordinary language terms substituted for their mathematical counterparts. For example, Acemoglu and Robinson's (Reference Acemoglu and Robinson2006) Proposition 6.1 above – which replaces some of the Pure Model's mathematical names with ordinary language ones – is really a part of the Interpretation phase, whereas Proposition 6.1.1 is the Solution phase statement underlying it.

The justification for the interpretation is generally offered in one or both of two ways: (1) by comparing Quasi-Model statements to historical experience – i.e. by re-describing an episode of current or historical experience as conforming roughly to the structure of the model, and/or (2) through quantitative/graphical presentation of statistical relationships that, it is claimed, were predicted by the model.Footnote 14 It is in this stage that the problems inherent in NNIE methodology become apparent. As implemented in current NNIE work, neither of these two strategies provides justification for the claims that the parsimonious formal models employed to explain complex institutional dynamics actually do so. In the remainder of this section, we will explain why the problems with these justificatory strategies undermine the claims of the NNIE regarding the efficacy and power of its methods.

The central problem with the first strategy is that, whereas historical experience is matched with some version of the model, it is not matched with the version of the model that is presented as the analytical engine of the work. Specifically, it is the Quasi-Model against which the experience is assessed rather than the Pure Model. As such, the most that this strategy could do is provide support for the claim that the Quasi-Model – a vague and informal statement of the structure of the Pure Model – is not inconsistent with historical experience. This may be helpful, but it is far short of the heroic claims of the NNIE.Footnote 15 Further, and perhaps most importantly, NNIE Quasi-Models are, in general, incapable of generating falsifiable hypotheses. As such, any work that depends on ‘tests’ of these hypotheses for justification of its Pure Model would not meet the criteria of ‘science’ in the Popperian sense.

This problem generally manifests itself in NNIE work through the adducing of evidence in a manner that is too nuanced, vague, or imprecise to correspond to the Pure Model (but that is well suited to correspond to the Quasi-Model). A good example of this problem can be found in Acemoglu and Robinson's (Reference Acemoglu and Robinson2006) testing of their model's ability to explain the process of democratization in Britain in the nineteenth and twentieth centuries. A portion of the claim being tested is that their model explains the relationship between democratization and the cost of revolution. Specifically, the authors claim that the relationship between the parameter μ and the equilibrium strategy of ‘elites’ (i.e. Agent 1 in the game in Appendix 1) matches the relationship between the cost of revolution and democratization in British history.Footnote 16 The following passage is presented as empirical evidence in favor of their model:

Beginning in 1832, the British political elites made a series of strategic concessions aimed at incorporating the previously disenfranchised into politics because the alternative was seen to be social unrest, chaos, and possibly revolution. The concessions were gradual because in 1832 social peace could be purchased by buying off the middle class. . . . Later, as the working classes reorganized through the Chartist movement and subsequently through trade unions, further concessions had to be made. The Great War and its fallout sealed the final offer of full democracy. (Acemoglu and Robinson, Reference Acemoglu and Robinson2006: 350–351)

The implication is that this series of events corresponds to the value of μ beginning low, and then rising in a manner that changes the equilibrium strategies of the players. As the value of μ increases, Agent 1's equilibrium strategy changes to include the action φ = A;Footnote 17 and, similarly, as circumstances in England changed to make mass organization less costly, the elite ultimately realized that their best choice was to offer democratizing reforms.

But the claim that this match between the historical fact pattern and the structure of the model constitutes a test of the Pure Model is not borne out. In fact, under closer scrutiny, one finds that the Pure Model is not involved in any important way in this test. While it may be true that the historical fact pattern shares with the Pure Model the one descriptive characteristic mentioned above (i.e. an increase in μ correlates with φ = A becoming part of an equilibrium strategy, just as an increase in the ‘cost of revolution’ correlates with democratization), there are many other characteristics of the Pure Model that are suppressed in this passage, that are not shared by the historical experience, and that are necessary parts of the Pure Model. For example, consider μ. In addition to having the feature that its level affects equilibrium strategies, it also has the following characteristics (among others): (1) it is one-dimensional; (2) its meaning is unambiguous and constant throughout the model; (3) it affects equilibrium strategies only in formally defined, determinate ways; (4) it is (and must be) capable of being held constant while the values of other elements of the model vary, and it is (and must be) capable of varying while the values of other elements of the model are held constant. Not all of these characteristics are constitutive of μ. For example, μ could be multi-dimensional. But characteristics (2), (3), and (4) are constitutive. The model would not be capable of the necessary manipulations if μ (and other elements) did not have these characteristics. In addition, all of the precision of the conclusions drawn from the model depend on elements like these. Yet none of these characteristics is shared by the elements of Britain's history that are meant to be analogous to μ. More importantly, it is difficult even to meaningfully conceptualize many of these historical elements as possessing such characteristics. As such, the historical fact pattern referenced above cannot be considered to be data for a test of the Pure Model as a representation of political dynamics. This is why the comparison is done not with the actual elements of the Pure Model, but rather with more nuanced and ambiguous versions of them, i.e. the Quasi-Model.

The same critique applies to Glaeser and Shleifer (Reference Glaeser and Shleifer2003). They also employ the first justificatory strategy in support of the insight-generating power of their Pure Model. The following statement is indicative:

We can use [our model] to understand the rise of regulation in the United States at the end of the nineteenth and the beginning of the twentieth centuries. Our interpretation is that ‘S’ – the scale of economic activity – rose dramatically over the nineteenth century. During the industrial revolution, firms grew sharply in size. The social costs of harm grew roughly proportionately, but the costs of subverting justice did not. As a result, a legal system that may have operated well during the agrarian period failed when faced with entities that had huge incentives to subvert it both legally and illegally. Because higher levels of S lead to subversion of both strict liability and negligence, adding regulation was the efficient response. (Glaeser and Shleifer, Reference Glaeser and Shleifer2003: 413)

The implication is that the growth of the scale of firms throughout the nineteenth century in the United States and the contemporaneous growth of industrial regulation correspond to the diminution of the statistic $\frac{X}{S}$ that occurs when S increases while all else (except D) is held equal. More generally, the authors suggest that the fact pattern of American regulatory history in the nineteenth and early twentieth centuries matches the relationship between the variables X, S, and D and the formal definitions of ‘laissez faire’, ‘strict liability’, ‘negligence’, and ‘regulation’. They further suggest that this matching counts as support for the aptness of the model and its ability to illuminate the actual causal mechanisms underlying American regulatory history of this period.

But this claim is unsupported, for precisely the same reason that the similar claim from Acemoglu and Robinson (Reference Acemoglu and Robinson2006) reviewed above was ultimately unsupported. Specifically, although the fact pattern of American regulatory history in this period can be redescribed in a manner that highlights certain characteristics and dynamics that are also among the characteristics and dynamics of the formal model, it is also true that the formal model contains many constitutive characteristics that are not and cannot be shared by the elements of historical experience adduced as empirical evidence. Again, as with Acemoglu and Robinson (Reference Acemoglu and Robinson2006), this is precisely why the authors actually deploy not the Pure Model but rather the Quasi-Model in their comparisons with historical experience. And while it may be true that the Quasi-Model matches well with historical experience, this is far short of what Glaeser and Shleifer (Reference Glaeser and Shleifer2003) claim.

One might argue that the foregoing critique of the first justificatory method rests on an overly rigid interpretation of the requirements of a ‘test’ of the Pure Model. But we would argue that, on the contrary, it is the NNIE's Pure Models themselves that are overly rigid. Both Acemoglu and Robinson (Reference Acemoglu and Robinson2006) and Glaeser and Shleifer (Reference Glaeser and Shleifer2003), in the end, abandon the Pure Model for precisely this reason, and test an informal version of it that is a much more plausible representation of the phenomena under study.

Specifically, in the case of Acemoglu and Robinson (Reference Acemoglu and Robinson2006), what their test ultimately amounts to is a judgment regarding whether or not a decrease in the ‘cost of revolution’/‘difficulty of overcoming the collective action problem’ has been followed in historical experience by moves toward democratization. But these categories are miles away from the precise, formally defined μ and φ = A of the Pure Model. To test the predictive power of a model with such precise categories, we would need, at the very least, to construct an equally precise, numerical index of the social phenomena ostensibly being represented: a real-number-valued variable representing the ‘cost of revolution’/‘difficulty of overcoming the collective action problem’ and a real-number-valued variable representing the level of democratization.Footnote 18 Instead, the authors engage in an ordinary language discussion of their judgments and interpretations of the relationship between the cost of revolution and level of democratization. The result is not a ‘test’ in the Popperian sense – i.e. a moment of truth, in which falsification is possible – but rather merely a redescription of events in a new vocabulary.

The second justificatory strategy – i.e. the quantitative/graphical presentation of statistical relationships that, it is claimed, were predicted by the model – encounters similar difficulties. Put briefly, the problem is that the relationship between the Pure Model's elements and the statistics that supposedly represent them in the quantitative/graphical representations is generally at least tenuous and at most implausible. For example, Acemoglu and Robinson (Reference Acemoglu and Robinson2006) offer the following connection between the predictions of their model and a scatter diagram (Figure 3.13 in their text) of an index of level of democracy in various countries versus the labor share of income in these countries:

[O]ur approach to democracy emphasizes the role of social conflict, especially between different groups. One implication of this approach is that inter-group inequality should have an effect on the equilibrium of political institutions and thus on the likelihood that a society ends up as a democracy. The problem, however, is that the relevant notion of inter-group inequality is often difficult to measure (for example, when it is between two different ethnic groups). Nevertheless, when the major conflict is between the rich and the poor, one variable that captures inter-group inequality is the share of labor income in GDP.

. . . Figure[] 3.13 . . . show[s] the relationship between the labor share in the 1990s and the relevant democracy indexes . . . [Figure 13.3] show[s] a positive association between the labor share and democracy. (Acemoglu and Robinson, Reference Acemoglu and Robinson2006: 58–9)

The authors take pains to explain that the representations of the level of democracy they use in Figure 3.13 actually are appropriate and meaningful measures of the level of democracy experienced in the countries in question (Acemoglu and Robinson, Reference Acemoglu and Robinson2006: 48–51). But even if we assume that these measures are appropriate and meaningful, the relevant question for the purposes of Acemoglu and Robinson's analysis is whether these measures correspond to the representation of democracy in their Pure Model. But again, the answer is that these measures correspond not to the Pure Model, but rather to the Quasi-Model. The Pure Model version of democracy corresponds to a value of the variable τ (tax rate) being chosen automatically (according to the Median Voter Theorem), with the outcome (calculated using an exogenously defined objective function for a group of identical representative agents) depending on various exogenously defined parameters and the objective function of a second agent. While it would not be wrong to claim that some of the characteristics of that formal model are also characteristics in some sense of the version of democracy represented by the democracy indices used by Acemoglu and Robinson's (Reference Acemoglu and Robinson2006), it is also true that the model includes many constitutive characteristics that are not and could not be shared by that version of democracy, and vice versa. To give just one example, the Freedom House political rights index – which is one of several indices of democracy used by Acemoglu and Robinson (Reference Acemoglu and Robinson2006) – takes into account (among other things) whether there are free and fair elections in a country and whether there are competitive political parties. These elements are not expressible within the conceptual vocabulary of the Median Voter Theorem, and yet Acemoglu and Robinson's (Reference Acemoglu and Robinson2006) Pure Model rests on the foundations of that theorem and all its attendant assumptions.

This critique also applies to NNIE work that uses more rigorous empirical methods, such as those cited in footnote 13 above. In short, (a) the theoretical relationships between various conceptual categories of the Pure Model are rigorously established (according to the standards of relevant mathematical practice), (b) the statistical relationships discovered between various data categories are rigorously established (according to the standards of econometric practice), but the connection between the referents of the categories in (a) and (b) remains purely conjectural, in the form of the assertion of the ‘Catalog of correspondences’.

The issues reviewed above are not limited to Acemoglu and Robinson (Reference Acemoglu and Robinson2006), Glaeser and Shleifer (Reference Glaeser and Shleifer2003), and Maskin and Tirole (Reference Maskin and Tirole2004), but rather are issues that inhere in NNIE methodology. By highlighting these issues, we are not claiming that NNIE work is a priori invalid. It is certainly possible for such work to generate insight into its subject matter. We do claim, however, that the role played by the NNIE's hyper-reductive formal models in this insight generation needs to be examined very carefully (in the manner suggested above) before we accept the claim that these models are actually doing (or are even capable of doing) the heavy-lifting they are presented as doing.

4. NNIE and the taming of institutions in the history of economic thought

For the Old Institutional Economics (OIE), institutions provided the social context in which individual actions occur and in which economic developments take place. Thorstein Veblen (Reference Veblen and Veblen1919: 239), for example, defined institutions as ‘settled habits of thought common to the generality of men’. This definition of institutions was premised on an understanding of individual behavior as endogenous to the set of social institutions, which themselves are molded by cultural and technological forces. Thus from the OIE perspective, institutions are embedded processes that result from technological and other social forces, and economic thought is concerned with both the formation of institutions and, especially, the role of institutions in the endogenous formation of preferences and technology and their consequences. From its inception, the OIE focused both on the forces that mold institutions and on the nature of the economy and economic change that result from having certain traditions and customs in place. Think, for example, of Veblen's writings on conspicuous consumption and on the theory of industrial change, or of Commons’ writings on the evolution and consequences of property law. Recent OIE writers continue to seek to explain institutions and their consequences. Hodgson, for example, notes that it is the appreciation of the role of ‘tradition, custom or legal constraint’ that gives institutionalist thought its capacity to understand social organization and its durable, routinized patterns of behavior. ‘It is this very durability and routinization, in a highly complex and sometimes volatile world’, he writes, ‘which makes social science with any practical application possible at all.’ (Hodgson, Reference Hodgson1988: 10)

The New Institutional Economics (NIE), exemplified by North's (Reference North1990, Reference North1991) writings on economic history and developed with respect to transaction costs and the theory of the firm by Williamson (Reference Williamson1975, Reference Williamson1985), takes institutions to be non-market entities that emerge as the efficient and thus rational solution to problems arising in purely market driven systems: individuals create institutions such as firms and hierarchies when these are more efficient than markets. In this traditional NIE view, institutions do not condition individual behavior, but instead are the result of that behavior and ultimately place a constraint on it.

The NIE conception of institutions thus broke from the OIE conception in at least two fundamental ways. First, in the NIE, institutions are endogenous to an economic cost–benefit calculus, with preferences and technologies treated as exogenous determinants of institutional forms. Second, since institutional formations are rooted in the logic of individual rational choice, they are understood to bring Pareto improvements at the level of society. In both of these ways, the NIE was fairly comfortably connected to the mainstream of marginalist economics, while the OIE had always seen itself as an alternative to – and a thorn in the side of – the marginalist approach. This is evident already in Veblen's famous 1919 essay ‘Why is Economics Not an Evolutionary Science?’.

We should note that NIE economists, and especially Douglass North, have expanded their notion of institutions, allowing for a greater interaction between culture (ideology, beliefs) and individual identity. In this context, institutions both order the external environment and are formed by it, the result being ‘a widening discussion of the role of ideology in determining individual behavior’ and a deeper consideration of the relevance of ‘inefficient institutions’.Footnote 19

The New New Institutional Economics identifies itself as falling squarely within the neoclassical tradition of the NIE. Acemoglu (Reference Acemoglu2005: 9) cites North (Reference North1990: 3) in his definition of institutions as ‘the rules of the game in a society or, more formally. . . the humanly devised constraints that shape human interaction’. But while the NNIE identifies in some respects with the NIE, it also seeks to extend the NIE in at least two respects. The first is the effort to go beyond traditional NIE concerns with economic institutions – for example, those of property rights protection and contract enforcement – and to extend the analysis to political institutions, including ‘form of government, constraints on politicians and elites, separation of powers, etc. [Political institutions] shape political incentives and the distribution of political power’ (Acemoglu, Reference Acemoglu2005: 10). This introduction of power is important in itself, and allows for the possibility of non-Pareto improvements in the formation of institutions, since ‘institutions are not typically chosen for the good of society, but imposed by groups with political power for their economic consequences’ (Acemoglu, Reference Acemoglu2005: 2). This possibility was not addressed in the NIE, as Williamson himself admitted, writing that, in NIE work, ‘efficiency arguments have mainly prevailed over power interpretations because the latter are tautological, but power issues refuse to go away’ (Williamson, Reference Williamson2000: 611).

The other contribution of the NNIE is the modeling of social institutions as sets of parameterized cost–benefit problems, and this has been the main focus of the methodological analysis of this paper. We have argued that the explanatory power of the NNIE hinges on the development of a ‘Quasi-Model’, which often corresponds only loosely to the rigorous formal model that gives NNIE work such professional distinction. The Quasi-Model – articulated in a mix of ordinary and formal language, whose ultimate referents are the phenomena of interest in their socially embedded context – is meant to imbue highly abstract but crucial model parameters with actual historical meaning in an effort to give the formal model relevance that it does not carry on its own. But, as we have argued above, the Quasi-Model ends up effectively replacing the Pure Model as the insight-generating engine of the analysis, rather than improving it. Consequently, the great promise of the NNIE approach – the ability to represent complex institutional dynamics with hyper-reductive models – never even gets off the ground.

If the OIE saw institutions as the all-important backdrop to social inquiry, they also placed the emphasis on understanding their function rather than on a full-fledged explanation of their particular form. The NIE, on the other hand, emphasized the rational choice foundation of institutional formation. The NNIE theory of institutions ostensibly adds precision to the analysis of institutions, but at the same time abandons the attempt to understand the nature and dynamics of institutions, representing them as merely a set of exogenous background conditions to cost–benefit analyses in which parameter values trivially lead to various socio-economic outcomes. In NNIE analyses, the (pure) model structure and taxonomy of institutional parameters are difficult to link to actual historical experience and thus are translated into a Quasi-Model that is subjected to casual verifications. In the end, what is accomplished is not illumination of the institutions in question, but rather a forceful fitting of those institutions into familiar optimization methodology. Even the innovative introduction of power into the consideration of institutional formation is lessened by the thinness with which the concept is formulated in the models.Footnote 20 In sum, the taming of institutions that is the major accomplishment of the NNIE has come at great cost to the theory of institutions and to the ability to link the theory of institutions to an empirical analysis of economics and history.

Appendix 1: Portion of the Pure Model of Acemoglu and Robinson (Reference Acemoglu and Robinson2006)

Strategy sets:

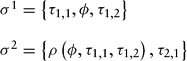
\begin{equation} \begin{array}{*{20}l} {\sigma ^1 = \left\{{\tau _{1,1}, \phi, \tau _{1,2}} \right\}} \\ \\ {\sigma ^2 = \left\{{\rho \left({\phi, \tau _{1,1}, \tau _{1,2}} \right),\tau _{2,1}} \right\}} \\ \end{array}\end{equation}

Parameters: θ, δ, μ, p ∈ [0, 1]

Choice variables:

Player 1: τ, φ ∈ {A, B}; Player 2: τ, ρ ∈ {α, β}

Other elements:

\begin{equation} \begin{array}{*{20}l} {y^p = \displaystyle \frac{{\left({1 - \theta} \right)\bar y}}{{\left({1 - \delta} \right)}}} \\ \\ {y^r = \displaystyle\frac{{\theta \bar y}}{\delta}} \\ {\tau _{1,1} =} & {\left\{{\mathop {\arg \max}\limits_{\tau \in [{0,1}]}y^i + \tau (\bar{y} - y^i) - C(\tau)\bar{y}} \right\}} \\[12pt] \, & {{\rm where}\,y^i = {\rm med}[Y];\ Y = \{{y^1, \ldots, y^n} \}} \\\end{array}\\tau _{2,1} \in[ {0,1} ]\end{equation}

Appendix 2: supplementary information for Solution phase statements of Acemoglu and Robinson (Reference Acemoglu and Robinson2006) and Glaeser and Shleifer (Reference Glaeser and Shleifer2003)

Acemoglu and Robinson (Reference Acemoglu and Robinson2006)

(6.6)
\begin{equation} \mu^ * = \theta - p\left({\tau ^p \left({\theta - \delta} \right) - \left({1 - \delta} \right)C\left({\tau ^p} \right)} \right)\end{equation}
(6.7)
\begin{equation} \mu \ge \theta - \left({\tau ^p \left({\theta - \delta} \right) - \left({1 - \delta} \right)C\left({\tau ^p} \right)} \right)\end{equation}

Glaeser and Shleifer (Reference Glaeser and Shleifer2003)

  1. C = per unit cost of precautionary action

  2. S = scale of the firm

  3. Pα = probability of an accident occurring, for type αs

  4. P1 = probability of an accident occurring for type βs when precaution is taken

  5. P2 = probability of an accident occurring for type βs when no precaution is taken

  6. πα = proportion of population that is type α.

Footnotes

1 We provide specific references throughout the course of the paper.

2 The work is absent, for example, from recent surveys of new developments in economic thought that are otherwise sympathetic to institutionalism; see Colander et al. (Reference Colander, Holt and Rosser2004), Colander (Reference Colander2005), Hodgson (Reference Hodgson2007), Davis (2008).

3 As early as 1975, Coddington (Reference Coddington1975) likened the contribution of general equilibrium theory to the understanding of actual economies to ‘the contribution of flatness to mountaineering’.

4 The lack of robustness was identified early on in the development of this paradigm, and was used to downplay the significance of its policy implications. See, for example, Grossman (Reference Grossman and Krugman1986). On the issue of robustness in economics generally, see Milberg (Reference Milberg and Gudeman2009).

5 In fact, the discussion of robustness has shifted more into the realm of empirics and in particular the support for a particular econometric result under different variable definitions, different choices of instrumental variables, and alternative model specifications. See, for example, Rodrik et al. (Reference Rodrik, Subramanian and Trebbi2004).

6 All models (mathematical or otherwise) of social phenomena are reductive to some extent. The term ‘hyper-reductive’ is meant to capture the NNIE's explicit goal of pushing the parsimony of these models as far as it can go.

7 These titles belong, respectively, to Glaeser and Shleifer (Reference Glaeser and Shleifer2003), Dixit et al. (Reference Dixit, Grossman and Gul2000), Murphy and Shleifer (Reference Murphy and Shleifer2004), Fang (Reference Fang2001), Maskin and Tirole (Reference Maskin and Tirole2004), and Hess and Orphanides (Reference Hess and Orphanides2001).

8 For a review of the nature and significance of the marginalist revolution, see Black et al. (Reference Black, Coats and Goodwin1973).

9 The framework draws from Spiegler (Reference Spiegler2005), Hughes (Reference Hughes1997) and Black (Reference Black1962). Note that the framework is a model of underlying structure and flow of argument. As such, it may be necessary to extract the elements of each phase from various parts of the text.

10 Of course, there are many other ways to characterize the analytical process of NNIE work. We will not argue here that the FPF is the only way to understand this work, only that it is one apt way of doing so.

11 The game in Appendix 1 substitutes purely mathematical language for many of the ordinary language terms used by Acemoglu and Robinson (Reference Acemoglu and Robinson2006). For purposes of translation: ‘The elites’ are Agent 1, ‘the citizens’ are Agent 2, A and B represent ‘democratizing’ and ‘not-democratizing’, respectively, and a and b represent ‘revolution’ and ‘no revolution’, respectively. Note also that Proposition 6.1 contains some elements that we have not defined above. We have provided the necessary supplemental information in Appendix 2.

12 For a different version of the model later in the book, Acemoglu and Robinson (Reference Acemoglu and Robinson2006: 149) themselves present two different versions of the subgame perfect Nash equilibrium as we do here. They do not, however, discuss the conceptual difference between the two. Rather, the conjectural version (which they refer to simply as an ‘alternative, more intuitive form’) of the solution is presented as an unproblematic elaboration of the pure model solution.

13 Similar hybrid Solution phase statements are found in Maskin and Tirole (Reference Maskin and Tirole2004: 1040–9). We omit discussion of these passages here purely for the sake of brevity.

14 Some NNIE work pursues this strategy through formal econometric testing. See, for example, Rodrik (Reference Rodrik1999), Blomberg and Harrington (Reference Blomberg and Harrington2000), Burton et al. (Reference Burton, Phipps and Curtis2002), Botticini and Siow (Reference Botticini and Siow2003), and Hanssen (Reference Hanssen2004).

15 Indeed, it is a standard feature of NNIE work to emphasize the Pure Model's role as the insight-generating engine of the analysis as the work's central distinguishing factor. For example, see Acemoglu and Robinson (Reference Acemoglu and Robinson2006: xiv).

16 In Acemoglu and Robinson (Reference Acemoglu and Robinson2006), μ is a catch-all index of the ease and attractiveness of mounting a revolution. They define it differently in different contexts. See p. 121 for μ as the cost of revolution in terms of destroyed assets, and p. 125 for μ as the magnitude of the collective-action problem of getting poor people to join the revolution.

17 See Appendix 1.

18 Of course it is possible to construct precise indices of the social phenomena under study, and the authors do so in the course of pursuing the second justificatory method mentioned above. But there are problems inherent in this practice as well, which we discuss below.

19 Hodgson (Reference Hodgson1999). For further development of this point, see Dequech (Reference Dequech2002), and Groenewegen et al. (Reference Groenewegen, Kerstholt and Nagalkerke1995). In this vein, there is a growing body of work in evolutionary institutional economics which seeks to provide formal-mathematical foundations for the origin and development of social norms and institutions. (See, for example, Sethi, Reference Sethi1996; Gintis, Reference Gintis2006) In general, this work is distinct from NNIE work in that while the evolutionary work attempts to model the origin, nature, and development of norms and institutions, NNIE work attempts to model the role of institutions in socio-economic activity by representing institutions as background conditions to individual or group optimization.

20 In Acemoglu and Robinson (Reference Acemoglu and Robinson2006), for example, power is expressed in two ways: (1) in the exogenously determined rules of their extensive form game governing the sequence of moves; and (2) in the exogenously determined parameters (typically one dimensional, real-valued elements of [0,1]) that alter cost-benefit calculations. For example, the parameter μ (discussed in detail above) is meant to express the costs of mounting a revolution. The lower the value of μ, the more power the ‘poor’ have.

References

Acemoglu, D. (2005), ‘Understanding Institutions’, presentation slides, Lionel Robbins Lectures, viewed 19 September 2008, <http://econ-www.mit.edu/faculty/acemoglu/selected>.CrossRef.>Google Scholar
Acemoglu, D. and Robinson, J. A. (2006), Economic Origins of Dictatorship and Democracy, Cambridge, UK: Cambridge University Press.Google Scholar
Barro, R. (1997), Determinants of Economic Growth: A Cross-Country Empirical Study, Cambridge, MA: MIT Press.Google Scholar
Black, M. (1962), Models and Metaphors, Ithaca, NY: Cornell University Press.CrossRefGoogle Scholar
Black, R. D. C., Coats, A. W., and Goodwin, C. D. W. (1973), The Marginal Revolution in Economics: Interpretation and Evaluation, Durham, NC: Duke University Press.Google Scholar
Blomberg, B. and Harrington, J. E. Jr., (2000), ‘A Theory of Rigid Extremists and Flexible Moderates with an Application to the US Congress’, American Economic Review, 90 (3): 605–620.CrossRefGoogle Scholar
Botticini, M. and Siow, A. (2003), ‘Why Dowries?’, American Economic Review, 93 (4): 1385–1398.Google Scholar
Burton, P., Phipps, S., and Curtis, L. (2002), ‘All in the Family: A Simultaneous Model of Parenting Style and Child Conduct’, American Economic Review, 92 (2): 368–372.CrossRefGoogle Scholar
Chang, H. (2007), Bad Samaritans: The Myth of Free Trade and the Secret History of Capitalism, New York: Bloomsbury Press.Google Scholar
Coddington, A. (1975), ‘The Rationale of General Equilibrium Theory’, Economic Inquiry, 13 (4): 539–558.CrossRefGoogle Scholar
Colander, D. (2005), ‘The Future of Economics: The Appropriately Educated Person in Pursuit of the Knowable’, Cambridge Journal of Economics, 29 (6): 927–941.CrossRefGoogle Scholar
Colander, D., Holt, R. and Rosser, B. Jr., (2004), ‘The Changing Face of Mainstream Economics’, Review of Political Economy, 16 (4): 485–499.Google Scholar
Davis, J. B. (2007), ‘The Turn in Economics and the Turn in Economic Methodology’, Journal of Economic Methodology, 14 (3): 275–90.CrossRefGoogle Scholar
Dequech, D. (2002), ‘The Demarcation between the “Old” and the “New” Institutional Economics: Recent Complications’, Journal of Economic Issues, 36 (2): 565–572.CrossRefGoogle Scholar
Dixit, A., Grossman, G. M., and Gul, F. (2000), ‘The Dynamics of Political Compromise’, Journal of Political Economy, 108 (3): 531–568.Google Scholar
Fang, H. (2001), ‘Social Culture and Economic Performance’, American Economic Review, 91 (4): 924–937.CrossRefGoogle Scholar
Gintis, H. (2006), ‘The Evolution of Private Property’, Journal of Economic Behavior and Organization, 64 (1): 1–16.CrossRefGoogle Scholar
Glaeser, E. L. and Shleifer, A. (2003), ‘The Rise of the Regulatory State’, Journal of Economic Literature, 41 (2): 401–425.CrossRefGoogle Scholar
Groenewegen, J., Kerstholt, F., and Nagalkerke, A. (1995), ‘On Integrating New and Old Institutionalism: Douglass North Building Bridges’, Journal of Economic Issues, 29 (2): 467–476.CrossRefGoogle Scholar
Grossman, G. (1986), ‘Strategic Export Promotion: A Critique’, in Krugman, P. R. (ed.), Strategic Trade Policy and the New International Economics, Cambridge, MA: MIT Press.Google Scholar
Guiso, L., Sapienza, P., and Zingales, L. (2006), ‘Does Culture Affect Economic Outcomes?’, Journal of Economic Perspectives, 20 (2): 23–48.CrossRefGoogle Scholar
Hanssen, F. A. (2004), ‘Is there a Politically Optimal Level of Judicial Independence?’, American Economic Review, 94 (3): 712–729.CrossRefGoogle Scholar
Hess, G. D. and Orphanides, A. (2001), ‘War and Democracy’, Journal of Political Economy, 109 (4): 776–810.Google Scholar
Hodgson, G. (1988), Economics and Institutions, London: Polity Press.Google Scholar
Hodgson, G. (1999), ‘Structures and Institutions: Reflection on Institutionalism, Structuration Theory, and Critical Realism’, presented at EAEPE conference, Prague.Google Scholar
Hodgson, G. (2007), ‘Evolutionary and Institutional Economics as the New Mainstream?’, Evolutionary Institutional Economics Review, 4 (1): 7–25.CrossRefGoogle Scholar
Hughes, R. I. G. (1997), ‘Models and Representation’, Philosophy of Science, 64, Supplement, Proceedings of the 1996 Biennial Meetings of the Philosophy of Science Association, Part II: S325–S336.CrossRefGoogle Scholar
Langlois, R. (2003), ‘The Vanishing Hand: The Changing Dynamics of Industrial Capitalism’, Industrial and Corporate Change, 12 (2): 351–385.CrossRefGoogle Scholar
Maskin, E. and Tirole, J. (2004), ‘The Politician and the Judge: Accountability in Government’, American Economic Review, 94 (4): 1034–1054.CrossRefGoogle Scholar
McCleary, R. M. and Barro, R. J. (2006), ‘Religion and Economy’, Journal of Economic Perspectives, 20 (2): 49–72.CrossRefGoogle Scholar
Milberg, W. (2009), ‘The New Social Science Imperialism and the Problem of Knowledge in Contemporary Economics’, in Gudeman, S. (ed.), Economic Persuasions, Oxford: Berghahn Books.Google Scholar
Moore, B. Jr., (1966), Social Origins of Dictatorship and Democracy: Lord and Peasant in the Making of the Modern World, Boston: Beacon Press.Google Scholar
Murphy, K. M. and Shleifer, A. (2004), ‘Persuasion in Politics’, American Economic Review, 94 (2): 435–439.CrossRefGoogle Scholar
North, D. (1990), Institutions, Institutional Change and Economic Performance, Cambridge, UK: Cambridge University Press.Google Scholar
North, D. (1991), ‘Institutions’, Journal of Economic Perspectives, 5 (1): 97–112.CrossRefGoogle Scholar
Rodrik, D. (1999), ‘Democracies Pay Higher Wages’, Quarterly Journal of Economics, 114 (3): 707–738.CrossRefGoogle Scholar
Rodrik, D., Subramanian, A. and Trebbi, F. (2004), ‘Institutions Rule: The Primacy of Institutions over Geography and Integration in Economic Development’, Journal of Economic Growth, 9 (2): 131–165.Google Scholar
Sethi, R. (1996), ‘Evolutionary Stability and Social Norms’, Journal of Economic Behavior and Organization, 29 (1): 113–140.Google Scholar
Solow, R. M. (1997), ‘Is There a Core of Usable Macroeconomics We Should All Believe In?’, American Economic Review, 87 (2): 230–232.Google Scholar
Spiegler, P. (2005), ‘A Constructive Critique of Economics’, doctoral dissertation, Harvard University.Google Scholar
Veblen, T. (1919), ‘Why Is Economics Not an Evolutionary Science?’, in Veblen, T., The Place of Science in Modern Civilization, New York: Cosimo.Google Scholar
Williamson, O. (1975), Markets and Hierarchies: Analysis and Antitrust Implications, New York: The Free Press.Google Scholar
Williamson, O. (1985), The Economic Institutions of Capitalism, New York: The Free Press.Google Scholar
Williamson, O. (2000), ‘The New Institutional Economics: Taking Stock, Looking Ahead’, Journal of Economic Literature, 38 (3): 595–613.Google Scholar
Figure 0

Figure 1. The four-part framework

Figure 1

Table 1. ‘Catalog of correspondences’ of Acemoglu and Robinson (2006)

Figure 2

Table 2. ‘Catalog of correspondences’ of Glaeser and Shleifer (2003) and Maskin and Tirole (2004)