INTRODUCTION
The link between environment and economic dynamics has been studied in a lot of contributions.1
For a recent survey see Xepapadeas (2005).
Recently, some papers have elucidated that more complex dynamics can emerge when one considers the interaction between environment and economic activity. Indeed, considering overlapping generations models where consumers have to choose between consumption and abatement, Seegmuller and Verchère (2004) and Zhang (1999) have shown the existence of deterministic cycles and chaos.
However, in these contributions, labor supply is inelastic and indeterminacy is ruled out. Nevertheless, elastic labor supply and the consumer choice between leisure and consumption often play key roles in the emergence of endogenous fluctuations.2
In this paper, we introduce an elastic labor supply in an overlapping generations economy with environment. Thus, consumers have to choose between consumption, environmental quality, and leisure. Moreover, they share their labor income between savings and abatement, because pollution negatively affects their preferences.Studying local dynamics, we prove that a flip bifurcation can occur, as well as local indeterminacy. This means that not only deterministic cycles can appear, but also endogenous fluctuations due to self-fulfilling expectations. Moreover, these fluctuations occur under weaker conditions than in previous existing works. Indeed, contrary to several contributions, the existence of indeterminacy and cycles needs neither weak substitution between production factors [Grandmont et al. (1998), Reichlin (1986)] nor increasing returns or imperfect competition [see Benhabib and Farmer (1999) for a survey]. We can further note that, in contrast to Seegmuller and Verchère (2004) and Zhang (1999), the occurrence of such fluctuations does not require a high level of the pollution emission rate. Consequently, this paper shows more generally that non-monotonic dynamics can easily occur in economies where an environmental dimension is taken into account.
The paper is organized as follows. In the next section, we present the model. In Section 3, we establish the existence of a steady state. Finally, in Section 4, we study local dynamics and provide interpretations of our findings.
THE MODEL
We consider a perfectly competitive overlapping generations model with discrete time t=1, 2, …, ∞ and a constant population size normalized to one. A generation of consumers is born in each period and households live two periods. When young, the representative consumer supplies labor lt, which is remunerated at the real wage rate wt. He shares his wage earnings between savings, through the purchase of aggregate capital kt, and environmental maintenance dt.3
As in John and Pecchenino (1994), we consider positive environmental maintenance or pollution abatement (dt≥0).
We assume that capital totally depreciates after one period of use.

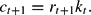
In this economy, the environmental quality decreases with respect to the pollution. At period t+1, the level of pollution is given by

The pollution, which is always strictly positive, increases linearly with respect to the capital stock inherited from the previous period and is a decreasing function of the environmental maintenance.5
Note that the pollution Pt+1 can be interpreted as a flow or a stock determined by Pt+1=(1−m)Pt+αkt−1−dt, with a natural rate of absorption m equal to 1. Because, in overlapping generations models, the length of period is assumed to be long, the assumption m=1 does not seem to be too restrictive.
Consumers derive utility from consumption, leisure, and environmental quality. Assuming additively separable preferences, the utility function of the representative household is given by
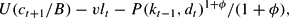
where B>0 and v>0 are two scaling parameters and ϕ>0. We can note that as usual in dynamic macroeconomic models, the disutility of labor is linear [see Hansen (1985)], whereas the disutility of pollution is increasing and convex. Furthermore, we assume the following:
Assumption 1. The function U(x) is continuous for all x≥0,
for x>0 and n large enough, with U′(x)>0, U″(x)≤0, and U′(x)+xU″(x)>0.
The representative consumer maximizes his utility function (4) under the constraints (1), (2), and (3). We deduce the two following equations:
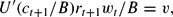
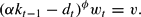
These two expressions define the consumer choice between leisure, environmental maintenance, and future consumption.
The final good is supplied by a representative firm using a constant-returns-to-scale technology. The production is given by yt = f(at)lt, where at = kt−1/lt denotes the capital-labor ratio and f(at) the intensive production function. In what follows, we assume the following:
Assumption 2. The intensive production function f(a) is continuous for a≥0, positively valued and differentiable as many times as needed for a>0, with f′(a)>0 and f″(a)<0.
The producers maximize their profits. Since the economy is perfectly competitive, we obtain the following equations:
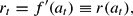

Substituting equations (1), (2), (7), and (8) into (5) and (6), we can define an intertemporal equilibrium as follows. An intertemporal equilibrium is a sequence (at, kt−1)t≥1 that satisfies the equations
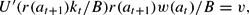
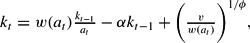

where k0>0 is given.
Note that inequalities (11) ensure strictly positive pollution and positive environmental maintenance. Taking these conditions as given, equations (9) and (10) define a two-dimensional dynamic system with one predetermined variable, the capital. One can further note that equation (10) means in fact that kt=w(at)lt−dt at equilibrium, where dt=αkt−1−Pt+1 and Pt+1=(v/w(at))1/ϕ. Note that in the limit case without any pollution (α=0), the trade-off between investments in productive capital and environmental maintenance disappears (dt=0), and equation (10) becomes kt=w(at)lt.
Before studying steady states, we define the following relationships. We denote as s(a)≡r(a)a/f(a)∈(0, 1) the capital share in income and furthermore, if σ(a) represents the elasticity of capital-labor substitution, 1/σ(a)=d ln w(a)/d ln a−d ln r(a)/d ln a. Because w′(a)=−ar′(a), we obtain the two following expressions:

EXISTENCE OF A STEADY STATE
A stationary solution of the dynamic system defined by (9), (10), and (11) is given by (a, k) such that

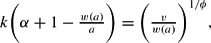
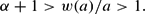
We can note that in Section 4 we are interested in fluctuations around a steady state. Since environmental maintenance has to be positive at each period, we assume strictly positive environmental maintenance in the steady state; that is, w(a)/a>1.
Following Cazzavillan et al. (1998), we ensure in what follows the existence of a normalized steady state (a, k)=(1, 1) by choosing appropriate values of the two scaling parameters B>0 and v>0.6
To be as short as possible, we do not discuss uniqueness or multiplicity of steady states. For such an analysis, the reader can refer to Seegmuller and Verchère (2005).
Assumption 3. α+1>w(1)>1.
Under Assumptions 1–3, there exists a unique solution v*>0 to the equation

Assume that limx→0xU′(x)<v*/w(1)<limx→+∞xU′(x). Then, under Assumption 1 and taking v* as given, there is a unique B* that satisfies

PROPOSITION 1. Assuming that limx→0xU′(x)<v*/w(1)<limx→+∞xU′(x) and Assumptions 1–3 are satisfied, then (a, k)=(1, 1) is a steady state of the dynamic system (9), (10) if and only if v* and B* are the unique solutions of (16) and (17).
LOCAL DYNAMICS
In this section, we analyze the occurrence of local indeterminacy and endogenous cycles. Furthermore, interpreting our results, we offer evidence that the consumer choice between leisure, environmental maintenance, and future consumption has a key role in the occurrence of endogenous fluctuations.
In order to do this, we study local dynamics in the neighborhood of the steady state (a, k)=(1, 1). If we denote s=s(1), we assume the following:
Assumption 4. s<1/2 and U″(x)=0.
This means that the capital share in income is smaller than one-half, which is usually assumed in macroeconomic dynamic models and verified by empirical studies, and the utility for consumption is linear. We introduce this last assumption for simplification.7
The reader can refer to Seegmuller and Verchère (2005), who relax this condition.
PROPOSITION 2. Assuming that there exists a steady state (Proposition 1) and Assumptions 1–4 are satisfied, the steady state is locally indeterminate for α<w(1)+1, a flip bifurcation occurs for α=w(1)+1, and the steady state is a saddle for α>w(1)+1.
proof. We first differentiate the dynamic system (9), (10) around (a, k)=(1, 1). Using (12) and after some computations, we obtain the trace T and the determinant D of the associated Jacobian matrix, which respectively represent the sum and the product of the two eigenvalues of the characteristic polynomial Q(λ)≡λ2−Tλ+D=0:

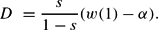
One can easily deduce that the two eigenvalues are defined by λ1=s/(1−s) and λ2=w(1)−α. Using Assumptions 3 and 4, we have λ1∈(0, 1) and λ2<1. Moreover, λ2>−1 for α<w(1)+1, λ2=−1 for α=w(1)+1 and λ2<−1 for α>w(1)+1. This concludes the proof.
This proposition establishes that both deterministic cycles and local indeterminacy, that is, fluctuations due to self-fulfilling prophecies, can occur. In contrast to previous results analyzing the existence of cycles in dynamic models with environment (see Seegmuller and Verchère (2004), Zhang (1999)), here the emission rate of pollution (α) must not be too high. Furthermore, endogenous fluctuations can occur when capital and labor are not weak substitutes as is often required [see, among others, Grandmont et al. (1998) or Reichlin (1986)]. Our results do not depend any more on the existence of increasing returns or imperfect competition [see Benhabib and Farmer (1999) for a survey].
We now interpret the occurrence of endogenous fluctuations by explaining how non-monotonic and cyclical trajectories can emerge due to consumer choices between consumption, environmental quality, and leisure.
Assume that one deviates from the steady state by an increase of the capital stock kt−1. Then, taking into account equation (3), young consumers expect that future pollution Pt+1 will increase, which implies a reduction of their utility. Because from relation (6) the real wage decreases, they increase their labor supply lt, and they also reallocate their savings from capital accumulation kt to environmental maintenance dt [see equation (1)]. Following this decrease of the capital stock, the next generation of consumers will expect a decreased pollution flow Pt+2 and then, by the reverse mechanism, both lt+1 and dt+1 will go down and kt+1 will go up, and so on successively along the fluctuations.
Finally, one can observe that the greater α is, the more volatile dt is, which can be a source of instability of the steady state and promote the determinacy of the equilibrium. This explains why fluctuations due to self-fulfilling expectations emerge only if α is not too high.
We would like to thank an associate editor and two anonymous referees for helpful comments and suggestions. This paper also benefited from comments of participants in the CEPET workshop at Udine June 2004, XIXth EEA Annual Congress August 2004, Journée à Générations Imbriquées at La Rochelle November 2004, and T2M Conference at Lyon January 2005. All remaining errors are our own responsibility.


