I. INTRODUCTION
In many metal-containing proteins, the metal is bound to amino acids forming discrete units, where the metal ion acts as active site carrying out biological processes. Knowledge of the structure of metal–amino acid complexes is of high relevance in understanding metal–protein interactions (Lehninger, Reference Lehninger1972; Sigel and Martin, Reference Sigel and Martin1982; Holm et al., Reference Holm, Kennepohl and Solomon1996). The study of these simple compounds is considered an excellent tool to increase the understanding of the biological processes, as the functionality is fully correlated with the atomic structure.
Zinc is one of the most common metal ions bound to proteins in living organisms. In proteins, Zn ions are often coordinated to the amino acid side chains of aspartic acid, glutamic acid, cysteine, and histidine. Four different biological functions for zinc in proteins have been identified: catalytic, co-catalytic, interface binding, and structurally stabilizing (Auld, Reference Auld2001). The Zn ion plays an important role in metalloprotein function, acting as active sites in many biological reactions (Gomis-Rüth, Reference Gomis-Rüth2003; Vahrenkamp, Reference Vahrenkamp2007). Therefore, amino acids are important biological ligands, as they are the basic building units of proteins. They are characterized by their torsional flexibility, which allows the molecules to adopt different conformations, or conformers. Cysteine is one of the most distinctive amino acids, because of the presence of the sulphur atom. The thiol group of cysteine can be dimerized to a disulphide under oxidative conditions, which is sometimes listed as a distinct amino acid under the name cystine. The S–S bonds play an important role in the formation of secondary and tertiary structures of the proteins.
In this work, we present the structure of a new Zn–cystine metal organic framework (MOF), with a stoichiometrical chemical formula of Zn(C3H5NO2S)2 [hereafter Zn(CYS)2]. Each half of the amino acid acts as a bidentate ligand to one Zn and as a monodentate to another Zn, having special attention to the disulphide bonds which play an important structural role.
II. EXPERIMENTAL
A. Synthesis
Zn(CYS)2 was prepared by evaporation of a supersaturated solution. Approximately 4 mmol of L-cysteine (99.5% Fluka) were dissolved in 40 ml of boiling water for 15 min. Then 2 mmol of ZnCO3 (Fluka 96466) dissolved in 5 ml of boiling water were added. The solution had a pH of 4.9 after 20 min, under a continuous magnetic stirring. NaOH (1 M) was added dropwise up to pH 7.1. The reaction mixture was stirred at 90 °C for 30 min, with a final pH of 8.4. During the reaction, the cystine group is obtained through oxidation of cysteine. Once the solution was filtered, the resulting mixture was left to stand at room temperature for 3 weeks, when it turned to a yellow-orange powder. Although other metal–amino acid such as Zn–histidine or Cu–isolucine have been grown as single crystals (Ferrer et al., Reference Ferrer, Rubio-Zuazo and Castro2013, Reference Ferrer, Jimenez-Villacorta, Rubio-Zuazo, da Silva and Castro2014), it has not been possible in this case. The powder was then collected and characterized by powder X-ray diffraction.
B. X-ray diffraction
The high-resolution powder diffraction (HRPD) pattern was collected at SpLine beamline (BM25A) of the Spanish CRG at the European Synchrotron Radiation Facility (ESRF, Grenoble) using a fixed wavelength of 0.825 02(5) Å [calibrated with NIST SRM 640c silicon powder; a = 5.431 1946(92) Å], at room temperature. The sample was finely powdered and loaded in a 0.3-mm-diameter borosilicate glass capillary to reduce the effect of possible preferential orientations, and was mounted on a spinning goniometer. Diffraction pattern recording was carried out in a 2θ-step scan mode with a step of 0.015°, counting 16 s of acquisition time per step. The incoming X-ray beam, with dimensions 10 mm × 0.5 mm (horizontal and vertical, respectively), was monitored to normalize the resulting data to the decay of the primary beam, while the diffracted beam was collected using a scintillation point detector (sample to detector distance of 850 mm). Data were collected in the 2θ range of 3°–45°, which correspond to a resolution of 1.08 Å.
III. STRUCTURE DETERMINATION AND RIETVELD REFINEMENT
The angular positions of the first 20 reflections (up to about 2θ = 21°) were determined using the peak search algorithm implemented in WinPLOTR program (Roisnel and Rodriguez-Carvajal, Reference Roisnel and Rodriguez-Carvajal2001). These positions were used to index the pattern using the DICVOL06 program (Louër and Boultif, Reference Louër and Boultif2007) in the orthorhombic system, yielding a unit cell with figure of merit (De Wolff, Reference De Wolff1968) of M(20) = 31.9. For space-group determination, the EXPO2004 program (Altomare et al., Reference Altomare, Caliandro, Camalli, Cuocci, Giacovazzo, Moliterni and Rizzi2004) was used, implementing a statistical algorithm to determine the most probable extinction group (Altomare et al., Reference Altomare, Camalli, Cuocci, da Silva, Giacovazzo, Moliterni and Rizzi2005). In this case, the extinction group found with the highest probability was P212121, which was confirmed by visual inspection of the systematic absences.
The structure of Zn(CYS)2 was solved using the parallel tempering algorithm implemented in the FOX program (Favre-Nicolin and Cerný, Reference Favre-Nicolin and Cerný2002). Templates of the structural fragments of the asymmetric unit (two cysteine molecules and one Zn atom; see Figure 1) were introduced in FOX (using only the non-H atoms) and they were previously built using the software package ChemBio Office (version 11.0). During the calculations, the observed and calculated intensities were compared only in the 2θ range from 3° to 25° and the cysteine molecules could translate and rotate randomly; the torsional angles could also change at random. The cost function was computed using the extracted Bragg peak intensities. After 15 million trials, the agreement factors were R wp = 2.8, and GoF = 22.194. Refinement of the crystal structure found by the FOX program was carried out by the Rietveld method (Rietveld, Reference Rietveld1969), using the FullProf program (Rodriguez-Carvajal, Reference Rodriguez-Carvajal2001) in the 2θ range from 3° to 45°, excluding three small regions around 5°, 17°, and 19°, where small Bragg peak intensity contributions coming from an unknown impurity were found. Atomic coordinates of all atoms were included in the refinement but, to ensure the convergence of the process, restraints on bond lengths and angles were introduced, thus limiting the number of free parameters. The values for the bond lengths and angles were taken from similar molecules and molecular fragments found on the Cambridge Structural Database (Allen, Reference Allen2002) [codes: BIKWIB (Menger and Caran, Reference Menger and Caran2000, COJTUQ (Faggiani et al., Reference Faggiani, Howard-Lock, Lock, Martins and Smalley1984), CUPENS (Thich et al., Reference Thich, Mastropaolo, Potenza and Schugar1974), CYSENC10 (Tucker, Reference Tucker1979), CYSTBR (Anbuchezhiyan et al., Reference Anbuchezhiyan, Ponnusamy and Muthamizhchelvan2010), LCYSTI10 (Oughton and Harrison, Reference Oughton and Harrison1959), and NURHEO (Seko et al., Reference Seko, Tsuge, Igashira-Kamiyama, Kawamoto and Konno2010)] and the standard deviations of the values assigned to bonds and angles were 0.02 Å and 1°, respectively. Two different isotropic temperature factors were introduced for the structure refinement, one for C, O, N, and S atoms and other one for the Zn atom. The peak function used for fitting the experimental data was the Thompson–Cox–Hastings Pseudo–Voigt (Thompson et al., Reference Thompson, Cox and Hastings1987), which can take into account the experimental resolution and the broadening because of size and strain effects, often present in this type of organic powder samples; the axial divergence asymmetry of the peaks was modelled using the Finger's treatment (Finger et al., Reference Finger, Cox and Jephcoat1994); a 12th-order Chebychev polynomial was used to model the background. Hydrogen atoms for cysteine molecules were introduced in FullProf at their calculated positions with the Olex2 program (Dolomanov et al., Reference Dolomanov, Bourhis, Gildea, Howard and Puschmann2009). During the Rietveld refinement, the positions of H atoms were restrained to that of their riding atom. Owing to the possibility of deformation or rotation of both cysteine molecules, the positions of H atoms were recalculated several times during the refinement procedure before it converged. On the final Rietveld fit, there were 81 adjustable parameters (scale factor, zero shift, atomic coordinates, temperature factors, unit-cell parameters, and peak-shape parameters), taking into account the introduced constraints. In Figure 2, the plot of the final Rietveld fit for Zn(CYS)2 compound is given. Crystallographic and refinement-related data are reported in Table I; the profiles of R p and R wp factors obtained from both Le Bail and Rietveld fits are shown for comparison, which indicates that the quality of the refinement is very good. Atomic coordinates and displacement parameters for non-H atoms are reported in Table II.

Figure 1. Structural fragments of Zn(CYS)2 compound. Only non-H atoms were used in the simulated annealing calculations.

Figure 2. (Color online) Final Rietveld refinement plot for Zn(CYS)2, showing the experimental (red circles), calculated (black line), and difference profiles (blue line); green tick marks indicate reflection positions.
Table I. Crystallographic data and Rietveld refinement summary for Zn(CYS)2 compound.
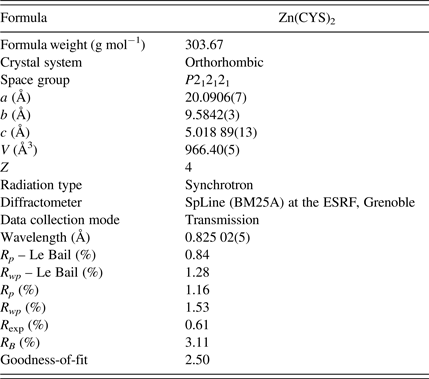
Table II. Fractional atomic coordinates and isotropic displacement parameters (Å2) of non-H atoms for Zn(CYS)2 compound.

IV. DISCUSSION
The asymmetric unit of the Zn(CYS)2 crystal structure presents a disulphide bond as the central part whose chains are linked to two zinc atoms (see Figure 3). The nitrogen atom of the amine group and one of the oxygen atoms of the carboxylic acid groups are bonded to one zinc ion, whereas the other oxygen atom of the same carboxylic acid group is bonded to a second zinc atom. Thus, both halves of the cystine act as a bidentate ligand to one Zn and as a monodentate to another Zn (see Figure 4).

Figure 3. (Color online) Asymmetric unit of Zn(CYS)2 compound, showing the atom-numbering scheme (yellow, S; grey, C; red, O; white, H; blue, N; green, Zn).

Figure 4. (Color online) Crystal structure of Zn(CYS)2 viewed along the c-axis (yellow, S; grey, C; red, O; white, H; blue, N; green, Zn).
Each zinc ion has four amino acid molecules around it, forming a distorted octahedral complex: N–Zn–N angle of 171.6(13)°, and O–Zn–O angles of 168.7(11) and 176.6(13)°. In the axial direction, the two cystines are linked to the zinc by one of the oxygens of the carboxylic acid group with distances of 2.34(3) and 2.50(3) Ǻ. In the equatorial plane, the other two cystines are bonded by the oxygens of the carboxylic acid group and the nitrogen of the amine, at distances of 2.15(3), 2.17(3), 2.12(3), and 2.06(3) Ǻ, respectively. The S–S bond distance is 1.974(16) Ǻ, and the disulphide bond has an important role on stabilizing the MOF.
It is remarkable that the different conformations were obtained for the two halves of the cystine. In one of them, the chiral C and the rest of the atoms are sitting roughly in the same plane; in the other half there is a clear difference around the chiral C atom, as one of the C atoms and the S atom are far from the plane formed by the carboxylic acid group, with an O–C–C–C torsion angle of about 90°. A geometry study of the crystal structure, carried out with the Mogul program (Bruno et al., Reference Bruno, Cole, Kessler, Luo, Motherwell, Purkis, Smith, Taylor, Cooper, Harris and Orpen2004), showed that all the bond lengths, bond angles, and torsion angles values are within the expected ranges, with the exception of the S7_2–C1_2–C2_2–N4_2 torsion angle; the difference between its value (41.52°) and the nearest value in the Mogul distribution is about 9°. Distorted zinc octahedra and disulphide bonds also alternate along the a-axis.
V. CONCLUSION
In this work, we report the structure determination of the novel Zn(CYS)2 compound from the synchrotron X-ray powder diffraction data, applying direct-space methods and Rietveld refinement. The zinc atom presents a distorted octahedral configuration and both halves of the cystine act as a bidentate ligand to one Zn and as a monodentate to another Zn. The Zn(CYS)2 crystal packing is stabilized by disulphide bonds. The CCDC 971360 entry contains supplementary crystallographic data for this paper. These data can be obtained free of charge from The Cambridge Crystallographic Data Centre via www.ccdc.cam.ac.uk/data_request/cif.
ACKNOWLEDGEMENTS
We thank the SpLine staff for their assistance in using the beamline BM25A-SpLine. The financial support of the Consejo Superior de Investigaciones Científicas and the Spanish Ministerio de Ciencia e Innovación (grant numbers PI201060E013 and MAT2011-23758) are also acknowledged.








