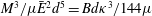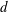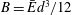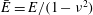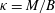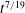1 Introduction
Viscous intrusion of fluid beneath an elastic sheet is controlled by the dynamics at the front, where the sheet is peeled away from the underlying substrate. Such coupling of the dynamics of viscous flow and sheet deformation has many and diverse applications. These include the geological formation and growth of laccoliths by magmatic intrusion at shallow depths (e.g. Bunger & Cruden Reference Bunger and Cruden2011; Michaut Reference Michaut2011), the dilation of elastic-walled Hele-Shaw cells (Pihler-Puzović et al. Reference Pihler-Puzović, Illien, Heil and Juel2012, Reference Pihler-Puzović, Peng, Lister and Heil2015; Lister, Peng & Neufeld Reference Lister, Peng and Neufeld2013; Ducloué et al. Reference Ducloué, Hazel, Thompson and Juel2017), cell adhesion and detachment (Hodges & Jensen Reference Hodges and Jensen2002; Leong & Chiam Reference Leong and Chiam2010), peeling of adhesive tape (McEwan & Taylor Reference McEwan and Taylor1966), growth of liquid blisters (Chopin, Vella & Boudaoud Reference Chopin, Vella and Boudaoud2008; Peng et al. Reference Peng, Pihler-Puzović, Heil and Lister2015), airway reopening (Jensen et al. Reference Jensen, Horsburgh, Halpern and Gaver2002; Grotberg & Jensen Reference Grotberg and Jensen2004; Heil & Hazel Reference Heil and Hazel2011) and the manufacture of flexible electronics and microelectromechanical systems (Hosoi & Mahadevan Reference Hosoi and Mahadevan2004; Rogers, Someya & Huang Reference Rogers, Someya and Huang2010; Gomez, Moulton & Vella Reference Gomez, Moulton and Vella2017).
The simplest model for flow in a thin fluid layer of viscosity
$\unicode[STIX]{x1D707}$
and thickness
$h(x,y,t)$
beneath a stiff elastic sheet of uniform thickness
$d$
is obtained by substituting the pressure
$p=B\unicode[STIX]{x1D6FB}^{4}h$
produced by bending stresses in the sheet into the Reynolds lubrication equation (e.g. Leal Reference Leal1992) to obtain
$$\begin{eqnarray}\frac{\unicode[STIX]{x2202}h}{\unicode[STIX]{x2202}t}=\frac{B}{12\unicode[STIX]{x1D707}}\unicode[STIX]{x1D735}\boldsymbol{\cdot }(h^{3}\unicode[STIX]{x1D735}\unicode[STIX]{x1D6FB}^{4}h),\end{eqnarray}$$
where
$B=Ed^{3}/12(1-\unicode[STIX]{x1D708}^{2})$
is the bending stiffness of the sheet,
$E$
and
$\unicode[STIX]{x1D708}$
are its Young’s modulus and Poisson’s ratio and
$\unicode[STIX]{x1D735}$
is the gradient operator in the
$x,y$
-plane.
The sixth-order equation (1.1) does not support solutions with a forwards propagating front at which
$h=0$
(Flitton & King Reference Flitton and King2004; Lister et al.
Reference Lister, Peng and Neufeld2013; Hewitt, Balmforth & de Bruyn Reference Hewitt, Balmforth and de Bruyn2015). In that respect, it is like the fourth-order thin-film equation for lubrication flows driven by a capillary pressure
$p=-\unicode[STIX]{x1D70E}\unicode[STIX]{x1D6FB}^{2}h$
, with surface tension
$\unicode[STIX]{x1D70E}$
, for which the so-called contact-line problem is often resolved by introducing a slip length or a prewetting film to model processes near the apparent contact line and regularize the equation (Hocking Reference Hocking1983; Hervet & de Gennes Reference Hervet and de Gennes1984). For a capillary-driven flow, the resulting contact-line speed depends only very weakly (logarithmically) on the details of this regularization (Bonn et al.
Reference Bonn, Eggers, Indekeu, Meunier and Rolley2009). However, for flow driven by elastic bending stresses, as described in the interior by (1.1), the speed of any propagating front is controlled by the peeling processes at the front, and the interior solution is then quasistatic with
$\unicode[STIX]{x1D735}p=\mathbf{0}$
at leading order.
Lister et al. (Reference Lister, Peng and Neufeld2013) considered the case where there is already a prewetting fluid film of some small thickness
$h_{0}$
between the elastic sheet and the underlying substrate, as in recent experiments on blister growth in a prefilled elastic-walled Hele-Shaw cell (Pihler-Puzović et al.
Reference Pihler-Puzović, Illien, Heil and Juel2012, Reference Pihler-Puzović, Peng, Lister and Heil2015; Peng et al.
Reference Peng, Pihler-Puzović, Heil and Lister2015; Ducloué et al.
Reference Ducloué, Hazel, Thompson and Juel2017). A local travelling-wave analysis near the front shows that the edge of the blister spreads at a speed
$v=(B^{2}h_{0}\unicode[STIX]{x1D705}^{5})^{1/2}/\unicode[STIX]{x1D707}$
, where the curvature
$\unicode[STIX]{x1D705}=h^{\prime \prime }$
at the edge of the blister is determined by the quasistatic interior solution. Hewitt et al. (Reference Hewitt, Balmforth and de Bruyn2015) considered an alternative situation where a precursor phase of low-viscosity vapour at some fixed pressure
$-p_{0}$
occupies the tip of the propagating front (see also Ball & Neufeld Reference Ball and Neufeld2018; Wang & Detournay Reference Wang and Detournay2018). This description, known as ‘fluid lag’ in models of fluid-driven fracture (e.g. Lister Reference Lister1990; Garagash & Detournay Reference Garagash and Detournay2000; Detournay Reference Detournay2016), is motivated by the possibility of exsolution or evaporation of gasses from the main fluid due to the low relative pressures in the peeling tip. A local travelling-wave analysis shows that the frontal speed is given by
$v=(B^{3}\unicode[STIX]{x1D705}^{7}/p_{0})^{1/2}/\unicode[STIX]{x1D707}$
, where the curvature
$\unicode[STIX]{x1D705}$
is again determined by matching to the interior solution.
In this paper we show that there is no need to invoke a prewetting film or precursor phase to find physical boundary conditions for propagating solutions to (1.1). Instead, we recognize that (1.1) was derived from a thin-sheet approximation to the equations of elasticity, based on the overall
$x$
and
$y$
length scales being much larger than
$d$
. This approximation breaks down within an
$O(d)$
distance from any front, and in this region the full equations of elasticity should be used instead to determine the stress and deformation fields. The full equations in this region lead to a local crack-propagation problem which is driven by the bending moment applied from the interior solution and is resisted by the combined effects of the viscous flow into the crack tip and the fracture toughness of any bonding between the sheet and the substrate. We show that when viscosity is significant the rate of propagation is given by
$v=B\unicode[STIX]{x1D705}^{3}d\,F/\unicode[STIX]{x1D707}$
, where
$F(k_{Ic},k_{IIc})$
is a function of the dimensionless fracture toughnesses,
$k_{Ic}$
and
$k_{IIc}$
, which may be zero for the case of no bonding.
If the viscous pressures are not significant, as in a dry crack, the problem reduces to one in fracture mechanics, for which the propagation criterion is simply that the stress intensity at the crack tip should exceed the fracture toughness. Motivated by obvious applications to the processes of delamination and spalling, Zlatin & Khrapkov (Reference Zlatin and Khrapkov1986), Thouless et al. (Reference Thouless, Evans, Ashby and Hutchinson1987) and Suo & Hutchinson (Reference Suo and Hutchinson1990) calculated the stress intensities at the tip of semi-infinite or finite cracks running parallel to the free surface of an elastic solid in terms of the remote loading. Dyskin, Germanovich & Ustinov (Reference Dyskin, Germanovich and Ustinov2000) and Bunger & Detournay (Reference Bunger and Detournay2005) showed how Zlatin and Khrapkov’s stress intensities can be used in conjunction with beam or plate theory to describe toughness-controlled growth of an inviscid pressurized blister. A key result is that the loading of the crack tip is dominated by the bending moment.
Zhang, Detournay & Jeffrey (Reference Zhang, Detournay and Jeffrey2002), Zhang, Jeffrey & Detournay (Reference Zhang, Jeffrey and Detournay2005) calculated solutions for fluid-driven propagation of a penny-shaped hydraulic fracture beneath a surface using the full elasticity equations for the whole problem to avoid making any assumptions about the depth-to-radius ratio. The problem considered here can be regarded as a near-tip asymptotic limit of their work, which is particularly suited to shallow viscously controlled fracture such as the laccolith problem. Our aim is to determine simple expressions for the rate of propagation at the tip that can then be used as boundary conditions for a general interior problem without further extensive computations.
We begin in § 2 by formulating a travelling-wave problem to describe propagation of a fluid-filled crack, and then describe its numerical solutions in § 3. Initially, we assume that the crack propagates with fluid filling the crack tip, but discover that if the bond between the sheet and the substrate is sufficiently weak, then there must be a region of dry shear failure ahead of the fluid front. We extend the calculations to describe this situation in § 4. Having obtained a full set of solutions for the propagation speed of the crack in terms of the applied bending moment, viscous resistance and toughness, we illustrate their application in § 5 to determine straightforwardly the rate of spread of an axisymmetric fluid-filled blister in a number of different regimes.
2 Formulation of the problem
2.1 Physical and mathematical description
Consider a semi-infinite elastic solid, from which an elastic sheet of uniform thickness
$d$
is being peeled off on one side by application of a constant bending moment
$M$
(see figure 1). The thin gap, or crack, on the peeling side is filled with incompressible fluid of viscosity
$\unicode[STIX]{x1D707}$
. (The additional effects of fluid lag could also be included in the model, but are omitted here for simplicity.)
Figure 1. A sketch of the geometry of the problem. A bending moment
$M$
peels an elastic sheet of thickness
$d$
away from an elastic solid. The relative displacement of the sheet from the solid is
$g$
in the
$x$
direction and
$h$
in the
$y$
direction, and the gap of width
$h$
is filled with viscous fluid. On the right is a close-up of the crack tip.
We assume that the sheet and the solid are initially bonded together at their interface, and that the strength of the bond can be described by fracture toughnesses
$K_{Ic}$
and
$K_{IIc}$
for tensile and shear failure respectively (mode I and mode II fracture). We assume that the strength of the interface is less than the strength of either elastic solid so that the crack produced by the applied bending moment propagates along the interface. Such interfacial planes of weakness arise naturally in laminated materials, between sedimentary strata in geology and in analogue experiments (e.g. Pollard & Johnson Reference Pollard and Johnson1973; Suo & Hutchinson Reference Suo and Hutchinson1990; Kavanagh et al.
Reference Kavanagh, Rogers, Boutelier and Cruden2017). To reduce the number of dimensionless parameters for simplicity, we assume that the sheet has the same elastic properties as the solid, though our calculations could easily be generalized to dissimilar materials using the techniques described in Suo & Hutchinson (Reference Suo and Hutchinson1990).
We take axes as shown in figure 1, with the crack aligned along the
$x$
-axis and the crack tip instantaneously at the origin. Let
$h(x)$
and
$g(x)$
be the normal and tangential elastic displacements of the crack walls relative to each other. These displacements can each be represented by a distribution of dislocations along the crack, of densities
$h^{\prime }(x)$
and
$g^{\prime }(x)$
respectively, where primes denote
$\text{d}/\text{d}x$
. The dislocation densities can be shown to require opposing tractions on the crack faces given by
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\unicode[STIX]{x1D70E}_{yy}(x)\\ \unicode[STIX]{x1D70E}_{xy}(x)\end{array}\right]=-\bar{E}\int _{0}^{\infty }\unicode[STIX]{x1D646}\left(\frac{\tilde{x}-x}{d}\right)\left[\begin{array}{@{}c@{}}h^{\prime }(\tilde{x})\\ g^{\prime }(\tilde{x})\end{array}\right]\frac{\text{d}\tilde{x}}{d},\end{eqnarray}$$
(e.g. Head Reference Head1953; Thouless et al.
Reference Thouless, Evans, Ashby and Hutchinson1987; Yang & Li Reference Yang and Li1997), where
$\bar{E}=E/(1-\unicode[STIX]{x1D708}^{2})$
is the modulus for plane strain, and
$$\begin{eqnarray}\unicode[STIX]{x1D646}(\unicode[STIX]{x1D709})=-\frac{4}{\unicode[STIX]{x03C0}}\left[\begin{array}{@{}cc@{}}\displaystyle \frac{4-3\unicode[STIX]{x1D709}^{2}}{\unicode[STIX]{x1D709}(\unicode[STIX]{x1D709}^{2}+4)^{3}} & \displaystyle \frac{3\unicode[STIX]{x1D709}^{2}-4}{2(\unicode[STIX]{x1D709}^{2}+4)^{3}}\\ \displaystyle \frac{4-3\unicode[STIX]{x1D709}^{2}}{2(\unicode[STIX]{x1D709}^{2}+4)^{3}} & \displaystyle \frac{\unicode[STIX]{x1D709}^{4}+\unicode[STIX]{x1D709}^{2}+4}{\unicode[STIX]{x1D709}(\unicode[STIX]{x1D709}^{2}+4)^{3}}\end{array}\right].\end{eqnarray}$$
For the fluid-loaded crack of interest here, we have
$\unicode[STIX]{x1D70E}_{yy}=-p$
, where
$p(x)$
is the fluid pressure, and
$\unicode[STIX]{x1D70E}_{xy}=0$
. (The viscous shear stresses due to flow have the wrong symmetry to contribute to the relative displacements, and are also much smaller than the fluid pressures.) Thus (2.1) can be regarded as an integral equation relating the crack shape to the fluid pressure.
We use lubrication theory to describe the viscous flow in the thin gap. Hence the fluid pressure gradients drive a flux
$$\begin{eqnarray}q=-\frac{h^{3}}{12\unicode[STIX]{x1D707}}\frac{\text{d}p}{\text{d}x}.\end{eqnarray}$$
We look for a travelling-wave solution of the form
$h(x+vt)$
, propagating leftwards with constant speed
$v$
. For such a solution, we deduce from mass conservation that
$q=-vh$
and hence
$$\begin{eqnarray}\frac{\text{d}p}{\text{d}x}=\frac{12\unicode[STIX]{x1D707}v}{h^{2}}.\end{eqnarray}$$
The coupled equations (2.4) and (2.1) require boundary conditions for propagation at the crack tip and for prescribing the applied bending moment.
The stress intensities
$K_{I}$
and
$K_{II}$
at the crack tip can be determined from the asymptotic behaviour (Rice Reference Rice and Liebovitz1968)
$$\begin{eqnarray}h(x)\sim \frac{K_{I}}{\bar{E}}\left(\frac{32x}{\unicode[STIX]{x03C0}}\right)^{1/2},\quad g(x)\sim \frac{K_{II}}{\bar{E}}\left(\frac{32x}{\unicode[STIX]{x03C0}}\right)^{1/2}\quad \text{as }x\rightarrow 0_{+},\end{eqnarray}$$
of the displacements near the tip. Assuming linear elastic fracture mechanics, the condition for crack propagation is that the stress intensity is equal to the fracture toughness (Kanninen & Popelar Reference Kanninen and Popelar1985). We assume for now that the crack is propagating as a simple mode-I (tensile) fracture, which requires
$K_{I}=K_{Ic}$
.
For
$x\gg d$
, the displacement of the sheet can be described asymptotically by beam theory (Dyskin et al.
Reference Dyskin, Germanovich and Ustinov2000), which gives
$$\begin{eqnarray}p(x)=\frac{\bar{E}d^{3}}{12}h^{\prime \prime \prime \prime }\quad \text{and}\quad m(x)=\frac{\bar{E}d^{3}}{12}h^{\prime \prime },\end{eqnarray}$$
where
$m(x)$
is the local bending moment. We are considering peeling driven by an applied remote bending moment
$M$
, and so
$m(x)\rightarrow M$
as
$x\rightarrow \infty$
, which gives a boundary condition on
$h^{\prime \prime }$
. Hence the gap
$h$
between the sheet and the solid widens rapidly to the right like
$x^{2}$
and, from (2.4), the pressure gradient decreases rapidly like
$x^{-4}$
, confirming that the viscous resistance is dominated by the
$O(d)$
neighbourhood of the tip. Since we are considering peeling-by-bending here rather than peeling-by-pulling (Lister et al.
Reference Lister, Peng and Neufeld2013), we assume that there is not any remote tension also being applied to the sheet (or that it is much smaller than
$M/d$
and thus negligible). Nevertheless, the upward curvature
$h^{\prime \prime }$
of the sheet implies that its lower surface is in extension with strain
$dh^{\prime \prime }/2$
(and its upper surface is in compression with strain
$-dh^{\prime \prime }/2$
). The remote loading conditions are thus equivalent to
$$\begin{eqnarray}\frac{\bar{E}d^{3}}{12}h^{\prime \prime }\sim M,\quad g^{\prime }\sim \frac{d}{2}h^{\prime \prime }\quad \text{as }x\rightarrow \infty .\end{eqnarray}$$
2.2 Non-dimensionalization
We define dimensionless variables as follows:
$$\begin{eqnarray}x=d\,\unicode[STIX]{x1D709},\quad h(x)=\frac{M}{\bar{E}d}H(\unicode[STIX]{x1D709}),\quad g(x)=\frac{M}{\bar{E}d}G(\unicode[STIX]{x1D709}),\end{eqnarray}$$
$$\begin{eqnarray}p=\frac{M}{d^{2}}P(\unicode[STIX]{x1D709}),\quad K_{I}=Md^{-3/2}k_{I},\quad K_{II}=Md^{-3/2}k_{II},\quad V=\frac{\unicode[STIX]{x1D707}\bar{E}^{2}d^{5}v}{M^{3}}.\end{eqnarray}$$
With these scalings, the equations become
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}P\\ 0\end{array}\right]=\int _{0}^{\infty }\unicode[STIX]{x1D646}(\tilde{\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D709})\left[\begin{array}{@{}c@{}}H^{\prime }(\tilde{\unicode[STIX]{x1D709}})\\ G^{\prime }(\tilde{\unicode[STIX]{x1D709}})\end{array}\right]\text{d}\tilde{\unicode[STIX]{x1D709}},\end{eqnarray}$$
$$\begin{eqnarray}H^{2}P^{\prime }=12V\quad \text{or}\quad P(\unicode[STIX]{x1D709})=-12V\int _{\unicode[STIX]{x1D709}}^{\infty }\frac{\text{d}\tilde{\unicode[STIX]{x1D709}}}{H(\tilde{\unicode[STIX]{x1D709}})^{2}},\end{eqnarray}$$
$$\begin{eqnarray}\lim _{\unicode[STIX]{x1D709}\rightarrow \infty }H^{\prime \prime }=12,\quad \lim _{\unicode[STIX]{x1D709}\rightarrow \infty }G^{\prime }=6,\end{eqnarray}$$
$$\begin{eqnarray}k_{I}=\unicode[STIX]{x1D712}\lim _{\unicode[STIX]{x1D709}\rightarrow 0}\sqrt{\unicode[STIX]{x1D709}}H^{\prime },\quad k_{II}=\unicode[STIX]{x1D712}\lim _{\unicode[STIX]{x1D709}\rightarrow 0}\sqrt{\unicode[STIX]{x1D709}}G^{\prime },\end{eqnarray}$$
where
$\unicode[STIX]{x1D712}=(\unicode[STIX]{x03C0}/8)^{1/2}$
. (We chose not to absorb
$\unicode[STIX]{x1D712}$
into our definitions of
$k_{I}$
and
$k_{II}$
in order to maintain consistency with Zlatin & Khrapkov (Reference Zlatin and Khrapkov1986) and Thouless et al. (Reference Thouless, Evans, Ashby and Hutchinson1987); Detournay and co-workers define
$K_{ic}^{\prime }=2K_{ic}/\unicode[STIX]{x1D712}$
.)
2.3 Numerical solution
It was found convenient to solve (2.10)–(2.12) numerically for a given value of
$V$
, and then infer the corresponding values of
$k_{I}(V)$
and
$k_{II}(V)$
from (2.13). The first of these relationships could then be inverted, with
$k_{I}=k_{Ic}$
, to give the speed
$V$
in terms of the toughness
$k_{Ic}$
, which is the natural physical interpretation.
We discretized the equations by taking
$n+1$
points
$\unicode[STIX]{x1D709}_{0}=0<\unicode[STIX]{x1D709}_{1}<\cdots <\unicode[STIX]{x1D709}_{n}$
at which to represent
$H^{\prime }$
and
$G^{\prime }$
. Typically,
$n\approx 500$
and
$\unicode[STIX]{x1D709}_{n}\approx 800$
. The choice of points and of the interpolation of
$H^{\prime }$
and
$G^{\prime }$
between the points both took account of the square-root singularities at the tip. (The details are described in appendix A.) Given the
$2(n+1)$
coefficients of the interpolating functions, the integrals in (2.10) and (2.11b
) can all be done analytically. We obtain
$n$
equations from equating the two expressions for
$P$
at
$n$
midpoints
$\unicode[STIX]{x1D709}_{i+1/2}\in [\unicode[STIX]{x1D709}_{i},\unicode[STIX]{x1D709}_{i+1}]$
,
$n$
equations from the condition
$\unicode[STIX]{x1D70E}_{xy}=0$
at those midpoints, and two equations from the limiting behaviour (2.12). This system of equations was solved by Newton’s method.
In order to apply the limits (2.12) to the information in
$\unicode[STIX]{x1D709}\leqslant \unicode[STIX]{x1D709}_{n}$
, we develop an asymptotic expansion using the beam approximation (2.6) for
$\unicode[STIX]{x1D709}\gg 1$
. In the dimensionless variables,
$P=H^{\prime \prime \prime \prime }/12$
, which we combine with (2.11a
) to obtain
$$\begin{eqnarray}H^{\prime \prime \prime \prime \prime }=144V/H^{2}.\end{eqnarray}$$
But we know from (2.12) that
$H(\unicode[STIX]{x1D709})=6\unicode[STIX]{x1D709}^{2}+o(\unicode[STIX]{x1D709}^{2})$
, as
$\unicode[STIX]{x1D709}\rightarrow \infty$
, and so we can solve (2.14) iteratively to find
$$\begin{eqnarray}\frac{1}{12}H^{\prime \prime }(\unicode[STIX]{x1D709})=1-\frac{V}{18\unicode[STIX]{x1D709}}-\frac{V^{2}}{18^{2}}\frac{\ln \unicode[STIX]{x1D709}}{\unicode[STIX]{x1D709}^{2}}+O(1/\unicode[STIX]{x1D709}^{2})\quad \text{and}\quad G^{\prime }=H^{\prime \prime }/2\end{eqnarray}$$
from (2.7b
). These conditions can be used at
$\unicode[STIX]{x1D709}_{n}$
in place of (2.12). (The
$O(1/\unicode[STIX]{x1D709}^{2})$
correction in (2.15) cannot be determined solely from the far-field behaviour.)
3 Results
For
$V=0$
the problem is static, there are no viscous pressures and (2.10)–(2.12) simply describe a semi-infinite crack beneath a free surface that is loaded by a remote bending moment. This problem was solved by Zlatin & Khrapkov (Reference Zlatin and Khrapkov1986), who found that
$(k_{I},k_{II})=(1.932,1.506)$
, which agrees with, and provides a check on, our numerical results.
Using the case
$V=0$
as a starting solution, we increased
$V$
, iterated the Newton scheme to convergence, and then repeated to obtain a sequence of solutions for increasing values of
$V$
. Two typical results for
$H^{\prime }$
,
$G^{\prime }$
and
$P$
with
$V=0.1$
and 0.65 are shown in figure 2, along with the expected asymptotic behaviour for
$\unicode[STIX]{x1D709}\ll 1$
and
$\unicode[STIX]{x1D709}\gg 1$
. (The behaviour of
$P$
follows from
$P^{\prime }=12V/H^{2}$
and the behaviour of
$H$
.) We note that the larger value of
$V$
requires a larger negative pressure in
$\unicode[STIX]{x1D709}\ll 1$
to suck fluid into the opening gap; the larger negative pressure in the tip reduces the values of
$H^{\prime }$
by pulling the crack walls together. In particular, it reduces the stress intensity
$k_{I}=\unicode[STIX]{x1D712}\lim _{\unicode[STIX]{x1D709}\rightarrow 0}\unicode[STIX]{x1D709}^{1/2}H^{\prime }(\unicode[STIX]{x1D709})$
. Alternatively put, some of the applied remote bending moment is supported by the negative fluid pressures, so that less stress is applied to the tip.
Figure 2. Numerical solutions for the dislocation densities
$H^{\prime }$
and
$G^{\prime }$
and the pressure
$P$
for speeds
$V=0.1$
and 0.65 (stress intensities
$k_{I}=1.83$
and 0.69). The second row of figures uses logarithmic scales to show the expected asymptotic behaviour (solid lines):
$H^{\prime }\sim (k_{I}/\unicode[STIX]{x1D712})\unicode[STIX]{x1D709}^{-1/2}$
,
$G^{\prime }\sim (k_{II}/\unicode[STIX]{x1D712})\unicode[STIX]{x1D709}^{-1/2}$
,
$P\sim (3\unicode[STIX]{x1D712}^{2}V/k_{I}^{2})\ln \unicode[STIX]{x1D709}$
as
$\unicode[STIX]{x1D709}\rightarrow 0$
, where
$\unicode[STIX]{x1D712}=(\unicode[STIX]{x03C0}/8)^{1/2}$
; and
$H^{\prime }\sim 12\unicode[STIX]{x1D709}$
,
$G^{\prime }\rightarrow 6$
,
$P\rightarrow 0$
as
$\unicode[STIX]{x1D709}\rightarrow \infty$
.
Figure 3. The mode-I stress intensity
$k_{I}$
as a function of the speed
$V$
(filled symbols). Also shown for discussion in § 4 is the mode-II stress intensity
$k_{II}$
(open symbols).
The variation of
$k_{I}$
with
$V$
is shown in figure 3, confirming a monotonic decrease of
$k_{I}$
as the viscous pressure drop in the tip increases. It is perhaps not surprising that as
$k_{I}\rightarrow 0$
(negligible toughness) the speed
$V$
tends to a finite limit
$V_{0}\approx 0.678$
determined entirely by the fluid-mechanical resistance to propagation. It is initially more surprising that the approach to this limit is singular, with
$k_{I}$
behaving locally like
$(V_{0}-V)^{0.316}$
.
Some insight can be obtained by considering the behaviour of
$H^{\prime }$
near the tip as
$V\rightarrow V_{0}$
(or
$k_{I}\rightarrow 0$
), as shown in figure 4. While
$H^{\prime }\sim (k_{I}/\unicode[STIX]{x1D712})\unicode[STIX]{x1D709}^{-1/2}$
as
$\unicode[STIX]{x1D709}\rightarrow 0$
, as
$k_{I}\rightarrow 0$
more and more of the near-tip solution looks like
$H^{\prime }\sim A\unicode[STIX]{x1D709}^{-1/3}+O(\unicode[STIX]{x1D709}^{-4/3})$
for
$A\approx 4.2$
, with the
$k_{I}\unicode[STIX]{x1D709}^{-1/2}$
behaviour confined to a boundary layer near
$\unicode[STIX]{x1D709}=0$
. This sort of boundary-layer structure was discovered and analysed by Garagash & Detournay (Reference Garagash and Detournay2005) in the context of finite or semi-infinite cracks propagating through an infinite elastic solid with a small dimensionless fracture toughness. We can establish the connection as follows.
Figure 4. The near-tip behaviour of
$H^{\prime }$
as
$k_{I}$
decreases towards 0. The
$\unicode[STIX]{x1D709}^{-1/2}$
behaviour is increasingly confined to a very thin region near
$\unicode[STIX]{x1D709}=0$
, while more and more of the solution tends towards
$H^{\prime }\sim \unicode[STIX]{x1D709}^{-1/3}$
. We did not calculate
$H^{\prime }$
directly for
$k_{I}=0$
, but show an extrapolation to it.
For a fluid-driven crack with
$k_{I}=0$
it should be anticipated that the crack-tip opening and pressure are governed by a viscous–elastic balance with
$H\propto \unicode[STIX]{x1D709}^{2/3}$
and
$P\propto \unicode[STIX]{x1D709}^{-1/3}$
as
$\unicode[STIX]{x1D709}\rightarrow 0$
(Spence & Sharp Reference Spence and Sharp1985; Lister Reference Lister1990; Desroches et al.
Reference Desroches, Detournay, Lenoach, Papanastasiou, Pearson, Thiercelin and Cheng1994). Crucially, this balance is locally determined in the tip, and is independent of more-remote loading or boundary conditions. For
$\unicode[STIX]{x1D709}\ll 1$
, the elasticity kernel (2.2) and integral (2.10) reduce to the much simplified form
$$\begin{eqnarray}P(\unicode[STIX]{x1D709})=\frac{1}{4\unicode[STIX]{x03C0}}\int _{0}^{\infty }\frac{H^{\prime }(\tilde{\unicode[STIX]{x1D709}})}{\tilde{\unicode[STIX]{x1D709}}-\unicode[STIX]{x1D709}}\,\text{d}\tilde{\unicode[STIX]{x1D709}},\end{eqnarray}$$
which is the same as that for a semi-infinite crack in an infinite solid.
For the case
$k_{I}=0$
, (3.1) and (2.11) have leading-order solutions
$$\begin{eqnarray}H_{0}=6(3V_{0}^{2})^{1/6}\unicode[STIX]{x1D709}^{2/3}+o(\unicode[STIX]{x1D709}^{2/3}),\quad P_{0}=-\left(\frac{V_{0}}{3\unicode[STIX]{x1D709}}\right)^{1/3}+o(\unicode[STIX]{x1D709}^{-1/3}).\end{eqnarray}$$
With
$V_{0}=0.678$
, equation (3.2) gives
$H^{\prime }\sim 4.22\unicode[STIX]{x1D709}^{-1/3}$
in agreement with figure 4.
However, for
$k_{I}>0$
(3.2) does not satisfy the tip condition (2.13). Garagash & Detournay (Reference Garagash and Detournay2005) showed how (2.13) can be satisfied for
$0<k_{I}\ll 1$
by introducing a so-called ‘LEFM’ (linear-elastic-fracture-mechanics) boundary layer on the small scale
$\unicode[STIX]{x1D709}=O(k_{I}^{6})$
, where
$H=O(k_{I}^{4})$
, and matching this inner solution to (3.2) as the leading-order outer solution. They also found that the boundary layer leads to
$O(k_{I}^{4-6s})$
corrections to the outer solution, where
$s\approx 0.139$
comes from solving a transcendental equation and
$u\equiv 4-6s\approx 3.168$
. In appendix B, we show how this correction term can be used to calculate an asymptotic prediction
$V\approx V_{0}-0.0950k_{I}^{u}$
as
$k_{I}\rightarrow 0$
. Figure 5 shows that there is remarkably good agreement with this linear prediction, even for relatively large values of
$k_{I}$
.
Figure 5. The numerical values of
$k_{I}^{u}$
are plotted as points against the values of
$V$
. A linear fit from the two smallest
$k_{I}$
values is plotted as a solid line, a quadratic fit from the three smallest
$k_{I}$
values is plotted as a dashed line. They are almost indistinguishable at this scale. The difference between the two fits at
$k_{I}=0$
is only
${\approx}0.002\,\%$
, which provides an estimate of the error in extrapolating to calculate
$V_{0}$
(not accounting for the discretization error due to
$n$
).
4 Dry cracking ahead of the fluid front
Thus far, we have been assuming for simplicity that the crack propagates as a simple mode-I (tensile) fracture, with speed
$V$
determined by the dimensionless criterion
$k_{I}(V)=k_{Ic}$
for tensile failure. However, owing to the asymmetry of the geometry about
$y=0$
, both the remote bending moment and the fluid pressure loading result in some mode-II (shear) loading of the crack tip and not just in tensile loading. The failure criterion for such mixed-mode loading of an interfacial crack is found experimentally to be fairly well represented by the elliptical form
$$\begin{eqnarray}k_{I}^{2}+\unicode[STIX]{x1D706}k_{II}^{2}=k_{Ic}^{2},\end{eqnarray}$$
where
$k_{I}$
and
$k_{II}$
are the stress intensities (2.13) at the tip,
$\unicode[STIX]{x1D706}^{1/2}=K_{Ic}/K_{IIc}=k_{Ic}/k_{IIc}$
is the ratio of the fracture toughnesses for pure tensile loading and pure shear loading and
$\unicode[STIX]{x1D706}$
is typically 0.1–0.2 (Jensen, Hutchinson & Kim Reference Jensen, Hutchinson and Kim1990; Yuuki et al.
Reference Yuuki, Liu, Ohira and Ono1994).
As
$V$
increases from 0 to the limiting speed 0.678 for the solutions calculated in § 3,
$k_{I}$
decreases monotonically from the static value 1.932 (Zlatin & Khrapkov Reference Zlatin and Khrapkov1986) down to
$0$
(see figure 3), and
$k_{II}$
decreases slowly and monotonically from the static value 1.506 to about 1.385. Provided
$1.385^{2}\unicode[STIX]{x1D706}<k_{Ic}^{2}<1.932^{2}+1.506^{2}\unicode[STIX]{x1D706}$
, there is thus a unique value of
$V$
and solution from § 3 that satisfies the failure criterion (4.1). However, if
$k_{IIc}=k_{Ic}\unicode[STIX]{x1D706}^{-1/2}<1.385$
even the fastest solution from § 3 has
$k_{II}>k_{IIc}$
(and
$k_{I}=0$
); the crack tip is under greater shear stress than it can withstand, and we would expect the crack to propagate faster as a result. We infer that shear failure at the crack tip must allow it to outrun the fluid front, such that there is a region of dry shear between the crack tip and the fluid front. (This phenomenon should be distinguished from the concept of ‘fluid lag’, which is caused by vapour in a low-pressure tip rather than dry shear failure.) We now analyse this possibility.
4.1 Equations
Suppose the crack tip is at
$\unicode[STIX]{x1D709}=-L$
and the fluid front is at
$\unicode[STIX]{x1D709}=0$
in the frame of a travelling-wave solution propagating to the left. Along the dry part of the crack,
$-L<\unicode[STIX]{x1D709}<0$
, the crack walls are in contact and so the normal displacement is zero,
$H(\unicode[STIX]{x1D709})=H^{\prime }(\unicode[STIX]{x1D709})=0$
. We assume here, for simplicity, that friction on the crack walls is negligible and so the tangential displacement
$G(\unicode[STIX]{x1D709})$
is such that the shear stress is zero,
$\unicode[STIX]{x1D70E}_{xy}=0$
. (Future work might explore the effects of different friction laws.) The elastic equation (2.10) is thus unaltered except for replacing the lower limit in the integral by
$-L$
. The lubrication equation (2.11) and far-field conditions (2.12) are likewise unaltered.
Now let
$$\begin{eqnarray}k_{I}\equiv \unicode[STIX]{x1D712}\lim _{\unicode[STIX]{x1D709}\rightarrow -L}\sqrt{\unicode[STIX]{x1D709}+L}H^{\prime }(\unicode[STIX]{x1D709}),\quad k_{II}\equiv \unicode[STIX]{x1D712}\lim _{\unicode[STIX]{x1D709}\rightarrow -L}\sqrt{\unicode[STIX]{x1D709}+L}G^{\prime }(\unicode[STIX]{x1D709}),\quad k_{I}^{f}\equiv \unicode[STIX]{x1D712}\lim _{\unicode[STIX]{x1D709}\rightarrow 0}\sqrt{\unicode[STIX]{x1D709}}H^{\prime }(\unicode[STIX]{x1D709}),\end{eqnarray}$$
where
$\unicode[STIX]{x1D712}=(\unicode[STIX]{x03C0}/8)^{1/2}$
, so that
$k_{I}$
and
$k_{II}$
denote the usual stress intensities for a crack tip at
$\unicode[STIX]{x1D709}=-L$
. Here
$H^{\prime }=0$
in the dry part
$\unicode[STIX]{x1D709}<0$
, and so
$k_{I}=0$
follows automatically. The criterion for crack-tip propagation at
$\unicode[STIX]{x1D709}=-L$
is thus
$k_{II}=k_{IIc}$
corresponding to simple shear failure. The third stress intensity
$k_{I}^{f}$
denotes the strength of the singularity at
$\unicode[STIX]{x1D709}=0$
that would, in general, result from solving the elastic problem with
$P(\unicode[STIX]{x1D709})$
prescribed in
$\unicode[STIX]{x1D709}>0$
and
$H=0$
prescribed in
$\unicode[STIX]{x1D709}<0$
. Here, however, the solid had already fractured at
$\unicode[STIX]{x1D709}=0$
and has no strength to support a non-zero stress intensity. Hence the location and speed of the fluid front must be such that
$k_{I}^{f}=0$
.
The physical boundary conditions at the fluid front and the crack tip are thus
$k_{I}^{f}=0$
and
$k_{II}=k_{IIc}$
, and these two conditions determine the dry length
$L$
and speed
$V$
of the solution. In practice, it is more convenient numerically to prescribe values of
$L$
and
$V$
, solve for the geometry to find the values of
$k_{I}^{f}(V,L)$
and
$k_{II}(V,L)$
, and then invert the first relationship to impose the physical condition
$k_{I}^{f}=0$
. Further details are given in § A.3.
Figure 6. Values of the stress intensities
$k_{I}^{f}$
at
$\unicode[STIX]{x1D709}=0$
and
$k_{II}$
at
$\unicode[STIX]{x1D709}=-L$
as functions of the dry crack length
$L$
ahead of the fluid front and the speed
$V$
of propagation. The desired physical solutions are those with
$k_{I}^{f}=0$
, which then implies a relationship between
$L$
and
$V$
.
Figure 7. The relationships between speed
$V_{0}$
, dry length
$L$
and stress intensity
$k_{II}$
for solutions with
$k_{I}^{f}=0$
. These give a unique solution with
$k_{I}^{f}=0$
and
$k_{II}=k_{IIc}$
for
$0\leqslant k_{IIc}\leqslant 1.385$
. Negative values of
$k_{II}<0$
(hollow squares) do not correspond to a physically attainable solution.
4.2 Results
In figure 6 we show the values of
$k_{I}^{f}$
and
$k_{II}$
for varying
$L$
at fixed
$V$
and for varying
$V$
at fixed
$L$
. The most significant observations are: (i) Increasing the length
$L$
of the dry region relieves the shear loading of the crack tip; the stress intensity
$k_{II}$
decreases monotonically from the values 1.506–1.385 obtained for
$L=0$
down to zero for
$L\approx 2.7$
, and we can thus find solutions with
$k_{II}=k_{IIc}$
. (ii) Increasing the speed
$V$
decreases the (unphysical) tensile stress intensity
$k_{I}^{f}$
at the fluid front, with
$k_{I}^{f}$
approaching zero (the desired value for an already-fractured solid) in the same power-law way as seen previously in figure 3 and analysed in appendix B.
For fixed
$L$
we extrapolate these results to find where
$k_{I}^{f}=0$
at some speed
$V_{0}(L)$
with a corresponding stress intensity
$k_{II}(L)$
. The relationships between
$V_{0}$
,
$L$
and
$k_{II}$
corresponding to the solutions with
$k_{I}^{f}=0$
are shown in figure 7. As hoped, we obtain a unique solution
$k_{II}=k_{IIc}$
for each value of
$k_{IIc}$
in the range 0–1.385 not covered by the solutions of § 3. As might be expected, both
$L$
and
$V_{0}$
increase as the toughness of the solid decreases, and reach finite limits as
$k_{IIc}\rightarrow 0$
. (The solutions with
$k_{II}<0$
for
$L\gtrsim 2.7$
are not physically attainable since they do not correspond to a stable equilibria, nor can they be reached by the tip extending from zero.) The relationship between
$V_{0}$
and
$k_{II}^{2}$
is approximately linear with
$V_{0}\rightarrow 1.15$
as
$k_{II}\rightarrow 0$
.
5 Summary and application to blisters
5.1 Summary of regimes
The results of §§ 3 and 4 allow us to find solutions for all values of the dimensionless fracture toughnesses
$k_{Ic}$
and
$k_{IIc}$
(see figure 8). First, from (4.1) and the static values of
$k_{I}$
and
$k_{II}$
(Zlatin & Khrapkov Reference Zlatin and Khrapkov1986), we deduce that if
$(1.932/k_{Ic})^{2}+(1.506/k_{IIc})^{2}<1$
then the material is too tough and the crack will not propagate. Secondly, if
$k_{IIc}<1.385$
then the material is sufficiently weak that the crack will propagate as described in § 4 with a dry shear crack of length
$L(k_{IIc})$
preceding the fluid front, and with the speed set by the condition
$k_{II}(V)=k_{IIc}$
. Thirdly, if
$k_{Ic}$
and
$k_{IIc}$
lie between the first and second regimes then the crack will propagate as described in § 3 with fluid filling the crack tip, and with the speed set by the condition that
$k_{I}(V)$
and
$k_{II}(V)$
satisfy (4.1). Recall that fluid lag was assumed negligible for simplicity, but could be included in future work. (While we have assumed a failure criterion of the form (4.1), the method could easily be generalized to any sensible criterion of the form
$G(k_{I},k_{II})=G_{c}$
.)
Figure 8. The failure criterion (4.1) for mixed-mode loading of the crack tip defines an ellipse
$(k_{I}/k_{Ic})^{2}+(k_{II}/k_{IIc})^{2}=1$
with semi-axes of lengths
$k_{ic}=K_{ic}d^{3/2}/M$
. For large
$K_{ic}$
(small
$M$
) the ellipse does not intersect either solution curve (dashed) and there is no propagation; for smaller
$K_{ic}$
(larger
$M$
) the ellipse intersects one of the two solution curves (circles) and the crack propagates either with a fluid-filled tip or with a preceding dry shear crack. The dimensionless speed
$V$
depends on the point of intersection.
Our calculations thus provide the dimensionless propagation speed
$V$
of the crack as a function of the remote loading, viscous resistance and fracture toughness. These solutions are near-tip asymptotics which describe the peeling process at the front of a larger-scale problem that provides the remote bending stress. In order to facilitate use of our results as an effective boundary condition for the larger-scale problem, without having to repeat all the numerical computations, we provide the following empirical fits for the relationships between speed and stress intensity from §§ 3 and 4:
$$\begin{eqnarray}\displaystyle & \displaystyle V=0.678-0.095k_{I}^{u}+0.0038k_{I}^{3u/2}\quad \text{(fluid-filled tip)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V=0.0377+7.0(1.5-k_{II})-12.3(1.5-k_{II})^{2}\quad \text{(fluid-filled tip)}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle V=1.15-0.248k_{IIc}^{2}\quad \text{(dry tip)}. & \displaystyle\end{eqnarray}$$
$v$
resulting from the bending moment
$M$
is obtained from 
$$\begin{eqnarray}v=\frac{M^{3}V(k_{Ic},k_{IIc})}{\unicode[STIX]{x1D707}\bar{E}^{2}d^{5}},\quad \text{where }k_{Ic}=\frac{K_{Ic}d^{3/2}}{M},k_{IIc}=\frac{K_{IIc}d^{3/2}}{M}.\end{eqnarray}$$
Alternatively, we can write (5.2) in terms of the bending stiffness
$B=\bar{E}d^{3}/12$
of the sheet and the curvature
$\unicode[STIX]{x1D705}=M/B$
behind the propagating front:
$$\begin{eqnarray}v=\frac{Bd}{144\unicode[STIX]{x1D707}}\unicode[STIX]{x1D705}^{3}V.\end{eqnarray}$$
To illustrate how these equations can be used as boundary conditions of an interior problem, we reconsider some of the axisymmetric blister problems described in Lister et al. (Reference Lister, Peng and Neufeld2013), but with the propagation rate determined by viscous-controlled fracture rather than by peeling from a prewetting film.
Figure 9. The empirical fits (5.1) (solid lines) are good approximations to the numerical solutions (symbols), allowing use as effective boundary conditions.
5.2 Application to axisymmetric propagation of blisters
Suppose an axisymmetric fluid blister of radius
$R(t)$
and thickness
$h(r,t)$
is formed by injecting a volumetric flux
$Q$
of fluid at
$r=0$
below an elastic sheet of thickness
$d\ll R$
resting on an elastic solid. If
$h\ll d$
then we can neglect stretching of the sheet above the blister, and the fluid pressure far from the edge (
$R-r\gg d$
) is given by the combination
$p=B\unicode[STIX]{x1D6FB}^{4}h+\unicode[STIX]{x1D70C}g(h-z)$
of bending stresses and hydrostatic pressure. As noted in the Introduction, because the sixth-order equation (1.1) (and its generalization to include gravity) does not support solutions with a propagating front, we expect an interior solution where
$\unicode[STIX]{x1D735}p=\mathbf{0}$
at leading order, which must be matched to a propagating frontal solution.
Solution of
$p=\text{const}.$
, with
$h(R)=h^{\prime }(R)=0$
yields
$$\begin{eqnarray}h(r)=h(0)\frac{f(R)-f(r)}{f(R)-f(0)},\quad \text{where }f(r)=\text{Im}\frac{\ell _{g}\text{I}_{0}(\unicode[STIX]{x1D714}r/\ell _{g})}{\unicode[STIX]{x1D714}\text{I}_{1}(\unicode[STIX]{x1D714}R/\ell _{g})},\unicode[STIX]{x1D714}=\text{e}^{\text{i}\unicode[STIX]{x03C0}/4},\end{eqnarray}$$
$\text{I}_{0}(z)$
and
$\text{I}_{1}(z)$
are modified Bessel functions, and
$\ell _{g}=(B/\unicode[STIX]{x1D70C}g)^{1/4}$
is the ‘elastogravity’ length scale at which bending stresses and gravity have comparable effects. The variation of these shapes with
$R/\ell _{g}$
is shown in figure 10. From the general solution (5.4) one can readily obtain expressions for the volume
$Qt$
and frontal curvature
$\unicode[STIX]{x1D705}=h^{\prime \prime }(R)$
and then use (5.3) to solve numerically for
$R(t)$
. However, it is more illuminating to consider the limits
$R\ll \ell _{g}$
and
$R\gg \ell _{g}$
.
Figure 10. The quasistatic interior solution (5.4) for the shape of a blister of radius
$R$
for various values of
$R/\ell _{g}$
(solid lines), where
$\ell _{g}=(B/\unicode[STIX]{x1D70C}g)^{1/4}$
is the elastogravity length, with the asymptotes as
$R/\ell _{g}\rightarrow 0,\infty$
(dashed).
For
$R\ll \ell _{g}$
bending stresses dominate the effects of gravity, and (5.4) can be simplified to
$$\begin{eqnarray}h(r,t)=\frac{3Qt}{\unicode[STIX]{x03C0}R^{2}(t)}\left(1-\frac{r^{2}}{R^{2}(t)}\right)^{2}.\end{eqnarray}$$
Assuming that the toughness of any bonding between the sheet and the solid is negligible, such that
$k_{Ic}=k_{IIc}=0$
, we obtain
$\text{d}R/\text{d}t$
from (5.3) with
$V=1.15$
and
$\unicode[STIX]{x1D705}=24Qt/\unicode[STIX]{x03C0}R^{4}$
. Integration yields
$$\begin{eqnarray}\displaystyle & \displaystyle R(t)=1.21\left(\frac{BdQ^{3}}{\unicode[STIX]{x1D707}}\right)^{1/13}t^{4/13}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle h(0,t)=0.66\left(\frac{\unicode[STIX]{x1D707}Q^{7}}{Bd}\right)^{1/13}t^{5/13}. & \displaystyle\end{eqnarray}$$
For
$R\gg \ell _{g}$
the effects of gravity dominate and the blister is flat-topped (like a large-Bond-number puddle) except within
$O(\ell _{g})$
of the edge where the bending stresses result in a peripheral shape
$$\begin{eqnarray}h=\frac{Qt}{\unicode[STIX]{x03C0}R^{2}}\left(1-\text{Im}\frac{\exp [\unicode[STIX]{x1D714}(R-r)/\ell _{g}]}{\unicode[STIX]{x1D714}}\right),\end{eqnarray}$$
with frontal curvature
$\unicode[STIX]{x1D705}=Qt/\unicode[STIX]{x03C0}R^{2}\ell _{g}^{2}$
. Again assuming negligible toughness and purely viscous control such that
$V=1.15$
, we integrate to obtain
$$\begin{eqnarray}\displaystyle & \displaystyle R(t)=0.33\left(\frac{BdQ^{3}}{\unicode[STIX]{x1D707}\ell _{g}^{6}}\right)^{1/7}t^{4/7}, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle h(0,t)=2.88\left(\frac{\unicode[STIX]{x1D707}Q\ell _{g}^{6}}{Bd}\right)^{1/7}t^{-1/7}. & \displaystyle\end{eqnarray}$$
From (5.6)–(5.7) we find that
$M\propto h^{\prime \prime }(R)\propto t^{-3/13}$
for
$R\ll \ell _{g}$
and from (5.9)–(5.10) that
$M\propto t^{-1/7}$
for
$R\gg \ell _{g}$
. It follows that if the toughness is not actually zero then from (5.2)
$k_{Ic}$
and
$k_{IIc}$
will increase with time, and the effects of toughness will eventually become significant. The resultant transition period toward toughness control has no analytical solution, but requires numerical solution using (5.5) or (5.8) to relate
$M=B\unicode[STIX]{x1D705}$
to the radius
$R$
, and then (5.2) to find
$\text{d}R/\text{d}t$
. The numerical problem is only an ordinary differential equation coupled to a few algebraic equations, and is easily programmed.
The long-term limit beyond this transition period is controlled by toughness rather than viscosity. In the toughness regime
$R$
increases with volume
$Qt$
in such a way that a quasistatic equilibrium is maintained, wherein the static stress intensities due to
$M$
(Zlatin & Khrapkov Reference Zlatin and Khrapkov1986) lie on the yield criterion (4.1). Thus
$M$
is given by the static yield criterion
$$\begin{eqnarray}M=d^{3/2}[(1.932/K_{Ic})^{2}+(1.506/K_{IIc})^{2}]^{-1/2},\end{eqnarray}$$
and both
$M$
and
$\unicode[STIX]{x1D705}=M/B$
are constant. Using (5.5) or (5.8), we find that
$$\begin{eqnarray}R\propto \left(\frac{BQt}{K_{Ic}d^{3/2}}\right)^{1/4}\quad (R\ll \ell _{g})\text{ or }R\propto \left(\frac{BQt}{\ell _{g}^{2}K_{Ic}d^{3/2}}\right)^{1/2}\quad (R\gg \ell _{g}),\end{eqnarray}$$
in agreement with detailed calculations by Bunger & Detournay (Reference Bunger and Detournay2005) and Bunger & Cruden (Reference Bunger and Cruden2011).
A transition of a different kind occurs if
$h$
in (5.7) increases to
$O(d)$
. In this case the tension due to stretching of the sheet above the blister can no longer be neglected and one should instead calculate the shape of the blister using the Föppl–von Kármán equations (see Jensen Reference Jensen1991; Lister et al.
Reference Lister, Peng and Neufeld2013). As
$h/d$
increases, this modifies the relationship giving the peripheral bending moment
$M$
in terms of the volume
$Qt$
and radius
$R$
. Moreover, it is found that the radial tension
$T$
increases to
$O(M/d)$
from
$O(Mh/d^{2})$
and so starts to contribute at leading order to the effective far-field loading of the near-tip problem. In particular, (2.12) needs to be modified to
$G^{\prime }\rightarrow 6+Td/M$
as
$\unicode[STIX]{x1D709}\rightarrow \infty$
, where the value of
$Td/M$
is determined by the interior blister solution. While this introduces another dimensionless parameter
$Td/M$
to the near-tip problem, and thus affects the numerical value of the dimensionless speed
$V$
, it does not change the dimensional scaling of the speed
$v$
in (5.2).
For
$d\ll h\ll R\ll \ell _{g}$
, the interior solution can be found by neglecting bending stresses and solving the membrane equations to obtain a roughly parabolic shape that approaches
$r=R$
with a slope
$\unicode[STIX]{x1D703}\propto Qt/R^{3}$
and tension
$T\propto \bar{E}d(Qt/R^{3})^{2}$
(see Lister et al.
Reference Lister, Peng and Neufeld2013) (This is the elastic analogue to the spherical-cap shape of a capillary drop with small contact angle.) This peripheral slope is matched to a static bending boundary layer where bending stresses re-enter the problem to give
$$\begin{eqnarray}h^{\prime }=\unicode[STIX]{x1D703}\{\text{e}^{(r-R)(T/B)^{1/2}}-1\}.\end{eqnarray}$$
The bending boundary-layer width,
$(B/T)^{1/2}=O(d/\unicode[STIX]{x1D703})$
, is much larger than the
$O(d)$
length scale of the near-tip viscous solution. The near-tip solution is thus nested within the boundary layer and forced by a bending moment
$M=(1/12)(BT)^{1/2}\unicode[STIX]{x1D703}\propto (B/d)(Qt/R^{3})^{2}$
and by the tension
$T\propto \bar{E}d(Qt/R^{3})^{2}$
. (The ratio
$Td/M$
is a constant for
$h\gg d$
.) We substitute the scale of the bending moment into the dimensional scaling of (5.2) and integrate to obtain
$$\begin{eqnarray}R\propto \left(\frac{\bar{E}dQ^{6}}{\unicode[STIX]{x1D707}}\right)^{1/19}t^{7/19}.\end{eqnarray}$$
Again
$M$
decreases, like
$t^{-6/19}$
, and there would be an eventual transition to toughness control.
5.3 Comparison with other spreading mechanisms
The examples given in the previous subsection show how straightforwardly to apply the propagation speed (5.2) as a boundary condition to determine growth by fracture of a fluid-driven blister in three different forcing regimes, in which the interior shape is dominated by bending stresses, gravity or tension respectively. In each case there is a transition from viscous control to toughness control for fixed-flux injection. These solutions are also easy to generalize to the case where the volume of fluid is of the form
$Qt^{\unicode[STIX]{x1D6FC}}$
, for some
$\unicode[STIX]{x1D6FC}$
, perhaps due to fixed-pressure or fixed-volume injection.
The same three forcing regimes were analysed by Lister et al. (Reference Lister, Peng and Neufeld2013) in the context of a blister that spreads by peeling of an elastic sheet away from a prewetting film of fluid between the sheet and the substrate. The interior solutions were the same, but the peeling process results in a propagation speed
$v\propto (B^{2}h_{0}\unicode[STIX]{x1D705}^{5})^{1/2}/\unicode[STIX]{x1D707}$
rather than (5.2).
Hewitt et al. (Reference Hewitt, Balmforth and de Bruyn2015) analysed the three regimes in the context of a two-dimensional blister that can spread because a low-viscosity precursor phase at a fixed pressure
$-p_{0}$
occupies the propagating front. If the extent of this fluid lag is much greater than
$O(d)$
then one can use beam theory to calculate a frontal speed
$v\propto (B^{3}\unicode[STIX]{x1D705}^{7}/p_{0})^{1/2}/\unicode[STIX]{x1D707}$
. This has recently been confirmed in axisymmetric experiments by Ball & Neufeld (Reference Ball and Neufeld2018) and extended to include toughness by Wang & Detournay (Reference Wang and Detournay2018). If the extent of the fluid lag is
$O(d)$
, or less, then one should instead generalize the elastohydrodynamic description in § 2 to replace the lubrication equation (2.11) by
$P=-P_{0}$
in some lag region
$0<\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{0}$
. In the context of hydraulic or magma fracture the large confining pressure means the lag length is very unlikely to be much greater than the thickness
$d$
of the overburden, and thus the generalized elastohydrodynamic description seems a more appropriate way to address lag in these cases than beam theory.
In table 1 we show the various spreading exponents for the three forcing regimes and the four spreading control mechanisms for the general case of fluid volume proportional to
$t^{\unicode[STIX]{x1D6FC}}$
. The exponents for each regime are quite similar in numerical value for
$\unicode[STIX]{x1D6FC}=1$
despite the different mechanisms. This table is actually far from exhaustive when considering the range of possible peeling regimes, and a fuller categorization is given by Peng (Reference Peng2017). We note that the exponents for toughness control are the same as those for simpler models with a prescribed interfacial energy of adhesion or with capillary adhesion (Peng Reference Peng2017; Ball & Neufeld Reference Ball and Neufeld2018).
Table 1. Spreading exponents
$\unicode[STIX]{x1D6FD}$
in
$R\propto t^{\unicode[STIX]{x1D6FD}}$
for the axisymmetric spread of a blister of volume
$Qt^{\unicode[STIX]{x1D6FC}}$
, in regimes driven by bending stresses, gravity or tension in the interior, and resisted by different mechanisms at the tip.
a Assuming the dominant viscous resistance is nested inside the bending boundary layer (5.13).
6 Conclusions
The peeling by fluid injection of an elastic sheet away from a substrate is often regularized by invoking a thin prewetting film or a low-viscosity phase in the tip. In this paper, we have instead analysed fluid-driven peeling without such precursors, by considering an elastic sheet either bonded to, or simply laid on, an elastic substrate. To resolve the ‘elastic contact-line problem’ that arises from a naive combination of lubrication theory and beam theory, we recognized that the beam approximation breaks down near the propagating tip, and instead the full equations of elasticity and fracture should be combined with lubrication theory to determine the coupled pressures and deformations in this region.
We have solved numerically the resultant local crack-propagation problem, which is driven by the bending moment
$M$
applied from the interior solution and resisted by the combined effects of viscous flow into the crack tip and the toughness of any bonding between sheet and substrate. This problem yielded a one-parameter family of solutions: for strong bonding and small bending moment, the load is supported (quasi-) statically by the toughness, and propagation is slow; for weak bonding and large bending moment, the load is supported instead by the flow-induced viscous pressure drop in the crack tip, and the propagation rate is determined by the local elastohydrodynamics. The singular asymptotic approach (figure 5) to a finite propagation rate for the case of no bonding is given in appendix B.
Between the two limiting regimes, our calculations provide simple expressions (5.1) and (5.2) to determine the dimensionless tip propagation speed
$V$
, which can then be used as effective boundary conditions for an interior problem without further extensive computations. The dimensional speed scales like
$M^{3}/\unicode[STIX]{x1D707}\bar{E}^{2}d^{5}=Bd\unicode[STIX]{x1D705}^{3}/144\unicode[STIX]{x1D707}$
, where
$d$
is the sheet’s thickness,
$B=\bar{E}d^{3}/12$
its stiffness,
$\bar{E}=E/(1-\unicode[STIX]{x1D708}^{2})$
its plane-strain modulus and
$\unicode[STIX]{x1D705}$
the limiting curvature at the edge of the interior solution. The expressions for the propagation speed have been used to derive new similarity solutions for the spread of a fluid-filled blister in a variety of different regimes (see table 1).
A geological application of these results is to the propagation and growth of laccoliths, which are large tabular near-surface magmatic intrusions that propagate along subsurface bedding planes rather than breaching the surface (Bunger & Cruden Reference Bunger and Cruden2011; Michaut Reference Michaut2011). For the case of constant-rate injection into weak rock, with vapour occupying only a small proportion of the tip, we find the radial extent increases like
$t^{4/13}$
up to the elastogravity length scale
$(B/\unicode[STIX]{x1D70C}g)^{1/4}$
and
$t^{4/17}$
beyond it. In future work it would be interesting to reappraise the geological data in comparison with these and other spreading regimes.
A novel feature of the solutions in § 4 is the presence of a region of dry shear failure ahead of the fluid front, with extent comparable to the
$O(d)$
thickness of the overlying sheet. This possibility is a consequence of the mixed-mode loading of the crack tip which arises from asymmetry between the finite-thickness sheet and the semi-infinite substrate. Since the crack is confined to a planar interface, the shear loading of the tip cannot be alleviated simply by kinking or curving away from the initial crack plane (cf. e.g. Cotterell & Rice Reference Cotterell and Rice1980; Meriaux & Lister Reference Meriaux and Lister2002). Geologically, evidence for such shear failure might be sought in a dry joint ahead of the magmatic tip.
We have focused on the simplest problem that demonstrates our main point, that the full equations of elasticity provide a way to resolve the apparent elastic contact-line problem in beam theory. As a result, our solutions effectively have just a single parameter describing the strength of any bonding. In the course of the analysis, a number of extensions to the simple problem have been suggested for future work. These include allowing some fluid lag, adding a significant tension to the remote bending moment, having friction on any region of shear failure, and allowing the sheet and substrate to have different elastic properties. While these complicate the problem, we anticipate that the physical ideas elucidated in this paper will remain central.
Acknowledgements
D.J.S. was supported by the Engineering and Physical Sciences Research Council under the UROP scheme. T.M.J.L. was supported by a summer studentship from Trinity College, Cambridge. All data accompanying this publication are directly available within the publication.
Appendix A. Numerical schemes
A.1 Fluid-filled crack
We discretized the problem (2.10)–(2.12) by taking
$n+1$
points
$\unicode[STIX]{x1D709}_{i}$
,
$i=0,\ldots ,n$
, at which to represent
$H^{\prime }$
and
$G^{\prime }$
. We used a set of points of the form
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}_{i}=\tan ^{2}(\unicode[STIX]{x1D719}i/m),\quad i=1,\ldots ,m<n, & \displaystyle\end{eqnarray}$$
$$\begin{eqnarray}\displaystyle & \displaystyle \unicode[STIX]{x1D709}_{i}=(\unicode[STIX]{x1D709}_{m}/\unicode[STIX]{x1D709}_{m-1})\unicode[STIX]{x1D709}_{i-1},\quad i=m+1,\ldots ,n, & \displaystyle\end{eqnarray}$$
where
$\unicode[STIX]{x1D719}$
and
$m$
were such that
$\unicode[STIX]{x1D709}_{m}=O(10)$
and
$\unicode[STIX]{x1D709}_{n}=O(10^{3})$
. This was chosen so that points are concentrated in a square-root manner in the important region near the tip, and spread out in a geometric progression in the far field
$\unicode[STIX]{x1D709}\gg 1$
, but it is otherwise fairly arbitrary.
For each interval
$\unicode[STIX]{x1D709}_{i-1}<\unicode[STIX]{x1D709}<\unicode[STIX]{x1D709}_{i}$
, we interpolated
$H^{\prime }$
and
$G^{\prime }$
using
$$\begin{eqnarray}\unicode[STIX]{x1D709}^{1/2}G^{\prime }(\unicode[STIX]{x1D709})=a_{i}\unicode[STIX]{x1D709}+b_{i},\quad \unicode[STIX]{x1D709}^{1/2}H^{\prime }(\unicode[STIX]{x1D709})=c_{i}\unicode[STIX]{x1D709}+d_{i},\quad i=1,\ldots ,t,\end{eqnarray}$$
$$\begin{eqnarray}G^{\prime }(\unicode[STIX]{x1D709})=a_{i}\unicode[STIX]{x1D709}+b_{i},\quad H^{\prime }(\unicode[STIX]{x1D709})=c_{i}\unicode[STIX]{x1D709}+d_{i},\quad i=t+1,\ldots ,n.\end{eqnarray}$$
The two sets of interpolating functions were chosen to represent the functional forms for
$\unicode[STIX]{x1D709}\ll 1$
and
$\unicode[STIX]{x1D709}\gg 1$
, but the division point
$t\approx n/2$
is fairly arbitrary. These interpolating functions allow the integrals in (2.10) and (2.11) to be performed analytically. We also need to extrapolate to
$\unicode[STIX]{x1D709}>\unicode[STIX]{x1D709}_{n}$
to complete the integrals, and continued to use a piecewise linear representation of
$H^{\prime }$
and
$G^{\prime }$
for simplicity, with slopes
$H^{\prime \prime }$
and
$G^{\prime \prime }$
given by
$$\begin{eqnarray}a_{n+1}=\frac{G_{\infty }^{\prime \prime }(\unicode[STIX]{x1D709}_{n})}{G_{\infty }^{\prime }(\unicode[STIX]{x1D709}_{n})}G_{n}^{\prime },\quad c_{n+1}=\frac{H_{\infty }^{\prime \prime }(\unicode[STIX]{x1D709}_{n})}{H_{\infty }^{\prime \prime }(\unicode[STIX]{x1D709}_{n-1})}c_{n},\end{eqnarray}$$
where
$H_{\infty }^{\prime \prime }$
and
$G_{\infty }^{\prime }$
are given by the asymptotic form (2.15).
We define a vector of
$2(n+1)$
unknowns
$\unicode[STIX]{x1D73D}=[\sqrt{\unicode[STIX]{x1D709}_{0}}H^{\prime }(\unicode[STIX]{x1D709}_{0}),\ldots ,\sqrt{\unicode[STIX]{x1D709}_{t}}H^{\prime }(\unicode[STIX]{x1D709}_{t}),H^{\prime }(\unicode[STIX]{x1D709}_{t+1}),\ldots ,H^{\prime }(\unicode[STIX]{x1D709}_{n}),\sqrt{\unicode[STIX]{x1D709}_{0}}G^{\prime }(\unicode[STIX]{x1D709}_{0}),\ldots ,\sqrt{\unicode[STIX]{x1D709}_{t}}G^{\prime }(\unicode[STIX]{x1D709}_{t}),G^{\prime }(\unicode[STIX]{x1D709}_{t+1}),\ldots ,G^{\prime }(\unicode[STIX]{x1D709}_{n})]$
, from which one can easily determine the interpolation, and thence evaluate the two components of the elasticity integral (2.10) at
$n$
intervening points
$\unicode[STIX]{x1D709}_{1/2},\ldots ,\unicode[STIX]{x1D709}_{n-1/2}$
. Using the linearity of these operations, we can thus define a square matrix
$\unicode[STIX]{x1D63C}$
such that
$$\begin{eqnarray}[P(\unicode[STIX]{x1D709}_{1/2}),\ldots ,P(\unicode[STIX]{x1D709}_{n-1/2}),\underbrace{0,\ldots ,0}_{n},G^{\prime }(\unicode[STIX]{x1D709}_{n}),H^{\prime \prime }(\unicode[STIX]{x1D709}_{n})]=\unicode[STIX]{x1D63C}\unicode[STIX]{x1D73D}.\end{eqnarray}$$
One can obtain analytical expressions for
$H(\unicode[STIX]{x1D709})$
by integrating the representation of
$H^{\prime }$
, and then for
$P(\unicode[STIX]{x1D709})$
by integrating
$H^{-2}$
in (2.11). Let
$\boldsymbol{p}(\unicode[STIX]{x1D73D})$
denote the vector of values found by evaluating
$P(\unicode[STIX]{x1D709}_{i-1/2})$
,
$i=1,\ldots ,n$
, in this way. Equating the two expressions for
$P$
and using the asymptotic conditions (2.15), we obtain the equation
$$\begin{eqnarray}\unicode[STIX]{x1D63C}\unicode[STIX]{x1D73D}=[\boldsymbol{p}(\unicode[STIX]{x1D73D}),\underbrace{0,\ldots ,0}_{n},G_{\infty }^{\prime }(\unicode[STIX]{x1D709}_{n}),H_{\infty }^{\prime \prime }(\unicode[STIX]{x1D709}_{n})],\end{eqnarray}$$
which can be solved by Newton’s method from quite arbitrary initial guesses. The accuracy of the numerical results was checked by varying the parameters of the discretization; the main considerations are that
$n$
and
$\unicode[STIX]{x1D709}_{n}$
should be sufficiently large.
A.2 Linear perturbation problem
For the linear perturbation problem in appendix B, we anticipate a singularity of the form
$\unicode[STIX]{x1D709}^{s-1}$
in
$\tilde{H}^{\prime }$
, with
$s=0.139$
, and the weighting in the interpolation (A 3) was changed to reflect this. (We still expect
$\tilde{G}^{\prime }$
to have a
$\unicode[STIX]{x1D709}^{-1/2}$
singularity.) Some of the integrals no longer have exact expressions, but can be carefully precalculated for the relevant intervals by numerical integration.
The lubrication equation (B 8b
) for the perturbation problem is linear in
$\tilde{H}$
. Therefore, the function
$\tilde{\boldsymbol{p}}(\tilde{\unicode[STIX]{x1D73D}})$
appearing in the equation analogous to (A 7) is linear, and we can solve this equation directly without recourse to Newton’s method.
The zero-toughness solution
$H_{0}$
was obtained by extrapolation with respect to
$k_{I}$
for each
$\unicode[STIX]{x1D709}_{i}>0.002$
. (Figure 4 shows that, away from the boundary layer near
$\unicode[STIX]{x1D709}=0$
,
$H^{\prime }(\unicode[STIX]{x1D709})$
for
$k_{I}=0.21$
is already a good approximation to
$H_{0}^{\prime }$
.) For
$\unicode[STIX]{x1D709}_{i}<0.002$
the linear trend in
$0.002<\unicode[STIX]{x1D709}<0.003$
was simply extended to
$\unicode[STIX]{x1D709}=0$
.
A.3 Dry cracking ahead of the fluid
To solve the problem in § 4.1 of dry shear failure at
$\unicode[STIX]{x1D709}=-L$
preceding a fluid front at
$\unicode[STIX]{x1D709}=0$
, we adapted the scheme for § 3 by adding more points to cover the interval
$-L\leqslant \unicode[STIX]{x1D709}<0$
. The spacing of points for
$\unicode[STIX]{x1D709}<0$
was chosen such that there was a concentration of points near
$-L$
and near
$0$
.
We also adapted the interpolation of
$G^{\prime }$
from (A 3a
) to reflect the
$(\unicode[STIX]{x1D709}+L)^{-1/2}$
singularity at
$\unicode[STIX]{x1D709}=-L$
, while continuing to allow
$H^{\prime }$
to have a
$\unicode[STIX]{x1D709}^{-1/2}$
singularity at
$\unicode[STIX]{x1D709}=0$
for the solutions with
$k_{I}\neq 0$
. Since
$H^{\prime }=0$
in
$\unicode[STIX]{x1D709}<0$
, we did not need to calculate
$P$
for
$\unicode[STIX]{x1D709}<0$
(although it is easily done): simply requiring that
$\unicode[STIX]{x1D70E}_{xy}=0$
at the intervening points in
$\unicode[STIX]{x1D709}<0$
provides enough additional equations to determine
$G^{\prime }$
in
$-L\leqslant \unicode[STIX]{x1D709}<0$
. The problem can then be solved as before with Newton’s method.
Appendix B. Small-toughness solution
In this appendix, we show how to predict the behaviour seen in figure 3 as
$k_{I}\rightarrow 0$
(or
$V\rightarrow V_{0}$
). Let
$H_{0}$
,
$G_{0}$
,
$P_{0}$
and
$V_{0}$
be the solution of (2.10)–(2.13) for
$k_{I}=0$
, with the asymptotic behaviour (3.2) as
$\unicode[STIX]{x1D709}\rightarrow 0$
. (The behaviour
$G_{0}^{\prime }\sim (k_{II}/\unicode[STIX]{x1D712})\unicode[STIX]{x1D709}^{-1/2}$
is not relevant to the following analysis.) We assume that for
$k_{I}\ll 1$
and away from
$\unicode[STIX]{x1D709}=0$
, we can set up a perturbation expansion of the form
$$\begin{eqnarray}\left.\begin{array}{@{}c@{}}H(\unicode[STIX]{x1D709})=H_{0}(\unicode[STIX]{x1D709})+\unicode[STIX]{x1D716}(k_{I})H_{1}(\unicode[STIX]{x1D709})+\cdots \,,\\ G(\unicode[STIX]{x1D709})=G_{0}(\unicode[STIX]{x1D709})+\unicode[STIX]{x1D716}(k_{I})G_{1}(\unicode[STIX]{x1D709})+\cdots \,,\\ P(\unicode[STIX]{x1D709})=P_{0}(\unicode[STIX]{x1D709})+\unicode[STIX]{x1D716}(k_{I})P_{1}(\unicode[STIX]{x1D709})+\cdots \,,\\ V=V_{0}+\unicode[STIX]{x1D716}(k_{I})V_{1}+\cdots \,,\end{array}\right\}\end{eqnarray}$$
with a small parameter
$\unicode[STIX]{x1D716}$
.
Near
$\unicode[STIX]{x1D709}=0$
this expansion must break down, because
$H\sim k_{I}\unicode[STIX]{x1D709}^{1/2}$
is much larger than
$H_{0}\sim V_{0}^{1/3}\unicode[STIX]{x1D709}^{2/3}$
. The balance
$k_{I}\unicode[STIX]{x1D709}^{1/2}\sim V^{1/3}\unicode[STIX]{x1D709}^{2/3}$
suggests the rescaling, with some convenient numerical factors,
$$\begin{eqnarray}\unicode[STIX]{x1D709}=\unicode[STIX]{x1D705}^{6}\unicode[STIX]{x1D713}^{-2}\hat{\unicode[STIX]{x1D709}},\quad H=\unicode[STIX]{x1D705}^{4}\unicode[STIX]{x1D713}^{-1}{\hat{H}},\quad P=\unicode[STIX]{x1D713}\unicode[STIX]{x1D705}^{-2}\hat{P},\quad \text{where }\unicode[STIX]{x1D713}=12V,\unicode[STIX]{x1D705}=(32/\unicode[STIX]{x03C0})^{1/2}k_{I}.\end{eqnarray}$$
In the rescaled variables, equations (3.1), (2.11) and (2.13) become
$$\begin{eqnarray}\hat{P}(\hat{\unicode[STIX]{x1D709}})=\frac{1}{4\unicode[STIX]{x03C0}}\int _{0}^{\infty }\frac{{\hat{H}}^{\prime }(\tilde{\unicode[STIX]{x1D709}})}{\tilde{\unicode[STIX]{x1D709}}-\hat{\unicode[STIX]{x1D709}}},\quad {\hat{H}}^{2}\hat{P}^{\prime }=1,\quad {\hat{H}}\sim \hat{\unicode[STIX]{x1D709}}^{1/2}\quad \text{as }\hat{\unicode[STIX]{x1D709}}\rightarrow 0,\end{eqnarray}$$
which are the same as the small-toughness boundary-layer equations derived and solved numerically by Garagash & Detournay (Reference Garagash and Detournay2005) in the context of a different problem. They showed that
$$\begin{eqnarray}{\hat{H}}\sim \unicode[STIX]{x1D6FD}\hat{\unicode[STIX]{x1D709}}^{2/3}+\unicode[STIX]{x1D6FD}_{1}\hat{\unicode[STIX]{x1D709}}^{s}\quad \text{as }\hat{\unicode[STIX]{x1D709}}\rightarrow \infty ,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FD}=3(4/3)^{1/6}$
,
$\unicode[STIX]{x1D6FD}_{1}=0.03719$
and
$s=0.013867$
. Reverting to the outer variables, we find that the matching condition for the outer solution is
$$\begin{eqnarray}H\sim b_{1}V^{2s-1}k_{I}^{4-6s}\unicode[STIX]{x1D709}^{s}+6(3V^{2})^{1/6}\unicode[STIX]{x1D709}^{2/3}\quad \text{as }\unicode[STIX]{x1D709}\rightarrow 0,\end{eqnarray}$$
where
$b_{1}=0.2439$
.
After comparing the expansion (B 1) with (B 5), we set
$\unicode[STIX]{x1D716}=b_{1}V_{0}^{2s-1}k_{I}^{4-6s}$
and write
$V^{1/3}=V_{0}^{1/3}(1+\unicode[STIX]{x1D716}V_{1}/3V_{0}+\cdots \,)$
. On substituting the expansion into (2.10)–(2.13) and equating terms of order
$\unicode[STIX]{x1D716}$
, we obtain the linear perturbation problem
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}P_{1}\\ 0\end{array}\right]=\int _{0}^{\infty }\unicode[STIX]{x1D646}(\unicode[STIX]{x1D709}-\tilde{\unicode[STIX]{x1D709}})\left[\begin{array}{@{}c@{}}H_{1}^{\prime }(\tilde{\unicode[STIX]{x1D709}})\\ G_{1}^{\prime }(\tilde{\unicode[STIX]{x1D709}})\end{array}\right]\text{d}\tilde{\unicode[STIX]{x1D709}},\quad H_{0}^{2}P_{1}^{\prime }+2H_{0}H_{1}P_{0}^{\prime }=V_{1},\end{eqnarray}$$
$$\begin{eqnarray}H_{1}^{\prime \prime }\rightarrow 0\quad \text{as }\unicode[STIX]{x1D709}\rightarrow \infty ,\quad H_{1}\sim \unicode[STIX]{x1D709}^{s}+\frac{V_{1}}{3V_{0}}H_{0}(\unicode[STIX]{x1D709})+\cdots \quad \text{as }\unicode[STIX]{x1D709}\rightarrow 0.\end{eqnarray}$$
These equations determine the value of
$V_{1}$
through the condition that the perturbed propagation speed is consistent with no perturbation to the far-field forcing
$H^{\prime \prime }\rightarrow 12$
.
For numerical solution, it is convenient to subtract
$V_{1}/3V_{0}$
times the zero-toughness solution to simplify (B 7b
), and then rescale to obtain
$$\begin{eqnarray}\left[\begin{array}{@{}c@{}}\tilde{P}\\ 0\end{array}\right]=\int _{0}^{\infty }\unicode[STIX]{x1D646}(\unicode[STIX]{x1D709}-\tilde{\unicode[STIX]{x1D709}})\left[\begin{array}{@{}c@{}}\tilde{H}^{\prime }(\tilde{\unicode[STIX]{x1D709}})\\ \tilde{G}^{\prime }(\tilde{\unicode[STIX]{x1D709}})\end{array}\right]\text{d}\tilde{\unicode[STIX]{x1D709}},\quad H_{0}^{2}\tilde{P}^{\prime }+2H_{0}\tilde{H}P_{0}^{\prime }=0,\end{eqnarray}$$
$$\begin{eqnarray}\tilde{H}^{\prime \prime }\rightarrow 12\quad \text{as }\unicode[STIX]{x1D709}\rightarrow \infty ,\quad \tilde{H}\sim \unicode[STIX]{x1D6FE}\unicode[STIX]{x1D709}^{s}+\cdots \text{ as }\unicode[STIX]{x1D709}\rightarrow 0,\end{eqnarray}$$
where
$\unicode[STIX]{x1D6FE}=-3V_{0}/V_{1}$
, and
$\tilde{H}=\unicode[STIX]{x1D6FE}[H_{1}-(V_{1}/3V_{0})H_{0}]$
etc.
Equations (B 8) and (B 9) were solved numerically as described in appendix A. We find that
$\unicode[STIX]{x1D6FE}=6.91$
and hence
$V_{1}=-14.0$
. The final asymptotic result
$$\begin{eqnarray}V\sim V_{0}-(3b_{1}/\unicode[STIX]{x1D6FE})V_{0}^{2s}k_{I}^{4-6s}=0.678-0.0950k_{I}^{4-6s}\quad \text{as }k_{I}\rightarrow 0\end{eqnarray}$$
shows excellent agreement with the results from the full numerical calculations (figure 5), providing a check both on the numerical calculations and on the understanding of the boundary-layer structure. The asymptotic result is also useful for moderately small
$k_{I}$
since it gives an excellent prediction of the speed of propagation without having to resolve the very thin
$O(k_{I}^{6})$
boundary-layer structure.
