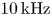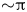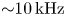1. Introduction
Drift-wave turbulence is a common phenomenon which occurs in inhomogeneous plasmas (Hasegawa & Mima Reference Hasegawa and Mima1977, Reference Hasegawa and Mima1978; Hasegawa & Wakatani Reference Hasegawa and Wakatani1983; Wakatani & Hasegawa Reference Wakatani and Hasegawa1984). Drift-wave turbulence is the result of a gradient in the electron pressure and, as most plasmas exhibit density and/or temperature gradients, drift-wave turbulence is omnipresent. For example, in magnetic confinement devices, drift-wave turbulence is what determines the transport perpendicular to the magnetic field lines (Tynan, Fujisawa & McKee Reference Tynan, Fujisawa and McKee2009). Moreover drift-wave turbulence is not just limited to laboratory plasmas, but is also observed to play a role in the magnetopause (Le et al. Reference Le, Daughton, Ohia, Chen, Liu, Wang, Nystrom and Bird2018). The experiments we discuss in this paper are especially relevant to turbulence characteristics observed in tokamak edge plasmas. At the plasma edge, aside from curvature driven interchange turbulence, resistive drift-wave turbulence is observed (Scott Reference Scott2005; Mosetto et al. Reference Mosetto, Halpern, Jolliet, Loizu and Ricci2013). Moreover, this is the region of the plasma where the impact of neutrals cannot be neglected (Fülöp, Catto & Helander Reference Fulöp, Catto and Helander1998; Omotani et al. Reference Omotani, Pusztai, Newton and Fülöp2016). The complex two-dimensional geometry in a tokamak with poloidal asymmetries, magnetic field ($\boldsymbol{B}$
-field) curvature and gradients makes the study of fundamental drift-wave turbulence more complicated, whereas linear machines such as the Large Plasma Device (LAPD) provide the ideal conditions to measure the changes in drift-wave turbulence and plasma parameters (Gekelman et al. Reference Gekelman, Pribyl, Lucky, Drandell, Leneman, Maggs, Vincena, Van Compernolle, Tripathi and Morales2016).
Drift-wave turbulence (DWT) occurs at various scale lengths and wavelengths which are determined by local and global plasma properties. DWT are negative energy modes driven by dissipation, where this dissipation can either be collisional (leading to resistive drift waves) or collisionless (Landau damping drives the mode). The dissipation causes the electron response to differ from an adiabatic response, as electrons are prevented by collisions or Landau damping to respond quickly to the variations in the potential (Horton Reference Horton1999). While plasmas in the core of a tokamak are typically collisionless, those at the plasma edge are considered collisional, similar to the plasmas we explore in this paper on the LAPD (D'Ippolito, Myra & Krasheninnikov Reference D'Ippolito, Myra and Krasheninnikov2002; Carter Reference Carter2006).
The drift waves we observe in LAPD are collisional and can be described using a fluid approximation (Carter Reference Carter2006; Friedman Reference Friedman2013; Schaffner Reference Schaffner2013). As LAPD is a flexible device, it has the possibility of also operating with substantial shear flow using biasing (Horton et al. Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004; Carter & Maggs Reference Carter and Maggs2009; Schaffner et al. Reference Schaffner, Carter, Rossi, Guice, Maggs, Vincena and Friedman2012; Schaffner Reference Schaffner2013). The substantial shear flow in these biasing experiments can lead to rotational interchange and Kelvin–Helmholtz instabilities. In the experiments discussed in this paper, no biasing is applied and as a result there is no substantial azimuthal flow shear, nor does the azimuthal flow shear change outside of error bars when we scan the density gradient.
The experiments show that the density perturbations increase with decreasing electron density ($n_e$
) gradient scale length, $L_n= n_e/ \boldsymbol {\nabla } n_e$
, another clear indication that the observed turbulence consists of collisional drift waves. Finally, the cross-phase between the density and potential fluctuations at low frequencies is $0^{\circ }$
, which agrees with expectations. The experiments discussed in this paper indicate that there are subtleties related to DWT that have not yet been captured by experimental observations, nor have they been predicted through nonlinear modelling and they can have a substantial effect on the particle flux.
Analytic theory predicts that resistive drift-wave turbulence is driven by a gradient in the electron density profile; i.e. a larger density gradient increase the linear growth rate (Kadomtsev Reference Kadomtsev1965; Horton Reference Horton1999; Goldston Reference Goldston2020). Experimentally, we cannot measure the growth rate directly and the assumption is often made that the turbulence intensity at a specific wavelength can be used as a proxy if nonlinear effects and the impact of turbulence spreading can be neglected in order to compare experiments with quasi-linear predictions, which if often done as a first approximation. However, in experiments where nonlinear turbulence mixing is strong and no coherent modes remain and the turbulence can be described as broadband, the integrated turbulence intensity over the whole spectrum can be used as a measure for the general turbulence drive. This crude approximation relies on the assumptions that turbulence spreading, nonlinear interactions and dissipation do not vary much across the scans that are being performed. This approximation would not be valid if there is a sudden change in for example shear flow, as seen in the biasing experiments. For a full validation, nonlinear simulations are necessary, which is beyond the scope of this paper.
In this paper, we vary the electron density gradient and temperature gradients separately and show that there is a correlation between the turbulence intensity and the local density gradient, as predicted by linear theory, see § 3.1. However, detailed analysis of turbulence measurements indicates that there are subtle deviations that are not captured using linear and quasi-linear approximations and none of these effects have been predicted by nonlinear simulations to the knowledge of the authors. The electron temperature gradient counter to the electron density gradient can both stabilize and destabilize drift waves. As long as the ratio of the normalized electron temperature gradient with respect to the normalized density gradient remains below $2/3$
, linear theory predicts the electron temperature gradient stabilizes the drift waves (Horton et al. Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004; Goldston Reference Goldston2020). Above this value, the electron temperature gradient is destabilizing as it provides a source of energy and can enhance the turbulence intensity in experiments. For the results reported in this paper, this ratio remains below $2/3$
and the density fluctuations are damped when an electron temperature gradient is present in comparison to a plasma region without an electron temperature gradient. The electron temperature gradient also affected the observed linear relationship between the measured density fluctuations and the local electron density gradient, see § 3.2.
We observe fully developed broadband turbulence in our experiments and the density fluctuations behaved similar to what would be expected from simplistic linear theory for independent wavelengths. The potential fluctuations and the cross-phase between the density and potential fluctuations are not coupled to trends observed in the density fluctuations. This indicates that these drift waves are resistive and do not follow the simplistic Boltzmann relationship that can be assumed in the collisionless limit described by Hasegawa & Mima (Reference Hasegawa and Mima1978). Resistive dissipation results in the decoupling of the density and potential fluctuations and their cross-phase. This has a direct effect on transport and the particle flux. Nonlinear modelling has shown that at large wavenumbers, $k$
, the quasi-linear flux and nonlinear flux match well. This changes at smaller $k$
(Camargo, Biskamp & Scott Reference Camargo, Biskamp and Scott1995). Moreover, we observe that the introduction of a temperature gradient results in a shift of ${\sim }{\rm \pi}$
in the cross-phase, altering it from positive to negative, indicating a reversal of the direction of particle flux from inward to outward.
In the next section we will first describe the experimental setup in LAPD. Next, we will discuss the impact of the density and the electron temperature gradient on the turbulence characteristics in § 3. Finally, we will discuss some of the nonlinear effects in § 4 and we discuss the impact of collisionality (and neutrals) and the parallel flow in § 5. We conclude with § 6.
2. Experimental setup
LAPD is a $24.4 \,{\rm m}$
long linear plasma device with a $0.5 \,{\rm m}$
radius (Gekelman et al. Reference Gekelman, Pribyl, Lucky, Drandell, Leneman, Maggs, Vincena, Van Compernolle, Tripathi and Morales2016). In our experiments, the circular magnetic field coils produce a uniform axial magnetic field of $1000 \,{\rm G}$
. A BaO cathode with a radius of $36.5 \,{\rm cm}$
produces a helium plasma column with a radius of ${\sim }29 \,{\rm cm}$
and length $17 \,{\rm m}$
in the center of LAPD, as the magnetic field flares close to the cathode. In these experiments, we can assume that the neutral helium density is fairly constant within the plasma column, as the mean free path of helium is of the same scale order as the radius of LAPD.
Drift-wave turbulence is directly linked to the electron density gradient. In this experiment the electron density gradient is varied using two different methods. First, we alter the central electron density by changing the current to the cathode. Second, we repeat this for three different gas fill pressures. This means that throughout these discharges the neutral density was varied along with the plasma density, allowing us to disentangle the impact of neutrals on turbulence vs the direct impact of plasma gradients. The fill pressures were $20 \,\mathrm {\mu }{\rm Torr}$
, $25 \,\mathrm {\mu }{\rm Torr}$
and $30 \,\mathrm {\mu }{\rm Torr}$
while the discharge current was increased from $2.0\,{\rm kA}$
to $6.0\,{\rm kA}$
in steps of $0.5 \,{\rm kA}$
. Pressure measurements reported were obtained on an ion gauge calibrated for a hydrogen fill gas which can be corrected for helium by dividing by 0.18.
The electron densities and temperatures trended with pressure/power as expected from a simple global discharge model (Lieberman & Lichtenberg Reference Lieberman and Lichtenberg2005). The electron temperature did not vary much, but the core electron density did increase with increasing power, as expected. In the core region (defined as $r= 0 - 21 \,{\rm cm}$
), line-averaged values of the electron density ranged from $n_e \sim 0.8 \times 10^{12} \,{\rm cm}^{-3}$
to $n_e \sim 2.2 \times 10^{12} \,{\rm cm}^{-3}$
. The electron temperature varied from $T_e =3.5 \,{\rm eV}$
to $T_e= 4.7 \,{\rm eV}$
. The whole data set will be used to look at global trends and correlations, but for detailed analysis of turbulence characteristics we will focus on three experiments. The three experiments were chosen to have a similar core electron temperature as well as similar parallel flow velocity, where the main difference is the variation in the electron density gradient. By imposing a limitation on lack of change in parallel velocity and core electron temperature, the three discharges do not represent the extremes of the database, but we avoid secondary effects that could impact the results. The electron density and temperature profiles for three representative experiments are shown in figure 1. The data for each point in these profiles, as well as all the turbulence data, were acquired using 15 pulses per radial location and multiple probe measurements during each current flat top. No large variations on profile measurements as well as turbulence spectra were observed.
Figure 1. Electron density and temperature profiles for three representative experiments that will be studied in more depth further in the paper. These experiments had nearly identical electron temperature profiles while the core electron density varied. These experiments had the same fill pressure of $20 \,\mathrm {\mu }{\rm Torr}$
and from low to higher density the current was $3.5 \,{\rm kA}$
, $4.0 \,{\rm kA}$
and $5.0 \,{\rm kA}$
.
The electron density and temperature profiles are measured along with the plasma velocity and turbulence characteristics using a bundle of three probes that are swept in $1 \,{\rm cm}$
increments through the horizontal plane of LAPD. These three probes consist of a Langmuir probe ($z = 8.946\,{\rm m}$
), a Mach probe ($z = 7.668\,{\rm m}$
) and a four-tipped probe ($z = 8.306\,{\rm m}$
). The Langmuir probe measures the electron temperature and plasma potential. The Mach probe measures the ion saturation current on its 6 faces which provides profiles of parallel and perpendicular (azimuthal) flow velocities.
The four-tipped probe has two tips to measure the ion saturation current as a proxy for the electron density. We extract the electron density from the measured current in real units and compare these with the line-integrated density measurements from the interferometer. The other two tips of the four-tipped probe were dedicated to measuring the floating potential as a proxy for the plasma potential. Simple sheath theory motivates these proxies through the following equations
where $I_{sat,i}$
is the ion saturation current, $e$
is the electric charge, $A$
is the probe area, $n_\infty$
is the plasma density far from the probe, $T_e$
is the electron temperature, $M_i$
is the ion mass, $m_e$
is the electron mass, $V_f$
is the floating potential and $\phi _p$
is the plasma potential. Note that both equations are strong functions of the electron temperature. Unfortunately, LAPD lacked a temperature fluctuation diagnostic at the time of the experiment so we have to assume that these are small and have a negligible impact on this analysis. The probe tips were vertically displaced by 3 mm so that we could apply a basic finite-difference form to the electrostatic approximation and thus obtain the azimuthal electric field. Moreover, the four-tipped probe recorded data at $100 \,{\rm MHz}$
with a 16 bit resolution, giving a fine enough time resolution for measuring electron density and electric field fluctuations and their cross-phase. The radial velocity fluctuations can be directly inferred from the electric field fluctuations. These combined turbulence measurements allow us to investigate the changes in particle flux and transport (Powers Reference Powers1974).
As drift waves require a pressure gradient, our analysis will focus on two areas highlighted in light blue and pink in figure 1. These areas occur at the plasma edge of these LAPD experiments and are characterized by first an increase in the density gradient starting at $r = 22 \,{\rm cm}$
up to $r = 29 \,{\rm cm}$
. Up to $r = 25 \,{\rm cm}$
the electron temperature remains constant and no significant gradient is observed. However, outside $r = 25 \,{\rm cm}$
an electron temperature gradient is observed. We choose $r = 25 \,{\rm cm}$
as this was the location at which we saw a consistent change in the turbulence characteristics across a wide range of experiments, as can be observed in figure 9. As these two gradients are staggered with respect to each other, we can independently investigate the impact of a density gradient and the addition of an electron temperature gradient. This distinction is important as theory has shown that the electron temperature gradient can stabilize drift-wave turbulence when $\eta _e = {\mathrm {d} \ln T_e}/{\mathrm {d} \ln n_e} < 2/3$
(Horton et al. Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004; Goldston Reference Goldston2020).
3. Drift-wave turbulence
Drift-wave turbulence is omnipresent in non-uniform plasma with a pressure gradient, $\boldsymbol {\nabla } P_e$
. The drift-wave dispersion relationship can be found in multiple textbooks and seminal papers and includes a real and an imaginary part (Kadomtsev Reference Kadomtsev1965; Hasegawa & Mima Reference Hasegawa and Mima1977, Reference Hasegawa and Mima1978; Camargo et al. Reference Camargo, Biskamp and Scott1995; Horton et al. Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004; Goldston Reference Goldston2020). Every derivation is slightly different depending on the choice of geometry, initial and boundary conditions. They, however, all reach the same conclusions, namely that for collisional drift-wave turbulence to be unstable you need resistivity, $\eta$
, and an electron density gradient, $\boldsymbol {\nabla } n_e$
, while the electron temperature gradient, $\boldsymbol {\nabla } T_e$
, can have a stabilizing effect as long as its gradient remains small with respect to the electron density gradient (Horton et al. Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004; Goldston Reference Goldston2020). As such, we should expect an increase in the magnitude of the density fluctuations as the electron density increases and a reduction or stabilization of these fluctuations as the electron temperature gradient increases as long as $\eta _e < 2/3$
. If this would be a collisionless plasma, the potential fluctuations would be linked to the density fluctuations through the Boltzmann relation and there would be no phase delay and the trends would be similar. However, as these are resistive drift waves, there is a phase delay between the density and potential fluctuations as a result of resistive damping and numerical analysis has shown that the relationship can change as a function of the wavelength (Camargo et al. Reference Camargo, Biskamp and Scott1995).
3.1. Impact of electron density gradient
To study the impact of electron density gradient on turbulence characteristics across all our experiments, we fit a linear function to all our edge plasma profiles, as shown in figure 1. This gradient is normalized using the average local electron density, $L_n = n_e/ \boldsymbol {\nabla } n_e$
. The average local electron density is the average electron density in the blue region of figure 1, which extends across the range $r=22-25 \,{\rm cm}$
. Next, for this same blue region in figure 1 we calculate the total electron density perturbation amplitude, $\tilde {n}$
. This total density perturbation is found by integrating the density fluctuations over their spectrum in the range $1-250 \,{\rm kHz}$
(see figure 3 for an example of the density fluctuations as a function of spectrum) and by taking the average of the total density perturbation in the radial region $r=22-25 \,{\rm cm}$
. These measurements are again normalized by the respective average local electron density. We observe that as $L_n$
increases and thus the density gradient decreases, the magnitude of the density fluctuations decreases as well (see figure 2a). The correlation appears to be linear, which would be in agreement with theoretical linear predictions. For example in Kadomtsev (Reference Kadomtsev1965), Horton et al. (Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004) and Goldston (Reference Goldston2020), the linear growth rate, $\gamma$
is directly inversely proportional to $L_n$
. In the quasi-linear estimate, we can assume that the mode amplitude saturates when it is able to remove its own drive, which means that $\tilde {n}/n \sim 1/(k_{\perp } L_n$
). We find a small spread in the data, with lower density fluctuations for a similar density gradient being linked to a higher total collisionality. Changes in collisionality would affect the exchange of energy from the parallel velocity of the electrons and the drift waves.
Figure 2. (a) Density fluctuation amplitude, $\tilde {n}$
, normalized by the respective local average density vs $L_n$
for $r = 22-25 \,{\rm cm}$
. The colour scheme is linked to the total collisionality in the plasma. (b) Normalized floating potential, $\tilde {V}_f/T_e$
, fluctuations as a function of $L_n$
for $r = 22-25 \,{\rm cm}$
. The colour scheme is determined by the average parallel velocity at the plasma edge.
The analysis of the floating potential fluctuations $\tilde {V}_f$
shows a more complex relationship (see figure 2b). At smaller $L_n$
there is a branch in the data, with a series of experiments observing constant $\tilde {V}_f/T_e$
values, which are unaffected by changes in $L_n$
. We find that all these experiments are characterized by a change in the direction of the parallel velocity (see figure 2b), while no substantial changes in the azimuthal direction are observed. Most transport simulations assume an adiabatic response and approximate deviations from the relationship between the density and potential fluctuations as a pure phase shift. $\tilde {n} = (1-{\rm i} \delta )\tilde {V}_{f}$
, where $\delta \ll 1$
(Camargo et al. Reference Camargo, Biskamp and Scott1995). The integrated density and potential fluctuation amplitudes as a function of $L_n$
deviate from this simple phase shift and nonlinear modelling of LAPD has indicated that for DWT most of the energy is carried in the density fluctuations (Friedman Reference Friedman2013).
The turbulence in this region of the plasma with only a density gradient present is broadband and fully developed both in the density as well as the potential fluctuations, see figure 3. The three experiments were chosen so that the parallel plasma velocity at the edge region has a similar magnitude and that there are no large differences in the electron temperature gradient. These experiments do not represent the extremes of our correlation data, but they allow us to focus on detailed changes in turbulence characteristics as a function of only the electron density and temperature gradients. So while the linear model should not be valid as no single mode is dominant, nonlinear interactions have distributed the energy to all scales and thus integrating over all scales still gives a good approximation for the intensity of the turbulence and its drive assuming quasi-linear saturation of the mode.
The experimental trends in changes in density fluctuations are compared with predictions from a linear eigenvalue code, Eigsolver (Popovich et al. Reference Popovich, Umansky, Carter and Friedman2010; Schaffner Reference Schaffner2013) developed to study linear stability in cylindrical geometry, see figure 4. Eigsolver solves the linearized Braginskii two-fluid model. Within cylindrical coordinates, the linearized equations can be solved as an eigenvalue problem assuming solutions of the form $f(\boldsymbol {r}) = f(r)\exp {({\rm i}m_\theta \theta +{\rm i}k_\parallel z-{\rm i}\omega t)}$
, where $k_\parallel = 2{\rm \pi} n_z/L_\parallel$
, $n_z$
is the parallel mode number, $L_\parallel \sim 17 \,{\rm m}$
is the plasma column length, $m_\theta$
is the poloidal mode number and $\omega$
is the eigenvalue. In this paper, we consider $n_z =0.5$
to focus on the longest wavelength drift wave ($\lambda = 2L_\parallel$
) while scanning in $m_\theta$
. We use experimental profiles with helium species, $Z=1$
(the temperature is too low for $Z=2$
helium) and $f_{ci}=383 \,{\rm kHz}$
. The electron collisionality is the sum of the electron–ion collisionality and the electron–neutral collisionality, $\nu _e = \nu _{ei}+\nu _{en} = 4.8 \,{\rm MHz}$
from experimental data; $\nu _{en}/\nu _{ei}\sim 0.1$
, so the resistivity is dominantly determined by electron–ion collisions. A poor correlation with just $\nu _{en}$
was observed in the data set. We assume a value of $\nu _{in} = 1.2 \,{\rm kHz}$
as reported in table 1 of Popovich et al. (Reference Popovich, Umansky, Carter and Friedman2010) as insufficient experimental information was available to determine the ion collisionality. Note that ion collisionality $\nu _{in}$
has a strong effect of stabilizing drift waves (Kasuya, Yagi & Itoh Reference Kasuya, Yagi and Itoh2005).
Figure 4. (a) The linear growth rate and (b) respective frequencies for three different $L_n$
vs $k_{\theta } \rho _s$
. The $L_n = 6.1 \,{\rm cm}$
simulation is based on the middle experiment in figure 1.
The density and temperature profiles are derived from a fit of the experimental density/temperature profiles from the $L_n=6.1\,{\rm cm}$
case shown in figure 1 over $r=15-45\,{\rm cm}$
. This is used as our control case. We set the plasma potential profile to that measured by the Langmuir probe for our control case and hold this fixed throughout to fix vorticity terms driving rotational interchange and Kelvin–Helmholtz instabilities in the linear simulations. No electron density data are available outside $r\sim 40\,{\rm cm}$
so we assume the density profile flattens outside this region. Similarly for the electron temperature, we assume it flattens outside $r\sim 30\,{\rm cm}$
at a value of $1 \,{\rm eV}$
. We investigate the impact of density/temperature gradients on growth rates by steepening/lessening of the gradient over its associated extent in the edge region around the initial values from the $L_n = 6.1\,{\rm cm}$
experimental profiles. The density gradient was varied spanning $L_n\sim 5.1-7.4\,{\rm cm}$
to encompass our experimental data set. The fastest growing eigenvalue was determined as the largest, positive growth rate with an associated density eigenmode peaking within the region $r=21-30\,{\rm cm}$
.
We observe as expected from linear theory and also observed experimentally that the largest positive growing eigenvalue decreases with increasing $L_n$
, see figure 4. This result is valid for all $k_\theta \rho _s$
for which the simulation was performed. Note that we converted from $m_\theta = k_\theta r$
, where we chose $r$
to be the location of the maximum in the density eigenfunction. The steepening of the density gradient (decreasing $L_n$
) globally increases the growth rates and the growth rate profiles peak at $k_\theta \rho _s \sim 0.9$
. The frequency $\omega <0$
indicates the modes are in the electron diamagnetic direction.
3.2. Impact of electron temperature gradient contribution
The electron temperature gradient can be both stabilizing and destabilizing for drift-wave turbulence. For resistive drift waves, as long as $\eta _e$
remains below $2/3$
, the electron temperature gradient is predicted to stabilize the turbulence drive (Horton et al. Reference Horton, Hoang, Bourdelle, Garbet, Ottaviani and Colas2004; Goldston Reference Goldston2020). In our experiments the electron temperature gradient was constant, but the electron density gradient varied and the maximum $\eta _e$
is approximately 2/3. Previous research performed on the Columbia linear device studied the impact of electron temperature gradient-driven turbulence for large $\eta _e$
(Fu et al. Reference Fu, Horton, Xiao, Lin, Sen and Sokolov2012). In those experiments, the electron density gradient was close to zero and the turbulence drive was thus linked directly to the temperature gradient. An increase in electron temperature fluctuations was observed with increasing temperature gradient, as expected. However, the increase in heat flux was larger than the increase in the fluctuation amplitude, suggesting nonlinear effects with a transfer of energy from high to lower modes. In the LAPD experiments discussed in this paper, we expect, based on linear theory, that the introduction of a small electron temperature gradient should have a damping effect on the turbulence drive and thus the fluctuations.
For the region where $r=22-25\,{\rm cm}$
with only a density gradient and no temperature gradient there is a steady increase in the amplitude of the density and potential fluctuations with increasing radius, see figure 5. Outside $r=25 \,{\rm cm}$
, the introduction of a temperature gradient results in the flattening of the amplitude of the density fluctuations vs radius, see figure 5(a). This suggests that the electron temperature gradient has a damping effect on the density fluctuations, as would be expected from theoretical predictions. However, little or no impact on the magnitude of the potential fluctuations is observed, see figure 5(b).
Figure 5. (a) Radial dependence of the integrated and normalized density fluctuations and (b) radial dependence of the integrated and normalized floating potential fluctuations for the three experiments with different edge density gradients introduced in figure 1.
The introduction of a small temperature gradient results in the decorrelation of the density gradient with the density fluctuations, see figure 6(a). Similar to the analysis in figure 2, we compare the averaged normalized density fluctuations in $r= 25-29 \,{\rm cm}$
, which corresponds to the pink region in figures 1 and 5. No correlation between the normalized density fluctuations and the local density gradient is observed, counter to the region in which no temperature gradient was present. The introduction of a temperature gradient masks the original correlation between the density fluctuations and $L_n$
as seen in figure 2(a). The temperature gradient decorrelates the normalized density fluctuations vs $L_n$
and turns it in a scatter plot, see figure 6(a).
Figure 6. (a) Density fluctuation amplitude, $\tilde {n}$
, normalized by the respective local average density vs $L_n$
for $r = 26-29 \,{\rm cm}$
. The colour scheme is linked to the total collisionality in the plasma. (b) Normalized floating potential $\tilde{V}_f/T_e$
fluctuations as a function of $L_n$
for $r = 26-29 \,{\rm cm}$
. The colour scheme is determined by the average parallel velocity at the plasma edge.
Linear theory can help quantify the impact of the temperature gradient. From Kadomtsev (Kadomtsev Reference Kadomtsev1965) we find that
the growth rate is being damped by ${\sim }{\omega ^* \eta _e}/{k_z v_{te}} = ({k_y}/{k_z v_{te} e B}) \boldsymbol {\nabla } T_e$
if we replace $\omega ^*$
with $k_y v_{de}$
. Here, $u$
is the parallel electron velocity, $v_{de}$
the electron drift velocity and $v_{te}$
is the electron thermal velocity. As the electron temperature and the temperature gradient are similar for all experiments and the $\boldsymbol{B}$
-field is a constant as well, the damping factor should be similar for all experiments, except for changes in $k_y/k_z$
.
Counter to the decorrelation of the density fluctuations with $L_n$
, the inclusion of a temperature gradient improves the correlation between the potential fluctuations and $L_n$
, see figure 6(b). We also observe that in figure 6 the data can be split into two linear trends, where the lower linear trend corresponds on average to lower or even negative parallel edge flow. These initial observations will be further explored in future work and will require new experiments and measurements. The three experiments we selected for a more detailed comparison had similar parallel flows to avoid the introduction of unexpected changes.
Using the Eigensolver code and fixing $L_n = 6.1 \,{\rm cm}$
, the temperature gradient for $r= 25-29 \,{\rm cm}$
was varied in the range $L_T \sim 8.7-12.5 \,{\rm cm}$
. In the experimental data set, the temperature gradient is $L_T \sim 10 \,{\rm cm}$
and the density gradient varied in this region. Figure 7 shows that steepening the temperature gradient (decreasing $L_T$
) weakly dampens the growth rates for these low values of $\eta _e$
. This is in line with the linear theory previously stated as we maintained a regime where $\eta _e \lesssim 2/3$
. The growth rate profiles peak at $k_\theta \rho _s\sim 0.9$
and the frequencies $\omega <0$
are in the electron direction.
Figure 7. (a) The linear growth rate and (b) respective frequencies for three different $L_T$
vs $k_{\theta } \rho _s$
. The $L_T = 10 \,{\rm cm}$
simulation is based on the middle experiment in figure 1.
4. Nonlinear effects
In our experiments we observe fully developed turbulence in the plasma regions of interest. Fully developed turbulence means that there is no single dominant mode or a complex interaction of two modes, but that the turbulence is broadband and well mixed. As a result, linear theory qualitatively agrees with the observed experimental trends in the density fluctuations. However, this trend is not replicated in the potential fluctuations. The turbulence in our experiments consists of resistive drift waves, which means the Boltzmann relationship does not apply. However, theory only shifts the fluctuations with a phase, but it should not affect the magnitude, something we do not observe experimentally, see § 3.
These observations are for an integrated value over the measured spectrum of both the density and potential fluctuations and we need to investigate the full spectrum for more information. In figure 3, we observed no deviation from broadband well-developed turbulence for both the density and potential fluctuations. In figure 8, we plot the density and potential spectra for the region with the electron temperature gradient. A small peak for both the density and the potential fluctuations can be observed around $10-11 \,{\rm kHz}$
. This small increase is more pronounced in the potential fluctuations than in the density fluctuations. As discussed, the temperature gradient should damp fluctuations, but how much depends on $k_y/k_z$
, the azimuthal wavenumber divided by the longitudinal wavenumber. Moreover, nonlinear effects such as wave interactions will also affect the final spectrum and turbulence characteristics. So it is unclear whether the reduction at low frequencies in the fluctuation spectrum is the direct result of this damping, or whether other phenomena play a role. Linear simulations in figure 7 did not indicate a shift to higher $k_y$
as a result of increases in the electron temperature gradient.
Figure 8. (a) Density fluctuation autopower spectra averaged in the range $r=26-29\,{\rm cm}$
for the three experiments. (b) Floating potential fluctuation autopower spectra averaged from in the range $r=26-29\,{\rm cm}$
for the three experiments.
As indicated earlier, linear theory assumes a Boltzmann-like relationship between the density and the potential fluctuations, $\tilde {n}/n = (\tilde {\phi }/T_e)(1+{\rm i}\delta )$
. Here, $\delta$
is the phase shift between the two and is related to the resistivity. The resistivity changes as the temperature and density change and so a gradual change in the cross-phase could be expected. However, if we look at the cross-phase as a function of radius and frequency, we observe that there is an abrupt change instead of a gradual change in the cross-phase in the presence of a temperature gradient for frequencies larger than ${\sim }8 \,{\rm kHz}$
, see figure 9. Moreover, the cross-phase changes from positive to negative at these frequencies, which also has a direct effect on the turbulent particle flux. In discharges with a lower $L_n$
, with $\eta _e$
closer to 2/3, this effect vanishes. More experiments at higher temperature gradients or lower density gradients are necessary to further investigate this dynamic.
Figure 9. Radial dependence of the cross-phase spectrum for the experiment with $L_n = 6.1 \,{\rm cm}$
. The red lines indicate the boundaries of the density gradient region and the magenta line indicates the start of the temperature gradient at larger radii.
While linear theory is able to predict the correlation between $L_n$
and the density fluctuations, along with the damping effect of the $T_e$
gradient, our experiments show that, to fully understand and predict these effects, nonlinear simulations might be necessary. What causes the decorrelation of the relationship between the density and potential fluctuations? Why does the introduction of a temperature gradient reverse the sign of the cross-phase between the density and temperature fluctuations at high frequencies and why is this effect less pronounced at higher $\eta _e$
?
5. Discussion
In this paper we show the correlation between the increase in the density fluctuations and an increase in the density gradient, which is damped by the introduction of an electron temperature gradient. By changing the density gradient we also change the collisionality of these plasmas, which could lead to a proportional increase in resistive drift-wave-driven turbulence. In these plasmas, as the core density increases and thus also the density gradient, the average collisionality also increases. The collisionality changes from $\nu _{ei} \sim 3$
to $11 \,{\rm MHz}$
. In our experiments, the impact of neutral gas on the collisionality is approximately a factor 10 lower than the impact of the electron–ion collisionality and ranges from $\nu _{en} \sim 0.1$
to $0.2 \,{\rm MHz}$
. As we varied both the gas prefill and the current to the cathode, our data set from figure 2 has typically 2–3 different collisionality values for a similar gradient, which might explain the spread in the correlation in figure 2. Garland et al. studied the effect of collisionality on the intermittency of the density and potential fluctuation in the TJ-K stellarator (Garland et al. Reference Garland, Reuther, Ramisch and Manz2017). In those stellarator experiments the collisionality was varied from the collisionless drift-wave regime to resistive drift waves using different plasma species. They show that, in the resistive drift-wave regime, the density and potential fluctuations become more alike and intermittent. In future work, we plan to expand our experimental data set to higher temperatures with similar density gradients at various gas fill pressures to investigate this transition from collisionless to resistive drift waves on LAPD. We can see that, in the center of our plasma column, with similar collisionality as in the edge region but no density gradient, the turbulence characteristics are vastly different, see figure 10 and 11.
Figure 10. Radial dependence of the density fluctuation spectrum for the experiment with $L_n = 6.1 \,{\rm cm}$
. The red lines indicate the boundaries of the density gradient region and the magenta line indicates the start of the temperature gradient at larger radii.
Figure 11. Radial dependence of the floating potential fluctuation spectrum for the experiment with $L_n = 6.1 \,{\rm cm}$
. The red lines indicate the boundaries of the density gradient region and the magenta line indicates the start of the temperature gradient at larger radii.
In the region with the temperature gradient we noticed a bifurcation in the behaviour of the potential fluctuations with respect to $L_n$
. The potential fluctuations are reduced for the same $L_n$
for a set of experiments in which the parallel velocity was negative in the center, where for all other discharges this velocity was positive in the center of the plasma column. Work on CSDX has looked into how turbulence can influence axial flows through Reynolds stress and zonal Flow interactions with the azimuthal flow (Vaezi et al. Reference Vaezi, Holland, Thakur and Tynan2017). More measurements and experiments are necessary to better understand whether this observed link between the potential fluctuations and the parallel flow is correlated or accidental. In figure 12, we show the difference in the parallel flow profiles for two discharges with similar $L_n \sim 5.2 \,{\rm cm}$
that exhibit very different potential fluctuation behaviour (see figure 2). The experiments in which the potential fluctuations are strongly reduced have a stronger counter-flow in the core and they cross-over into positive flow close to $r = {\sim }25 \,{\rm cm}$
. For all these experiments, where the change in parallel flow direction occurs further out in the density gradient region, we observe a strong reduction in the potential fluctuations, which is not observed in the discharges where the change in parallel flow direction occurs further inward. Future research will focus on trying to understand how changes in the prefill as well as the collisionality and other plasma parameters affect the parallel flows. Based on our current observations, it is unlikely that this is purely set by turbulence, as we observe very different axial flows for similar plasma gradients. Changes in the neutral pressure and collisionality can affect the axial flow, similar to the scrape-off layer of a tokamak, where at larger collisionalities the plasma filaments become electrically disconnected from the target sheaths (Garcia et al. Reference Garcia, Pitts, Horacek, Madsen, Naulin, Nielsen and Rasmussen2007; D'Ippolito et al. Reference D'Ippolito, Russell, Myra, Thakur, Tynan and Holland2012). As a result, it seems more likely that the axial flow and its shear profile has an impact on the turbulence being generated than vice versa in our LAPD experiments.
Figure 12. Parallel flow measured with the Mach probe vs radius for 2 experiments with a similar $L_n \sim 5.2 \,{\rm cm}$
. The parallel flow profiles are shifted as a result of the change in fill pressure and cathode current.
Nonlinear Braginskii simulations for typical LAPD plasmas have suggested that transport can be driven by the Kelvin–Helmholtz instability (Rogers & Ricci Reference Rogers and Ricci2010). Indeed, we measure relative amplitudes between the density fluctuations and the floating potential fluctuations indicative of turbulence driven by a combination of rotational interchange, Kelvin–Helmholtz and drift waves (Perez et al. Reference Perez, Horton, Bengtson and Carter2006). However, the measured edge temperature gradients are constant within error throughout the data set. Therefore, the rotational interchange and Kelvin–Helmholtz drive can be assumed to be constant for the different experimental conditions and not be the cause for diverging experimental observations. Moreover, prior experiments on LAPD have shown that a very large shear is needed for any rotational instabilities to become dominant (Schaffner Reference Schaffner2013). Finally, the setup of LAPD experiments has very different boundary conditions than those used in the simulations by Rogers & Ricci (Reference Rogers and Ricci2010) nor are their profiles similar to the experiments presented in this paper. While there is no indication based on the profiles, nor from prior experimental observations on LAPD of any rotational instability playing a role in these experiments, nonlinear simulations similar to those reported in Rogers & Ricci (Reference Rogers and Ricci2010) are part of future work to fully understand the nonlinear dynamics at play.
6. Conclusion
In summary, in this paper we show that, for fully developed turbulence, linear predictions of resistive drift-wave turbulence provide a good initial estimate of the behaviour of the density fluctuations. There is a clear linear correlation between the density fluctuations and the density gradient when the electron temperature gradient is close to zero. The introduction of a small electron temperature gradient damps the density and potential fluctuations, as predicted by linear theory, but also alters the cross-phase between them. Moreover, the introduction of an electron temperature gradient eliminates the correlation between the density fluctuations and the density gradient and sets the density fluctuations to a fixed ‘constant’ value.
Acknowledgements
Editor Cary Forest thanks the referees for their advice in evaluating this article.
Funding
This work was performed using the Basic Plasma Science Facility at UCLA which is supported by DOE and NSF. This material is based upon work supported by the Department of Energy (DE-SC0007880, DE-FC02-07ER54918); National Science Foundation (NSF PHY 1561912, NSF PHY 2144099).
Declaration of interests
The authors report no conflict of interest.
Data availability statement
The data in the figures that support the findings of this study are openly available in https://doi.org/10.5281/zenodo.6877546.
