1. INTRODUCTION
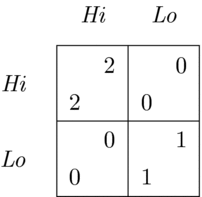
The standard solution concept used in orthodox game theory is based on the notion of individualistic best-response reasoning. Best-response reasoning is a process by which a player in a game arrives at his or her strategy choice. Its label derives from the fact that a player always picks his or her most preferred choice option from those available, given his or her beliefs about others’ actions. When each player’s chosen strategy in a game is a best response to the strategies chosen by other players, they are said to be in a Nash equilibrium – a profile of strategies from which no player has an incentive to deviate by unilaterally changing his or her strategy. This solution concept is sometimes criticized for its inability to single out what at times appears to be the only obvious choice to make in games with multiple Nash equilibria. A simple example is the Hi-Lo game, in which two players simultaneously and independently from each other choose one from a pair of options: Hi or Lo. If both choose Hi, they get a payoff of 2 each. If both choose Lo, they get a payoff of 1 each. If one chooses Hi while the other chooses Lo, they both get 0. The game is shown in Figure 1, where one player chooses between the two options identified by rows and the other – by columns. The bottom-left and the top-right number in each cell represents row and column player’s payoff respectively.
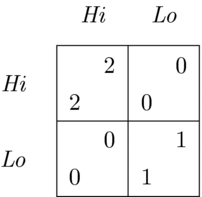
Figure 1. The Hi-Lo game.
There are two Nash equilibria in this game in pure strategies: (Hi, Hi) and (Lo, Lo). The first (second) entry in these pairs corresponds to row (column) player’s strategy. There is a third Nash equilibrium in mixed strategies, in which both players randomize between the available options by playing Hi and Lo with probabilities 1/3 and 2/3 respectively. This yields each player an expected payoff of 2/3. Thereby, individualistic best-response reasoning identifies a number of rational solutions of this game and, as a result, does not resolve the game definitively for the interacting players, leaving them with an equilibrium selection problem.Footnote 1 For many people, however, (Lo, Lo) and the mixed strategy equilibrium do not appear as convincing rational solutions, while the attainment of the outcome (Hi, Hi), which is unambiguously the best outcome for both players, appears to be a clear definitive resolution of this game. It is true that if one player expected the other to play Lo, then choosing Lo would be his or her best response to the other player’s choice. In other words, choosing Lo would be the rational thing to do. However, it would be odd if anyone formed an expectation that a rational individual would play Lo in the first place. Results from experiments support this by revealing that over 90% of the time people do opt for Hi in this game.Footnote 2
This prompted the development of the theory of team reasoning, which suggests that certain contextual and/or structural features of games may trigger a shift in peoples’ mode of reasoning from individualistic best-responding to reasoning as members of a team – a group of individuals who act together in the attainment of some common goal.Footnote 3 By suggesting various versions of this goal, the theory can be operationalized to select (Hi, Hi) as the only solution of the Hi-Lo game for those who reason as members of a team. As such, it is able to provide convincing resolutions of some interpersonal interactions where best-response reasoning falls short. As we will show shortly, it can also account for some instances of non-Nash-equilibrium play.
The theory of team reasoning has been developed in a number of different ways, producing various (sometimes competing) principles underlying team play in games. What, in our view, needs further development is a specification of team interests or team goals that applies, if such generalization is possible, across a wide range of games. In this paper we attempt to do that by suggesting a function of team interests based on the notion of mutually advantageous play discussed by Sugden (Reference Sugden2011, Reference Sugden2015). Our function is compatible with the orthodox conception of payoffs in games, which means that its application does not require payoffs to be interpersonally comparable. Thus our approach differs from those that use aggregative functions of team interests, such as the maximization of the average or the sum of players’ personal payoffs.
This paper is structured as follows. In Section 2 we discuss the theory of team reasoning in more detail and explain how it differs from simple payoff transformations in games. In Section 3 we discuss a few properties for potential functions of team interests to satisfy and show why aggregative functions may be ill-suited for this purpose. In Section 4 we propose measures of individual and mutual advantage in games and present a function of team interests as the maximization of mutual advantage attained by interacting players. After reviewing the function’s prescriptions in a few examples and discussing some of its properties we revisit the topic of interpersonal comparability of payoffs and distinguish it from interpersonal comparability of advantage based on our working definition of the latter. We then discuss the problem of coordination of players’ actions in games in which our function produces multiple solutions. In Section 5 we present some tentative ideas about why and under what circumstances people may reason as members of a team and with Section 6 we conclude.
2. TEAM REASONING
When a person reasons individualistically, he or she focuses on the question ‘what it is that I should do in order to best promote my interests?’. The answer to this question identifies a strategy that is associated with the highest expected personal payoff to the individual, given his or her beliefs about the actions of others. This is what is meant by individualistic best-response reasoning underlying the identification of Nash equilibria in games. When a person reasons as a member of a team, he or she focuses on the question ‘what it is that we should do in order to best promote our interests?’. The answer to this question identifies a strategy profile – one strategy for each player in a game – that leads to the attainment of the best possible outcome for the group of individuals acting together as a team.Footnote 4 As explained by Gold and Sugden (Reference Gold and Sugden2007a, 121), ‘when an individual reasons as a member of a team, she considers which combination of actions by members of the team would best promote the team’s objective, and then performs her part of that combination’.Footnote 5
If in the Hi-Lo game the outcome (Hi, Hi) is identified as uniquely optimal for a team, team reasoning can be said to resolve this game definitively for those players who endorse it. This would be so, for example, if the team’s objective were to maximize the average or the sum of the interacting players’ payoffs. In that case, an individual who endorsed this mode of reasoning when choosing his or her strategy would identify (Hi, Hi) as the uniquely optimal outcome for the team and choose Hi – his or her part in the attainment of this outcome.
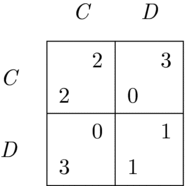
A well-known example of a case where team reasoning can prescribe the attainment of a non-Nash-equilibrium outcome is the Prisoner’s Dilemma game shown in Figure 2. Here two players simultaneously and independently from each other decide whether to cooperate (play C) or defect (play D). There is only one Nash equilibrium in this game, (D, D), since, from each player’s personal point of view, playing D is the best response to whatever the other player is going to do. It is thus said that cooperation is not rationalizable in terms of best-response reasoning: whatever one player may believe about the other’s choice, C is always inferior to D. In other words, C is a strictly dominated strategy – dominated by the strategy D. If, however, any of the outcomes associated with the play of C are ranked at the top from the point of view of a team, strategy C can be selected for the attainment of this outcome in terms of team reasoning.
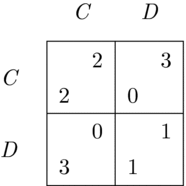
Figure 2. The Prisoner’s Dilemma game.
If, as earlier, the team’s goal were to maximize the average or the sum of individuals’ payoffs, team play would select the outcome (C, C). As such, with reference to results from numerous experiments showing that in a one-shot version of the Prisoner’s Dilemma game people tend to cooperate about 50% of the time, the theory of team reasoning operationalized this way provides a suggestion of why that is the case.Footnote 6
2.1. Motivations and Payoff Transformations
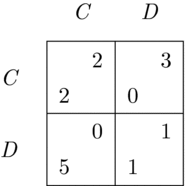
An important point stressed by a number of game theorists and rational choice theorists is that payoff structures of games have to capture all motivationally relevant aspects of players’ evaluations of the possible outcomes of those games.Footnote 7 Otherwise, without knowing precisely what games people play in terms of their true motivations, it would often be impossible to say anything about whether their choices are rational and why they make the choices that they do. To illustrate this, consider the Prisoner’s Dilemma game in terms of monetary payoffs shown in Figure 3(a). Suppose that the row player is a pure altruist when it comes to decisions involving money – he or she always strives to maximize the other player’s monetary gain. The column player, on the other hand, prefers to maximize his or her personal monetary payoff, but is averse to inequitable distributions of gains among individuals. Suppose that his or her inequity aversion is such that any unequal distribution of monetary gains is just as good in his or her eyes as personally gaining nothing. The correct representation of these players’ motivations transforms the monetary Prisoner’s Dilemma game into the game shown in Figure 3(b). There is one Nash equilibrium in the transformed game, (C, C), and the players would rationally cooperate if they both endorsed individualistic best-response reasoning and believed each other to do likewise. If we analysed observed cooperation using the original monetary payoff structure of the game, we may incorrectly conclude their choices to be irrational or presume the players to be reasoning as members of a team when that may not actually be so.
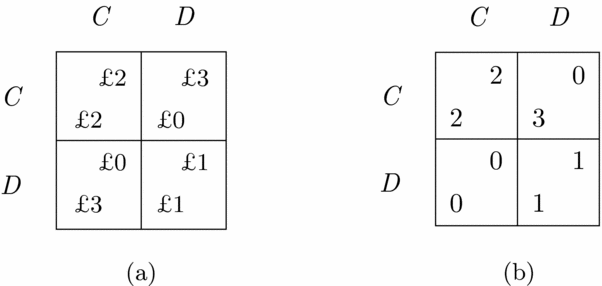
Figure 3. Monetary Prisoner’s Dilemma game (a) and its transformation (b).
This raises the question of whether it is possible to represent a shift in a player’s mode of reasoning to reasoning as a member of a team using a payoff transformation to reflect his or her motivation to attain the team’s objective in a similar way as in the case of altruism and inequity aversion above. To see that it is not, consider again the Hi-Lo game discussed earlier. Suppose that, from the point of view of a team, the outcome (Hi, Hi) is deemed to be the best, the outcome (Lo, Lo) is deemed to be the second-best and the outcomes (Hi, Lo) and (Lo, Hi) – the worst. Replacing any of the two players’ original payoffs in each cell of the game matrix with those corresponding to the team’s ranking of the four outcomes does not change the payoff structure of the original game in any way. As a result, the set of Nash equilibria and, hence, rational solutions in terms of best-response reasoning in the transformed game would be the same as in its original version, which is exactly what the theory of team reasoning was developed to contest. The key difference here is that individualistic best-response reasoning prescribes evaluating and choosing a particular strategy based on the expected personal payoff associated with that strategy, whereas team reasoning prescribes evaluating outcomes of a game from the perspective of a team (given the interacting players’ personal preferential rankings of those outcomes) and then choosing a strategy that is associated with the optimal outcome for the team. As such, the motivational shift that takes place with a switch from one mode of reasoning to another cannot be captured by transforming players’ payoff numbers in the cells of considered game matrices.Footnote 8
Another question is whether a shift from best-response reasoning to reasoning as a member of a team (or vice versa), in addition to changing the way a player reasons about which course of action it is best to take, may also change the way he or she personally values different outcomes of a game. In other words, whether such a shift transforms the payoff structure of a game itself. While this is an interesting possibility and one that has not been widely discussed in the literature on the theory of team reasoning to date, we assume here that this does not happen. We believe, however, there to be a reasonable ground for taking this approach. If a shift in the mode of reasoning may change the way a player personally values different outcomes, interactions between individuals could become games of incomplete information about each other’s payoffs and, as such, would take us far away from the type of games which the theory of team reasoning was developed to address. First, the solutions prescribed by best-response, team, and possible other modes of reasoning in cases of incomplete information about payoff structures of games would often be significantly different from those when payoff structures are commonly known. Players’ strategy choices would depend not only on modes of reasoning they use in a particular strategic interaction, but also on their beliefs about which payoff structures correctly define the games they play. Second, the theory of team reasoning was originally developed to resolve certain types of games in which best-response reasoning was deemed to fall short. In the case of the Hi-Lo game, for example, it was meant to resolve precisely this game with its particular payoff structure and when this structure was commonly known by interacting players. As such, for the rest of this paper we assume common knowledge of payoff structures of games and that shifts in modes of reasoning leave players’ personal payoffs associated with possible outcomes of games unchanged.Footnote 9
The last point to note is that reasoning as a member of a team does not imply the sharing of the attained personal payoffs among members of a team. In other words, the attained payoffs are assumed not to be transferable. If players were able to share their gains with others, such strategies and the associated payoff distributions would have to be included in representations of their strategic interactions.
2.2. Team Reasoning and Team Interests: Two Questions
The theory of team reasoning needs to address two important questions: ‘when do people reason as members of a team?’ and ‘what do people do when they reason as members of a team?’. In other words, it needs to suggest why and under what circumstances people may reason as members of a team and, once they do, what it is that they take team interests to be. In this paper we predominantly focus on the second question, though we will suggest some tentative ideas concerning the first question at the end.
3. TEAM INTERESTS
Suggestions about what team-reasoning decision-makers’ interests are vary in a number of ways. Two particular aspects in terms of which they differ are the extent to which team interests require individuals to sometimes sacrifice their personal interests for the benefit of other members of a team and whether the identification of team-optimal outcomes requires the interacting decision-makers’ payoffs to be interpersonally comparable. We discuss them in turn.
3.1. Self-Sacrifice and Mutual Advantage
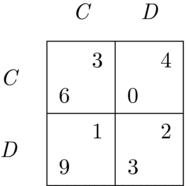
Bacharach (Reference Bacharach2006) mentions Pareto efficiency as a minimal condition for any function of team interests to satisfy: if one strategy profile is superior to another in terms of Pareto efficiency, a team prefers the former to the latter.Footnote 10 A function that satisfies this criterion is the maximization of the average or the sum of the interacting players’ payoffs, and it is discussed as an example in some of the early developments of the theory (e.g. Bacharach Reference Bacharach1999, Reference Bacharach2006) as well as in some more recent works (e.g. Colman et al. Reference Colman, Pulford and Rose2008, Reference Colman, Pulford and Lawrence2014; Smerilli Reference Smerilli2012). Even though it is used merely as an example, it is able to resolve some games definitively in intuitively compelling ways. It is easy to see that in the Hi-Lo and the Prisoner’s Dilemma games discussed earlier it selects the outcomes (Hi, Hi) and (C, C). One feature of this function, however, is that it may sometimes advocate a complete sacrifice of some individuals’ personal interests for the benefit of others. Consider a slight variation of the Prisoner’s Dilemma game shown in Figure 4. Here this function would prescribe the attainment of the outcome (D, C). As such, it would advocate a complete sacrifice of the column player’s personal interests for the benefit of the row player alone.
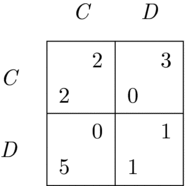
Figure 4. A variation of the Prisoner’s Dilemma game.
Although no alternative formal representations of team interests have been proposed, Sugden (Reference Sugden2011, Reference Sugden2015) discusses the notion of mutual advantage as another criterion for a function of team interests to satisfy. The idea is that an outcome selected by a team should be mutually beneficial from every team member’s perspective. Although he does not present an explicit function, Sugden proposes to define mutually advantageous outcomes as those that are associated with decision-makers’ personal payoffs satisfying a particular threshold. The suggested threshold is each player’s personal maximin payoff level in a game – the highest payoff that a player can guarantee himself or herself irrespective of what other players in the game are going to do. For both players in the Hi-Lo game this is 0. In the Prisoner’s Dilemma game of Figures 2 and 4 this is 1 (the lowest possible payoff associated with strategy D).
For Sugden, an outcome of a game is mutually beneficial if everyone’s maximin threshold is met and each player’s participation is necessary for the attainment of payoffs associated with that outcome. Notice that, according to this definition, all Nash equilibria in the Hi-Lo game are mutually beneficial. This is because every equilibrium is associated with personal payoffs higher than each player’s maximin threshold and each player’s play of the strategy associated with a particular equilibrium is necessary for the attainment of those payoffs. Thus, the above definition of mutual advantage does not exclude Pareto inefficient outcomes and, by itself, it does not suggest a further ranking of outcomes for a team once all mutually beneficial outcomes are established.
3.2. Interpersonal Comparisons of Utility
Any function of team interests that aggregates decision-makers’ payoffs requires them to be interpersonally comparable. In the Prisoner’s Dilemma game of Figure 4 this suggests, for example, that the row player prefers the outcome (D, C) to the outcome (C, C) to a greater extent than the column player prefers (C, D) to (D, D). Such comparisons go beyond the standard assumptions of expected utility theory, which make numerical representations of individuals’ preferences possible, but do not automatically grant their interpersonal comparability. This means, for example, that the representation of row player’s preferences in Figure 4 allows us to say that he or she prefers the outcome (C, C) to (D, D), or that he or she prefers the outcome (D, C) to (C, C) by a greater extent than he or she prefers (D, D) to (C, D). However, it does not allow us to claim that the row player’s well-being, in some objective sense, is the same in the outcome (C, C) as that of the column player.
It is a result of expected utility theory that any payoff function that numerically represents a decision-maker’s preferences is unique up to positive affine transformations. This means that if u is a payoff function that maps every strategy profile in a game to a real number in a way that correctly represents an individual’s preferences over outcomes, then so is any function u′ = au + c, where a > 0 and c are constants. (For a detailed discussion of why this is so, see, for example, Luce and Raiffa Reference Luce and Raiffa1957, ch. 2.) What follows from this is that the payoff structure of the Prisoner’s Dilemma game of Figure 2 represents exactly the same preferences of the interacting players as the one in Figure 5.Footnote 11 As such, we would expect solutions of this game to be invariant under positive affine transformations of players’ payoffs and a function of team interests to select the same outcome(s) as optimal for a team in both cases. The maximization of the average or the sum of the two players’ payoffs, however, selects different outcomes: (C, C) in the case of Figure 2 and (D, C) in the case of Figure 5.
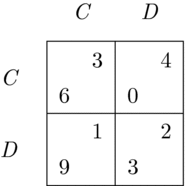
Figure 5. Another representation of preferences in the Prisoner’s Dilemma game.
Any version of the theory of team reasoning that uses aggregative functions of team interests will be applicable only in those contexts in which interpersonal comparisons of payoffs are possible. Since this goes beyond the standard assumptions of expected utility theory, the possibility to make such comparisons may need a separate justification.Footnote 12 The function of team interests which we present in the next section is applicable in both cases. We will first present a version that applies to situations in which interpersonal comparisons of payoffs are not warranted. We will then explain how it can be modified to apply in cases in which payoffs are interpersonally comparable.
4. TEAM INTERESTS AS MAXIMUM MUTUAL ADVANTAGE
Let us return to Sugden’s (Reference Sugden2011, Reference Sugden2015) notion of team interests as the attainment of mutually beneficial outcomes. By itself, the identification of mutually beneficial outcomes does not suggest how much of mutual benefit is gained. For the latter we need measures of individual and mutual advantage in terms of which considered outcomes could be evaluated. We propose the following definitions.
-
Individual advantage: An outcome of a game is individually advantageous to a particular player if that player’s attained personal payoff is higher than his or her reference point – a payoff level from which the advantage to that player is measured. The extent of individual advantage gained is the extent by which that outcome advances the player’s personal payoff from his or her reference point relative to the largest advancement possible, where the latter is associated with the attainment of an outcome that he or she prefers the most in the game.
-
Mutual advantage: An outcome of a game is mutually advantageous to the interacting players if each player’s attained personal payoff is higher than his or her reference point – a payoff level from which the advantage to that player is measured. The extent of mutual advantage associated with an outcome is the largest extent of individual advantage that is gained by every player in that outcome.
By definition, the maximum value of individual or mutual advantage is 1. To avoid working with decimals we can express these in percentage terms, which simply means that the values are multiplied by a factor of 100. For example, if, in a two-player game, both players’ reference points are associated with a payoff of 0 and their most preferred outcomes with a payoff of 100, a particular outcome associated with payoffs of 30 and 20 to the two players is said to offer 20 units of mutual advantage. The additional 10 units of individual advantage to one player is not mutual.
Note that individual advantage, defined as above, is simply a player’s personal payoff when that player’s payoff function is normalized so that his or her most preferred outcome of a game is assigned the payoff value 1, while his or her reference payoff is set to 0. This can always be achieved through a positive affine transformation of that player’s original payoffs (recall that any such transformation of a player’s payoffs represents the same preferences over considered outcomes). Note also that if some player’s most preferred outcome is associated with the same payoff as his or her reference point, nothing in the game is individually advantageous to that player and, consequently, nothing is mutually advantageous to a group of decision-makers that includes that player as well.
Given these measures of individual and mutual advantage, team interests can now be defined as the attainment of outcomes that are associated with maximum mutual advantage to the interacting players. In addition to this we impose the constraint that each player’s personal payoff should be at least as high as his or her personal maximin threshold – the personal payoff that the player can guarantee himself or herself irrespective of what other players do. Similarly as for Sugden (Reference Sugden2015), this is due to the idea that team play, driven by a joint pursuit of team interests, should be at least as beneficial to every player partaking in it as the payoff that the player can guarantee himself or herself individually. Subject to this constraint, since the extent of mutual advantage is the largest extent of individual advantage that is gained by every player, this is identical to the maximization of the minimum extent of individual advantage across the interacting players.Footnote 13
4.1. Formalization
For a formal presentation of the proposed function of team interests, let I = {1, . . ., m} be a finite set of m players and S
i
be a set of pure strategies available to player i ∈ I. A pure strategy outcome is defined as a strategy profile s = (s
1, . . ., s
m
), where s
i
∈ S
i
is a particular pure strategy of player i. Let S = ×
i ∈ I
S
i
be the set of all possible pure strategy profiles in a game, and
![]() $u_i : S \rightarrow \mathbb {R}$
be a payoff function that maps every pure strategy profile to a personal payoff for player i. A mixed strategy of player i is a probability distribution over S
i
. Let Σ
i
be a set of all such probability distributions and σ
i
∈ Σ
i
be a particular mixed strategy of player i, where σ
i
(s
i
) denotes probability assigned to s
i
. A mixed strategy outcome (henceforth, outcome) is defined as a strategy profile σ = (σ1, . . ., σ
m
). Let Σ = ×
i ∈ I
Σ
i
be the set of all possible mixed strategy profiles and u
i
(σ) = ∑
s ∈ S
(∏
i ∈ I
σ
i
(s
i
))u
i
(s) be expected payoff to player i associated with the mixed strategy profile σ.
$u_i : S \rightarrow \mathbb {R}$
be a payoff function that maps every pure strategy profile to a personal payoff for player i. A mixed strategy of player i is a probability distribution over S
i
. Let Σ
i
be a set of all such probability distributions and σ
i
∈ Σ
i
be a particular mixed strategy of player i, where σ
i
(s
i
) denotes probability assigned to s
i
. A mixed strategy outcome (henceforth, outcome) is defined as a strategy profile σ = (σ1, . . ., σ
m
). Let Σ = ×
i ∈ I
Σ
i
be the set of all possible mixed strategy profiles and u
i
(σ) = ∑
s ∈ S
(∏
i ∈ I
σ
i
(s
i
))u
i
(s) be expected payoff to player i associated with the mixed strategy profile σ.
In what follows, we present the function when mixed strategy play is allowed.Footnote 14 (For a version of the function when only pure strategies are considered simply replace σ i , σ, Σ i , and Σ with s i , s, S i , and S.) Let u max i ≔ maxσ ∈ Σ ui (σ) denote player i’s personal payoff associated with his or her most preferred outcome, let u ref i denote i’s reference payoff from which individual advantage to i is measured, and let u maximin i ≔ maxσ i ∈ Σ i {minσ−i ∈ Σ−i ui (σ)} denote i’s maximin payoff level in the game (where σ−i ∈ Σ−i denotes a combination of strategies of all players other than i).
So long as u ref i ≠ ui max, the extent of individual advantage to player i associated with a particular strategy profile σ is
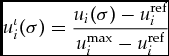 $$\begin{equation}
u_i^\iota (\sigma ) = \frac{u_i(\sigma )-u_i^{\rm {ref}}}{u_i^{\rm {max}}-u_i^{\rm {ref}}}
\end{equation}$$
$$\begin{equation}
u_i^\iota (\sigma ) = \frac{u_i(\sigma )-u_i^{\rm {ref}}}{u_i^{\rm {max}}-u_i^{\rm {ref}}}
\end{equation}$$
(Notice that if i’s payoff function u i is normalized so that u max i = 1 and u ref i = 0, then u ι i (σ) = ui (σ).) Having defined u ι i (σ), the extent of mutual advantage associated with σ is
When u
ref
i
≠ ui
max for all i ∈ I, the proposed function of team interests
![]() $\tau : \mathcal {P}(\Sigma ) \rightarrow \mathcal {P}(\Sigma )$
, where τ(Σ) = Στ⊆Σ, selects a subset from the set of all possible strategy profiles in a game such that each selected strategy profile maximizes the extent of mutual advantage to the interacting players, subject to each player’s personal payoff being at least as high as his or her maximin payoff level in the game. Formally, each element σ ∈ Στ is such that
$\tau : \mathcal {P}(\Sigma ) \rightarrow \mathcal {P}(\Sigma )$
, where τ(Σ) = Στ⊆Σ, selects a subset from the set of all possible strategy profiles in a game such that each selected strategy profile maximizes the extent of mutual advantage to the interacting players, subject to each player’s personal payoff being at least as high as his or her maximin payoff level in the game. Formally, each element σ ∈ Στ is such that
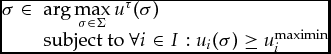 $$\begin{eqnarray}
\begin{array}{rl} \sigma \in &\ {\arg \max\limits_{\sigma \in \Sigma }}\, u^\tau (\sigma ) \\
&\ \mbox{subject to}\ \forall i \in I : u_i(\sigma ) \ge u_i^{\rm {maximin}} \end{array}
\end{eqnarray}$$
$$\begin{eqnarray}
\begin{array}{rl} \sigma \in &\ {\arg \max\limits_{\sigma \in \Sigma }}\, u^\tau (\sigma ) \\
&\ \mbox{subject to}\ \forall i \in I : u_i(\sigma ) \ge u_i^{\rm {maximin}} \end{array}
\end{eqnarray}$$
or, inserting (1) and (2) into (3),
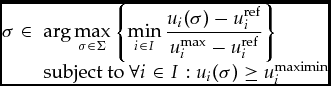 $$\begin{eqnarray}
\begin{array}{rl} \sigma \in &\ {\arg \max\limits_{\sigma \in \Sigma }} \left\{ {\min\limits_{i \in I} }\, \displaystyle\frac{u_i(\sigma )-u_i^{\rm {ref}}}{u_i^{\rm {max}}-u_i^{\rm {ref}}} \right\} \\
&\ \mbox{subject to}\ \forall i \in I : u_i(\sigma ) \ge u_i^{\rm {maximin}} \end{array}
\end{eqnarray}$$
$$\begin{eqnarray}
\begin{array}{rl} \sigma \in &\ {\arg \max\limits_{\sigma \in \Sigma }} \left\{ {\min\limits_{i \in I} }\, \displaystyle\frac{u_i(\sigma )-u_i^{\rm {ref}}}{u_i^{\rm {max}}-u_i^{\rm {ref}}} \right\} \\
&\ \mbox{subject to}\ \forall i \in I : u_i(\sigma ) \ge u_i^{\rm {maximin}} \end{array}
\end{eqnarray}$$
If u ref i = ui max for some i ∈ I, u ι i is undefined and nothing is individually advantageous to player i. Consequently, nothing is mutually advantageous to the group of players I and so τ(Σ) = ∅. To summarize,
4.2. Applicability and Two Properties
The application of the above function of team interests is limited to cases in which u ref i and u max i can be identified for every payer i in a game. A sufficient condition for this to be so is having a finite number of players and pure strategies available to each player. With an infinite number of players and/or pure strategies this may not be so. Consider, for example, a decision situation in which a number of firms compete to employ a prospective employee by offering a salary. Since there is no upper bound on the salary a firm could offer in theory, there is no upper bound on the payoff the potential employee may attain.Footnote 15 In this and similar scenarios our proposed function of team interests could only be applied if all players’ payoff functions were bounded from above and below. There may be cases, however, in which all players’ payoff functions are bounded, but the infinite number of strategies allow one’s payoff to approach a particular value, but never quite reach it. Suppose that the aforementioned competing firms are prohibited from paying anyone more than some set salary level. If infinitesimal fractions of monetary units were meaningful, theoretically this would mean than the maximum payoff for the prospective employee could not be identified. In such and similar scenarios our discussed function could only be applied by approximating each player’s u ref i and u max i payoffs.
Two properties of τ can be derived without further specification of u
ref
i
. First, provided there is a finite number of players and pure strategies available to each player, and u
ref
i
≠ ui
max for all i ∈ I, the set of strategy profiles selected by τ is nonempty. This is so because, for every player i in a game, there always exists at least one maximin strategy
![]() $\sigma _i^{\rm {maximin}} \in \arg \max _{\sigma _i \in \Sigma _i} \lbrace \min _{\sigma _{-i} \in \Sigma _{-i}} u_i(\sigma )\rbrace$
, such that ui
(σmaximin
i
, σ−i
) ⩾ u
maximin
i
. As such, there is at least one strategy profile σmaximin = (σmaximin
1, . . ., σ
m
maximin), such that ui
(σmaximin) ⩾ u
maximin
i
for every player i ∈ I, which satisfies the constraint in (3) and (4). Since the function τ selects strategy profiles associated with maximum mutual advantage from those that satisfy the above constraint and since there is at least one strategy profile that satisfies it, it follows that Στ is nonempty.
$\sigma _i^{\rm {maximin}} \in \arg \max _{\sigma _i \in \Sigma _i} \lbrace \min _{\sigma _{-i} \in \Sigma _{-i}} u_i(\sigma )\rbrace$
, such that ui
(σmaximin
i
, σ−i
) ⩾ u
maximin
i
. As such, there is at least one strategy profile σmaximin = (σmaximin
1, . . ., σ
m
maximin), such that ui
(σmaximin) ⩾ u
maximin
i
for every player i ∈ I, which satisfies the constraint in (3) and (4). Since the function τ selects strategy profiles associated with maximum mutual advantage from those that satisfy the above constraint and since there is at least one strategy profile that satisfies it, it follows that Στ is nonempty.
Another property of τ is that every strategy profile that it selects is efficient in the weak sense of Pareto efficiency.Footnote
16
To see this, suppose that τ selects the strategy profile σ
x
∈ Σ when there exists another strategy profile σ
y
∈ Σ, such that u
i
(σ
y
) > u
i
(σ
x
) for every player i ∈ I (in other words, σ
x
is not Pareto efficient in the weak sense). As long as u
ref
i
≠ ui
max for every i ∈ I, it follows that min
i ∈ I
u
ι
i
(σ
y
) > min
i ∈ I
u
ι
i
(σ
x
). Hence,
![]() $\sigma ^x \notin \arg \max _{\sigma \in \Sigma } \lbrace \min _{i \in I} u_i^\iota (\sigma ) \rbrace$
, and so σ
x
∉Στ.
$\sigma ^x \notin \arg \max _{\sigma \in \Sigma } \lbrace \min _{i \in I} u_i^\iota (\sigma ) \rbrace$
, and so σ
x
∉Στ.
4.3. Reference Points
The above function of team interests can be applied with any set of personal reference points, relative to which individual and, based on these, mutual advantages are measured. We discuss three possible reference points here and focus on one of them in more detail when reviewing examples in the next section.
Since every outcome of a game is reachable via players’ joint actions, one possibility is to set each player’s reference point to be the worst payoff that he or she can attain in that game. It is the payoff associated with a player’s least preferred outcome: u ref i = minσ ∈ Σ ui (σ). However, this approach may be criticized on the basis that not all outcomes of games should be considered on an equal footing when it comes to establishing players’ personal reference points, relative to which individual advantages are to be measured. It may be argued that outcomes that are not rationalizable in terms of best-response reasoning should be left out from the set considered for this purpose. Since this would exclude strictly dominated strategies, outcomes defined in terms of such strategies would not be used for establishing reference points.Footnote 17 Letting Σ br ⊆Σ denote the set of strategy profiles that are rationalizable in terms of best-response reasoning, this modifies the previous reference point to the following: u ref i = minσ ∈ Σ br ui (σ).
The fact that the notion of rationalizability is associated with best-response reasoning raises the question of whether it should be applied in establishing reference points for identifying mutually advantageous outcomes when using a mode of reasoning that is not based on best-response considerations. There are two ways to justify the use of the restricted set Σ br instead of Σ. The first is to argue that decision-makers approach their considered games in terms of best-response reasoning to begin with, and that, having drawn conclusions about outcomes they could potentially reach through the application of this mode of reasoning, they evaluate everything that follows – including their considerations about what is mutually advantageous – relative to those conclusions. We will briefly return to this idea later in Section 5. The second approach is to argue that players’ reference points, relative to which individual advantages are measured to subsequently establish the extents of mutual advantage, are, essentially, individualistic. These are thresholds, such that anything that is preferentially inferior to them is not individually advantageous to respective decision-makers. Hence it may be argued that their establishment should be based on individualistic reasoning and, as such, best-response rationalization is a plausible restriction to impose.
The third possible reference point is a player’s personal maximin payoff level in a game: u ref i = maxσ i ∈ Σ i {minσ−i ∈ Σ−i ui (σ)}. This approach is closest to the definition of mutual advantage discussed by Sugden (Reference Sugden2015) and it ensures that the maximin constraint in the function τ is automatically met. However, the previous criticism could still apply: strategy profiles associated with players’ maximin payoffs may be excluded from the set of outcomes that are rationalizable in terms of best-response reasoning. Also, outcomes associated with these thresholds, when they lie close, in relative preferential terms, to players’ most preferred outcomes of games, may, at times, serve as useful definitive resolutions of those games when individualistic best-response reasoning leads to indeterminacies. As such, maximin thresholds themselves may be mutually advantageous. We will illustrate such a case shortly.
4.4. Examples
In this section we show what the function τ selects in a few simple examples. Two of these – the Hi-Lo and the Prisoner’s Dilemma games – we already introduced. The other two are a version of the Chicken game and a game we labelled the High Maximin shown in Figure 6. In our discussion here we compute the extents of individual and mutual advantage using the second of the three possible reference points discussed in the previous section: u ref i = minσ ∈ Σ br ui (σ). We present a detailed derivation of results in the Chicken game first and summarize the function’s prescriptions for the remaining games afterwards.
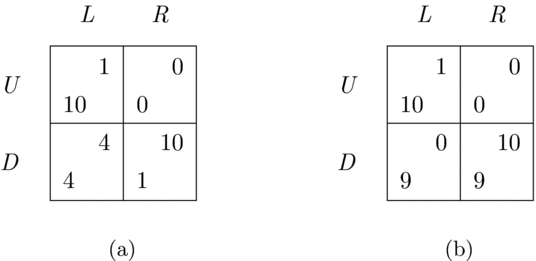
Figure 6. The Chicken (a) and the High Maximin (b) games.
There are three Nash equilibria in the presented version of the Chicken game: (U, L), (D, R), and (U
![]() $\frac{6}{7}$
, D
$\frac{6}{7}$
, D
![]() $\frac{1}{7}$
; L
$\frac{1}{7}$
; L
![]() $\frac{1}{7}$
, R
$\frac{1}{7}$
, R
![]() $\frac{6}{7}$
). The third is a mixed strategy equilibrium, in which row player randomizes between U and D with probabilities 6/7 and 1/7, while column player randomizes between L and R with probabilities 1/7 and 6/7 respectively. This yields both players an expected payoff of 10/7. Any combination of strategies associated with the three Nash equilibria is rationalizable in terms of best-response reasoning. As such, for both players, the least preferred rationalizable outcome from the set Σ
br
is (U, R), the maximin payoff level is 1 (the lowest possible payoff associated with strategies D and L), and the most preferred outcome yields a payoff of 10. Thus, for both players, u
ref
i
= 0, u
max
i
= 10, and u
maximin
i
= 1. The extents of individual and mutual advantage, u
ι
i
and u
τ, associated with the four pure strategy outcomes of the game are shown below (sorted by u
τ). These, as noted earlier, are expressed in percentage terms (u
ι
i
and u
τ are multiplied by a factor of 100).
$\frac{6}{7}$
). The third is a mixed strategy equilibrium, in which row player randomizes between U and D with probabilities 6/7 and 1/7, while column player randomizes between L and R with probabilities 1/7 and 6/7 respectively. This yields both players an expected payoff of 10/7. Any combination of strategies associated with the three Nash equilibria is rationalizable in terms of best-response reasoning. As such, for both players, the least preferred rationalizable outcome from the set Σ
br
is (U, R), the maximin payoff level is 1 (the lowest possible payoff associated with strategies D and L), and the most preferred outcome yields a payoff of 10. Thus, for both players, u
ref
i
= 0, u
max
i
= 10, and u
maximin
i
= 1. The extents of individual and mutual advantage, u
ι
i
and u
τ, associated with the four pure strategy outcomes of the game are shown below (sorted by u
τ). These, as noted earlier, are expressed in percentage terms (u
ι
i
and u
τ are multiplied by a factor of 100).

When only pure strategies are considered the maximally mutually advantageous outcome is (D, L) and, since it satisfies the maximin constraint for both players, it is the unique outcome selected by τ. The result is slightly different, albeit also yielding a unique solution, if mixed strategies are considered as well. In the latter case, maximum mutual advantage is associated with the mixed strategy profile (U
![]() $\frac{3}{14}$
, D
$\frac{3}{14}$
, D
![]() $\frac{11}{14}$
; L
$\frac{11}{14}$
; L
![]() $\frac{11}{14}$
, R
$\frac{11}{14}$
, R
![]() $\frac{3}{14}$
), which yields both players an expected payoff (with reference to the payoff structure in Figure 6(a)) of approximately 4.32. The corresponding approximate extent of mutual advantage is 43.2, which is higher than that associated with (D, L). As a result, S
τ = {(D, L)} when only pure strategies are considered and
$\frac{3}{14}$
), which yields both players an expected payoff (with reference to the payoff structure in Figure 6(a)) of approximately 4.32. The corresponding approximate extent of mutual advantage is 43.2, which is higher than that associated with (D, L). As a result, S
τ = {(D, L)} when only pure strategies are considered and
![]() $\Sigma ^\tau = \lbrace \mbox{({\em U} $\frac{3}{14}$, {\em D} $\frac{11}{14}$; {\em L} $\frac{11}{14}$, {\em R} $\frac{3}{14}$)}\rbrace$
when mixed strategies are considered as well. Either way, S
τ and Στ are singletons, which means that the function τ resolves this game definitively for those who reason as members of a team. Also note that in both cases τ selects a non-Nash-equilibrium outcome.
$\Sigma ^\tau = \lbrace \mbox{({\em U} $\frac{3}{14}$, {\em D} $\frac{11}{14}$; {\em L} $\frac{11}{14}$, {\em R} $\frac{3}{14}$)}\rbrace$
when mixed strategies are considered as well. Either way, S
τ and Στ are singletons, which means that the function τ resolves this game definitively for those who reason as members of a team. Also note that in both cases τ selects a non-Nash-equilibrium outcome.
Results for the remaining three games are summarized in Table 1. The top section of the table shows parameter values and the selected outcomes in S τ when only pure strategies are considered (u maximin i is abbreviated for row and column player as u mxm row and u mxm col respectively). The bottom section shows these values and the selected outcomes in Στ when mixed strategies are considered as well.
Table 1. Summary of results in four examples.

*In Στ for the High Maximin, 0 ⩽ p ⩽ 1/10.
In the case of mixed strategies in the Hi-Lo game, the maximin strategy for both players is to randomize between Hi and Lo as in the mixed strategy Nash equilibrium. Irrespective of whether mixed strategies are considered or not, however, (Hi, Hi) is the unique outcome selected by τ.
The three Nash equilibria in the High Maximin game are (U, L), (D, R), and (U
![]() $\frac{10}{11}$
, D
$\frac{10}{11}$
, D
![]() $\frac{1}{11}$
; L
$\frac{1}{11}$
; L
![]() $\frac{9}{10}$
, R
$\frac{9}{10}$
, R
![]() $\frac{1}{10}$
). The mixed strategy equilibrium yields expected payoff of 9 and 10/11 to row and column player respectively. In the case of mixed strategies, column player can secure an expected payoff of at least 10/11 by randomizing between L and R with probabilities 10/11 and 1/11. As in the Chicken game, the output of τ depends on whether mixed strategies are considered or not. If they are, any strategy profile in which the row player plays D while the column player randomizes between L and R with probabilities 0 ⩽ p ⩽ 1/10 and 1 − p respectively is maximally mutually advantageous and is included in the set Στ, which means that Στ is not a singleton. This still resolves the game definitively for the interacting players, since τ prescribes a unique strategy choice to row player and it is up to column player alone to select any outcome from the set Στ using 0 ⩽ p ⩽ 1/10 of his or her choice. If only pure strategies are considered, τ selects (D, R). Note that mutually advantageous play in both cases yields row player his or her maximin payoff. As such, this is an example of a case where a personal payoff associated with maximally mutually advantageous outcome(s) is also one player’s maximin level. By contrast, if u
ref
i
were set for both players to their personal maximin payoffs, τ would select the outcome (U, L) with and without mixed strategy play.
$\frac{1}{10}$
). The mixed strategy equilibrium yields expected payoff of 9 and 10/11 to row and column player respectively. In the case of mixed strategies, column player can secure an expected payoff of at least 10/11 by randomizing between L and R with probabilities 10/11 and 1/11. As in the Chicken game, the output of τ depends on whether mixed strategies are considered or not. If they are, any strategy profile in which the row player plays D while the column player randomizes between L and R with probabilities 0 ⩽ p ⩽ 1/10 and 1 − p respectively is maximally mutually advantageous and is included in the set Στ, which means that Στ is not a singleton. This still resolves the game definitively for the interacting players, since τ prescribes a unique strategy choice to row player and it is up to column player alone to select any outcome from the set Στ using 0 ⩽ p ⩽ 1/10 of his or her choice. If only pure strategies are considered, τ selects (D, R). Note that mutually advantageous play in both cases yields row player his or her maximin payoff. As such, this is an example of a case where a personal payoff associated with maximally mutually advantageous outcome(s) is also one player’s maximin level. By contrast, if u
ref
i
were set for both players to their personal maximin payoffs, τ would select the outcome (U, L) with and without mixed strategy play.
Lastly, in the Prisoner’s Dilemma game the function τ selects (C, C). Parameter values in Table 1 are based on the Prisoner’s Dilemma game of Figure 2, but the result is the same for all versions of this game discussed earlier.
4.5. No Irrelevant Player or Strategy
A point to note is that the function τ does not ignore any player in its determination of team-optimal outcomes. This means that no player can be dismissed on grounds of being irrelevant. One consequence of this is that the presence of a player who is indifferent between all outcomes of a game, with u ref i = ui max, renders Στ = ∅. Since such a player personally does not care about how the game is going to be resolved, there is nothing that would motivate him or her to seek out mutually advantageous solutions. Although in cases involving more than two players this leaves the possibility for the remaining decision-makers to consider what is mutually advantageous for them based on their predicted actions of those outside of their group, mutually advantageous play is not possible for all players in the game as members of one team.
Also, as the Prisoner’s Dilemma example shows, the addition of strictly dominated strategies to a game can result in changes in the set of outcomes selected for a team.Footnote 18 This means that such strategies cannot be treated as irrelevant either. With regards to this point, however, the function τ can be adapted to a more orthodox interpretation of what counts as feasible in games by limiting its output to outcomes that are rationalizable in terms of best-response reasoning. For this approach, all outcomes outside of the set Σ br are excluded from those considered as potential outputs of τ, and u ref i with u max i are assigned payoff values associated with each player’s least and most preferred outcome(s) in Σ br . Returning to our examples, in the Hi-Lo game this would yield the same results as previously. In the Chicken and the High Maximin games the outcomes selected by τ when mixed strategies are considered would be the same as those selected for pure strategy play earlier (this is because previously selected mixed strategy profiles are not rationalizable in terms of best-response reasoning and, as such, they would be excluded). Lastly, in the Prisoner’s Dilemma game nothing would count as mutually advantageous, since only one outcome is rationalizable in terms of best-response reasoning. This version of τ would allow to regard all strictly dominated strategies as irrelevant.
4.6. Interpersonal Comparisons of Advantage
Earlier we noted that the standard expected utility theory makes numerical representations of decision-makers’ preferences possible, but does not automatically grant their interpersonal comparability, and suggested that the function τ applies in cases when interpersonal comparisons of payoffs are not warranted in this sense. The presented function, however, does make an interpersonal comparison of one sort: it equates a unit of individual advantage gained by one player in a game with that gained by another. We argue that even when the comparison of the former sort is not warranted, the comparison of the latter sort is nevertheless permissible.
Interpersonal comparisons of decision-makers’ payoffs tend to associate their preference satisfaction with some interpersonally comparable notion of attained well-being or other form of welfare. If, in the context of games, we were to contemplate the possibility that for one player stakes might be significantly higher than they are for another in this sense, we would indeed be making an implicit assumption that their attained payoffs can be interpersonally compared. Our proposed measures of individual and mutual advantage, expressed as extents of relative advancement of players’ personal interests towards their most preferred outcomes of games, however, are meant to be applied when such comparisons are not possible (or, to put differently, when such comparisons provide no meaningful information). The reason they can be applied is the fact that the scales for these measures can be established using commonly known and objectively identifiable points in games without the need to make interpersonal comparisons of the attained payoffs. In order to use these measures, decision-makers need to know each other’s preferences over the possible outcomes of games and their personal reference points, but they need not be able to make any interpersonal comparisons of their attained well-being in some objectively or subjectively comparable way. Without comparing their attained well-being players can still compare the extents to which their personal interests are advanced within the context of some particular decision problem they are trying to solve.Footnote 19
The interpersonal comparisons implied by the function τ are thus quite different from those not warranted by the standard expected utility theory. When decision-makers consider mutually advantageous play in games, they equate units of measures of their individual advantage – the advancement of their personal interests relative to what they personally deem to be the best and the worst case outcomes of their interactions – while not being able to equate units of the attained personal well-being. All they know is how much a particular outcome is individually advantageous to a player relative to that player’s reference point and his or her most preferred outcome of a game.Footnote 20
This does not mean that interpersonal comparisons of payoffs are never possible or that we never make them in our interactions with each other. Binmore (Reference Binmore2005, Reference Binmore, Ross and Kincaid2009) argues, for example, that we may have evolved the ability to make such comparisons over the course of our evolutionary development. This, however, does not preclude the applicability of the above function for identifying mutually advantageous outcomes. A step that needs to be added before the function is applied in cases when players’ payoffs are interpersonally comparable is the rescaling of players’ measures of individual advantage u ι i using appropriate scaling factors to equate these units in accordance with how their attained personal payoffs interpersonally compare.
4.7. Mutual Advantage and Coordination
There will be many games in which the function τ selects more than one outcome. In some situations, such as the High Maximin game of Figure 6(b), this will not cause a difficulty for decision-makers to coordinate their actions, but in many cases it will. We may thus consider whether the expected success of coordinating actions on some particular outcome should be reflected in the measure of mutual advantage associated with that outcome.
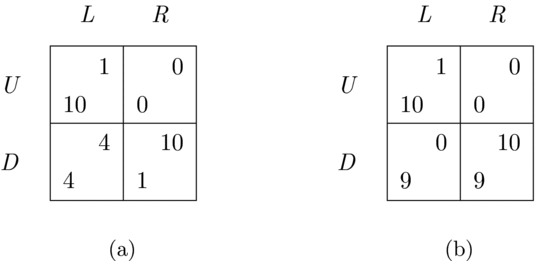
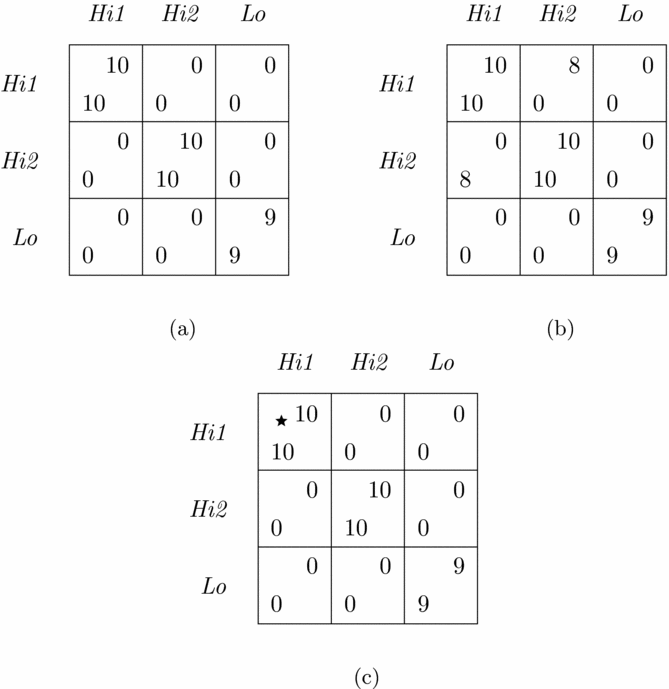
Consider the expanded version of the Hi-Lo game shown in Figure 7(a). There are seven Nash equilibria in this game, three in pure strategies and four in mixed. (The four mixed strategy equilibria yield each player an expected payoff of at most 5.) The function τ selects two outcomes as maximally mutually advantageous: (Hi1, Hi1) and (Hi2, Hi2). As such, it leaves team-reasoning decision-makers facing a coordination problem. Since the selected outcomes are indistinguishable (apart from strategy labels and their positions in the matrix representation of the game, both of which can aid to coordinate players’ actions – a point which we ignore for the time being), if the two players, without communicating with each other, were to simultaneously attempt to attain any one of the two, they could expect to succeed with probability 1/2. This would yield each player an expected payoff of 5. The outcome (Lo, Lo), however, is unique in the sense that it is the only outcome of the game that yields both players a payoff of 9. It may thus be beneficial for the interacting players, instead of attempting to coordinate their actions on one of the two indistinguishable outcomes, to focus on the attainment of the outcome (Lo, Lo). This would guarantee each player a certain personal payoff of 9 instead of the expected payoff of 5.
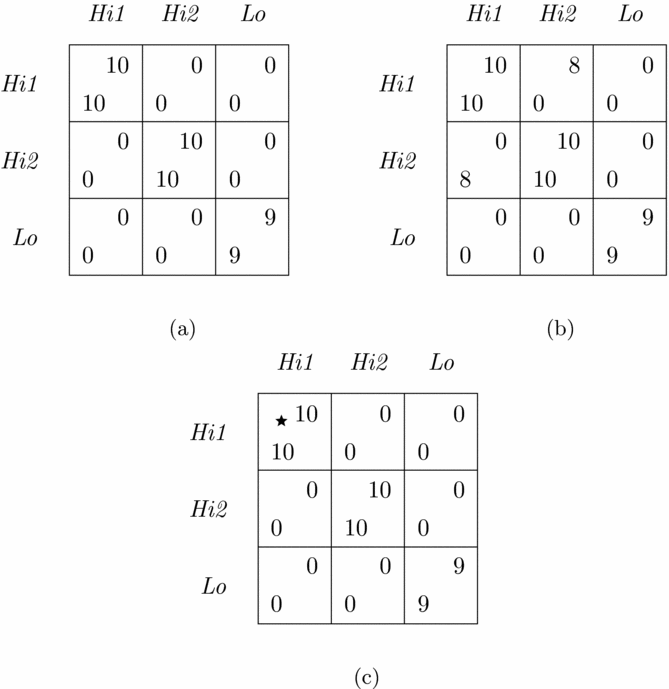
Figure 7. The expanded Hi-Lo game (a) and its variations (b), (c).
Bardsley et al. (Reference Bardsley, Mehta, Starmer and Sugden2010) and Faillo et al. (Reference Faillo, Smerilli and Sugden2016) discuss the idea of incorporating perceived coordination success rates when it comes to evaluating the attainment of one from a number of indistinguishable outcomes of a game into the function of team interests itself and use it to interpret results from a number of experiments.Footnote 21 It is easy to modify the measure of mutual advantage u τ to do this. In a case of a coordination problem due to multiplicity of outcomes that are indistinguishable from a team’s perspective and in the absence of any further coordination aid for the interacting players to rely on, the original measures of mutual advantage associated with the indistinguishable outcomes can be divided by the number of indistinguishable outcomes in question. In the game of Figure 7(a), this would yield the extent of mutual advantage associated with outcomes (Hi1, Hi1) and (Hi2, Hi2) to be 50, while that associated with the outcome (Lo, Lo) would remain to be 90. Operationalized this way, the function τ would now select the outcome (Lo, Lo) as uniquely optimal for a team. However, although payoff pairs associated with the pure strategy Nash equilibria in this game can themselves aid to coordinate team-reasoning decision-makers’ actions in this way, coordination of actions may often be possible due to factors that are not related to payoffs associated with outcomes that are deemed indistinguishable from a team’s perspective. For one example, consider a variation of this game shown in Figure 7(b). The pure strategy Nash equilibria here are the same as earlier and the function τ, based on the original measure u τ, selects the same pair of outcomes, (Hi1, Hi1) and (Hi2, Hi2), as optimal for a team. Although the two outcomes are just as indistinguishable as they were before, in this case the personal payoff of 8 to row and column player in the outcome (Hi2, Hi1) and (Hi1, Hi2) off the matrix diagonal respectively can aid to coordinate players’ actions for the attainment of the outcome (Hi2, Hi2). Even though it is still the payoff structure of the game that aids players to resolve their coordination problem in this case, it is not a payoff pair associated with any of the outcomes on which the interacting players try to coordinate their actions that does so.
Another example is shown in Figure 7(c). Here everything is the same as in the original version of the game, except for the fact that the outcome (Hi1, Hi1) is marked with a star. The salience of this outcome has nothing to do with the payoff structure of the game, but the presence of the star serves as a potential aid to coordinate actions. In fact, there is a number of coordination aids to choose from: (i) the presence of the star among outcomes that are maximally mutually advantageous in terms of the original measure u τ, (ii) its absence, and (iii) the uniqueness of the payoff pair associated with the Nash equilibrium (Lo, Lo). Which of these is most appropriate will depend on decision-makers’ beliefs about which of these aids is most likely to be recognized and considered by others.
Our intention with these examples is to show that decision-makers’ ability to coordinate their actions on a particular outcome of a game may often depend on factors that have nothing to do with how mutually advantageous it would be for the players to end up at that outcome in terms of their personal payoffs associated with it. Furthermore, the possibility of there being multiple coordination aids for players to choose from may leave them facing a coordination problem of a different kind – one related to the choice of a coordination aid to resolve the game they play. The interacting players’ choice of the latter will depend on their beliefs about which aids are most likely to be recognized, considered, and adopted by other players. These beliefs may, in turn, depend on decision-makers’ cultural backgrounds, the prevalent social norms in their societies, and other factors unrelated to the payoff structure of the game itself.Footnote 22 Because of this it may often be fruitful to keep the question of which outcomes of games are maximally mutually advantageous in terms of players’ attainable payoffs separate from the question of how to successfully coordinate their actions. Keeping the two questions separate allows the latter to be informed by the former: in the presence of many potential coordination aids to choose from, the measure u τ may help narrow down which of these should be employed in order to remain as faithful as possible to the mutual advancement of players’ personal interests. In this light, it is the fact that the outcome (Hi, Hi) in the original version of the Hi-Lo game of Figure 1 is maximally mutually advantageous to the interacting players in terms of the attainable personal payoffs that makes them coordinate their actions on this outcome rather than the less mutually advantageous one, (Lo, Lo).
5. WHY TEAM REASON?
As we noted at the end of Section 2, one of the two important questions that the theory of team reasoning needs to address concerns why and under what circumstances people may reason as members of a team. A number of possibilities have been suggested to date. According to a view attributed to Bacharach (Reference Bacharach2006), the adopted mode of reasoning depends on a decision-maker’s psychological frame of mind, which, in turn, may depend on a number of circumstantial factors, but need not necessarily be driven by conscious deliberation. Sugden’s (Reference Sugden2003) version of the theory suggests that a decision-maker may choose to endorse a particular mode of reasoning, but that this choice may lie outside of rational evaluation itself. Hurley (Reference Hurley and Gold2005a, Reference Hurley2005b), on the other hand, suggests that team reasoning may be consciously chosen as a result of rational deliberation. We do not review these developments in detail here (for a survey see, for example, Gold and Sugden Reference Gold and Sugden2007a, Reference Gold, Sugden, Peter and Schmid2007b, or Karpus and Gold Reference Karpus, Gold and Kiverstein2017), but discuss some tentative suggestions in connection to the function τ.
We started by noting that the development of the theory of team reasoning was partly motivated by the fact that, in some games, the application of best-response reasoning produced multiple solutions without discriminating between them, even though some of these solutions seemed less compelling than others. This prompts a suggestion that decision-makers, who first approach games from the point of view of best-response reasoning, may switch to considering which outcomes of games are mutually advantageous when best-response reasoning is unable to resolve their decision problems definitively. The decision-makers’ subsequent endorsement of team reasoning to guide their actions can depend on their beliefs about its endorsement by others as well as the outcomes they can expect to attain from the application of best-response considerations, and the first of these factors may depend on the second. With regards to the function τ, this provides a justification for measuring individual and mutual advantages associated with considered outcomes relative to reference points established using the notion of best-response rationalizability. This is so because decision-makers who first approach games from the point of view of best-response reasoning would make further evaluations of outcomes relative to conclusions they can draw from assumed (common) application of the best-response approach.
This can explain why decision-makers may switch from best-response reasoning to reasoning as members of a team in games such as the Hi-Lo, the Chicken, and the High Maximin discussed earlier, but not in games such as the Prisoner’s Dilemma which best-response reasoning resolves definitively. Deliberation about what is mutually advantageous in latter cases, however, may be prompted by considerations relating efficiency. If best-response solutions are inefficient (say, in terms of the weak sense of Pareto efficiency) and, as a consequence, this triggers such deliberation, decision-makers may end up facing two competing definitive resolutions of games. As a result, such scenarios may turn into complicated dilemmas about which mode of reasoning decision-makers should endorse when choosing their actions, with inefficient best-response solutions pitted against efficient mutually advantageous ones from which players may be tempted to deviate. This fits the aforementioned findings from experiments with the Prisoner’s Dilemma game that show cooperation rates to be around 50% in one-shot versions of this game.Footnote 23
If, on the other hand, players first approach games from the point of view of team reasoning, they may switch to best-response considerations when unilateral deviations from the attainment of mutually advantageous outcomes are beneficial to them personally, or when team reasoning fails to resolve the considered games definitively. This possibility can explain why decision-makers may switch from reasoning as members of a team to best-response reasoning in games such as the Prisoner’s Dilemma, the Chicken, and the High Maximin (depending on which outcome of the latter game is considered to be maximally mutually advantageous), but not in games such as the Hi-Lo. With regards to the function τ, if decision-makers approach games from the point of view of team reasoning to begin with, their reference points need not necessarily be established using the notion of best-response rationalizability. However, if players end up vacillating between the two modes of reasoning when deciding on which one to endorse when choosing their actions, they will pit the perceived benefits associated with the two modes of reasoning against each other. This way, the advantages of endorsing team reasoning will be measured relative to potential outcomes that can be expected to result from the application of best-response considerations, which provides further grounds for the establishment of decision-makers’ reference points to take into account the notion of best-response rationalizability, even if at the start it did not.Footnote 24
6. CONCLUSION
In this paper we predominantly focused on discussing a possible representation of team-reasoning decision-makers’ interests based on the notion of mutual advantage in games. A few differences aside, the spirit of our working definition of mutual advantage is broadly in line with Sugden’s (Reference Sugden2015). Our proposed method for measuring extents of individual and mutual advantage allows us to further discriminate between outcomes identified as mutually beneficial and to define team-reasoning decision-makers’ interests as the attainment of maximum mutual advantage in their interactions with each other. We argued our proposed function of team interests to be applicable when interacting players’ payoffs are not interpersonally comparable, but also suggested its modification for cases when such comparisons are possible.
Our goal was not to provide a complete account of the theory of team reasoning and, at most, we offered only tentative ideas concerning factors that may motivate people to seek out mutually advantageous solutions and switch between competing modes of reasoning in various types of games. In our account, we focused on the question of what properties an outcome must have in order for it to be identified as a maximally mutually advantageous solution purely on the basis of information available to the interacting players about their personal interests in a particular game. The question of how team-reasoning decision-makers coordinate their actions in the face of multiple such solutions warrants further investigation and discussion. Since players’ ability to coordinate their actions may often depend on factors that are not related to payoff structures of games alone, a single generalizable formal model of their final choices may not be possible. Sugden (Reference Sugden2015, 156) notes that mutually beneficial cooperation may thus consist in ‘conforming to complex and sometimes arbitrary conventions that could not be reconstructed by abstract rational analysis’. While we agree that resolutions of coordination problems may be based on arbitrary rules and conventions, we nevertheless believe there to be some general principles underlying interacting players’ identification of maximally mutually beneficial outcomes before the question of how to coordinate their actions is addressed.
Further empirical research is needed to test competing theories about modes of reasoning that people actually use in their interactions with each other. Since many strategies can often be explained in terms of multiple accounts of what players try to achieve in games they play, these studies may need to consider a broader evidence base than mere observations of decision-makers’ choices. In a related discussion of the problem of undetermination of theory by evidence, Dietrich and List (Reference Dietrich and List2016, 273) suggest that our evaluation of theories concerning decision-makers’ choices in games may need to consider ‘novel choice situations, psychological data over and above choice behaviour, verbal reports, related social phenomena, and occasionally (for plausibility checks) even introspection’. In a recent experiment involving a similar scenario to the Chicken game discussed in this paper, Rubinstein and Salant (Reference Rubinstein and Salant2016) asked participating decision-makers to report their beliefs about other players’ actions either before or after making their own choice. They found a sizeable portion of decision-makers not to best respond to their elicited beliefs, in line with the prediction of the attainment of one of the maximally mutually advantageous outcomes based on the function of team interests presented in this paper. Elicitation of interacting players’ beliefs about each other’s actions and further development of such experimental techniques will be fruitful for empirical testing of ideas discussed here.
ACKNOWLEDGEMENTS
We would particularly like to thank Yair Antler, Jason Alexander, Garth Baughman, Mike Coxhead, Ben Davies, Julien Dutant, Natalie Gold, Clayton Littlejohn, David Pappineau, Klemens Puppe, Andis Sofianos, Robert Sugden, Spyros Terovitis, James Thom, Edward Webb, and Nicolas Wüthrich for their invaluable comments and suggestions on various earlier versions of this work. We would also like to thank participants of the following events for lively discussions, all of which we greatly benefited from in the development of this paper: the UECE Lisbon Meetings 2014 Conference on Game Theory and Applications held at Lisboa School of Economics and Management (ISEG) in November 2014, the Warwick Economics PhD Conference 2015 held at the University of Warwick in February 2015, the Decisions, Games and Logic 2015 Conference held at the London School of Economics in June 2015, the 26th International Conference on Game Theory held at the Stony Brook University in July 2015, and the Workshop on Game Theory and Social Choice at the Corvinus University of Budapest in December 2015. Last but by no means least, we were able to improve this paper considerably thanks to very detailed and insightful suggestions we received from three anonymous reviewers of this journal and its editor, Richard Bradley. Jurgis Karpus is grateful for research funding from the European Research Council under the European Union’s Seventh Framework Programme (FP/2007–2013) / ERC Grant Agreement n. 283849.