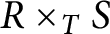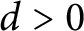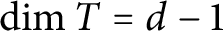1 Introduction
The fiber product of homomorphisms
$R \overset {f}{\longrightarrow } T \overset {g}{\longleftarrow } S$
of rings is defined by
$$\begin{align*}R\times_TS = \big\{(a, b) \in R \times S \mid f(a) = g(b)\big\}, \end{align*}$$
which forms a subring of
$R \times S$
. The notion of fiber products, in general, appears not only in commutative algebra but in diverse branches of mathematics, and it often plays a crucial role. Much research has been conducted regarding a relation of ring theoretic properties (e.g., Cohen-Macaulay, Gorenstein) between the fiber products and the base rings. The reader may consult [Reference Ananthnarayan, Avramov and Moore1, Reference Christensen, Striuli and Veliche5, Reference D’Anna7, Reference Moore30, Reference Nasseh and Sather-Wagstaff31, Reference Nasseh, Sather-Wagstaff, Takahashi and VandeBogert32, Reference Ogoma33, Reference Shapiro34] for details. By [Reference Ogoma33], the fiber product of one-dimensional Cohen–Macaulay local rings over the residue class field is Gorenstein if and only if the base rings are discrete valuation rings (DVRs), and hence the fiber products are rarely Gorenstein rings. Nevertheless, for example, the fiber product of hypersurfaces might have good properties even though it is not Gorenstein, which we will clarify in this paper.
An almost Gorenstein ring is one of the generalizations of a Gorenstein ring, defined by a certain embedding of the rings into their canonical modules. The motivation of the theory derives from the strong desire to stratify Cohen–Macaulay rings, finding new and interesting classes that naturally cover the Gorenstein rings. The class of almost Gorenstein rings could be a very nice candidate for such classes. Originally, the theory of almost Gorenstein rings was established by V. Barucci and R. Fröberg [Reference Barucci and Fröberg2] in the case where the local rings are analytically unramified of dimension one. They mainly considered the numerical semigroup rings and gave pioneering results. However, the notion given by [Reference Barucci and Fröberg2] was not flexible for the analysis of analytically ramified case, so in 2013, the second author, N. Matsuoka, and T. T. Phuong [Reference Goto, Matsuoka and Phuong12] proposed the notion of over one-dimensional Cohen-Macaulay local rings, using the first Hilbert coefficient of canonical ideals. Finally, in 2015, the first and second authors, and R. Takahashi [Reference Goto, Takahashi and Taniguchi19] gave the definition of almost Gorenstein graded/local rings of arbitrary dimension, by means of Ulrich modules.
The purpose of this paper is to explore the question of when the fiber product is an almost Gorenstein ring. The main result of this paper is stated as follows.
Theorem 1.1 Let
$(R, \mathfrak m), (S, \mathfrak n)$
be Cohen–Macaulay local rings with
$d=\dim R=\dim S>0$
, and let T be a regular local ring with
$\dim T=d-1$
possessing an infinite residue class field. Let
$f: R \to T$
,
$g: S \to T$
be surjective homomorphisms. Suppose that
$A=R \times _T S$
has a canonical module
$\mathrm {K}_A$
and that
$\mathrm {Q}(A)$
is a Gorenstein ring. Then the following conditions are equivalent.
-
(i) The fiber product
$A=R\times _TS$
is an almost Gorenstein ring. -
(ii) R and S are almost Gorenstein rings.
In what follows, unless otherwise specified, let R be a Cohen–Macaulay local ring with maximal ideal
$\mathfrak {m}$
. Let
$\mathrm {Q}(R)$
be the total quotient ring of R and
$\overline {R}$
the integral closure of R in
$\mathrm {Q}(R)$
. For each finitely generated R-module M, let
$\mu _R(M)$
(resp.
$\ell _R(M)$
) denote the number of elements in a minimal system of generators of M (resp. the length of M). For R-submodules X, Y of
$\mathrm {Q}(R)$
, let
$X:Y = \{a \in \mathrm {Q}(R) \mid a Y \subseteq X\}$
. We denote by
$\mathrm {K}_R$
a canonical module of R if one exists. We set
$\mathrm {r}(R) = \ell _R(\operatorname {Ext}^d_R(R/\mathfrak m, R))$
the Cohen–Macaulay type of R, where
$d = \dim R$
.
2 Basic Facts
The purpose of this section is to summarize some basic properties of fiber products. For a moment, let R, S, T be arbitrary commutative rings, and let
$f:R \to T$
,
$g: S \to T$
denote homomorphisms of rings. We set
$$\begin{align*}A = R\times_TS = \big\{(a, b) \in R \times S \mid f(a) = g(b)\big\} \end{align*}$$
and call it the fiber product of R and S over T with respect to f and g, which forms a subring of
$B=R \times S$
. We then have a commutative diagram
of rings, where
$p_1 : A \to R, (x, y)\mapsto x$
,
$p_2: A \to S, (x, y)\mapsto y$
stand for the projections. Hence, we get an exact sequence
$$\begin{align*}0 \longrightarrow A \overset{i}{\longrightarrow} B \overset{\varphi}{\longrightarrow} T \end{align*}$$
of A-modules, where
$\varphi = \Big [\begin{array}{@{}c@{}} f \\ -g \end{array}\Big ] $
. The map
$\varphi $
is surjective if either f or g is surjective. In addition, if both f and g are surjective, then T is cyclic as an A-module, and B is a module-finite extension over A. This partially justifies the following (see e.g., [Reference Ananthnarayan, Avramov and Moore1, Lemmas 1.2 and 1.5]).
Lemma 2.1 Suppose that
$f:R \to T$
and
$g: S \to T$
are surjective. Then the following assertions hold true.
-
(i) A is a Noetherian ring if and only if R and S are Noetherian rings.
-
(ii)
$(A, J)$
is a local ring if and only if
$(R, \mathfrak m)$
and
$(S, \mathfrak n)$
are local rings. When this is the case,
$J = (\mathfrak m \times \mathfrak n) \cap A$
. -
(iii) If
$(R, \mathfrak m), (S, \mathfrak n)$
are Cohen–Macaulay local rings with
$\dim R=\dim S = d>0$
and
$\operatorname {depth} T\ge d-1$
, then
$(A, J)$
is a Cohen–Macaulay local ring and
$\dim A = d$
.
In the case of local rings, we have the following. Although Proposition 2.2(iii) follows from the result of Ogoma ([Reference Ogoma33]), let us give a brief proof for the sake of completeness. For a Noetherian local ring R, we denote by
$\mathrm {e}(R)$
(resp.
$v(R)$
) the multiplicity (resp. the embedding dimension) of R.
Proposition 2.2 Suppose that
$(R, \mathfrak m)$
,
$(S, \mathfrak n)$
are Noetherian local rings with a common residue class field
$k=R/\mathfrak m=S/\mathfrak n$
, and
$f : R \to k$
,
$g : S \to k$
denote the canonical surjective maps. Then the following assertions hold true.
-
(i)
$v(A) = v(R) + v(S)$
. -
(ii) If
$\dim R=\dim S>0$
, then
$\mathrm {e}(A) = \mathrm {e}(R) + \mathrm {e}(S)$
. -
(iii) If R, S are Cohen–Macaulay local rings with
$\dim R=\dim S=1$
, then
$A=R\times _k S$
is Gorenstein if and only if R and S are DVRs.
Proof Since
$J=\mathfrak m\times \mathfrak n$
is the maximal ideal of A, we get
$J^{\ell } = \mathfrak m^{\ell + 1}\times \mathfrak n^{\ell + 1}$
for every
$\ell \ge 0$
.
-
(i) This part follows from the equalities
$\ell _A(J/J^2) = \ell _k([\mathfrak m/\mathfrak m^2] \oplus [\mathfrak n/\mathfrak n^2]) =\ell _R(\mathfrak m/\mathfrak m^2) + \ell _S(\mathfrak n/\mathfrak n^2)$
. -
(ii) Remember that f and g are surjective. We then have the equalities
for every
$$ \begin{align*} \ell_A(A/J^{\ell+1}) &= \ell_A(A/J) + \ell_A(J/J^{\ell +1}) \\ &= 1 + \big[\ell_R(\mathfrak m/\mathfrak m^{\ell + 1}) + \ell_S(\mathfrak n/\mathfrak n^{\ell + 1})\big] \\ &= 1+\big\{[\ell_R(R/\mathfrak m^{\ell + 1})-1] + [\ell_S(S/\mathfrak n^{\ell + 1})-1]\big\}\\ &= \big[\ell_R(R/\mathfrak m^{\ell +1})+ \ell_S(S/\mathfrak n^{\ell +1})\big] -1 \end{align*} $$
$\ell \ge 0$
, which yield that
$\mathrm {e}(A) = \mathrm {e}(R) + \mathrm {e}(S)$
, because
$\dim A = \dim R = \dim S> 0$
.
-
(iii) Suppose that A is a Gorenstein ring. By applying the functor
$\operatorname {Hom}_A(-, A)$
to the exact sequence
$0 \to A \overset {i}{\to } B \overset {\varphi }{\to } k \to 0$
of A-modules
$\Big(\text{\rm here},\ \varphi = \Big [\begin{array}{@{}c@{}} f \\ -g \end{array}\Big ]\Big) $
, we get which implies
$$\begin{align*}0 \longrightarrow A:B \overset{i}{\longrightarrow} A \longrightarrow \operatorname{Ext}^1_A(A/J, A) \longrightarrow 0, \end{align*}$$
$J = A:B$
, because
$\operatorname {Ext}^1_A(A/J, A) \cong A/J$
. As A is Gorenstein, we have
$B= A:(A:B)$
, so the equalities hold where the fourth equality comes from the fact that A is not a DVR (note that B is a module-finite birational extension of A). Consequently,
$$\begin{align*}R \times S = B= A:(A:B) = A:J = J:J = (\mathfrak m : \mathfrak m) \times (\mathfrak n : \mathfrak n) \end{align*}$$
$R=\mathfrak m:\mathfrak m$
and
$S=\mathfrak n:\mathfrak n$
, whence R and S are DVRs (see e.g., [Reference Goto, Matsuoka and Phuong12, Lemma 3.15]). The converse implication follows from assertion (ii). This completes the proof.▪
3 Survey on Almost Gorenstein Rings
This section is devoted to the definition and some basic properties of almost Gorenstein rings, which we will use throughout this paper. Let
$(R, \mathfrak m)$
be a Cohen–Macaulay local ring with
$d=\dim R$
, possessing a canonical module
$\mathrm {K}_R$
.
Definition 3.1 ([Reference Goto, Takahashi and Taniguchi19, Definition 1.1])
We say that R is an almost Gorenstein local ring, if there exists an exact sequence
$$\begin{align*}0 \longrightarrow R \longrightarrow \mathrm{K}_R \longrightarrow C \longrightarrow 0 \end{align*}$$
of R-modules such that
$\mu _R(C) = \mathrm {e}^0_{\mathfrak m}(C)$
, where
$\mu _R(C)$
denotes the number of elements in a minimal system of generators for C and
$$\begin{align*}\mathrm{e}^0_{\mathfrak m}(C) = \lim_{n \to \infty}\frac{\ell_R(C/\mathfrak m^{n+1}C)}{n^{d-1}}\cdot (d-1)! \end{align*}$$
is the multiplicity of C with respect to
$\mathfrak {m}$
.
Notice that every Gorenstein ring is an almost Gorenstein ring, and the converse holds if the ring R is Artinian ([Reference Goto, Takahashi and Taniguchi19, Lemma 3.1 (3)]). Definition 3.1 requires that if R is an almost Gorenstein ring, then R might not be Gorenstein, but the ring R can be embedded into its canonical module
$\mathrm {K}_R$
so that the difference
$\mathrm {K}_R/R$
should have good properties. For any exact sequence
$$\begin{align*}0 \longrightarrow R \longrightarrow \mathrm{K}_R \longrightarrow C \longrightarrow 0 \end{align*}$$
of R-modules, C is a Cohen–Macaulay R-module with
$\dim _RC=d-1$
, provided
$C \,{\ne}\, (0)$
([Reference Goto, Takahashi and Taniguchi19, Lemma 3.1 (2)]). Suppose that R possesses an infinite residue class field
$R/ \mathfrak m$
. Set
$R_1=R/[(0):_RC]$
and let
$\mathfrak m_1$
denote the maximal ideal of
$R_1$
. Choose elements
$f_1, f_2, \dots , f_{d-1} \in \mathfrak m$
such that
$(f_1, f_2, \dots , f_{d-1})R_1$
forms a minimal reduction of
$\mathfrak m_1$
. We then have
$$\begin{align*}\mathrm{e}_{\mathfrak m}^0(C) = \mathrm{e}_{\mathfrak m_1}^0(C) = \ell_R\big(C/(f_1, f_2, \dots, f_{d-1})C\big) \ge \ell_R(C/\mathfrak m C) = \mu_R(C). \end{align*}$$
Therefore,
$\mathrm {e}_{\mathfrak m}^0(C) \ge \mu _R(C),$
and we say that C is an Ulrich R-module if
$\mathrm {e}_{\mathfrak m}^0(C) = \mu _R(C)$
, since C is a maximally generated maximal Cohen–Macaulay
$R_1$
-module in the sense of [Reference Brennan, Herzog and Ulrich3]. Hence, C is an Ulrich R-module if and only if
$\mathfrak m C = (f_1, f_2, \dots , f_{d-1})C$
. If
$d=1$
, then the Ulrich property for C is equivalent to saying that C is a vector space over
$R/\mathfrak m$
. In addition, we have the following fact.
Fact 3.2 ([Reference Goto, Matsuoka and Phuong12, Theorem 3.11], [Reference Goto, Takahashi and Taniguchi19, Proposition 3.4], [Reference Kobayashi24, Theorem 2.14])
Suppose that
$d=1$
and there exists an R-submodule K of the total ring
$\mathrm {Q}(R)$
of fractions such that
$R \subseteq K \subseteq \overline {R}$
and
$K \cong \mathrm {K}_R$
as an R-module, where
$\overline {R}$
stands for the integral closure of R in
$\mathrm {Q}(R)$
. Then the following conditions are equivalent.
-
(i) R is an almost Gorenstein ring.
-
(ii)
$\mathfrak m K \subseteq R$
, that is,
$\mathfrak m K = \mathfrak m$
. -
(iii)
$\mathfrak m K \cong \mathfrak m$
as an R-module.
In this paper, we say that an R-submodule K of
$\mathrm {Q}(R)$
is a fractional canonical ideal of R, if
$R \subseteq K \subseteq \overline {R}$
and
$K \cong \mathrm {K}_R$
as an R-module.
One can construct many examples of almost Gorenstein rings (e.g., [Reference Celikbas, Celikbas, Goto and Taniguchi4, Reference Ghezzi, Goto, Hong and Vasconcelos8, Reference Goto, Kien, Matsuoka and Truong10, Reference Goto, Matsuoka and Phuong12, Reference Goto, Matsuoka, Taniguchi and Yoshida13, Reference Goto, Matsuoka, Taniguchi and Yoshida14, Reference Goto, Matsuoka, Taniguchi and Yoshida15, Reference Goto, Matsuoka, Taniguchi and Yoshida16, Reference Goto, Rahimi, Taniguchi and Truong18, Reference Goto, Takahashi and Taniguchi19, Reference Goto, Takahashi and Taniguchi20, Reference Higashitani23, Reference Matsuoka and Murai28, Reference Miyazaki29, Reference Taniguchi35]). The significant examples of almost Gorenstein rings are one-dimensional Cohen–Macaulay local rings of finite Cohen–Macaulay representation type and two-dimensional rational singularities. Because the origin of the theory of almost Gorenstein rings are the theory of numerical semigroup rings, there are numerous examples of almost Gorenstein numerical semigroup rings (see [Reference Barucci and Fröberg2, Reference Goto, Matsuoka and Phuong12]).
4 Proof of Theorem 1.1
This section mainly focuses on proving Theorem 1.1. Theorem 1.1 is reduced, by induction on
$\dim A$
, to the case where
$\dim A =1$
. Let us start from the key result of dimension one. First, we fix our notation and assumptions.
Setting 4.1 Let
$(R, \mathfrak m)$
,
$(S, \mathfrak n)$
be one-dimensional Cohen–Macaulay local rings with a common residue class field
$k = R/\mathfrak m = S/\mathfrak n$
, and let
$f : R \to k$
,
$g : S \to k$
be the canonical surjective maps. Then
$A = R\times _k S$
is a one-dimensional Cohen–Macaulay local ring with maximal ideal
$J = \mathfrak m \times \mathfrak n$
. Since
$B=R\times S$
is a module-finite birational extension over A,
$\mathrm {Q}(A) = \mathrm {Q}(R) \times \mathrm {Q}(S)$
and
$\overline {A} = \overline {R} \times \overline {S}$
.
Throughout this section, unless otherwise specified, we assume that
$\mathrm {Q}(A)$
is a Gorenstein ring, A admits a canonical module
$\mathrm {K}_A$
, and the field
$k=A/J$
is infinite. Hence, all the rings
$A, R$
, and S possess fractional canonical ideals (see [Reference Goto, Matsuoka and Phuong12, Corollary 2.9]).
We denote by K (resp. L) the fractional canonical ideal of R (resp. S). Thus, K is an R-submodule of
$\mathrm {Q}(R)$
such that
$R \subseteq K \subseteq \overline {R}$
,
$K \cong \mathrm {K}_R$
as an R-module, and L is an S-submodule of
$\mathrm {Q}(S)$
such that
$S \subseteq L \subseteq \overline {S}$
,
$L \cong \mathrm {K}_S$
as an S-module.
To prove Theorem 1.1 in the case where
$\dim A=1$
, we can assume that A is not a Gorenstein ring. Hence, either R or S is not a DVR (see Proposition 2.2).
4.1 The Case Where R and S are not DVRs
In this subsection, suppose that both R and S are not DVRs. We then have
$K \ne \overline {R}$
, since
$K:K = R$
([Reference Herzog and Kunz22, Bemerkung 2.5]). As
$\ell _R([K:\mathfrak m]/K) = \ell _R(\operatorname {Ext}^1_R(R/\mathfrak m, K)) =1$
, we obtain
$K:\mathfrak m \subseteq \overline {R}$
. In addition, we also have
$R : \mathfrak m \not \subseteq K$
. Indeed, if
$R : \mathfrak m \subseteq K$
, then
$K \supseteq R:\mathfrak m = (K:K):\mathfrak m = K:\mathfrak m K$
. Thus,
$R = K:K \subseteq K:( K:\mathfrak m K) = \mathfrak m K \subseteq \mathfrak m \overline {R}$
. This makes a contradiction. Hence,
$R : \mathfrak m \not \subseteq K,$
and therefore
$$\begin{align*}K:\mathfrak m = K + R{\cdot}g_1 \end{align*}$$
for some
$g_1 \in (R:\mathfrak m) \backslash K$
. Similarly, because S is not a DVR, we can choose
$g_2 \in (S:\mathfrak n) \backslash L$
such that
$L:\mathfrak n = L + S{\cdot }g_2$
. We set
$$\begin{align*}X = (K\times L) + A{\cdot}\psi \end{align*}$$
with
$\psi = (g_1, g_2) \in \overline {A} = \overline {R} \times \overline {S}$
. Then X is an A-submodule of
$\overline {A}$
, satisfying
$A \subseteq B \subseteq X \,{\subseteq}\, \overline {A}$
. Furthermore, we have the following lemma, which plays a key role in our argument.
Lemma 4.2
$X \cong \mathrm {K}_A$
as an A-module. Hence, X is a fractional canonical ideal of A and
$\mathrm {r}(A) = \mathrm {r}(R) + \mathrm {r}(S) + 1$
.
Proof First, we notice that
$X:J = (K:\mathfrak m) \times (L:\mathfrak n)$
. In fact, take an element
$\alpha \in X:J$
and write
$\alpha = (x, y)$
, where
$x \in \mathrm {Q}(R)$
,
$y \in \mathrm {Q}(S)$
. Since
$J\cdot (x, y) \subseteq X = (K\times L) + A{\cdot }\psi $
, we have
$$\begin{align*}(m, 0)(x, y) = (mx, 0) \in X \quad\text{and}\quad (0, n)(x, y) = (0, ny) \in X \end{align*}$$
for each
$m \in \mathfrak m$
and
$n \in \mathfrak n$
. Hence,
$(mx, 0) = (k, \ell ) + (a, b)(g_1, g_2)$
for some
$(k, \ell ) \in K \times L$
,
$(a, b) \in A$
. Therefore,
$$\begin{align*}mx = k + ag_1\quad \text{and} \quad 0 = \ell + bg_2, \end{align*}$$
which yield that
$b \in \mathfrak n$
. Moreover, because
$(a, b) \in A$
, we get
$a \in \mathfrak m$
. Consequently, we have
$ag_1 \in \mathfrak m(R:\mathfrak m) \subseteq R$
, whence
$x \in K:\mathfrak m$
. Similarly,
$y \in L:\mathfrak n$
, as desired.
Note that X is a faithful maximal Cohen–Macaulay A-module with
$\dim _AX = 1$
. We now choose the regular elements
$a \in \mathfrak m$
on R and
$b \in \mathfrak n$
on S. Then
$(a, b) \in A$
is a regular element on A. Therefore,
$$\begin{align*}(a, b)X:_X J = (a, b)X:_{\mathrm{Q}(A)}J = (a, b) [X:_{\mathrm{Q}(A)}J ] \end{align*}$$
so that
$[(a, b)X:_X J]/(a, b)X \cong [X:_{\mathrm {Q}(A)}J ]/X$
as an A-module. We are now going to prove that
$ [X:_{\mathrm {Q}(A)}J ]/X$
is cyclic as an A-module. Indeed, choose an element
$\alpha \in X:J$
and write
$\alpha = (x, y)$
, where
$x \in \mathrm {Q}(R)$
and
$y \in \mathrm {Q}(S)$
. Then, since
$X:J = (K+Rg_1) \times (L+Sg_2)$
, we have
$$\begin{align*}x = k + cg_1 \quad\text{and}\quad y = \ell + dg_2, \end{align*}$$
where
$k \in K$
,
$\ell \in L$
,
$c \in R$
, and
$d \in S$
. Notice that the projection
$p_1 : A \to R, (a, b) \mapsto a$
is surjective. There exists
$c'\in S$
such that
$(c, c')\in A$
and
$p_1(c, c') = c$
. Similarly, let us choose
$d' \in R$
such that
$(d', d-c') \in A$
and
$p_2(d', d-c')=d-c'$
. Hence, we have the equalities
$$ \begin{align*} \alpha &= (x, y) = (k, \ell) + (cg_1, 0) + (0, dg_2) \\ & = (k, \ell) + (c, c')(g_1, g_2) + (0, (d-c')g_2) \\ & = (k, \ell) + (c, c')(g_1, g_2) + (d', d-c')(0, g_2), \end{align*} $$
whence
$\alpha \in (K \times L) + A{\cdot } \psi + A\cdot (0, g_2) = X + A\cdot (0, g_2)$
. Therefore,
$\left [X:_{\mathrm {Q}(A)}J\right ]/X$
is a cyclic A-module. Hence,
$X \cong \mathrm {K}_A$
as an A-module.
Remember that
$R:\mathfrak m = \mathfrak m:\mathfrak m$
and
$S:\mathfrak n = \mathfrak n : \mathfrak n$
, because R and S are not DVRs (see [Reference Goto, Matsuoka and Phuong12, Lemma 3.15]). We then have
$\mathfrak m (K :\mathfrak m) = \mathfrak m K$
and
$\mathfrak n (L:\mathfrak n) = \mathfrak n L$
. Hence,
$$ \begin{align*} JX &= J (K \times L) + J \psi = (\mathfrak m K \times \mathfrak n L) + (\mathfrak m g_1 \times \mathfrak n g_2) \\ & = \mathfrak m (K :\mathfrak m) \times \mathfrak n (L : \mathfrak n) = \mathfrak m K \times \mathfrak n L. \end{align*} $$
Therefore, we have
$$ \begin{align*} \mathrm{r}(A) &= \ell_A(X/JX) = \ell_A(X/[K\times L]) + \ell_A([K \times L]/[\mathfrak m K \times \mathfrak n L]) \\ &= 1 + \ell_R(K/\mathfrak m K) + \ell_S(L/\mathfrak n L) = 1 + \mathrm{r}(R) + \mathrm{r}(S), \end{align*} $$
which completes the proof. ▪
As a consequence of Lemma 4.2, we have the following corollary, which ensures that Theorem 1.1 holds when R and S are not DVRs, and
$\dim A=1$
.
Corollary 4.3 Suppose that R and S are not DVRs. Then the fiber product
$A=R\times _kS$
is an almost Gorenstein ring if and only if R and S are almost Gorenstein rings.
Proof Notice that
$JX = (\mathfrak m\times \mathfrak n)((K\times L) + A{\cdot }\psi ) = \mathfrak m(K+Rg_1) \times \mathfrak n (L+Sg_2) = \mathfrak m(K:\mathfrak m) \times \mathfrak n(L:\mathfrak n) = \mathfrak m K \times \mathfrak n L$
, where the last equality follows from the fact that R and S are not DVRs. Therefore,
$A=R\times _kS$
is an almost Gorenstein ring if and only if
$JX=J$
(Fact 3.2). The latter condition is equivalent to saying that
$\mathfrak m K = \mathfrak m$
and
$\mathfrak n L = \mathfrak n$
, that is, R and S are almost Gorenstein rings, as desired. ▪
Let us note one example.
Example 4.4 Let k be a field and let
$a, b, c, d \ge 2$
be integers. We set
$R=k[\!\![X, Y]\!\!]/(X^a-Y^b)$
,
$S=k[\!\![Z, W]\!\!]/(Z^c-W^d)$
and consider the canonical surjections
$f:R \to k$
,
$g:S \to k$
. Then
$$\begin{align*}R\times_kS \cong k[\!\![ X, Y, Z, W ]\!\!]/{(X, Y)(Z, W) + (X^a-Y^b, Z^c-W^d)} \end{align*}$$
is an almost Gorenstein local ring with
$\mathrm {r}(R)=3$
.
For a one-dimensional case, we will show that the conditions stated in Theorem 1.1 are equivalent to saying that the fiber product
$A=R\times _k S$
is a generalized Gorenstein ring, which naturally covers the class of almost Gorenstein rings. Similarly, for almost Gorenstein rings, the notion is defined by a certain specific embedding of the rings into their canonical modules. Let us now recall the definition of generalized Gorenstein rings, in particular, of dimension one, which was recently proposed by the second author and S. Kumashiro (see [Reference Goto and Kumashiro11] for the precise definition).
Definition 4.5 ([Reference Goto and Kumashiro11, Definition 1.2])
Let
$(R, \mathfrak m)$
be a Cohen–Macaulay local ring with
$\dim R=1$
, possessing a fractional canonical ideal K of R; that is, K is an R-submodule of
$\overline {R}$
such that
$R \subseteq K \subseteq \overline {R}$
and
$K \cong \mathrm {K}_R$
as an R-module. We say that R is a generalized Gorenstein ring, if either R is Gorenstein, or R is not a Gorenstein ring, and
$K/R$
is a free
$R/\mathfrak {a}$
-module, where
$\mathfrak {a} = R:K$
.
Notice that, by [Reference Goto, Matsuoka and Phuong12, Theorem 3.11], R is a non-Gorenstein almost Gorenstein ring if and only if
$\mathfrak {a} = \mathfrak m$
, so that the generalized Gorenstein condition is weaker than the almost Gorenstein condition.
We begin with the following proposition.
Proposition 4.6
$\ell _A(X/A) = \ell _R(K/R) + \ell _S(L/S) + 2$
.
Proof Remember that
$X = (K\times L) + A{\cdot }\psi $
and
$JX = J(K \times L)$
. Since
$JX \subseteq J \overline {A}$
, we then have
$J=JX \cap A$
. Hence, we get the equalities
$$ \begin{align*} \ell_A(X/ A) & = \ell_A(X/ JX + A) + \ell_A(JX+A/A) \\ & = \mu_A(X/A) + \ell_A(JX/J) \\ & = \mathrm{r}(R) + \mathrm{r}(S) + \ell_R(\mathfrak m K/\mathfrak m) + \ell_S(\mathfrak n L/\mathfrak n) \\ & = \mathrm{r}(R) + \mathrm{r}(S) + [\ell_R(K/R) + 1 -\mathrm{r}(R)] + [\ell_S(L/S) + 1 -\mathrm{r}(S)] \\ & = \ell_R(K/R) + \ell_S(L/S) +2, \end{align*} $$
as claimed. ▪
Lemma 4.7 Let
$(R, \mathfrak m)$
be a Cohen–Macaulay local ring with
$\dim R=1$
, possessing a fractional canonical ideal K of R. If R is not a Gorenstein ring, then
$\mathfrak {a} {\cdot }(K:\mathfrak m) = \mathfrak {a} K$
, where
$\mathfrak {a} = R:K$
.
Proof Since R is not a DVR,
$K:\mathfrak m = K + Rg$
for some
$g \in (R:\mathfrak m) \backslash K$
. For each
$a \in \mathfrak {a}$
and
$k \in K$
, we obtain
$(ag)k = (ak)g \in \mathfrak m g \subseteq R$
, because
$ak \in \mathfrak {a} K \cap R \subseteq \mathfrak m K \cap R \subseteq \mathfrak m \overline {R}\cap R = \mathfrak m$
. Hence,
$ag \in R:K = \mathfrak {a} \subseteq \mathfrak {a} K$
, so that
$\mathfrak {a} (K:\mathfrak m) = \mathfrak {a} K + \mathfrak {a} g = \mathfrak {a} K,$
which completes the proof. ▪
By setting
$\mathfrak {a}_1 = R:K$
and
$\mathfrak {a}_2 = S:L$
, we have the following lemma.
Lemma 4.8 The following assertions hold true.
-
(i) Suppose that R and S are not Gorenstein rings. Then
$A:X = \mathfrak {a}_1 \times \mathfrak {a}_2$
. -
(ii) Suppose that R is Gorenstein, but S is not a Gorenstein ring. Then
$A:X = \mathfrak m \times \mathfrak {a}_2$
.
-
(i) By Lemma 4.7, we get
$\mathfrak {a}_1 (K:\mathfrak m) = \mathfrak {a}_1 K$
and
$\mathfrak {a}_2 (L:\mathfrak n) = \mathfrak {a}_2 L$
. Hence, whence
$$ \begin{align*} X\cdot(\mathfrak{a}_1 \times \mathfrak{a}_2) &= (\mathfrak{a}_1 K + \mathfrak{a}_1 g) \times (\mathfrak{a}_2 L + \mathfrak{a}_2 g_2)\\& = \mathfrak{a}_1 (K:\mathfrak m) \times \mathfrak{a}_2 (L:\mathfrak n) = \mathfrak{a}_1 K \times \mathfrak{a}_2 L \\ &\subseteq (\mathfrak m \overline{R} \cap R) \times (\mathfrak n \overline{S}\cap S) = \mathfrak m \times \mathfrak n \subseteq A, \end{align*} $$
$\mathfrak {a}_1 \times \mathfrak {a}_2 \subseteq A:X$
. Conversely, for every
$(x, y) \in A:X$
, we have
$(K \times L)\cdot (x, y) \subseteq A$
. For each
$k \in K$
, we get
$(k, 0)(x, y) = (kx, 0) \in A$
, so that
$kx \in \mathfrak m$
. Hence
$x \in R:K=\mathfrak {a}_1$
. Similarly,
$y \in S:L=\mathfrak {a}_2$
, as wanted.
-
(ii) This part follows from the same argument as in the proof of (i).▪
As a consequence, we have the following corollary.
Corollary 4.9 Suppose that R and S are not DVRs. Then the fiber product
$A=R\times _kS$
is a generalized Gorenstein ring if and only if R and S are almost Gorenstein rings.
Proof The ‘if’ part is due to Corollary 4.3. We now prove the ‘only if’ part. Suppose that
$A=R\times _kS$
is a generalized Gorenstein ring. We can assume that either R or S is not a Gorenstein ring. Notice that there is an isomorphism
$(A/A:X)^{\oplus (r+s)} \cong X/A$
of A-modules, where
$r=\mathrm {r}(R)$
,
$s = \mathrm {r}(S)$
denote the Cohen–Macaulay types of R and S, respectively. Hence, by Proposition 4.6,
$ (r+s) \cdot \ell _A(A/A:X) = \ell _R(K/R) + \ell _S(L/S) + 2. $
Suppose now that both R and S are not Gorenstein rings. Then, because
$\ell _A(A/A:X) = \ell _R(R/\mathfrak {a}_1) + \ell _S(S/\mathfrak {a}_2) - 1$
, we have
$$ \begin{align*} (r+s)& \cdot \big[\ell_R(R/\mathfrak{a}_1) + \ell_S(S/\mathfrak{a}_2) - 1\big] \\& = \ell_R(K/R) + \ell_S(L/S) + 2 \\ &\le (r-1)\ell_R(R/\mathfrak{a}_1) + (s-1) \ell_S(S/\mathfrak{a}_2) + 2, \end{align*} $$
which yields that
$ \left [\ell _S(S/\mathfrak {a}_2)\kern1.5pt{-}\kern1.5pt1\right ](r\kern1.5pt{+}\kern1.5pt1) \kern1.5pt{+}\kern1.5pt \left [\ell _R(R/\mathfrak {a}_1) \kern1.5pt{-}\kern1.5pt1\right ](s\kern1.5pt{+}\kern1.5pt1) \le 0. $
Hence,
$\ell _R(R/\mathfrak {a}_1) \kern1.5pt{=} \ell _S(S/\mathfrak {a}_2) = 1$
, so that
$\mathfrak {a}_1 = \mathfrak m$
,
$\mathfrak {a}_2 = \mathfrak n$
. By Fact 3.2, we conclude that R and S are almost Gorenstein rings. On the other hand, we consider the case where R is Gorenstein, but S is not a Gorenstein ring. We then have
$ (r+s)\cdot \left [\ell _S(S/\mathfrak {a}_2)\right ] \le (s-1)\cdot \ell _S(S/\mathfrak {a}_2) + 2, $
which implies
$\ell _S(S/\mathfrak {a}_2) = 1$
. Hence, S is an almost Gorenstein ring. ▪
4.2 The Case where R is a DVR and S is not a DVR
In this subsection, we assume that R is a DVR and S is not a DVR. Choose an A-submodule X of
$\mathrm {Q}(A)$
such that
$A \subseteq X \subseteq \overline {A}$
and
$X \cong \mathrm {K}_A$
as an A-module. Then, because
$\mathrm {K}_B = X :B \cong R \times L$
as a B-module, we have
$X:B = \xi \cdot (R \times L)$
for some invertible element
$\xi =(\xi _1, \xi _2)\in \mathrm {Q}(A)$
. Applying the functor
$\operatorname {Hom}_A(-, X)$
to the exact sequence
$0 \to A \overset {\iota }{\to } B \overset {\varphi }{\to } k= A/J \to 0$
where
$\varphi = \Big [\begin {array}{c}f \\ -g\end {array}\Big ] $
, we obtain the sequence
$$\begin{align*}0 \longrightarrow X:B \longrightarrow X \longrightarrow A/J \longrightarrow 0 \end{align*}$$
of A-modules. Hence,
$JX \subseteq X:B \subseteq X$
. Thus, we have the following inclusions.
Lemma 4.10 One has
$$ \begin{align*} X:B &\subseteq\ X \subseteq (X:B):J = (\xi_1R \times \xi_2L):J \\ &= \xi_1(R:\mathfrak m) \times \xi_2 (L:\mathfrak n). \end{align*} $$
In particular,
$J(X:B) \subseteq JX \subseteq J\cdot [\xi _1(R:\mathfrak m) \times \xi _2(L:\mathfrak n)]$
.
We are now in a position to prove Theorem 1.1 for the one-dimensional case.
Proposition 4.11 Suppose that R is a DVR and S is not a DVR. Then the fiber product
$A=R\times _kS$
is an almost Gorenstein ring if and only if S is an almost Gorenstein ring.
Proof Suppose that A is an almost Gorenstein ring. Then, since
$JX=J$
, we get
$$\begin{align*}\mathfrak n{\cdot}\xi_2L \subseteq \mathfrak n \subseteq \mathfrak n{\cdot}\xi_2(L:\mathfrak n) = \xi_2{\cdot}\mathfrak n L, \end{align*}$$
because
$\mathfrak n (L:\mathfrak n) = \mathfrak n L$
. Thus,
$\mathfrak n=\xi _2{\cdot }\mathfrak n L \cong \mathfrak n L$
, and hence S is an almost Gorenstein ring. Conversely, suppose that S is an almost Gorenstein ring. We then have
$\xi \in X$
, because
$\xi = \xi \cdot (1, 1) \in \xi \cdot (K\times L) = X:B \subseteq X$
. Since
$X \subseteq \overline {A} = R \times \overline {S}$
, we get
$\xi _1 \in R$
. Therefore,
$$ \begin{align*} JX &\subseteq J\cdot \left[\xi_1(R:\mathfrak m) \times \xi_2(L:\mathfrak n) \right]\\ &= \xi_1\cdot\mathfrak m(R:\mathfrak m) \times \xi_2\cdot \mathfrak n \\ &\subseteq \xi_1 R \times \xi_2\cdot \mathfrak n, \end{align*} $$
where the second equality comes from the fact that S is an almost Gorenstein ring, but not a DVR. Moreover, we have
$$\begin{align*}JX \subseteq A\cdot(1, 0)\cdot \xi + J \xi. \end{align*}$$
Indeed, for each
$a \in R$
, there exists
$\alpha \in A$
such that
$p_1 (\alpha ) = a$
. Hence,
$\alpha = (a, b)$
for some
$b \in S$
. Then, for every
$n \in \mathfrak n$
, we get the equalities
$$ \begin{align*} (a\xi_1, \xi_2n) &= (a, b)(\xi_1, 0) + (0, \xi_2 n) \\ &= (a, b)(1, 0)\xi + (0, n) \xi, \end{align*} $$
which imply the required inclusion. Therefore, we have
$$\begin{align*}JX = [JX \cap A\cdot(1, 0)\cdot \xi] + J \xi. \end{align*}$$
If
$JX \cap A\cdot (1, 0)\cdot \xi \subseteq J\xi $
, then
$JX = J\xi \cong J$
. Let us now assume that
$JX \cap A\cdot (1, 0)\cdot \xi \not \subseteq J \xi $
. Take an element
$\varphi \in JX \cap A\cdot (1, 0)\cdot \xi $
such that
$\varphi \not \in J \xi $
. Write
$\varphi = (a, b)(1,0) \xi $
, where
$(a, b) \in A$
. Then, since
$\varphi \in JX \subseteq J(R \times \overline {S}) = \mathfrak m \times \mathfrak n \overline {S}$
, we get
$a\xi _1 \in \mathfrak m$
. Furthermore,
$a\xi _1 \not \in \mathfrak m \xi _1$
, because
$\varphi \not \in J\xi $
. Hence,
$a \not \in \mathfrak m$
and
$\xi _1 \in \mathfrak m$
. Consequently,
$$\begin{align*}JX \subseteq J (R \times \mathfrak n) = \xi_1 R \times \xi_2 \mathfrak n \subseteq JX \end{align*}$$
yields that
$JX = \xi (R\times \mathfrak n) \cong \xi (\mathfrak m\times \mathfrak n) = \xi J\cong J$
. In any case, because
$JX \cong J$
, we conclude that A is an almost Gorenstein ring. ▪
To explore the generalized Gorenstein properties of fiber products, we need more auxiliaries.
Proposition 4.12 The following assertions hold true.
-
(i)
$X:J = R \times \xi _2 (S:L)$
. -
(ii)
$X:B=\mathfrak m \times \xi _2 L$
and
$\xi _2 \rho =1$
for some
$\rho \in (L:\mathfrak n)\backslash L$
. -
(iii)
$X=(X:B) + A$
. -
(iv)
$A:X = \mathfrak m \times \rho (S:L)$
.
Proof (i), (ii) Since
$(X: B):J = X:BJ = X:J \subseteq \overline {A} = R \times \overline {S}$
, we have
$X:J = \xi _1(R:\mathfrak m) \times \xi _2 (L:\mathfrak n)$
and
$\xi _1(R:\mathfrak m) \subseteq R$
, whence
$\xi _1 \in R:(R:\mathfrak m) = \mathfrak m$
. Because
${A \subseteq X \subseteq X:J}$
, we get
$R \subseteq \xi _1 (R:\mathfrak m)$
. Thus,
$\mathfrak m = (\xi _1)$
. Consequently,
$X: B = \xi (R \times L) = \mathfrak m \times \xi _2 L$
, while
$X:J = R \times \xi _2 (L:\mathfrak n)$
. Since
$1 \in X:J$
and
$1 \notin X:B$
, there exists
$\rho \in (L:\mathfrak n)\backslash L$
such that
$\xi _2 \rho =1$
.
(iii) Since
$\ell _A(X/X:B) = 1$
, we get
$X = (X:B) + A$
.
(iv) Notice that
$A:X = A:_A(X:B)$
. For each
$(a, b) \in A:X$
,
$a \mathfrak m \times b {\cdot }\xi _2 L \subseteq A$
. We then have
$b {\cdot }\xi _2 L \subseteq \mathfrak n$
, so that
$b {\cdot }\xi _2 \subseteq \mathfrak n :L = S:L$
. Hence,
$b \in \rho (S:L)$
. Since
$\rho (S:L) \subseteq (L:\mathfrak n)(S:L) = (S:L)L \subseteq \mathfrak n$
, we conclude that
$a \in \mathfrak m$
. Thus,
$A:X \subseteq \mathfrak m \times \rho (S:L) \subseteq A$
. Because
$(\mathfrak m \times \rho (S:L))(X:B) = \mathfrak m^2 \times (S:L)L \subseteq \mathfrak m^2 \times \mathfrak n \subseteq A$
, we have that
$A:X = \mathfrak m \times \rho (S:L)$
. ▪
We apply Proposition 4.12 to get the following corollary.
Corollary 4.13
$(A:X) X = \mathfrak m \times (S:L) L$
.
Proof The assertion follows from Proposition 4.12 and
$\rho (S:L) \subseteq (S:L)L$
. ▪
We need one more general lemma.
Lemma 4.14 Let
$(R, \mathfrak m)$
be a Cohen–Macaulay local ring with
$\dim R=1$
, possessing a fractional canonical ideal K of R. Suppose that R is not a Gorenstein ring. We set
$\mathfrak {a} = R:K$
. Then the following assertions hold true.
-
(i)
$\mathfrak {a} = \mathfrak {a} {\cdot }(R:\mathfrak m) \subseteq \mathfrak {a} K$
. -
(ii)
$\mathfrak {a} = \mathfrak {a} K$
if and only if
$K^2 = K^3$
.
-
(i) For each
$a \in \mathfrak {a}$
and
$x \in (R:\mathfrak m)$
, we have
$(ax)k = (ak)x \in \mathfrak m x \subseteq R$
for every
$k \in K$
, because
$ak \in \mathfrak {a} K \subseteq \mathfrak m K \subseteq \mathfrak m \overline {R}$
. Hence,
$ax \in R:K = \mathfrak {a} \subseteq \mathfrak {a} K$
, so that
$\mathfrak {a} = \mathfrak {a} {\cdot }(R:\mathfrak m) \subseteq \mathfrak {a} K,$
which completes the proof. -
(ii) If
$K^2 = K^3$
, then
$\mathfrak {a} = R:K = R:R[K],$
which forms an ideal of
$R[K]$
. Hence,
$\mathfrak {a} K = \mathfrak {a}$
. Conversely, if
$\mathfrak {a} = \mathfrak {a} K$
, then
$\mathfrak {a} = \mathfrak {a} K^n$
for every
$n>0$
, so that
$\mathfrak {a} = R:R[K]$
. Hence,
$K^2 = K^3$
, because
$\mathfrak {a} = R:K=K:K^2$
and
$R:R[K] = R:K^2 = K:K^3$
.▪
Corollary 4.15 The following conditions are equivalent.
-
(i)
$X^2 = X^3.$
-
(ii)
$L^2 = L^3.$
When this is the case,
$\ell _A(A/(A:X)) = \ell _S(S/(S:L))$
.
-
(i) ⇒ (ii) Suppose that
$X^2 = X^3$
. By Lemma 4.14, we get
$(A:X)X = (A:X)$
, so that
$\mathfrak m \times (S:L)L = \mathfrak m \times \rho (S:L)$
. Hence,
$(S:L)L^n =\rho ^n (S:L)$
for all
$n>0$
. Thus,
$(S:L)S[L] = \rho ^n (S:L) = (S:L)$
for each
$n \gg 0$
, because
$\rho $
is an invertible element of
$S[L]$
. Therefore,
$L^2 = L^3$
. -
(ii) ⇒ (i) If
$L^2 = L^3$
, then
$S:L = S:S[L],$
which is an ideal of
$S[L]$
, so that
$\rho (S:L) = (S:L) = (S:L)L$
. Hence,
$X^2=X^3$
, by Proposition 4.12(iv) and Corollary 4.13. The last assertion follows from the fact that
$\rho (S:L) = (S:L)$
. ▪
Finally, we reach the following theorem.
Theorem 4.16 Suppose that R is a DVR and S is not a DVR. Then the fiber product
$A=R\times _kS$
is a generalized Gorenstein ring if and only if S is an almost Gorenstein ring.
Proof We only prove the ‘only if’ part. Suppose that A is a generalized Gorenstein ring. By [Reference Goto and Kumashiro11, Theorem 4.8], we then have
$A[X]/A \cong (A/A:X)^{\oplus (\ell + 1)}$
as an A-module, where
$\ell = \mathrm {r}(S)$
. By [Reference Goto and Kumashiro11, Theorem 4.8], we get
$X^2 = X^3$
, that is ,
$L^2 = L^3$
. Hence, we have the equalities
$$\begin{align*}\ell_A(A[X]/A) = (\ell + 1)\ell_A\big(A/(A:X)\big) = (\ell + 1) \ell_S\big(S/(S:L)\big). \end{align*}$$
Since
$X \subseteq X:J \subseteq A[X]$
(see [Reference Goto, Matsuoka and Phuong12, Corollary 3.8 (1)]), we have
$X^n \subseteq (X:J)^n \subseteq A[X]$
for every
$n>0$
, so that
$X^n = (X:J)^n =A[X]$
for every
$n \gg 0$
. Similarly, we have
$L^n = (L:\mathfrak n)^n = S[L]$
for every
$n \gg 0$
. Therefore,
$$\begin{align*}A[X] = \big[R \times \xi_2(L:\mathfrak n)\big]^n = R \times \xi_2^n{\cdot} S[L] = R \times \xi_2^{n+1}{\cdot} S[L] \quad \text{for all} \ n \gg 0, \end{align*}$$
which yields
$S[L] = \xi _2{\cdot } S[L]$
. Thus,
$\xi _2, \rho \in S[L],$
and hence
$A[X]=R \times S[L]$
. Hence,
$\ell _A(A[X]/A) = 1 + \ell _S(S[L]/S)$
. On the other hand, by the sequence
$$\begin{align*}0 \longrightarrow L/S \longrightarrow S[L]/S \longrightarrow S[L]/L \longrightarrow 0 \end{align*}$$
of S-modules, we get
$$\begin{align*}\ell_S(S[L]/S) \le (\ell-1) \cdot \ell_S(S/(S:L)) + \ell_S(S/(S:L)) =\ell \cdot \ell_S(S/(S:L)), \end{align*}$$
because
$S[L]/L \cong \mathrm {K}_{S/(S:L)}$
(see [Reference Goto and Kumashiro11, Theorem 4.8]). Therefore,
$$\begin{align*}(\ell + 1) \ell_S\big(S/(S:L)\big) \le 1 + \ell \cdot \ell_S\big(S/(S:L)\big), \end{align*}$$
which implies
$\ell _S(S/(S:L)) =1$
, so that
$\mathfrak n = S:L$
. Hence, S is almost Gorenstein. ▪
We now go back to the notation as in Setting 4.1. By combining Corollaries 4.3, 4.9, Proposition 4.11, and Theorem 4.16, we have the following theorem.
Theorem 4.17 The following conditions are equivalent.
-
(i) The fiber product
$A=R\times _kS$
is an almost Gorenstein ring. -
(ii) The fiber product
$A=R\times _kS$
is a generalized Gorenstein ring. -
(iii) R and S are almost Gorenstein rings.
Letting
$S=R$
, we get the following corollary.
Corollary 4.18 The following conditions are equivalent.
-
(i) The fiber product
$R \times _k R$
is an almost Gorenstein ring. -
(ii) The fiber product
$R \times _k R$
is a generalized Gorenstein ring. -
(iii) The idealization
$R \ltimes \mathfrak m$
is an almost Gorenstein ring. -
(iv) R is an almost Gorenstein ring.
Proof The proof follows from Theorem 4.17 and [Reference Goto, Matsuoka and Phuong12, Theorem 6.5]. ▪
We are now ready to prove Theorem 1.1. Let
$(R, \mathfrak m)$
,
$(S, \mathfrak n)$
be Cohen-Macaulay local rings with
$d=\dim R=\dim S>0$
,
$(T,\mathfrak m_T)$
a regular local ring with
$\dim T=d-1$
, and let
$f: R \to T$
,
$g: S \to T$
be surjective homomorphisms. Suppose that the residue class field
$T/\mathfrak m_T$
of T is infinite. We then consider the fiber product
$A=R\times _TS$
, which is a Cohen–Macaulay local ring with
$\dim A = d$
.
With this notation, we begin with the following proposition.
Proposition 4.19 The fiber product
$A=R\times _TS$
is a Gorenstein ring if and only if R and S are regular local rings.
Proof By Proposition 2.2, we can assume
$d \ge 2$
. Choose a regular system
$x_1, x_2, \dots , x_{d-1}$
of parameters for T. The surjectivities of f and g show that
$x_1, x_2, \dots , x_{d-1}$
forms a regular sequence on R and S. Let us write
$x_i = f(a_i) = g(b_i)$
for some
$a_i \in \mathfrak m$
and
$b_i \in \mathfrak n$
. We then have an isomorphism
$$ \begin{align*} A/(\alpha_1, \alpha_2, \dots, \alpha_{d-1}) \cong R/(a_1, a_2, \dots, a_{d-1}) \\\times_{T/(x_1, x_2, \dots, x_{d-1})} S/(b_1, b_2, \dots, b_{d-1}) \end{align*} $$
of rings, which yields the required assertion, by induction arguments. ▪
We finally reach the proof of Theorem 1.1.
Proof of Theorem 1.1
We set
$d = \dim A$
. By Theorem 4.17, we can assume that
$d \ge 2$
and that the assertion holds for
$d-1$
.
-
(i) ⇒ (ii) We can assume A is not a Gorenstein ring. Let us consider an exact sequence
of A-modules with
$$\begin{align*}0 \longrightarrow A \longrightarrow \mathrm{K}_A \longrightarrow C \longrightarrow 0 \end{align*}$$
$\mu _A(C) = \mathrm {e}^0_J(C)$
, where
$J = (\mathfrak m \times \mathfrak n) \cap A$
denotes the maximal ideal of A. Since A has an infinite residue class field, we choose a regular element
$\alpha =(a, b) \in J$
on A so that
$\alpha $
is a superficial element for C with respect to J, and
$(f\circ p_1)(\alpha )$
forms a part of a regular system of parameters of T. We then have that
$a \in \mathfrak {m}$
and
$b \in \mathfrak n$
are regular elements of R and S, respectively. Hence, we have an isomorphism
$A/(\alpha ) \cong R/(a) \times _{T/aT}S/(b)$
as rings. Then the hypothesis on d shows that
$R/(a)$
and
$S/(b)$
are almost Gorenstein rings. Therefore, by [Reference Goto, Takahashi and Taniguchi19, Theorem 3.7], R and S are almost Gorenstein rings.
-
(ii) ⇒ (i) First, we consider the case where R and S are Gorenstein rings. Choose a regular system of parameters
$x_1, x_2, \dots , x_{d-1} \in \mathfrak m_T$
of T and write
$x_i = f(a_i) = g(b_i)$
with
$a_i \in \mathfrak m$
and
$b_i \in \mathfrak n$
. For each
$1 \le i \le d-1$
, we set
$\alpha _i =(a_i, b_i) \in J$
. Then
$\alpha _1, \alpha _2, \dots , \alpha _{d-1}$
forms a regular sequence on
$A,$
and there is an isomorphism of rings. As
$$ \begin{align*} A/(\alpha_1, \alpha_2, \dots, \alpha_{d-1}) \cong R/(a_1, a_2, \dots, a_{d-1}) \\\times_{T/(x_1, x_2, \dots, x_{d-1})} S/(b_1, b_2, \dots, b_{d-1}) \end{align*} $$
$R/(a_1, a_2, \dots , a_{d-1})$
,
$S/(b_1, b_2, \dots , b_{d-1})$
are Gorenstein and
$T/(x_1, x_2, \dots , x_{d-1})$
is a field, we conclude that
$A/(\alpha _1, \alpha _2, \dots , \alpha _{d-1})$
is an almost Gorenstein ring, and so is A. Let us assume that R is Gorenstein, and S is an almost Gorenstein ring, but not a Gorenstein ring. Choose an exact sequence of S-modules such that
$$\begin{align*}0 \longrightarrow S \longrightarrow \mathrm{K}_S \longrightarrow D \longrightarrow 0 \end{align*}$$
$\mu _S(D) = \mathrm {e}^0_{\mathfrak n}(D)$
. Let us take an S-regular element
$b \in \mathfrak n$
such that b is a superficial element for D with respect to
$\mathfrak n$
, and
$g(b) \in \mathfrak m_T$
is a part of a regular system of parameters of T. Let us choose
$a \in \mathfrak m$
such that
$f(a) = g(b)$
. Then
$\alpha = (a, b) \in J$
is a regular element on A and
$A/(\alpha ) \cong R/(a) \times _{T/aT} S/(b)$
. The induction hypothesis shows that
$A/(\alpha )$
is an almost Gorenstein ring, whence A is almost Gorenstein. Finally, we are assuming that R and S are non-Gorenstein, almost Gorenstein rings. Consider the exact sequences of R-modules, and of S-modules, respectively. We then choose an A-regular element
$$\begin{align*}0 \longrightarrow R \longrightarrow\mathrm{K}_R \longrightarrow C \longrightarrow 0\quad\text{and} \quad 0 \longrightarrow S \longrightarrow \mathrm{K}_S \longrightarrow D \longrightarrow 0 \end{align*}$$
$\alpha =(a, b) \in J$
such that
$a \in \mathfrak m$
is a superficial element for C with respect to
$\mathfrak m$
,
$b \in \mathfrak n$
is a superficial element for D with respect to
$\mathfrak n$
, and
$(f \circ p_1)(\alpha ) \in \mathfrak m_T$
is a part of a regular system of parameters of T. Then
$A/(\alpha ) \cong R/(a) \times _{T/aT} S/(b)$
. Hence,
$A/(\alpha )$
is an almost Gorenstein ring, whence A is almost Gorenstein, as desired. ▪
5 Further Results in Dimension One
The notion of almost Gorenstein ring in our sense originated from the works [Reference Barucci and Fröberg2] of V. Barucci and R. Fröberg in 1997, and [Reference Goto, Matsuoka and Phuong12] of the second author, N. Matsuoka, and T. T. Phuong in 2013, where they dealt with the notion of one-dimensional Cohen–Macaulay local rings. Although the second author and S. Kumashiro have already provided a beautiful generalization of almost Gorenstein rings, say generalized Gorenstein rings, there are other directions of the generalization for one-dimensional almost Gorenstein rings, which we call
$2$
-almost Gorenstein and nearly Gorenstein rings.
Let us maintain the notation as in Setting 4.1. The goals of this section are stated as follows.
Theorem 5.1 The following conditions are equivalent.
-
(i) The fiber product
$A=R\times _kS$
is a
$2$
-almost Gorenstein ring. -
(ii) Either R is a
$2$
-almost Gorenstein ring and S is an almost Gorenstein ring, or R is an almost Gorenstein ring and S is a
$2$
-almost Gorenstein ring.
Theorem 5.2 The following conditions are equivalent.
-
(i) The fiber product
$A=R\times _kS$
is a nearly Gorenstein ring. -
(ii) R and S are nearly Gorenstein rings.
Before going ahead, we recall the definition of
$2$
-almost Gorenstein rings and nearly Gorenstein rings. For a while, let
$(R, \mathfrak m)$
be a Cohen-Macaulay local ring with
$\dim R=1$
, possessing a fractional canonical ideal K of R, i.e., K is an R-submodule of
$\mathrm {Q}(R)$
such that
$R \subseteq K \subseteq \overline {R}$
and
$K \cong \mathrm {K}_R$
as an R-module.
With this notation, T. D. M. Chau, the second author, S. Kumashiro, and N. Matsuoka proposed the notion of
$2$
-almost Gorenstein rings.
Definition 5.3 ([Reference Chau, Goto, Kumashiro and Matsuoka6])
We say that R is a
$2$
-almost Gorenstein ring, if
$K^2 = K^3$
and
$\ell _R(K^2/K) =2$
.
By [Reference Chau, Goto, Kumashiro and Matsuoka6, Theorem 3.7], the condition of
$K^2 = K^3$
and
$\ell _R(K^2/K)=2$
is equivalent to saying that
$\ell _R(R/\mathfrak {c}) = 2$
, where
$\mathfrak {c} = R:R[K]$
. The latter condition is independent of the choice of fractional canonical ideals K (see [Reference Chau, Goto, Kumashiro and Matsuoka6, Theorem 2.5]). Furthermore, because R is an almost Gorenstein ring but not a Gorenstein ring if and only if
$\ell _R(R/\mathfrak {c})=1$
, that is,
$\mathfrak {c} =\mathfrak m$
([Reference Goto, Matsuoka and Phuong12, Theorem 3.16]),
$2$
-almost Gorenstein rings could be considered to be one of the successors of almost Gorenstein rings.
Let us now state the definition of nearly Gorenstein rings, which is defined by J. Herzog, T. Hibi, and D. I. Stamate, by using the trace of canonical ideals. The notion is defined for arbitrary dimension; however, let us focus our attention on the case where
$\dim R=1$
, because there is no relation between almost Gorenstein and nearly Gorenstein rings for higher dimensions (see [Reference Herzog, Hibi and Stamate21]). For an R-module X, let
$$\begin{align*}\varphi : \operatorname{Hom}_R(X, R) \otimes_R X \longrightarrow R \end{align*}$$
be the R-linear map defined by
$\varphi (f \otimes x) = f(x)$
for every
$f \in \operatorname {Hom}_R(X, R)$
and
$x \in X$
. We set
$\mathrm {tr}_R(X) = \operatorname {Im} \varphi $
and call it the trace of X. The reader may consult [Reference Goto, Isobe and Kumashiro9, Reference Herzog, Hibi and Stamate21, Reference Kobayashi and Takahashi25, Reference Lindo26, Reference Lindo and Pande27] for further information on trace ideals and modules.
Definition 5.4 ([Reference Herzog, Hibi and Stamate21])
We say that R is a nearly Gorenstein ring, if
$\mathfrak m \subseteq \mathrm {tr}_R(K)$
.
For every fractional ideal X in R, we have
$\mathrm {tr}_R(X) = (R:X){\cdot } X$
(see [Reference Lindo26, Lemma 2.3]). By [Reference Herzog, Hibi and Stamate21, Proposition 6.1], almost Gorenstein ring is nearly Gorenstein, and the converse is not true in general, but it holds if R has minimal multiplicity, that is,
$v(R) \,{=}\, \mathrm {e}(R)$
.
We close this paper by proving Theorems 5.1 and 5.2.
Proof of Theorem 5.1
Thanks to Proposition 2.2, we can assume that either R or S is not a DVR. Suppose that both R and S are not DVRs. Then
$X = (K \times L) + Ag$
forms a fractional canonical ideal of A, where
$\psi = (g_1, g_2) \in \overline {A}$
,
$g_1 \in (R:\mathfrak m)\backslash K$
, and
$g_2 \in (L:\mathfrak n)\backslash L$
. By Theorem 4.17, we can assume that either R or S is not a Gorenstein ring. Suppose that R and S are not Gorenstein rings. We then have
$A:X = (R:K) \times (S:L)$
, so that
$$\begin{align*}\ell_A(A/(A:X)) =\ell_A(B/(A:X)) -1= \ell_R(R/(R:K)) + \ell_S(S/(S:L)) - 1. \end{align*}$$
Hence,
$\ell _A(A/(A:X)) = 2$
holds if and only if either
$\ell _R(R/(R:K)) =1$
and
$\ell _S(S/(S:L)) = 2$
, or
$\ell _R(R/(R:K)) = 2$
and
$\ell _S(S/(S:L)) =1$
. If R is Gorenstein and S is a non-Gorenstein ring, then
$A:X = \mathfrak {m} \times (S:L)$
so that
$$\begin{align*}\ell_A(A/(A:X)) = \ell_R(R/\mathfrak{m}) + \ell_S(S/(S:L)) - 1 = \ell_S(S/(S:L)), \end{align*}$$
which yields the required assertion. ▪
Proof of Theorem 5.2
By Proposition 2.2 and Corollary 4.13, we can assume that R and S are not DVRs. If R and S are Gorenstein, then by Corollary 4.3,
$A=R\times _kS$
is an almost Gorenstein ring, so that A is nearly Gorenstein ([Reference Herzog, Hibi and Stamate21, Proposition 6.1]). Thus, we can also assume that either R or S is not a Gorenstein ring. Suppose that R and S are not Gorenstein rings. By Lemma 4.8(i), we have that
$A:X = \mathfrak {a}_1 \times \mathfrak {a}_2$
, where
$\mathfrak {a}_1 = R:K$
,
$\mathfrak {a}_2 = S:L$
. Since
$$ \begin{align*} (A:X)X &= (\mathfrak{a}_1 \times \mathfrak{a}_2)((K\times L) + A\cdot(g_1, g_2))\\& = \mathfrak{a}_1(K:\mathfrak m) \times \mathfrak{a}_2(L:\mathfrak n) = \mathfrak{a}_1 K \times \mathfrak{a}_2 L, \end{align*} $$
we see that
$A=R\times _kS$
is a nearly Gorenstein ring if and only if
$\mathfrak {a}_1 K= \mathfrak m$
and
$\mathfrak {a}_2 L =\mathfrak n$
, in other words, R and S are nearly Gorenstein. Let us now consider the case where R is Gorenstein, but S is not a Gorenstein ring. In this case,
$A:X = \mathfrak m \times \mathfrak {a}_2$
, so that
$$\begin{align*}(A:X)X = (\mathfrak m \times \mathfrak{a}_2)\big((R\times L) + A\cdot(g_1, g_2)\big) = \mathfrak m(R:\mathfrak m) \times \mathfrak{a}_2 L. \end{align*}$$
Therefore, condition (ii) is equivalent to saying that
$\mathfrak {a}_2 L=\mathfrak n$
, that is, S is a nearly Gorenstein ring. This completes the proof. ▪
Acknowledgment
The authors are grateful to the referee for his/her careful reading of the manuscript.
